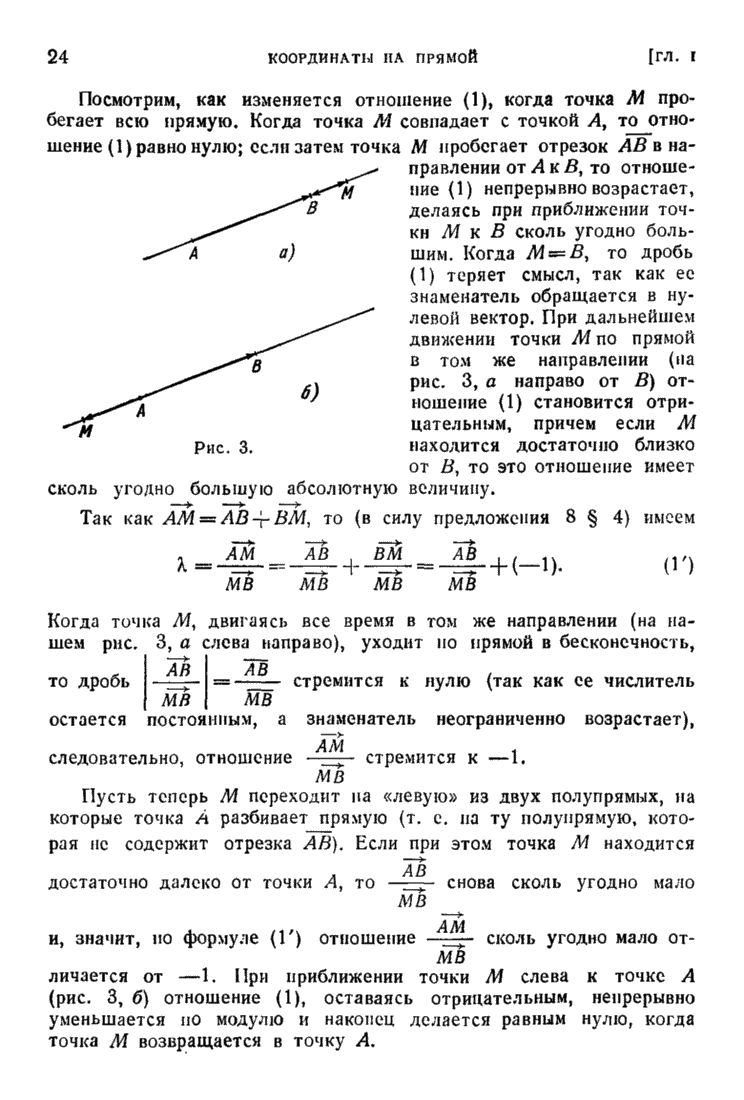
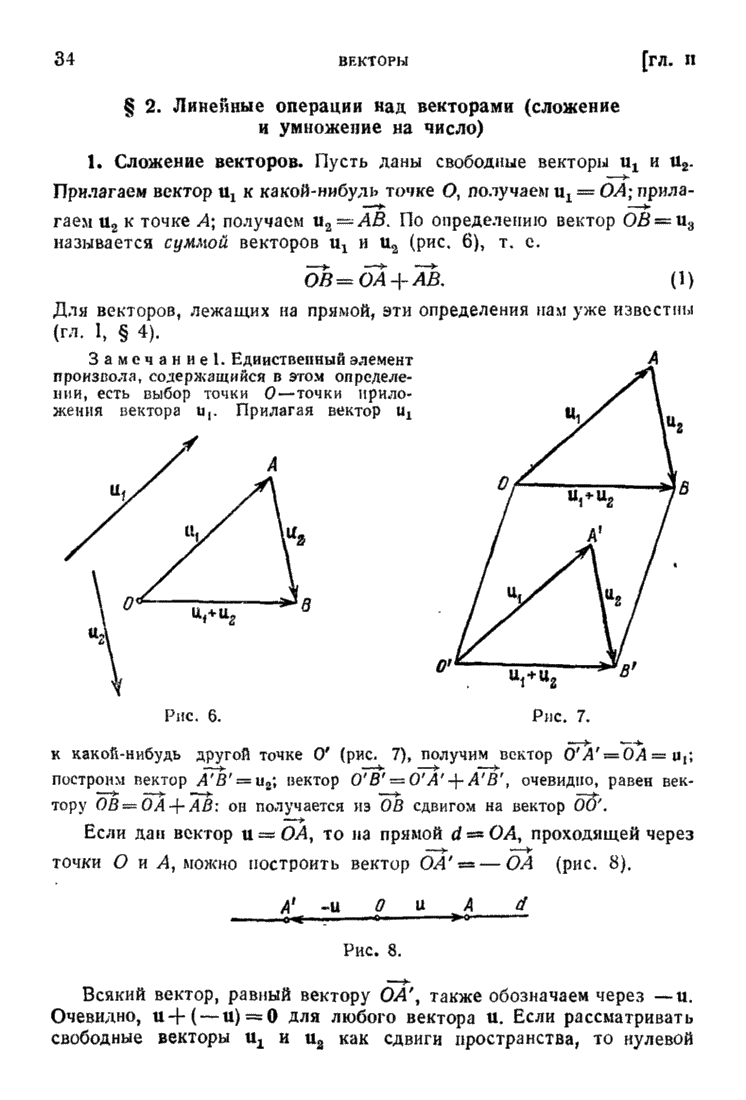
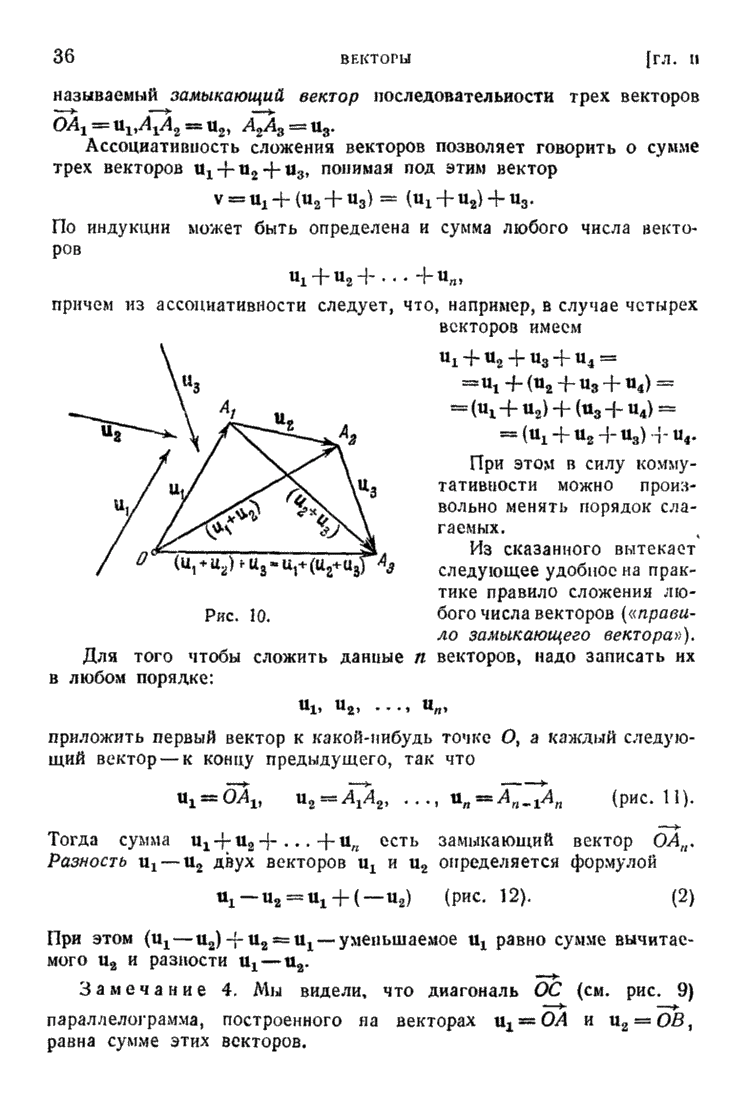
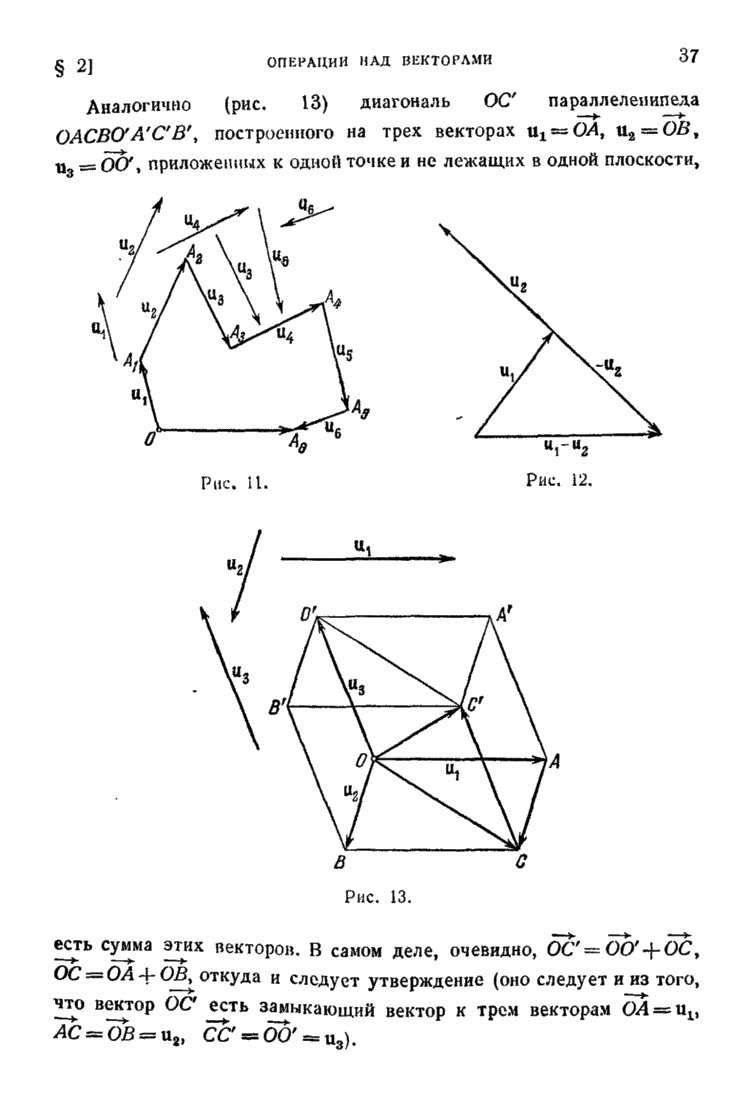
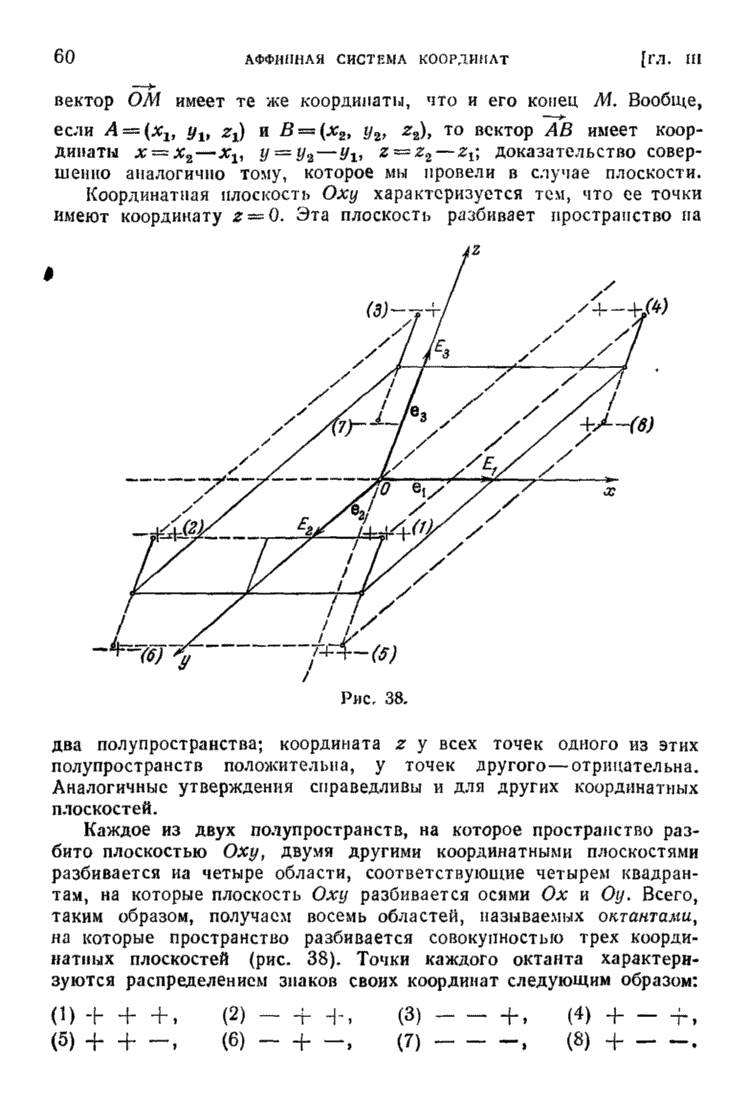
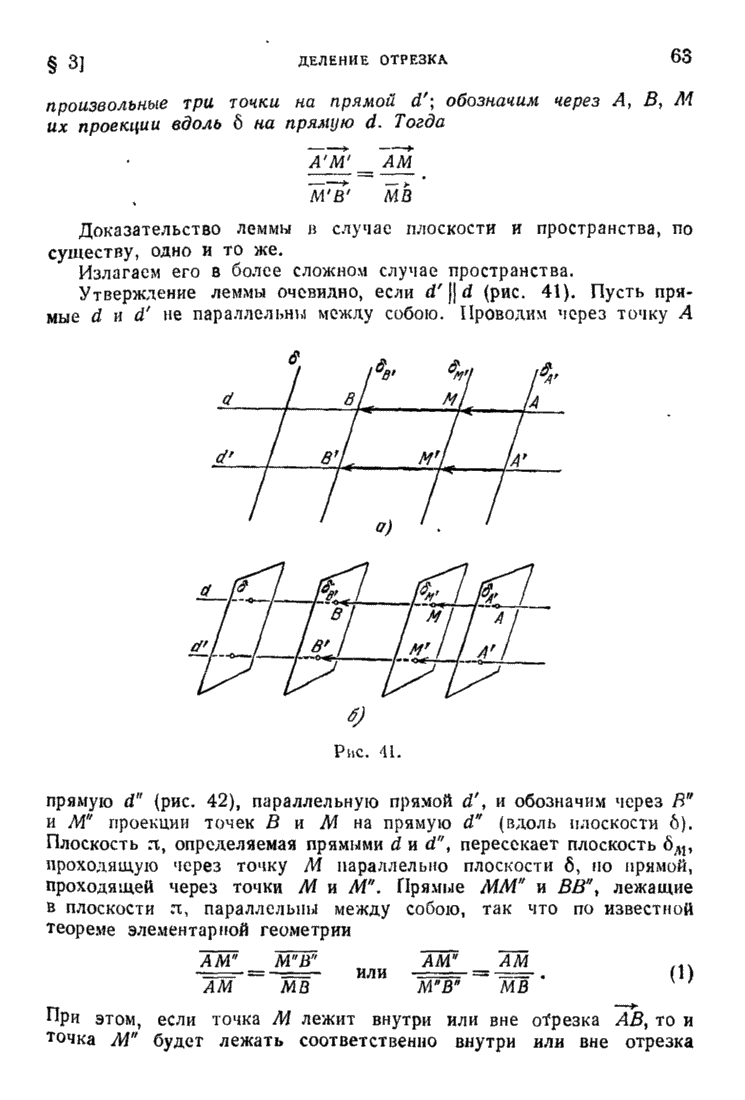
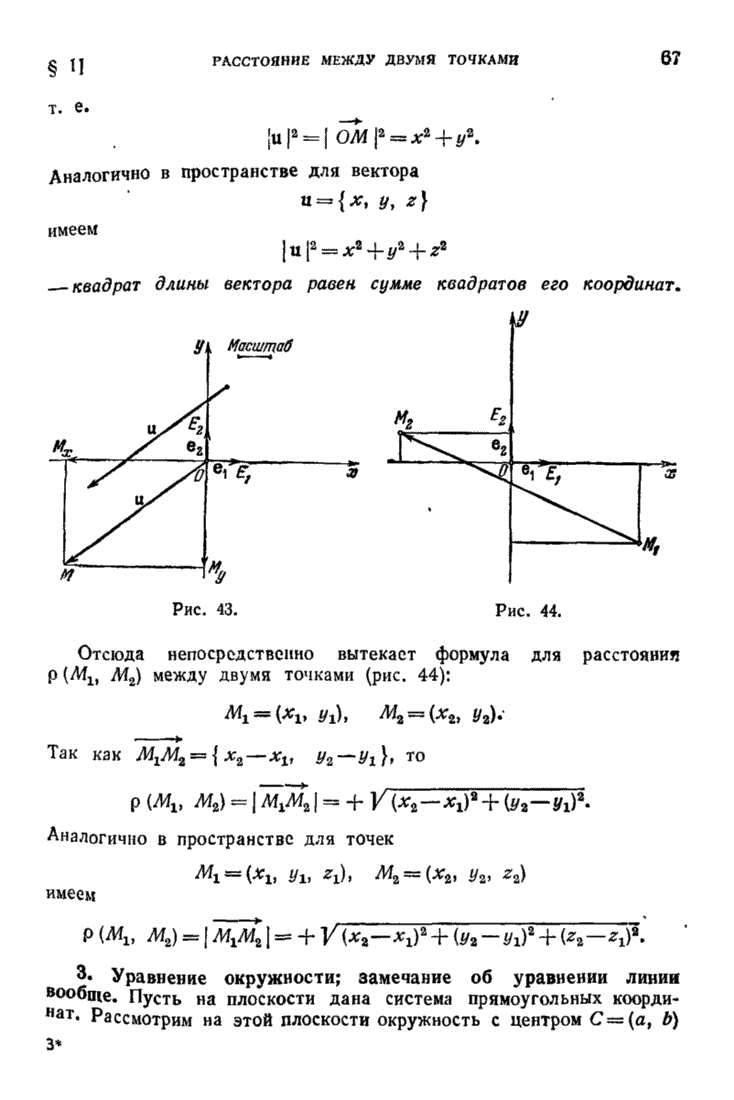
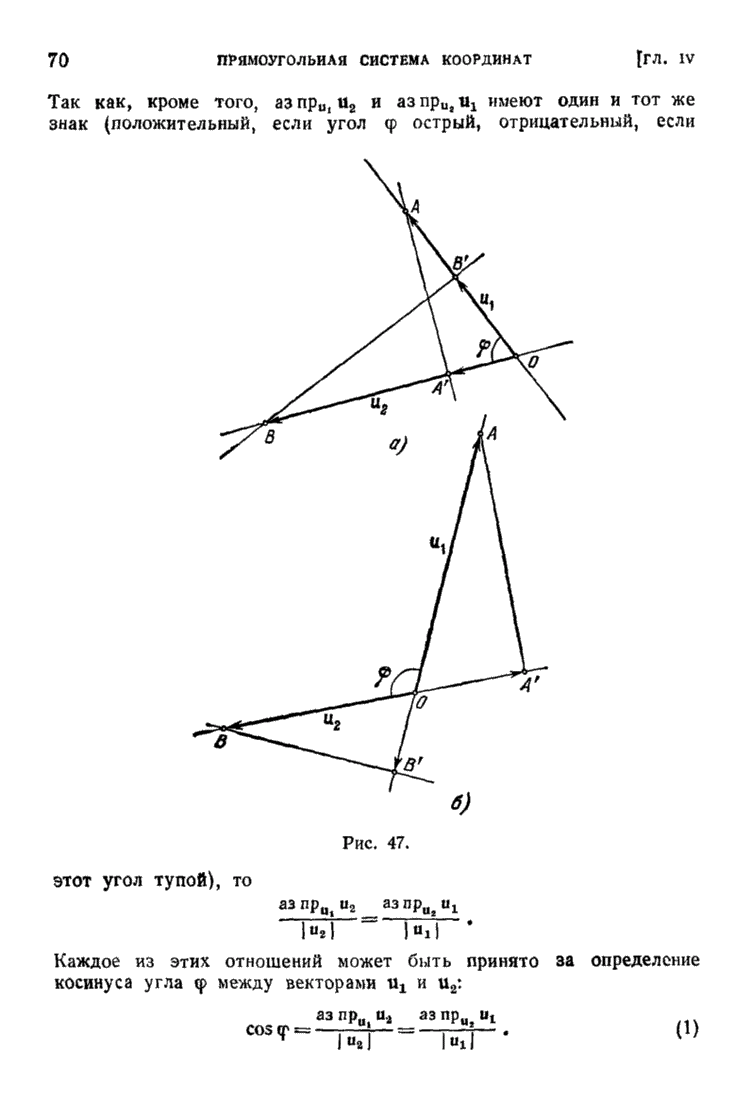
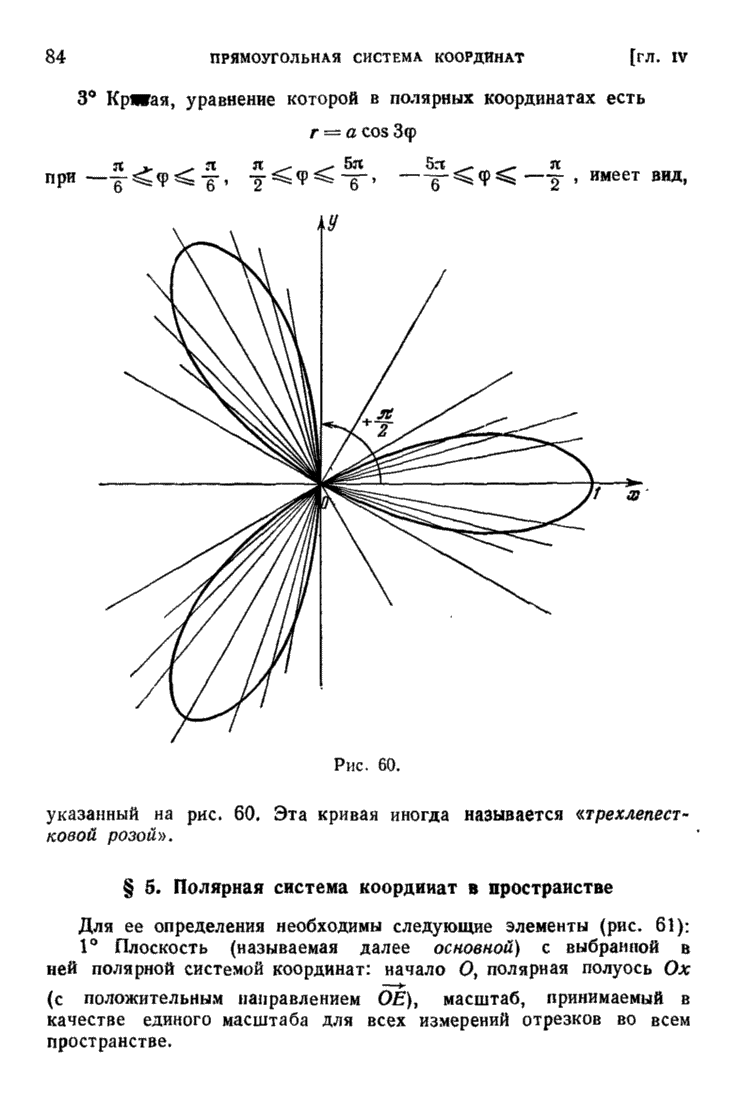
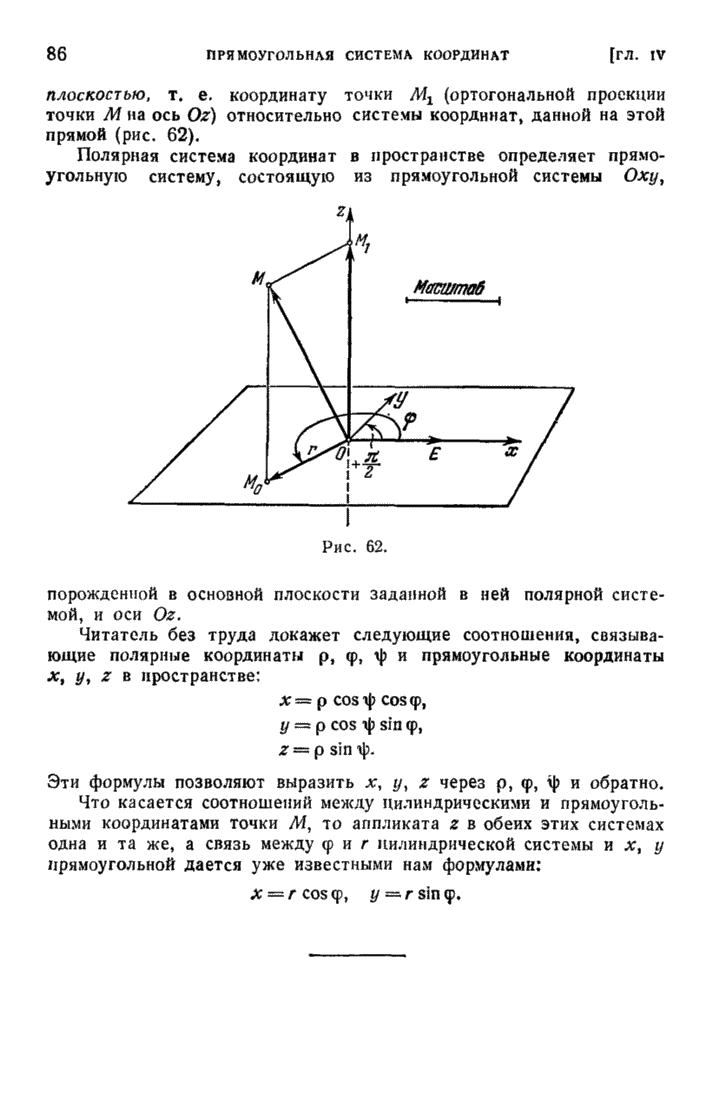
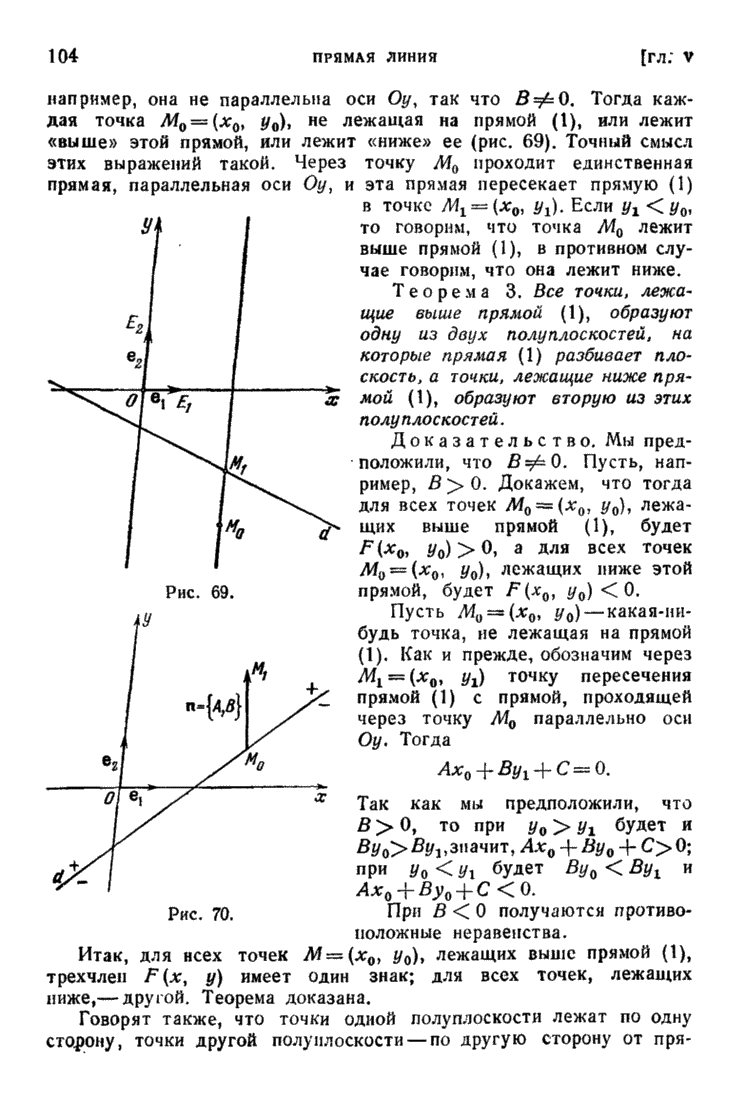
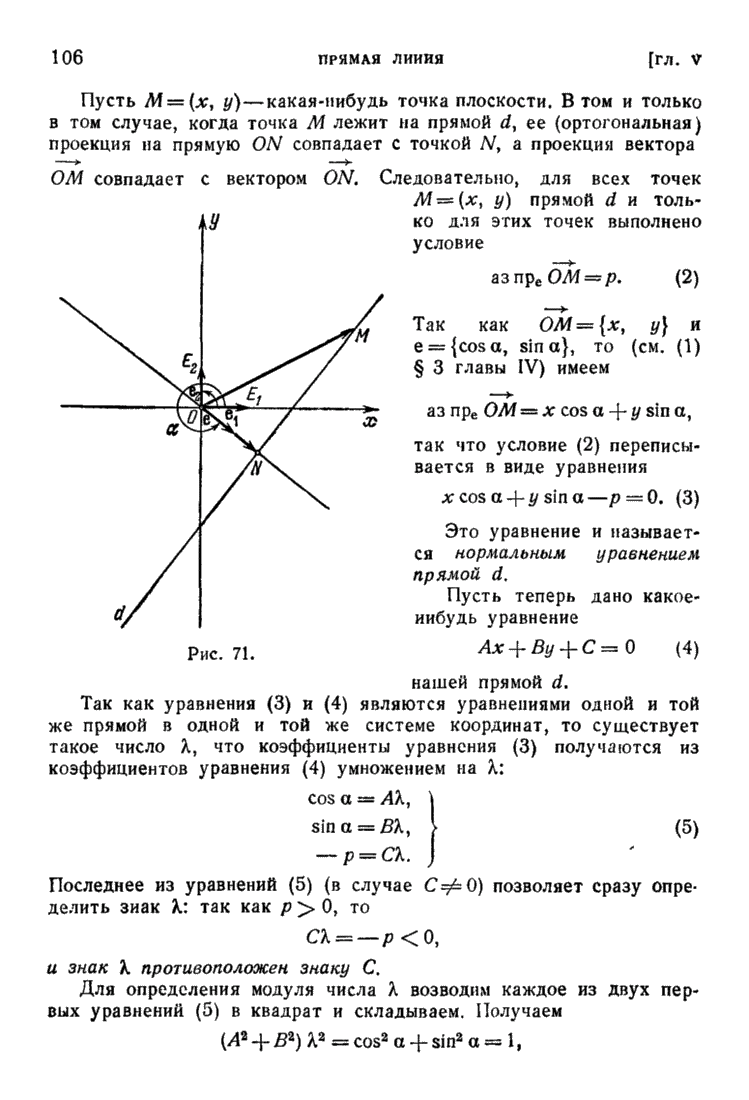
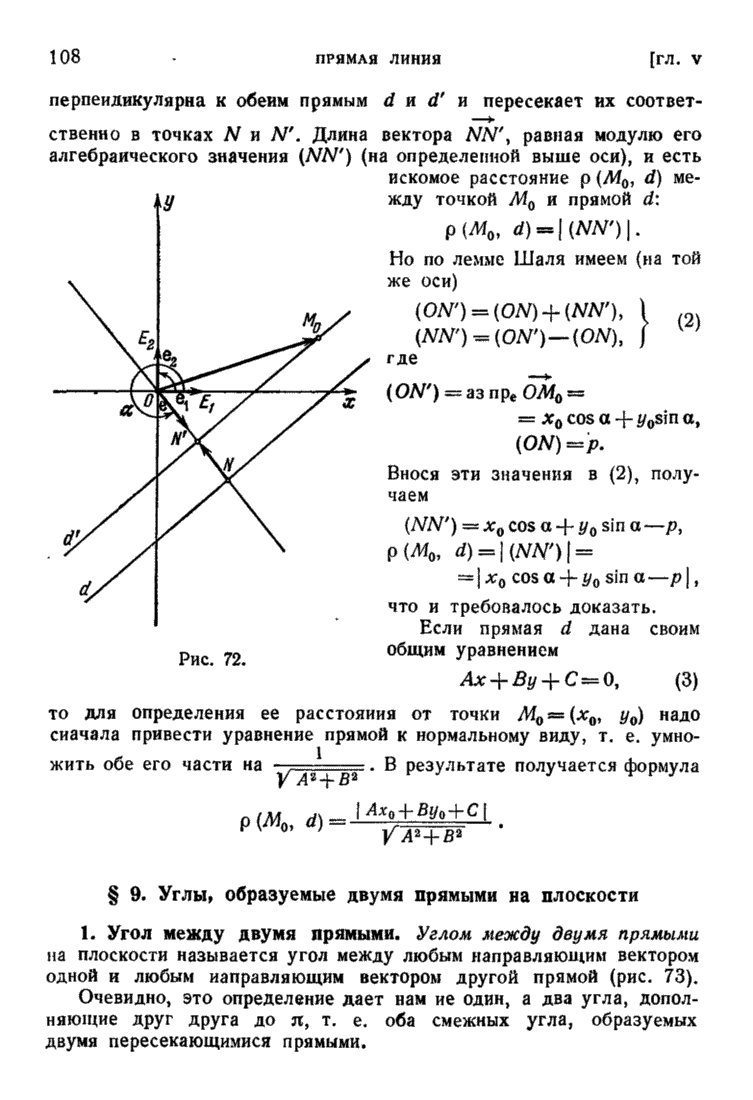
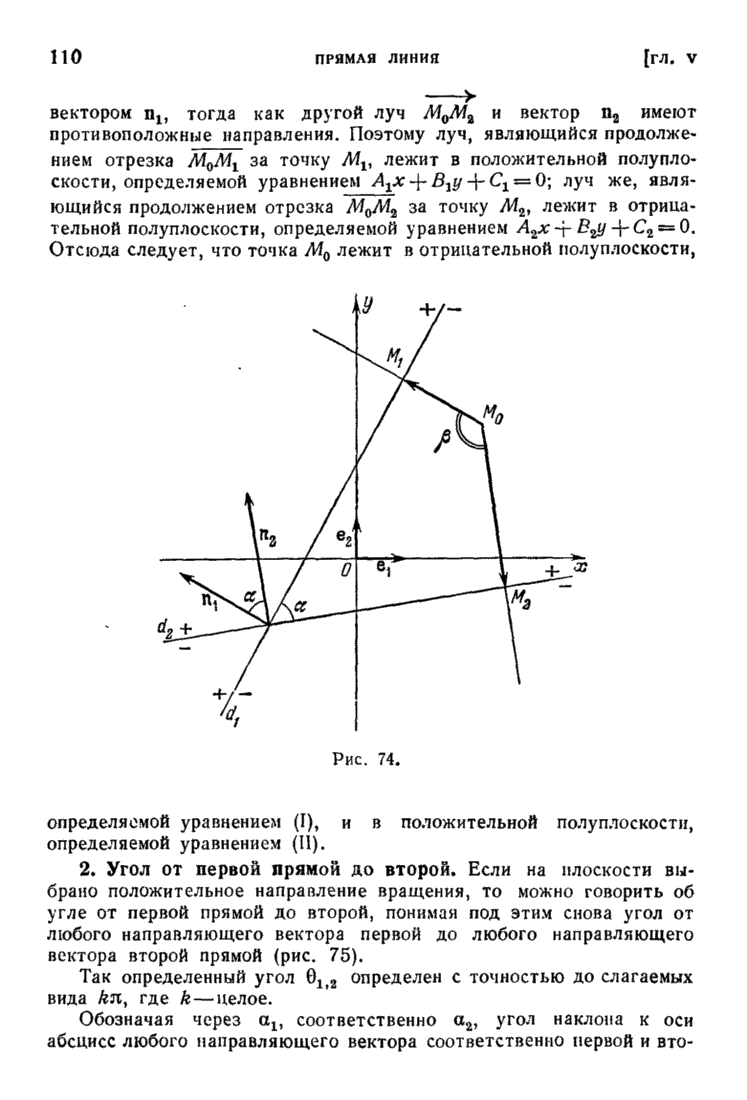
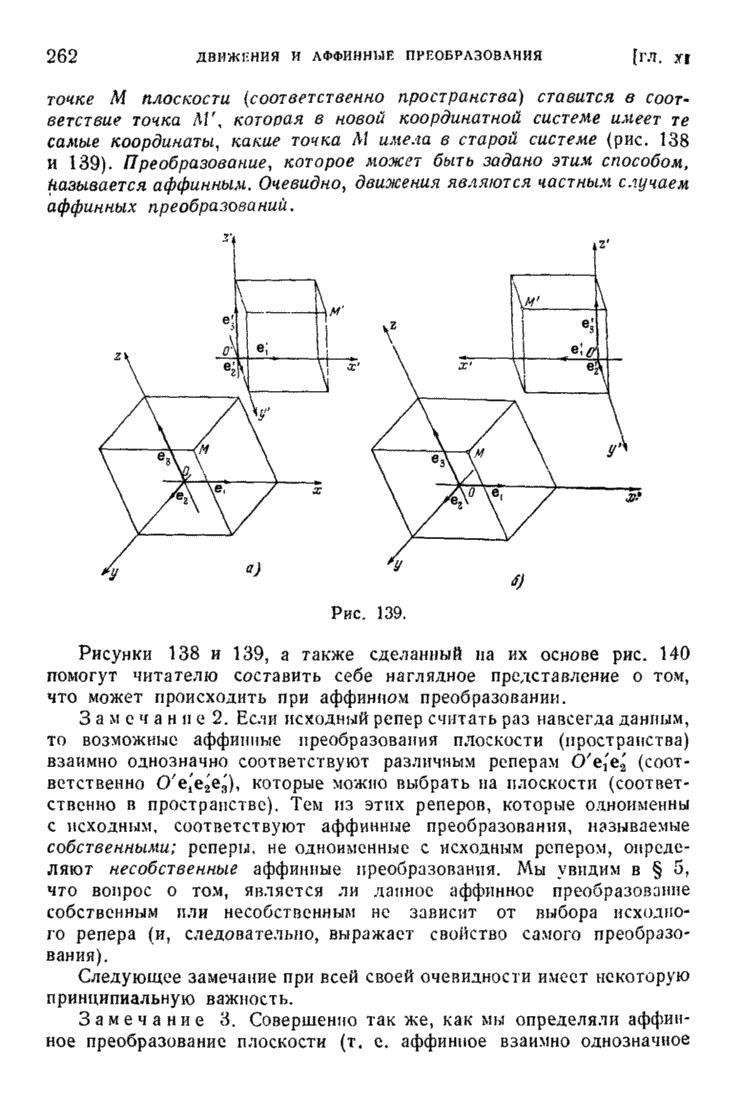
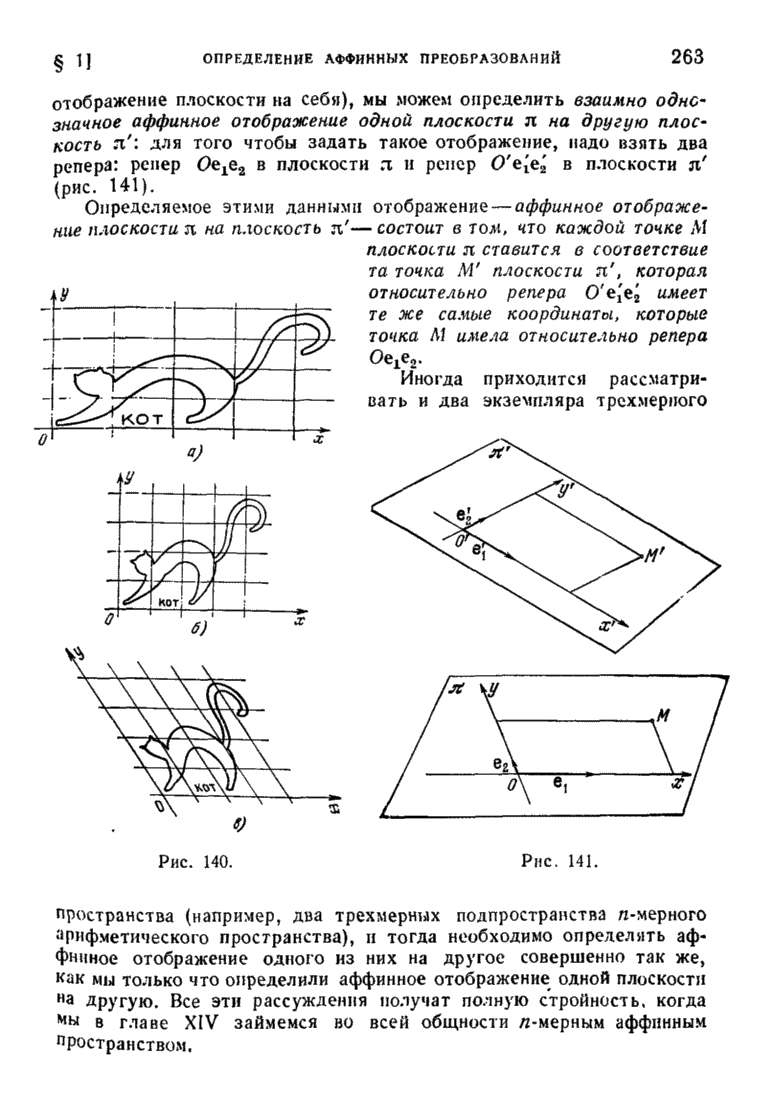
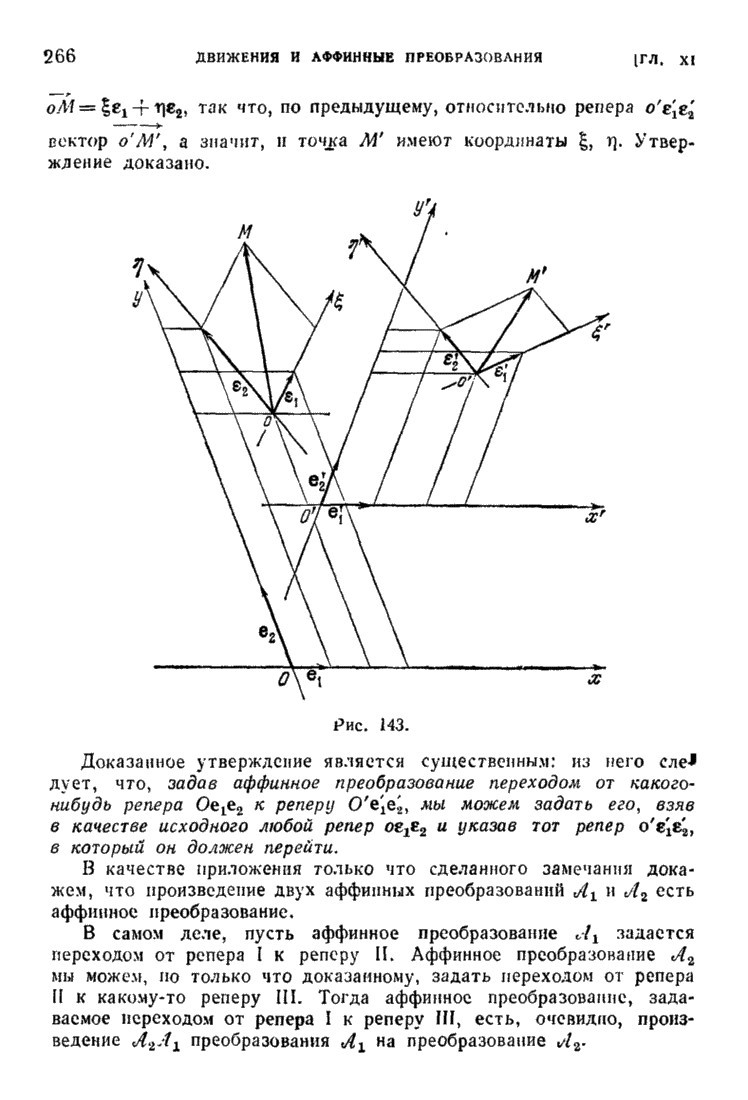
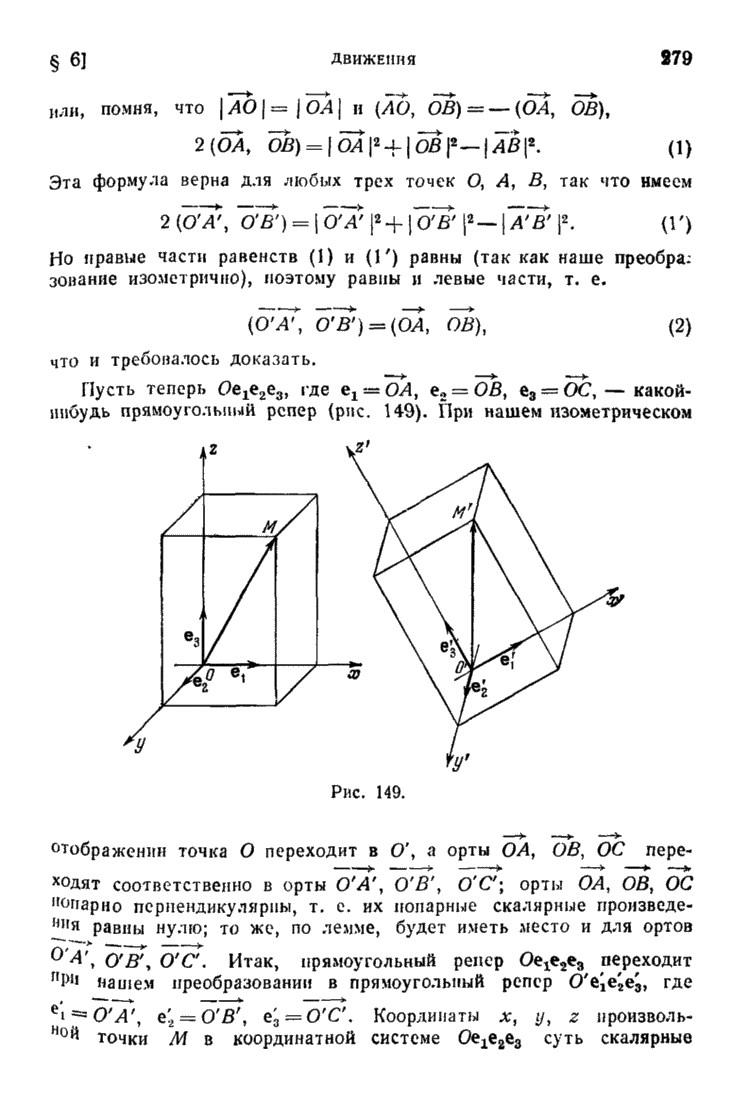
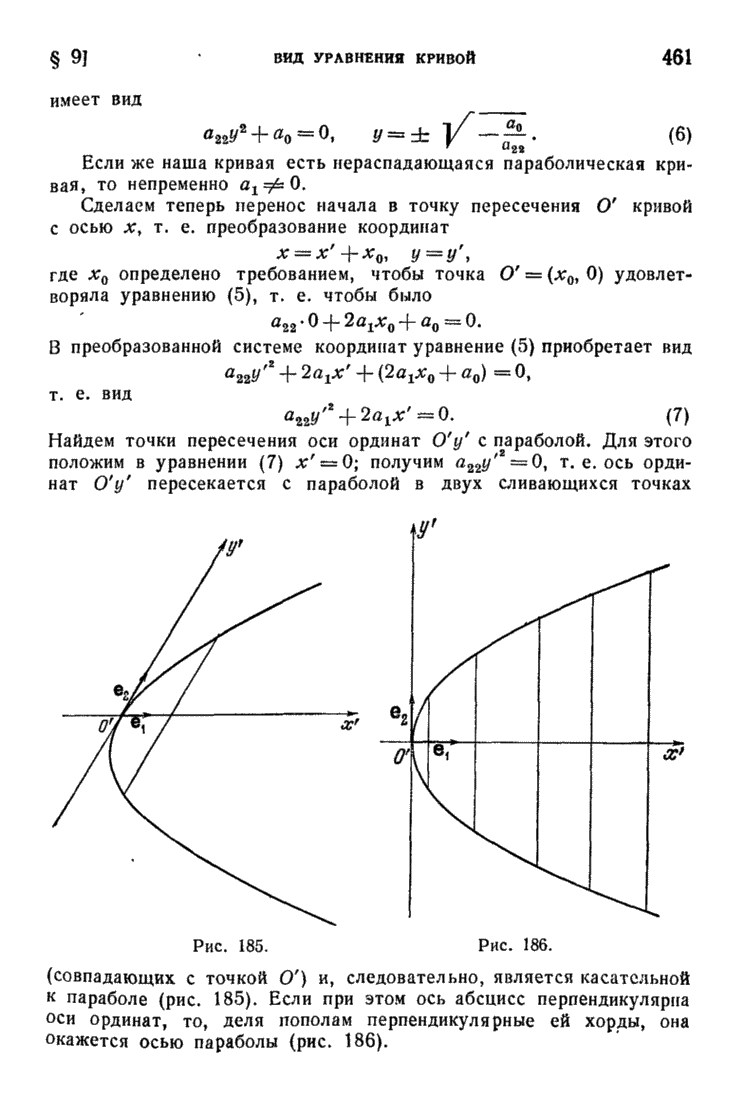
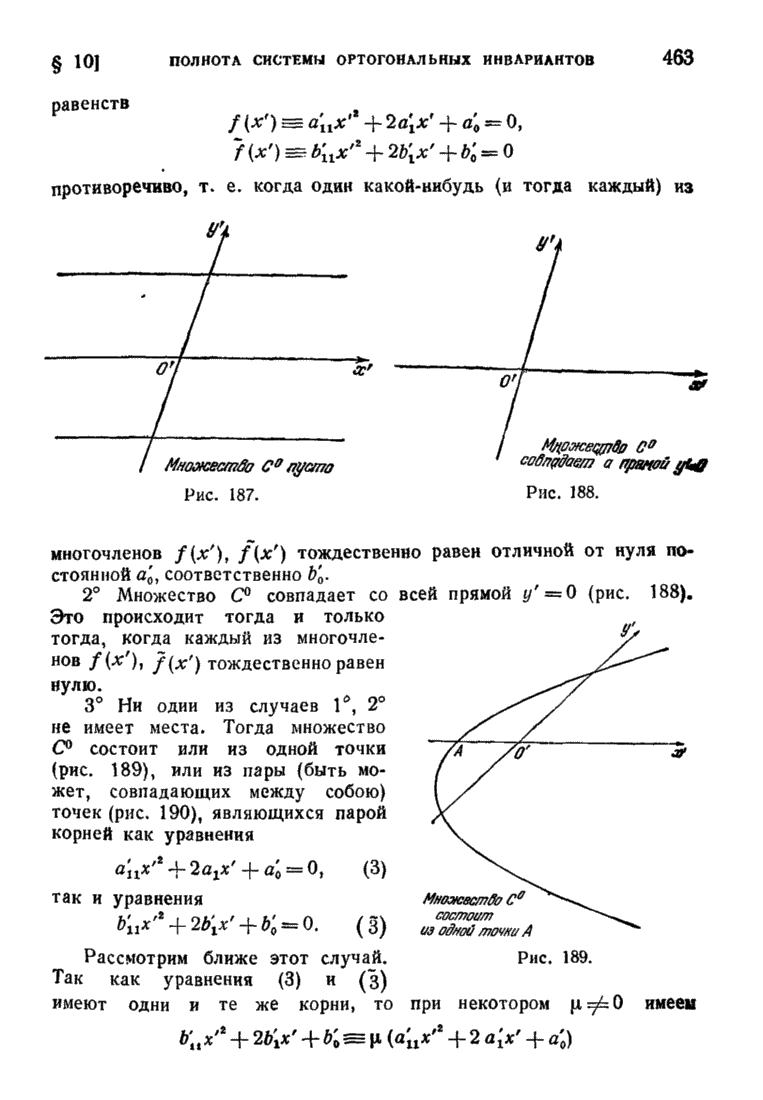
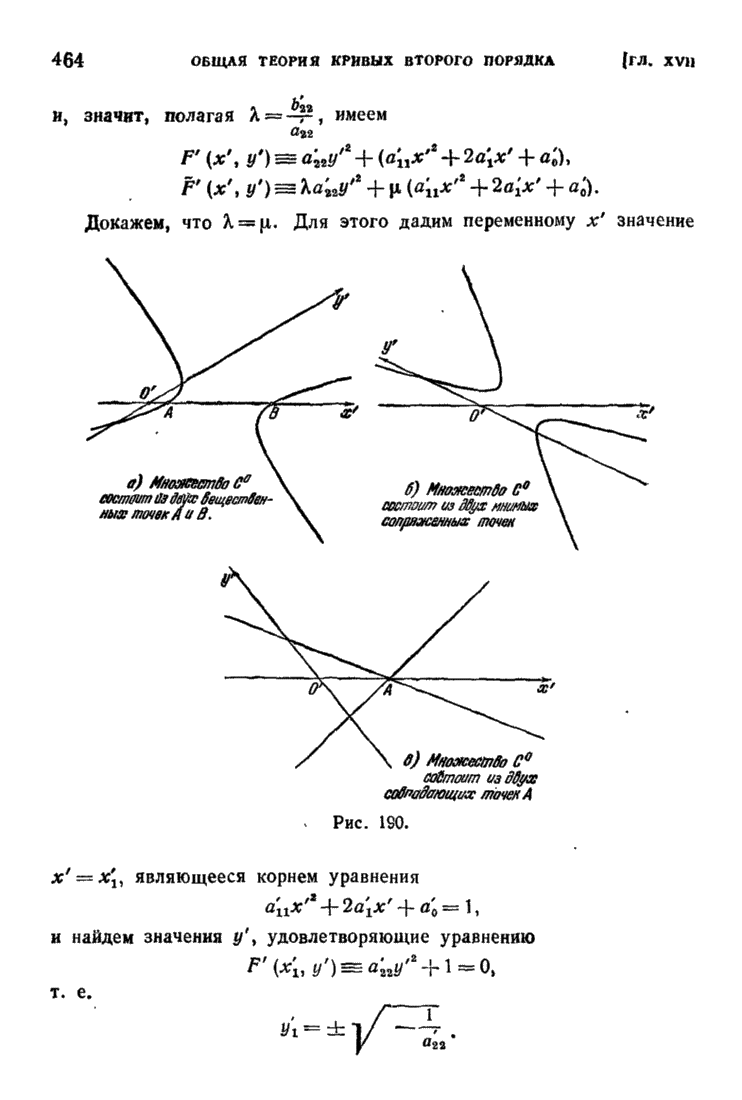
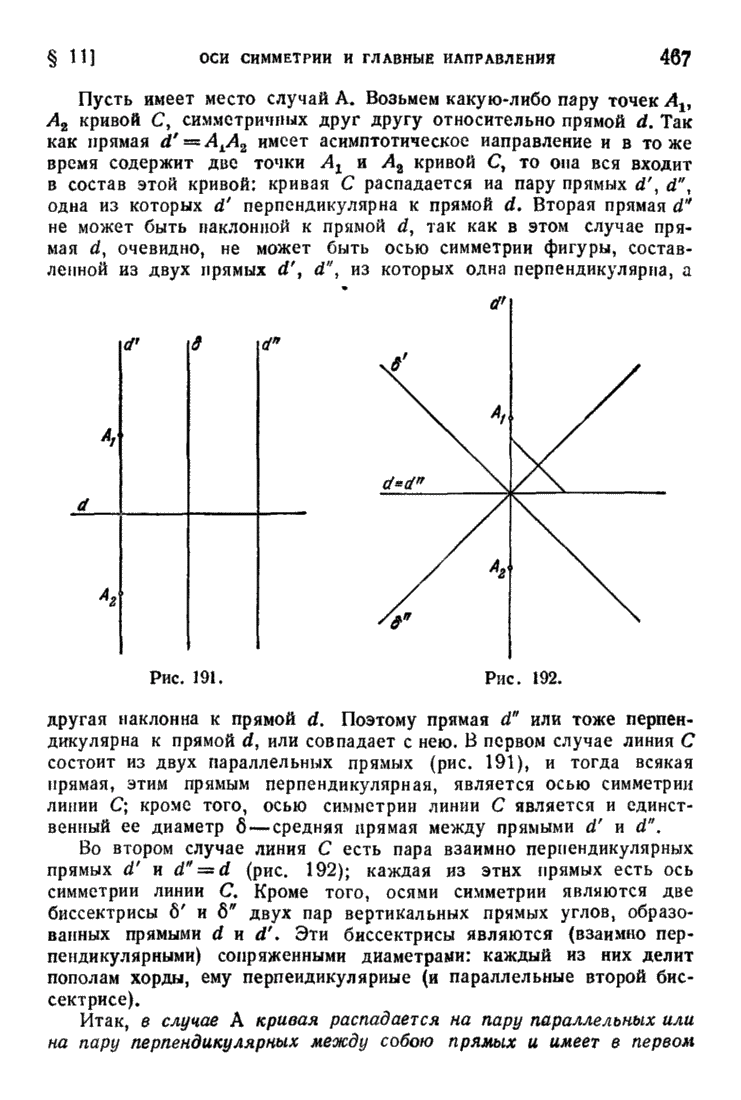
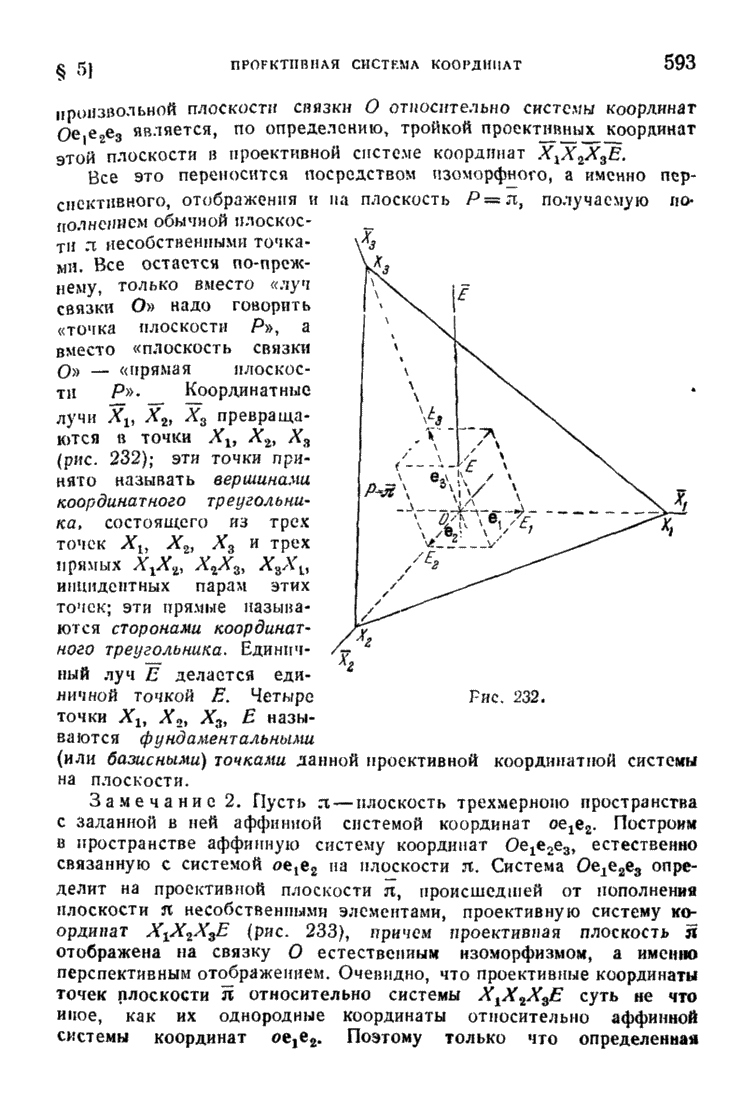
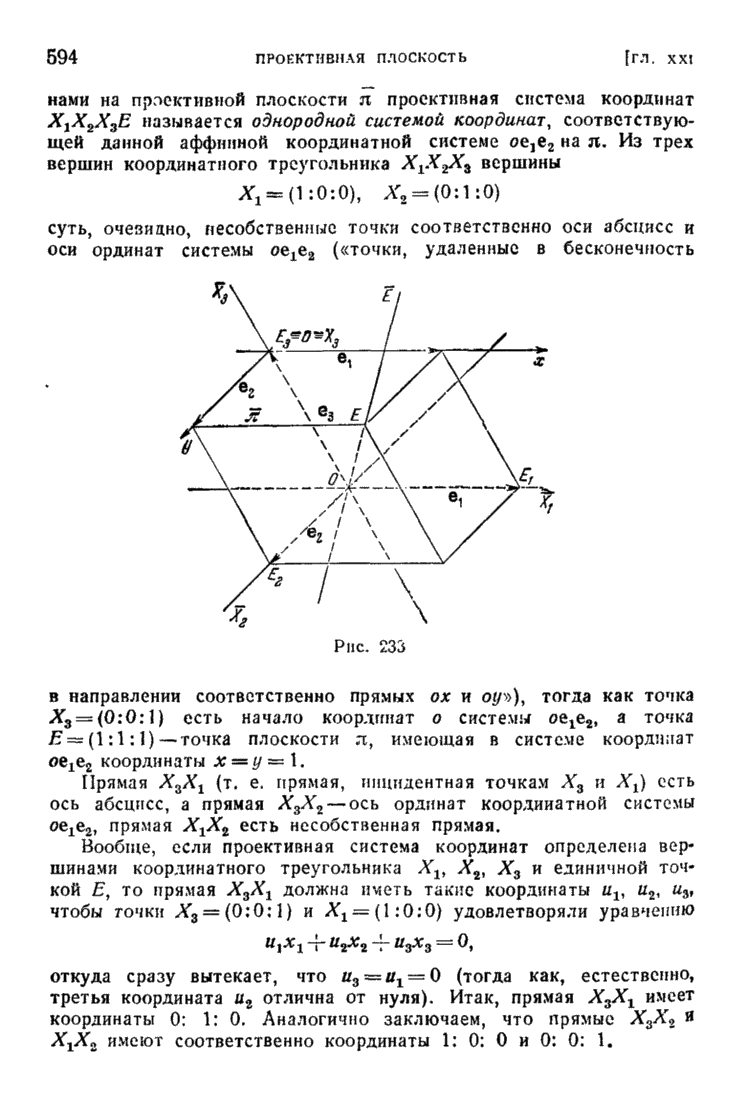
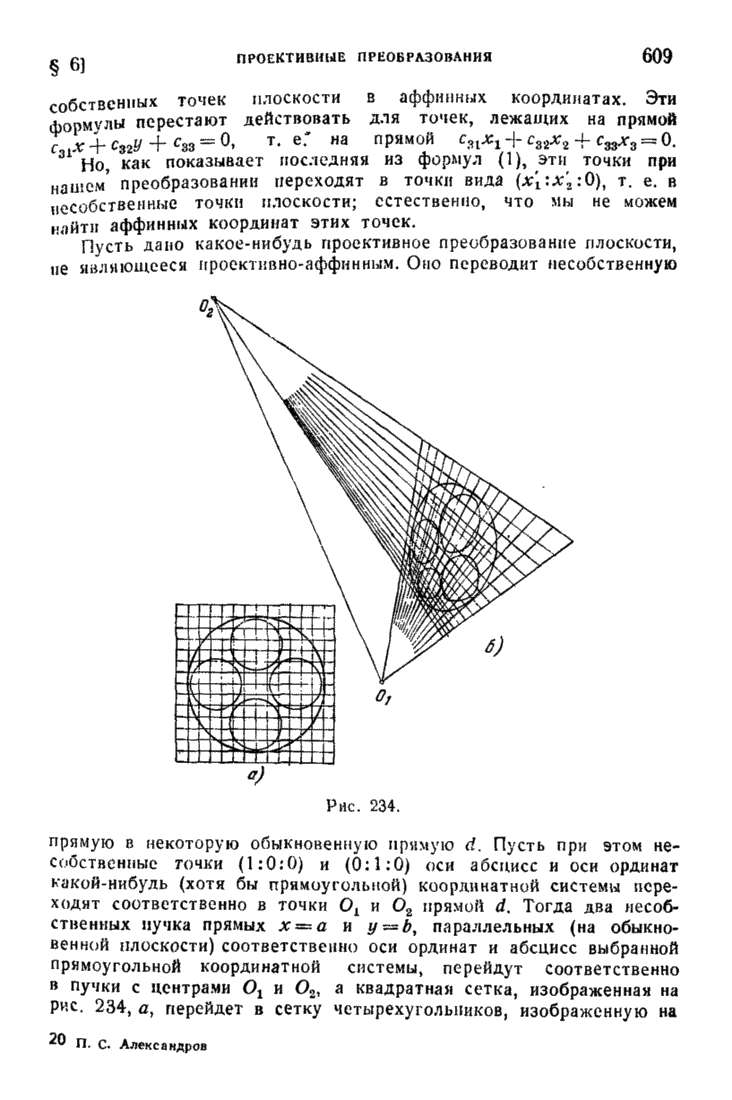
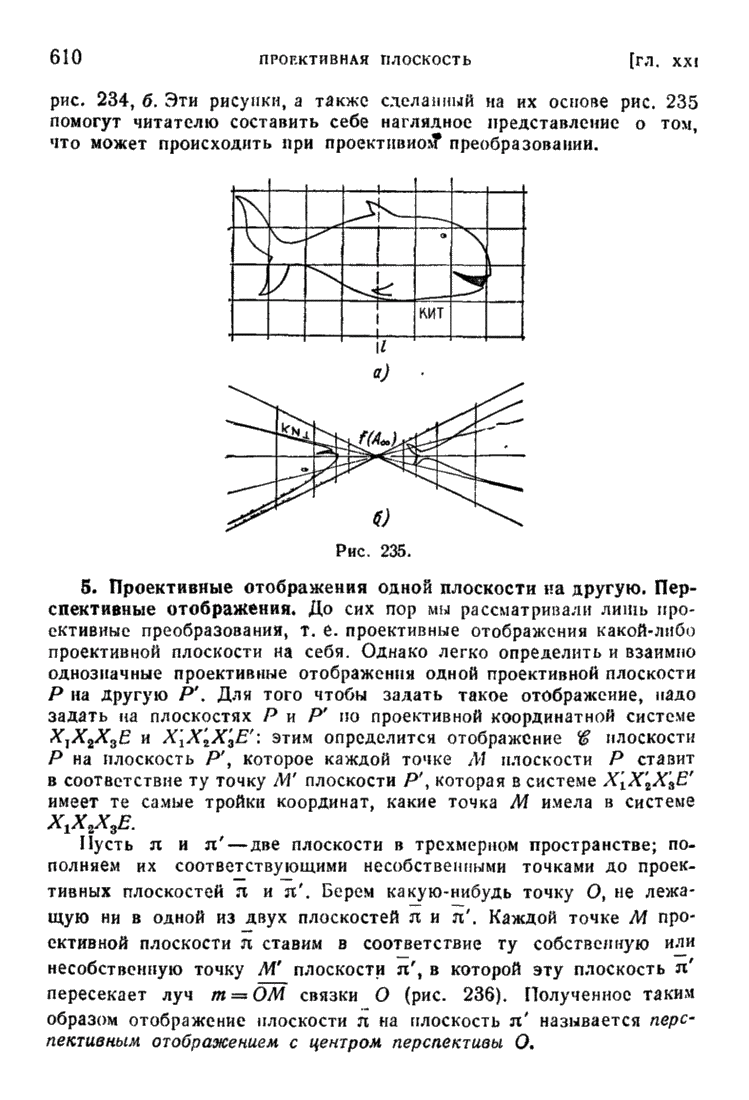
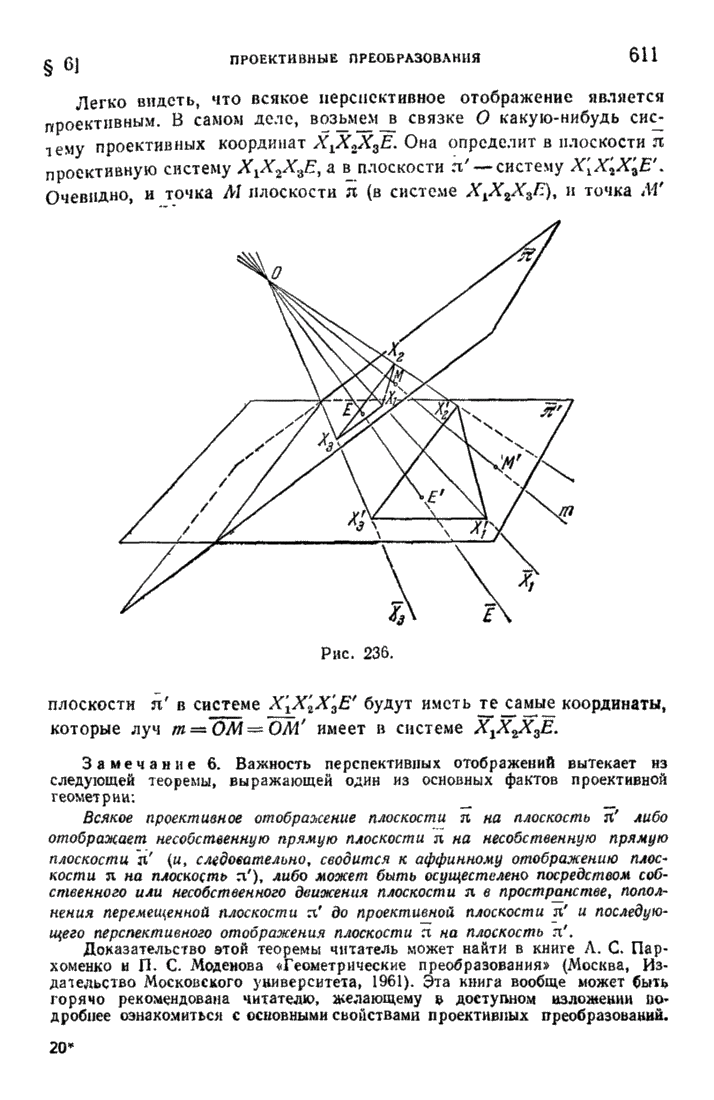
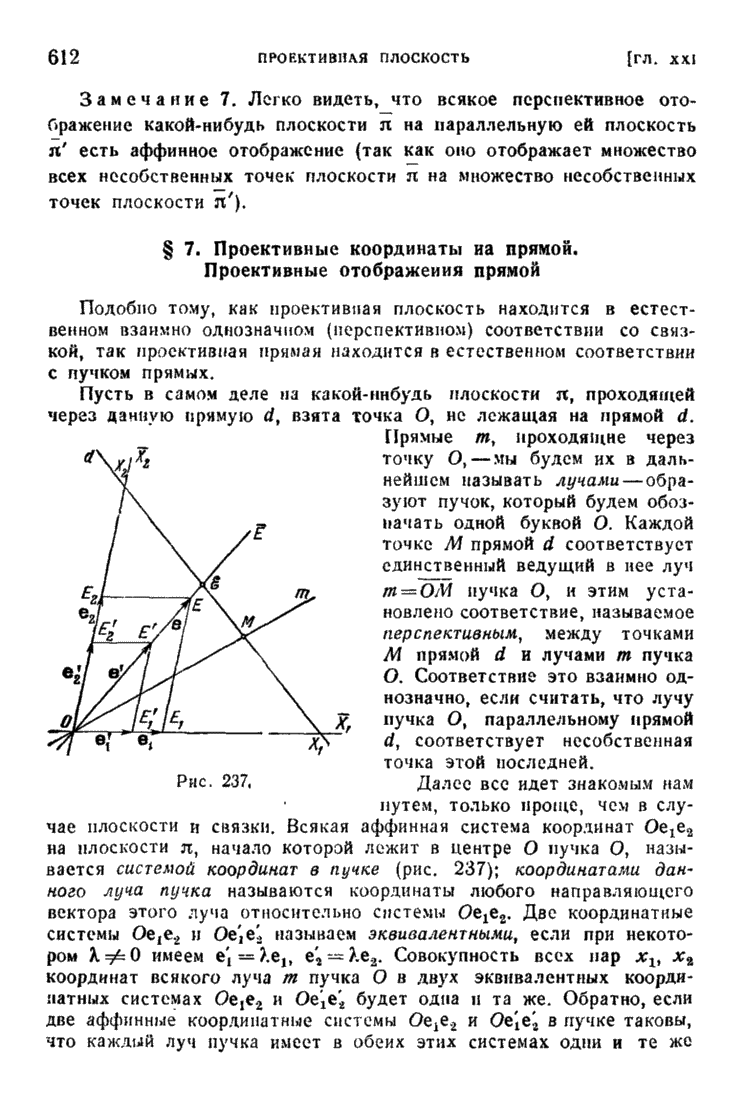
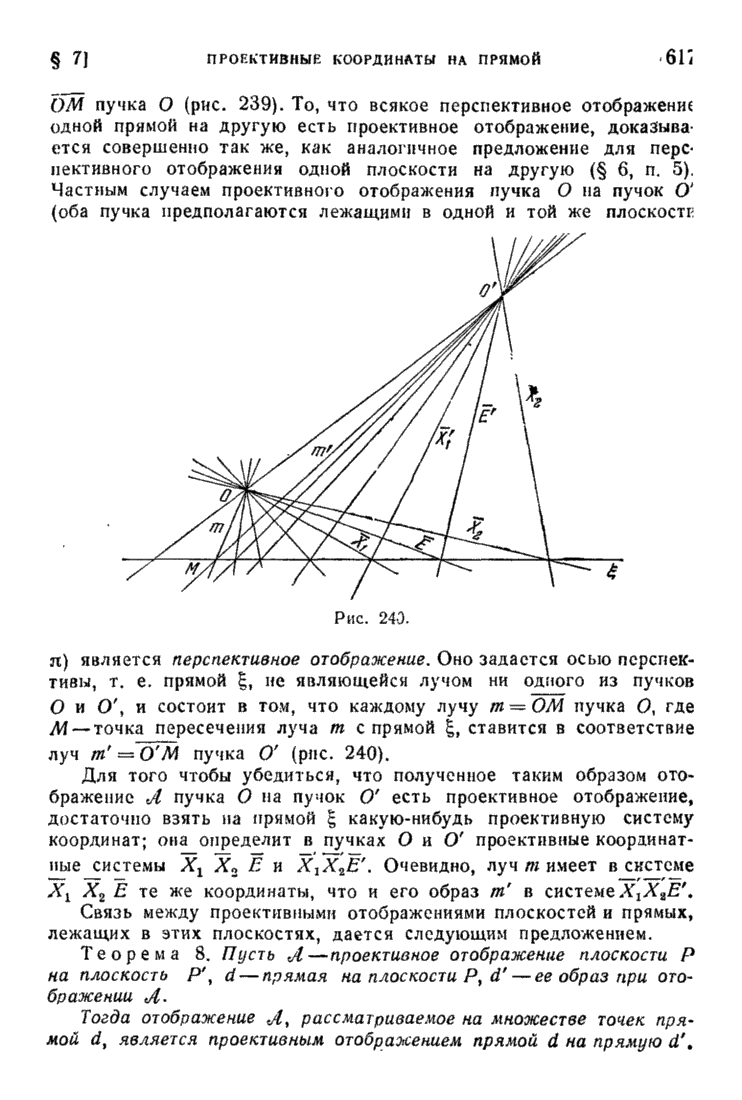
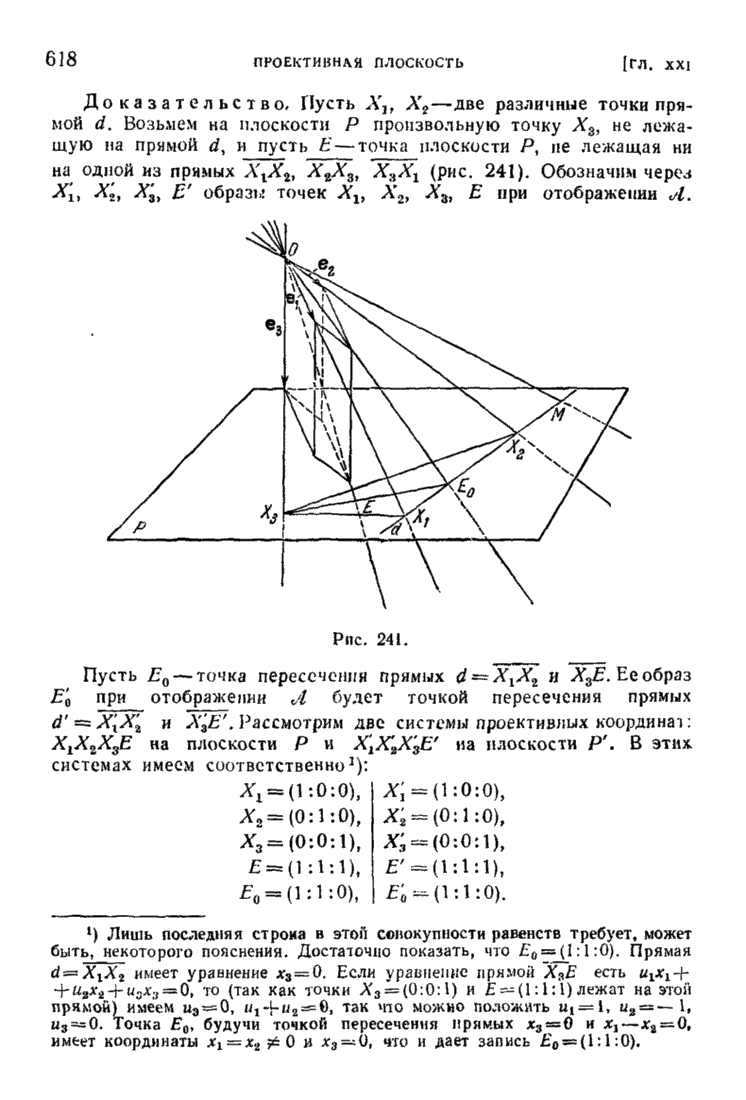
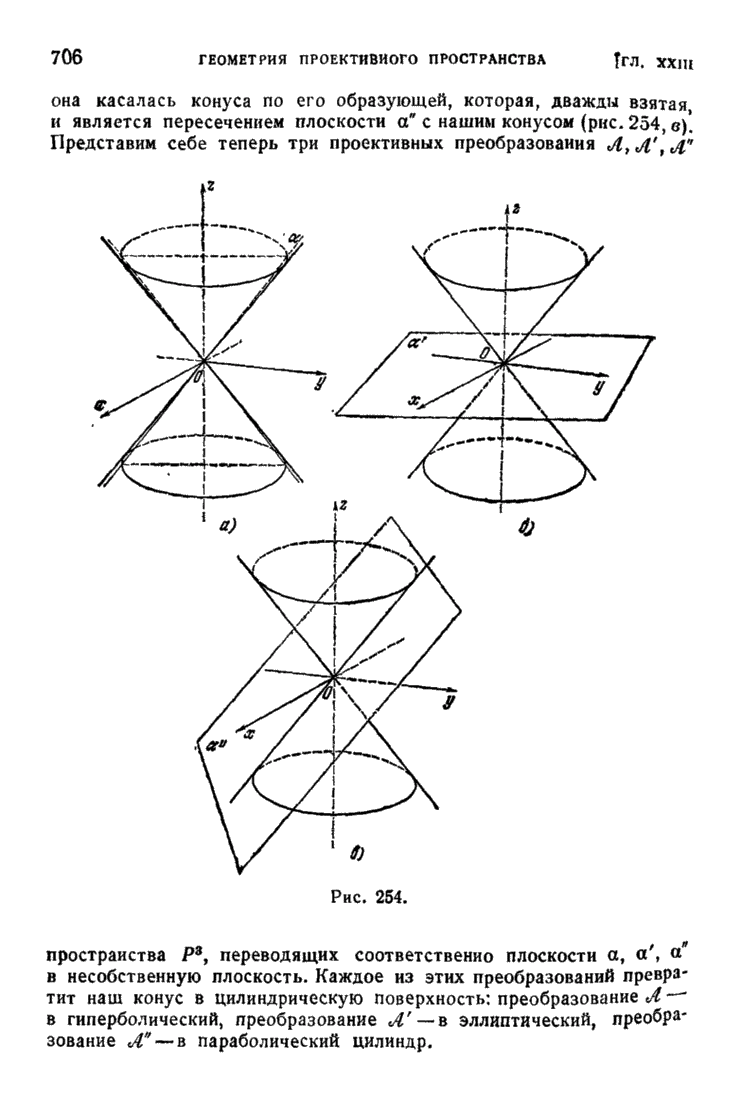
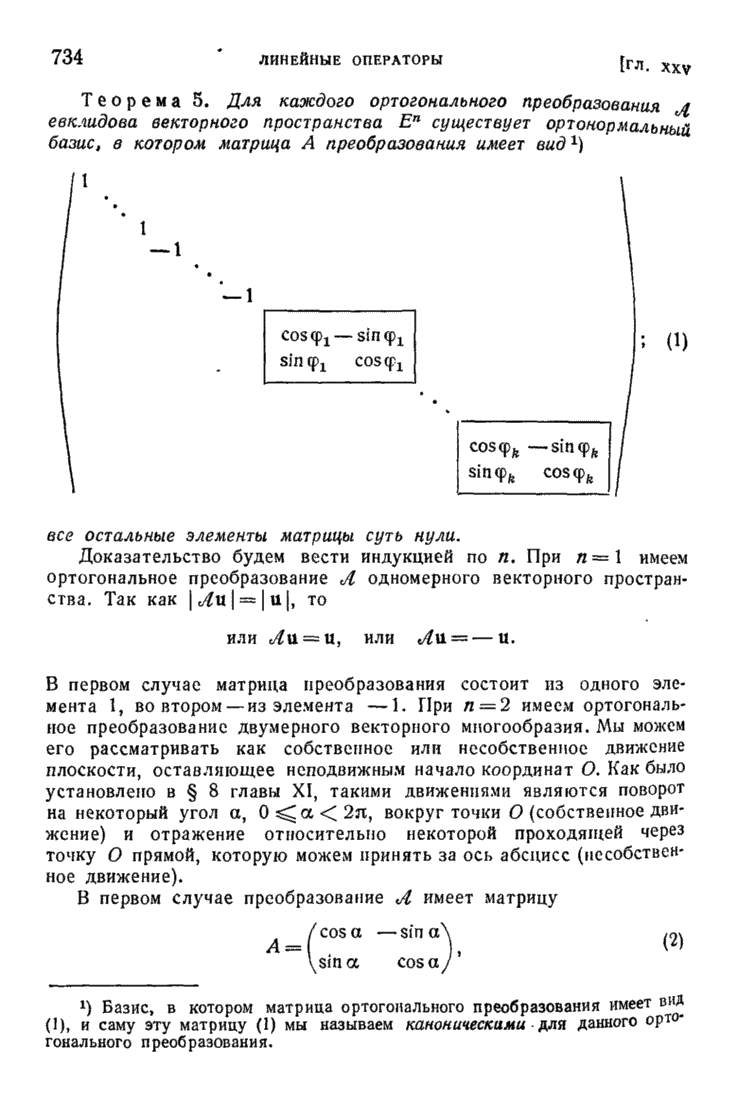
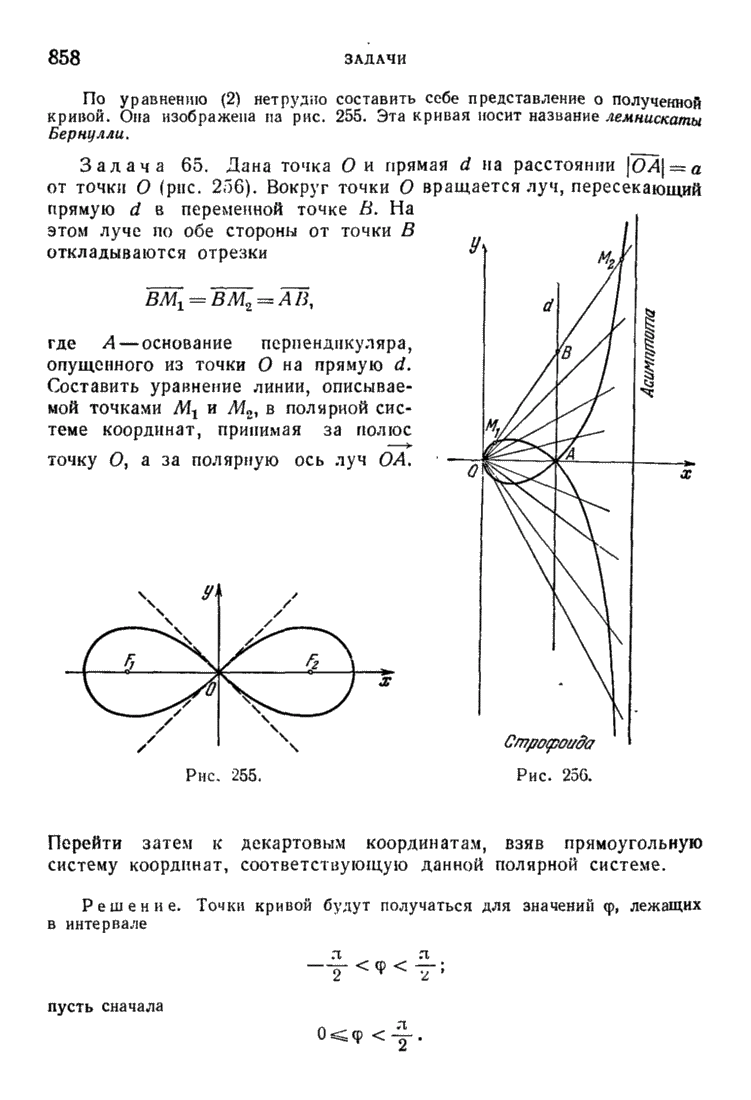
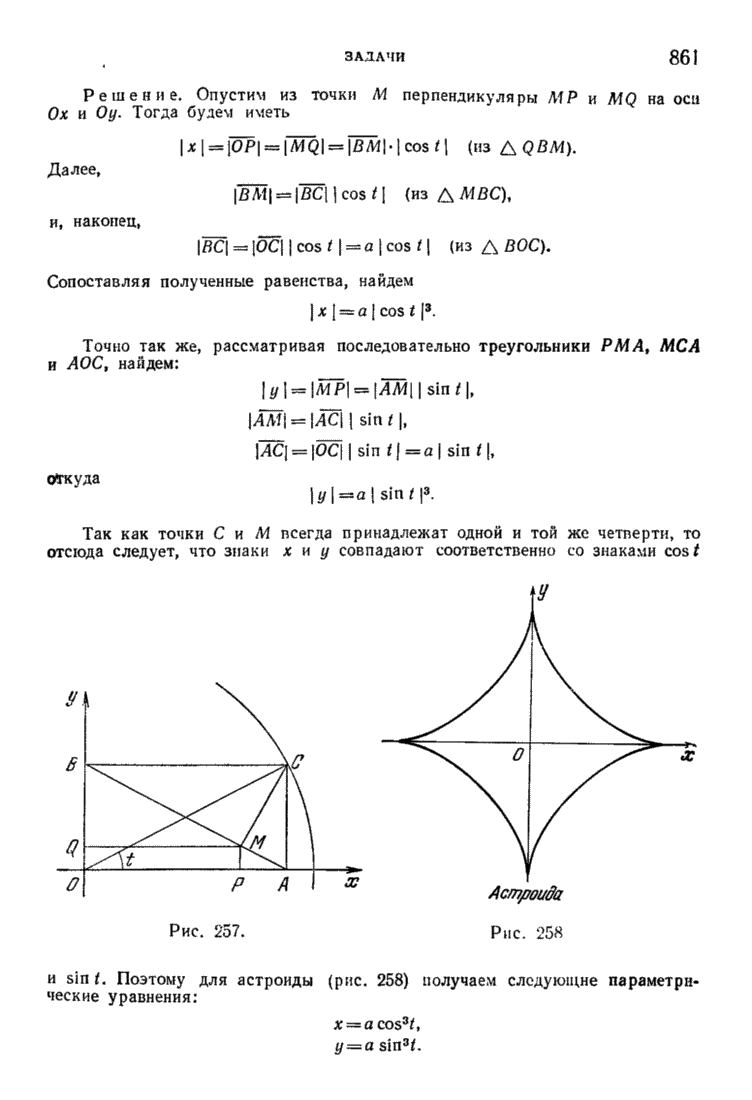
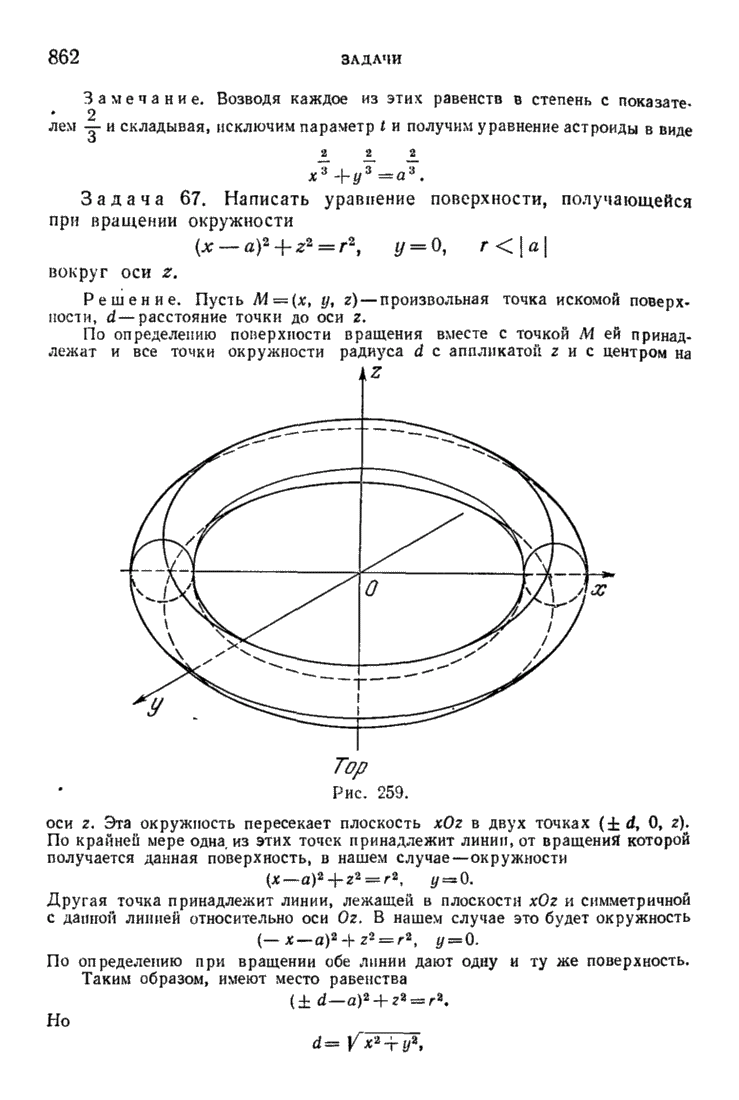
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
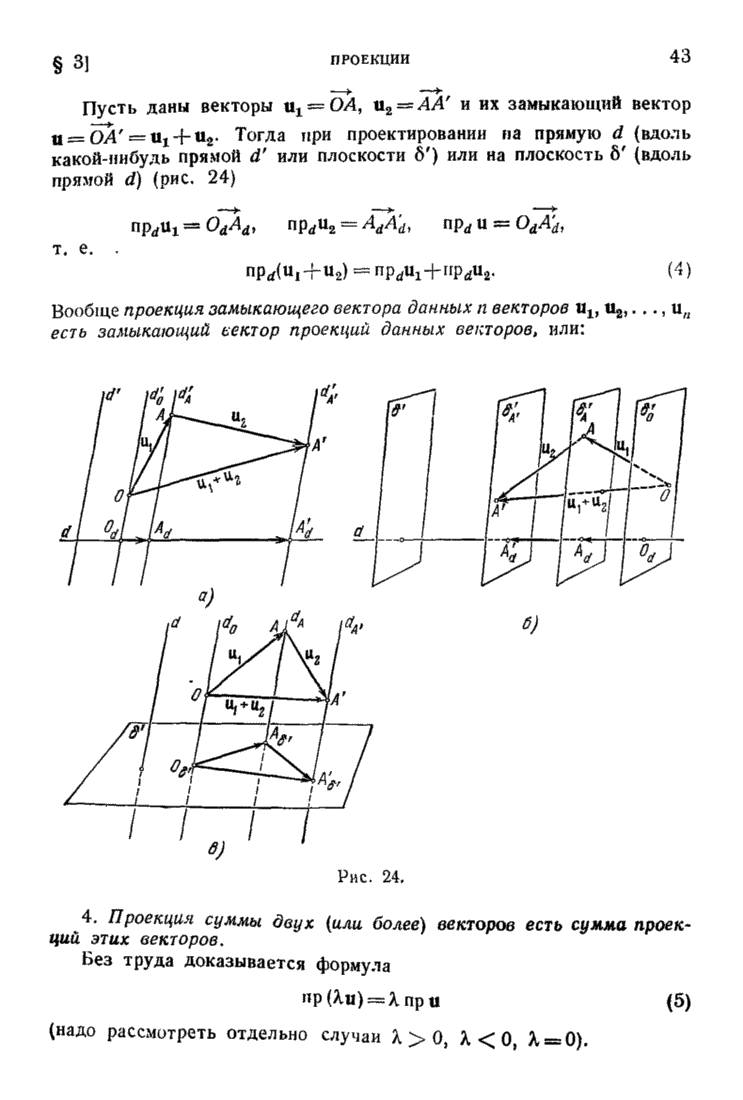
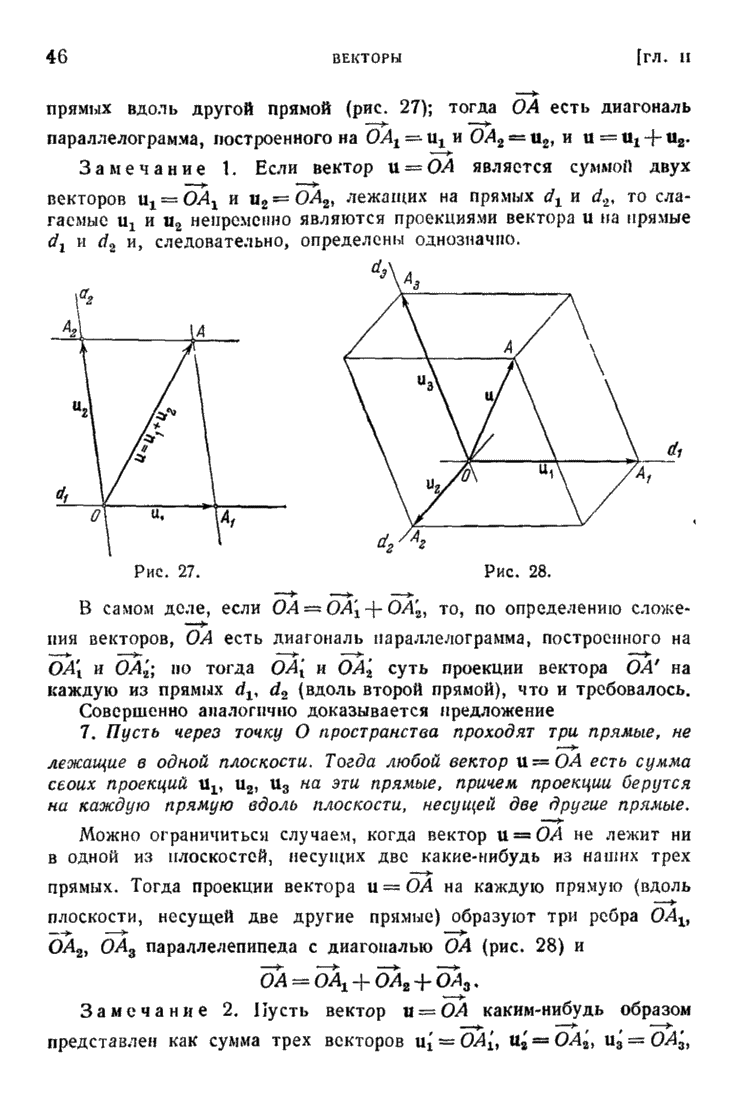
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 4. Векторная и параметрическая форма уравнения прямой. Уравнение прямой, проходящей через две заданные точки
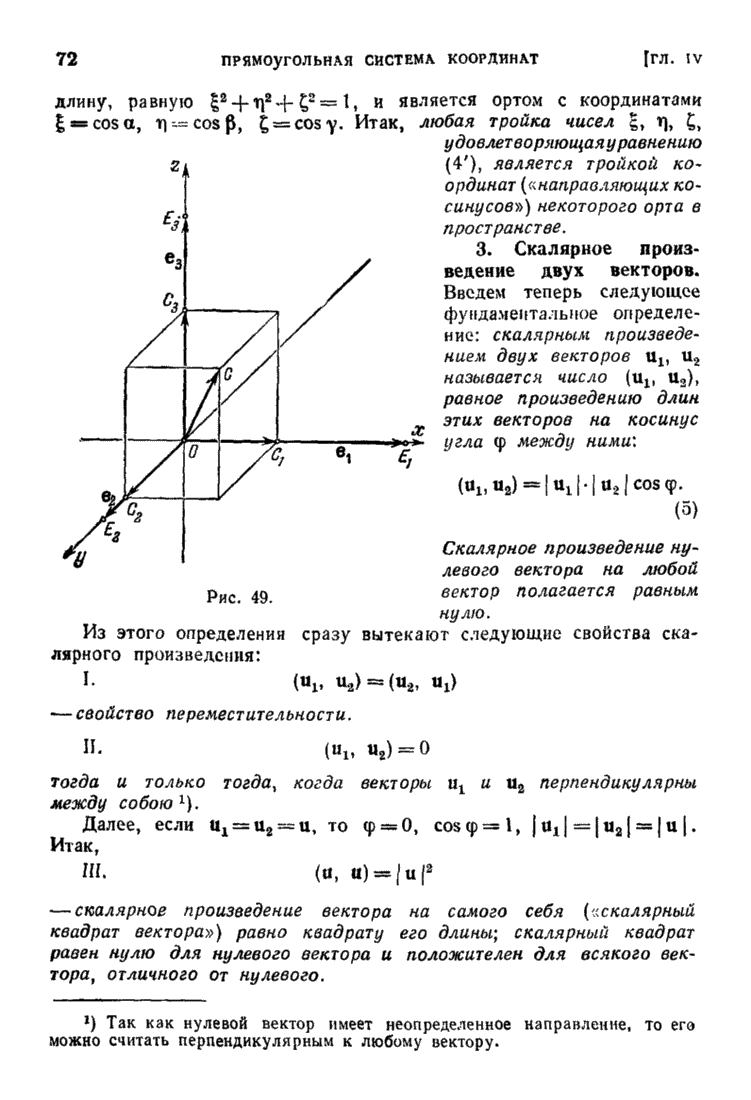
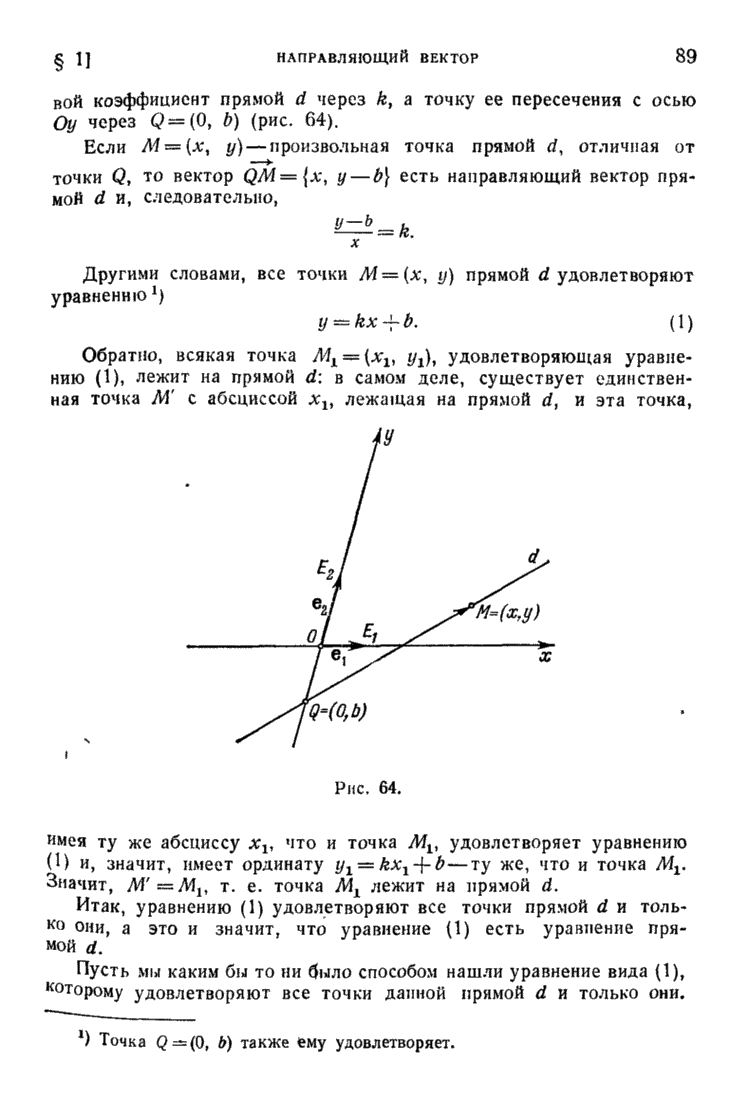
Пусть дана какая-нибудь точка  и вектор
и вектор  , который считаем приложенным к точке
, который считаем приложенным к точке  :
:

Эти данные определяют прямую d как геометрическое место концов всевозможных векторов вида

где t пробегает все вещественные числовые значения. Вектор  , очевидно, является направляющим вектором прямой d. Можно сказать, что наша прямая есть геометрическое место всех точек М, удовлетворяющих уравнению (1), а само это уравнение можно назвать уравнением прямой в векторной форме (или векторным уравнением прямой). Ясно, что каждая прямая может быть задана, таким образом, какой-нибудь своей точкой
, очевидно, является направляющим вектором прямой d. Можно сказать, что наша прямая есть геометрическое место всех точек М, удовлетворяющих уравнению (1), а само это уравнение можно назвать уравнением прямой в векторной форме (или векторным уравнением прямой). Ясно, что каждая прямая может быть задана, таким образом, какой-нибудь своей точкой  и (приложенным к этой точке) направляющим вектором
и (приложенным к этой точке) направляющим вектором  .
.
Существенным преимуществом уравнения (1) является то, что оно позволяет задать прямую не только на плоскости, но и в пространстве: ведь все до сих пор сказанное в этом параграфе в равной мере относится и к прямой на плоскости, и к прямой в пространстве. Разница (и то очень несущественная) начнется лишь тогда, когда мы будем «расписывать» уравнение (1) по координатам входящих в него векторов  . Этих координат будет в случае плоскости две, а в пространственном случае — три.
. Этих координат будет в случае плоскости две, а в пространственном случае — три.
Если на плоскости раз навсегда дана точка О (начало координат), то уравнение (1) эквивалентно уравнению

которым часто тоже пользуются (в механике и физике) под названием векторного уравнения прямой.
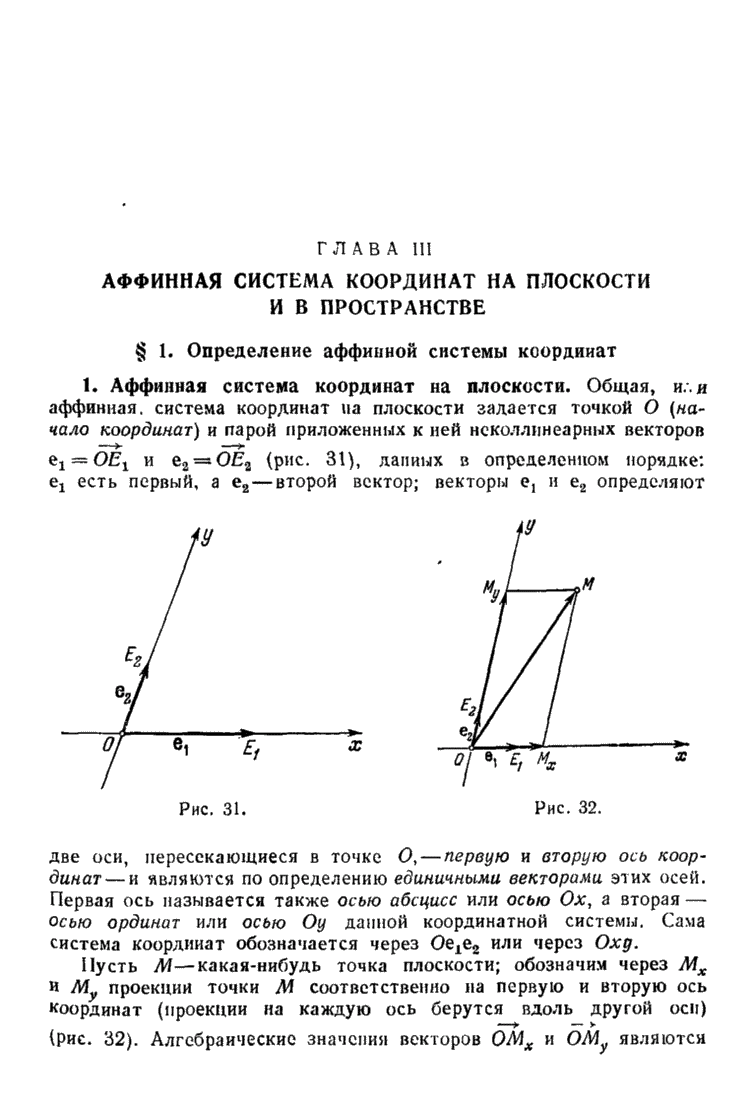
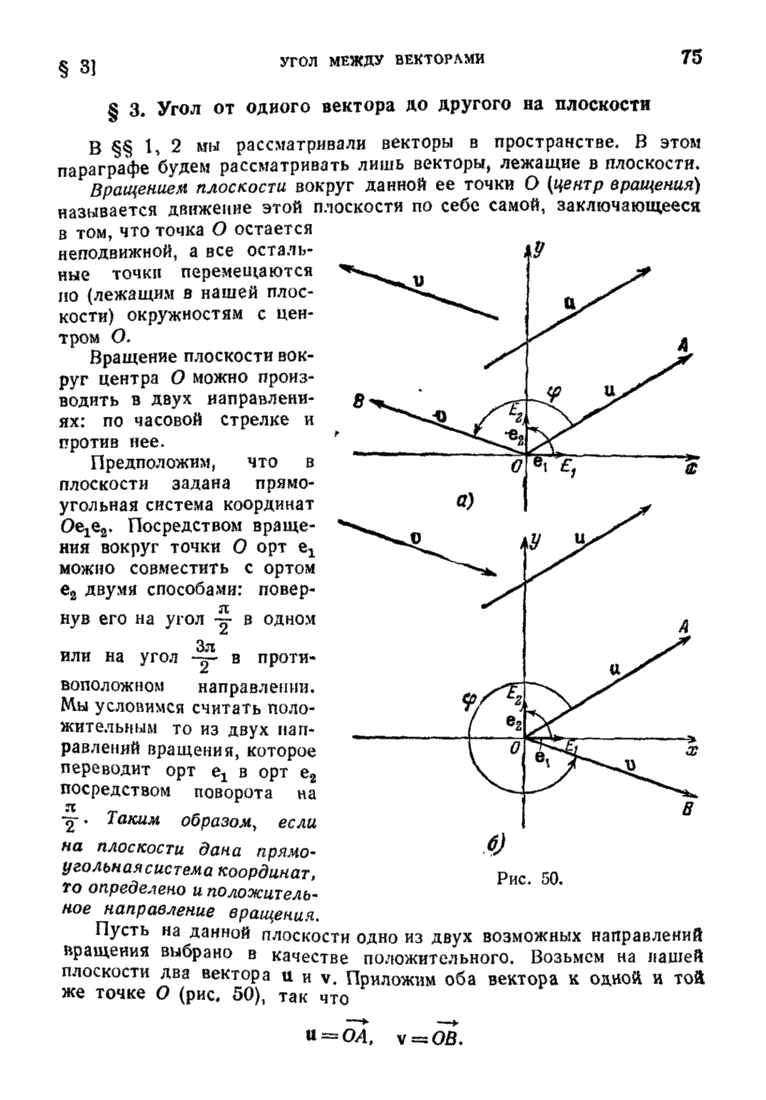
Пусть сначала дело происходит в плоскости (снабженной некоторой аффинной системой координат (рис. 66)). Тогда вектор  задан двумя своими координатами:
задан двумя своими координатами:

 , а координаты переменной точки М суть х и у, то уравнение (1) записывается в виде системы двух уравнений:
, а координаты переменной точки М суть х и у, то уравнение (1) записывается в виде системы двух уравнений:

Итак, наша прямая состоит из всех тех и только тех точек  , координаты каждой из которых при некотором вещественном значении параметра t могут быть записаны в виде (2). Поэтому система уравнений (2) называется системой параметрических уравнений данной прямой или, короче, ее параметрическим уравнением (единственное число оправдано тем, что в действительности система двух уравнений (2) является лишь координатной записью одного уравнения
, координаты каждой из которых при некотором вещественном значении параметра t могут быть записаны в виде (2). Поэтому система уравнений (2) называется системой параметрических уравнений данной прямой или, короче, ее параметрическим уравнением (единственное число оправдано тем, что в действительности система двух уравнений (2) является лишь координатной записью одного уравнения  .
.
Система уравнений (2) равносильна одной пропорции

которая часто называется каноническим уравнением прямой на плоскости.

Рис. 66.
Если прямая задана двумя своими точками  то ее направляющий вектор
то ее направляющий вектор  имеет координаты
имеет координаты

и уравнение (3) превращается в

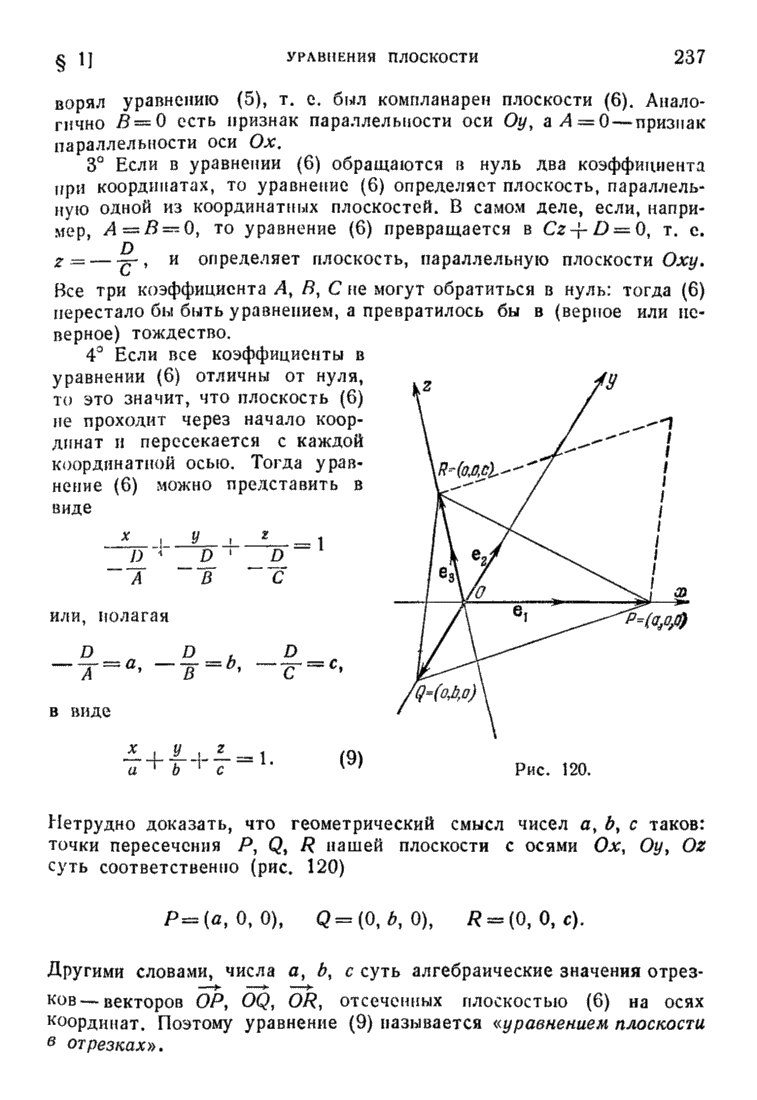
Это и есть уравнение прямой, проходящей через две заданные точки  .
.
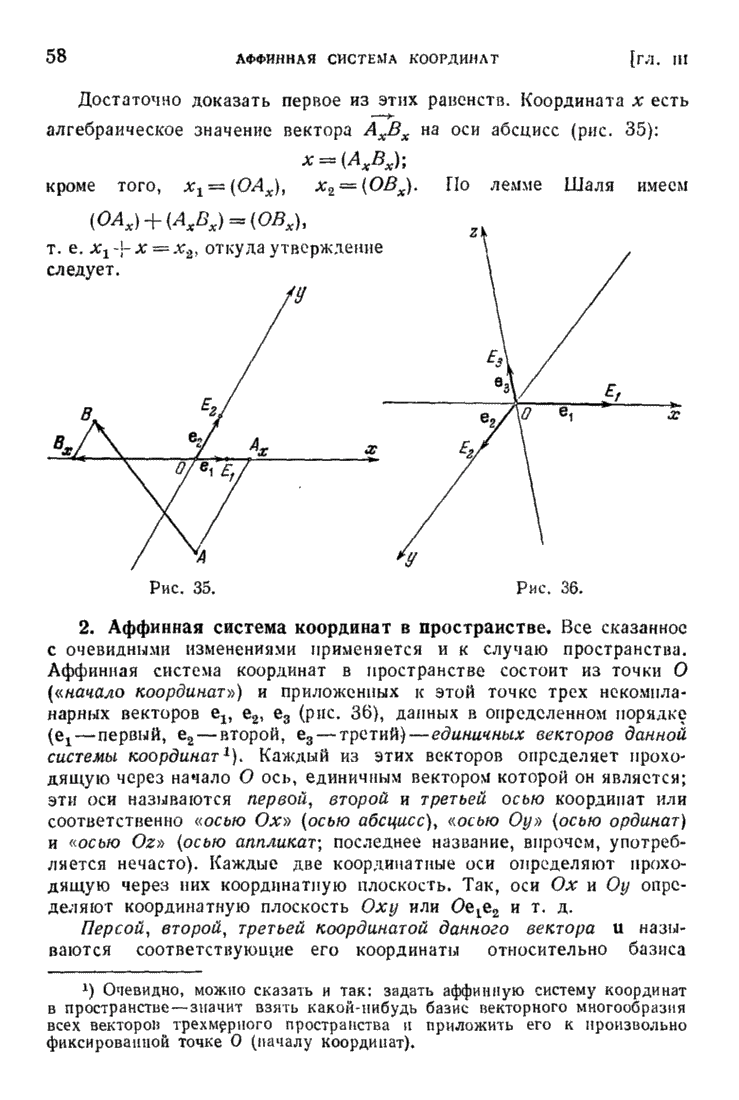
Переходим к случаю, когда прямая d, определенная своей точкой  и направляющим вектором
и направляющим вектором  , задается в пространстве, снабженном аффинной системой координат. Тогда
, задается в пространстве, снабженном аффинной системой координат. Тогда

и уравнение (1) в координатной записи превращается в систему трех уравнений

Эта система равносильна пропорции

(теперь уже трехчленной), называемой каноническим уравнением прямой в пространстве. Не следует забывать, что пропорция (6) при подробной записи превращается не в одно, а в два уравнения, например в

третье уравнение  является следствием первых двух, которым и удовлетворяют все точки прямой в пространстве.
является следствием первых двух, которым и удовлетворяют все точки прямой в пространстве.
Замечание. Если среди координат  направляющего вектора
направляющего вектора  одна какая-нибудь равна нулю, например
одна какая-нибудь равна нулю, например  , то вектор
, то вектор  и прямая d параллельны координатной плоскости
и прямая d параллельны координатной плоскости  , это видно и из уравнения (5), где теперь
, это видно и из уравнения (5), где теперь  для всех точек прямой d. Если одновременно две координаты направляющего вектора
для всех точек прямой d. Если одновременно две координаты направляющего вектора  равны нулю, например
равны нулю, например  ,
,  , то имеем
, то имеем  в этом случае направляющий вектор
в этом случае направляющий вектор  , а значит, и наша прямая параллельна оси
, а значит, и наша прямая параллельна оси  .
.
Если прямая в пространстве задается двумя своими точками  , то для ее направляющего вектора
, то для ее направляющего вектора  имеем
имеем  и пропорция (6) превращается в пропорцию
и пропорция (6) превращается в пропорцию

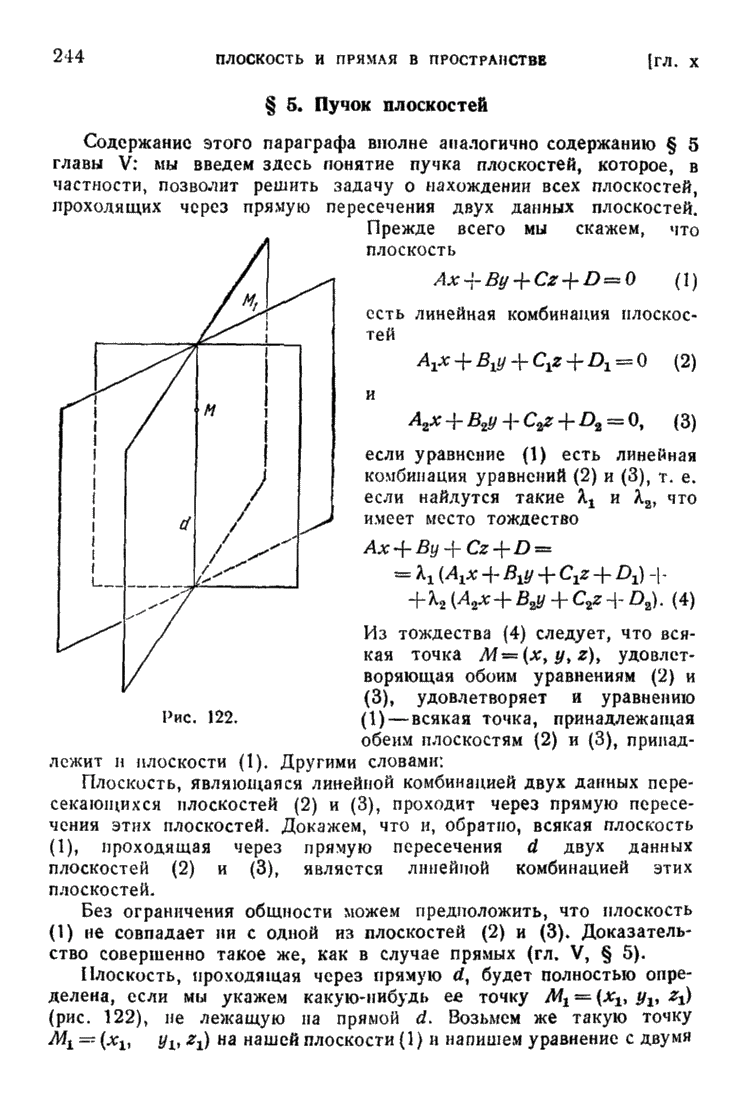
которая и определяет прямую (в пространстве), проходящую через две заданные точки.
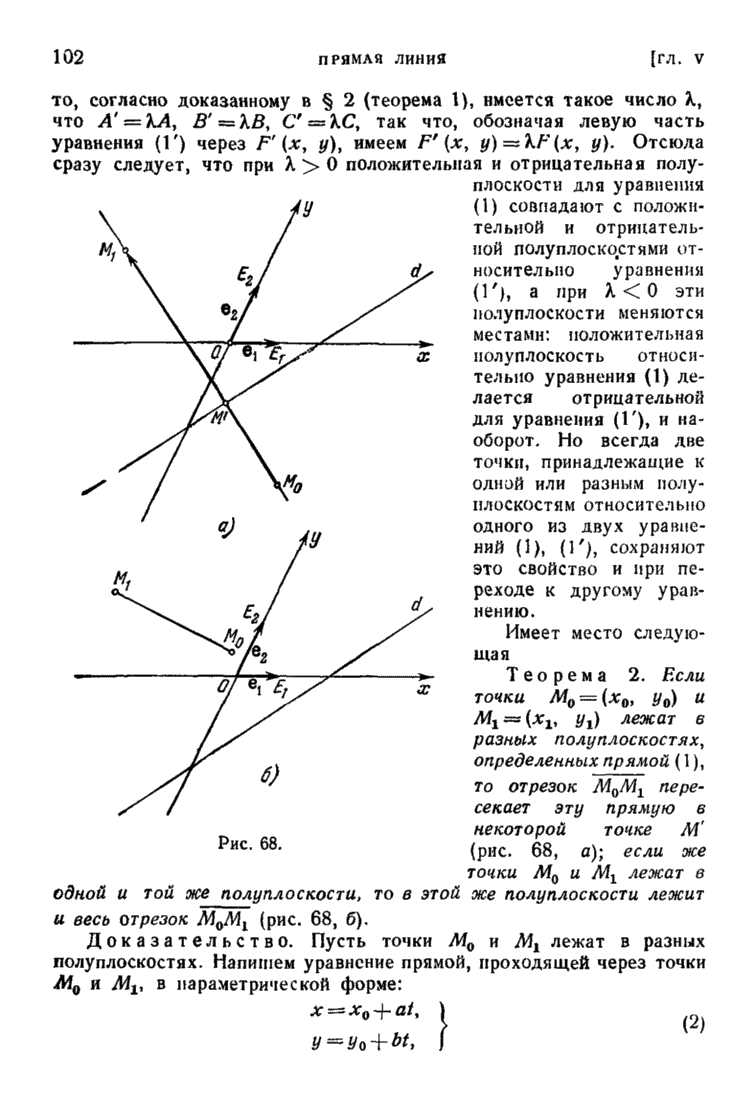
Условие параллельности (в широком смысле) двух прямых, заданных их каноническими уравнениями

заключается в коллинеарности их направляющих векторов, т. е. в пропорции

Для совпадения прямых (6) и (6) необходимо и достаточно, чтобы кроме условия (8) выполнялось еще и условие

означающее требование, чтобы точка  прямой (6) лежала на прямой (6) (или — что в данном случае равносильно — чтобы точка
прямой (6) лежала на прямой (6) (или — что в данном случае равносильно — чтобы точка  ) прямой (6) лежала на прямой
) прямой (6) лежала на прямой  .
.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ГЛАВА I. КООРДИНАТЫ НА ПРЯМОЙ
- § 1. Отношение отрезков
- § 2. Направленные отрезки (векторы); их отношение
- § 3. Ось. Алгебраическое значение (координата) вектора на оси
- § 4. Сложение векторов на прямой
- § 5. Система координат на прямой
- § 6. Деление отрезка в данном отношении
- § 7. Пропорциональность пар чисел
- § 8. Бесконечно удаленная точка прямой
- § 9. Пропорциональность двух последовательностей, состоящих из и чисел
- ГЛАВА II. ВЕКТОРЫ
- § 1. Равенство векторов. Свободный вектор
- § 2. Линейные операции над векторами (сложение и умножение на число)
- § 3. Проекции
- § 4. Коллинеарные и компланарные векторы; координаты вектора относительного данного базиса
- § 5. Линейная зависимость и независимость векторов
- § 6. Геометрический смысл линейной зависимости векторов
- § 7. Векторные многообразия
- ГЛАВА III. АФФИННАЯ СИСТЕМА КООРДИНАТ НА ПЛОСКОСТИ И В ПРОСТРАНСТВЕ
- § 1. Определение аффинной системы координат
- § 2. Перенос начала координат
- § 3. Деление отрезка в данном отношении
- ГЛАВА IV. ПРЯМОУГОЛЬНАЯ СИСТЕМА КООРДИНАТ. ПОЛЯРНЫЕ КООРДИНАТЫ
- § 1. Прямоугольная система координат на плоскости и в пространстве. Расстояние между двумя точками. Уравнение окружности и сферы
- § 2. Скалярное произведение векторов; угол между двумя векторами
- § 3. Угол от одного вектора до другого на плоскости
- § 4. Полярная система координат на плоскости
- § 5. Полярная система координат в пространстве
- ГЛАВА V. ПРЯМАЯ ЛИНИЯ
- § 1. Направляющий вектор и угловой коэффициент прямой (в произвольной аффинной системе координат). Уравнение прямой
- § 2. Расположение двух прямых на плоскости
- § 3. Частные случаи общего уравнения прямой
- § 4. Векторная и параметрическая форма уравнения прямой. Уравнение прямой, проходящей через две заданные точки
- § 5. Задача: когда прямая Ax+By+C=0 на плоскости проходит через точку пересечения двух заданных прямых A1x+B1y+C1=0 и A2x+B2y+C2=0?
- § 6. Две полуплоскости, определяемые данной прямой на плоскости
- § 7. Прямая на плоскости в прямоугольной системе координат. Нормальное уравнение прямой на плоскости
- § 8. Расстояние от точки до прямой (на плоскости)
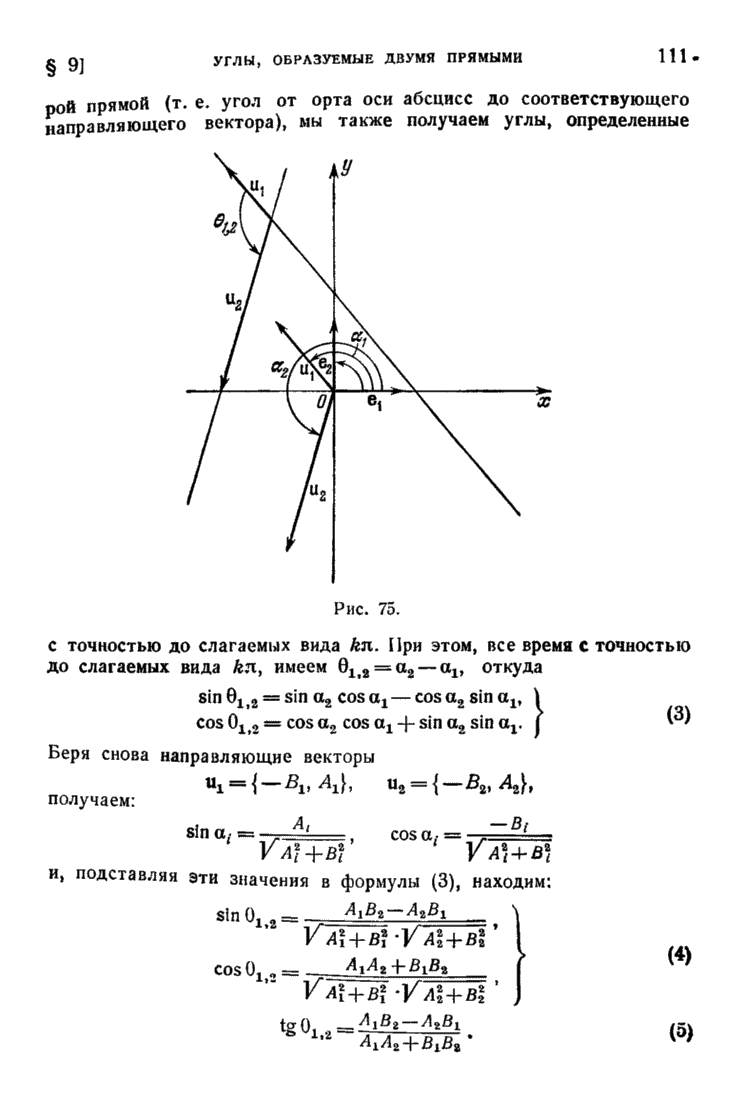
- § 9. Углы, образуемые двумя прямыми на плоскости
- § 10. Прямая в пространстве, снабженном прямоугольной системой координат
- ГЛАВА VI. ПАРАБОЛА. ЭЛЛИПС. ГИПЕРБОЛА
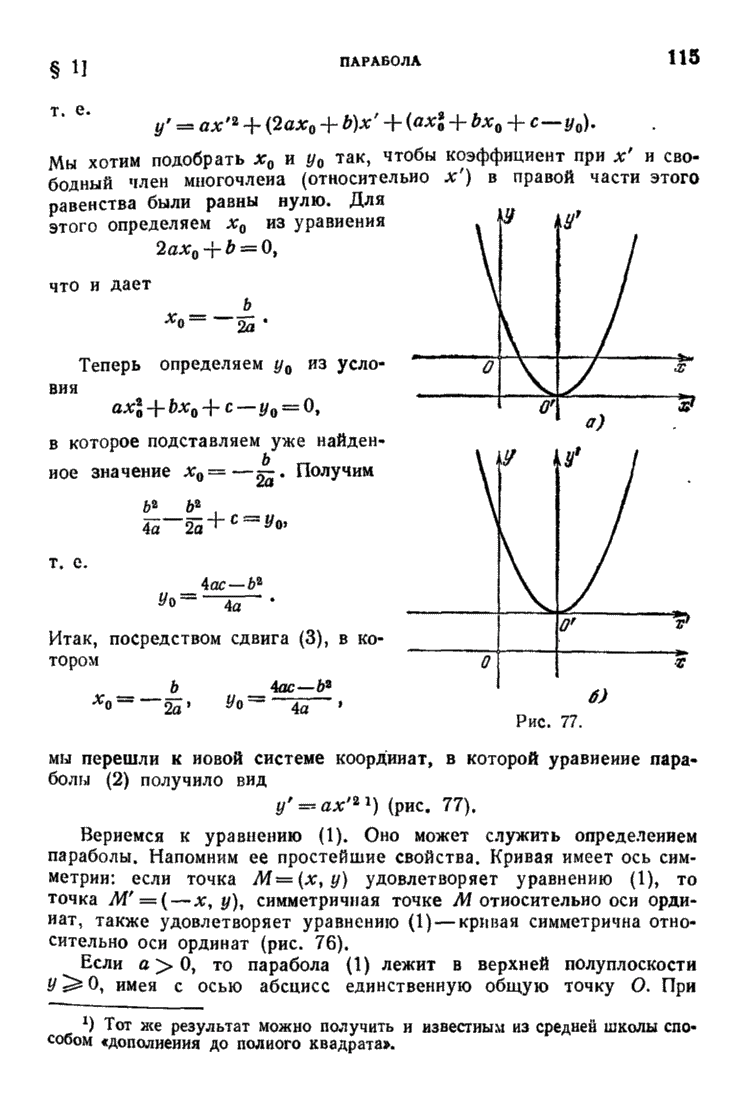
- § 1. Парабола
- § 2. Определение и каноническое уравнение эллипса
- § 3. Параметрическая запись уравнения эллипса; построение эллипса по точкам. Эллипс как результат сжатия окружности к одному из ее диаметров
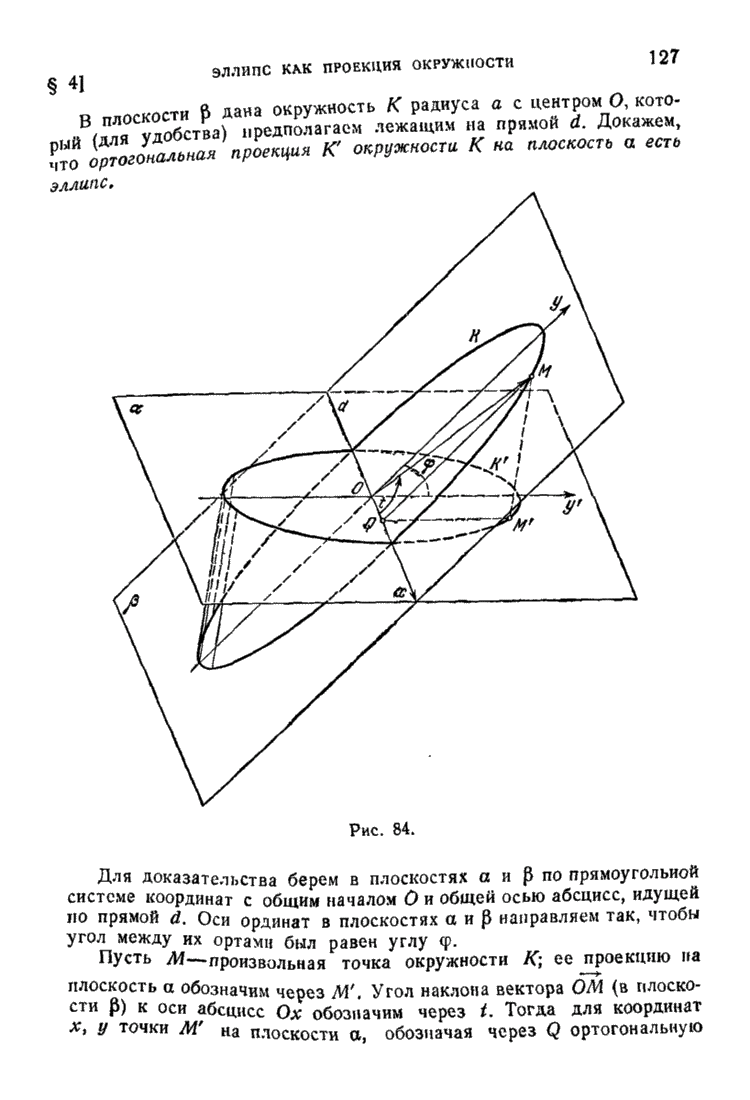
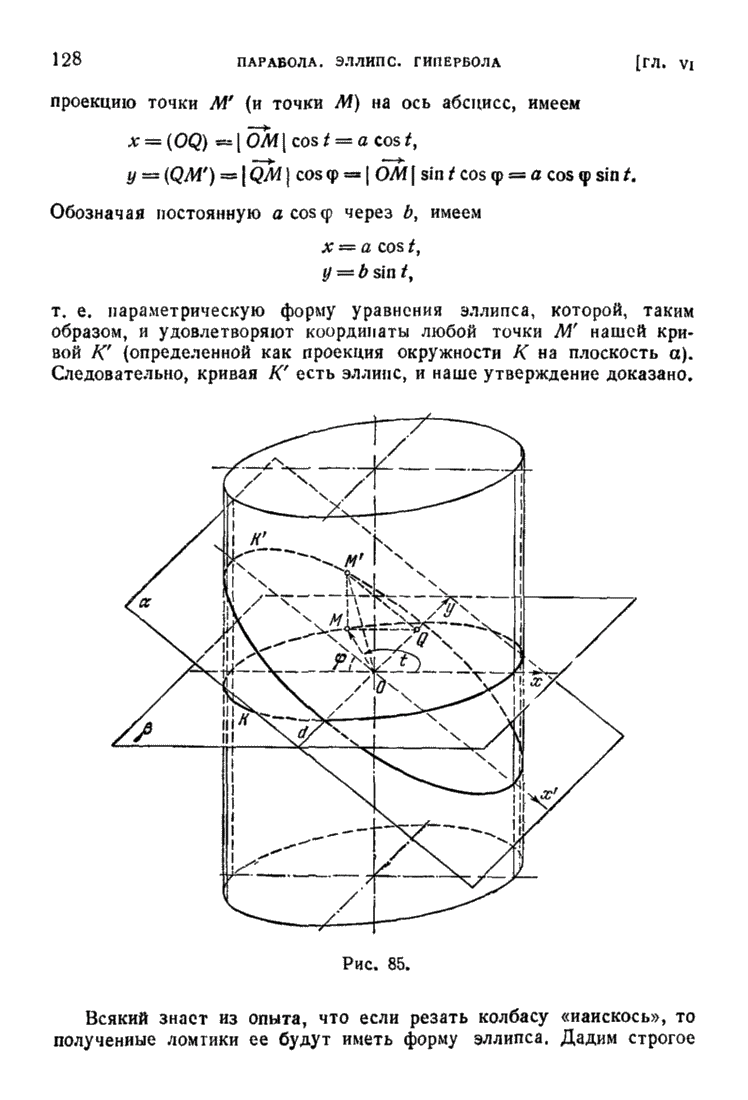
- § 4. Эллипс как проекция окружности и как сечение круглого цилиндра
- § 5. Определение гиперболы. Каноническое уравнение гиперболы
- § 6. Основной прямоугольник и асимптоты гиперболы
- § 7. Директрисы эллипса и гиперболы
- § 8. Фокальный параметр эллипса и гиперболы. Уравнение при вершине
- § 9. Уравнение эллипса, гиперболы и параболы в полярных координатах
- ГЛАВА VII. ДЕТЕРМИНАНТЫ
- § 1. Плошадь ориентированного параллелограмма и треугольника
- § 2. Детерминант второго порядка. Матрицы
- § 4. Разложение детерминанта третьего порядка по элементам какой-либо строки. Приложение к системе трех уравнений с тремя неизвестными (правило Крамера)
- § 5. Системы трех уравнений с тремя неизвестными с детерминантом системы, равным нулю
- § 6. Арифметическое n-мерное векторное многообразие (пространство). Общее определение матрицы. Детерминанты любого порядка
- § 7. Разложение детерминанта n-го порядка по элементам данной строки (данного столбца)
- § 8. Правило Крамера для решений систем и уравнений с n неизвестными
- § 9. Общее определение миноров матрицы. Теорема Лапласа
- § 10. Умножение детерминантов
- § 11. Детерминант n-го порядка как линейная нечетная нормированная функция от n векторов
- ГЛАВА VIII. ПРЕОБРАЗОВАНИЕ КООРДИНАТ. МАТРИЦЫ
- § 1. Переход от одной аффинной системы координат к другой
- § 2. Перемножение матриц. Новое определение обратной матрицы
- § 3. Переход от одной прямоугольной системы координат к другой
- § 4. Действия над матрицами в общем случае
- ГЛАВА IX. ПРЕОБРАЗОВАНИЕ КООРДИНАТ (ПРОДОЛЖЕНИЕ): ОРИЕНТАЦИЯ ПЛОСКОСТИ И ПРОСТРАНСТВА; УГЛЫ ЭЙЛЕРА; ОБЪЕМ ОРИЕНТИРОВАННОГО ПАРАЛЛЕЛЕПИПЕДА; ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ДВУХ ВЕКТОРОВ
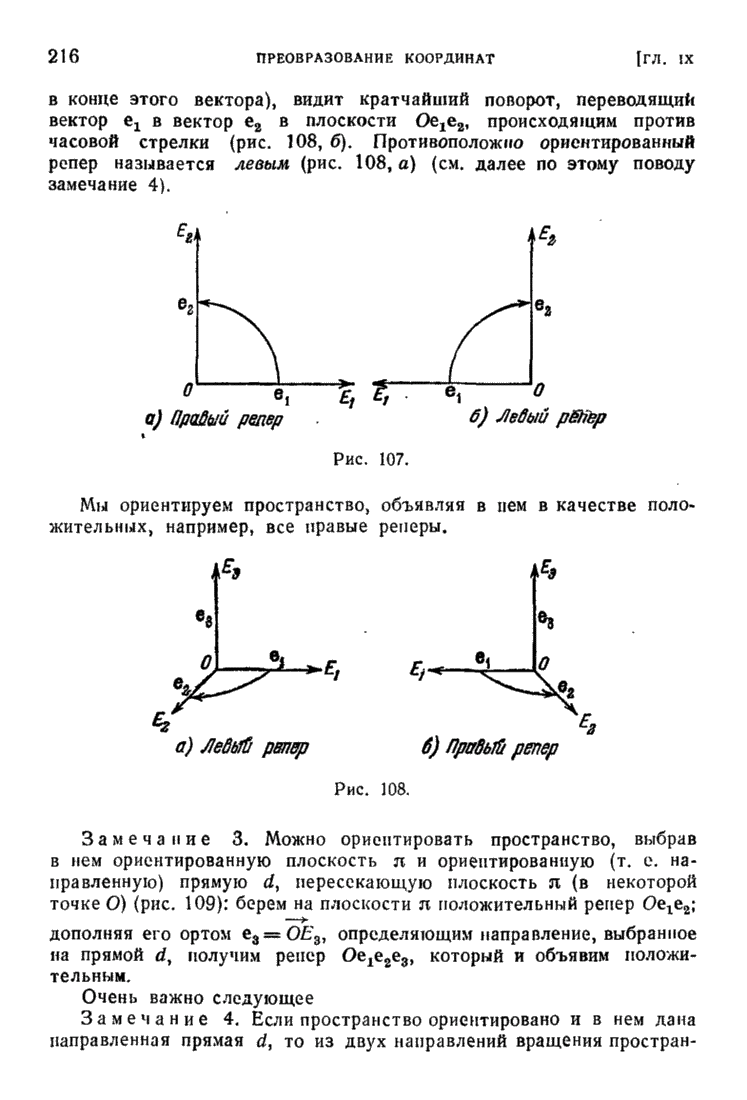
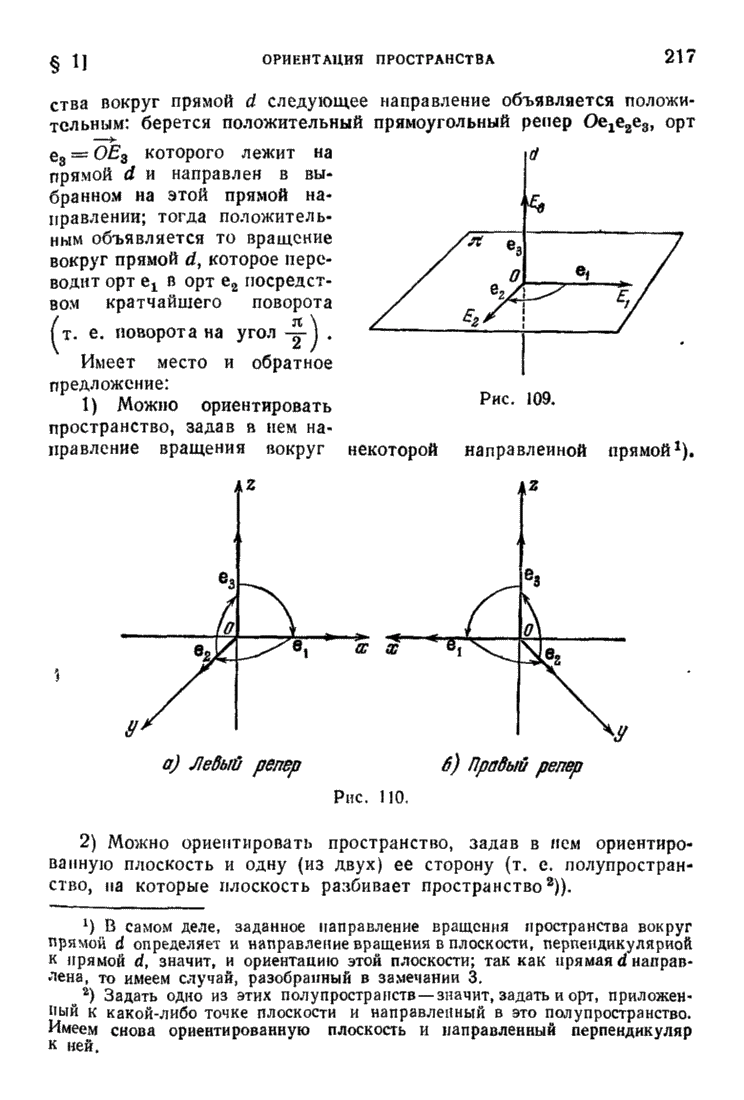
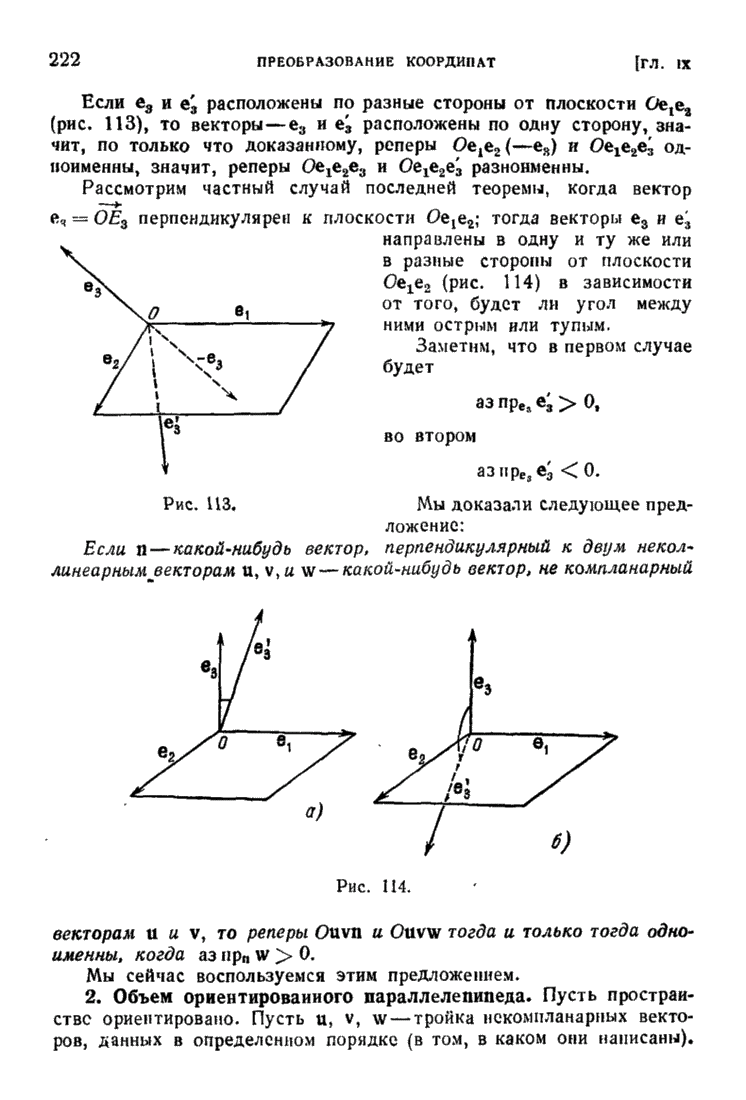
- § 1. Ориентация пространства (плоскости)
- § 2. Углы Эйлера
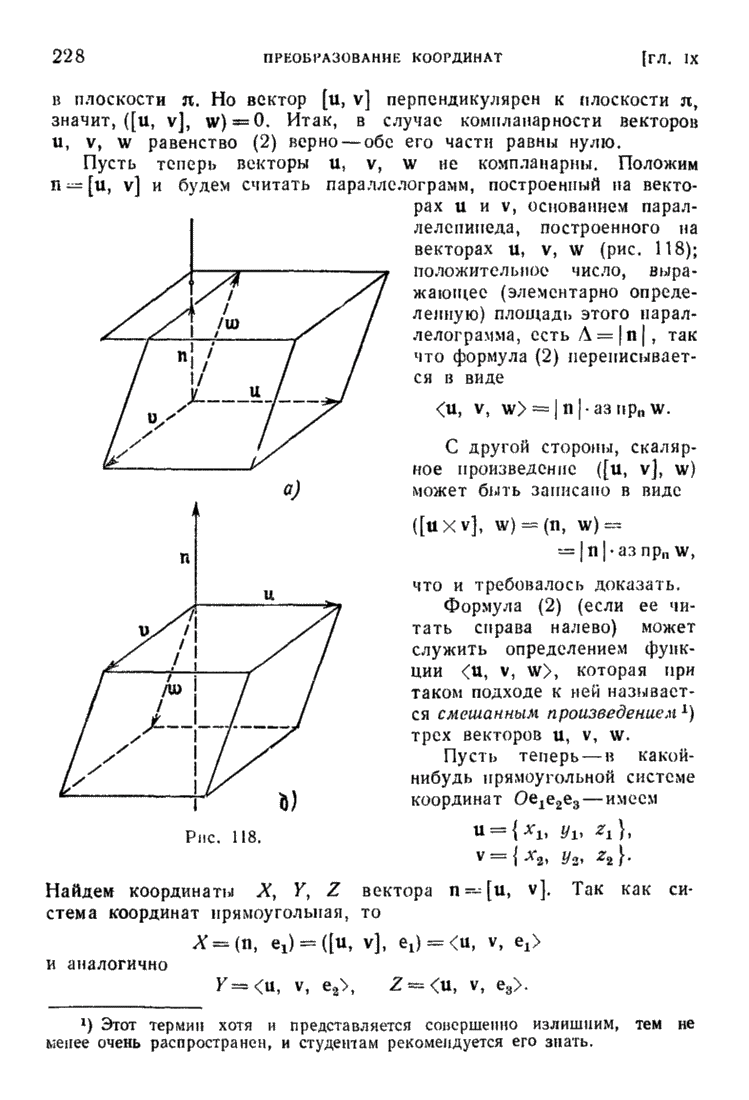
- § 3. Объем ориентированного параллелепипеда
- § 4. Векторное произведение двух векторов
- ГЛАВА X. ПЛОСКОСТЬ И ПРЯМАЯ В ПРОСТРАНСТВЕ
- § 1. Уравнения плоскости
- § 2. Множество решений системы двух однородных линейных уравнений с тремя неизвестными
- § 3. Взаимное расположение двух плоскостей
- § 4. Прямая как пересечение двух плоскостей
- § 5. Пучок плоскостей
- § 6. Взаимное расположение двух прямых в пространстве
- § 7. О двух полупространствах, определяемых данной плоскостью
- § 8. Плоскость в прямоугольной системе координат; нормальное уравнение плоскости; расстояние от точки до плоскости
- § 9. Угол между прямой и плоскостью; угол между двумя плоскостями
- § 10. Две задачи
- ГЛАВА XI. ДВИЖЕНИЯ И АФФИННЫЕ ПРЕОБРАЗОВАНИЯ
- § 1. Определение движений и аффинных преобразований
- § 2. Преобразование векторов при аффинном преобразовании плоскости и пространства. Основные свойства аффинных преобразований
- § 3. Аналитическое выражение аффинных преобразований
- § 4. Сохранение отношений площадей и объемов при аффинных преобразованиях
- § 5. Получение собственных аффинных преобразований посредством деформации тождественного преобразования. Следствия
- § 6. Движения как изометрические преобразования
- § 7. Преобразования подобия
- § 8. Классификация движений прямой и плоскости
- ГЛАВА XII. ВЕКТОРНЫЕ ПРОСТРАНСТВА (МНОГООБРАЗИЯ) ЛЮБОГО КОНЕЧНОГО ЧИСЛА ИЗМЕРЕНИЙ. СИСТЕМЫ ЛИНЕЙНЫХ ОДНОРОДНЫХ УРАВНЕНИЙ
- § 1. Определение векторного пространства
- § 2. Размерность. Базис. Координаты
- § 3. Теорема об изоморфизме между любыми двумя векторными пространствами одной и той же конечной размерности n
- § 4. Подпространства векторного пространства. Дальнейшие теоремы о линейной зависимости векторов и о базисе векторного пространства
- § 5. Алгебраическая (в частности, прямая) сумма подпространств
- § 6. Линейные отображения векторных пространств
- § 7. Теорема о ранге матрицы
- § 8. Системы линейных однородных уравнения
- ГЛАВА XIII. ЛИНЕЙНЫЕ, БИЛИНЕЙНЫЕ И КВАДРАТИЧНЫЕ ФУНКЦИИ НА ВЕКТОРНЫХ ПРОСТРАНСТВАХ
- § 1. Линейные функции
- § 2. Билинейные функции и билинейные формы
- § 3. Матрица билинейной и квадратичной формы и ее преобразование при переходе к новому базису (при преобразовании переменных)
- § 4. Ранг билинейной и квадратичной формы (билинейной и квадратичной функции)
- § 5. Существование канонического базиса для всякой квадратичной и всякой билинейной функции («приведение квадратичных форм к каноническому виду»)
- ГЛАВА XIV. ТОЧЕЧНО-ВЕКТОРНОЕ АФФИННОЕ n-МЕРНОЕ ПРОСТРАНСТВО
- § 1. Определение n-мерного аффинного пространства
- § 2. Системы координат. Арифметическое пространство. Изоморфизм всех n-мерных пространств между собою
- § 3. r-мерные плоскости n-мерного аффинного пространства; r-мерные параллелепипеды
- § 4. Геометрически независимые системы точек. Барицентрические координаты. Симплексы
- § 5. Системы линейных уравнений
- § 6. Аффинные преобразования n-мерного аффинного пространства
- ГЛАВА XV. АЛГЕБРАИЧЕСКИЕ ЛИНИИ И ПОВЕРХНОСТИ. КОМПЛЕКСНАЯ ПЛОСКОСТЬ И КОМПЛЕКСНОЕ ПРОСТРАНСТВО
- § 1. Определение алгебраических линий и поверхностей
- § 2. Преобразование многочлена второй степени при преобразовании координат
- § 3. Аффинная эквивалентность линий и поверхностей
- § 4. Комплексная плоскость
- § 5. Прямая линия на комплексной плоскости
- § 6. Замечание о действительных и мнимых линиях
- § 7. Комплексное пространство
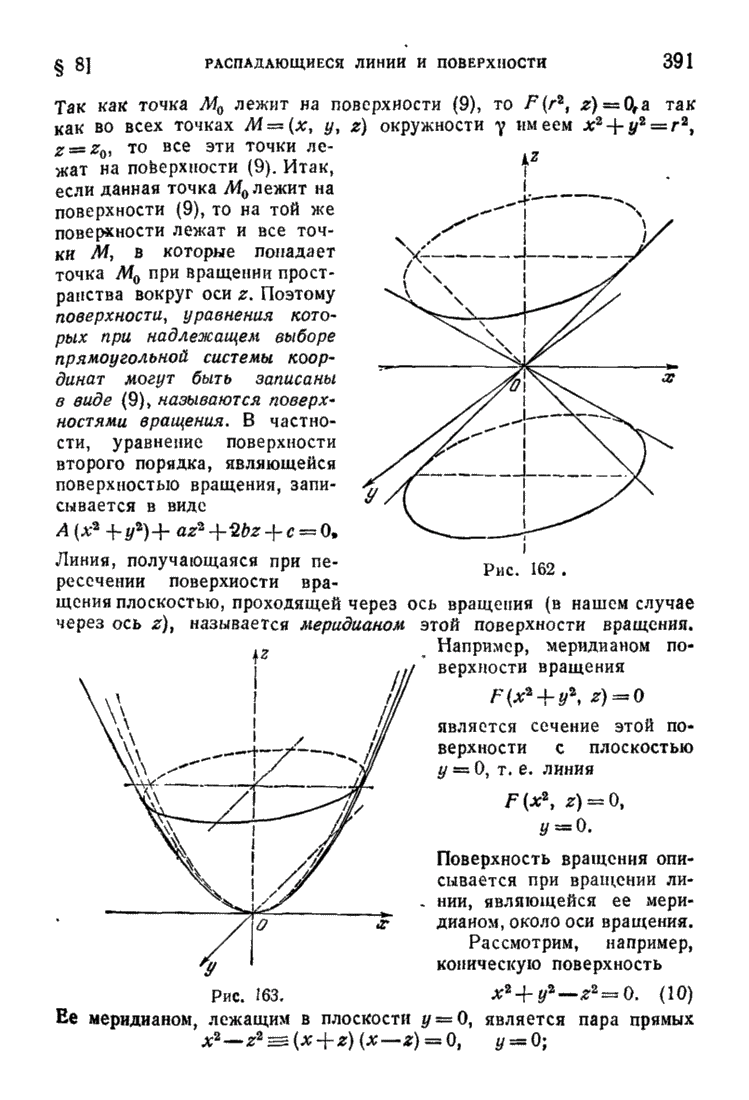
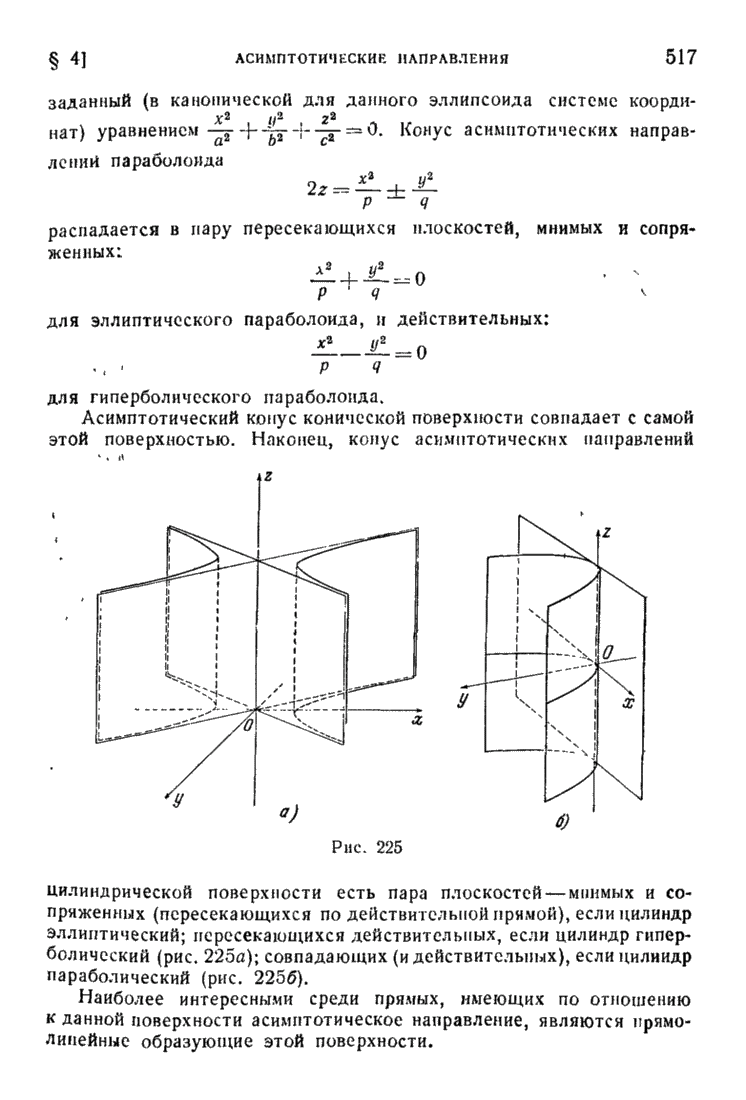
- § 8. Распадающиеся линии и поверхности. Цилиндрические и конические поверхности. Поверхности вращения
- § 9. Несколько заключительных замечаний о линиях и поверхностях
- ГЛАВА XVI. Различные виды кривых второго порядка
- § 1. О линиях, определяемых уравнениями второй степени с двумя неизвестными
- § 2. Инварианты многочлена второй степени
- § 3. Центральный случай
- § 4. Параболический случай
- § 5. Аффинная классификация кривых второго порядка
- § 6. Несколько заключительных замечаний
- ГЛАВА XVII. ОБЩАЯ ТЕОРИЯ КРИВЫХ ВТОРОГО ПОРЯДКА
- § 1. Пересечение алгебраической кривой с прямой. Асимптотические направления и асимптоты алгебраической кривой
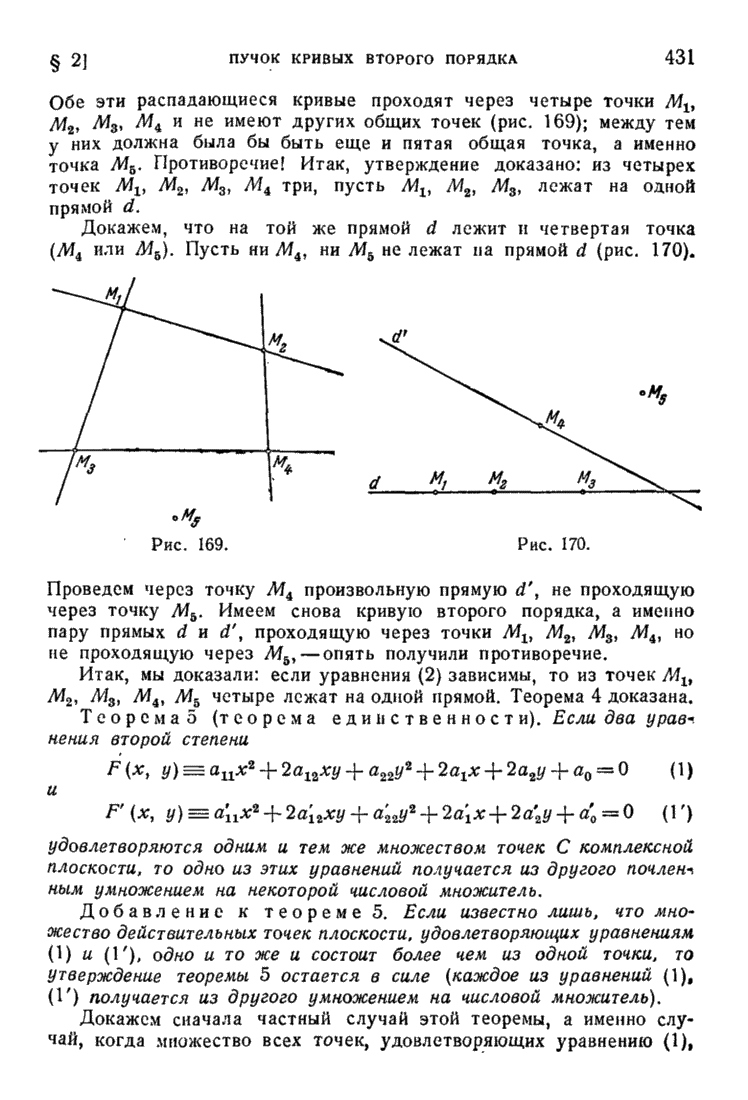
- § 2. Теорема единственности для кривых второго порядка. Пучок кривых второго порядка
- § 3. Асимптотические направления кривых второго порядка
- § 4. Пересечение кривой второго порядка с прямой иеасимптотического направления. Касательные
- § 5. Пересечение кривой второго порядка с прямой асимптотического направления. Геометрическая характеристика асимптотических и неасимптотических направлений
- § 6. Центр кривой второго порядка
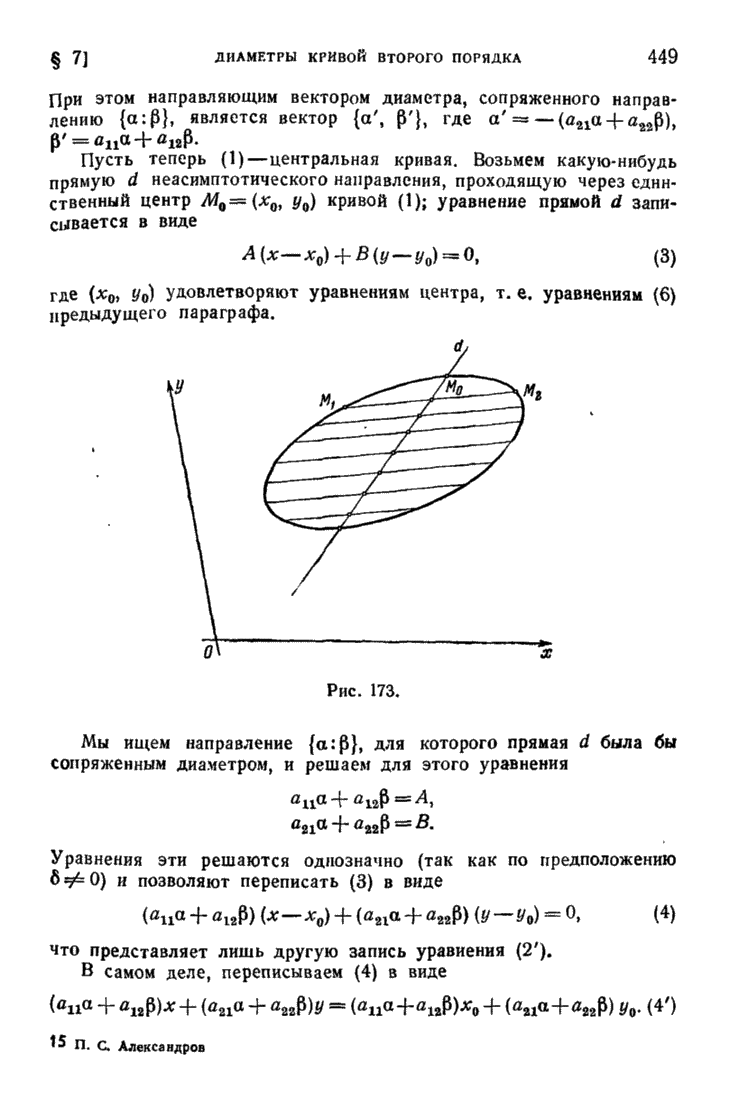
- § 7. Диаметры кривой второго порядка
- § 8. Взаимно сопряженные векторы (направления). Диаметры и касательные
- § 9. Вид уравнения кривой, если оси координат имеют сопряженные направления
- § 10. Второе доказательство теоремы единственности. О полноте системы ортогональных инвариантов
- § 11. Оси симметрии и главные направления кривой второго порядка
- § 12. Основная теорема об аффинных преобразованиях
- ГЛАВА XVIII. КРАТКОЕ ОПИСАНИЕ РАЗЛИЧНЫХ ВИДОВ ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА
- § 1. Распадающиеся поверхности
- § 2. Цилиндрические поверхности
- § 3. Конусы второго порядка
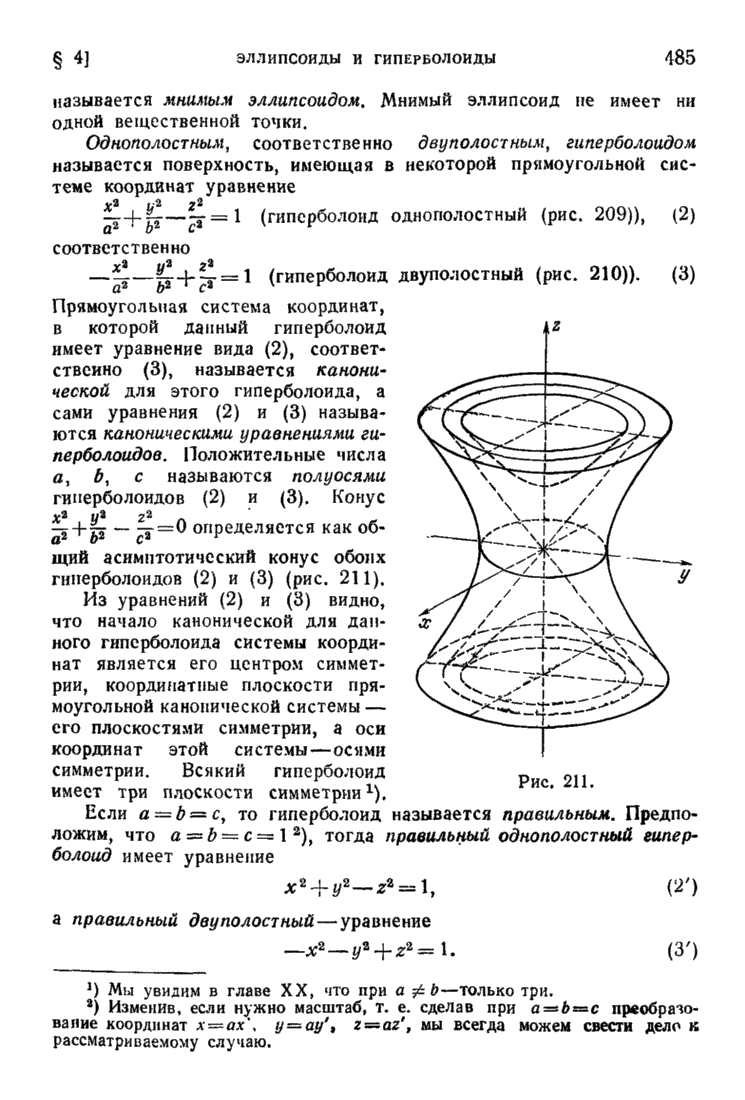
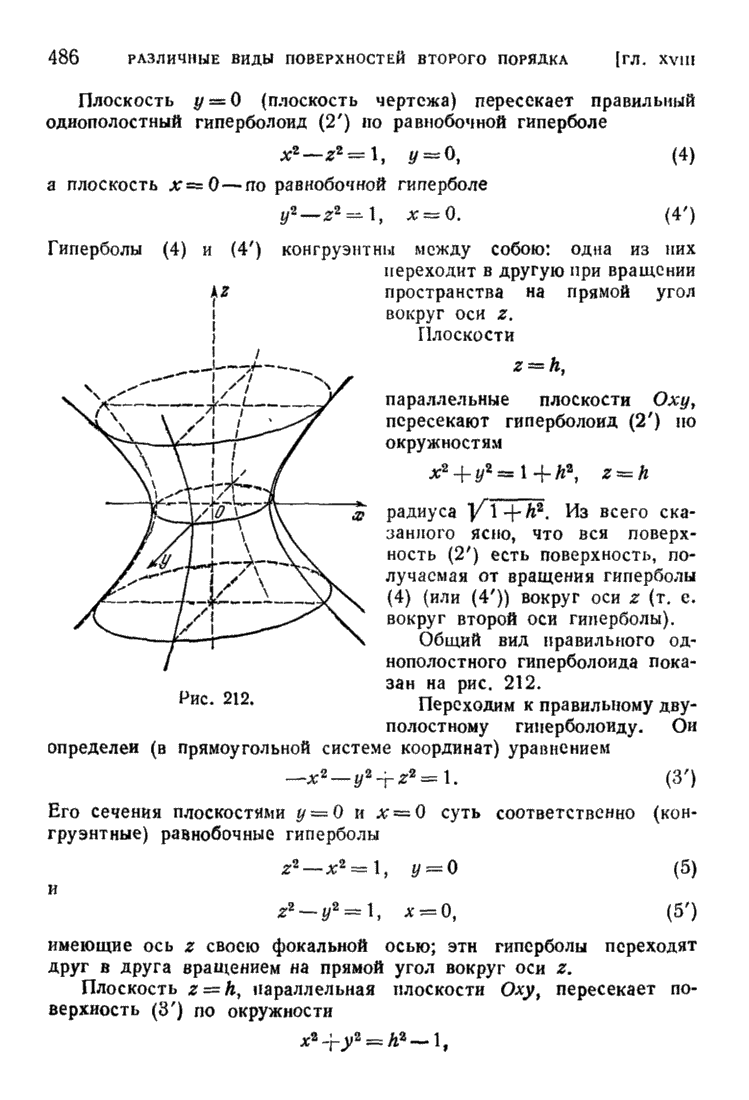
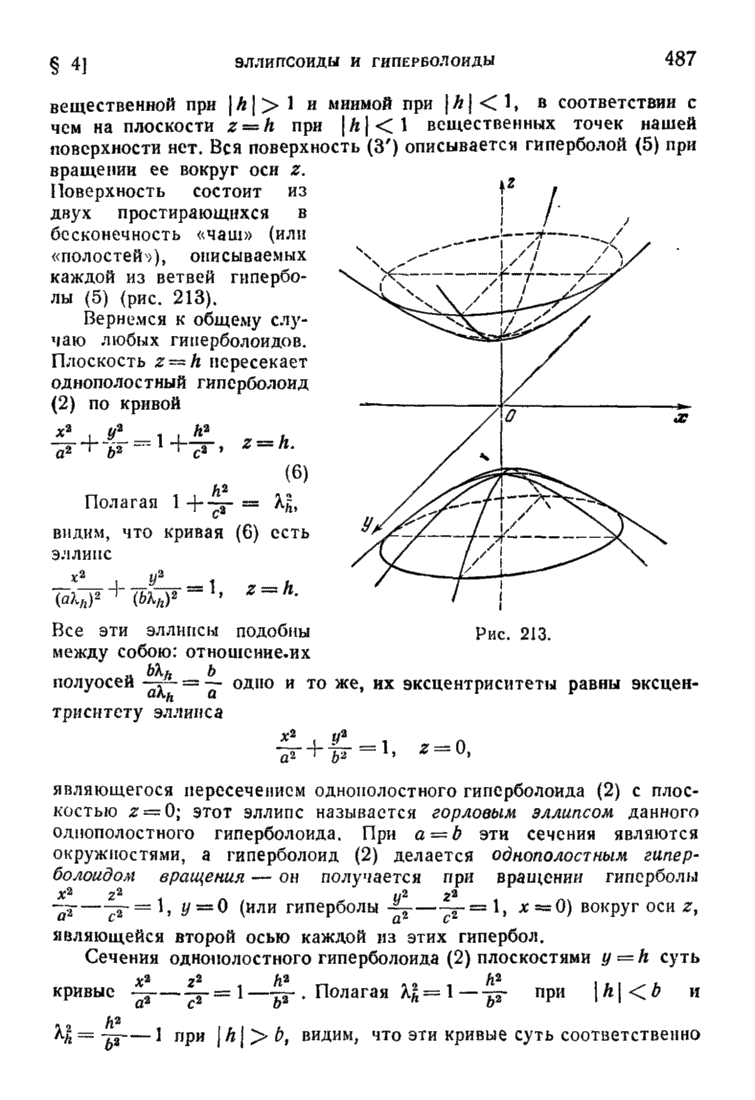
- § 4. Эллипсоиды и гиперболоиды
- § 5. Параболоиды
- § 6. Прямолинейные образующие
- ГЛАВА XIX. ОБЩАЯ ТЕОРИЯ ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА. I (ПЕРЕСЕЧЕНИЕ С ПЛОСКОСТЬЮ И С ПРЯМОЙ; АСИМПТОТИЧЕСКИЕ НАПРАВЛЕНИЯ; КАСАТЕЛЬНАЯ ПЛОСКОСТЬ; ЦЕНТР)
- § 1. Ранг и детерминант малой и большой матрицы многочлена второй степени
- § 2. Пересечение поверхности второго порядка с плоскостью
- § 3. Пересечение поверхности второго порядка с прямой. Асимптотические направления. Касательные прямые и касательная плоскость. Особые точки поверхности второго порядка
- § 4. Асимптотические направления, конус асимптотических направлений, прямолинейные образующие поверхностей второго порядка
- § 5. Центр поверхности второго порядка
- ГЛАВА XX. ОБЩАЯ ТЕОРИЯ ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА. II (ДИАМЕТРАЛЬНЫЕ ПЛОСКОСТИ; ОСОБЫЕ И ГЛАВНЫЕ НАПРАВЛЕНИЯ; АФФИННАЯ КЛАССИФИКАЦИЯ)
- § 1. Диаметральные плоскости. Особые направления
- § 2. Диаметральные плоскости поверхностей различных видов
- § 3. Сопряженные направления
- § 4. Уравнение поверхности второго порядка относительно координатной системы с сопряженными направлениями осей
- § 5. Теорема единственности
- § 6. Главные направления
- § 7. Приведение к каноническому виду уравнения поверхности второго порядка
- § 8. Аффинная классификация поверхностей второго порядка
- ГЛАВА XXI. ПРОЕКТИВНАЯ ПЛОСКОСТЬ
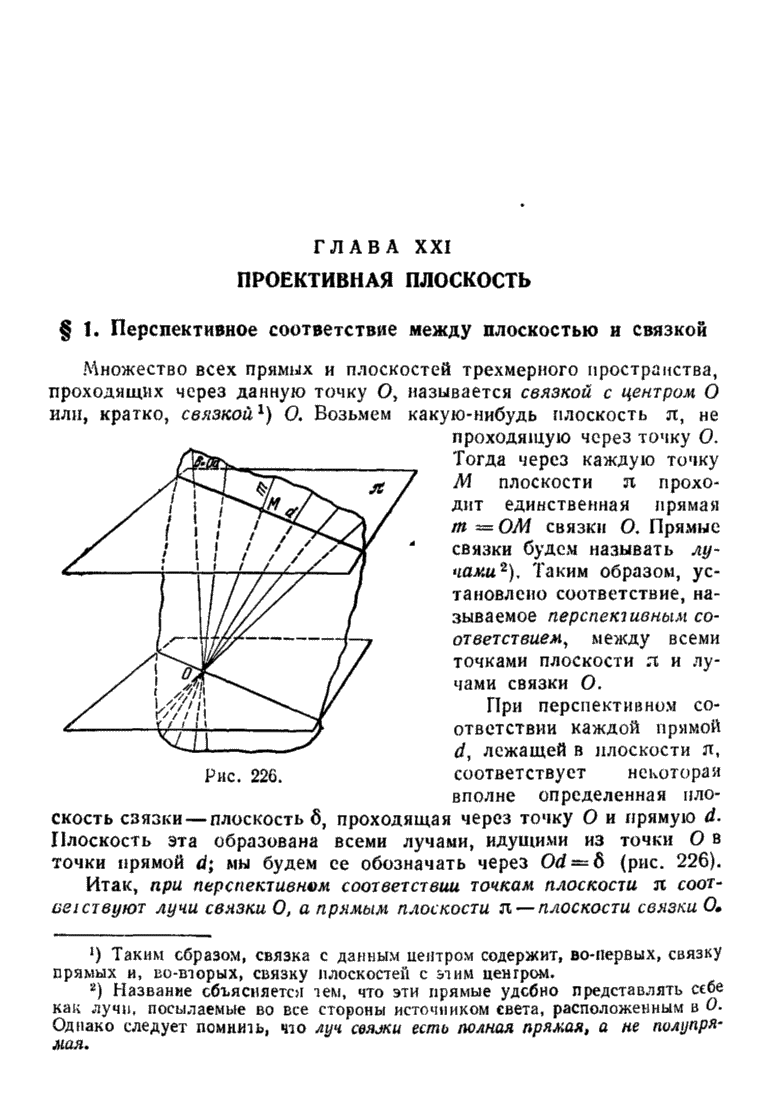
- § 1. Перспективное соответствие между плоскостью и связкой
- § 2. Однородные координаты точек на плоскости и лучел в связке
- § 3. Координаты прямой; арифметическая проективная плоскость; общее определение проективной плоскости
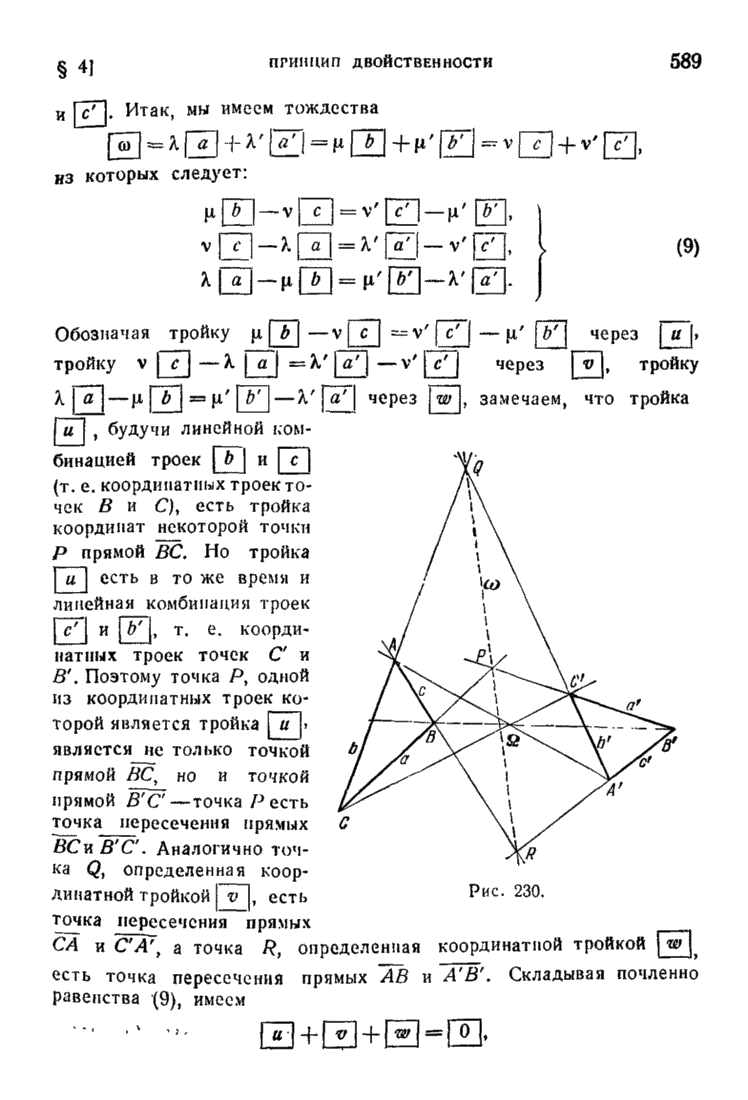
- § 4. Принцип двойственности для проективной плоскости
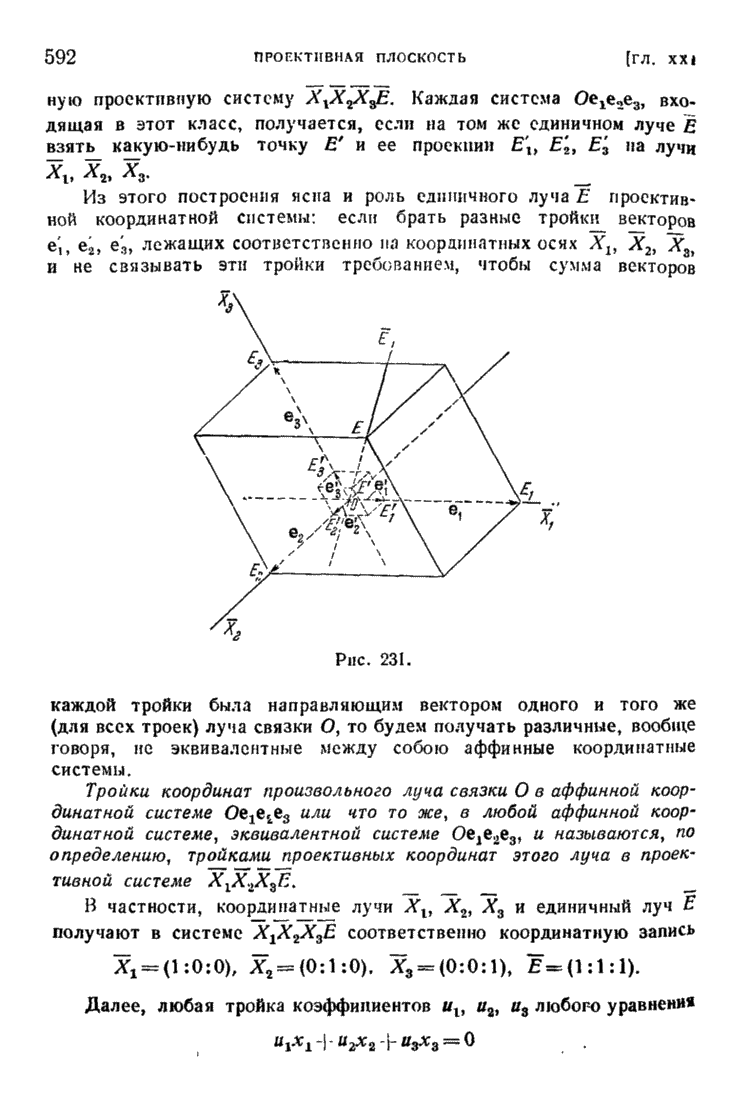
- § 5. Проективная система координат в связке и на проективной плоскости
- § 6. Проективные преобразования и отображения проективной плоскости
- § 7. Проективные координаты на прямой. Проективные отображения прямой
- § 8. Двойное отношение
- ГЛАВА XXII. КРИВЫЕ ВТОРОГО ПОРЯДКА НА ПРОЕКТИВНОЙ ПЛОСКОСТИ
- § 1. Определение. Теорема единственности
- § 2. Пересечение кривой второго порядка с прямой. Касательные; асимптоты
- § 3. Пучок кривых второго порядка. Второе доказательство теоремы единственности. Теорема Паскаля. Теорема Штейнера
- § 4. Поляры и полюсы
- § 5. Коррелятивное, в частности полярное, соответствие. Тангенциальное уравнение кривой
- § 6. Диаметры как поляры несобственных точек
- § 7. Автополярный треугольник
- § 8. Проективная классификация кривых второго порядка
- ГЛАВА XXIII. НАЧАЛЬНЫЕ СВЕДЕНИЯ ИЗ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ ПРОЕКТИВНОГО ПРОСТРАНСТВА
- § 1. Проективное пространство; его плоскости и прямые
- § 2. Проективные координаты. Проективные преобразования.
- § 3. Понятие об n-мерном проективном пространстве
- § 4. Поверхности второго порядка в проективном пространстве. Теорема единственности
- § 5. Пересечение поверхности второго порядка с плоскостью и с прямой. Касательные прямые. Касательная плоскость. Прямолинейные образующие
- § 6. Полюсы и полярные плоскости
- § 7. Проективная классификация поверхностей второго порядка
- § 8. Распределение по проективным классам поверхностей различных аффинных классов. Проективно-аффинная классификация поверхностей второго порядка
- ГЛАВА XXIV. ЕВКЛИДОВО n-МЕРНОЕ ПРОСТРАНСТВО
- § 1. Введение. Ортогональные матрицы
- § 2. Положительно определенные симметричные билинейные функции в векторном пространстве
- § 3. Определение евклидовых пространств и простейших относящихся к ним понятий
- § 4. Неравенство Коши—Буняковского и его следствия. Углы
- § 5. Подпространства евклидовых пространств. Ортогональное дополнение к данному подпространству
- ГЛАВА XXV. ЛИНЕЙНЫЕ ОПЕРАТОРЫ, БИЛИНЕЙНЫЕ И КВАДРАТИЧНЫЕ ФУНКЦИИ В ЕВКЛИДОВЫХ ПРОСТРАНСТВАХ. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
- § 1. Инвариантные подпространства и собственные векторы линейного оператора в любом векторном пространстве
- § 2. Ортогональные преобразования n-мерного евклидова пространства
- § 3. Движения трехмерного евклидова пространства
- § 4. Преобразования подобия. Дальнейшие проблемы
- § 5. Самосопряженные операторы
- § 6. Теорема о структуре произвольного линейного преобразования евклидова пространства
- § 7. Билинейные и квадратичные формы в евклидовых пространствах
- § 8. (n-1)-мерные многообразия (поверхности) второго поряд] в -мерном аффинном и евклидовом пространствах
- ПРИБАВЛЕНИЕ. ПЕРЕСТАНОВКИ, МНОЖЕСТВА И ИХ ОТОБРАЖЕНИЯ; ГРУППЫ
- § 1. Перестановки
- § 2. Множества
- § 3. Отображения или функции
- § 4. Разбиение множества на подмножества. Отношение эквивалентности
- § 5. Определение группы
- § 6. Простейшие теоремы о группах
- § 7. Эквивалентность подмножеств данного множества по отношению к дайной группе его преобразований
- ЗАДАЧИ
- Задачи к главе IV
- Задачи к главе V
- Задачи к главе VI
- Задачи к главе VIII
- Задачи к главе IX
- Задачи к главе X
- Задачи к главе XI
- Задачи к главе XII
- Задачи к главе XIII
- Задачи к главе XIV
- Задачи к главе XV
- Задачи к главам XVI и XVII
- Задачи к главе XVIII
- Задачи к главам XIX и XX
- Задачи к главе XXI
- Задачи к главе XXII