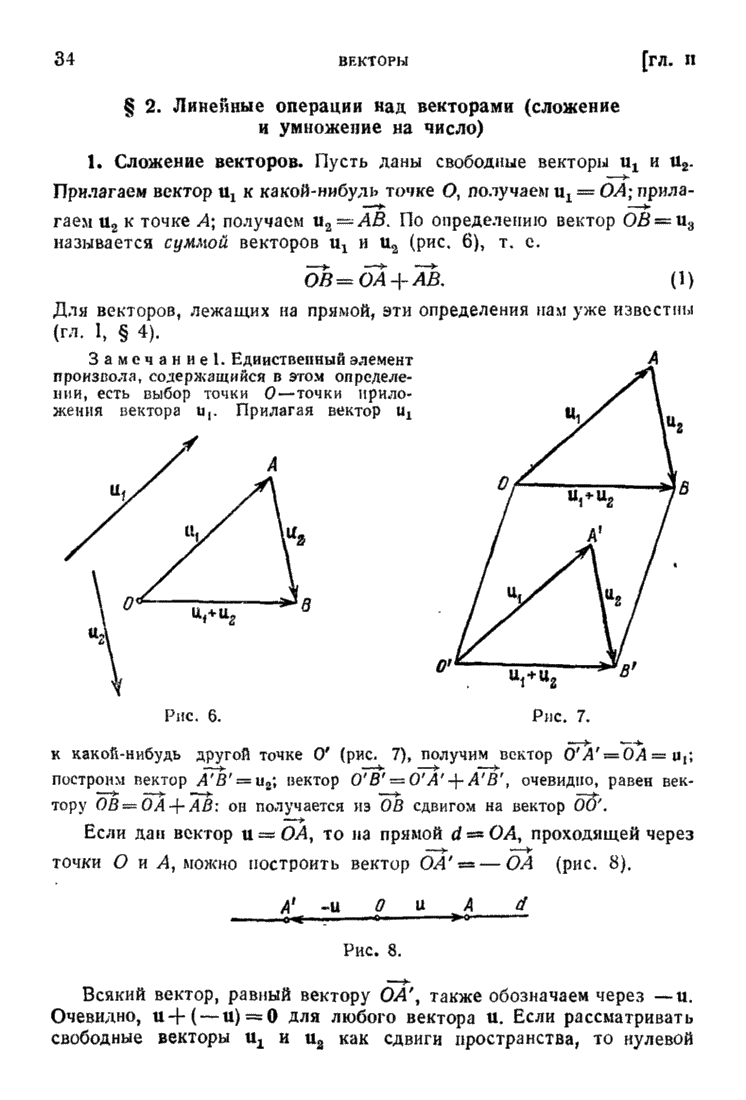
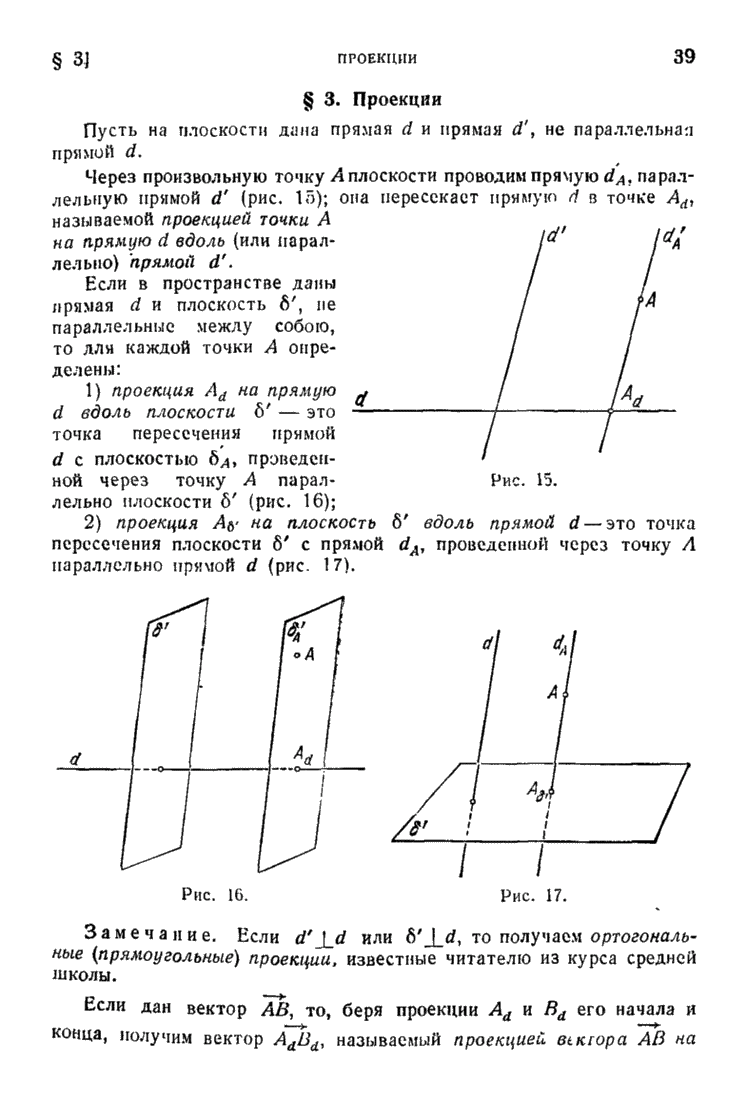
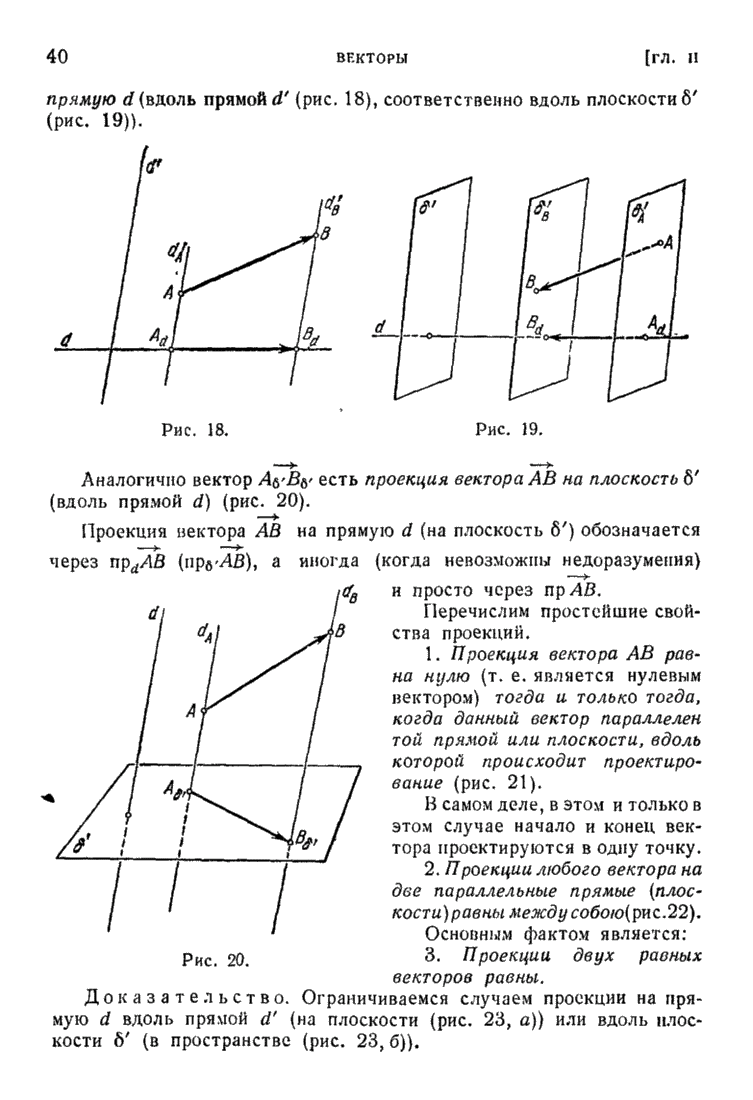
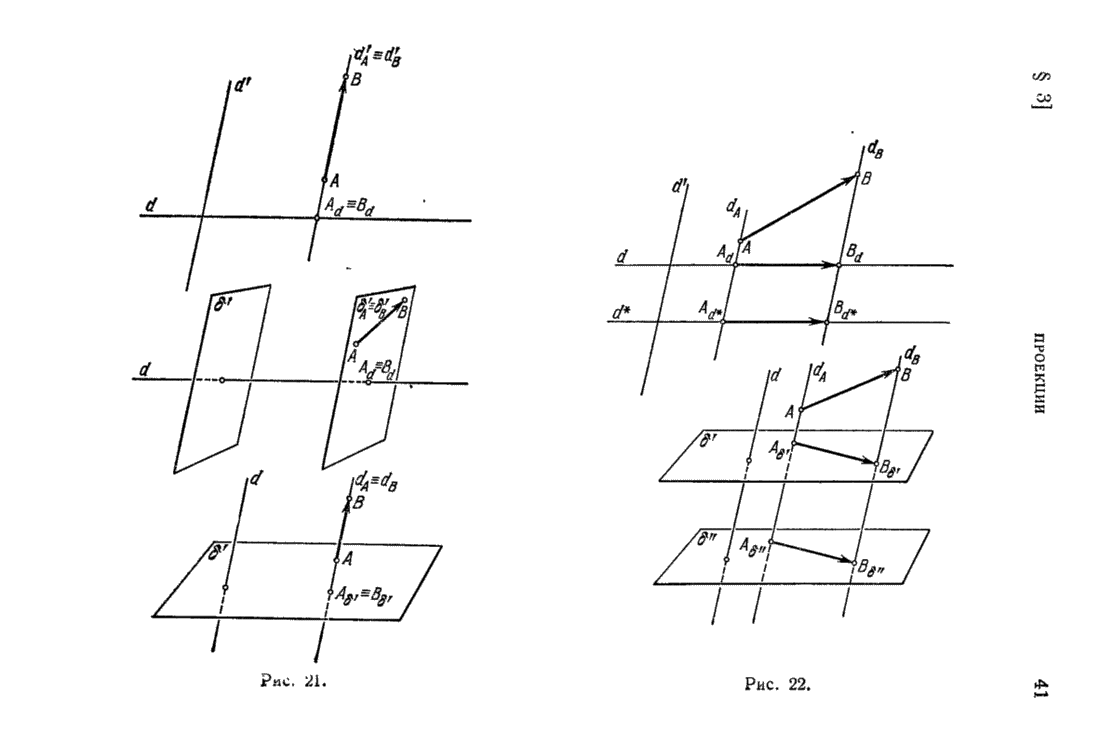
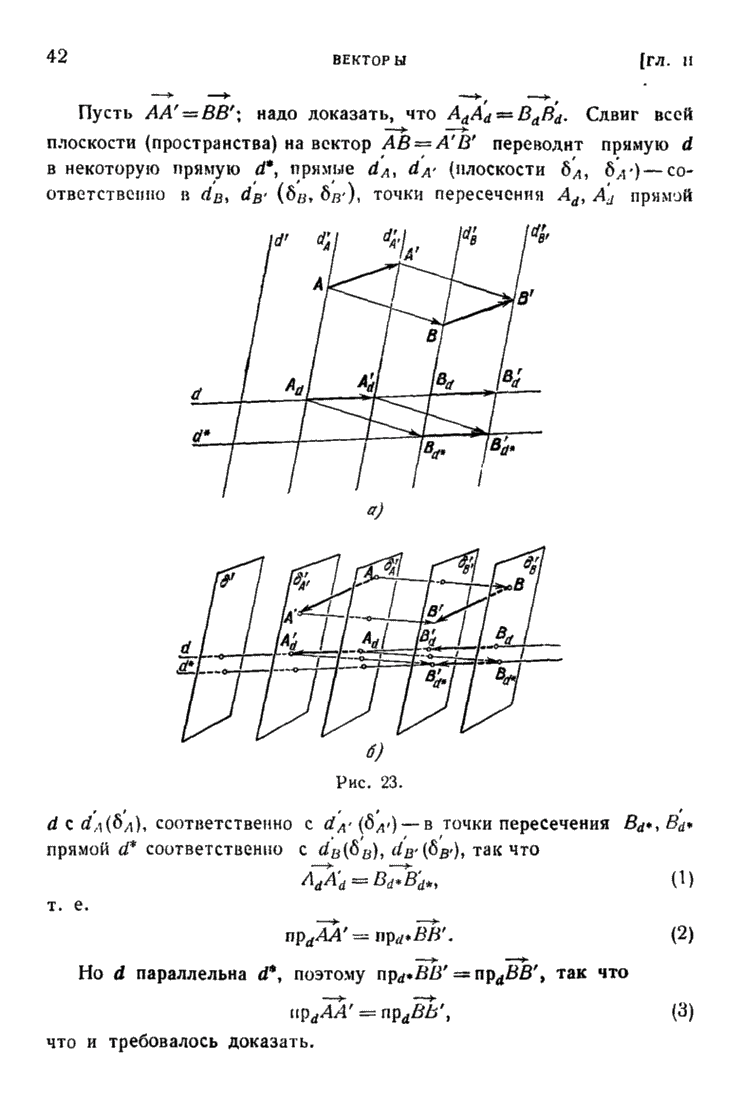
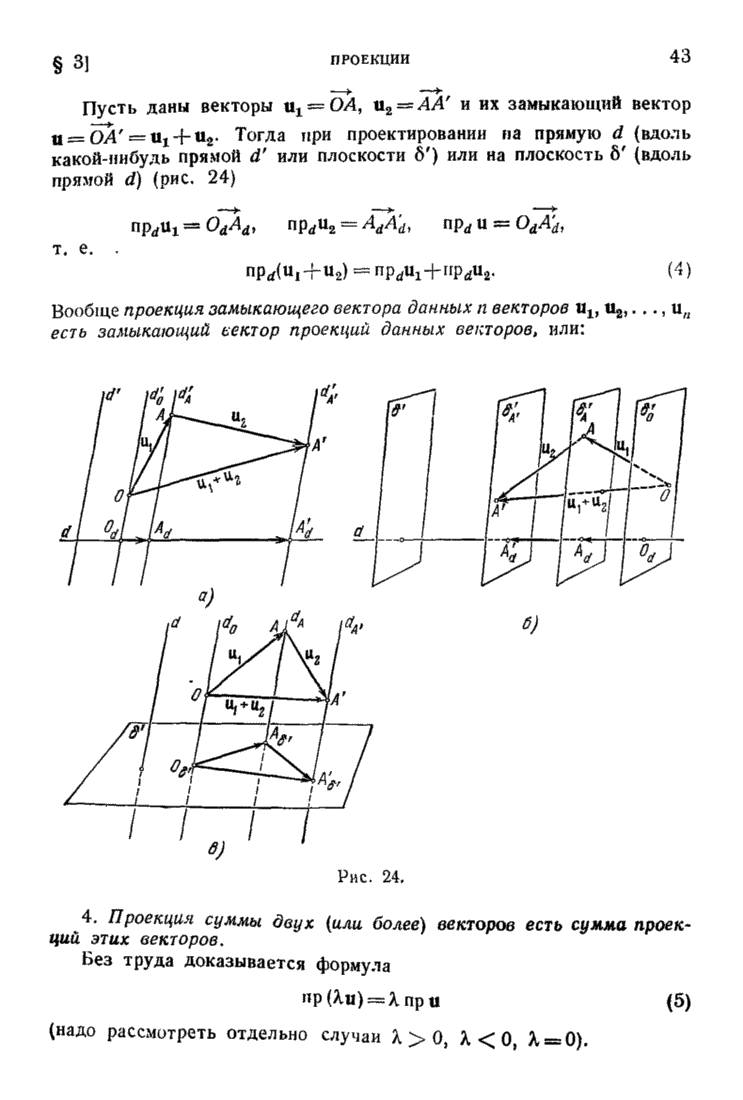
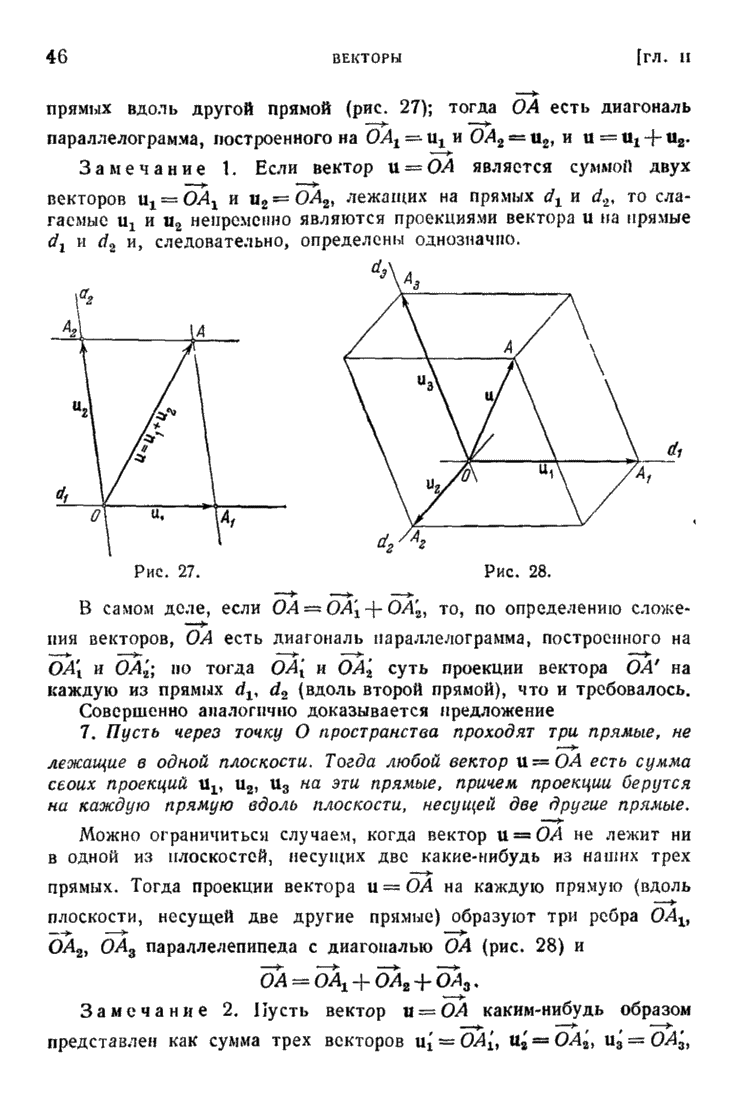
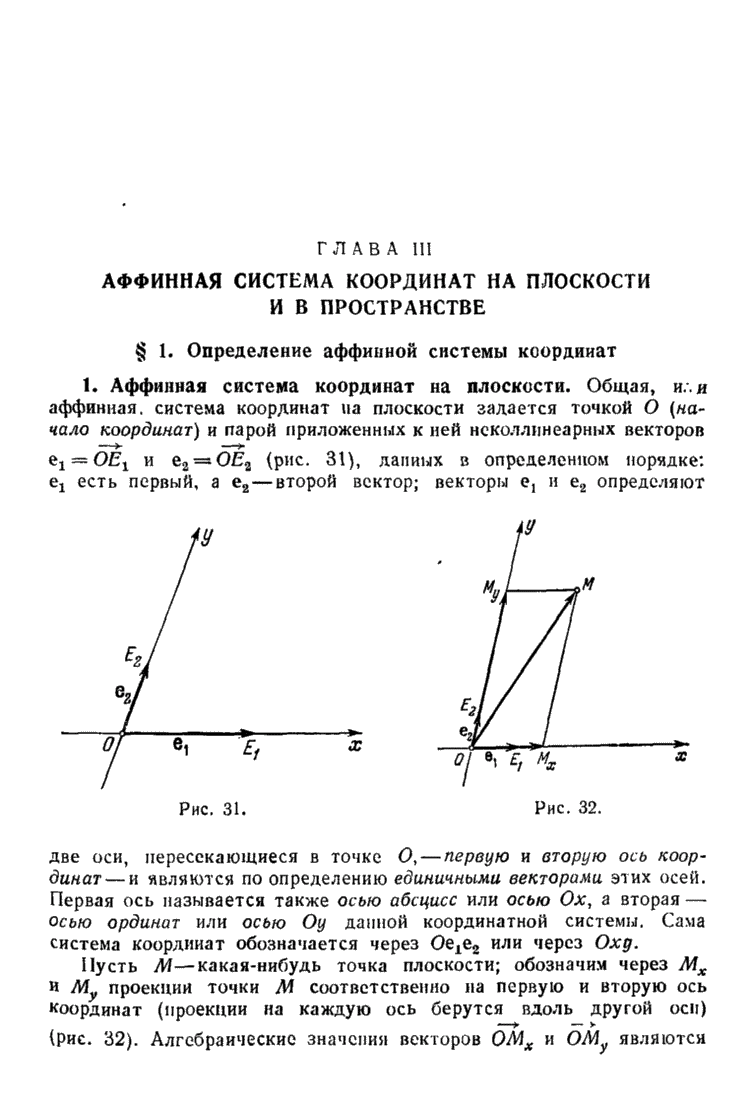
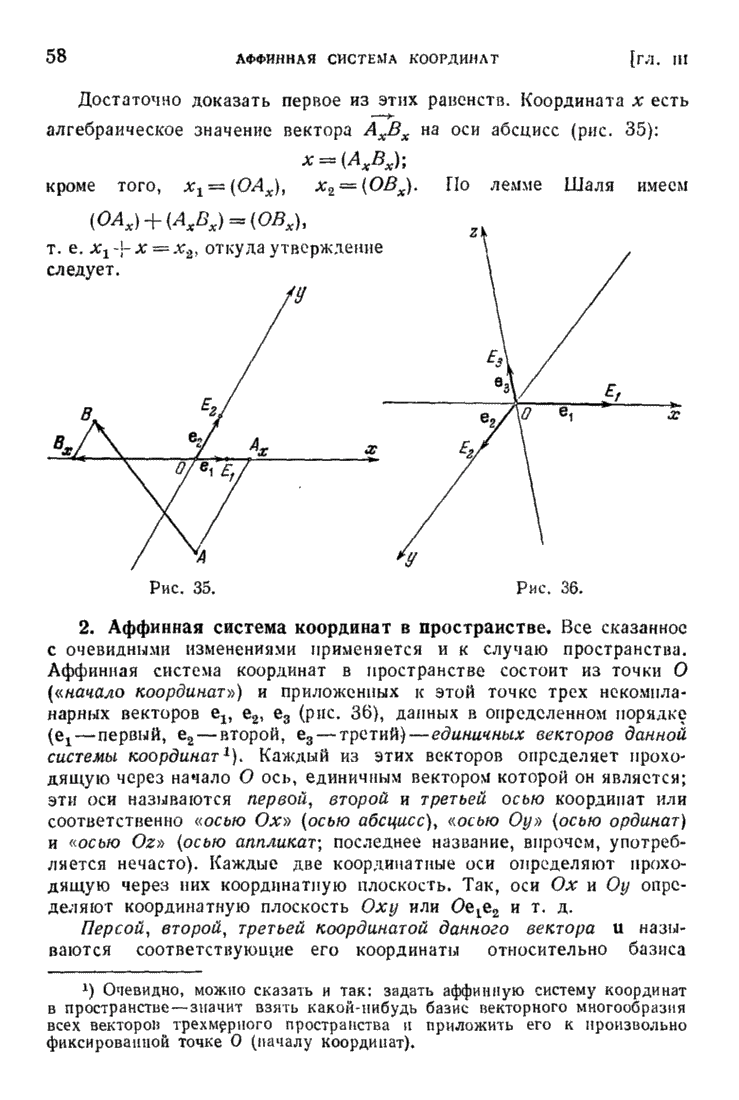
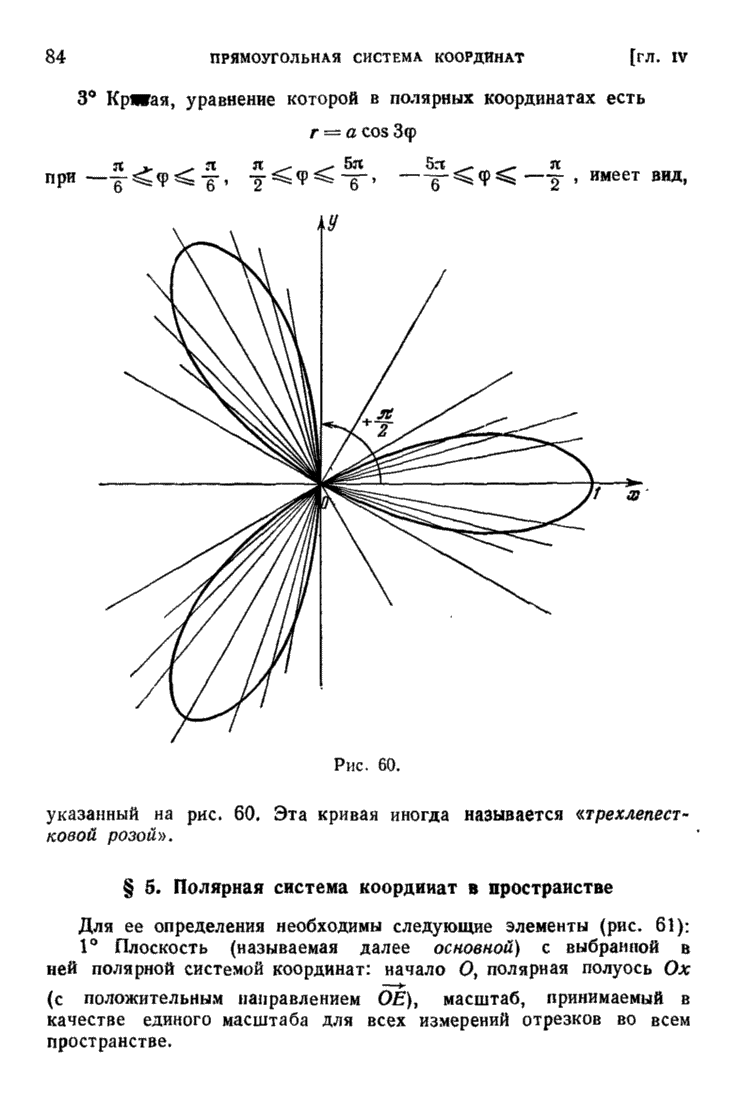
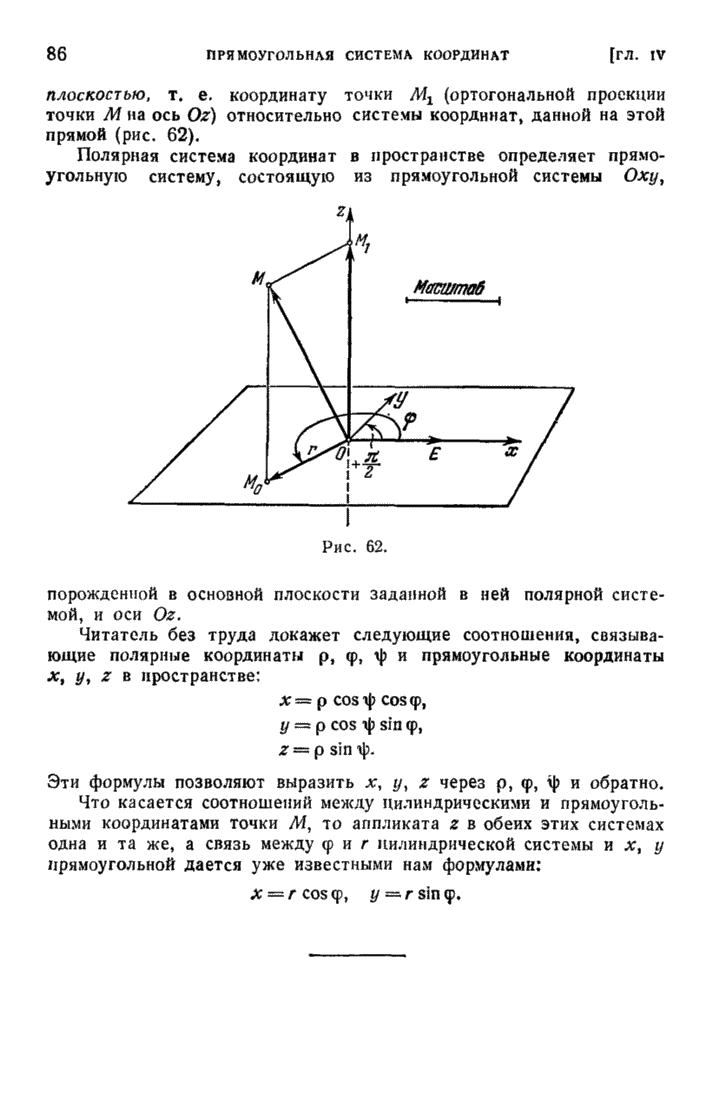
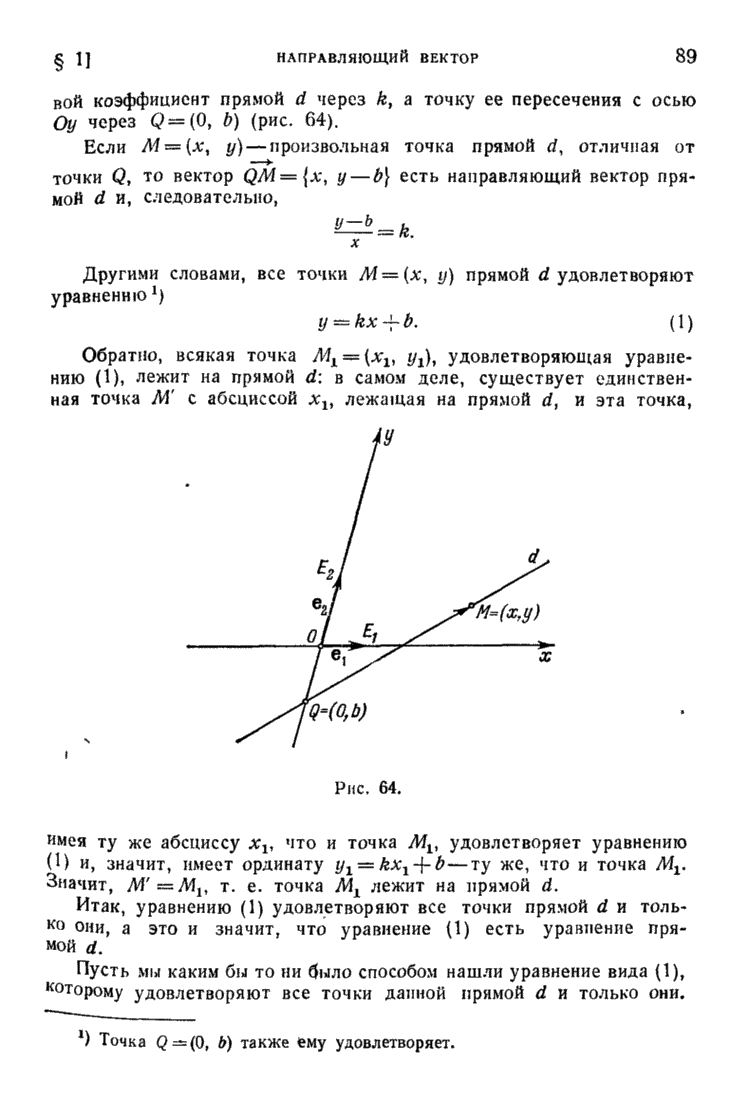
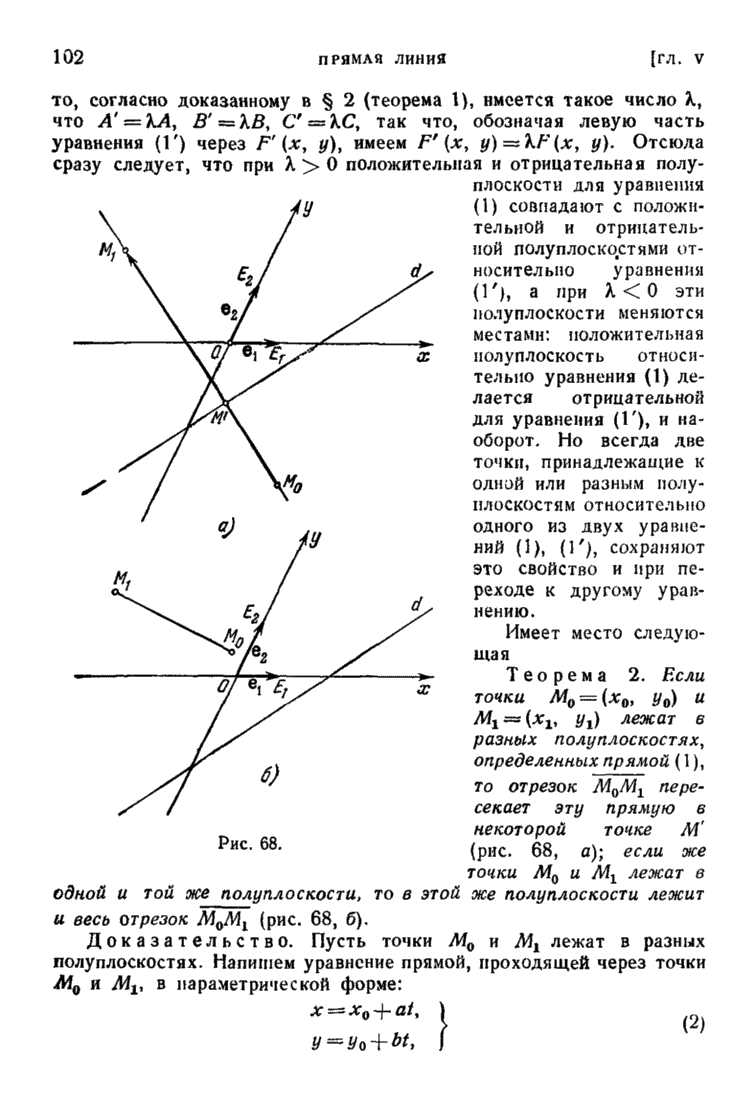
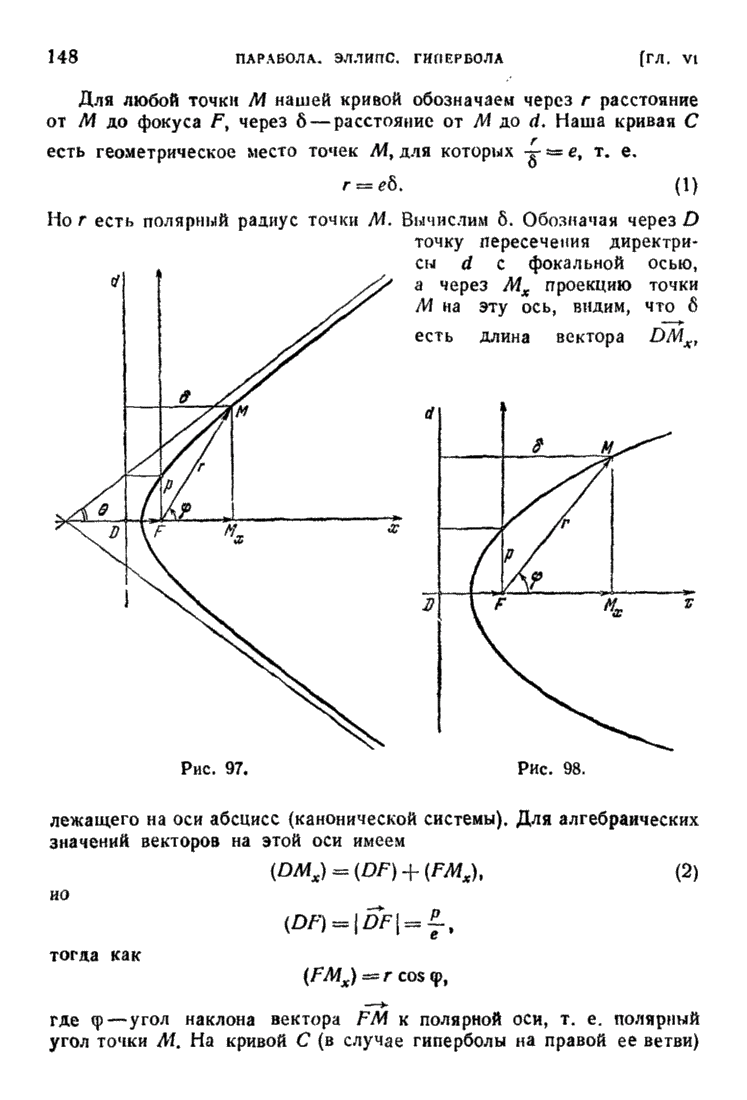
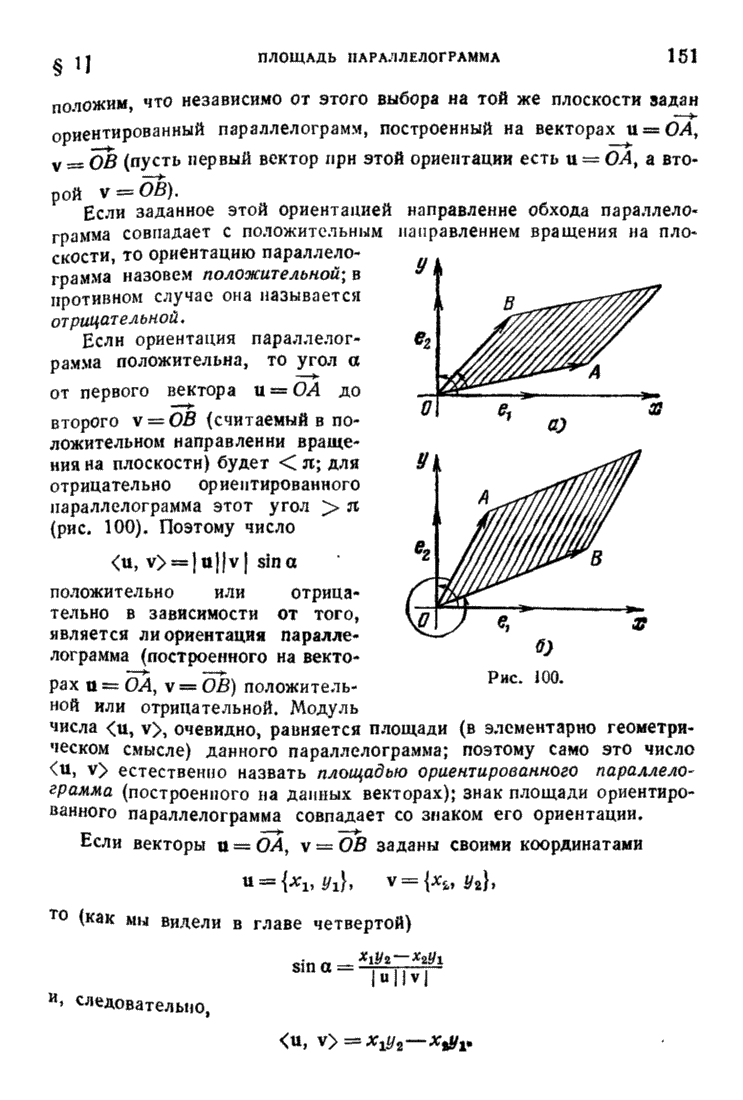
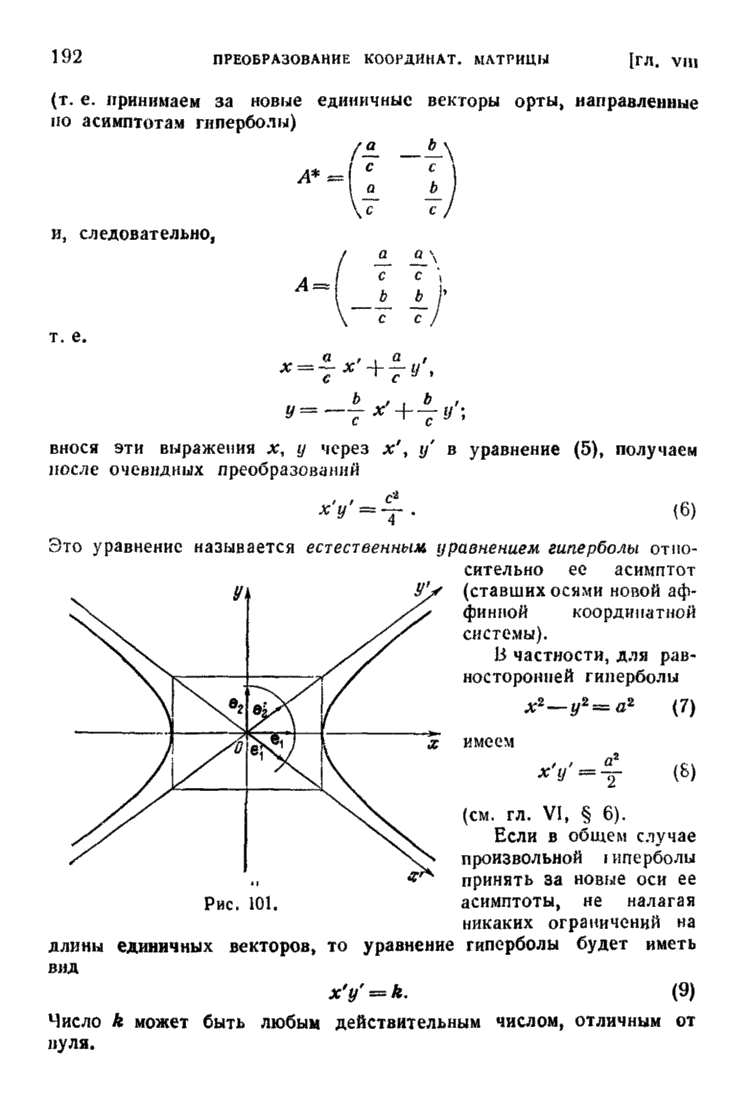
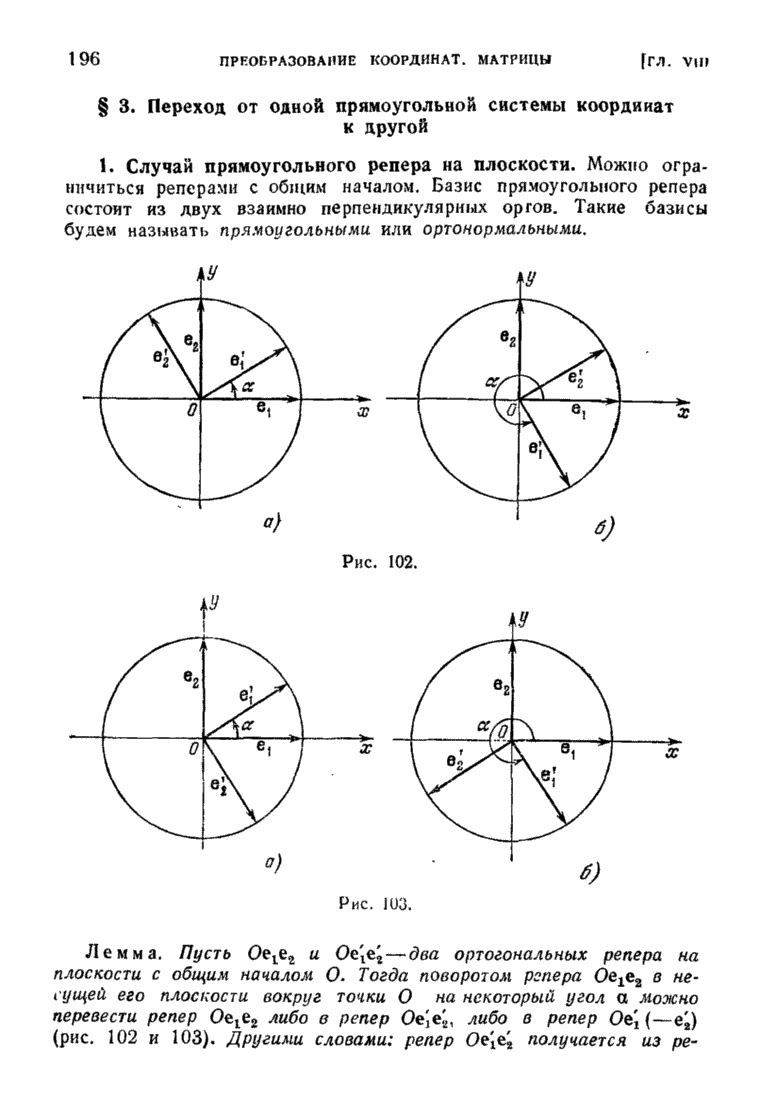
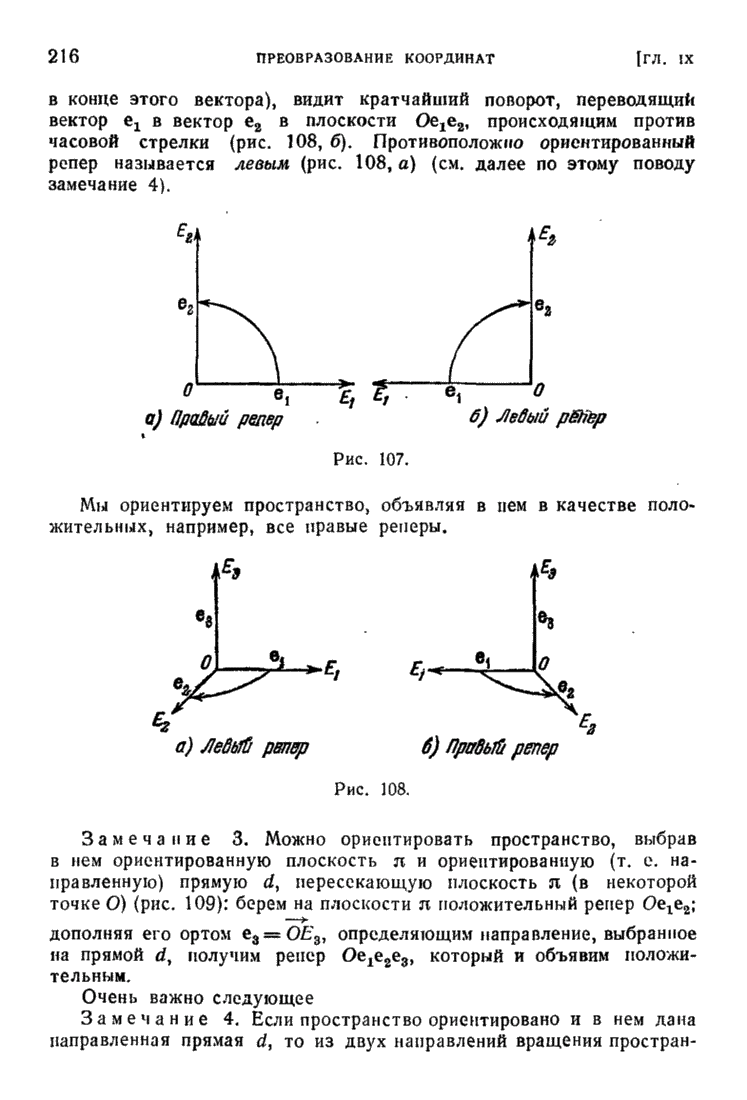
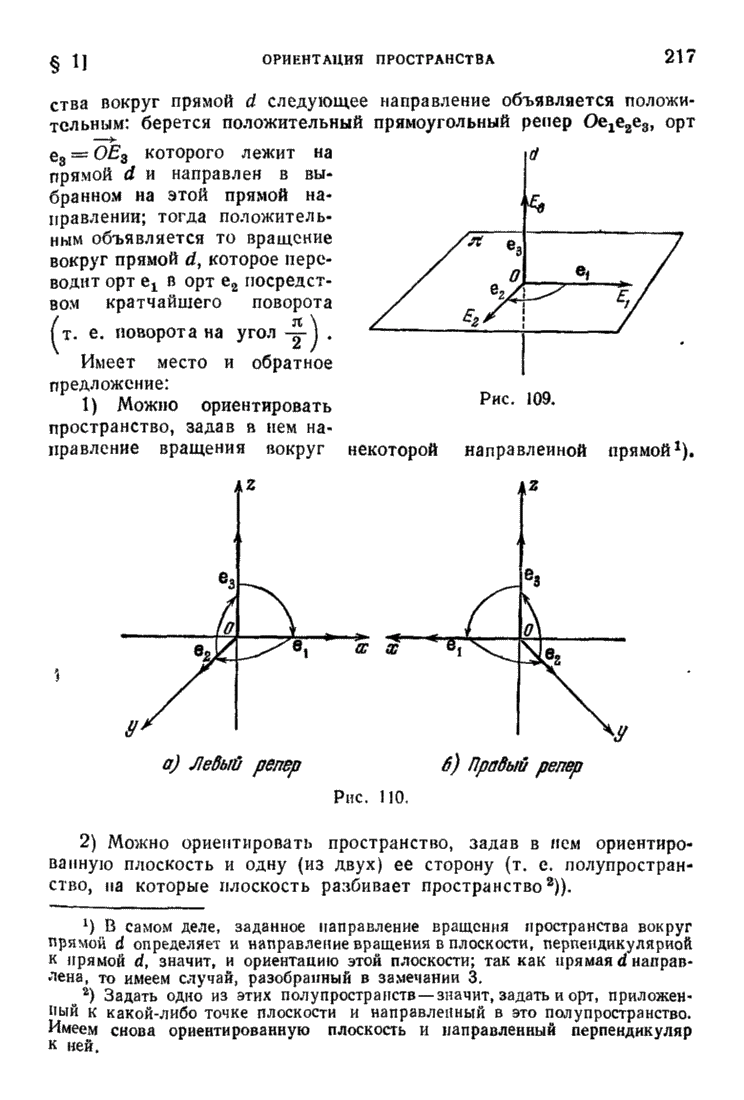
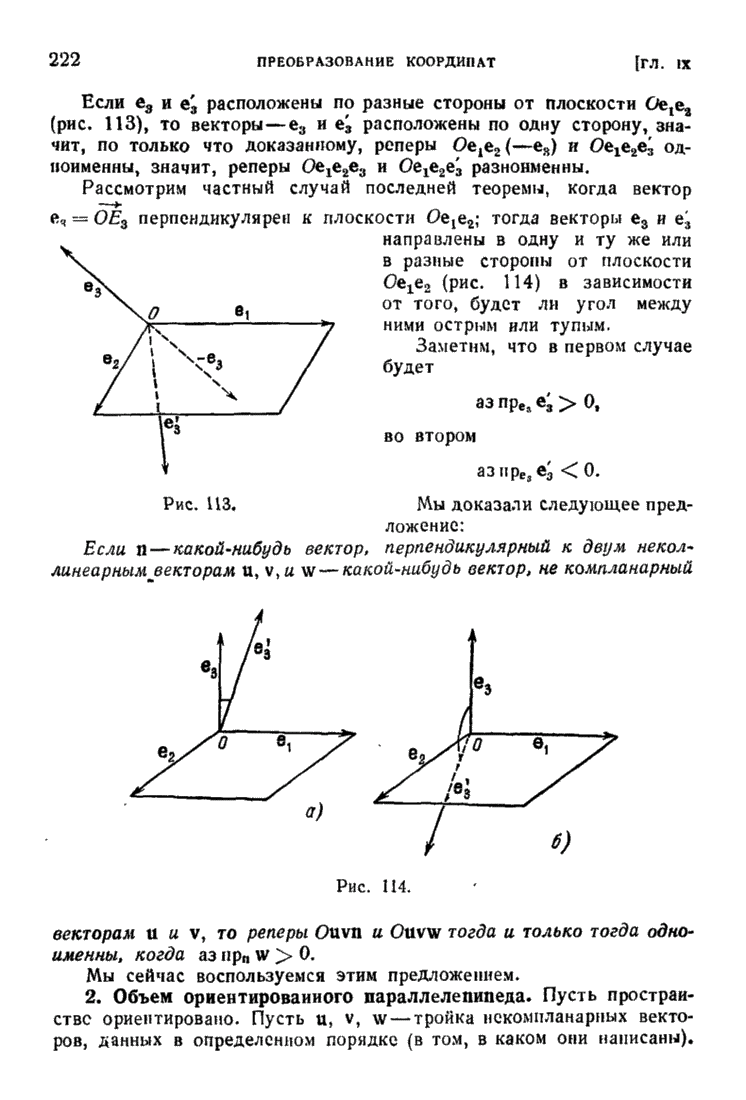
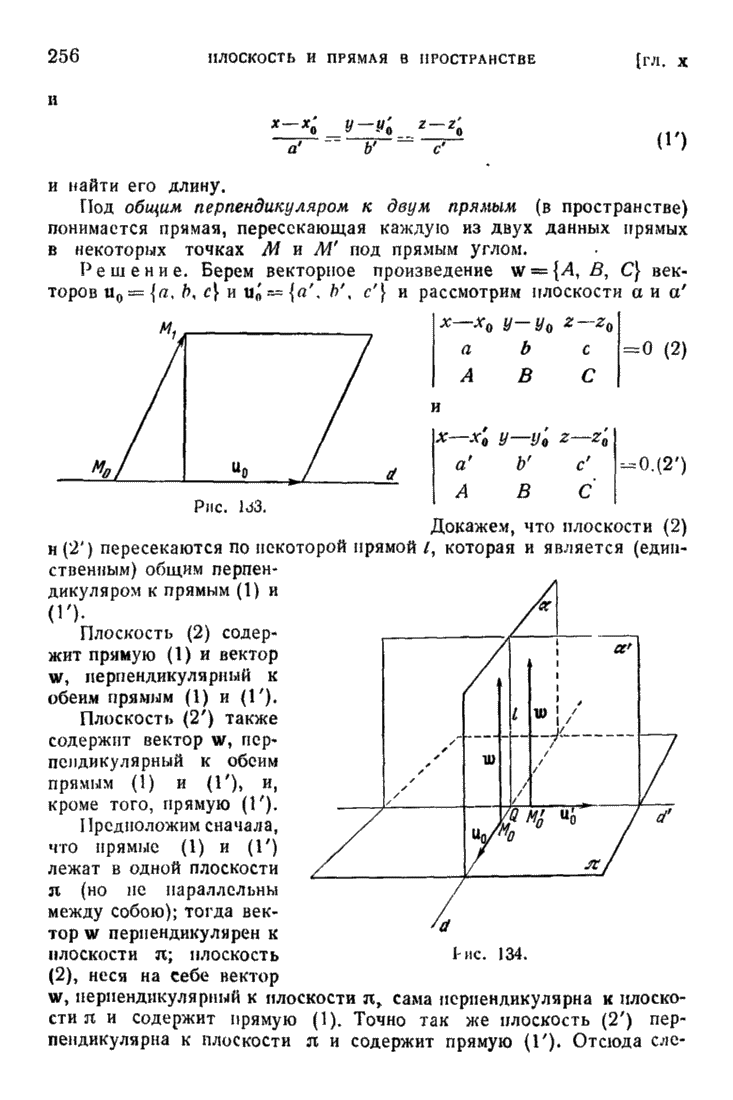
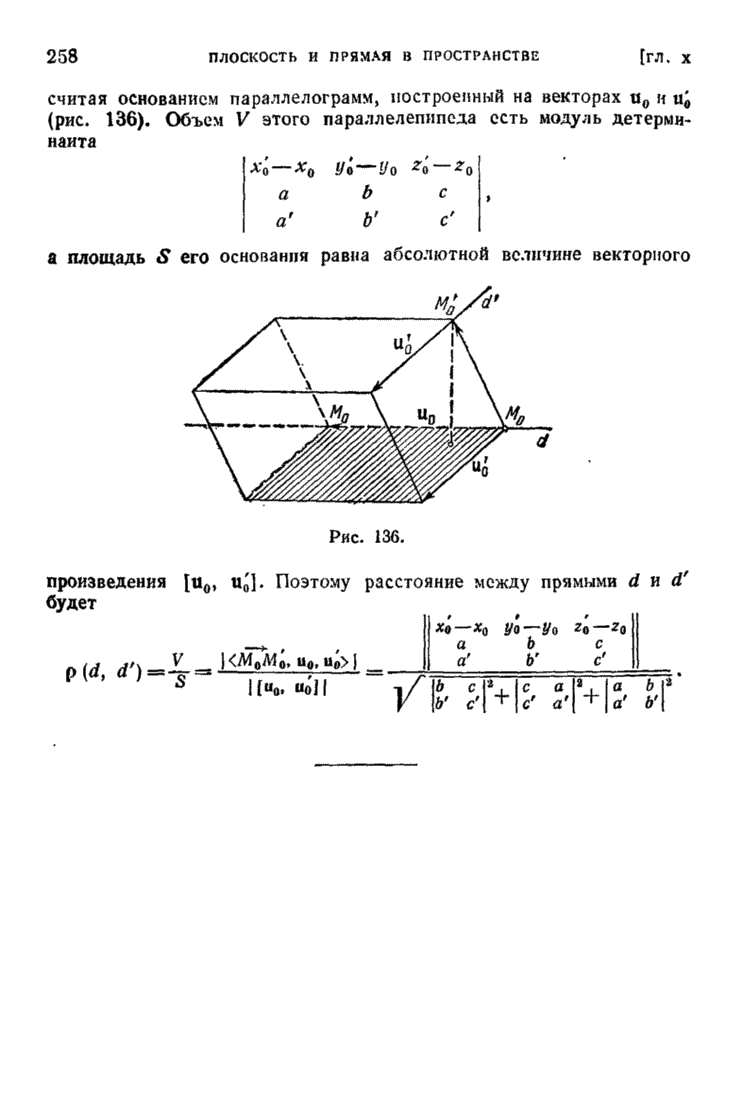
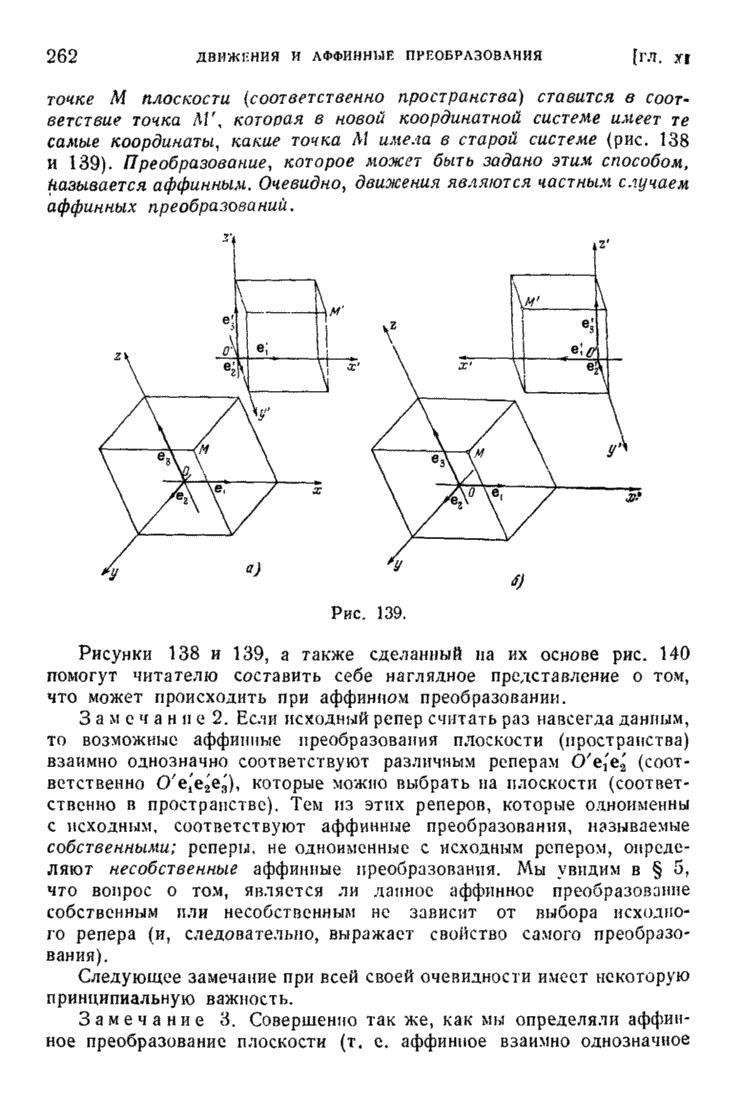
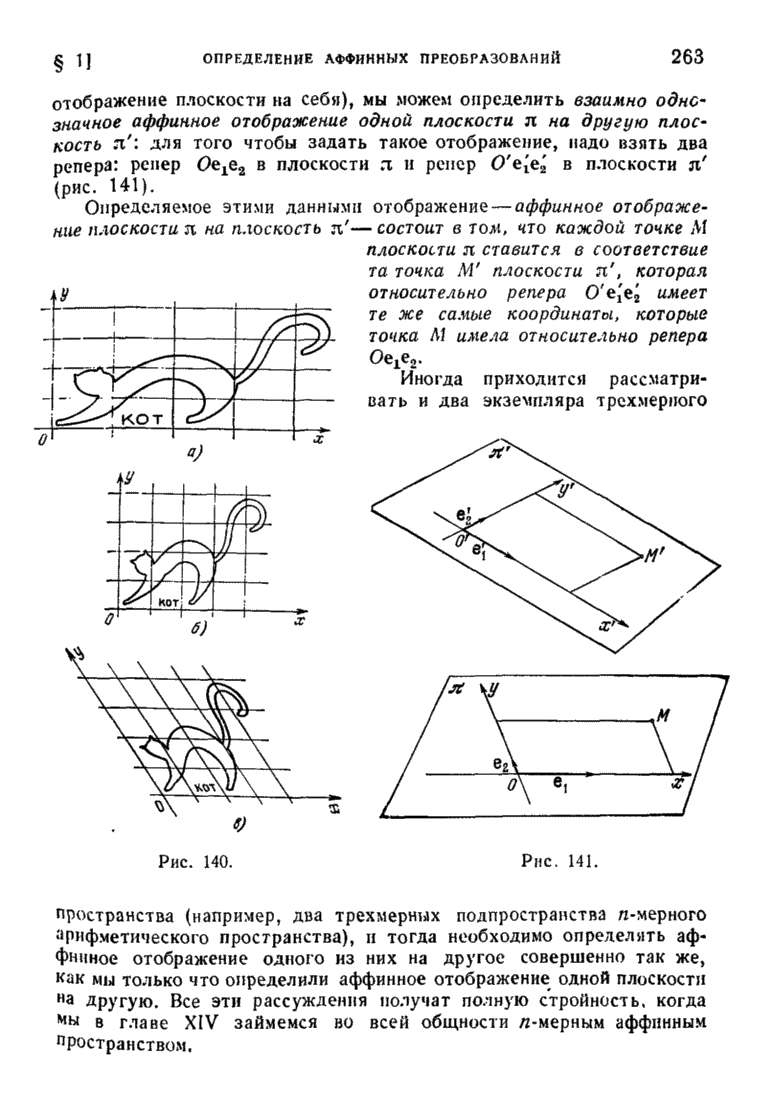
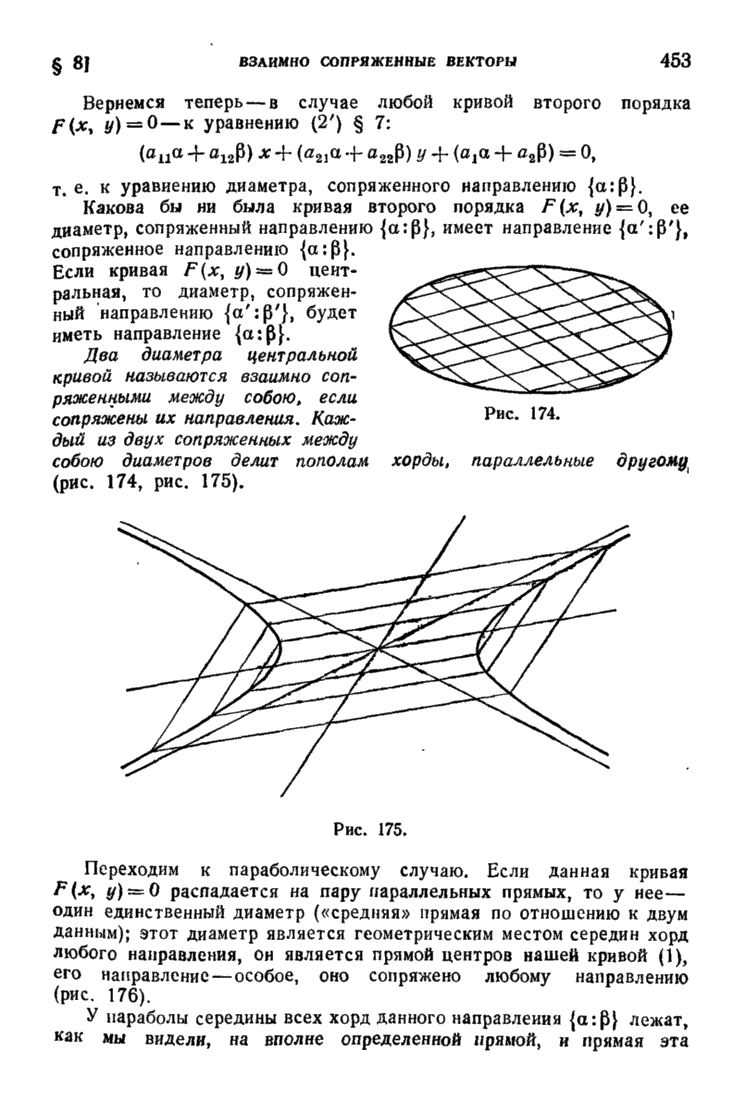
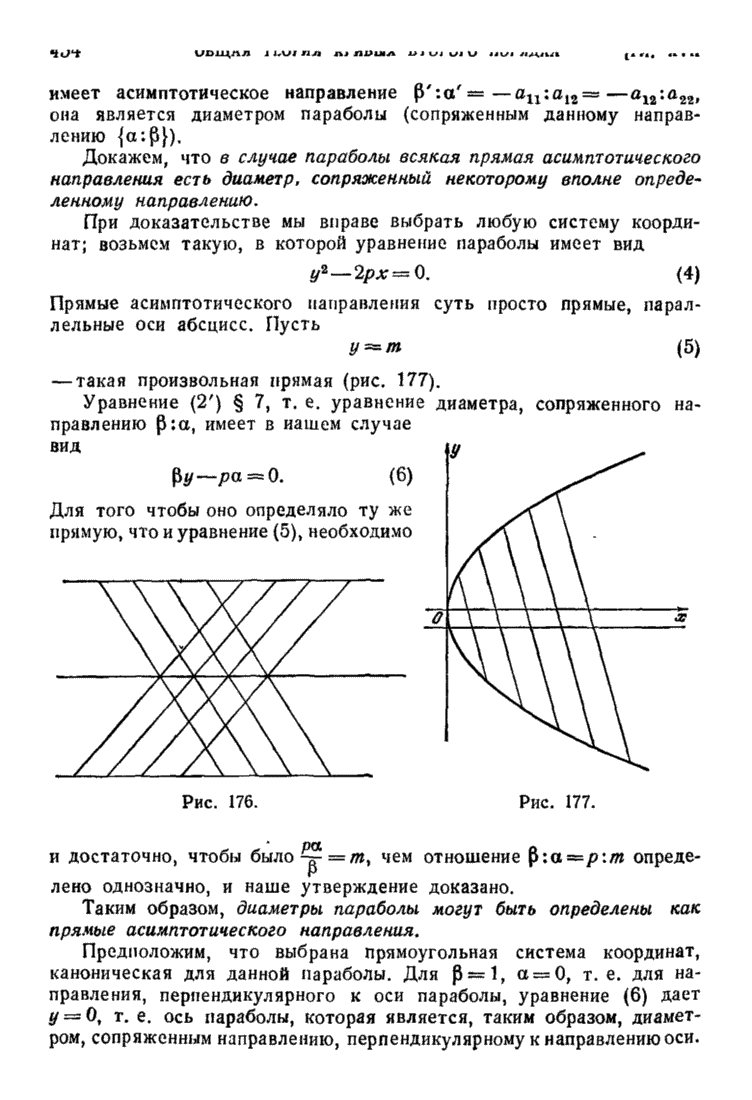
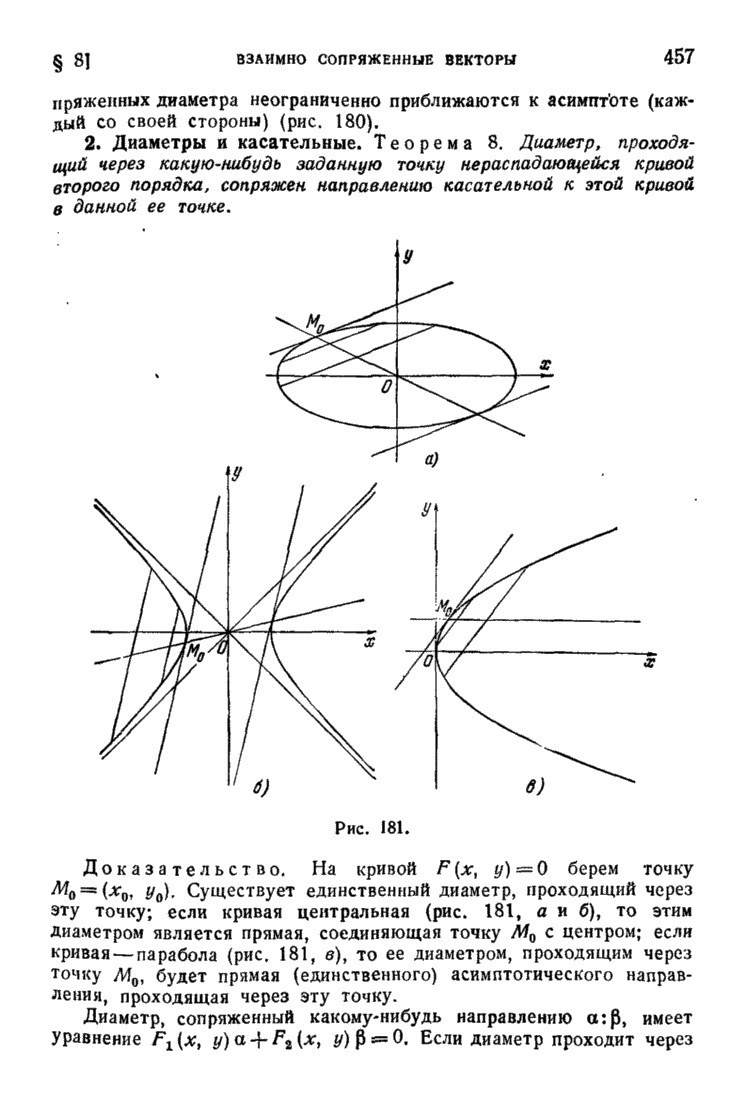
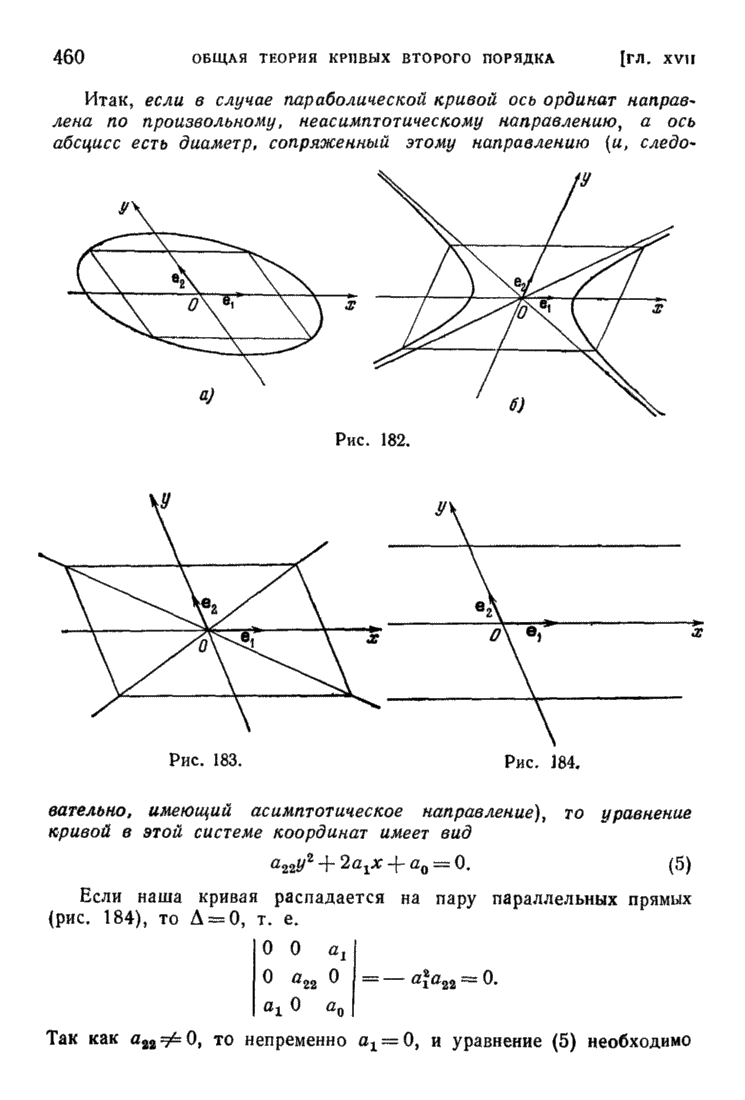
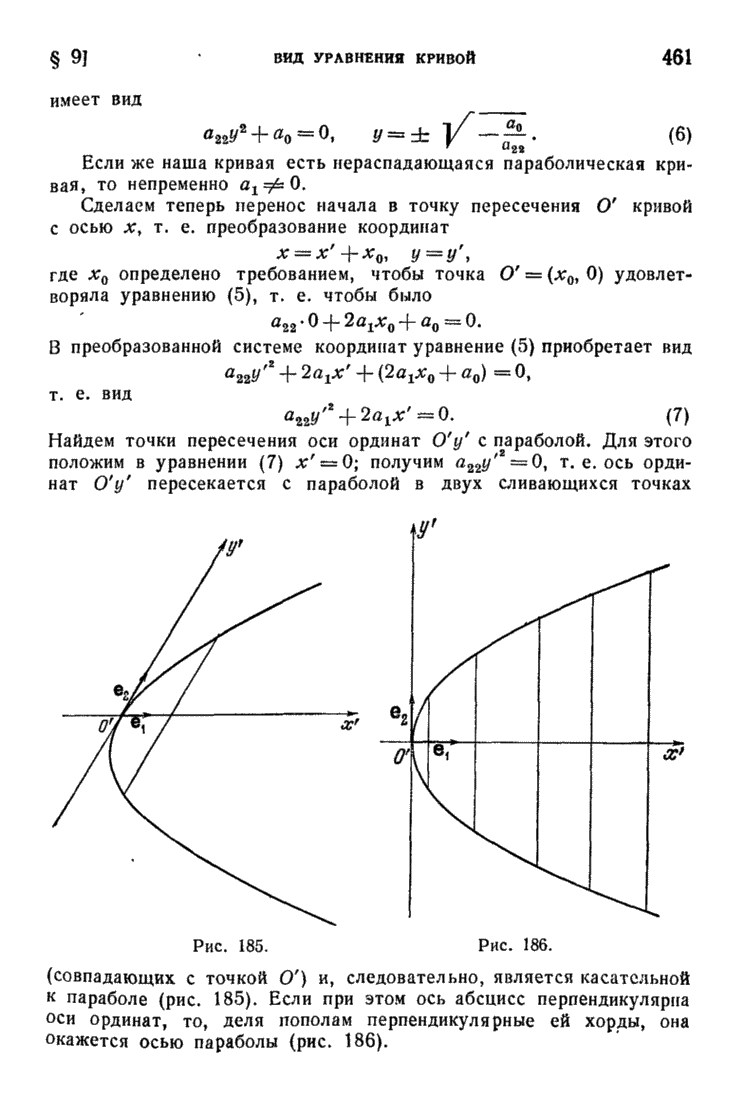
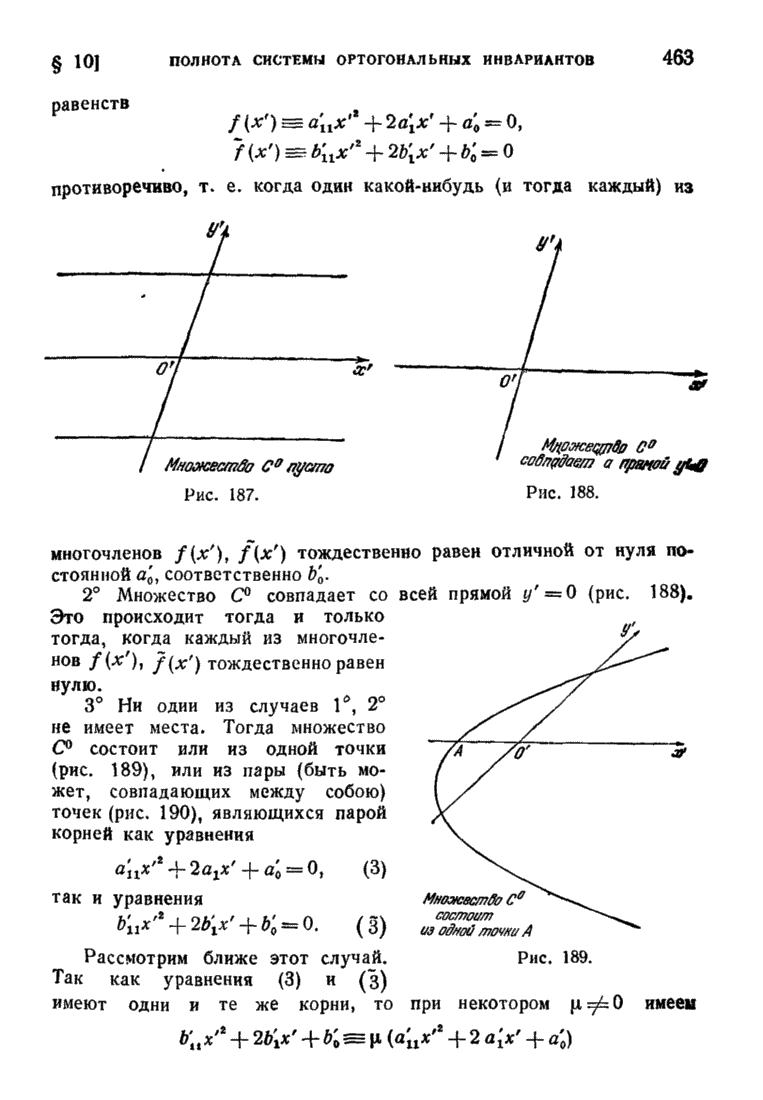
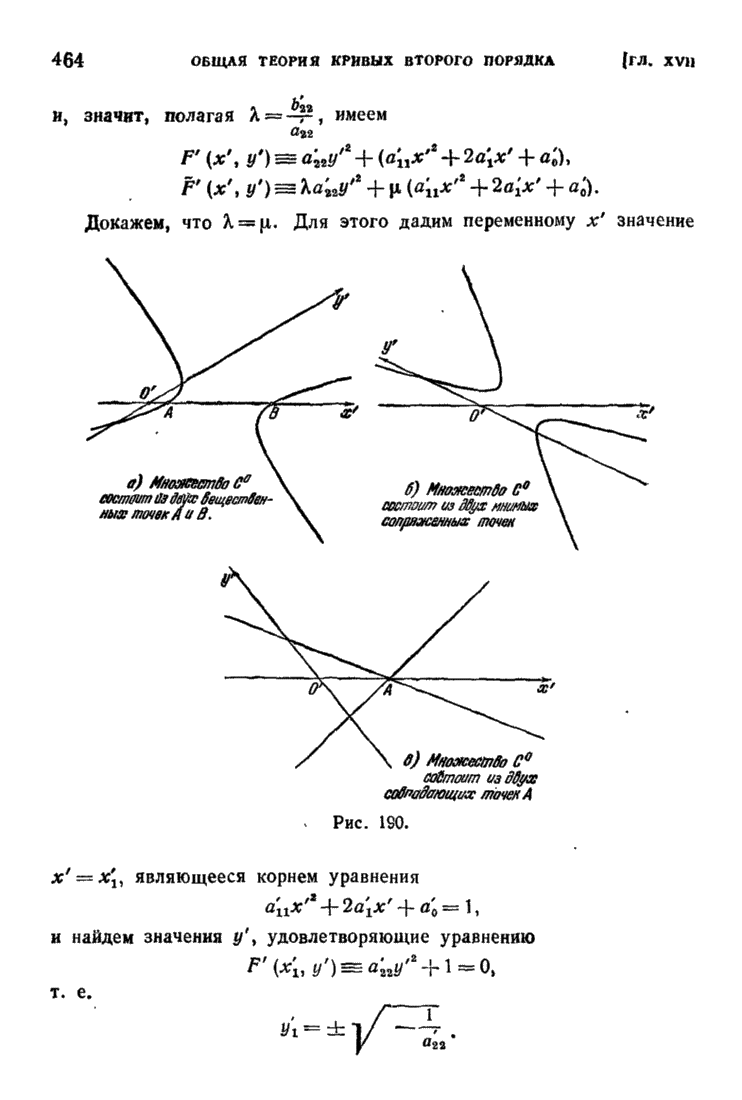
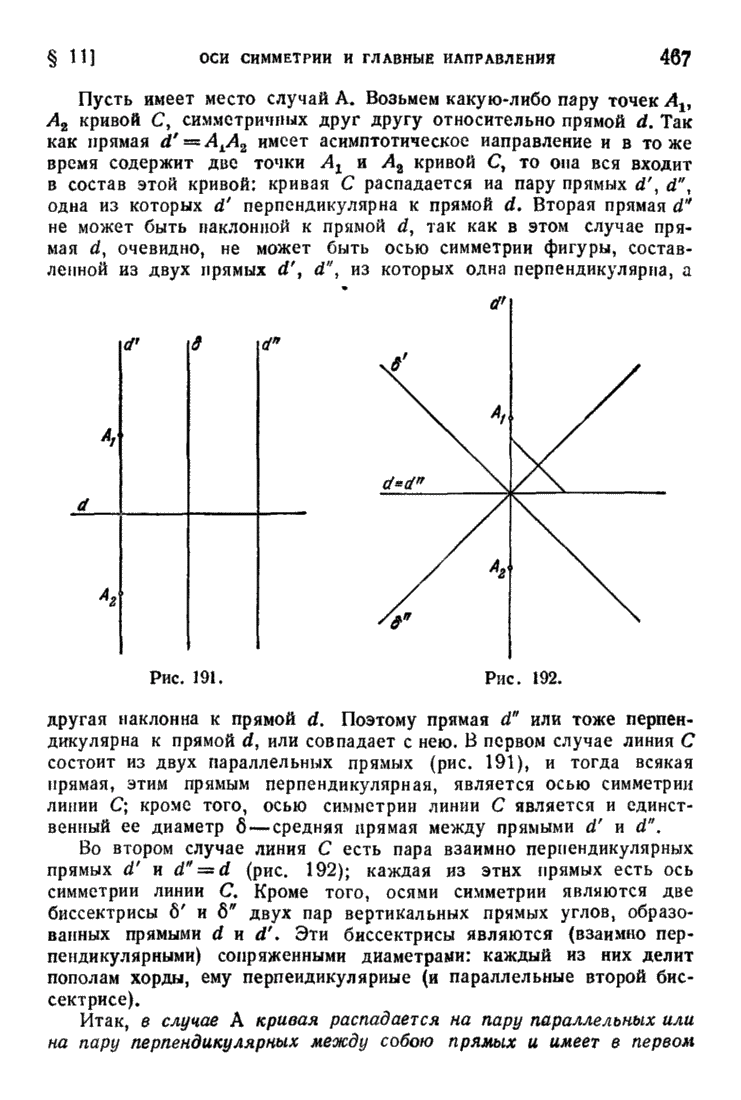
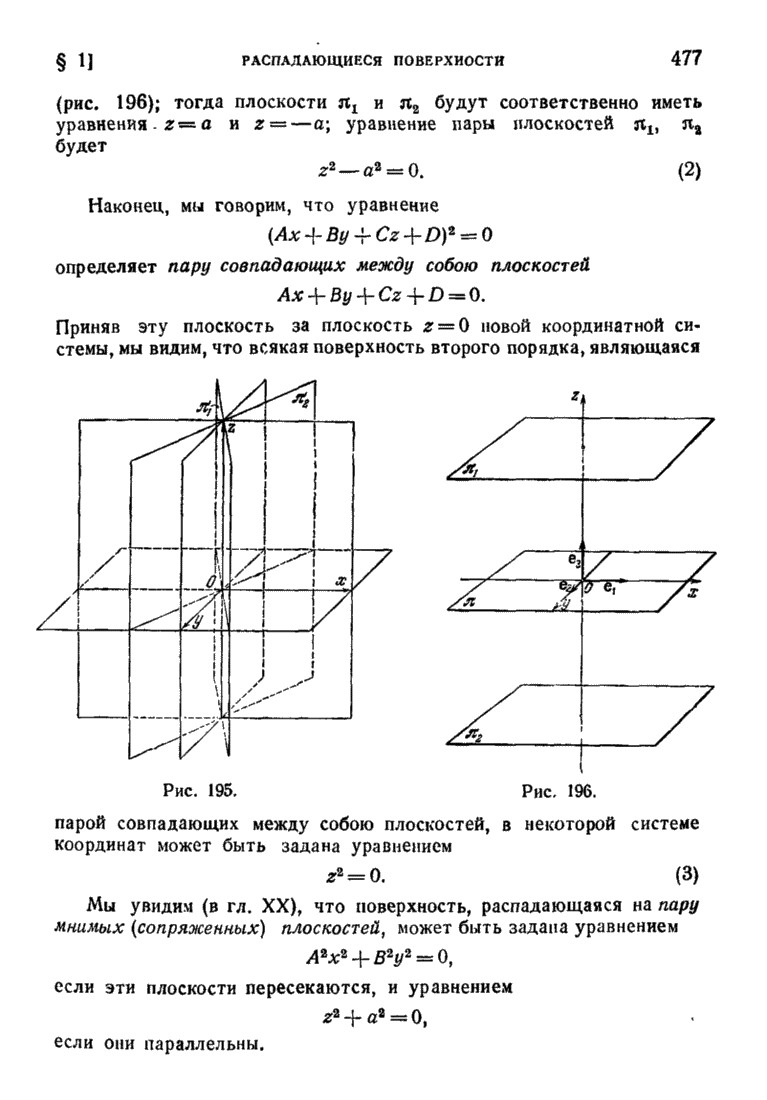
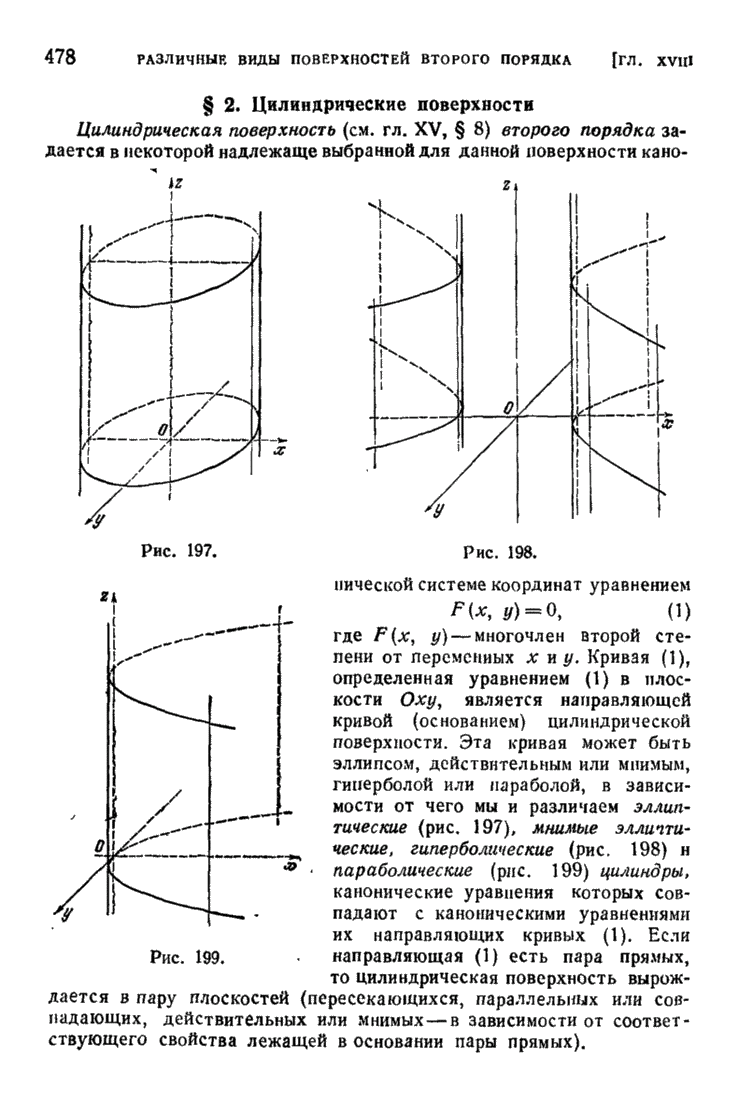
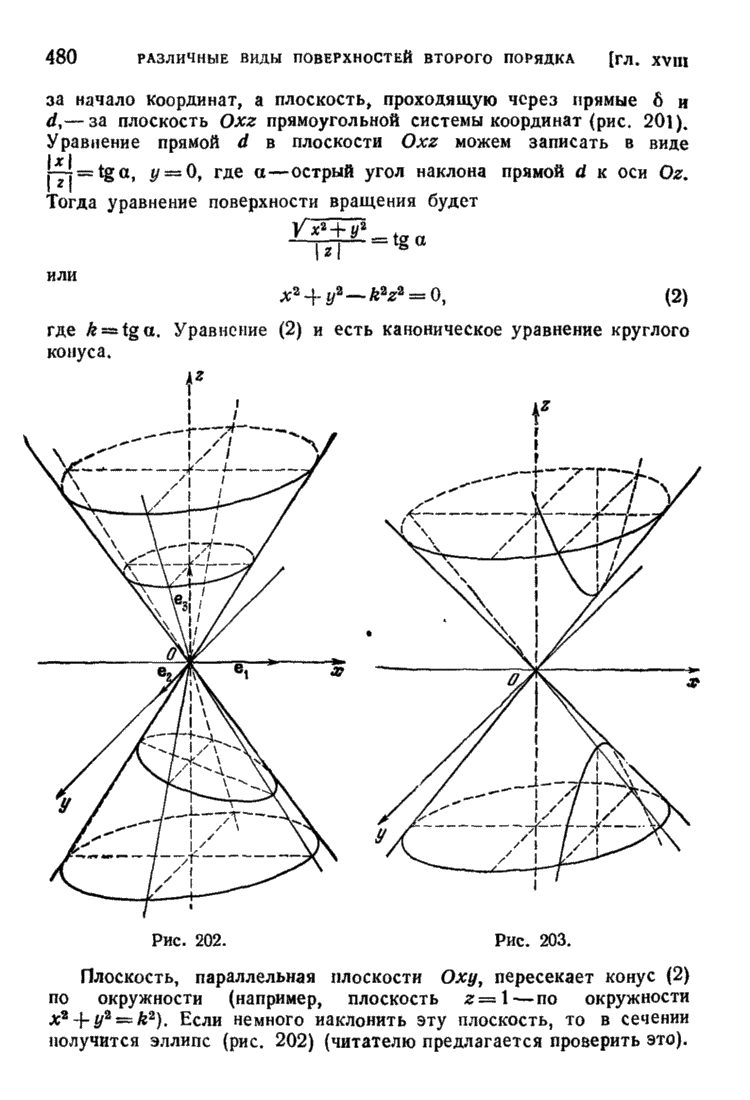
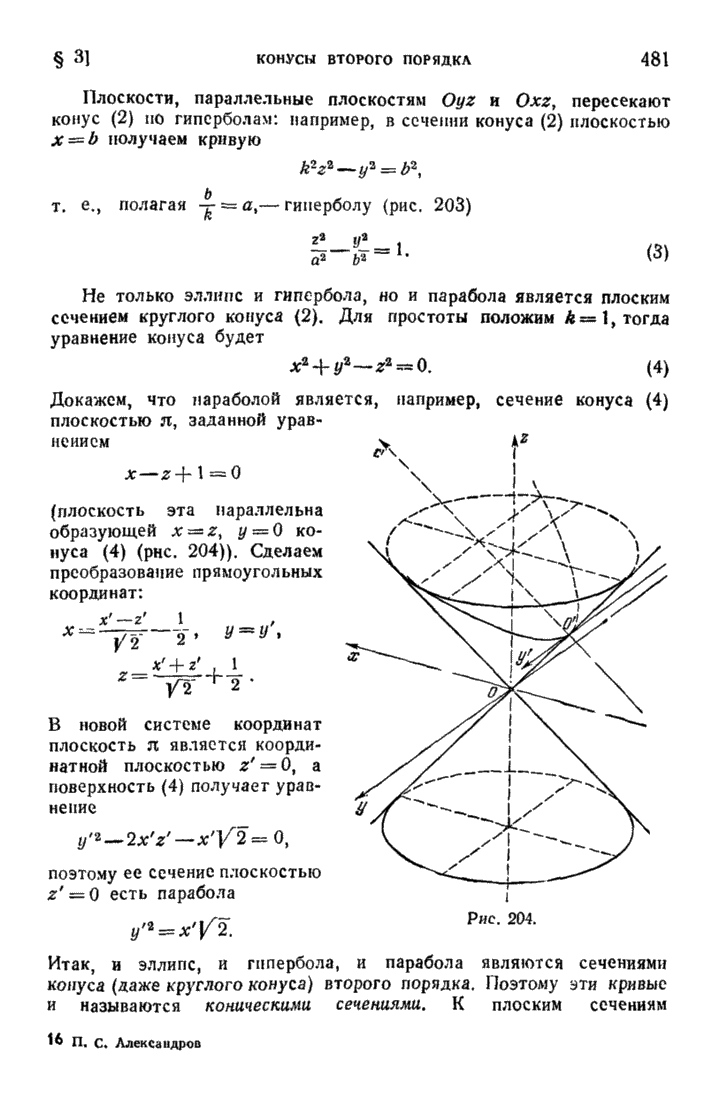
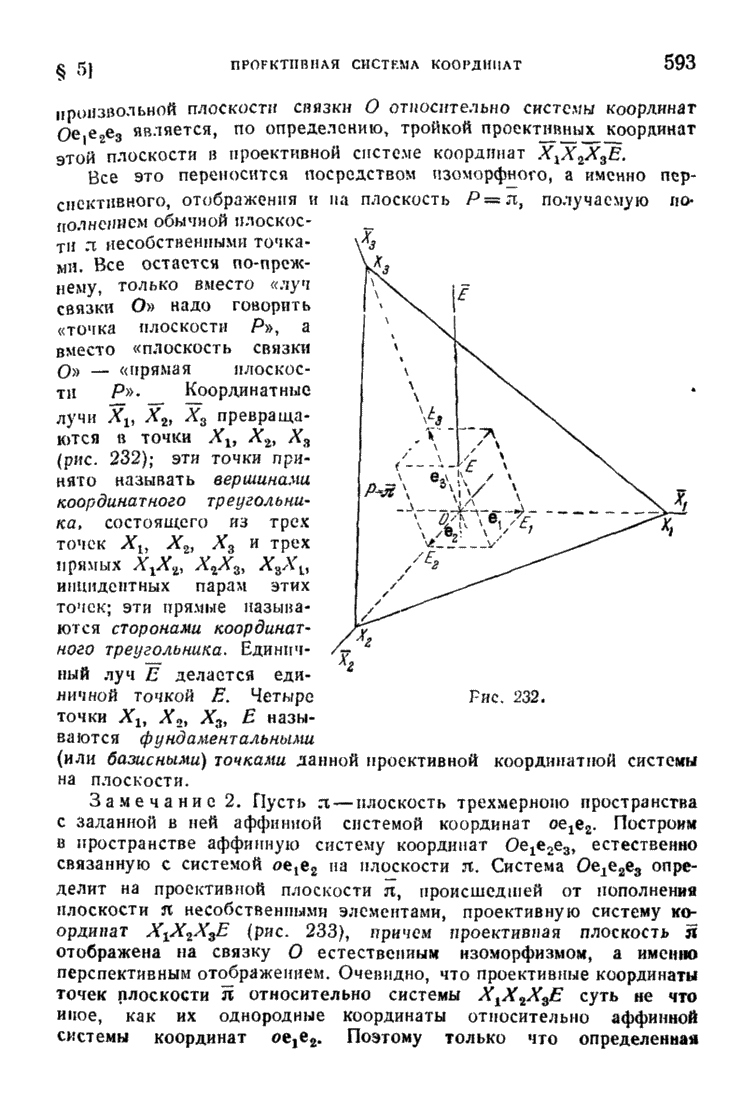
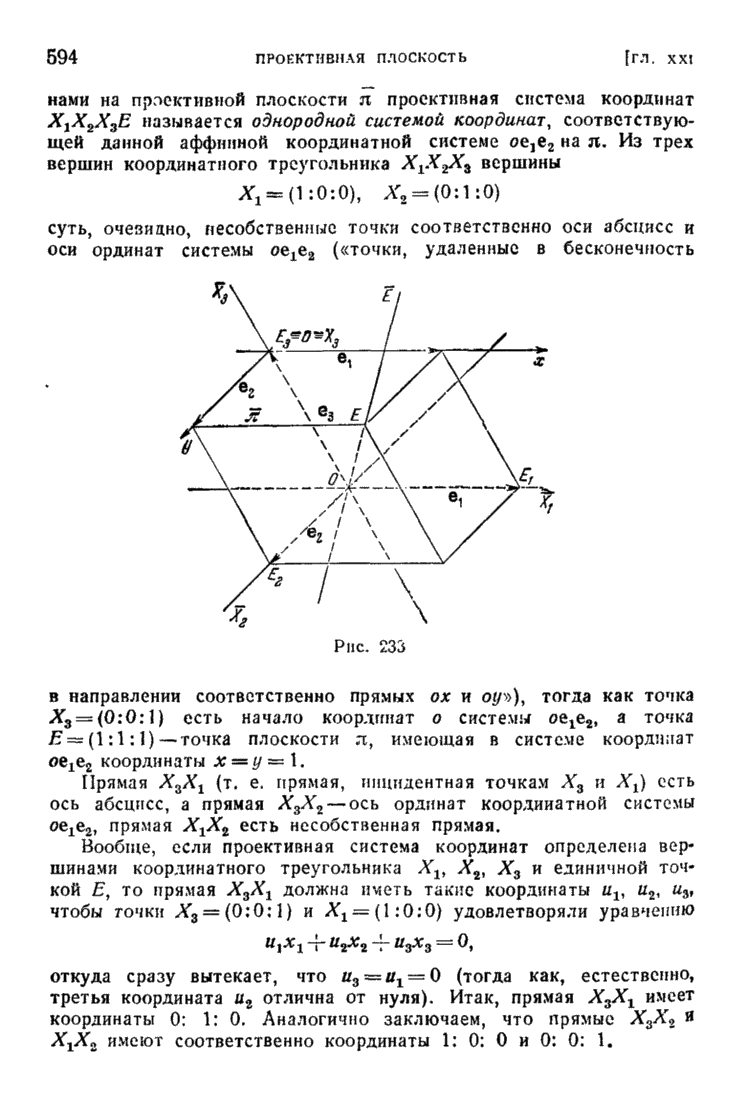
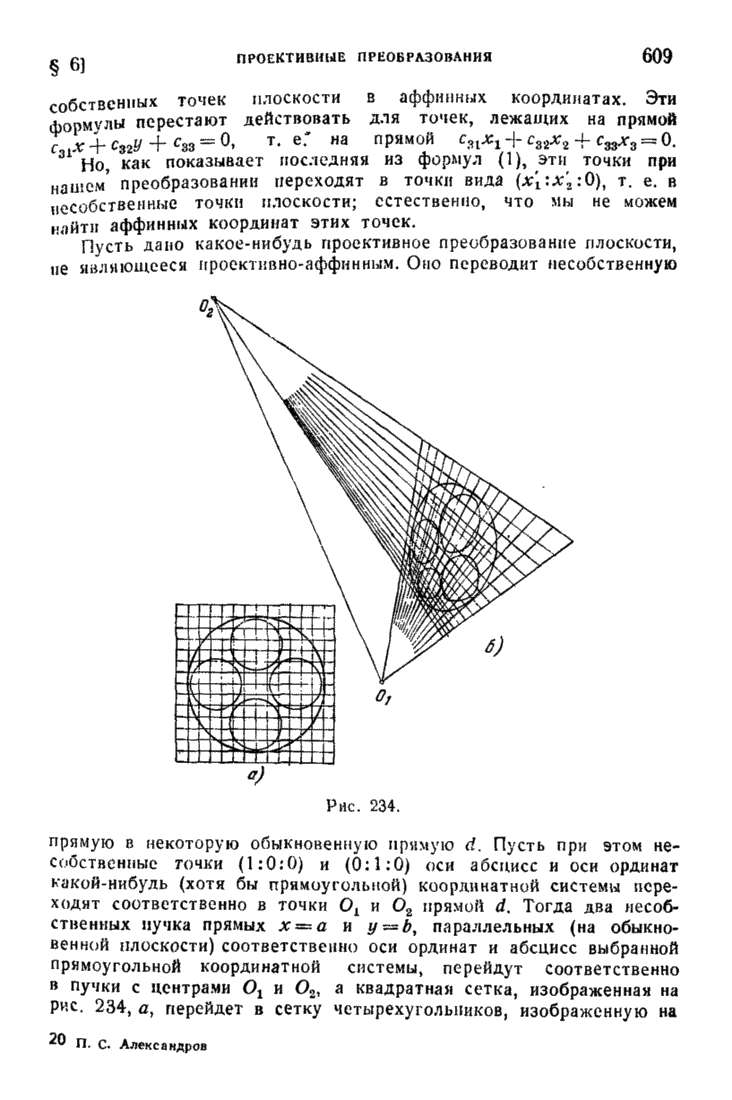
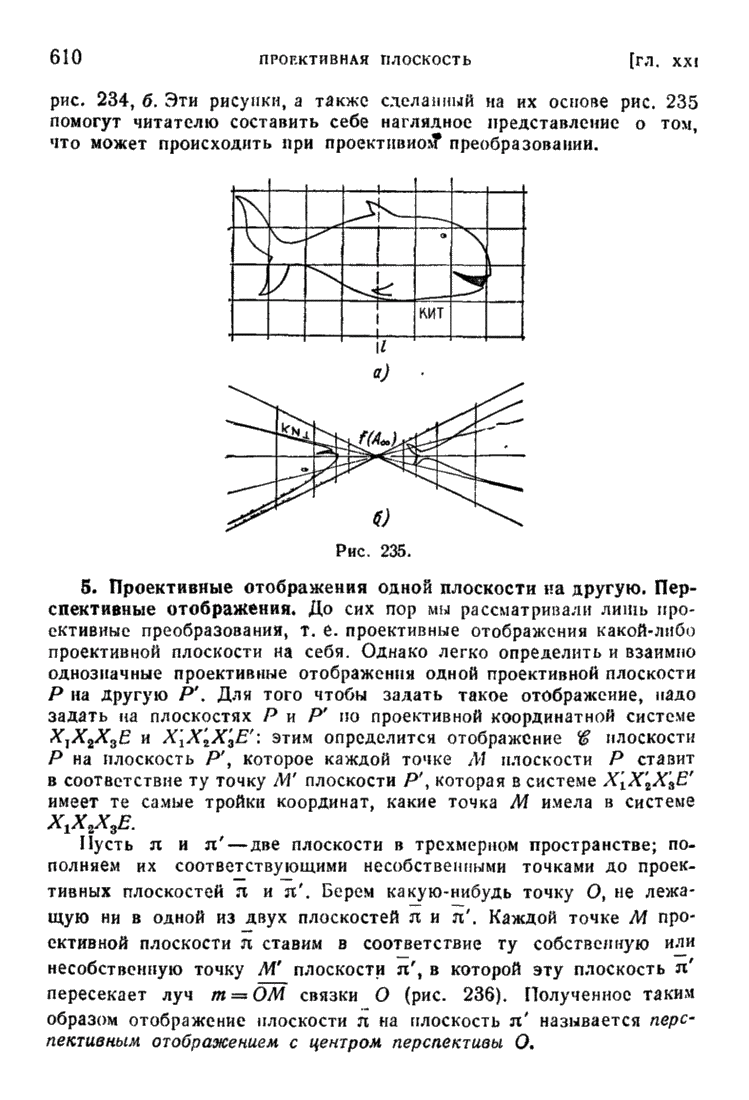
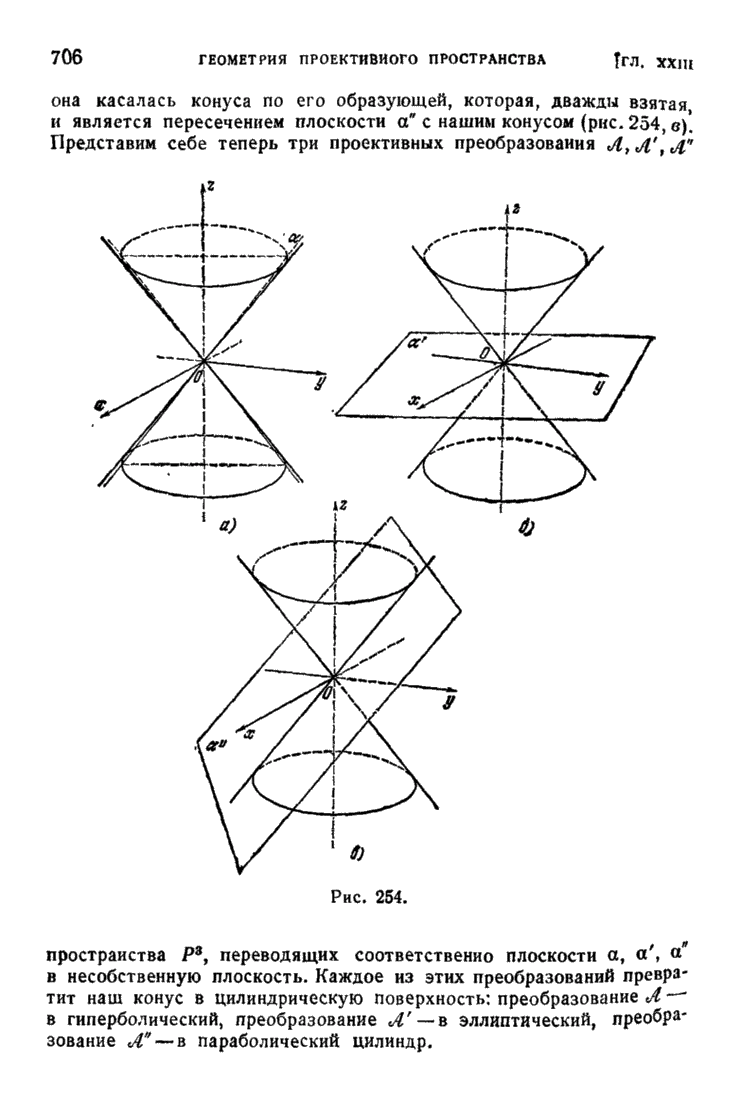
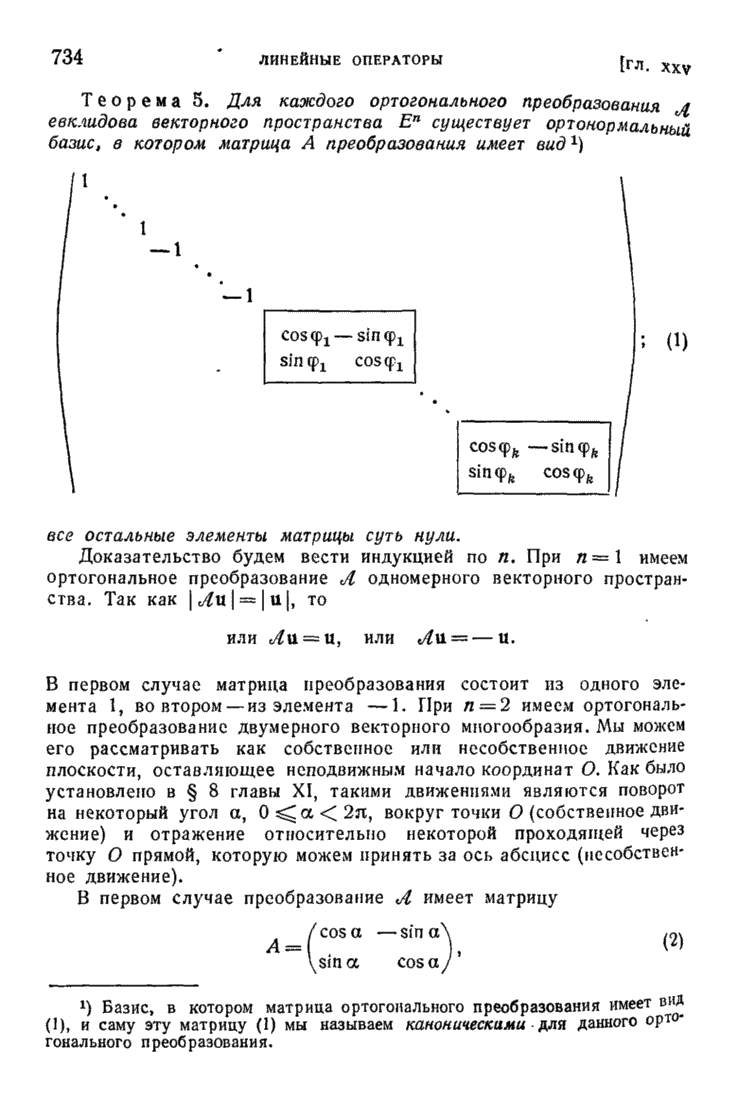
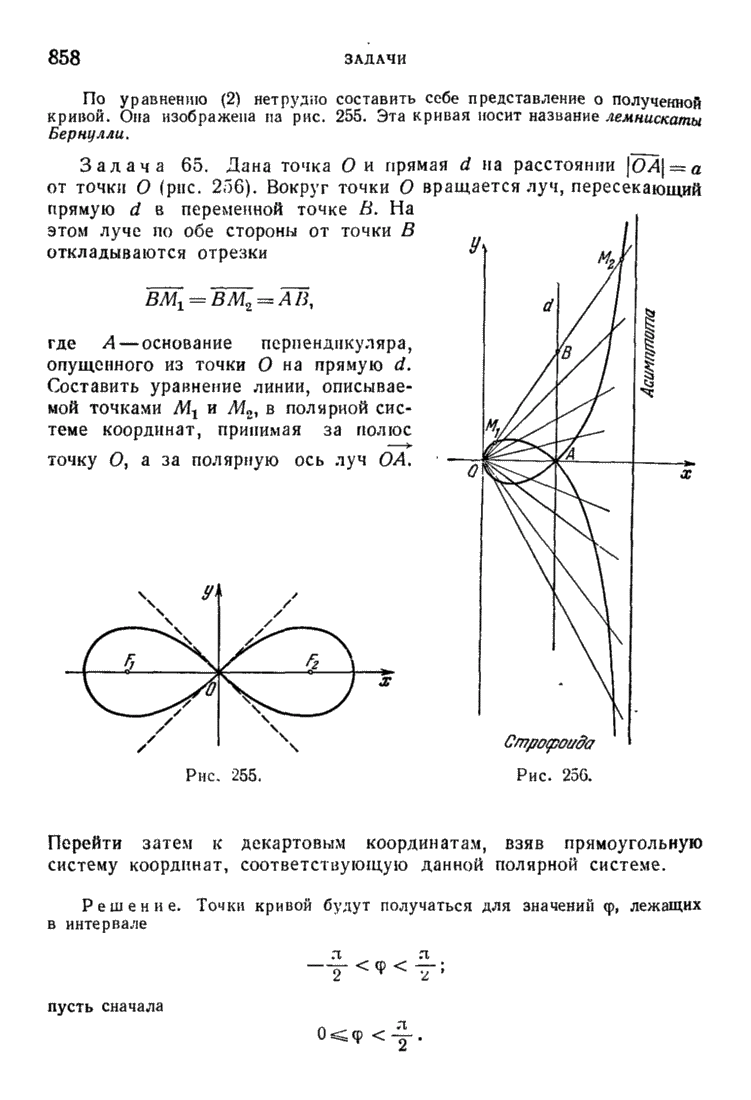
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 4. Геометрически независимые системы точек. Барицентрические координаты. Симплексы
Начнем со следующей простой леммы.
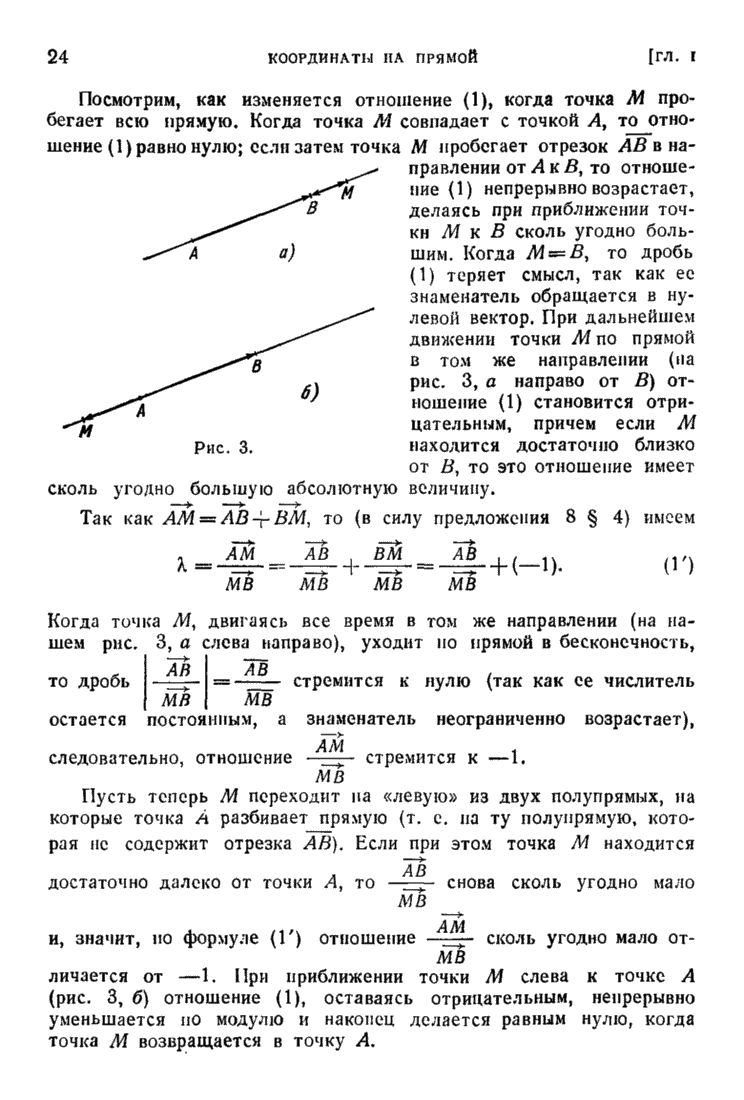
Пусть  . Всякая
. Всякая  -мерная плоскость
-мерная плоскость  в
в  -мерном аффинном пространстве
-мерном аффинном пространстве  содержится в некоторой
содержится в некоторой  -мерной плоскости.
-мерной плоскости.
В самом деле, возьмем в  какую-нибудь линейно независимую систему, состоящую из
какую-нибудь линейно независимую систему, состоящую из  векторов их,
векторов их,  . Так как
. Так как  , то эта система может быть дополнена до линейно независимой системы, состоящей из
, то эта система может быть дополнена до линейно независимой системы, состоящей из  векторов
векторов  )
)  . Эти векторы порождают
. Эти векторы порождают  -мерное подпространство
-мерное подпространство  векторного пространства
векторного пространства  всех векторов, лежащих в
всех векторов, лежащих в  . Произвольная точка А и векторное многообразие
. Произвольная точка А и векторное многообразие  определяют
определяют  -мерную плоскость
-мерную плоскость  , очевидно, содержащую плоскость
, очевидно, содержащую плоскость  .
.
Пусть в пространстве  дано множество, состоящее из конечного числа,
дано множество, состоящее из конечного числа,  , точек
, точек

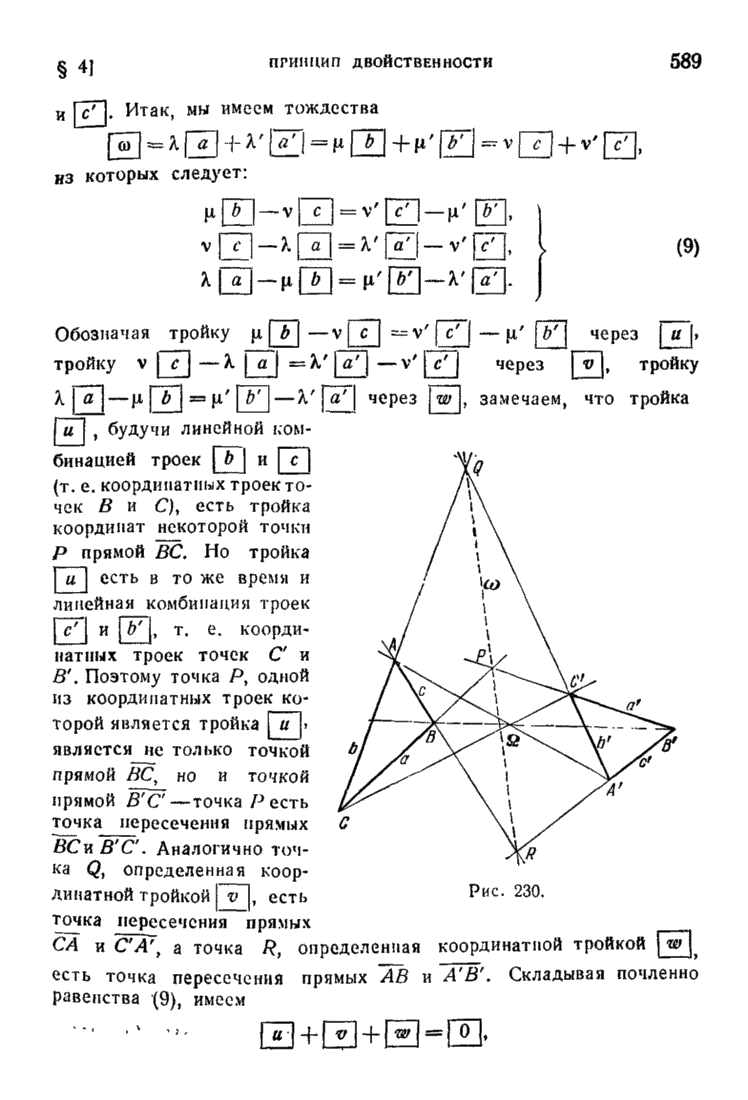
Рассмотрим всевозможные векторы  , ведущие из любой из этих точек в любую другую. Подпространство, порожденное всеми этими векторами (в пространстве всех вообще векторов, лежащих в
, ведущие из любой из этих точек в любую другую. Подпространство, порожденное всеми этими векторами (в пространстве всех вообще векторов, лежащих в  ), обозначим через
), обозначим через  , его размерность — через
, его размерность — через  . Так как
. Так как

то все векторы  линейно выражаются через векторы, ведущие из одной какой-нибудь фиксированной точки (1), например из точки
линейно выражаются через векторы, ведущие из одной какой-нибудь фиксированной точки (1), например из точки  , во все остальные, так что множество, состоящее из векторов
, во все остальные, так что множество, состоящее из векторов

является системой образующих пространства  , максимальное число линейно независимых среди них равно размерности
, максимальное число линейно независимых среди них равно размерности  всего пространства
всего пространства  , и, значит,
, и, значит,

Нумерацию точек (1) выберем так, чтобы первые  среди векторов
среди векторов  , т. е.
, т. е.

составляли линейно независимую систему. Тогда  -мерная плоскость
-мерная плоскость  , натянутая на точку
, натянутая на точку  и векторы (3), содержа все векторы (2), содержит и все концы этих векторов, т. е. все точки (1).
и векторы (3), содержа все векторы (2), содержит и все концы этих векторов, т. е. все точки (1).
Не существует плоскости размерности  , которая содержала бы все точки (1), так как тогда в этой плоскости лежали бы и все векторы (3), что противоречит их линейной независимости. Всякая плоскость, содержащая все точки (1), содержит как точку
, которая содержала бы все точки (1), так как тогда в этой плоскости лежали бы и все векторы (3), что противоречит их линейной независимости. Всякая плоскость, содержащая все точки (1), содержит как точку  так и векторы (3), значит, содержит и плоскость
так и векторы (3), значит, содержит и плоскость  , натянутую на них. Итак, доказано следующее предложение:
, натянутую на них. Итак, доказано следующее предложение:
Пусть дано конечное множество точек

пространства  . Тогда определено наименьшее число
. Тогда определено наименьшее число  , являющееся размерностью плоскости пространства
, являющееся размерностью плоскости пространства  , содержащей все эти точки (1); это число (которое можно было бы назвать «мерой независимости» точек
, содержащей все эти точки (1); это число (которое можно было бы назвать «мерой независимости» точек  ) равно наибольшему числу линейно независимых среди векторов, ведущих из какой-нибудь определенной точки системы (1) (например, из точки
) равно наибольшему числу линейно независимых среди векторов, ведущих из какой-нибудь определенной точки системы (1) (например, из точки  ) во все остальные точки этой системы. При этом имеется одна - единственная
) во все остальные точки этой системы. При этом имеется одна - единственная  -мерная плоскость, содержащая все точки (1), и эта
-мерная плоскость, содержащая все точки (1), и эта  -мерная плоскость
-мерная плоскость  называется плоскостью, натянутой на точки
называется плоскостью, натянутой на точки  .
.
Дополним этот результат следующим определением:
Если  , т. е. если мера независимости точек
, т. е. если мера независимости точек  имеет наибольшее возможное значение
имеет наибольшее возможное значение  , то точки
, то точки  называются геометрически, независимыми (или просто независимыми) между собою в пространстве
называются геометрически, независимыми (или просто независимыми) между собою в пространстве  .
.
Из предыдущего следует:
Точки  тогда и только тогда геометрически независимы, когда векторы
тогда и только тогда геометрически независимы, когда векторы  линейно независимы, или, что то же, когда точки (1) (векторы
линейно независимы, или, что то же, когда точки (1) (векторы  ) не лежат ни в какой плоскости размерности
) не лежат ни в какой плоскости размерности  .
.
Во всякой  -мерной плоскости пространства
-мерной плоскости пространства  можно (бесконечным числом различных способов) выбрать независимую систему из
можно (бесконечным числом различных способов) выбрать независимую систему из  точек; всякая независимая система из
точек; всякая независимая система из  точек
точек  -мерного аффинного пространства
-мерного аффинного пространства  содержится в единственной
содержится в единственной  -мерной плоскости этого пространства.
-мерной плоскости этого пространства.
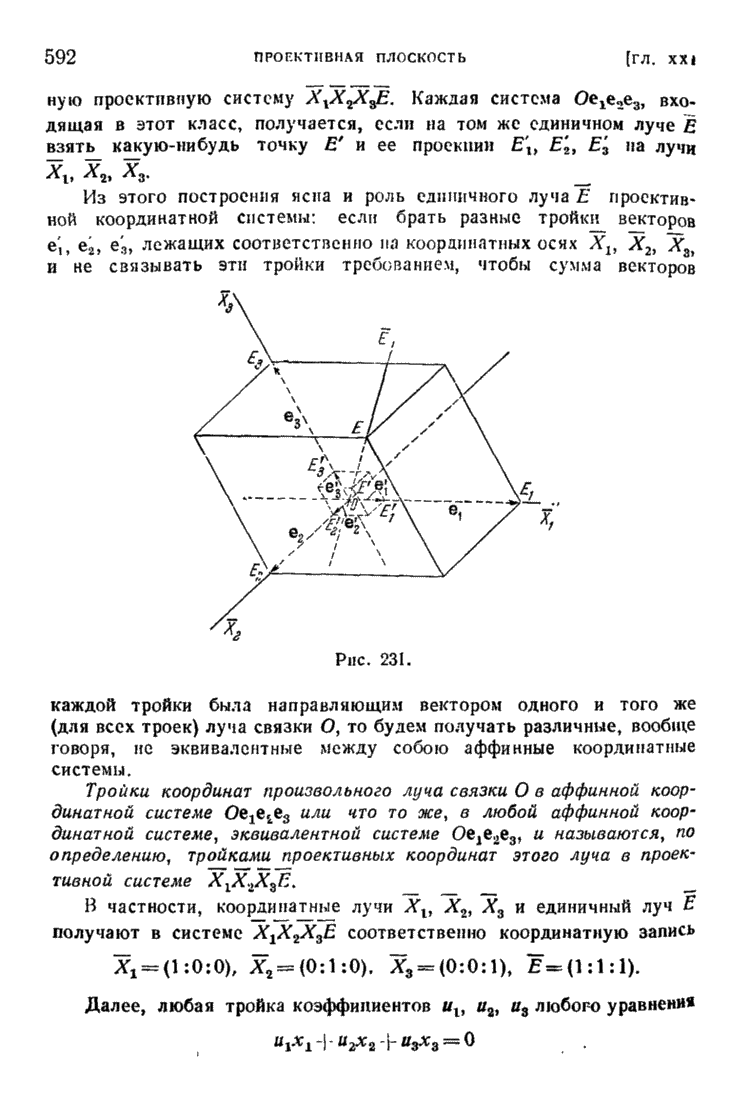
Рассмотрим в пространстве  независимую систему из
независимую систему из  точек, заданных своими координатами (в какой-нибудь системе координат пространства
точек, заданных своими координатами (в какой-нибудь системе координат пространства  ):
):

Единственную  -мерную плоскость, содержащую эти точки, обозначим через
-мерную плоскость, содержащую эти точки, обозначим через  .
.
Положим

Тогда

Плоскость  натянута на точку
натянута на точку  и векторы
и векторы  , поэтому координаты
, поэтому координаты  любой точки
любой точки  плоскости
плоскости  однозначно записываются в виде
однозначно записываются в виде

Давая параметрам  всевозможные действительные значения, получим из уравнений (5) всевозможные точки
всевозможные действительные значения, получим из уравнений (5) всевозможные точки  плоскости
плоскости  и только точки этой плоскости.
и только точки этой плоскости.
Положим

Тогда система равенств (5) переходит в систему равенств 

что мы кратко переписываем в виде одного равенства  .
.

— точка М есть взвешенная сумма точек  , взятых соответственно с весами
, взятых соответственно с весами  , кг Веса
, кг Веса  , в равенстве (6) пробегают всевозможные действительные значения, связанные единственным соотношением
, в равенстве (6) пробегают всевозможные действительные значения, связанные единственным соотношением

т. е.

Для каждой точки  единственным образом определяются удовлетворяющие условию (7) числа
единственным образом определяются удовлетворяющие условию (7) числа  - веса точки М во взвешенной сумме (6).
- веса точки М во взвешенной сумме (6).
Обратно, всякий набор чисел  , удовлетворяющих условию (7), однозначно определяет по формулам (6) или (6) точку если дана независимая система точек
, удовлетворяющих условию (7), однозначно определяет по формулам (6) или (6) точку если дана независимая система точек  .
.
Коэффициенты  в представлении (6) или (6) называются барицентрическими координатами точки М относительно системы точек
в представлении (6) или (6) называются барицентрическими координатами точки М относительно системы точек  в
в  -мерной плоскости
-мерной плоскости  , определенной этими точками.
, определенной этими точками.
Множество  точек все барицентрические координаты которых (относительно системы
точек все барицентрические координаты которых (относительно системы  ) положительны называется
) положительны называется  -мерным открытым симплексом с вершинами
-мерным открытым симплексом с вершинами  точки, барицентрические координаты которых относительно той же системы
точки, барицентрические координаты которых относительно той же системы  неотрицательны, образуют, по определению, замкнутый симплекс с вершинами
неотрицательны, образуют, по определению, замкнутый симплекс с вершинами  .
.
Очевидно, замкнутый симплекс содержит в себе открытый симплекс с теми же вершинами.
Мы уже видели, что одномерный симплекс с вершинами  есть просто отрезок
есть просто отрезок  (открытый, соответственно
(открытый, соответственно 
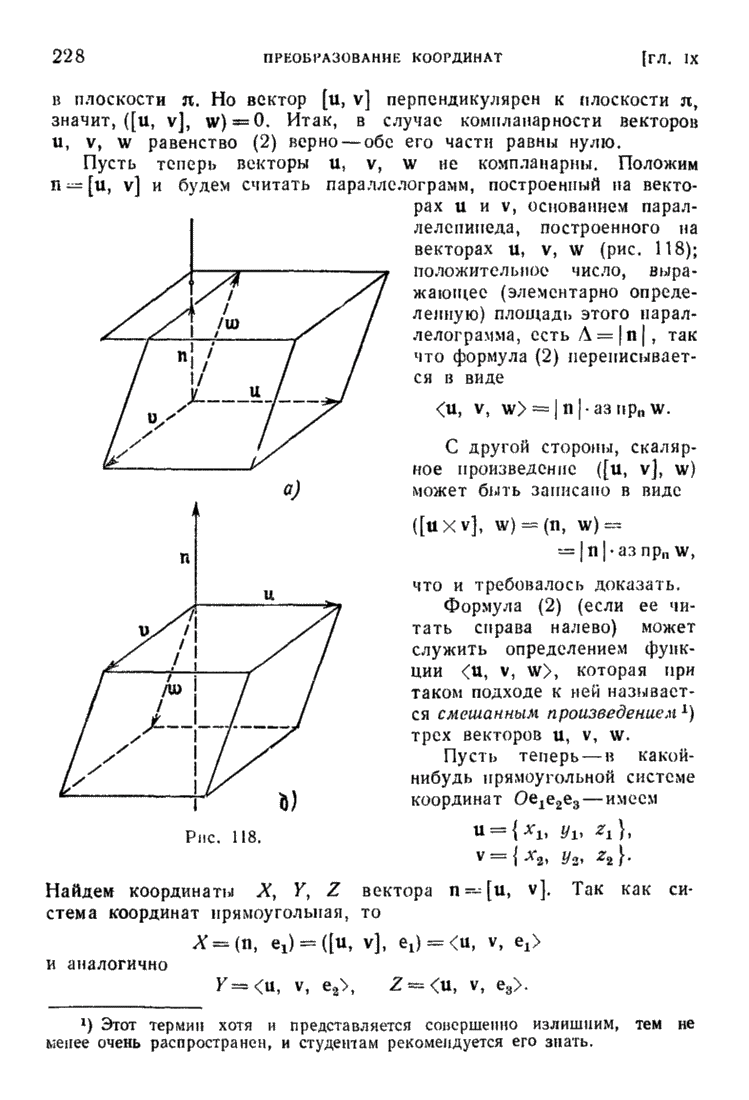
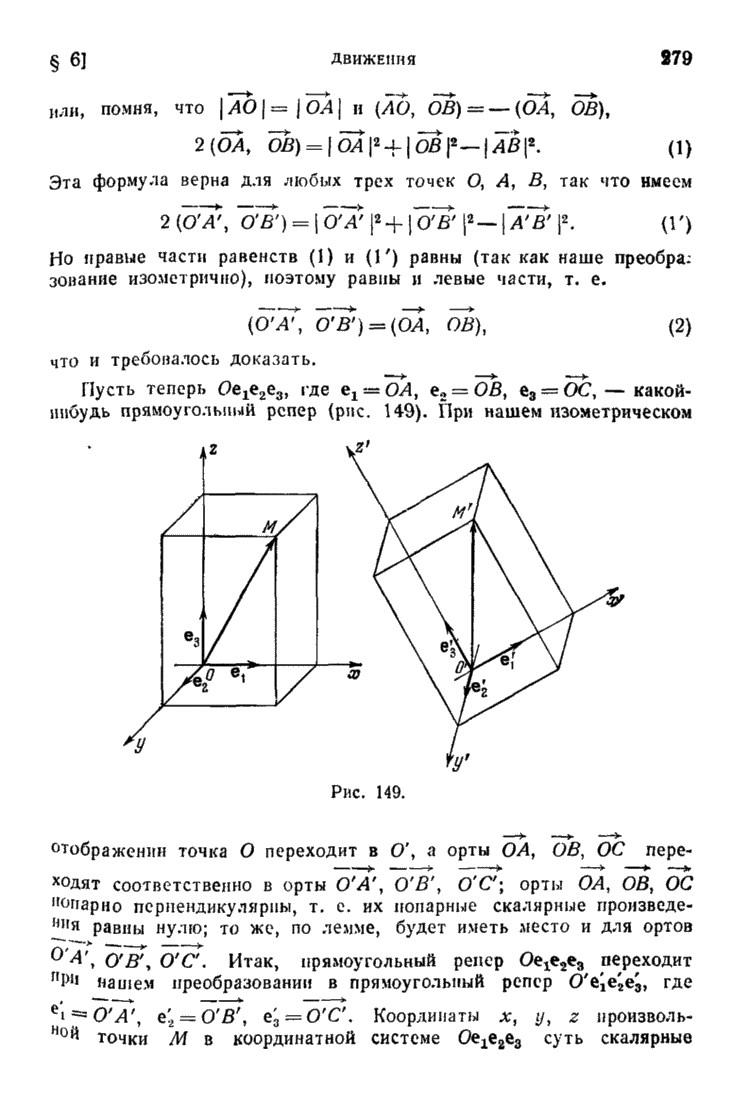
Легко доказать, что двумерный симплекс с вершинами  есть просто открытый треугольник (т. е. множество всех внутренних точек этого треугольника).
есть просто открытый треугольник (т. е. множество всех внутренних точек этого треугольника).
В самом деле, всякая внутренняя точка М треугольника есть внутренняя точка единственного отрезка вида  , где М есть (внутренняя) точка отрезка
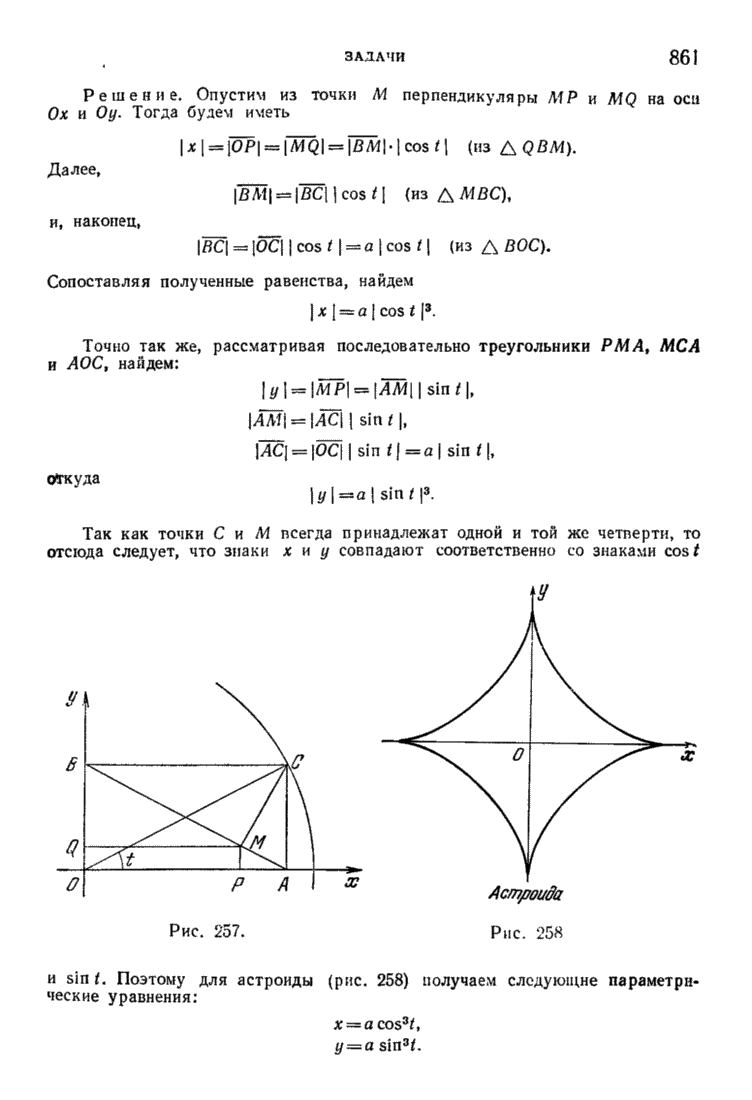
, где М есть (внутренняя) точка отрезка  (рис. 154).
(рис. 154).
Поэтому

Подставляя  в (8'), получим
в (8'), получим

т. е.

где


Рис. 154.
При этом все числа  положительны и
положительны и

Обратно, пусть  , причем
, причем  Можно написать
Можно написать

где

значит,

Точка  есть внутренняя точка отрезка
есть внутренняя точка отрезка  , где
, где  , так что М есть внутренняя точка отрезка
, так что М есть внутренняя точка отрезка  , т. е. внутренняя точка треугольника
, т. е. внутренняя точка треугольника  .
.
Читателю предоставляется самому убедиться (основываясь на только что доказанном и продолжая рассуждать аналогичным образом), что трехмерный открытый симплекс с вершинами  есть (открытый) тетраэдр
есть (открытый) тетраэдр  .
.
Замечание. Множество X точек  -мерного пространства
-мерного пространства  называется выпуклым, если, каковы бы ни были две точки Р и Q этого множества, оно содержит и все точки отрезка
называется выпуклым, если, каковы бы ни были две точки Р и Q этого множества, оно содержит и все точки отрезка  .
.
Все пространство  , а также всякая лежащая в нем плоскость, является выпуклым множеством. Выпуклым множеством является также и симплекс любого числа измерений (как открытый, так и замкнутый), а также любой параллелепипед (пусть читатель докажет все эти утверждения). Выпуклым является также как пустое множество, так и всякое одноточечное множество, т. е. множество, состоящее лишь из одной точки. Имея в виду последнее утверждение, читатель легко докажет важную теорему: пересечение любой (конечной или бесконечной) совокупности выпуклых множеств, лежащих в данном
, а также всякая лежащая в нем плоскость, является выпуклым множеством. Выпуклым множеством является также и симплекс любого числа измерений (как открытый, так и замкнутый), а также любой параллелепипед (пусть читатель докажет все эти утверждения). Выпуклым является также как пустое множество, так и всякое одноточечное множество, т. е. множество, состоящее лишь из одной точки. Имея в виду последнее утверждение, читатель легко докажет важную теорему: пересечение любой (конечной или бесконечной) совокупности выпуклых множеств, лежащих в данном  , есть выпуклое множество. Всякое множество X, лежащее в
, есть выпуклое множество. Всякое множество X, лежащее в  , содержится в некотором выпуклом множестве (за которое можно взять, например, все пространство
, содержится в некотором выпуклом множестве (за которое можно взять, например, все пространство  ). Поэтому можно говорить о (непустой) совокупности всех выпуклых множеств
). Поэтому можно говорить о (непустой) совокупности всех выпуклых множеств  , содержащих данное произвольное множество
, содержащих данное произвольное множество  .
.
Следовательно, определено и выпуклое множество X, являющееся пересечением всех выпуклых множеств Z, содержащих данное множество X. Множество X называется «выпуклым замыканием» (или выпуклой оболочкой) множества X. Оно является наименьшим выпуклым множеством, лежащим в данном  и содержащим данное множество X.
и содержащим данное множество X.
Последнее утверждение имеет следующий смысл: каково бы ни было выпуклое множество Y, содержащее множество X, множество Y содержит и X. Полезным упражнением для читателя было бы доказательство следующей важной теоремы. Пусть  -конечное множество точек
-конечное множество точек  , образующих в
, образующих в  геометрически независимую систему. Тогда выпуклое замыкание X множества X есть замкнутый симплекс с вершинами
геометрически независимую систему. Тогда выпуклое замыкание X множества X есть замкнутый симплекс с вершинами 
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ГЛАВА I. КООРДИНАТЫ НА ПРЯМОЙ
- § 1. Отношение отрезков
- § 2. Направленные отрезки (векторы); их отношение
- § 3. Ось. Алгебраическое значение (координата) вектора на оси
- § 4. Сложение векторов на прямой
- § 5. Система координат на прямой
- § 6. Деление отрезка в данном отношении
- § 7. Пропорциональность пар чисел
- § 8. Бесконечно удаленная точка прямой
- § 9. Пропорциональность двух последовательностей, состоящих из и чисел
- ГЛАВА II. ВЕКТОРЫ
- § 1. Равенство векторов. Свободный вектор
- § 2. Линейные операции над векторами (сложение и умножение на число)
- § 3. Проекции
- § 4. Коллинеарные и компланарные векторы; координаты вектора относительного данного базиса
- § 5. Линейная зависимость и независимость векторов
- § 6. Геометрический смысл линейной зависимости векторов
- § 7. Векторные многообразия
- ГЛАВА III. АФФИННАЯ СИСТЕМА КООРДИНАТ НА ПЛОСКОСТИ И В ПРОСТРАНСТВЕ
- § 1. Определение аффинной системы координат
- § 2. Перенос начала координат
- § 3. Деление отрезка в данном отношении
- ГЛАВА IV. ПРЯМОУГОЛЬНАЯ СИСТЕМА КООРДИНАТ. ПОЛЯРНЫЕ КООРДИНАТЫ
- § 1. Прямоугольная система координат на плоскости и в пространстве. Расстояние между двумя точками. Уравнение окружности и сферы
- § 2. Скалярное произведение векторов; угол между двумя векторами
- § 3. Угол от одного вектора до другого на плоскости
- § 4. Полярная система координат на плоскости
- § 5. Полярная система координат в пространстве
- ГЛАВА V. ПРЯМАЯ ЛИНИЯ
- § 1. Направляющий вектор и угловой коэффициент прямой (в произвольной аффинной системе координат). Уравнение прямой
- § 2. Расположение двух прямых на плоскости
- § 3. Частные случаи общего уравнения прямой
- § 4. Векторная и параметрическая форма уравнения прямой. Уравнение прямой, проходящей через две заданные точки
- § 5. Задача: когда прямая Ax+By+C=0 на плоскости проходит через точку пересечения двух заданных прямых A1x+B1y+C1=0 и A2x+B2y+C2=0?
- § 6. Две полуплоскости, определяемые данной прямой на плоскости
- § 7. Прямая на плоскости в прямоугольной системе координат. Нормальное уравнение прямой на плоскости
- § 8. Расстояние от точки до прямой (на плоскости)
- § 9. Углы, образуемые двумя прямыми на плоскости
- § 10. Прямая в пространстве, снабженном прямоугольной системой координат
- ГЛАВА VI. ПАРАБОЛА. ЭЛЛИПС. ГИПЕРБОЛА
- § 1. Парабола
- § 2. Определение и каноническое уравнение эллипса
- § 3. Параметрическая запись уравнения эллипса; построение эллипса по точкам. Эллипс как результат сжатия окружности к одному из ее диаметров
- § 4. Эллипс как проекция окружности и как сечение круглого цилиндра
- § 5. Определение гиперболы. Каноническое уравнение гиперболы
- § 6. Основной прямоугольник и асимптоты гиперболы
- § 7. Директрисы эллипса и гиперболы
- § 8. Фокальный параметр эллипса и гиперболы. Уравнение при вершине
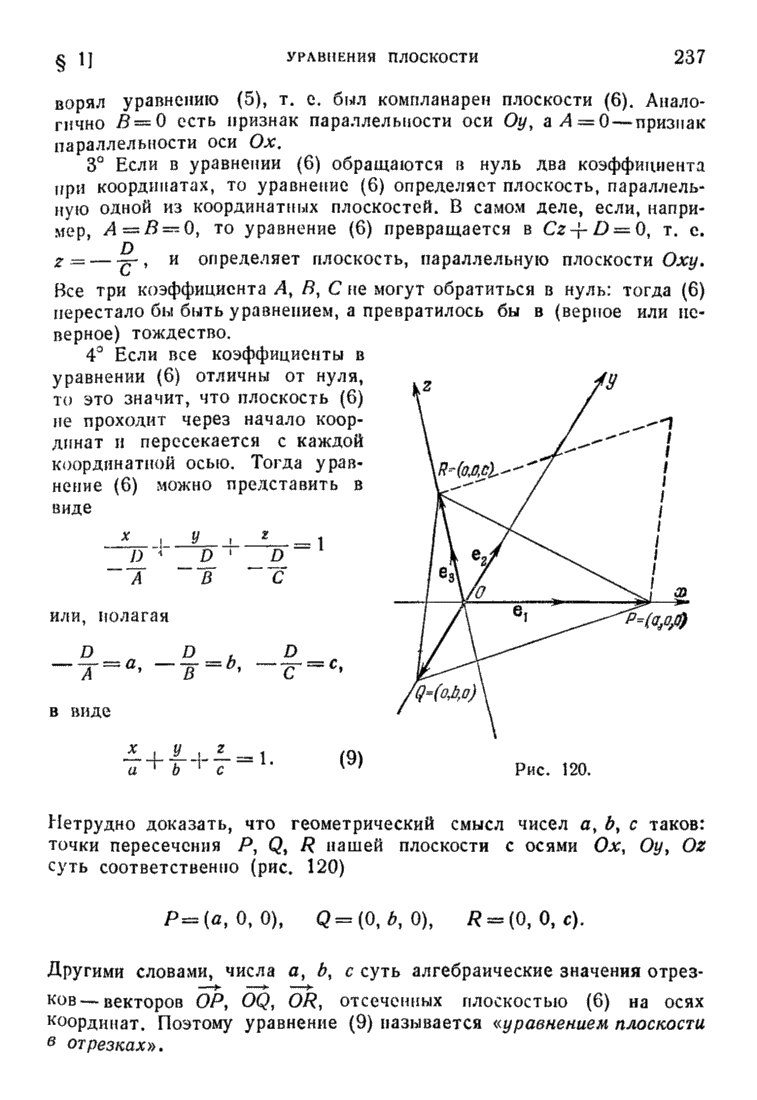
- § 9. Уравнение эллипса, гиперболы и параболы в полярных координатах
- ГЛАВА VII. ДЕТЕРМИНАНТЫ
- § 1. Плошадь ориентированного параллелограмма и треугольника
- § 2. Детерминант второго порядка. Матрицы
- § 4. Разложение детерминанта третьего порядка по элементам какой-либо строки. Приложение к системе трех уравнений с тремя неизвестными (правило Крамера)
- § 5. Системы трех уравнений с тремя неизвестными с детерминантом системы, равным нулю
- § 6. Арифметическое n-мерное векторное многообразие (пространство). Общее определение матрицы. Детерминанты любого порядка
- § 7. Разложение детерминанта n-го порядка по элементам данной строки (данного столбца)
- § 8. Правило Крамера для решений систем и уравнений с n неизвестными
- § 9. Общее определение миноров матрицы. Теорема Лапласа
- § 10. Умножение детерминантов
- § 11. Детерминант n-го порядка как линейная нечетная нормированная функция от n векторов
- ГЛАВА VIII. ПРЕОБРАЗОВАНИЕ КООРДИНАТ. МАТРИЦЫ
- § 1. Переход от одной аффинной системы координат к другой
- § 2. Перемножение матриц. Новое определение обратной матрицы
- § 3. Переход от одной прямоугольной системы координат к другой
- § 4. Действия над матрицами в общем случае
- ГЛАВА IX. ПРЕОБРАЗОВАНИЕ КООРДИНАТ (ПРОДОЛЖЕНИЕ): ОРИЕНТАЦИЯ ПЛОСКОСТИ И ПРОСТРАНСТВА; УГЛЫ ЭЙЛЕРА; ОБЪЕМ ОРИЕНТИРОВАННОГО ПАРАЛЛЕЛЕПИПЕДА; ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ДВУХ ВЕКТОРОВ
- § 1. Ориентация пространства (плоскости)
- § 2. Углы Эйлера
- § 3. Объем ориентированного параллелепипеда
- § 4. Векторное произведение двух векторов
- ГЛАВА X. ПЛОСКОСТЬ И ПРЯМАЯ В ПРОСТРАНСТВЕ
- § 1. Уравнения плоскости
- § 2. Множество решений системы двух однородных линейных уравнений с тремя неизвестными
- § 3. Взаимное расположение двух плоскостей
- § 4. Прямая как пересечение двух плоскостей
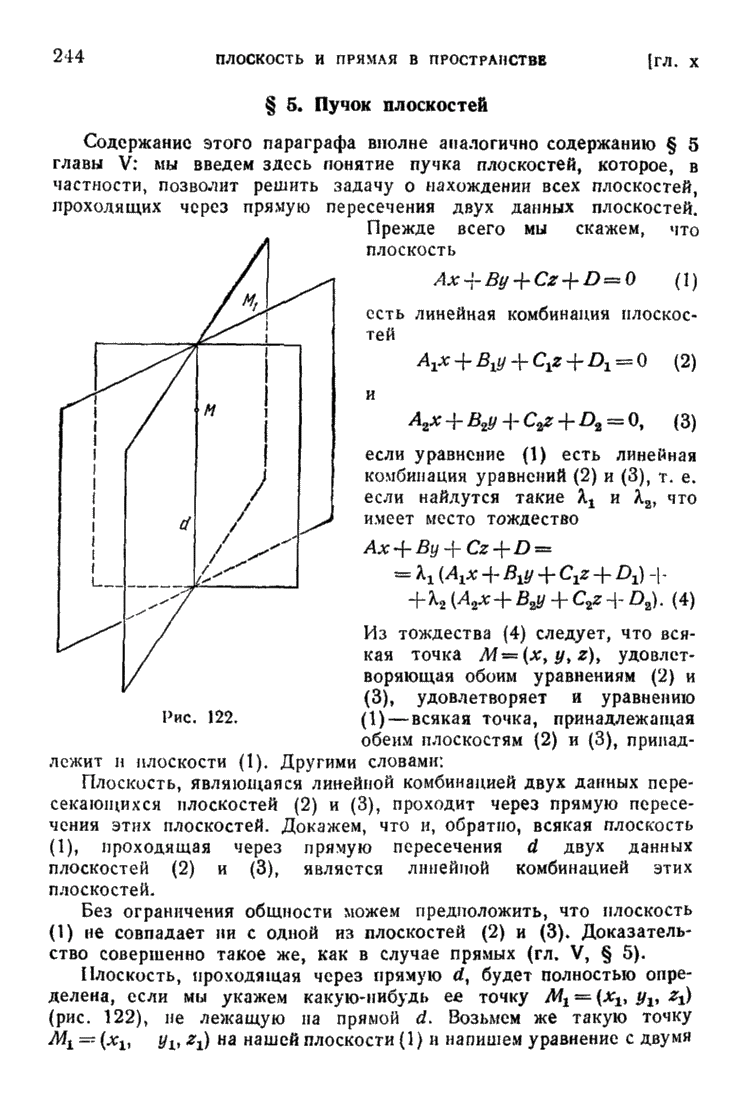
- § 5. Пучок плоскостей
- § 6. Взаимное расположение двух прямых в пространстве
- § 7. О двух полупространствах, определяемых данной плоскостью
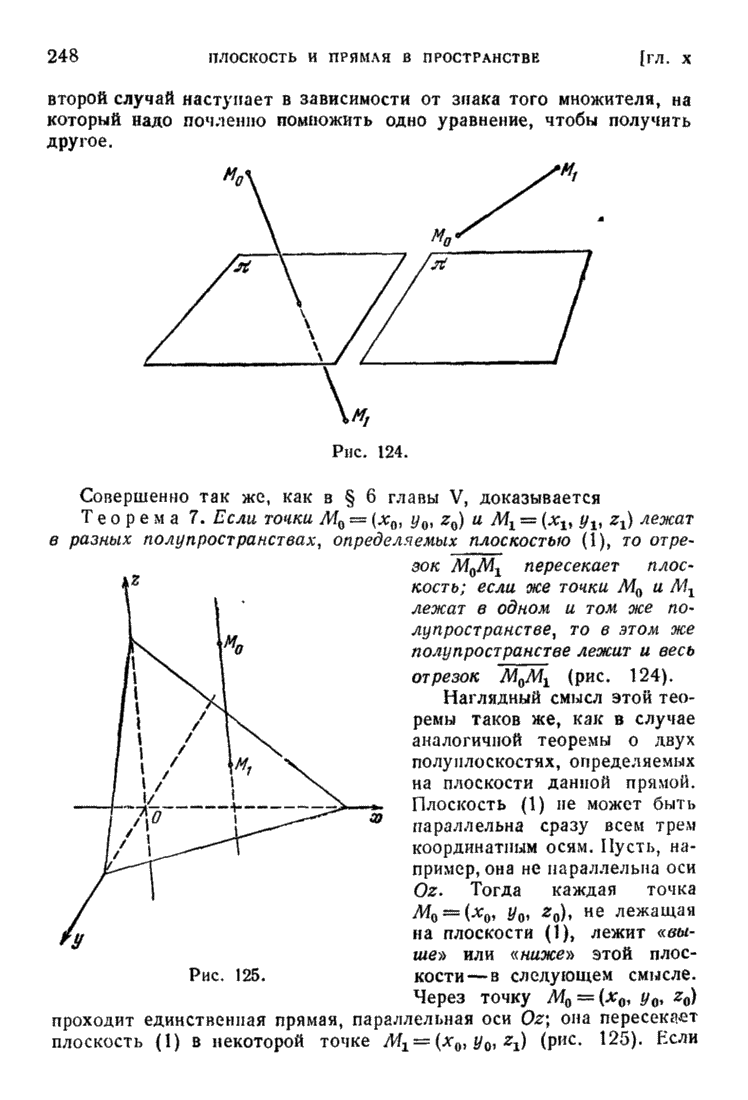
- § 8. Плоскость в прямоугольной системе координат; нормальное уравнение плоскости; расстояние от точки до плоскости
- § 9. Угол между прямой и плоскостью; угол между двумя плоскостями
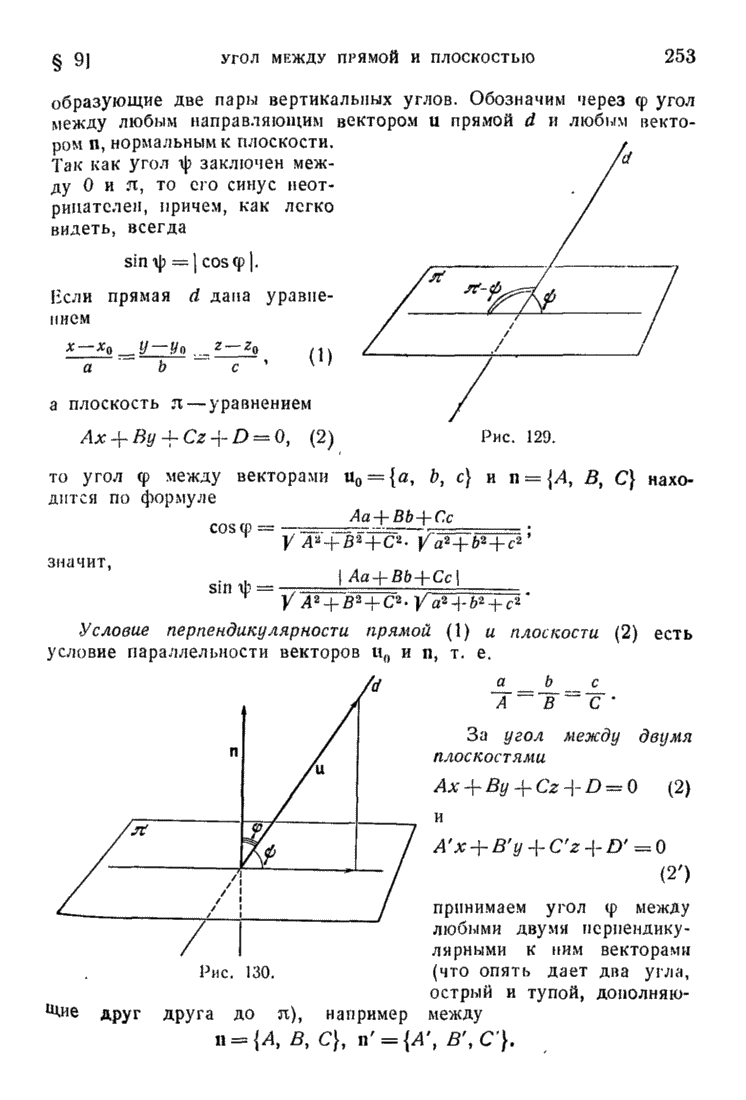
- § 10. Две задачи
- ГЛАВА XI. ДВИЖЕНИЯ И АФФИННЫЕ ПРЕОБРАЗОВАНИЯ
- § 1. Определение движений и аффинных преобразований
- § 2. Преобразование векторов при аффинном преобразовании плоскости и пространства. Основные свойства аффинных преобразований
- § 3. Аналитическое выражение аффинных преобразований
- § 4. Сохранение отношений площадей и объемов при аффинных преобразованиях
- § 5. Получение собственных аффинных преобразований посредством деформации тождественного преобразования. Следствия
- § 6. Движения как изометрические преобразования
- § 7. Преобразования подобия
- § 8. Классификация движений прямой и плоскости
- ГЛАВА XII. ВЕКТОРНЫЕ ПРОСТРАНСТВА (МНОГООБРАЗИЯ) ЛЮБОГО КОНЕЧНОГО ЧИСЛА ИЗМЕРЕНИЙ. СИСТЕМЫ ЛИНЕЙНЫХ ОДНОРОДНЫХ УРАВНЕНИЙ
- § 1. Определение векторного пространства
- § 2. Размерность. Базис. Координаты
- § 3. Теорема об изоморфизме между любыми двумя векторными пространствами одной и той же конечной размерности n
- § 4. Подпространства векторного пространства. Дальнейшие теоремы о линейной зависимости векторов и о базисе векторного пространства
- § 5. Алгебраическая (в частности, прямая) сумма подпространств
- § 6. Линейные отображения векторных пространств
- § 7. Теорема о ранге матрицы
- § 8. Системы линейных однородных уравнения
- ГЛАВА XIII. ЛИНЕЙНЫЕ, БИЛИНЕЙНЫЕ И КВАДРАТИЧНЫЕ ФУНКЦИИ НА ВЕКТОРНЫХ ПРОСТРАНСТВАХ
- § 1. Линейные функции
- § 2. Билинейные функции и билинейные формы
- § 3. Матрица билинейной и квадратичной формы и ее преобразование при переходе к новому базису (при преобразовании переменных)
- § 4. Ранг билинейной и квадратичной формы (билинейной и квадратичной функции)
- § 5. Существование канонического базиса для всякой квадратичной и всякой билинейной функции («приведение квадратичных форм к каноническому виду»)
- ГЛАВА XIV. ТОЧЕЧНО-ВЕКТОРНОЕ АФФИННОЕ n-МЕРНОЕ ПРОСТРАНСТВО
- § 1. Определение n-мерного аффинного пространства
- § 2. Системы координат. Арифметическое пространство. Изоморфизм всех n-мерных пространств между собою
- § 3. r-мерные плоскости n-мерного аффинного пространства; r-мерные параллелепипеды
- § 4. Геометрически независимые системы точек. Барицентрические координаты. Симплексы
- § 5. Системы линейных уравнений
- § 6. Аффинные преобразования n-мерного аффинного пространства
- ГЛАВА XV. АЛГЕБРАИЧЕСКИЕ ЛИНИИ И ПОВЕРХНОСТИ. КОМПЛЕКСНАЯ ПЛОСКОСТЬ И КОМПЛЕКСНОЕ ПРОСТРАНСТВО
- § 1. Определение алгебраических линий и поверхностей
- § 2. Преобразование многочлена второй степени при преобразовании координат
- § 3. Аффинная эквивалентность линий и поверхностей
- § 4. Комплексная плоскость
- § 5. Прямая линия на комплексной плоскости
- § 6. Замечание о действительных и мнимых линиях
- § 7. Комплексное пространство
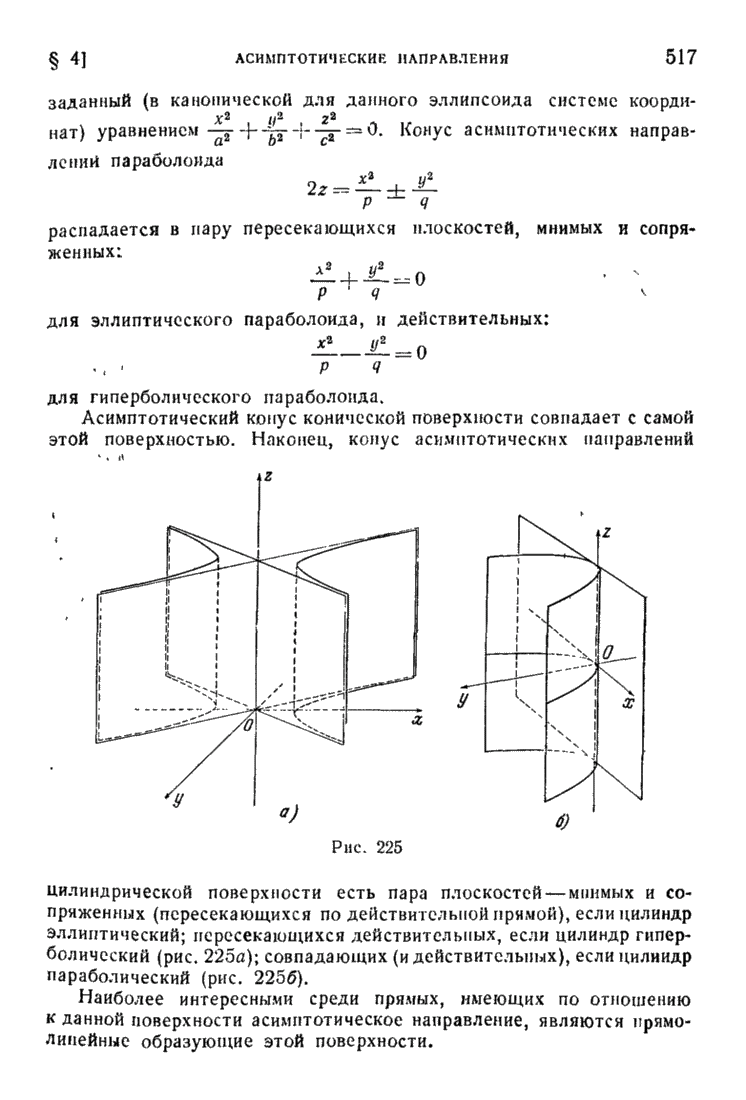
- § 8. Распадающиеся линии и поверхности. Цилиндрические и конические поверхности. Поверхности вращения
- § 9. Несколько заключительных замечаний о линиях и поверхностях
- ГЛАВА XVI. Различные виды кривых второго порядка
- § 1. О линиях, определяемых уравнениями второй степени с двумя неизвестными
- § 2. Инварианты многочлена второй степени
- § 3. Центральный случай
- § 4. Параболический случай
- § 5. Аффинная классификация кривых второго порядка
- § 6. Несколько заключительных замечаний
- ГЛАВА XVII. ОБЩАЯ ТЕОРИЯ КРИВЫХ ВТОРОГО ПОРЯДКА
- § 1. Пересечение алгебраической кривой с прямой. Асимптотические направления и асимптоты алгебраической кривой
- § 2. Теорема единственности для кривых второго порядка. Пучок кривых второго порядка
- § 3. Асимптотические направления кривых второго порядка
- § 4. Пересечение кривой второго порядка с прямой иеасимптотического направления. Касательные
- § 5. Пересечение кривой второго порядка с прямой асимптотического направления. Геометрическая характеристика асимптотических и неасимптотических направлений
- § 6. Центр кривой второго порядка
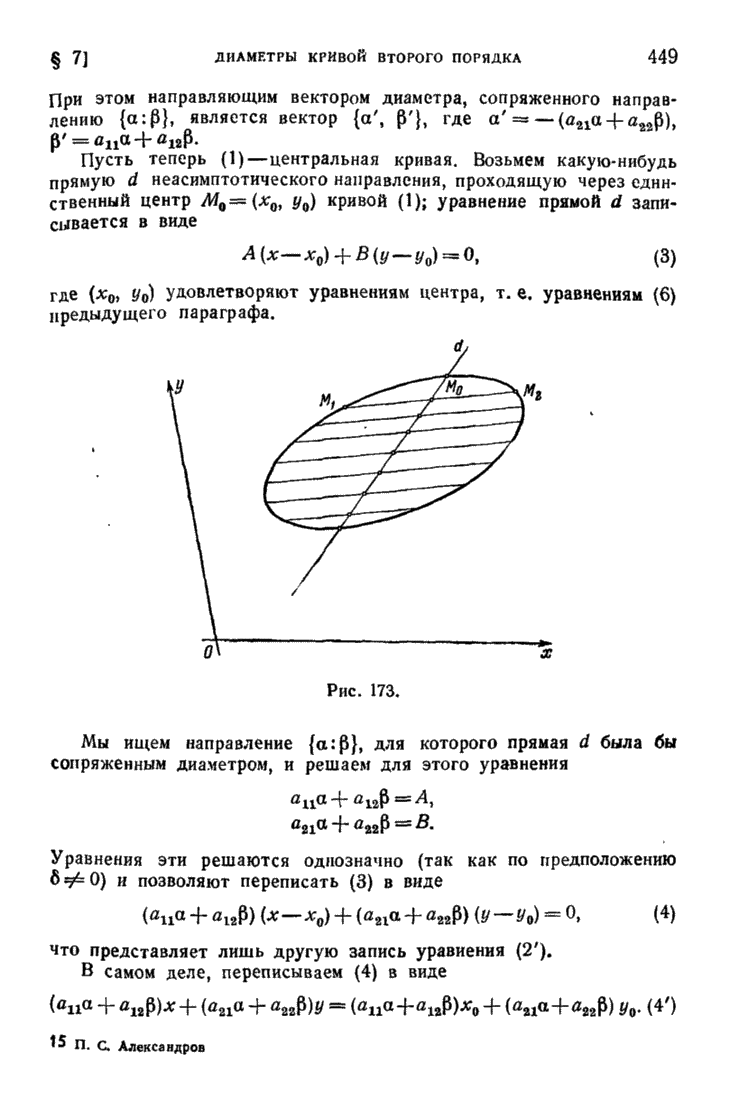
- § 7. Диаметры кривой второго порядка
- § 8. Взаимно сопряженные векторы (направления). Диаметры и касательные
- § 9. Вид уравнения кривой, если оси координат имеют сопряженные направления
- § 10. Второе доказательство теоремы единственности. О полноте системы ортогональных инвариантов
- § 11. Оси симметрии и главные направления кривой второго порядка
- § 12. Основная теорема об аффинных преобразованиях
- ГЛАВА XVIII. КРАТКОЕ ОПИСАНИЕ РАЗЛИЧНЫХ ВИДОВ ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА
- § 1. Распадающиеся поверхности
- § 2. Цилиндрические поверхности
- § 3. Конусы второго порядка
- § 4. Эллипсоиды и гиперболоиды
- § 5. Параболоиды
- § 6. Прямолинейные образующие
- ГЛАВА XIX. ОБЩАЯ ТЕОРИЯ ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА. I (ПЕРЕСЕЧЕНИЕ С ПЛОСКОСТЬЮ И С ПРЯМОЙ; АСИМПТОТИЧЕСКИЕ НАПРАВЛЕНИЯ; КАСАТЕЛЬНАЯ ПЛОСКОСТЬ; ЦЕНТР)
- § 1. Ранг и детерминант малой и большой матрицы многочлена второй степени
- § 2. Пересечение поверхности второго порядка с плоскостью
- § 3. Пересечение поверхности второго порядка с прямой. Асимптотические направления. Касательные прямые и касательная плоскость. Особые точки поверхности второго порядка
- § 4. Асимптотические направления, конус асимптотических направлений, прямолинейные образующие поверхностей второго порядка
- § 5. Центр поверхности второго порядка
- ГЛАВА XX. ОБЩАЯ ТЕОРИЯ ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА. II (ДИАМЕТРАЛЬНЫЕ ПЛОСКОСТИ; ОСОБЫЕ И ГЛАВНЫЕ НАПРАВЛЕНИЯ; АФФИННАЯ КЛАССИФИКАЦИЯ)
- § 1. Диаметральные плоскости. Особые направления
- § 2. Диаметральные плоскости поверхностей различных видов
- § 3. Сопряженные направления
- § 4. Уравнение поверхности второго порядка относительно координатной системы с сопряженными направлениями осей
- § 5. Теорема единственности
- § 6. Главные направления
- § 7. Приведение к каноническому виду уравнения поверхности второго порядка
- § 8. Аффинная классификация поверхностей второго порядка
- ГЛАВА XXI. ПРОЕКТИВНАЯ ПЛОСКОСТЬ
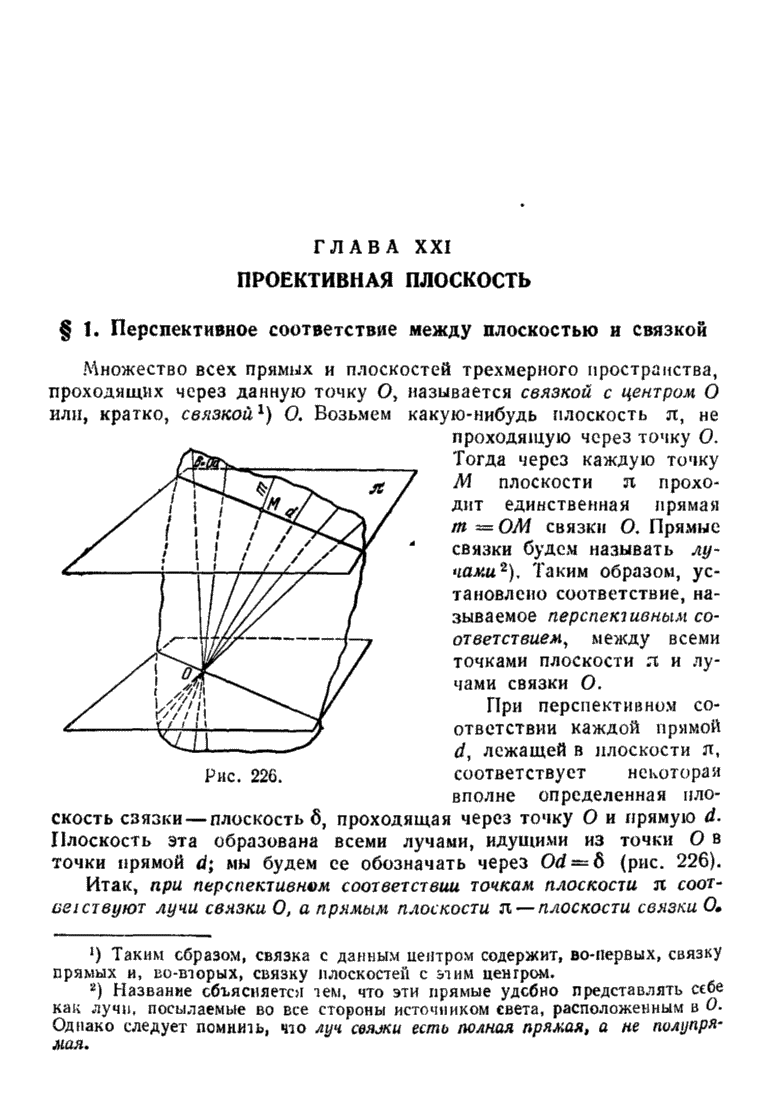
- § 1. Перспективное соответствие между плоскостью и связкой
- § 2. Однородные координаты точек на плоскости и лучел в связке
- § 3. Координаты прямой; арифметическая проективная плоскость; общее определение проективной плоскости
- § 4. Принцип двойственности для проективной плоскости
- § 5. Проективная система координат в связке и на проективной плоскости
- § 6. Проективные преобразования и отображения проективной плоскости
- § 7. Проективные координаты на прямой. Проективные отображения прямой
- § 8. Двойное отношение
- ГЛАВА XXII. КРИВЫЕ ВТОРОГО ПОРЯДКА НА ПРОЕКТИВНОЙ ПЛОСКОСТИ
- § 1. Определение. Теорема единственности
- § 2. Пересечение кривой второго порядка с прямой. Касательные; асимптоты
- § 3. Пучок кривых второго порядка. Второе доказательство теоремы единственности. Теорема Паскаля. Теорема Штейнера
- § 4. Поляры и полюсы
- § 5. Коррелятивное, в частности полярное, соответствие. Тангенциальное уравнение кривой
- § 6. Диаметры как поляры несобственных точек
- § 7. Автополярный треугольник
- § 8. Проективная классификация кривых второго порядка
- ГЛАВА XXIII. НАЧАЛЬНЫЕ СВЕДЕНИЯ ИЗ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ ПРОЕКТИВНОГО ПРОСТРАНСТВА
- § 1. Проективное пространство; его плоскости и прямые
- § 2. Проективные координаты. Проективные преобразования.
- § 3. Понятие об n-мерном проективном пространстве
- § 4. Поверхности второго порядка в проективном пространстве. Теорема единственности
- § 5. Пересечение поверхности второго порядка с плоскостью и с прямой. Касательные прямые. Касательная плоскость. Прямолинейные образующие
- § 6. Полюсы и полярные плоскости
- § 7. Проективная классификация поверхностей второго порядка
- § 8. Распределение по проективным классам поверхностей различных аффинных классов. Проективно-аффинная классификация поверхностей второго порядка
- ГЛАВА XXIV. ЕВКЛИДОВО n-МЕРНОЕ ПРОСТРАНСТВО
- § 1. Введение. Ортогональные матрицы
- § 2. Положительно определенные симметричные билинейные функции в векторном пространстве
- § 3. Определение евклидовых пространств и простейших относящихся к ним понятий
- § 4. Неравенство Коши—Буняковского и его следствия. Углы
- § 5. Подпространства евклидовых пространств. Ортогональное дополнение к данному подпространству
- ГЛАВА XXV. ЛИНЕЙНЫЕ ОПЕРАТОРЫ, БИЛИНЕЙНЫЕ И КВАДРАТИЧНЫЕ ФУНКЦИИ В ЕВКЛИДОВЫХ ПРОСТРАНСТВАХ. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
- § 1. Инвариантные подпространства и собственные векторы линейного оператора в любом векторном пространстве
- § 2. Ортогональные преобразования n-мерного евклидова пространства
- § 3. Движения трехмерного евклидова пространства
- § 4. Преобразования подобия. Дальнейшие проблемы
- § 5. Самосопряженные операторы
- § 6. Теорема о структуре произвольного линейного преобразования евклидова пространства
- § 7. Билинейные и квадратичные формы в евклидовых пространствах
- § 8. (n-1)-мерные многообразия (поверхности) второго поряд] в -мерном аффинном и евклидовом пространствах
- ПРИБАВЛЕНИЕ. ПЕРЕСТАНОВКИ, МНОЖЕСТВА И ИХ ОТОБРАЖЕНИЯ; ГРУППЫ
- § 1. Перестановки
- § 2. Множества
- § 3. Отображения или функции
- § 4. Разбиение множества на подмножества. Отношение эквивалентности
- § 5. Определение группы
- § 6. Простейшие теоремы о группах
- § 7. Эквивалентность подмножеств данного множества по отношению к дайной группе его преобразований
- ЗАДАЧИ
- Задачи к главе IV
- Задачи к главе V
- Задачи к главе VI
- Задачи к главе VIII
- Задачи к главе IX
- Задачи к главе X
- Задачи к главе XI
- Задачи к главе XII
- Задачи к главе XIII
- Задачи к главе XIV
- Задачи к главе XV
- Задачи к главам XVI и XVII
- Задачи к главе XVIII
- Задачи к главам XIX и XX
- Задачи к главе XXI
- Задачи к главе XXII