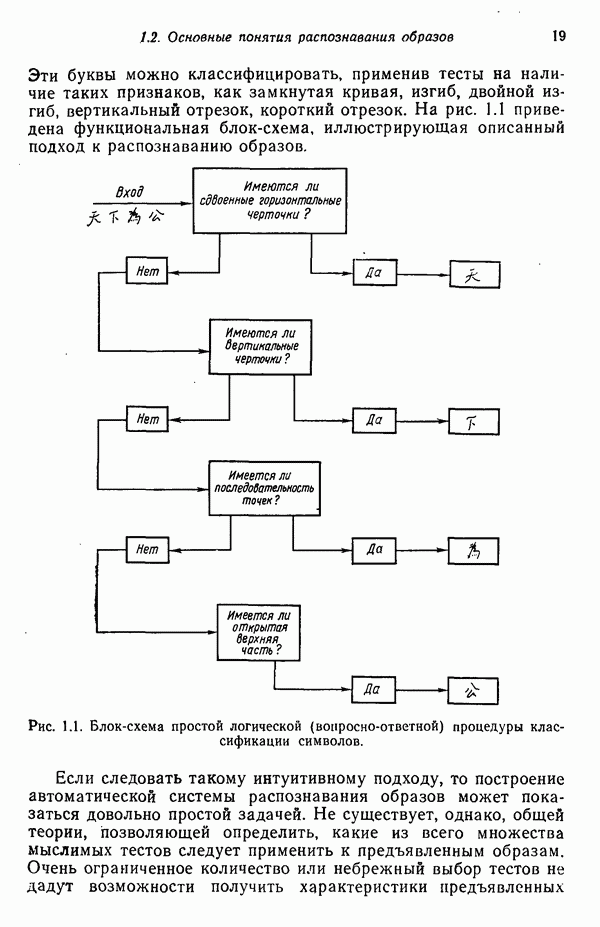
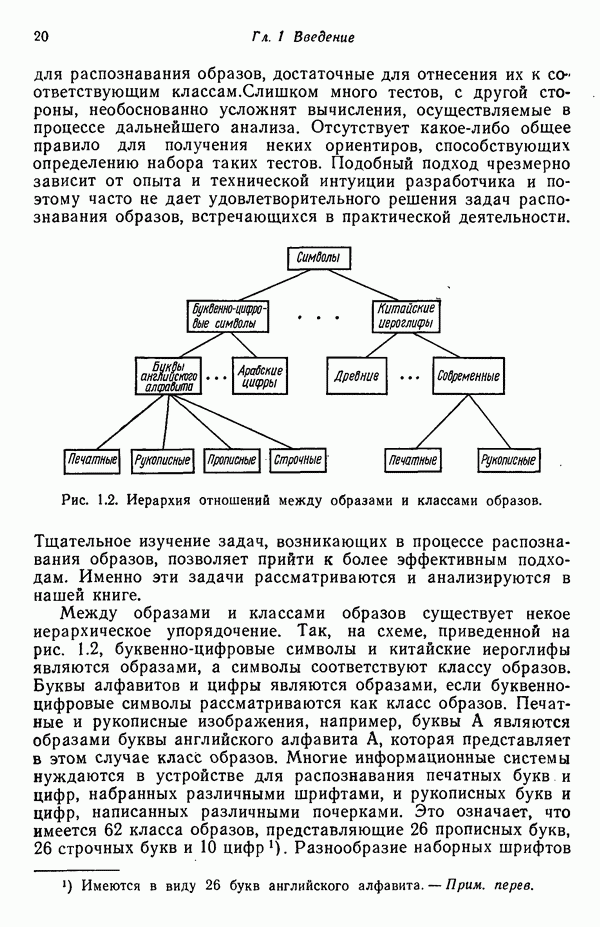
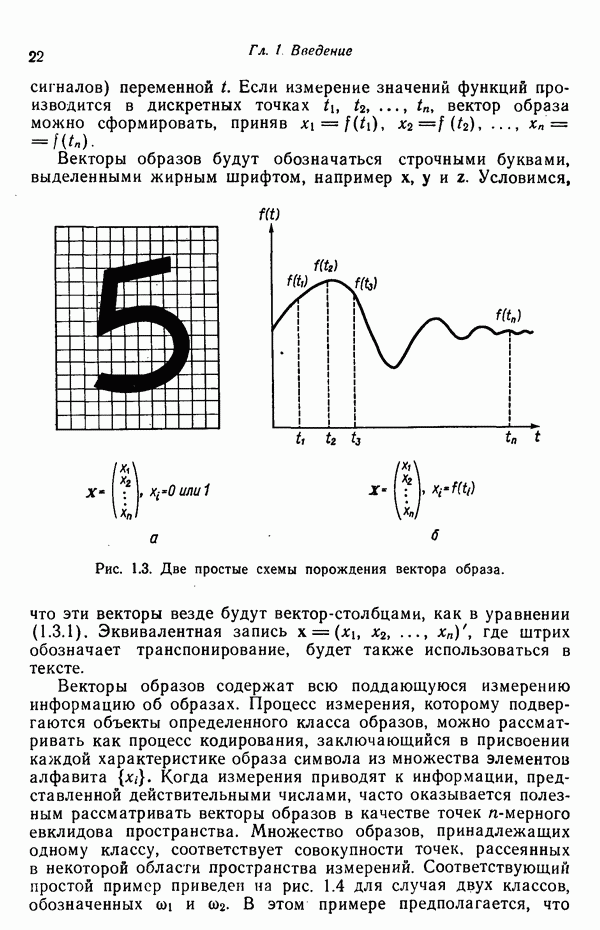
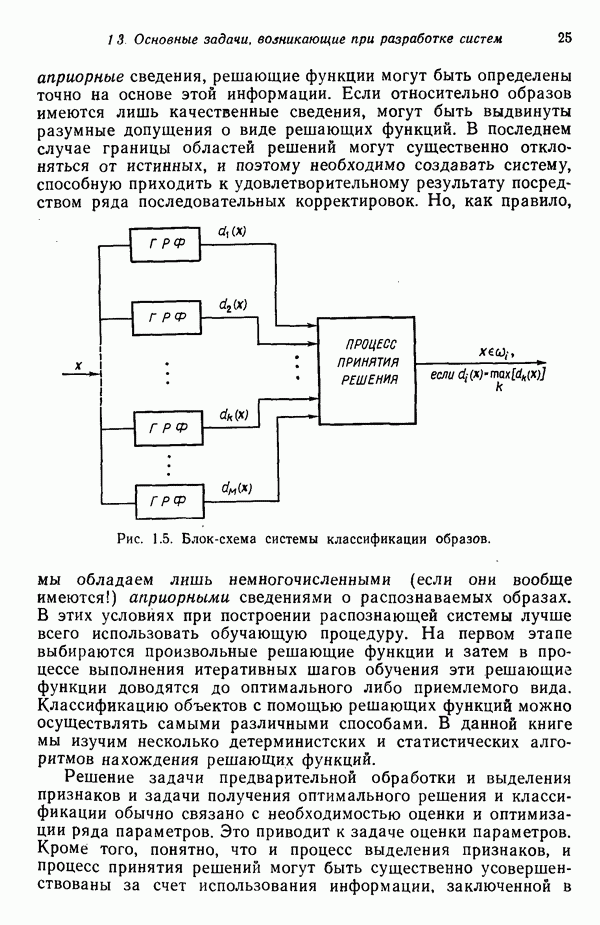
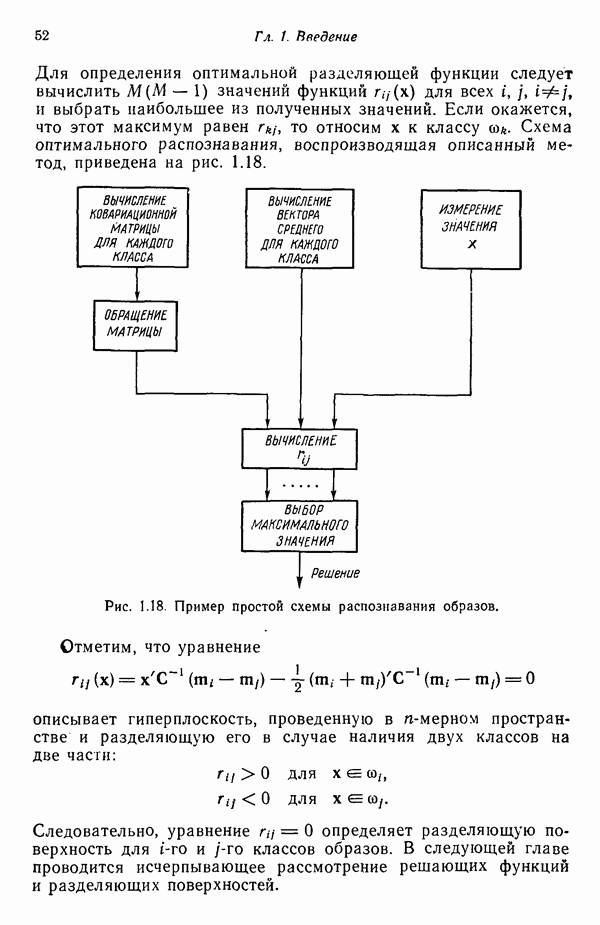
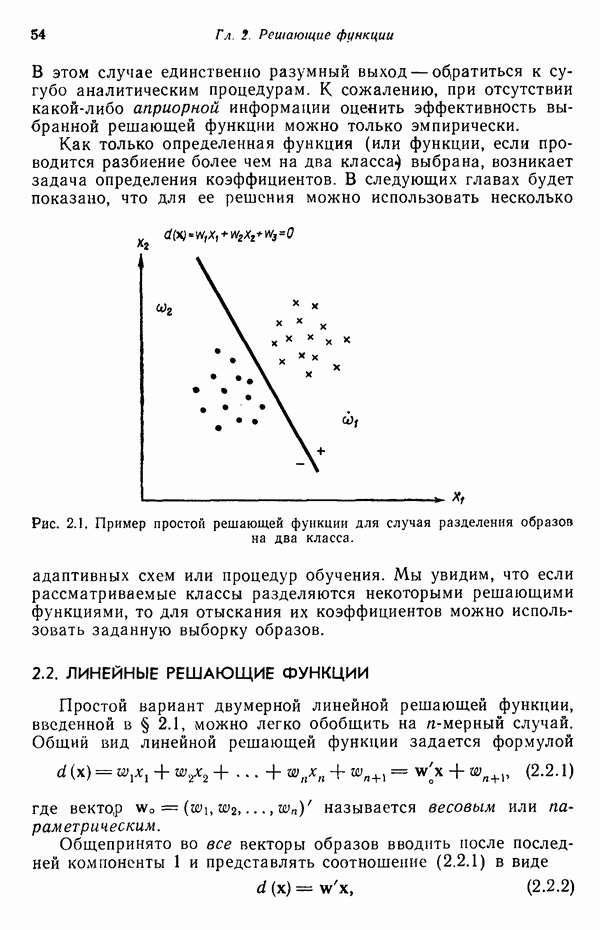
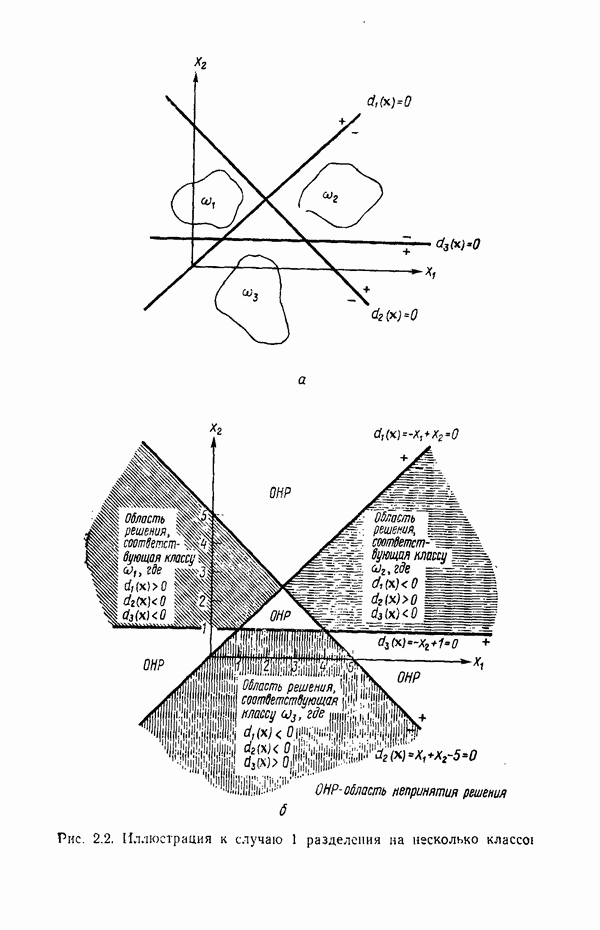
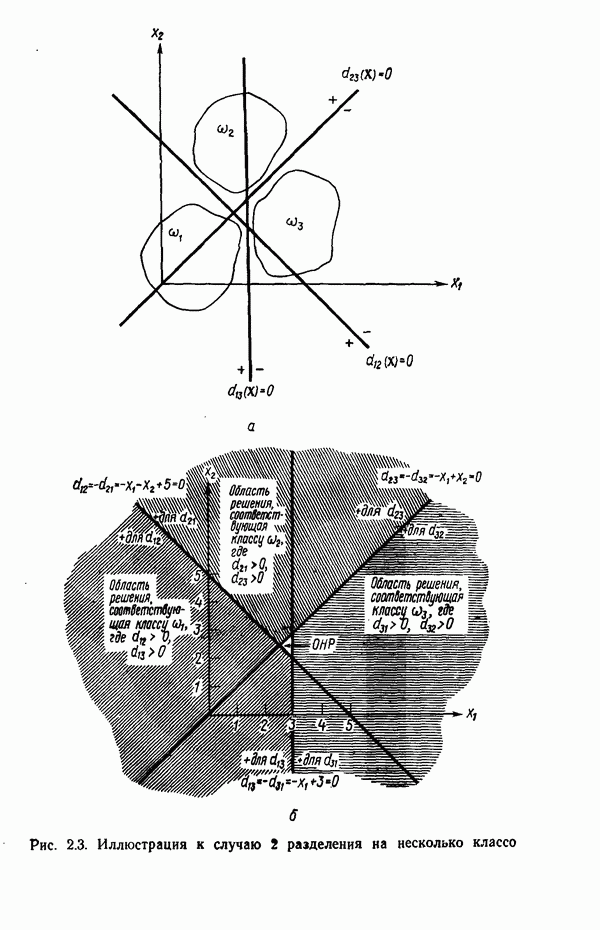
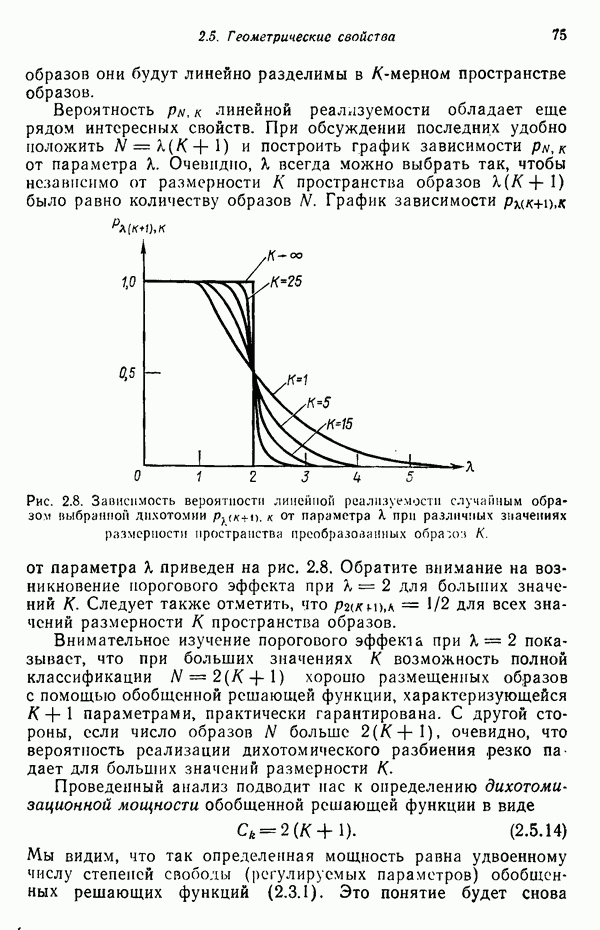
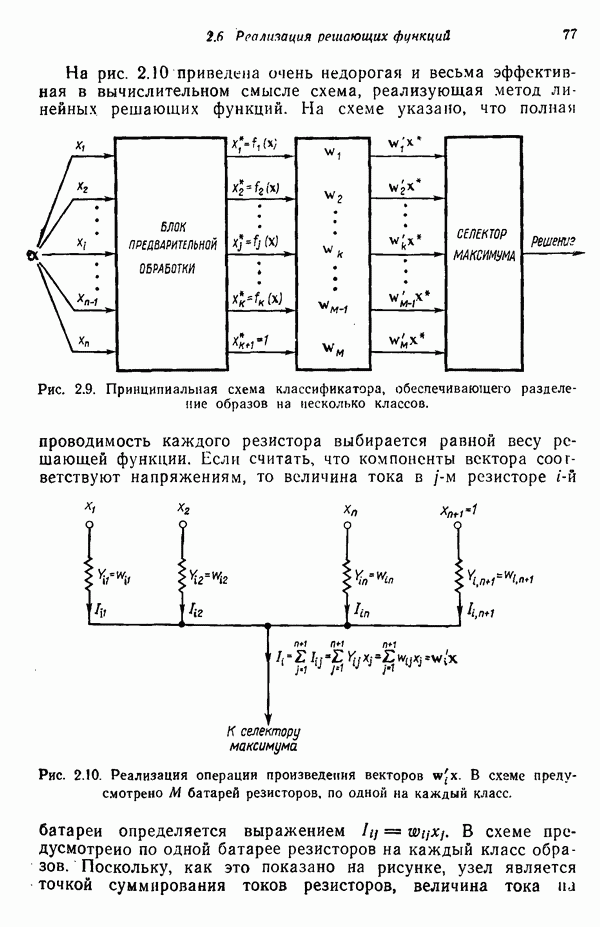
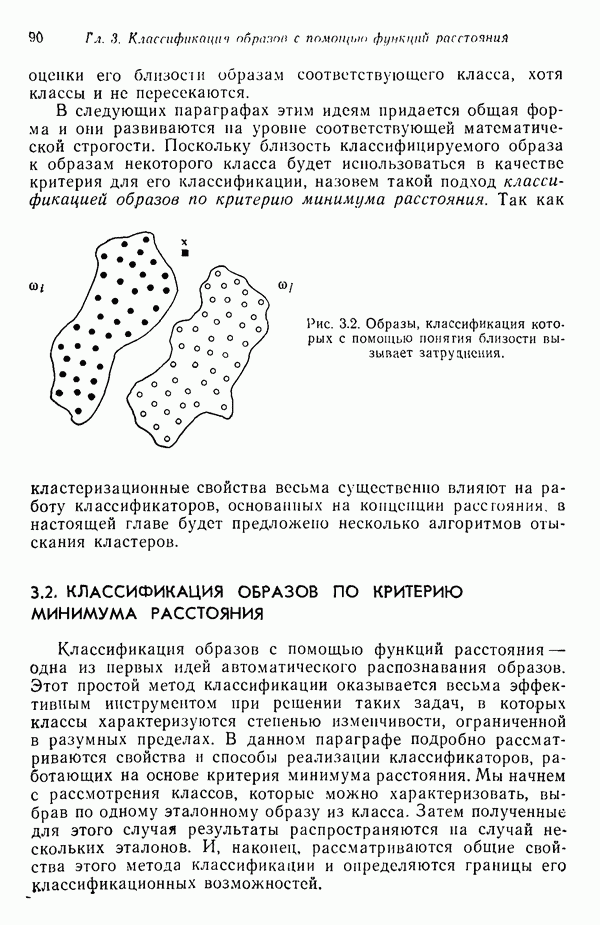
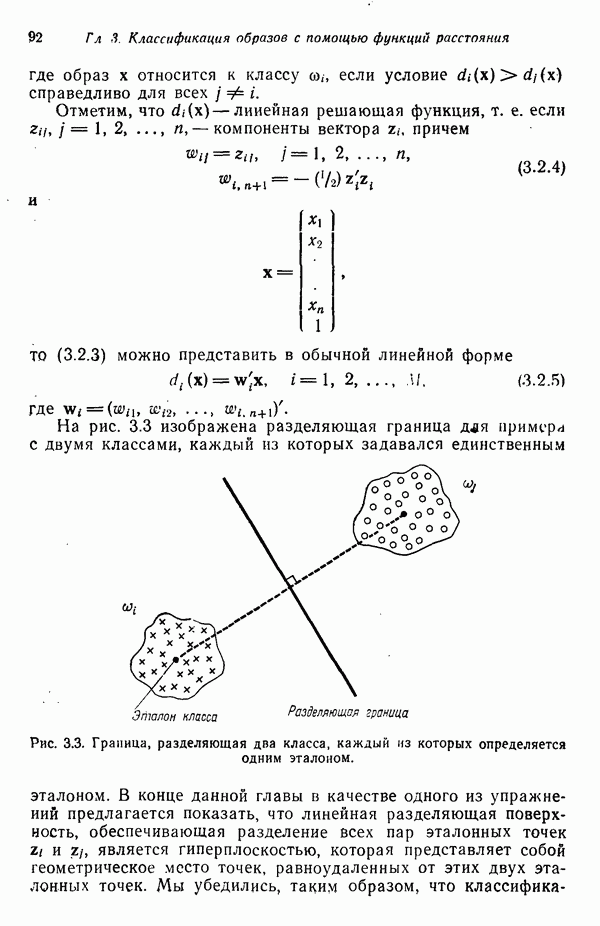
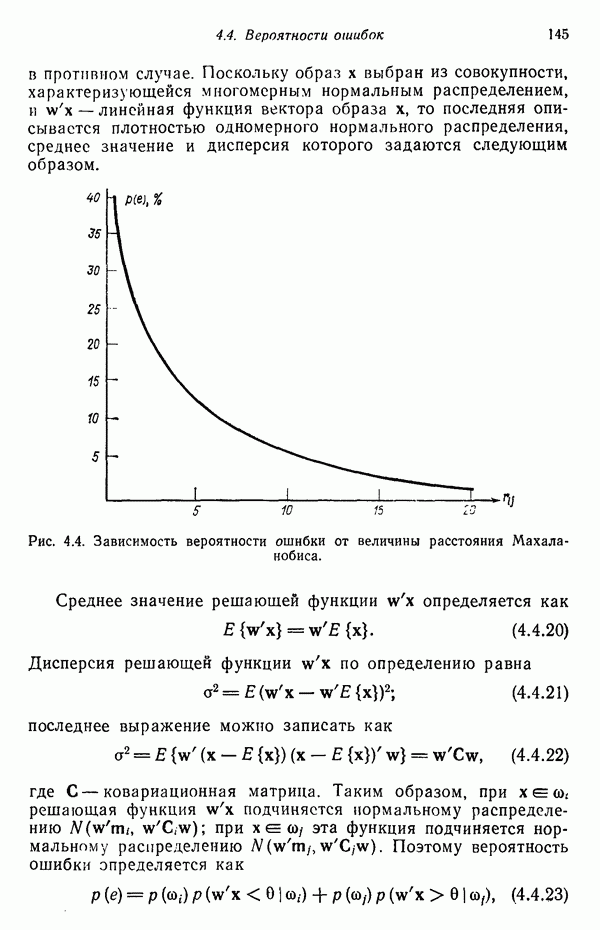
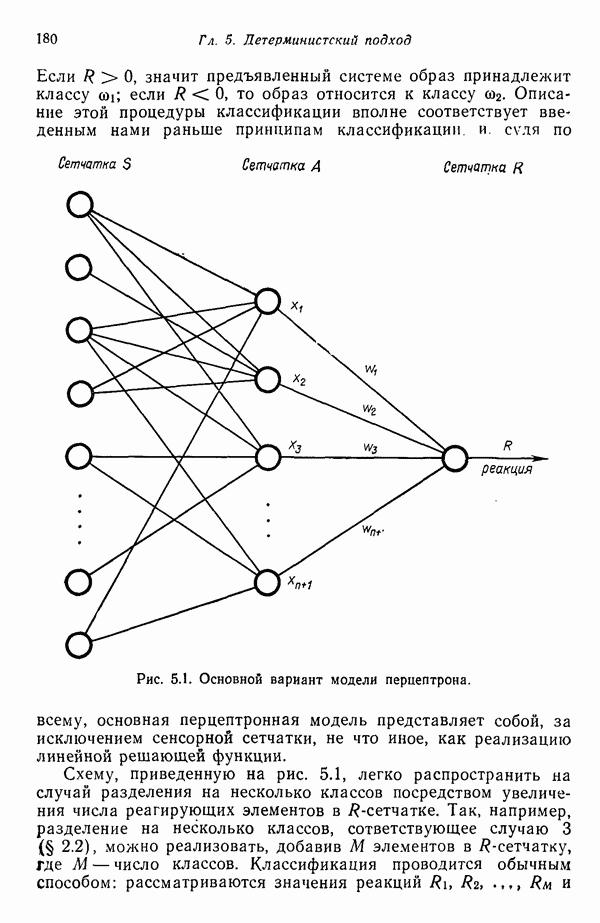
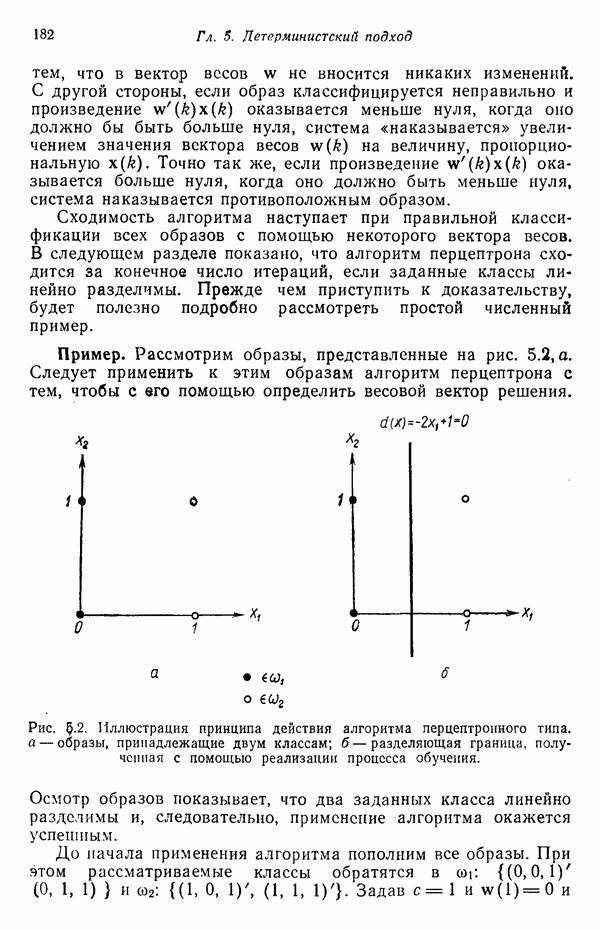
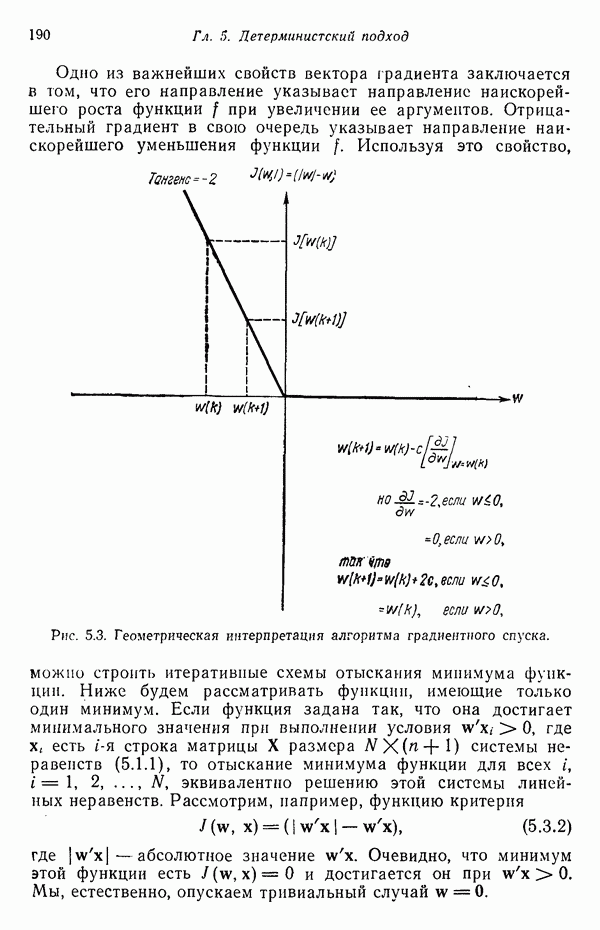
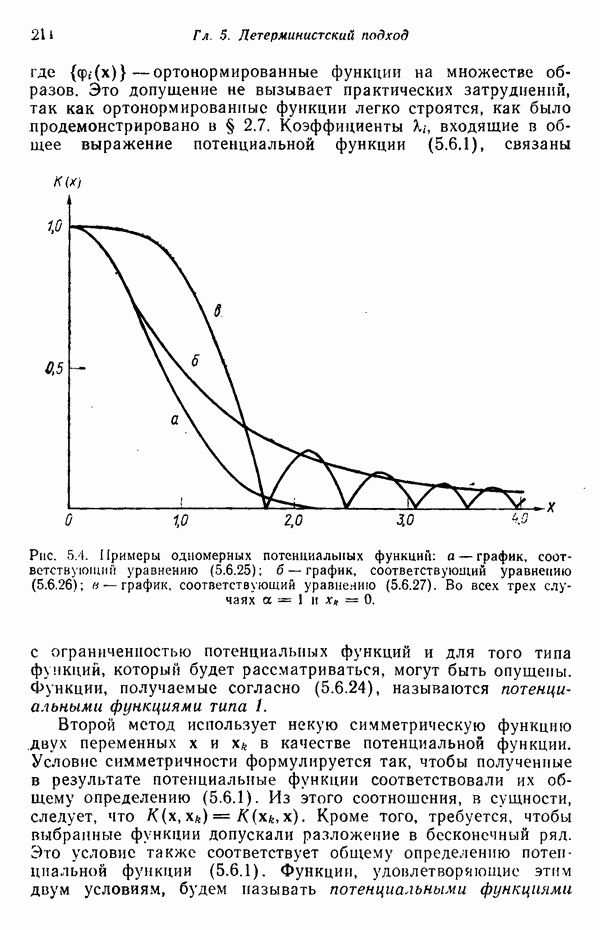
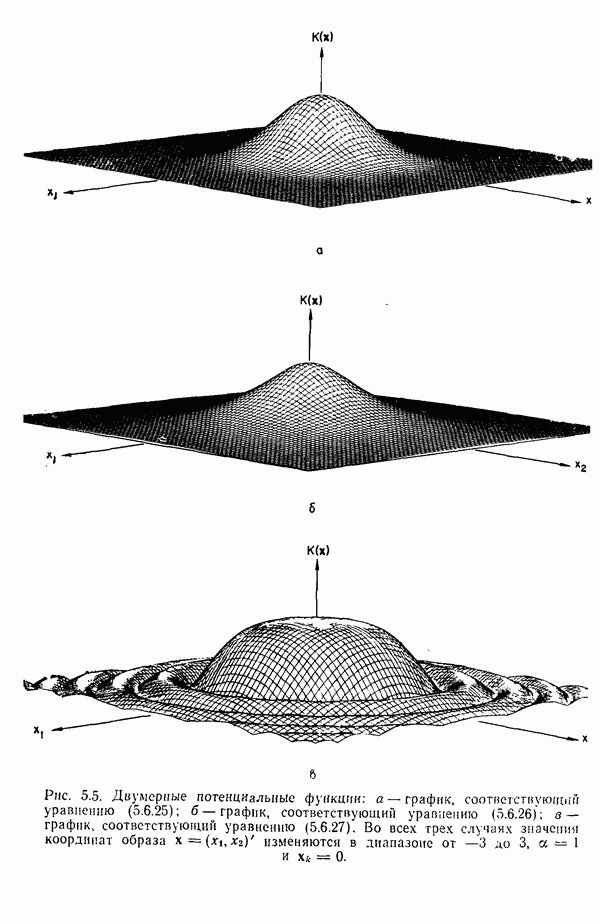
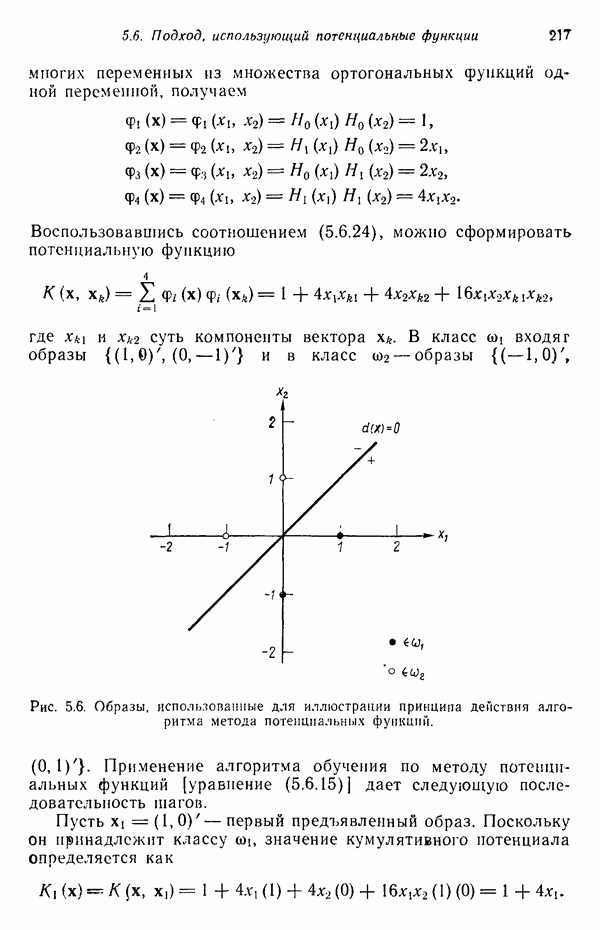
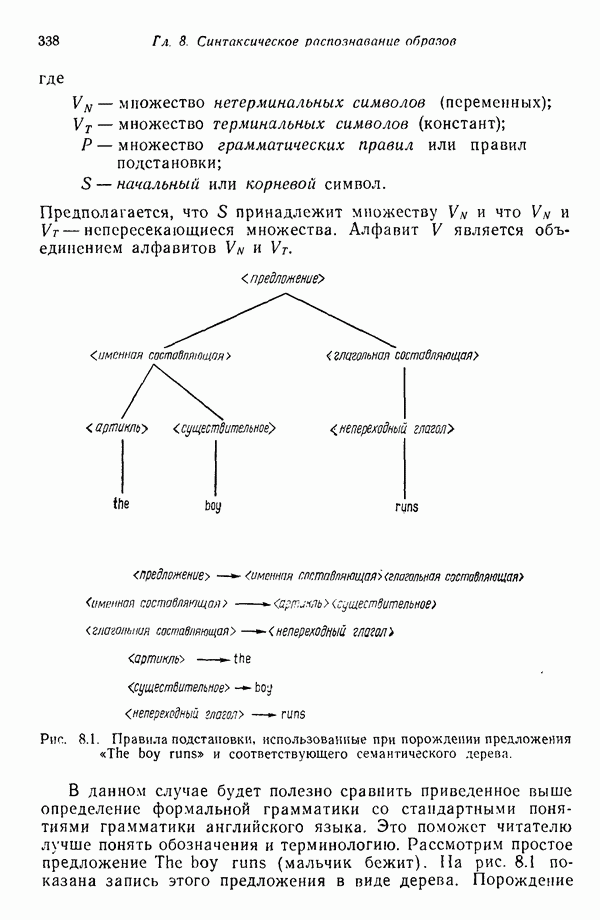
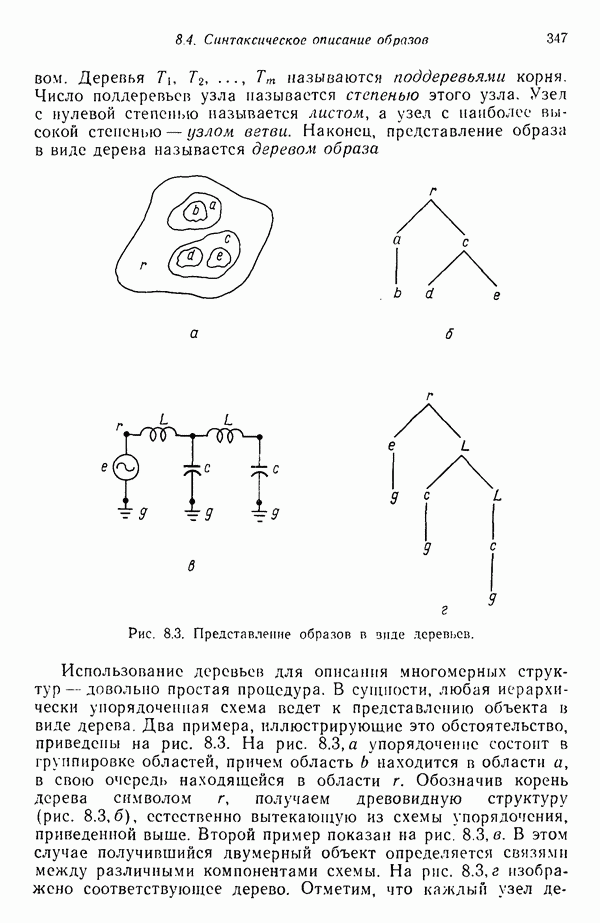
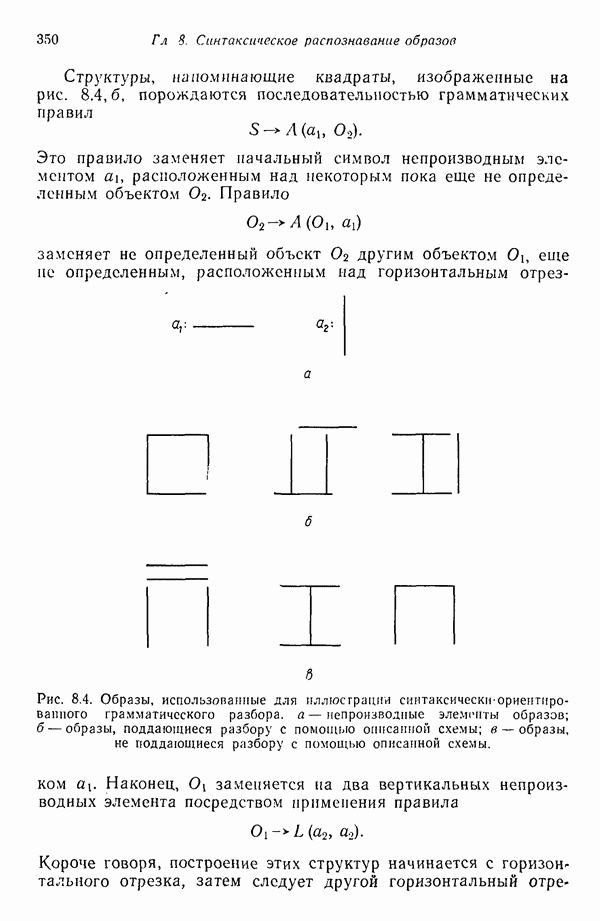
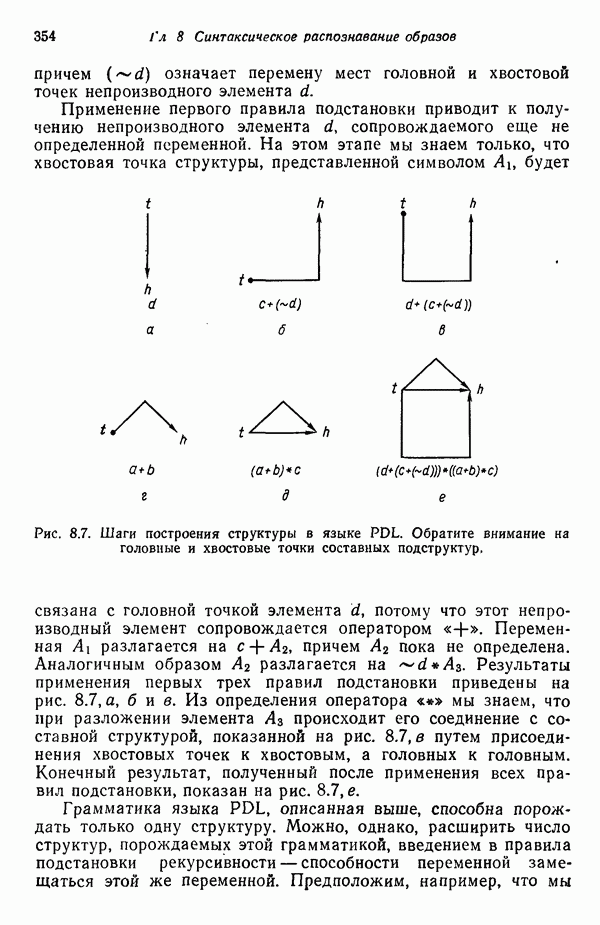
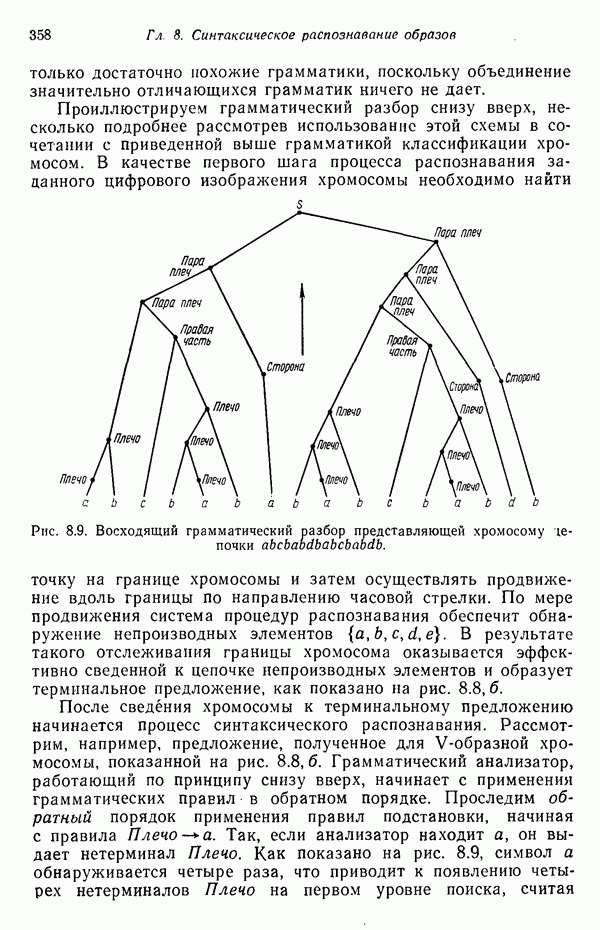
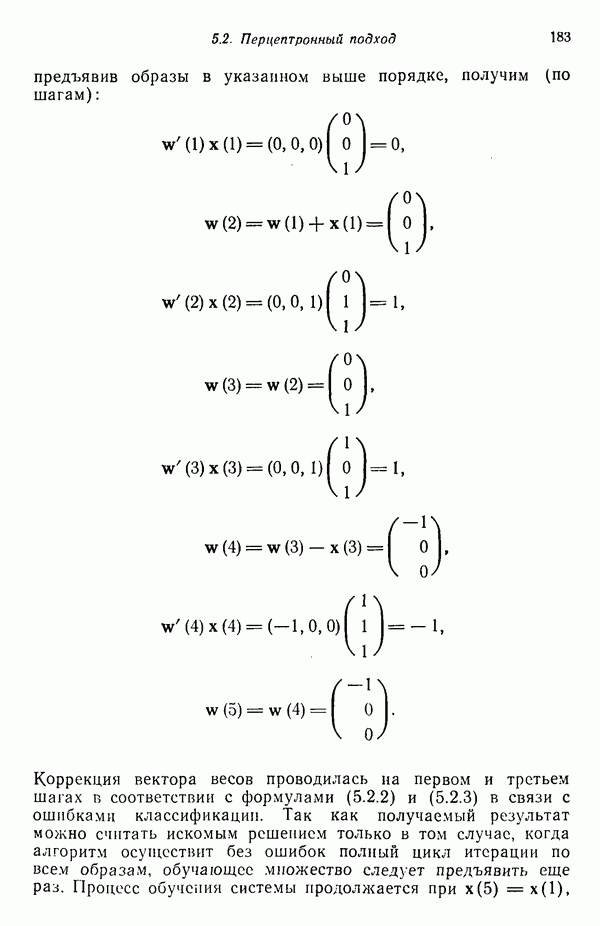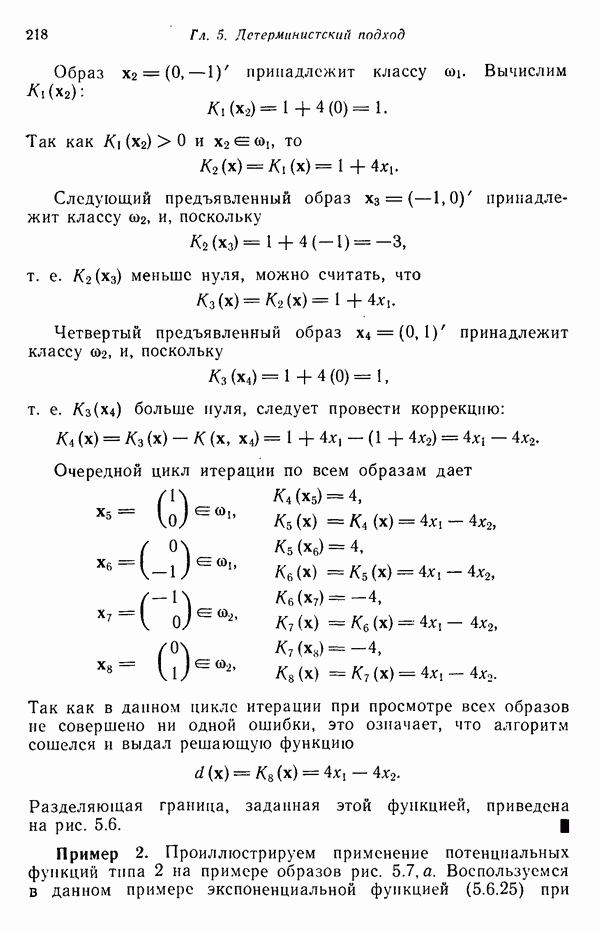| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
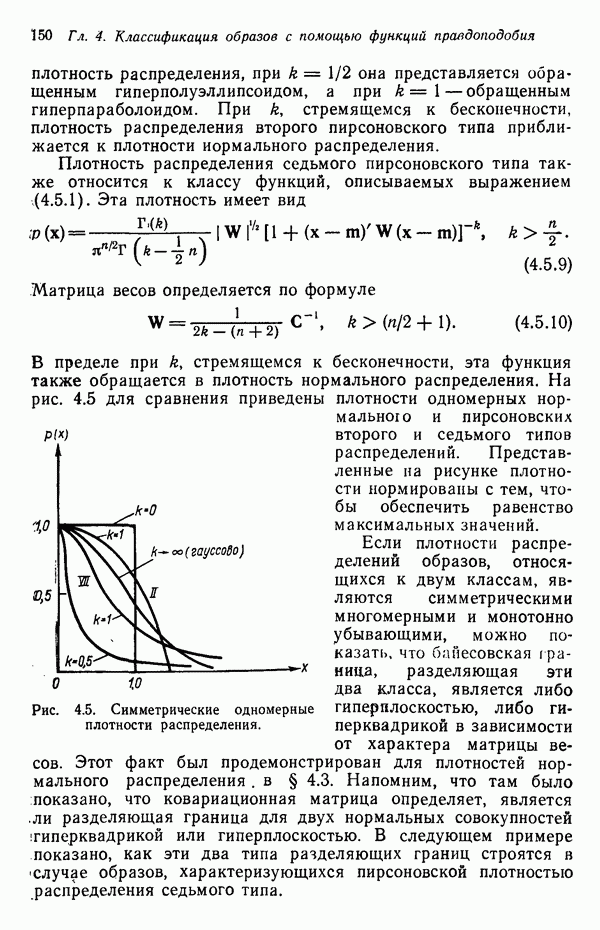
4.6.4. Аппроксимация плотностей распределения функциями
В пп. 4.6.2 и 4.6.3 были рассмотрены частные случаи оценки параметров плотности распределения — предполагалось, что тип распределения известен. Часто, однако, это допущение неприемлемо и возникает необходимость оценивать плотность распределения непосредственно.
Пусть  — оценка плотности распределения
— оценка плотности распределения  причем, как и раньше, под
причем, как и раньше, под  подразумевается
подразумевается  . Мы пытаемся найти такую оценку, которая обеспечила бы минимизацию среднеквадратичной ошибки (интегрального квадратичного показателя качества), определяемой как
. Мы пытаемся найти такую оценку, которая обеспечила бы минимизацию среднеквадратичной ошибки (интегрального квадратичного показателя качества), определяемой как

где  — весовая функция. Воспользуемся разложением оценки
— весовая функция. Воспользуемся разложением оценки  в ряд
в ряд

где  — коэффициенты, подлежащие определению, а
— коэффициенты, подлежащие определению, а  — множество заданных базисных функций. В § 2.7 обсуждался способ построения таких функций. Известное разложение в ряд Фурье является частным случаем разложения (4.6.48) - он возникает, если базисные функции имеют синусоидальный характер.
— множество заданных базисных функций. В § 2.7 обсуждался способ построения таких функций. Известное разложение в ряд Фурье является частным случаем разложения (4.6.48) - он возникает, если базисные функции имеют синусоидальный характер.
Подстановка (4.6.48) в соотношение (4.6.47) дает

Требуется найти такие коэффициенты  которые обеспечат минимизацию интеграла вероятности ошибки
которые обеспечат минимизацию интеграла вероятности ошибки  Необходимое условие минимальности интеграла вероятности ошибки
Необходимое условие минимальности интеграла вероятности ошибки  заключается в том, что
заключается в том, что

Взяв частную производную, получим

Взглянув на правую часть уравнения (4.6.51), нетрудно убедиться в том, что она по определению равна математическому ожиданию функции  . В соответствии с нашим предыдущим анализом математическое ожидание можно аппроксимировать выборочным средним, т. е.
. В соответствии с нашим предыдущим анализом математическое ожидание можно аппроксимировать выборочным средним, т. е.

Подстановка этой аппроксимирующей оценки в уравнение (4.6.51) дает

Если базисные функции  выбраны таким образом, что они ортогональны весовой функции
выбраны таким образом, что они ортогональны весовой функции  то из определения
то из определения
ортогональности [см. (2.7.4)] следует

Подстановка (4.6.54) в уравнение (4.6.53) приводит к следующему соотношению, позволяющему вычислить искомые коэффициенты:

Если базисные функции  ортонормированны, то
ортонормированны, то  для всех
для всех  Кроме того, поскольку члены
Кроме того, поскольку члены  не зависят от
не зависят от  , следовательно, для всех коэффициентов одинаковы, то их можно исключить из аппроксимирующего выражения без всякого ущерба для классификационной мощности коэффициентов. В таком случае
, следовательно, для всех коэффициентов одинаковы, то их можно исключить из аппроксимирующего выражения без всякого ущерба для классификационной мощности коэффициентов. В таком случае

После того как коэффициенты определены, с помощью формулы (4.6.48) формируется оценка плотности распределения 
Использование процедуры, рассмотренной в п. 4.6.2, позволяет представить выражение (4.6.56) в более удобной рекуррентной форме. Если  представляет коэффициент, определенный по выборке объема
представляет коэффициент, определенный по выборке объема  , то выражение для коэффициента при увеличении выборки на один объект имеет следующий вид:
, то выражение для коэффициента при увеличении выборки на один объект имеет следующий вид:

где  . При использовании этой формулы для определения новых коэффициентов необходимы только уже известные коэффициенты
. При использовании этой формулы для определения новых коэффициентов необходимы только уже известные коэффициенты  что существенно упрощает вычислительную процедуру.
что существенно упрощает вычислительную процедуру.
Для того чтобы применение выражений (4.6.48) и (4.6.55) или (4.6.56) приводило к успеху, необходимо иметь в виду два существенных обстоятельства. Во-первых, следует полностью отдавать себе отчет в том, что качество аппроксимации с помощью выбранной системы базисных функций зависит от числа  членов разложения. Поскольку, по всей вероятности, вид плотности распределения
членов разложения. Поскольку, по всей вероятности, вид плотности распределения  нам не известен, оценить качество аппроксимации
нам не известен, оценить качество аппроксимации  при помощи непосредственного сравнения невозможно. С другой стороны, так как оценка
при помощи непосредственного сравнения невозможно. С другой стороны, так как оценка 
отыскивается для того, чтобы построить байесовский классификатор, то заботиться следует только о качестве распознавания, доступном этому классификатору. Последнее можно установить непосредственно в эксперименте с обучающей выборкой. Если при некоторой оценке  качество классификации оказывается неудовлетворительным, следует попробовать увеличить число базисных функций и посмотреть, приводит ли улучшение качества оценки
качество классификации оказывается неудовлетворительным, следует попробовать увеличить число базисных функций и посмотреть, приводит ли улучшение качества оценки  к улучшению качества классификатора. Эту процедуру можно продолжать вплоть до наступления «насыщения» (когда введение дополнительных членов не производит никакого либо очень малый эффект) или до тех пор, пока число членов не начнет превосходить допустимую величину.
к улучшению качества классификатора. Эту процедуру можно продолжать вплоть до наступления «насыщения» (когда введение дополнительных членов не производит никакого либо очень малый эффект) или до тех пор, пока число членов не начнет превосходить допустимую величину.
Вторым важным моментом является выбор базисных функций. Так, например, если плотность распределения  имеет синусоидальный характер, а для разложения оценки
имеет синусоидальный характер, а для разложения оценки  использован степенной ряд, то очевидно, что число членов будет значительно больше, чем при выборе синусоидальных базисных функций. Естественно, при отсутствии априорных сведений о характере плотности распределения
использован степенной ряд, то очевидно, что число членов будет значительно больше, чем при выборе синусоидальных базисных функций. Естественно, при отсутствии априорных сведений о характере плотности распределения  базисные функции в первую очередь должны выбираться исходя из простоты реализации. Все, что можно было бы сказать об общих правилах выбора базисных функций, сводится к тому, что при выполнении условия линейной независимости и некоторых других не очень жестких ограничений на вид плотности распределения
базисные функции в первую очередь должны выбираться исходя из простоты реализации. Все, что можно было бы сказать об общих правилах выбора базисных функций, сводится к тому, что при выполнении условия линейной независимости и некоторых других не очень жестких ограничений на вид плотности распределения  можно доказать сходимость
можно доказать сходимость  при
при  Отметим, что ортогональность является частным случаем линейной независимости.
Отметим, что ортогональность является частным случаем линейной независимости.
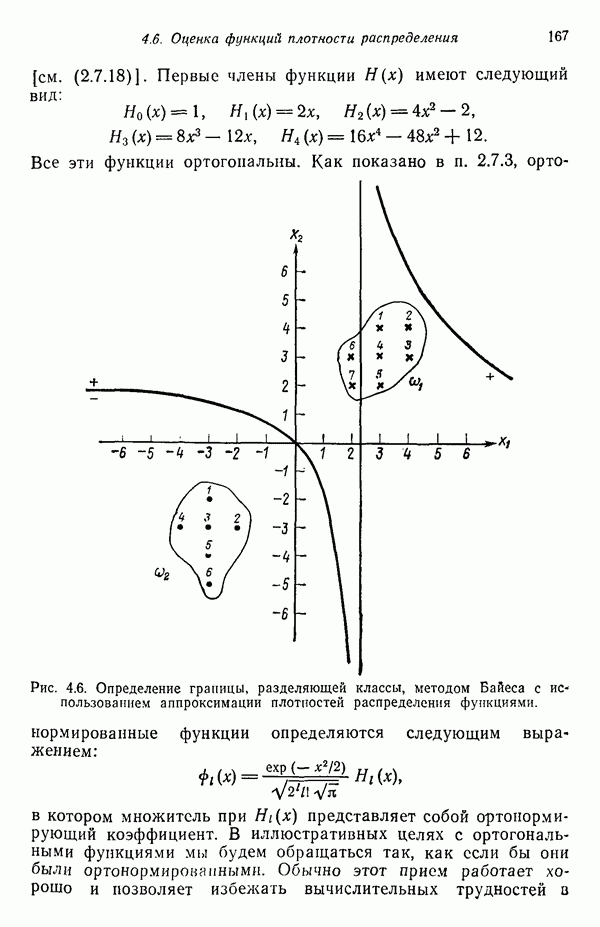
Пример. Рассмотрим классы, приведенные на рис. 4.6. Для этих классов требуется сформировать байесовский классификатор, воспользовавшись плотностями распределений, полученными непосредственной оценкой по обучающим выборкам. Эти плотности можно аппроксимировать, применив выражения вида (4.6.48):

в котором первый индекс коэффициента указывает класс  .
.
Как следует из (4.6.54), базисные функции  считаются ортогональными в области определения образов. Особенно удобны для применения многочлены Эрмита, рассмотренные в § 2.7, поскольку областью их ортогональности является интервал
считаются ортогональными в области определения образов. Особенно удобны для применения многочлены Эрмита, рассмотренные в § 2.7, поскольку областью их ортогональности является интервал  . В одномерном случае эти функции определяются рекуррентным соотношением
. В одномерном случае эти функции определяются рекуррентным соотношением

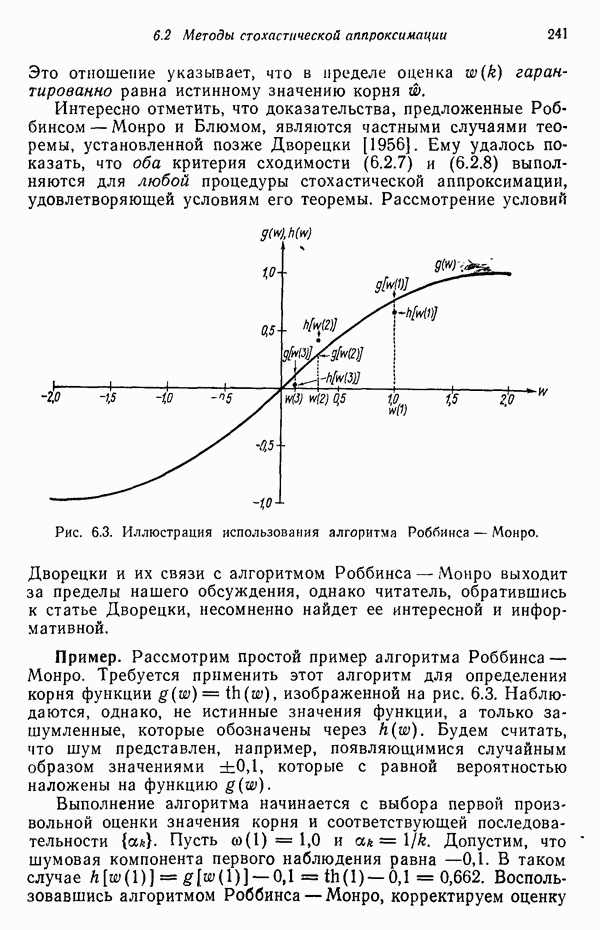
Рис. 4.6. (см. скан) Определение границы, разделяющей классы, методом Байеса с использованием аппроксимации плотностей распределения функциями.
[см. (2.7.18)]. Первые члены функции  имеют следующий вид:
имеют следующий вид:

Все эти функции ортогональны. Как показано в п. 2.7.3, ортонормированные функции определяются следующим выражением:

в котором множитель при  представляет собой ортонормирующий коэффициент. В иллюстративных целях с ортогональными функциями мы будем обращаться так, как если бы они были ортонормироваиными. Обычно этот прием работает хорошо и позволяет избежать вычислительных трудностей в
представляет собой ортонормирующий коэффициент. В иллюстративных целях с ортогональными функциями мы будем обращаться так, как если бы они были ортонормироваиными. Обычно этот прием работает хорошо и позволяет избежать вычислительных трудностей в
(4.6.55) при больших значениях  . В частности, при
. В частности, при  для многочленов Эрмита
для многочленов Эрмита  .
.
Множество ортогональных функций для двумерного случая легко получить, формируя произвольные попарные комбинации одномерных функций. Пусть  . Четыре члена низшего порядка двумерного ортогонального множества выглядят следующим образом:
. Четыре члена низшего порядка двумерного ортогонального множества выглядят следующим образом:

Должно быть очевидно, что порядок формирования этих функций не единственный. Для получения любой функции  можно использовать произвольную парную комбинацию функций одной переменной. Любой иной выбор
можно использовать произвольную парную комбинацию функций одной переменной. Любой иной выбор  просто приведет к получению более сложных членов.
просто приведет к получению более сложных членов.
Теперь задача заключается в определении коэффициентов  разложения
разложения  Используя допущение об ортонормированности функций, эти коэффициенты можно вычислить посредством (4.6.56). Для класса
Используя допущение об ортонормированности функций, эти коэффициенты можно вычислить посредством (4.6.56). Для класса 

где  — число образов, входящих в класс
— число образов, входящих в класс  изменяется в диапазоне от 1 до
изменяется в диапазоне от 1 до  . Для образов класса
. Для образов класса  представленного на рис. 4.6, применение данной процедуры дает
представленного на рис. 4.6, применение данной процедуры дает

где первый индекс образа указывает, какому классу он принадлежит (в данном случае  ). Так как
). Так как  , то
, то

Следующий коэффициент определяется выражением

и так как реализация функции  эквивалентна удвоению первой компоненты образа
эквивалентна удвоению первой компоненты образа  то
то

Аналогично получим

Применение этой же процедуры к образам класса  приводит к следующим коэффициентам:
приводит к следующим коэффициентам:

Следовательно, согласно (4.6.48), аппроксимация плотности распределения  такова:
такова:

В таком случае искомые решающие функции имеют вид

Если предположить, что  то
то

В таком случае уравнением разделяющей границы будет

Соответствующая граница показана на рис. 4.6. Поскольку данная задача требует разделения образов на два класса, разность решающих функций  представляет классификационную решающую функцию. Следует отметить также, что в данном случае с равным успехом можно было воспользоваться линейной аппроксимацией плотностей распределения
представляет классификационную решающую функцию. Следует отметить также, что в данном случае с равным успехом можно было воспользоваться линейной аппроксимацией плотностей распределения  . В этом можно убедиться, приравняв нулю нелинейный член последнего выражения. Хотя мы для того, чтобы проиллюстрировать процедуры во всех подробностях, с самого начала работали с нелинейной решающей функцией.
. В этом можно убедиться, приравняв нулю нелинейный член последнего выражения. Хотя мы для того, чтобы проиллюстрировать процедуры во всех подробностях, с самого начала работали с нелинейной решающей функцией.
должно быть очевидно, что в большинстве задач в первую очередь используется линейная аппроксимация. Только получение неприемлемых результатов заставляет увеличивать сложность аппроксимации.
Важный частный случай аппроксимации посредством функций возникает при оценке плотностей распределения для двоичных образов. Если имеется образ  и каждая его компонента
и каждая его компонента  принимает значения 1 или 0, то общее число возможных различных образов равно
принимает значения 1 или 0, то общее число возможных различных образов равно  причем каждому из них соответствует «своя» вершина единичного
причем каждому из них соответствует «своя» вершина единичного  -мерного куба. В таком случае нам нужно определять не плотность непрерывного распределения, а плотность дискретного распределения
-мерного куба. В таком случае нам нужно определять не плотность непрерывного распределения, а плотность дискретного распределения  где индекс
где индекс  пробегает значения от 1 до
пробегает значения от 1 до  другими словами, нас интересует вероятность появления каждого из
другими словами, нас интересует вероятность появления каждого из  возможных векторов образов. Результаты настоящего раздела нетрудно использовать для решения данной задачи посредством соответствующего выбора базисных функций
возможных векторов образов. Результаты настоящего раздела нетрудно использовать для решения данной задачи посредством соответствующего выбора базисных функций  . В качестве последних можно использовать полиномиальные функции Радемахера — Уолша, которые часто применяются при разложении дискретных функций. Искомое множество содержит
. В качестве последних можно использовать полиномиальные функции Радемахера — Уолша, которые часто применяются при разложении дискретных функций. Искомое множество содержит  членов, полученных перемножением различных членов вида
членов, полученных перемножением различных членов вида  в количестве пуля, одного, двух, трех и т. д. — вплоть до
в количестве пуля, одного, двух, трех и т. д. — вплоть до  Эта процедура проиллюстрирована в табл. 4.1.
Эта процедура проиллюстрирована в табл. 4.1.
Эти дискретные полиномиальные функции ортогональны относительно весовой функции  (см. п. 2.7.1), так как
(см. п. 2.7.1), так как

где суммирование проводится по всем  значениям двоичных векторов
значениям двоичных векторов 
Если в разложении используется только  базисных функций, то приближенное значение плотности дискретного распределения
базисных функций, то приближенное значение плотности дискретного распределения  имеет, согласно (4.6.48), следующий вид:
имеет, согласно (4.6.48), следующий вид:

где коэффициенты определяются из (4.6.55) при  , т. е.
, т. е.

Соответствующие коэффициенты для ортонормированиых функций задаются соотношением (4.6.56).
Таблица 4.1 (см. скан). Формирование полиномиальных функций Радемахера — Уолша
Поскольку в данном случае полное множество базисных функций состоит из  элементов, сходимость аппроксимированной плотности распределения
элементов, сходимость аппроксимированной плотности распределения  к истинной плотности распределения
к истинной плотности распределения  обеспечивается при
обеспечивается при  (общее число различных двоичных образов).
(общее число различных двоичных образов).
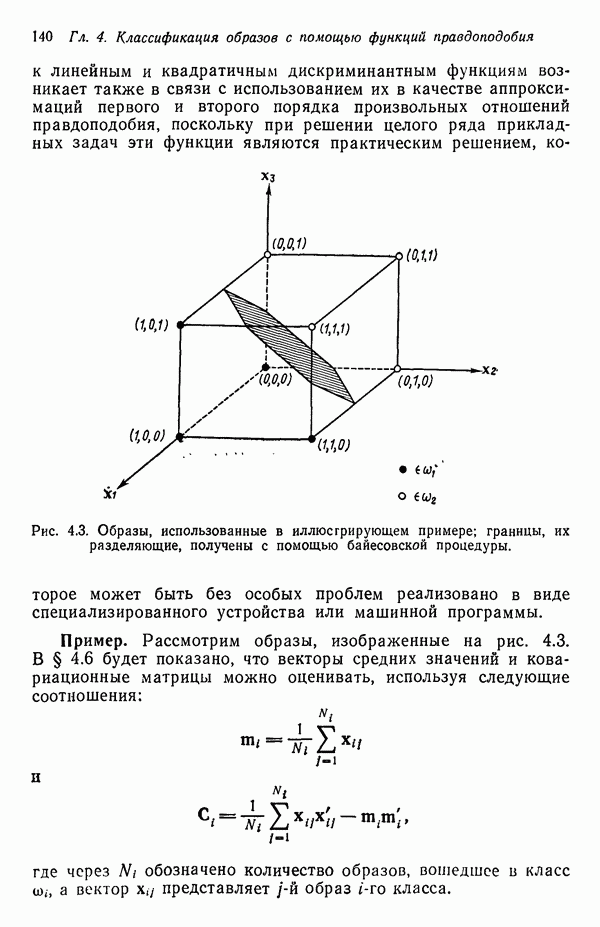
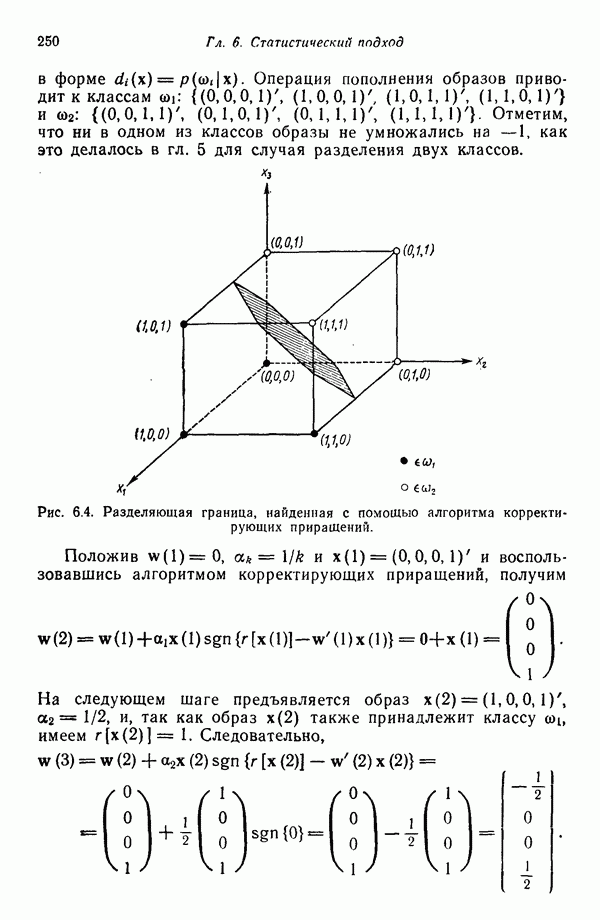
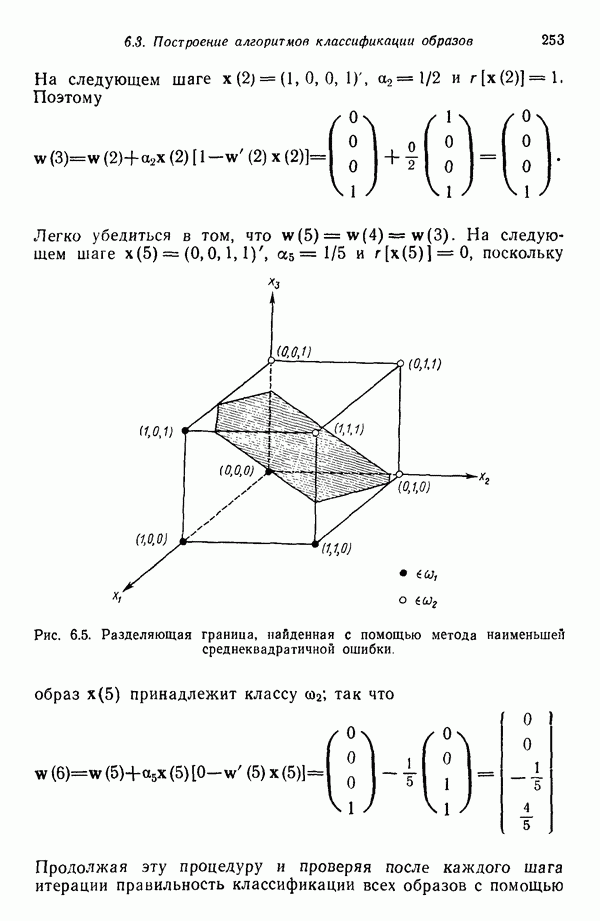
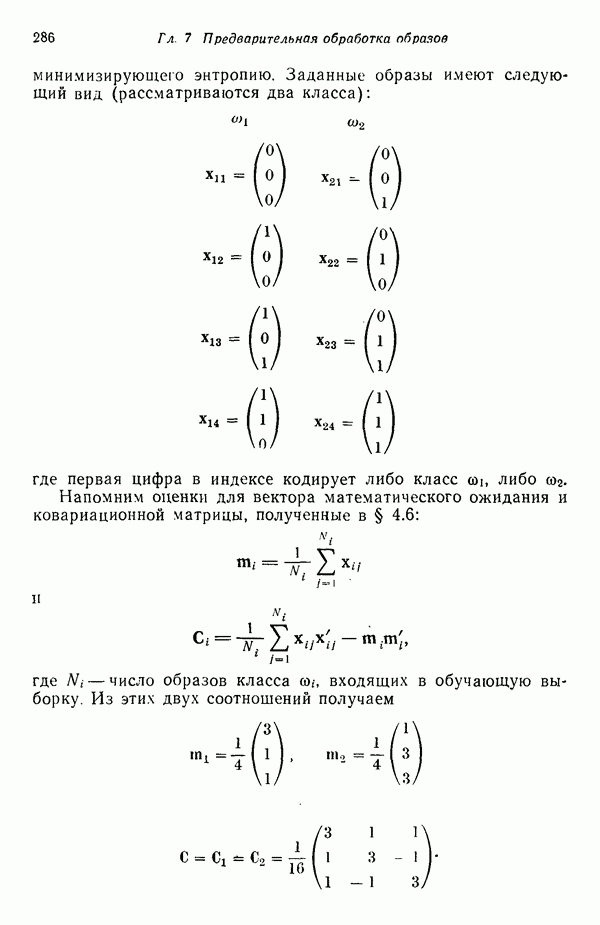
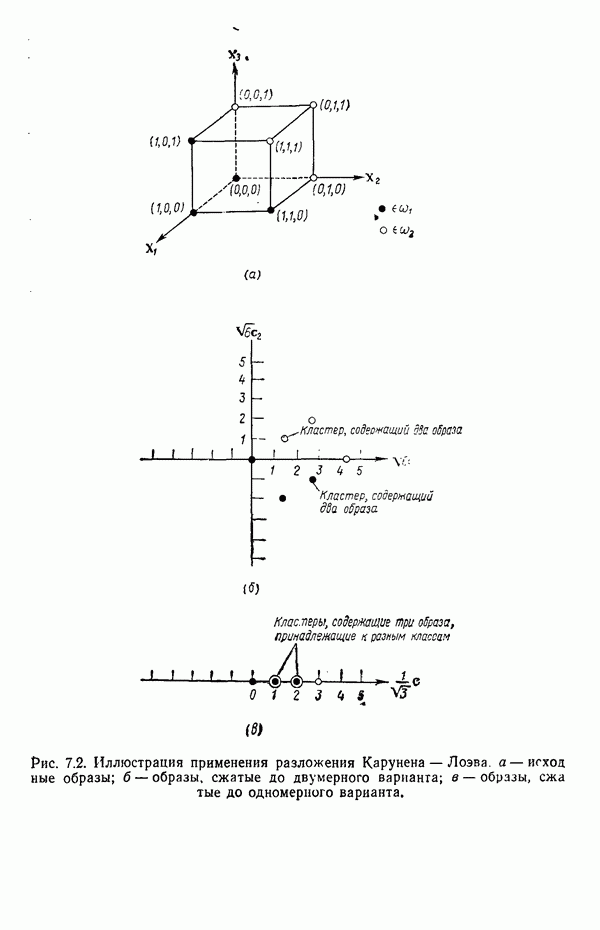
Пример. В качестве примера аппроксимации посредством дискретных функций рассмотрим снова образы, представленные на рис. 4.3. Образы принадлежат двум классам:  .
.
Решив воспользоваться линейиой аппроксимацией плотности распределения  , из табл. 4.1 получаем
, из табл. 4.1 получаем  , где все
, где все  принимают значения 0 или 1.
принимают значения 0 или 1.
Коэффициенты для класса  согласно (4.6.59), суть
согласно (4.6.59), суть

где  представляет количество образов, входящих в класс
представляет количество образов, входящих в класс  . Проведя суммирование по образам класса
. Проведя суммирование по образам класса  получим
получим

Применение такой же процедуры к классу  дает
дает

В таком случае аппроксимации плотностей распределения выглядят следующим образом:

Приняв, что  получим следующие решающие функции:
получим следующие решающие функции:

Одну решающую функцию, обеспечивающую разделение обоих классов, можно получить, положив  Таким образом,
Таким образом,

после умножения на 16 эта функция принимает вид

Легко убедиться в том, что  для всех образов класса
для всех образов класса  для всех образов класса
для всех образов класса  Использование ортонормированных функций дает такие же результаты.
Использование ортонормированных функций дает такие же результаты.
Следует отметить, что решающая функция  имеет смысл только для двоичных образов
имеет смысл только для двоичных образов  . Следовательно, в данном случае понятие разделяющей поверхности в том виде, как оно вводилось выше, перестает работать. Функция
. Следовательно, в данном случае понятие разделяющей поверхности в том виде, как оно вводилось выше, перестает работать. Функция  имеет только восемь значений — по одному на каждый из восьми различных двоичных образов, которые могут существовать в трехмерном пространстве.
имеет только восемь значений — по одному на каждый из восьми различных двоичных образов, которые могут существовать в трехмерном пространстве.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
- Глава 1. ВВЕДЕНИЕ
- 1.1. ПРОБЛЕМА ОБРАБОТКИ ИНФОРМАЦИИ
- 1.2. ОСНОВНЫЕ ПОНЯТИЯ РАСПОЗНАВАНИЯ ОБРАЗОВ
- 1.3. ОСНОВНЫЕ ЗАДАЧИ, ВОЗНИКАЮЩИЕ ПРИ РАЗРАБОТКЕ СИСТЕМ РАСПОЗНАВАНИЯ ОБРАЗОВ
- 1.4. КРАТКОЕ ОПИСАНИЕ КОНЦЕПЦИЙ И МЕТОДОЛОГИИ
- 2. Принцип общности свойств
- 3. Принцип кластеризации
- 1.5. ПРИМЕРЫ АВТОМАТИЧЕСКИХ СИСТЕМ РАСПОЗНАВАНИЯ ОБРАЗОВ
- 1.6. ПРОСТАЯ МОДЕЛЬ РАСПОЗНАВАНИЯ ОБРАЗОВ
- Глава 2. РЕШАЮЩИЕ ФУНКЦИИ
- 2.2. ЛИНЕЙНЫЕ РЕШАЮЩИЕ ФУНКЦИИ
- 2.3. ОБОБЩЕННЫЕ РЕШАЮЩИЕ ФУНКЦИИ
- 2.4. ПРОСТРАНСТВО ОБРАЗОВ И ПРОСТРАНСТВО ВЕСОВ
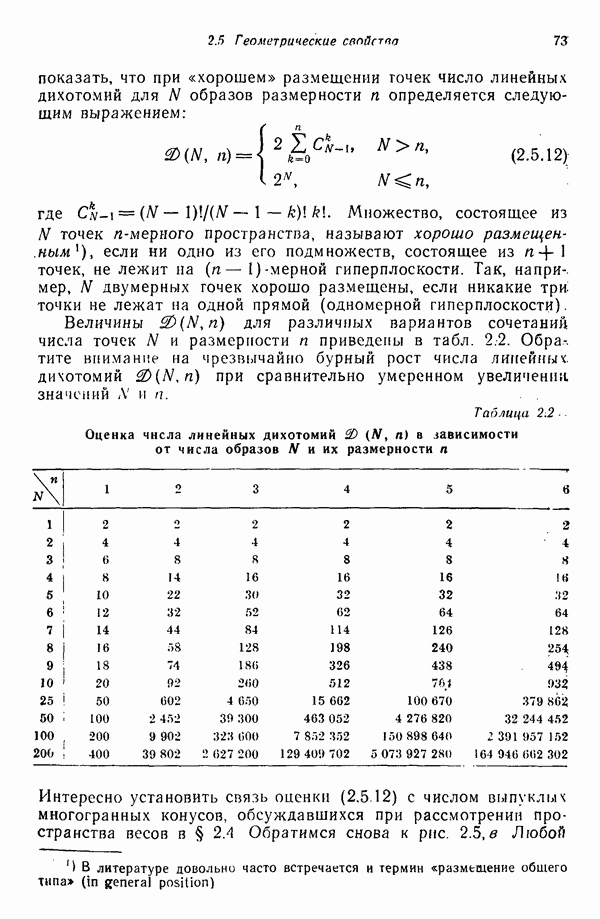
- 2.5. ГЕОМЕТРИЧЕСКИЕ СВОЙСТВА
- 2.5.2. Дихотомии
- 2.5.3. Дихотомизационная мощность обобщенных решающих функций
- 2.6. РЕАЛИЗАЦИЯ РЕШАЮЩИХ ФУНКЦИЙ
- 2.7. ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ
- 2.7.2. Построение функций многих переменных
- 2.7.3. Ортогональные и ортонормированные системы функций
- 2.8. ЗАКЛЮЧИТЕЛЬНЫЕ ЗАМЕЧАНИЯ
- Глава 3. КЛАССИФИКАЦИЯ ОБРАЗОВ С ПОМОЩЬЮ ФУНКЦИЙ РАССТОЯНИЯ
- 3.2. КЛАССИФИКАЦИЯ ОБРАЗОВ ПО КРИТЕРИЮ МИНИМУМА РАССТОЯНИЯ
- 3.2.2. Множественность эталонов
- 3.2.3. Обобщение принципов классификации по минимуму расстояния
- 3.2.4. Синтез системы распознавания. Пример
- 3.3. ВЫЯВЛЕНИЕ КЛАСТЕРОВ
- 3.3.2. Критерии кластеризации
- 3.3.3. Простой алгоритм выявления кластеров
- 3.3.4. Алгоритм максиминного расстояния
- 3.3.5. Алгоритм К внутригрупповых средних
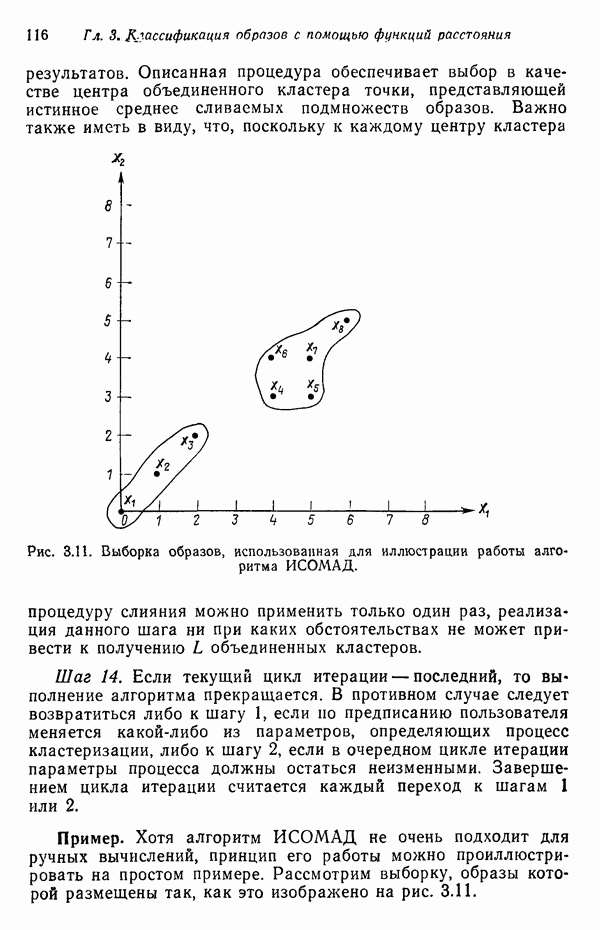
- 3.3.6. Алгоритм ИСОМАД
- 3.3.7. Оценка результатов процесса кластеризации
- 3.3.8. Кластеризация, основанная на теории графов
- 3.4. РАСПОЗНАВАНИЕ ОБРАЗОВ БЕЗ УЧИТЕЛЯ
- 3.5. ЗАКЛЮЧИТЕЛЬНЫЕ ЗАМЕЧАНИЯ
- Глава 4. КЛАССИФИКАЦИЯ ОБРАЗОВ С ПОМОЩЬЮ ФУНКЦИЙ ПРАВДОПОДОБИЯ
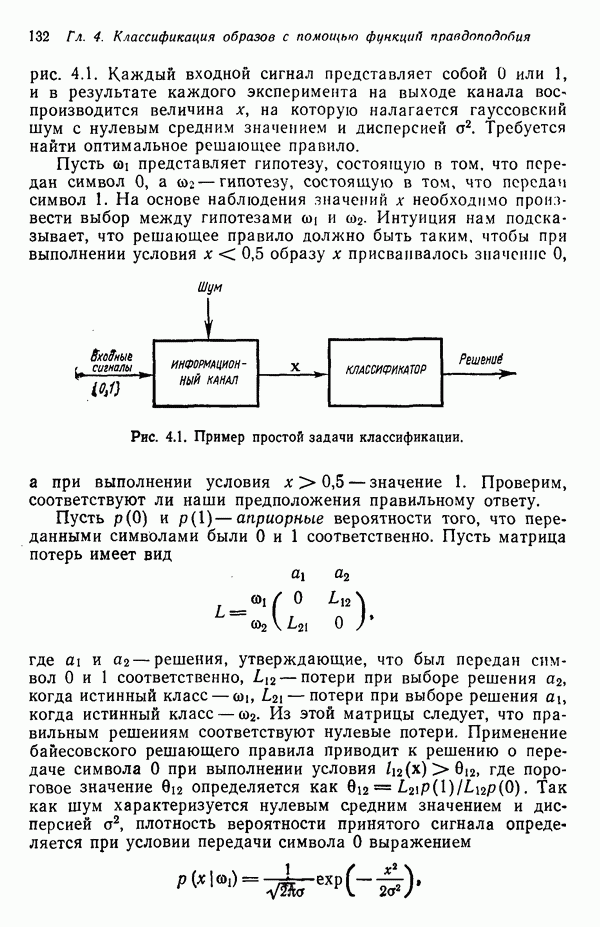
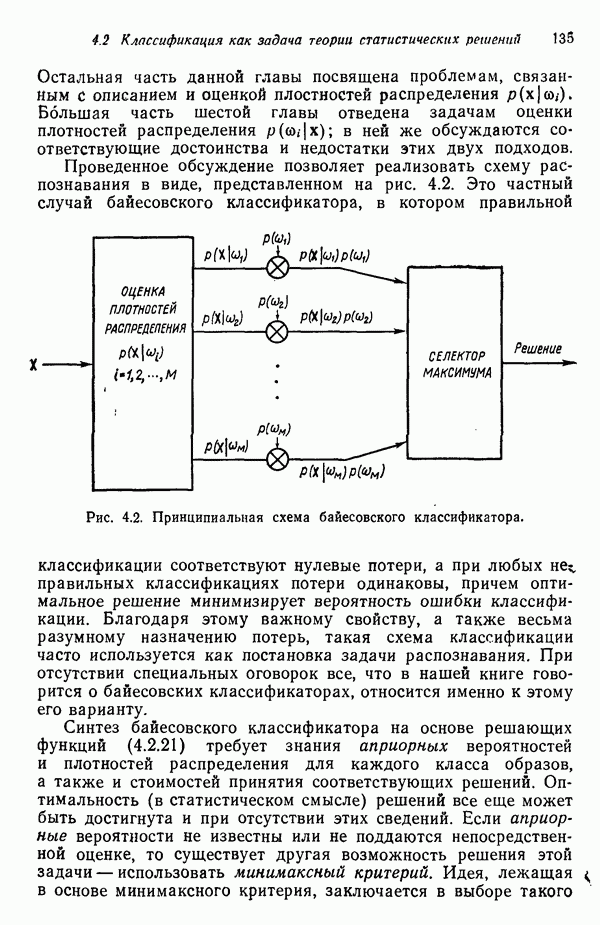
- 4.2. КЛАССИФИКАЦИЯ ОБРАЗОВ КАК ЗАДАЧА ТЕОРИИ СТАТИСТИЧЕСКИХ РЕШЕНИЙ
- 4.3. БАЙЕСОВСКИЙ КЛАССИФИКАТОР В СЛУЧАЕ ОБРАЗОВ, ХАРАКТЕРИЗУЮЩИХСЯ НОРМАЛЬНЫМ РАСПРЕДЕЛЕНИЕМ
- 4.4. ВЕРОЯТНОСТИ ОШИБОК
- 4.5. ВАЖНОЕ СЕМЕЙСТВО ПЛОТНОСТЕЙ РАСПРЕДЕЛЕНИЯ
- 4.6. ОЦЕНКА ФУНКЦИЙ ПЛОТНОСТИ РАСПРЕДЕЛЕНИЯ
- 4.6.2. Оценка вектора средних значений и ковариационной матрицы
- 4.6.3. Оценка вектора средних значений и ковариационной матрицы с помощью байесовской обучающей процедуры
- 4.6.4. Аппроксимация плотностей распределения функциями
- 4.7. ЗАКЛЮЧИТЕЛЬНЫЕ ЗАМЕЧАНИЯ
- Глава 5. ОБУЧАЕМЫЕ КЛАССИФИКАТОРЫ ОБРАЗОВ. ДЕТЕРМИНИСТСКИЙ ПОДХОД
- 5.2. ПЕРЦЕПТРОННЫЙ ПОДХОД
- 5.2.1. Принцип подкрепления — наказания
- 5.2.2. Доказательство сходимости
- 5.2.3. Разновидности перцептронного подхода
- 5.3. ПОСТРОЕНИЕ АЛГОРИТМОВ КЛАССИФИКАЦИИ ОБРАЗОВ
- 5.3.2. Алгоритм перцептрона
- 5.3.3. Алгоритм, основанный на минимизации среднеквадратичной ошибки
- 5.3.4. Доказательство сходимости НСКО-алгоритма
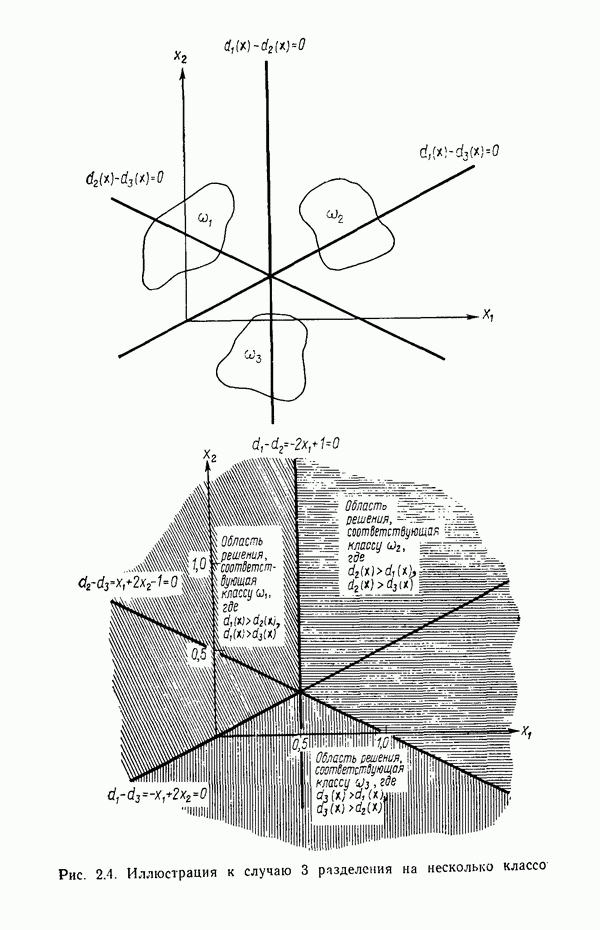
- 5.4. КЛАССИФИКАЦИЯ ДЛЯ СЛУЧАЯ НЕСКОЛЬКИХ КЛАССОВ
- 5.5. ОБУЧЕНИЕ И ОБОБЩЕНИЕ
- 5.6. ПОДХОД, ОСНОВАННЫЙ НА ИСПОЛЬЗОВАНИИ ПОТЕНЦИАЛЬНЫХ ФУНКЦИЙ
- 5.6.2. Выбор потенциальных функций
- 5.6.3. Геометрическая интерпретация коррекции весов
- 5.6.4. Сходимость алгоритмов обучения
- 5.6.5. Обобщение на случай нескольких классов
- 5.7. ЗАКЛЮЧИТЕЛЬНЫЕ ЗАМЕЧАНИЯ
- Глава 6. ОБУЧАЕМЫЕ КЛАССИФИКАТОРЫ ОБРАЗОВ. СТАТИСТИЧЕСКИЙ ПОДХОД
- 6.2. МЕТОДЫ СТОХАСТИЧЕСКОЙ АППРОКСИМАЦИИ
- 6.2.2. Скорость сходимости
- 6.2.3. Обобщение на многомерный случай
- 6.3. ПОСТРОЕНИЕ АЛГОРИТМОВ КЛАССИФИКАЦИИ ОБРАЗОВ
- 6.3.2. Алгоритм корректирующих приращений
- 6.3.3. Алгоритм наименьшей среднеквадратичной ошибки
- 6.4. МЕТОД ПОТЕНЦИАЛЬНЫХ ФУНКЦИЙ
- 6.5. ЗАКЛЮЧИТЕЛЬНЫЕ ЗАМЕЧАНИЯ
- Глава 7. ПРЕДВАРИТЕЛЬНАЯ ОБРАБОТКА ОБРАЗОВ И ВЫБОР ПРИЗНАКОВ
- 7.2. РАССТОЯНИЯ
- 7.3. ПРЕОБРАЗОВАНИЯ КЛАСТЕРИЗАЦИИ И УПОРЯДОЧЕНИЕ ПРИЗНАКОВ
- 7.4. РОЛЬ КЛАСТЕРИЗАЦИИ В ВЫБОРЕ ПРИЗНАКОВ
- 7.5. ВЫБОР ПРИЗНАКОВ ПРИ ПОМОЩИ МИНИМИЗАЦИИ ЭНТРОПИИ
- 7.6. ВЫБОР ПРИЗНАКОВ ПРИ ПОМОЩИ РАЗЛОЖЕНИЙ ПО СИСТЕМЕ ОРТОГОНАЛЬНЫХ ФУНКЦИЙ
- 7.6.2. Разложение Карунена — Лоэва
- 7.7. ВЫБОР ПРИЗНАКОВ ПОСРЕДСТВОМ АППРОКСИМАЦИИ ФУНКЦИЯМИ
- 7.7.2. Метод стохастической аппроксимации
- 7.7.3. Ядерная аппроксимация
- 7.7.4. Использование функций признаков при классификации
- 7.8. КОНЦЕПЦИЯ ДИВЕРГЕНЦИИ
- 7.9. ВЫБОР ПРИЗНАКОВ НА ОСНОВЕ МАКСИМИЗАЦИИ ДИВЕРГЕНЦИИ
- 7.10. ВЫБОР ДВОИЧНЫХ ПРИЗНАКОВ
- 7.11 ЗАКЛЮЧИТЕЛЬНЫЕ ЗАМЕЧАНИЯ
- Глава 8. СИНТАКСИЧЕСКОЕ РАСПОЗНАВАНИЕ ОБРАЗОВ
- 8.2. ПОНЯТИЯ ТЕОРИИ ФОРМАЛЬНЫХ ЯЗЫКОВ
- 8.2.2. Типы грамматик
- 8.3. ПОСТАНОВКА ЗАДАЧИ СИНТАКСИЧЕСКОГО РАСПОЗНАВАНИЯ ОБРАЗОВ
- 8.4. СИНТАКСИЧЕСКОЕ ОПИСАНИЕ ОБРАЗОВ
- 8.5. ГРАММАТИКИ, ИСПОЛЬЗУЕМЫЕ В РАСПОЗНАВАНИИ ОБРАЗОВ
- 8.5.2. Распознавание образов, представленных графами
- 8.5.3. Распознавание древовидных структур
- 8.6. СТАТИСТИЧЕСКИЙ АНАЛИЗ
- 8.6.2. Оценка вероятностей правил подстановки с помощью процедур обучения
- 8.7. ОБУЧЕНИЕ И ГРАММАТИЧЕСКИЙ ВЫВОД
- 8.7.2. Вывод двумерных грамматик
- 8.8. АВТОМАТЫ КАК РАСПОЗНАЮЩИЕ УСТРОЙСТВА
- 8.9. ЗАКЛЮЧИТЕЛЬНЫЕ ЗАМЕЧАНИЯ
- СПИСОК ЛИТЕРАТУРЫ
- СПИСОК ОБОЗНАЧЕНИЙ