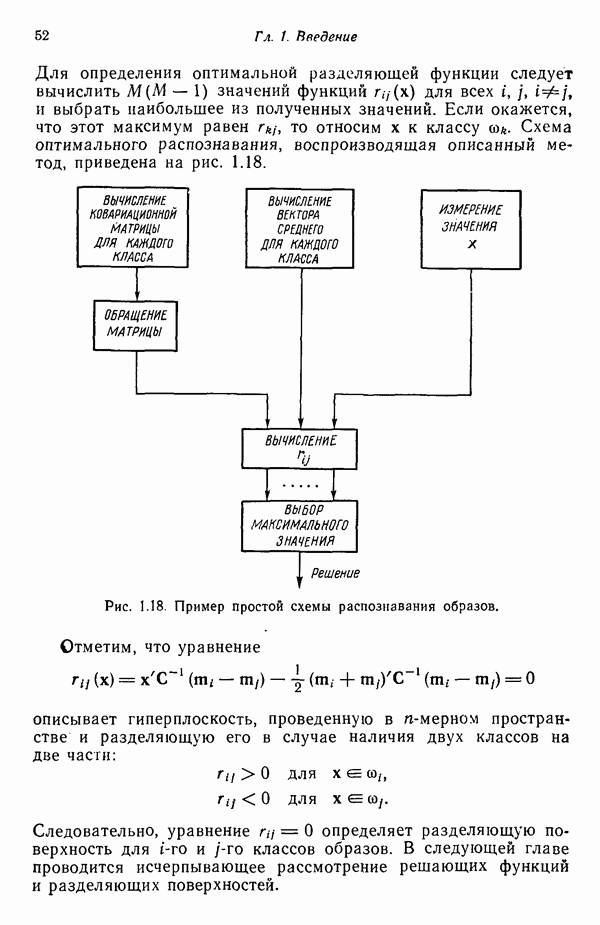
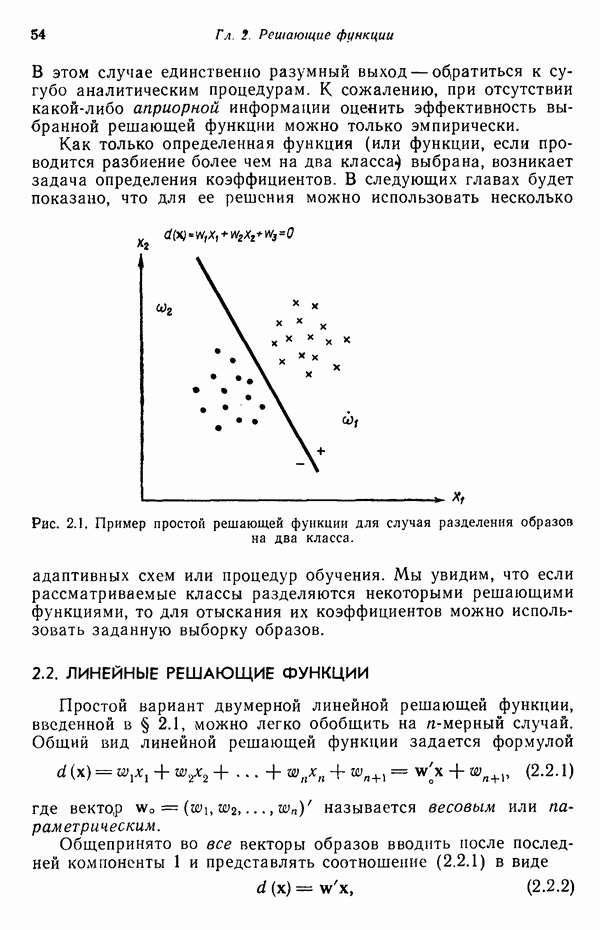
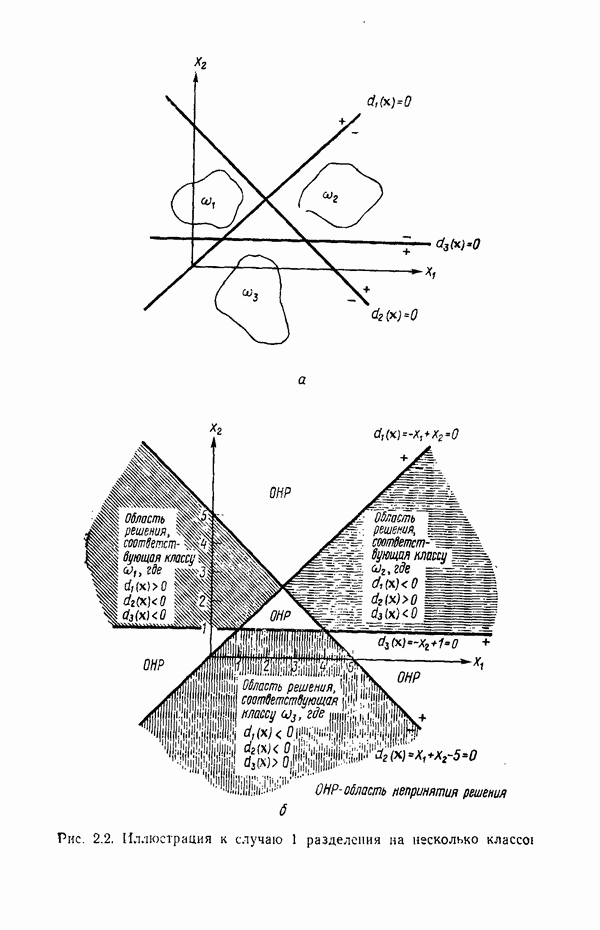
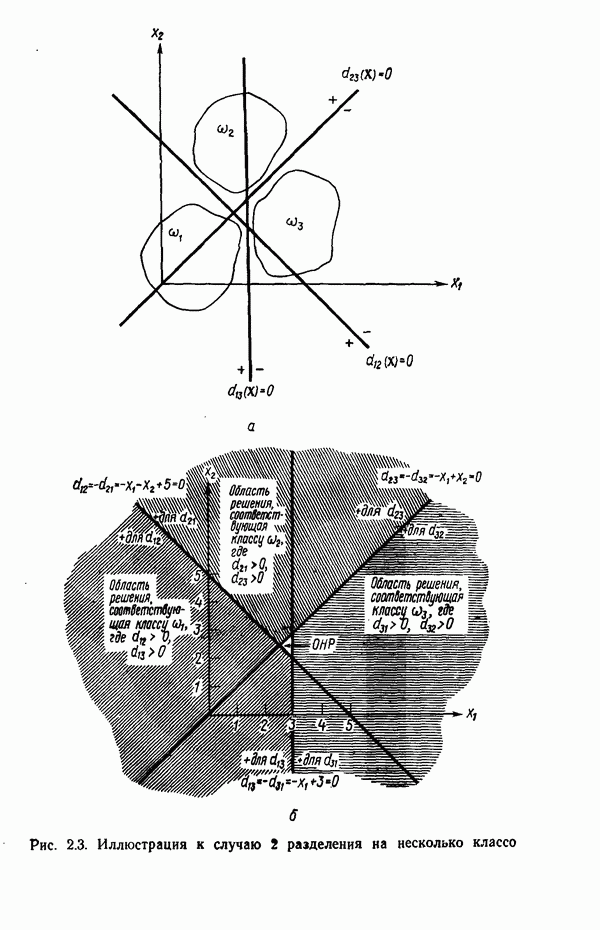
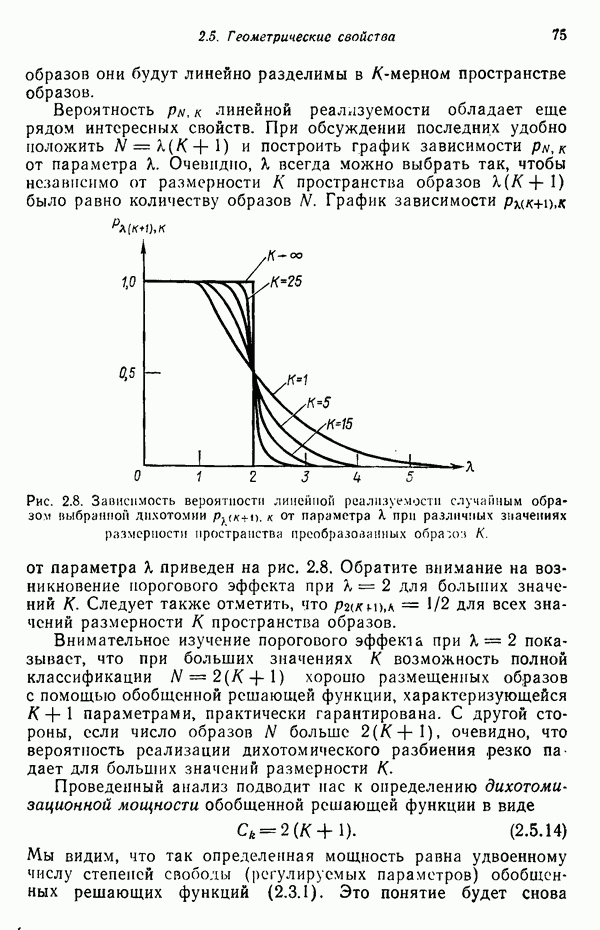
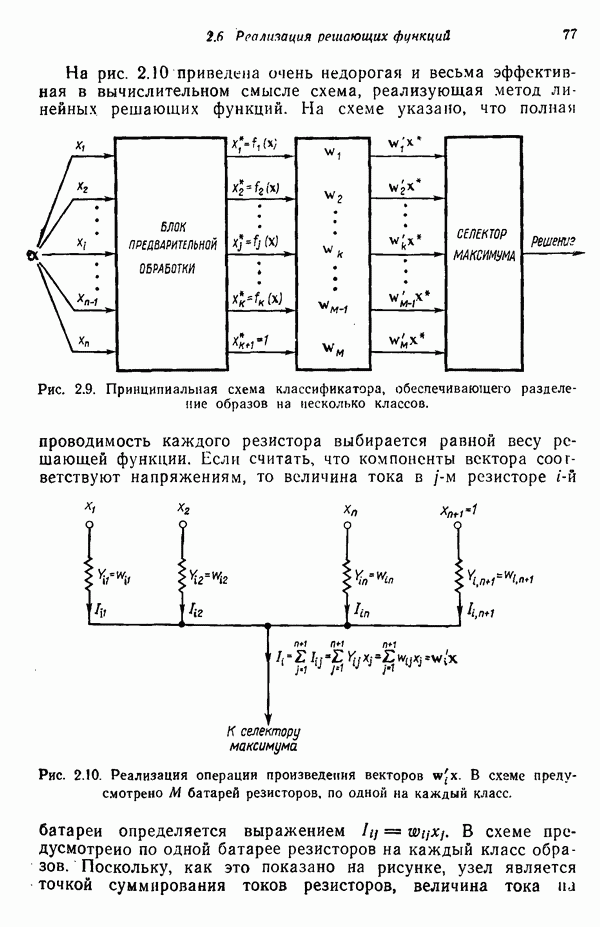
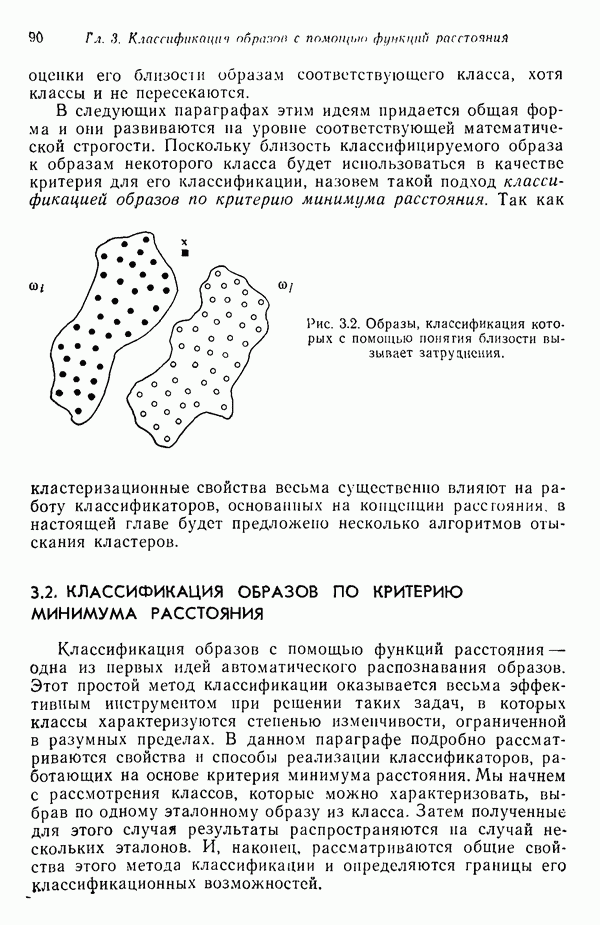
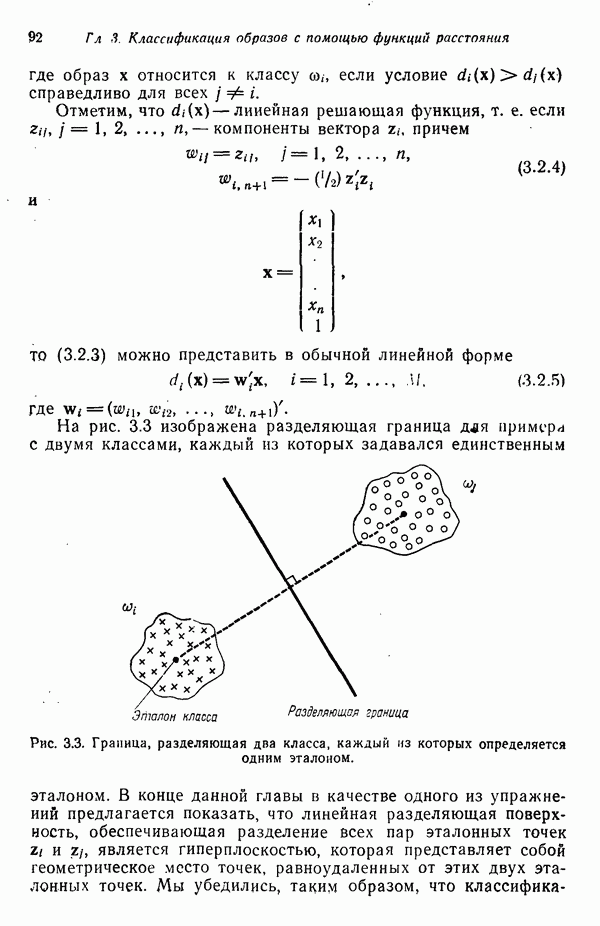
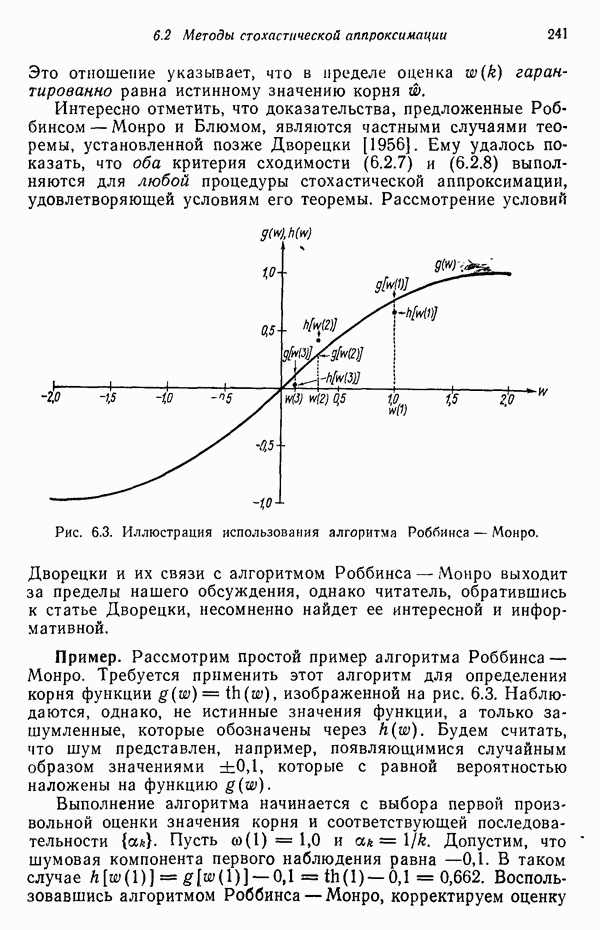
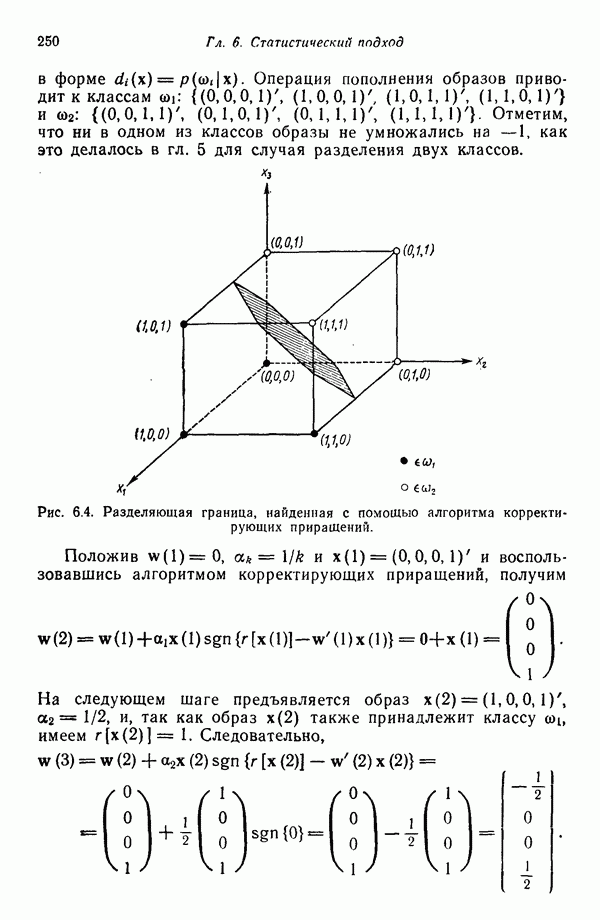
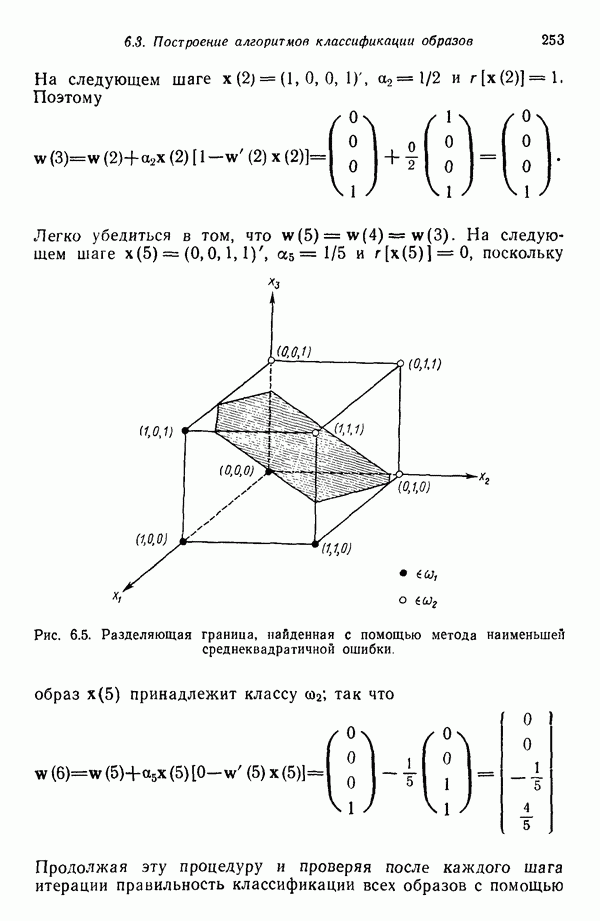
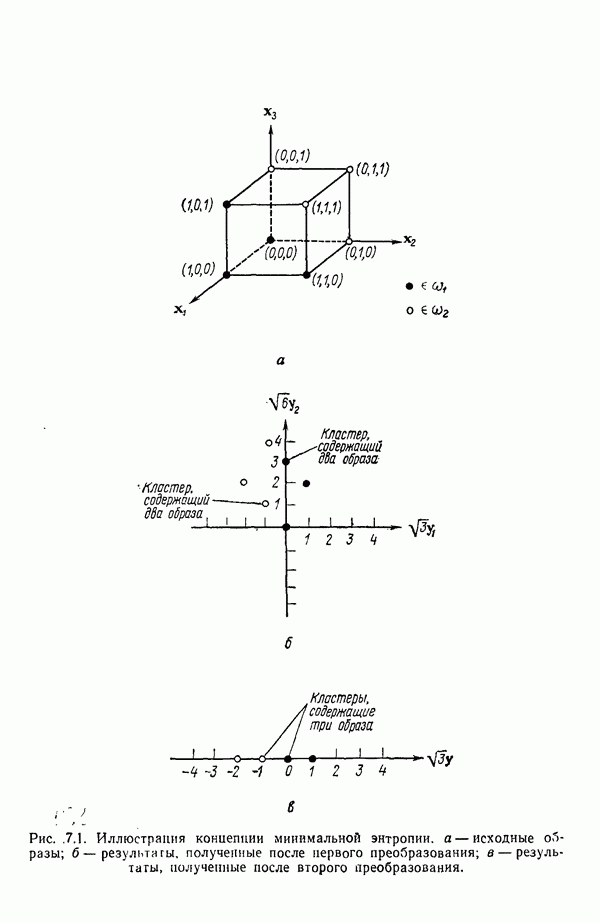
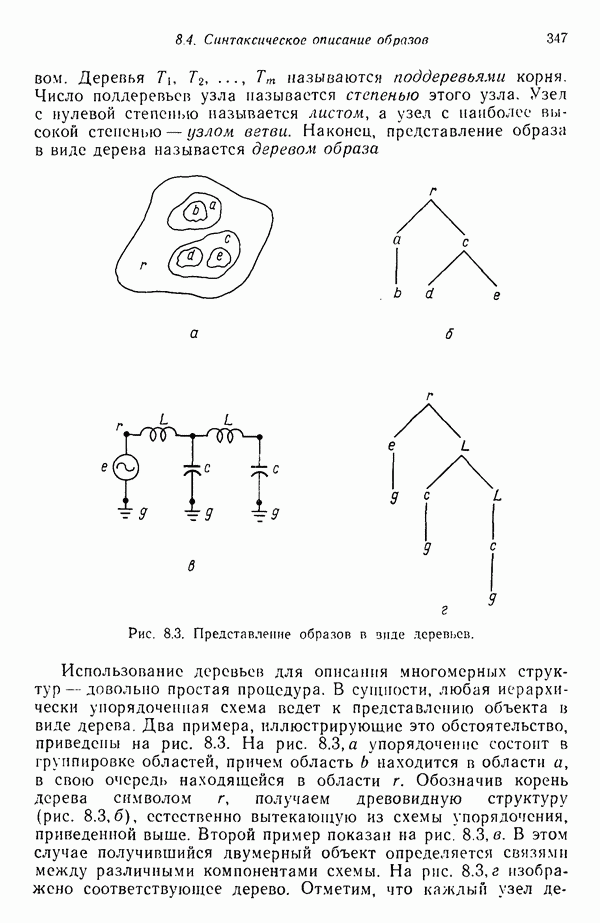
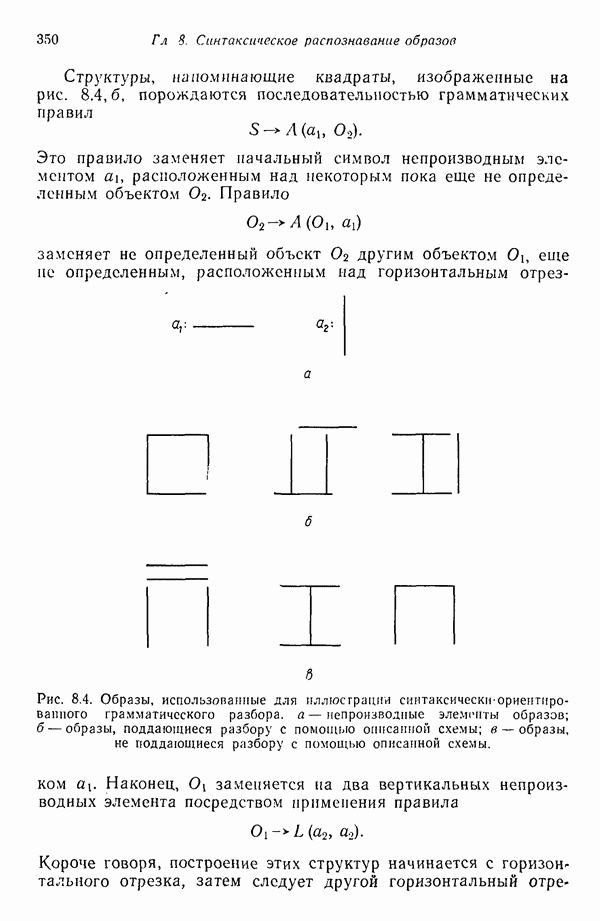
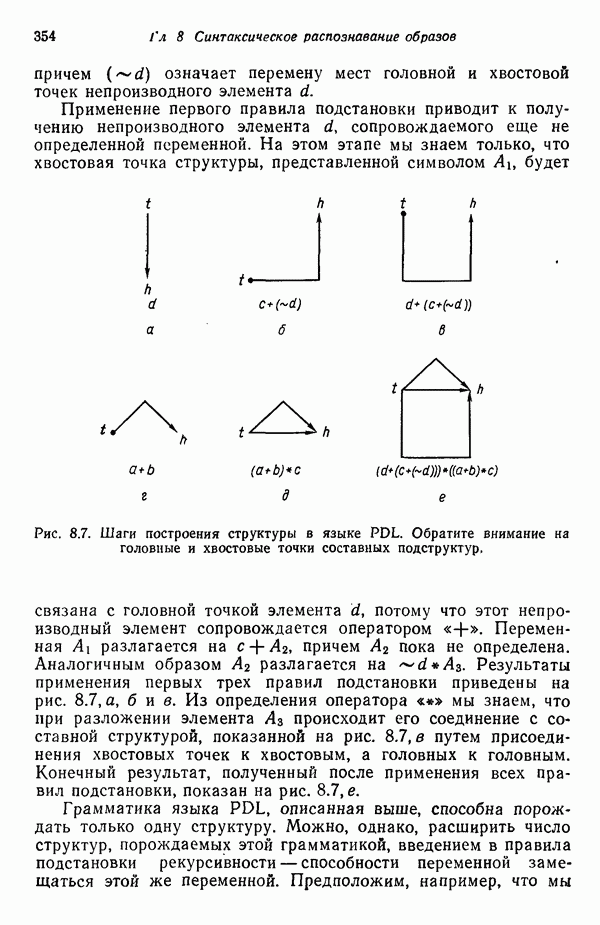
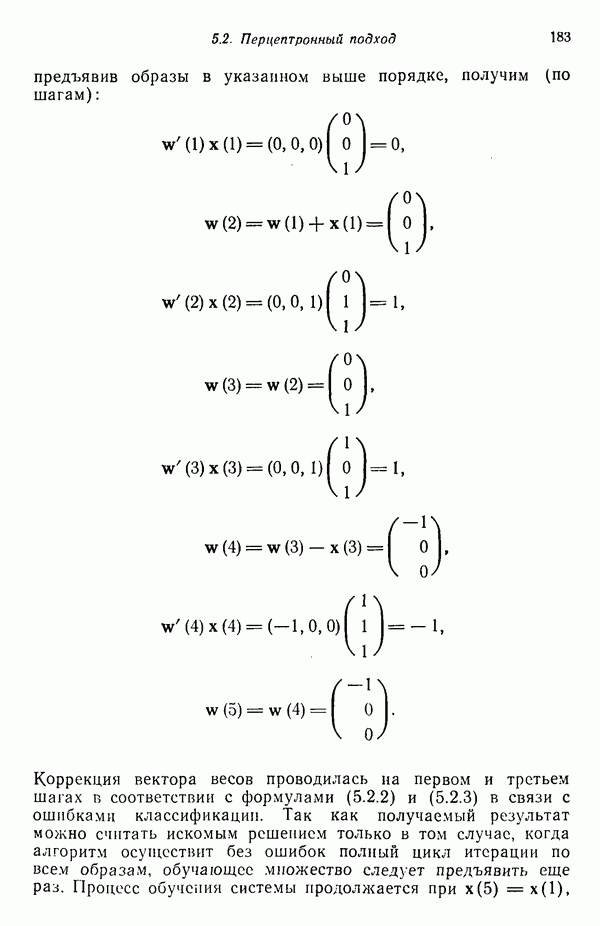| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
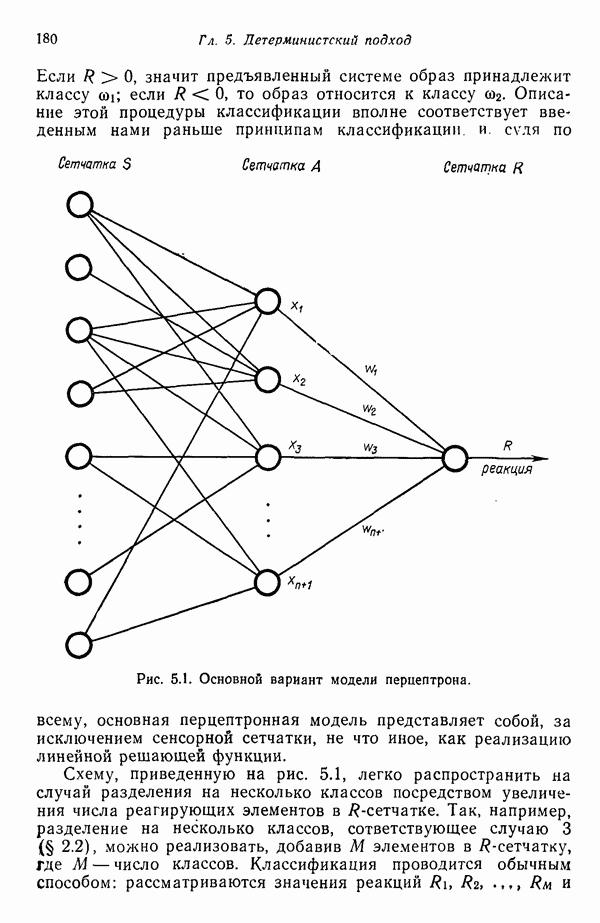
7.3. ПРЕОБРАЗОВАНИЯ КЛАСТЕРИЗАЦИИ И УПОРЯДОЧЕНИЕ ПРИЗНАКОВ
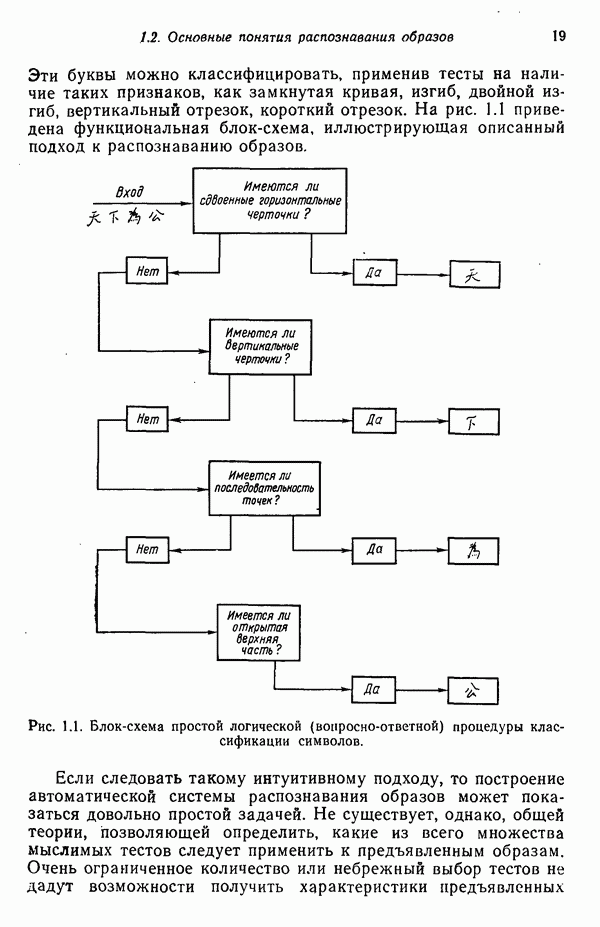
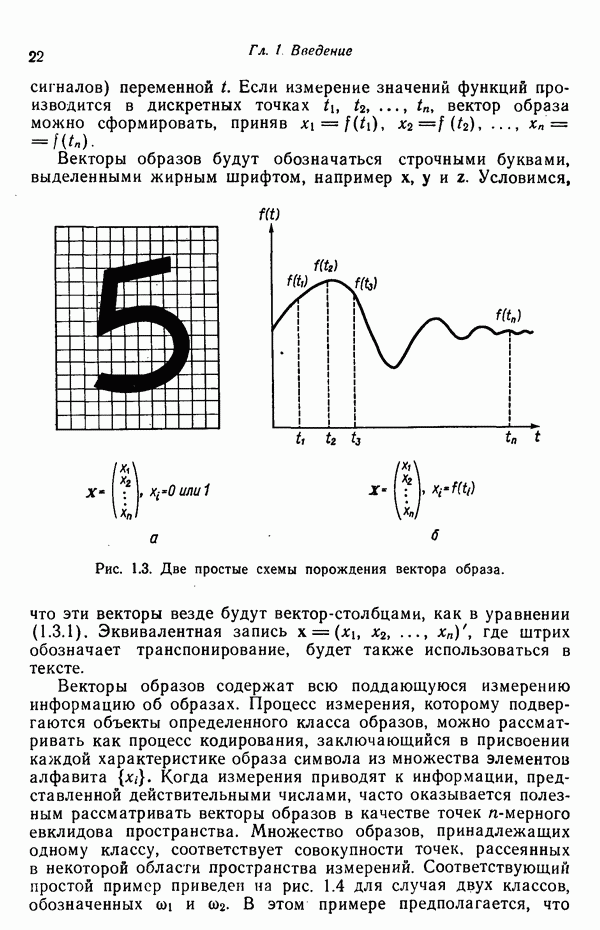
Не все измерения характеристик образа, соответствующие отдельным координатным осям в равной степени важны для определения класса, которому принадлежат сходные образы. При сопоставлении двух образов последовательным сравнением признаков измерениям с меньшей значимостью следует приписать меньшие веса. Назначение весов признаков можно осуществить посредством линейного преобразования, которое обеспечит более благоприятную группировку точек, представляющих образы, в новом пространстве.
Рассмотрим векторы образов  которые после применения к ним преобразования
которые после применения к ним преобразования  перешли в векторы
перешли в векторы  . В таком случае
. В таком случае

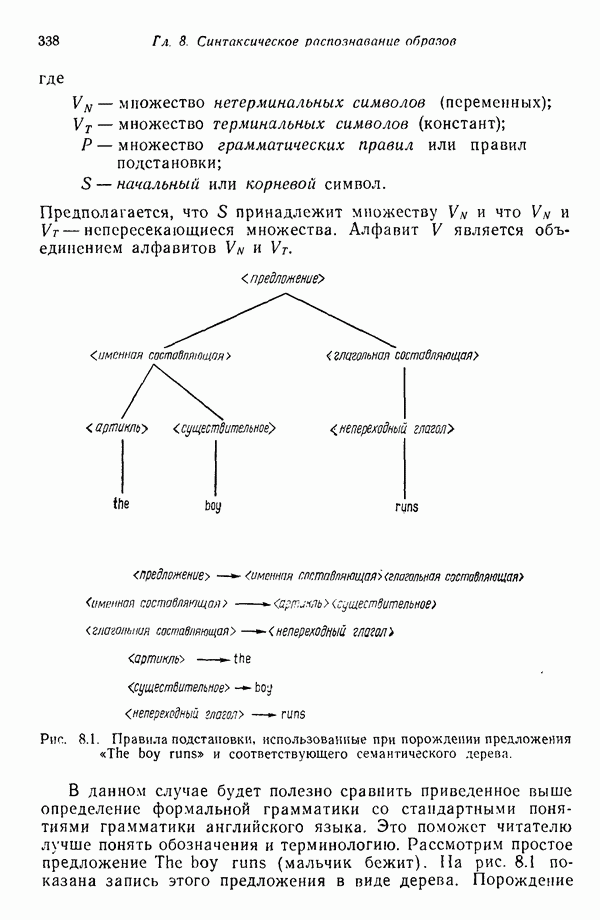
где

причем элементы  суть весовые коэффициенты.
суть весовые коэффициенты.
Итак,

Каждый элемент преобразованного вектора образа представляет собой линейную комбинацию элементов исходного вектора образа. В новом пространстве евклидово расстояние между векторами  определяется как
определяется как

В тех случаях, когда линейное преобразование сводится к изменению масштабных коэффициентов координатных осей, матрица  является диагональной, т. е. ее ненулевые элементы расположены только на главной диагонали. В таком случае выражение для евклидова расстояния сводится к
является диагональной, т. е. ее ненулевые элементы расположены только на главной диагонали. В таком случае выражение для евклидова расстояния сводится к

где элементы  представляют весовые коэффициенты при признаках. Задача преобразования кластеризации заключается в том, чтобы определить весовые коэффициенты признаков
представляют весовые коэффициенты при признаках. Задача преобразования кластеризации заключается в том, чтобы определить весовые коэффициенты признаков  минимизирующие расстояние между
минимизирующие расстояние между  с учетом определенных ограничений, наложенных на коэффициенты тюкк.
с учетом определенных ограничений, наложенных на коэффициенты тюкк.
Из материала предыдущего параграфа следует, что в новом пространстве внутреннее расстояние для множества точек, представляющих образы, определяется как

где  — несмещенная оценка выборочной дисперсии компонент, соответствующих координатной оси
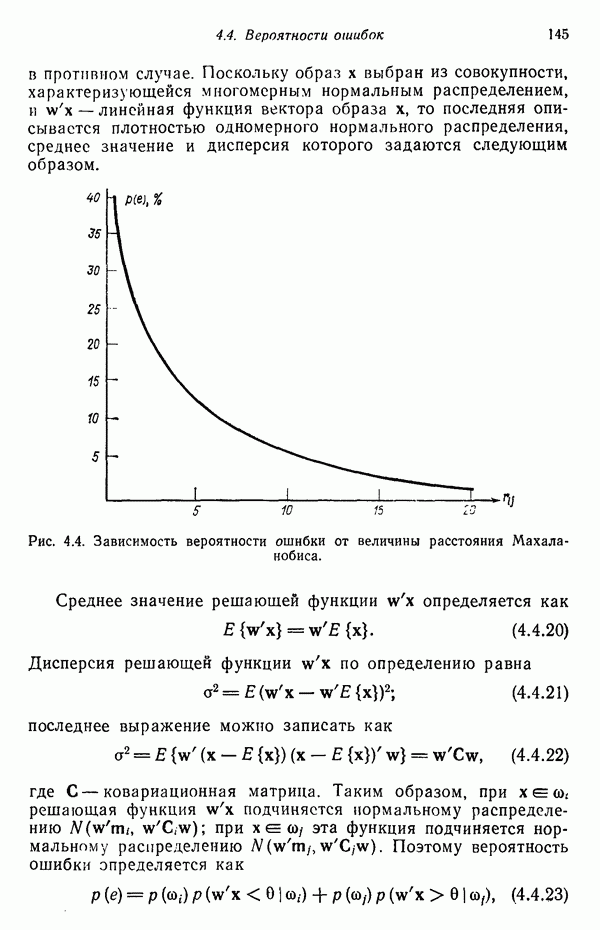
— несмещенная оценка выборочной дисперсии компонент, соответствующих координатной оси  При осуществлении процедуры минимизации будем рассматривать два случая.
При осуществлении процедуры минимизации будем рассматривать два случая.
Случай 1. Ограничение  .
.
Минимизация  при таком ограничении эквивалентна минимизации величины
при таком ограничении эквивалентна минимизации величины

Возьмем частную производную от  но весовому коэффициенту
но весовому коэффициенту  и приравняем ее нулю. После проведения соответствующих упрощений получим
и приравняем ее нулю. После проведения соответствующих упрощений получим

где  — множитель Лагранжа, определяемый выражением
— множитель Лагранжа, определяемый выражением

Итак, весовой коэффициент признака равен

Из (7.3.5) заключаем, что значения коэффициента  малы, если дисперсия
малы, если дисперсия  велика. Это означает, что при измерении расстояния малые веса следует приписывать признакам, которым свойственна значительная изменчивость. Если же, с другой стороны, дисперсия
велика. Это означает, что при измерении расстояния малые веса следует приписывать признакам, которым свойственна значительная изменчивость. Если же, с другой стороны, дисперсия  мала, то соответствующему признаку должен быть приписан существенный вес.
мала, то соответствующему признаку должен быть приписан существенный вес.
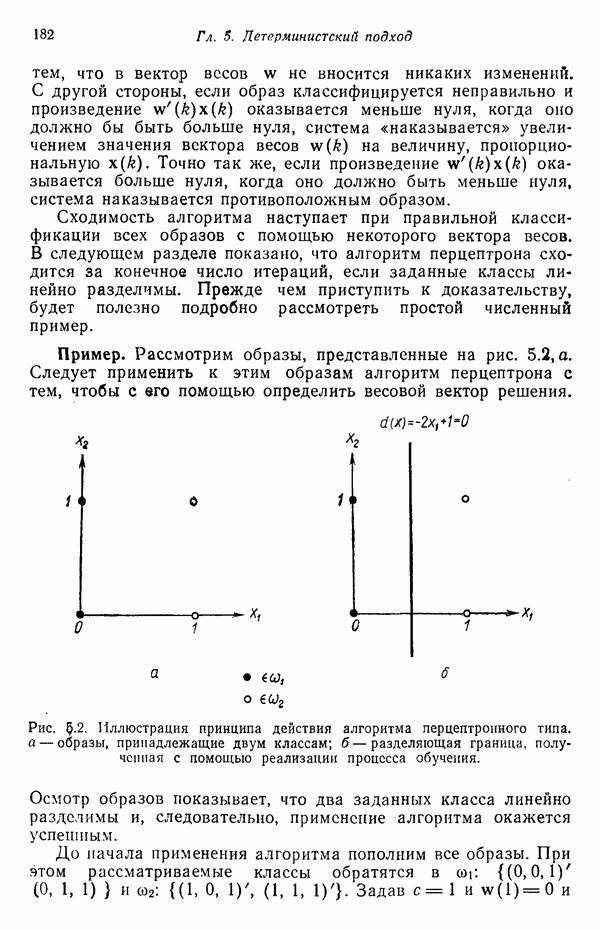
В данном случае преобразование кластеризации было осуществлено посредством «взвешивания» признаков. Интуитивно понятно, что малая дисперсия  определяет большую надежность
определяет большую надежность  измерения, а большая дисперсия а? меньшую надежность
измерения, а большая дисперсия а? меньшую надежность  измерения. Результатам более надежных измерений присваиваются большие веса.
измерения. Результатам более надежных измерений присваиваются большие веса.
Случай 2. Ограничение 
Минимизация  при таком ограничении эквивалентна минимизации выражения
при таком ограничении эквивалентна минимизации выражения

Взяв частную производную от (7.3.8) по весовому коэффициенту  и приравняв ее нулю, получим
и приравняв ее нулю, получим

где  — множитель Лагранжа, определяемый выражением
— множитель Лагранжа, определяемый выражением

Таким образом, весовой коэффициент признака определяется выражением

значение этого коэффициента обратно пропорционально среднеквадратичному отклонению  измерения.
измерения.
Формулы (7.3.7) и (7.3.11) определяют матрицу преобразования  с учетом введенных выше ограничений. Если векторы образов переводятся из пространства X в пространство X с помощью преобразования
с учетом введенных выше ограничений. Если векторы образов переводятся из пространства X в пространство X с помощью преобразования

то внутреннее расстояние множества в пространстве X минимизируется. Теперь требуется провести второе преобразование

для того, чтобы выделить компоненты, имеющие малую (или большую) дисперсию, обеспечив таким образом возможность провести упорядочение и выбор признаков. Это преобразование превратит ковариационную матрицу точек, представляющих образы в пространстве X, в диагональную. Более того, матрица преобразования А должна быть ортонормированной для того, чтобы расстояния оставались неизменными.
Задача заключается в выражении матрицы А посредством собственных векторов известной ковариационной матрицы. Пусть С — ковариационная матрица для точек, представляющих образы в пространстве X, а  — аналогичные ковариационные матрицы в пространствах X и X соответственно. Пусть
— аналогичные ковариационные матрицы в пространствах X и X соответственно. Пусть  — вектор математического ожидания точек, отвечающих образам в пространстве X, и
— вектор математического ожидания точек, отвечающих образам в пространстве X, и  — векторы математического ожидания в пространствах
— векторы математического ожидания в пространствах  соответственно. В таком случае
соответственно. В таком случае

и

где

В этом выражении Е — оператор математического ожидания. Ковариационная матрица в пространстве X определяется как

поскольку  .
.
Подобным же образом можно легко показать, что

Так как матрица А — ортонормированная, то

В таком случае мы приходим к

это выражение представляет преобразование подобия.
Хорошо известно, что преобразование подобия дает диагональную матрицу С, если в качестве матрицы  выбирается модальная матрица матрицы С, т. е. столбцами матрицы
выбирается модальная матрица матрицы С, т. е. столбцами матрицы  являются собственные векторы матрицы С либо строками матрицы А являются собственные векторы матрицы С. Итак, строками матрицы А являются собственные векторы матрицы
являются собственные векторы матрицы С либо строками матрицы А являются собственные векторы матрицы С. Итак, строками матрицы А являются собственные векторы матрицы  Это преобразование, которое является скорее конгруэнтным, нежели преобразованием подобия, не позволяет легко выразить собственные векторы матрицы
Это преобразование, которое является скорее конгруэнтным, нежели преобразованием подобия, не позволяет легко выразить собственные векторы матрицы  через собственные векторы матрицы С.
через собственные векторы матрицы С.
Пусть  нормированные собственные векторы матрицы С и
нормированные собственные векторы матрицы С и  — соответствующие характеристические числа. Тогда
— соответствующие характеристические числа. Тогда


Матрица А выбирается так, чтобы

и так как собственные векторы образуют ортонормированное множество, то  . В таком случае
. В таком случае

Воспользовавшись уравнением (7.3.18), можно записать

так как  при
при  . Можно показать, что
. Можно показать, что

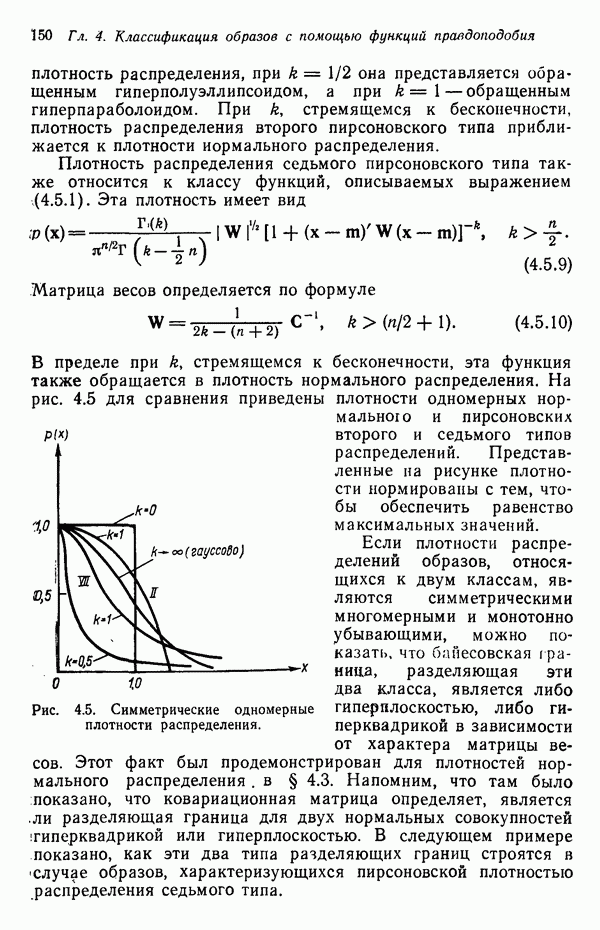
Матрица А преобразует ковариационную матрицу С в диагональную, элементами которой являются несмещенные оценки выборочной дисперсии. Результаты измерений, которым соответствуют малые дисперсии, более надежны и могут считаться более существенными признаками.
Описанная процедура исследования ковариационной матрицы не позволяет связать простой зависимостью собственные векторы матрицы  с собственными векторами исходной ковариационной матрицы С. Можно, однако, найти простое выражение, связывающее строки матрицы А с элементами исходной ковариационной матрицы, если обратить последовательность операций
с собственными векторами исходной ковариационной матрицы С. Можно, однако, найти простое выражение, связывающее строки матрицы А с элементами исходной ковариационной матрицы, если обратить последовательность операций  Выбирается ортонормированная матрица А, строки которой являются собственными векторами ковариационной матрицы С. Матрица А преобразует матрицу С в диагональную матрицу С. Затем от матрицы преобразования
Выбирается ортонормированная матрица А, строки которой являются собственными векторами ковариационной матрицы С. Матрица А преобразует матрицу С в диагональную матрицу С. Затем от матрицы преобразования  требуется, чтобы она была диагональной и минимизировала внутримножественное расстояние в пространстве X с учетом заданного ограничения. Если выбрано ограничение
требуется, чтобы она была диагональной и минимизировала внутримножественное расстояние в пространстве X с учетом заданного ограничения. Если выбрано ограничение

то

где  элементы ковариационной матрицы С, приведенной к диагональному виду:
элементы ковариационной матрицы С, приведенной к диагональному виду:

Ковариационная матрица после преобразования кластеризации будет иметь вид

Так как все матрицы  и
и  — диагональные, а произведением диагональных матриц всегда будет диагональная матрица, то очевидно, что, как и требовалось, матрица С — диагональная.
— диагональные, а произведением диагональных матриц всегда будет диагональная матрица, то очевидно, что, как и требовалось, матрица С — диагональная.
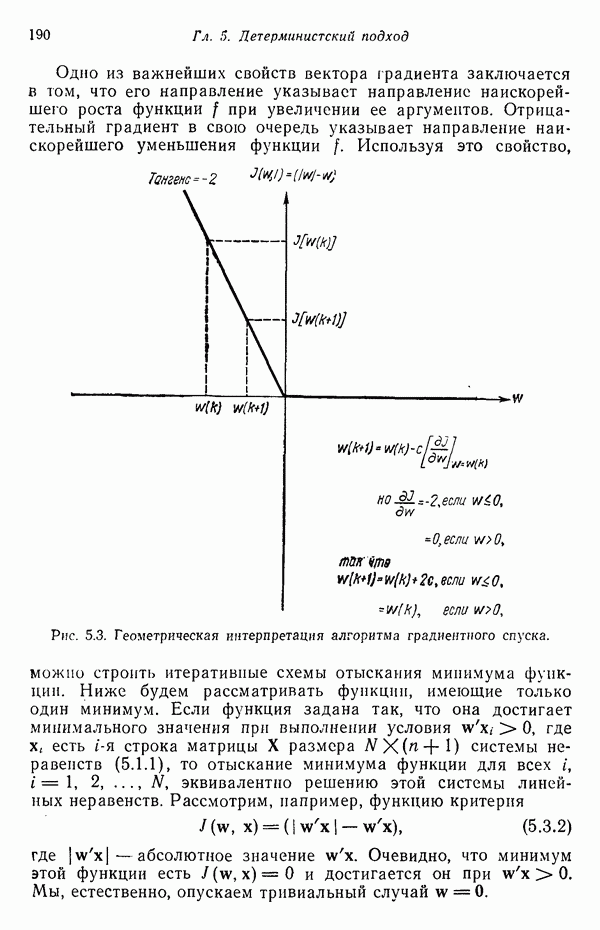
Соотношения среднеквадратичного расстояния и отношения правдоподобия
Здесь устанавливается связь между отношением правдоподобия, рассмотренным в гл. 4, и среднеквадратичным расстоянием; для этого используются преобразования, описанные выше. Рассмотрим плотность нормального распределения

где С — ковариационная матрица,  — вектор математического ожидания для класса образов в пространстве X. Отметим, что кривые равной вероятности соответствуют тем значениям
— вектор математического ожидания для класса образов в пространстве X. Отметим, что кривые равной вероятности соответствуют тем значениям  при которых значение аргумента
при которых значение аргумента  показательной функции остается постоянным.
показательной функции остается постоянным.
Для исследования ковариационной матрицы осуществляется ортонормирующее преобразование

где строками матрицы А служат нормированные собственные векторы ковариационной матрицы С. Это преобразование облегчает установление связи между отношением правдоподобия и среднеквадратичным расстоянием. После преобразования вектор математического ожидания и ковариационная матрица определяются как

и

соответственно.
Пусть  собственные векторы матрицы
собственные векторы матрицы  — соответствующие характеристические числа. В таком случае, согласно (7.3.27), имеем
— соответствующие характеристические числа. В таком случае, согласно (7.3.27), имеем

На основе формул (7.3.27) и (7.3.28) получаем

и

Итак, плотность распределения в пространстве X определяется выражением

Это выражение для плотности распределения показывает, что кривыми равной вероятности являются эллипсоиды с центрами в точке т. Направления главных осей совпадают с собственными векторами ковариационной матрицы, а диаметры пропорциональны квадратному корню от соответствующих характеристических чисел или среднеквадратичных отклонений, поскольку  Это становится более очевидным после разложения показательной функции:
Это становится более очевидным после разложения показательной функции:

где  — координата вектора
— координата вектора  соответствующая
соответствующая  собственному вектору,
собственному вектору,  — среднее всех значений координат, соответствующих этому собственному вектору
— среднее всех значений координат, соответствующих этому собственному вектору
Среднеквадратичное расстояние, отделяющее точку — произвольный образ  — от множества точек (образов)
— от множества точек (образов)  определяется как
определяется как

Усреднение проводится но всем  точкам, входящим в заданное множество. В первую очередь осуществляется преобразование оргонормировки, причем собственные векторы ковариационной
точкам, входящим в заданное множество. В первую очередь осуществляется преобразование оргонормировки, причем собственные векторы ковариационной
матрицы становятся строками матрицы А:

поскольку А — ортоиормироваиная матрица и  Расстояние при выполнении этого преобразования остается неизменным.
Расстояние при выполнении этого преобразования остается неизменным.
При выполнении преобразования кластеризации

среднеквадратичное расстояние принимает вид

Выбранная матрица  является диагональной, и ее элементы равны величинам, обратным среднеквадратичным отклонениям координат образов множества
является диагональной, и ее элементы равны величинам, обратным среднеквадратичным отклонениям координат образов множества  соответствующих отдельным собственным векторам. Было показано, что преобразование такого вида минимизирует внутреннее расстояние множества образов.
соответствующих отдельным собственным векторам. Было показано, что преобразование такого вида минимизирует внутреннее расстояние множества образов.
Матрица  — диагональная, и ее элементы равны величинам, обратным дисперсиям координат образов множества
— диагональная, и ее элементы равны величинам, обратным дисперсиям координат образов множества  Так как эти дисперсии суть соответствующие характеристические числа, т. е.
Так как эти дисперсии суть соответствующие характеристические числа, т. е.  , получаем
, получаем

Следовательно, среднеквадратичное расстояние определяется выражением

которое после выполнения соответствующих операций можно представить в виде

Поскольку усреднение проводится по всем  точкам множества образов, оно не зависит от процесса суммирования. Поэтому
точкам множества образов, оно не зависит от процесса суммирования. Поэтому
(7.3.39) можно привести к

где 

то формула (7.3.40) превращается в

В таком случае, если опустить константу  среднеквадратичное расстояние для класса
среднеквадратичное расстояние для класса  определяется выражением
определяется выражением

и, аналогичным образом, среднеквадратичное расстояние для класса  — выражением
— выражением

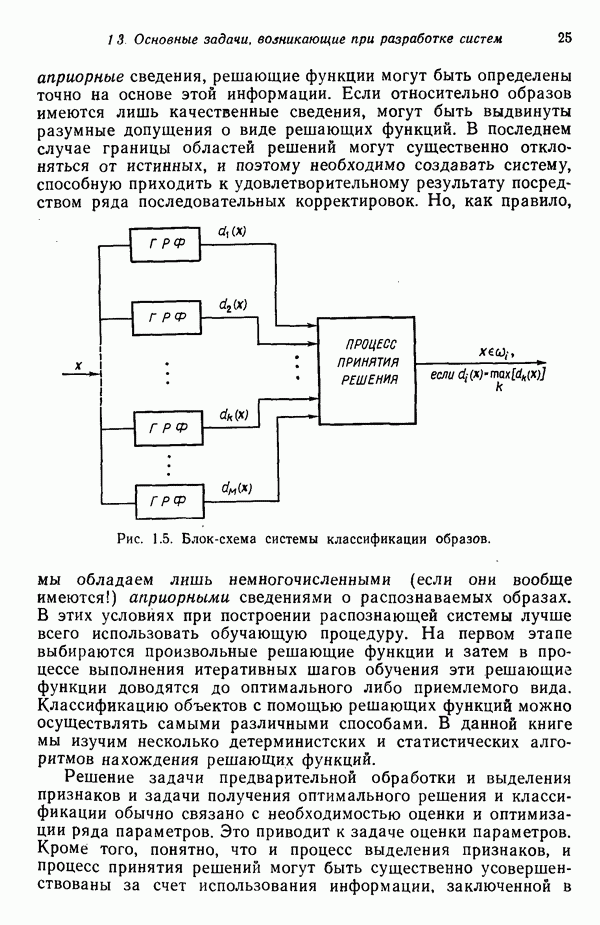
Исходя из принципа расстояния, решающее правило можно сформулировать в таком виде:  в том и только том случае, если
в том и только том случае, если

Для образов, подчиняющихся нормальному распределению, плотность распределения или функция правдоподобия для класса  определяется как
определяется как

После осуществления ортонормирующего преобразования выражение (7.3.45) принимает вид

Точно так же для класса  находим плотность распределения
находим плотность распределения

Если мы прологарифмируем и опустим постоянные члены, то получим решающие функции

и

В таком случае решающее правило, основанное на этих двух функциях, гласит, что  тогда и только тогда, когда
тогда и только тогда, когда  , где
, где  — пороговая величина.
— пороговая величина.
На основе проведенного анализа можно сделать вывод о том, что аппроксимация заданных выборок наблюдений для классов образов плотностями нормального распределения эквивалентна нахождению среднеквадратичных расстояний для соответствующих классов после осуществления преобразования кластеризации над пространством измерений.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
- Глава 1. ВВЕДЕНИЕ
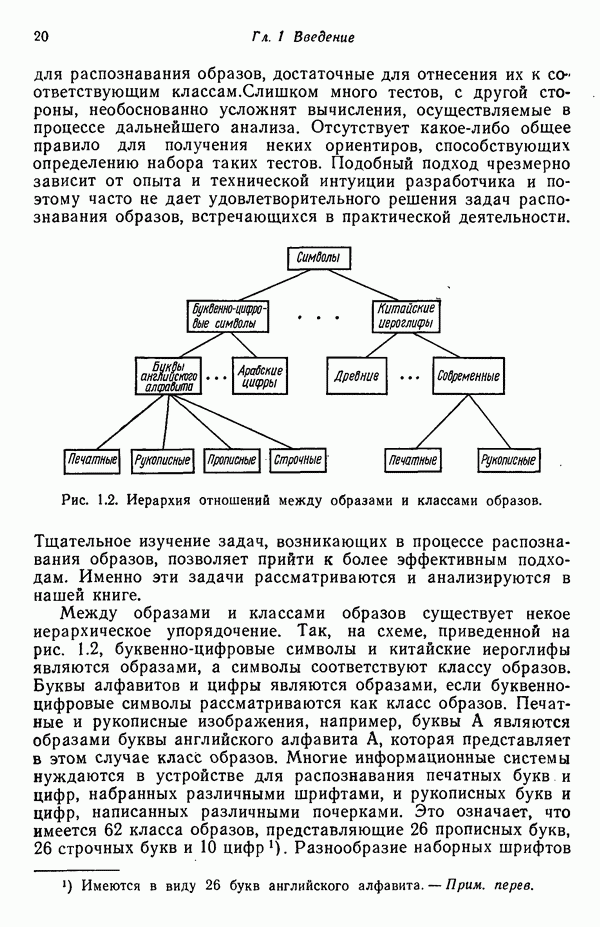
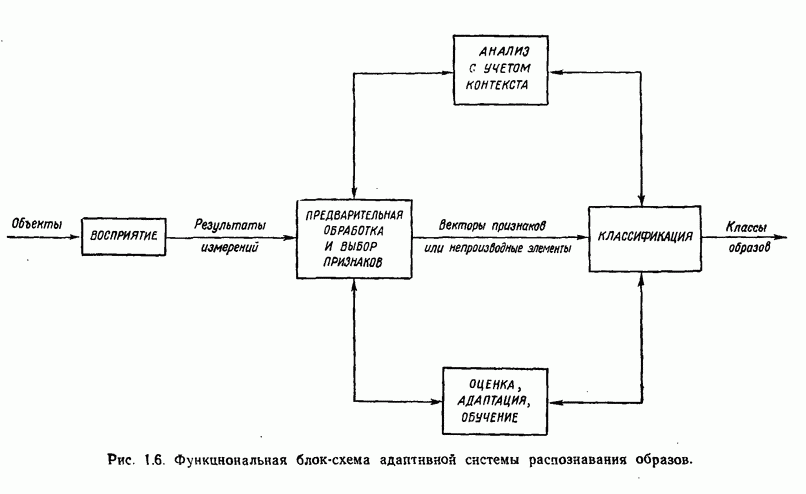
- 1.1. ПРОБЛЕМА ОБРАБОТКИ ИНФОРМАЦИИ
- 1.2. ОСНОВНЫЕ ПОНЯТИЯ РАСПОЗНАВАНИЯ ОБРАЗОВ
- 1.3. ОСНОВНЫЕ ЗАДАЧИ, ВОЗНИКАЮЩИЕ ПРИ РАЗРАБОТКЕ СИСТЕМ РАСПОЗНАВАНИЯ ОБРАЗОВ
- 1.4. КРАТКОЕ ОПИСАНИЕ КОНЦЕПЦИЙ И МЕТОДОЛОГИИ
- 2. Принцип общности свойств
- 3. Принцип кластеризации
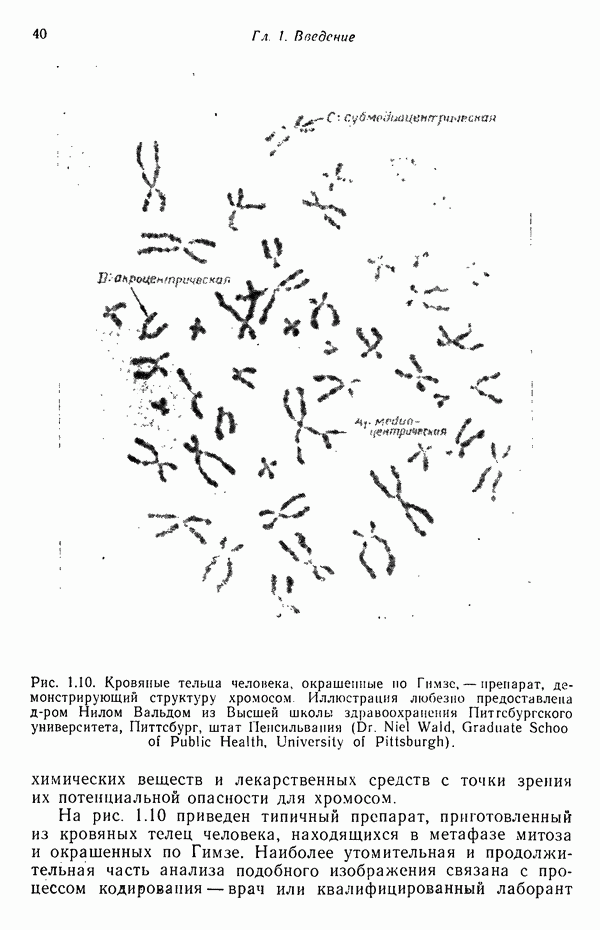
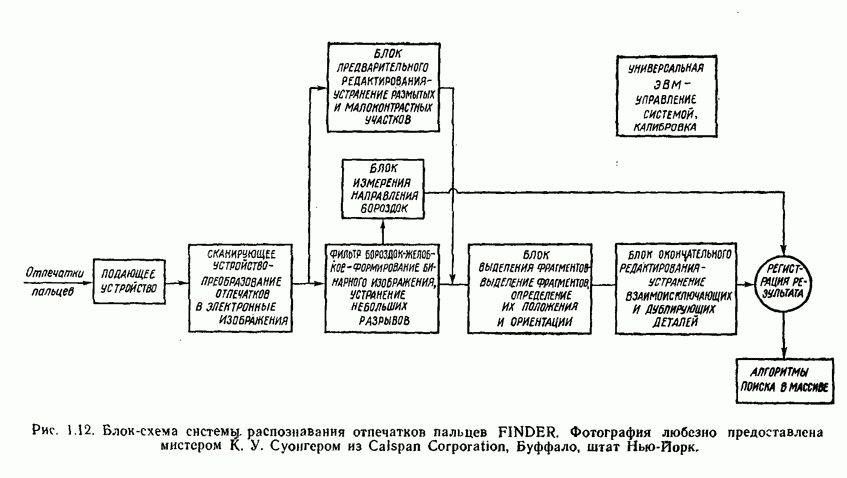
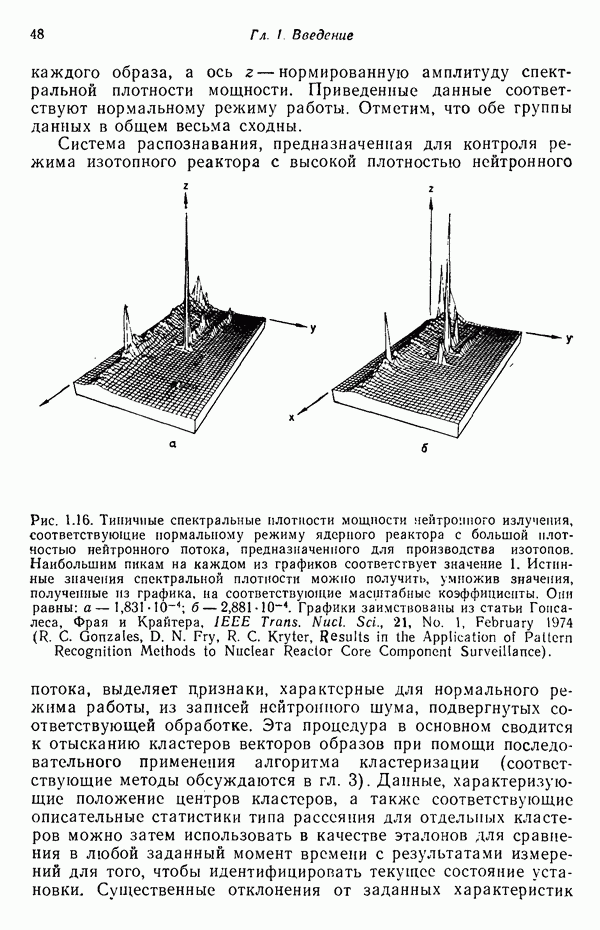
- 1.5. ПРИМЕРЫ АВТОМАТИЧЕСКИХ СИСТЕМ РАСПОЗНАВАНИЯ ОБРАЗОВ
- 1.6. ПРОСТАЯ МОДЕЛЬ РАСПОЗНАВАНИЯ ОБРАЗОВ
- Глава 2. РЕШАЮЩИЕ ФУНКЦИИ
- 2.2. ЛИНЕЙНЫЕ РЕШАЮЩИЕ ФУНКЦИИ
- 2.3. ОБОБЩЕННЫЕ РЕШАЮЩИЕ ФУНКЦИИ
- 2.4. ПРОСТРАНСТВО ОБРАЗОВ И ПРОСТРАНСТВО ВЕСОВ
- 2.5. ГЕОМЕТРИЧЕСКИЕ СВОЙСТВА
- 2.5.2. Дихотомии
- 2.5.3. Дихотомизационная мощность обобщенных решающих функций
- 2.6. РЕАЛИЗАЦИЯ РЕШАЮЩИХ ФУНКЦИЙ
- 2.7. ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ
- 2.7.2. Построение функций многих переменных
- 2.7.3. Ортогональные и ортонормированные системы функций
- 2.8. ЗАКЛЮЧИТЕЛЬНЫЕ ЗАМЕЧАНИЯ
- Глава 3. КЛАССИФИКАЦИЯ ОБРАЗОВ С ПОМОЩЬЮ ФУНКЦИЙ РАССТОЯНИЯ
- 3.2. КЛАССИФИКАЦИЯ ОБРАЗОВ ПО КРИТЕРИЮ МИНИМУМА РАССТОЯНИЯ
- 3.2.2. Множественность эталонов
- 3.2.3. Обобщение принципов классификации по минимуму расстояния
- 3.2.4. Синтез системы распознавания. Пример
- 3.3. ВЫЯВЛЕНИЕ КЛАСТЕРОВ
- 3.3.2. Критерии кластеризации
- 3.3.3. Простой алгоритм выявления кластеров
- 3.3.4. Алгоритм максиминного расстояния
- 3.3.5. Алгоритм К внутригрупповых средних
- 3.3.6. Алгоритм ИСОМАД
- 3.3.7. Оценка результатов процесса кластеризации
- 3.3.8. Кластеризация, основанная на теории графов
- 3.4. РАСПОЗНАВАНИЕ ОБРАЗОВ БЕЗ УЧИТЕЛЯ
- 3.5. ЗАКЛЮЧИТЕЛЬНЫЕ ЗАМЕЧАНИЯ
- Глава 4. КЛАССИФИКАЦИЯ ОБРАЗОВ С ПОМОЩЬЮ ФУНКЦИЙ ПРАВДОПОДОБИЯ
- 4.2. КЛАССИФИКАЦИЯ ОБРАЗОВ КАК ЗАДАЧА ТЕОРИИ СТАТИСТИЧЕСКИХ РЕШЕНИЙ
- 4.3. БАЙЕСОВСКИЙ КЛАССИФИКАТОР В СЛУЧАЕ ОБРАЗОВ, ХАРАКТЕРИЗУЮЩИХСЯ НОРМАЛЬНЫМ РАСПРЕДЕЛЕНИЕМ
- 4.4. ВЕРОЯТНОСТИ ОШИБОК
- 4.5. ВАЖНОЕ СЕМЕЙСТВО ПЛОТНОСТЕЙ РАСПРЕДЕЛЕНИЯ
- 4.6. ОЦЕНКА ФУНКЦИЙ ПЛОТНОСТИ РАСПРЕДЕЛЕНИЯ
- 4.6.2. Оценка вектора средних значений и ковариационной матрицы
- 4.6.3. Оценка вектора средних значений и ковариационной матрицы с помощью байесовской обучающей процедуры
- 4.6.4. Аппроксимация плотностей распределения функциями
- 4.7. ЗАКЛЮЧИТЕЛЬНЫЕ ЗАМЕЧАНИЯ
- Глава 5. ОБУЧАЕМЫЕ КЛАССИФИКАТОРЫ ОБРАЗОВ. ДЕТЕРМИНИСТСКИЙ ПОДХОД
- 5.2. ПЕРЦЕПТРОННЫЙ ПОДХОД
- 5.2.1. Принцип подкрепления — наказания
- 5.2.2. Доказательство сходимости
- 5.2.3. Разновидности перцептронного подхода
- 5.3. ПОСТРОЕНИЕ АЛГОРИТМОВ КЛАССИФИКАЦИИ ОБРАЗОВ
- 5.3.2. Алгоритм перцептрона
- 5.3.3. Алгоритм, основанный на минимизации среднеквадратичной ошибки
- 5.3.4. Доказательство сходимости НСКО-алгоритма
- 5.4. КЛАССИФИКАЦИЯ ДЛЯ СЛУЧАЯ НЕСКОЛЬКИХ КЛАССОВ
- 5.5. ОБУЧЕНИЕ И ОБОБЩЕНИЕ
- 5.6. ПОДХОД, ОСНОВАННЫЙ НА ИСПОЛЬЗОВАНИИ ПОТЕНЦИАЛЬНЫХ ФУНКЦИЙ
- 5.6.2. Выбор потенциальных функций
- 5.6.3. Геометрическая интерпретация коррекции весов
- 5.6.4. Сходимость алгоритмов обучения
- 5.6.5. Обобщение на случай нескольких классов
- 5.7. ЗАКЛЮЧИТЕЛЬНЫЕ ЗАМЕЧАНИЯ
- Глава 6. ОБУЧАЕМЫЕ КЛАССИФИКАТОРЫ ОБРАЗОВ. СТАТИСТИЧЕСКИЙ ПОДХОД
- 6.2. МЕТОДЫ СТОХАСТИЧЕСКОЙ АППРОКСИМАЦИИ
- 6.2.2. Скорость сходимости
- 6.2.3. Обобщение на многомерный случай
- 6.3. ПОСТРОЕНИЕ АЛГОРИТМОВ КЛАССИФИКАЦИИ ОБРАЗОВ
- 6.3.2. Алгоритм корректирующих приращений
- 6.3.3. Алгоритм наименьшей среднеквадратичной ошибки
- 6.4. МЕТОД ПОТЕНЦИАЛЬНЫХ ФУНКЦИЙ
- 6.5. ЗАКЛЮЧИТЕЛЬНЫЕ ЗАМЕЧАНИЯ
- Глава 7. ПРЕДВАРИТЕЛЬНАЯ ОБРАБОТКА ОБРАЗОВ И ВЫБОР ПРИЗНАКОВ
- 7.2. РАССТОЯНИЯ
- 7.3. ПРЕОБРАЗОВАНИЯ КЛАСТЕРИЗАЦИИ И УПОРЯДОЧЕНИЕ ПРИЗНАКОВ
- 7.4. РОЛЬ КЛАСТЕРИЗАЦИИ В ВЫБОРЕ ПРИЗНАКОВ
- 7.5. ВЫБОР ПРИЗНАКОВ ПРИ ПОМОЩИ МИНИМИЗАЦИИ ЭНТРОПИИ
- 7.6. ВЫБОР ПРИЗНАКОВ ПРИ ПОМОЩИ РАЗЛОЖЕНИЙ ПО СИСТЕМЕ ОРТОГОНАЛЬНЫХ ФУНКЦИЙ
- 7.6.2. Разложение Карунена — Лоэва
- 7.7. ВЫБОР ПРИЗНАКОВ ПОСРЕДСТВОМ АППРОКСИМАЦИИ ФУНКЦИЯМИ
- 7.7.2. Метод стохастической аппроксимации
- 7.7.3. Ядерная аппроксимация
- 7.7.4. Использование функций признаков при классификации
- 7.8. КОНЦЕПЦИЯ ДИВЕРГЕНЦИИ
- 7.9. ВЫБОР ПРИЗНАКОВ НА ОСНОВЕ МАКСИМИЗАЦИИ ДИВЕРГЕНЦИИ
- 7.10. ВЫБОР ДВОИЧНЫХ ПРИЗНАКОВ
- 7.11 ЗАКЛЮЧИТЕЛЬНЫЕ ЗАМЕЧАНИЯ
- Глава 8. СИНТАКСИЧЕСКОЕ РАСПОЗНАВАНИЕ ОБРАЗОВ
- 8.2. ПОНЯТИЯ ТЕОРИИ ФОРМАЛЬНЫХ ЯЗЫКОВ
- 8.2.2. Типы грамматик
- 8.3. ПОСТАНОВКА ЗАДАЧИ СИНТАКСИЧЕСКОГО РАСПОЗНАВАНИЯ ОБРАЗОВ
- 8.4. СИНТАКСИЧЕСКОЕ ОПИСАНИЕ ОБРАЗОВ
- 8.5. ГРАММАТИКИ, ИСПОЛЬЗУЕМЫЕ В РАСПОЗНАВАНИИ ОБРАЗОВ
- 8.5.2. Распознавание образов, представленных графами
- 8.5.3. Распознавание древовидных структур
- 8.6. СТАТИСТИЧЕСКИЙ АНАЛИЗ
- 8.6.2. Оценка вероятностей правил подстановки с помощью процедур обучения
- 8.7. ОБУЧЕНИЕ И ГРАММАТИЧЕСКИЙ ВЫВОД
- 8.7.2. Вывод двумерных грамматик
- 8.8. АВТОМАТЫ КАК РАСПОЗНАЮЩИЕ УСТРОЙСТВА
- 8.9. ЗАКЛЮЧИТЕЛЬНЫЕ ЗАМЕЧАНИЯ
- СПИСОК ЛИТЕРАТУРЫ
- СПИСОК ОБОЗНАЧЕНИЙ