| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
17.2. РАСПРОСТРАНЕНИЕ ОПТИЧЕСКИХ ВОЛН В ПЛОСКОМ ВОЛНОВОДЕ
Плоский оптический волновод представляет собой плоский и тонкий (порядка длины волны света) слой, в котором показатель преломления выше, чем в прилегающих слоях настолько, чтобы между волноводным слоем и прилегающими выполнялись условия отсечки. В частном (но наиболее важном) случае таким слоем является поверхностный слой кристалла, в котором за счет определенной обработки повышен показатель преломления. Такой слой с одной стороны граничит с матрицей (подложкой), в которой показатель преломления остался неизменным, а с другой - с внешней средой (воздух). Поскольку показатель преломления воздуха  и заведомо меньше, чем показатель преломления подложки
и заведомо меньше, чем показатель преломления подложки  то волноводный режим в слое с повышенным показателем преломления наступает при выполнении условия отсечки на границе слой - подложка. Рассматривая распространение оптических волн в плоском волноводе, можно установить его основные характеристики и их связь с параметрами, характеризующими сам волновод. Следуя [5], рассмотрим распространение в оптическом волноводе плоской оптической ТЕ-волны. Напомним, что ТЕ-волной является оптическая волна, для которой электрический
то волноводный режим в слое с повышенным показателем преломления наступает при выполнении условия отсечки на границе слой - подложка. Рассматривая распространение оптических волн в плоском волноводе, можно установить его основные характеристики и их связь с параметрами, характеризующими сам волновод. Следуя [5], рассмотрим распространение в оптическом волноводе плоской оптической ТЕ-волны. Напомним, что ТЕ-волной является оптическая волна, для которой электрический  вектор параллелен плоскостям отражения. В нашем случае (рис. 17.2) для плоскостей отражения (границ раздела слоев)
вектор параллелен плоскостям отражения. В нашем случае (рис. 17.2) для плоскостей отражения (границ раздела слоев)  при распространении волн в плоскости
при распространении волн в плоскости  электрический вектор должен бьггь направлен вдоль оси у и имеет компоненты
электрический вектор должен бьггь направлен вдоль оси у и имеет компоненты  Полагаем: слои не ограничены в размерах в направлениях z и у, так что стоячие волны в этих направлениях не образуются.
Полагаем: слои не ограничены в размерах в направлениях z и у, так что стоячие волны в этих направлениях не образуются.

Рис. 17.2. Система координат в трехслойном волноводе
Воспользовавшись решением (17.2) уравнения Максвелла (17.1) для плоской волны, распространяющейся вдоль  с постоянной распространения
с постоянной распространения  в волноводном слое толщиной
в волноводном слое толщиной  запишем для амплитуды поля
запишем для амплитуды поля

При выполнении условий отсечки функция  в соседних слоях имеет вид
в соседних слоях имеет вид

А, В, С, q, h, p - постоянные, которые можно определить из условий непрерывности на границах раздела слоев функций  - компонента вектора магнитного поля ТЕ-волны;
- компонента вектора магнитного поля ТЕ-волны;  - магнитная проницаемость). Подстановка (17.9) в (17.8) и (17.1) позволяет определить константы
- магнитная проницаемость). Подстановка (17.9) в (17.8) и (17.1) позволяет определить константы  и
и  через показатели преломления
через показатели преломления  число распространения
число распространения  и волновое число
и волновое число 

Используя условие непрерывности на границе  и
и
1) приравнивая (17.9, а) и (17.9, 6) при  получим
получим  т.е.
т.е. 
2) приравнивая производные (17.9, а) и (17.9, 6) по  при
при  получим
получим 

Используя условие непрерывности на границе  и
и
1) приравнивая  получим
получим

2) приравнивая производные (17.9, б) и (17.9, в) по х с подстановкой значений  и
и  получим
получим

Разделив правую и левую части этого равенства на  получим
получим


Рис. 17.3. Форма мод симметричного (а) и асимметричного (б) волновода

Решение (17.11) дает набор разрешенных значений  которым согласно (17.10) соответствует набор значений
которым согласно (17.10) соответствует набор значений  определяющий набор оптических мод, существующих в волноводе.
определяющий набор оптических мод, существующих в волноводе.
Часто нет необходимости знать весь набор значений  достаточно выяснить, может ли в волноводе распространяться данная конкретная мода. Этот вопрос легко решить для так называемого «симметричного» волновода. Симметричным называют такой волновод, в котором волноводный слой находится между слоями с одинаковыми показателями преломления. Такие волноводы могут создаваться, например, в многослойных интегральных схемах на основе
достаточно выяснить, может ли в волноводе распространяться данная конкретная мода. Этот вопрос легко решить для так называемого «симметричного» волновода. Симметричным называют такой волновод, в котором волноводный слой находится между слоями с одинаковыми показателями преломления. Такие волноводы могут создаваться, например, в многослойных интегральных схемах на основе  . В симметричном волноводе
. В симметричном волноводе  , следовательно,
, следовательно,

С учетом этого выражение (17.11) превращается в равенство

Из (17.13) следует, что

Подставляя  из (17.12) в (17.13), получаем
из (17.12) в (17.13), получаем

Выражая к через длину волны  из (17.15) получим условие, при котором мода с номером
из (17.15) получим условие, при котором мода с номером  может распространяться в волноводе
может распространяться в волноводе

Выражение (17.16) показывает, каково должно быть  для того, чтобы в слое толщиной
для того, чтобы в слое толщиной  могла распространяться мода
могла распространяться мода  где
где  - число волн, укладывающихся на длине
- число волн, укладывающихся на длине  (рис. 17.3).
(рис. 17.3).

Рис. 17.4. Распространение волны с волновым вектором  в среде с наибольшим показателем преломления. А и
в среде с наибольшим показателем преломления. А и  - точки, в которых фаза волны одинакова;
- точки, в которых фаза волны одинакова;  точки отражения от поверхности раздела;
точки отражения от поверхности раздела;  - расстояние между границами раздела сред
- расстояние между границами раздела сред
В том случае, если  волновод является несимметричным. В частности, асимметричным является волновод, у которого оптически плотный слой создан на поверхности подложки и граничит с воздухом или покрыт слоем металла. В этом случае в
волновод является несимметричным. В частности, асимметричным является волновод, у которого оптически плотный слой создан на поверхности подложки и граничит с воздухом или покрыт слоем металла. В этом случае в  и для нахождения условия распространения мод типа (17.13) нужно решать уравнение (17.11) графически или на ЭВМ. В [5] предложено приближенное решение, позволяющее найти соотношение между
и для нахождения условия распространения мод типа (17.13) нужно решать уравнение (17.11) графически или на ЭВМ. В [5] предложено приближенное решение, позволяющее найти соотношение между  для асимметричного волновода. Это решение основано на сходстве распределения поля в асимметричном волноводе, имеющем толщину
для асимметричного волновода. Это решение основано на сходстве распределения поля в асимметричном волноводе, имеющем толщину  и в симметричном волноводе удвоенной толщины
и в симметричном волноводе удвоенной толщины  Это сходство видно из сравнения рис. 17.3, а и рис.
Это сходство видно из сравнения рис. 17.3, а и рис.  на котором представлены две ТЕ-моды низшего порядка симметричного
на котором представлены две ТЕ-моды низшего порядка симметричного  и асимметричного
и асимметричного  волноводов. Видно, что нижняя половина моды симметричного волновода
волноводов. Видно, что нижняя половина моды симметричного волновода  хорошо соответствует моде
хорошо соответствует моде  асимметричного волновода половинной толщины. Учитывая это обстоятельство, можно для нахождения условия отсечки в асимметричном волноводе толщиной
асимметричного волновода половинной толщины. Учитывая это обстоятельство, можно для нахождения условия отсечки в асимметричном волноводе толщиной  воспользоваться выражением (17.16) для симметричного волновода удвоенной толщины
воспользоваться выражением (17.16) для симметричного волновода удвоенной толщины 

Асимметричный волновод поддерживает только те моды, которые соответствуют нечетным модам симметричного волновода удвоенной толщины. Следовательно, условие отсечки для асимметричного волновода толщиной  определяется выражением
определяется выражением

Здесь та состоит из нечетных значений  т. е.
т. е. 
С учетом этого (17.18) можно переписать в виде

Из сравнения (17.16) и (17.19) видно, что в асимметричном волноводе можно отсечь все моды, а в симметричном волноводе моду 
отсечь нельзя  равенство (17.16) превращается в
равенство (17.16) превращается в 
Направления волновых векторов дискретных мод, существующих в данном волноводе, можно найти, рассмотрев изменение фазы волны на пути между точками волновода, оптическая длина пути между которыми равна длине волны - точки А и  на рис. 17.4. Волна
на рис. 17.4. Волна  за период
за период  проходит путь
проходит путь  На этом пути фаза волны меняется на величину
На этом пути фаза волны меняется на величину

где  - изменение фазы данной моды на пути
- изменение фазы данной моды на пути  - изменение фазы волны при отражении от границ раздела 2 - 1 и 2 - 3;
- изменение фазы волны при отражении от границ раздела 2 - 1 и 2 - 3;

Выражение (17.20) можно переписать в виде

Величины сдвигов фаз при отражении можно найти [6] из равенств

Углы распространения мод колебаний, разрешенных в данном волноводе, можно определить, решая численными методами уравнение

Величина

определяющая скорость распространения волны в направлении переноса электромагнитной энергии в волноводе, получила название эффективный показатель преломления волновода.
Для определения  оптических мод, существующих в волноводе, можно использовать ввод излучения в волновод с помощью оптического волокна (в торец) или призмы и призменный вывод (рис. 17.5). Использовав соотношения
оптических мод, существующих в волноводе, можно использовать ввод излучения в волновод с помощью оптического волокна (в торец) или призмы и призменный вывод (рис. 17.5). Использовав соотношения


Рис. 17.5. Схема определения 
откуда  и
и

Эта величина определяет скорость переноса фазы волн в направлении  волновода.
волновода.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Часть I. ЛАЗЕРНЫЕ КРИСТАЛЛЫ
- Глава 1. ХАРАКТЕРИСТИКИ КРИСТАЛЛОВ, ИСПОЛЬЗУЕМЫХ ДЛЯ ГЕНЕРАЦИИ ЛАЗЕРНОГО ИЗЛУЧЕНИЯ
- 1.2. ОПТИЧЕСКИЙ РЕЗОНАТОР
- 1.3. ПОРОГОВЫЕ УСЛОВИЯ ДЛЯ УСИЛЕНИЯ СВЕТА
- 1.3.2. Пороговые условия в непрерывном режиме
- 1.4. ЭНЕРГЕТИЧЕСКИЕ ХАРАКТЕРИСТИКИ И К.П.Д. ЛАЗЕРА
- 1.5. ИОНЫ-АКТИВАТОРЫ
- 1.6. ТЕПЛОВЫЕ СВОЙСТВА КРИСТАЛЛОВ
- 1.7. ТРЕБОВАНИЯ, ПРЕДЪЯВЛЯЕМЫЕ К КРИСТАЛЛАМ
- Глава 2. КРИСТАЛЛЫ-ОКСИДЫ
- 2.1.2. Структура кристаллов
- Макронеоднородность кристаллов
- Примеси
- Центры окраски в кристаллах соединений …
- Окраска корунда
- Окраска иттрий-атоминиевого граната
- Дополнительная окраска и рекомбинационные процессы в кристаллах алюмината иттрия
- 2.2. КРИСТАЛЛИЧЕСКИЕ СРЕДЫ ДЛЯ ВЫСОКОЭФФЕКТИВНЫХ НЕОДИМОВЫХ ЛАЗЕРОВ
- 2.2.2. ВЫРАЩИВАНИЕ И РОСТОВЫЕ ДЕФЕКТЫ КРИСТАЛЛОВ ГАЛЛИЕВЫХ ГРАНАТОВ
- 2.2.3. РАЗУПОРЯДОЧЕНИЕ В ГАЛЛИЕВЫХ ГРАНАТАХ
- 2.2.4. ЦЕНТРЫ ОКРАСКИ В ГАЛЛИЕВЫХ ГРАНАТАХ
- Глава 3. КРИСТАЛЛЫ ФТОРИДОВ
- 3.1. Кристаллы YLiF4
- 3.2. Кристаллы …
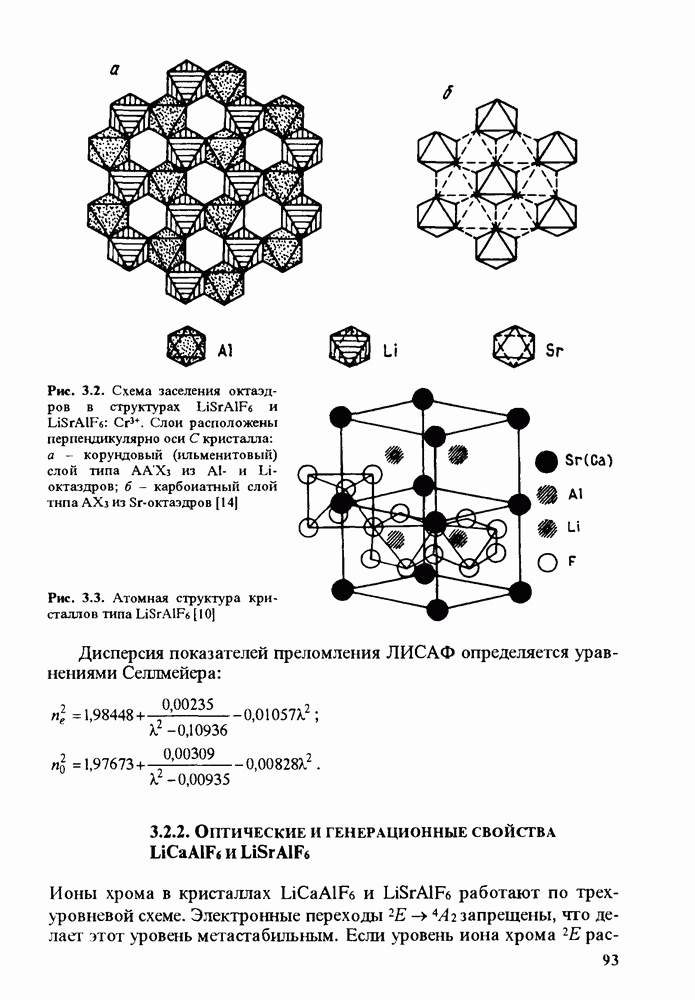
- 3.2.2. ОПТИЧЕСКИЕ И ГЕНЕРАЦИОННЫЕ СВОЙСТВА
- Глава 4. КРИСТАЛЛЫ ДЛЯ ЛАЗЕРОВ С ПЕРЕСТРАИВАЕМОЙ ЧАСТОТОЙ
- 4.1. АЛЕКСАНДРИТ
- 4.2. КОРУНД С ТИТАНОМ
- 4.3. ЦЕНТРЫ ОКРАСКИ — АКТИВАТОРЫ ЛАЗЕРНЫХ КРИСТАЛЛОВ
- Глава 5. ДЕФЕКТЫ ЛАЗЕРНЫХ КРИСТАЛЛОВ, ВОЗНИКАЮЩИЕ ПРИ ПЛАСТИЧЕСКОЙ ДЕФОРМАЦИИ
- 5.2. ДВОЙНИКОВАНИЕ
- Глава 6. КРИСТАЛЛЫ ДЛЯ ПРОХОДНОЙ ОПТИКИ МОЩНЫХ ЛАЗЕРОВ
- 6.1. СОБСТВЕННЫЕ МЕХАНИЗМЫ ОПТИЧЕСКОГО РАЗРУШЕНИЯ
- 6.2. НЕСОБСТВЕННЫЕ МЕХАНИЗМЫ ОПТИЧЕСКОГО РАЗРУШЕНИЯ
- 6.2.1. ОПТИЧЕСКОЕ РАЗРУШЕНИЕ ПОВЕРХНОСТИ
- 6.2.2. РАЗРУШЕНИЕ В ОБЪЕМЕ КРИСТАЛЛА
- 6.3. ОПТИЧЕСКАЯ ПРОЧНОСТЬ В СФОКУСИРОВАННЫХ И ШИРОКО АПЕРТУРНЫХ ПУЧКАХ
- 6.4. ОПТИЧЕСКАЯ ПРОЧНОСТЬ КРИСТАЛЛОВ ПРИ ВОЗДЕЙСТВИИ ИМПУЛЬСНОПЕРИОДИЧЕСКОГО ИЗЛУЧЕНИЯ
- 6.5. ВЫБОР МАТЕРИАЛА ДЛЯ ПРОХОДНОЙ ОПТИКИ МОЩНЫХ ЛАЗЕРОВ
- 6.6. ВОЗМОЖНОСТИ ПОВЫШЕНИЯ ОПТИЧЕСКОЙ ПРОЧНОСТИ КРИСТАЛЛОВ И ОПТИЧЕСКИХ ЭЛЕМЕНТОВ
- Часть II. НЕЛИНЕЙНО-ОПТИЧЕСКИЕ И ЭЛЕКТРООПТИЧЕСКИЕ КРИСТАЛЛЫ
- Глава 7. ЛИНЕЙНЫЙ ЭЛЕКТРООПТИЧЕСКИЙ ЭФФЕКТ И ХАРАКТЕРИСТИКИ ЭЛЕКТРО-ОПТИЧЕСКОГО КАЧЕСТВА КРИСТАЛЛОВ
- 7.2. ПОЛЯРИЗАЦИОННО-ОПТИЧЕСКИЕ ЗАТВОРЫ И МОДУЛЯТОРЫ СВЕТА
- 7.3. ЭЛЕКТРООПТИЧЕСКИЕ ЗАТВОРЫ НА РЕГУЛЯРНОЙ ДОМЕННОЙ СТРУКТУРЕ
- Глава 8. РАСПРОСТРАНЕНИЕ СВЕТА В НЕЛИНЕЙНЫХ ОПТИЧЕСКИХ СРЕДАХ
- 8.2. УСЛОВИЯ СОХРАНЕНИЯ ЭНЕРГИИ И ИМПУЛЬСА ПРИ ВЗАИМОДЕЙСТВИИ ФОТОНОВ В НЕЛИНЕЙНЫХ СРЕДАХ
- 8.3. РЕАЛИЗАЦИЯ УСЛОВИЙ СИНХРОНИЗМА
- 8.4. ЭФФЕКТИВНЫЕ КОЭФФИЦИЕНТЫ НЕЛИНЕЙНОСТИ
- 8.5. РАССОГЛАСОВАНИЕ ФАЗ ВЗАИМОДЕЙСТВУЮЩИХ ВОЛН ПОД ДЕЙСТВИЕМ ВНЕШНИХ ФАКТОРОВ. ПОЛОСА ПРОПУСКАНИЯ
- 8.6. РАСЧЕТ ПРЕОБРАЗОВАТЕЛЯ ЧАСТОТЫ
- 8.7. КВАЗИСИНХРОННОЕ ВЗАИМОДЕЙСТВИЕ
- Глава 9. КРИСТАЛЛЫ НА ОСНОВЕ ОКСИДОВ
- 9.2. ВЫРАЩИВАНИЕ КРИСТАЛЛОВ
- 9.3. ФАЗОВЫЕ ПЕРЕХОДЫ В КИСЛОРОДНООКТАЭДРИЧЕСКИХ КРИСТАЛЛАХ
- 9.4. ДЕФЕКТЫ СТРУКТУРЫ
- 9.4.1. МАКРОНЕОДНОРОДНОСТЬ КРИСТАЛЛОВ
- 9.4.2. ДВОЙНИКОВАНИЕ
- Механическое двойникование кристаллов ниобата лития
- 9.5. МОНОДОМЕНИЗАЦИЯ КРИСТАЛЛОВ
- 9.6. ПОЛУЧЕНИЕ РЕГУЛЯРНЫХ ДОМЕННЫХ СТРУКТУР
- 9.6.2. ПОСЛЕРОСТОВАЯ ЭЛЕКТРОТЕРМИЧЕСКАЯ ОБРАБОТКА
- 9.6.3. ПОЛУЧЕНИЕ РЕГУЛЯРНЫХ ДОМЕННЫХ СТРУКТУР В ПОВЕРХНОСТНЫХ СЛОЯХ
- 9.6.4. ПОЛУЧЕНИЕ РЕГУЛЯРНЫХ ДОМЕННЫХ СТРУКТУР СКАНИРОВАНИЕМ ПО КРИСТАЛЛУ ЭЛЕКТРОННЫМ ЛУЧОМ
- 9.7. ДИСЛОКАЦИИ И ПЛАСТИЧНОСТЬ КИСЛОРОДНО-ОКТАЭДРИЧЕСКИХ КРИСТАЛЛОВ
- 9.8. ТОЧЕЧНЫЕ ДЕФЕКТЫ
- 9.8.1. ВЛИЯНИЕ ОТКЛОНЕНИЯ ОТ СТЕХИОМЕТРИИ НА СВОЙСТВА КРИСТАЛЛОВ НИОБАТА ЛИТИЯ
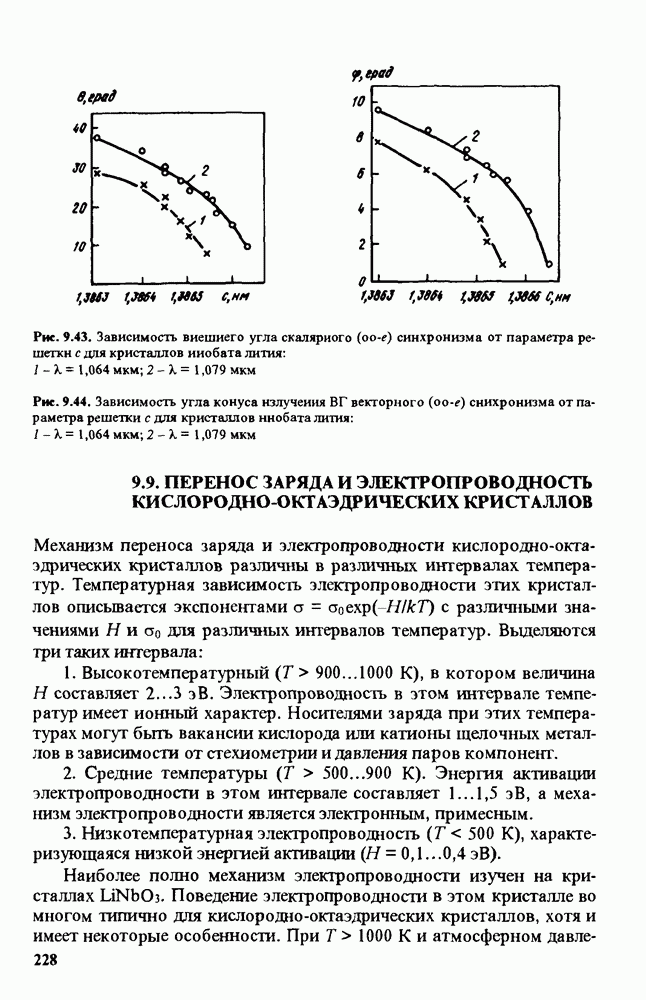
- 9.9. ПЕРЕНОС ЗАРЯДА И ЭЛЕКТРОПРОВОДНОСТЬ КИСЛОРОДНО-ОКТАЭДРИЧЕСКИХ КРИСТАЛЛОВ
- 9.10. ФОТОРЕФР АКТИВНЫЙ ЭФФЕКТ В КИСЛОРОДНО-ОКТАЭДРИЧЕСКИХ КРИСТАЛЛАХ
- 9.10.2. МЕХАНИЗМЫ ВОЗНИКНОВЕНИЯ ПРОСТРАНСТВЕННОГО ЗАРЯДА
- 9.10.3. ВОЗМОЖНОСТЬ ОСЛАБЛЕНИЯ ФОТОРЕФРАКЦИИ
- 9.10.4. ФОТОРЕФРАКЦИЯ В ПРАКТИЧЕСКИ ВАЖНЫХ КРИСТАЛЛАХ
- 9.11. ОПТИЧЕСКАЯ НЕОДНОРОДНОСТЬ И НЕСТАБИЛЬНОСТЬ СВОЙСТВ КРИСТАЛЛОВ
- 9.11.2. ОПТИЧЕСКАЯ НЕОДНОРОДНОСТЬ КРИСТАЛЛОВ НИОБАТА ЛИТИЯ
- Глава 10. КРИСТАЛЛЫ ГРУППЫ KDP
- 10.1. ОСНОВНЫЕ СВОЙСТВА КРИСТАЛЛОВ ГРУППЫ KDP
- 10.2. СТРУКТУРА И МЕТОДЫ ВЫРАЩИВАНИЯ КРИСТАЛЛОВ
- 10.3. ВЛИЯНИЕ ПРИМЕСЕЙ И КИСЛОТНОСТИ РАСТВОРА НА РОСТ КРИСТАЛЛОВ KDP И ADP
- 10.4. СКОРОСТНОЕ ВЫРАЩИВАНИЕ КРИСТАЛЛОВ
- 10.5. ПЛАСТИЧНОСТЬ И ДИСЛОКАЦИИ В КРИСТАЛЛАХ ГРУППЫ KDP
- Глава 11. ИОДАТ ЛИТИЯ
- 11.1. СТРУКТУРА И ВЫРАЩИВАНИЕ КРИСТАЛЛОВ ИОДАТА ЛИТИЯ
- 11.2. ВХОЖДЕНИЕ ПРИМЕСЕЙ В КРИСТАЛЛ …
- 11.3. ГАБИТУС КРИСТАЛЛОВ … И ВЫРАЩИВАНИЕ ПРОФИЛИРОВАННЫХ КРИСТАЛЛОВ
- 11.4. ЭЛЕКТРИЧЕСКИЕ СВОЙСТВА КРИСТАЛЛОВ …
- 11.5. ОПТИЧЕСКИЕ И НЕЛИНЕЙНООПТИЧЕСКИЕ СВОЙСТВА КРИСТАЛЛОВ …
- Глава 12. ТИТАНИЛФОСФАТ КАЛИЯ
- 12.1. ОСОБЕННОСТИ КРИСТАЛЛОВ ТИТАНИЛФОСФАТА КАЛИЯ
- 12.2. СТРУКТУРА КРИСТАЛЛОВ КТР
- 12.3. ВЫРАЩИВАНИЕ КРИСТАЛЛОВ
- 12.4. СВОЙСТВА КТР
- 12.5. ОПТИЧЕСКАЯ НЕЛИНЕЙНОСТЬ КРИСТАЛЛОВ КТР
- Глава 13. БОРАТЫ
- 13.2. ОПТИЧЕСКИЕ И НЕЛИНЕЙНООПТИЧЕСКИЕ СВОЙСТВА БОРАТОВ
- Часть III. КРИСТАЛЛЫ В АКУСТООПТИКЕ
- Глава 14. ОСНОВНЫЕ ПРИНЦИПЫ АКУСТООПТИКИ
- 14.2. АКУСТООПТИЧЕСКАЯ ДИФРАКЦИЯ БРЭГГА В АНИЗОТРОПНЫХ КРИСТАЛЛАХ
- 14.2.2. АКУСТООПТИЧЕСКОЕ ВЗАИМОДЕЙСТВИЕ в ПЛОСКОСТИ, ЛЕЖАЩЕЙ ПОД УГЛОМ К ОПТИЧЕСКОЙ ОСИ КРИСТАЛЛА
- 14.3. ИНТЕНСИВНОСТЬ ДИФРАКЦИИ И АКУСТООПТИЧЕСКАЯ ЭФФЕКТИВНОСТЬ СРЕДЫ
- 14.4. КОЛЛИНЕАРНОЕ АКУСТООПТИЧЕСКОЕ ВЗАИМОДЕЙСТВИЕ. ВЛИЯНИЕ СИНХРОНИЗМА НА ЭФФЕКТИВНОСТЬ ДИФРАКЦИИ
- Глава 15. ОСНОВНЫЕ ОБЛАСТИ ПРИМЕНЕНИЯ АКУСТООПТИЧЕСКОГО ВЗАИМОДЕЙСТВИЯ
- 15.2. АКУСТООПТИЧЕСКИЙ ДЕФЛЕКТОР
- 15.3. АКУСТООПТИЧЕСКИЙ ФИЛЬТР
- 15.3.2. ПРИМЕРЫ РЕАЛИЗАЦИИ КОЛЛИНЕАРНОГО ВЗАИМОДЕЙСТВИЯ ПРИ СОЗДАНИИ АКУСТООПТИЧЕСКИХ ФИЛЬТРОВ
- Глава 16. АКУСТООПТИЧЕСКОЕ КАЧЕСТВО КРИСТАЛЛОВ
- 16.1. СВЯЗЬ АКУСТООПТИЧЕСКОГО КАЧЕСТВА И ОСНОВНЫХ СВОЙСТВ КРИСТАЛЛОВ
- 16.2. МОНОКРИСТАЛЛИЧЕСКИЙ КВАРЦ
- 16.2.2. ДЕФЕКТЫ КВАРЦА
- 16.3. ПАРАТЕЛЛУРИТ
- 16.3.1. СТРУКТУРА И СВОЙСТВА ПАРАТЕЛЛУРИТА
- 16.3.2. ВЫРАЩИВАНИЕ ПАРАТЕЛЛУРИТА
- 16.3.3. ДЕФЕКТЫ СТРУКТУРЫ ПАРАТЕЛЛУРИТА
- 16.3.4. ПРИМЕНЕНИЕ TEO2 В АКУСГООПТИЧЕСКИХ ПРИБОРАХ
- 16.4. МОЛИБДАТЫ ЩЕЛОЧНОЗЕМЕЛЬНЫХ ИОНОВ
- 16.4.2. ВЫРАЩИВАНИЕ МОНОКРИСТАЛЛОВ
- 16.4.3. ДЕФЕКТЫ СТРУКТУРЫ
- 16.4.4. ПРИМЕНЕНИЕ МОЛИБДАТОВ В АКУСТООПТИКЕ
- Часть IV. КРИСТАЛЛИЧЕСКИЕ ЭЛЕМЕНТЫ ИНТЕГРАЛЬНОЙ ОПТИКИ
- Глава 17 ОПТИЧЕСКИЕ ВОЛНОВОДЫ, ИХ СВОЙСТВА И ХАРАКТЕРИСТИКИ
- 17.2. РАСПРОСТРАНЕНИЕ ОПТИЧЕСКИХ ВОЛН В ПЛОСКОМ ВОЛНОВОДЕ
- 17.3. ПОТЕРИ В ВОЛНОВОДЕ
- Глава 18. МЕТОДЫ ПОЛУЧЕНИЯ ВОЛНОВОДОВ
- 18.1. Ti-ДИФФУЗИОННАЯ ТЕХНОЛОГИЯ
- 18.1.2. ДИФФУЗИОННЫЙ ОТЖИГ
- 18.2. ПОЛУЧЕНИЕ ОПТИЧЕСКИХ ВОЛНОВОДОВ МЕТОДОМ ИОННОГО ОБМЕНА (ПРОТОННОГО ЗАМЕЩЕНИЯ)
- 18.2.1. ДИФФУЗИОННЫЕ ПРОЦЕССЫ ПРИ ИОННОМ ОБМЕНЕ
- 18.2.2. ПОЛУЧЕНИЕ ВОЛНОВОДОВ МЕТОДОМ ПЗ В КРИСТАЛЛАХ
- 18.3. ПОЛУЧЕНИЕ ОПТИЧЕСКИХ ВОЛНОВОДОВ С ПОМОЩЬЮ ИОННОЙ ИМПЛАНТАЦИИ
- БИБЛИОГРАФИЧЕСКИЙ СПИСОК