| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
Глава 8. РАСПРОСТРАНЕНИЕ СВЕТА В НЕЛИНЕЙНЫХ ОПТИЧЕСКИХ СРЕДАХ
8.1. ИНТЕНСИВНОСТЬ ВЗАИМОДЕЙСТВУЮЩИХ ЛУЧЕЙ
8.1.1. Взаимодействие трех оптических полей
Взаимодействие электрических полей с близкими частотами колебаний удобно рассматривать, используя связь поляризации и электрического поля в виде, заданном выражением (II. 1). В результате взаимодействия электромагнитных полей  в нелинейных оптических средах возникает нелинейная поляризация
в нелинейных оптических средах возникает нелинейная поляризация  которая, следуя выражению (II.3) может быть задана в виде
которая, следуя выражению (II.3) может быть задана в виде

Нелинейная поляризация порождает новое электромагнитное поле  так что в результате нелинейного взаимодействия в среде будут существовать три взаимно связанных электрических поля. Зададим взаимодействующие электрические поля в виде волн, распространяющихся в направлении
так что в результате нелинейного взаимодействия в среде будут существовать три взаимно связанных электрических поля. Зададим взаимодействующие электрические поля в виде волн, распространяющихся в направлении 

где  - частоты;
- частоты;
 - волновые векторы;
- волновые векторы;
 - комплексные амплитуды трех взаимодействующих волн.
- комплексные амплитуды трех взаимодействующих волн.
Подставляя (8.2) в (8.1) с учетом того, что тензор диэлектрической проницаемости симметричен, получим для нелинейной поляризации

Амплитуды взаимодействующих полей можно получить, решая уравнения Максвелла с учетом нелинейной поляризации. Для немагнитной и непроводящей среды уравнение Максвелла имеет вид

где индукция  определяется электрическим полем и нелинейной составляющей поляризации с помощью материального уравнения
определяется электрическим полем и нелинейной составляющей поляризации с помощью материального уравнения

в котором линейная составляющая поляризации включена в  описывает нелинейную часть поляризации. Подставляя (8.5) в (8.4), получим
описывает нелинейную часть поляризации. Подставляя (8.5) в (8.4), получим

Рассмотрим решение (8.6) так, как это сделано в [1]. Запишем производные от напряженности поля и поляризации, требуемые для подстановки в (8.6). Вторые производные напряженности поля по времени

и аналогичные выражения для 
Для вторых производных поляризации по времени, используя (8.3), получим

Дважды дифференцируя (8.2) по z и полагая, что амплитуда поля настолько слабо зависит от z, что можно пренебречь вторыми производными амплитуды по полю, получим

Подставив (8.7), (8.8) и (8.9) в (8.6), учитывая, что  и полагая, что (8.6) удовлетворяется для каждой частной компоненты отдельно, получим систему уравнений для трех связанных волн
и полагая, что (8.6) удовлетворяется для каждой частной компоненты отдельно, получим систему уравнений для трех связанных волн

Общее решение этой системы уравнений не выражается в элементарных функциях. Однако для некоторых важных частных случаев такое решение может быть получено. Если поле  возникает в результате взаимодействия мощных полей
возникает в результате взаимодействия мощных полей  так, что передача энергии от полей
так, что передача энергии от полей  мала и амплитуды полей
мала и амплитуды полей  слабо меняются в зависимости от координаты, то можно считать
слабо меняются в зависимости от координаты, то можно считать  Тогда в системе (8.10) остается одно
Тогда в системе (8.10) остается одно  уравнение для
уравнение для  Обозначив
Обозначив

из (8.10) получим для 

Интегрируя (8.12), получаем 

Заменив  и используя соотношения
и используя соотношения  запишем (8.13) в виде
запишем (8.13) в виде

Плотность потока мощности или интенсивность излучения выражается через амплитуды электрического поля

Следовательно,

Вычислим отдельно произведение выражений, стоящих в скобках 

Подстановкой (8.17) в (8.16) получаем

В том случае, если  т.е. для Геннадии второй гармоники начального излучения (излучения накачки) из (8.18), получаем
т.е. для Геннадии второй гармоники начального излучения (излучения накачки) из (8.18), получаем

Коэффициент x связывает комплексные амплитуды нелинейной поляризации и электрического поля. Часто используется другой коэффициент  связывающий действительные амплитуды электрического поля
связывающий действительные амплитуды электрического поля  и нелинейной поляризации Р. Рассмотрим соотношение X и
и нелинейной поляризации Р. Рассмотрим соотношение X и  используя выражения, описывающие удвоение частоты. Действительная амплитуда поляризации
используя выражения, описывающие удвоение частоты. Действительная амплитуда поляризации  удвоенной частоты, определяемая действительной амплитудой поля записывается как
удвоенной частоты, определяемая действительной амплитудой поля записывается как

Здесь  и - комплексно сопряженные амплитуды поляризации удвоенной частоты, равные
и - комплексно сопряженные амплитуды поляризации удвоенной частоты, равные

В то же время, определяя  с помощью комплексных амплитуд поля, получаем
с помощью комплексных амплитуд поля, получаем

Используя для определения поля действительную амплитуду, запишем

Отсюда следует, что комплексная и действительная амплитуды поля связаны как

Подставляя (8.24) в (8.22), получим

Сравнивая (8.21) и (8.25), видим, что

Используя (8.26) и обозначив  запишем (8.18) и
запишем (8.18) и

| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- Часть I. ЛАЗЕРНЫЕ КРИСТАЛЛЫ
- Глава 1. ХАРАКТЕРИСТИКИ КРИСТАЛЛОВ, ИСПОЛЬЗУЕМЫХ ДЛЯ ГЕНЕРАЦИИ ЛАЗЕРНОГО ИЗЛУЧЕНИЯ
- 1.2. ОПТИЧЕСКИЙ РЕЗОНАТОР
- 1.3. ПОРОГОВЫЕ УСЛОВИЯ ДЛЯ УСИЛЕНИЯ СВЕТА
- 1.3.2. Пороговые условия в непрерывном режиме
- 1.4. ЭНЕРГЕТИЧЕСКИЕ ХАРАКТЕРИСТИКИ И К.П.Д. ЛАЗЕРА
- 1.5. ИОНЫ-АКТИВАТОРЫ
- 1.6. ТЕПЛОВЫЕ СВОЙСТВА КРИСТАЛЛОВ
- 1.7. ТРЕБОВАНИЯ, ПРЕДЪЯВЛЯЕМЫЕ К КРИСТАЛЛАМ
- Глава 2. КРИСТАЛЛЫ-ОКСИДЫ
- 2.1.2. Структура кристаллов
- Макронеоднородность кристаллов
- Примеси
- Центры окраски в кристаллах соединений …
- Окраска корунда
- Окраска иттрий-атоминиевого граната
- Дополнительная окраска и рекомбинационные процессы в кристаллах алюмината иттрия
- 2.2. КРИСТАЛЛИЧЕСКИЕ СРЕДЫ ДЛЯ ВЫСОКОЭФФЕКТИВНЫХ НЕОДИМОВЫХ ЛАЗЕРОВ
- 2.2.2. ВЫРАЩИВАНИЕ И РОСТОВЫЕ ДЕФЕКТЫ КРИСТАЛЛОВ ГАЛЛИЕВЫХ ГРАНАТОВ
- 2.2.3. РАЗУПОРЯДОЧЕНИЕ В ГАЛЛИЕВЫХ ГРАНАТАХ
- 2.2.4. ЦЕНТРЫ ОКРАСКИ В ГАЛЛИЕВЫХ ГРАНАТАХ
- Глава 3. КРИСТАЛЛЫ ФТОРИДОВ
- 3.1. Кристаллы YLiF4
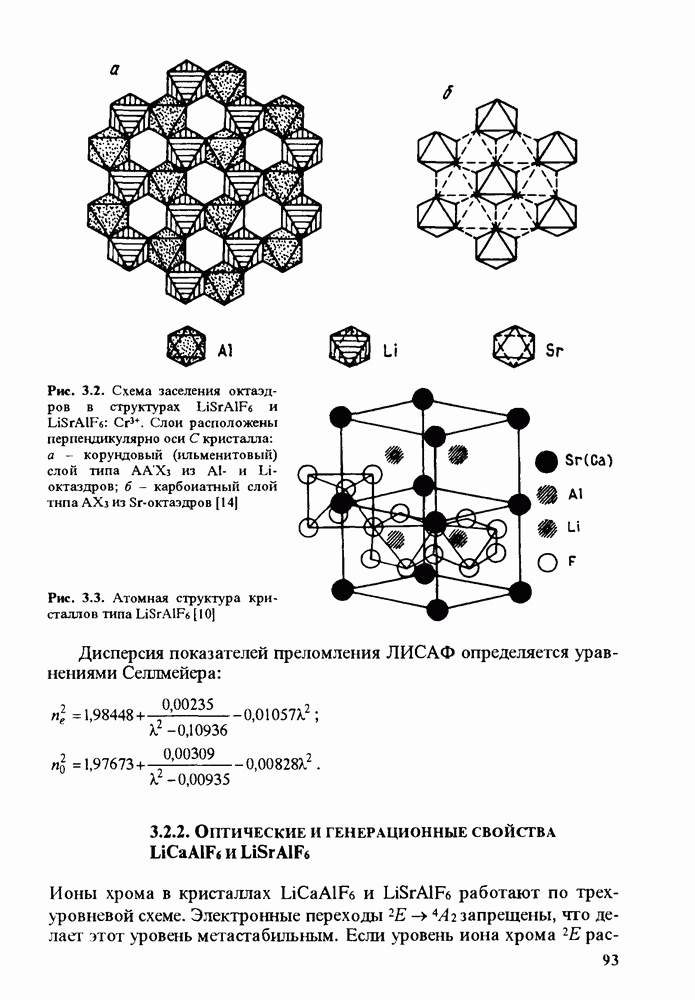
- 3.2. Кристаллы …
- 3.2.2. ОПТИЧЕСКИЕ И ГЕНЕРАЦИОННЫЕ СВОЙСТВА
- Глава 4. КРИСТАЛЛЫ ДЛЯ ЛАЗЕРОВ С ПЕРЕСТРАИВАЕМОЙ ЧАСТОТОЙ
- 4.1. АЛЕКСАНДРИТ
- 4.2. КОРУНД С ТИТАНОМ
- 4.3. ЦЕНТРЫ ОКРАСКИ — АКТИВАТОРЫ ЛАЗЕРНЫХ КРИСТАЛЛОВ
- Глава 5. ДЕФЕКТЫ ЛАЗЕРНЫХ КРИСТАЛЛОВ, ВОЗНИКАЮЩИЕ ПРИ ПЛАСТИЧЕСКОЙ ДЕФОРМАЦИИ
- 5.2. ДВОЙНИКОВАНИЕ
- Глава 6. КРИСТАЛЛЫ ДЛЯ ПРОХОДНОЙ ОПТИКИ МОЩНЫХ ЛАЗЕРОВ
- 6.1. СОБСТВЕННЫЕ МЕХАНИЗМЫ ОПТИЧЕСКОГО РАЗРУШЕНИЯ
- 6.2. НЕСОБСТВЕННЫЕ МЕХАНИЗМЫ ОПТИЧЕСКОГО РАЗРУШЕНИЯ
- 6.2.1. ОПТИЧЕСКОЕ РАЗРУШЕНИЕ ПОВЕРХНОСТИ
- 6.2.2. РАЗРУШЕНИЕ В ОБЪЕМЕ КРИСТАЛЛА
- 6.3. ОПТИЧЕСКАЯ ПРОЧНОСТЬ В СФОКУСИРОВАННЫХ И ШИРОКО АПЕРТУРНЫХ ПУЧКАХ
- 6.4. ОПТИЧЕСКАЯ ПРОЧНОСТЬ КРИСТАЛЛОВ ПРИ ВОЗДЕЙСТВИИ ИМПУЛЬСНОПЕРИОДИЧЕСКОГО ИЗЛУЧЕНИЯ
- 6.5. ВЫБОР МАТЕРИАЛА ДЛЯ ПРОХОДНОЙ ОПТИКИ МОЩНЫХ ЛАЗЕРОВ
- 6.6. ВОЗМОЖНОСТИ ПОВЫШЕНИЯ ОПТИЧЕСКОЙ ПРОЧНОСТИ КРИСТАЛЛОВ И ОПТИЧЕСКИХ ЭЛЕМЕНТОВ
- Часть II. НЕЛИНЕЙНО-ОПТИЧЕСКИЕ И ЭЛЕКТРООПТИЧЕСКИЕ КРИСТАЛЛЫ
- Глава 7. ЛИНЕЙНЫЙ ЭЛЕКТРООПТИЧЕСКИЙ ЭФФЕКТ И ХАРАКТЕРИСТИКИ ЭЛЕКТРО-ОПТИЧЕСКОГО КАЧЕСТВА КРИСТАЛЛОВ
- 7.2. ПОЛЯРИЗАЦИОННО-ОПТИЧЕСКИЕ ЗАТВОРЫ И МОДУЛЯТОРЫ СВЕТА
- 7.3. ЭЛЕКТРООПТИЧЕСКИЕ ЗАТВОРЫ НА РЕГУЛЯРНОЙ ДОМЕННОЙ СТРУКТУРЕ
- Глава 8. РАСПРОСТРАНЕНИЕ СВЕТА В НЕЛИНЕЙНЫХ ОПТИЧЕСКИХ СРЕДАХ
- 8.2. УСЛОВИЯ СОХРАНЕНИЯ ЭНЕРГИИ И ИМПУЛЬСА ПРИ ВЗАИМОДЕЙСТВИИ ФОТОНОВ В НЕЛИНЕЙНЫХ СРЕДАХ
- 8.3. РЕАЛИЗАЦИЯ УСЛОВИЙ СИНХРОНИЗМА
- 8.4. ЭФФЕКТИВНЫЕ КОЭФФИЦИЕНТЫ НЕЛИНЕЙНОСТИ
- 8.5. РАССОГЛАСОВАНИЕ ФАЗ ВЗАИМОДЕЙСТВУЮЩИХ ВОЛН ПОД ДЕЙСТВИЕМ ВНЕШНИХ ФАКТОРОВ. ПОЛОСА ПРОПУСКАНИЯ
- 8.6. РАСЧЕТ ПРЕОБРАЗОВАТЕЛЯ ЧАСТОТЫ
- 8.7. КВАЗИСИНХРОННОЕ ВЗАИМОДЕЙСТВИЕ
- Глава 9. КРИСТАЛЛЫ НА ОСНОВЕ ОКСИДОВ
- 9.2. ВЫРАЩИВАНИЕ КРИСТАЛЛОВ
- 9.3. ФАЗОВЫЕ ПЕРЕХОДЫ В КИСЛОРОДНООКТАЭДРИЧЕСКИХ КРИСТАЛЛАХ
- 9.4. ДЕФЕКТЫ СТРУКТУРЫ
- 9.4.1. МАКРОНЕОДНОРОДНОСТЬ КРИСТАЛЛОВ
- 9.4.2. ДВОЙНИКОВАНИЕ
- Механическое двойникование кристаллов ниобата лития
- 9.5. МОНОДОМЕНИЗАЦИЯ КРИСТАЛЛОВ
- 9.6. ПОЛУЧЕНИЕ РЕГУЛЯРНЫХ ДОМЕННЫХ СТРУКТУР
- 9.6.2. ПОСЛЕРОСТОВАЯ ЭЛЕКТРОТЕРМИЧЕСКАЯ ОБРАБОТКА
- 9.6.3. ПОЛУЧЕНИЕ РЕГУЛЯРНЫХ ДОМЕННЫХ СТРУКТУР В ПОВЕРХНОСТНЫХ СЛОЯХ
- 9.6.4. ПОЛУЧЕНИЕ РЕГУЛЯРНЫХ ДОМЕННЫХ СТРУКТУР СКАНИРОВАНИЕМ ПО КРИСТАЛЛУ ЭЛЕКТРОННЫМ ЛУЧОМ
- 9.7. ДИСЛОКАЦИИ И ПЛАСТИЧНОСТЬ КИСЛОРОДНО-ОКТАЭДРИЧЕСКИХ КРИСТАЛЛОВ
- 9.8. ТОЧЕЧНЫЕ ДЕФЕКТЫ
- 9.8.1. ВЛИЯНИЕ ОТКЛОНЕНИЯ ОТ СТЕХИОМЕТРИИ НА СВОЙСТВА КРИСТАЛЛОВ НИОБАТА ЛИТИЯ
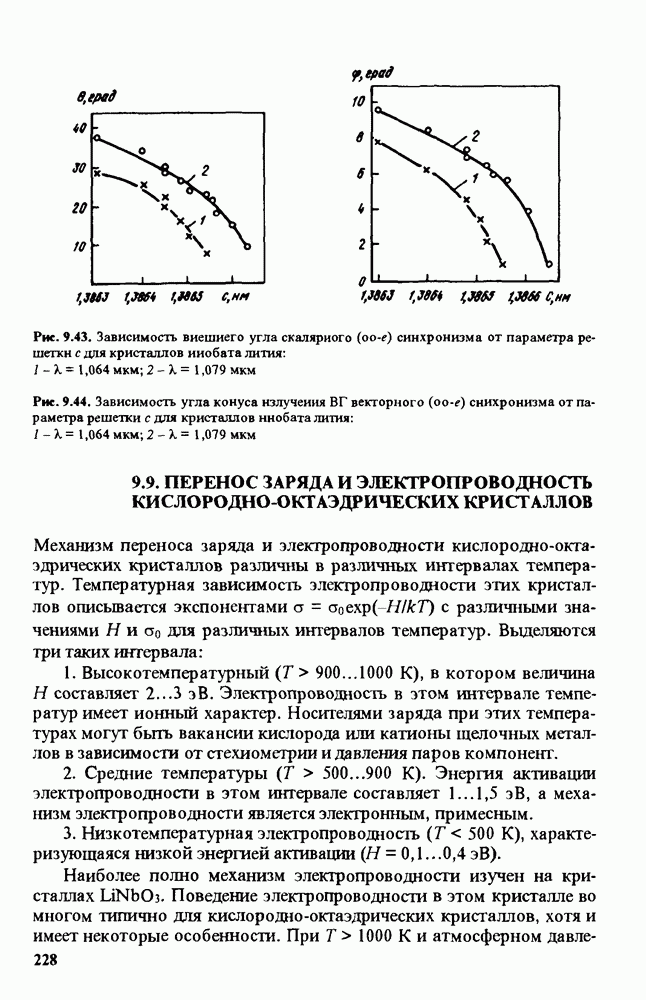
- 9.9. ПЕРЕНОС ЗАРЯДА И ЭЛЕКТРОПРОВОДНОСТЬ КИСЛОРОДНО-ОКТАЭДРИЧЕСКИХ КРИСТАЛЛОВ
- 9.10. ФОТОРЕФР АКТИВНЫЙ ЭФФЕКТ В КИСЛОРОДНО-ОКТАЭДРИЧЕСКИХ КРИСТАЛЛАХ
- 9.10.2. МЕХАНИЗМЫ ВОЗНИКНОВЕНИЯ ПРОСТРАНСТВЕННОГО ЗАРЯДА
- 9.10.3. ВОЗМОЖНОСТЬ ОСЛАБЛЕНИЯ ФОТОРЕФРАКЦИИ
- 9.10.4. ФОТОРЕФРАКЦИЯ В ПРАКТИЧЕСКИ ВАЖНЫХ КРИСТАЛЛАХ
- 9.11. ОПТИЧЕСКАЯ НЕОДНОРОДНОСТЬ И НЕСТАБИЛЬНОСТЬ СВОЙСТВ КРИСТАЛЛОВ
- 9.11.2. ОПТИЧЕСКАЯ НЕОДНОРОДНОСТЬ КРИСТАЛЛОВ НИОБАТА ЛИТИЯ
- Глава 10. КРИСТАЛЛЫ ГРУППЫ KDP
- 10.1. ОСНОВНЫЕ СВОЙСТВА КРИСТАЛЛОВ ГРУППЫ KDP
- 10.2. СТРУКТУРА И МЕТОДЫ ВЫРАЩИВАНИЯ КРИСТАЛЛОВ
- 10.3. ВЛИЯНИЕ ПРИМЕСЕЙ И КИСЛОТНОСТИ РАСТВОРА НА РОСТ КРИСТАЛЛОВ KDP И ADP
- 10.4. СКОРОСТНОЕ ВЫРАЩИВАНИЕ КРИСТАЛЛОВ
- 10.5. ПЛАСТИЧНОСТЬ И ДИСЛОКАЦИИ В КРИСТАЛЛАХ ГРУППЫ KDP
- Глава 11. ИОДАТ ЛИТИЯ
- 11.1. СТРУКТУРА И ВЫРАЩИВАНИЕ КРИСТАЛЛОВ ИОДАТА ЛИТИЯ
- 11.2. ВХОЖДЕНИЕ ПРИМЕСЕЙ В КРИСТАЛЛ …
- 11.3. ГАБИТУС КРИСТАЛЛОВ … И ВЫРАЩИВАНИЕ ПРОФИЛИРОВАННЫХ КРИСТАЛЛОВ
- 11.4. ЭЛЕКТРИЧЕСКИЕ СВОЙСТВА КРИСТАЛЛОВ …
- 11.5. ОПТИЧЕСКИЕ И НЕЛИНЕЙНООПТИЧЕСКИЕ СВОЙСТВА КРИСТАЛЛОВ …
- Глава 12. ТИТАНИЛФОСФАТ КАЛИЯ
- 12.1. ОСОБЕННОСТИ КРИСТАЛЛОВ ТИТАНИЛФОСФАТА КАЛИЯ
- 12.2. СТРУКТУРА КРИСТАЛЛОВ КТР
- 12.3. ВЫРАЩИВАНИЕ КРИСТАЛЛОВ
- 12.4. СВОЙСТВА КТР
- 12.5. ОПТИЧЕСКАЯ НЕЛИНЕЙНОСТЬ КРИСТАЛЛОВ КТР
- Глава 13. БОРАТЫ
- 13.2. ОПТИЧЕСКИЕ И НЕЛИНЕЙНООПТИЧЕСКИЕ СВОЙСТВА БОРАТОВ
- Часть III. КРИСТАЛЛЫ В АКУСТООПТИКЕ
- Глава 14. ОСНОВНЫЕ ПРИНЦИПЫ АКУСТООПТИКИ
- 14.2. АКУСТООПТИЧЕСКАЯ ДИФРАКЦИЯ БРЭГГА В АНИЗОТРОПНЫХ КРИСТАЛЛАХ
- 14.2.2. АКУСТООПТИЧЕСКОЕ ВЗАИМОДЕЙСТВИЕ в ПЛОСКОСТИ, ЛЕЖАЩЕЙ ПОД УГЛОМ К ОПТИЧЕСКОЙ ОСИ КРИСТАЛЛА
- 14.3. ИНТЕНСИВНОСТЬ ДИФРАКЦИИ И АКУСТООПТИЧЕСКАЯ ЭФФЕКТИВНОСТЬ СРЕДЫ
- 14.4. КОЛЛИНЕАРНОЕ АКУСТООПТИЧЕСКОЕ ВЗАИМОДЕЙСТВИЕ. ВЛИЯНИЕ СИНХРОНИЗМА НА ЭФФЕКТИВНОСТЬ ДИФРАКЦИИ
- Глава 15. ОСНОВНЫЕ ОБЛАСТИ ПРИМЕНЕНИЯ АКУСТООПТИЧЕСКОГО ВЗАИМОДЕЙСТВИЯ
- 15.2. АКУСТООПТИЧЕСКИЙ ДЕФЛЕКТОР
- 15.3. АКУСТООПТИЧЕСКИЙ ФИЛЬТР
- 15.3.2. ПРИМЕРЫ РЕАЛИЗАЦИИ КОЛЛИНЕАРНОГО ВЗАИМОДЕЙСТВИЯ ПРИ СОЗДАНИИ АКУСТООПТИЧЕСКИХ ФИЛЬТРОВ
- Глава 16. АКУСТООПТИЧЕСКОЕ КАЧЕСТВО КРИСТАЛЛОВ
- 16.1. СВЯЗЬ АКУСТООПТИЧЕСКОГО КАЧЕСТВА И ОСНОВНЫХ СВОЙСТВ КРИСТАЛЛОВ
- 16.2. МОНОКРИСТАЛЛИЧЕСКИЙ КВАРЦ
- 16.2.2. ДЕФЕКТЫ КВАРЦА
- 16.3. ПАРАТЕЛЛУРИТ
- 16.3.1. СТРУКТУРА И СВОЙСТВА ПАРАТЕЛЛУРИТА
- 16.3.2. ВЫРАЩИВАНИЕ ПАРАТЕЛЛУРИТА
- 16.3.3. ДЕФЕКТЫ СТРУКТУРЫ ПАРАТЕЛЛУРИТА
- 16.3.4. ПРИМЕНЕНИЕ TEO2 В АКУСГООПТИЧЕСКИХ ПРИБОРАХ
- 16.4. МОЛИБДАТЫ ЩЕЛОЧНОЗЕМЕЛЬНЫХ ИОНОВ
- 16.4.2. ВЫРАЩИВАНИЕ МОНОКРИСТАЛЛОВ
- 16.4.3. ДЕФЕКТЫ СТРУКТУРЫ
- 16.4.4. ПРИМЕНЕНИЕ МОЛИБДАТОВ В АКУСТООПТИКЕ
- Часть IV. КРИСТАЛЛИЧЕСКИЕ ЭЛЕМЕНТЫ ИНТЕГРАЛЬНОЙ ОПТИКИ
- Глава 17 ОПТИЧЕСКИЕ ВОЛНОВОДЫ, ИХ СВОЙСТВА И ХАРАКТЕРИСТИКИ
- 17.2. РАСПРОСТРАНЕНИЕ ОПТИЧЕСКИХ ВОЛН В ПЛОСКОМ ВОЛНОВОДЕ
- 17.3. ПОТЕРИ В ВОЛНОВОДЕ
- Глава 18. МЕТОДЫ ПОЛУЧЕНИЯ ВОЛНОВОДОВ
- 18.1. Ti-ДИФФУЗИОННАЯ ТЕХНОЛОГИЯ
- 18.1.2. ДИФФУЗИОННЫЙ ОТЖИГ
- 18.2. ПОЛУЧЕНИЕ ОПТИЧЕСКИХ ВОЛНОВОДОВ МЕТОДОМ ИОННОГО ОБМЕНА (ПРОТОННОГО ЗАМЕЩЕНИЯ)
- 18.2.1. ДИФФУЗИОННЫЕ ПРОЦЕССЫ ПРИ ИОННОМ ОБМЕНЕ
- 18.2.2. ПОЛУЧЕНИЕ ВОЛНОВОДОВ МЕТОДОМ ПЗ В КРИСТАЛЛАХ
- 18.3. ПОЛУЧЕНИЕ ОПТИЧЕСКИХ ВОЛНОВОДОВ С ПОМОЩЬЮ ИОННОЙ ИМПЛАНТАЦИИ
- БИБЛИОГРАФИЧЕСКИЙ СПИСОК