| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
1.5. ИОНЫ-АКТИВАТОРЫ
В лазерах, рабочим телом которых служат ионные кристаллы, активаторами, обеспечивающими необходимую систему уровней, являются либо специально вводимые в кристалл примеси, либо собственные ионы. Часто это ионы, вводимые в кристалл в виде примесей, реже - ионы, входящие в химическую формулу данного кристалла или собственные точечные дефекты. Энергетическое состояние иона, или терм Иона, определяется набором квантовых чисел, записанным в определенной форме.
Терм иона, свободного от воздействия внешних полей, в частности, от воздействия кристаллического поля, определяется квантовыми числами электронов, образующих валентные орбитали.
Главное квантовое число - номер орбитали  Изменение главного квантового числа от
Изменение главного квантового числа от  до
до  (переход между соседними орбиталями) приводит к испусканию кванта с частотой
(переход между соседними орбиталями) приводит к испусканию кванта с частотой

где  - постоянная Ридберга,
- постоянная Ридберга,  - масса электрона.
- масса электрона.
Изменение энергетического состояния ионов, сопровождающееся испусканием или поглощением квантов энергии видимого и ближнего  оптического диапазона, определяется изменением орбитального момента или спина внешних, валентных электронов.
оптического диапазона, определяется изменением орбитального момента или спина внешних, валентных электронов.
Орбитальный момент количества движения М, определяется орбитальным квантовым числом  где
где  - магнетон Бора). Разрешенными являются моменты, для которых
- магнетон Бора). Разрешенными являются моменты, для которых  . Для записи орбитального квантового числа используются буквы:
. Для записи орбитального квантового числа используются буквы:

Квантуется не только момент количества движения, но и его проекция на выделенное направление. Размер проекции может меняться 
Спин  - квантовое число, определяющее момент количества вращения электрона вокруг своей оси
- квантовое число, определяющее момент количества вращения электрона вокруг своей оси  Для одного электрона
Для одного электрона  имеет значения -1/2 и
имеет значения -1/2 и 
Терм одноэлектронного иона (атома), имеющего один электрон, определяется набором квантовых чисел, характеризующих этот электрон. Терм многоэлектронного иона (атома) должен учитывать взаимодействие электронов, образующих валентную оболочку. Основное взаимодействие - это взаимодействие однотипных моментов (связь Рассела - Саундерса). Для этого взаимодействия результирующий орбитальный момент системы валентных электронов иона образуется как геометрическая сумма орбитальных моментов электронов, а спин иона - как геометрическая сумма спинов электронов. Зная квантовые числа  для всех
для всех  электронов в ионе, можно определить максимально возможные орбитальное и спиновое квантовые числа иона. Квантовые числа атома (иона) обозначаются теми же, но заглавными буквами, что и квантовые числа электрона. Таким образом, квантовые числа атома (иона) определяются как
электронов в ионе, можно определить максимально возможные орбитальное и спиновое квантовые числа иона. Квантовые числа атома (иона) обозначаются теми же, но заглавными буквами, что и квантовые числа электрона. Таким образом, квантовые числа атома (иона) определяются как

Квадратные скобки показывают, что проводится не алгебраическое, а геометрическое суммирование.
Взаимодействие орбитального момента и спина (спин-орбиталь-ное взаимодействие) тоже квантуется. Допустимые взаимные ориентировки спина и орбитального момента определяются побочным квантовым числом  являющегося геометрической суммой
являющегося геометрической суммой  и
и 
Принят следующий вид записи терма многоэлектронного атома:

где  - орбитальное квантовое число атома;
- орбитальное квантовое число атома;
 - побочное квантовое число;
- побочное квантовое число;  - степень вырождения данного уровня, определяемая спин-орбитальным взаимодействием.
- степень вырождения данного уровня, определяемая спин-орбитальным взаимодействием.
В соответствии с правилом Хунда состояние с наименьшей энергией (стабильное) для данного атома (иона) имеет наибольшее из возможных значение спина и орбитального квантового числа  где
где  - число электронов в оболочке, застроенной меньше чем наполовину (для оболочек, застроенных более чем наполовину,
- число электронов в оболочке, застроенной меньше чем наполовину (для оболочек, застроенных более чем наполовину,  - число вакантных мест в оболочке).
- число вакантных мест в оболочке).
Запись терма в форме (1.44) относится к свободному атому (иону). Если влияние кристаллического поля на валентные орбитали мало, то эта форма записи терма может быть использована для атомов (ионов), находящихся в кристалле. Влияние кристаллического поля на ион-активатор можно считать малым, если оно значительно меньше энергии оптического перехода. Для видимого диапазона длин волн эта энергия составляет  так что малым взаимодействием можно считать взаимодействие на уровне
так что малым взаимодействием можно считать взаимодействие на уровне  Такое взаимодействие приводит к слабому расщеплению или уширению спектральных линий видимого диапазона, возникающих при изменении терма иона-активатора.
Такое взаимодействие приводит к слабому расщеплению или уширению спектральных линий видимого диапазона, возникающих при изменении терма иона-активатора.
При взаимодействии внешних электронов с кристаллическим полем на уровне  это поле существенно влияет на терм иона-активатора. В этом случае связь
это поле существенно влияет на терм иона-активатора. В этом случае связь  разрывается и терм иона должен записываться с учетом взаимодействия иона с кристаллическим полем. Во внешнем поле
разрывается и терм иона должен записываться с учетом взаимодействия иона с кристаллическим полем. Во внешнем поле  и
и  прецессируют отдельно, не образуя единого вектора полного момента. Энергии отдельных подуровней определяются проекциями моментов
прецессируют отдельно, не образуя единого вектора полного момента. Энергии отдельных подуровней определяются проекциями моментов  и
и  на направление кристаллического поля. Связь
на направление кристаллического поля. Связь  в этом случае приводит лишь к возмущению уровней, определяемых кристаллическим полем.
в этом случае приводит лишь к возмущению уровней, определяемых кристаллическим полем.
Ионы-активаторы, слабо взаимодействующие с кристаллическим полем, можно найти среди ионов с недостроенными внутренними валентными оболочками, экранированными от влияния кристаллического поля внешними оболочками. Такие атомы (ионы) находятся в
группах лантанидов и актинидов. Использование актинидов в качестве активаторов лазерных сред невозможно из-за их радиоактивности, поэтому основными ионами-активаторами лазерных матриц, имеющими слабое взаимодействие с кристаллическим полем, являются лантаниды (редкие земли).
Другая группа атомов, имеющих недостроенную внутреннюю оболочку, - группа переходных металлов. Отличие редких земель (РЗ) от переходных металлов (ПМ) определяется местом незаполненных оболочек соответствующих ионов. В оболочках лантанидов незаполненной валентной оболочкой является оболочка  тогда как уже достроены
тогда как уже достроены  и
и  -оболочки, появляются электроны на оболочках
-оболочки, появляются электроны на оболочках  Поэтому даже при потере валентных электронов с
Поэтому даже при потере валентных электронов с  и
и  -орбиталей
-орбиталей  -орбитали остаются хорошо экранированными от воздействия внешнего кристаллического поля присутствием электронов на
-орбитали остаются хорошо экранированными от воздействия внешнего кристаллического поля присутствием электронов на  и
и  -орбиталях (конфигурация благородного газа
-орбиталях (конфигурация благородного газа  В результате воздействие кристаллического поля на оптические термы ионов-лантанидов является слабым. Термы этих ионов в кристаллическом поле можно рассматривать как термы свободных ионов, испытывающих слабое возмущение от воздействия кристаллического поля. В переходных металлах при незаполненной
В результате воздействие кристаллического поля на оптические термы ионов-лантанидов является слабым. Термы этих ионов в кристаллическом поле можно рассматривать как термы свободных ионов, испытывающих слабое возмущение от воздействия кристаллического поля. В переходных металлах при незаполненной  -оболочке заполняется только одна
-оболочке заполняется только одна  -оболочка, электроны которой теряются при ионизации. Поэтому экранирование валентных
-оболочка, электроны которой теряются при ионизации. Поэтому экранирование валентных  -орбиталей в
-орбиталей в  слабее, чем экранирование валентных
слабее, чем экранирование валентных  -орбиталей
-орбиталей  и уровни, определяющие оптические переходы в
и уровни, определяющие оптические переходы в  формируются с участием кристаллического поля.
формируются с участием кристаллического поля.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Часть I. ЛАЗЕРНЫЕ КРИСТАЛЛЫ
- Глава 1. ХАРАКТЕРИСТИКИ КРИСТАЛЛОВ, ИСПОЛЬЗУЕМЫХ ДЛЯ ГЕНЕРАЦИИ ЛАЗЕРНОГО ИЗЛУЧЕНИЯ
- 1.2. ОПТИЧЕСКИЙ РЕЗОНАТОР
- 1.3. ПОРОГОВЫЕ УСЛОВИЯ ДЛЯ УСИЛЕНИЯ СВЕТА
- 1.3.2. Пороговые условия в непрерывном режиме
- 1.4. ЭНЕРГЕТИЧЕСКИЕ ХАРАКТЕРИСТИКИ И К.П.Д. ЛАЗЕРА
- 1.5. ИОНЫ-АКТИВАТОРЫ
- 1.6. ТЕПЛОВЫЕ СВОЙСТВА КРИСТАЛЛОВ
- 1.7. ТРЕБОВАНИЯ, ПРЕДЪЯВЛЯЕМЫЕ К КРИСТАЛЛАМ
- Глава 2. КРИСТАЛЛЫ-ОКСИДЫ
- 2.1.2. Структура кристаллов
- Макронеоднородность кристаллов
- Примеси
- Центры окраски в кристаллах соединений …
- Окраска корунда
- Окраска иттрий-атоминиевого граната
- Дополнительная окраска и рекомбинационные процессы в кристаллах алюмината иттрия
- 2.2. КРИСТАЛЛИЧЕСКИЕ СРЕДЫ ДЛЯ ВЫСОКОЭФФЕКТИВНЫХ НЕОДИМОВЫХ ЛАЗЕРОВ
- 2.2.2. ВЫРАЩИВАНИЕ И РОСТОВЫЕ ДЕФЕКТЫ КРИСТАЛЛОВ ГАЛЛИЕВЫХ ГРАНАТОВ
- 2.2.3. РАЗУПОРЯДОЧЕНИЕ В ГАЛЛИЕВЫХ ГРАНАТАХ
- 2.2.4. ЦЕНТРЫ ОКРАСКИ В ГАЛЛИЕВЫХ ГРАНАТАХ
- Глава 3. КРИСТАЛЛЫ ФТОРИДОВ
- 3.1. Кристаллы YLiF4
- 3.2. Кристаллы …
- 3.2.2. ОПТИЧЕСКИЕ И ГЕНЕРАЦИОННЫЕ СВОЙСТВА
- Глава 4. КРИСТАЛЛЫ ДЛЯ ЛАЗЕРОВ С ПЕРЕСТРАИВАЕМОЙ ЧАСТОТОЙ
- 4.1. АЛЕКСАНДРИТ
- 4.2. КОРУНД С ТИТАНОМ
- 4.3. ЦЕНТРЫ ОКРАСКИ — АКТИВАТОРЫ ЛАЗЕРНЫХ КРИСТАЛЛОВ
- Глава 5. ДЕФЕКТЫ ЛАЗЕРНЫХ КРИСТАЛЛОВ, ВОЗНИКАЮЩИЕ ПРИ ПЛАСТИЧЕСКОЙ ДЕФОРМАЦИИ
- 5.2. ДВОЙНИКОВАНИЕ
- Глава 6. КРИСТАЛЛЫ ДЛЯ ПРОХОДНОЙ ОПТИКИ МОЩНЫХ ЛАЗЕРОВ
- 6.1. СОБСТВЕННЫЕ МЕХАНИЗМЫ ОПТИЧЕСКОГО РАЗРУШЕНИЯ
- 6.2. НЕСОБСТВЕННЫЕ МЕХАНИЗМЫ ОПТИЧЕСКОГО РАЗРУШЕНИЯ
- 6.2.1. ОПТИЧЕСКОЕ РАЗРУШЕНИЕ ПОВЕРХНОСТИ
- 6.2.2. РАЗРУШЕНИЕ В ОБЪЕМЕ КРИСТАЛЛА
- 6.3. ОПТИЧЕСКАЯ ПРОЧНОСТЬ В СФОКУСИРОВАННЫХ И ШИРОКО АПЕРТУРНЫХ ПУЧКАХ
- 6.4. ОПТИЧЕСКАЯ ПРОЧНОСТЬ КРИСТАЛЛОВ ПРИ ВОЗДЕЙСТВИИ ИМПУЛЬСНОПЕРИОДИЧЕСКОГО ИЗЛУЧЕНИЯ
- 6.5. ВЫБОР МАТЕРИАЛА ДЛЯ ПРОХОДНОЙ ОПТИКИ МОЩНЫХ ЛАЗЕРОВ
- 6.6. ВОЗМОЖНОСТИ ПОВЫШЕНИЯ ОПТИЧЕСКОЙ ПРОЧНОСТИ КРИСТАЛЛОВ И ОПТИЧЕСКИХ ЭЛЕМЕНТОВ
- Часть II. НЕЛИНЕЙНО-ОПТИЧЕСКИЕ И ЭЛЕКТРООПТИЧЕСКИЕ КРИСТАЛЛЫ
- Глава 7. ЛИНЕЙНЫЙ ЭЛЕКТРООПТИЧЕСКИЙ ЭФФЕКТ И ХАРАКТЕРИСТИКИ ЭЛЕКТРО-ОПТИЧЕСКОГО КАЧЕСТВА КРИСТАЛЛОВ
- 7.2. ПОЛЯРИЗАЦИОННО-ОПТИЧЕСКИЕ ЗАТВОРЫ И МОДУЛЯТОРЫ СВЕТА
- 7.3. ЭЛЕКТРООПТИЧЕСКИЕ ЗАТВОРЫ НА РЕГУЛЯРНОЙ ДОМЕННОЙ СТРУКТУРЕ
- Глава 8. РАСПРОСТРАНЕНИЕ СВЕТА В НЕЛИНЕЙНЫХ ОПТИЧЕСКИХ СРЕДАХ
- 8.2. УСЛОВИЯ СОХРАНЕНИЯ ЭНЕРГИИ И ИМПУЛЬСА ПРИ ВЗАИМОДЕЙСТВИИ ФОТОНОВ В НЕЛИНЕЙНЫХ СРЕДАХ
- 8.3. РЕАЛИЗАЦИЯ УСЛОВИЙ СИНХРОНИЗМА
- 8.4. ЭФФЕКТИВНЫЕ КОЭФФИЦИЕНТЫ НЕЛИНЕЙНОСТИ
- 8.5. РАССОГЛАСОВАНИЕ ФАЗ ВЗАИМОДЕЙСТВУЮЩИХ ВОЛН ПОД ДЕЙСТВИЕМ ВНЕШНИХ ФАКТОРОВ. ПОЛОСА ПРОПУСКАНИЯ
- 8.6. РАСЧЕТ ПРЕОБРАЗОВАТЕЛЯ ЧАСТОТЫ
- 8.7. КВАЗИСИНХРОННОЕ ВЗАИМОДЕЙСТВИЕ
- Глава 9. КРИСТАЛЛЫ НА ОСНОВЕ ОКСИДОВ
- 9.2. ВЫРАЩИВАНИЕ КРИСТАЛЛОВ
- 9.3. ФАЗОВЫЕ ПЕРЕХОДЫ В КИСЛОРОДНООКТАЭДРИЧЕСКИХ КРИСТАЛЛАХ
- 9.4. ДЕФЕКТЫ СТРУКТУРЫ
- 9.4.1. МАКРОНЕОДНОРОДНОСТЬ КРИСТАЛЛОВ
- 9.4.2. ДВОЙНИКОВАНИЕ
- Механическое двойникование кристаллов ниобата лития
- 9.5. МОНОДОМЕНИЗАЦИЯ КРИСТАЛЛОВ
- 9.6. ПОЛУЧЕНИЕ РЕГУЛЯРНЫХ ДОМЕННЫХ СТРУКТУР
- 9.6.2. ПОСЛЕРОСТОВАЯ ЭЛЕКТРОТЕРМИЧЕСКАЯ ОБРАБОТКА
- 9.6.3. ПОЛУЧЕНИЕ РЕГУЛЯРНЫХ ДОМЕННЫХ СТРУКТУР В ПОВЕРХНОСТНЫХ СЛОЯХ
- 9.6.4. ПОЛУЧЕНИЕ РЕГУЛЯРНЫХ ДОМЕННЫХ СТРУКТУР СКАНИРОВАНИЕМ ПО КРИСТАЛЛУ ЭЛЕКТРОННЫМ ЛУЧОМ
- 9.7. ДИСЛОКАЦИИ И ПЛАСТИЧНОСТЬ КИСЛОРОДНО-ОКТАЭДРИЧЕСКИХ КРИСТАЛЛОВ
- 9.8. ТОЧЕЧНЫЕ ДЕФЕКТЫ
- 9.8.1. ВЛИЯНИЕ ОТКЛОНЕНИЯ ОТ СТЕХИОМЕТРИИ НА СВОЙСТВА КРИСТАЛЛОВ НИОБАТА ЛИТИЯ
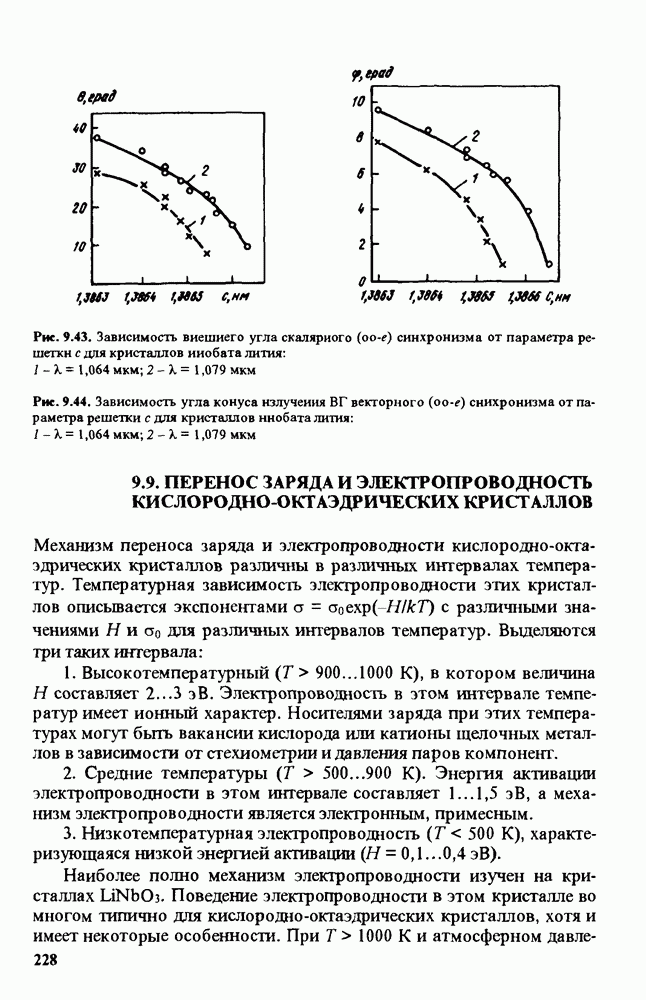
- 9.9. ПЕРЕНОС ЗАРЯДА И ЭЛЕКТРОПРОВОДНОСТЬ КИСЛОРОДНО-ОКТАЭДРИЧЕСКИХ КРИСТАЛЛОВ
- 9.10. ФОТОРЕФР АКТИВНЫЙ ЭФФЕКТ В КИСЛОРОДНО-ОКТАЭДРИЧЕСКИХ КРИСТАЛЛАХ
- 9.10.2. МЕХАНИЗМЫ ВОЗНИКНОВЕНИЯ ПРОСТРАНСТВЕННОГО ЗАРЯДА
- 9.10.3. ВОЗМОЖНОСТЬ ОСЛАБЛЕНИЯ ФОТОРЕФРАКЦИИ
- 9.10.4. ФОТОРЕФРАКЦИЯ В ПРАКТИЧЕСКИ ВАЖНЫХ КРИСТАЛЛАХ
- 9.11. ОПТИЧЕСКАЯ НЕОДНОРОДНОСТЬ И НЕСТАБИЛЬНОСТЬ СВОЙСТВ КРИСТАЛЛОВ
- 9.11.2. ОПТИЧЕСКАЯ НЕОДНОРОДНОСТЬ КРИСТАЛЛОВ НИОБАТА ЛИТИЯ
- Глава 10. КРИСТАЛЛЫ ГРУППЫ KDP
- 10.1. ОСНОВНЫЕ СВОЙСТВА КРИСТАЛЛОВ ГРУППЫ KDP
- 10.2. СТРУКТУРА И МЕТОДЫ ВЫРАЩИВАНИЯ КРИСТАЛЛОВ
- 10.3. ВЛИЯНИЕ ПРИМЕСЕЙ И КИСЛОТНОСТИ РАСТВОРА НА РОСТ КРИСТАЛЛОВ KDP И ADP
- 10.4. СКОРОСТНОЕ ВЫРАЩИВАНИЕ КРИСТАЛЛОВ
- 10.5. ПЛАСТИЧНОСТЬ И ДИСЛОКАЦИИ В КРИСТАЛЛАХ ГРУППЫ KDP
- Глава 11. ИОДАТ ЛИТИЯ
- 11.1. СТРУКТУРА И ВЫРАЩИВАНИЕ КРИСТАЛЛОВ ИОДАТА ЛИТИЯ
- 11.2. ВХОЖДЕНИЕ ПРИМЕСЕЙ В КРИСТАЛЛ …
- 11.3. ГАБИТУС КРИСТАЛЛОВ … И ВЫРАЩИВАНИЕ ПРОФИЛИРОВАННЫХ КРИСТАЛЛОВ
- 11.4. ЭЛЕКТРИЧЕСКИЕ СВОЙСТВА КРИСТАЛЛОВ …
- 11.5. ОПТИЧЕСКИЕ И НЕЛИНЕЙНООПТИЧЕСКИЕ СВОЙСТВА КРИСТАЛЛОВ …
- Глава 12. ТИТАНИЛФОСФАТ КАЛИЯ
- 12.1. ОСОБЕННОСТИ КРИСТАЛЛОВ ТИТАНИЛФОСФАТА КАЛИЯ
- 12.2. СТРУКТУРА КРИСТАЛЛОВ КТР
- 12.3. ВЫРАЩИВАНИЕ КРИСТАЛЛОВ
- 12.4. СВОЙСТВА КТР
- 12.5. ОПТИЧЕСКАЯ НЕЛИНЕЙНОСТЬ КРИСТАЛЛОВ КТР
- Глава 13. БОРАТЫ
- 13.2. ОПТИЧЕСКИЕ И НЕЛИНЕЙНООПТИЧЕСКИЕ СВОЙСТВА БОРАТОВ
- Часть III. КРИСТАЛЛЫ В АКУСТООПТИКЕ
- Глава 14. ОСНОВНЫЕ ПРИНЦИПЫ АКУСТООПТИКИ
- 14.2. АКУСТООПТИЧЕСКАЯ ДИФРАКЦИЯ БРЭГГА В АНИЗОТРОПНЫХ КРИСТАЛЛАХ
- 14.2.2. АКУСТООПТИЧЕСКОЕ ВЗАИМОДЕЙСТВИЕ в ПЛОСКОСТИ, ЛЕЖАЩЕЙ ПОД УГЛОМ К ОПТИЧЕСКОЙ ОСИ КРИСТАЛЛА
- 14.3. ИНТЕНСИВНОСТЬ ДИФРАКЦИИ И АКУСТООПТИЧЕСКАЯ ЭФФЕКТИВНОСТЬ СРЕДЫ
- 14.4. КОЛЛИНЕАРНОЕ АКУСТООПТИЧЕСКОЕ ВЗАИМОДЕЙСТВИЕ. ВЛИЯНИЕ СИНХРОНИЗМА НА ЭФФЕКТИВНОСТЬ ДИФРАКЦИИ
- Глава 15. ОСНОВНЫЕ ОБЛАСТИ ПРИМЕНЕНИЯ АКУСТООПТИЧЕСКОГО ВЗАИМОДЕЙСТВИЯ
- 15.2. АКУСТООПТИЧЕСКИЙ ДЕФЛЕКТОР
- 15.3. АКУСТООПТИЧЕСКИЙ ФИЛЬТР
- 15.3.2. ПРИМЕРЫ РЕАЛИЗАЦИИ КОЛЛИНЕАРНОГО ВЗАИМОДЕЙСТВИЯ ПРИ СОЗДАНИИ АКУСТООПТИЧЕСКИХ ФИЛЬТРОВ
- Глава 16. АКУСТООПТИЧЕСКОЕ КАЧЕСТВО КРИСТАЛЛОВ
- 16.1. СВЯЗЬ АКУСТООПТИЧЕСКОГО КАЧЕСТВА И ОСНОВНЫХ СВОЙСТВ КРИСТАЛЛОВ
- 16.2. МОНОКРИСТАЛЛИЧЕСКИЙ КВАРЦ
- 16.2.2. ДЕФЕКТЫ КВАРЦА
- 16.3. ПАРАТЕЛЛУРИТ
- 16.3.1. СТРУКТУРА И СВОЙСТВА ПАРАТЕЛЛУРИТА
- 16.3.2. ВЫРАЩИВАНИЕ ПАРАТЕЛЛУРИТА
- 16.3.3. ДЕФЕКТЫ СТРУКТУРЫ ПАРАТЕЛЛУРИТА
- 16.3.4. ПРИМЕНЕНИЕ TEO2 В АКУСГООПТИЧЕСКИХ ПРИБОРАХ
- 16.4. МОЛИБДАТЫ ЩЕЛОЧНОЗЕМЕЛЬНЫХ ИОНОВ
- 16.4.2. ВЫРАЩИВАНИЕ МОНОКРИСТАЛЛОВ
- 16.4.3. ДЕФЕКТЫ СТРУКТУРЫ
- 16.4.4. ПРИМЕНЕНИЕ МОЛИБДАТОВ В АКУСТООПТИКЕ
- Часть IV. КРИСТАЛЛИЧЕСКИЕ ЭЛЕМЕНТЫ ИНТЕГРАЛЬНОЙ ОПТИКИ
- Глава 17 ОПТИЧЕСКИЕ ВОЛНОВОДЫ, ИХ СВОЙСТВА И ХАРАКТЕРИСТИКИ
- 17.2. РАСПРОСТРАНЕНИЕ ОПТИЧЕСКИХ ВОЛН В ПЛОСКОМ ВОЛНОВОДЕ
- 17.3. ПОТЕРИ В ВОЛНОВОДЕ
- Глава 18. МЕТОДЫ ПОЛУЧЕНИЯ ВОЛНОВОДОВ
- 18.1. Ti-ДИФФУЗИОННАЯ ТЕХНОЛОГИЯ
- 18.1.2. ДИФФУЗИОННЫЙ ОТЖИГ
- 18.2. ПОЛУЧЕНИЕ ОПТИЧЕСКИХ ВОЛНОВОДОВ МЕТОДОМ ИОННОГО ОБМЕНА (ПРОТОННОГО ЗАМЕЩЕНИЯ)
- 18.2.1. ДИФФУЗИОННЫЕ ПРОЦЕССЫ ПРИ ИОННОМ ОБМЕНЕ
- 18.2.2. ПОЛУЧЕНИЕ ВОЛНОВОДОВ МЕТОДОМ ПЗ В КРИСТАЛЛАХ
- 18.3. ПОЛУЧЕНИЕ ОПТИЧЕСКИХ ВОЛНОВОДОВ С ПОМОЩЬЮ ИОННОЙ ИМПЛАНТАЦИИ
- БИБЛИОГРАФИЧЕСКИЙ СПИСОК