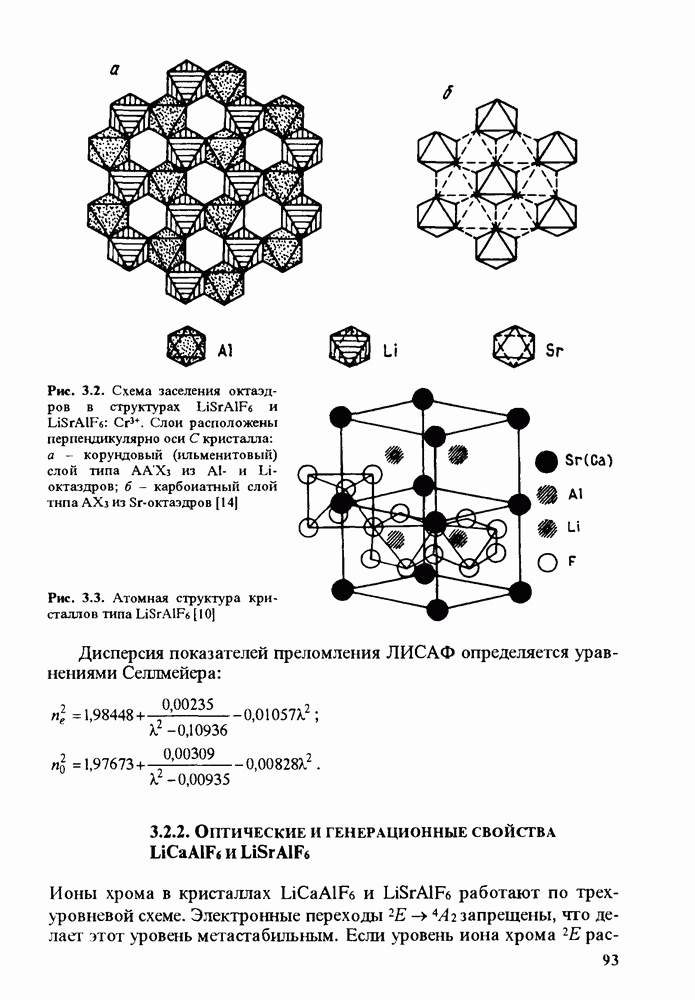
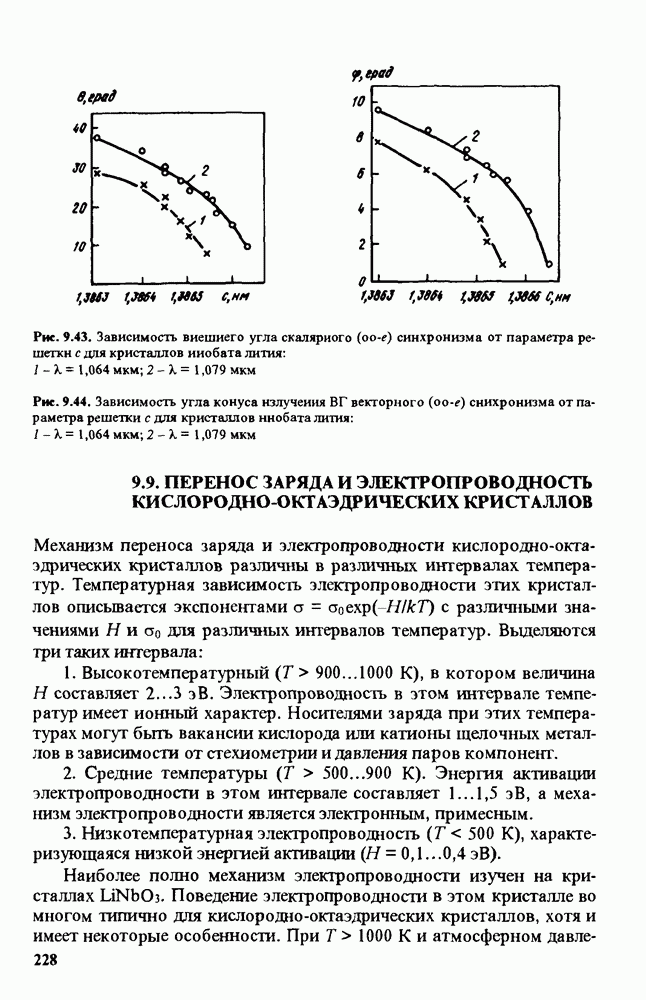
8.4. ЭФФЕКТИВНЫЕ КОЭФФИЦИЕНТЫ НЕЛИНЕЙНОСТИ

Здесь, как и ранее, ограничимся рассмотрением коэффициентов квадратичной нелинейности. Используя коэффициент связи между действительными компонентами полей и нелинейной поляризации запишем уравнение для квадратичной поляризации в тензорной форме

Для конкретного светового луча, направление и поляризация которого определены относительно кристаллофизической системы координат (обычно это направление синхронизма), может быть выполнено суммирование коэффициентов Как было показано ранее, при генерации гармоник в условиях синхронизма могут различаться поляризации начального луча и его гармоники. В более общем случае (при генерации суммарных или разностных частот) могут различаться поляризации всех компонент поля и нелинейной поляризации, участвующих во взаимодействии. Тогда каждая данная компонента нелинейной поляризации (и соответствующая ей компонента поля) появляется в результате воздействия на среду суммарной компоненты поля накачки, возникшей в результате суммирования компонент поля различных поляризаций. Например, при - -взаимодействии компонента нелинейной поляризации возникает в результате воздействия на среду компонент поля по оси х и обыкновенной и необыкновенной поляризаций. Если в системе координат (рис. 8.7) направление волновой нормали волны-накачки задано углами и Ф, то эти же углы определяют и направления обыкновенной и необыкновенной Ее компонент поля накачки, находящихся в плоскости, нормальной к т.

Рис. 8.7. Система координат для расчета эффективного коэффициента нелинейности. Оси координат главные оси тензора

Как следует из рис. 8.7, поле обыкновенной поляризации имеет компоненты:

Поле необыкновенной поляризации имеет компоненты:

Таким образом, компоненты поля в общем виде можно записать для поля обыкновенной поляризации

и для поля необыкновенной поляризации:

В (8.51) и (8.52) а и b матрицы вида

Зная компоненты нелинейной поляризации Р, и используя эти матрицы, определим обыкновенную и необыкновенную нелинейные поляризации, как В результате для различных видов взаимодействия можно получить для нелинейной поляризации выражения, приведенные в табл. 8.1.

Выражения в квадратных скобках представляют собой комбинации компонентов тензора коэффициентов квадратичной нелинейной поляризуемости и тригонометрических функций. Эти выражения можно объединить под названием «эффективный коэффициент нелинейности» Выражения для в зависимости от рассчитаны для всех точечных групп симметрии и приведены в известных книгах по кристаллофизике и нелинейной оптике, в частности в [1] и [3].

В табл. 8.2 приведены выражения для вычисленные для случая, когда выполняются так называемые «условия Клейнмана». Эти

Таблица 8.1. Поляризация при различных типах взаимодействия фотонов

Таблица 8.2. Выражения для взаимодействии I типа при выполнении условия Клейнмана

условия состоят в том, что для рассматриваемого взаимодействия должно выполняться равенство Это равенство будет выполняться, если тензор диэлектрической проницаемости (как и тензоры диэлектрической восприимчивости и поляризуемости), определяющий распространение в среде волн накачки симметричен Ясно, что условие Клейнмана выполняется в большинстве практически важных случаев, в частности при генерации оптических гармоник.