| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
8.2. УСЛОВИЯ СОХРАНЕНИЯ ЭНЕРГИИ И ИМПУЛЬСА ПРИ ВЗАИМОДЕЙСТВИИ ФОТОНОВ В НЕЛИНЕЙНЫХ СРЕДАХ
Записав условия сохранения энергии и импульса при взаимодействии фотонов, можно получить существенную информацию о результатах такого взаимодействия. Взаимодействие трех фотонов Ф можно представить как реакцию

где  - частоты начального излучения (излучения накачки);
- частоты начального излучения (излучения накачки);  - частота результирующего излучения;
- частота результирующего излучения;
 - волновые векторы начального излучения (излучения накачки);
- волновые векторы начального излучения (излучения накачки);
 - волновой вектор результирующего излучения.
- волновой вектор результирующего излучения.
Для такого взаимодействия законы сохранения имеют следующий вид. Закон сохранения энергии:

откуда следует соотношение частот взаимодействующих волн

В том случае, если начальное излучение имеет один источник и, следовательно, одну частоту  результатом выполнения закона сохранения энергии является генерация второй гармоники начального излучения (накачки)
результатом выполнения закона сохранения энергии является генерация второй гармоники начального излучения (накачки)

Закон сохранения импульса имеет вид

или

т.е. закон сохранения импульса выполняется, если волновой вектор результирующего излучения есть векторная сумма волновых векторов волн накачки.
Подставив в (8.34) выражения для волновых векторов  (здесь
(здесь  - частота и показатель преломления соответствующей волны,
- частота и показатель преломления соответствующей волны,  - волновая нормаль), получим
- волновая нормаль), получим


Рис. 8.1. Схема синхронизации фаз поля излучения накачки  нелинейной поляризации
нелинейной поляризации  и поля результирующего излучения
и поля результирующего излучения  при оптическом нелинейном взаимодействии
при оптическом нелинейном взаимодействии
В частном случае для генерации второй гармоники при  и выполнении равенства (8.32) получим
и выполнении равенства (8.32) получим

Выражения (8.34) и (8.36) определяют условия синхронизации волн при их взаимодействии в нелинейной среде. Рассмотрим условия синхронизации волн более детально на примере генерации второй гармоники. На рис. 8.1 показано распространение волн электрического поля начального излучения  входящего в нелинейную среду на границе среды, обозначенной цифрой I.
входящего в нелинейную среду на границе среды, обозначенной цифрой I.
Это поле, распространяясь со скоростью  порождает нелинейную поляризацию
порождает нелинейную поляризацию  распространяющуюся с той же скоростью. Нелинейная поляризация (колебание электрических диполей с частотой
распространяющуюся с той же скоростью. Нелинейная поляризация (колебание электрических диполей с частотой  порождает электромагнитное излучение
порождает электромагнитное излучение  скорость распространения которого в общем случае отличается от скорости распространения начальной волны, т.е.
скорость распространения которого в общем случае отличается от скорости распространения начальной волны, т.е.  из-за зависимости показателя преломления от частоты. Интенсивность излучения гармоники на некотором расстоянии от поверхности нелинейной среды (позиция II) определяется интерференцией волн гармоники, рожденных ранее [в позиции
из-за зависимости показателя преломления от частоты. Интенсивность излучения гармоники на некотором расстоянии от поверхности нелинейной среды (позиция II) определяется интерференцией волн гармоники, рожденных ранее [в позиции  ] и возникающих в данной точке [позиция
] и возникающих в данной точке [позиция  Если в позиции II сдвиг по фазе
Если в позиции II сдвиг по фазе  находится в пределах
находится в пределах  поле
поле  будет усиливать поле
будет усиливать поле  . С ростом сдвига по фазе в интервале от
. С ростом сдвига по фазе в интервале от  до
до  поле
поле

Рис. 8.2. Зависимость интенсивности результирующего излучения от длины взаимодействия 
 ослабляется полем
ослабляется полем  и при сдвиге фаз равном
и при сдвиге фаз равном  поле
поле  гасит поле
гасит поле  (рис. 8.1). При дальнейшем распространении волн сдвиг фаз продолжает возрастать и при сдвиге фаз, равном
(рис. 8.1). При дальнейшем распространении волн сдвиг фаз продолжает возрастать и при сдвиге фаз, равном  (позиция III на рис. 8.1), результирующее поле гармоники вновь усиливается в результате интерференции волн, возникающих в позиции III и пришедших из позиции I. Таким образом, по пути распространения волн накачки в нелинейной среде будет меняться сдвиг фаз волн гармоники, возникающих в данной точке и возникших ранее. Различие скоростей распространения волн
(позиция III на рис. 8.1), результирующее поле гармоники вновь усиливается в результате интерференции волн, возникающих в позиции III и пришедших из позиции I. Таким образом, по пути распространения волн накачки в нелинейной среде будет меняться сдвиг фаз волн гармоники, возникающих в данной точке и возникших ранее. Различие скоростей распространения волн  определит разность фаз между ними
определит разность фаз между ними  , следовательно, интенсивности результирующего излучения от координаты.
, следовательно, интенсивности результирующего излучения от координаты.
Количественная зависимость интенсивности результирующего излучения от рассогласования фаз следует из выражений (8.18, 8.19). Эта зависимость определяется величиной

Здесь рассогласование фаз определяется величиной  или для генерации второй гармоники
или для генерации второй гармоники

Условие  соответствует выполнению закона сохранения импульса и условию согласования фаз взаимодействующих волн.
соответствует выполнению закона сохранения импульса и условию согласования фаз взаимодействующих волн.
Из (8.18) следует, что зависимость интенсивности результирующего излучения от длины нелинейной среды  или, что то же самое, от координаты при распространении излучения в нелинейной среде, является периодической функцией
или, что то же самое, от координаты при распространении излучения в нелинейной среде, является периодической функцией  от
от  с быстро уменьшающимися экстремумами (рис. 8.2). Положения экстремумов интенсивности результирующего излучения по длине распространения света в среде получаем, дифференцируя
с быстро уменьшающимися экстремумами (рис. 8.2). Положения экстремумов интенсивности результирующего излучения по длине распространения света в среде получаем, дифференцируя  по
по 

Экстремумы результирующего излучения появляются при  где
где  - целые числа.
- целые числа.
Первый максимум наблюдается при  . Длина
. Длина  на которой наблюдается повышение интенсивности результирующего излучения, получила название «когерентная длина».
на которой наблюдается повышение интенсивности результирующего излучения, получила название «когерентная длина».
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- Часть I. ЛАЗЕРНЫЕ КРИСТАЛЛЫ
- Глава 1. ХАРАКТЕРИСТИКИ КРИСТАЛЛОВ, ИСПОЛЬЗУЕМЫХ ДЛЯ ГЕНЕРАЦИИ ЛАЗЕРНОГО ИЗЛУЧЕНИЯ
- 1.2. ОПТИЧЕСКИЙ РЕЗОНАТОР
- 1.3. ПОРОГОВЫЕ УСЛОВИЯ ДЛЯ УСИЛЕНИЯ СВЕТА
- 1.3.2. Пороговые условия в непрерывном режиме
- 1.4. ЭНЕРГЕТИЧЕСКИЕ ХАРАКТЕРИСТИКИ И К.П.Д. ЛАЗЕРА
- 1.5. ИОНЫ-АКТИВАТОРЫ
- 1.6. ТЕПЛОВЫЕ СВОЙСТВА КРИСТАЛЛОВ
- 1.7. ТРЕБОВАНИЯ, ПРЕДЪЯВЛЯЕМЫЕ К КРИСТАЛЛАМ
- Глава 2. КРИСТАЛЛЫ-ОКСИДЫ
- 2.1.2. Структура кристаллов
- Макронеоднородность кристаллов
- Примеси
- Центры окраски в кристаллах соединений …
- Окраска корунда
- Окраска иттрий-атоминиевого граната
- Дополнительная окраска и рекомбинационные процессы в кристаллах алюмината иттрия
- 2.2. КРИСТАЛЛИЧЕСКИЕ СРЕДЫ ДЛЯ ВЫСОКОЭФФЕКТИВНЫХ НЕОДИМОВЫХ ЛАЗЕРОВ
- 2.2.2. ВЫРАЩИВАНИЕ И РОСТОВЫЕ ДЕФЕКТЫ КРИСТАЛЛОВ ГАЛЛИЕВЫХ ГРАНАТОВ
- 2.2.3. РАЗУПОРЯДОЧЕНИЕ В ГАЛЛИЕВЫХ ГРАНАТАХ
- 2.2.4. ЦЕНТРЫ ОКРАСКИ В ГАЛЛИЕВЫХ ГРАНАТАХ
- Глава 3. КРИСТАЛЛЫ ФТОРИДОВ
- 3.1. Кристаллы YLiF4
- 3.2. Кристаллы …
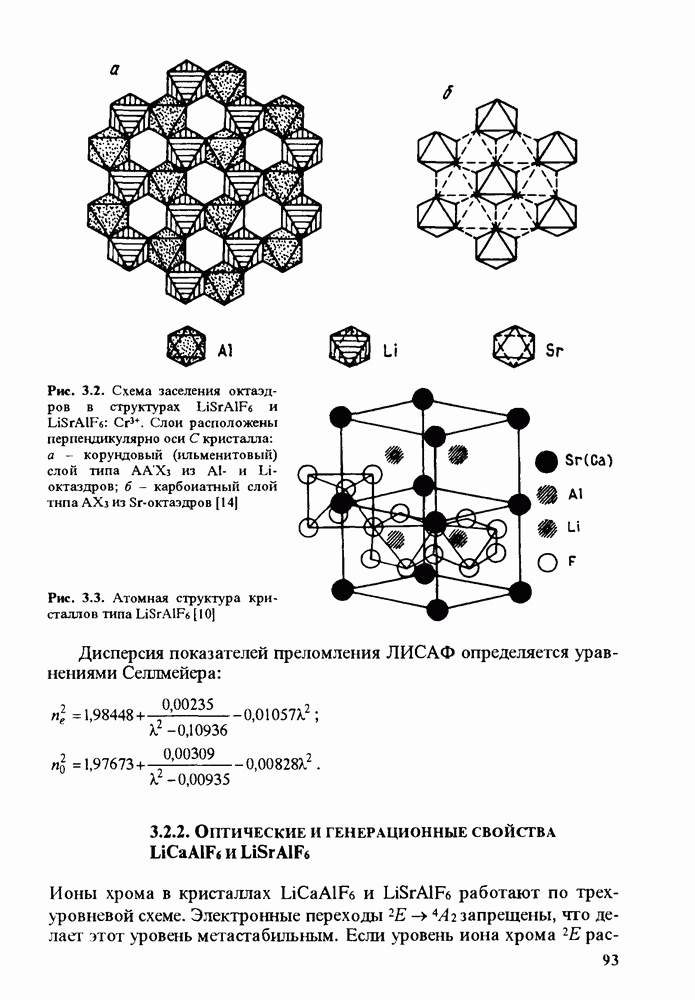
- 3.2.2. ОПТИЧЕСКИЕ И ГЕНЕРАЦИОННЫЕ СВОЙСТВА
- Глава 4. КРИСТАЛЛЫ ДЛЯ ЛАЗЕРОВ С ПЕРЕСТРАИВАЕМОЙ ЧАСТОТОЙ
- 4.1. АЛЕКСАНДРИТ
- 4.2. КОРУНД С ТИТАНОМ
- 4.3. ЦЕНТРЫ ОКРАСКИ — АКТИВАТОРЫ ЛАЗЕРНЫХ КРИСТАЛЛОВ
- Глава 5. ДЕФЕКТЫ ЛАЗЕРНЫХ КРИСТАЛЛОВ, ВОЗНИКАЮЩИЕ ПРИ ПЛАСТИЧЕСКОЙ ДЕФОРМАЦИИ
- 5.2. ДВОЙНИКОВАНИЕ
- Глава 6. КРИСТАЛЛЫ ДЛЯ ПРОХОДНОЙ ОПТИКИ МОЩНЫХ ЛАЗЕРОВ
- 6.1. СОБСТВЕННЫЕ МЕХАНИЗМЫ ОПТИЧЕСКОГО РАЗРУШЕНИЯ
- 6.2. НЕСОБСТВЕННЫЕ МЕХАНИЗМЫ ОПТИЧЕСКОГО РАЗРУШЕНИЯ
- 6.2.1. ОПТИЧЕСКОЕ РАЗРУШЕНИЕ ПОВЕРХНОСТИ
- 6.2.2. РАЗРУШЕНИЕ В ОБЪЕМЕ КРИСТАЛЛА
- 6.3. ОПТИЧЕСКАЯ ПРОЧНОСТЬ В СФОКУСИРОВАННЫХ И ШИРОКО АПЕРТУРНЫХ ПУЧКАХ
- 6.4. ОПТИЧЕСКАЯ ПРОЧНОСТЬ КРИСТАЛЛОВ ПРИ ВОЗДЕЙСТВИИ ИМПУЛЬСНОПЕРИОДИЧЕСКОГО ИЗЛУЧЕНИЯ
- 6.5. ВЫБОР МАТЕРИАЛА ДЛЯ ПРОХОДНОЙ ОПТИКИ МОЩНЫХ ЛАЗЕРОВ
- 6.6. ВОЗМОЖНОСТИ ПОВЫШЕНИЯ ОПТИЧЕСКОЙ ПРОЧНОСТИ КРИСТАЛЛОВ И ОПТИЧЕСКИХ ЭЛЕМЕНТОВ
- Часть II. НЕЛИНЕЙНО-ОПТИЧЕСКИЕ И ЭЛЕКТРООПТИЧЕСКИЕ КРИСТАЛЛЫ
- Глава 7. ЛИНЕЙНЫЙ ЭЛЕКТРООПТИЧЕСКИЙ ЭФФЕКТ И ХАРАКТЕРИСТИКИ ЭЛЕКТРО-ОПТИЧЕСКОГО КАЧЕСТВА КРИСТАЛЛОВ
- 7.2. ПОЛЯРИЗАЦИОННО-ОПТИЧЕСКИЕ ЗАТВОРЫ И МОДУЛЯТОРЫ СВЕТА
- 7.3. ЭЛЕКТРООПТИЧЕСКИЕ ЗАТВОРЫ НА РЕГУЛЯРНОЙ ДОМЕННОЙ СТРУКТУРЕ
- Глава 8. РАСПРОСТРАНЕНИЕ СВЕТА В НЕЛИНЕЙНЫХ ОПТИЧЕСКИХ СРЕДАХ
- 8.2. УСЛОВИЯ СОХРАНЕНИЯ ЭНЕРГИИ И ИМПУЛЬСА ПРИ ВЗАИМОДЕЙСТВИИ ФОТОНОВ В НЕЛИНЕЙНЫХ СРЕДАХ
- 8.3. РЕАЛИЗАЦИЯ УСЛОВИЙ СИНХРОНИЗМА
- 8.4. ЭФФЕКТИВНЫЕ КОЭФФИЦИЕНТЫ НЕЛИНЕЙНОСТИ
- 8.5. РАССОГЛАСОВАНИЕ ФАЗ ВЗАИМОДЕЙСТВУЮЩИХ ВОЛН ПОД ДЕЙСТВИЕМ ВНЕШНИХ ФАКТОРОВ. ПОЛОСА ПРОПУСКАНИЯ
- 8.6. РАСЧЕТ ПРЕОБРАЗОВАТЕЛЯ ЧАСТОТЫ
- 8.7. КВАЗИСИНХРОННОЕ ВЗАИМОДЕЙСТВИЕ
- Глава 9. КРИСТАЛЛЫ НА ОСНОВЕ ОКСИДОВ
- 9.2. ВЫРАЩИВАНИЕ КРИСТАЛЛОВ
- 9.3. ФАЗОВЫЕ ПЕРЕХОДЫ В КИСЛОРОДНООКТАЭДРИЧЕСКИХ КРИСТАЛЛАХ
- 9.4. ДЕФЕКТЫ СТРУКТУРЫ
- 9.4.1. МАКРОНЕОДНОРОДНОСТЬ КРИСТАЛЛОВ
- 9.4.2. ДВОЙНИКОВАНИЕ
- Механическое двойникование кристаллов ниобата лития
- 9.5. МОНОДОМЕНИЗАЦИЯ КРИСТАЛЛОВ
- 9.6. ПОЛУЧЕНИЕ РЕГУЛЯРНЫХ ДОМЕННЫХ СТРУКТУР
- 9.6.2. ПОСЛЕРОСТОВАЯ ЭЛЕКТРОТЕРМИЧЕСКАЯ ОБРАБОТКА
- 9.6.3. ПОЛУЧЕНИЕ РЕГУЛЯРНЫХ ДОМЕННЫХ СТРУКТУР В ПОВЕРХНОСТНЫХ СЛОЯХ
- 9.6.4. ПОЛУЧЕНИЕ РЕГУЛЯРНЫХ ДОМЕННЫХ СТРУКТУР СКАНИРОВАНИЕМ ПО КРИСТАЛЛУ ЭЛЕКТРОННЫМ ЛУЧОМ
- 9.7. ДИСЛОКАЦИИ И ПЛАСТИЧНОСТЬ КИСЛОРОДНО-ОКТАЭДРИЧЕСКИХ КРИСТАЛЛОВ
- 9.8. ТОЧЕЧНЫЕ ДЕФЕКТЫ
- 9.8.1. ВЛИЯНИЕ ОТКЛОНЕНИЯ ОТ СТЕХИОМЕТРИИ НА СВОЙСТВА КРИСТАЛЛОВ НИОБАТА ЛИТИЯ
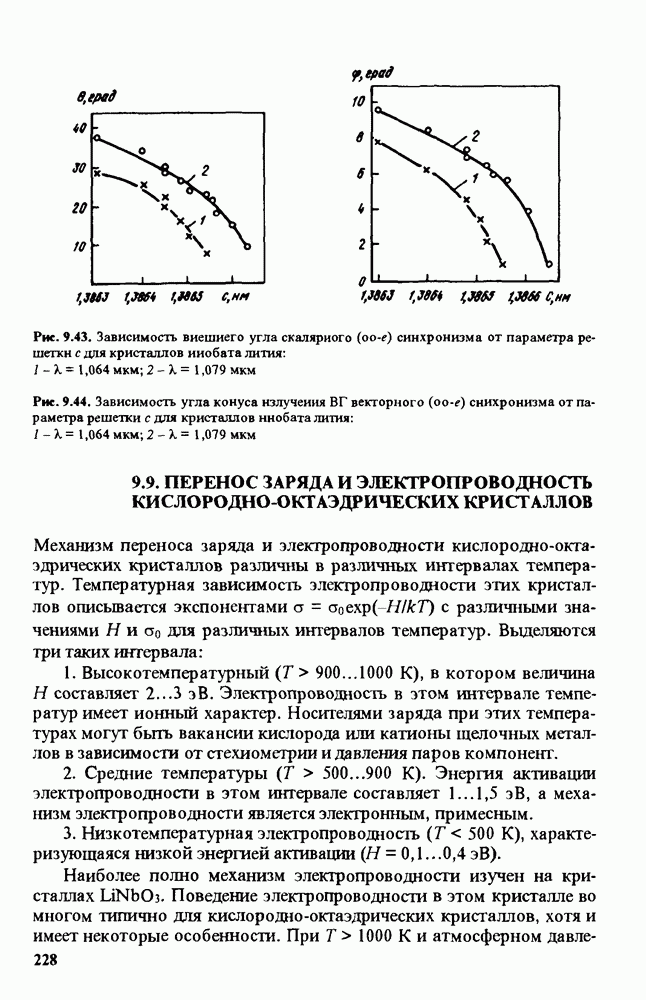
- 9.9. ПЕРЕНОС ЗАРЯДА И ЭЛЕКТРОПРОВОДНОСТЬ КИСЛОРОДНО-ОКТАЭДРИЧЕСКИХ КРИСТАЛЛОВ
- 9.10. ФОТОРЕФР АКТИВНЫЙ ЭФФЕКТ В КИСЛОРОДНО-ОКТАЭДРИЧЕСКИХ КРИСТАЛЛАХ
- 9.10.2. МЕХАНИЗМЫ ВОЗНИКНОВЕНИЯ ПРОСТРАНСТВЕННОГО ЗАРЯДА
- 9.10.3. ВОЗМОЖНОСТЬ ОСЛАБЛЕНИЯ ФОТОРЕФРАКЦИИ
- 9.10.4. ФОТОРЕФРАКЦИЯ В ПРАКТИЧЕСКИ ВАЖНЫХ КРИСТАЛЛАХ
- 9.11. ОПТИЧЕСКАЯ НЕОДНОРОДНОСТЬ И НЕСТАБИЛЬНОСТЬ СВОЙСТВ КРИСТАЛЛОВ
- 9.11.2. ОПТИЧЕСКАЯ НЕОДНОРОДНОСТЬ КРИСТАЛЛОВ НИОБАТА ЛИТИЯ
- Глава 10. КРИСТАЛЛЫ ГРУППЫ KDP
- 10.1. ОСНОВНЫЕ СВОЙСТВА КРИСТАЛЛОВ ГРУППЫ KDP
- 10.2. СТРУКТУРА И МЕТОДЫ ВЫРАЩИВАНИЯ КРИСТАЛЛОВ
- 10.3. ВЛИЯНИЕ ПРИМЕСЕЙ И КИСЛОТНОСТИ РАСТВОРА НА РОСТ КРИСТАЛЛОВ KDP И ADP
- 10.4. СКОРОСТНОЕ ВЫРАЩИВАНИЕ КРИСТАЛЛОВ
- 10.5. ПЛАСТИЧНОСТЬ И ДИСЛОКАЦИИ В КРИСТАЛЛАХ ГРУППЫ KDP
- Глава 11. ИОДАТ ЛИТИЯ
- 11.1. СТРУКТУРА И ВЫРАЩИВАНИЕ КРИСТАЛЛОВ ИОДАТА ЛИТИЯ
- 11.2. ВХОЖДЕНИЕ ПРИМЕСЕЙ В КРИСТАЛЛ …
- 11.3. ГАБИТУС КРИСТАЛЛОВ … И ВЫРАЩИВАНИЕ ПРОФИЛИРОВАННЫХ КРИСТАЛЛОВ
- 11.4. ЭЛЕКТРИЧЕСКИЕ СВОЙСТВА КРИСТАЛЛОВ …
- 11.5. ОПТИЧЕСКИЕ И НЕЛИНЕЙНООПТИЧЕСКИЕ СВОЙСТВА КРИСТАЛЛОВ …
- Глава 12. ТИТАНИЛФОСФАТ КАЛИЯ
- 12.1. ОСОБЕННОСТИ КРИСТАЛЛОВ ТИТАНИЛФОСФАТА КАЛИЯ
- 12.2. СТРУКТУРА КРИСТАЛЛОВ КТР
- 12.3. ВЫРАЩИВАНИЕ КРИСТАЛЛОВ
- 12.4. СВОЙСТВА КТР
- 12.5. ОПТИЧЕСКАЯ НЕЛИНЕЙНОСТЬ КРИСТАЛЛОВ КТР
- Глава 13. БОРАТЫ
- 13.2. ОПТИЧЕСКИЕ И НЕЛИНЕЙНООПТИЧЕСКИЕ СВОЙСТВА БОРАТОВ
- Часть III. КРИСТАЛЛЫ В АКУСТООПТИКЕ
- Глава 14. ОСНОВНЫЕ ПРИНЦИПЫ АКУСТООПТИКИ
- 14.2. АКУСТООПТИЧЕСКАЯ ДИФРАКЦИЯ БРЭГГА В АНИЗОТРОПНЫХ КРИСТАЛЛАХ
- 14.2.2. АКУСТООПТИЧЕСКОЕ ВЗАИМОДЕЙСТВИЕ в ПЛОСКОСТИ, ЛЕЖАЩЕЙ ПОД УГЛОМ К ОПТИЧЕСКОЙ ОСИ КРИСТАЛЛА
- 14.3. ИНТЕНСИВНОСТЬ ДИФРАКЦИИ И АКУСТООПТИЧЕСКАЯ ЭФФЕКТИВНОСТЬ СРЕДЫ
- 14.4. КОЛЛИНЕАРНОЕ АКУСТООПТИЧЕСКОЕ ВЗАИМОДЕЙСТВИЕ. ВЛИЯНИЕ СИНХРОНИЗМА НА ЭФФЕКТИВНОСТЬ ДИФРАКЦИИ
- Глава 15. ОСНОВНЫЕ ОБЛАСТИ ПРИМЕНЕНИЯ АКУСТООПТИЧЕСКОГО ВЗАИМОДЕЙСТВИЯ
- 15.2. АКУСТООПТИЧЕСКИЙ ДЕФЛЕКТОР
- 15.3. АКУСТООПТИЧЕСКИЙ ФИЛЬТР
- 15.3.2. ПРИМЕРЫ РЕАЛИЗАЦИИ КОЛЛИНЕАРНОГО ВЗАИМОДЕЙСТВИЯ ПРИ СОЗДАНИИ АКУСТООПТИЧЕСКИХ ФИЛЬТРОВ
- Глава 16. АКУСТООПТИЧЕСКОЕ КАЧЕСТВО КРИСТАЛЛОВ
- 16.1. СВЯЗЬ АКУСТООПТИЧЕСКОГО КАЧЕСТВА И ОСНОВНЫХ СВОЙСТВ КРИСТАЛЛОВ
- 16.2. МОНОКРИСТАЛЛИЧЕСКИЙ КВАРЦ
- 16.2.2. ДЕФЕКТЫ КВАРЦА
- 16.3. ПАРАТЕЛЛУРИТ
- 16.3.1. СТРУКТУРА И СВОЙСТВА ПАРАТЕЛЛУРИТА
- 16.3.2. ВЫРАЩИВАНИЕ ПАРАТЕЛЛУРИТА
- 16.3.3. ДЕФЕКТЫ СТРУКТУРЫ ПАРАТЕЛЛУРИТА
- 16.3.4. ПРИМЕНЕНИЕ TEO2 В АКУСГООПТИЧЕСКИХ ПРИБОРАХ
- 16.4. МОЛИБДАТЫ ЩЕЛОЧНОЗЕМЕЛЬНЫХ ИОНОВ
- 16.4.2. ВЫРАЩИВАНИЕ МОНОКРИСТАЛЛОВ
- 16.4.3. ДЕФЕКТЫ СТРУКТУРЫ
- 16.4.4. ПРИМЕНЕНИЕ МОЛИБДАТОВ В АКУСТООПТИКЕ
- Часть IV. КРИСТАЛЛИЧЕСКИЕ ЭЛЕМЕНТЫ ИНТЕГРАЛЬНОЙ ОПТИКИ
- Глава 17 ОПТИЧЕСКИЕ ВОЛНОВОДЫ, ИХ СВОЙСТВА И ХАРАКТЕРИСТИКИ
- 17.2. РАСПРОСТРАНЕНИЕ ОПТИЧЕСКИХ ВОЛН В ПЛОСКОМ ВОЛНОВОДЕ
- 17.3. ПОТЕРИ В ВОЛНОВОДЕ
- Глава 18. МЕТОДЫ ПОЛУЧЕНИЯ ВОЛНОВОДОВ
- 18.1. Ti-ДИФФУЗИОННАЯ ТЕХНОЛОГИЯ
- 18.1.2. ДИФФУЗИОННЫЙ ОТЖИГ
- 18.2. ПОЛУЧЕНИЕ ОПТИЧЕСКИХ ВОЛНОВОДОВ МЕТОДОМ ИОННОГО ОБМЕНА (ПРОТОННОГО ЗАМЕЩЕНИЯ)
- 18.2.1. ДИФФУЗИОННЫЕ ПРОЦЕССЫ ПРИ ИОННОМ ОБМЕНЕ
- 18.2.2. ПОЛУЧЕНИЕ ВОЛНОВОДОВ МЕТОДОМ ПЗ В КРИСТАЛЛАХ
- 18.3. ПОЛУЧЕНИЕ ОПТИЧЕСКИХ ВОЛНОВОДОВ С ПОМОЩЬЮ ИОННОЙ ИМПЛАНТАЦИИ
- БИБЛИОГРАФИЧЕСКИЙ СПИСОК