9.8.1. ВЛИЯНИЕ ОТКЛОНЕНИЯ ОТ СТЕХИОМЕТРИИ НА СВОЙСТВА КРИСТАЛЛОВ НИОБАТА ЛИТИЯ

Практическая важность кристаллов ниобата лития, выращиваемых из несгехиометрического, конгруэнтно плавящегося состава, потребовала обратить особое внимание на зависимость его свойств от стехиометрии. Анализ соотношения компонентов в исходных оксидах, шихте и кристалле показал, что недостаток в конгруэнтном составе определяется дефицитом кислорода в исходном оксиде ниобия (V) и примесным составом используемых реактивов [94]. Переход от конгруэнтного состава к сгехиометрическому, т.е. возрастание соотношения означает относительное снижение молярной доли катиона имеющего меньший ионный радиус но больший заряд, чем ион Как следует

из рис. 9.38, с ростом параметр решетки по оси уменьшается. Этот эффект нельзя объясншъ исходя из соотношения ионных радиусов катионов. Очевидно, основное влияние на изменение параметра решетки оказывает возрастание молярной доли высоковалентного катиона. Частичное замещение одновалентного лития пятивалентным ниобием приводит к стягиванию анионов и к уменьшению параметра решетки.

Исследование зависимости температуры Кюри от содержания мольной доли в кристалле [95 - 98] дают зависимость, близкую к линейной (рис. 9.39)

где Т - температура Кюри, - мольная доля

Измерения проведены для составов исходного расплава что соответствует содержанию в кристалле

Для оптического применения ниобата лития важнейшей является зависимость от стехиометрии показателей преломления. Эта зависимость в свою очередь определяет влияние стехиометрии на условия синхронизма при нелинейно-оптическом взаимодействии. С увеличением отношения от 0,8 до 1,2 обыкновенный показатель преломления практически не меняется, а нелинейный показатель линейно уменьшается от 2,22 до 2,19 (рис. 9.40) [94]. Как следствие этого, изменяется температура -градусного (некритического) синхронизма (рис. 9.41) [83].

Рис. 9.38. Зависимость параметра решетки с от стехиометрии кристалла ниобата лития

Рис. 9.39. Зависимость температуры Кюри от содержания в кристалле

Прямое определение соотношения в расплаве очень трудоемко и точность его не превосходит Поэтому для определения стехиометрии кристалла используются приведенные зависимости физических характеристик от его состава. Чаще всего для оценки соотношения используются измерения температуры Кюри [согласно (9.7) величина определяется соотношением ] и измерение или угла фазового синхронизма при генерации оптической гармоники, но и при использовании этих методов возникают определенные трудности.

Определение по измерениям температуры Кюри затруднено из-за необходимости нагрева кристалла до высоких температур Существенным недостатком метода оценки по величине является длительность измерений.

Кроме того, скорости нагрева или охлаждения массивных образцов при относительно низких температурах должны быть достаточно малы, чтобы обеспечить низкие градиенты температур и избежать возникновения больших пироэлектрических полей, которые могут привести к длительно сохраняющейся оптической неоднородности или даже к растрескиванию кристалла. Более простым является измерение угла синхронизма при постоянной (комнатной) температуре. Но в этом случае часто необходимо готовить образцы специальной ориентации с двумя оптически полированными поверхностями, что затрудняет использование метода для измерения на кристаллических булях. На кафедре физики кристаллов МИСиС был предложен метод оценки, использующий особенности векторного синхронизма в ниобате лития.

Рис. 9.40. Зависимость показателя преломления кристаллов от соотношения в расплаве:

Рис. 9.41. Зависимость температуры -градусного (некритического) синхронизма от состава расплава в кристаллах для мкм [83]

Рис. 9.42. Схема построения направлений излучения второй гармоники для векторного синхронизма в оптически отрицательном кристалле. Сечение поверхностей волновых векторов плоскостью

В отличие от скалярного синхронизма, угол которого задан условием векторный синхронизм может давать излучение в интервале углов от до . При векторном синхронизме взаимодействуют два луча с различными направлениями волновых векторов. Если падающие волны (волны накачки) имеют широкий набор волновых векторов, то условие векторного синхронизма реализуется для множества лучей, дающих конус излучения второй гармоники (рис. 9.42).

Реально наблюдаемая картина представляет собой совокупность лучей по образующей конуса. Это объясняется тем, что наибольшую интенсивность имеют лучи, которые возникают при взаимодействии центрального, имеющего большую интенсивность, луча с рассеянными лучами. Результат взаимодействия рассеянных лучей практически не заметен из-за малой интенсивности рассеянных лучей. Как следует из рис. 9.42, луч основной частоты, направленный по угол между и , пересекает поверхность в точке В. Проведя из точки В окружность радиусом получим точки - пересечения этой окружности с сечением плоскостью Направления и являются направлениями векторного синхронизма, так как

Векторы и имеют углы с осью если ОА не совпадает с .

В объеме поверхность волновых векторов является эллипсоидом вращения, а вокруг точки В строится сфера радиусом

Излучение второй гармоники образует конус с вершиной, расположенной на входной, рассеивающей свет поверхности кристалла. На экране, расположенном за кристаллом, наблюдается светлое кольцо, являющееся результатом сечения конуса плоскостью экрана. Внутри кольца находится светлая точка, которая возникает в

результате несинхронного преобразования основного луча в излучение Положение точки определяется углом падения основного излучения на кристалл, а форма кольца представляет собой овалоид, описываемый уравнением четвертого порядка. Этот овалоид можно представить как эллипс, при этом ошибка не превосходит 0,5 %. В частном случае при распространении основного излучения по нормали к оптической оси кристалла кольцо излучения можно апроксимировать окружностью. Светлая точка в этом случае располагается в центре кольца. В случае поворота кристалла в плоскости вокруг оси 1 при том, что направление основного луча остается нормальным оптической оси, радиус кольца излучения уменьшается, а светлая точка смещается из центра кольца. Если оптическая ось кристалла не лежит в плоскости поворота, на экране наблюдается овал со смещенной светлой точкой. Наклон оси овала равен наклону оптической оси кристалла относительно плоскости поворота.

Для характеристики условий векторного синхронизма можно использовать угол конуса излучения Определение наиболее удобно проводить при падении основного излучения по нормали к оптической оси кристалла. Измеряются расстояния между светлой точкой и кольцом а размер кольца оценивается как Кроме того, можно измерять расстояние светлой точки от центра кольца Величины связаны зависимостью где - максимальный радиус кольца излучения Величина неизвестна, и ее можно определить из пары измерений и проведенных при различных углах Исключив таким образом рассчитав и зная базу измерения можно определить как

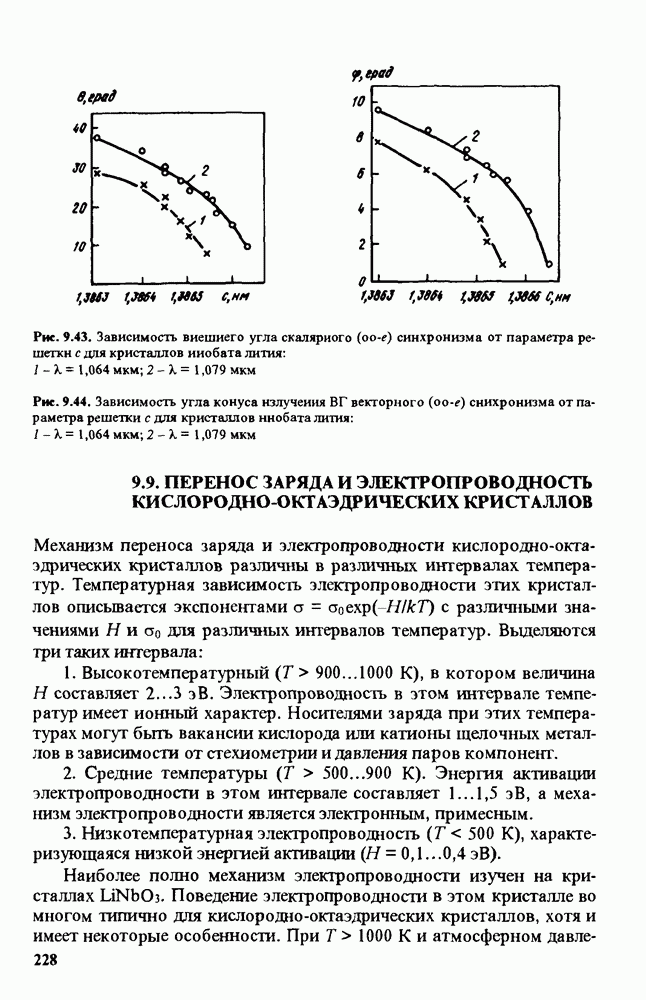
Для того чтобы использовать величину при определении стехиометрии ниобата лития, необходимо знать связь с какой-либо характеристикой кристалла ниобата лития, зависимость которой от стехиометрии кристалла достаточно надежно установлена. В качестве такой базовой характеристики был избран параметр решетки (см. рис. 9.38). С использованием кристаллов, имеющих различную стехиометрию, измерены зависимости от параметра решетки величин углов скалярного синхронизма (рис. 9.43) и угла (рис. 9.44). Зависимость, показанную на рис. 9.44, можно использовать для определения с помощью измерения векторного синхронизма. Эти измерения отличаются простотой, так как не требуют вращения кристалла и могут быть легко автоматизированы с использованием фотоматрицы для регистрации светлого кольца и обработкой изображения кольца на ЭВМ. С использованием этих методов показано, что конгруэнтный состав находится в интервале

Рис. 9.43. Зависимость внешнего угла скалярного синхронизма от параметра решетки с дня кристаллов ниобата лития: мкм; мкм

Рис. 9.44. Зависимость угла конуса излучения векторного синхронизма от параметра решетки с для кристаллов ниобата лития: мкм; мкм