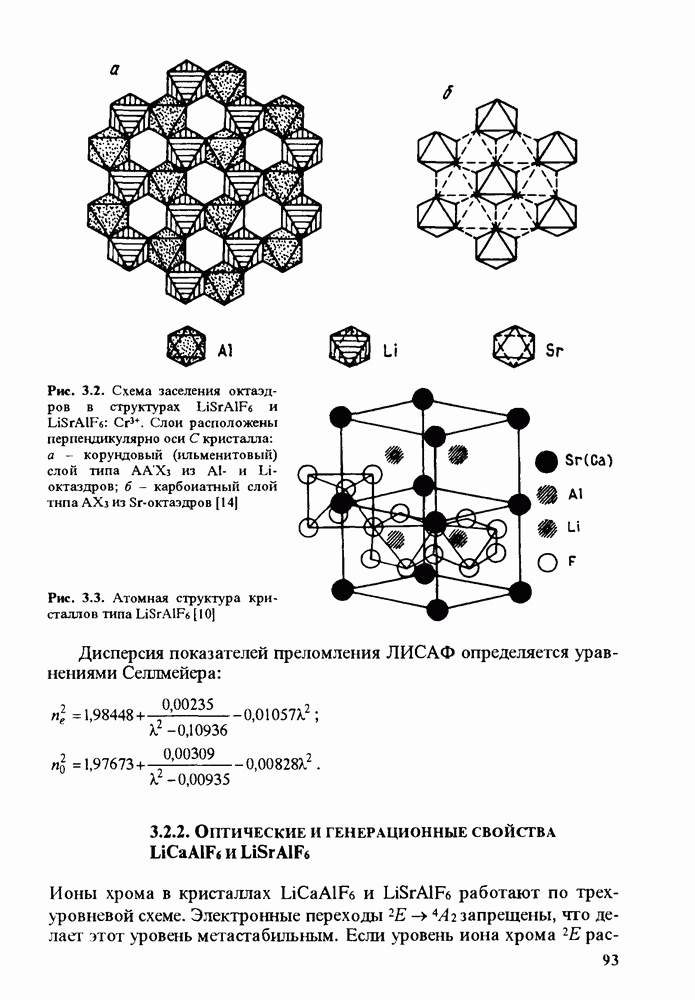
14.3. ИНТЕНСИВНОСТЬ ДИФРАКЦИИ И АКУСТООПТИЧЕСКАЯ ЭФФЕКТИВНОСТЬ СРЕДЫ

Эффективность акустооптической среды (в частности, кристалла) определяется соотношением интенсивностей дифрагированного и начального лучей, которое можно получить в среде при данном уровне акустического воздействия. Для оценки эффективности материала нужно иметь количественную характеристику, выражающую АО эффективность через известные, фундаментальные свойства материала. Такую характеристику можно получить, рассмотрев зависимость интенсивности дифрагированных пучков от интенсивности акустического луча и свойств среды. С этой целью для определения интенсивности дифрагированных пучков и напряженности поля света в среде найдем решение уравнения Максвелла в системе координат, показанной на рис. 14.8

где Е напряженность поля в акустооптической среде, нормированная на напряженность поля, входящего в среду излучения.

Показатель преломления модулирован акустической волной и поэтому зависит от координаты и времени, как зависит от координаты и времени деформация среды акустической волной. С учетом упругооптического эффекта показатель преломления можно записать

где показатель преломления среды в отсутствии звукового поля;

- изменение показателя преломления, вносимое звуковой волной вследствие упругооптического эффекта.

Для простоты будем считать среду изотропной. Определим напряженность поля световой волны

Амплитуда зависит от звуковых колебаний, является периодической функцией от х и может быть представлена в виде разложения Фурье по

Рис. 14.8. Система координат для решения уравнения Максвелла

Подставляя (14.19) в (14.18), получим

где - волновые векторы дифрагированных волн порядка есть

Выражение (14.20) описывает систему волн с направлениями волновых векторов и амплитудами Решение для поля оптических волн можно искать в виде

где

После подстановки (14.22) в (14.16) имеем

Поскольку меняются во времени с частотой звуковой волны, т.е. медленно по сравнению с изменением напряженности поля световой волны Е, то первый и второй производной по времени в (14.25) можно пренебречь и (14.20) переписать в виде

так как

Изменение показателя преломления «1 определяется звуковыми колебаниями и для синусоидальной звуковой волны «1 можно задать как

следовательно,

Подставляя в с учетом (14.22 - 14.24) и из (14.27), приравнивая коэффициенты при экспонентах с одинаковыми степенями, пренебрегая вторыми производными по координатам и переходя к полным производным, получим

Обозначив

и приведя подобные члены, перепишем (14.30) как

Фт. (14.32)

Введя параметр характеризующий длину акусто оптического взаимодействия, и обозначив в (14.31) комбинации переменных как

можно переписать (14.32) в виде

Фт. (14.36)

Разделим переменные и подставим в виде

Подставив (14.37) в (14.36), имеем

Величина правой части выражения (14.38) определяет тип дифракции. Предельная величина правой части равна нулю при Это условие определяет который при приводит к

что соответствует условию дифракции Брэгга, а есть угол Брэгга. Известно, что дифракция Брэгга - это дифракция на «толстых» дифракционных решетках, т.е. дифракция, при которой падающий и дифрагированные лучи пересекают несколько (много) периодов дифракционной решетки. В (14.38) число акустических волн, пересекаемых оптическими лучами, определяется величиной Действительно, выражая волновые векторы через длины волн в (14.35), с учетом (14.39) получим

Угол распространения падающего светового луча при котором луч пересекает одну акустическую волну, определяется как следовательно, . Так как для дифракции Брэгга (дифракции на толстых решетках) должно выполняться условие то дифракции Брэгга соответствуют значения т.е. при дифракции Брэгга оптический луч пересекает более акустических волн. При величинах близких к 1, реализуется другой вид дифракции, при котором число акустических волн, пересекаемых оптическими лучом, близко или меньше единицы. Это дифракция оптических волн, волновые векторы которых почти нормальны волновым векторам акустических волн, или дифракция происходит на тонких акустических лучах. Такой вид дифракции известен как «дифракция Рамана - Ната» и реализуется уже при

Величина задает определенную связь между размером пьезопреобразователя, определяющим ширину звукового луча и свойствами материала при реализации того или иного вида дифракции. В частности, для дифракции Брэгга необходимо, чтобы размер пьезопреобразователя соответствовал условию

где V - скорость и частота звуковых волн.

Для получения характеристик акусгооптического качества материала можно ограничиться рассмотрением дифракции Брэгга, тем более что этот вид дифракции наиболее часто используется при создании акустооптических устройств. Для дифракции Брэгга правая часть уравнения (14.38) равна нулю. Это соответствует синхронизации основной и дифрагированной волн, и (14.38) можно записать как

Для двух лучей с амплитудами поля и из (14.30) получим систему уравнений

решением которой являются где - амплитуда поля света, падающего в акустооптическую среду.

Поскольку интенсивность света I - на выходе из АО ячейки получим для интенсивностей двух дифрагированных лучей

Как следует из (14.22), величина прямо зависит от изменения показателя преломления а величина определяется упругооптическим эффектом

где - тензор упруго оптических коэффициентов;

тензор упругой деформации, создаваемой акустической волной.

Упругая деформация в звуковой волне и интенсивность звука связаны как

где - плотность звуковой энергии;

V - скорость звука в среде;

С - константа упругой жесткости; - плотность среды.

В результате для относительной интенсивности дифрагированного луча при дифракции Брэгга получим

В скобках (подчеркнуто) собраны величины, характеризующие материал. Эту комбинацию величин можно использовать для общей характеристики акустооптической эффективности материалов и принято обозначать

В зависимости от конкретных применений на первый план могут выходить различные характеристики АО прибора: разрешающая способность, полоса пропускания и т.д. Это может усиливать или ослаблять влияние различных характеристик материала на АО эффективность. Поэтому при различных применениях материала комбинация величин, характеризующая АО эффективность, может меняться и для характеристики АО эффективности материала в конкретном приборе приходится использовать комбинации величин, отличающиеся от (14.48). Эти характеристики можно ввести, рассмотрев принципы работы некоторых основных АО устройств.