| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
II. АНАЛИЗ ПРИМЕРОВ.
1. В рассуждении допущена ошибка: второй клиент гостиницы остался без комнаты, так как об его существовании просто «забыли» при распределении номеров гостиницы.
Однако здесь нельзя ограничиться одним указанием ошибки. Следует объяснить, почему эта грубая ошибка далеко не каждому сразу бросается в глаза.
Объяснение же этого факта состоит в том, что понятие нзлого положительного числа не является однозначным: оно может быть и количественным и порядковым. Путем сознательного смешения понятий количественного и порядкового
чисел и достигается иллюзия правдоподобности приведенного рассуждения. В самом деле, мы рассуждали так: «в итоге расселения в первой комнате оказалось два человека» — число количественное; «третий человек был помещен во второй комнате» - число порядковое. Подобная структура рассуждения и дала возможность отвлечь внимание читающего текст софизма от факта пропуска второго клиента.
Этот софизм указывает на необходимость четко уяснить себе, какой смысл вкладывается в используемый термин, особенно тогда, когда он принадлежит к числу неоднозначных математических терминов.
2. В рассуждении допущено намеренное отождествление понятий порядкового и количественного чисел.
Ошибка возникает потому, что для пальцев правой руки совпадение порядкового и количественного чисел не имеет места.
3. Отметим, что, взяв вместо денежных единиц единицы длины и поступая точно так же, мы не получим ничего неверного:

или

Получив от умножения чисел, выражающих метры, число, выражающее уже не простые (линейные), а квадратные метры, мы догадываемся,  чем была допущена ошибка, когда мы имели дело с деньгами: умножить а рублей на
чем была допущена ошибка, когда мы имели дело с деньгами: умножить а рублей на
1 рубль нельзя, так как никаких «квадратных рублен» и «квадратных копеек» не существует.
Иногда говорят, что множимое может быть и отвлеченным, и именованным числом, множитель же должен быть обязательно числом отвлеченным. Уже такое умножение, как  показывает, что это неверно. Можно указать еще сколько угодно примеров умножения именованного числа на именованное. Так, количество работы, которую надо затратить для выполнения некоторого задания, выражают обычно числом рабочих дней, т. е. произведением числа рабочих на число дней, в течение которых они будут заняты; работу транспорта характеризуют числом пассажиро-километров (произведением числа пассажиров на число километров). Каждый раз умножение двух именованных чисел приводит к некоторой новой, сложной единице. Почленное умножение
показывает, что это неверно. Можно указать еще сколько угодно примеров умножения именованного числа на именованное. Так, количество работы, которую надо затратить для выполнения некоторого задания, выражают обычно числом рабочих дней, т. е. произведением числа рабочих на число дней, в течение которых они будут заняты; работу транспорта характеризуют числом пассажиро-километров (произведением числа пассажиров на число километров). Каждый раз умножение двух именованных чисел приводит к некоторой новой, сложной единице. Почленное умножение
Двух равенств между именованными числами законно всегда, когда существует соответствующая сложная единица. Так, имея равенства:

мы можем перемножить их почленно и получим совершенно правильный результат:

Это показывает, что для подъема груза в  на высоту в
на высоту в  надо затратить в миллион раз больше работы, чем для подъема груза в
надо затратить в миллион раз больше работы, чем для подъема груза в  на высоту
на высоту 
4. Ошибка состоит в том, что мы занимаемую единицу возводили в ранг десятка.
Возникает вопрос: случайно ли сумма таким образом полученных разностей равна 45?
Нет, не случайно. В самом деле мы занимали пять раз по единице и каждую из занимаемых единиц считали десятком.
Таким образом образовалась сумма пяти лишних девяток, составляющих 45
Допускаемая грубая ошибка не каждым сразу обнаруживается в результате ложной аналогии с выполнением вычитания чисел, записанных по принципам позиционной десятичной системы счисления.
Имела место попытка предлагать тезис этого софизма «45 — 45—45» в качестве задачи для отыскания ее «решения». «Как из 45 (сумма, которая составляется из сложения чисел от 1 до 9) вычесть 45, чтобы в итоге получилось  (Журнал «Огонек», 1953, № 26, стр. 32.) Разумеется, подобная постановка вопроса должна вызвать решительный протест со стороны представителей методико-математической мысли.
(Журнал «Огонек», 1953, № 26, стр. 32.) Разумеется, подобная постановка вопроса должна вызвать решительный протест со стороны представителей методико-математической мысли.
5. Грубая ошибка маленького Пети, как показывает опытная проверка, не всем детям сразу бросается в глаза, а объяснить ее затрудняются многие. Это происходит потому, что в основе рассуждений мальчика, как это ни странно, лежит правильная мысль. Она состоит в том, что точное деление (деление без остатка) сводится к последовательному вычитанию делителя из делимого до получения разности, равной нулю.
Производя деление 40 на 8, Петя должен был установить, сколько раз из 40 можно вычесть 8. Он установил, что это можно сделать четыре раза  и еще один раз
и еще один раз 
т. е. выполнить Деление так:

Однако в силу неправильного использования записи при вычислении единицы первого слагаемого возведены Петей в ранг десятков:  оказались у него приравненными
оказались у него приравненными  т. е. 41. В этом его ошибка.
т. е. 41. В этом его ошибка.
6. Из курса арифметики известно, что от деления членов отношения на одно и то же число, отличное от нуля, величина отношения не изменяется. Вопреки этому, в анализируемом рассуждении величина отношения, в данном случае равная единице, умножалась на число, являющееся общим наибольшим делителем членов отношения.
В рассуждении создана иллюзия правдоподобия на основе ложной аналогии с распределительным свойством умножения относительно сложения..
Существенно заметить, что подобные ошибки становятся невозможными при использовании в качестве знака деления черты дроби. В самом деле:

и

7. Неправильность полученных ответов бросается в глаза (за исключением пятого, неправильность которого не столь очевидна). Все они получены в предположении, что между теми двумя величинами, о которых идет речь в задаче, имеется прямо или обратно пропорциональная зависимость; в действительности же зависимость между величинами, с которыми мы имеем дело в каждой из этих задач, более сложная.
Решая первую задачу, мы пришли к заключению, что за 4 часа самолет поднимется на 60 км. Это было бы верно, если бы высота набиралась пропорционально времени: во сколько раз больше продолжительность подъема, во столько раз больше и достигнутая высота. В действительности же такой пропорциональности нет: по мере того как увеличивается высота подъема, растет и время, нужное для подъема на каждый следующий метр, и всякий самолет имеет свой «потолок», т. е. такую высоту подъема, превзойти которую он уже не может.
Во второй задаче решение дано в предположении, что скорость моторной лодки пропорциональна числу
лошадиных сил (мощности) мотора. Оказалось, что сравнительно небольшой мотор, всего в 10 лошадиных сил, даст лодке скорость в  в час, т. е. скорость курьерского поезда. Этот расчет тоже неправилен, так как в действительности увеличение скорости моторной лодки, как и вообще всякого судна с механическим двигателем, происходит гораздо медленнее, чем увеличение мощности мотора. Опыты показывают, что мощность растет приблизительно пропорционально кубу скорости: чтобы увеличить скорость в а раз, надо увеличить мощность не в а раз, а в
в час, т. е. скорость курьерского поезда. Этот расчет тоже неправилен, так как в действительности увеличение скорости моторной лодки, как и вообще всякого судна с механическим двигателем, происходит гораздо медленнее, чем увеличение мощности мотора. Опыты показывают, что мощность растет приблизительно пропорционально кубу скорости: чтобы увеличить скорость в а раз, надо увеличить мощность не в а раз, а в  раз. Чтобы дать лодке скорость в
раз. Чтобы дать лодке скорость в  в час, т. е. увеличить скорость в 8 раз по сравнению с уже имеющейся и указанной в условии задачи
в час, т. е. увеличить скорость в 8 раз по сравнению с уже имеющейся и указанной в условии задачи  в час), мощность мотора надо увеличить в
в час), мощность мотора надо увеличить в  раз, т. е. мотор в 1,25 лошадиных силы надо заменить мотором в
раз, т. е. мотор в 1,25 лошадиных силы надо заменить мотором в  Замена же мотора в 1,25 силы мотором в 10 сил, т. е. в 8 раз более мощным, даст лишь удвоение скорости, так как
Замена же мотора в 1,25 силы мотором в 10 сил, т. е. в 8 раз более мощным, даст лишь удвоение скорости, так как  и моторная лодка будет делать вместо 8 всего
и моторная лодка будет делать вместо 8 всего  в час).
в час).
Решение третьей задачи гласит, что челопек, пробегающий  за 10,2 сек., пробежит за час больше
за 10,2 сек., пробежит за час больше  Как показывает опыт, силы человека при таком быстром беге очень быстро истощаются, и каждые следующие
Как показывает опыт, силы человека при таком быстром беге очень быстро истощаются, и каждые следующие  челочек будет бежать уже гораздо дольше, а затем и вовсе остановится. О пропорциональности между продолжительностью пробега, начатого с такой большой скоростью, и пройденным расстоянием не может быть и речи.
челочек будет бежать уже гораздо дольше, а затем и вовсе остановится. О пропорциональности между продолжительностью пробега, начатого с такой большой скоростью, и пройденным расстоянием не может быть и речи.
Четвертая задача решена в предположении, что человек бросает диск на расстояние, обратно пропорциональное весу диска. Полученный фантастический ответ (диск забрасывается на  почти полкилометра!) показывает неправильность этого предположения. Объясняется это тем, что лишь при очень небольших изменениях веса бросаемого диска пролетаемое им расстояние изменяется приблизительно обратно пропорционально весу (точнее: если бросать снаряд в безвоздушном пространстве под одним и тем же углом к горизонту и сообщать ему одно и то же количество энергии, то для увеличения пролетаемого им расстояния в 2, 3, 4, вообще в а раз, надо вес снаряда уменьшить в
почти полкилометра!) показывает неправильность этого предположения. Объясняется это тем, что лишь при очень небольших изменениях веса бросаемого диска пролетаемое им расстояние изменяется приблизительно обратно пропорционально весу (точнее: если бросать снаряд в безвоздушном пространстве под одним и тем же углом к горизонту и сообщать ему одно и то же количество энергии, то для увеличения пролетаемого им расстояния в 2, 3, 4, вообще в а раз, надо вес снаряда уменьшить в  раза,
раза,  раз,
раз,  раз, вообще
раз, вообще  раз). Когда диск бросают в воздухе, то при уменьшении веса диска и увеличении его скорости все большее и большее влияние на дальность его полета оказывает сопротивление воздуха. Кроме того, диску очень малого веса нельзя сообщить при бросании его рукой всего того количества энергии, какое можно сообщить
раз). Когда диск бросают в воздухе, то при уменьшении веса диска и увеличении его скорости все большее и большее влияние на дальность его полета оказывает сопротивление воздуха. Кроме того, диску очень малого веса нельзя сообщить при бросании его рукой всего того количества энергии, какое можно сообщить
Диску более тяжелому. В силу этих причин очень малые диски летят не дальше, а ближе более тяжелых, и расчет дальности полета, основанный на применении обратно пропорциональной зависимости, даег результаты совершенно неправильные.
При решении пятой задачи мы исходили из предположения, что количество ударов и время находятся в прямой пропорциональной зависимости. Однако эти две величины связаны между собой иной, причем более сложной зависимостью.
Это ясно из следующих соображений.
Так как любые из двух последовательных ударов отделены друг от друга одним промежутком, то, очевидно, шесть ударов, следующих один за другим, отделены друг от друга пятью промежутками. Итак, за 6 сек. происходит  ударов, отделенных друг от друга пятью промежутками, длительность каждого из которых составляет 1,2 сек.
ударов, отделенных друг от друга пятью промежутками, длительность каждого из которых составляет 1,2 сек.
Паше утверждение об отсутствии пропорциональности следует из того факта, что, считая двенадцать ударов, мы имеем не десять, а одиннадцать промежутков между ними.
Теперь не представляет труда дать ответ на вопрос задачи: за какое время часы сделают 12 ударов?
Очевидно, часы сделают 12 ударов за (12-г 0 секунд, где мы буквой  обозначили длительность в секундах промежутка времени между двумя последовательными ударами
обозначили длительность в секундах промежутка времени между двумя последовательными ударами  сек.).
сек.).
Из всего сказанного надо сделать вывод о необходимости соблюдения большой осторожности при решении задач посредством тройного правила: всякий раз, прежде чем применить это правило, надо убедиться, что рассматриваемые в задаче величины действительно находятся в пропорциональной зависимости. Можно привести сколько угодно примеров нелепых выводов, основанных на применении тройного правила в случаях, когда его применять нельзя. Мы с ними еще встретимся.
8. Здесь допущена ошибка при вычислении процента экономии топлива. При наличии всех трех усовершенствований расчет экономии топлива должен быть проведен следующим образом: 40% экономии топлива, получающиеся от введения первого изобретения, нужно взять от всего количества топлива, потребляемого машиной. 35% экономии от введения второго изобретения вычисляются от остатка после вычета экономии от первого усовершенствования. 25% экономии топлива, получающиеся от введения третьего усовершенствования, вычисляются от второго остатка. Расчет
будет верен и в том случае, если мы проведем вычисление в другом порядке, т. е. начнем со второго или третьего усовершенствования. Возьмем конкретный пример. Допустим, что машина потребляет  топлива; тогда расчет должен быть проведен следующим образом:
топлива; тогда расчет должен быть проведен следующим образом:

Следовательно, при наличии трех усовершенствований в  нужно будет заложить вместо
нужно будет заложить вместо  только
только 
Результат может быть выражен так:

Это выражение показывает, что общий процент экономии не зависит от того, в каком порядке мы вводим отдельные усовершенствования.
В ошибочном решении этой задачи мы сталкиваемся с использованием ложной аналогии.
Привыкая принимать при решении очень многих задач данное первоначальное количество за 100% (например, в рассматриваемой задаче: «если принять количество топлива, употребляемого машиной, за  ученики довольно часто склонны полагать, что проценты следует всегда вычислять от указанного в задаче первоначального количества («основного, стопроцентного числа»), и считают возможным пренебрегать необходимостью учитывать изменение этого количества (новое, другое «основное, стопроцентное число») в результате определенных действий (в данном случае в результате последовательного введения усовершенствований, дающих экономию топлива).
ученики довольно часто склонны полагать, что проценты следует всегда вычислять от указанного в задаче первоначального количества («основного, стопроцентного числа»), и считают возможным пренебрегать необходимостью учитывать изменение этого количества (новое, другое «основное, стопроцентное число») в результате определенных действий (в данном случае в результате последовательного введения усовершенствований, дающих экономию топлива).
9. Необходимо твердо помнить, что при вычислении среднего процента х по нескольким группам (или, как говорят статистики, по нескольким частным совокупностям) простое среднее арифметическое из чисел  выражающих соответствующий процент по каждой группе отдельно, дает правильный ответ лишь в том случае, когда все эти группы одинаковой численности (имеют одинаковый вес). Если же среди этих групп не все одинаковой численности, средний процент х необходимо вычислять по формуле взвешенного среднего, а именно:
выражающих соответствующий процент по каждой группе отдельно, дает правильный ответ лишь в том случае, когда все эти группы одинаковой численности (имеют одинаковый вес). Если же среди этих групп не все одинаковой численности, средний процент х необходимо вычислять по формуле взвешенного среднего, а именно:

где  - числа, выражающие численность (вес)
- числа, выражающие численность (вес)
каждой группы. В случае  Эта формула приводится к формуле простого, т. е. не взвешенного среднего арифметического
Эта формула приводится к формуле простого, т. е. не взвешенного среднего арифметического 
10. Для осознания ошибки начнем с противопоставления правильного рассуждения ложному.
Пусть имеем ежегодный прирост в 40% по сравнению с предшествующим годом. К началу первого года производительность была 100%  к концу его она стала уже
к концу его она стала уже  Новый
Новый  -процентный прирост за второй год надо вычислить не от первоначальной производительности в 100%, а от той, какая была к началу второго года, т. е. от
-процентный прирост за второй год надо вычислить не от первоначальной производительности в 100%, а от той, какая была к началу второго года, т. е. от  Следовательно, прирост за второй год равен 40% от 140%, т. е. 56%, и к концу второго года производительность составит 140%
Следовательно, прирост за второй год равен 40% от 140%, т. е. 56%, и к концу второго года производительность составит 140%  Прибавив сюда 40% от 196%, найдем, что к концу третьего года мы будем иметь уже
Прибавив сюда 40% от 196%, найдем, что к концу третьего года мы будем иметь уже  К концу четвертого года будем иметь 274,4% плюс 40% от 274,4%, или
К концу четвертого года будем иметь 274,4% плюс 40% от 274,4%, или  а к концу пятого года уже 384,16% плюс 40% от 384,16%, или
а к концу пятого года уже 384,16% плюс 40% от 384,16%, или 
Таким образом, ежегодный прирост производительности в 40% даст не утроение, а более чем пятикратное увеличение производительности за пятилетку.
Чтобы иметь за пятилетку утроение, мы должны взять за год не 40% прироста, а меньше. Взяв 20%, убедимся, что к концу первого, второго и так далее лет пятилетки мы будем иметь 120%, 144%, 172,8%, 207,36%, 248,83%, и утроения за пятилетку не получим. При 25% ежегодного прироста утроение за пятилетку уже обеспечено — к концу пятилетки получим 305,18% производительности. Ежегодный прирост в 30% даст к концу пятилетки 371,2996.
Ошибка первого рассуждения, которое привело к заключению, что 30% ежегодного прироста утроения за пятилетку не дадут, состояла в том, что там не были учтены проценты на проценты: 30% прироста за год надо считать не от производительности к началу пятилетки, принятой нами за  а от производительности к началу каждого года. Другими словами, здесь мы имеем дело не с простыми, а со сложными процентами. Более точный расчет, основанный на применении формулы сложных процентов:
а от производительности к началу каждого года. Другими словами, здесь мы имеем дело не с простыми, а со сложными процентами. Более точный расчет, основанный на применении формулы сложных процентов:

(для решения нашей задачи надо взять  и провести вычисление
и провести вычисление  посредством логарифмов), приводит к
посредством логарифмов), приводит к
заключению, что ежегодный прирост в  уже обеспечивает утроение за пятилетку
уже обеспечивает утроение за пятилетку  а ежегодный прирост в
а ежегодный прирост в  его не обеспечивает
его не обеспечивает 
11. Рассмотрим задачу: если человек проходит по  в час, то сколько он пройдет за
в час, то сколько он пройдет за  часа? Решим эту задачу, не пользуясь никаким правилом умножения дробей, ни старым, ни новым.
часа? Решим эту задачу, не пользуясь никаким правилом умножения дробей, ни старым, ни новым.
За час человек пройдет  км или
км или  за 2 часа
за 2 часа  за четверть часа
за четверть часа  См), а всего за
См), а всего за  часа
часа  или
или  или
или 
Казалось бы, задачу эту можно решить одним действием — умножением  на
на  . Действительно, при любом целом числе часов пройденный путь равен пути, пройденному в 1 час, повторенному столько раз, сколько часов продолжалось движение, т. е. равен произведению
. Действительно, при любом целом числе часов пройденный путь равен пути, пройденному в 1 час, повторенному столько раз, сколько часов продолжалось движение, т. е. равен произведению  на число часов. Естественно ожидать, что и при дробном числе часов результат должен получаться посредством того же действия умножения. Но если принять новое правило умножения, то произведение на
на число часов. Естественно ожидать, что и при дробном числе часов результат должен получаться посредством того же действия умножения. Но если принять новое правило умножения, то произведение на  как мы видели выше, оказывается равным
как мы видели выше, оказывается равным  как должно быть. Обычное же правило умножения в настоящем случае дает:
как должно быть. Обычное же правило умножения в настоящем случае дает:

т. е. именно тот результат, который мы получили выше, обходясь без дробей (посредством раздробления километров в метры).
Итак, «новое правило» умножения смешанных чисел приходится забраковать. Но интересно выяснить, почему сложение (и вычитание) смешанных чисел можно выполнять, складывая (и вычитая) отдельно целые и отдельно дроби, а умножение выполнять таким образом (т. е. умножая целое на целое, а дробь на дробь) нельзя.
Чтобы к сумме двух чисел прибавить третье число, нужно это третье число прибавить к одному из слагаемых, оставляя другое неизменным. Например, чтобы к  прибавить
прибавить
2, мы должны взять либо  либо
либо  В обоих случаях получается правильный результат (15). Мы имеем здесь формулу:
В обоих случаях получается правильный результат (15). Мы имеем здесь формулу:

выражающую так называемое «сочетательное» свойство суммы. Используя «переместителыюе свойство» суммы  мы получим
мы получим  и придем к другому выражению «сочетательного свойства» суммы:
и придем к другому выражению «сочетательного свойства» суммы:

Чтобы произведение двух чисел умножить на третье число, надо умножить на это третье число один из сомножителей, оставляя второй неизменным. Например, чтобы умножить 3-4 на 5, надо взять либо  либо
либо  В обоих случаях получается правильный результат (60). Здесь имеем формулу:
В обоих случаях получается правильный результат (60). Здесь имеем формулу:

выражающую «сочетательное» свойство произведения.
Мы рассмотрели случаи, когда дважды выполняется одно и то же действие: два раза сложение или два раза умножение. Теперь возьмем случай, когда выполняется сначала сложение, затем умножение. Чтобы сумму двух чисел умножить на третье число, оказывается, нельзя ограничиться умножением одного лишь из данных чисел: надо умножить каждое слагаемое. Например, чтобы умножить на 5 сумму  нельзя взять
нельзя взять  или
или  необходимо взять
необходимо взять  Таким образом здесь нельзя ограничиться простым сочетанием третьего числа с одним из двух первых. Здесь второе действие (умножение) как бы распределяется между двумя числами, над которыми производится первое действие (сложение). Говорят, что произведение суммы обладает распределительным свойством, которое выражается формулой:
Таким образом здесь нельзя ограничиться простым сочетанием третьего числа с одним из двух первых. Здесь второе действие (умножение) как бы распределяется между двумя числами, над которыми производится первое действие (сложение). Говорят, что произведение суммы обладает распределительным свойством, которое выражается формулой:

Итак, прибавляя к сумме двух чисел третье число, мы должны применять сочетательное свойство, а умножая сумму двух чисел на третье число, должны применять распределительное свойство.
Теперь вернемся к действиям над дробями. Всякое смешанное число можно рассматривать как сумму двух чисел,
целого и правильной дроби, например,  Складывая два смешанных числа, например,
Складывая два смешанных числа, например,  и
и  , мы можем прибавить к
, мы можем прибавить к  сначала 2, потом Чтобы прибавить к
сначала 2, потом Чтобы прибавить к  число 2, мы увеличим на 2 первое слагаемое (6), а второе оставим без изменения. Получим
число 2, мы увеличим на 2 первое слагаемое (6), а второе оставим без изменения. Получим 
К эгой сумме двух слагаемых  и остается прибавить еще Пользуясь еще раз сочетательным свойством, оставим первое слагаемое
и остается прибавить еще Пользуясь еще раз сочетательным свойством, оставим первое слагаемое  без изменения, а второе увеличим на Окончательно имеем:
без изменения, а второе увеличим на Окончательно имеем:

Рассмотрим умножение смешанных чисел  Чтобы умножить
Чтобы умножить  на
на  мы должны, используя распределительное свойство, умиожить на 2- как первое слагаемое (6), так и второе слагаемое а затем произведения сложить:
мы должны, используя распределительное свойство, умиожить на 2- как первое слагаемое (6), так и второе слагаемое а затем произведения сложить:

Но для получения произведения  или
или  или
или  опять используем распределительное свойство:
опять используем распределительное свойство:

Точно так же поступаем и для получения произведения —  а именно:
а именно:

В конце концов оказывается, что наше произведение двух смешанных чисел равно сумме четырех частных произведений, а именно:

Теперь ясно, что, умножая целое на целое и дробь на дробь, мы получаем не все произведение, а лишь часть его: теряются второе и третье частные произведения  т. е. произведение целой части первого сомножителя на дробную часть второго и целой части второго на дробную часть первого.
т. е. произведение целой части первого сомножителя на дробную часть второго и целой части второго на дробную часть первого.

Черт. 12
Применяя умножение для вычисления площади прямоугольника но основанию и высоте, мы можем очень наглядно представить все четыре частных произведения, входящие в произведение двух смешанных чисел. Взяв, например, прямоугольник со сторонами  и
и  , видим (черт. 12), что его площадь состоит из 4 частей: большого прямоугольника со сторонами 6 и 2, узкой длинной полоски — прямоугольника со сторонами 6 и -1, более широкой полоски справа — прямоугольника со сторонами у и 2, маленького прямоугольника со сторонами
, видим (черт. 12), что его площадь состоит из 4 частей: большого прямоугольника со сторонами 6 и 2, узкой длинной полоски — прямоугольника со сторонами 6 и -1, более широкой полоски справа — прямоугольника со сторонами у и 2, маленького прямоугольника со сторонами  и 1. Площадь большого прямоугольника содержит 12 квадратов
и 1. Площадь большого прямоугольника содержит 12 квадратов  единиц), площадь узкой длинной полоски — 6 четвертей квадрата, или
единиц), площадь узкой длинной полоски — 6 четвертей квадрата, или  у квадрата, площадь полоски справа — две половины, или 1 целый квадрат, а площадь маленького прямоугольника есть половина одной четверти, или одна восьмая квадрата. Всего имеем
у квадрата, площадь полоски справа — две половины, или 1 целый квадрат, а площадь маленького прямоугольника есть половина одной четверти, или одна восьмая квадрата. Всего имеем  квадрата, как и должно быть.
квадрата, как и должно быть.
Если обозначить целые и дробные части обоих сомножителей буквами, то мы получим не что иное, как известное из курса алгебры правило умножения двучленов:

наглядно изображенное на чертеже 13.
12. Из второй корзины (15 груш на  продавец мог брать по 15 штук всего 10 раз. Добавляя к каждым 15 грушам по 10 штук из первой корзины (10 груш на
продавец мог брать по 15 штук всего 10 раз. Добавляя к каждым 15 грушам по 10 штук из первой корзины (10 груш на  он вынет из нее только 100 груш.
он вынет из нее только 100 груш.
Составленные таким образом десять совокупностей по 25 груш он продаст за  После этого останется 50 груш только из первой корзины; из них каждый десяток груш он должен был продавать по рублю и получить за все 50 груш
После этого останется 50 груш только из первой корзины; из них каждый десяток груш он должен был продавать по рублю и получить за все 50 груш  на самом же деле он эти 50 груш продал за
на самом же деле он эти 50 груш продал за  (по
(по  за 25 штук) и, таким сбразом, потерпел
за 25 штук) и, таким сбразом, потерпел  убытка.
убытка.
Разъясняя этот софизм, надо напомнить ученикам и правильный оасчет стоимости 25 гпуш в случае продажи смеси.

Черт. 13
Так как стоимость 150 груш, находящихся в первой корзине, составляет  а стоимость 150 груш, находящихся во второй корзине, составляет
а стоимость 150 груш, находящихся во второй корзине, составляет  то стоимость каждой груши смеси составит
то стоимость каждой груши смеси составит  Следовательно, стоимость 25 груш составит
Следовательно, стоимость 25 груш составит  же совокупностей по 25 груш из множества груш двух корзин можно выделить
же совокупностей по 25 груш из множества груш двух корзин можно выделить  При их продаже будет выручено
При их продаже будет выручено  т. е. столько же, что и при раздельной продаже по различным ценам.
т. е. столько же, что и при раздельной продаже по различным ценам.
В анализируемом рассуждении мы столкнулись с отклонением от тезиса: под видом изменения способа решения одна задача заменена другой, не равносильной первой.
Задача, эквивалентная первоначальной, формулируется так: «Каждые 25 груш, составленные из 10 груш первой корзины и 15 груш второй, продаются по  остаток груш первой корзины продается по ранее установленной для них цене».
остаток груш первой корзины продается по ранее установленной для них цене».
В ошибочном же рассуждении исходная задача подменена следующей, ей не эквивалентной: «150 груш одного сорта, стоящие  и 150 груш другого сорта, стоящие
и 150 груш другого сорта, стоящие 
решили смешать и продавать по  за 25 штук. Какая сумма будет выручена при реализации груш по указанной цене (сопоставить с первоначально установленной стоимостью этого товара)?»
за 25 штук. Какая сумма будет выручена при реализации груш по указанной цене (сопоставить с первоначально установленной стоимостью этого товара)?»
13. В этом рассуждении допущена та же самая ошибка, что и в рассуждении 
Оно предназначено для самостоятельного опровержения учащимися, которое становится им доступным на основе предварительного анализа подобного же рассуждения под руководством учителя.
14. В завещании умершего родителя допущена оплошность. В самом деле, сумма долей  составляет
составляет  а не единицу. Точное выполнение завещания предполагает передачу старшему сыну у голов табуна, среднему и младшему
а не единицу. Точное выполнение завещания предполагает передачу старшему сыну у голов табуна, среднему и младшему  Это в сумме составит
Это в сумме составит  а от одной лошади остаются вне требований раздела.
а от одной лошади остаются вне требований раздела.
Старик сосед своими действиями подсказал такую подмену тезиса завещания, благодаря которой бралось не от 7, а от 8 единиц. Однако такое решение вопроса неточностью реализует завещание, так как старший сын получил больше на  лошади среднии на
лошади среднии на  а младшии на
а младшии на  Эти прибавки в своей сумме исчерпывают оставшиеся вне раздела
Эти прибавки в своей сумме исчерпывают оставшиеся вне раздела  от одной лошади.
от одной лошади.
15. В рассуждении допущено уклонение от тезиса: вопрос о числе, составляющем произведение двух единиц на три, подмеиеп вопросом о числе обломков спички, полученных в результате определенного процесса, привлеченного для ложной иллюстрации анализируемого рассуждения.
Мы называем иллюстрацию ложной потому, что в ней в качестве множимого сначала выступают две половины от целой спички, а затем две четверти от той же спички.
| << Предыдущий параграф | Следующий параграф >> |
- ИЗ ПРЕДИСЛОВИЯ К ПЕРВОМУ ИЗДАНИЮ
- Глава I. ОБ УПРАЖНЕНИЯХ НА ОПРОВЕРЖЕНИЕ ОШИБОЧНЫХ МАТЕМАТИЧЕСКИХ РАССУЖДЕНИЙ И ИХ КЛАССИФИКАЦИИ
- 1. МАТЕМАТИЧЕСКИЕ СОФИЗМЫ И ИХ ПЕДАГОГИЧЕСКАЯ РОЛЬ.
- II. КЛАССИФИКАЦИЯ УПРАЖНЕНИЙ НА ОПРОВЕРЖЕНИЕ ЛОЖНЫХ МАТЕМАТИЧЕСКИХ РАССУЖДЕНИЙ.
- 2. Распространение на исключительные случаи.
- 3. Приписывание свойств определенного вида всему роду.
- 4. Неправильное применение принципа непосредственных умозаключений путем обращения.
- 5. Подмена точных определений геометрической интуицией.
- 6. Ошибки построения.
- 7. Ошибки, являющиеся следствием буквального толкования сокращенной (условной) формулировки некоторых геометрических утверждений.
- 8. Нарушение смысла условных записей.
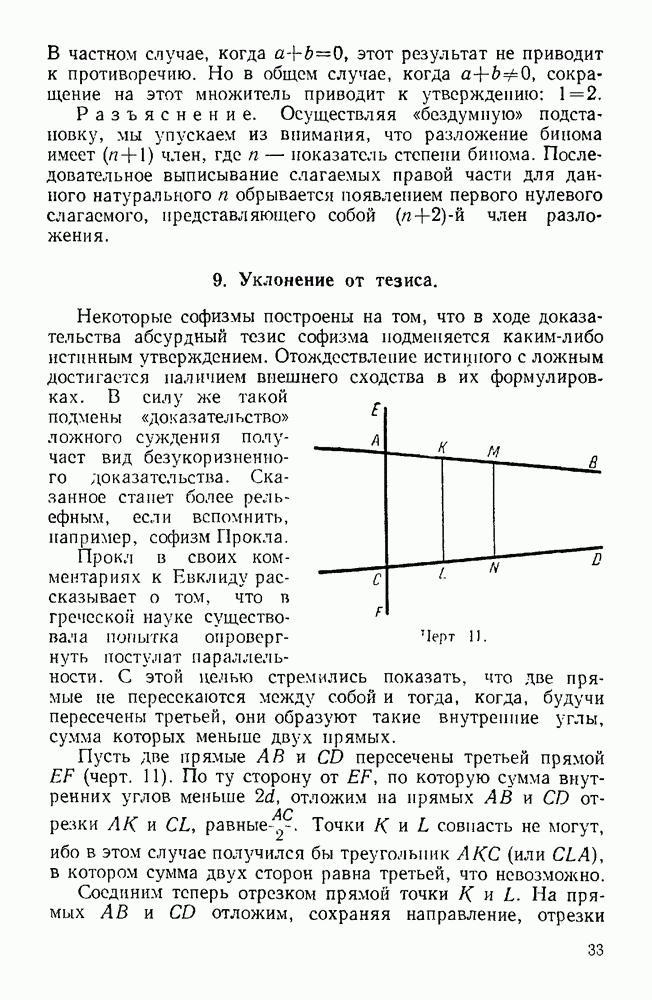
- 9. Уклонение от тезиса.
- Глава II. АРИФМЕТИКА.
- I. ПРИМЕРЫ ЛОЖНЫХ РАССУЖДЕНИЙ.
- 2. На двух нормальных руках одиннадцать пальцев.
- 3. Квадратные рубли.
- 4. 45 — 45 = 45
- 5. 40 : 8 = 41
- 6. Дважды два — пять!
- 7. Есть ли здесь пропорциональность?
- 8. 100% экономии.
- 9. Как вычислять средний процент?
- 10. Что даст ежегодный прирост в 40% за пять лет?
- 11. Новое правило умножения дробей.
- 12. Куда делся рубль?
- 13. Откуда появился лишний гривенник?
- 14. Завещание отца.
- 15. 2-3=4.
- II. АНАЛИЗ ПРИМЕРОВ.
- Глава III. АЛГЕБРА.
- I. ПРИМЕРЫ ЛОЖНЫХ РАССУЖДЕНИЙ.
- 19. Делимость многочленов и делимость чисел.
- 20. Произвольно взятое число а равно нулю.
- 21. 7 = 13.
- 22. Положительная единица равна отрицательной единице.
- 23. Другое «доказательство» равенства положительной и отрицательной единиц.
- 24. Мнимая единица и действительная отрицательная единица равны.
- 25. i^2 = 1
- 26. Всякое отрицательное число больше положительного, имеющего то же абсолютное значение.
- 27. Если a > b, то a > 2b
- 28. Если а и b положительные числа, то a > b и b > a.
- 29. Положительное число меньше нуля.
- 30. Сумма натуральных чисел, каждое из которых превосходит единицу, больше их произведения.
- 31. Чему равен квадратный корень из числа a^2?
- 32. Еще одно «доказательство» равенства нулю произвольно взятого числа.
- 33. Число не изменяется, если в нем переставить любые цифры!
- 34. Что говорит теорема о существовании корня в алгебре комплексных чисел?
- 35. Об одном спэсобе получать правильные результаты, применение которого требует большой осторожности.
- 36. О сумме 1-1+1-1 + …
- 37. Всегда ли целое больше своей части?
- 38. Еще одно «доказательство» равенства двух произвольно взятых чисел.
- 39. Сумма двух произвольных одинаковых чисел равна нулю.
- 40. Число не изменится, если к нему прибавить 1.
- 41. Ахиллес и черепаха.
- 42. О некоторых ученических ошибках.
- II. АНАЛИЗ ПРИМЕРОВ.
- Глава IV. ГЕОМЕТРИЯ.
- 1. ПРИМЕРЫ ЛОЖНЫХ РАССУЖДЕНИЙ.
- 44. Отрезок прямой равен своей правильной части.
- 45. Все треугольники равновелики.
- 46. Сумма оснований любой трапеции равна нулю.
- 47. Объемлемая и объемлющая.
- 48. Еще о пропорциональности.
- 49. Две окружности разного радиуса имеют одну и ту же длину.
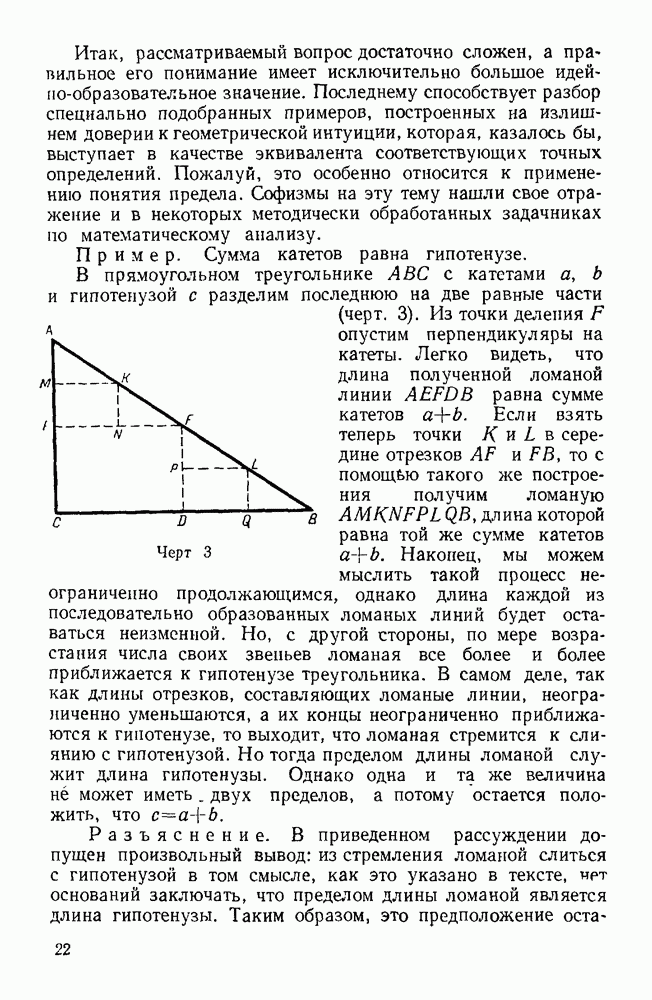
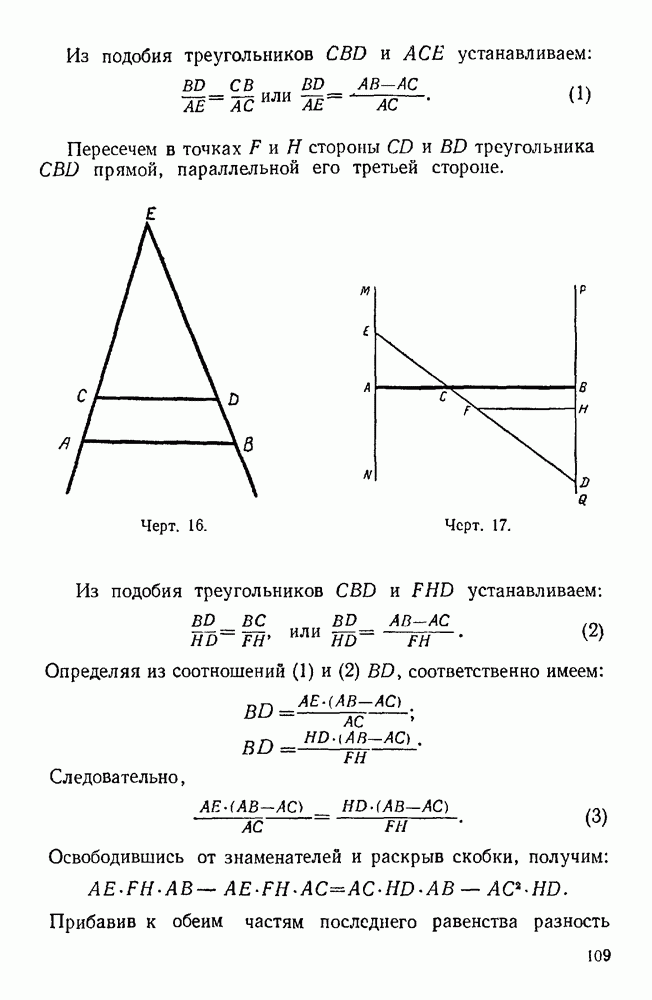
- 50. Сумма катетов равна гипотенузе.
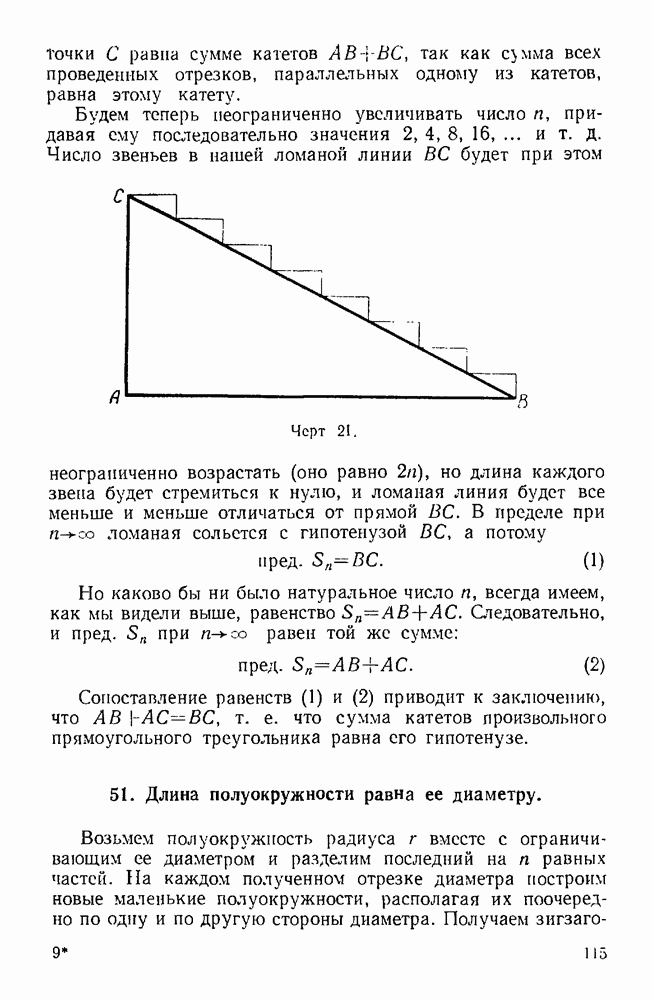
- 51. Длина полуокружности равна ее диаметру.
- 52. Боковая поверхность круглого прямого конуса с радиусом основания r и высотой h выражается формулой P=pi*r(r+h).
- 53. В данной точке на прямой можно восставить два перпендикуляра к этой прямой.
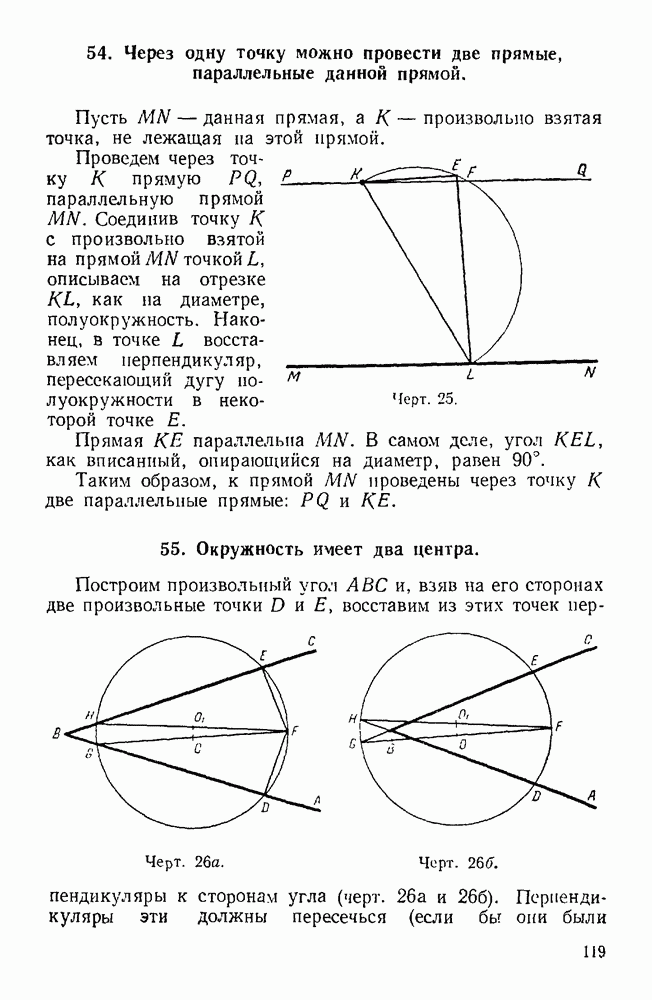
- 54. Через одну точку можно провести две прямые, параллельные данной прямой.
- 55. Окружность имеет два центра.
- 56. Из точки на прямую можно опустить два перпендикуляра.
- 57. Через две данные точки можно провести две прямые.
- 58. Любой треугольник — равнобедренный.
- 59. Катет прямоугольного треугольника равен его гипотенузе.
- 60. Прямой угол равен тупому (планиметрический вариант).
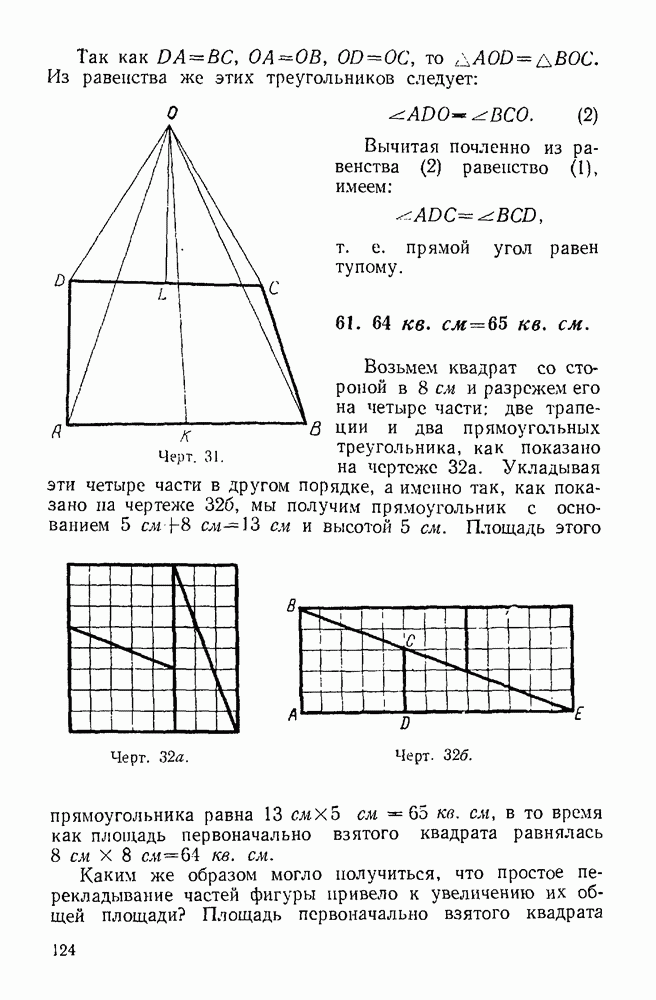
- 61. 64 кв. см = 65 кв. см.
- 62. Задача о заплате.
- II. АНАЛИЗ ПРИМЕРОВ.
- III. РАССКАЗЫ-ОБЪЯСНЕНИЯ ПО ПОВОДУ ОШИБОЧНЫХ РАССУЖДЕНИЙ.
- 64. Трисекция угла.
- 65. Еще о трисекции угла.
- 66. Квадратура круга.
- 67. Об одном доказательстве теоремы о сумме внутренних углов треугольника.
- 68. Как вычислять объем усеченной пирамиды?
- Глава V. ТРИГОНОМЕТРИЯ.
- 70. Синус угла уменьшается, если к углу прибавить 360°.
- 71. Косинус любого острого угла больше единицы.
- 72. 1/4 > 1/2
- 73. 2^2 = 4^2
- 74. Площадь прямоугольника равна нулю.
- 75. Существуют равные треугольники, у которых не все стороны равны.
- 76. Каждый треугольник — прямоугольный.
- II. АНАЛИЗ ПРИМЕРОВ
- Глава VI. ПРИБЛИЖЕННЫЕ ВЫЧИСЛЕНИЯ. РАССКАЗЫ-ОБЪЯСНЕНИЯ ПО ПОВОДУ ОШИБОЧНЫХ РАССУЖДЕНИЙ
- 78. Все большие числа приближенно равны между собой.
- 79. О точности произведения приближенных чисел.
- 80. Верна ли формула …
- 81. Сколько цифр надо знать в подкоренном числе, чтобы получить корень с заданной точностью?
- 82. Зачем освобождаются от иррациональности в знаменателе?