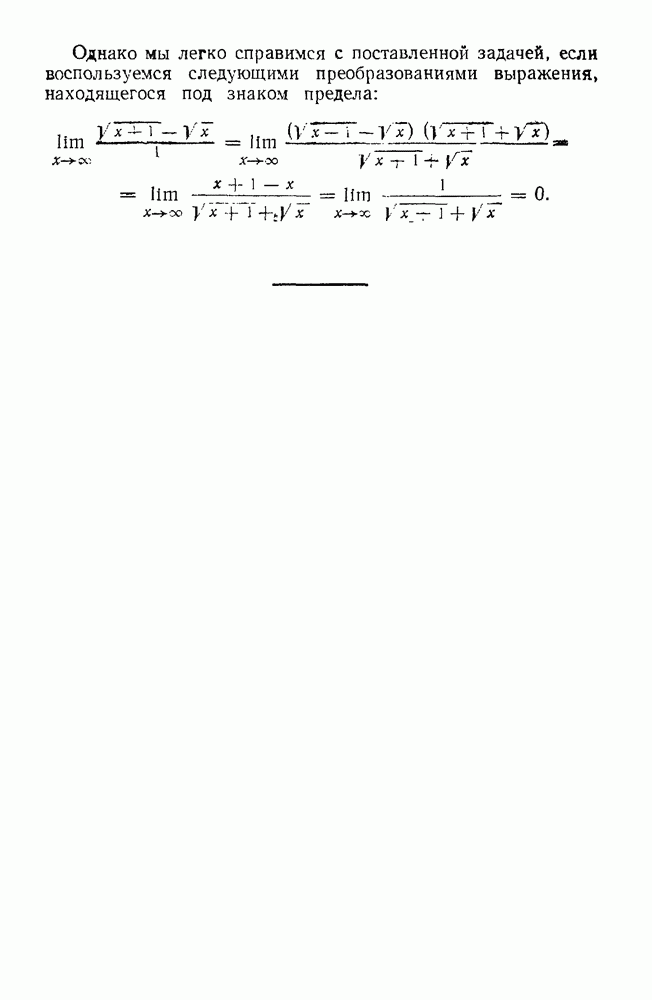| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
Глава IV. ГЕОМЕТРИЯ.
1. ПРИМЕРЫ ЛОЖНЫХ РАССУЖДЕНИЙ.
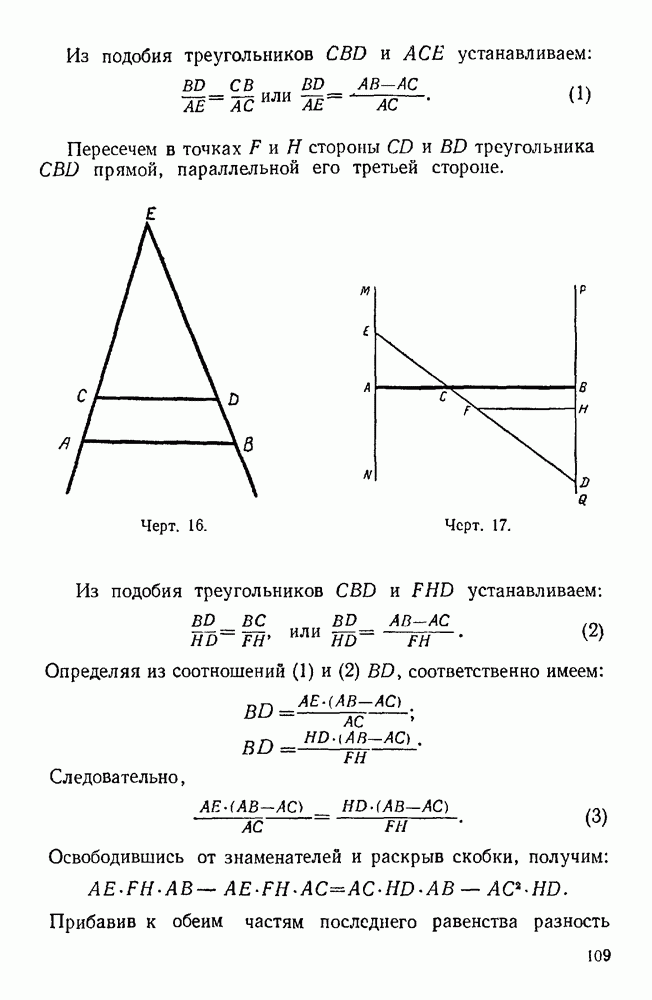
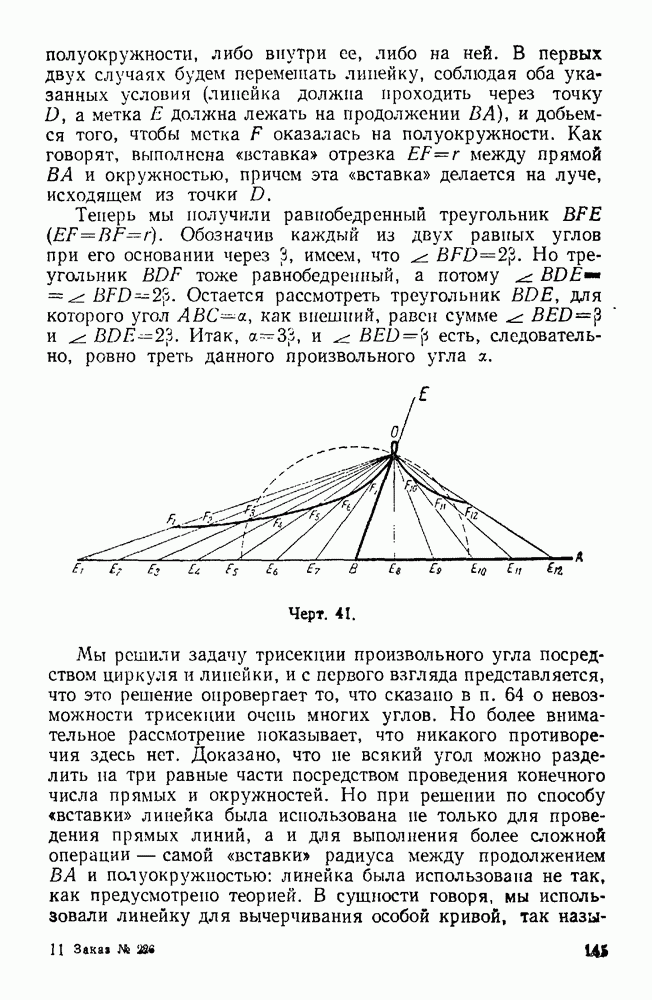
43. Отрезки параллельных прямых, заключенные между сторонами угла, равны.
Возьмем произвольный угол и пересечем его стороны двумя произвольными параллельными прямыми. Пусть  и
и  будут отрезки параллельных, заключенные между сторонами этого угла, а точка Е — его вершина (черт. 16).
будут отрезки параллельных, заключенные между сторонами этого угла, а точка Е — его вершина (черт. 16).
Как известно, параллельные прямые отсекают от сторон угла пропорциональные отрезки; следовательно,

и

Умножив обе части равенства (1) на разность  производим следующие преобразования:
производим следующие преобразования:

Разделив обе части последнего равенства на разность  получим равенство
получим равенство  таким образом отрезки параллельных, заключенные между сторонами данного угла, всегда равны.
таким образом отрезки параллельных, заключенные между сторонами данного угла, всегда равны.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ИЗ ПРЕДИСЛОВИЯ К ПЕРВОМУ ИЗДАНИЮ
- Глава I. ОБ УПРАЖНЕНИЯХ НА ОПРОВЕРЖЕНИЕ ОШИБОЧНЫХ МАТЕМАТИЧЕСКИХ РАССУЖДЕНИЙ И ИХ КЛАССИФИКАЦИИ
- 1. МАТЕМАТИЧЕСКИЕ СОФИЗМЫ И ИХ ПЕДАГОГИЧЕСКАЯ РОЛЬ.
- II. КЛАССИФИКАЦИЯ УПРАЖНЕНИЙ НА ОПРОВЕРЖЕНИЕ ЛОЖНЫХ МАТЕМАТИЧЕСКИХ РАССУЖДЕНИЙ.
- 2. Распространение на исключительные случаи.
- 3. Приписывание свойств определенного вида всему роду.
- 4. Неправильное применение принципа непосредственных умозаключений путем обращения.
- 5. Подмена точных определений геометрической интуицией.
- 6. Ошибки построения.
- 7. Ошибки, являющиеся следствием буквального толкования сокращенной (условной) формулировки некоторых геометрических утверждений.
- 8. Нарушение смысла условных записей.
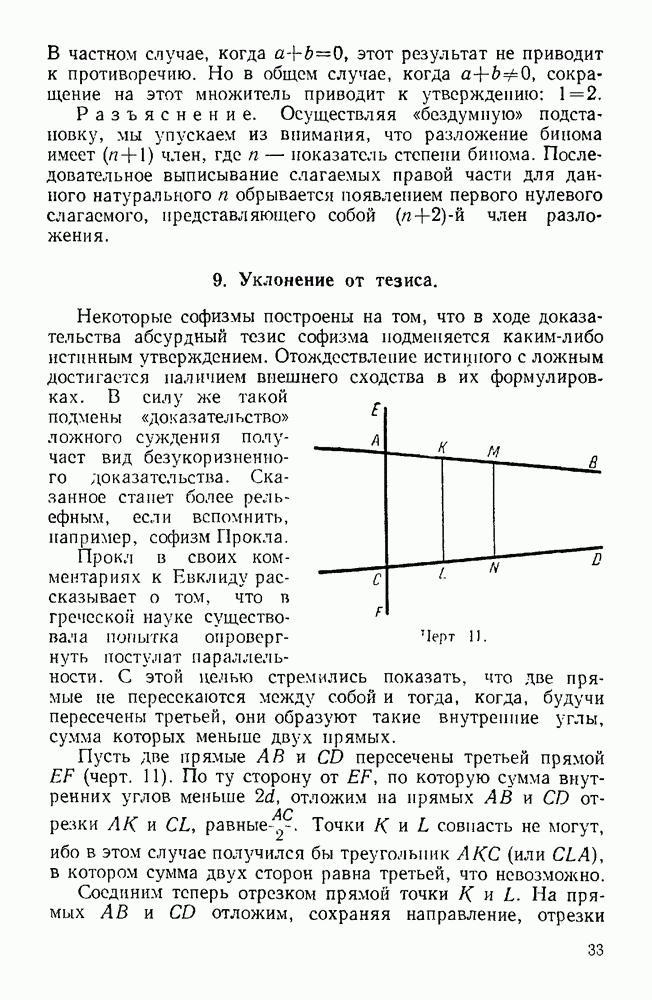
- 9. Уклонение от тезиса.
- Глава II. АРИФМЕТИКА.
- I. ПРИМЕРЫ ЛОЖНЫХ РАССУЖДЕНИЙ.
- 2. На двух нормальных руках одиннадцать пальцев.
- 3. Квадратные рубли.
- 4. 45 — 45 = 45
- 5. 40 : 8 = 41
- 6. Дважды два — пять!
- 7. Есть ли здесь пропорциональность?
- 8. 100% экономии.
- 9. Как вычислять средний процент?
- 10. Что даст ежегодный прирост в 40% за пять лет?
- 11. Новое правило умножения дробей.
- 12. Куда делся рубль?
- 13. Откуда появился лишний гривенник?
- 14. Завещание отца.
- 15. 2-3=4.
- II. АНАЛИЗ ПРИМЕРОВ.
- Глава III. АЛГЕБРА.
- I. ПРИМЕРЫ ЛОЖНЫХ РАССУЖДЕНИЙ.
- 19. Делимость многочленов и делимость чисел.
- 20. Произвольно взятое число а равно нулю.
- 21. 7 = 13.
- 22. Положительная единица равна отрицательной единице.
- 23. Другое «доказательство» равенства положительной и отрицательной единиц.
- 24. Мнимая единица и действительная отрицательная единица равны.
- 25. i^2 = 1
- 26. Всякое отрицательное число больше положительного, имеющего то же абсолютное значение.
- 27. Если a > b, то a > 2b
- 28. Если а и b положительные числа, то a > b и b > a.
- 29. Положительное число меньше нуля.
- 30. Сумма натуральных чисел, каждое из которых превосходит единицу, больше их произведения.
- 31. Чему равен квадратный корень из числа a^2?
- 32. Еще одно «доказательство» равенства нулю произвольно взятого числа.
- 33. Число не изменяется, если в нем переставить любые цифры!
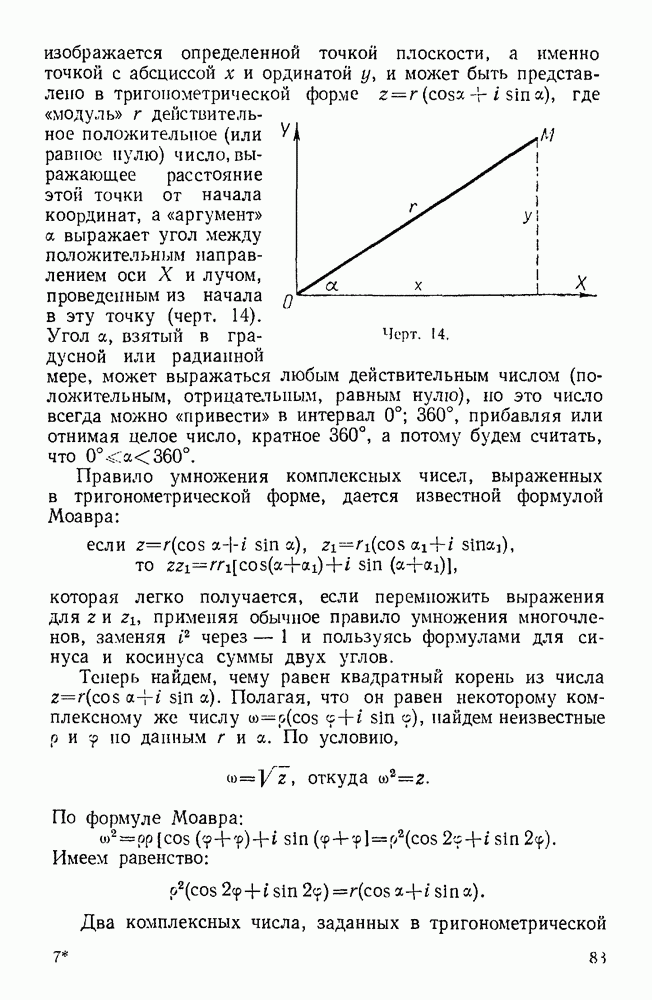
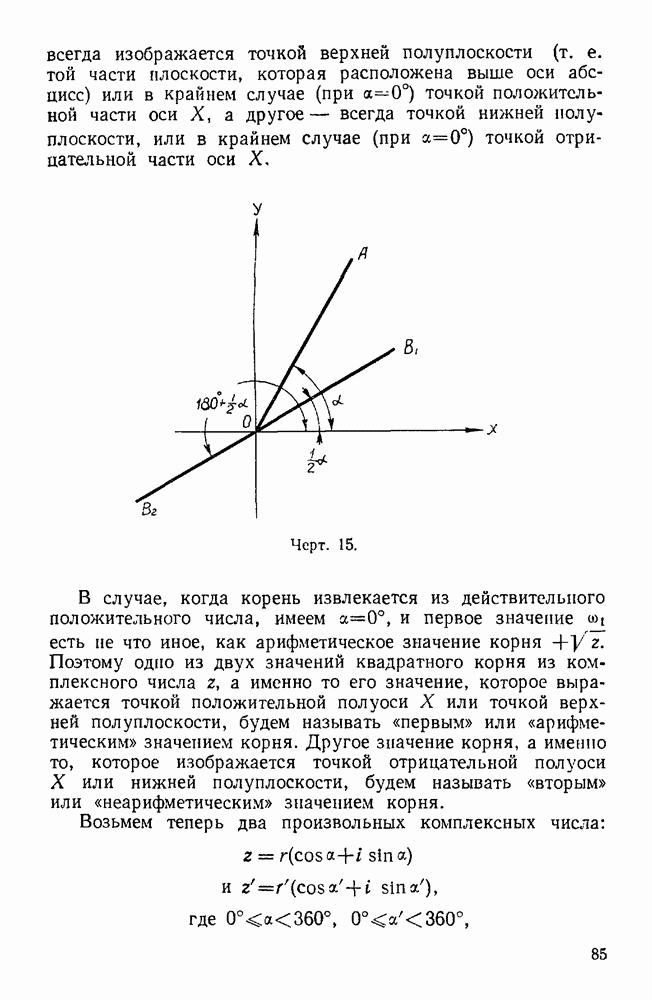
- 34. Что говорит теорема о существовании корня в алгебре комплексных чисел?
- 35. Об одном спэсобе получать правильные результаты, применение которого требует большой осторожности.
- 36. О сумме 1-1+1-1 + …
- 37. Всегда ли целое больше своей части?
- 38. Еще одно «доказательство» равенства двух произвольно взятых чисел.
- 39. Сумма двух произвольных одинаковых чисел равна нулю.
- 40. Число не изменится, если к нему прибавить 1.
- 41. Ахиллес и черепаха.
- 42. О некоторых ученических ошибках.
- II. АНАЛИЗ ПРИМЕРОВ.
- Глава IV. ГЕОМЕТРИЯ.
- 1. ПРИМЕРЫ ЛОЖНЫХ РАССУЖДЕНИЙ.
- 44. Отрезок прямой равен своей правильной части.
- 45. Все треугольники равновелики.
- 46. Сумма оснований любой трапеции равна нулю.
- 47. Объемлемая и объемлющая.
- 48. Еще о пропорциональности.
- 49. Две окружности разного радиуса имеют одну и ту же длину.
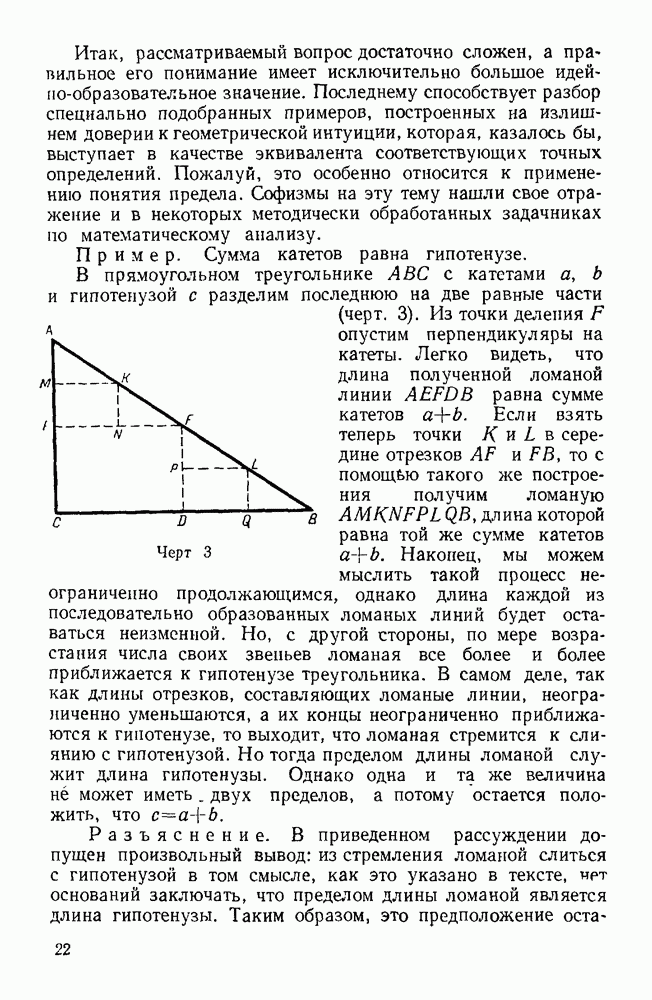
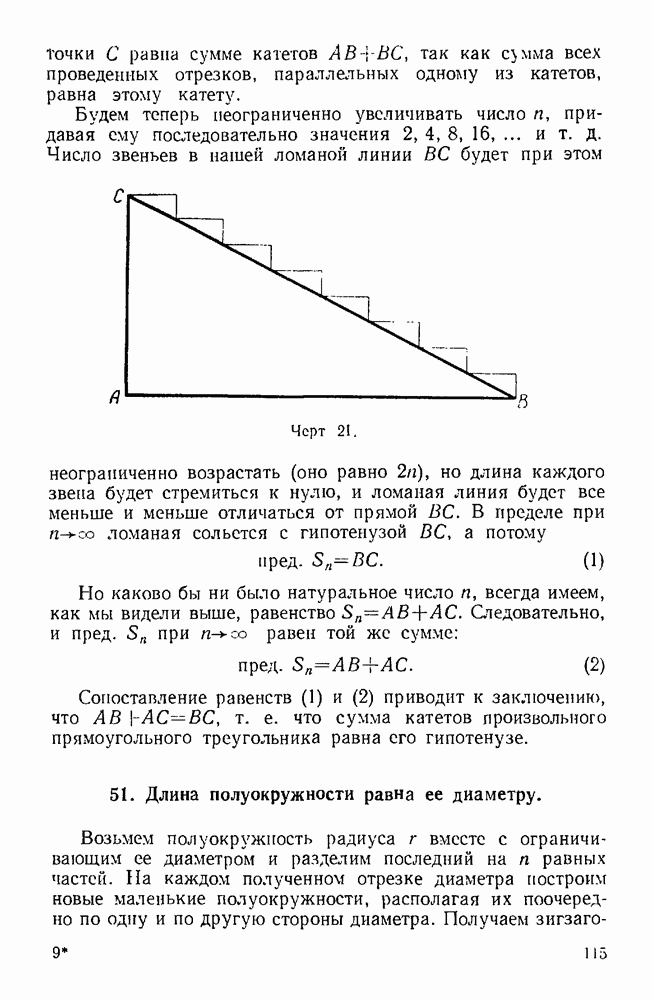
- 50. Сумма катетов равна гипотенузе.
- 51. Длина полуокружности равна ее диаметру.
- 52. Боковая поверхность круглого прямого конуса с радиусом основания r и высотой h выражается формулой P=pi*r(r+h).
- 53. В данной точке на прямой можно восставить два перпендикуляра к этой прямой.
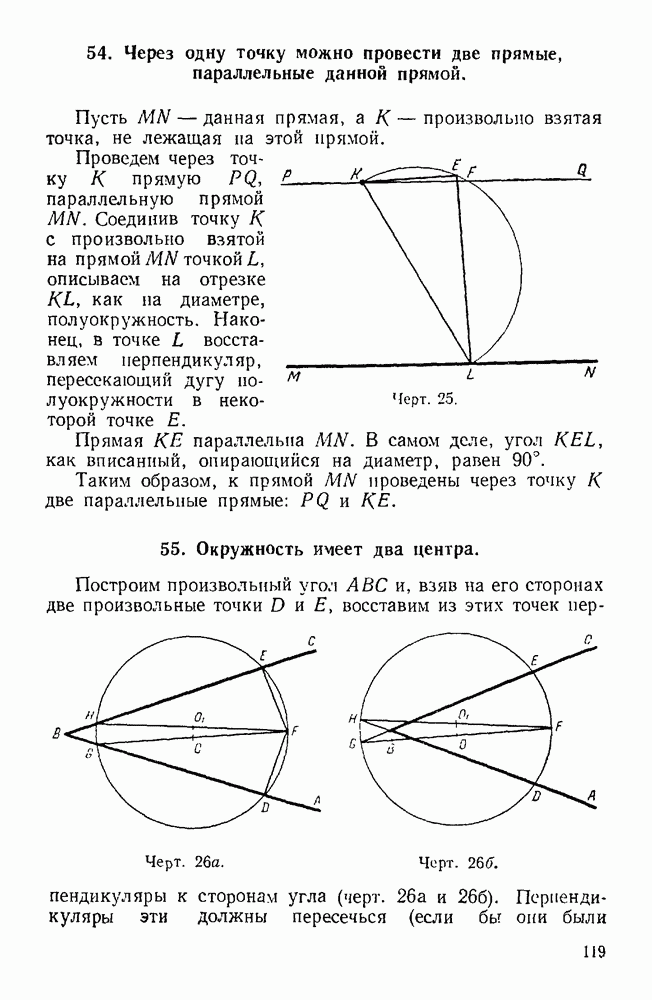
- 54. Через одну точку можно провести две прямые, параллельные данной прямой.
- 55. Окружность имеет два центра.
- 56. Из точки на прямую можно опустить два перпендикуляра.
- 57. Через две данные точки можно провести две прямые.
- 58. Любой треугольник — равнобедренный.
- 59. Катет прямоугольного треугольника равен его гипотенузе.
- 60. Прямой угол равен тупому (планиметрический вариант).
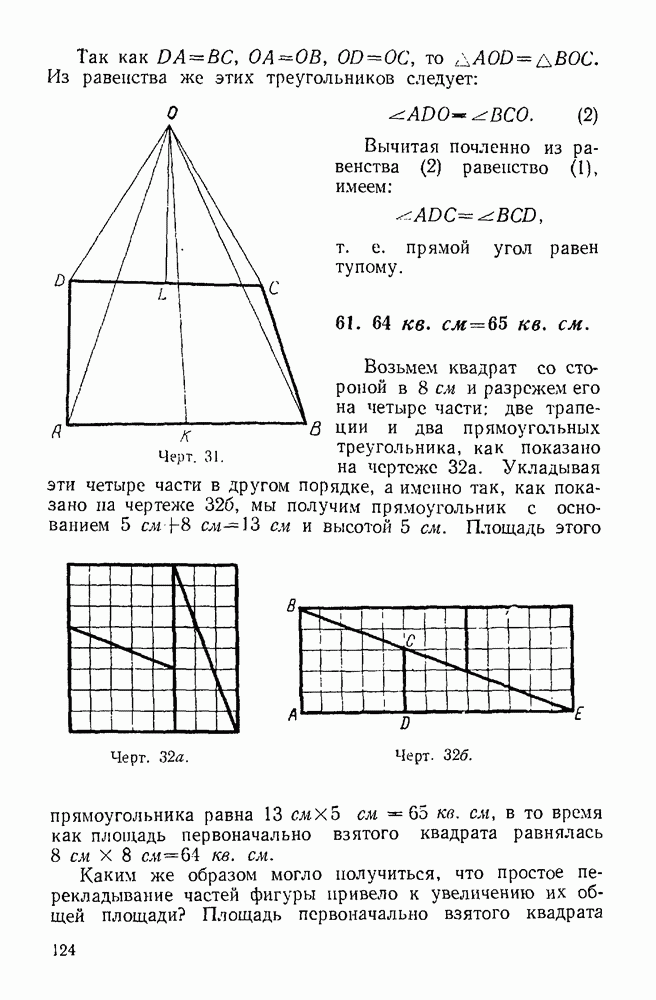
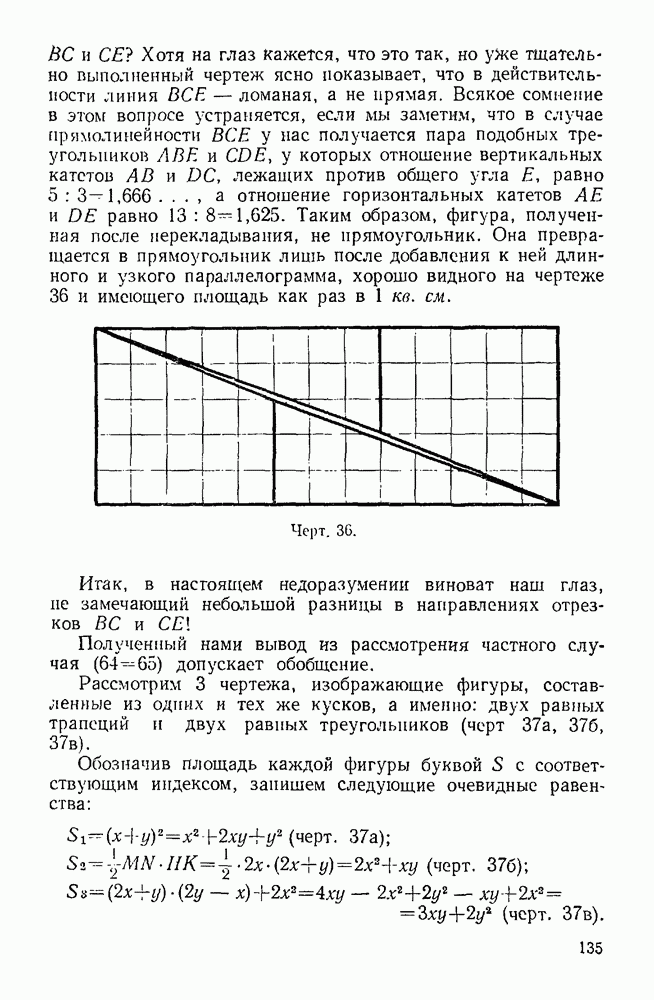
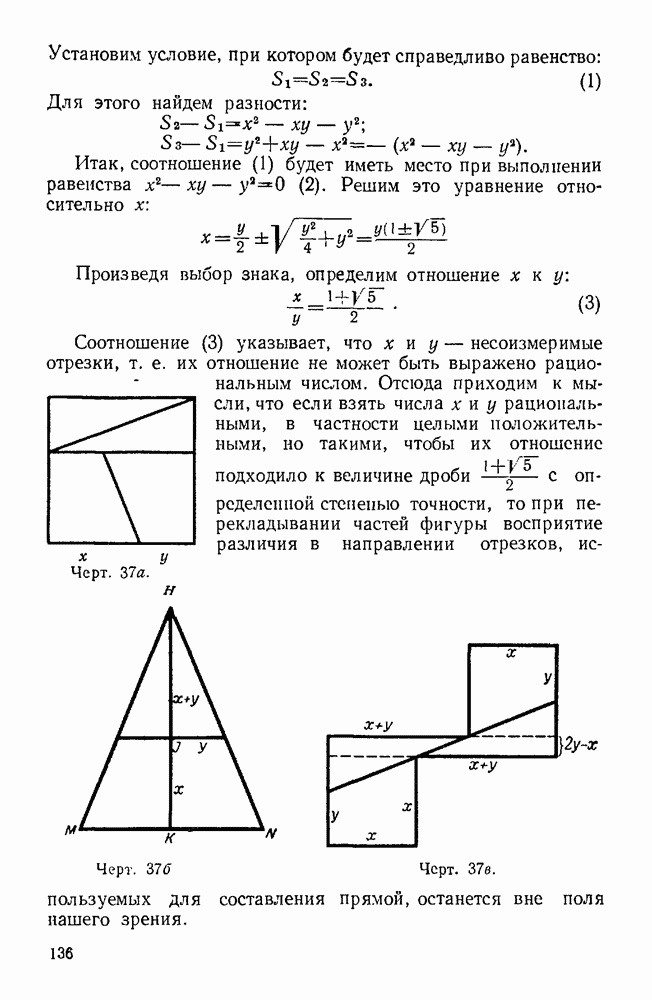
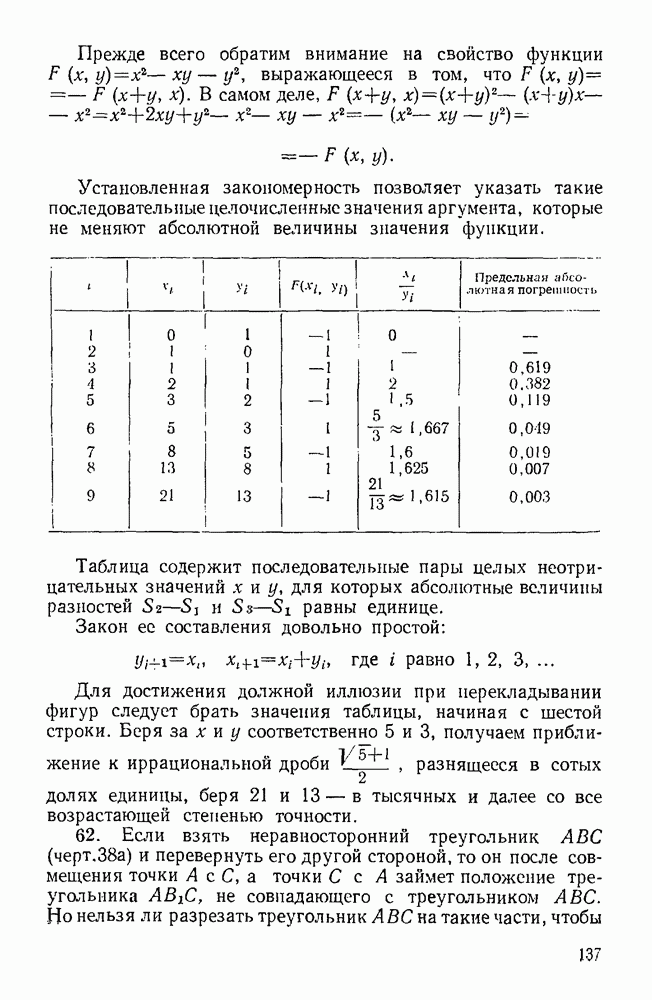
- 61. 64 кв. см = 65 кв. см.
- 62. Задача о заплате.
- II. АНАЛИЗ ПРИМЕРОВ.
- III. РАССКАЗЫ-ОБЪЯСНЕНИЯ ПО ПОВОДУ ОШИБОЧНЫХ РАССУЖДЕНИЙ.
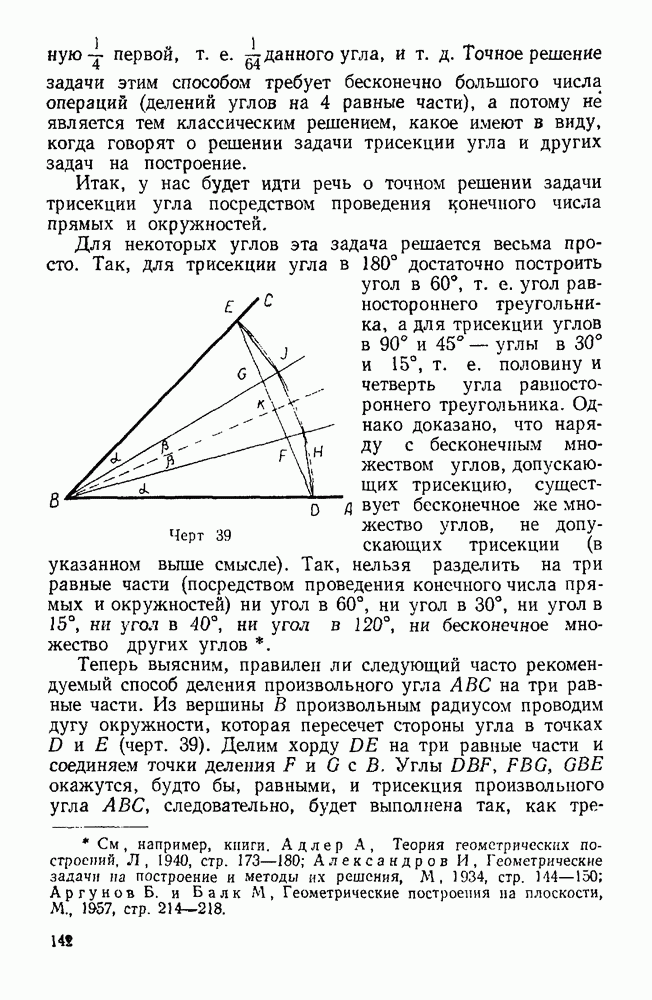
- 64. Трисекция угла.
- 65. Еще о трисекции угла.
- 66. Квадратура круга.
- 67. Об одном доказательстве теоремы о сумме внутренних углов треугольника.
- 68. Как вычислять объем усеченной пирамиды?
- Глава V. ТРИГОНОМЕТРИЯ.
- 70. Синус угла уменьшается, если к углу прибавить 360°.
- 71. Косинус любого острого угла больше единицы.
- 72. 1/4 > 1/2
- 73. 2^2 = 4^2
- 74. Площадь прямоугольника равна нулю.
- 75. Существуют равные треугольники, у которых не все стороны равны.
- 76. Каждый треугольник — прямоугольный.
- II. АНАЛИЗ ПРИМЕРОВ
- Глава VI. ПРИБЛИЖЕННЫЕ ВЫЧИСЛЕНИЯ. РАССКАЗЫ-ОБЪЯСНЕНИЯ ПО ПОВОДУ ОШИБОЧНЫХ РАССУЖДЕНИЙ
- 78. Все большие числа приближенно равны между собой.
- 79. О точности произведения приближенных чисел.
- 80. Верна ли формула …
- 81. Сколько цифр надо знать в подкоренном числе, чтобы получить корень с заданной точностью?
- 82. Зачем освобождаются от иррациональности в знаменателе?