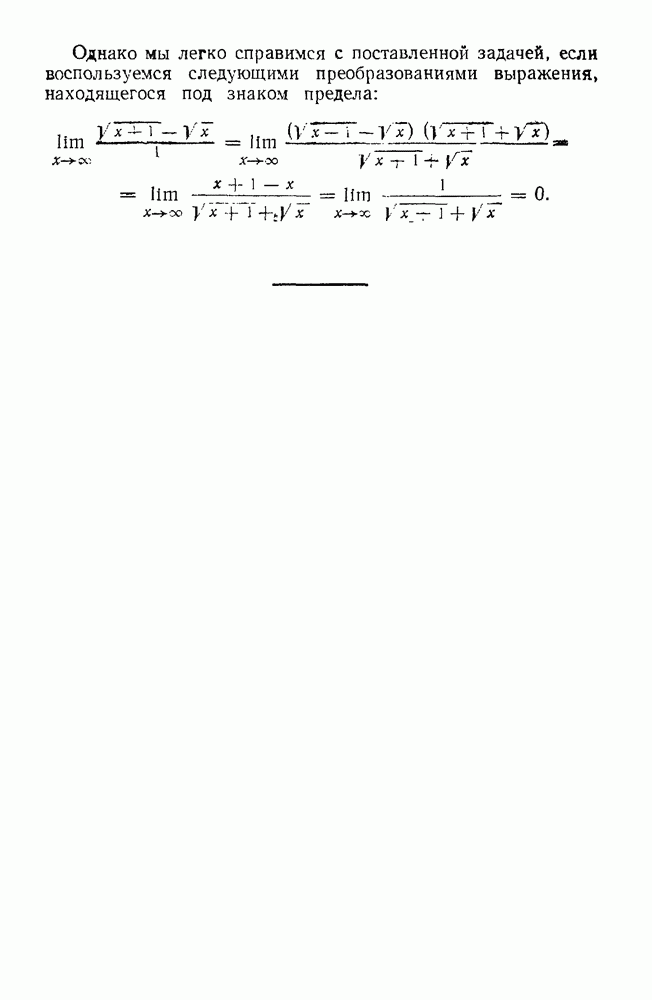| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
II. АНАЛИЗ ПРИМЕРОВ
69. Ошибка допущена при переходе от верного равенства (2) к неверному равенству (3). Ложность равенства (3) объясняется тем, что оно получено в результате деления обеих частей равенства (2) на разность  которая равна нулю.
которая равна нулю.
70. В результате почленного умножения двух неравенств одинакового смысла, все части которых положительны, получается новое неравенство того же смысла. Умножение же неравенств, не удовлетворяющих этому требованию, может давать что угодно: и неравенство другого смысла, и даже равенство.
В неравенствах (1) левые и правые части равны по абсолютной величине, но различны по знакам:

Почленное их перемножение приводит к двум равным по абсолютной величине произведениям, имеющим знак плюс, а потому равным друг другу. Неравенство (2) в силу этого неправильно и должно быть заменено равенством:

которое приводит к общеизвестной формуле:

71. При переходе от равенства (1) к неравенству (2) мы умножили на 2 левую часть равенства (1).
Но действительно ли это умножение на 2 есть увеличение? Всегда ли  Перенося в этом последнем неравенстве число а из правой части в левую, убеждаемся, что из неравенства
Перенося в этом последнем неравенстве число а из правой части в левую, убеждаемся, что из неравенства  вытекает неравенство
вытекает неравенство  Следователь не, если а не больше нуля, а меньше нуля или равно нулю, то неравенство
Следователь не, если а не больше нуля, а меньше нуля или равно нулю, то неравенство  не может иметь места.
не может иметь места.
Итак, переход от равенства  к неравенству
к неравенству  возможен исключительно при
возможен исключительно при  Но косинус острого угла всегда заключен между нулем и единицей, десятичный логарифм этого косинуса отрицателен, а потому из равенства
Но косинус острого угла всегда заключен между нулем и единицей, десятичный логарифм этого косинуса отрицателен, а потому из равенства  а не вытекает неравенство
а не вытекает неравенство

72. Ошибка допущена при переходе от равенства (2) к неравенству (3). Здесь упускается из внимания, что так как  правильной дроби, то
правильной дроби, то  отрицателен, а потому в соотношении (3) должен быть поставлен не знак больше, а, наоборот, знак меньше: удвоенное отрицательное число меньше этого отрицательного числа.
отрицателен, а потому в соотношении (3) должен быть поставлен не знак больше, а, наоборот, знак меньше: удвоенное отрицательное число меньше этого отрицательного числа.
73. Ошибка основана на забвении определения арифметического корня. В соответствии с этим определянием  а он равен
а он равен  т. е.
т. е.  если
если  если
если 
В анализируемом примере:  если
если  если х не принадлежит множеству значений, указанному двойным неравенством. В частности, при значении х равном
если х не принадлежит множеству значений, указанному двойным неравенством. В частности, при значении х равном  левая часть соотношения (3) должна быть взята в виде:
левая часть соотношения (3) должна быть взята в виде:  Абсурдный вывод, естественно, устраняется.
Абсурдный вывод, естественно, устраняется.
74. Ошибка настоящего рассуждения заключается, конечно, в неправильном вычислении высоты прямоугольника. Приписывая отрезку определенный знак  или
или  мы тем самым указываем, в каком направлении этот отрезок откладывается, или, что то же, в каком направлении мы этот отрезок проходим. Для линии синуса знак плюс указывает, что она откладывается вверх от горизонтального диаметра, минус - вниз. Рассматривая такие направленные отрезки и обозначая каждый отрезок двумя буквами, всегда предполагают, что первая буква означает начало отрезка, вторая —
мы тем самым указываем, в каком направлении этот отрезок откладывается, или, что то же, в каком направлении мы этот отрезок проходим. Для линии синуса знак плюс указывает, что она откладывается вверх от горизонтального диаметра, минус - вниз. Рассматривая такие направленные отрезки и обозначая каждый отрезок двумя буквами, всегда предполагают, что первая буква означает начало отрезка, вторая —
его конец. Поэтому два направленных отрезка  не тождественны: имея одинаковую длину, они имеют противоположные направления, и в силу этого
не тождественны: имея одинаковую длину, они имеют противоположные направления, и в силу этого  .
.
На чертеже 43 отрезок  откладывается вверх, а потому
откладывается вверх, а потому  отрезок же
отрезок же  вниз, и следовательно,
вниз, и следовательно,  а. Чтобы получить высоту прямоугольника со знаком плюс, мы должны двигаться от точки
а. Чтобы получить высоту прямоугольника со знаком плюс, мы должны двигаться от точки  к точке М в одном и том же направлении, а именио вверх. Поэтому формула (1) неверна, правильной же является формула
к точке М в одном и том же направлении, а именио вверх. Поэтому формула (1) неверна, правильной же является формула  или, что то же
или, что то же  Замечая, что
Замечая, что  , имеем:
, имеем:

как и должно быть.
Разъяснить настоящий софизм можно было бы гораздо короче, просто указав, что при вычислении площади прямоугольника мы должны брать лишь длины его основания и высоты, не принимая во внимание их знаков. Однако, во-первых, нередко и площадям приписывают определенные знаки  во-вторых, важно выяснить, как, зная направленные отрезки, ведущие от некоторой данной точки к концам некоторого интересующего нас отрезка, получить длину этого отрезка (в пашей задаче вопрос заключался именно в этом: надо было пайти длину отрезка
во-вторых, важно выяснить, как, зная направленные отрезки, ведущие от некоторой данной точки к концам некоторого интересующего нас отрезка, получить длину этого отрезка (в пашей задаче вопрос заключался именно в этом: надо было пайти длину отрезка  зная направленные отрезки, ведущие от точки Р к точкам
зная направленные отрезки, ведущие от точки Р к точкам 
75. На основе анализа трех признаков равенства треугольников методом неполной индукции сделан ложный вывод: «Итак, для утверждения равенства двух треугольников требуется знать (т. е. достаточно знать!) о равенстве трех элементов их, среди которых представлен по крайней мере один линейный».
На самом же деле, равенство трех основных элементов одного треугольника трем основным элементам другого треугольника, включая по крайней мере и один линейный элемент, является необходимым, но недостаточным условием для равенства рассматриваемых фигур. Взглянув на чертеж 45, мы легко убеждаемся в недостаточности этого условия.
Приняв ложное утверждение за истинное и применив его к анализу примера, в котором речь идет о подобных треугольниках со сторонами 18, 12, 8 и 27, 18, 12, мы пришли к утверждению нелепости: существуют равные треугольники, у которых не все стороны равны.
Этот софизм мы уже рассматривали в геометрии  Там же было дано подробное раскрытие его.
Там же было дано подробное раскрытие его.

Черт. 45.
76. Ошибка сделана при переходе от соотношения (5) к соотношению (6). Она состоит в неправильном применении принципа непосредственных умозаключений путем обращения. Тот факт, что равные углы имеют равные синусы, не дает еще основания заключать о справедливости обратного утверждения. Здесь можно утверждать только следующее: «Если синусы двух углов равны, то и утлы могут быть равны».
Относительно углов  возможно сделать три предположения:
возможно сделать три предположения:
1)  . В этом частном случае мы действительно будем иметь прямоугольный треугольник. Но этот случай, как видно из дальнейшего, не исчерпывает всех возможных случаев.
. В этом частном случае мы действительно будем иметь прямоугольный треугольник. Но этот случай, как видно из дальнейшего, не исчерпывает всех возможных случаев.
2)  . В этом случае
. В этом случае  что не противоречит смыслу задачи и связывает углы треугольника известным соотношением. Однако этот случай не дает никаких оснований для абсурдного вывода о наличии прямого угла в любом треугольнике.
что не противоречит смыслу задачи и связывает углы треугольника известным соотношением. Однако этот случай не дает никаких оснований для абсурдного вывода о наличии прямого угла в любом треугольнике.
3)  . Этот случай невозможен, так как разность суммы двух любых углов треугольника и его третьего угла не может быть равна 360°.
. Этот случай невозможен, так как разность суммы двух любых углов треугольника и его третьего угла не может быть равна 360°.
Как видим, абсурдный вывод устраняется.
| << Предыдущий параграф | Следующий параграф >> |
- ИЗ ПРЕДИСЛОВИЯ К ПЕРВОМУ ИЗДАНИЮ
- Глава I. ОБ УПРАЖНЕНИЯХ НА ОПРОВЕРЖЕНИЕ ОШИБОЧНЫХ МАТЕМАТИЧЕСКИХ РАССУЖДЕНИЙ И ИХ КЛАССИФИКАЦИИ
- 1. МАТЕМАТИЧЕСКИЕ СОФИЗМЫ И ИХ ПЕДАГОГИЧЕСКАЯ РОЛЬ.
- II. КЛАССИФИКАЦИЯ УПРАЖНЕНИЙ НА ОПРОВЕРЖЕНИЕ ЛОЖНЫХ МАТЕМАТИЧЕСКИХ РАССУЖДЕНИЙ.
- 2. Распространение на исключительные случаи.
- 3. Приписывание свойств определенного вида всему роду.
- 4. Неправильное применение принципа непосредственных умозаключений путем обращения.
- 5. Подмена точных определений геометрической интуицией.
- 6. Ошибки построения.
- 7. Ошибки, являющиеся следствием буквального толкования сокращенной (условной) формулировки некоторых геометрических утверждений.
- 8. Нарушение смысла условных записей.
- 9. Уклонение от тезиса.
- Глава II. АРИФМЕТИКА.
- I. ПРИМЕРЫ ЛОЖНЫХ РАССУЖДЕНИЙ.
- 2. На двух нормальных руках одиннадцать пальцев.
- 3. Квадратные рубли.
- 4. 45 — 45 = 45
- 5. 40 : 8 = 41
- 6. Дважды два — пять!
- 7. Есть ли здесь пропорциональность?
- 8. 100% экономии.
- 9. Как вычислять средний процент?
- 10. Что даст ежегодный прирост в 40% за пять лет?
- 11. Новое правило умножения дробей.
- 12. Куда делся рубль?
- 13. Откуда появился лишний гривенник?
- 14. Завещание отца.
- 15. 2-3=4.
- II. АНАЛИЗ ПРИМЕРОВ.
- Глава III. АЛГЕБРА.
- I. ПРИМЕРЫ ЛОЖНЫХ РАССУЖДЕНИЙ.
- 19. Делимость многочленов и делимость чисел.
- 20. Произвольно взятое число а равно нулю.
- 21. 7 = 13.
- 22. Положительная единица равна отрицательной единице.
- 23. Другое «доказательство» равенства положительной и отрицательной единиц.
- 24. Мнимая единица и действительная отрицательная единица равны.
- 25. i^2 = 1
- 26. Всякое отрицательное число больше положительного, имеющего то же абсолютное значение.
- 27. Если a > b, то a > 2b
- 28. Если а и b положительные числа, то a > b и b > a.
- 29. Положительное число меньше нуля.
- 30. Сумма натуральных чисел, каждое из которых превосходит единицу, больше их произведения.
- 31. Чему равен квадратный корень из числа a^2?
- 32. Еще одно «доказательство» равенства нулю произвольно взятого числа.
- 33. Число не изменяется, если в нем переставить любые цифры!
- 34. Что говорит теорема о существовании корня в алгебре комплексных чисел?
- 35. Об одном спэсобе получать правильные результаты, применение которого требует большой осторожности.
- 36. О сумме 1-1+1-1 + …
- 37. Всегда ли целое больше своей части?
- 38. Еще одно «доказательство» равенства двух произвольно взятых чисел.
- 39. Сумма двух произвольных одинаковых чисел равна нулю.
- 40. Число не изменится, если к нему прибавить 1.
- 41. Ахиллес и черепаха.
- 42. О некоторых ученических ошибках.
- II. АНАЛИЗ ПРИМЕРОВ.
- Глава IV. ГЕОМЕТРИЯ.
- 1. ПРИМЕРЫ ЛОЖНЫХ РАССУЖДЕНИЙ.
- 44. Отрезок прямой равен своей правильной части.
- 45. Все треугольники равновелики.
- 46. Сумма оснований любой трапеции равна нулю.
- 47. Объемлемая и объемлющая.
- 48. Еще о пропорциональности.
- 49. Две окружности разного радиуса имеют одну и ту же длину.
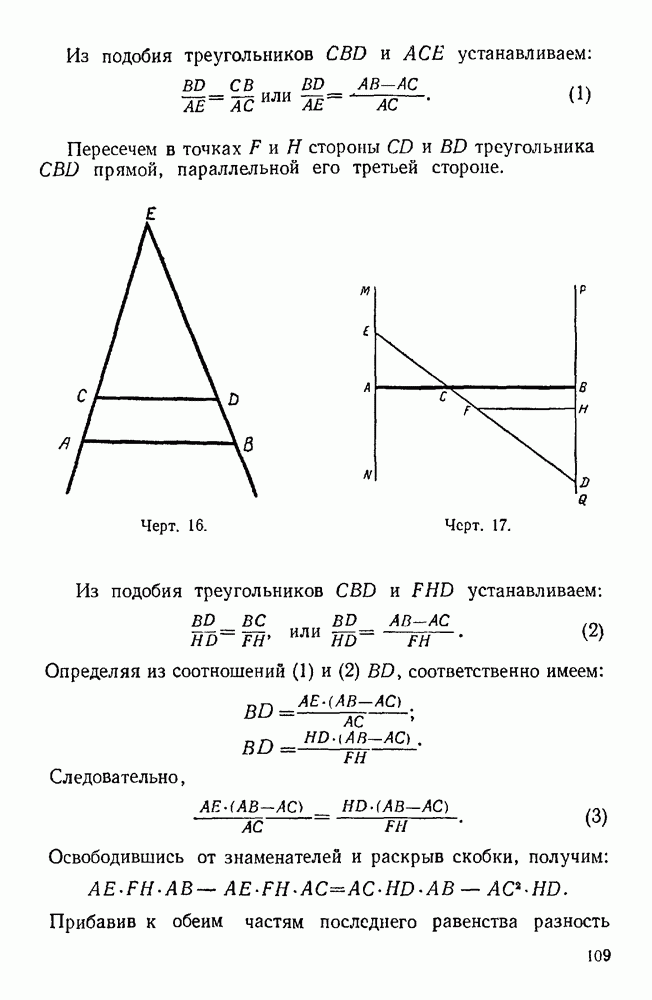
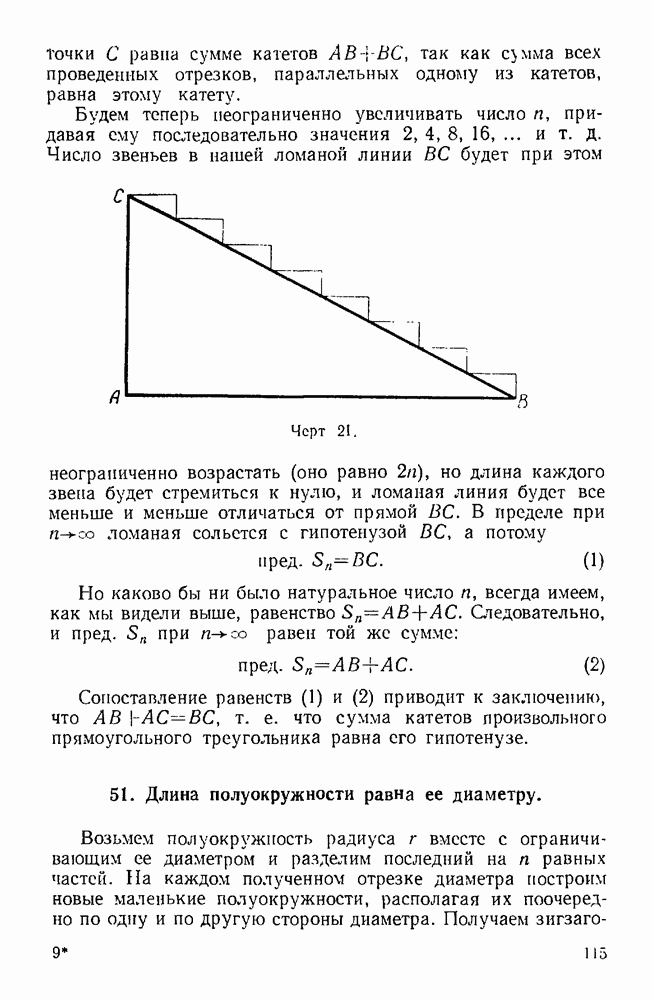
- 50. Сумма катетов равна гипотенузе.
- 51. Длина полуокружности равна ее диаметру.
- 52. Боковая поверхность круглого прямого конуса с радиусом основания r и высотой h выражается формулой P=pi*r(r+h).
- 53. В данной точке на прямой можно восставить два перпендикуляра к этой прямой.
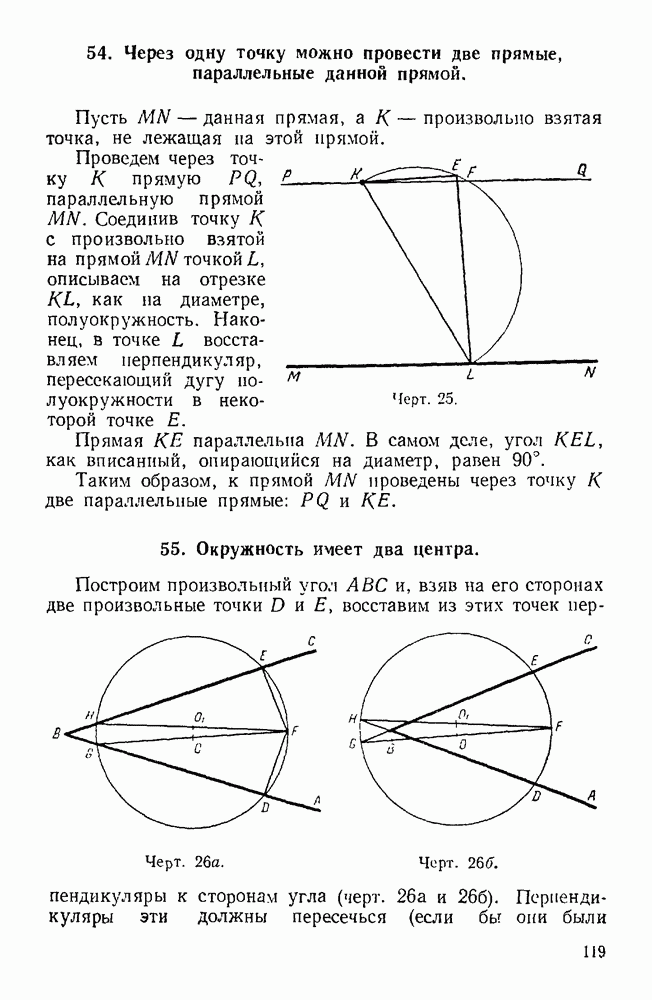
- 54. Через одну точку можно провести две прямые, параллельные данной прямой.
- 55. Окружность имеет два центра.
- 56. Из точки на прямую можно опустить два перпендикуляра.
- 57. Через две данные точки можно провести две прямые.
- 58. Любой треугольник — равнобедренный.
- 59. Катет прямоугольного треугольника равен его гипотенузе.
- 60. Прямой угол равен тупому (планиметрический вариант).
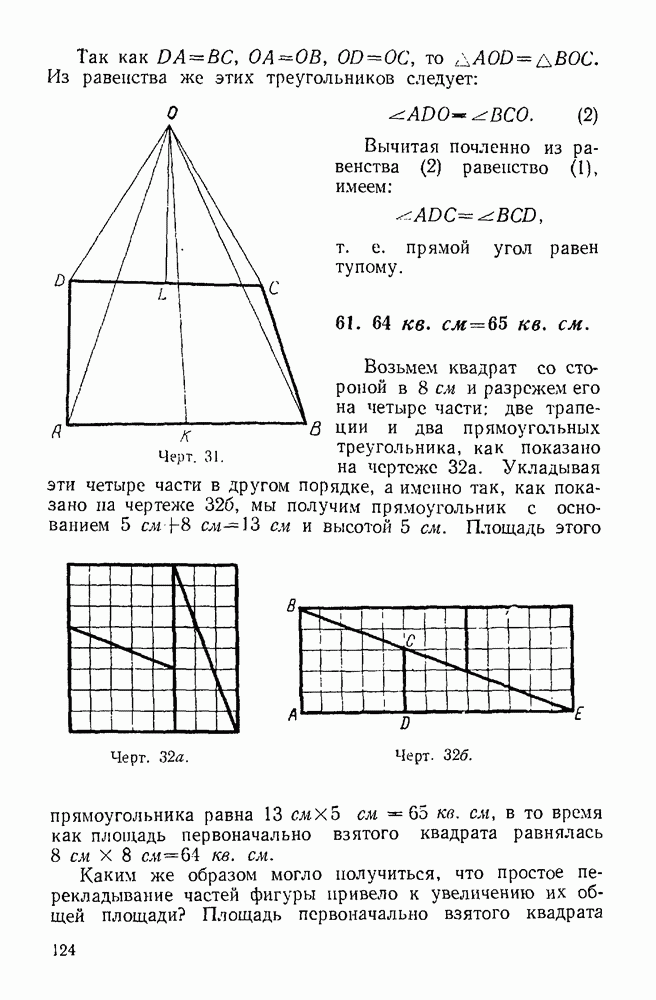
- 61. 64 кв. см = 65 кв. см.
- 62. Задача о заплате.
- II. АНАЛИЗ ПРИМЕРОВ.
- III. РАССКАЗЫ-ОБЪЯСНЕНИЯ ПО ПОВОДУ ОШИБОЧНЫХ РАССУЖДЕНИЙ.
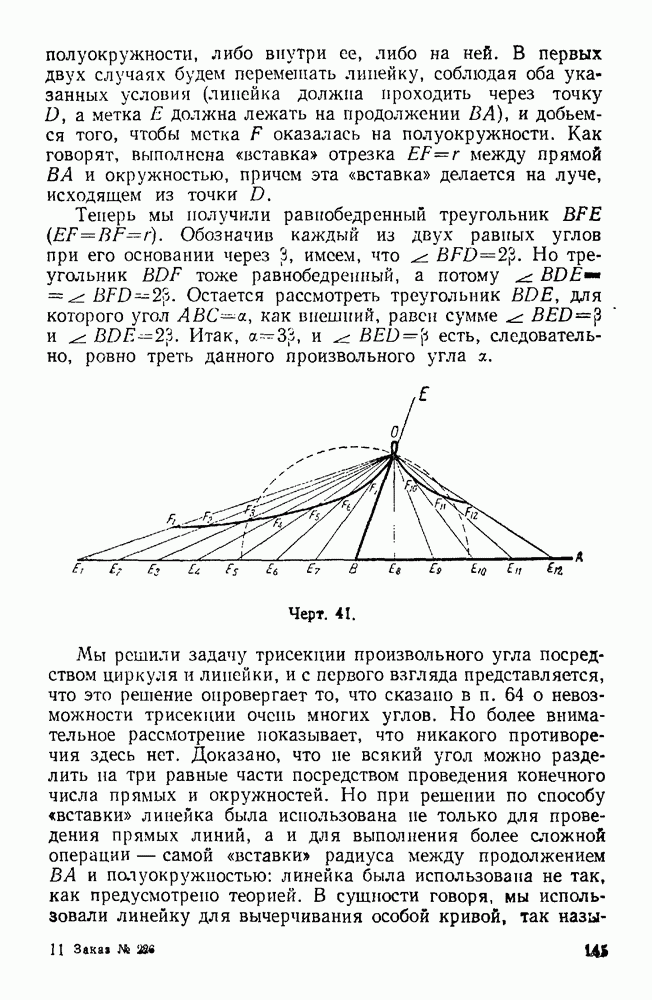
- 64. Трисекция угла.
- 65. Еще о трисекции угла.
- 66. Квадратура круга.
- 67. Об одном доказательстве теоремы о сумме внутренних углов треугольника.
- 68. Как вычислять объем усеченной пирамиды?
- Глава V. ТРИГОНОМЕТРИЯ.
- 70. Синус угла уменьшается, если к углу прибавить 360°.
- 71. Косинус любого острого угла больше единицы.
- 72. 1/4 > 1/2
- 73. 2^2 = 4^2
- 74. Площадь прямоугольника равна нулю.
- 75. Существуют равные треугольники, у которых не все стороны равны.
- 76. Каждый треугольник — прямоугольный.
- II. АНАЛИЗ ПРИМЕРОВ
- Глава VI. ПРИБЛИЖЕННЫЕ ВЫЧИСЛЕНИЯ. РАССКАЗЫ-ОБЪЯСНЕНИЯ ПО ПОВОДУ ОШИБОЧНЫХ РАССУЖДЕНИЙ
- 78. Все большие числа приближенно равны между собой.
- 79. О точности произведения приближенных чисел.
- 80. Верна ли формула …
- 81. Сколько цифр надо знать в подкоренном числе, чтобы получить корень с заданной точностью?
- 82. Зачем освобождаются от иррациональности в знаменателе?