| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
35. Об одном спэсобе получать правильные результаты, применение которого требует большой осторожности.
Как известно, всякая несократимая дробь  у которой знаменатель
у которой знаменатель  содержит хотя бы один первоначальный множитель, отличный от 2 и 5, при обращении в десятичную дробь дает бесконечную периодическую дробь. Поставим себе обратную задачу: имея какую-нибудь бесконечную периодическую дробь, найти ту обыкновенную дробь, от обращения которой в десятичную она получилась. При этом ограничимся «чистыми» периодическими дробями, т. е. такими, у которых период начинается сразу после знака дробности.
содержит хотя бы один первоначальный множитель, отличный от 2 и 5, при обращении в десятичную дробь дает бесконечную периодическую дробь. Поставим себе обратную задачу: имея какую-нибудь бесконечную периодическую дробь, найти ту обыкновенную дробь, от обращения которой в десятичную она получилась. При этом ограничимся «чистыми» периодическими дробями, т. е. такими, у которых период начинается сразу после знака дробности.
Пусть дана, например, дробь  т. е. чистая периодическая дробь с целой частью 0 и периодом 24. Обозначив величину этой дроби через х, возьмем равенство
т. е. чистая периодическая дробь с целой частью 0 и периодом 24. Обозначив величину этой дроби через х, возьмем равенство

и умножим обе его части на 100; получим:

Замечаем, что это последнее равенство можно переписать в новом конечном виде (бесконечное повторение периода исключено):

Мы получили уравнение первой степени, решение которого дает  проверки обращаемое десятичную дробь и после деления 8 на 33 действительно получаем данную периодическую дробь
проверки обращаемое десятичную дробь и после деления 8 на 33 действительно получаем данную периодическую дробь 
Этим способом можно обратить в обыкновенную дробь любую чистую периодическую дробь, но только умножать надо не всегда на 100: если в периоде  цифр, то умножать надо на
цифр, то умножать надо на  Для обращения в обыкновенную дробь «смешанной» периодической дроби, т. е. такой, у которой между знаком дробности и периодом находятся еще цифры, надо предварительно преобразовать смешанную дробь так, чтобы свести вопрос к обращению чистой периодической дроби. Например, если дана дробь
Для обращения в обыкновенную дробь «смешанной» периодической дроби, т. е. такой, у которой между знаком дробности и периодом находятся еще цифры, надо предварительно преобразовать смешанную дробь так, чтобы свести вопрос к обращению чистой периодической дроби. Например, если дана дробь  то сначала умножаем обе части этого равенства на 10, а потом, получив
то сначала умножаем обе части этого равенства на 10, а потом, получив

полагаем  и находим
и находим  и
и  Проверка (делением 5 на 6) показывает, что задача решена правильно.
Проверка (делением 5 на 6) показывает, что задача решена правильно.
Характерной особенностью примененного нами метода было исключение бесконечного повторения периода.
Вот еще задача, где применяется аналогичный прием.
Надо найти  предполагая, что действие извлечения квадратного корня повторяется неограниченное количество раз. Полагая
предполагая, что действие извлечения квадратного корня повторяется неограниченное количество раз. Полагая  возводим обе части эюго равенства в квадрат и убеждаемся, что после переноса числа 2 налево в правой части опять получается выражение, обозначенное нами через
возводим обе части эюго равенства в квадрат и убеждаемся, что после переноса числа 2 налево в правой части опять получается выражение, обозначенное нами через  Делая замену, исключаем бесконечное множество корней и приходим к квадратному уравнению, из которого и определяем
Делая замену, исключаем бесконечное множество корней и приходим к квадратному уравнению, из которого и определяем 

Пригодным, разумеется, является лишь положительный корень. Итак, искомое выражение равно 2.
Правильность нашего утверждения легко проверить, произведя следующие вычисления:

Как видим, последовательность чисел

которую можно продолжать как угодно далеко, состоит из чисел, действительно приближающихся к указанному значению 2, как к своему пределу (насколько можно об этом судить по нашему небольшому вычислению, проведенному с точностью до тысячных).
Наш прием исключения бесконечного ряда повторяющихся операций в рассмотренных двух случаях привел к правильным результатам. Но рассмотрим еще одно применение этого приема.
Возьмем какое угодно положительное число а и обозначим буквой х сумму бесконечного множества слагаемых, равных а; затем производим исключение бесконечности и приходим к неожиданному заключению, что 

Применение нашего приема исключения бесконечности привело здесь к противоречию между заключением  и исходным условием
и исходным условием 
Вот еще пример: обозначив через х значение алгебраической суммы бесконечного множества слагаемых

имеем:

Ответ явно неверный, так как, находя суммы последовательно возрастающего числа слагаемых, мы получим ряд целых чисел:

не обнаруживающих никакого приближения к найденному нами числу -1. Итак, примененный нами способ устранения бесконечности, дающий иногда правильные результаты, иногда дает результаты явно неправильные, а потому его применение требует осторожности: необходимо выяснить, при каких условиях этот прием дает правильные результаты.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ИЗ ПРЕДИСЛОВИЯ К ПЕРВОМУ ИЗДАНИЮ
- Глава I. ОБ УПРАЖНЕНИЯХ НА ОПРОВЕРЖЕНИЕ ОШИБОЧНЫХ МАТЕМАТИЧЕСКИХ РАССУЖДЕНИЙ И ИХ КЛАССИФИКАЦИИ
- 1. МАТЕМАТИЧЕСКИЕ СОФИЗМЫ И ИХ ПЕДАГОГИЧЕСКАЯ РОЛЬ.
- II. КЛАССИФИКАЦИЯ УПРАЖНЕНИЙ НА ОПРОВЕРЖЕНИЕ ЛОЖНЫХ МАТЕМАТИЧЕСКИХ РАССУЖДЕНИЙ.
- 2. Распространение на исключительные случаи.
- 3. Приписывание свойств определенного вида всему роду.
- 4. Неправильное применение принципа непосредственных умозаключений путем обращения.
- 5. Подмена точных определений геометрической интуицией.
- 6. Ошибки построения.
- 7. Ошибки, являющиеся следствием буквального толкования сокращенной (условной) формулировки некоторых геометрических утверждений.
- 8. Нарушение смысла условных записей.
- 9. Уклонение от тезиса.
- Глава II. АРИФМЕТИКА.
- I. ПРИМЕРЫ ЛОЖНЫХ РАССУЖДЕНИЙ.
- 2. На двух нормальных руках одиннадцать пальцев.
- 3. Квадратные рубли.
- 4. 45 — 45 = 45
- 5. 40 : 8 = 41
- 6. Дважды два — пять!
- 7. Есть ли здесь пропорциональность?
- 8. 100% экономии.
- 9. Как вычислять средний процент?
- 10. Что даст ежегодный прирост в 40% за пять лет?
- 11. Новое правило умножения дробей.
- 12. Куда делся рубль?
- 13. Откуда появился лишний гривенник?
- 14. Завещание отца.
- 15. 2-3=4.
- II. АНАЛИЗ ПРИМЕРОВ.
- Глава III. АЛГЕБРА.
- I. ПРИМЕРЫ ЛОЖНЫХ РАССУЖДЕНИЙ.
- 19. Делимость многочленов и делимость чисел.
- 20. Произвольно взятое число а равно нулю.
- 21. 7 = 13.
- 22. Положительная единица равна отрицательной единице.
- 23. Другое «доказательство» равенства положительной и отрицательной единиц.
- 24. Мнимая единица и действительная отрицательная единица равны.
- 25. i^2 = 1
- 26. Всякое отрицательное число больше положительного, имеющего то же абсолютное значение.
- 27. Если a > b, то a > 2b
- 28. Если а и b положительные числа, то a > b и b > a.
- 29. Положительное число меньше нуля.
- 30. Сумма натуральных чисел, каждое из которых превосходит единицу, больше их произведения.
- 31. Чему равен квадратный корень из числа a^2?
- 32. Еще одно «доказательство» равенства нулю произвольно взятого числа.
- 33. Число не изменяется, если в нем переставить любые цифры!
- 34. Что говорит теорема о существовании корня в алгебре комплексных чисел?
- 35. Об одном спэсобе получать правильные результаты, применение которого требует большой осторожности.
- 36. О сумме 1-1+1-1 + …
- 37. Всегда ли целое больше своей части?
- 38. Еще одно «доказательство» равенства двух произвольно взятых чисел.
- 39. Сумма двух произвольных одинаковых чисел равна нулю.
- 40. Число не изменится, если к нему прибавить 1.
- 41. Ахиллес и черепаха.
- 42. О некоторых ученических ошибках.
- II. АНАЛИЗ ПРИМЕРОВ.
- Глава IV. ГЕОМЕТРИЯ.
- 1. ПРИМЕРЫ ЛОЖНЫХ РАССУЖДЕНИЙ.
- 44. Отрезок прямой равен своей правильной части.
- 45. Все треугольники равновелики.
- 46. Сумма оснований любой трапеции равна нулю.
- 47. Объемлемая и объемлющая.
- 48. Еще о пропорциональности.
- 49. Две окружности разного радиуса имеют одну и ту же длину.
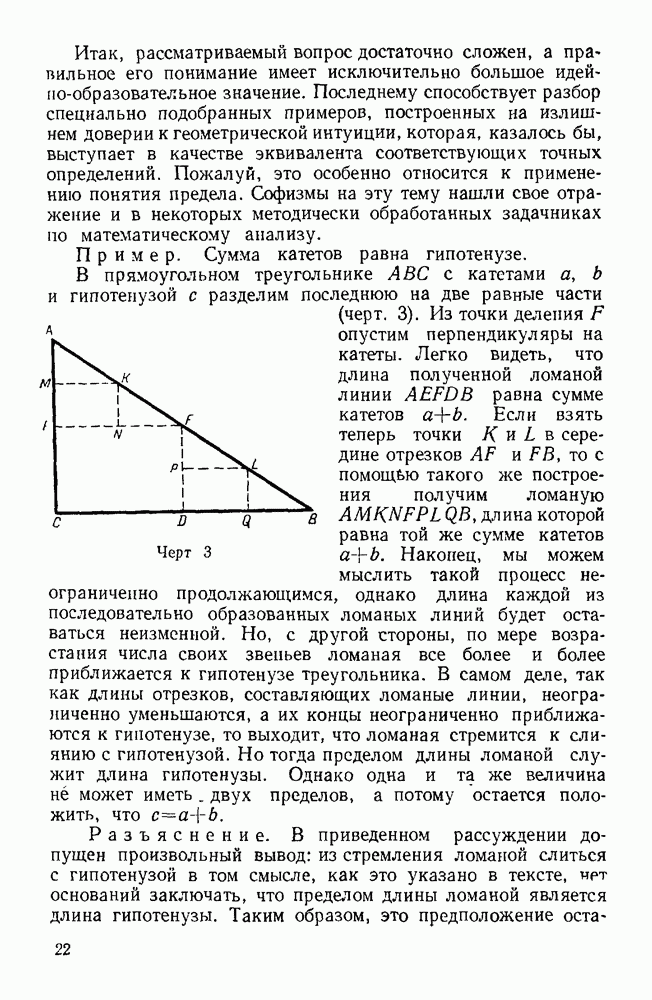
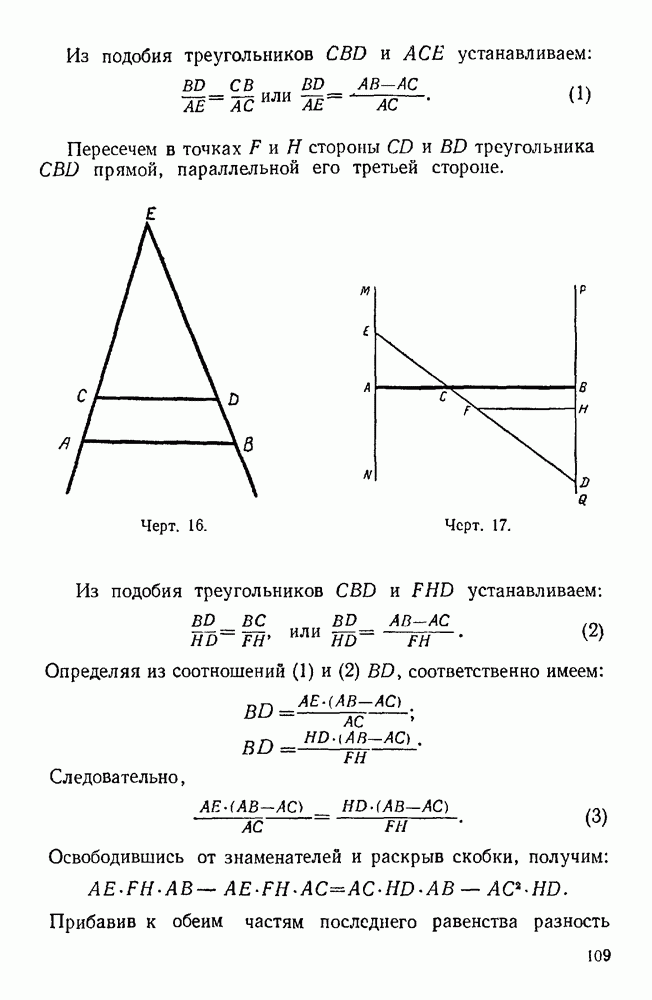
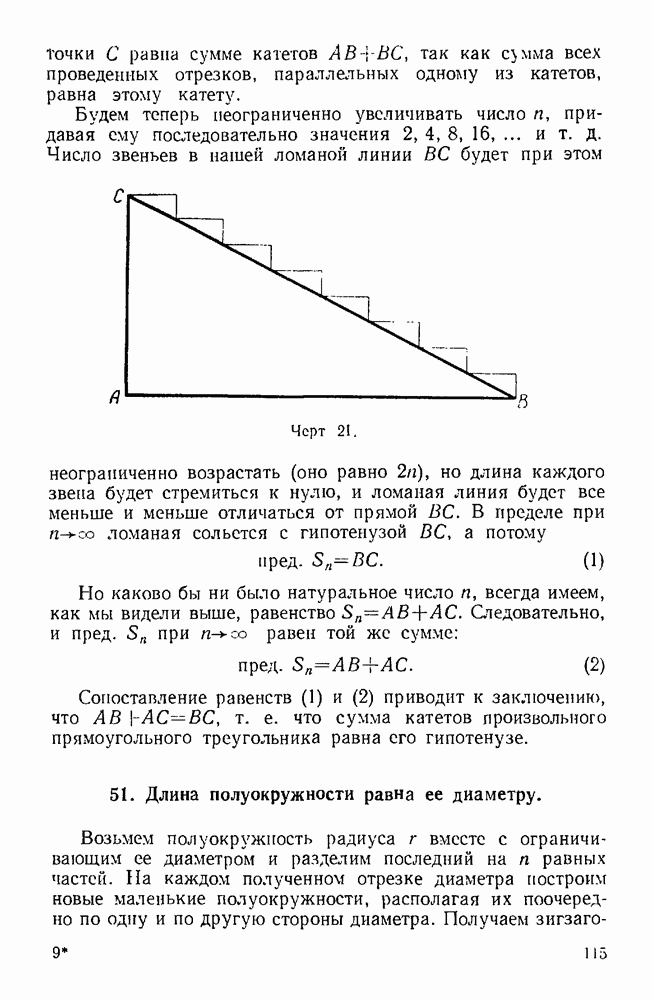
- 50. Сумма катетов равна гипотенузе.
- 51. Длина полуокружности равна ее диаметру.
- 52. Боковая поверхность круглого прямого конуса с радиусом основания r и высотой h выражается формулой P=pi*r(r+h).
- 53. В данной точке на прямой можно восставить два перпендикуляра к этой прямой.
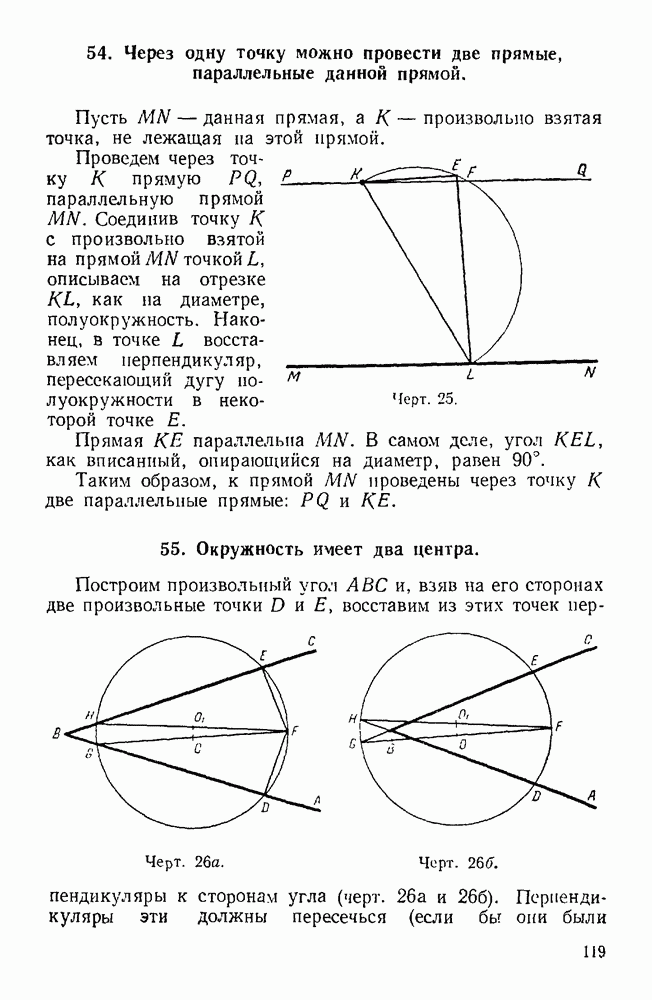
- 54. Через одну точку можно провести две прямые, параллельные данной прямой.
- 55. Окружность имеет два центра.
- 56. Из точки на прямую можно опустить два перпендикуляра.
- 57. Через две данные точки можно провести две прямые.
- 58. Любой треугольник — равнобедренный.
- 59. Катет прямоугольного треугольника равен его гипотенузе.
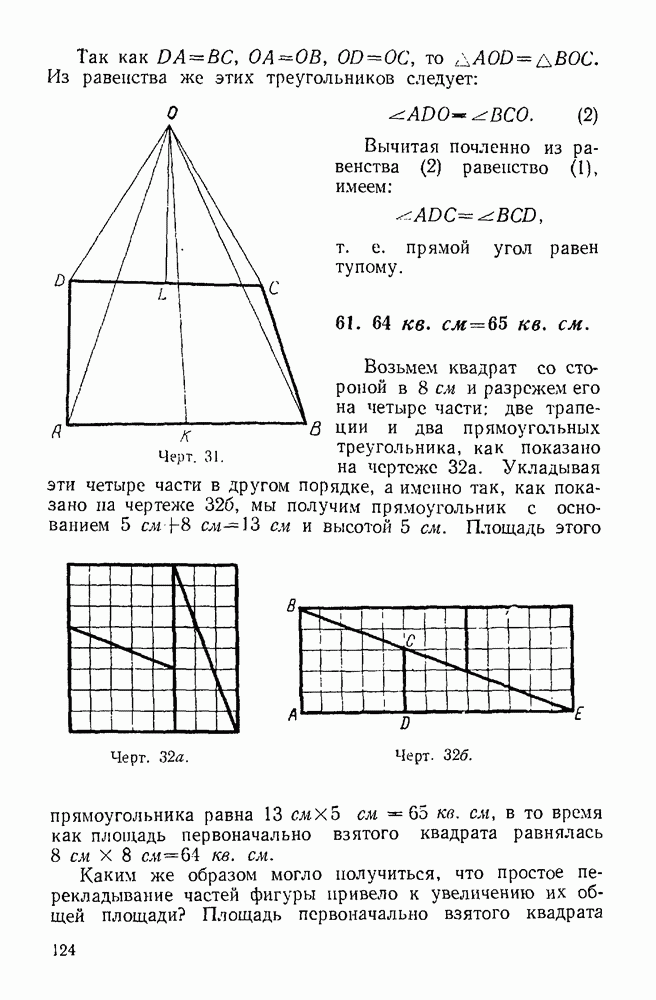
- 60. Прямой угол равен тупому (планиметрический вариант).
- 61. 64 кв. см = 65 кв. см.
- 62. Задача о заплате.
- II. АНАЛИЗ ПРИМЕРОВ.
- III. РАССКАЗЫ-ОБЪЯСНЕНИЯ ПО ПОВОДУ ОШИБОЧНЫХ РАССУЖДЕНИЙ.
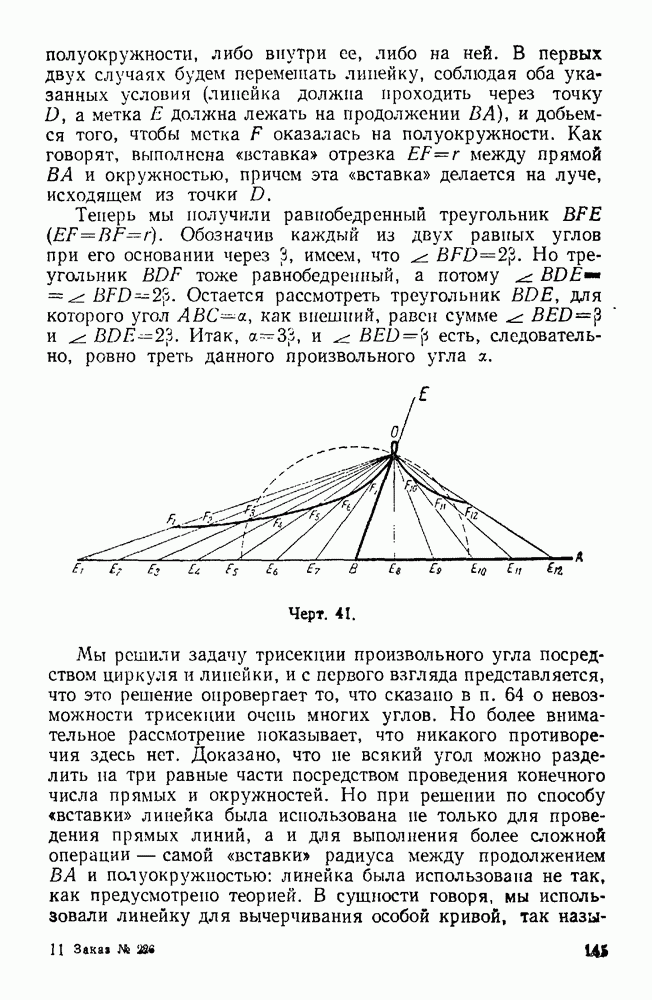
- 64. Трисекция угла.
- 65. Еще о трисекции угла.
- 66. Квадратура круга.
- 67. Об одном доказательстве теоремы о сумме внутренних углов треугольника.
- 68. Как вычислять объем усеченной пирамиды?
- Глава V. ТРИГОНОМЕТРИЯ.
- 70. Синус угла уменьшается, если к углу прибавить 360°.
- 71. Косинус любого острого угла больше единицы.
- 72. 1/4 > 1/2
- 73. 2^2 = 4^2
- 74. Площадь прямоугольника равна нулю.
- 75. Существуют равные треугольники, у которых не все стороны равны.
- 76. Каждый треугольник — прямоугольный.
- II. АНАЛИЗ ПРИМЕРОВ
- Глава VI. ПРИБЛИЖЕННЫЕ ВЫЧИСЛЕНИЯ. РАССКАЗЫ-ОБЪЯСНЕНИЯ ПО ПОВОДУ ОШИБОЧНЫХ РАССУЖДЕНИЙ
- 78. Все большие числа приближенно равны между собой.
- 79. О точности произведения приближенных чисел.
- 80. Верна ли формула …
- 81. Сколько цифр надо знать в подкоренном числе, чтобы получить корень с заданной точностью?
- 82. Зачем освобождаются от иррациональности в знаменателе?