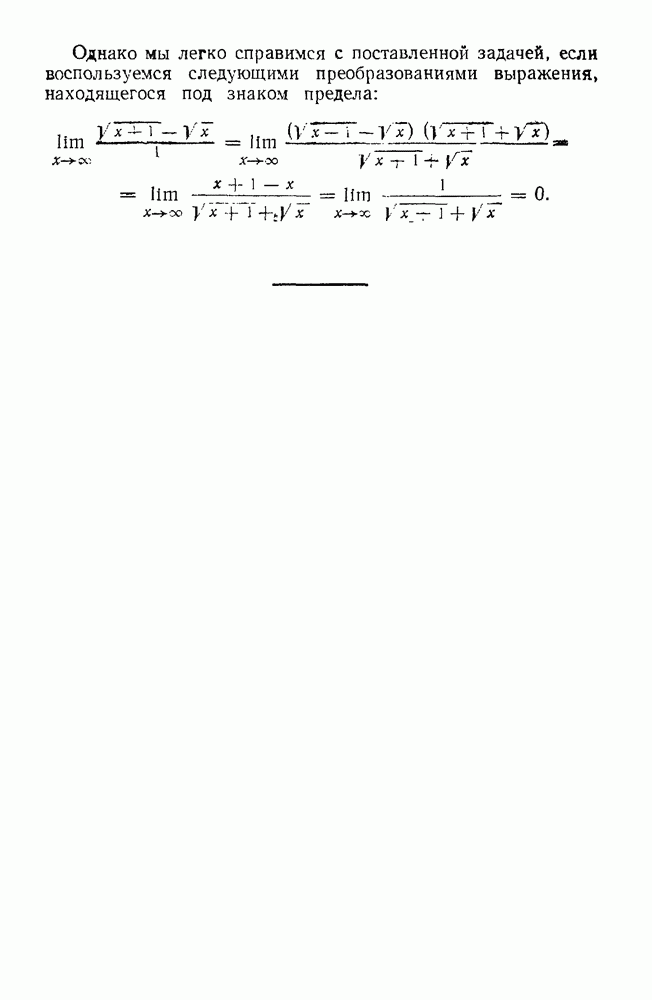| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
6. Ошибки построения.
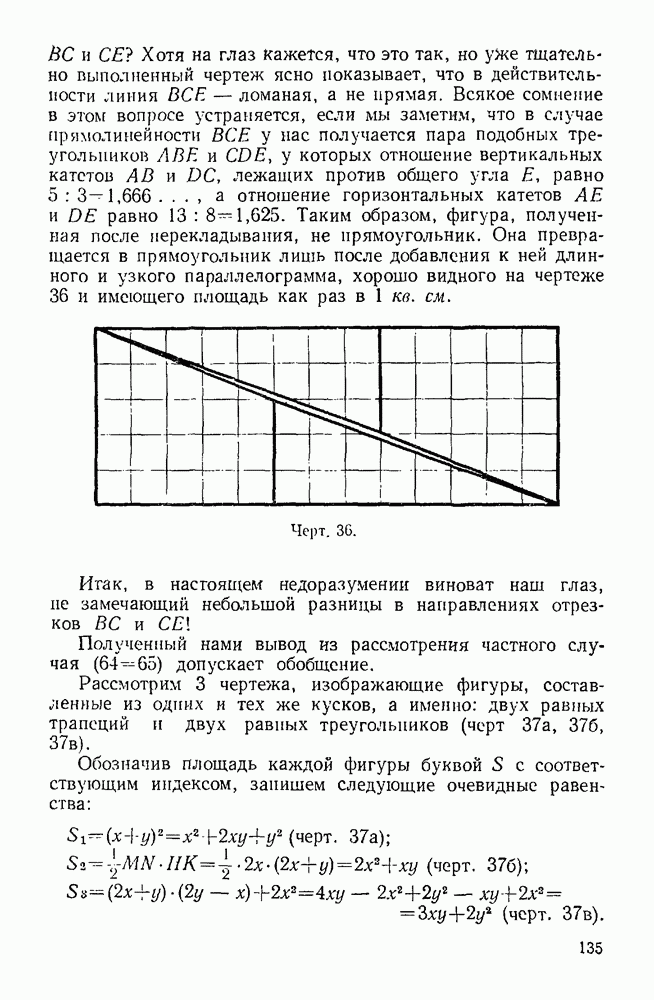
Мы уже рассматривали вопрос об ошибках, могущих возникнуть при пользовании верным чертежом. Здесь мы проанализируем основные типы заблуждений, возникающих в силу той или иной ошибки чертежа.
Взгляд некоторых математиков на сведение на нет роли чертежа в геометрии не мог найти сколько-нибудь значительного числа последователей. И это вполне закономерно, так как вся многовековая история геометрии убедительно свидетельствует об исключительно большом значении чертежа в выявлении новых геометрических положений и изыскании способов их доказательства. Однако проблема взаимоотношения логики и иитуиции в процессе творчества и преподавания и в связи с этим проблема правильного использования наглядных изображений остается до сих пор в числе актуальных вопросов методологии и методики математики.
Во всяком случае учащимися должно быть хорошо осознано, что геометрическое наглядное представление еще не гарантирует истину или по крайней мере логическую строгость; что нельзя судить об условиях теоремы по тому впечатлению, которое производит чертеж. Одновременно с этим учащиеся должны проникнуться сознанием, что верный чертеж, как правило, помогает сделать правильную догадку, оказывая неоценимую услугу познанию; неправильный же чертеж, наоборот, способствует порождению различных
ошибок. Исключительной педагогической сложностью и важностью этой проблемы объясняется то особое внимание, которым она пользуется в нашей методико-математической прессе последних лет (работы проф. И. Ф. Четверухина, проф. Д. Л. Франка, доц. Г. А. Владимирского и др.).
При изложении геометрических доказательств, связанных с точками пересечения различных линий, в учебниках обычно ведутся рассуждения на основании готового чертежа, в котором точки пересечения взяты в надлежащем месте. Вопрос о том, пересекаются ли рассматриваемые линии, и если да, то где находится точка их пересечения, как правило, не обсуждается. Однако умение осмысленно и правильно решать перечисленные вопросы имеет весьма существенное значение для овладения методами геометрических доказательств.
Пониманию учащимися целесообразности высказанных требований и проверке развития их критического чутья служат геометрические софизмы, основанные на ошибках в построении, среди которых мы выделяем шесть разновидностей.
Совпадающие точки рассматриваются как различные.
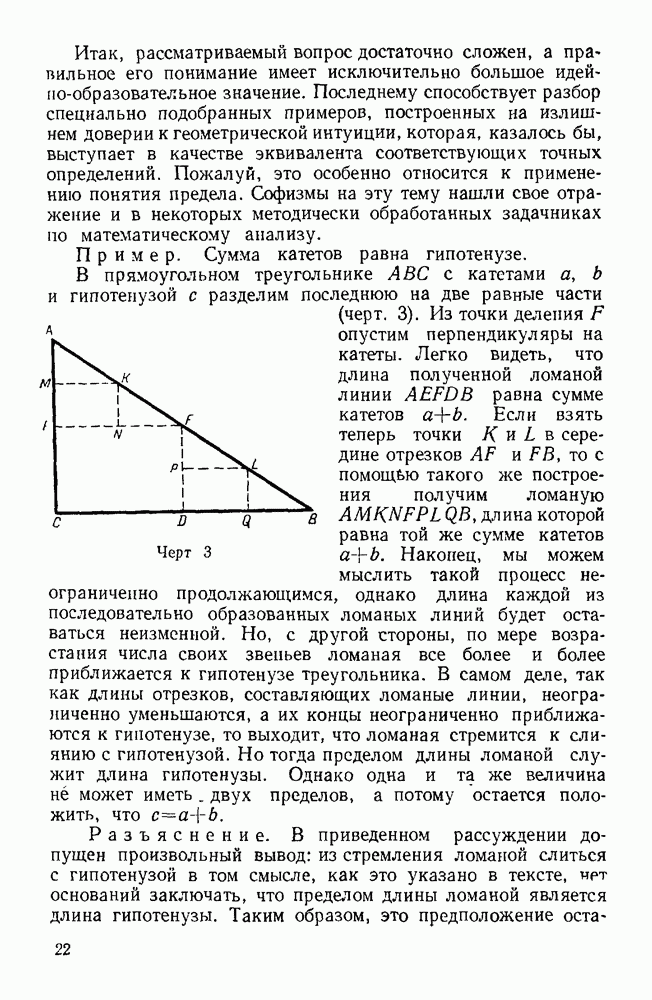
Пример. Внешний угол треугольника равен внутреннему, с ним не смежному.

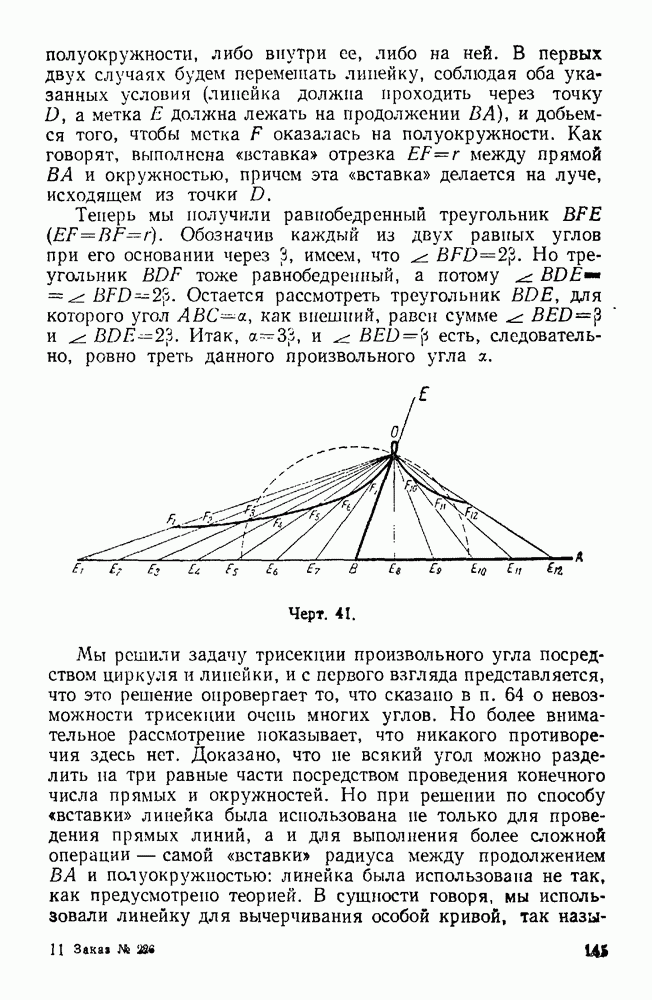
Черт. 4.
Пусть в четырехугольнике  дополняет
дополняет  до
до  . Так как любые три точки, не лежащие на одной прямой, вполне определяют положение окружности, то, следовательно, можно утверждать, что через точки
. Так как любые три точки, не лежащие на одной прямой, вполне определяют положение окружности, то, следовательно, можно утверждать, что через точки  проходит едчнетвенпая окружность. Точку пересечения этой окружности со стороной
проходит едчнетвенпая окружность. Точку пересечения этой окружности со стороной  обозначим через Е. Соединив ее отрезком прямой с точкой В, получаем четырехугольник
обозначим через Е. Соединив ее отрезком прямой с точкой В, получаем четырехугольник  вписанный в окружность. В нем сумма двух любых противоположных углов составляет
вписанный в окружность. В нем сумма двух любых противоположных углов составляет 
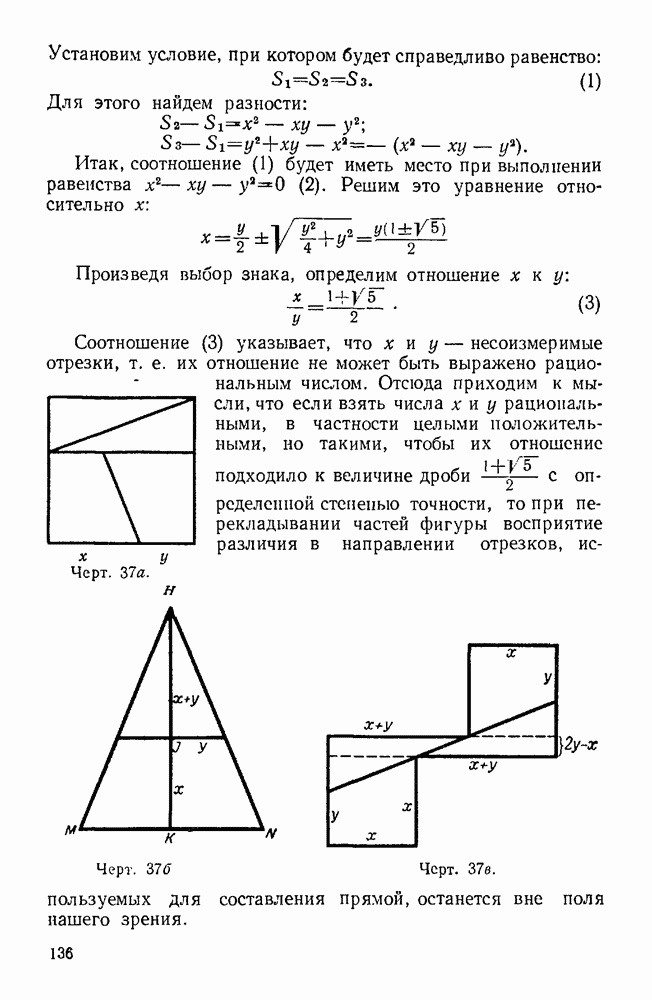
Подводя итоги, выписываем два соотношения:
1)  2)
2)  . Из них, как легко
. Из них, как легко
видеть, следует, что  внешний угол
внешний угол  равен внутреннему, с ним не смежному.
равен внутреннему, с ним не смежному.
Разъяснение. Так как в первоначально взятом четырехугольнике сумма противоположных углов равна  то все его вершины, в том числе и С, должны лежать на окружности. Выходит, что точки
то все его вершины, в том числе и С, должны лежать на окружности. Выходит, что точки  и С не различные, а совпадающие. В силу этого треугольник
и С не различные, а совпадающие. В силу этого треугольник  вообще исчезает.
вообще исчезает.
Различные точки рассматриваются как совпадающие.
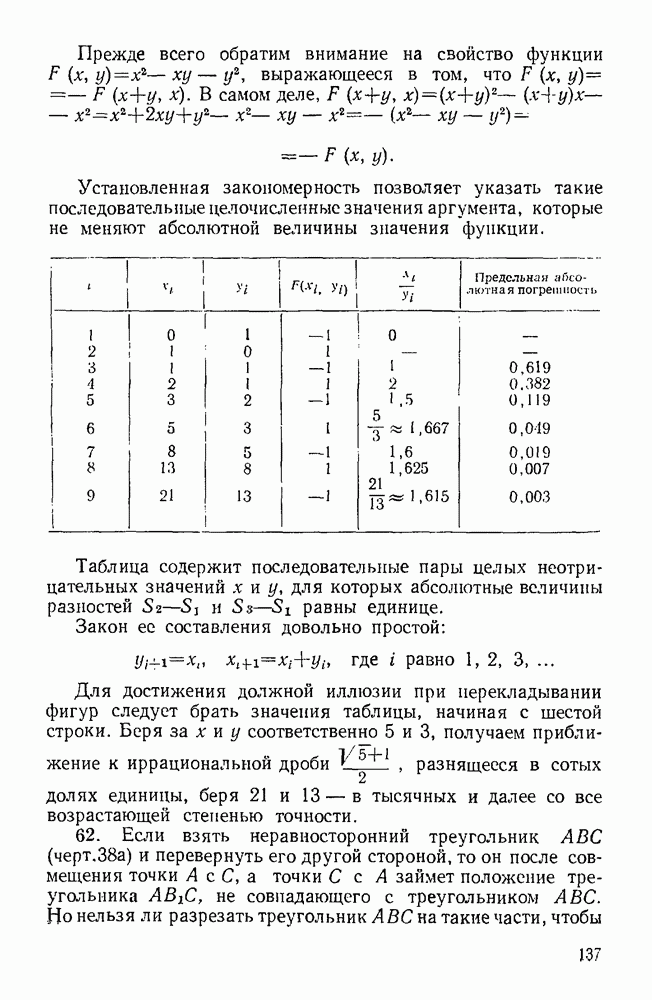
Пример. Площадь равностороннего треугольника равна нулю.
В равностороннем треугольнике  проводим высоту
проводим высоту  (черт. 5). Рассматриваемый треугольник равновелик прямоугольнику
(черт. 5). Рассматриваемый треугольник равновелик прямоугольнику  смежными сторонами которого являются отрезки
смежными сторонами которого являются отрезки  и
и  На продолжении
На продолжении  откладываем отрезок
откладываем отрезок  равный
равный  На отрезке
На отрезке  как на диаметре, описываем полуокружность, которая пересечется с продолжением
как на диаметре, описываем полуокружность, которая пересечется с продолжением  в некоторой точке К. Тогда
в некоторой точке К. Тогда  Квадрат
Квадрат  как и прямоугольник
как и прямоугольник  равновелик треугольнику
равновелик треугольнику 

Черт. 5.
Представляя  сдвинутым вдоль
сдвинутым вдоль  так, что С совпадает с
так, что С совпадает с  заметим, что квадрат
заметим, что квадрат  состоит из фигуры
состоит из фигуры  и фигуры, равновеликой
и фигуры, равновеликой  следовательно, квадрат
следовательно, квадрат  равновелик трапеции
равновелик трапеции  Отсюда следует, что площадь равностороннего треугольника
Отсюда следует, что площадь равностороннего треугольника  равна нулю.
равна нулю.
Разъяснение. Утверждение, что при указанном параллельном перенесении точка Е совпадает с точкой Н, ошибочно. Для того чтобы в этом убедиться и иметь возможность оценить численную величину ошибки, найдем отрезки  и
и 

где буквой а обозначена сторона 

Откуда находим:

точка берется там, где она не может быть.
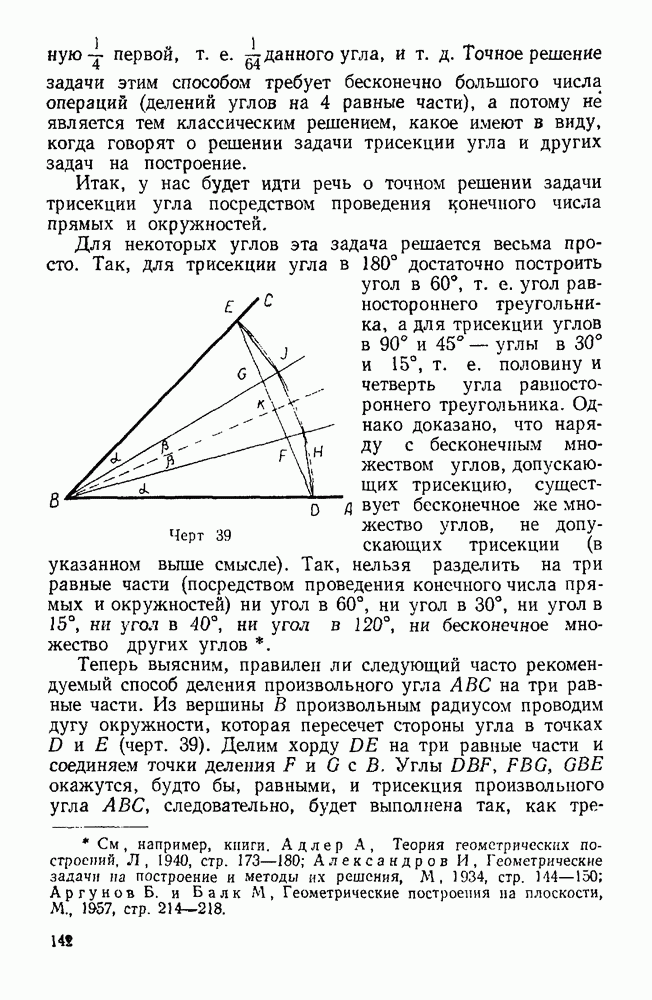
Пример. Каждая точка диаметра окружности лежит на самой окружности.

Черт. 6.
Пусть С — любая точка диаметра  Построив к точкам
Построив к точкам  четвертую гармоническую
четвертую гармоническую  делим пополам отрезок
делим пополам отрезок  и обозначаем его середину через 11. Тогда, если М обозначает центр окружности, имеем по известной теореме
и обозначаем его середину через 11. Тогда, если М обозначает центр окружности, имеем по известной теореме 
Напомним читателю вывод этой теоремы. Из чертежа не. посредственно усматриваем, что пропорцию

имеющую место для четырех гармонических точек  можно переписать так:
можно переписать так:

Воспользовавшись свойством пропорции, по которому сумма членов первого отношения так относится к их разности,
как сумма членов второго отношения к их разности, заключаем:

откуда

Заметив, что  и
и  утверждаем:
утверждаем:

С другой стороны, если перпендикуляр в точке Н к АВ пересечет окружность в точке Е, то

3)  . Вычитая почленно 3) из 2), будем иметь:
. Вычитая почленно 3) из 2), будем иметь:

Но из 1) и 4) следует, что  откуда
откуда  т. е. точка С лежит на окружности, и так как С есть произвольно взятая точка диаметра, то это справедливо для любой точки диаметра
т. е. точка С лежит на окружности, и так как С есть произвольно взятая точка диаметра, то это справедливо для любой точки диаметра 
Разъяснение. В пропорции

произведем перестановку крайних членов:

Так как  то, следовательно, и
то, следовательно, и  должно быть больше
должно быть больше  А потому точка И, которая должна быть серединой отрезка
А потому точка И, которая должна быть серединой отрезка  лежит не внутри круга, а вне его, правее точки В.
лежит не внутри круга, а вне его, правее точки В.
Итак, ошибка явилась следствием неправильного чертежа: точка И нами была взята там, где она не может быть.
Классическим софизмом этого типа является «доказательство» утверждения, что нет треугольников, отличных от равнобедренных. Индийский математик Сундара  приводит его в качестве примера такой ошибки, самую возможность появления которой исключают геометрические упражнения с куском бумаги. «Было бы совершенно правильно, — утверждает
приводит его в качестве примера такой ошибки, самую возможность появления которой исключают геометрические упражнения с куском бумаги. «Было бы совершенно правильно, — утверждает  требовать от учеников складывания этих чертежей на бумаге. Это давало бы им отчетливые и точные фигуры и невольно запечатлевало бы в их умах истины предложений».
требовать от учеников складывания этих чертежей на бумаге. Это давало бы им отчетливые и точные фигуры и невольно запечатлевало бы в их умах истины предложений».
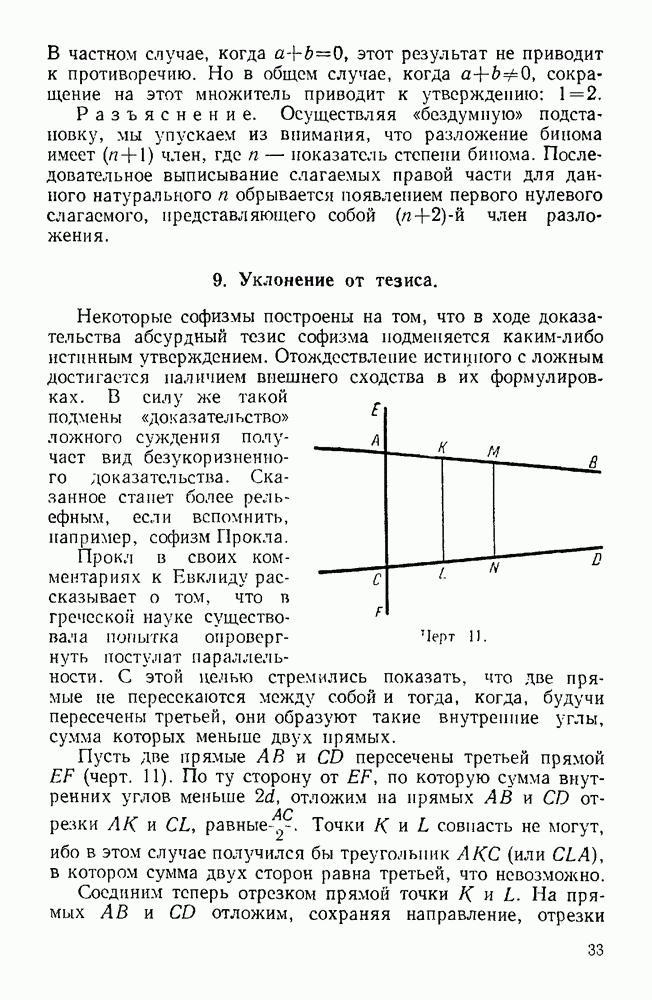
Предположенная точка пересечения на самом деле отсутствует.
Профессор Н. Ф. Четверухин в своей фундаментальной работе «Чертежи пространственных фигур в курсе геометрии» (М., 1946), анализируя педагогическую постановку задачи о построении изображений, подчеркивает следующее положение: «Особенно же велико значение изображений пространственных фигур в воспитании пространственного воображения (разрядка автора. —  у учащихся, в выработке у них более тонкого, более развитого пространственного мышления, столь необходимого в условиях современной сложной техники» (стр. 7). Некоторую роль в решении этой ответственной задачи может играть и разбор стереометрических вариантов некоторых софизмов.
у учащихся, в выработке у них более тонкого, более развитого пространственного мышления, столь необходимого в условиях современной сложной техники» (стр. 7). Некоторую роль в решении этой ответственной задачи может играть и разбор стереометрических вариантов некоторых софизмов.

Черт. 7.
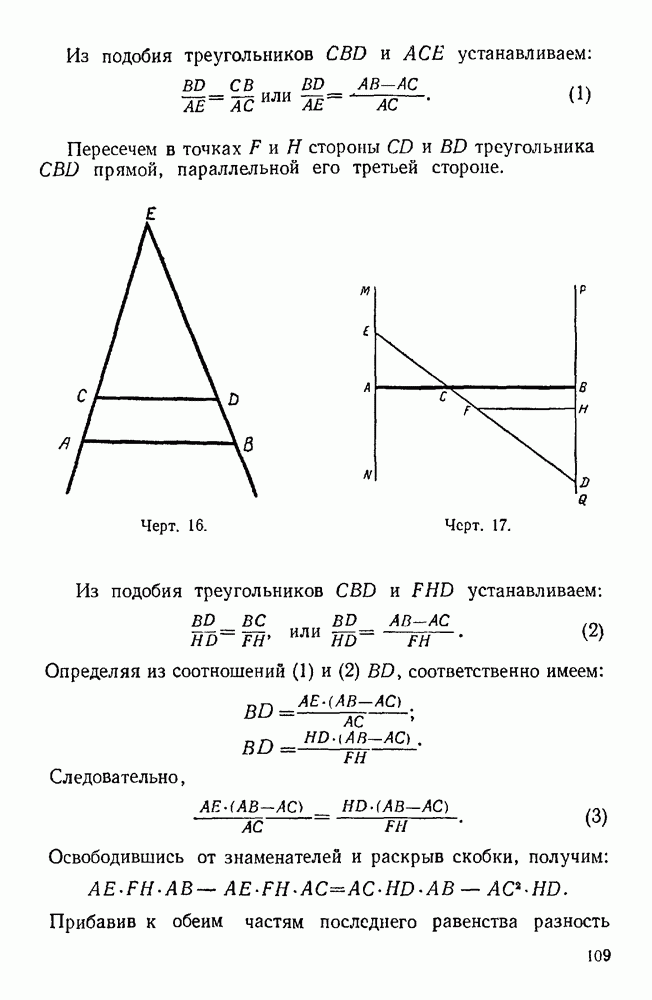
Пример. Прямой угол равен тупому.
Пусть имеем четырехугольник  (черт. 7), у которого
(черт. 7), у которого  сторона
сторона  образует со стороной А В прямой угол и равна стороне
образует со стороной А В прямой угол и равна стороне  образующей
образующей  тупой угол.
тупой угол.
Восстановим из середины стороны А В перпендикуляр к плоскости четырехугольника  а из середины стороны
а из середины стороны  перпендикуляр к этой прямой, пересекающий перпендикуляр к
перпендикуляр к этой прямой, пересекающий перпендикуляр к  в некоторой точке
в некоторой точке  Соединим точку
Соединим точку  с точками
с точками 
Из прямой теоремы о трех перпендикулярах легко усмотреть, что  т. е.
т. е. 
Замечая, что по построению  (как наклонные к одной прямой, имеющие равные проекции) и
(как наклонные к одной прямой, имеющие равные проекции) и  (как наклонные к прямой
(как наклонные к прямой  имеющие равные проекции), а по условию
имеющие равные проекции), а по условию  утверждаем, что
утверждаем, что 
Из равенства этих треугольников имеем:  Применяя обратную теорему о трех перпендикулярах, утверждаем, что
Применяя обратную теорему о трех перпендикулярах, утверждаем, что  перпендикулярна к
перпендикулярна к  а потому
а потому  что и требовалось доказать.
что и требовалось доказать.
Разъяснение. При использованном построении  является равнобедренным, что и приводит к противоречию, так как при равенстве наклонных
является равнобедренным, что и приводит к противоречию, так как при равенстве наклонных  и
и  их проекции
их проекции  и
и  оказываются неравными, что видно из рассмотрения
оказываются неравными, что видно из рассмотрения  и
и  но
но  так как Отсюда вывод, что прямые
так как Отсюда вывод, что прямые  и
и  не могут иметь общей точки.
не могут иметь общей точки.
Источник анализируемой весьма грубой ошибки состоит в том, что при построении постулировалось существование точки пересечения 5 как точки пересечения плоскости (перпендикулярной к прямой  и делящей отрезок
и делящей отрезок  пополам) и прямой (перпендикуляром к данной плоскости, восставленным к ней из середины отрезка
пополам) и прямой (перпендикуляром к данной плоскости, восставленным к ней из середины отрезка  Короче говоря, при построении исходили из предположения, что плоскость и прямая всегда пересекаются.
Короче говоря, при построении исходили из предположения, что плоскость и прямая всегда пересекаются.
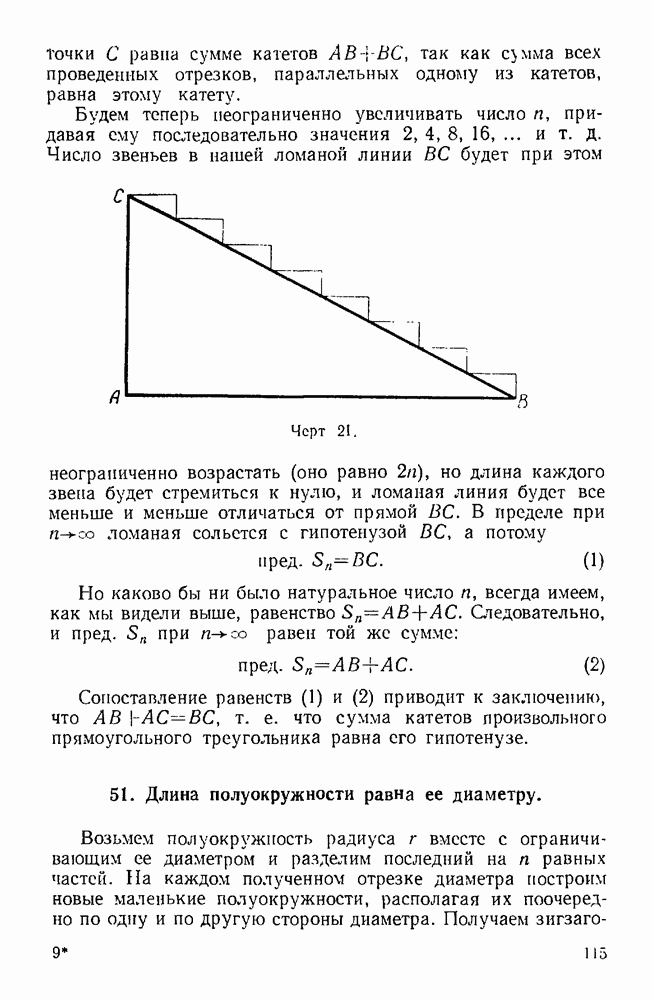
Ломаная принимается за прямую.
Пример. Софизм  и его обобщение.
и его обобщение.
Этот софизм исключительно ценец по своему идейно-образовательному значению. Обобщенная трактовка этого софизма, привлекающая теорию непрерывных дробей, изложена Игнатьевым. Более элементарное изложение этого обобщения дано в главе IV.
Прямая принимается за ломаную
Ошибка, обратная предыдущей.
Пример. Два треугольника равны, если они имеют по две соответственно равных стороны и по равному углу, противолежащему одной из них.
Легко увидеть, что в этом предложении «обобщен» четвертый признак равенства треугольников. В самом деле, обычный признак предусматривает, что угол берется против большей стороны. В приведенной же формулировке это ограничение снято.
Итак, даны треугольники 

Черт. 8
и  причем
причем  требуется доказать, что
требуется доказать, что 
Доказательство. Приложим  и
и  один к другому так, чтобы их равные стороны
один к другому так, чтобы их равные стороны  и
и  совместились (черт. 8), причем точка В совпала бы с точкой
совместились (черт. 8), причем точка В совпала бы с точкой
В, точка С — с точкой С. Соединяем точки  На основании равенства отрезков
На основании равенства отрезков  заключаем, что
заключаем, что  равнобедренный, а, следовательно,
равнобедренный, а, следовательно,  А так как по условию теоремы дано, что
А так как по условию теоремы дано, что  то в зависимости от вида треугольника с помощью сложения или вычитания получаем соотношение:
то в зависимости от вида треугольника с помощью сложения или вычитания получаем соотношение:  Значит,
Значит,  равнобедренный, а потому
равнобедренный, а потому  Ссылкой на третий признак равенства треугольников заканчивается доказательство теоремы.
Ссылкой на третий признак равенства треугольников заканчивается доказательство теоремы.
Разъяснение. По условию имеем:

Из  находим:
находим:

Из  находим:
находим:

Так как в соотношениях (1) и (2) правые части равны, то равны и левые:

Относительно углов  возможно сделать три предположения:
возможно сделать три предположения:
1)  . В этом случае мы имеем действительно равные треугольники. Их равенство устанавливаем по
. В этом случае мы имеем действительно равные треугольники. Их равенство устанавливаем по  или
или  признакам равенства треугольников.
признакам равенства треугольников.

Черт. 9
2)  . В этом случае
. В этом случае  Следовательно, приведенный чертеж ненравилен: стороны
Следовательно, приведенный чертеж ненравилен: стороны  и
и  лежат на одной прямой (черт. 9). Прямая была принята за ломаную, и все наше доказательство, как построенное на неправильном чертеже, рушится.
лежат на одной прямой (черт. 9). Прямая была принята за ломаную, и все наше доказательство, как построенное на неправильном чертеже, рушится.
Таково конкретное проявление ошибки. Однако источник ее в другом — в неполном перечислении возможных случаев.
3)  Этот случай невозможен, так как разность двух углов треугольника не может быть равна 360°.
Этот случай невозможен, так как разность двух углов треугольника не может быть равна 360°.
Опровержение же утверждения «теоремы» легко достигается путем построения треугольников, удовлетворяющих требованиям «теоремы», но неравных между собой (см. черт. 45, стр 161).
| << Предыдущий параграф | Следующий параграф >> |
- ИЗ ПРЕДИСЛОВИЯ К ПЕРВОМУ ИЗДАНИЮ
- Глава I. ОБ УПРАЖНЕНИЯХ НА ОПРОВЕРЖЕНИЕ ОШИБОЧНЫХ МАТЕМАТИЧЕСКИХ РАССУЖДЕНИЙ И ИХ КЛАССИФИКАЦИИ
- 1. МАТЕМАТИЧЕСКИЕ СОФИЗМЫ И ИХ ПЕДАГОГИЧЕСКАЯ РОЛЬ.
- II. КЛАССИФИКАЦИЯ УПРАЖНЕНИЙ НА ОПРОВЕРЖЕНИЕ ЛОЖНЫХ МАТЕМАТИЧЕСКИХ РАССУЖДЕНИЙ.
- 2. Распространение на исключительные случаи.
- 3. Приписывание свойств определенного вида всему роду.
- 4. Неправильное применение принципа непосредственных умозаключений путем обращения.
- 5. Подмена точных определений геометрической интуицией.
- 6. Ошибки построения.
- 7. Ошибки, являющиеся следствием буквального толкования сокращенной (условной) формулировки некоторых геометрических утверждений.
- 8. Нарушение смысла условных записей.
- 9. Уклонение от тезиса.
- Глава II. АРИФМЕТИКА.
- I. ПРИМЕРЫ ЛОЖНЫХ РАССУЖДЕНИЙ.
- 2. На двух нормальных руках одиннадцать пальцев.
- 3. Квадратные рубли.
- 4. 45 — 45 = 45
- 5. 40 : 8 = 41
- 6. Дважды два — пять!
- 7. Есть ли здесь пропорциональность?
- 8. 100% экономии.
- 9. Как вычислять средний процент?
- 10. Что даст ежегодный прирост в 40% за пять лет?
- 11. Новое правило умножения дробей.
- 12. Куда делся рубль?
- 13. Откуда появился лишний гривенник?
- 14. Завещание отца.
- 15. 2-3=4.
- II. АНАЛИЗ ПРИМЕРОВ.
- Глава III. АЛГЕБРА.
- I. ПРИМЕРЫ ЛОЖНЫХ РАССУЖДЕНИЙ.
- 19. Делимость многочленов и делимость чисел.
- 20. Произвольно взятое число а равно нулю.
- 21. 7 = 13.
- 22. Положительная единица равна отрицательной единице.
- 23. Другое «доказательство» равенства положительной и отрицательной единиц.
- 24. Мнимая единица и действительная отрицательная единица равны.
- 25. i^2 = 1
- 26. Всякое отрицательное число больше положительного, имеющего то же абсолютное значение.
- 27. Если a > b, то a > 2b
- 28. Если а и b положительные числа, то a > b и b > a.
- 29. Положительное число меньше нуля.
- 30. Сумма натуральных чисел, каждое из которых превосходит единицу, больше их произведения.
- 31. Чему равен квадратный корень из числа a^2?
- 32. Еще одно «доказательство» равенства нулю произвольно взятого числа.
- 33. Число не изменяется, если в нем переставить любые цифры!
- 34. Что говорит теорема о существовании корня в алгебре комплексных чисел?
- 35. Об одном спэсобе получать правильные результаты, применение которого требует большой осторожности.
- 36. О сумме 1-1+1-1 + …
- 37. Всегда ли целое больше своей части?
- 38. Еще одно «доказательство» равенства двух произвольно взятых чисел.
- 39. Сумма двух произвольных одинаковых чисел равна нулю.
- 40. Число не изменится, если к нему прибавить 1.
- 41. Ахиллес и черепаха.
- 42. О некоторых ученических ошибках.
- II. АНАЛИЗ ПРИМЕРОВ.
- Глава IV. ГЕОМЕТРИЯ.
- 1. ПРИМЕРЫ ЛОЖНЫХ РАССУЖДЕНИЙ.
- 44. Отрезок прямой равен своей правильной части.
- 45. Все треугольники равновелики.
- 46. Сумма оснований любой трапеции равна нулю.
- 47. Объемлемая и объемлющая.
- 48. Еще о пропорциональности.
- 49. Две окружности разного радиуса имеют одну и ту же длину.
- 50. Сумма катетов равна гипотенузе.
- 51. Длина полуокружности равна ее диаметру.
- 52. Боковая поверхность круглого прямого конуса с радиусом основания r и высотой h выражается формулой P=pi*r(r+h).
- 53. В данной точке на прямой можно восставить два перпендикуляра к этой прямой.
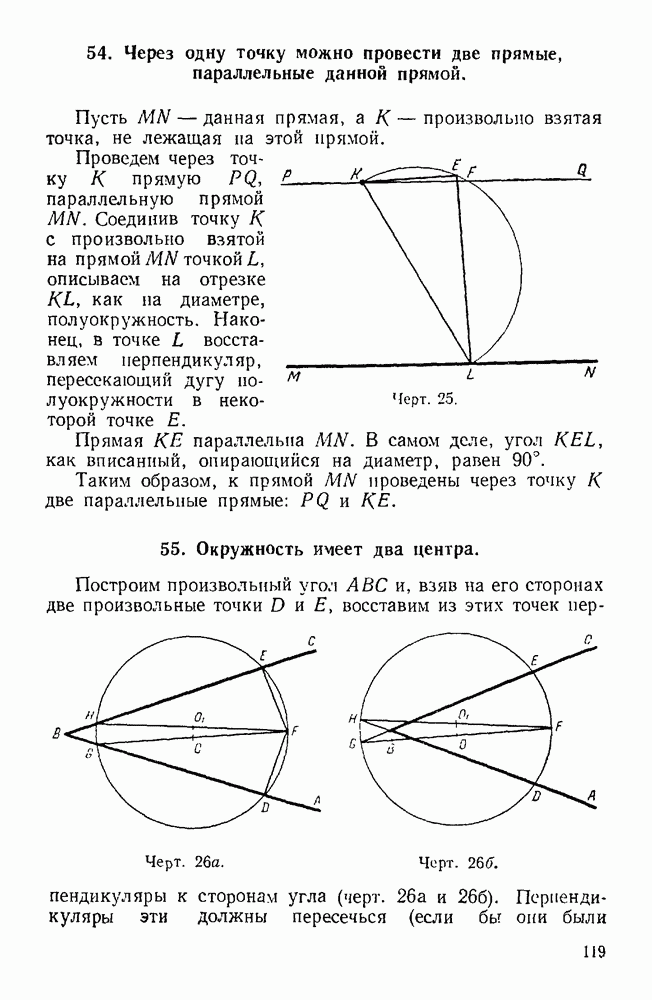
- 54. Через одну точку можно провести две прямые, параллельные данной прямой.
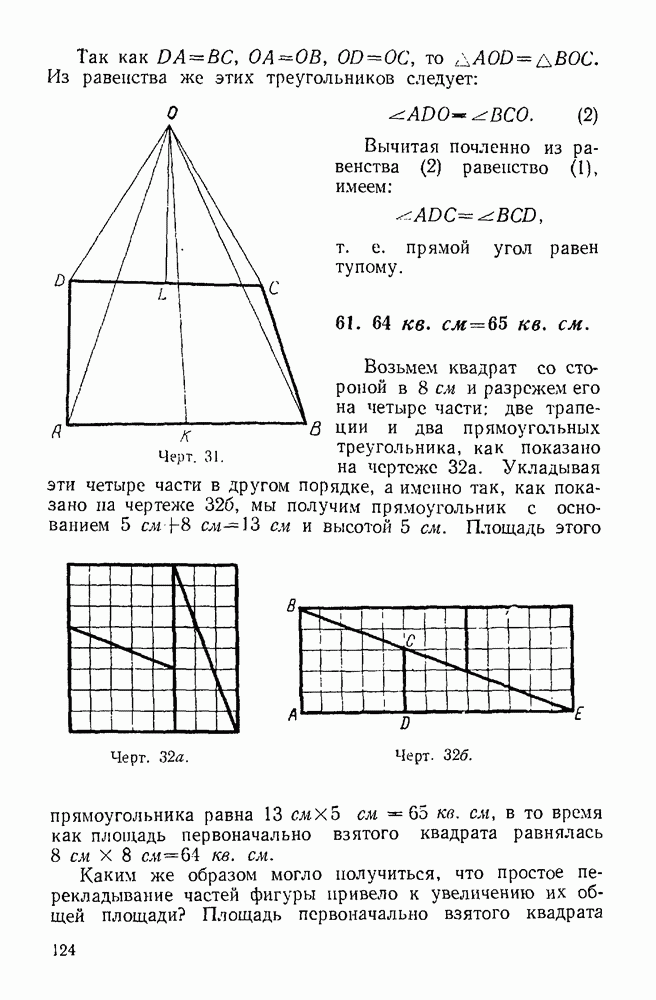
- 55. Окружность имеет два центра.
- 56. Из точки на прямую можно опустить два перпендикуляра.
- 57. Через две данные точки можно провести две прямые.
- 58. Любой треугольник — равнобедренный.
- 59. Катет прямоугольного треугольника равен его гипотенузе.
- 60. Прямой угол равен тупому (планиметрический вариант).
- 61. 64 кв. см = 65 кв. см.
- 62. Задача о заплате.
- II. АНАЛИЗ ПРИМЕРОВ.
- III. РАССКАЗЫ-ОБЪЯСНЕНИЯ ПО ПОВОДУ ОШИБОЧНЫХ РАССУЖДЕНИЙ.
- 64. Трисекция угла.
- 65. Еще о трисекции угла.
- 66. Квадратура круга.
- 67. Об одном доказательстве теоремы о сумме внутренних углов треугольника.
- 68. Как вычислять объем усеченной пирамиды?
- Глава V. ТРИГОНОМЕТРИЯ.
- 70. Синус угла уменьшается, если к углу прибавить 360°.
- 71. Косинус любого острого угла больше единицы.
- 72. 1/4 > 1/2
- 73. 2^2 = 4^2
- 74. Площадь прямоугольника равна нулю.
- 75. Существуют равные треугольники, у которых не все стороны равны.
- 76. Каждый треугольник — прямоугольный.
- II. АНАЛИЗ ПРИМЕРОВ
- Глава VI. ПРИБЛИЖЕННЫЕ ВЫЧИСЛЕНИЯ. РАССКАЗЫ-ОБЪЯСНЕНИЯ ПО ПОВОДУ ОШИБОЧНЫХ РАССУЖДЕНИЙ
- 78. Все большие числа приближенно равны между собой.
- 79. О точности произведения приближенных чисел.
- 80. Верна ли формула …
- 81. Сколько цифр надо знать в подкоренном числе, чтобы получить корень с заданной точностью?
- 82. Зачем освобождаются от иррациональности в знаменателе?