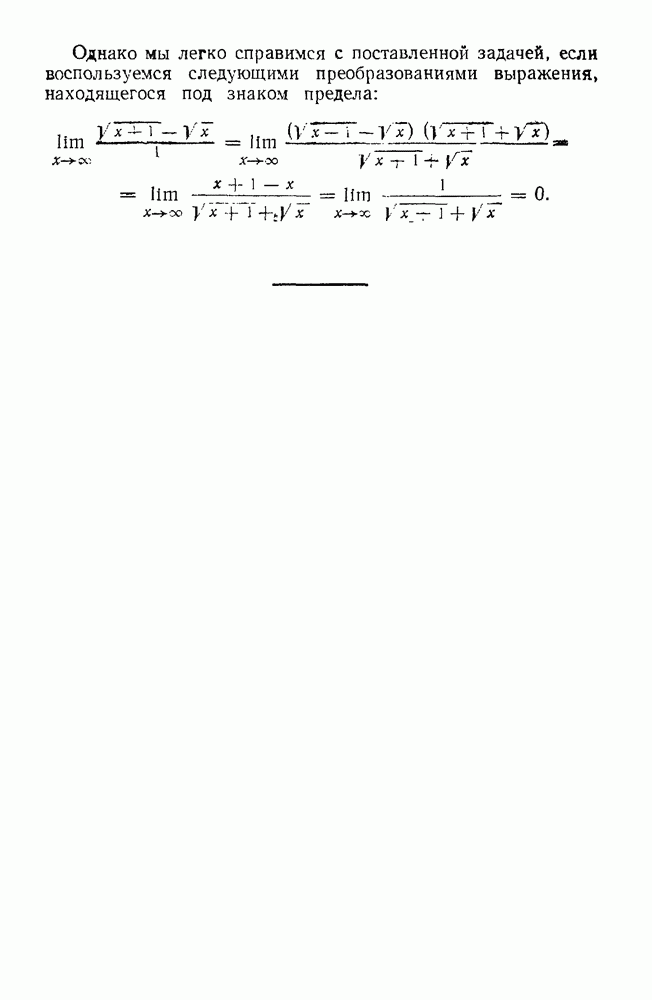| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
II. КЛАССИФИКАЦИЯ УПРАЖНЕНИЙ НА ОПРОВЕРЖЕНИЕ ЛОЖНЫХ МАТЕМАТИЧЕСКИХ РАССУЖДЕНИЙ.
В истории развития науки математические софизмы (в свое время парадоксы) играли существенную роль: они способствовали усилению требований содержательного анализа и строгого доказательства и порой приводили к длительному отказу, по крайней мере официальному, от использования тех понятий и методов, которые не были еще доступны для строго логической обработки. Отсюда понятен и рано возникший интерес к изучению, систематизации и педагогическому использованию заведомо ложных доказательств.
Осознание педагогической роли математических упражнений на опровержение ложных доказательств порождает стремление к выявлению и характеристике их основных видов как необходимого условия для рационального отбора и использования этого материала в школе.
Первый опыт составления сборника геометрических софизмов был предпринят автором «Начал» Евклидом из Александрии. К великому сожалению, этот труд Евклида, носивший название «Псевдария», считается безнадежно утерянным.
О его назначении и содержании рассказывает нам Прокл (410—485). Из слов Прокла видно, что работа предназначалась для начинающих изучать геометрию. Она ставила своей задачей научить учащихся обнаруживать ложные заключения и тем самым иметь возможность их избегать.
Для обнаружения ошибок Евклидом были предложены остроумные методы, которые он, перечисляя в определенном порядке, сопровождает соответствующими упражнениями. Ложному выводу Евклид противопоставляет истинный и показывает, как иногда интуиция может служить источником заблуждения.
Выдающийся русский педагог-математик В. И. Обреимов (1843—1910) предложил свой «опыт группировки» упражнений указанного типа и перечислил эти группы.
Первые три группы классификации В. И. Обреимова (равенство неравных, неравенство равных и меньшее превышает большее) охватывают те ложные доказательства, тезисы которых противоречат применению критериев сравнения, т. е. понятий больше, меньше и равно.
Четвертая группа — геометрические несообразности. В нее включены такие умозаключения, в которых нелепый вывод возникает из-за ошибки чертежа при безукоризненном проведении всех остальных логических рассуждений.
Пятая группа — «мнимое реально». Здесь нашли себе место ложные доказательства, связанные с неправильной трактовкой понятия мнимого числа.
Классификация В. И. Обреимова не свободна от недостатков. Во-первых, при перечислении видов делимого понятия не выдержан принцип единственности основания деления: критерии сравнения, с одной стороны, и принадлежность к геометрии или к данному разделу курса алгебры (мнимые числа), с другой. Во-вторых, за основание первых трех групп классификации В. И. Обреимова выбран чисто внешний, весьма общий и несущественный для характеристики ложных доказательств признак деления. В силу этого материал, относящийся к уяснению одной и той же ошибки, разбросан по разным разделам. Недоразумения в связи с делением на нуль изложены в первом и во втором разделах, а недоразумения из-за отсутствия перемены знака при умножении обеих частей неравенства на отрицательное число — во втором и третьем разделах, и т. п.
Положительным моментом классификации В. И. Обреимова является выделение в особую группу ложных доказательств, основанных на ошибках построения.
Перейдем теперь к рассмотрению указаний на классификацию ложных доказательств немецкого ученого Германа Шуберта (1848—1911). Он высказывается за выделение четырех видов ложных доказательств, основанных на делении на нуль, на двузначности квадратного корпя, на геометрическом обмане (ошибка в построении) и на приписывании сумме бесконечного множества чисел бесконечно большой величины.
Ценным в предложении Г. Шуберта является распределение ложных доказательств по характеру тех ошибок, которые приводят к ложным выводам. Однако классификация по избранному принципу осталась неразвернутой. Перечисленные Г. Шубертом четыре вида ложных доказательств не исчерпывают даже минимального объема рассматриваемого понятия. В частности, ничего не сказано о ложных доказательствах, построенных на излишнем доверии к геометрической интуиции в тех случаях, когда прямой геометрический обман не имеет места.
Французский педагог и историк математики Е. Фурре относит к геометрическим софизмам все те софизмы, формулировки которых касаются геометрических объектов. Таким образом, сюда включаются и геометрические воплощения алгебраических софизмов, основанные на допущении чисто алгебраических ошибок. Разумеется, эти ошибки могут быть замаскированы не только различными геометрическими предложениями, но и относящимися к другим отделам математики. Ясно, что классификация, основанная на внешней форме ошибочного рассуждения, есть чисто внешняя классификация.
Геометрические софизмы в указанном широком смысле этого термина Е. Фурре разделяет на два вида: основанные на ошибках в построении и основанные на ошибках в рассуждении. В ошибках рассуждения Е. Фурре различает ошибки, связанные с отклонением от точных определений и с выполнением недозволенных опесаций над числами.
Теперь мы предложим вниманию читателя наш опыт классификации упражнений на опровержение ложных математических рассуждений по важнейшим разделам ошибок в речи и мышлении, которые, обычно не именуя их, упорно предотвращает учитель всей практикой своей повседневной работы как при изучении теории, так и при выполнении упражнений.
Предлагаемая классификация рассчитана прежде всего на учителя. С этой целью в ней подчеркивается уже названием каждого вида специфическое педагогическое назначение того или иного упражнения, что создает возможности для быстрой ориентировки в материале и предупреждает бессистемность в его использовании
Наш педагогический опыт позволяет утверждать, что эта классификация полезна и ученикам старших классов, у которых рассуждения начинают совершаться не только в соответствии с определенными принципами, но и на основе осознания этих принципов. В этот переходный период учащиеся ощущают настоятельную потребность в проверке точности своих познаний, их логической обоснованности, степени своего понимания и удовлетворительности словесного выражения.
Мы далеки от мысли, что предлагаемая классификация свободна от недостатков. Она, конечно, не свободна от тех недостатков, которые характерны, например, для классификации арифметических задач по существенным особенностям
способов их решения. Использование более широкого опыта работы и критика помогут внести в нее необходимые коррективы. Однако мы позволяем себе думать, что и в настоящем виде она представляет некоторый шаг вперед по сравнению с существующими классификациями, преследующими, как и данная, чисто педагогические цели.
Перейдем теперь к конкретному рассмотрению вопроса.
1. Неправильности речи.
Систематический анализ софизмов был дан впервые Аристотелем (384—322 до н. э.) в особом трактате, посвященном софистическим опровержениям, в котором все ошибки разделяются на два класса: «неправильности речи» и ошибки «вне речи», т. е. в мышлении.
Нет необходимости доказывать, что каждый правильно спланированный и проведенный урок по предмету математики является одновременно и уроком по развитию речи учащихся. На страницах методической литературы неоднократно подчеркивалось благотворное влияние математики на совершенствование речи ученика в смысле ее точности и последовательности. Однако эти цели не достигаются автоматически. Для их достижения необходима повседневная работа учителя математики над словом ученика, над формой выражения его мысли как при устных ответах, так и при выполнении различных письменных работ. Интенсивному искоренению неправильностей, встречающихся в речи учащихся, способствует привлечение самих учащихся к корректированию ответов своих товарищей. Следует отчетливо довести до сознания учащихся, что неправильности речи не только затрудняют изучение математики, но и являются одним из источников различных заблуждений.
Двусмысленность слова.
Как правило, каждое понятие в математике обозначается своим особым термином. В исключительных же случаях, т. е. когда один и тот же термин употребляется в разных смыслах, необходимы специальные указания, в каком именно смысле здесь употреблен данный термин, если это неясно из самого контекста. К числу неоднозначных математических терминов относятся, например, следующие: квадрат (показатель степени и геометрическая фигура), корень (в смысле
решения уравнения и как синоним слова радикал), число (количественное и порядковое, отвлеченное и именованное, точное и приближенное).
Пример. Отец и сын прибыли в город на постоянное жительство. Мальчик, знавший из рассказов рсдчтелей, что в городе 25 тыс жителей, поспешил уже на вокзале заявить, что теперь в городе жителей 25 002. Отец засмеялся и начал что-то объяснять сыну Что сказал отец?
Двусмысленность произношения.
Здесь речь идет об искажении первоначального смысла фразы из-за измененной постановки ударения в каком-нибудь слове.
Пример. Сто сорок да сто сорок будет двести сорок
Двусмысленность конструкции.
Имеется в виду такая конструкция предложения, которая допускает разное восприятие его смысла.
Пример. Сколько будет трижды три и семь?
Со смыслом этой фразы согласуются два различных, друг друга исключающих, порядка действий, а именно: 
Ошибка распределения
Эта ошибка имеет место, когда термину, употребленному в собирательном смысле, придается значение разделительного.
Пример. Все углы треугольника равны двум прямым углам.
Здесь слово «все» употреблено в смысле «сумма». Однако вывод термина неудачен, так как можно его понимать и в смысле «каждый». Мысль становится абсурдной: «Каждый угол треугольника равен сумме двух прямых углов».
Ошибка составления.
Ошибка, противоположная предыдущей. Она возникает тогда, когда термину, употребленному в разделительном смысле, придается значение собирательного.
Пример. Все углы треугольника меньше двух прямых углов.
Здесь слово «все» употреблено в смысле «каждый». Однако выбор термина нельзя признать удачным, так как его можно понимать и в смысле «сумма». Мысль для системы евклидовой
геометрии становится абсурдной: «Сумма углов треугольника меньше двух прямых углов».
Разбор ошибок «вне речи» мы начнем с ложных доказательств, построенных на поспешных, непродуманных обобщениях. Рассмотрение некоторых из них в школе весьма полезно, так как «прежде всего совершенно ясно замечается тенденция к расширенному пониманию тех правил, с которыми оперирует элементарная память» (Д. Д. Мордухай-Болтовской).
| << Предыдущий параграф | Следующий параграф >> |
- ИЗ ПРЕДИСЛОВИЯ К ПЕРВОМУ ИЗДАНИЮ
- Глава I. ОБ УПРАЖНЕНИЯХ НА ОПРОВЕРЖЕНИЕ ОШИБОЧНЫХ МАТЕМАТИЧЕСКИХ РАССУЖДЕНИЙ И ИХ КЛАССИФИКАЦИИ
- 1. МАТЕМАТИЧЕСКИЕ СОФИЗМЫ И ИХ ПЕДАГОГИЧЕСКАЯ РОЛЬ.
- II. КЛАССИФИКАЦИЯ УПРАЖНЕНИЙ НА ОПРОВЕРЖЕНИЕ ЛОЖНЫХ МАТЕМАТИЧЕСКИХ РАССУЖДЕНИЙ.
- 2. Распространение на исключительные случаи.
- 3. Приписывание свойств определенного вида всему роду.
- 4. Неправильное применение принципа непосредственных умозаключений путем обращения.
- 5. Подмена точных определений геометрической интуицией.
- 6. Ошибки построения.
- 7. Ошибки, являющиеся следствием буквального толкования сокращенной (условной) формулировки некоторых геометрических утверждений.
- 8. Нарушение смысла условных записей.
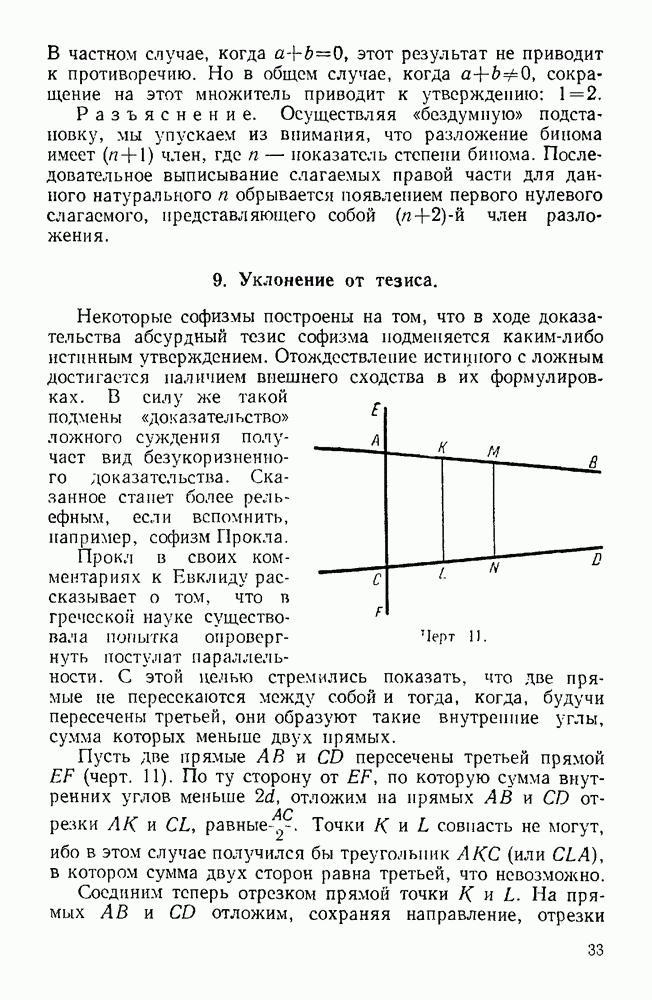
- 9. Уклонение от тезиса.
- Глава II. АРИФМЕТИКА.
- I. ПРИМЕРЫ ЛОЖНЫХ РАССУЖДЕНИЙ.
- 2. На двух нормальных руках одиннадцать пальцев.
- 3. Квадратные рубли.
- 4. 45 — 45 = 45
- 5. 40 : 8 = 41
- 6. Дважды два — пять!
- 7. Есть ли здесь пропорциональность?
- 8. 100% экономии.
- 9. Как вычислять средний процент?
- 10. Что даст ежегодный прирост в 40% за пять лет?
- 11. Новое правило умножения дробей.
- 12. Куда делся рубль?
- 13. Откуда появился лишний гривенник?
- 14. Завещание отца.
- 15. 2-3=4.
- II. АНАЛИЗ ПРИМЕРОВ.
- Глава III. АЛГЕБРА.
- I. ПРИМЕРЫ ЛОЖНЫХ РАССУЖДЕНИЙ.
- 19. Делимость многочленов и делимость чисел.
- 20. Произвольно взятое число а равно нулю.
- 21. 7 = 13.
- 22. Положительная единица равна отрицательной единице.
- 23. Другое «доказательство» равенства положительной и отрицательной единиц.
- 24. Мнимая единица и действительная отрицательная единица равны.
- 25. i^2 = 1
- 26. Всякое отрицательное число больше положительного, имеющего то же абсолютное значение.
- 27. Если a > b, то a > 2b
- 28. Если а и b положительные числа, то a > b и b > a.
- 29. Положительное число меньше нуля.
- 30. Сумма натуральных чисел, каждое из которых превосходит единицу, больше их произведения.
- 31. Чему равен квадратный корень из числа a^2?
- 32. Еще одно «доказательство» равенства нулю произвольно взятого числа.
- 33. Число не изменяется, если в нем переставить любые цифры!
- 34. Что говорит теорема о существовании корня в алгебре комплексных чисел?
- 35. Об одном спэсобе получать правильные результаты, применение которого требует большой осторожности.
- 36. О сумме 1-1+1-1 + …
- 37. Всегда ли целое больше своей части?
- 38. Еще одно «доказательство» равенства двух произвольно взятых чисел.
- 39. Сумма двух произвольных одинаковых чисел равна нулю.
- 40. Число не изменится, если к нему прибавить 1.
- 41. Ахиллес и черепаха.
- 42. О некоторых ученических ошибках.
- II. АНАЛИЗ ПРИМЕРОВ.
- Глава IV. ГЕОМЕТРИЯ.
- 1. ПРИМЕРЫ ЛОЖНЫХ РАССУЖДЕНИЙ.
- 44. Отрезок прямой равен своей правильной части.
- 45. Все треугольники равновелики.
- 46. Сумма оснований любой трапеции равна нулю.
- 47. Объемлемая и объемлющая.
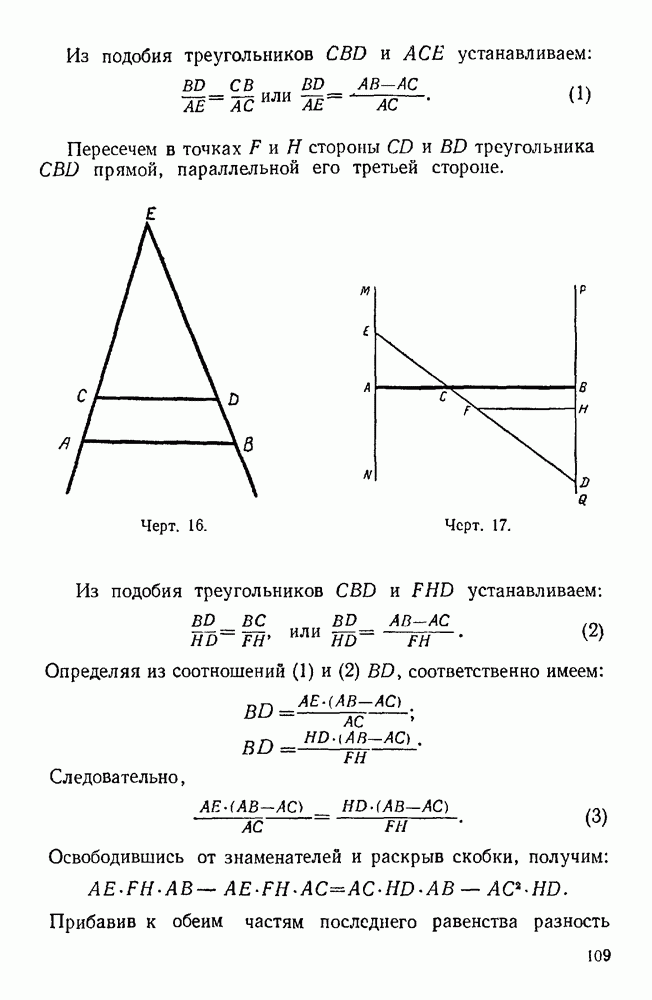
- 48. Еще о пропорциональности.
- 49. Две окружности разного радиуса имеют одну и ту же длину.
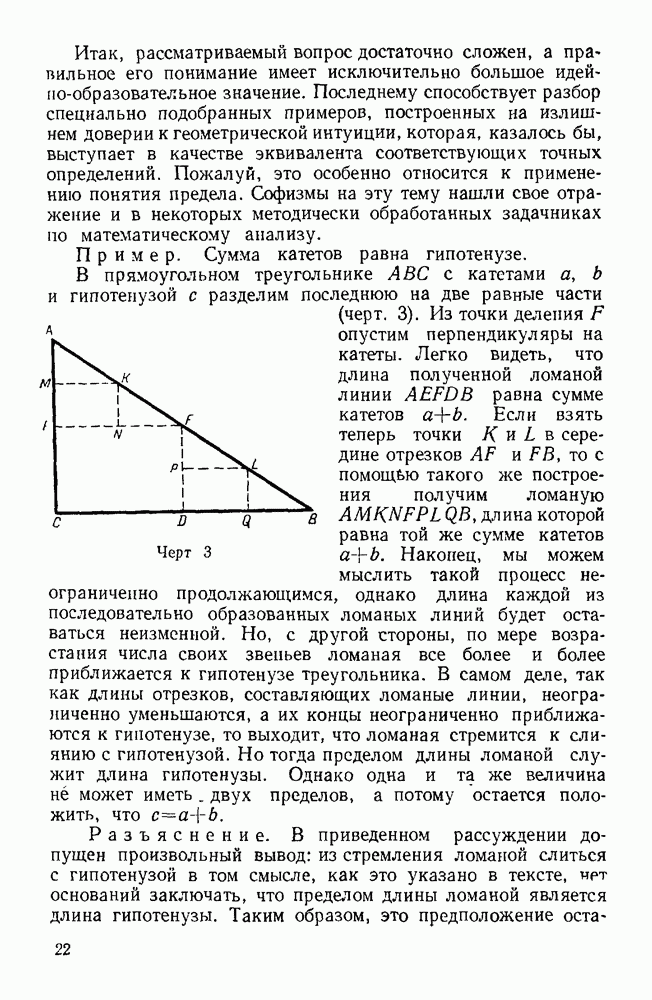
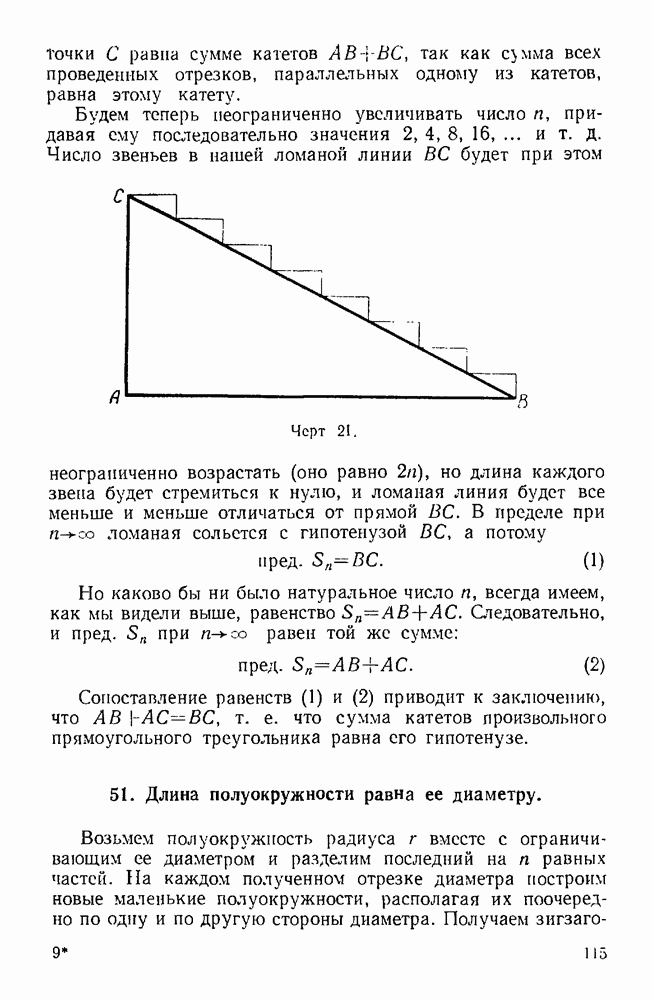
- 50. Сумма катетов равна гипотенузе.
- 51. Длина полуокружности равна ее диаметру.
- 52. Боковая поверхность круглого прямого конуса с радиусом основания r и высотой h выражается формулой P=pi*r(r+h).
- 53. В данной точке на прямой можно восставить два перпендикуляра к этой прямой.
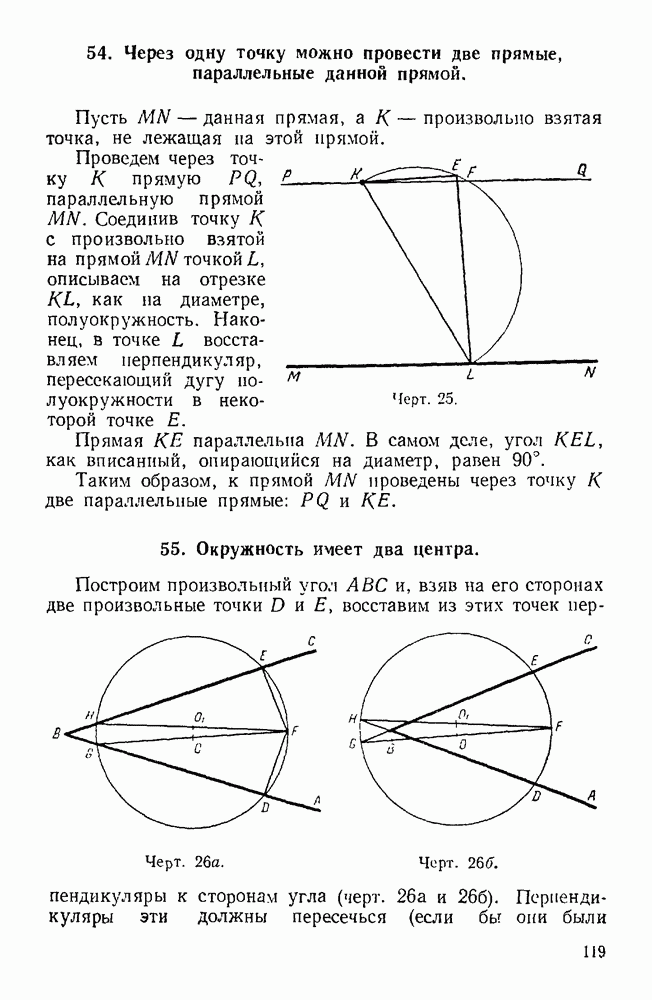
- 54. Через одну точку можно провести две прямые, параллельные данной прямой.
- 55. Окружность имеет два центра.
- 56. Из точки на прямую можно опустить два перпендикуляра.
- 57. Через две данные точки можно провести две прямые.
- 58. Любой треугольник — равнобедренный.
- 59. Катет прямоугольного треугольника равен его гипотенузе.
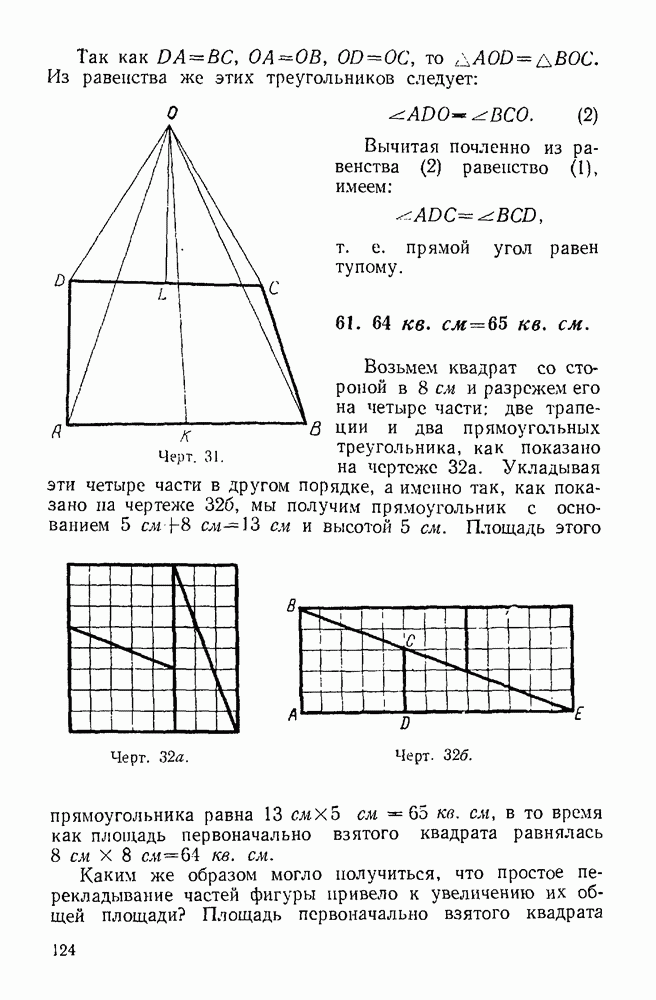
- 60. Прямой угол равен тупому (планиметрический вариант).
- 61. 64 кв. см = 65 кв. см.
- 62. Задача о заплате.
- II. АНАЛИЗ ПРИМЕРОВ.
- III. РАССКАЗЫ-ОБЪЯСНЕНИЯ ПО ПОВОДУ ОШИБОЧНЫХ РАССУЖДЕНИЙ.
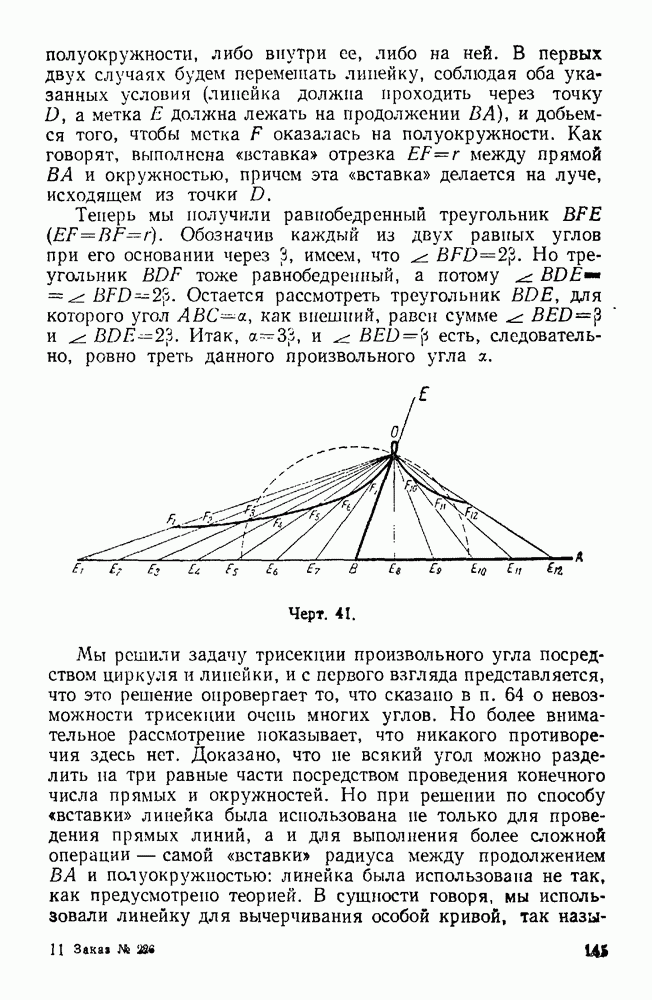
- 64. Трисекция угла.
- 65. Еще о трисекции угла.
- 66. Квадратура круга.
- 67. Об одном доказательстве теоремы о сумме внутренних углов треугольника.
- 68. Как вычислять объем усеченной пирамиды?
- Глава V. ТРИГОНОМЕТРИЯ.
- 70. Синус угла уменьшается, если к углу прибавить 360°.
- 71. Косинус любого острого угла больше единицы.
- 72. 1/4 > 1/2
- 73. 2^2 = 4^2
- 74. Площадь прямоугольника равна нулю.
- 75. Существуют равные треугольники, у которых не все стороны равны.
- 76. Каждый треугольник — прямоугольный.
- II. АНАЛИЗ ПРИМЕРОВ
- Глава VI. ПРИБЛИЖЕННЫЕ ВЫЧИСЛЕНИЯ. РАССКАЗЫ-ОБЪЯСНЕНИЯ ПО ПОВОДУ ОШИБОЧНЫХ РАССУЖДЕНИЙ
- 78. Все большие числа приближенно равны между собой.
- 79. О точности произведения приближенных чисел.
- 80. Верна ли формула …
- 81. Сколько цифр надо знать в подкоренном числе, чтобы получить корень с заданной точностью?
- 82. Зачем освобождаются от иррациональности в знаменателе?