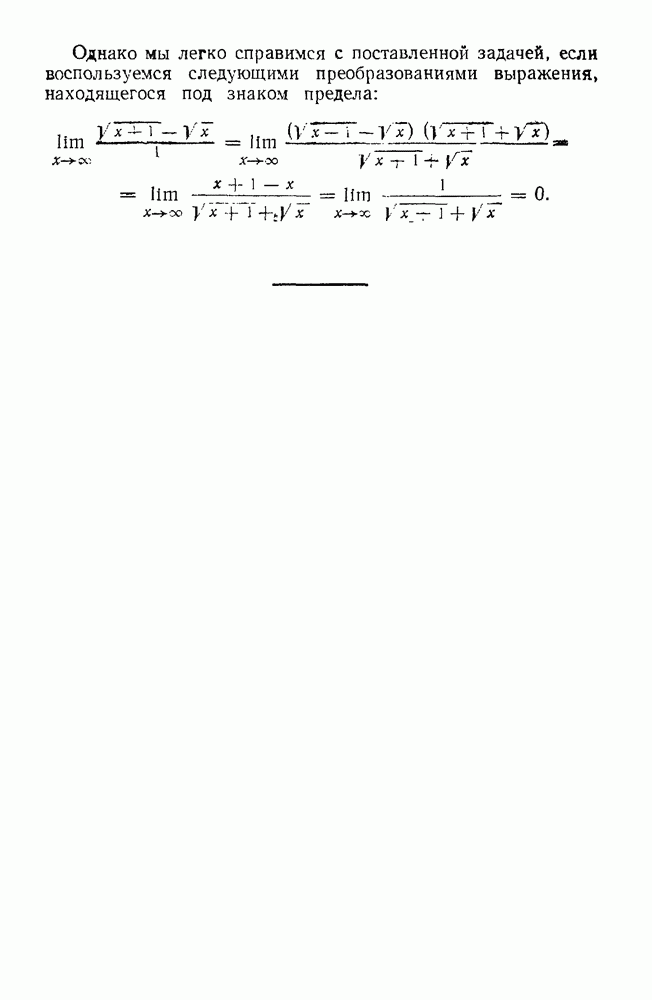| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
II. АНАЛИЗ ПРИМЕРОВ.
16. Если исходить из того, что в математике как науке все действия производятся над отвлеченными числами, то переход от соотношения (1) к (2) не имеет смысла.
Однако можно дать и другое объяснение этой ошибки, указав на то, что никаких «квадратных рублей» и «квадратных копеек» не существует, а потому операция извлечения корпя из обеих частей соотношения (1) бессмысленна.
Иллюзорная правдоподобность этого рассуждения основывается на неоднозначности термина «число», в данном случае на смешении понятия отвлеченного числа с именованным.
17. Ученик, очевидно, забыл о неоднозначности термина «корень» (в данном случае: истинный и посторонний). В частности, забыл он и о том, что при решении иррационального уравнения могут быть получены посторонние корни. Только этим можно объяснить, почему он рассматривал проверку лишь в плане подтверждения истинности произведенных им преобразований и вычислений, а не в качестве органической части предлагаемого им решения.
Не допустив этого, нельзя понять его смущения в связи с получением неверного равенства  которое представляло возможность сделать правильный вывод.
которое представляло возможность сделать правильный вывод.
Выявим причину смущения ученика.
С этой целью нам следует ответить на два вопроса:
1) Почему появился посторонний корень?
2) Корнем какого уравнения он является?
Для достижения возможно большей ясности полезно использовать прием решения, несколько отличный от использованного учеником. Он состоит в том, что мы уравнение (1) преобразуем к виду  а затем умножаем левую и правую его части на такой множитель, чтобы в левой части иметь разность квадратов двух функциональных выражений.
а затем умножаем левую и правую его части на такой множитель, чтобы в левой части иметь разность квадратов двух функциональных выражений.
Итак, уравнение (1) представляем в виде:

Умножим обе части его на множитель:

Тогда, очевидно, получим:

Мы пришли к уравнению (2), стр. 57, корни которого равны 4 и 1.
Корень  является посторонним Для уравнения (1). Он появился в результате умножения обеих частей уравнения на множитель
является посторонним Для уравнения (1). Он появился в результате умножения обеих частей уравнения на множитель  корнем которого он и является. В самом деле,
корнем которого он и является. В самом деле, 
Способ решения, использованный учеником, конечно, равносилен способу сейчас рассмотренному, но с помощью последнего отчетливее выявляется тот множитель, который может дать посторонние корни.
18. Отсутствие корней у уравнения (1) легко усмотреть из того факта, что его левая часть  неотрицательна и имеет смысл при
неотрицательна и имеет смысл при  а правая часть
а правая часть  при этом условии отрицательна. Следовательно, полученные решения
при этом условии отрицательна. Следовательно, полученные решения  являются корнями фуикции
являются корнями фуикции  в чем легко убедиться непосредственной подстановкой.
в чем легко убедиться непосредственной подстановкой.
19. Самая тщательная проверка доказательства делимости разности  на
на  не обнаруживает никакой ошибки. Точно так же не вызывает никаких сомнений и рассмотренный частный случай: при
не обнаруживает никакой ошибки. Точно так же не вызывает никаких сомнений и рассмотренный частный случай: при  разность
разность  не делится на
не делится на 
Попробуем найти частное от деления  на
на  оно равно:
оно равно:

Дроби, появившиеся во всех членах частного, кроме последнего, заставляют насторожиться и сразу указывают, в чем источник путаницы: слово «делиться» в алгебре и в арифметике имеет различный смысл.
Когда в алгебре говорят, что один многочлен, расположенный по степеням какой-нибудь главной буквы, например х, «делится» на другой многочлен, расположенный по степеням того же х, то под этим разумеют возможность получения целого частного, т. е. многочлена, тоже расположенного по степеням  Будут ли при этом коэффициенты отдельных членов частного числами целыми или дробными — совершенно безразлично. Например, двучлен
Будут ли при этом коэффициенты отдельных членов частного числами целыми или дробными — совершенно безразлично. Например, двучлен  делится на
делится на  а и дает в частном
а и дает в частном  коэффициенты а
коэффициенты а  могут при этом оказаться и целыми и дробными. Двучлен
могут при этом оказаться и целыми и дробными. Двучлен  делится на
делится на  и дает в частном
и дает в частном  коэффициент
коэффициент  опять-таки может иметь при этом и целое значение (например, при
опять-таки может иметь при этом и целое значение (например, при  и дробное (например, при
и дробное (например, при 
В арифметике же в применении к натуральным числам слово «делится» имеет совсем другой смысл: если натуральное число а делится на натуральное число  то существует такое натуральное же число с, которое, будучи умножено на
то существует такое натуральное же число с, которое, будучи умножено на  дает а.
дает а.
Поэтому из делимости одного многочлена на другой (в алгебраическом смысле!) еще не вытекает делимость (в арифметическом смысле!) тех чисел, которые получатся, если заменить в многочленах буквы числами. Делимость чисел будет вытекать из делимости многочленов лишь в том случае, когда все коэффициенты частного — целые алгебраические выражения, а не дроби (при условии, разумеется, что все буквы заменяются натуральными числами и что делитель получает значение, отличное от нуля).
Отметим еще одно различие между делением многочленов и делением натуральных чисел. При делении многочлена на многочлен степень остатка (относительно главной буквы) всегда ниже степени делителя, при делении же натуральных чисел остаток всегда меньше делителя. Деление многочленов, выполненное совершенно правильно, может после замены букв числами привести к такому случаю деления чисел, которое не будет правильным в арифметическом смысле. Например, при делении многочлена  на
на  получаем в частном
получаем в частном  и в остатке
и в остатке  Если заменить х через 3, делимое принимает значение 15, делитель 4, а частное и остаток равны
Если заменить х через 3, делимое принимает значение 15, делитель 4, а частное и остаток равны  (вместо правильных значений 3 и 3), т. е. остаток оказывается больше делителя.
(вместо правильных значений 3 и 3), т. е. остаток оказывается больше делителя.
Итак, не всегда правильное в алгебраическом смысле, правильно и с точки зрения арифметической!
20. В рассуждении допущена грубая ошибка. Из уравнения  где а — произвольно взятое действительное число, отличное от пуля, не следует, конечно, что
где а — произвольно взятое действительное число, отличное от пуля, не следует, конечно, что 
В самом деле, решение уравнения  приводит к следующим выводам:
приводит к следующим выводам:

Так как но условию  то уравнение
то уравнение  не имеет решений: нет такого числа, которое, будучи умножено на нуль, дает число, отличное от нуля.
не имеет решений: нет такого числа, которое, будучи умножено на нуль, дает число, отличное от нуля.
Однако у читателя возможно возникло сомнение: законен ли переход от 
Подобный переход вполне законен, если возведенные в куб числа оба действительные: кубический корень из действительного числа, если ограничиваться только действительными значениями, имеет только одно значение (положительное, если подкоренное число положительно, и отрицательное, если оно отрицательно).
Из сказанного следует, что полученный результат — уравнение (2) не имеет корней — указывает на отсутствие корней во множестве действительных чисел у уравнения (1).
21. Корнем уравнения (1) является число 10, в чем легко убедиться.
При  соотношение (2) принимает такой вид:
соотношение (2) принимает такой вид:

Так как частное от деления нуля на любое число, отличное от нуля, равно 0, то, очевидно, из соотношения  нельзя делать заключения о равенстве
нельзя делать заключения о равенстве  если
если 
Мы здесь встретились с использованием ложной аналогии, а именно: с распространением некоторого утверждения (если  то
то  на случай исключения
на случай исключения 
22. Во множестве действительных чисел соотношение (1) не имеет смысла: любая степень положительного числа есть положительное число.
Соотношение (1) приобретает смысл, если рассматривать вопрос в множестве комплексных чисел. В этом случае, положив  мы имеем правильное соотношение
мы имеем правильное соотношение  не приводящее, как известно, к противоречиям.
не приводящее, как известно, к противоречиям.
Однако при такой постановке вопроса мы выходим за те пределы, в которых проводилось анализируемое ошибочное рассуждение.
23. Понятие арифметического корня во множестве комплексных чисел не вводится.
Правильное вычисление произведения  предполагает следующий ход рассуждений:
предполагает следующий ход рассуждений:

который приводит к тому же результату, что и извлечение квадратного корня из единицы: 
Если же взять для каждого из сомножителей произведения  одно и тоже значение корня квадратного из минус единицы, то мы получим в результате —1.
одно и тоже значение корня квадратного из минус единицы, то мы получим в результате —1.
В самом деле:

24. И в этом рассуждении, как и в рассуждении  мы подвергли забвению положение о том, что во множестве комплексных чисел понятие арифметического корня не вводится.
мы подвергли забвению положение о том, что во множестве комплексных чисел понятие арифметического корня не вводится.
Преобразования, выполненные в строке (2), ошибочны.
Для лучшего осознания допущенных здесь ошибок противопоставляем ложному рассуждению истинное:

Если множители подкоренного выражения взять с одинаковыми знаками, то 
Если множители подкоренного выражения взять с разными знаками, то 
Следовательно, в результате извлечения корня 4-й степени из произведения  получено четыре значения х, а именно:
получено четыре значения х, а именно: 
Легко проверить правильность полученных результатов. В самом деле, числа  должны удовлетворять уравнению
должны удовлетворять уравнению  , что и имеет место:
, что и имеет место: 
Тот же результат можно получить, решая уравнение  способом разложения левой части па множители:
способом разложения левой части па множители:

Итак, уравнению (1) удовлетворяет каждое из четырех чисел:  Одно из значений х, естественно, должно совпадать с исходным предположением, что и имеет место.
Одно из значений х, естественно, должно совпадать с исходным предположением, что и имеет место.
Неверное заключение отпало.
Поставим теперь вопрос шире, рассматривая правило умножения квадратных корней не только из отрицательных чисел, а из чисел комплексных, т. е. чисел вида  где х и у числа действительные. Как известно из курса математики X класса средней школы, всякое такое число
где х и у числа действительные. Как известно из курса математики X класса средней школы, всякое такое число
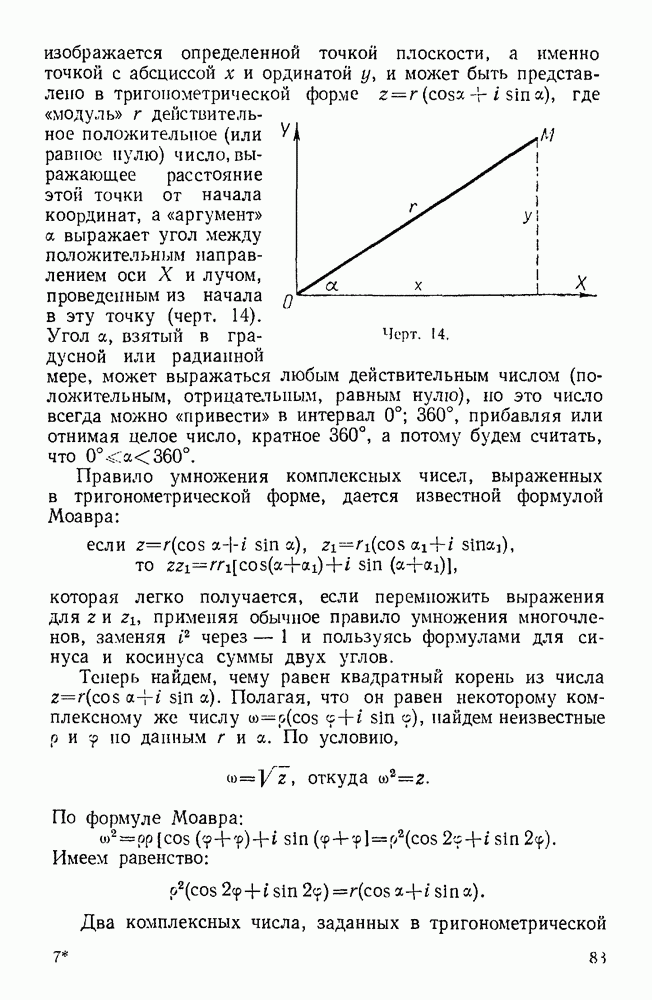
изображается определенной точкой плоскости, а именно точкой с абсциссой х и ординатой у, и может быть представлено в тригонометрической форме  где «модуль»
где «модуль»  действительное положительное (или равное пулю) число, выражающее расстояние этой точки от начала координат, а «аргумент» а выражает угол между положительным направлением оси X и лучом, проведенным из начала в эту точку (черт. 14).
действительное положительное (или равное пулю) число, выражающее расстояние этой точки от начала координат, а «аргумент» а выражает угол между положительным направлением оси X и лучом, проведенным из начала в эту точку (черт. 14).
Угол а, взятый в градусной или радианной мере, может выражаться любым действительным числом (положительным, отрицательным, равным нулю), по это число всегда можно «привести» в интервал  прибавляя или отнимая целое число, кратное 360°, а потому будем считать, что
прибавляя или отнимая целое число, кратное 360°, а потому будем считать, что 

Черт. 14,
Правило умножения комплексных чисел, выраженных в тригонометрической форме, дается известной формулой Моавра:

которая легко получается, если перемножить выражения для  применяя обычное правило умножения многочленов, заменяя
применяя обычное правило умножения многочленов, заменяя  через — 1 и пользуясь формулами для синуса и косинуса суммы двух углов.
через — 1 и пользуясь формулами для синуса и косинуса суммы двух углов.
Теперь найдем, чему равен квадратный корень из числа  Полагая, что он равен некоторому комплексному же числу
Полагая, что он равен некоторому комплексному же числу  найдем неизвестные
найдем неизвестные  по данным
по данным  и а. По условию,
и а. По условию,

По формуле Моавра:

Имеем равенство:

Два комплексных числа, заданных в тригонометрической
форме, равны (и изображают, следовательно, одну и ту же точку плоскости) тогда и только тогда, когда их модули равны, а аргументы либо равны, либо отличаются друг от друга на целое число, кратное 360°. Отсюда заключаем, что  где
где  любое целое число. Модуль
любое целое число. Модуль  как действительное неотрицательное число, равен арифметическому (положительному) значению квадратного корня из неотрицательного действительного числа
как действительное неотрицательное число, равен арифметическому (положительному) значению квадратного корня из неотрицательного действительного числа  а аргумент
а аргумент  имеет бесконечное множество значений, определяемых формулой
имеет бесконечное множество значений, определяемых формулой  при произвольном целом
при произвольном целом  Однако если из всего этого бесконечного множества значений
Однако если из всего этого бесконечного множества значений  выбросить те, какие отличаются от других на целое число, кратное 360°, то останутся только два значения, соответствующие числам
выбросить те, какие отличаются от других на целое число, кратное 360°, то останутся только два значения, соответствующие числам  а именно:
а именно:

и мы приходим к заключению, что существует два и только два значения квадратного корня из числа

а именно:

причем

На чертеже 15 точка А изображает данное число  точки
точки  оба значения
оба значения  (здесь
(здесь  а именно точка
а именно точка  первое значение
первое значение  точка
точка  второе значение
второе значение 
Аргумент а, как мы видели выше, всегда можно считать удовлетворяющим неравенству  а потому
а потому

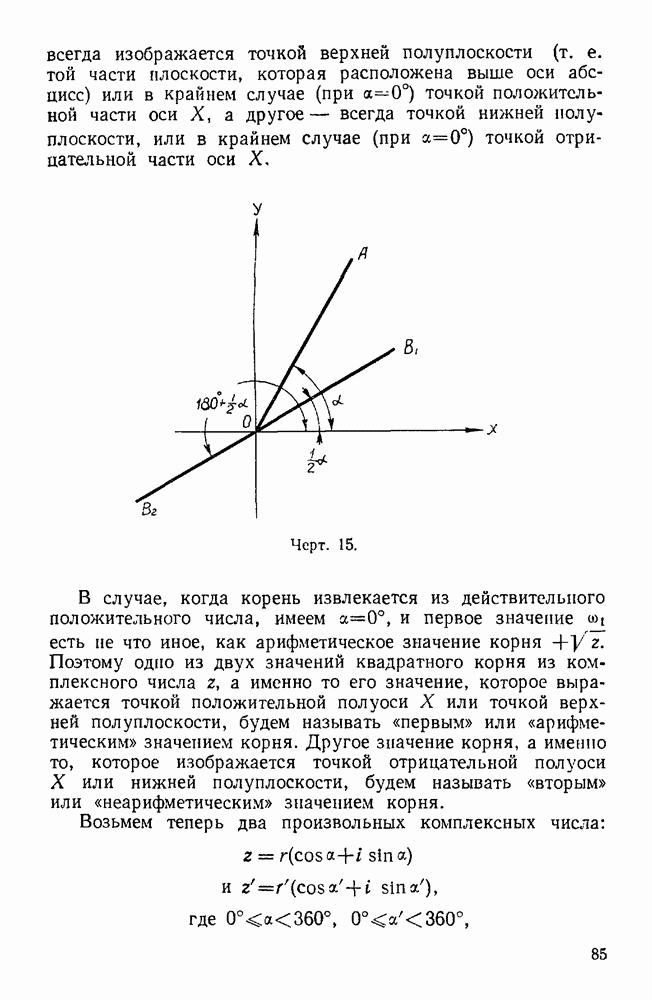
Таким образом, из двух значений квадратного корня одно
всегда изображается точкой верхней полуплоскости (т. е. той части плоскости, которая расположена выше оси абсцисс) или в крайнем случае  точкой положительной части оси X, а другое — всегда точкой нижней полуплоскости, или в крайнем случае
точкой положительной части оси X, а другое — всегда точкой нижней полуплоскости, или в крайнем случае  точкой отрицательной части оси X,
точкой отрицательной части оси X,

Черт. 15.
В случае, когда корень извлекается из действительного положительного числа, имеем  и первое значение
и первое значение  есть не что иное, как арифметическое значение корня
есть не что иное, как арифметическое значение корня  Поэтому одно из двух значений квадратного корня из комплексного числа
Поэтому одно из двух значений квадратного корня из комплексного числа  а именно то его значение, которое выражается точкой положительной полуоси X или точкой верхней полуплоскости, будем называть «первым» или «арифметическим» значением корня. Другое значение корня, а именно то, которое изображается точкой отрицательной полуоси X или нижней полуплоскости, будем называть «вторым» или «неарифметическим» значением корня.
а именно то его значение, которое выражается точкой положительной полуоси X или точкой верхней полуплоскости, будем называть «первым» или «арифметическим» значением корня. Другое значение корня, а именно то, которое изображается точкой отрицательной полуоси X или нижней полуплоскости, будем называть «вторым» или «неарифметическим» значением корня.
Возьмем теперь два произвольных комплексных числа:

и найдем «первые» значения их квадратных корней:

Перомножим их, применяя правило Моавра:

Кроме того, найдем произведение чисел  и оба значения квадратного корня из него:
и оба значения квадратного корня из него:

Теперь у нас подготовлено все нужное для решения вопроса о том, дает ли произведение «первых» значений квадратного корня из двух произвольных комплексных чисел «первое» значение квадратного корня из произведения этих чисел, или нет.
Как видим, произведение «первых» значений квадратного корня из чисел

а именно

равно одному из значений квадратного корня из числа  а именно числу:
а именно числу:

Но возникает вопрос, является ли это последнее число и «первым» значением корня из  или этим «первым» значением является другое значение корня из
или этим «первым» значением является другое значение корня из  обозначенное у нас буквой
обозначенное у нас буквой 
Из условий  выводим, что
выводим, что  Значит, точка, изображающая число и, может лежать и на положительной части оси Х при
Значит, точка, изображающая число и, может лежать и на положительной части оси Х при  и выше оси
и выше оси  и на отрицательной части оси X (при
и на отрицательной части оси X (при  , и ниже оси X (при
, и ниже оси X (при  Таким образом, произведение «первых» значений корней из
Таким образом, произведение «первых» значений корней из  может быть равно в некоторых случаях «первому» значению корня из
может быть равно в некоторых случаях «первому» значению корня из  а в других случаях «второму» его значению.
а в других случаях «второму» его значению.
Рассматривая вместо значений полусуммы аргументов  значение целой суммы
значение целой суммы  и объединяя попарно установленные выше четыре случая, придем к следующим двум случаям:
и объединяя попарно установленные выше четыре случая, придем к следующим двум случаям:
Случай I. Если  то либо
то либо  либо
либо  число и изображается либо точкой положительной части оси X, либо точкой верхней полуплоскости; и равно «первому» значению корня из
число и изображается либо точкой положительной части оси X, либо точкой верхней полуплоскости; и равно «первому» значению корня из 
Случай II. Если  то либо а
то либо а  либо
либо  число и изображается либо точкой отрицательной части оси X, либо точкой нижней полуплоскости; и равно «второму» значению корня из
число и изображается либо точкой отрицательной части оси X, либо точкой нижней полуплоскости; и равно «второму» значению корня из 
Теперь получаем окончательный вывод: произведение «первых» значений квадратных корней из комплексных чисел  равно «первому» значению квадратного корня из произведения этих чисел, тогда и только тогда, когда сумма аргументов этих чисел меньше 360° (предполагается, что аргументы приведены в границы
равно «первому» значению квадратного корня из произведения этих чисел, тогда и только тогда, когда сумма аргументов этих чисел меньше 360° (предполагается, что аргументы приведены в границы  .
.
Замечая, что «второе» значение квадратного корня равно «первому» его значению, взятому с противоположным знаком, легко составим, пользуясь последним предложением, следующую «таблицу-умпожения» квадратных корней из комплексных чисел («первое» значение квадратного корня будем обозначать знаком плюс, поставленным перед знаком корпя, «второе» — знаком минус); как и раньше, будем предполагать, что аргументы а и а чисел  заключаются между 0° и 360°.
заключаются между 0° и 360°.

Вернемся теперь к тому частному случаю умножения корней, которым мы занимались в начале настоящего параграфа: пусть  два действительных отрицательных числа. Всякое такое число можно написать в виде
два действительных отрицательных числа. Всякое такое число можно написать в виде  где х действительное отрицательное число, а потому такое число
где х действительное отрицательное число, а потому такое число  изображается точкой отрицательной полуоси
изображается точкой отрицательной полуоси  Следовательно,
Следовательно,

и здесь мы имеем случай II: произведение «первых» значений квадратных корней из двух действительных отрицательных чисел равно «второму» значению квадратного корня из произведения этих чисел.
25. Для осознания ошибки противопоставим неправильному рассуждению, которое привело к абсурдному выводу, правильное.
Исходя из соотношения  и используя операцию извлечения квадратного корня, будем иметь:
и используя операцию извлечения квадратного корня, будем иметь:

т. е.

а отсюда

Это соотношение ни к какому противоречию не приводит при соответствующем выборе знаков. В самом деле:

26. Внимательно просматривая все рассуждение в поисках ошибки, которая привела нас к этому абсурдному выводу, мы обнаруживаем, что она заключается в той «очевидной истине», с формулировки которой мы начали этот
параграф. Для чисел положительных это утверждение правильно: если а  причем все четыре числа
причем все четыре числа  положительны, то, полагая а
положительны, то, полагая а  заключаем, что
заключаем, что  но отношение с
но отношение с  тоже равно
тоже равно  а если отношение двух положительных чисел больше 1, то первое число больше второго; следовательно,
а если отношение двух положительных чисел больше 1, то первое число больше второго; следовательно, 
Для чисел рациональных, как показывает настоящий софизм, это заключение может быть и неверным. Кроме рассмотренной в нем пропорции  можно привести сколько угодно других, для которых «очевидная истина» начала настоящего параграфа не оправдывается. Например:
можно привести сколько угодно других, для которых «очевидная истина» начала настоящего параграфа не оправдывается. Например:

В настоящем софизме мы имеем очень поучительный пример того, как легко ошибиться, доверяясь «очевидной истине», т. е. принимая без доказательства некоторое утверждение, представляющееся с первого взгляда правильным. Принимая некоторое утверждение без доказательства, мы должны виести его в список аксиом. Все же утверждения, не включаемые в список аксиом, должны рассматриваться как теоремы и подлежат доказательству (на основе принятых аксиом и определений, а также ранее доказанных теорем). Слово «очевидно» хорошо бы вовсе изгнать из употребления в математических рассуждениях: вместо ссылки на «очевидность» необходима либо ссылка на определенную аксиому, либо доказательство, т. е. сведение нового утверждения к аксиомам и ранее доказанным теоремам.
С другой стороны, настоящий софизм показывает пример того, как может перестать быть верным утверждение, доказанное для некоторых чисел (в данном случае положительных), после перехода к числам более общего вида (в данном случае рациональным). Уже при переходе от целых чисел к дробным ученик, привыкнув к тому, что умножение на целое связано с увеличением (при множителе, большем 1), а деление — с уменьшением взятого числа, с большим трудом привыкает к тому, что при умножении и делении на правильную дробь все происходит наоборот.
В дальнейшем мы встретим еще ряд примеров ошибок, происходящих от подобного применения теорем, справедливых при некоторых условиях, в таких случаях, когда эти условия не выполняются.
27. Легко убедиться, взяв хотя бы числовые значения,
Что ошибка сделана при переходе от неравенства (1) к неравенству (2), т. е. при делении обеих частей неравенства (1) на разность  а, имеющую при
а, имеющую при  отрицательное значение. Дело в том, что деление обеих частей неравенства на одно и то же число приводит к неравенству того же смысла, т. е. к неравенству с тем же из двух знаков
отрицательное значение. Дело в том, что деление обеих частей неравенства на одно и то же число приводит к неравенству того же смысла, т. е. к неравенству с тем же из двух знаков  лишь тогда, когда делитель положителен; при отрицательном же делителе смысл неравенства изменяется. Доказательство этого свойства неравенств можно найти в любом руководстве алгебры. Если при переходе от неравенства (1) к неравенству (2) примем во внимание перемену смысла неравенства, то получим, что
лишь тогда, когда делитель положителен; при отрицательном же делителе смысл неравенства изменяется. Доказательство этого свойства неравенств можно найти в любом руководстве алгебры. Если при переходе от неравенства (1) к неравенству (2) примем во внимание перемену смысла неравенства, то получим, что  и неверный вывод о том, что
и неверный вывод о том, что  отпадает.
отпадает.
28. Теорема об умножении неравенств, приведенная в начале  формулирована у нас неточно: она верпа лишь для неравенств, все части которых положительны. Вот ее точная формулировка: можно перемножать почленно два неравенства одного и того же смысла, если все части его положительны; новое неравенство будет того же смысла, что и каждое из данных неравенств. Если же применять эту теорему к таким неравенствам, как
формулирована у нас неточно: она верпа лишь для неравенств, все части которых положительны. Вот ее точная формулировка: можно перемножать почленно два неравенства одного и того же смысла, если все части его положительны; новое неравенство будет того же смысла, что и каждое из данных неравенств. Если же применять эту теорему к таким неравенствам, как  может получиться нелепость:
может получиться нелепость:  т. е.
т. е.  Неосторожное умножение неравенств и привело к абсурдному выводу, что
Неосторожное умножение неравенств и привело к абсурдному выводу, что 
29. Ошибка допущена при умножении обеих частей неравенства  на
на  . Дело в том, что разность чисел
. Дело в том, что разность чисел  и а отрицательна, так как по условию
и а отрицательна, так как по условию  Следовательно, умножая на
Следовательно, умножая на  , т. е. на число отрицательное, надо было изменить знак неравенства на противоположный. Однако этого сделано не было, что и привело к абсурдному выводу.
, т. е. на число отрицательное, надо было изменить знак неравенства на противоположный. Однако этого сделано не было, что и привело к абсурдному выводу.
30. Ошибка допущена при переходе от равенства (2) к неравенству (3). Здесь сознательно подвергнут забвению тот факт, что так как логарифм правильной дроби отрицателен, то в соотношении (3) должен быть поставлен не знак больше, а, наоборот, знак меньше: удвоенное отрицательное число меньше этого отрицательного числа.
31. Тщательно проверяя оба решения, мы находим только один сомнительный пункт: имеем ли мы право считать, что  Другими словами: всегда ли арифметическое значение квадратного корня из квадрата какого-нибудь числа равно этому числу, всегда ли
Другими словами: всегда ли арифметическое значение квадратного корня из квадрата какого-нибудь числа равно этому числу, всегда ли  Последняя формула, очевидно, верна при
Последняя формула, очевидно, верна при  но при
но при  она должна быть заменена другой, а именно формулой
она должна быть заменена другой, а именно формулой
 так как, если а отрицательно, то для получения арифметического (положительного) значения корня надо взять не
так как, если а отрицательно, то для получения арифметического (положительного) значения корня надо взять не  . Обе эти формулы можно соединить в одну:
. Обе эти формулы можно соединить в одну:

Решая поставленную выше задачу вторым способом, мы брали  Это верно, если
Это верно, если  т. е. если
т. е. если  Но в дальнейшем мы заменяли х числом 3, т. е. делали разность
Но в дальнейшем мы заменяли х числом 3, т. е. делали разность  отрицательной. Значит, для получения положительного значения квадратного корня из
отрицательной. Значит, для получения положительного значения квадратного корня из  при таком значении х, надо брать не
при таком значении х, надо брать не  или
или  Правильным будет такое решение:
Правильным будет такое решение:

Получено то же, что и при вычислении первым способом.
32. Равенство  верно, если
верно, если  и неверно, если
и неверно, если 
Если 
Вообще, если  то имеет место равенство:
то имеет место равенство:

Из сказанного ясно, что в анализируемом рассуждении из соотношения  должно следовать не соотношение
должно следовать не соотношение  которое является ложным, а соотношение:
которое является ложным, а соотношение:

Из последнего равенства заключаем:

которое не противоречит соотношению  и не дает оснований для нелепых выводов.
и не дает оснований для нелепых выводов.
Анализируемое ложное рассуждение сыграло настолько значительную роль в истории развития математики, что на этом вопросе следует остановиться несколько подробнее.
В истории математики XVIII в. весьма заметное место по своему научному и методологическому содержанию занимает дискуссия о том, существуют ли действительные значения логарифмов отрицательных чисел.
При разработке проблем интегрирования Лейбниц (1646— 1716) и Иоганн Бернулли (1667—1748) столкнулись с вопросом о логарифмах отрицательных чисел. Вначале они, заботясь лишь о выработке определенных алгоритмов
интегрирования, чисто формально подходили к логарифмированию чисел той или иной природы. Но в 1712—1713 годах между названными учеными возникает оживленный спор в форме переписки, посвященный уже существу проблемы. В своих письмах Бернулли оспаривает мнение Лейбница, что логарифмы отрицательных чисел мнимы, утверждая, что они действительны, так как, по его убеждению, 
В 1745 году переписка Лейбница и Бернулли была обнародована. Ознакомившись с ней, Л. Эйлер (1707—1783) в 1749 году опубликовал статью «О споре между Бернулли и Лейбницем о логарифмах отрицательных и мнимых чисел», в которой дал блестящее решение вопроса. Установив правоту Лейбница, Эйлер не удовлетворяется его аргументацией, достигая решения вопроса с помощью своей формулы для мнимых показателей.
Однако публикацией работы Эйлера спор еще не заканчивается. Авторитетную поддержку взгляд Бернулли находит у Даламбера (1717—1783). Он ее осуществляет публикацией в 1761 году полемической статьи «О логарифмах отрицательных чисел» и в том же духе написанной статьей о логарифмах для XX тома знаменитой «Энциклопедии» (1778). Точка зрения Бернулли — Даламбера разделяется и некоторыми другими математиками XVIII в.
Отголоском этого интересного спора и является сохранившийся до нашего времени весьма распространенный софизм, носящий имя И. Бернулли.
Бернулли, исходя из бесспорного равенства  утверждал, что так как
утверждал, что так как  то
то  а потому
а потому  Отсюда он делал вывод, что логарифмы отрицательных чисел имеют действительные значения.
Отсюда он делал вывод, что логарифмы отрицательных чисел имеют действительные значения.
Здесь при переходе от равенства  к равенству
к равенству  совершается ошибка. Дело в том, что в то время как множества значений
совершается ошибка. Дело в том, что в то время как множества значений  совпадают, множества значений
совпадают, множества значений  не только не совпадают, но даже и не имеют общей части.
не только не совпадают, но даже и не имеют общей части.
Разберемся в этом вопросе подробнее.
Из формулы Эйлера для мнимых показателей  у непосредственно усматриваем, что
у непосредственно усматриваем, что  где
где  равно
равно 
Из формулы, дающей тригонометрическую форму
комплексного числа  равно
равно  находим, что
находим, что  откуда
откуда 
Возможность равенства  исключена, ибо множества
исключена, ибо множества  где
где  равно
равно  не пересекаются, т. е. не имеют ни одного общего элемента.
не пересекаются, т. е. не имеют ни одного общего элемента.
Итак, из равенства  незаконно заключить, что
незаконно заключить, что  Из равенства можно только заключить, что
Из равенства можно только заключить, что  . Здесь в каждой части выступают в качестве слагаемых, вообще говоря, неравные значения
. Здесь в каждой части выступают в качестве слагаемых, вообще говоря, неравные значения  и неравные значения
и неравные значения  В самом деле, переходя от последнего соотношения к соотношению:
В самом деле, переходя от последнего соотношения к соотношению:

видим, что, например, при  равенство удовлетворяется.
равенство удовлетворяется.
33. Ошибку настоящего ложного доказательства легко обнаружить, рассматривая разности  которые появляются при вычитании
которые появляются при вычитании  из
из  Будут ли эти разности цифрами в обычном смысле этого слова, т. е. всегда ли каждая из них является одним из чисел 0, 1, 2, 3,4, 5,
Будут ли эти разности цифрами в обычном смысле этого слова, т. е. всегда ли каждая из них является одним из чисел 0, 1, 2, 3,4, 5,

и разность  отрицательна. Легко понять, что если числа
отрицательна. Легко понять, что если числа  имеют одну и ту же сумму цифр, то по крайней мере одна из разностей
имеют одну и ту же сумму цифр, то по крайней мере одна из разностей  отрицательна (исключением является лишь тот случай, когда
отрицательна (исключением является лишь тот случай, когда  и когда перестановка цифр действительно числа не меняет). В самом деле, переписывая равенство
и когда перестановка цифр действительно числа не меняет). В самом деле, переписывая равенство  в виде
в виде

убеждаемся, что если одна из этих разностей положительна,
то по крайней мере одна из двух других должна иметь отрицательное значение
Итак, записав разность  в виде
в виде  мы не имеем права утверждать, что в числе
мы не имеем права утверждать, что в числе  имеется
имеется  сотен,
сотен,  десятков,
десятков,  единиц Вместо разностей надо взять их абсолютные значения
единиц Вместо разностей надо взять их абсолютные значения

Сумма цифр числа  равна не алгебраической сумме
равна не алгебраической сумме

а арифметической сумме

и все дальнейшие преобразования, проведенные в нашем «доказательстве», отпадают
34 Недоразумение разрешается очень просто Теорема о существовании корня в алгебре комплексных чисел относится лишь к уравнению вида

где  некоторое натуральное число,
некоторое натуральное число,  имеет одно из значений
имеет одно из значений  а все коэффициенты
а все коэффициенты  произвольные комплексные числа, причем
произвольные комплексные числа, причем  Относительно такого уравнения доказано, что оно всегда имеет по крайней мере один корень (действительный или мнимый) Надо твердо помнить, что эта теорема высшей алгебры (или теорема Гаусса, как ее называют по имени великого немецкого математика, впервые почти безупречно ее доказавшего) относится только к уравнениям вида (2) и что она ничего не говорит об уравнениях другого вида, как, например, об уравнении (1) Существенна и сделанная выше оговорка относительно значений коэффициентов Если, например, мы возьмем уравнение
Относительно такого уравнения доказано, что оно всегда имеет по крайней мере один корень (действительный или мнимый) Надо твердо помнить, что эта теорема высшей алгебры (или теорема Гаусса, как ее называют по имени великого немецкого математика, впервые почти безупречно ее доказавшего) относится только к уравнениям вида (2) и что она ничего не говорит об уравнениях другого вида, как, например, об уравнении (1) Существенна и сделанная выше оговорка относительно значений коэффициентов Если, например, мы возьмем уравнение

то окажется, что никакого корня оно не имеет какое число мы ни возьмем вместо х, всегда произведение 0-х будет 0, и левая часть уравнения всегда окажется равной 1, равенство левой и правой частей, таким образом, невозможно ни при каком значении х Это обстоятельство ничуть не
противоречит теореме Гаусса: в уравнении (3) коэффициент старшего члена  между тем как в условиях теоремы указывается, что
между тем как в условиях теоремы указывается, что 
Из теоремы Гаусса легко выводится следствие, гласяшес, что левая часть уравнения (2) всегда разлагается на  линейных множителей, т. е. что уравнение (2) всегда можно представить в виде:
линейных множителей, т. е. что уравнение (2) всегда можно представить в виде:

Числа  , которые могут быть и действительными (положительными, равными нулю, отрицательными) и мнимыми, как неравными, так и равными друг другу, представляют собой не что иное, как корни уравнений (2) и (4); замена в уравнении
, которые могут быть и действительными (положительными, равными нулю, отрицательными) и мнимыми, как неравными, так и равными друг другу, представляют собой не что иное, как корни уравнений (2) и (4); замена в уравнении  одним из этих чисел
одним из этих чисел  а" превращает уравнение (4) в тождество
а" превращает уравнение (4) в тождество  Поэтому это следствие теоремы Гаусса можно формулировать иначе: всякое уравнение вида (2) имеет (при
Поэтому это следствие теоремы Гаусса можно формулировать иначе: всякое уравнение вида (2) имеет (при  ровно
ровно  корней, т. е. столько корней, сколько единиц в показателе его степени.
корней, т. е. столько корней, сколько единиц в показателе его степени.
Зная следствие теоремы Гаусса лишь в последней его формулировке, можно прийти в недоумение, встретившись, например, с уравнением  Ведь оно имеет лишь один корень
Ведь оно имеет лишь один корень  так как никакое неравное нулю число, ни действительное, ни мнимое, не даст 0 после возведения в куб. Следствие теоремы Гаусса в первой его формулировке в применении к уравнению
так как никакое неравное нулю число, ни действительное, ни мнимое, не даст 0 после возведения в куб. Следствие теоремы Гаусса в первой его формулировке в применении к уравнению  гласит, что левую часть этого уравнения можно разложить на три линейных множителя вида
гласит, что левую часть этого уравнения можно разложить на три линейных множителя вида  Но это сделать очень легко:
Но это сделать очень легко:  Теперь становится ясным, что уравнение
Теперь становится ясным, что уравнение  имеет три корня, но что все эти корпи равны между собой.
имеет три корня, но что все эти корпи равны между собой.
Применяя следствие теоремы Гаусса, иикогда не следует забывать о возможности равенства некоторых (или даже всех) корней уравнения.
35. Во всех рассмотренных нами примерах, как в первых двух, когда использованный способ решения дал правильные результаты, так и в последних двух, когда он привел к неверным выводам, все выполненные нами преобразования не вызывают никакого сомнения: все делалось в строгом соответствии с правилами алгебры. Единственная операция, для которой нельзя указать основания в виде некоторого правила алгебры, это само обозначение результата бесконечной совокупности операций буквой х, над которой мы в дальнейшем производим действия, предполагая, конечно, что эта буква х обозначает некоторое определенное, хотя нам пока
еще неизвестное число Ведь все правила алгебры относятся к действиям над числами. Причина появления в результатах наших рассуждений в примерах третьем и четвертом нелепых выводов в том и заключается, что в этих примерах не существует определенного числа, которое получалось бы после бесконечного повторения рассматриваемых операций Выражаясь точнее, можно сказать, что в примере третьем мы имеем дело с бесконечной последовательностью чисел

которая при  не имеет никакого предела, так как эти числа неограниченно возрастают как бы велико ни было данное число А, всегда можно указать такой номер
не имеет никакого предела, так как эти числа неограниченно возрастают как бы велико ни было данное число А, всегда можно указать такой номер  что все члены нашей последовательности, имеющие номера выше
что все члены нашей последовательности, имеющие номера выше  будут больше А (для этого достаточно взять
будут больше А (для этого достаточно взять  Обозначив «сумму» бесконечного множестьа равных чисел буквой х и произведя над х действия так, как будто этот х обозначал число, мы и пришли к нелепому выводу
Обозначив «сумму» бесконечного множестьа равных чисел буквой х и произведя над х действия так, как будто этот х обозначал число, мы и пришли к нелепому выводу
Подобным же образом обстоит дело и в примере четвертом Здесь мы имеем последовательность чисел  которая никакого предельного значения не имеет Неправильным было само обозначение этого несуществующего предельного значения буквой х и действия над этим х, как над определенным числом
которая никакого предельного значения не имеет Неправильным было само обозначение этого несуществующего предельного значения буквой х и действия над этим х, как над определенным числом
Теперь появляется вопрос а как узнать существует ли предельное значение у рассматриваемой бесконечной последовательности чисел или нет? Ответ на этот вопрос дают различные признаки существования предела у бесконечных последовательностей Простейший признак такого рода изучается в IX классе если дана бесконечная последовательность возрастающих чисел

но каждое из этих чисел меньше некоторого числа  то числа
то числа  стремятся к пределу, который либо меньше
стремятся к пределу, который либо меньше  либо равен
либо равен 
В первом рассмотренном выше примере мы имели последовательность бесконечного множества возрастающих чисел

но каждое из этих чисел меньше, например, 0,3. Следовательно, предельное значение существует. Обозначив его буксой х, мы можем спокойно оперировать над х, как это было сделано выше, и придем к заключению, что Точно так же и во втором примере мы имеем бесконечную последовательность возрастающих чисел:

но каждое из этих чисел меньше 2, так как каждое подкоренное выражение меньше 4. Следовательно, и здесь предельное значение существует, и его можно обозначить через 
Итак, применяя прием исключения бесконечности, мы только тогда можем быть уверены в правильности получаемого результата, когда предварительно установим, что искомое предельное значение действительно существует.
36. Читатель, уже ознакомившийся с  конечно, давно понял, в чем тут дело: наша сумма бесконечно большого множества слагаемых вообще не имеет никакого определенного значения, так как последовательное суммирование все большего и большего числа слагаемых не дает приближения ни к какому предельному значению:
конечно, давно понял, в чем тут дело: наша сумма бесконечно большого множества слагаемых вообще не имеет никакого определенного значения, так как последовательное суммирование все большего и большего числа слагаемых не дает приближения ни к какому предельному значению:

Ошибка первого рассуждения, которое привело к значению 0,5, заключалась в том, что мы производили над х действия, не установив предварительно, что буква х означает определенное число.
Во втором рассуждении, которое дало  мы воспользовались сочетательным свойством алгебраической суммы: в любой алгебраической сумме, состоящей из определенного числа слагаемых, можно заключить произвольное число слагаемых в скобки. Перенесение этого сочетательного свойства на сумму бесконечного множества слагаемых ничем не оправдано, и полученный результат (определенное числовое значение, а именно 0, для выражения, явно не имеющего никакого определенного числового значения) обнаруживает, что такое перенесение может привести к неверному заключению.
мы воспользовались сочетательным свойством алгебраической суммы: в любой алгебраической сумме, состоящей из определенного числа слагаемых, можно заключить произвольное число слагаемых в скобки. Перенесение этого сочетательного свойства на сумму бесконечного множества слагаемых ничем не оправдано, и полученный результат (определенное числовое значение, а именно 0, для выражения, явно не имеющего никакого определенного числового значения) обнаруживает, что такое перенесение может привести к неверному заключению.
В третьем рассуждении, приведшем к значению  мы опять незаконно использовали это сочетательное свойство алгебраической суммы в применении к сумме бесконечного множества слагаемых.
мы опять незаконно использовали это сочетательное свойство алгебраической суммы в применении к сумме бесконечного множества слагаемых.
В четвертом рассуждении, в котором мы нашли, что  , мы имеем опять-таки незаконное использование
, мы имеем опять-таки незаконное использование
сочетательного свойства, но, кроме того, незаконное же использование свойства переместительного: как известно, значение алгебраической суммы определенного числа слагаемых не изменяется от перемещения слагаемых, если каждое слагаемое переносить с тем знаком, какой стоит перед ним: перемещая же слагаемые в сумме, содержащей бесконечное множество слагаемых, мы в некоторых случаях изменяем значение этой суммы.
Итак, все наши четыре рассуждения — сплошное нагромождение ошибок, основанных на применении к сумме бесконечного множества слагаемых таких приемов, которые законны лишь в применении к суммам определенного числа слагаемых.
Ошибки охарактеризованного типа имеют поучительную историю, а потому остановимся на некоторых подробностях.
Операции сложения и вычитания в области действительных чисел всегда выполнимы и однозначны. Математикам XVIII в. это было хорошо известно по крайней мере в применении к рациональным числам, но они не были склонны ограничить применение принципов арифметики областью сумм с ограниченным числом слагаемых. На пути же произвольного расширения материала арифметических суждений возникли непримиримые противоречия. «Сохранение» однозначности за операцией сложения заставляло прибегать к уловкам, подчас остроумным, но явно стоящим в противоречии с законом достаточного основания.
Желая, например, найти «сумму» ряда  вычислители писали
вычислители писали  откуда, перенося первое слагаемое правой части в левую, находили
откуда, перенося первое слагаемое правой части в левую, находили  т. е.
т. е.  а потому заключал и, что
а потому заключал и, что 
Но от математиков не могли ускользнуть и другие вполне прозрачные «ответы», как, например:

Естественно возникал вопрос: на каком же решении, как единственно верном, надо остановиться?
Итальянский математик Гвидо Гранди, желая установить аргументы для подтверждения справедливости ответа  излагает любопытные размышления. Допустим, рассуждает Гранди, что некий отец, умирая, оставил своим двум
излагает любопытные размышления. Допустим, рассуждает Гранди, что некий отец, умирая, оставил своим двум
сыновьям драгоценный камень. В своем завещании родитель указал, что по прошествии каждого года наследство должно переходить от одного сына к другому. Подсчитаем же исходя из приведенных условий долю богатства каждого наследника. Выражая для этой цели год обладания камнем одним из братьев за  а год, в течение которого он будет у другого брата, за —1, получим ряд:
а год, в течение которого он будет у другого брата, за —1, получим ряд:  который должен равняться
который должен равняться  так как братья имеют одинаковые права на оставленное им наследство.
так как братья имеют одинаковые права на оставленное им наследство.
Вокруг этого вопроса возникла длительная и оживленная дискуссия-переписка, в которой, кроме самого Гранди, приняли участие Лейбниц, Вольф, Вариньон и Николай Бернулли старший. Лейбниц указал, что ряд  не имеет никакого отношения к примеру Гранди. Ведь братья будут в равной степени обладать камнем, если они будут иметь его, например, сто лет, по сумма ста членов ряда равна все-таки нулю, а не половине. Однако и Лейбниц считал ответ -1 единственно правильным, мотивируя его истинность метафизическими рассуждениями о законе справедливости в природе.
не имеет никакого отношения к примеру Гранди. Ведь братья будут в равной степени обладать камнем, если они будут иметь его, например, сто лет, по сумма ста членов ряда равна все-таки нулю, а не половине. Однако и Лейбниц считал ответ -1 единственно правильным, мотивируя его истинность метафизическими рассуждениями о законе справедливости в природе.
Равенство рассматриваемого ряда половине отстаивал и Эйлер, утверждая, что так как при последовательном суммировании получается то 1, то 0, а ряд не имеет конца, то должно получиться среднее, т. е.  .
.
Этот любопытный спор математиков XVIII в. был разрешен установлением точного понятия о сходящемся ряде и осознанием незаконности формального распространения свойств сумм с определенным числом слагаемых на ряды. Ряд, послуживший предметом дискуссии, является, как известно, расходящимся, т. е. таким, для которого понятие суммы вообще не имеет смысла.
37. Прежде всего заметим, что математики предпочитают говорить не о равенстве бесконечных множеств, а об их «эквивалентности»: два множества, конечные или
бесконечные, называются эквивалентными, если каждому элементу первого соответствует один и только один элемент второго, и обратно, каждому элементу второго множества соответствует один и только один элемент первого.
Итак, имеем два факта: 1) множество  есть часть множества
есть часть множества  множества
множества  тем не менее эквиваленты.
тем не менее эквиваленты.
Во избежание недоразумений отметим еще раз, что речь идет о множествах бесконечных, состоящих из всех квадратных и всех натуральных чисел. Если взять конечное множество из натуральных чисел, не превышающих, например, один миллион, и множество квадратных чисел, тоже не превышающих один миллион, то никакой эквивалентности в этих двух множествах мы, конечно, не обнаружим: на миллион натуральных чисел у нас придется лишь тысяча чисел квадратных, часть окажется меньше своего целого.
Если же рассматривать все натуральные и все квадратные числа, не ограничивая ничем их величину, то окажется, что множество  будучи частью множества
будучи частью множества  в то же время эквивалентно ему: часть равна своему целому.
в то же время эквивалентно ему: часть равна своему целому.
Получив такой вывод, мы непременно усомнимся в правильности наших рассуждений, так как привыкли считать одной из основных общематематических истин, что часть меньше своего целого (это утверждение составляет одну из аксиом 1 книги «Начал» Евклида). Но рассуждения безупречны, и этот вывод приходится принять. Аксиома «часть меньше своего целого» верна лишь для конечных множеств, бесконечное же множество может быть и равно своей части. На вопрос, какое множество называется бесконечным, иногда отвечают так: бесконечным называется всякое множество, у которого есть часть, эквивалентная всему множеству.
Кроме алгебры конечных чисел, существует еще алгебра бесконечных (или «трансфинитных») чисел. Ее изучает математическая наука, носящая название «Теория множеств». Как видим, обе эти алгебры резко отличны одна от другой. Мы получаем новое подтверждение сказанного в  : если мы обозначаем некоторую величину буквой х и выполняем над этим х операции по правилам обыкновенной алгебры, мы только тогда можем быть уверены в правильности полученных выводов, если предварительно убедимся, что х определенное число.
: если мы обозначаем некоторую величину буквой х и выполняем над этим х операции по правилам обыкновенной алгебры, мы только тогда можем быть уверены в правильности полученных выводов, если предварительно убедимся, что х определенное число.
38. Взяв вместо а и  какие-нибудь определенные числа, например,
какие-нибудь определенные числа, например,  легко убедимся, что равенства (1) и (2) верны, равенства (3) и (4) уже неверны. Следовательно, ошибка допущена при переходе от равенства (2) к равенству
легко убедимся, что равенства (1) и (2) верны, равенства (3) и (4) уже неверны. Следовательно, ошибка допущена при переходе от равенства (2) к равенству
(3). Этот переход был сделан на основе того соображения, что извлечение корня одной и той же степени из двух равных чисел должно привести к равным же результатам. Это, конечно, совершенно справедливо, если мы имеем дело с одними положительными числами: если х и у два положительных числа, а  произвольное натуральное число, то из равенства
произвольное натуральное число, то из равенства  вытекает равенство
вытекает равенство  Действительно, если бы было
Действительно, если бы было  или
или  то и
то и  было бы больше или меньше
было бы больше или меньше  При
При  теорему эту можно формулировать так: если два квадрата имеют одну и ту же площадь, то стороны их равны.
теорему эту можно формулировать так: если два квадрата имеют одну и ту же площадь, то стороны их равны.
Все это так, если числа  у — положительные. Если же они оба (или одно из них) могут быть и положительными и отрицательными, то из равенства степеней этих чисел еще нельзя заключить о равенстве самих чисел. Например, при
у — положительные. Если же они оба (или одно из них) могут быть и положительными и отрицательными, то из равенства степеней этих чисел еще нельзя заключить о равенстве самих чисел. Например, при  мы имеем равенство квадратов, так как
мы имеем равенство квадратов, так как  но здесь
но здесь 
Принимая во внимание правило знаков при возведении рациональных чисел в квадрат, легко придем к такому заключению: если квадраты двух рациональных чисел равны, то самые эти числа либо равны, либо противоположны (т. е. имеют одно и то же абсолютное значение, но разные знаки). Короче: из равенства  вытекает одно из равенств:
вытекает одно из равенств:  или
или  Какое именно — надо выяснять каждый раз особо на основании тех сведений о числах
Какое именно — надо выяснять каждый раз особо на основании тех сведений о числах  какими мы располагаем.
какими мы располагаем.
В изложенном выше рассуждении, которое привело нас к ложному заключению о равенстве чисел а и  мы имели равенство
мы имели равенство  Если
Если  как было предположено, то
как было предположено, то  число положительное,
число положительное,  а число отрицательное. Таким образом, здесь мы имеем дело с числами рациональными и должны считаться с тем, что из равенства квадратов этих чисел вытекает одно из двух: либо эти числа
а число отрицательное. Таким образом, здесь мы имеем дело с числами рациональными и должны считаться с тем, что из равенства квадратов этих чисел вытекает одно из двух: либо эти числа  а равны друг другу, либо противоположны. Но числа
а равны друг другу, либо противоположны. Но числа  а имеют разные знаки; возможность их равенства отпадает, остается лишь возможность их противоположности. Равенство (3) в приведенном выше рассуждении надо заменить таким:
а имеют разные знаки; возможность их равенства отпадает, остается лишь возможность их противоположности. Равенство (3) в приведенном выше рассуждении надо заменить таким:

откуда

а не

как было получено выше, и нелепый вывод устранен.
Для разъяснения настоящего софизма часто ограничиваются просто указанием на то, что извлечеиие квадратного корня дает результат с двумя знаками (плюс и минус). Для полной ясности необходимо добавить еще несколько указаний. Извлекая квадратный корень из обеих частей равенства (2), мы должны писать результат в виде 
— а), где любой знак левой части может браться одновременно с любым знаком правой части. Вместо одного равенства (3) мы имеем теперь четыре равенства:

Меняя знаки обеих частей в последних двух равенствах на противоположные, мы сведем эти четыре равенства к двум:

а пользуясь двойным знаком  даже к одному:
даже к одному:

в котором надо еще произвести выбор знака.
Ошибки, обусловленные переходом от  встречаются очень часто. Необходимо твердо помнить, что из
встречаются очень часто. Необходимо твердо помнить, что из  вытекают два равенства:
вытекают два равенства:  или, короче,
или, короче,  и никогда не забывать о необходимости выяснения вопроса о выборе знака.
и никогда не забывать о необходимости выяснения вопроса о выборе знака.
39. Ошибочным является равенство (2): из равенства (1) вытекает, что либо  либо
либо  В силу условия
В силу условия  имеем:
имеем:  а потому равенство (2) отпадает (при
а потому равенство (2) отпадает (при  число
число  равное —а, не может равняться х, равному а) и должно быть заменено другим:
равное —а, не может равняться х, равному а) и должно быть заменено другим:  Но из него следует, что
Но из него следует, что  Мы пришли к исходному равенству, устранив нелепый вывод.
Мы пришли к исходному равенству, устранив нелепый вывод.
40. Как в  ошибка допущена при извлечении квадратного корня из обеих частей равенства (1): из равенства (1) следует, что выражения в скобках либо равны, и тогда имеет место равенство (2), либо эти выражения равны по абсолютной величине, но противоположны по знаку, и тогда вместо (2) надо написать равенство:
ошибка допущена при извлечении квадратного корня из обеих частей равенства (1): из равенства (1) следует, что выражения в скобках либо равны, и тогда имеет место равенство (2), либо эти выражения равны по абсолютной величине, но противоположны по знаку, и тогда вместо (2) надо написать равенство:

Легко убедиться в правильности равенства (3), а не (2).
41. Посмотрим, как расположены те точки  и т. д., о которых была речь, и сколько времени надо точке М, чтобы пройти отрезки
и т. д., о которых была речь, и сколько времени надо точке М, чтобы пройти отрезки  и т. д. По условию,
и т. д. По условию,  Отрезок
Отрезок  точка
точка  двигаясь со скоростью
двигаясь со скоростью  в сек., проходит за то время, в течение которого точка
в сек., проходит за то время, в течение которого точка  двигаясь со скоростью
двигаясь со скоростью  в сек., проходит отрезок
в сек., проходит отрезок  т. е. за
т. е. за  легко видеть, что
легко видеть, что  Точно так же устанавливаем, что для перехода от В к
Точно так же устанавливаем, что для перехода от В к  точке М нужна 1 сек. (в течение которой точка
точке М нужна 1 сек. (в течение которой точка  пройдет отрезок
пройдет отрезок  а для перехода от
а для перехода от  нужно 0,1 сек. (за этот промежуток точка
нужно 0,1 сек. (за этот промежуток точка  пройдет отрезок
пройдет отрезок  Повторяя эти рассуждения, легко убедимся, что расстояния (в метрах) между точками
Повторяя эти рассуждения, легко убедимся, что расстояния (в метрах) между точками  и так далее образуют бесконечно убывающую геометрическую прогрессию:
и так далее образуют бесконечно убывающую геометрическую прогрессию:

а промежутки времени (в секундах), в течение которых точка М проходит эти расстояния, образуют другую такую же прогрессию:

Приведенное выше рассуждение, «доказывающее», что точка М никогда не догонит точку  действительно доказывает, что точка М не догонит точку
действительно доказывает, что точка М не догонит точку  в течение времени, равного сумме любого числа
в течение времени, равного сумме любого числа  промежутков
промежутков  Но сумма
Но сумма  членов этой прогрессии равна:
членов этой прогрессии равна:

 и всегда меньше числа
и всегда меньше числа  Следовательно, наше рассуждение доказывает лишь то, что точка М не догонит точки
Следовательно, наше рассуждение доказывает лишь то, что точка М не догонит точки  ни в какой промежуток времени, меньший
ни в какой промежуток времени, меньший  А в этом утверждении ничего абсурдного нет: точка М сближается с точкой
А в этом утверждении ничего абсурдного нет: точка М сближается с точкой  на
на  в сек.) и догонит ее, т. е. сблизится на все первоначально бывшее между ними расстояние в
в сек.) и догонит ее, т. е. сблизится на все первоначально бывшее между ними расстояние в  как раз через
как раз через  но не раньше.
но не раньше.
Только что рассмотренный софизм был указан греческим философом Зеноном.
В древнейшей греческой математике в число основных аксиом этой науки входило утверждение, по которому «сумма бесконечно большого числа любых, хотя бы и чрезвычайно малых, протяженных величин обязательно должна быть бесконечно большой». На этот момент обращает внимание комментатор Аристотеля Симпликий (умер в 549 г.)
С признанием приведенной аксиомы связаны знаменитые «апории» — доказательства Зенона, жившего в V в. до н. э. Диоген Лаэрций (писатель конца II и начала III в.) свидетельствует, что Зенон обладал необыкновенным даром красноречия, написал произведения, выявляющие большую силу его ума и глубокую ученость, и приобрел известность в философии и политике. В философии его имя связано с отрицанием возможности выразить движение в научном понятии, а в политике с активной поддержкой сил реакции в открытой политической борьбе против античной демократии.
Зенон выступал как противник некоторой вполне определенной математической теории, по которой одновременно постулировалось существование минимального, далее неделимого, отрезка пространства или времени и бесконечная делимость величин. Своим скептическим воззрениям античный философ придал блестящую форму великолепно построенных апагогических доказательств.
«Есть четыре рассуждения Зенона о движении («Дихотомия», «Ахиллес и черепаха», «Стрела», «Ристалище» —  говорит Аристотель, — доставляющие большие затруднения тем, которые хотят их разрешить». «Второе, — продолжает Аристотель, — так называемый Ахиллес. Оно заключается в том, что существо более медленное в беге никогда не будет настигнуто самым быстрым, ибо преследующему необходимо раньше прийти в место, откуда уже двинулось убегающее, так что более медленное всегда имеет некоторое преимущество».
говорит Аристотель, — доставляющие большие затруднения тем, которые хотят их разрешить». «Второе, — продолжает Аристотель, — так называемый Ахиллес. Оно заключается в том, что существо более медленное в беге никогда не будет настигнуто самым быстрым, ибо преследующему необходимо раньше прийти в место, откуда уже двинулось убегающее, так что более медленное всегда имеет некоторое преимущество».
Психологической основой приведенного парадокса является интуитивное отождествление суммы бесконечного множества членов с бесконечно большой величиной, хотя на самом деле речь идет лишь о сумме бесконечно убывающей геометрической прогрессии  равной
равной
дроби  где
где  указывает, во сколько раз Ахиллес двигается быстрее черепахи.
указывает, во сколько раз Ахиллес двигается быстрее черепахи.
Уровень философской и математической культуры Греции времен Зенона Элейского не позволяет допустить, что описанная грубая ошибка могла бы ввести в заблуждение выдающихся мыслителей этой эпохи. Заметить, что сумма как угодно большого числа членов подобного ряда не превзойдет все-таки некоторого числа, не могло составить для них большого труда. Все дело в том, что греческий ученый подходил к разрешению этого вопроса, исходя из безоговорочного признания двух противоречивых воззрений: неограниченной делимости и существования последних элементов деления. Истинный смысл «Ахилла» и состоит в иллюстрации того факта, что сумма бесконечно большого числа неделимых является всегда величиной бесконечно большой.
На подобном толковании парадокса Зенона сходятся авторитетные историки и математики. Впервые эта гипотеза была выставлена П. Таннери. Крупнейший советский знаток Эллады С. Я. Лурье, разделяя мнение Целлера, Нестле и Гиса, оспаривает точку зрения Таннери, что в противниках Зенона следует видеть пифагорейцев. Лурье указывает, что «все, что нам известно об Анаксагоре, говорит за то, что он, с античной точки зрения, был повинен как раз в том противоречии, на котором сыграл Зенон». Однако профессор Лурье не утверждает, что Зенон имел в виду именно Анаксагора (500—428), считая, что современное состояние науки не дает еще достаточных оснований для решения этого вопроса.
Таким представляется «Ахилл» Зенона в плане воззрений современной ему философии и математики.
Но уже Аристотель лишает апорий Зенона о движении той базы, на которой они возникли. Он признает бесконечную делимость непрерывных величин и отрицает существование последних элементов деления (неделимых). Благодаря этому у Аристотеля та сумма, о которой говорится в «Ахилле», не является уже величиной бесконечно большой.
Аристотелево объяснение парадокса Зенона лишило его математической базы. Однако дискуссия о подлинных гносеологических истоках апорий Зенона не сходила со страниц историко-философской литературы на протяжении многих столетий. Только диалектика позволила до конца показать несостоятельность философии Зенона, в частности, его
апорий. В. И. Ленин, вскрывший сущность Зеноновьтх апорий, подчеркивал, что пространство делится в данном случае абстрактно, в уме, что па самом деле, т. е. в процессе движения, оно и делимо, и неделимо одновременно, так как реальное движение представляет собой противоречивое единство непрерывности и прерывности пространства и времени.
42. 
Весьма распространенная ошибка: сокращение на общий множитель знаменателя с одним из слагаемых числителя.
Исследование дает:  или
или  так как знаменатель с не может быть равен нулю. Из соотношения
так как знаменатель с не может быть равен нулю. Из соотношения  следует, что равенство (3) будет справедливо только в двух частных случаях: во-первых, когда
следует, что равенство (3) будет справедливо только в двух частных случаях: во-первых, когда  и формула (3) принимает вид во-вторых, когда
и формула (3) принимает вид во-вторых, когда  и формула (3) принимает вид
и формула (3) принимает вид
II. 
Типичная и весьма упорная ошибка.
Исследование дает:

Из последнего равенства следует, что или  или
или

Однако трехчлен  ни при каких действительных отличных от нуля значениях
ни при каких действительных отличных от нуля значениях  и с в нуль не обратится. В самом деле, если
и с в нуль не обратится. В самом деле, если  то или
то или  или
или  если
если  то
то  А потому во всех случаях
А потому во всех случаях

Выходит, что «формула» (4) оказалась справедливой только в том тривиальном случае, когда 
Мы не случайно остановились  примерах, относящихся к тождественным преобразованиям над алгебраическими дробями и к действиям над ними. Дело в том, что очень большое число массовых ошибок учащихся падает именно на эти вопросы.
примерах, относящихся к тождественным преобразованиям над алгебраическими дробями и к действиям над ними. Дело в том, что очень большое число массовых ошибок учащихся падает именно на эти вопросы.
III. 
Ошибки этого типа весьма распространены и требуют упорной работы по их предупреждению.
Исследование дает:

Формула (5) имеет место во множестве действительных чисел, когда  и выполнено соотношение (6).
и выполнено соотношение (6).
Если, например,  то
то  и
и

| << Предыдущий параграф | Следующий параграф >> |
- ИЗ ПРЕДИСЛОВИЯ К ПЕРВОМУ ИЗДАНИЮ
- Глава I. ОБ УПРАЖНЕНИЯХ НА ОПРОВЕРЖЕНИЕ ОШИБОЧНЫХ МАТЕМАТИЧЕСКИХ РАССУЖДЕНИЙ И ИХ КЛАССИФИКАЦИИ
- 1. МАТЕМАТИЧЕСКИЕ СОФИЗМЫ И ИХ ПЕДАГОГИЧЕСКАЯ РОЛЬ.
- II. КЛАССИФИКАЦИЯ УПРАЖНЕНИЙ НА ОПРОВЕРЖЕНИЕ ЛОЖНЫХ МАТЕМАТИЧЕСКИХ РАССУЖДЕНИЙ.
- 2. Распространение на исключительные случаи.
- 3. Приписывание свойств определенного вида всему роду.
- 4. Неправильное применение принципа непосредственных умозаключений путем обращения.
- 5. Подмена точных определений геометрической интуицией.
- 6. Ошибки построения.
- 7. Ошибки, являющиеся следствием буквального толкования сокращенной (условной) формулировки некоторых геометрических утверждений.
- 8. Нарушение смысла условных записей.
- 9. Уклонение от тезиса.
- Глава II. АРИФМЕТИКА.
- I. ПРИМЕРЫ ЛОЖНЫХ РАССУЖДЕНИЙ.
- 2. На двух нормальных руках одиннадцать пальцев.
- 3. Квадратные рубли.
- 4. 45 — 45 = 45
- 5. 40 : 8 = 41
- 6. Дважды два — пять!
- 7. Есть ли здесь пропорциональность?
- 8. 100% экономии.
- 9. Как вычислять средний процент?
- 10. Что даст ежегодный прирост в 40% за пять лет?
- 11. Новое правило умножения дробей.
- 12. Куда делся рубль?
- 13. Откуда появился лишний гривенник?
- 14. Завещание отца.
- 15. 2-3=4.
- II. АНАЛИЗ ПРИМЕРОВ.
- Глава III. АЛГЕБРА.
- I. ПРИМЕРЫ ЛОЖНЫХ РАССУЖДЕНИЙ.
- 19. Делимость многочленов и делимость чисел.
- 20. Произвольно взятое число а равно нулю.
- 21. 7 = 13.
- 22. Положительная единица равна отрицательной единице.
- 23. Другое «доказательство» равенства положительной и отрицательной единиц.
- 24. Мнимая единица и действительная отрицательная единица равны.
- 25. i^2 = 1
- 26. Всякое отрицательное число больше положительного, имеющего то же абсолютное значение.
- 27. Если a > b, то a > 2b
- 28. Если а и b положительные числа, то a > b и b > a.
- 29. Положительное число меньше нуля.
- 30. Сумма натуральных чисел, каждое из которых превосходит единицу, больше их произведения.
- 31. Чему равен квадратный корень из числа a^2?
- 32. Еще одно «доказательство» равенства нулю произвольно взятого числа.
- 33. Число не изменяется, если в нем переставить любые цифры!
- 34. Что говорит теорема о существовании корня в алгебре комплексных чисел?
- 35. Об одном спэсобе получать правильные результаты, применение которого требует большой осторожности.
- 36. О сумме 1-1+1-1 + …
- 37. Всегда ли целое больше своей части?
- 38. Еще одно «доказательство» равенства двух произвольно взятых чисел.
- 39. Сумма двух произвольных одинаковых чисел равна нулю.
- 40. Число не изменится, если к нему прибавить 1.
- 41. Ахиллес и черепаха.
- 42. О некоторых ученических ошибках.
- II. АНАЛИЗ ПРИМЕРОВ.
- Глава IV. ГЕОМЕТРИЯ.
- 1. ПРИМЕРЫ ЛОЖНЫХ РАССУЖДЕНИЙ.
- 44. Отрезок прямой равен своей правильной части.
- 45. Все треугольники равновелики.
- 46. Сумма оснований любой трапеции равна нулю.
- 47. Объемлемая и объемлющая.
- 48. Еще о пропорциональности.
- 49. Две окружности разного радиуса имеют одну и ту же длину.
- 50. Сумма катетов равна гипотенузе.
- 51. Длина полуокружности равна ее диаметру.
- 52. Боковая поверхность круглого прямого конуса с радиусом основания r и высотой h выражается формулой P=pi*r(r+h).
- 53. В данной точке на прямой можно восставить два перпендикуляра к этой прямой.
- 54. Через одну точку можно провести две прямые, параллельные данной прямой.
- 55. Окружность имеет два центра.
- 56. Из точки на прямую можно опустить два перпендикуляра.
- 57. Через две данные точки можно провести две прямые.
- 58. Любой треугольник — равнобедренный.
- 59. Катет прямоугольного треугольника равен его гипотенузе.
- 60. Прямой угол равен тупому (планиметрический вариант).
- 61. 64 кв. см = 65 кв. см.
- 62. Задача о заплате.
- II. АНАЛИЗ ПРИМЕРОВ.
- III. РАССКАЗЫ-ОБЪЯСНЕНИЯ ПО ПОВОДУ ОШИБОЧНЫХ РАССУЖДЕНИЙ.
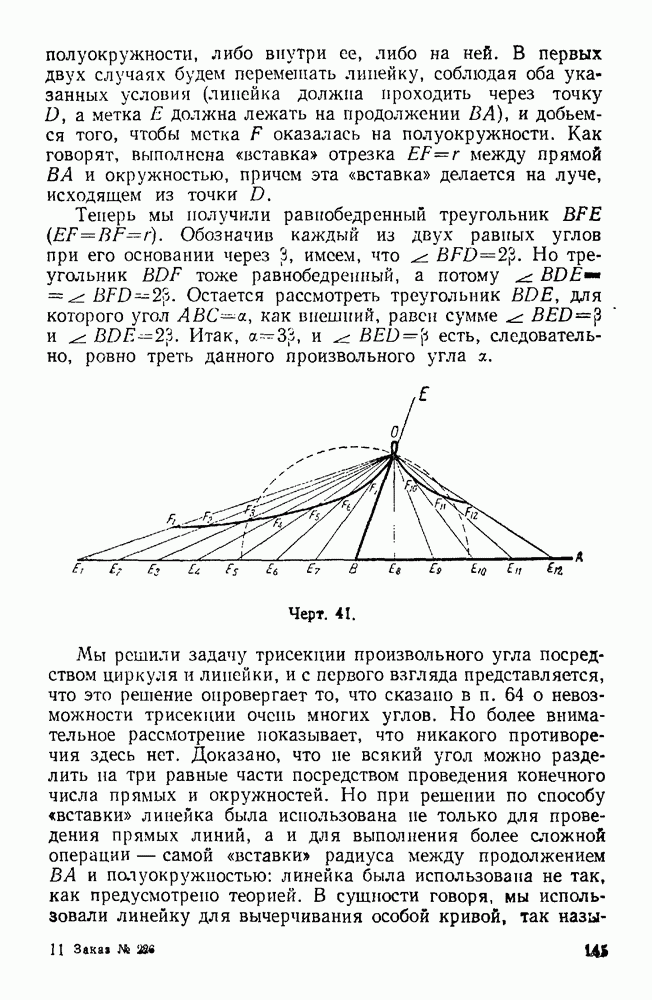
- 64. Трисекция угла.
- 65. Еще о трисекции угла.
- 66. Квадратура круга.
- 67. Об одном доказательстве теоремы о сумме внутренних углов треугольника.
- 68. Как вычислять объем усеченной пирамиды?
- Глава V. ТРИГОНОМЕТРИЯ.
- 70. Синус угла уменьшается, если к углу прибавить 360°.
- 71. Косинус любого острого угла больше единицы.
- 72. 1/4 > 1/2
- 73. 2^2 = 4^2
- 74. Площадь прямоугольника равна нулю.
- 75. Существуют равные треугольники, у которых не все стороны равны.
- 76. Каждый треугольник — прямоугольный.
- II. АНАЛИЗ ПРИМЕРОВ
- Глава VI. ПРИБЛИЖЕННЫЕ ВЫЧИСЛЕНИЯ. РАССКАЗЫ-ОБЪЯСНЕНИЯ ПО ПОВОДУ ОШИБОЧНЫХ РАССУЖДЕНИЙ
- 78. Все большие числа приближенно равны между собой.
- 79. О точности произведения приближенных чисел.
- 80. Верна ли формула …
- 81. Сколько цифр надо знать в подкоренном числе, чтобы получить корень с заданной точностью?
- 82. Зачем освобождаются от иррациональности в знаменателе?