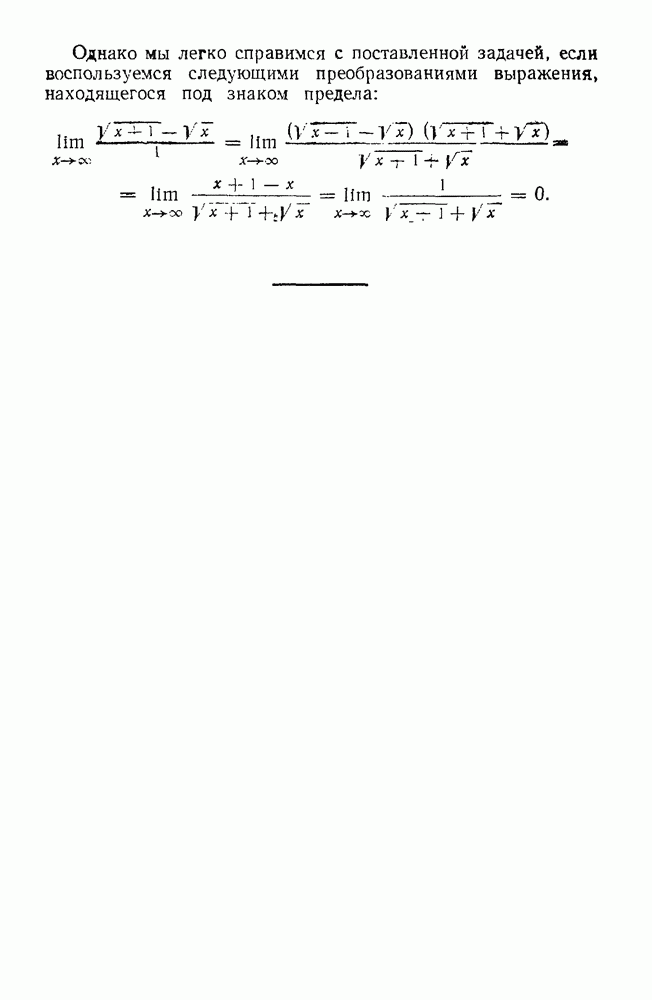| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
42. О некоторых ученических ошибках.
В заключение настоящей главы, отведенной рассмотрению ошибок в алгебраических рассуждениях, проанализируем две очень простые, но, к сожалению, очень часто допускаемые ошибки, а затем предложим несколько вопросов для самостоятельных размышлений читателя.
Первая из них относится к сокращению алгебраических дробей: зачеркивают одинаковые буквы в числителе и знаменателе дроби, не заботясь о том, означают ли эти буквы множители всего числителя и всего знаменателя или нет.
Так, производят сокращение дроби  на х и получают дробь
на х и получают дробь  забывая о том, что сократить дробь — значит разделить ее числитель и знаменатель на одно и то же число
забывая о том, что сократить дробь — значит разделить ее числитель и знаменатель на одно и то же число
и что, хотя для деления одночленного числителя  на х достаточно зачеркнуть в нем х, для деления двучленного знаменателя
на х достаточно зачеркнуть в нем х, для деления двучленного знаменателя  на х надо разделить на х каждый член, как
на х надо разделить на х каждый член, как  так и
так и  После деления на х данная дробь примет такой вид:
После деления на х данная дробь примет такой вид:

а вовсе не  . Наше «сокращение» привело к неудобной «трехэтажной» дроби, и делать его здесь, конечно, не следует.
. Наше «сокращение» привело к неудобной «трехэтажной» дроби, и делать его здесь, конечно, не следует.
Итак, надо твердо помнить, что при сокращении алгебраических дробей можно зачеркивать лишь одинаковые множители всего числителя и всего знаменателя. Не соблюдая этого правила, легко прийти к такому заключению:

Совершаемая при таком «сокращении» ошибка сводится к нарушению распределительного закона (или распределительного свойства) для частного от деления алгебраической суммы. Закон этот говорит, что для деления суммы на некоторое число надо разделить на это число каждый член этой суммы, и выражается формулой:

Другая, тоже очень распространенная, ошибка заключается в почленном извлечении корня из суммы: считают, что для извлечения корня из суммы надо извлечь корень из каждого слагаемого отдельно, т. е. что  Ясно, что это неверно: ведь
Ясно, что это неверно: ведь  равно
равно  а не
а не  . Равенство
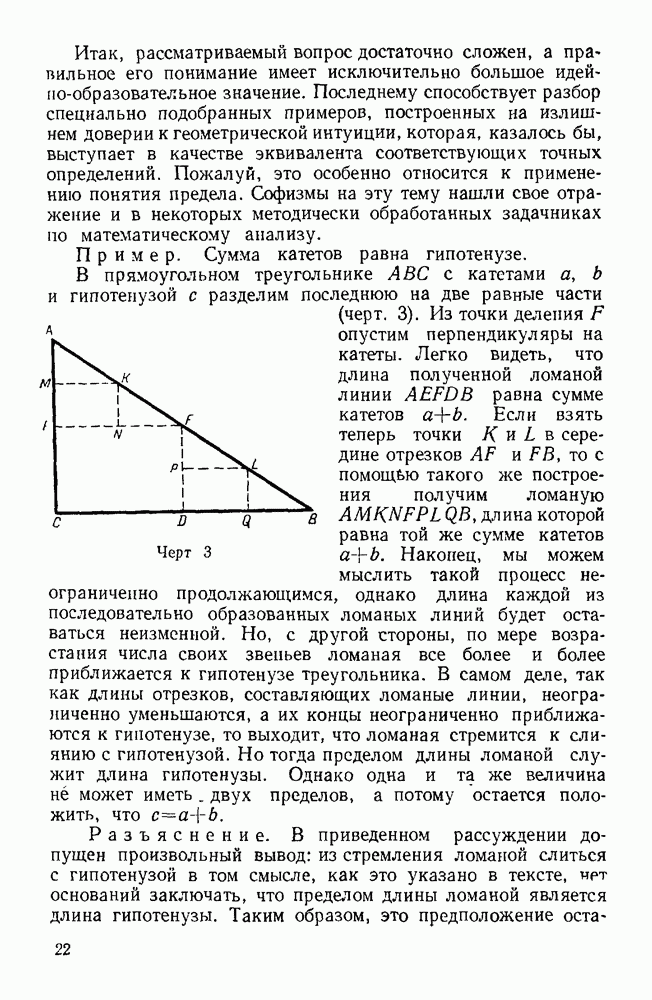
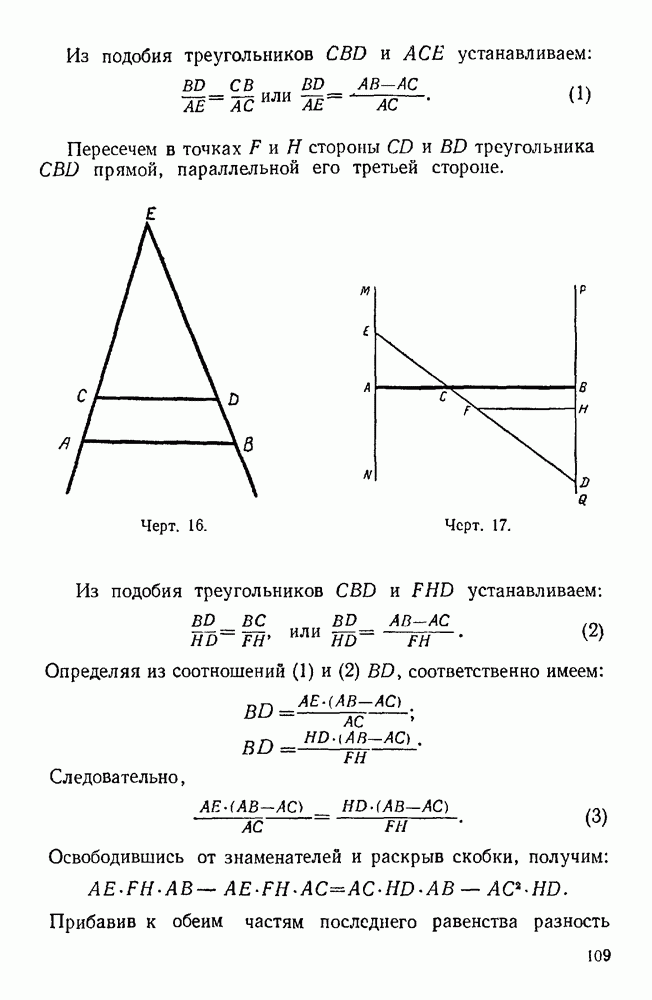
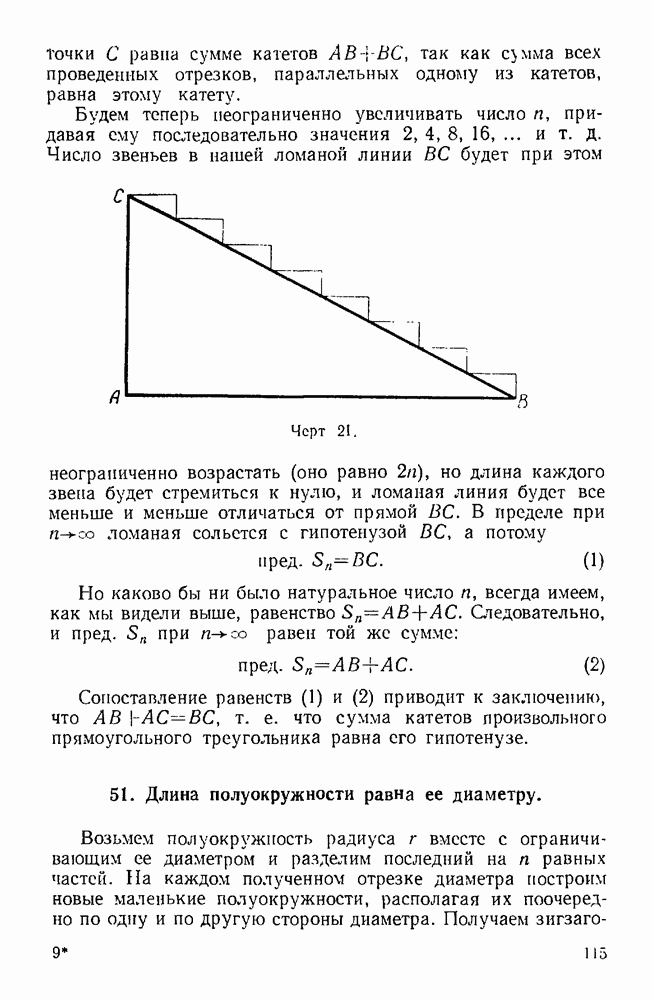
. Равенство  является очевидной нелепостью и с точки зрения геометрии: ведь оно выражает равенство гипотенузы и суммы катетов в произвольном прямоугольном треугольнике! Оказывается, что действие извлечения корня не обладает распределительным свойством по отношению к сумме и разности, но обладает им по отношению к произведению и частному:
является очевидной нелепостью и с точки зрения геометрии: ведь оно выражает равенство гипотенузы и суммы катетов в произвольном прямоугольном треугольнике! Оказывается, что действие извлечения корня не обладает распределительным свойством по отношению к сумме и разности, но обладает им по отношению к произведению и частному:

Отметим, что действия второй ступени (умножение и деление) обладают распределительным свойством по отношению к результатам действий первой ступзни (сложению и вычитанию). Действия третьей ступени (возведение в степень и извлечение корня) обладают распределительным свойством по отношению к результатам действий второй ступени и не обладают им по отношению к результатам действий первой ступени.
Всякий ошибочный ответ противоречит одному из исходных принципов или одному из ранее полученных выводов данной отрасли знания. Возникает возможность постановки вопроса: существуют ли условия, и если да, то какие, при соблюдении которых ошибочное (в общем случае) утверждение оказывается справедливым.
В практике преподавания следует воспользоваться некоторыми из ученических ошибок как поводом для проведения весьма ценных в педагогическом отношении элементарных исследований. От учащихся здесь требуется установить, при каком дополнительном условии ошибочное соотношение окажемся справедливым. Подобными упражнениями достигается углубленное осознание теории и допущенной ошибки. Эти же упражнения играют известную роль в развитии функционального мышления учащихся, так как на каждое выражение вырабатывается взгляд как на функцию входящих в него букв.
Конкретизируем высказанные утверждения на анализе одного примера.
Ученик VII класса, выполняя действие сложения двух дробей, сложил их числители и знаменатели отдельно, первую сумму взял за числитель, вторую за знаменатель, т. е. выполнил сложение дробей так:

Несмотря на явную неправильность формулы (1), если под буквами разуметь произвольные числа, можно указать бесконечное множество таких значений для  с и
с и  при которых равенство (1) будет иметь место. К числу таких значений принадлежат, например, следующие:
при которых равенство (1) будет иметь место. К числу таких значений принадлежат, например, следующие:  Вообще равенство (1) будет удовлетворяться любой системой из четырех чисел, взятых при условии:
Вообще равенство (1) будет удовлетворяться любой системой из четырех чисел, взятых при условии:

К последнему соотношению приходим с помощью следующих элементарных выкладок:

или

Придавая произвольные значения  исключая
исключая  и находя соответствующие значения а по формуле (2), получим бесконечное множество систем из четырех чисел, удовлетворяющих формуле (1).
и находя соответствующие значения а по формуле (2), получим бесконечное множество систем из четырех чисел, удовлетворяющих формуле (1).
Равенство (1) справедливо тогда и только тогда, когда выполнено дополнительное условие (2). Подобные формулы не имеют, конечно, практического значения. С их помощью можно только пополнить коллекцию арифметических курьезов.
Формула  не связана ни с какими ограничениями, если не считать требования, чтобы
не связана ни с какими ограничениями, если не считать требования, чтобы  были отличными от нуля, выражающего запрет деления на нуль. Разумеется, только эта формула выражает правило сложения алгебраических дробей.
были отличными от нуля, выражающего запрет деления на нуль. Разумеется, только эта формула выражает правило сложения алгебраических дробей.
Теперь предложим упражнения для самостоятельного проведения подобных исследований.

В каких частных случаях эта грубейшая ошибка не приведет к заблуждению?

Тот же вопрос.

Аналогичный вопрос.
| << Предыдущий параграф | Следующий параграф >> |
- ИЗ ПРЕДИСЛОВИЯ К ПЕРВОМУ ИЗДАНИЮ
- Глава I. ОБ УПРАЖНЕНИЯХ НА ОПРОВЕРЖЕНИЕ ОШИБОЧНЫХ МАТЕМАТИЧЕСКИХ РАССУЖДЕНИЙ И ИХ КЛАССИФИКАЦИИ
- 1. МАТЕМАТИЧЕСКИЕ СОФИЗМЫ И ИХ ПЕДАГОГИЧЕСКАЯ РОЛЬ.
- II. КЛАССИФИКАЦИЯ УПРАЖНЕНИЙ НА ОПРОВЕРЖЕНИЕ ЛОЖНЫХ МАТЕМАТИЧЕСКИХ РАССУЖДЕНИЙ.
- 2. Распространение на исключительные случаи.
- 3. Приписывание свойств определенного вида всему роду.
- 4. Неправильное применение принципа непосредственных умозаключений путем обращения.
- 5. Подмена точных определений геометрической интуицией.
- 6. Ошибки построения.
- 7. Ошибки, являющиеся следствием буквального толкования сокращенной (условной) формулировки некоторых геометрических утверждений.
- 8. Нарушение смысла условных записей.
- 9. Уклонение от тезиса.
- Глава II. АРИФМЕТИКА.
- I. ПРИМЕРЫ ЛОЖНЫХ РАССУЖДЕНИЙ.
- 2. На двух нормальных руках одиннадцать пальцев.
- 3. Квадратные рубли.
- 4. 45 — 45 = 45
- 5. 40 : 8 = 41
- 6. Дважды два — пять!
- 7. Есть ли здесь пропорциональность?
- 8. 100% экономии.
- 9. Как вычислять средний процент?
- 10. Что даст ежегодный прирост в 40% за пять лет?
- 11. Новое правило умножения дробей.
- 12. Куда делся рубль?
- 13. Откуда появился лишний гривенник?
- 14. Завещание отца.
- 15. 2-3=4.
- II. АНАЛИЗ ПРИМЕРОВ.
- Глава III. АЛГЕБРА.
- I. ПРИМЕРЫ ЛОЖНЫХ РАССУЖДЕНИЙ.
- 19. Делимость многочленов и делимость чисел.
- 20. Произвольно взятое число а равно нулю.
- 21. 7 = 13.
- 22. Положительная единица равна отрицательной единице.
- 23. Другое «доказательство» равенства положительной и отрицательной единиц.
- 24. Мнимая единица и действительная отрицательная единица равны.
- 25. i^2 = 1
- 26. Всякое отрицательное число больше положительного, имеющего то же абсолютное значение.
- 27. Если a > b, то a > 2b
- 28. Если а и b положительные числа, то a > b и b > a.
- 29. Положительное число меньше нуля.
- 30. Сумма натуральных чисел, каждое из которых превосходит единицу, больше их произведения.
- 31. Чему равен квадратный корень из числа a^2?
- 32. Еще одно «доказательство» равенства нулю произвольно взятого числа.
- 33. Число не изменяется, если в нем переставить любые цифры!
- 34. Что говорит теорема о существовании корня в алгебре комплексных чисел?
- 35. Об одном спэсобе получать правильные результаты, применение которого требует большой осторожности.
- 36. О сумме 1-1+1-1 + …
- 37. Всегда ли целое больше своей части?
- 38. Еще одно «доказательство» равенства двух произвольно взятых чисел.
- 39. Сумма двух произвольных одинаковых чисел равна нулю.
- 40. Число не изменится, если к нему прибавить 1.
- 41. Ахиллес и черепаха.
- 42. О некоторых ученических ошибках.
- II. АНАЛИЗ ПРИМЕРОВ.
- Глава IV. ГЕОМЕТРИЯ.
- 1. ПРИМЕРЫ ЛОЖНЫХ РАССУЖДЕНИЙ.
- 44. Отрезок прямой равен своей правильной части.
- 45. Все треугольники равновелики.
- 46. Сумма оснований любой трапеции равна нулю.
- 47. Объемлемая и объемлющая.
- 48. Еще о пропорциональности.
- 49. Две окружности разного радиуса имеют одну и ту же длину.
- 50. Сумма катетов равна гипотенузе.
- 51. Длина полуокружности равна ее диаметру.
- 52. Боковая поверхность круглого прямого конуса с радиусом основания r и высотой h выражается формулой P=pi*r(r+h).
- 53. В данной точке на прямой можно восставить два перпендикуляра к этой прямой.
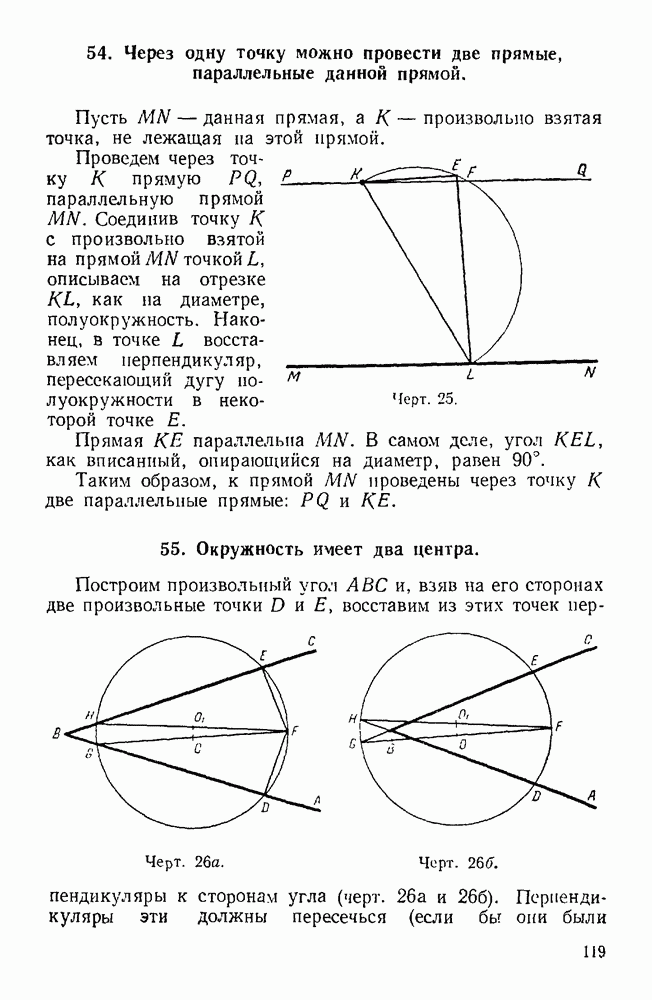
- 54. Через одну точку можно провести две прямые, параллельные данной прямой.
- 55. Окружность имеет два центра.
- 56. Из точки на прямую можно опустить два перпендикуляра.
- 57. Через две данные точки можно провести две прямые.
- 58. Любой треугольник — равнобедренный.
- 59. Катет прямоугольного треугольника равен его гипотенузе.
- 60. Прямой угол равен тупому (планиметрический вариант).
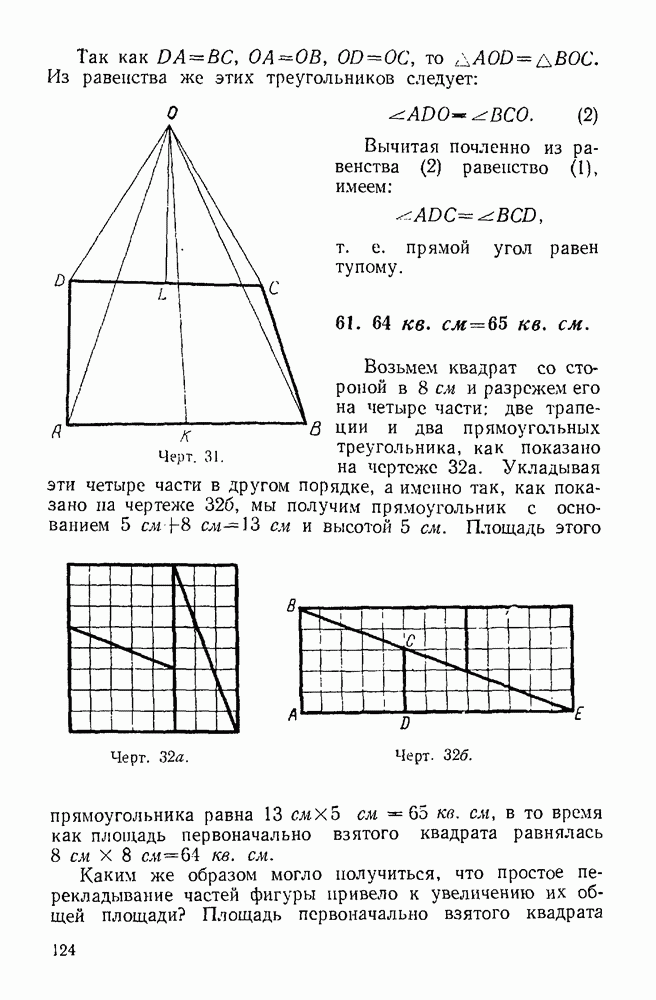
- 61. 64 кв. см = 65 кв. см.
- 62. Задача о заплате.
- II. АНАЛИЗ ПРИМЕРОВ.
- III. РАССКАЗЫ-ОБЪЯСНЕНИЯ ПО ПОВОДУ ОШИБОЧНЫХ РАССУЖДЕНИЙ.
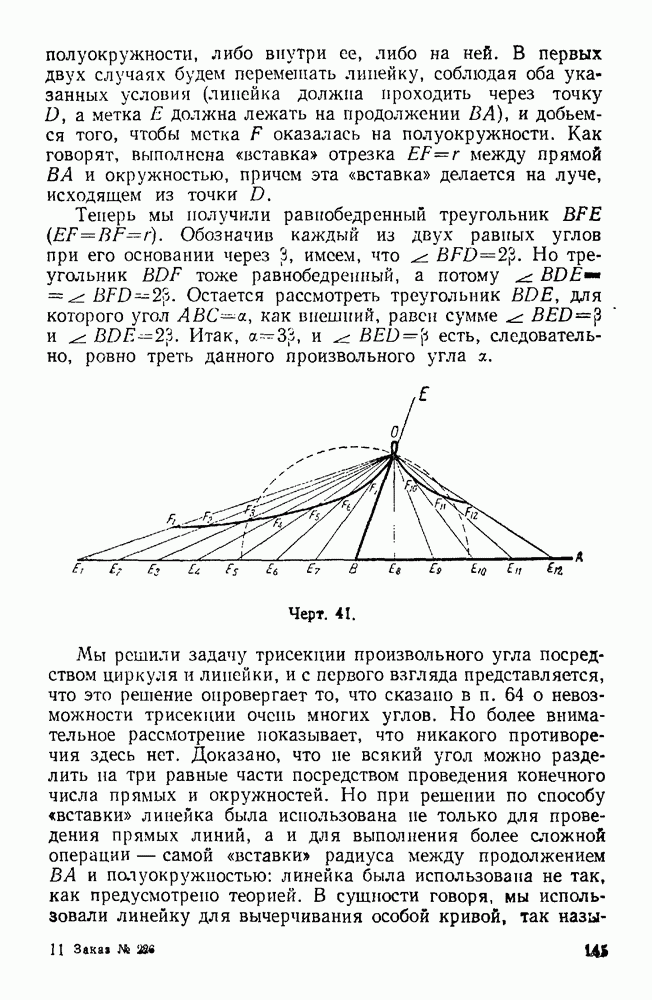
- 64. Трисекция угла.
- 65. Еще о трисекции угла.
- 66. Квадратура круга.
- 67. Об одном доказательстве теоремы о сумме внутренних углов треугольника.
- 68. Как вычислять объем усеченной пирамиды?
- Глава V. ТРИГОНОМЕТРИЯ.
- 70. Синус угла уменьшается, если к углу прибавить 360°.
- 71. Косинус любого острого угла больше единицы.
- 72. 1/4 > 1/2
- 73. 2^2 = 4^2
- 74. Площадь прямоугольника равна нулю.
- 75. Существуют равные треугольники, у которых не все стороны равны.
- 76. Каждый треугольник — прямоугольный.
- II. АНАЛИЗ ПРИМЕРОВ
- Глава VI. ПРИБЛИЖЕННЫЕ ВЫЧИСЛЕНИЯ. РАССКАЗЫ-ОБЪЯСНЕНИЯ ПО ПОВОДУ ОШИБОЧНЫХ РАССУЖДЕНИЙ
- 78. Все большие числа приближенно равны между собой.
- 79. О точности произведения приближенных чисел.
- 80. Верна ли формула …
- 81. Сколько цифр надо знать в подкоренном числе, чтобы получить корень с заданной точностью?
- 82. Зачем освобождаются от иррациональности в знаменателе?