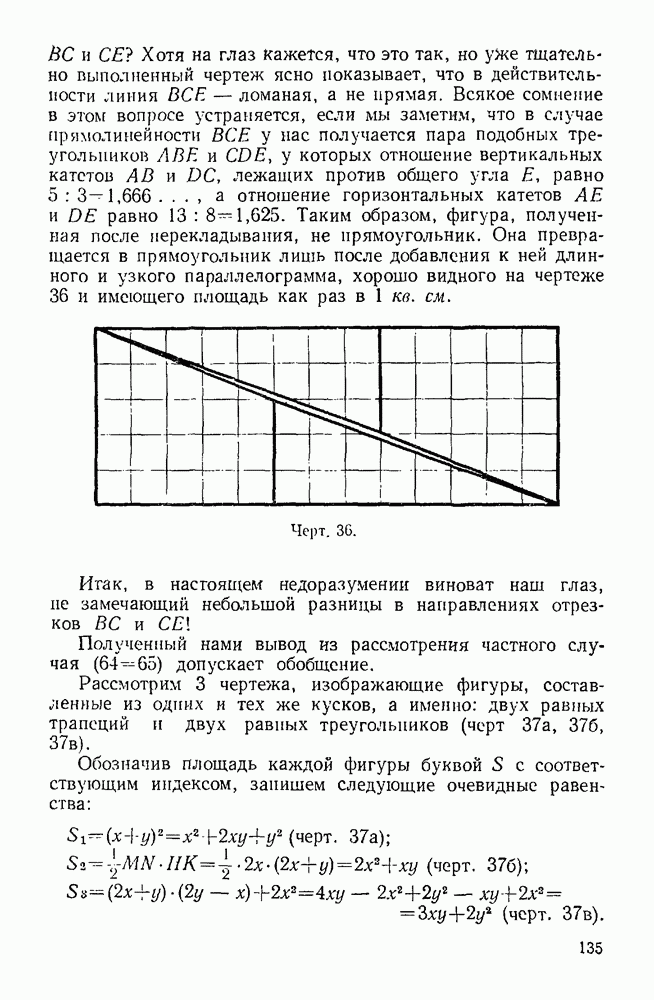
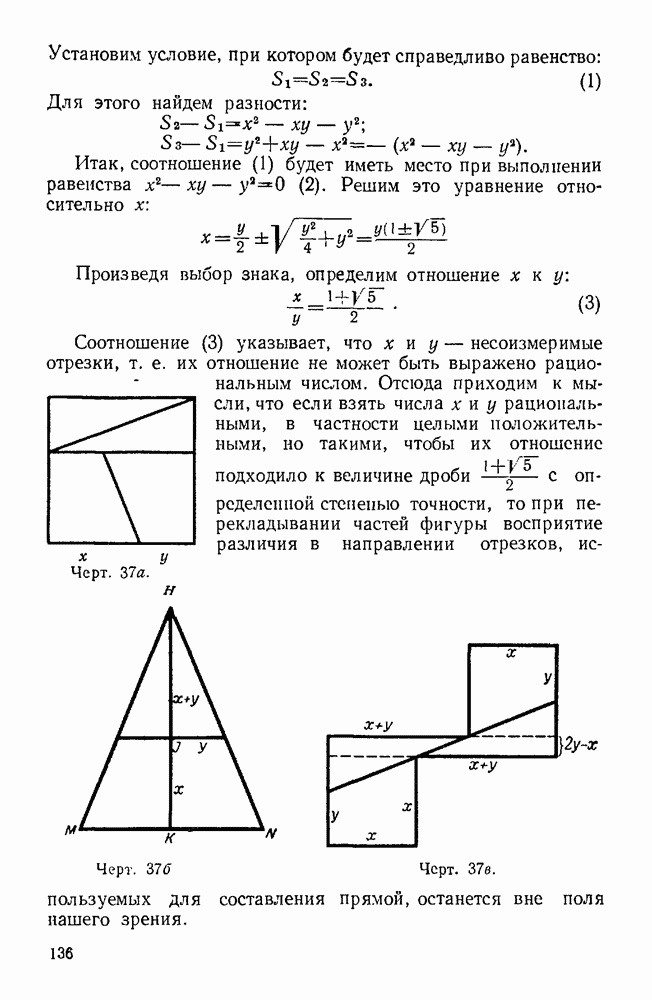
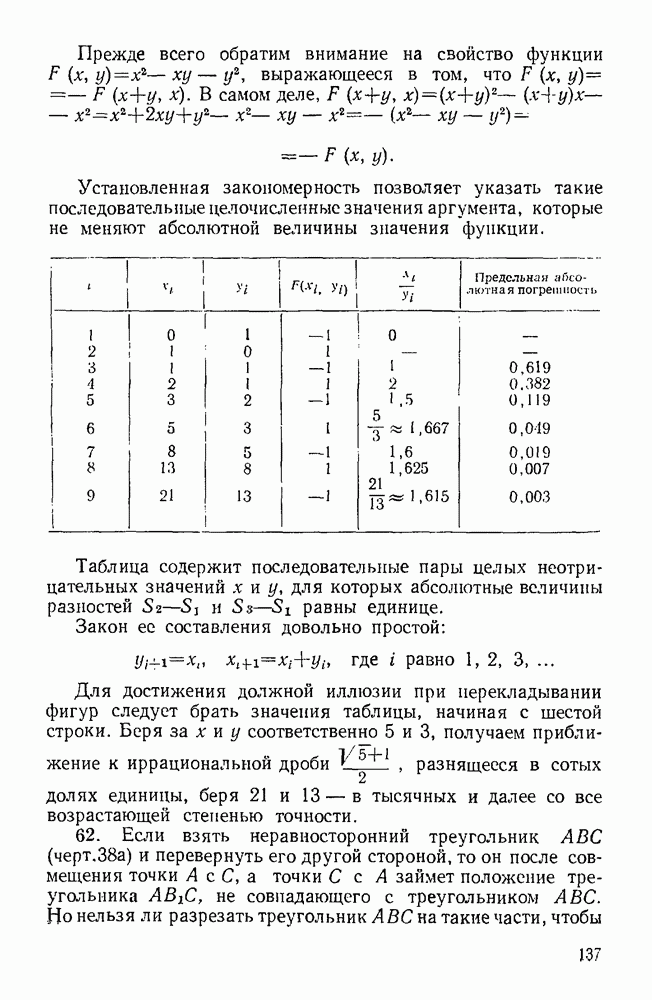
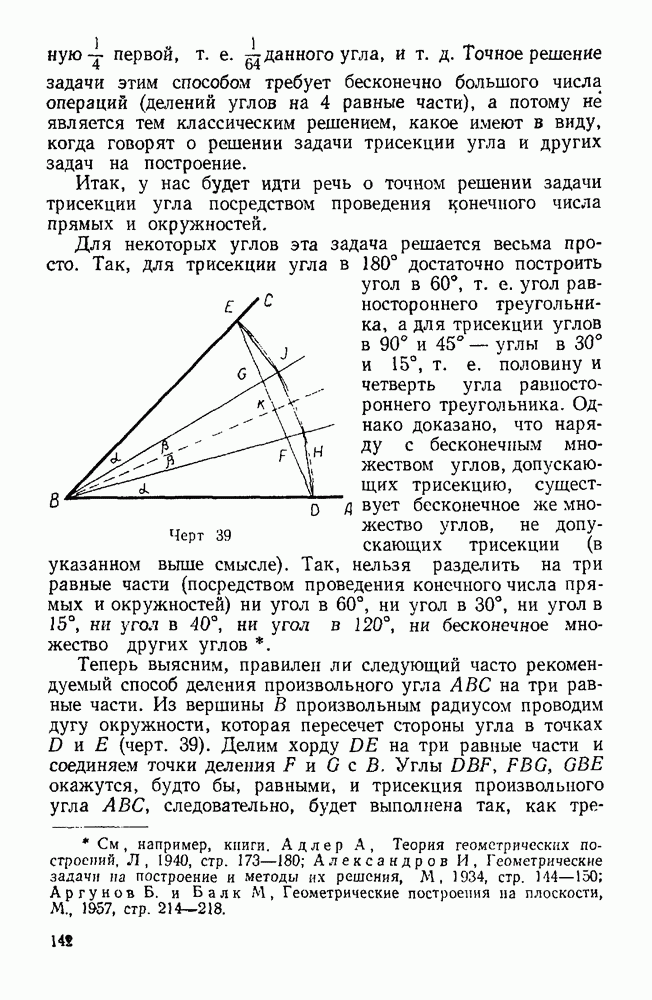
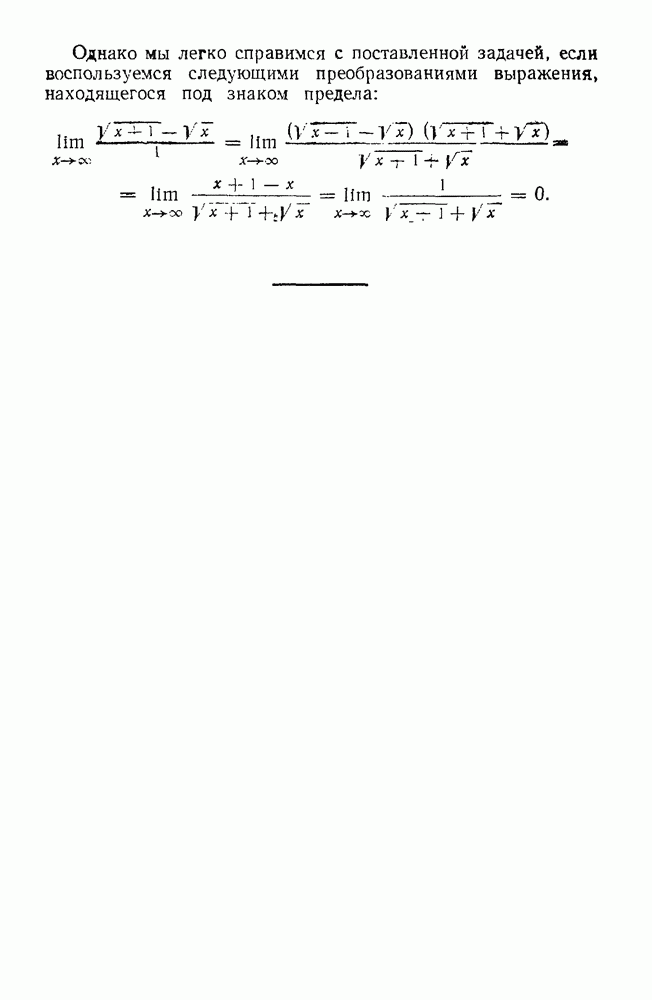| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
5. Подмена точных определений геометрической интуицией.
Доказательство всякого математического суждения должно быть основано: на первичных понятиях, на точных определениях всех остальных понятий, аксиомах, ранее доказанных теоремах данной научной области и только на них. Определения устраняют неопределенность используемых понятий (терминов), которая часто служит причиной разнообразных заблуждений. Известное правило Паскаля (1623— 1662) предупреждает, что для проверки нужно подставлять определения вместо терминов.
Одпако нередко возникают ошибки из попыток учащихся устанавливать в качестве дополнительных оснований доказательства какие-либо данные опыта, извлекаемые из наглядного изображения. Это дало повод для появления еще в середине прошлого века среди ярко выраженных умов аналитического склада тенденции к изгнанию чертежа из математики.
Созерцание чертежа производит на начинающих изучение курса математики сильное впечатление. Оно выступает в качестве бесспорного факта, которому надлежит только подыскать подходящее объяснение. Даже студенты под влиянием наглядного образа порой склонны забывать о точных определениях тех или иных понятий, особенно там, где зрительное впечатление, казалось бы, полностью дает непосредственный ответ на поставленный вопрос, не требуя косвенной проверки.
Итак, рассматриваемый вопрос достаточно сложен, а правильное его понимание имеет исключительно большое идейно-образовательное значение. Последнему способствует разбор специально подобранных примеров, построенных на излишнем доверии к геометрической интуиции, которая, казалось бы, выступает в качестве эквивалента соответствующих точных определений. Пожалуй, это особенно относится к применению понятия предела. Софизмы на эту тему нашли свое отражение и в некоторых методически обработанных задачниках по математическому анализу.
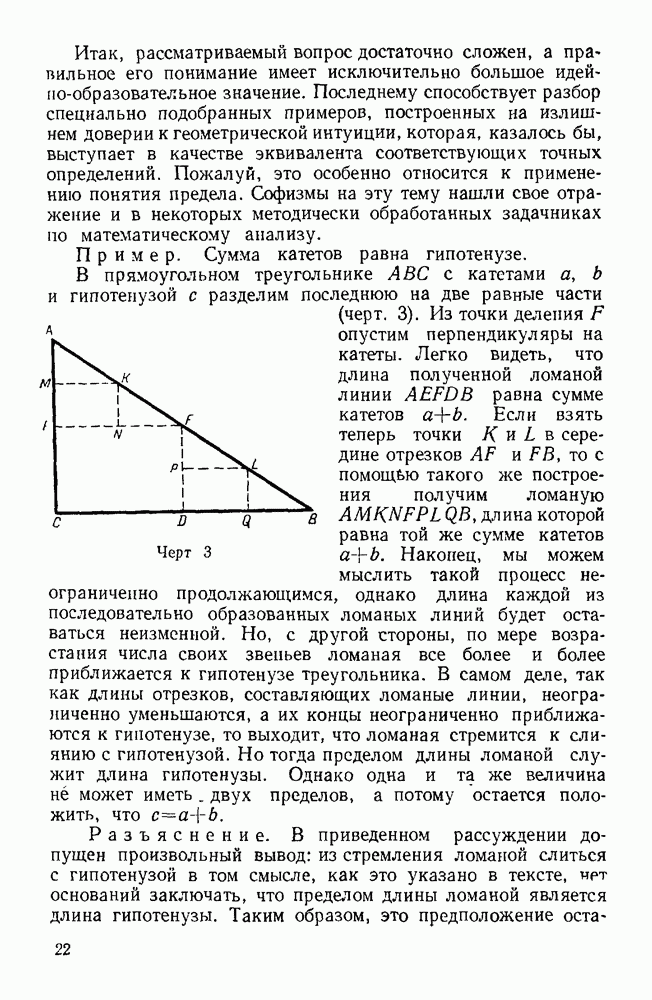
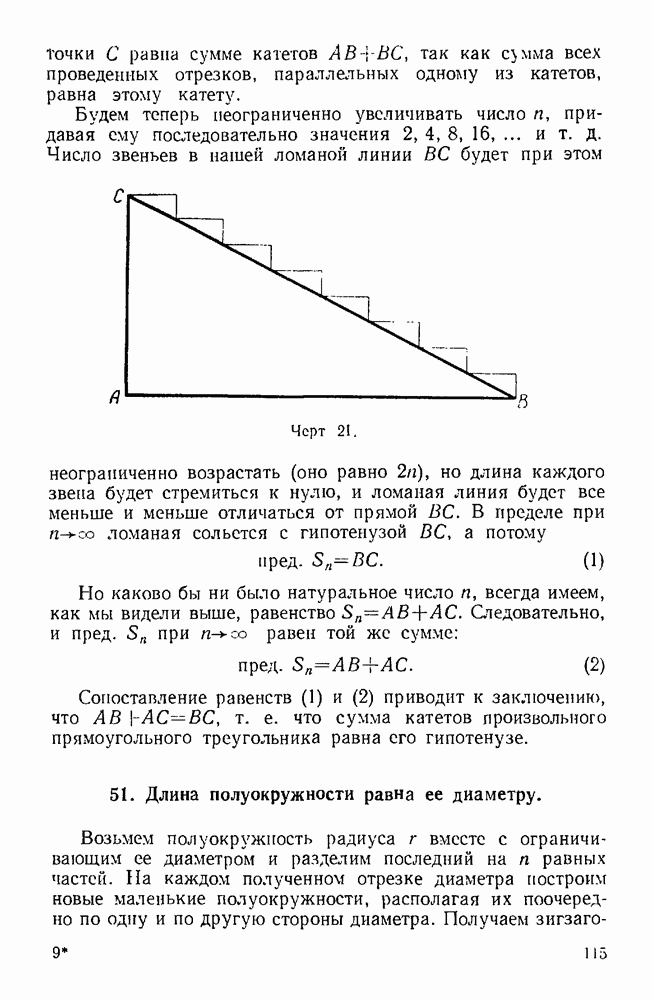
Пример. Сумма катетов равна гипотенузе.
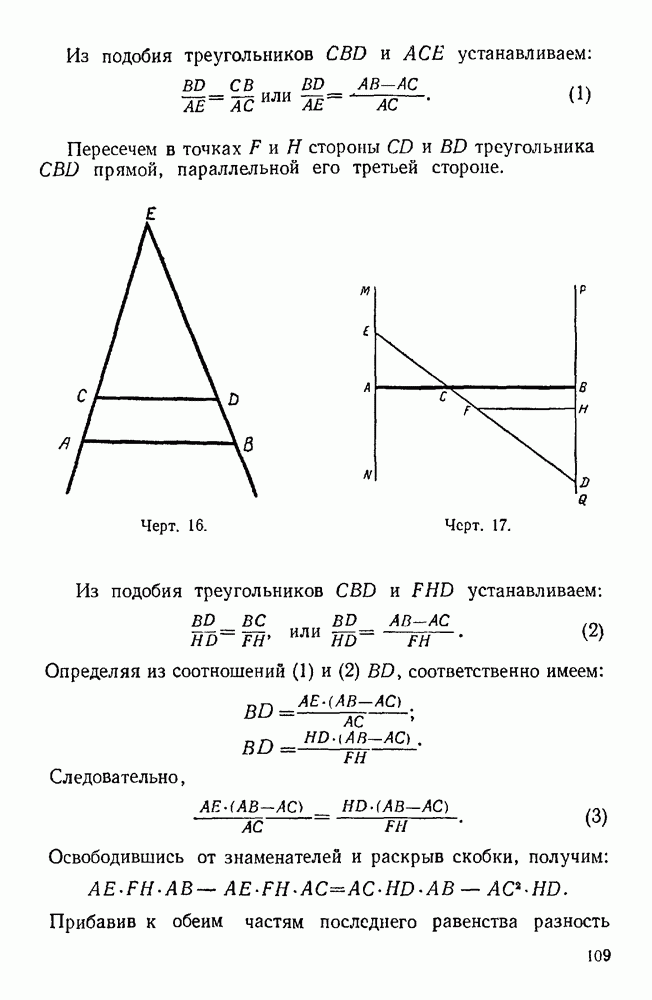
В прямоугольном треугольнике  с катетами
с катетами  и гипотенузой с разделим последнюю на две равные части (черт. 3). Из точки деления
и гипотенузой с разделим последнюю на две равные части (черт. 3). Из точки деления  опустим перпендикуляры на катеты. Легко видеть, что длина полученной ломаной линии
опустим перпендикуляры на катеты. Легко видеть, что длина полученной ломаной линии  равна сумме катетов
равна сумме катетов  Если взять теперь точки
Если взять теперь точки  в середине отрезков
в середине отрезков  и
и  то с помощью такого же построения получим ломаную
то с помощью такого же построения получим ломаную  длина которой равна той же сумме катетов
длина которой равна той же сумме катетов  Наконец, мы можем мыслить такой процесс неограниченно продолжающимся, однако длина каждой из последовательно образованных ломаных линий будет оставаться неизменной. Но, с другой стороны, по мере возрастания числа своих звеньев ломаная все более и более приближается к гипотенузе треугольника. В самом деле, так как длины отрезков, составляющих ломаные линии, неограниченно уменьшаются, а их концы неограниченно приближаются к гипотенузе, то выходит, что ломаная стремится к слиянию с гипотенузой. Но тогда пределом длины ломаной служит длина гипотенузы. Однако одна и та же величина не может иметь
Наконец, мы можем мыслить такой процесс неограниченно продолжающимся, однако длина каждой из последовательно образованных ломаных линий будет оставаться неизменной. Но, с другой стороны, по мере возрастания числа своих звеньев ломаная все более и более приближается к гипотенузе треугольника. В самом деле, так как длины отрезков, составляющих ломаные линии, неограниченно уменьшаются, а их концы неограниченно приближаются к гипотенузе, то выходит, что ломаная стремится к слиянию с гипотенузой. Но тогда пределом длины ломаной служит длина гипотенузы. Однако одна и та же величина не может иметь  двух пределов, а потому остается положить, что
двух пределов, а потому остается положить, что 

Черт. 3
Разъяснение. В приведенном рассуждении допущен произвольный вывод: из стремления ломаной слиться с гипотенузой в том смысле, как это указано в тексте, нет оснований заключать, что пределом длины ломаной является длина гипотенузы. Таким образом, это предположение
осталось необоснованным. Обосновать его и нельзя, так как оно ложно В самом деле, мы здесь не находимся в условиях применимости понятия предела: разность между переменной величиной, в частном случае постоянной (длина ломаной), и ее предполагаемым пределом (гипотенузой) не является ни бесконечно малой величиной, ни ее частным случаем — нулем.
Для лучшего понимания вопроса и во избежание механического переноса этого вывода на определение длины окружности следует провести контрастное сопоставление.
Выдающийся популяризатор знаний почетный академик
Н. А. Морозов (1854—1946) считал, что софизмы типа «гипотенуза прямоугольного треугольника равна сумме его катетов» «имеют научный интерес, так как обращают наше внимание на важные особенности математических методов или самых наших математических представлений и генезиса этих представлений в наших головах».
| << Предыдущий параграф | Следующий параграф >> |
- ИЗ ПРЕДИСЛОВИЯ К ПЕРВОМУ ИЗДАНИЮ
- Глава I. ОБ УПРАЖНЕНИЯХ НА ОПРОВЕРЖЕНИЕ ОШИБОЧНЫХ МАТЕМАТИЧЕСКИХ РАССУЖДЕНИЙ И ИХ КЛАССИФИКАЦИИ
- 1. МАТЕМАТИЧЕСКИЕ СОФИЗМЫ И ИХ ПЕДАГОГИЧЕСКАЯ РОЛЬ.
- II. КЛАССИФИКАЦИЯ УПРАЖНЕНИЙ НА ОПРОВЕРЖЕНИЕ ЛОЖНЫХ МАТЕМАТИЧЕСКИХ РАССУЖДЕНИЙ.
- 2. Распространение на исключительные случаи.
- 3. Приписывание свойств определенного вида всему роду.
- 4. Неправильное применение принципа непосредственных умозаключений путем обращения.
- 5. Подмена точных определений геометрической интуицией.
- 6. Ошибки построения.
- 7. Ошибки, являющиеся следствием буквального толкования сокращенной (условной) формулировки некоторых геометрических утверждений.
- 8. Нарушение смысла условных записей.
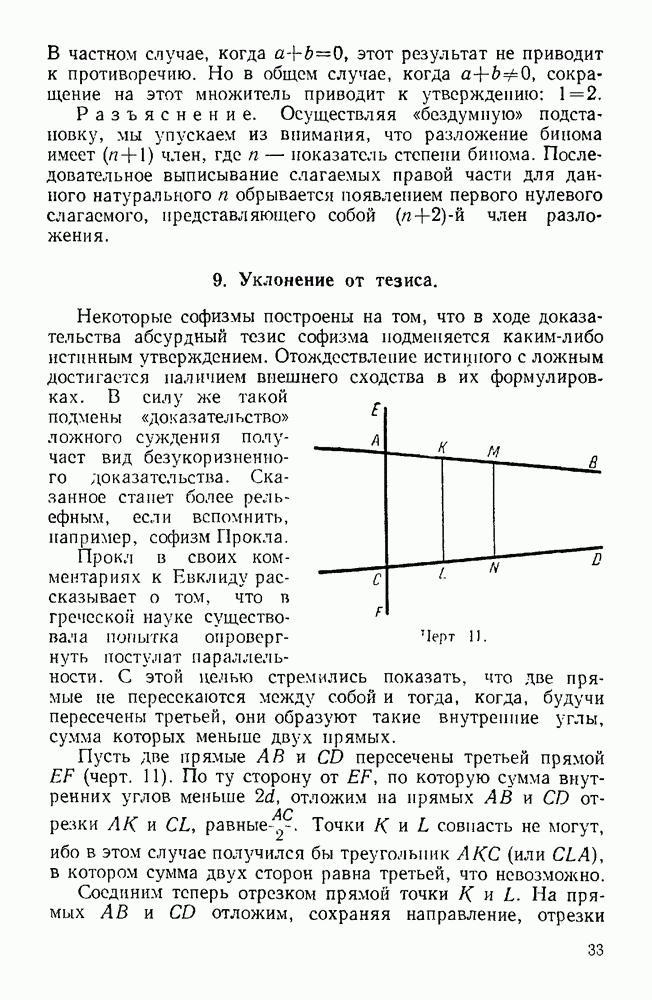
- 9. Уклонение от тезиса.
- Глава II. АРИФМЕТИКА.
- I. ПРИМЕРЫ ЛОЖНЫХ РАССУЖДЕНИЙ.
- 2. На двух нормальных руках одиннадцать пальцев.
- 3. Квадратные рубли.
- 4. 45 — 45 = 45
- 5. 40 : 8 = 41
- 6. Дважды два — пять!
- 7. Есть ли здесь пропорциональность?
- 8. 100% экономии.
- 9. Как вычислять средний процент?
- 10. Что даст ежегодный прирост в 40% за пять лет?
- 11. Новое правило умножения дробей.
- 12. Куда делся рубль?
- 13. Откуда появился лишний гривенник?
- 14. Завещание отца.
- 15. 2-3=4.
- II. АНАЛИЗ ПРИМЕРОВ.
- Глава III. АЛГЕБРА.
- I. ПРИМЕРЫ ЛОЖНЫХ РАССУЖДЕНИЙ.
- 19. Делимость многочленов и делимость чисел.
- 20. Произвольно взятое число а равно нулю.
- 21. 7 = 13.
- 22. Положительная единица равна отрицательной единице.
- 23. Другое «доказательство» равенства положительной и отрицательной единиц.
- 24. Мнимая единица и действительная отрицательная единица равны.
- 25. i^2 = 1
- 26. Всякое отрицательное число больше положительного, имеющего то же абсолютное значение.
- 27. Если a > b, то a > 2b
- 28. Если а и b положительные числа, то a > b и b > a.
- 29. Положительное число меньше нуля.
- 30. Сумма натуральных чисел, каждое из которых превосходит единицу, больше их произведения.
- 31. Чему равен квадратный корень из числа a^2?
- 32. Еще одно «доказательство» равенства нулю произвольно взятого числа.
- 33. Число не изменяется, если в нем переставить любые цифры!
- 34. Что говорит теорема о существовании корня в алгебре комплексных чисел?
- 35. Об одном спэсобе получать правильные результаты, применение которого требует большой осторожности.
- 36. О сумме 1-1+1-1 + …
- 37. Всегда ли целое больше своей части?
- 38. Еще одно «доказательство» равенства двух произвольно взятых чисел.
- 39. Сумма двух произвольных одинаковых чисел равна нулю.
- 40. Число не изменится, если к нему прибавить 1.
- 41. Ахиллес и черепаха.
- 42. О некоторых ученических ошибках.
- II. АНАЛИЗ ПРИМЕРОВ.
- Глава IV. ГЕОМЕТРИЯ.
- 1. ПРИМЕРЫ ЛОЖНЫХ РАССУЖДЕНИЙ.
- 44. Отрезок прямой равен своей правильной части.
- 45. Все треугольники равновелики.
- 46. Сумма оснований любой трапеции равна нулю.
- 47. Объемлемая и объемлющая.
- 48. Еще о пропорциональности.
- 49. Две окружности разного радиуса имеют одну и ту же длину.
- 50. Сумма катетов равна гипотенузе.
- 51. Длина полуокружности равна ее диаметру.
- 52. Боковая поверхность круглого прямого конуса с радиусом основания r и высотой h выражается формулой P=pi*r(r+h).
- 53. В данной точке на прямой можно восставить два перпендикуляра к этой прямой.
- 54. Через одну точку можно провести две прямые, параллельные данной прямой.
- 55. Окружность имеет два центра.
- 56. Из точки на прямую можно опустить два перпендикуляра.
- 57. Через две данные точки можно провести две прямые.
- 58. Любой треугольник — равнобедренный.
- 59. Катет прямоугольного треугольника равен его гипотенузе.
- 60. Прямой угол равен тупому (планиметрический вариант).
- 61. 64 кв. см = 65 кв. см.
- 62. Задача о заплате.
- II. АНАЛИЗ ПРИМЕРОВ.
- III. РАССКАЗЫ-ОБЪЯСНЕНИЯ ПО ПОВОДУ ОШИБОЧНЫХ РАССУЖДЕНИЙ.
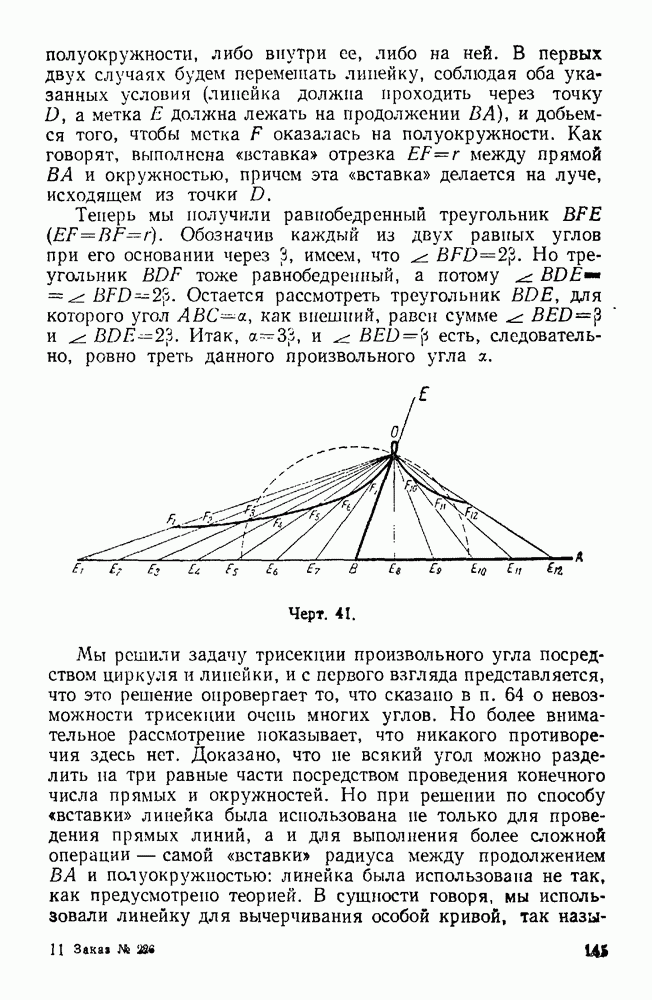
- 64. Трисекция угла.
- 65. Еще о трисекции угла.
- 66. Квадратура круга.
- 67. Об одном доказательстве теоремы о сумме внутренних углов треугольника.
- 68. Как вычислять объем усеченной пирамиды?
- Глава V. ТРИГОНОМЕТРИЯ.
- 70. Синус угла уменьшается, если к углу прибавить 360°.
- 71. Косинус любого острого угла больше единицы.
- 72. 1/4 > 1/2
- 73. 2^2 = 4^2
- 74. Площадь прямоугольника равна нулю.
- 75. Существуют равные треугольники, у которых не все стороны равны.
- 76. Каждый треугольник — прямоугольный.
- II. АНАЛИЗ ПРИМЕРОВ
- Глава VI. ПРИБЛИЖЕННЫЕ ВЫЧИСЛЕНИЯ. РАССКАЗЫ-ОБЪЯСНЕНИЯ ПО ПОВОДУ ОШИБОЧНЫХ РАССУЖДЕНИЙ
- 78. Все большие числа приближенно равны между собой.
- 79. О точности произведения приближенных чисел.
- 80. Верна ли формула …
- 81. Сколько цифр надо знать в подкоренном числе, чтобы получить корень с заданной точностью?
- 82. Зачем освобождаются от иррациональности в знаменателе?