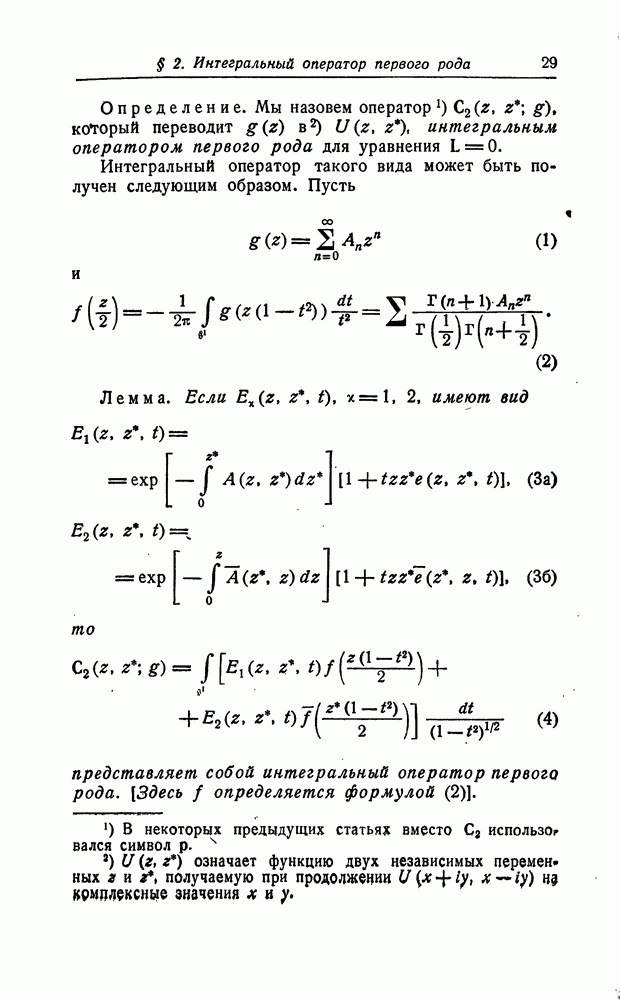§ 6. Оператор, порождающий решения системы уравнений в частных производных

В предыдущих параграфах рассматривались операторы, преобразующие аналитические функции одного комплексного переменного в решения одного уравнения в частных производных. В этом параграфе мы рассмотрим оператор, преобразующий аналитические функции двух комплексных переменных в решения системы уравнений в частных производных.

Мы рассмотрим систему уравнений

где независимые комплексные переменные, целые функции указанных переменных. (Если ввести обычным образом переменные записав и ограничиться лишь действительными значениями новых переменных, будет, разумеется, совпадать с сопряженным к

В. простейшем возможном случае, а именно, когда система (1) сразу решается; решение выражается формулой

где каждая из функций аналитична по указанным аргументам, т. е. функция удовлетворяет системе

Если потребовать, кроме того, чтобы было действительным решением системы (1) в том смысле, что принимает действительные значения при то тем самым число произвольных функций, входящих в формулу (2), сводится от четырех к двум. Действительно, эти четыре функции будут теперь связаны соотношениями

Возвратимся к общему случаю системы (1). Можно образовать действительные решения системы (1) таким способом, при котором, с одной стороны, обобщается представление, определяемое формулами (2) и (3) в простейшем случае с другой стороны, обобщаются представления, полученные ранее для решений одного уравнения в частных производных. Это выполняется следующим образом.

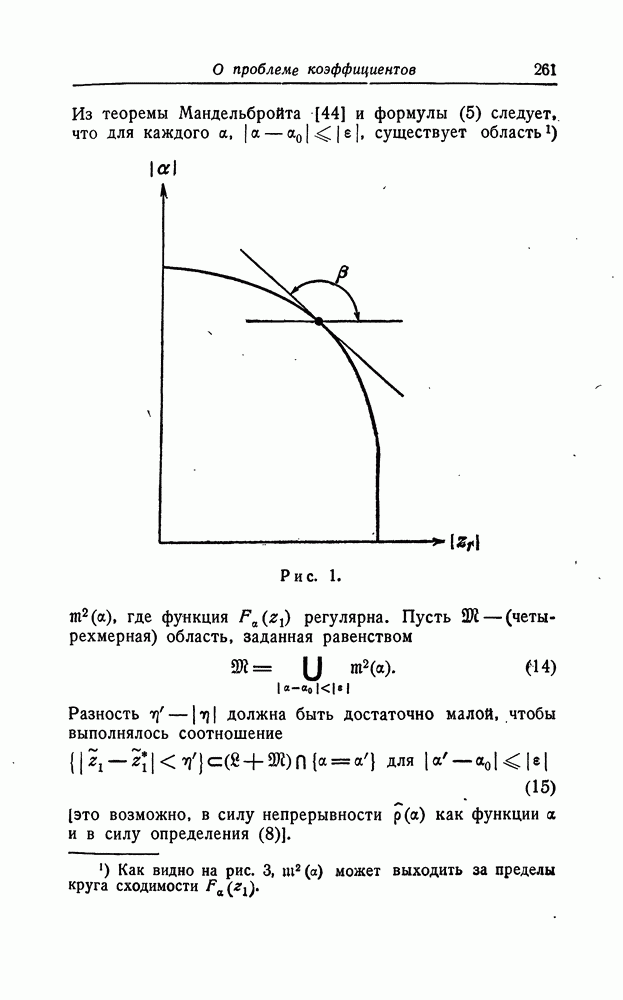
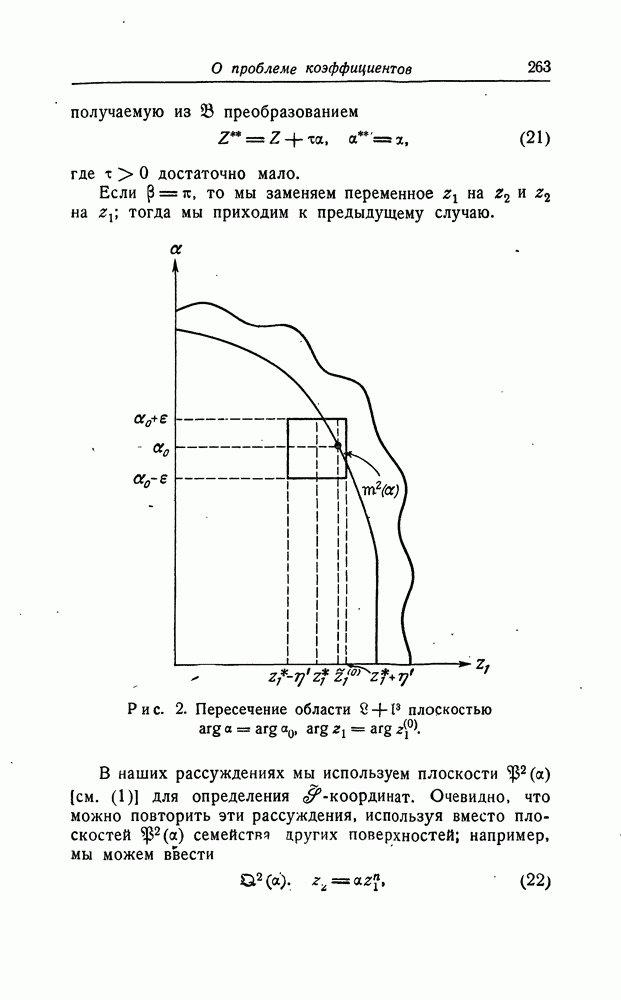
Покажем сначала, что можно найти решение системы (1), аналитическое в некоторой области восьмимерного пространства и совпадающее с данной выше функцией (2) при выполнении одного из четырех условий:

Это доказательство мы проводим непосредственным применением метода последовательных приближений. Чтобы

упростить выкладки, определим при помощи рекуррентных соотношений величины

где

Эти рекуррентные соотношения определены, если регулярная аналитическая функция в и все переменные изменяются в этой области.

При помощи индукции доказываем, что в силу (3), (4) и имеем

С другой стороны, используя (5), мы получаем из (4), что

Заметим, далее, что в силу второго уравнения из (3) и в силу (4), (4) и имеем

Из этого уравнения мы хотим по индукции вывести дифференциальную рекуррентную формулу

В самом деле, предположим, что эта формула уже доказана для всех индексов, меньших или равных

Умножая уравнение (4) на и используя формулы и снова (4), получаем

Таким образом, формула (8) справедлива для и индукция закончена.

Рассмотрим теперь ряд

Легко видеть, что этот ряд сходится, как экспоненциальный, в рассматриваемой области и представляет здесь аналитическую функцию четырех комплексных переменных. Действительно, пусть

в некоторой замкнутой подобласти из Согласно (4) и (40. имеем

и

Таким образом, функция аналитична в и в силу (6) и (8) удовлетворяет системе уравнений в частных производных (1). Далее, по построению, имеем для

Следовательно, совпадает с если выполнено одно из этих условий.

С другой стороны, ясно, что определяет решение единственным образом. Действительно, равенства

определяют сначала единственным образом в силу первого уравнения (1), так как мы имеем дело с обычной задачей с начальными условиями при фиксированном Аналогично находим Фиксируя теперь переменные определим решая задачу с начальными условиями известны] для второго уравнения (1).

Итак, мы показали, что система (1) имеет регулярное аналитическое решение в области 358, в которой аналитичны оба коэффициента Мы можем выбрать аналитическую функцию произвольно. Описанный процесс можно интерпретировать как применение линейного интегрального оператора к исходной функции Далее мы выразим этот оператор в замкнутой и более удобной форме и назовем его, как в случае одного уравнения, интегральным оператором первого рода.

Во многих приложениях мы приходим к системе дифференциальных уравнений в частных производных, исходя из задачи для действительных переменных следующего типа. Мы хотим определить действительнозначные функции удовлетворяющие системе уравнений

где

Положим тогда мы можем записать систему (16) в виде

где

Таким образом, мы снова приходим к системе (1) с дополнительным условием

Предположим, что аналитичны в области 558. Если действительное решение в "действительной подобласти области характеризуемой равенствами (19), то возникает задача продолжения этого решения в Мы хотим показать, что это всегда возможно. Таким путем мы сможем связать представление действительных решений системы определенным выше интегральным оператором, который тесно связан со значениями этого решения в комплексной области .

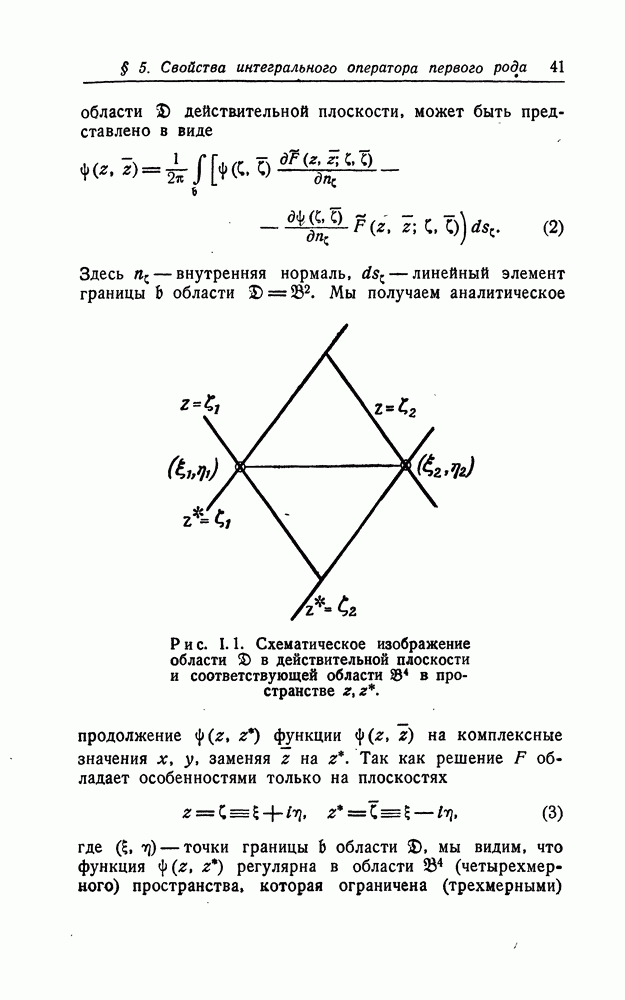
Введем понятие комплексной оболочки действительной области. Пусть область точек (или, в комплексной форме, точек определим ее комплексную (четырехмерную) оболочку как множество пар комплексных чисел таких, что ; обозначим ее через (см. стр. 42).

Пусть мы имеем четырехмерную область точек или, в комплексной форме, определим комплексную (восьмимерную) оболочку области как множество всех четверок комплексных чисел таких, что все четыре точки принадлежат Обозначим ее через

Сформулируем теперь следующий результат. Пусть решение системы (16), дифференцируемое четыре раза по всем переменным в выпуклой области

действительного пространства Тогда Функция может быть аналитически продолжена в если коэффициенты регулярные аналитические функции в

Доказательство. Рассмотрим сначала как функцию от при фиксированных значениях Так как удовлетворяет уравнению в частных производных

мы можем, в силу наших предположений относительно и классической теоремы об аналитичности решений линейных эллиптических дифференциальных уравнений, продолжить в комплексную область. Пусть область изменения при фиксированном Ясно, что тогда будет регулярной аналитической функцией в

Рассмотрим теперь функцию аналитически зависящую от . В силу (16) имеет место равенство

аналитических функций для Следовательно, по принципу перманентности это равенство справедливо всюду в

Далее, фиксируем и исследуем (20) как дифференциальное уравнение для функции рассматриваемой как функция от Мы снова можем продолжить ее в комплексную область. Мы должны определить область изменения для заданных Таким путем определяется двумерная область будет регулярной аналитической функцией по в комплексной оболочке Эта оболочка, очевидно, характеризуется тем, что лежит в Следовательно, мы доказали, что зависит аналитически от каждой пары переменных

если что доказывает наше утверждение.

Мы доказали, что действительное решение системы (16), определенное в области , может быть аналитически продолжено в комплексную оболочку Таким образом, мы получаем две аналитические функции

регулярные соответственно в пересечениях с многообразиями

Докажем теперь обратное утверждение: две аналитические функции определяют решение

В самом деле, так как решение действительно, имеем тождество

Следовательно, из (21) и (22) получаем

Это показывает, что все значения функции для которых один элемент из пары один элемент из пары равны нулю, выражаются через Таким образом, используя упомянутый выше результат, мы можем построить решение проведенным выше итерационным процессом, выразив его через две аналитические функции и I двух комплексных переменных.

Итак, функцию можно получить из с помощью усложненного интегрального оператора, линейного по обеим этим аналитическим функциям и задающего линейное отображение семейства пар аналитических функций в пространство решений рассматриваемой системы дифференциальных уравнений. Мы можем дать несколько более удобный интегральный оператор, определяющий то же самое отображение и тесно связанный с описанным выше оператором.

Этот новый интегральный оператор можно получить при помощи аналогичного оператора, широко используемого в теории одного уравнения в частных производных. Действительно, пусть

где функция F аналитична по Тогда мы можем найти ядро такое, что оно является действительнозначной аналитической функцией всех этих переменных при и

является решением уравнения (25) при любой аналитической функции (см. стр. 26 и 29). Аналогично, пусть соответствующее ядро для дифференциального уравнения

Следовательно, существует пара порождающих функций , которые являются целыми функциями от и аналитичны по в замкнутом единичном круге и при этом любое решение системы (1), действительное в разъясненном выше смысле, для действительных значений может быть выражено в виде

где аналитические функции соответственно от регулярные в окрестности начала координат.

В формуле (28) мы имеем еще некоторую свободу в выборе и так как, не изменяя интеграла, мы можем добавить к произвольную функцию и вычесть из функцию Пользуясь этой свободой, мы можем потребовать, чтобы было

Формула (28) позволяет продолжить полученное решение в комплексную область. Используя то, что ядра принимают действительные значения, и их фундаментальное свойство: мы получаем простые интегральные соотношения между аналитическими функциями фигурирующими в формуле (28), и рассмотренными ргнае аналитическими функциями

Таким образом, мы легко определим если заданы Обратно, по заданным мы из (30) можем единственным образом найти Определим сначала из первого уравнения (30), сравнивая коэффициенты. Для первого члена получаем

Это показывает, что должно быть действительным. Последнее следует также из равенства

так как действительно при . С другой стороны, определяется из (30) с точностью до аддитивной мнимой постоянной, но это не влияет на интегральный оператор (28). Определив функцию мы вводим ее во второе уравнение (30) и находим снова методом сравнения коэффициентов. Заметим, что условие (29) автоматически выполняется в силу соотношений

которые следуют из (21) и (23).

Таким образом, установлена эквивалентность интегрального оператора (28) и оператора, описанного ранее (стр. 153—160), и определено значение функций

Кроме (28), получено еще одно представление для решений системы (1). Для всякой системы (1) существуют четыре функции и , целые по всем указанным переменным и такие, что каждое действительное решение системы (1) может быть выражено в форме

(см. скан)

где аналитические функции двух комплексных переменных, регулярные в окрестности начала координат.

Используя представление (33), можно найти оценки для некоторых классов решений системы (1). В качестве примера такого рода результатов мы сформулируем без доказательства следующую теорему.

Теорема 6.1. Поставам в соответствие функциям фигурирующим в формуле (33), функции зависящие только от и такие, что

при Пусть решение системы (1) представляется в виде (33), где функция предполагается регулярной в области а значение действительным. Далее, пусть при продолжении на комплексные значения, функция обладает тем свойством, что при любом являются однозначными функциями от при и удовлетворяют неравенствам

где а и удобно выбранные постоянные. Тогда в области

имеем

Доказательство, данное в работе [36, § 3], по существу состоит в использовании представления (33) наряду с теоремой об искажении Кёбе.

Операторы вида (28) применялись в [14, 123] для исследования некоторых классов систем (1), определенных следующим образом.

Говорят, что система (1) принадлежит классу если в представлении для ее решений можно выбрать порождающие функции вида

В [36] получены необходимые и достаточные условия, чтобы система (1) принадлежала классу и установлены соотношения между функциями в (1) и коэффициентами в (37). Например, система двух «волновых» уравнений принадлежит классу Кроме того, доказан следующий результат.

Теорема 6.2. Пусть любое решение некоторой системы класса соответствующее рациональным функциям и в представлении (33). Тогда удовлетворяет обыкновенным линейным дифференциальным уравнениям по каждой из переменных Коэффициенты этих уравнений являются рациональными функциями коэффициентов из (37). Порядок уравнений зависит только от в (37), но не зависит от

Теорема 6.2 позволяет исследовать решения систем класса с помощью теории Фукса для обыкновенных дифференциальных уравнений.

Мы видели, что в случае одного уравнения в частных производных интегральные операторы позволяют изучать

проблему коэффициентов, т. е. находить соотношения между свойствами решений и коэффициентами их разложений в ряд. В [36, 123] доказано, что подобные возможности существуют и для систем вида (1). Соответствующее исследование опирается на интегральные операторы, представленные в форме (33). Для этих операторов очень просты соотношения между решением и соответствующими аналитическими функциями а именно

(см. [42]). В [123] показано, что сначала мы получаем соотношения между подпоследовательностями коэффициентов ряда

и свойствами Как и в случае одного дифференциального уравнения, можно получить информацию о поведении и из других подпоследовательностей. Это можно сделать с помощью соотношений между различными подпоследовательностями.

[7, 8, 10, 14, 28, 34, 36, 38, 42, 81, 82, 93, 94, 113, 123, 201, 2211