| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 8. Интегральный оператор для уравнений с неаналитическими коэффициентами
В этом параграфе мы рассмотрим уравнения вида

Это уравнение исследовалось в гл. I в предположении, что с — целая функция. Результаты, подобные полученным в гл. I, очевидным образом переносятся на случай, когда с регулярна в ограниченной области, и не нуждаются в подробном обсуждении. Случай, когда с аналитична, но имеет некоторые особенности, рассматривался в § 1—4 настоящей главы.
Сделаем теперь общее предположение, что коэффициент с — действительная функция двух действительных переменных, определенная и всего лишь непрерывно дифференцируемая в замкнутой ограниченной односвязной области плоскости х, у.
Введем сначала интегральный оператор, преобразующий аналитические функции комплексного переменного в решения уравнения (1), определенные в 
Теорема 8.1. Пусть  гармоническая функция в замкнутой ограниченной односвязной области
гармоническая функция в замкнутой ограниченной односвязной области  ограниченной регулярной жордановой кривой
ограниченной регулярной жордановой кривой  Если область
Если область  достаточно мала и
достаточно мала и  непрерывно дифференцируемая функция в
непрерывно дифференцируемая функция в  то функция
то функция

где

являетсярешением уравнения (1) в 
Доказательство. Покажем сначала, что ряд (2) и его первые производные по х и у сходятся абсолютно и равномерно в  . Пусть
. Пусть  круг радиуса
круг радиуса  с центром в произвольной точке
с центром в произвольной точке  содержащий
содержащий  Продолжим
Продолжим  в
в  таким образом, чтобы получающаяся в результате продолжения функция
таким образом, чтобы получающаяся в результате продолжения функция  была равномерно ограничена, а
была равномерно ограничена, а  непрерывно дифференцируема в
непрерывно дифференцируема в  . (Такое продолжение с и Н возможно, см. [209].) Тогда существуют такие положительные константы
. (Такое продолжение с и Н возможно, см. [209].) Тогда существуют такие положительные константы  что
что

Далее, полагая

получаем

и

Пусть  Тогда ряд для
Тогда ряд для  и для его первых производных по х и у мажорируется рядом
и для его первых производных по х и у мажорируется рядом

а ряд в правой части сходится. Здесь  зависят от выбора точки
зависят от выбора точки  Если
Если  изменяется в
изменяется в  , то эти три величины имеют конечные верхние грани. Используя их, мы получим верхнюю грань для
, то эти три величины имеют конечные верхние грани. Используя их, мы получим верхнюю грань для  и его двух первых производных во всей области
и его двух первых производных во всей области  . Это доказывает абсолютную и равномерную сходимость ряда (2) и его первых производных по х и у.
. Это доказывает абсолютную и равномерную сходимость ряда (2) и его первых производных по х и у.
Для первой производной  существует представление, отличное от полученного почленным дифференцированием правой части равенства (2),
существует представление, отличное от полученного почленным дифференцированием правой части равенства (2),
Так как ряд в правой части равенства (2) сходится абсолютно, мы можем записать

где

Далее  Если мы положим
Если мы положим

то

Интегрирование по частям в правой части формулы (10) дает

Аналогично

Первый член в правой части формулы (12) ведет себя как ньютоновский потенциал с распределением массы вдоль кривой  Так как
Так как  регулярная жорданова кривая, этот интеграл существует в каждой точке
регулярная жорданова кривая, этот интеграл существует в каждой точке  Таким образом,
Таким образом,  существует и имеет непрерывные производные первого и второго порядков в
существует и имеет непрерывные производные первого и второго порядков в 
Используя (12) и аналогичное выражение для  применяя хорошо известные рассуждения, убеждаемся в том, что
применяя хорошо известные рассуждения, убеждаемся в том, что  удовлетворяет уравнению (1).
удовлетворяет уравнению (1).
Введем другой класс решений уравнения (1). Пусть  — достаточно малая область, звездная по отношению к началу координат, и
— достаточно малая область, звездная по отношению к началу координат, и  имеет счетное число особенностей в
имеет счетное число особенностей в  в точках
в точках  Обозначим через
Обозначим через  область, получаемую разрезом
область, получаемую разрезом  вдоль отрезков
вдоль отрезков  Пусть
Пусть  — ветвь
— ветвь  , определенная в
, определенная в  , и пусть
, и пусть

Определение.  есть оператор того же вида, что и
есть оператор того же вида, что и  [см. (2)], если
[см. (2)], если  заменить на
заменить на  .
.
Если существует функция  то мы скажем, что
то мы скажем, что 
Определение. Пусть  — регулярная гармоническая функция в замкнутой подобласти
— регулярная гармоническая функция в замкнутой подобласти  области
области  . Если
. Если  то соответствующее решение
то соответствующее решение  называется
называется  -регулярным решением уравнения (1) в
-регулярным решением уравнения (1) в 
Определение. Функции

называются  - степенными решениями уравнения (1) в
- степенными решениями уравнения (1) в  .
.
Для решений  справедливы многие результаты, аналогичные полученным в гл. I, § 5, 6 в случае,
справедливы многие результаты, аналогичные полученным в гл. I, § 5, 6 в случае,
дифференциальных уравнений с целыми коэффициентами. Приведем несколько примеров.
Пусть  решение уравнения (1),
решение уравнения (1),  -регулярное в замкнутой подобласти
-регулярное в замкнутой подобласти  области
области  Тогда если
Тогда если  достаточно малый круг с центром в начале координат, то решение
достаточно малый круг с центром в начале координат, то решение  может быть разложено в ряд по
может быть разложено в ряд по  -степенным решениям в
-степенным решениям в  Если
Если  односвязная область, то
односвязная область, то  можно аппроксимировать в
можно аппроксимировать в  линейной комбинацией
линейной комбинацией  -степенных решений
-степенных решений 
Эти утверждения немедленно следуют из того факта, что аналитическую функцию в круге  можно разложить в ряд
можно разложить в ряд  и из теоремы Рунге.
и из теоремы Рунге.
Определение. Особенность функции  где
где

называется  -полюсом порядка нуль.
-полюсом порядка нуль.
Пусть решение  является
является  -регулярным в круге
-регулярным в круге  и представляется там в виде
и представляется там в виде

Тогда  имеет
имеет  -полюс нулевого порядка в замкнутом круге
-полюс нулевого порядка в замкнутом круге  тогда и только тогда, когда существует постоянная
тогда и только тогда, когда существует постоянная  такая, что
такая, что

при всех достаточно больших  лежащих на границе
лежащих на границе 
Этот результат немедленно следует из соответствующей теоремы для функций комплексного переменного. В самом деле, если аналитическая функция  имеет логарифмический полюс в точке а, и это ее единственная особенность в то ее коэффициенты
имеет логарифмический полюс в точке а, и это ее единственная особенность в то ее коэффициенты
удовлетворяют неравенству (16), и обратно (см. [61, т. II, стр. 325]).
Замечание. Если о коэффициенте с в уравнении (1) известно только, что это непрерывная функция, то можно при некоторых дополнительных предположениях получить аналогичные результаты. В этом случае функции  являются обобщенными решениями в смысле Соболева (см. [200, стр. 3, 4]). [4, 17, 18, 23, 24, 27, 29, 31, 36, 40—43, 45—51, 56—58, 67, 83, 84, 86. 91, 122, 133, 135, 136, 138, 140, 142—146, 160, 161, 176, 178, 191, 207—209, 212, 213, 215, 216, 218, 219, 225, 227, 228]
являются обобщенными решениями в смысле Соболева (см. [200, стр. 3, 4]). [4, 17, 18, 23, 24, 27, 29, 31, 36, 40—43, 45—51, 56—58, 67, 83, 84, 86. 91, 122, 133, 135, 136, 138, 140, 142—146, 160, 161, 176, 178, 191, 207—209, 212, 213, 215, 216, 218, 219, 225, 227, 228]
ЛИТЕРАТУРА
(см. скан)
(см. скан)
(см. скан)
(см. скан)
(см. скан)
(см. скан)
(см. скан)
(см. скан)
(см. скан)
(см. скан)
(см. скан)
(см. скан)
(см. скан)
(см. скан)
(см. скан)
(см. скан)
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ВВЕДЕНИЕ
- Глава I. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ С ЦЕЛЫМИ КОЭФФИЦИЕНТАМИ С ДВУМЯ НЕЗАВИСИМЫМИ ПЕРЕМЕННЫМИ
- § 1. Представление решений уравнений с частными производными
- § 2. Интегральный оператор первого рода
- § 3. Дальнейшие представления интегральных операторов
- § 4. Представление оператора первого рода посредством интегралов
- § 5. Свойства интегрального оператора первого рода
- § 6. Некоторые дальнейшие свойства интегрального оператора первого рода
- § 7. Дифференциальное уравнение
- § 8. Интегральные операторы экспоненциального типа
- § 9. Дифференциальное уравнение …
- 10. Дифференциальные уравнения высшего порядка
- Глава II. ГАРМОНИЧЕСКИЕ ФУНКЦИИ ТРЕХ ПЕРЕМЕННЫХ
- § 2. Характеристическое пространство
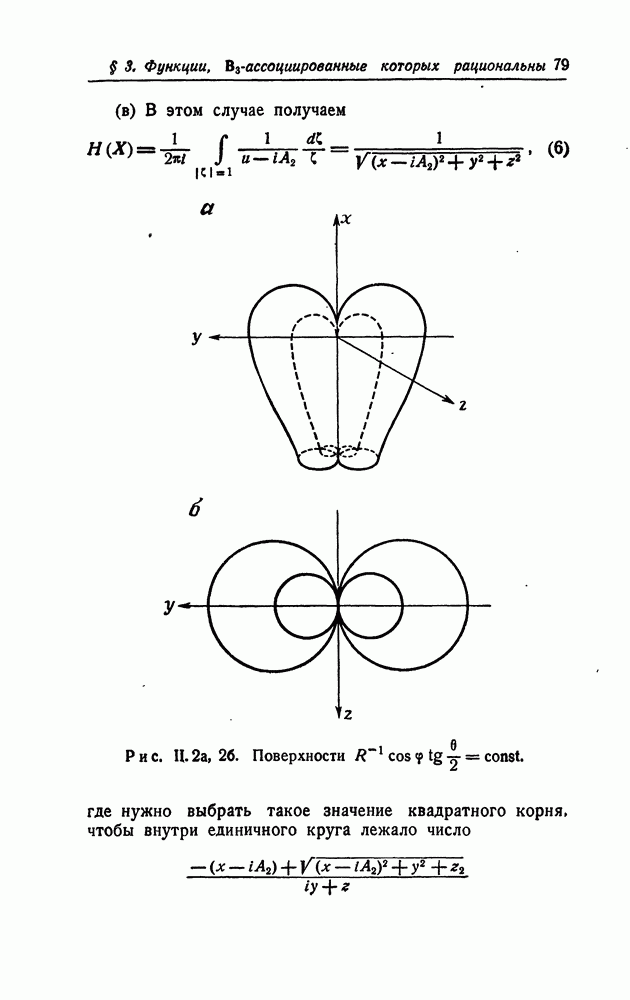
- § 3. Гармонические функции, В3-ассоциированные функции которых рациональны
- § 4. Периоды
- § 5. Связь между коэффициентами разложения гармонической функции в ряд и ее особенностями
- § 6. Другой тип интегральных представлений гармонических функций
- § 7. Поведение в целом функций класса с рациональной ассоциированной
- Глава III. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ С ТРЕМЯ ПЕРЕМЕННЫМИ
- § 2. Разложение в ряд решений уравнения …
- § 3. Интегральный оператор, порождающий решения уравнения
- § 4. Второй интегральный оператор, порождающий решения уравнения …
- § 5. Интегральный оператор, порождающий решения уравнения
- § 6. Интегральный оператор, порождающий решения уравнения …
- Глава IV. СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
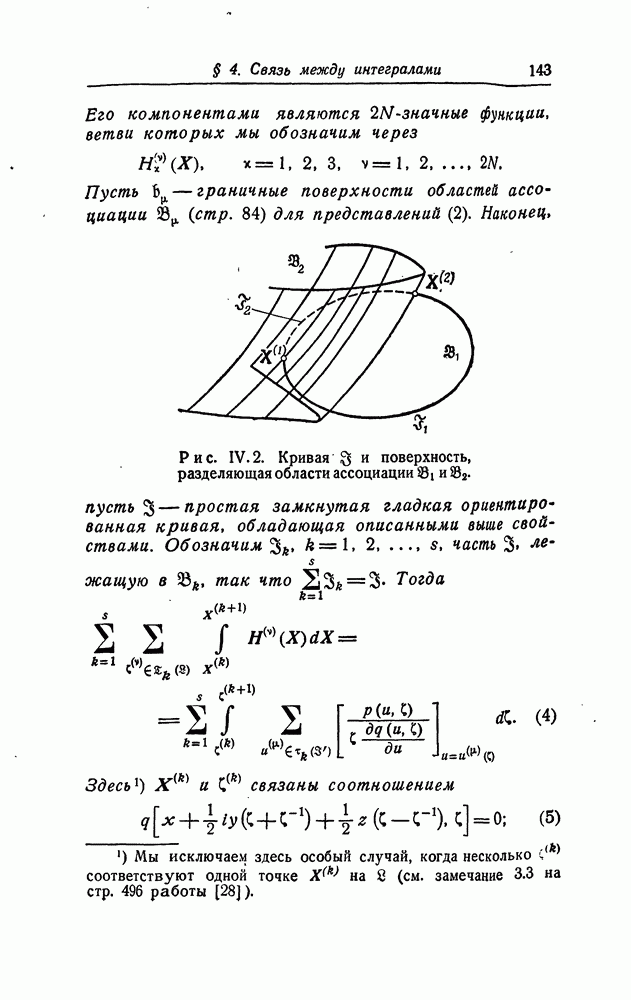
- § 2. Гармонические векторы в целом и их представление посредством интегралов
- § 3. Интегралы от гармонических векторов
- § 4. Связь интегралов от алгебраических гармонических векторов трех переменных с интегралами от алгебраических функций одного комплексного переменного
- § 5. Обобщение теорем о вычетах на случай уравнения …
- § 6. Оператор, порождающий решения системы уравнений в частных производных
- Глава V. УРАВНЕНИЯ СМЕШАННОГО ТИПА И ЭЛЛИПТИЧЕСКИЕ УРАВНЕНИЯ С СИНГУЛЯРНЫМИ И НЕАНАЛИТИЧЕСКИМИ КОЭФФИЦИЕНТАМИ
- § 2. Обобщение представления (1.12) решений уравнения (1.6)
- § 3. Оператор (1.11б) в общем случае
- § 4. Порождающие функции, аналогичные решениям гипергеометрического уравнения
- § 5. О решении задачи Коши в целом
- § 6. Обобщенные уравнения Коши — Римана
- § 7. Дифференциальное уравнение … с новым типом особенности функции N
- § 8. Интегральный оператор для уравнений с неаналитическими коэффициентами
- ПРИЛОЖЕНИЕ. ОПЕРАТОРЫ, ПОРОЖДАЮЩИЕ РЕШЕНИЯ НЕКОТОРЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ТРЕМЯ ПЕРЕМЕННЫМИ, И ИХ СВОЙСТВА
- 1. Определение компонент H2 и H3 гармонического вектора по данной компоненте H1
- 2. Связь между интегралами от алгебраических гармонических векторов от трех переменных с интегралами от алгебраических функций комплексного переменного.
- 3. Обобщение предыдущих результатов на случай дифференциального уравнения …
- О ПРОБЛЕМЕ КОЭФФИЦИЕНТОВ В ТЕОРИИ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ
- 2. Формулы для определения области регулярности функции двух комплексных переменных по коэффициентам ее разложения в ряд.
- 3. Формула для определения расположения некоторых особенностей f(z1, z2) по коэффициентам ее разложения в ряд.
- 4. Обобщение результатов п. 2,3 на случай одной системы дифференциальных уравнений.
- 5. Применение интегральных рператоров в теории целых функций.
- ПРИМЕНЕНИЕ ИНТЕГРАЛЬНЫХ ОПЕРАТОРОВ ПРИ ИЗУЧЕНИИ АЛГЕБРЫ ГАРМОНИЧЕСКИХ ФУНКЦИЙ ТРЕХ ПЕРЕМЕННЫХ И ПРОБЛЕМЫ КОЭФФИЦИЕНТОВ