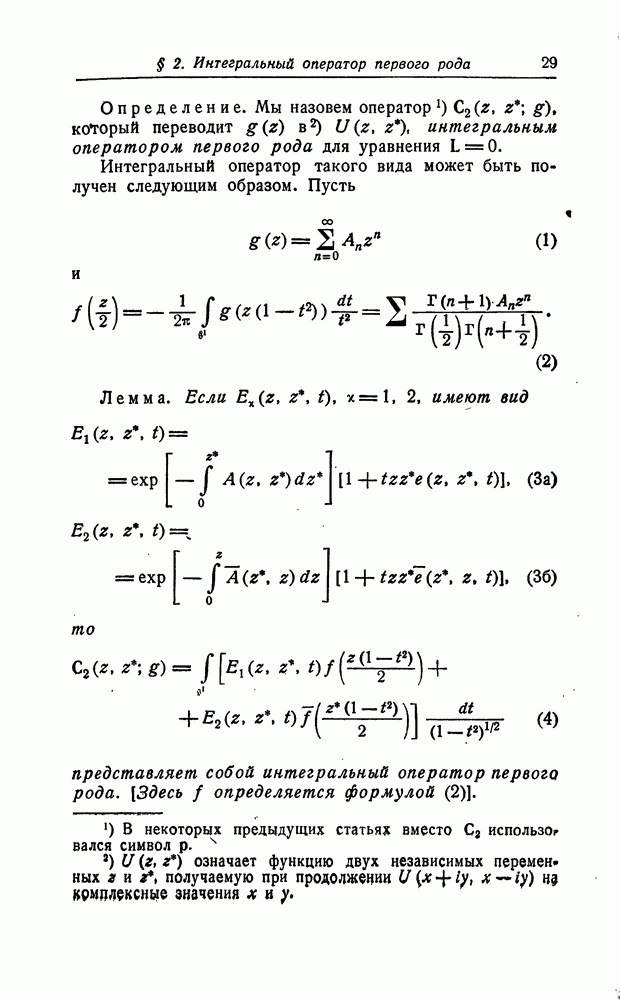| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4. Обобщение результатов п. 2,3 на случай одной системы дифференциальных уравнений.
Шиффер и автор [23, 12] определили интегральные операторы, порождающие решения системы двух линейных уравнений с частными производными

В работе [12] (см. теорему 1 на стр. 995) показано, что для каждой системы (1) существуют четыре порождающие функции

(целые по  такие, что каждое действительное решение
такие, что каждое действительное решение  регулярное в начале координат, может быть
регулярное в начале координат, может быть
представлено в виде
(см. скан)
Здесь  аналитические функции соответственно от
аналитические функции соответственно от  регулярные в начале координат,
регулярные в начале координат,  где А — сопряженное к
где А — сопряженное к  Обратно, если
Обратно, если  аналитические функции, то правая часть (3) является решением системы (1). Области, в которых имеют место представления (4) и (5), называются областями представления соответственно операторов
аналитические функции, то правая часть (3) является решением системы (1). Области, в которых имеют место представления (4) и (5), называются областями представления соответственно операторов  Для определения функций
Для определения функций  можно использовать следующие уравнения:
можно использовать следующие уравнения:

Пусть решение системы (1) имеет разложение 

в окрестности начала координат. Тогда

Порождающие функции  являются целыми функциями переменных
являются целыми функциями переменных  при
при  Таким образом, порождаемое решение определено и голоморфно в каждой области 35, такой, что
Таким образом, порождаемое решение определено и голоморфно в каждой области 35, такой, что  голоморфна в
голоморфна в  и
и  обладает следующим свойством: точку
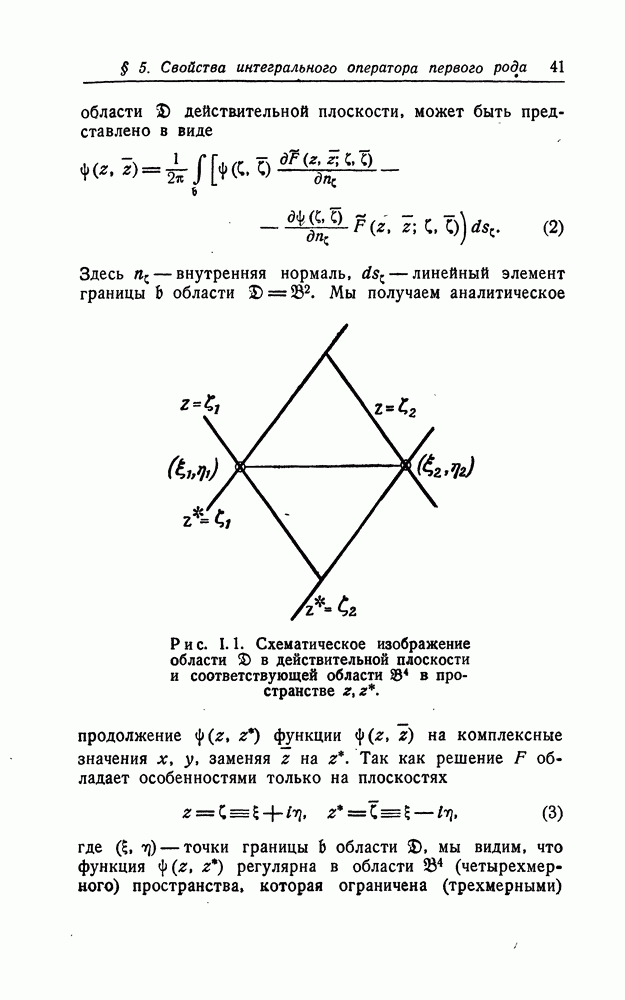
обладает следующим свойством: точку  можно соединить с началом координат посредством
можно соединить с началом координат посредством  . Здесь — прямое произведение двух простых кривых, одной из плоскости
. Здесь — прямое произведение двух простых кривых, одной из плоскости  другой из плоскости
другой из плоскости 
Функция  регулярна в
регулярна в  односвязная область, обладающая упомянутым выше свойством. Таким образом, также регулярна в
односвязная область, обладающая упомянутым выше свойством. Таким образом, также регулярна в 
Замечание 4.1. Решение  можно рассматривать либо в четырехмерном пространстве
можно рассматривать либо в четырехмерном пространстве  т. е. для действительных
т. е. для действительных  сопряженное к
сопряженное к  либо в восьмимерном пространстве
либо в восьмимерном пространстве  Тогда мы предполагаем, что
Тогда мы предполагаем, что  В этом случае
В этом случае  два независимых переменных.
два независимых переменных.
В дальнейшем мы предположим, что  Кроме функций
Кроме функций  мы также рассмотрим функции
мы также рассмотрим функции  последнем случае областью регулярности будет уже не
последнем случае областью регулярности будет уже не  а область
а область  которая получается при
которая получается при
замене точек  области
области  точками
точками  Аналогично, следует заменить плоскости (2.1) плоскостями
Аналогично, следует заменить плоскости (2.1) плоскостями

(Трехмерные) гиперповерхности  следует заменить гиперповерхностями, получаемыми тем же путем, что и в
следует заменить гиперповерхностями, получаемыми тем же путем, что и в  при помощи плоскостей
при помощи плоскостей  вместо
вместо  Новые гиперповерхности мы обозначим так:
Новые гиперповерхности мы обозначим так:

Так как функции  см. (2), являются целыми функциями по
см. (2), являются целыми функциями по  то применение результатов из
то применение результатов из  дает аналогичные результаты для решений
дает аналогичные результаты для решений  системы (1).
системы (1).
Теорема 4.1. Пусть 

— действительное решение системы (1). Предположим,  коэффициенты
коэффициенты 

удовлетворяют условиям леммы 2.1. Тогда функция  голоморфна в
голоморфна в  [ел. (2.6), (2.7), (2.8), (2.8а)]. Если коэффициенты
[ел. (2.6), (2.7), (2.8), (2.8а)]. Если коэффициенты  ряда
ряда

удовлетворяют условиям леммы  функция
функция  регулярна в
регулярна в 
Теорема 4.1 следует почти сразу из формул (8) и (9) и из того, что  — целые
— целые
функции от  Функция регулярна во всякой области, в которой регулярна
Функция регулярна во всякой области, в которой регулярна  С другой стороны, разложение для функции
С другой стороны, разложение для функции  дается в правой части (9). Аналогично доказывается второе утверждение теоремы 4.1.
дается в правой части (9). Аналогично доказывается второе утверждение теоремы 4.1.
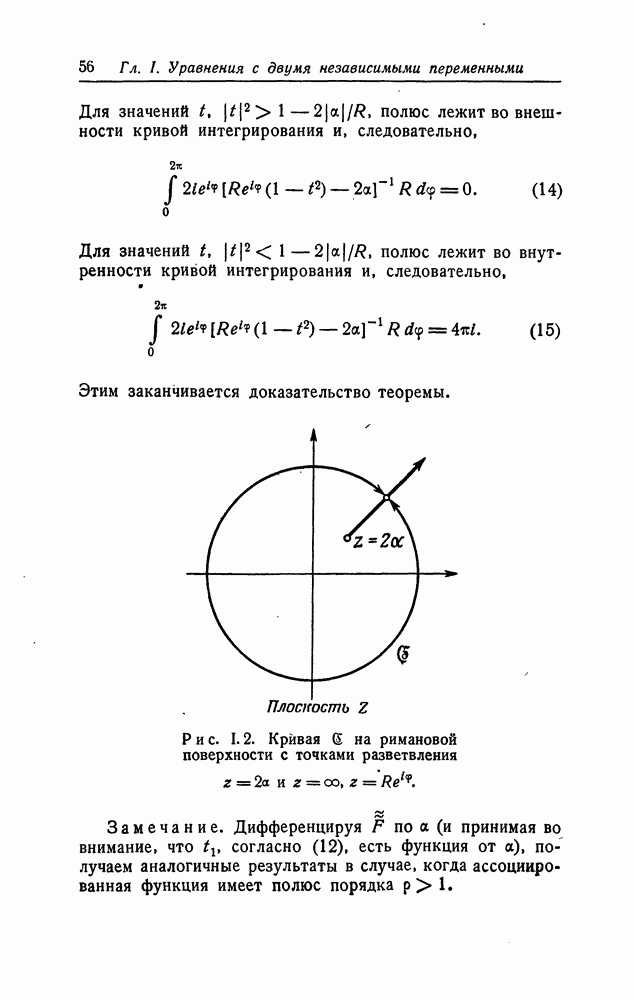
Если мы применим оператор  к функции
к функции  имеющей в
имеющей в  полюсы, то мы получим особенности, которые, вообще говоря, будут линиями разветвления. Это следует из того, что, согласно формуле (13) из [12, стр. 997], наш оператор
полюсы, то мы получим особенности, которые, вообще говоря, будут линиями разветвления. Это следует из того, что, согласно формуле (13) из [12, стр. 997], наш оператор  можно записать в виде
можно записать в виде

Здесь  целые функции, просто связанные с
целые функции, просто связанные с  ( см. [12]).
( см. [12]).
Предположим, что функция  в достаточно малой окрестности допускает представление
в достаточно малой окрестности допускает представление  где
где  регулярные функции. Тогда
регулярные функции. Тогда

и

бесконечнозначные функции от 
В соответствии с этим множества 11, где аналитические функции  имеют бесконечность конечного порядка и однозначны, преобразуются оператором
имеют бесконечность конечного порядка и однозначны, преобразуются оператором  в множества
в множества  , где
, где  имеют бесконечность того же порядка, что и
имеют бесконечность того же порядка, что и  но бесконечнозначны.
но бесконечнозначны.
Замечание 4.2. Интегральным представлением (4) функции определены в "области ассоциации" рассматриваемого интегрального оператора, т. е. в области, где имеет  место представление в виде (4). Аналитическим продолжением функцию
место представление в виде (4). Аналитическим продолжением функцию  можно определить во всей области ее существования. Таким образом, используя теорию функций комплексных переменных, мы можем в некоторых случаях делать выводы о поведении также вне области ассоциации.
можно определить во всей области ее существования. Таким образом, используя теорию функций комплексных переменных, мы можем в некоторых случаях делать выводы о поведении также вне области ассоциации.
Теорема 4.2. Пусть  действительное решение системы (1), имеющее разложение в ряд (8) в окрестности начала координат. Обозначим через
действительное решение системы (1), имеющее разложение в ряд (8) в окрестности начала координат. Обозначим через  функции (3.4), которые получаются из (3.5) заменой коэффициентов
функции (3.4), которые получаются из (3.5) заменой коэффициентов  на
на 
1. Если  удовлетворяют условиям (3.7), (3.8) леммы 3.1, то функция
удовлетворяют условиям (3.7), (3.8) леммы 3.1, то функция  имеет самое большее
имеет самое большее  особых множеств разветвления
особых множеств разветвления  и не имеет других особенностей на границе (3.6).
и не имеет других особенностей на границе (3.6).
2. Пусть соотношение (3.9) выполнено для  Тогда имеет самое большее конечное число линий разветвления
Тогда имеет самое большее конечное число линий разветвления  .
.
3. Если (3.10) имеет место для  то в каждой конечной области имеет только конечное число особых множеств на границе области ассоциации.
то в каждой конечной области имеет только конечное число особых множеств на границе области ассоциации.
4. Если  удовлетворяют соотношению (3.11), то функция имеет конечное число множеств разветвления 33 в каждой области (3.12) и бесконечно много множеств разветвления в окрестности (3.13).
удовлетворяют соотношению (3.11), то функция имеет конечное число множеств разветвления 33 в каждой области (3.12) и бесконечно много множеств разветвления в окрестности (3.13).
Аналогичные соотношения справедливы для  В последнем случае
В последнем случае  следует определить,
следует определить, 
пользуя коэффициенты (3.5); линии разветвления 2 совпадают с множествами (12).
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ВВЕДЕНИЕ
- Глава I. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ С ЦЕЛЫМИ КОЭФФИЦИЕНТАМИ С ДВУМЯ НЕЗАВИСИМЫМИ ПЕРЕМЕННЫМИ
- § 1. Представление решений уравнений с частными производными
- § 2. Интегральный оператор первого рода
- § 3. Дальнейшие представления интегральных операторов
- § 4. Представление оператора первого рода посредством интегралов
- § 5. Свойства интегрального оператора первого рода
- § 6. Некоторые дальнейшие свойства интегрального оператора первого рода
- § 7. Дифференциальное уравнение
- § 8. Интегральные операторы экспоненциального типа
- § 9. Дифференциальное уравнение …
- 10. Дифференциальные уравнения высшего порядка
- Глава II. ГАРМОНИЧЕСКИЕ ФУНКЦИИ ТРЕХ ПЕРЕМЕННЫХ
- § 2. Характеристическое пространство
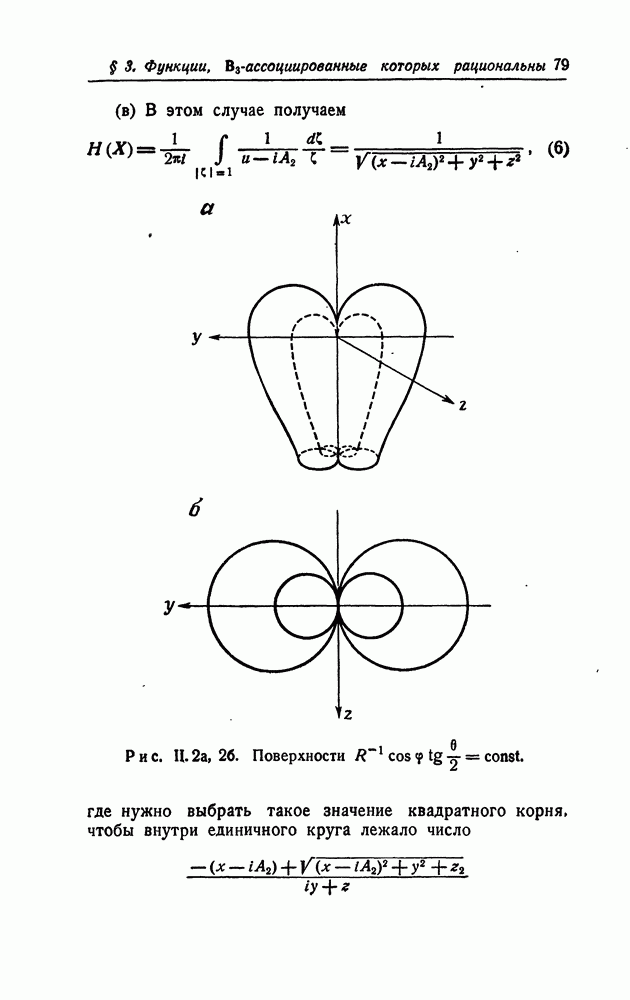
- § 3. Гармонические функции, В3-ассоциированные функции которых рациональны
- § 4. Периоды
- § 5. Связь между коэффициентами разложения гармонической функции в ряд и ее особенностями
- § 6. Другой тип интегральных представлений гармонических функций
- § 7. Поведение в целом функций класса с рациональной ассоциированной
- Глава III. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ С ТРЕМЯ ПЕРЕМЕННЫМИ
- § 2. Разложение в ряд решений уравнения …
- § 3. Интегральный оператор, порождающий решения уравнения
- § 4. Второй интегральный оператор, порождающий решения уравнения …
- § 5. Интегральный оператор, порождающий решения уравнения
- § 6. Интегральный оператор, порождающий решения уравнения …
- Глава IV. СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- § 2. Гармонические векторы в целом и их представление посредством интегралов
- § 3. Интегралы от гармонических векторов
- § 4. Связь интегралов от алгебраических гармонических векторов трех переменных с интегралами от алгебраических функций одного комплексного переменного
- § 5. Обобщение теорем о вычетах на случай уравнения …
- § 6. Оператор, порождающий решения системы уравнений в частных производных
- Глава V. УРАВНЕНИЯ СМЕШАННОГО ТИПА И ЭЛЛИПТИЧЕСКИЕ УРАВНЕНИЯ С СИНГУЛЯРНЫМИ И НЕАНАЛИТИЧЕСКИМИ КОЭФФИЦИЕНТАМИ
- § 2. Обобщение представления (1.12) решений уравнения (1.6)
- § 3. Оператор (1.11б) в общем случае
- § 4. Порождающие функции, аналогичные решениям гипергеометрического уравнения
- § 5. О решении задачи Коши в целом
- § 6. Обобщенные уравнения Коши — Римана
- § 7. Дифференциальное уравнение … с новым типом особенности функции N
- § 8. Интегральный оператор для уравнений с неаналитическими коэффициентами
- ПРИЛОЖЕНИЕ. ОПЕРАТОРЫ, ПОРОЖДАЮЩИЕ РЕШЕНИЯ НЕКОТОРЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ТРЕМЯ ПЕРЕМЕННЫМИ, И ИХ СВОЙСТВА
- 1. Определение компонент H2 и H3 гармонического вектора по данной компоненте H1
- 2. Связь между интегралами от алгебраических гармонических векторов от трех переменных с интегралами от алгебраических функций комплексного переменного.
- 3. Обобщение предыдущих результатов на случай дифференциального уравнения …
- О ПРОБЛЕМЕ КОЭФФИЦИЕНТОВ В ТЕОРИИ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ
- 2. Формулы для определения области регулярности функции двух комплексных переменных по коэффициентам ее разложения в ряд.
- 3. Формула для определения расположения некоторых особенностей f(z1, z2) по коэффициентам ее разложения в ряд.
- 4. Обобщение результатов п. 2,3 на случай одной системы дифференциальных уравнений.
- 5. Применение интегральных рператоров в теории целых функций.
- ПРИМЕНЕНИЕ ИНТЕГРАЛЬНЫХ ОПЕРАТОРОВ ПРИ ИЗУЧЕНИИ АЛГЕБРЫ ГАРМОНИЧЕСКИХ ФУНКЦИЙ ТРЕХ ПЕРЕМЕННЫХ И ПРОБЛЕМЫ КОЭФФИЦИЕНТОВ