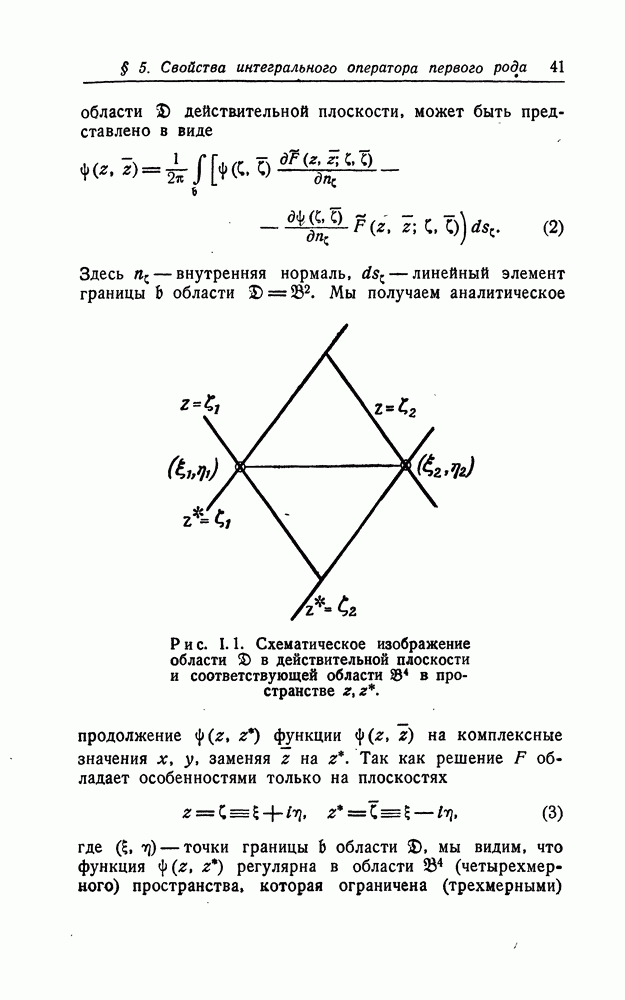
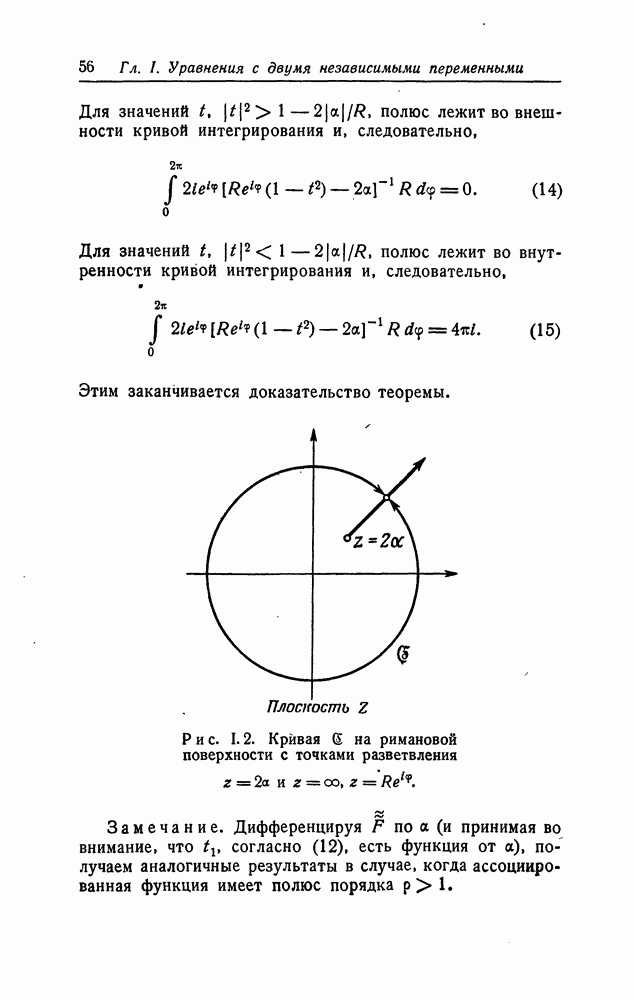
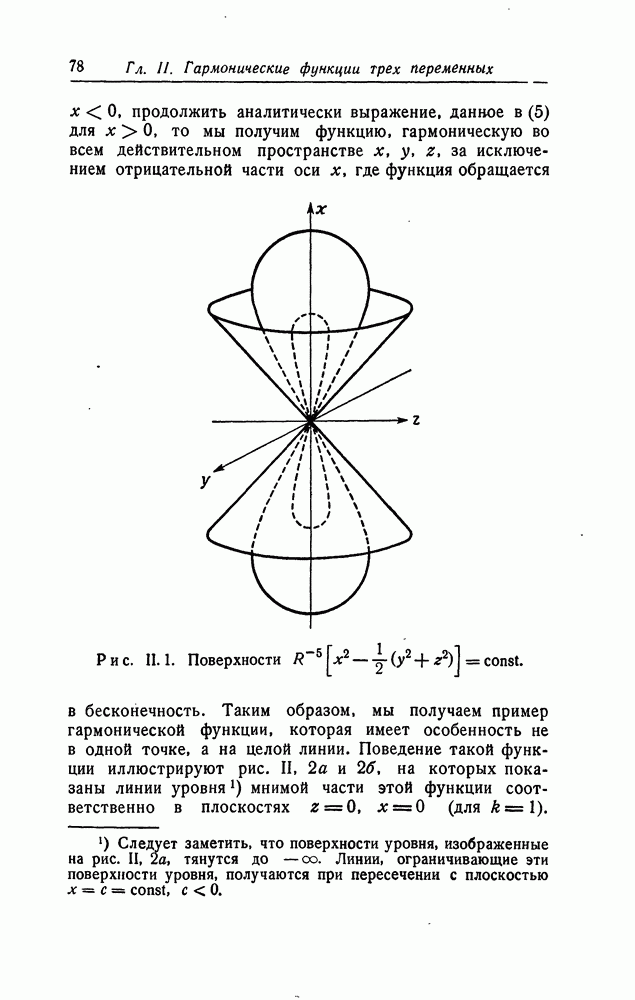
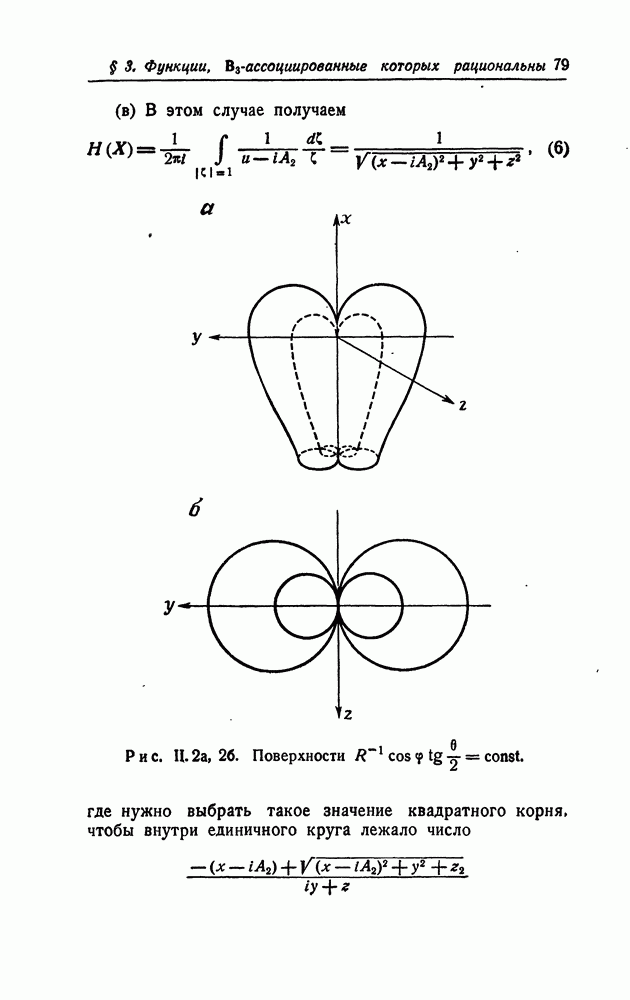
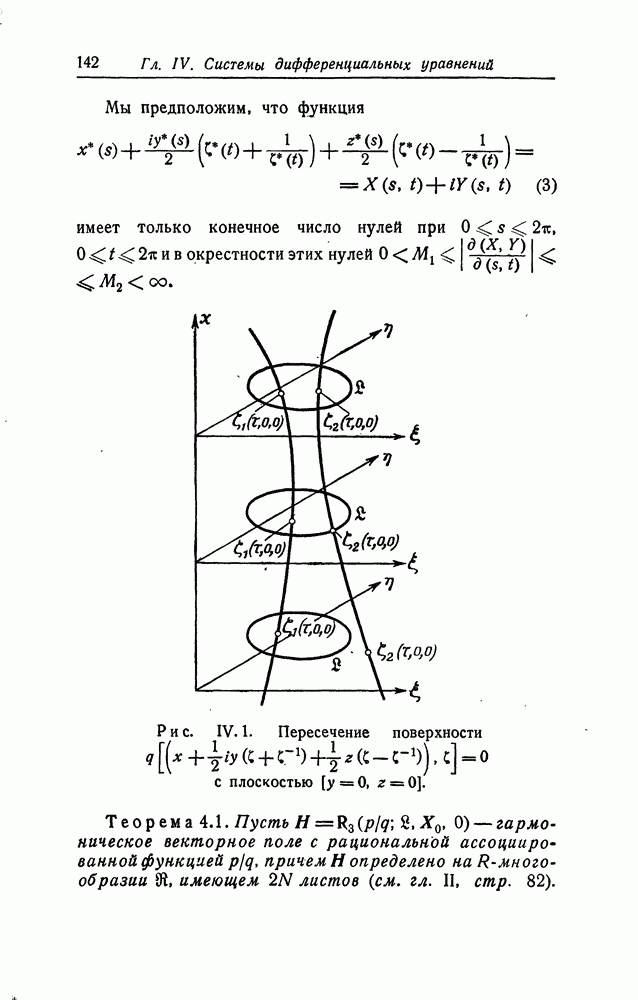
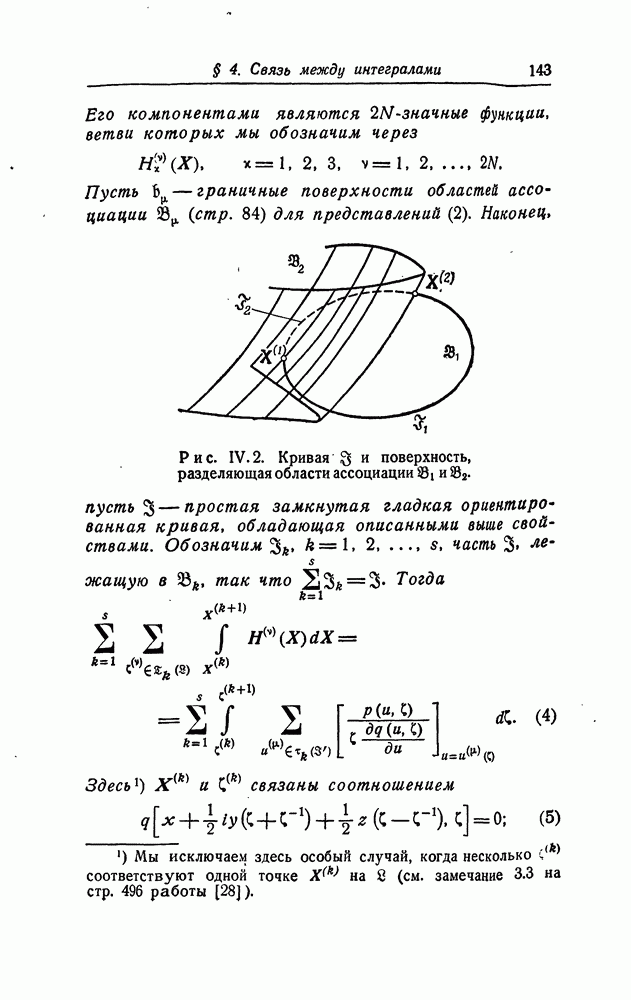
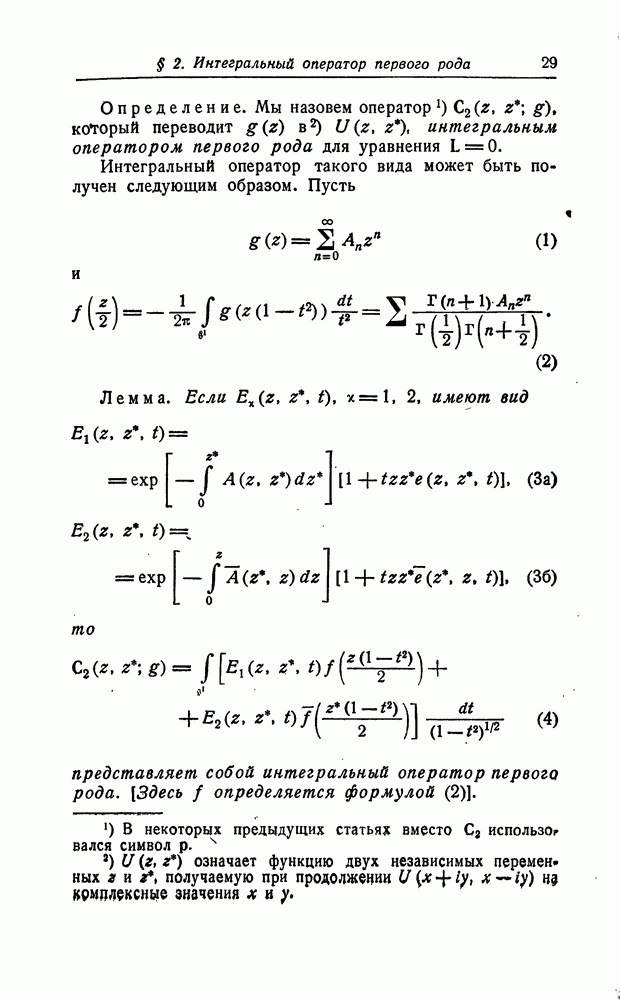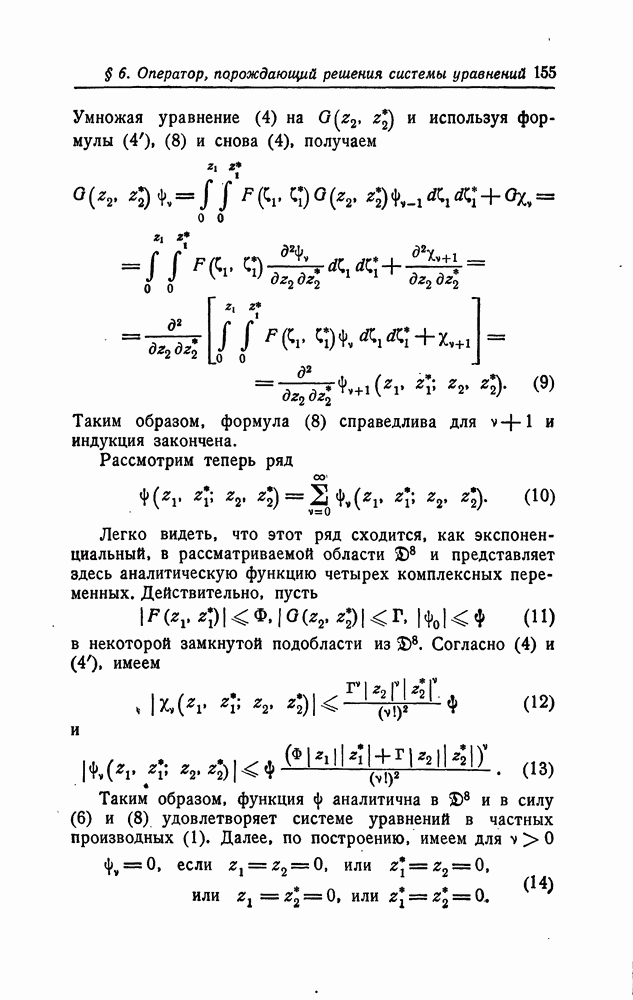| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
1. Определение компонент H2 и H3 гармонического вектора по данной компоненте H1
Пусть  гармоническая функция, регулярная в достаточно малой окрестности
гармоническая функция, регулярная в достаточно малой окрестности  начала координат О.
начала координат О.
Как указывалось в [8,15], данной функции  соответствует целое семейство сопряженных функций
соответствует целое семейство сопряженных функций

Здесь  любые две сопряженные функции,
любые две сопряженные функции,  произвольная аналитическая функция, регулярная в начале координат.
произвольная аналитическая функция, регулярная в начале координат.
Пусть  — односвязная область, удовлетворяющая приводимым ниже условиям
— односвязная область, удовлетворяющая приводимым ниже условиям  и
и  Мы покажем, что для всякой функции
Мы покажем, что для всякой функции  регулярной в
регулярной в  можно найти две функции
можно найти две функции  регулярные в
регулярные в  такие, что
такие, что  будет гармоническим вектором.
будет гармоническим вектором.
Дадее мы рассмотрим различные представления тройки 
Пусть  регулярна в односвязной области
регулярна в односвязной области  ,
,  трехмерного пространства
трехмерного пространства  (Как показано в [8], существуют области
(Как показано в [8], существуют области  такие, что не каждая функция
такие, что не каждая функция  регулярная в
регулярная в  имеет сопряженные
имеет сопряженные  также регулярные в
также регулярные в 
Сейчас мы опишем класс областей, в которых сопряженные  всегда существуют.
всегда существуют.
Предположим, что  односвязная область, содержащая начало координат и обладающая следующими свойствами.
односвязная область, содержащая начало координат и обладающая следующими свойствами.
(А) Пересечение  области
области  с плоскостью
с плоскостью  содержит проекции пересечений
содержит проекции пересечений  области
области  с любой плоскостью
с любой плоскостью  Пересечение
Пересечение  со всякой прямой, параллельной оси х (если оно не пусто), является связным сегментом.
со всякой прямой, параллельной оси х (если оно не пусто), является связным сегментом.
Теорема 1.1. Пусть  — область, удовлетворяющая условиям
— область, удовлетворяющая условиям  и
и  и пусть
и пусть  гармоническая функция, регулярная в
гармоническая функция, регулярная в  .
.
Тогда найдутся две функции  регулярные в
регулярные в  , такие, что
, такие, что  будет гармоническим вектором в
будет гармоническим вектором в 
Доказательство. Так как функция  регулярна в
регулярна в  она регулярна в большей области
она регулярна в большей области 
Предположим, что  удовлетворяет условиям
удовлетворяет условиям  и
и  и что ее граница
и что ее граница  имеет нормаль в каждой точке. Функцию
имеет нормаль в каждой точке. Функцию  можно рассматривать в
можно рассматривать в  как потенциал простого слоя
как потенциал простого слоя

где  элемент площади поверхности
элемент площади поверхности  Пусть
Пусть  где
где  , и
, и

Тогда

Функции  равномерно ограничены в
равномерно ограничены в  , следовательно,
, следовательно,  регулярные гармонические функции в
регулярные гармонические функции в  (см. [8, стр. 489]).
(см. [8, стр. 489]).
При дифференцировании правых частей равенств (1.2) и (1.3) мы можем поменять порядок интегрирования и дифференцирования. Так как  гармонический вектор, то
гармонический вектор, то  также гармонический вектор в
также гармонический вектор в  . Представление (1.4) для
. Представление (1.4) для  можно видоизменить. Каждую гармоническую функцию
можно видоизменить. Каждую гармоническую функцию  регулярную в
регулярную в  можно представить в
можно представить в  в виде
в виде

(см. [42, т. II, стр. 235]). Таким образом,

Здесь

Если заданы функции  и
и  связанные соотношением
связанные соотношением  то вектор
то вектор  где
где

будет гармоническим вектором. Здесь С — произвольная постоянная.
Таким образом, имеется свобода в выборе второй компоненты  для данной гармонической функции
для данной гармонической функции  интересно найти вектор
интересно найти вектор  или множество векторов, обладающих определенными свойствами.
или множество векторов, обладающих определенными свойствами.
Рассмотрим сначала представление для некоторого подкласса гармонических векторов. Будем говорить, что  если
если  гармоническая функция, четная по х.
гармоническая функция, четная по х.
Лемма 1.1. Для каждой объемной сферической функции  сопряженная функция
сопряженная функция  определяется формулой
определяется формулой

Доказательство. Функции

(см. [15, стр. 70],  образуют полную систему в классе
образуют полную систему в классе  и
и

[Правая часть равенства (1.10а) является нечетной гармонической функцией от  она не имеет членов, не зависящих от х, см. (1.16).]
она не имеет членов, не зависящих от х, см. (1.16).]
Пусть  - ортонормальная система полиномов, полная в классе
- ортонормальная система полиномов, полная в классе  в области
в области  . [Полиномы
. [Полиномы  удовлетворяют соотношениям
удовлетворяют соотношениям

Здесь  элемент объема
элемент объема 
Используя (1.10) и  мы определим множество гармонических векторов
мы определим множество гармонических векторов

Теорема 1.2 Пусть

— гармоническая функция класса  регулярная
регулярная  области
области  причем область
причем область  удовлетворяет
удовлетворяет
условиям  и
и  Тогда существует гармонический вектор
Тогда существует гармонический вектор  который представляется в
который представляется в  в виде
в виде

Вернемся теперь к рассмотрению общего случая гармонических функций, т. е. функций, не обязательно принадлежащих классу 
Найдем представление для вектора, первая компонента которого — заданная гармоническая функция  регулярная в
регулярная в 
Пусть  граничная кривая области
граничная кривая области  Для каждой точки
Для каждой точки  кривой
кривой  построим круг
построим круг  с центром
с центром  и радиусом
и радиусом  Пусть
Пусть

Расстояние от каждой точки  до граничной кривой
до граничной кривой  области
области  не меньше
не меньше 
Как мы доказали ранее, для каждого решения  регулярного в
регулярного в  , существует сопряженная функция
, существует сопряженная функция 
Пусть  сопряженная к
сопряженная к  Так как
Так как  то
то

где  функция от у и z. Образуя лапласиан для (1.16), получаем
функция от у и z. Образуя лапласиан для (1.16), получаем

Подставляя  находим, что
находим, что  решение уравнения
решение уравнения

Мы можем записать решение уравнения (1.18) в форме

(см. [42, т. I, стр. 315 и далее]). Каждая гармоническая функция  регулярная в
регулярная в  может быть разложена в
может быть разложена в  в ряд по ортогональным полиномам (X), т. е. по гармоническим полиномам, удовлетворяющим условию (1.11):
в ряд по ортогональным полиномам (X), т. е. по гармоническим полиномам, удовлетворяющим условию (1.11):

Этот ряд сходится равномерно и абсолютно в каждой замкнутой подобласти, лежащей в  Таким образом, сопряженная
Таким образом, сопряженная  может быть представлена в
может быть представлена в  в виде
в виде

где

Замечание. Функции  уже не образуют ортонормальную систему в
уже не образуют ортонормальную систему в  .
.
Так как (1.20) — гармоническая функция и ряд сходится абсолютно и равномерно во всякой замкнутой подобласти в 93, ряды для производных сходятся также равномерно во всякой области  Мы можем менять порядок суммирования и интегрирования в выражении
Мы можем менять порядок суммирования и интегрирования в выражении

Таким образом, сопряженная  к гармонической функции (1.20), регулярной в
к гармонической функции (1.20), регулярной в  , может быть представлена в
, может быть представлена в  в виде (1.21), (1.21а). Далее,
в виде (1.21), (1.21а). Далее,

является гармонической функцией в

Следовательно,  гармонические сопряженные к
гармонические сопряженные к 
Функция

гармонична  гармонический вектор в
гармонический вектор в  для любого
для любого 
Теорема 1.3. Гармонический вектор  первая компонента которого задана формулой (1.20),
первая компонента которого задана формулой (1.20),
может быть представлен в подобласти  области
области  в виде
в виде

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ВВЕДЕНИЕ
- Глава I. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ С ЦЕЛЫМИ КОЭФФИЦИЕНТАМИ С ДВУМЯ НЕЗАВИСИМЫМИ ПЕРЕМЕННЫМИ
- § 1. Представление решений уравнений с частными производными
- § 2. Интегральный оператор первого рода
- § 3. Дальнейшие представления интегральных операторов
- § 4. Представление оператора первого рода посредством интегралов
- § 5. Свойства интегрального оператора первого рода
- § 6. Некоторые дальнейшие свойства интегрального оператора первого рода
- § 7. Дифференциальное уравнение
- § 8. Интегральные операторы экспоненциального типа
- § 9. Дифференциальное уравнение …
- 10. Дифференциальные уравнения высшего порядка
- Глава II. ГАРМОНИЧЕСКИЕ ФУНКЦИИ ТРЕХ ПЕРЕМЕННЫХ
- § 2. Характеристическое пространство
- § 3. Гармонические функции, В3-ассоциированные функции которых рациональны
- § 4. Периоды
- § 5. Связь между коэффициентами разложения гармонической функции в ряд и ее особенностями
- § 6. Другой тип интегральных представлений гармонических функций
- § 7. Поведение в целом функций класса с рациональной ассоциированной
- Глава III. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ С ТРЕМЯ ПЕРЕМЕННЫМИ
- § 2. Разложение в ряд решений уравнения …
- § 3. Интегральный оператор, порождающий решения уравнения
- § 4. Второй интегральный оператор, порождающий решения уравнения …
- § 5. Интегральный оператор, порождающий решения уравнения
- § 6. Интегральный оператор, порождающий решения уравнения …
- Глава IV. СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- § 2. Гармонические векторы в целом и их представление посредством интегралов
- § 3. Интегралы от гармонических векторов
- § 4. Связь интегралов от алгебраических гармонических векторов трех переменных с интегралами от алгебраических функций одного комплексного переменного
- § 5. Обобщение теорем о вычетах на случай уравнения …
- § 6. Оператор, порождающий решения системы уравнений в частных производных
- Глава V. УРАВНЕНИЯ СМЕШАННОГО ТИПА И ЭЛЛИПТИЧЕСКИЕ УРАВНЕНИЯ С СИНГУЛЯРНЫМИ И НЕАНАЛИТИЧЕСКИМИ КОЭФФИЦИЕНТАМИ
- § 2. Обобщение представления (1.12) решений уравнения (1.6)
- § 3. Оператор (1.11б) в общем случае
- § 4. Порождающие функции, аналогичные решениям гипергеометрического уравнения
- § 5. О решении задачи Коши в целом
- § 6. Обобщенные уравнения Коши — Римана
- § 7. Дифференциальное уравнение … с новым типом особенности функции N
- § 8. Интегральный оператор для уравнений с неаналитическими коэффициентами
- ПРИЛОЖЕНИЕ. ОПЕРАТОРЫ, ПОРОЖДАЮЩИЕ РЕШЕНИЯ НЕКОТОРЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ТРЕМЯ ПЕРЕМЕННЫМИ, И ИХ СВОЙСТВА
- 1. Определение компонент H2 и H3 гармонического вектора по данной компоненте H1
- 2. Связь между интегралами от алгебраических гармонических векторов от трех переменных с интегралами от алгебраических функций комплексного переменного.
- 3. Обобщение предыдущих результатов на случай дифференциального уравнения …
- О ПРОБЛЕМЕ КОЭФФИЦИЕНТОВ В ТЕОРИИ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ
- 2. Формулы для определения области регулярности функции двух комплексных переменных по коэффициентам ее разложения в ряд.
- 3. Формула для определения расположения некоторых особенностей f(z1, z2) по коэффициентам ее разложения в ряд.
- 4. Обобщение результатов п. 2,3 на случай одной системы дифференциальных уравнений.
- 5. Применение интегральных рператоров в теории целых функций.
- ПРИМЕНЕНИЕ ИНТЕГРАЛЬНЫХ ОПЕРАТОРОВ ПРИ ИЗУЧЕНИИ АЛГЕБРЫ ГАРМОНИЧЕСКИХ ФУНКЦИЙ ТРЕХ ПЕРЕМЕННЫХ И ПРОБЛЕМЫ КОЭФФИЦИЕНТОВ