ПРИМЕНЕНИЕ ИНТЕГРАЛЬНЫХ ОПЕРАТОРОВ ПРИ ИЗУЧЕНИИ АЛГЕБРЫ ГАРМОНИЧЕСКИХ ФУНКЦИЙ ТРЕХ ПЕРЕМЕННЫХ И ПРОБЛЕМЫ КОЭФФИЦИЕНТОВ

Современная теория функций, развитая Неванлинной и другими, показывает, что различные соотношения между ростом и распределением значений рациональных функций имеют место (в модифицированной форме) для мероморфных функций. Используя интегральные операторы, мы определим правило композиции в линейном пространстве гармонических функций трех переменных так, чтобы различные подалгебры и коалгебры полученной алгебры обладали сходными свойствами. (Мы получим алгебру относительно сложения и определенной ниже композиции.)

1. Введение

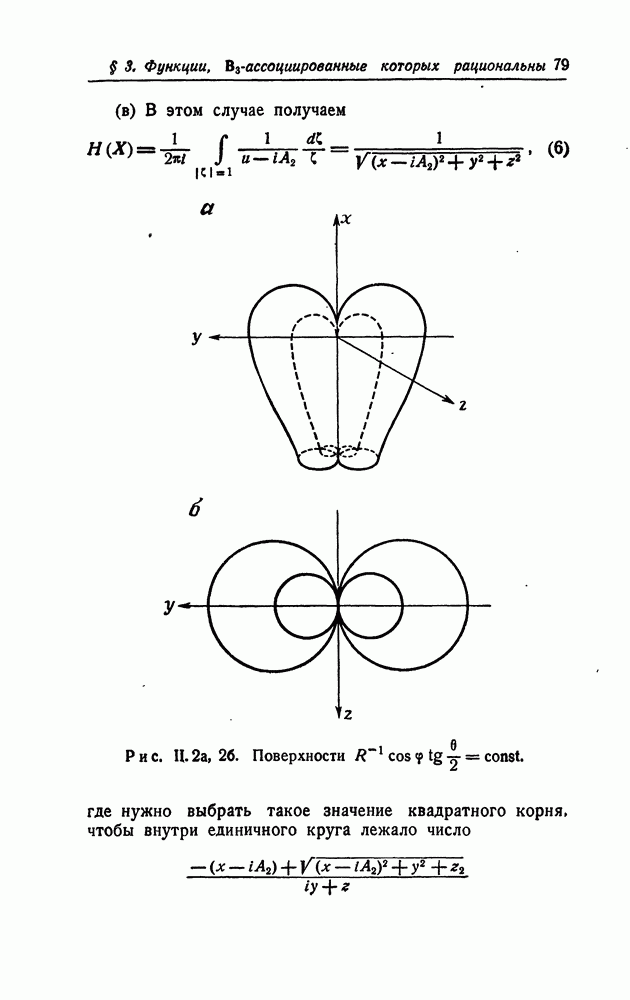
Различные интегральные операторы преобразуют аналитические функции одного (или нескольких) комплексных переменных в решения линейного уравнения с частными производными (см. [3, 4, 8, 15]). Эти операторы отображают аналитические функции в решения прежде всего в малом, т. е. рассматриваются в достаточно малой окрестности начала координат О. Мы называем функцию ассоциированной с относительно такого оператора. Во многих случаях при помощи аналитического продолжения мы получаем соотношения между ассоциированными функциями (аналитическими функциями одного или нескольких комплексных переменных) и решениями в области ассоциации (т. е. в области, где имеет место представление или в целом, т. е. во всей области существования решения (см. [15, стр. 83]).

Решения линейных уравнений с частными производными с целыми коэффициентами образуют линейное

пространство, в то время как аналитические функции образуют алгебру. Используя интегральные операторы, мы можем определить композицию решений соответствующую произведению ассоциированных функций. Таким способом мы получаем алгебру решений рассматриваемых дифференциальных уравнений, где обычное умножение заменено композицией, соответствующей произведению ассоциированных функций (см. [3, стр. 647]).

Интересно изучить решения соответствующие различным алгебрам (со сложением и обычным умножением) ассоциированных функций, например алгебрам

1) всех аналитических функций, регулярных в

2) всех аналитических функций, обладающих определенными особенностями в начале координат О,

3) рациональных функций, регулярных в О,

4) мероморфных функций, регулярных в О (см. [4, 8, 16]).

Многие соотношения, справедливые для ассоциированных функций можно "преобразовать" в теоремы о соответствующих решениях данного уравнения

Как пример применения этой идеи мы рассмотрим в настоящей статье алгебру гармонических функций трех переменных, порождаемых мероморфными функциями, регулярными в точке О.

Эти рассмотрения тесно связаны с проблемой коэффициентов для гармонических функций трех действительных переменных, т. е. с вопросом о том, как можно найти распределение особенностей гармонической функции по коэффициентам ее разложения в ряд в окрестности точки О.

В случае подалгебр и коалгебр, исследованном в п. 3, 4, мы рассматриваем функции разложения в ряд которых имеют специальный вид: многие коэффициенты ряда либо равны нулю, либо равны друг другу. В п. 5 мы изучаем проблему коэффициентов в общем случае и даем критерий возможности продолжения функции в область 6 определенной структуры (см. стр. 294 и далее).

2. Алгебра гармонических функций трех действительных переменных.

Аналитические функции одного комплексного переменного образуют подпространство

а комплексных гармонических функций двух действительных переменных. Пространство а имеет базис

Произведением двух аналитических функций является аналитическая функция (если то и

поэтому а представляет собой алгебру функций.

В дальнейшем мы введем линейное пространство гармонических функций (регулярных в окрестности начала координат О) трех действительных переменных х, у, z; мы определим композицию элементов и покажем, что является алгеброй относительно сложения и этой композиции. Пусть линейное пространство комплексных гармонических функций, которые в достаточно малой окрестности начала координат разлагаются в ряд вида

Здесь

декартовы, а сферические координаты трехмерного пространства,

присоединенные функции Лежандра. Функции определяются формулой

(см. [15, стр. 70—73], [16, стр. 212] и [54, стр. 392]).

Замечание. Это означает, что функции в достаточно малой окрестности начала координат можно представить в виде

где Функция принадлежит если

где - целые функции от и для

Замечание. Если коэффициенты изменяются над полем комплексных чисел, так что ряды (3) сходятся в то изменяется над пространством комплексных гармонических функций, регулярных в начале координат.

Если потребовать выполнения равенств

то мы получим пространство действительных гармонических функций, регулярных в начале координат.

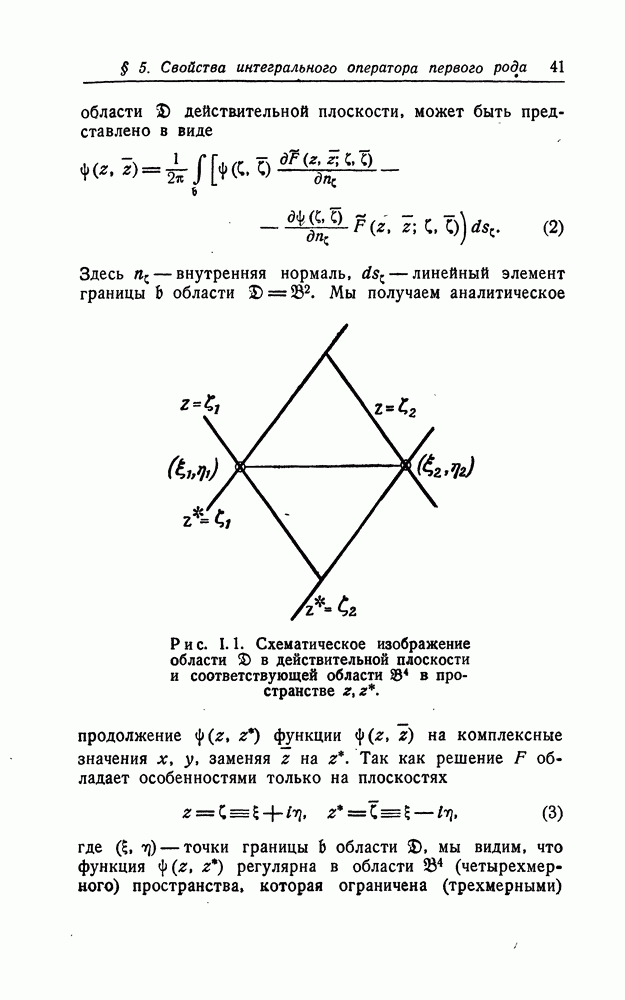
Представление (3) было вначале установлено в Вся область, в которой справедлива формула (3), называется областью ассоциации представления (3) (см. [15, стр. 15, 83]).

Очевидно, что линейное пространство. Покажем, что можно определить композицию, которая превратит в алгебру.

Для пространство изоморфно алгебре А функций двух комплексных переменных и и С, которые образуют линейное пространство с базисом

Определим композицию двух функций

формулой

Композиция ассоциативна, коммутативна и дистрибутивна. Функция является единицей по отношению к определенной композиции. Умножение на комплексную константу и композиция с этой константой дают один и тот же результат. Таким образом, есть алгебра по отношению к сложению и композиции, определенной по формуле (6) (см. [3, стр. 647]). (Следует заметить, что в формуле (1) на стр. 644 в работе [3] необходимо поменять местами

Замечание. Можно рассматривать композицию либо действительных, либо комплексных гармонических функций. Такую композицию можно определить независимо от интегрального оператора, представляя коэффициенты разложения в окрестности начала координат в виде комбинаций величин

В случае двух переменных мы рассмотрим либо класс а, состоящий из аналитических функций комплексного переменного (подкласс комплексных гармонических функций), либо класс действительных гармонических функций.

Гармоническая функция двух действительных переменных может быть записана в виде

где -аналитическая функция одного комплексного переменного. Определим

композицию, положив

В случае гармонических функций трех переменных мы либо введем класс комплексных гармонических функций и определим композицию так, как это сделано в работе [3, стр. 647] (такое определение используется в настоящей статье), или. мы можем определить композицию для действительных гармонических функций (см. [16, стр. 216]).

Здесь мы рассмотрим подалгебру алгебры состоящую из гармонических функций которые соответствуют мероморфным функциям (регулярным в окрестности начала координат) и разлагаются в ряд вида (3).

Как указывалось в п. 1, отображение на А определено сначала в достаточно малой окрестности начала координат. При помощи аналитического продолжения используя работы Неванлинны и других, мы получим результаты, которые относятся к поведению в целом. Алгебра имеет различные подалгебры и коалгебры, изоморфные алгебре аналитических функций одного комплексного переменного. Интерпретация результатов теории функций одного комплексного переменного приводит к интересным соотношениям для этих подалгебр и коалгебр. Пусть — подалгебра или коалгебра алгебры изоморфная линейному пространству соответственно с базисом

где фиксированные положительные целые числа. Примеры подалгебры и коалгебры алгебры дают соответственно и В п. 3 мы рассмотрим случаи таких подалгебр и коалгебр с базисом (9).

Замечание. Если композиция элементов подпространства С некоторой алгебры принадлежит С, то С

называется подалгеброй. Если такие композиции являются элементами другого подпространства то С называется коалгеброй. Гармоническая функция, принадлежащая подалгебре может иметь только особенности, описанные в работе [15, стр. 77—78, случаи (а) и (б)]. Среди них мы имеем линии разветвления второго порядка в плоскостях . (Линия разветвления может стягиваться в точку. В этом случае функция однозначна в окрестности особенности. Однако если мы продолжим эту функцию на комплексные значения, то она становится многозначной. В этом случае мы говорим, что линия разветвления вырожденная. В комплексном пространстве, т. е. для комплексных значений х, у, z, ветви связны.)

В случае подалгебр и коалгебр алгебры соответствующих целым большим 1, функции имеют особенности вдоль алгебраических кривых. Эти особенности изучены в [4, 8]. Как указывалось в [11], применение результатов Адамара позволяет определить расположение и тип особенностей по коэффициентам разложения в ряд (3).

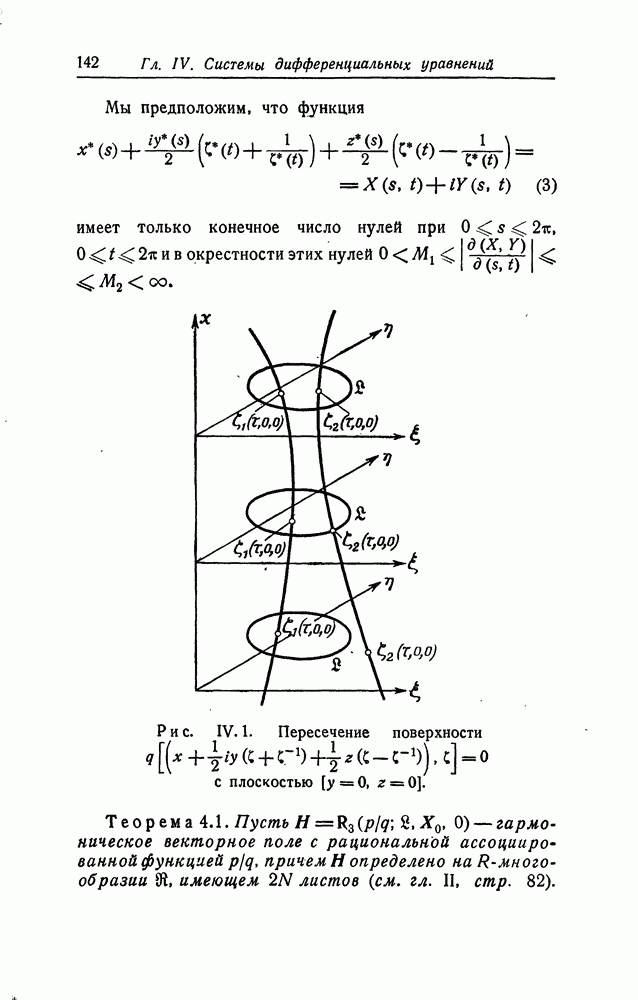
3. Особенности функции ..., где — целая гармоническая функция.

Теорема 3.1. Пусть

фиксированные неотрицательные целые числа,

и

Тогда функция

обратная к имеет особенности типа полюса, структура которых описана в [15, стр. 77—83] и [8], и представляется в виде

Здесь алгебраическая гармоническая функция, ассоциированная с которой функция имеет особенность в начале координат] алгебраические гармонические функции, которые будут описаны в дальнейшем, целая гармоническая функция и гармонические полиномы степени наименьшее целое число, большее

Замечание. зависит от Заметим, что мы полагаем для так как в этом случае

Доказательство. Коэффициенты удовлетворяют условию (2), следовательно,

является целой функцией порядка стр. 231]). Так как полином, то функция

также имеет порядок (см. [49, стр. 14, 30] или [50, стр. 321]), Так как целая функция от то

мероморфная функция, которую можно представить в виде

(см. [50, стр. 304]), где полиномы, обеспечивающие сходимость, постоянные, целая функция и рациональная функция с особенностью в начале координат. Порядок равен (см. [35, стр. 351]) и ряд

сходится (см. [49, стр. 31]). В дальнейшем X будет обозначать целое число, Таким образом, мы можем взять полиномы степени , см. [50, стр. 305]. Заменим на и применим к оператор Пусть

Так как сумму 2 в формуле (6) можно разбить на две части так, чтобы при и члены были регулярными функциями от . Так как ряд 2 сходится абсолютно и равномерно, указанный интеграл будет регулярной гармонической функцией от Рассмотрим в сумме 2 член

Для каждого значения не лежащего на отделяющей поверхности (см. [15, стр. 83]) [т. е. на

поверхности, где для некоторого значения имеем

первый интеграл в формуле (8) является алгебраической гармонической функцией, которая будет описана в дальнейшем. Второй интеграл представляет собой конечную линейную комбинацию сферических функций степени, не превосходящей Изменяя кривую интегрирования мы меняем отделяющую поверхность. Таким образом, путь интегрирования может пройти через любые точки за исключением тех, которые принадлежат линии особенностей в порождаемой гармонической функции, см. [8, стр. 471 и далее].

В соответствии с этими рассуждениями мы видим, что в данном случае

является алгебраической гармонической функцией, определенной интегрированием на одном пространственном листе ее области существования. Аналитическим продолжением мы можем определить на остальных листах. Существует только конечное число членов (8), которые имеют особенности в Разность между значениями в соответствующих точках на различных листах является конечной величиной, если только функция не имеет особенности в одной из таких точек. (Соответствующими являются точки, координаты которых х, у, z в однолистном пространстве совпадают.) Каждая функция (9) конечнозначна. Рассматривая ее аналитическое продолжение вдоль линии, лежащей полностью в мы можем определить значения функции получаемые аналитическим продолжением (8). Это завершает доказательство теоремы 3.1.

Приступим теперь к более подробному описанию функции см. (3). Предположим сначала, что

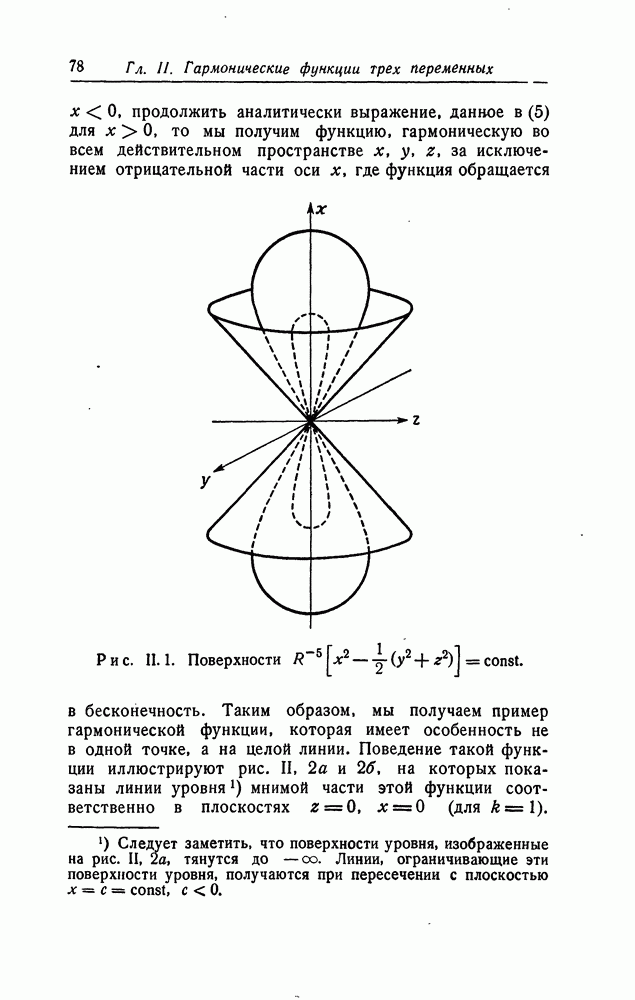
Особенности гармонических функций

где полиномы от , изучены в работе [8]. Для имеем

Мы различаем два случая.

I. К < Р. Тогда

Здесь являются (модифицированными) сферическими функциями (см. [15, стр. 70]). Знаменатель в (11.) является полиномом по С степени

II. . Имеем

Знаменатель — полином степени по С.

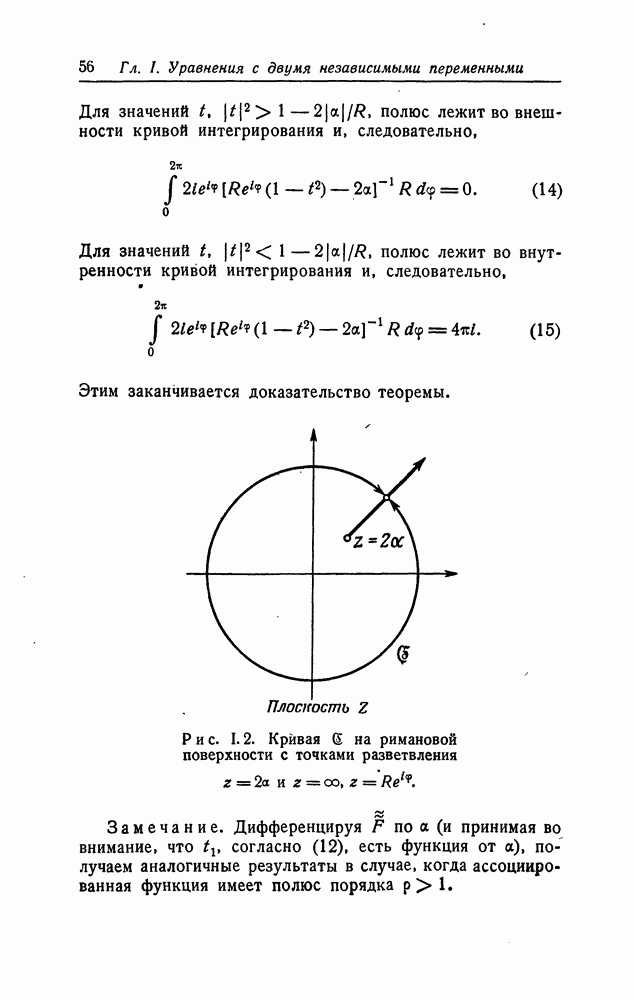
Замечание. Следует заметить, что если степень знаменателя в формулах (11) или (12) больше степени числителя, то при вычислении интеграла мы будем действовать, как в [8, стр. 476, формула Согласно [8, стр. 476], интеграл

имеет особенности вдоль кривой (которая в действительном пространстве может стягиваться в точку):

где дискриминант для

Если этот дискриминант не равен тождественно нулю, то его можно записать в виде определителя. В случае I этот определитель имеет порядок Его первая строка имеет вид

В случае II порядок определителя равен и первая строка имеет вид

Величина называется параметром

Если целое число, большее 1, то мы получим более сложные функции, зависящие от и производных

(см. [4, стр. 644 и след.]). Здесь корни уравнения —знаменатели правых частей (11) или (12). В случае целое, должны быть сосчитаны раз, и соответствующие особенности имеют более сложную структуру. В этом случае (13) также является уравнением особых кривых.

Если то функции, описанные в [15, стр. 77 и далее]. Эти функции имеют линии разветвления на сферах с центром в начале координат и радиусами (Заметим, что линия разветвления в действительном пространстве может стягиваться в точку, см. [15, стр.

Очевидно, наши результаты обобщаются на случай гармонических функций с мероморфной ассоциированной, если предположить, что коэффициенты их разложения

в ряд удовлетворяют условиям Адамара:

(Мы предполагаем здесь, что В этом случае ассоциированная с функция мероморфна на всей плоскости. Обратная величина для мероморфной функции есть снова мероморфная функция, которая может быть представлена в виде (3). Однако, чтобы определить степень полиномов обеспечивающих сходимость произведения, мы нуждаемся в некоторых дополнительных сведениях, которые позволяют определить порядок характеристической функции ассоциированной функции

4. Особенности функции ... для целой функции ... более общего вида.

В п. 3 рассматривались функции весьма специального вида. Коэффициенты разложения гармонической функции по сферическим функциям (X) образуют треугольную матрицу

(см. [16, стр. 208]). Коэффициенты функций [см. (3.1)] являются суммами сферических функций. Все коэффициенты строке равны нулю, если то время как для по крайней мере один из отличен от нуля.

Замечание. Гармонические функции такого вида называют специальными гармоническими функциями, или функциями, разложения которых соответствуют одному столбцу.

Однако несколько модифицированный метод может быть применен и в случае гармонических функций, разложения которых не обязательно соответствуют одному столбцу.

Связь между коэффициентами функции двух комплексных переменных и свойствами ее особенностей изучалась в работе [18]. Используя эти исследования, можно получить результаты в общем случае, т. е. когда коэффициенты разложения образуют матрицу (1).

Теорема 4.1. Пусть

(В, D - постоянные) — разложение в ряд некоторой целой гармонической функции, и пусть

— гармонический полином. Далее, предположим, что

Обратная величина [относительно композиции (2.6)] функции является гармонической функцией, представимой в виде

Здесь

[см. (11)] являются алгебраическими гармоническими функциями, регулярными в начале координат, гармонические полиномы степени, не превосходящей целая гармоническая функция и алгебраическая функция, ассоциированная

с которой функция имеет особенность в начале координат (к — наименьшее целое число, большее

Доказательство. В силу (2.3а) ассоциированная функция для есть

Так как коэффициенты ап, удовлетворяют условию (4), ассоциированная для обратной величины где может быть записана в виде

где рациональная функция, имеющая особенность в начале координат, целая функция от обеспечивающие сходимость полиномы. Заметим, что мы действуем так же, как в заменяя, однако, на

Так же, как и ранее, мы получим верхнюю грань для степени Повторяя рассуждения из п. 3, мы придем к утверждению теоремы.

Приступим теперь к описанию функций в случае Если то

полином степени Пусть решения уравнения

Тогда

Если то мы получим более сложное выражение. Так как удовлетворяют условию (4), мы можем выбрать полиномы, обеспечивающие сходимость, степень которых по равна следовательно, сферические функции степени .

5. Аналитическое продолжение гармонической функции трех действительных переменных, заданной своим разложением в ряд.

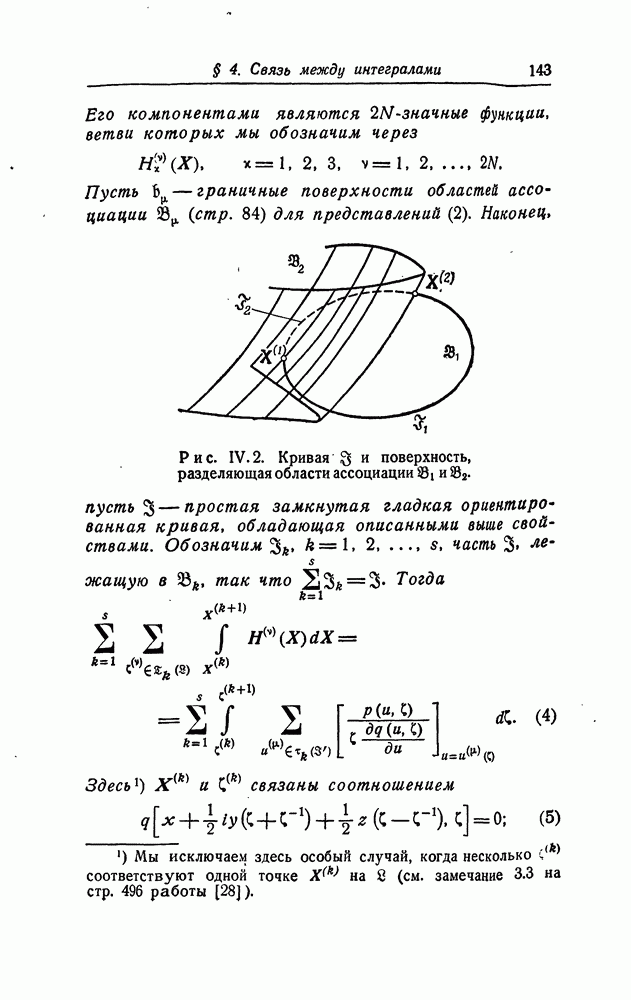
В рассуждениях из п. 3 и 4 используются результаты, касающееся проблемы коэффициентов для особенностей гармонических функций, которые разлагаются в ряд весьма специальной структуры. В то время как в общем случае коэффициенты разложения по сферическим функциям образуют треугольную матрицу (4.1), в п. 3 мы рассматривали только разложение, соответствующее одному столбцу, а в п. 4 мы делали весьма ограничительные предположения о коэффициентах при сферических функциях одной и той же степени. Использование керн-функции позволяет дать критерии для рядов значительно более общей структуры (см. также [18]).

Пусть — декартовы координаты в трехмерном пространстве, и пусть односвязная область, содержащая внутри начало координат О и лежащая в плоскости . Ортогональным преобразованием постоянная, область отображается на область в плоскости

Через каждую точку области проводим прямую

(Бесконечный) цилиндр мы обозначим через Предположим, что изменяется непрерывно при Пересечение всех цилиндров обозначим через 6, т. е.

Теорема 5.1. Пусть гармоническая функция разлагается в ряд

Если для всякого и любого вектора коэффициенты удовлетворяют неравенству

где коэффициенты разложения в ряд керн-функции (двумерной) области то функция может быть аналитически продолжена в область

Доказательство. В силу (2) функция

является ассоциированной с

Бергман и Шиффер стр. 240]) доказали следующую теорему. Пусть функция, симметричная и аналитическая по обоим аргументам в окрестности начала координат; пусть — керн-функция области и пусть

— разложения функций Если для любого комплексного вектора выполняется неравенство

то аналитична для

Шиффер и Ситяк [56] связывают с функцией выражение

Подставляя в (6)

Шиффер и Ситяк получили отсюда условия регулярности функции в области выраженные через коэффициенты разложения в ряд функции

Если для фиксированного функция регулярна в области то функция регулярна в области трехмерного пространства. Таким образом, интеграл регулярен в пересечении всех областей

Замечание. Метод, описанный в [9, стр. 14—20], позволяет решать вопрос о возможности продолжения

функции, заданной своим разложением в окрестности начала координат О, в область Этим способом мы получаем другой критерий возможности аналитического продолжения функции (2). Однако в этом случае мы должны определить так называемые двоякоортогональные функции, т. е. функции, которые ортогональны одновременно в и в достаточно малом шаре с центром в начале координат.

Литература к приложению

(см. скан)

(см. скан)

(см. скан)

(см. скан)

(см. скан)