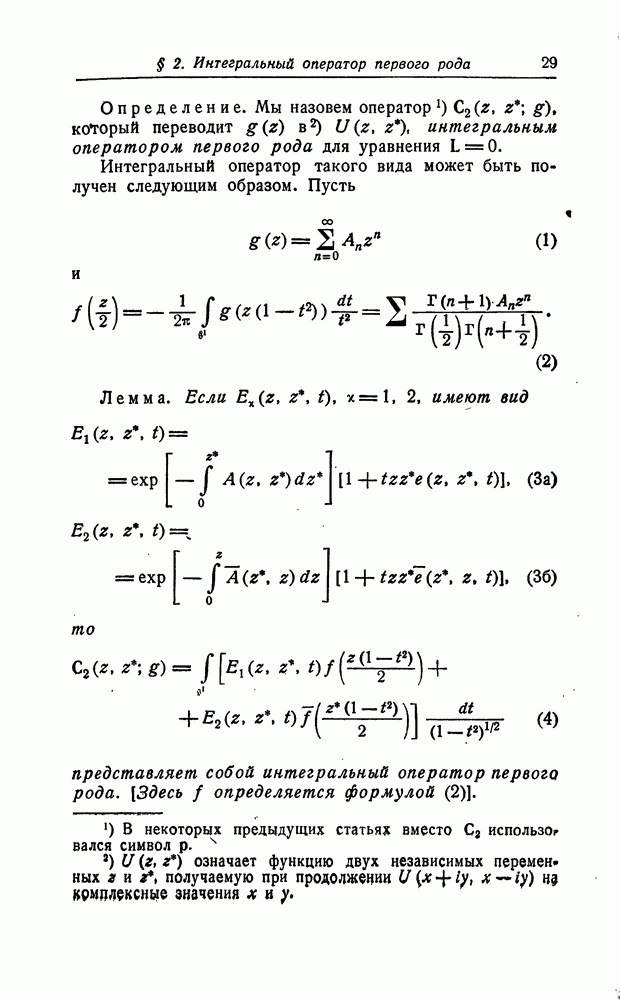| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 7. Дифференциальное уравнение

В частном случае, когда дифференциальное уравнение имеет вид

 целая функция от
целая функция от  интегральный оператор первого рода допускает более простую, чем в общем случае, форму. Благодаря этому в данном случае можно получить различные дополнительные результаты.
интегральный оператор первого рода допускает более простую, чем в общем случае, форму. Благодаря этому в данном случае можно получить различные дополнительные результаты.
Теорема 7.1. В случае дифференциального уравнения (1) порождающая функция  для интегрального оператора первого рода является действительной функцией переменных
для интегрального оператора первого рода является действительной функцией переменных 
Доказательство. Напишем

где  — функции, введенные в (2.7) и (2.9). Покажем, что функции
— функции, введенные в (2.7) и (2.9). Покажем, что функции  зависят только от
зависят только от  Переходя от
Переходя от  в системе (2.9), мы получим следующие уравнения:
в системе (2.9), мы получим следующие уравнения:

Формальное вычисление показывает, что уравнение (За) может быть записано в виде

так что  зависит только от
зависит только от  Если предположить, что
Если предположить, что  то
то  будет удовлетворять уравнению (4). Переходим по индукции к случаю
будет удовлетворять уравнению (4). Переходим по индукции к случаю  Предположим, что
Предположим, что  зависят только от
зависят только от  тогда равенства (36) и (4) будут выполнены, если
тогда равенства (36) и (4) будут выполнены, если  будет решением уравнения
будет решением уравнения

и если

Сходимость ряда  доказывается, как выше.
доказывается, как выше.
Итак, в противоположность общему случаю, в этом частном случае порождающая функция  оказывается действительной и мы можем говорить о сопряженных решениях уравнения (1), которые в окрестности начала координат представляются в виде
оказывается действительной и мы можем говорить о сопряженных решениях уравнения (1), которые в окрестности начала координат представляются в виде

Пара решений V и получается, если использовать в качестве ассоциированной функции одну и ту же аналитическую функцию  одного комплексного переменного и отделить соответственно действительную и мнимую части полученного в результате комплексного решения. Действительное решение, регулярное в начале координат, может быть записано в виде
одного комплексного переменного и отделить соответственно действительную и мнимую части полученного в результате комплексного решения. Действительное решение, регулярное в начале координат, может быть записано в виде

а сопряженное к нему решение определяется формулой

Замечание. Когда  функции
функции  имеют вид
имеют вид

Таким образом, в этом особенно простом случае имеем

где  функция Бесселя. (Следовательно, можно рассматривать
функция Бесселя. (Следовательно, можно рассматривать  как обобщения бесселевых функций.)
как обобщения бесселевых функций.)
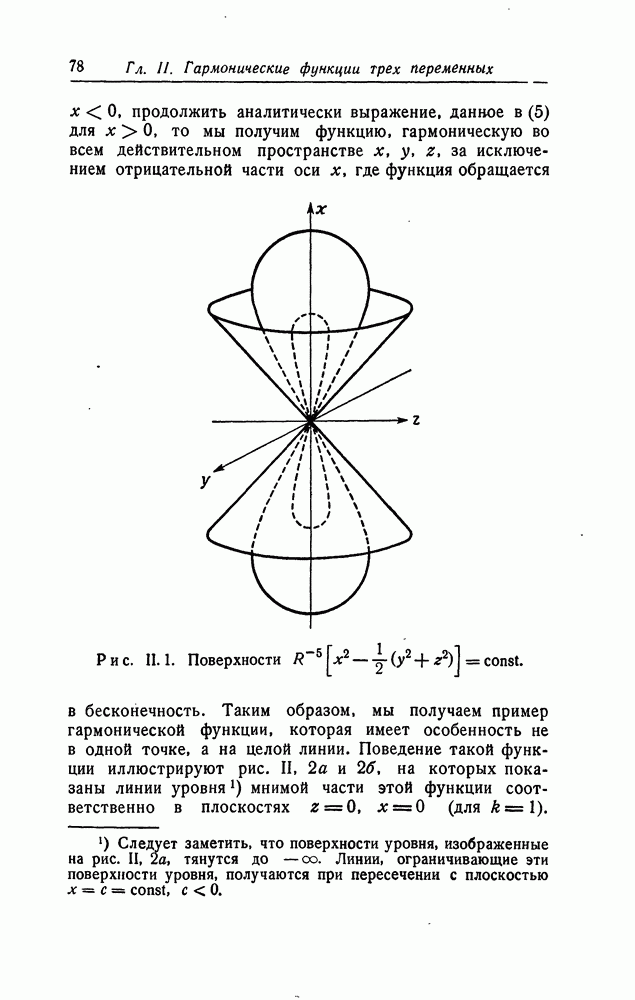
Как установлено выше, любое действительное решение уравнения (1), регулярное в начале координат, может быть разложено в ряд (86), сходящийся в. некоторой окрестности начала координат. Можно доказать более сильный результат: ряд (8а) сходится внутри наибольшего круга с центром в начале координат, внутри которого регулярно решение. Многие результаты о соотношениях между двумя сопряженными гармоническими функциями можно обобщить на пары сопряженных решений (7а) и (76) уравнения (1).
По аналогии с регулярными решениями можно рассматривать также решения с различными особенностями, которые получаются, если использовать в качестве ассоциированной функции аналитическую функцию с особенностями. В частности, мы можем рассматривать решения с особенностями типа полюса, т. е. функции, для которых ассоциированная функция имеет полюсы. Интересно, что теорему о вычетах можно до некоторой степени распространить на решения уравнения (1). Об этом говорят следующие две теоремы.
Теорема 7.2. Пусть  [см. (7а)
[см. (7а)  два сопряженных решения уравнения (1), регулярных в круге
два сопряженных решения уравнения (1), регулярных в круге 
Тогда

где  (Доказательство элементарно и не приводится здесь.)
(Доказательство элементарно и не приводится здесь.)
Теорема 7.3. Пусть сопряженные решения  имеют особенность типа полюса первого порядка в точке
имеют особенность типа полюса первого порядка в точке  ассоциированная функция
ассоциированная функция  допускает в круге
допускает в круге  представление
представление

где  регулярна в круге
регулярна в круге  Тогда
Тогда

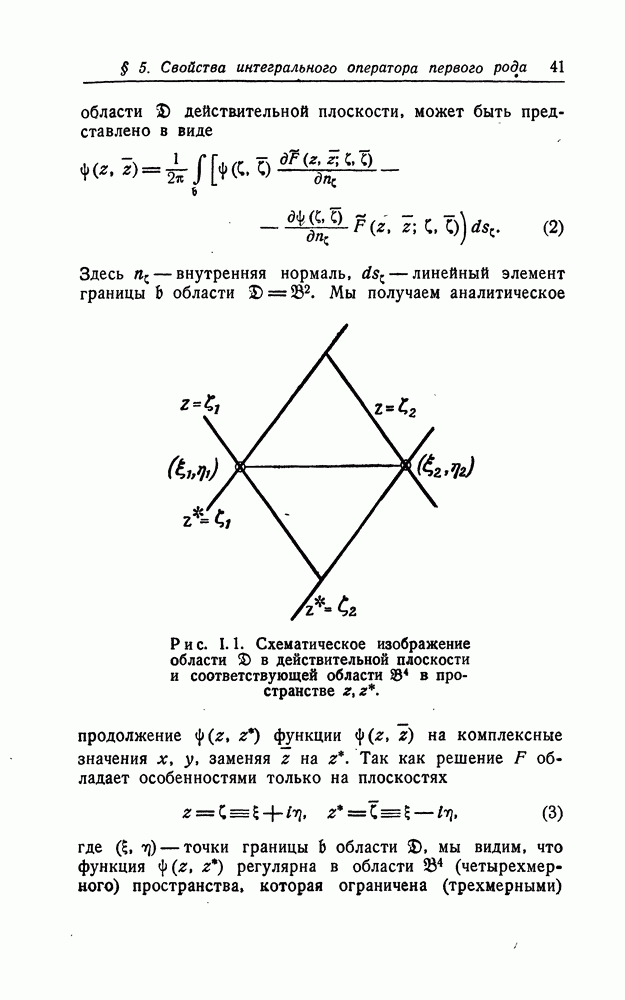
Замечание. Как указывалось в § 6, функции  имеют точку разветвления бесконечного порядка в точке
имеют точку разветвления бесконечного порядка в точке  Если мы разрежем риманову поверхность функции F вдоль луча с началом в точке
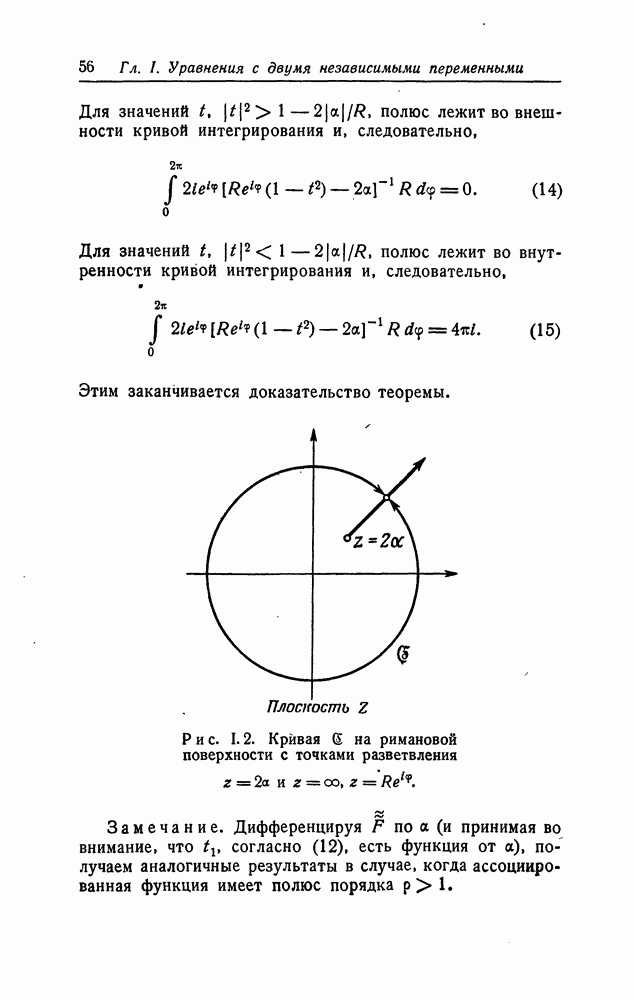
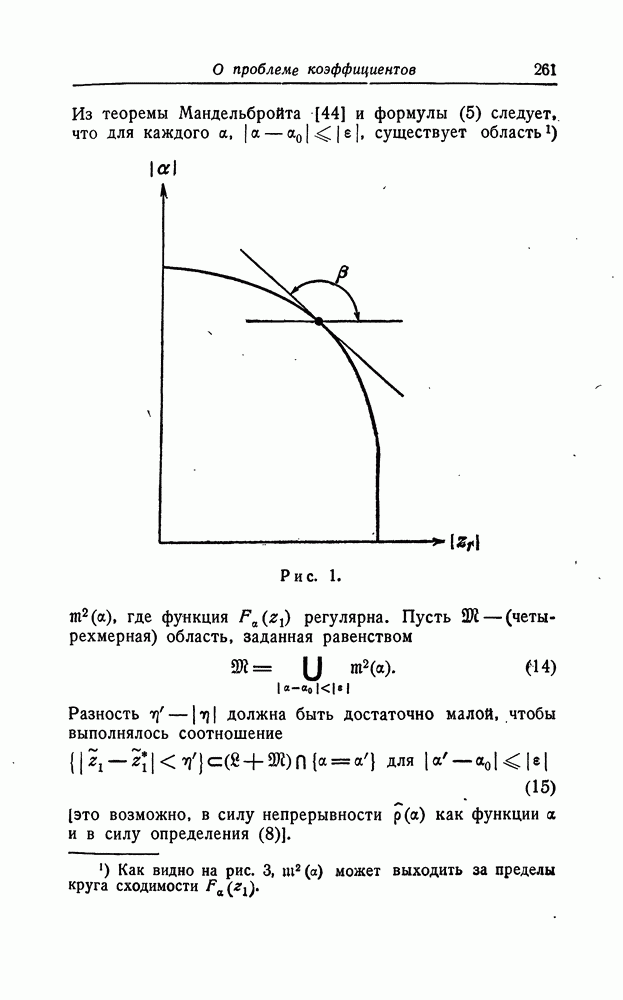
Если мы разрежем риманову поверхность функции F вдоль луча с началом в точке  направленного по радиусу в сторону, противоположную началу координат, то кривая 6 станет незамкнутой кривой, концы которой лежат один над другим на различных листах римановой поверхности (см. рис. 1.2).
направленного по радиусу в сторону, противоположную началу координат, то кривая 6 станет незамкнутой кривой, концы которой лежат один над другим на различных листах римановой поверхности (см. рис. 1.2).
Очевидно, что достаточно доказать наше утверждение для ассоциированной функции  Кривой
Кривой  соответствуют в плоскости
соответствуют в плоскости  кривые
кривые 
Из (7а) и (76) следует, что

где  (В силу абсолютной сходимости двойного интеграла мы можем менять порядок интегрирований
(В силу абсолютной сходимости двойного интеграла мы можем менять порядок интегрирований
Для значений  полюс лежит во внешности кривой интегрирования и, следовательно,
полюс лежит во внешности кривой интегрирования и, следовательно,

Для значений  полюс лежит во внутренности кривой интегрирования и, следовательно,
полюс лежит во внутренности кривой интегрирования и, следовательно,

Этим заканчивается доказательство теоремы.

Рис. 1.2. Кривая  на римановой поверхности с точками разветвления
на римановой поверхности с точками разветвления 
Замечание. Дифференцируя F по а (и принимая во внимание, что  согласно (12), есть функция от а), получаем аналогичные результаты в случае, когда ассоциированная функция имеет полюс порядка
согласно (12), есть функция от а), получаем аналогичные результаты в случае, когда ассоциированная функция имеет полюс порядка 
Продолжая функции  на комплексные значения аргументов, мы получим интересные обобщения соотношений (10) и (12).
на комплексные значения аргументов, мы получим интересные обобщения соотношений (10) и (12).
Предположим, что кривая интегрирования  лежит на поверхности
лежит на поверхности

где  целая аналитическая функция одного комлексного переменного z. Тогда мы можем заменить величину
целая аналитическая функция одного комлексного переменного z. Тогда мы можем заменить величину  функцией
функцией  и получить результаты, аналогичные сформулированным в теоремах 2 и 3, стр. 54, 55.
и получить результаты, аналогичные сформулированным в теоремах 2 и 3, стр. 54, 55.
Рассмотренный выше метод можно обобщить на случай, когда ассоциированная функция  является алгебраической функцией а и когда рассматривается кривая интегрирования, такая, что для всех значений
является алгебраической функцией а и когда рассматривается кривая интегрирования, такая, что для всех значений  геометрическим местом точек
геометрическим местом точек  является замкнутая кривая на римановой поверхности ассоциированной функции
является замкнутая кривая на римановой поверхности ассоциированной функции  (Так как кривая интегрирования
(Так как кривая интегрирования  может оказаться незамкнутой на римановой поверхности, мы заменяем ее кривой
может оказаться незамкнутой на римановой поверхности, мы заменяем ее кривой  где
где  выбрано так, чтобы
выбрано так, чтобы  была замкнутой кривой на римановой поверхности функции
была замкнутой кривой на римановой поверхности функции  Результаты такого рода рассматриваются в работе [10, § 3].
Результаты такого рода рассматриваются в работе [10, § 3].
Замечание. В работе [10] исследуется уравнение  рассуждения могут быть немедленно распространены на случай дифференциального уравнения (1).
рассуждения могут быть немедленно распространены на случай дифференциального уравнения (1).
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ВВЕДЕНИЕ
- Глава I. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ С ЦЕЛЫМИ КОЭФФИЦИЕНТАМИ С ДВУМЯ НЕЗАВИСИМЫМИ ПЕРЕМЕННЫМИ
- § 1. Представление решений уравнений с частными производными
- § 2. Интегральный оператор первого рода
- § 3. Дальнейшие представления интегральных операторов
- § 4. Представление оператора первого рода посредством интегралов
- § 5. Свойства интегрального оператора первого рода
- § 6. Некоторые дальнейшие свойства интегрального оператора первого рода
- § 7. Дифференциальное уравнение
- § 8. Интегральные операторы экспоненциального типа
- § 9. Дифференциальное уравнение …
- 10. Дифференциальные уравнения высшего порядка
- Глава II. ГАРМОНИЧЕСКИЕ ФУНКЦИИ ТРЕХ ПЕРЕМЕННЫХ
- § 2. Характеристическое пространство
- § 3. Гармонические функции, В3-ассоциированные функции которых рациональны
- § 4. Периоды
- § 5. Связь между коэффициентами разложения гармонической функции в ряд и ее особенностями
- § 6. Другой тип интегральных представлений гармонических функций
- § 7. Поведение в целом функций класса с рациональной ассоциированной
- Глава III. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ С ТРЕМЯ ПЕРЕМЕННЫМИ
- § 2. Разложение в ряд решений уравнения …
- § 3. Интегральный оператор, порождающий решения уравнения
- § 4. Второй интегральный оператор, порождающий решения уравнения …
- § 5. Интегральный оператор, порождающий решения уравнения
- § 6. Интегральный оператор, порождающий решения уравнения …
- Глава IV. СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- § 2. Гармонические векторы в целом и их представление посредством интегралов
- § 3. Интегралы от гармонических векторов
- § 4. Связь интегралов от алгебраических гармонических векторов трех переменных с интегралами от алгебраических функций одного комплексного переменного
- § 5. Обобщение теорем о вычетах на случай уравнения …
- § 6. Оператор, порождающий решения системы уравнений в частных производных
- Глава V. УРАВНЕНИЯ СМЕШАННОГО ТИПА И ЭЛЛИПТИЧЕСКИЕ УРАВНЕНИЯ С СИНГУЛЯРНЫМИ И НЕАНАЛИТИЧЕСКИМИ КОЭФФИЦИЕНТАМИ
- § 2. Обобщение представления (1.12) решений уравнения (1.6)
- § 3. Оператор (1.11б) в общем случае
- § 4. Порождающие функции, аналогичные решениям гипергеометрического уравнения
- § 5. О решении задачи Коши в целом
- § 6. Обобщенные уравнения Коши — Римана
- § 7. Дифференциальное уравнение … с новым типом особенности функции N
- § 8. Интегральный оператор для уравнений с неаналитическими коэффициентами
- ПРИЛОЖЕНИЕ. ОПЕРАТОРЫ, ПОРОЖДАЮЩИЕ РЕШЕНИЯ НЕКОТОРЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ТРЕМЯ ПЕРЕМЕННЫМИ, И ИХ СВОЙСТВА
- 1. Определение компонент H2 и H3 гармонического вектора по данной компоненте H1
- 2. Связь между интегралами от алгебраических гармонических векторов от трех переменных с интегралами от алгебраических функций комплексного переменного.
- 3. Обобщение предыдущих результатов на случай дифференциального уравнения …
- О ПРОБЛЕМЕ КОЭФФИЦИЕНТОВ В ТЕОРИИ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ
- 2. Формулы для определения области регулярности функции двух комплексных переменных по коэффициентам ее разложения в ряд.
- 3. Формула для определения расположения некоторых особенностей f(z1, z2) по коэффициентам ее разложения в ряд.
- 4. Обобщение результатов п. 2,3 на случай одной системы дифференциальных уравнений.
- 5. Применение интегральных рператоров в теории целых функций.
- ПРИМЕНЕНИЕ ИНТЕГРАЛЬНЫХ ОПЕРАТОРОВ ПРИ ИЗУЧЕНИИ АЛГЕБРЫ ГАРМОНИЧЕСКИХ ФУНКЦИЙ ТРЕХ ПЕРЕМЕННЫХ И ПРОБЛЕМЫ КОЭФФИЦИЕНТОВ