| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3.3. Управление с самонастройкой
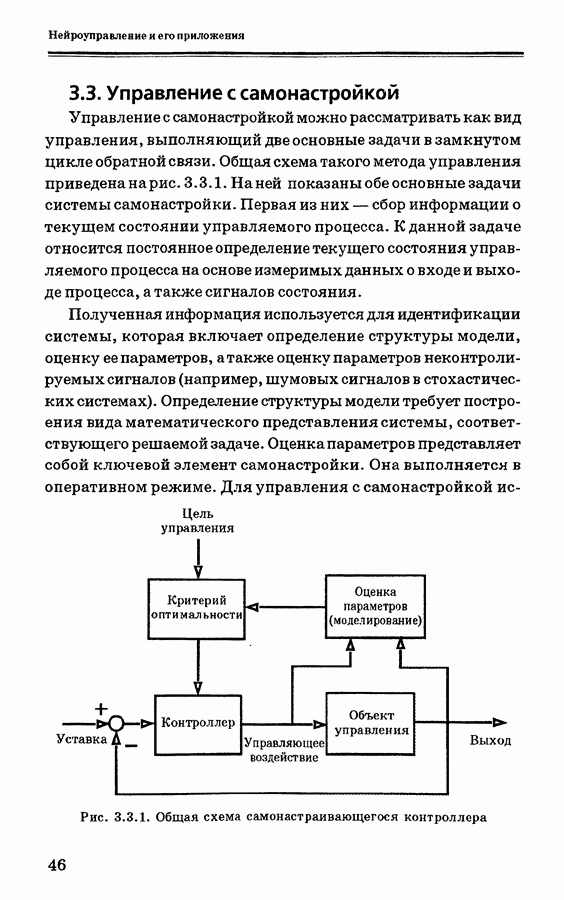
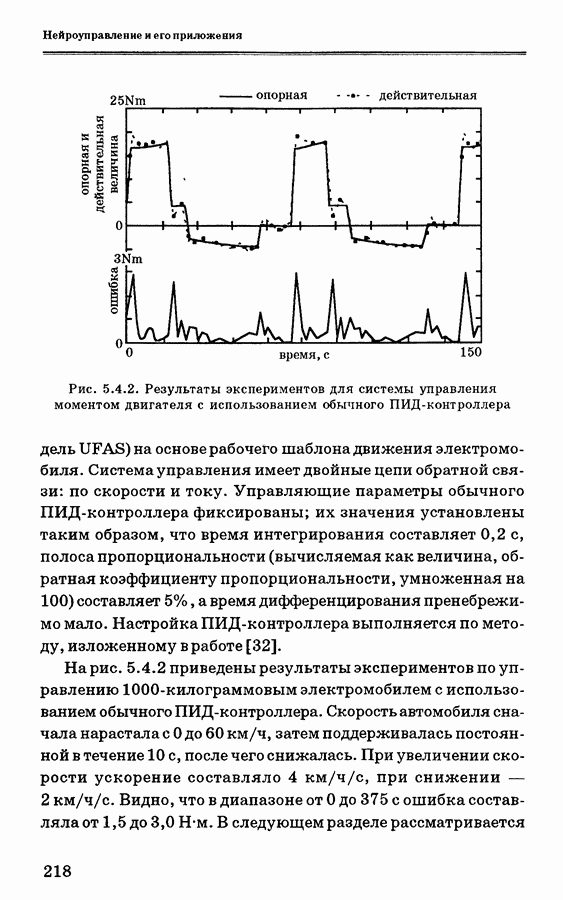
Управление с самонастройкой можно рассматривать как вид управления, выполняющий две основные задачи в замкнутом цикле обратной связи. Общая схема такого метода управления приведена на рис. 3.3.1. На ней показаны обе основные задачи системы самонастройки. Первая из них — сбор информации о текущем состоянии управляемого процесса. К данной задаче относится постоянное определение текущего состояния управляемого процесса на основе измеримых данных о входе и выходе процесса, а также сигналов состояния.
Полученная информация используется для идентификации системы, которая включает определение структуры модели, оценку ее параметров, а также оценку параметров неконтролируемых сигналов (например, шумовых сигналов в стохастических системах). Определение структуры модели требует построения вида математического представления системы, соответствующего решаемой задаче. Оценка параметров представляет собой ключевой элемент самонастройки. Она выполняется в оперативном режиме. Для управления с самонастройкой

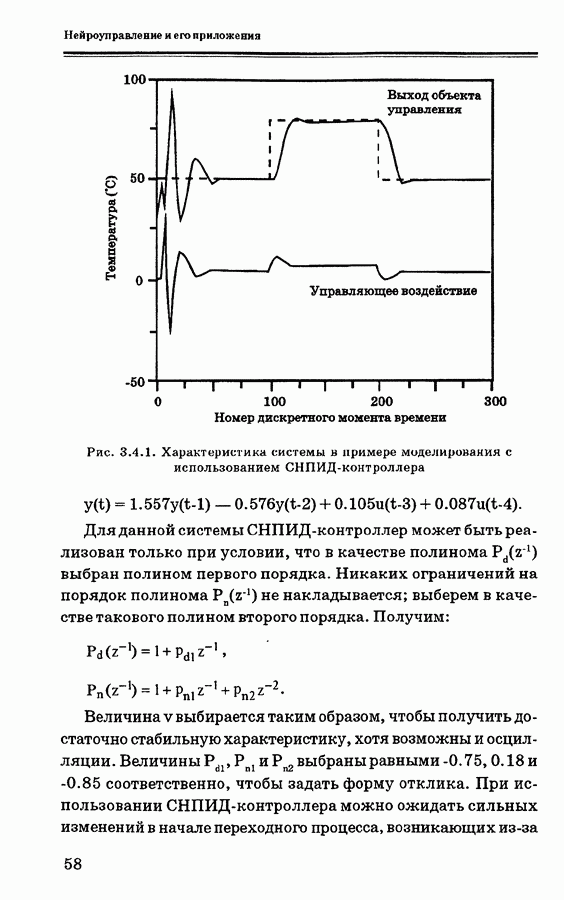
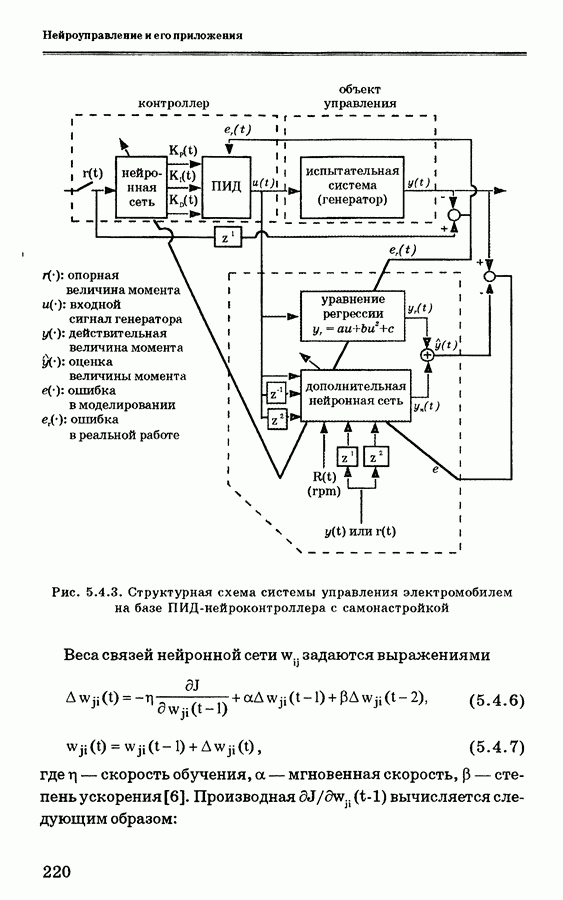
Рис. 3.3.1. Общая схема самонастраивающегося контроллера
используется несколько схем рекурсивной оценки параметров. Наиболее распространенная схема—рекурсивный метод оценки на основе метода наименьших квадратов [31], [32] или его расширение — UD факторизационный метод [33], который является более надежным.
Вторая задача системы самонастройки — задача проектирования (контроллера); ее решение обычно базируется на оптимизации критерия оптимальности управления. Цель управления задается для каждой конкретной системы; при этом требуется принять решения в отношении того, как контроллер должен адаптироваться или настраиваться. На этой основе рассчитывается новый набор параметров контроллера (взамен прежних параметров в цикле управления). Эта часть процесса известна как этап ратификации или утверждения; одно из основных достоинств системы самонастройки состоит в том, что данный процесс выполняется в оперативном режиме и в реальном времени. При традиционном методе процесс утверждения обычно выполняется в автономном режиме; результаты часто оказываются неудовлетворительными, и весь процесс моделирования и проектирования приходится повторять. Расчет закона управления выполняется на основе процедуры, называемой эквивалентом определенности; в ней неопределенность текущих оценок параметров игнорируется.
Подход к оцениванию параметров передаточной функции по процессу и воздействию называется методом косвенной самонастройки, или методом полной определенности. Примером реализации метода такого типа может служить самонастраивающийся регулятор Острема (Astrom) и Виттенмарка (Wittenmark) [6], известный также под названием системы управления по минимуму дисперсии. Критерий оптимальности такого регулятора — минимизация дисперсии выходного процесса  по всем моментам дискретного времени
по всем моментам дискретного времени  Это может быть достигнуто следующим образом: сначала предсказывается будущая вёлична выходного процесса на
Это может быть достигнуто следующим образом: сначала предсказывается будущая вёлична выходного процесса на  шагов вперед —
шагов вперед —  затем текущая величина управляющего
затем текущая величина управляющего
воздействия  устанавливается таким образом, чтобы сделать этот выход нулевым. Однако в этом методе не делается попыток оптимизации уставок, атакже возможны чрезмерно большие величины управляющих воздействий. Другим недостатком данного метода является нестабильность замкнутого цикла из-за потери нулей процесса, если процесс не является минимально-фазовым. Для преодоления этих сложностей Кларк (Clarke) и Гаутроп (Gawthrop) [18], [19] изменили критерий: минимизируется нетолько дисперсия выхода, но и функция, включающая управляющее воздействие, выход, атакже изменения уставки. Таким образом обеспечивается возможность использования большего набора целей функционирования. В этом критерии управляющий сигнал подвергается «штрафу» таким образом, что уменьшаются его избыточные пики, и обеспечиваются возможности оптимального отслеживания уставки. Кроме того, модифицированный критерий обеспечивает стабильное управление неминимально-фазовым процессом. Такой тип самонастраивающегося контроллера известен также под названием УОМД (управление по обобщенному минимуму дисперсии). В последнее время в литературе приводятся различные усовершенствования и расширения этого контроллера [34—39].
устанавливается таким образом, чтобы сделать этот выход нулевым. Однако в этом методе не делается попыток оптимизации уставок, атакже возможны чрезмерно большие величины управляющих воздействий. Другим недостатком данного метода является нестабильность замкнутого цикла из-за потери нулей процесса, если процесс не является минимально-фазовым. Для преодоления этих сложностей Кларк (Clarke) и Гаутроп (Gawthrop) [18], [19] изменили критерий: минимизируется нетолько дисперсия выхода, но и функция, включающая управляющее воздействие, выход, атакже изменения уставки. Таким образом обеспечивается возможность использования большего набора целей функционирования. В этом критерии управляющий сигнал подвергается «штрафу» таким образом, что уменьшаются его избыточные пики, и обеспечиваются возможности оптимального отслеживания уставки. Кроме того, модифицированный критерий обеспечивает стабильное управление неминимально-фазовым процессом. Такой тип самонастраивающегося контроллера известен также под названием УОМД (управление по обобщенному минимуму дисперсии). В последнее время в литературе приводятся различные усовершенствования и расширения этого контроллера [34—39].
Для вывода алгоритма работы таких контроллеров рассматривается система в форме модели управляемой авторегрессии — скользящего среднего (УАРСС) (Controlled Auto-Regressive Moving Average (CARMA) model). Систему можно представить в виде следующей математической модели:

где  — выходной процесс,
— выходной процесс,  — входной процесс (управляющее воздействие),
— входной процесс (управляющее воздействие),  — некоррелированная случайная последовательность с нулевым математическим ожиданием и ковариацией (среднеквадратическим отклонением) a, d — время задержки,
— некоррелированная случайная последовательность с нулевым математическим ожиданием и ковариацией (среднеквадратическим отклонением) a, d — время задержки,  — целочисленное время.
— целочисленное время.  выражаются через оператор z-преобразования:
выражаются через оператор z-преобразования:

Предполагается, что корни полинома  располагаются внутри круга единичного радиуса. Никаких предположений о корнях полиномов
располагаются внутри круга единичного радиуса. Никаких предположений о корнях полиномов  не делается, т.е. считается, что за пределами единичного круга могут находиться как корни
не делается, т.е. считается, что за пределами единичного круга могут находиться как корни  (что означает неустойчивость объекта управления в разомкнутом состоянии), так и корни
(что означает неустойчивость объекта управления в разомкнутом состоянии), так и корни  (объект управления неминимально-фазовый).
(объект управления неминимально-фазовый).
В этом случае используется критерий качества в виде:

где  — математическое ожидание,
— математическое ожидание,  — задаваемые пользователем полиномы,
— задаваемые пользователем полиномы,  — уставка,
— уставка,  — дробно-рациональная передаточная функция:
— дробно-рациональная передаточная функция:

Здесь  — полиномы степени
— полиномы степени  соответственно. Данный критерий качества в некоторых отношениях отличается от критерия качества по минимуму дисперсии, предложенного Остремом. Управление по последнему критерию направлено только на стабилизацию выходного процесса
соответственно. Данный критерий качества в некоторых отношениях отличается от критерия качества по минимуму дисперсии, предложенного Остремом. Управление по последнему критерию направлено только на стабилизацию выходного процесса  вблизи нулевого значения при действии случайных возмущений. Однако во многих реальных ситуациях требуется поддерживать при случайных возмущениях выход системы на некотором постоянном уровне. В УОМД-контроллере используется как стабилизация, так и серворегулирование. Кроме того, УОМД-контроллер придает такой вес управляющему воздействию, что он препятствует появлению излишне больших значений этого воздействия при подавлении последствий от нулей, находящихся вне области устойчивости. В рассматриваемом подходе
вблизи нулевого значения при действии случайных возмущений. Однако во многих реальных ситуациях требуется поддерживать при случайных возмущениях выход системы на некотором постоянном уровне. В УОМД-контроллере используется как стабилизация, так и серворегулирование. Кроме того, УОМД-контроллер придает такой вес управляющему воздействию, что он препятствует появлению излишне больших значений этого воздействия при подавлении последствий от нулей, находящихся вне области устойчивости. В рассматриваемом подходе
вводится понятие псевдовыхода, задаваемого следующим  выражением:
выражением:

Таким образом, систему можно рассматривать как обобщенный выход системы с прогнозирующим элементом, фильтрующим действием на входе и с уставкой. Многие стратегии самонастройки основываются на прогнозирующей схеме управления; горизонтом прогнозирования при этом является временная задержка  Оптимальное прогнозирование выхода в момент
Оптимальное прогнозирование выхода в момент  может быть получено в момент
может быть получено в момент  если вход выбран таким образом, что возмущения нейтрализуются. Для получения оптимального прогноза псевдовыхода рассмотрим уравнение тождества (тождественное равенство) в следующей форме:
если вход выбран таким образом, что возмущения нейтрализуются. Для получения оптимального прогноза псевдовыхода рассмотрим уравнение тождества (тождественное равенство) в следующей форме:

где

и

Умножая уравнения (3.3.1) на  получим:
получим:

Подставляя  из уравнения (3.3.8) в уравнение (3.3.12), получим:
из уравнения (3.3.8) в уравнение (3.3.12), получим:

Здесь  Прибавляя
Прибавляя  к обеим частям уравнения (3.3.13), получим:
к обеим частям уравнения (3.3.13), получим:

что эквивалентно выражению:

Обозначив через  оптимальный прогноз величины
оптимальный прогноз величины  полученный на основе измерений до момента времени
полученный на основе измерений до момента времени  а через
а через  — ошибку прогноза, а также полагая
— ошибку прогноза, а также полагая  получим:
получим:

и

Здесь  Учитывая, что ошибки в последующие моменты времени
Учитывая, что ошибки в последующие моменты времени  не коррелированы с текущими и предыдущими измерениями на входе и выходе, управление по минимальной дисперсии
не коррелированы с текущими и предыдущими измерениями на входе и выходе, управление по минимальной дисперсии  достигается путем выбора
достигается путем выбора  таким, чтобы
таким, чтобы  обращалось в ноль. Таким образом, получим
обращалось в ноль. Таким образом, получим

Так как в момент времени  величины
величины  известны, выражение прогноза
известны, выражение прогноза  можно уменьшить до
можно уменьшить до

Таким образом, оптимальный прогноз  на
на  шагов вперед задается следующим выражением:
шагов вперед задается следующим выражением:

Параметры контроллера  можно легко получить из тождества (3.13), если полиномы
можно легко получить из тождества (3.13), если полиномы  известны. Если же они неизвестны, то для оценки элементов
известны. Если же они неизвестны, то для оценки элементов  можно использовать рекурсивный метод наименьших квадратов, рассматриваемый ниже. Векторы параметров регрессии и данных следующие:
можно использовать рекурсивный метод наименьших квадратов, рассматриваемый ниже. Векторы параметров регрессии и данных следующие:

где  — оценки элементов
— оценки элементов  соответственно.
соответственно.
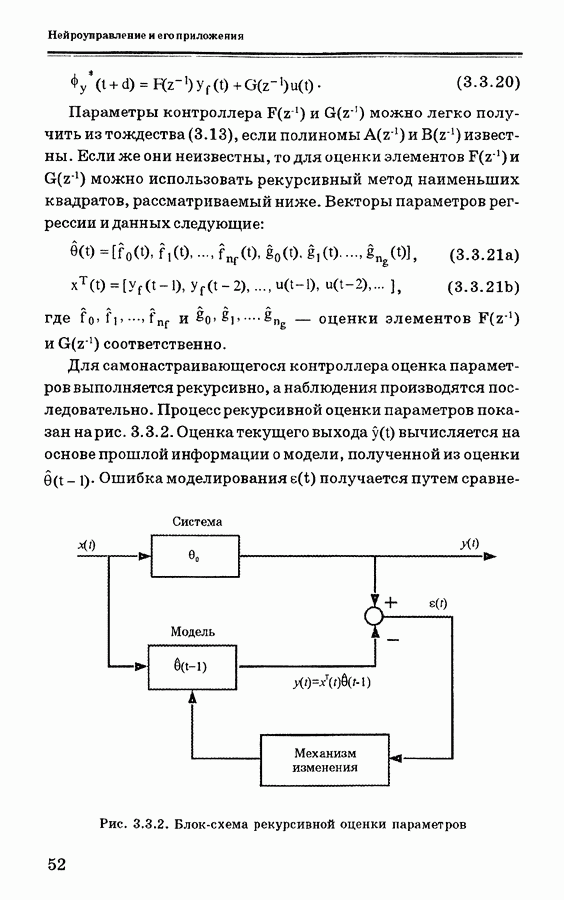
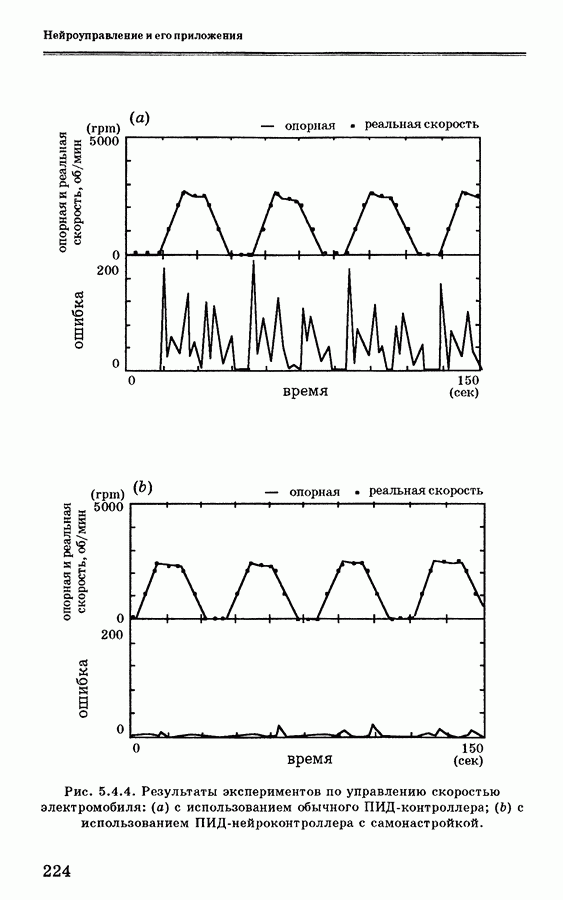
Для самонастраивающегося контроллера оценка параметров выполняется рекурсивно, а наблюдения производятся последовательно. Процесс рекурсивной оценки параметров показан на рис. 3.3.2. Оценка текущего выхода  вычисляется на основе прошлой информации о модели, полученной из оценки
вычисляется на основе прошлой информации о модели, полученной из оценки  Ошибка моделирования
Ошибка моделирования  получается путем
получается путем

Рис. 3.3.2. Блок-схема рекурсивной оценки параметров
сравнения оценки выхода с наблюдаемым выходом. Затем ошибка минимизируется в смысле наименьших квадратов, а оценка  корректируется в соответствии с новым значением
корректируется в соответствии с новым значением  Оценки
Оценки  могут быть получены с помощью трех важных рекурсивных уравнений:
могут быть получены с помощью трех важных рекурсивных уравнений:

где  — ковариационная матрица, задаваемая выражением:
— ковариационная матрица, задаваемая выражением:

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРОВ ПЕРЕВОДА
- 1. ВВЕДЕНИЕ
- 1.1. Общие сведения об интеллектуальном управлении
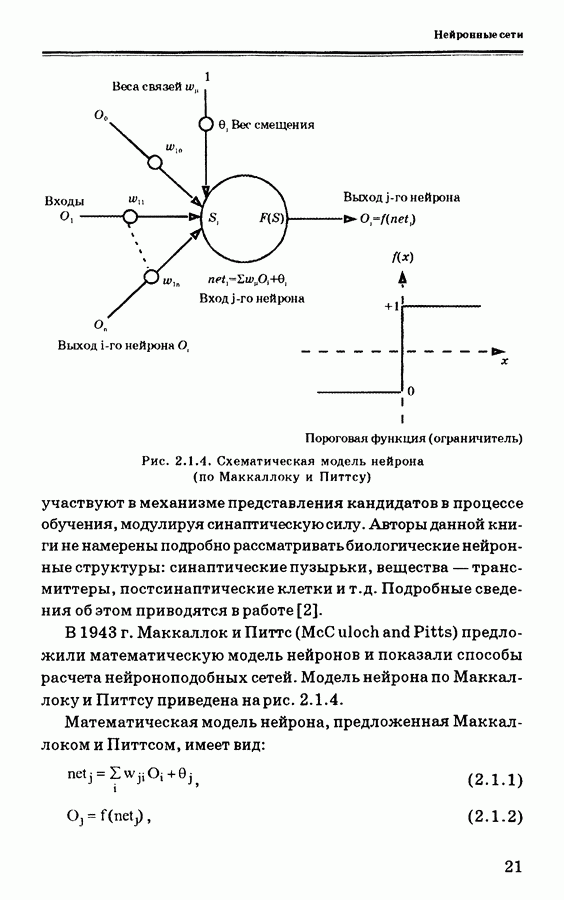
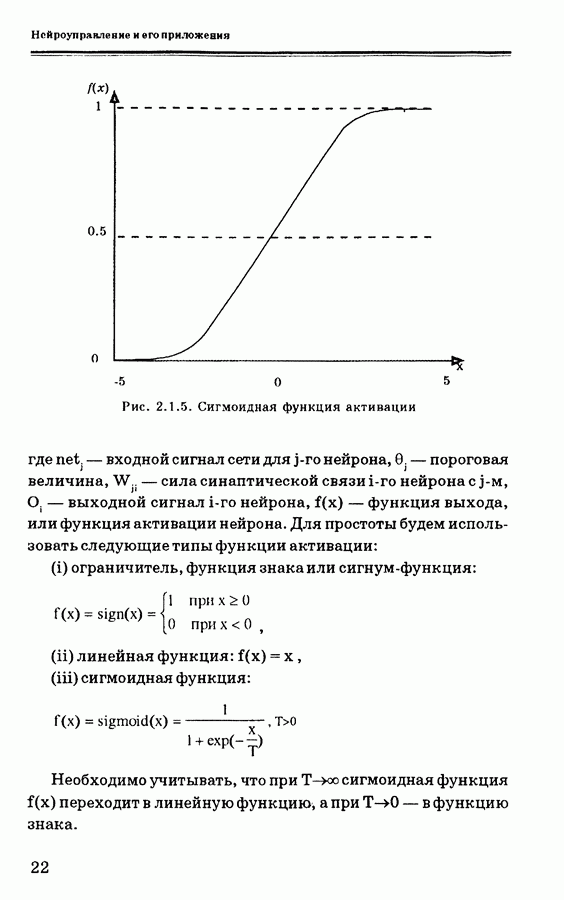
- 2. НЕЙРОННЫЕ СЕТИ
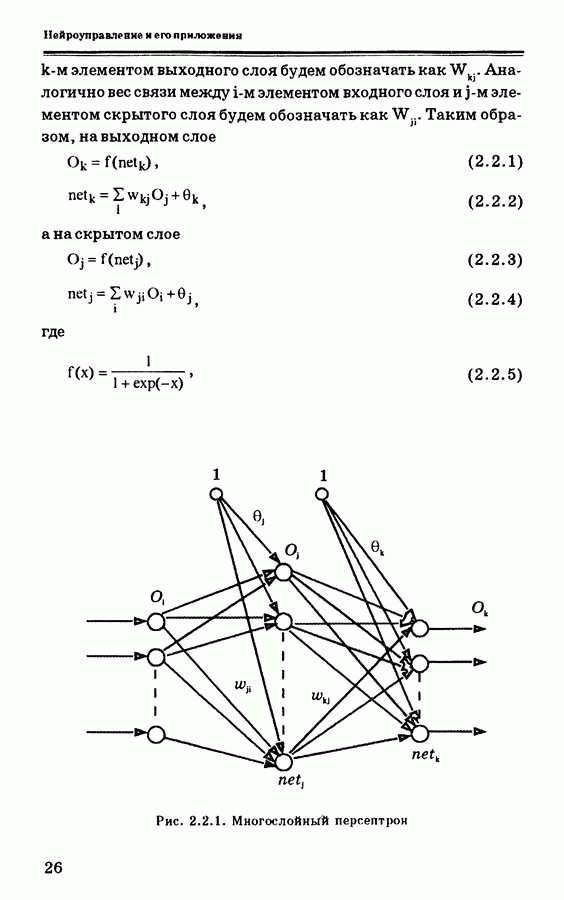
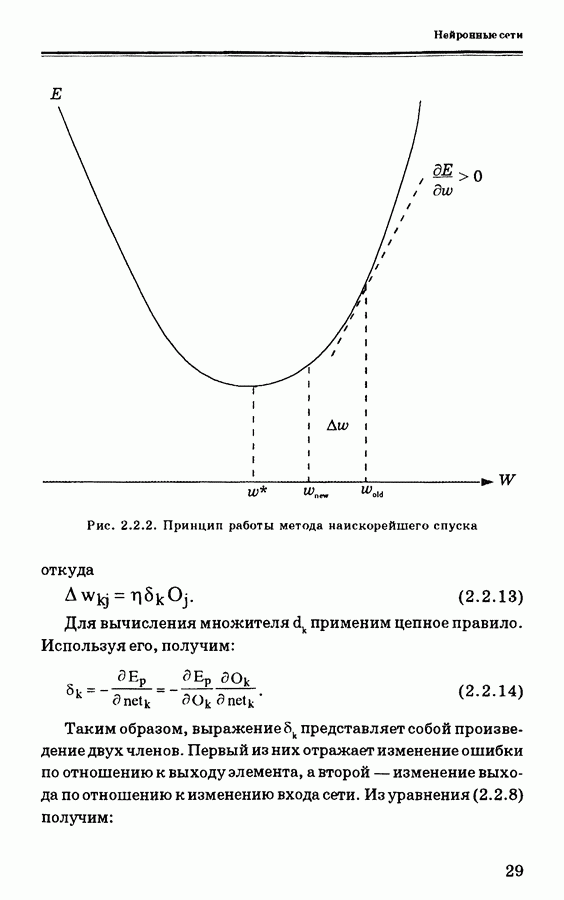
- 2.2. Алгоритм обратного распространения
- 2.2.2. Вывод алгоритма обратного распространения
- 2.2.2.2. Правило для скрытого слоя
- 2.2.3. Алгоритм обратного распространения: порядок реализации
- 2.2.4. Обсуждение алгоритма обратного распространения
- 2.3. Заключение
- 3. ТРАДИЦИОННЫЕ СХЕМЫ УПРАВЛЕНИЯ
- 3.2. ПИ- и ПИД-контроллеры с дискретным временем
- 3.3. Управление с самонастройкой
- 3.4. Самонастраивающиеся ПИ- и ПИД- контроллеры
- 3.5. ПИД-управление с самонастройкой: многомерный подход
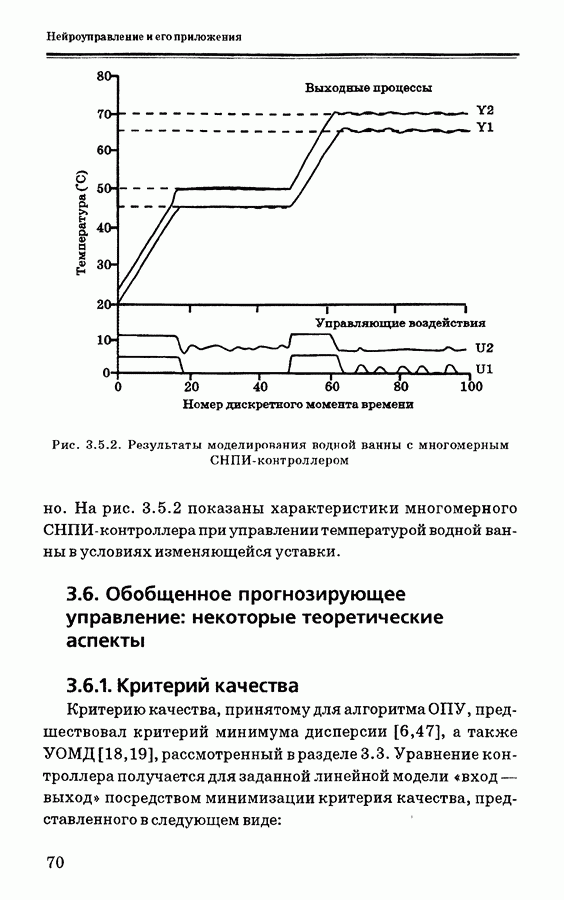
- 3.5.1. Пример моделирования
- 3.6. Обобщенное прогнозирующее управление: некоторые теоретические аспекты
- 3.6.2. Модель объекта управления и решение задачи оптимизации
- 3.7. Управление на основе нечеткой логики
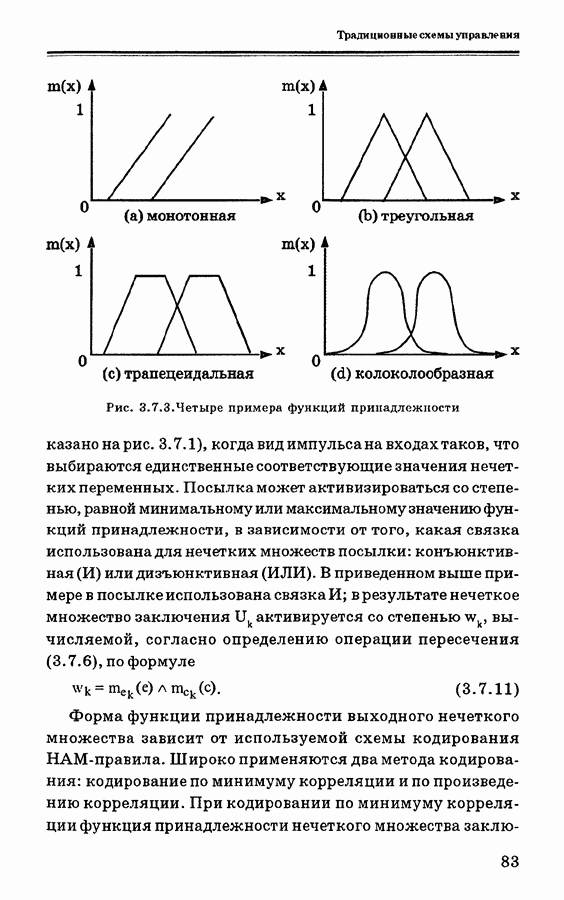
- 3.7.1. Краткие сведения по теории нечетких множеств и нечетких систем
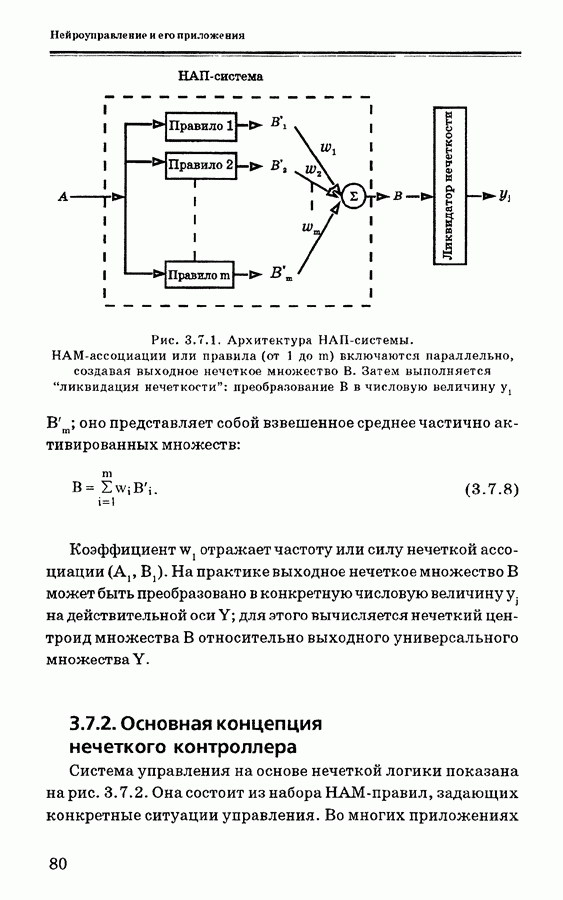
- 3.7.2. Основная концепция нечеткого контроллера
- 3.8. Заключение
- 4. ТЕХНОЛОГИИ НЕЙРОННОГО УПРАВЛЕНИЯ
- 4.2. Общие сведения о нейронном управлении
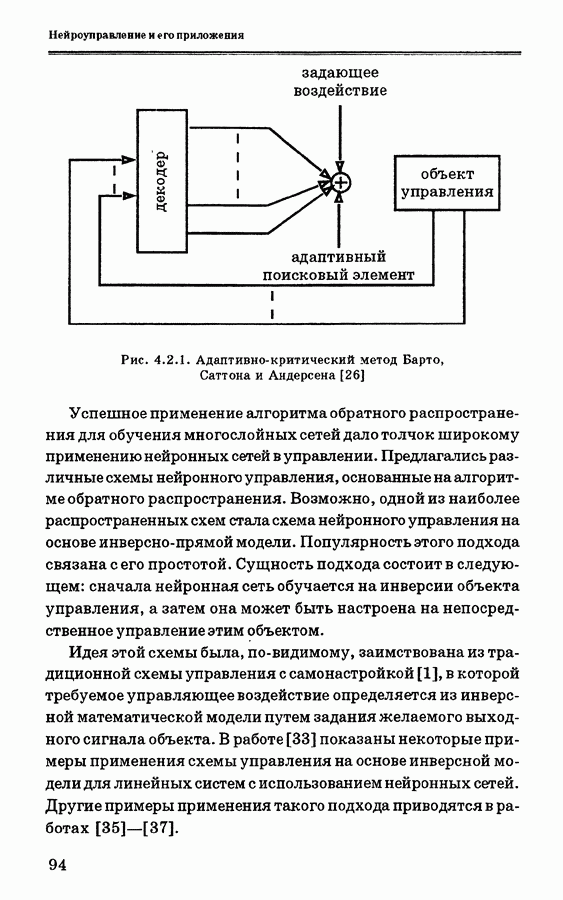
- 4.2.1. Подходы к нейронному управлению
- 4.2.2. Общая схема управления
- 4.3. Последовательная схема нейронного управления
- 4.4. Расширение последовательной схемы нейронного управления
- 4.4.2. Нейроморфные структуры управления
- 4.4.3. Конфигурации обучения
- 4.4.4. Эффективное оперативное управление
- 4.4.5. Алгоритмы обучения
- 4.4.6. Оценка алгоритмов обучения на основе моделирования
- 4.5. Параллельная схема управления
- 4.6. Алгоритм обучения по ошибке обратной связи
- 4.7. Расширение применения нейроконтроллеров параллельного типа
- 4.7.2. Линеаризованная система управления
- 4.7.3. Система управления с нейронными сетями
- 4.7.4. Нелинейный алгоритм наблюдения для нейронной сети
- 4.7.5. Нелинейный контроллер для нейронной сети
- 4.7.6. Численное моделирование
- 4.8. Схема нейронного управления с самонастройкой
- 4.9. ПИД-нейроконтроллер с самонастройкой
- 4.9.1. Вывод уравнений ПИД-нейроконтроллера с самонастройкой
- 4.9.2. Примеры эмуляции
- 4.10. Схема нейронного управления с эмулятором и контроллером (схема обратного распространения во времени)
- 4.11. Заключение
- 5. ПРИЛОЖЕНИЯ НЕЙРОННОГО УПРАВЛЕНИЯ
- 5.2. Применение нейронного управления в системе регулирования процессов в водяной ванне и сравнение его с другими схемами управления
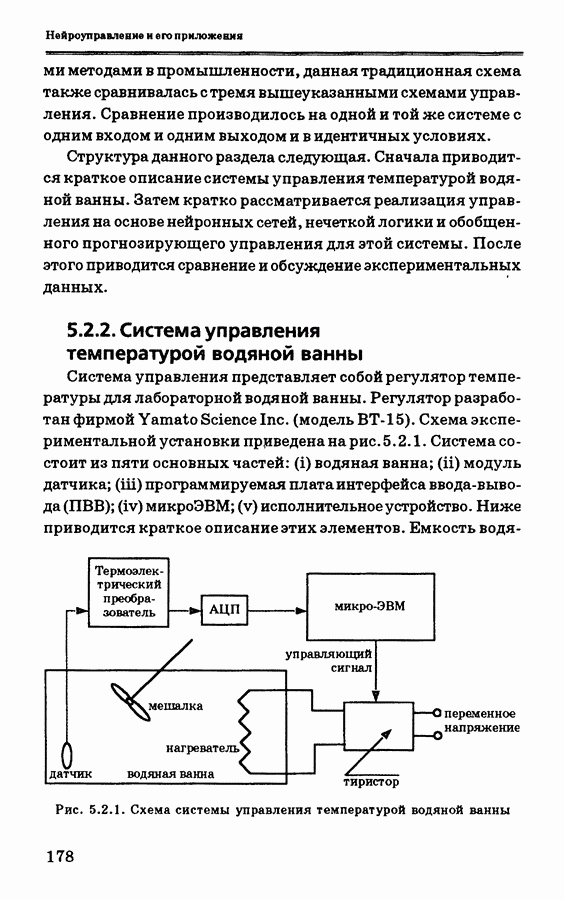
- 5.2.2. Система управления температурой водяной ванны
- 5.2.3. Схема нейронного управления
- 5.2.4. Схема управления на основе нечеткой логики
- 5.2.5. Схема обобщенного прогнозирующего управления
- 5.2.6. Экспериментальные данные и их анализ
- 5.2.7. Заключение
- 5.3. Система стабилизации инвертированного маятника на основе нейронных сетей
- 5.3.2. Система стабилизации инвертированного маятника
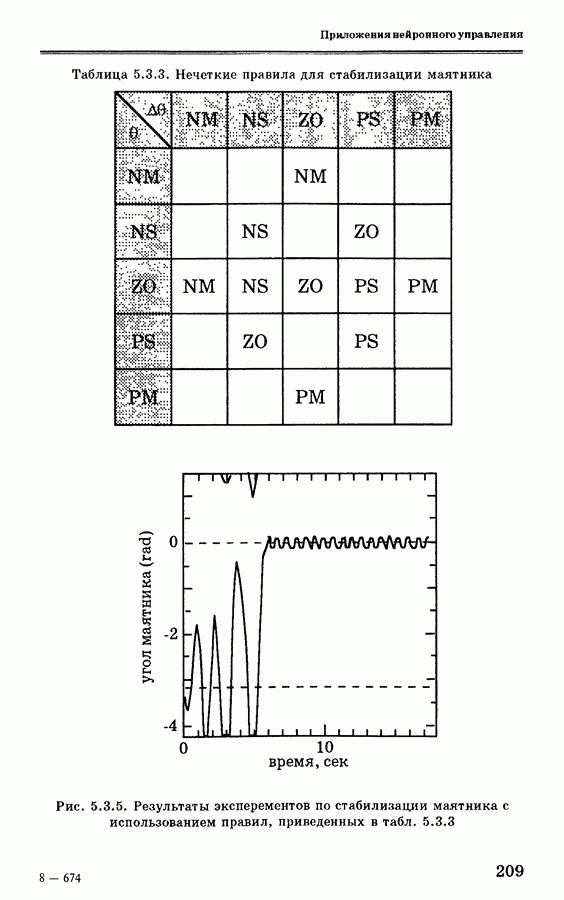
- 5.3.3. Инициализация поворотного управления с использованием нечеткой логики
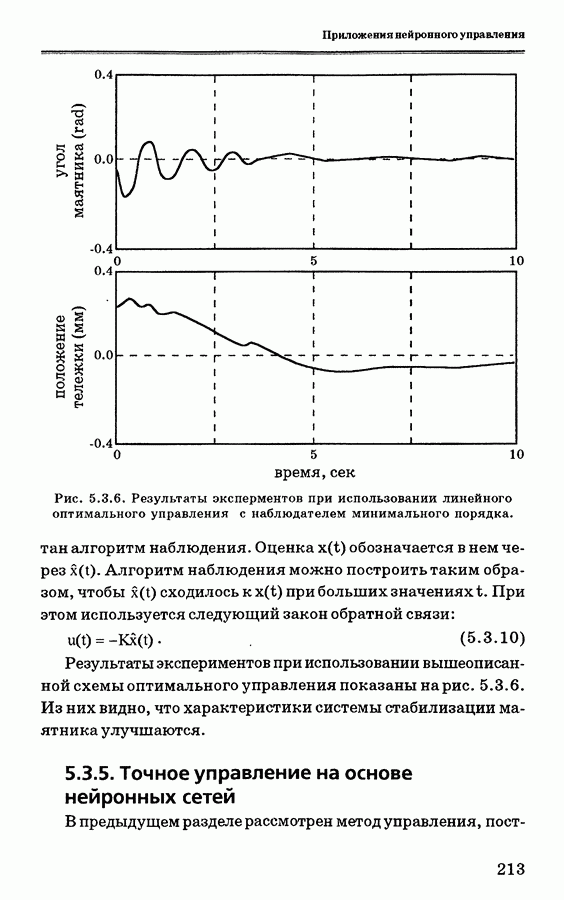
- 5.3.4. Применение стратегии оптимального управления для стабилизации маятника
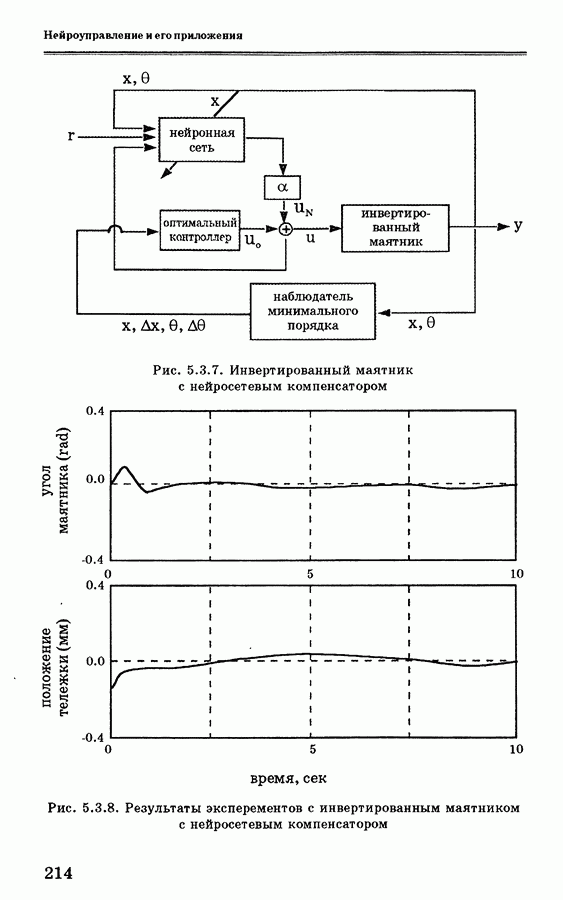
- 5.3.5. Точное управление на основе нейронных сетей
- 5.3.6. Заключение
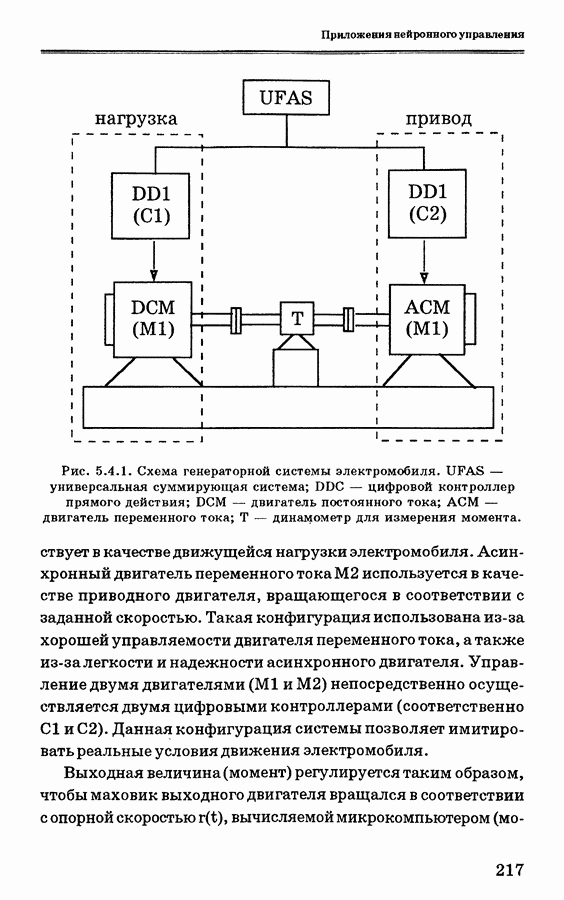
- 5.4. Применение ПИД-нейроконтроллера с самонастройкой для управления скоростью электромобиля
- 5.4.2. Система управления электромобилем
- 5.4.3. ПИД-нейроконтроллер с самонастройкой
- 5.4.4. Применение нейронной сети для управления скоростью электромобиля
- 5.4.5. Заключение
- 5.5. Применение нейронных сетей для управления печью
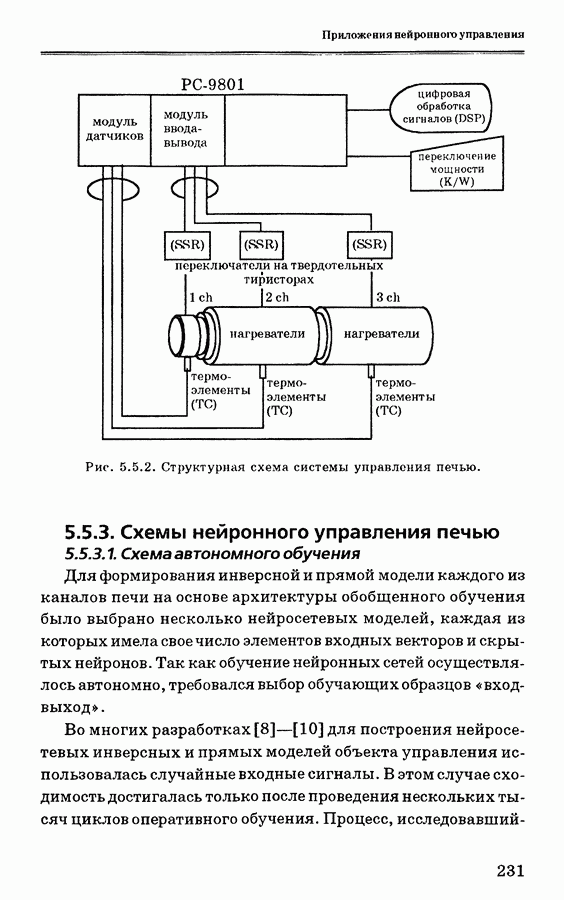
- 5.5.2. Система управления печью
- 5.5.3. Схемы нейронного управления печью
- 5.5.4. Анализ экспериментальных данных
- 5.6. Заключительные замечания и выводы
- Литература
- ЛИСТИНГ ПРОГРАММЫ