| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
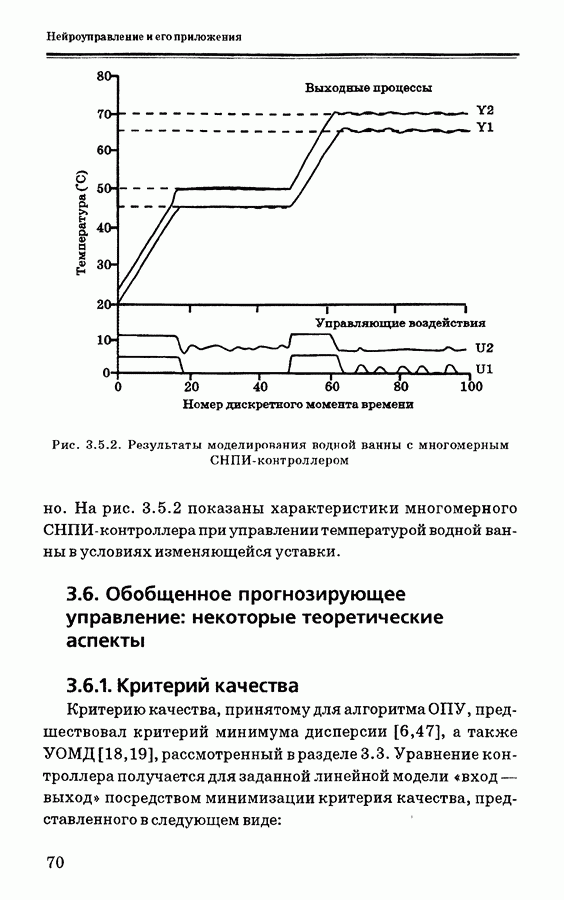
3.6. Обобщенное прогнозирующее управление: некоторые теоретические аспекты
3.6.1. Критерий качества
Критерию качества, принятому для алгоритма ОПУ, предшествовал критерий минимума дисперсии [6,47], а также УОМД [18,19], рассмотренный в разделе 3.3. Уравнение контроллера получается для заданной линейной модели «вход — выход» посредством минимизации критерия качества, представленного в следующем виде:

Очевидное различие между вышеприведенным критерием качества и критерием для УОМД заключается в постановке задачи оптимизации, которая описывается не через значения про цесса  а через конечную разность
а через конечную разность  Она введенав разделе 3.2 и обозначает приращение управляющего воздействия в системе. В момент времени
Она введенав разделе 3.2 и обозначает приращение управляющего воздействия в системе. В момент времени  критерий минимизируется относительно разности
критерий минимизируется относительно разности  Использование инкрементных входных сигналов обеспечивает появление нулевой статической ошибки при ненулевом постоянном опорном сигнале. Однако использование инкрементного управления затрудняет установление точно определенных границ величины
Использование инкрементных входных сигналов обеспечивает появление нулевой статической ошибки при ненулевом постоянном опорном сигнале. Однако использование инкрементного управления затрудняет установление точно определенных границ величины  . В результате она может достигать очень больших величин. Чтобы предотвратить такое увеличение и при этом сохранить дисперсию как можно меньшей, необходимо при обеспечении устойчивости замкнутой системы поддерживать достаточно малое значение весового коэффициента?. Таким образом, весовой коэффициент приращения управляющего воздействия
. В результате она может достигать очень больших величин. Чтобы предотвратить такое увеличение и при этом сохранить дисперсию как можно меньшей, необходимо при обеспечении устойчивости замкнутой системы поддерживать достаточно малое значение весового коэффициента?. Таким образом, весовой коэффициент приращения управляющего воздействия  включается в окончательное выражение только для ограничения управляющего сигнала.
включается в окончательное выражение только для ограничения управляющего сигнала.
Другим свойством ОПУ является способность к управлению неминимально-фазовыми и неустойчивыми в разомкнутом состоянии системами, в частности, системами с не полностью известными величинами транспортного запаздывания. Для удовлетворения этим требованиям, критерий (3.6.1) преобразуется к следующему виду:

при условии  при
при 
Здесь  — горизонт управления,
— горизонт управления,  — минимальный горизонт качества,
— минимальный горизонт качества,  — максимальный горизонт качества,
— максимальный горизонт качества,  — последовательность весовых коэффициентов управления. Добавление ограничения на приращение управляющего воздействия можно интерпретировать как назначение
— последовательность весовых коэффициентов управления. Добавление ограничения на приращение управляющего воздействия можно интерпретировать как назначение
бесконечных весовых коэффициентов на изменения управляющего воздействия через некоторое время. Это, в свою очередь, не только обеспечивает быстрое достижение контроллером своей цели и стабилизацию неминимально-фазового объекта управления, но и существенно снижает накладные расходы, связанные с вычислениями. Правильный выбор весовых коэффициентов управления и горизонтов стоимости обеспечивает также достижение хороших показателей качества и асимптотической устойчивости замкнутой системы и для систем, устойчивых в разомкнутом состоянии [48].
Процедура минимизации выполняется на нескольких  будущих значениях выхода с учетом нескольких (NU) будущих инкрементных управляющих воздействий. Результат алгоритма в некоторой степени зависит от того, входит ли действительное запаздывание в интервал между величинами
будущих значениях выхода с учетом нескольких (NU) будущих инкрементных управляющих воздействий. Результат алгоритма в некоторой степени зависит от того, входит ли действительное запаздывание в интервал между величинами  Обычно значение величины
Обычно значение величины  выбирается равным значению времени запаздывания. В процедуре минимизации используется также концепция управления по удаляющемуся горизонту, в которой управляющие воздействия
выбирается равным значению времени запаздывания. В процедуре минимизации используется также концепция управления по удаляющемуся горизонту, в которой управляющие воздействия  вырабатываются, но фактически применяется только значение
вырабатываются, но фактически применяется только значение  . В момент
. В момент  решается новая задача минимизации. Управление по такому критерию обеспечивает как хорошие показатели качества, так и асимптотическую устойчивость разнообразных объектов управления.
решается новая задача минимизации. Управление по такому критерию обеспечивает как хорошие показатели качества, так и асимптотическую устойчивость разнообразных объектов управления.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРОВ ПЕРЕВОДА
- 1. ВВЕДЕНИЕ
- 1.1. Общие сведения об интеллектуальном управлении
- 2. НЕЙРОННЫЕ СЕТИ
- 2.2. Алгоритм обратного распространения
- 2.2.2. Вывод алгоритма обратного распространения
- 2.2.2.2. Правило для скрытого слоя
- 2.2.3. Алгоритм обратного распространения: порядок реализации
- 2.2.4. Обсуждение алгоритма обратного распространения
- 2.3. Заключение
- 3. ТРАДИЦИОННЫЕ СХЕМЫ УПРАВЛЕНИЯ
- 3.2. ПИ- и ПИД-контроллеры с дискретным временем
- 3.3. Управление с самонастройкой
- 3.4. Самонастраивающиеся ПИ- и ПИД- контроллеры
- 3.5. ПИД-управление с самонастройкой: многомерный подход
- 3.5.1. Пример моделирования
- 3.6. Обобщенное прогнозирующее управление: некоторые теоретические аспекты
- 3.6.2. Модель объекта управления и решение задачи оптимизации
- 3.7. Управление на основе нечеткой логики
- 3.7.1. Краткие сведения по теории нечетких множеств и нечетких систем
- 3.7.2. Основная концепция нечеткого контроллера
- 3.8. Заключение
- 4. ТЕХНОЛОГИИ НЕЙРОННОГО УПРАВЛЕНИЯ
- 4.2. Общие сведения о нейронном управлении
- 4.2.1. Подходы к нейронному управлению
- 4.2.2. Общая схема управления
- 4.3. Последовательная схема нейронного управления
- 4.4. Расширение последовательной схемы нейронного управления
- 4.4.2. Нейроморфные структуры управления
- 4.4.3. Конфигурации обучения
- 4.4.4. Эффективное оперативное управление
- 4.4.5. Алгоритмы обучения
- 4.4.6. Оценка алгоритмов обучения на основе моделирования
- 4.5. Параллельная схема управления
- 4.6. Алгоритм обучения по ошибке обратной связи
- 4.7. Расширение применения нейроконтроллеров параллельного типа
- 4.7.2. Линеаризованная система управления
- 4.7.3. Система управления с нейронными сетями
- 4.7.4. Нелинейный алгоритм наблюдения для нейронной сети
- 4.7.5. Нелинейный контроллер для нейронной сети
- 4.7.6. Численное моделирование
- 4.8. Схема нейронного управления с самонастройкой
- 4.9. ПИД-нейроконтроллер с самонастройкой
- 4.9.1. Вывод уравнений ПИД-нейроконтроллера с самонастройкой
- 4.9.2. Примеры эмуляции
- 4.10. Схема нейронного управления с эмулятором и контроллером (схема обратного распространения во времени)
- 4.11. Заключение
- 5. ПРИЛОЖЕНИЯ НЕЙРОННОГО УПРАВЛЕНИЯ
- 5.2. Применение нейронного управления в системе регулирования процессов в водяной ванне и сравнение его с другими схемами управления
- 5.2.2. Система управления температурой водяной ванны
- 5.2.3. Схема нейронного управления
- 5.2.4. Схема управления на основе нечеткой логики
- 5.2.5. Схема обобщенного прогнозирующего управления
- 5.2.6. Экспериментальные данные и их анализ
- 5.2.7. Заключение
- 5.3. Система стабилизации инвертированного маятника на основе нейронных сетей
- 5.3.2. Система стабилизации инвертированного маятника
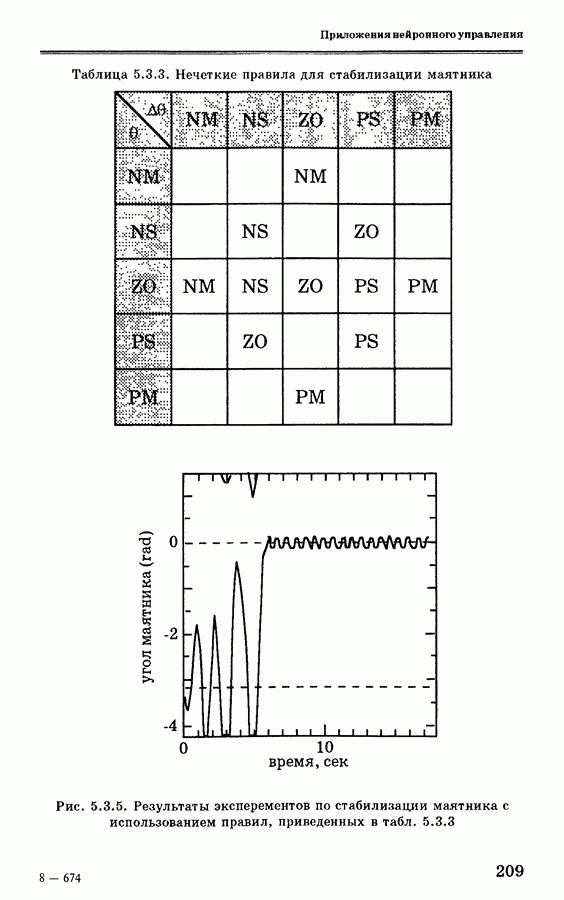
- 5.3.3. Инициализация поворотного управления с использованием нечеткой логики
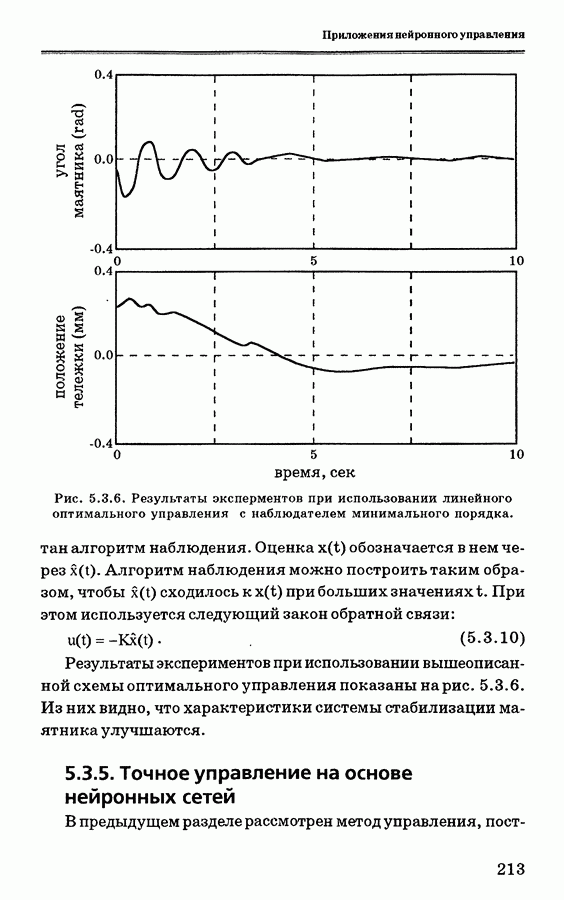
- 5.3.4. Применение стратегии оптимального управления для стабилизации маятника
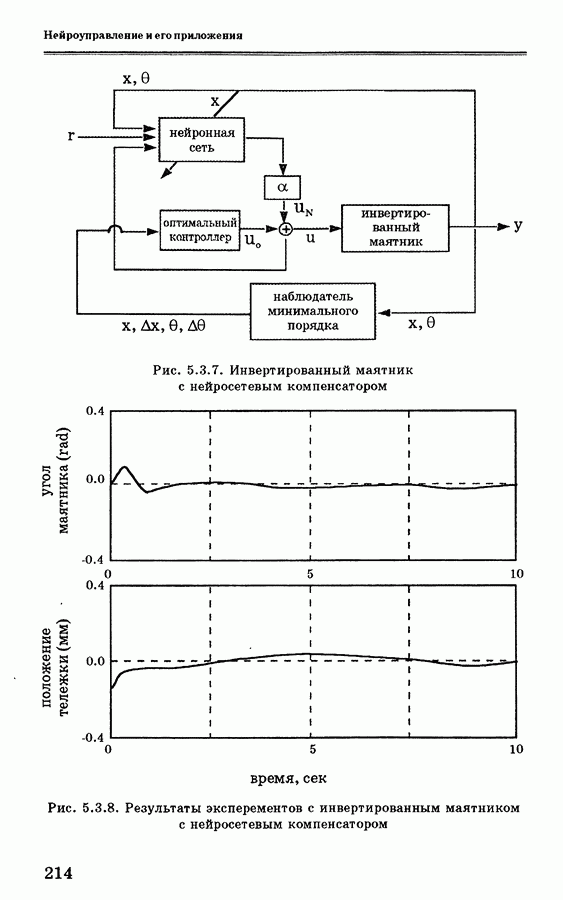
- 5.3.5. Точное управление на основе нейронных сетей
- 5.3.6. Заключение
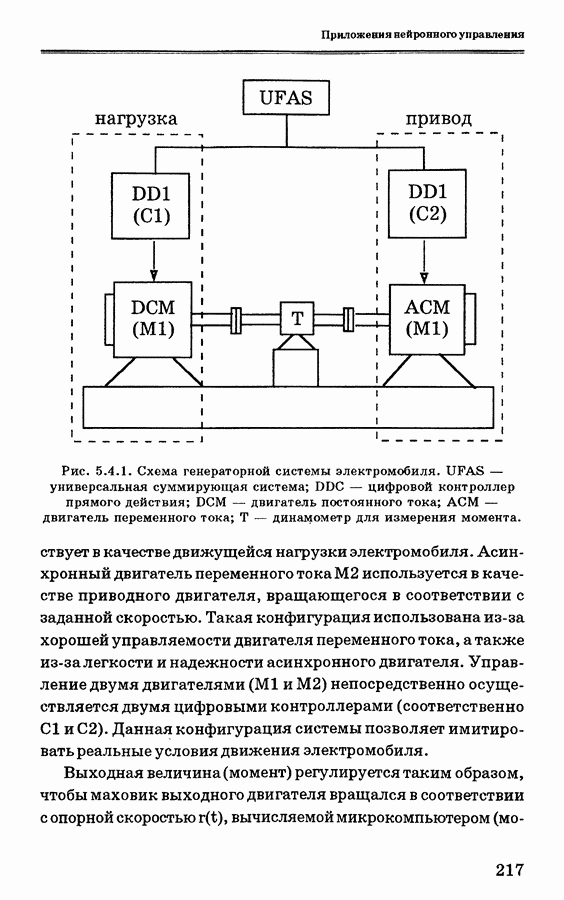
- 5.4. Применение ПИД-нейроконтроллера с самонастройкой для управления скоростью электромобиля
- 5.4.2. Система управления электромобилем
- 5.4.3. ПИД-нейроконтроллер с самонастройкой
- 5.4.4. Применение нейронной сети для управления скоростью электромобиля
- 5.4.5. Заключение
- 5.5. Применение нейронных сетей для управления печью
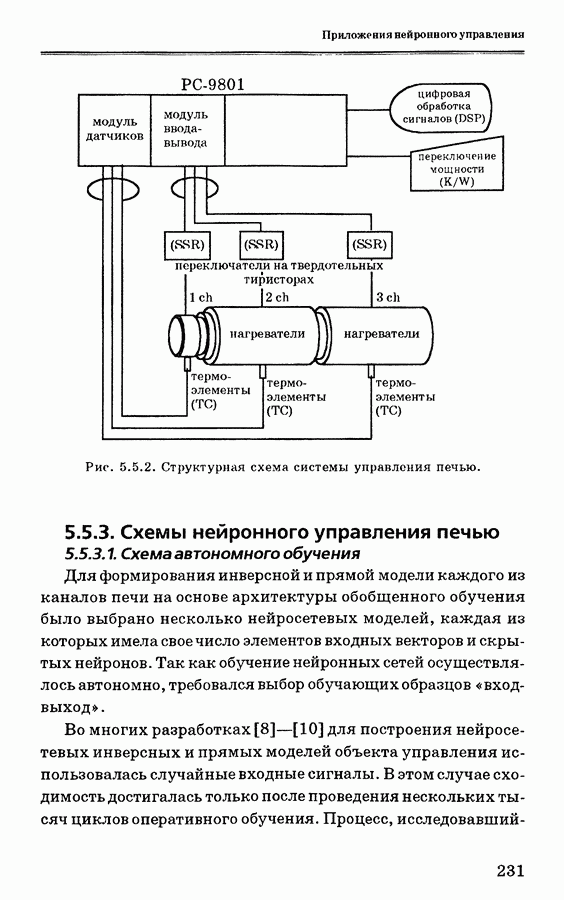
- 5.5.2. Система управления печью
- 5.5.3. Схемы нейронного управления печью
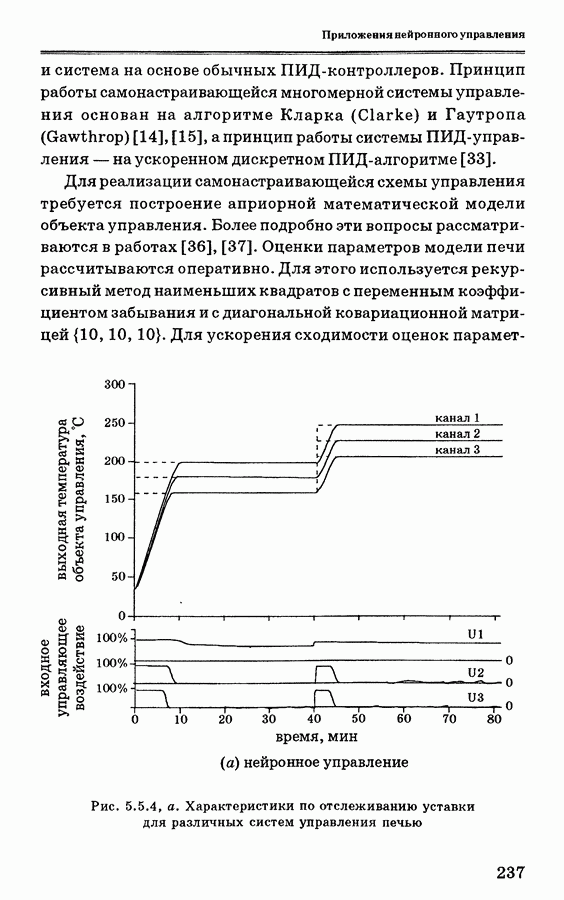
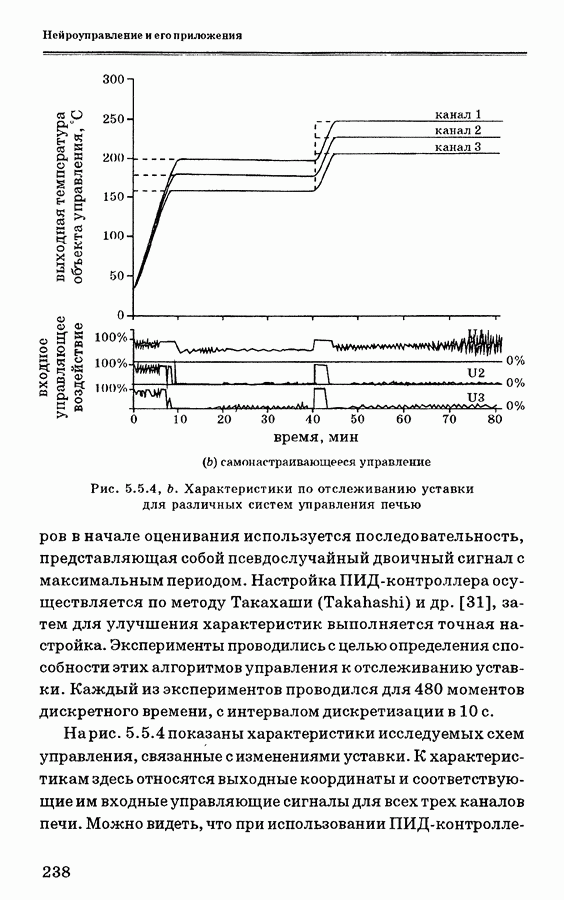
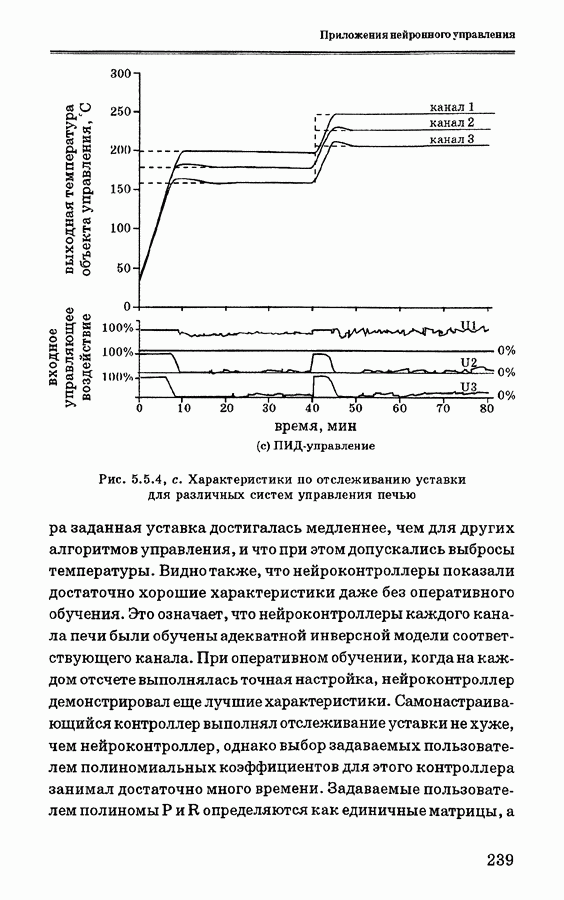
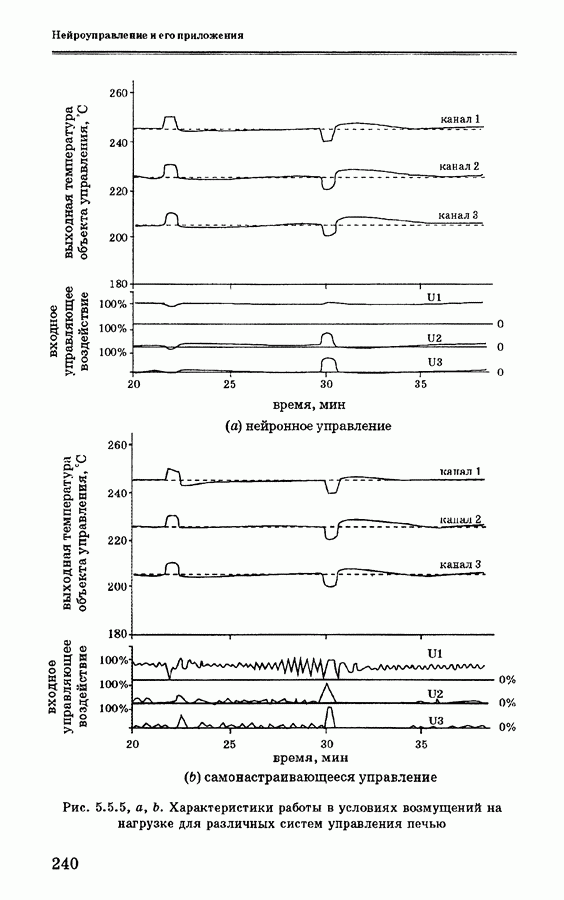
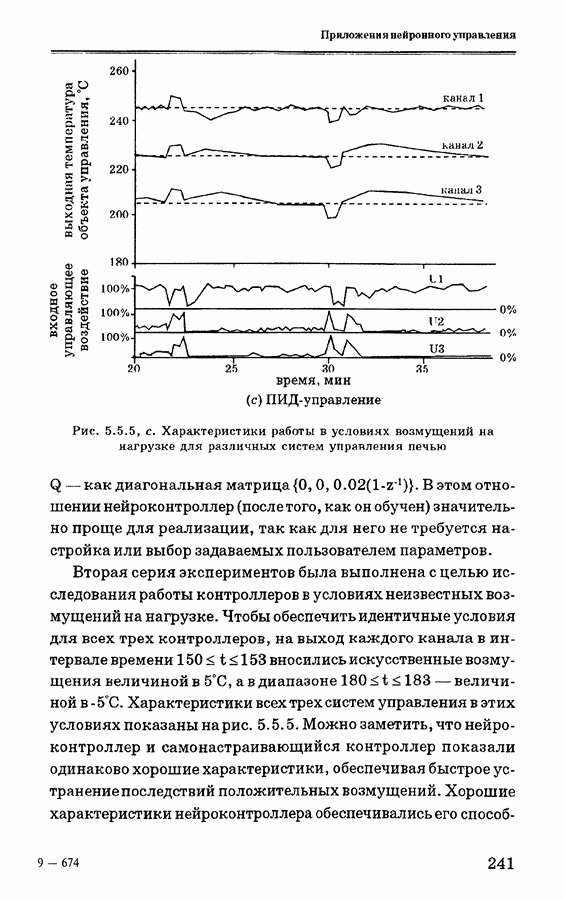
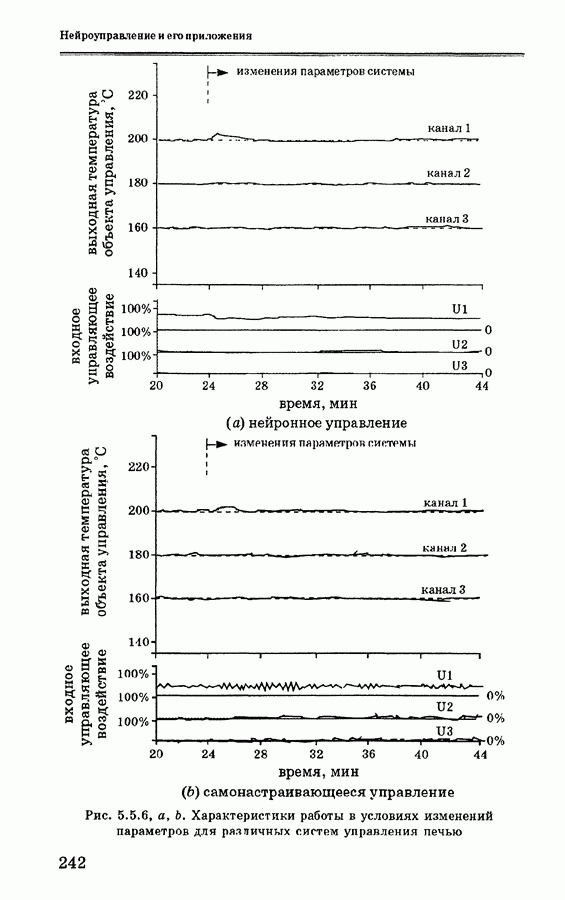
- 5.5.4. Анализ экспериментальных данных
- 5.6. Заключительные замечания и выводы
- Литература
- ЛИСТИНГ ПРОГРАММЫ