| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
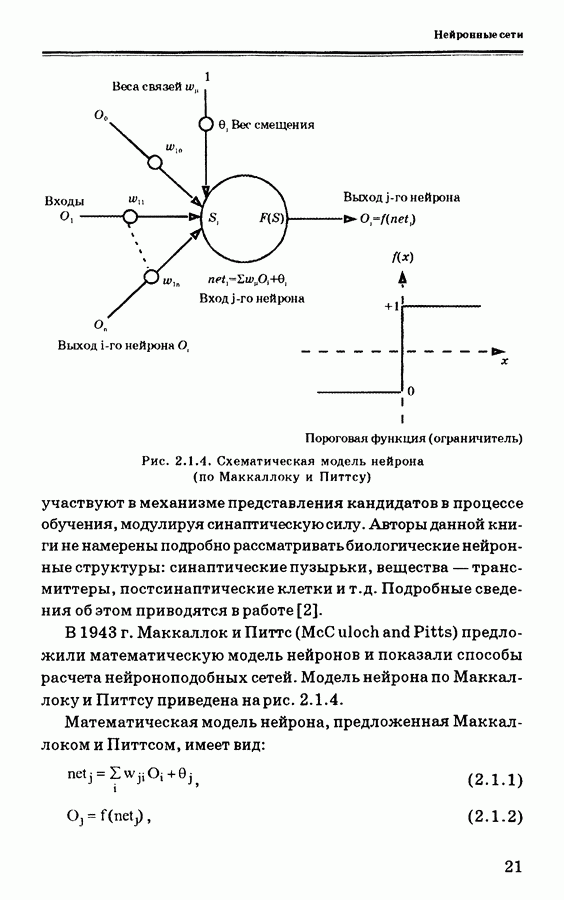
2.2.2. Вывод алгоритма обратного распространения
Вывод строится на основе одного из градиентных методов, например метода наискорейшего спуска. Здесь показан процесс адаптации весов связей между слоями в многослойной нейронной сети. Зададим сначала функцию ошибки и критерий адаптации весов, пропорциональный отношению производной меры ошибки к каждому из весов. Получим сначала алгоритм обратного распространения для конкретного образа  т.е. найдем минимизирующую последовательность
т.е. найдем минимизирующую последовательность  Для простоты будем опускать индекс
Для простоты будем опускать индекс 
Тогда

2.2.2.1. Правило для выходного слоя
В соответствии с методом наискорейшего спуска

где  — необходимое изменение веса связи
— необходимое изменение веса связи  т.е.
т.е.

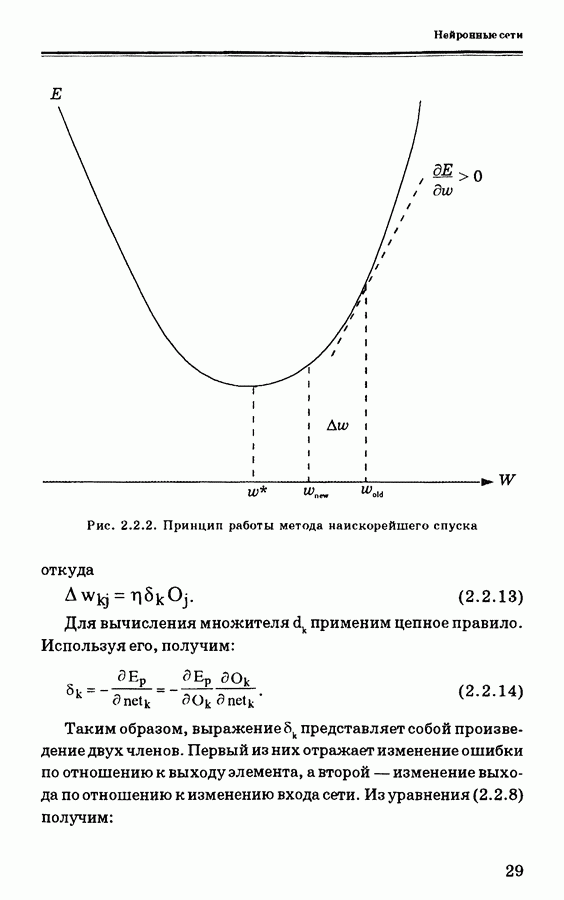
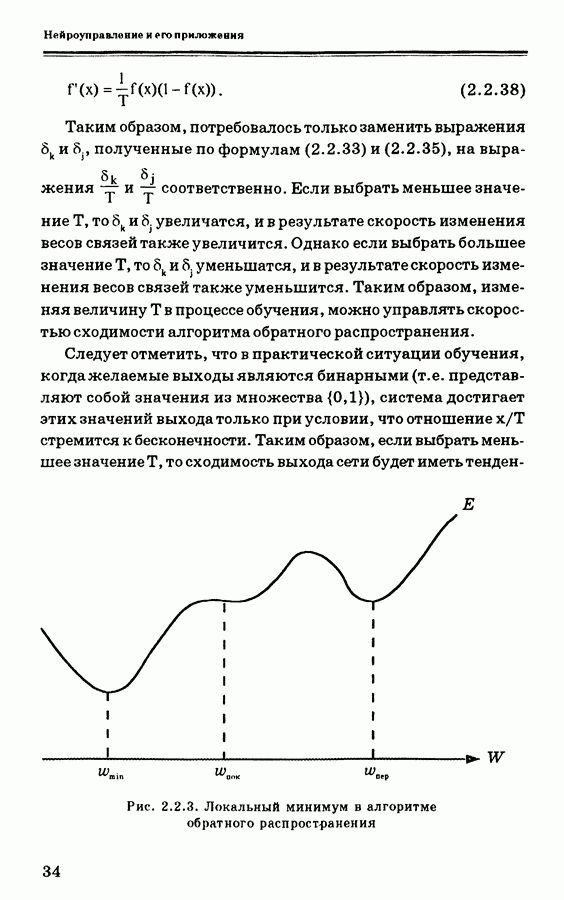
Такое изменение показано на рис. 2.2.2. Следует обратить внимание, что метод наискорейшего спуска может сходиться к локальному минимуму, как показано на рис. 2.2.3. Поэтому возьмем

где  — скорость обучения.
— скорость обучения.
Введем величину обобщенного сигнала ошибки  задаваемую выражением
задаваемую выражением

Затем, используя известное цепное правило, получим:

Это означает, что выражение может быть представлено как произведение двух членов. Один из них представляет собой изменение ошибки в зависимости от изменения входного сигнала сети, а второй — влияние конкретного веса связи на входной сигнал сети. Из выражения (2.2.2) получим:

Рис. 2.2.2. (см. скан) Принцип работы метода наискорейшего спуска
откуда

Для вычисления множителя  применим цепное правило. Используя его, получим:
применим цепное правило. Используя его, получим:

Таким образом, выражение  представляет собой произведение двух членов. Первый из них отражает изменение ошибки по отношению к выходу элемента, а второй — изменение выхода по отношению к изменению входа сети. Из уравнения (2.2.8) получим:
представляет собой произведение двух членов. Первый из них отражает изменение ошибки по отношению к выходу элемента, а второй — изменение выхода по отношению к изменению входа сети. Из уравнения (2.2.8) получим:

а из выражения (2.2.1) -

где  — производная от
— производная от  по х.
по х.
Из выражения (2.2.5) получим:

откуда

Таким образом, имеем:

| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРОВ ПЕРЕВОДА
- 1. ВВЕДЕНИЕ
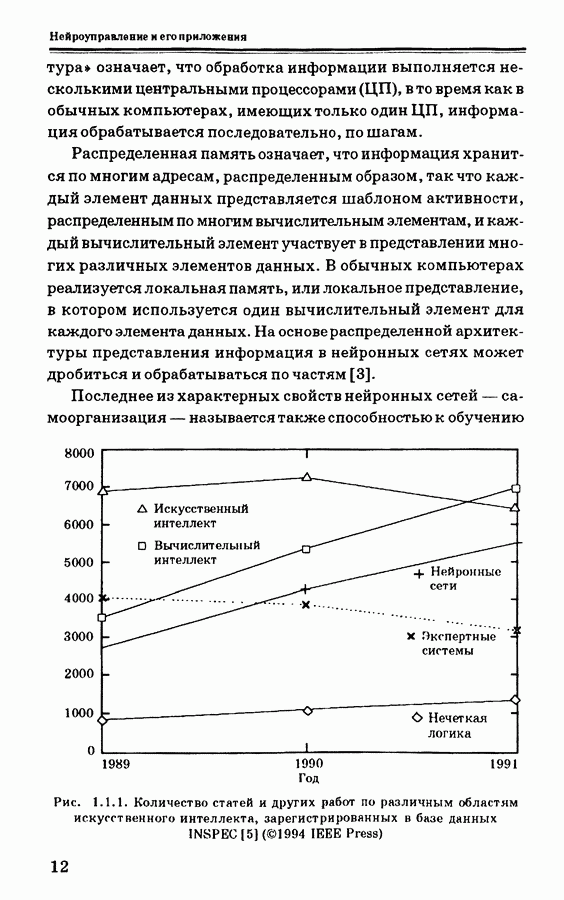
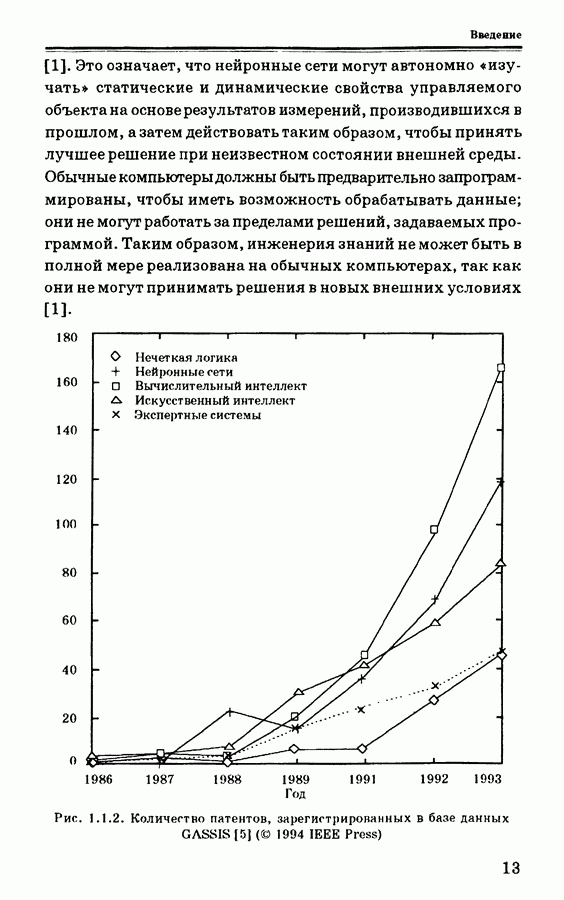
- 1.1. Общие сведения об интеллектуальном управлении
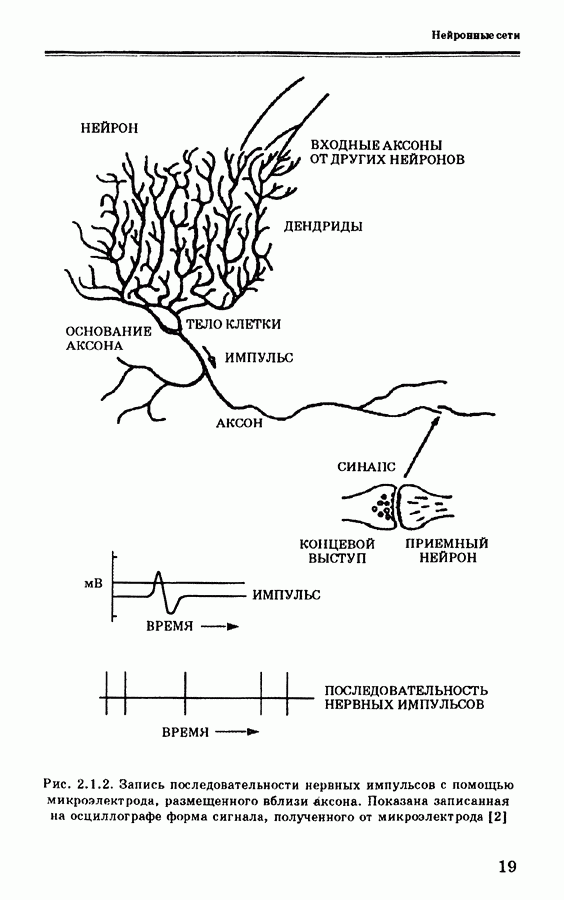
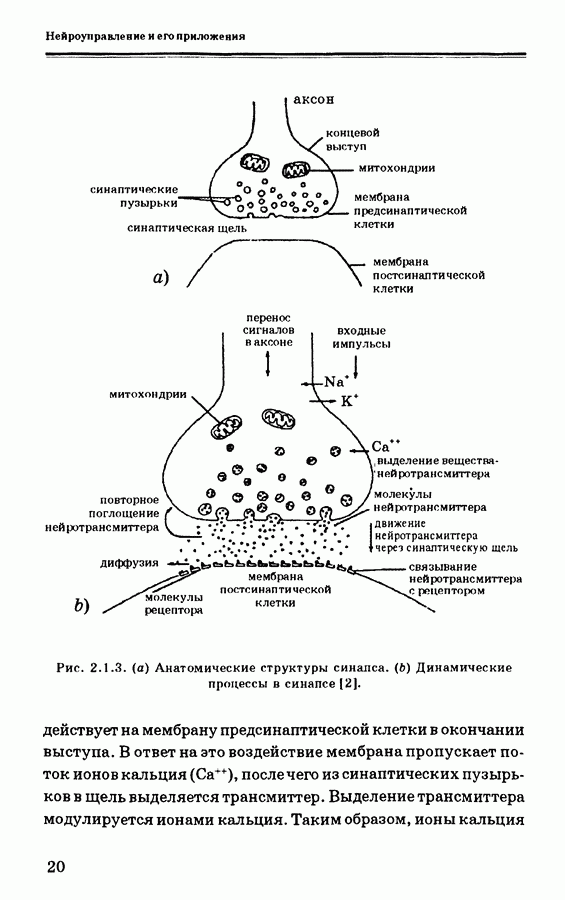
- 2. НЕЙРОННЫЕ СЕТИ
- 2.2. Алгоритм обратного распространения
- 2.2.2. Вывод алгоритма обратного распространения
- 2.2.2.2. Правило для скрытого слоя
- 2.2.3. Алгоритм обратного распространения: порядок реализации
- 2.2.4. Обсуждение алгоритма обратного распространения
- 2.3. Заключение
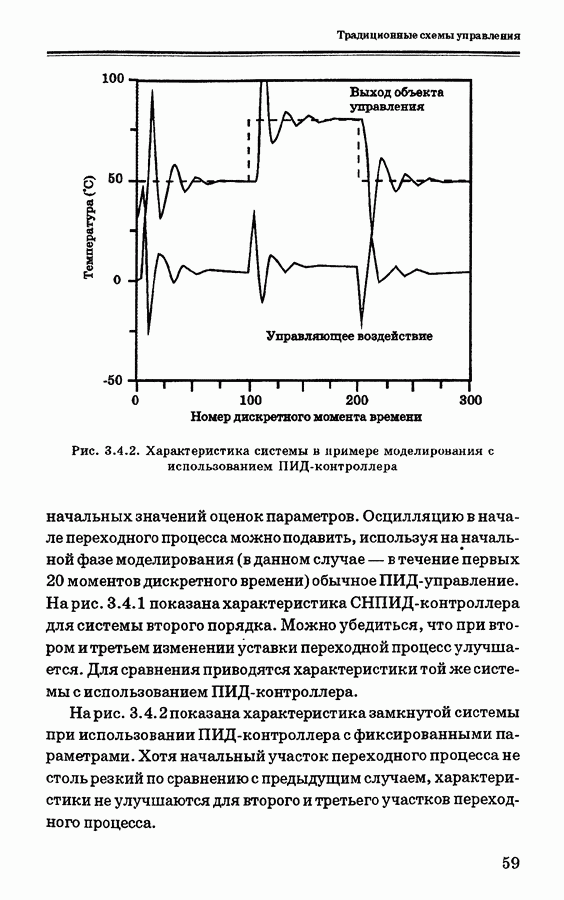
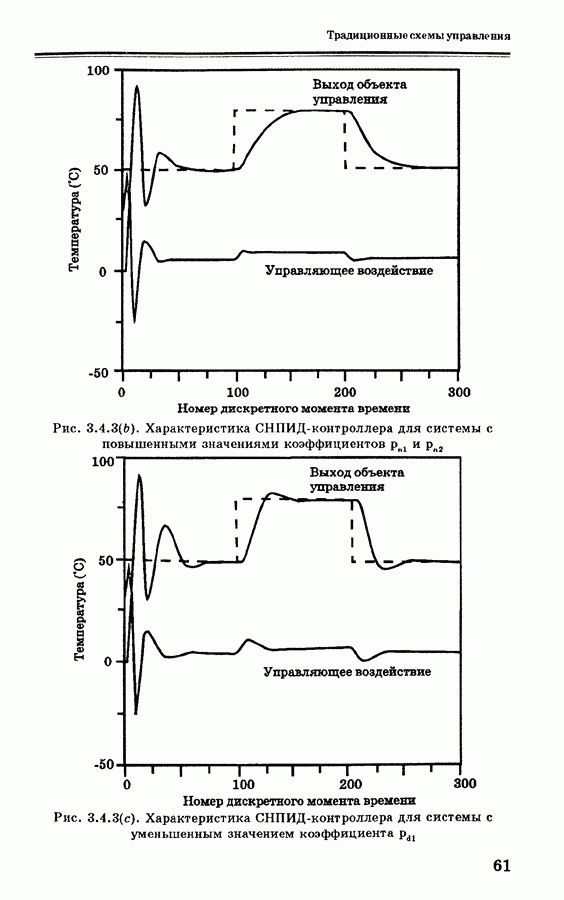
- 3. ТРАДИЦИОННЫЕ СХЕМЫ УПРАВЛЕНИЯ
- 3.2. ПИ- и ПИД-контроллеры с дискретным временем
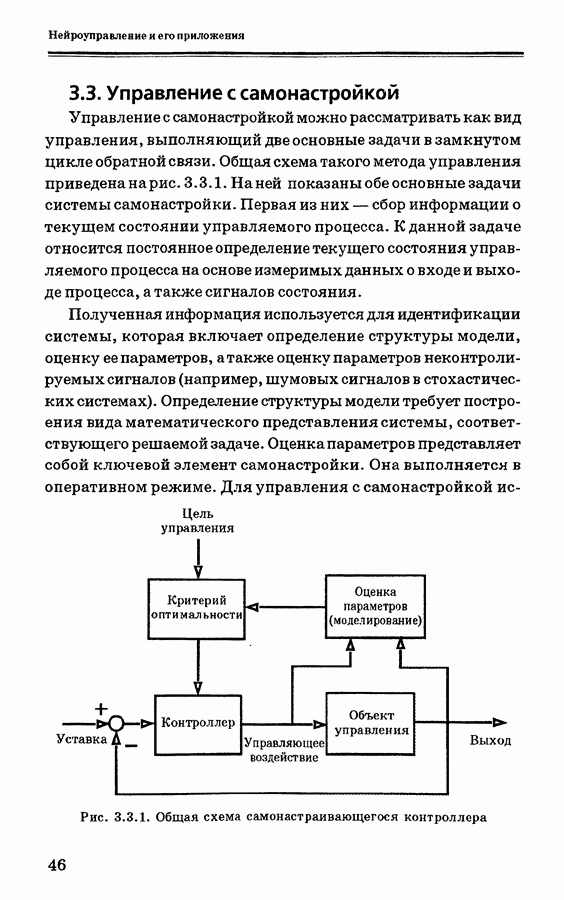
- 3.3. Управление с самонастройкой
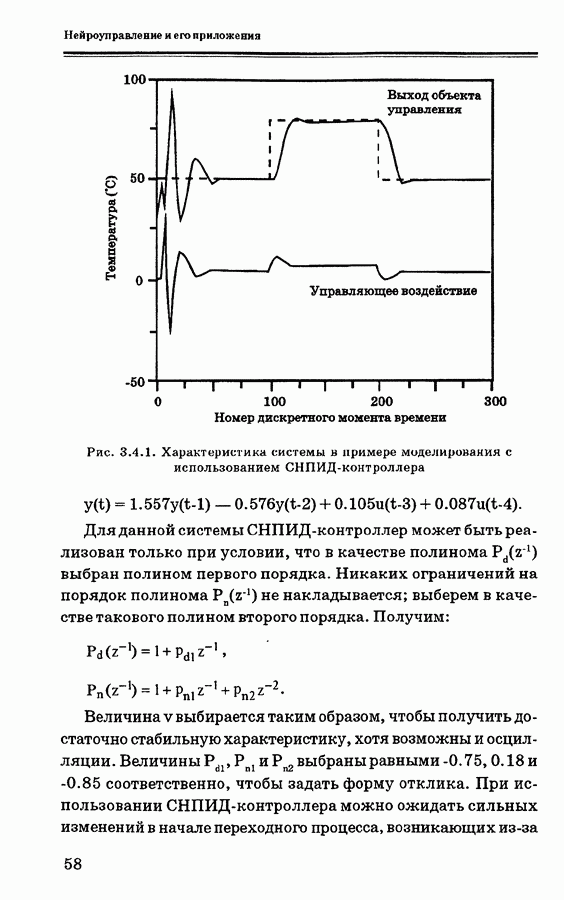
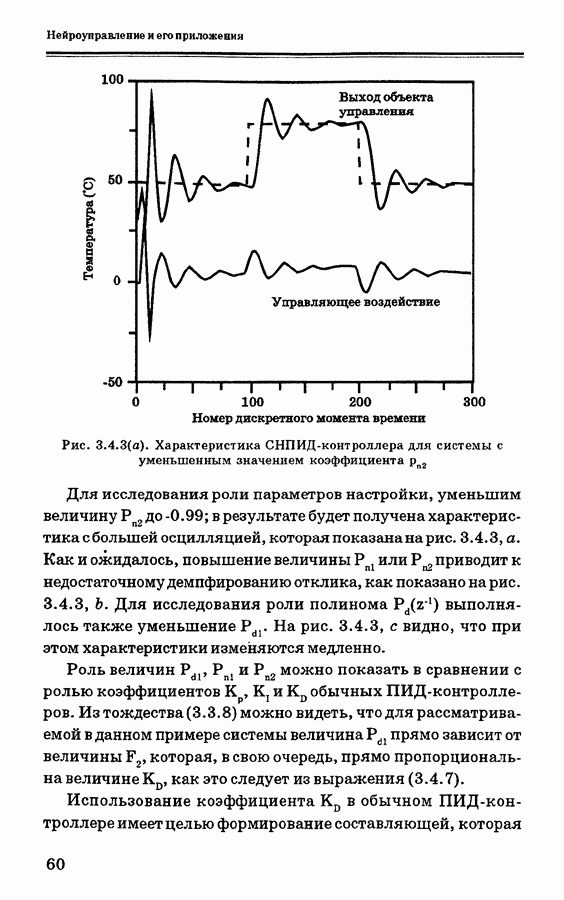
- 3.4. Самонастраивающиеся ПИ- и ПИД- контроллеры
- 3.5. ПИД-управление с самонастройкой: многомерный подход
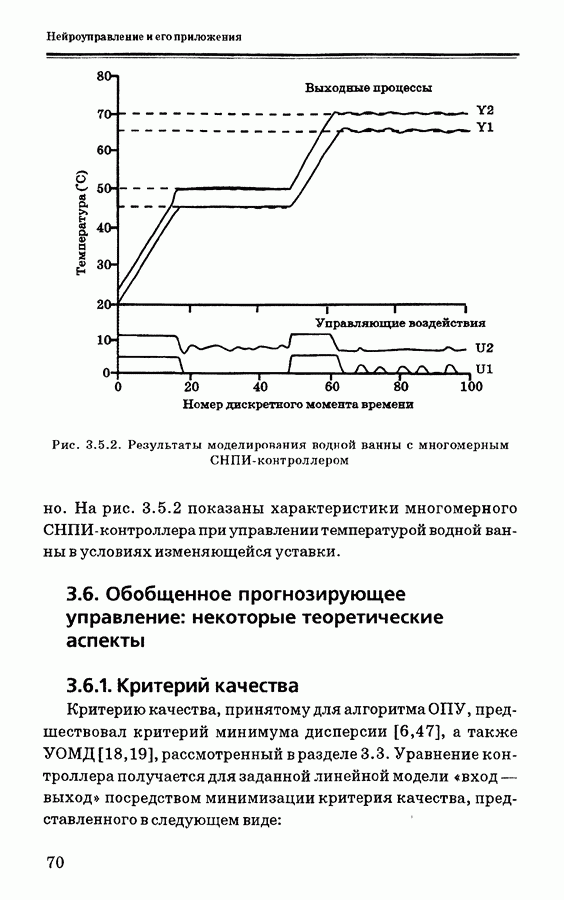
- 3.5.1. Пример моделирования
- 3.6. Обобщенное прогнозирующее управление: некоторые теоретические аспекты
- 3.6.2. Модель объекта управления и решение задачи оптимизации
- 3.7. Управление на основе нечеткой логики
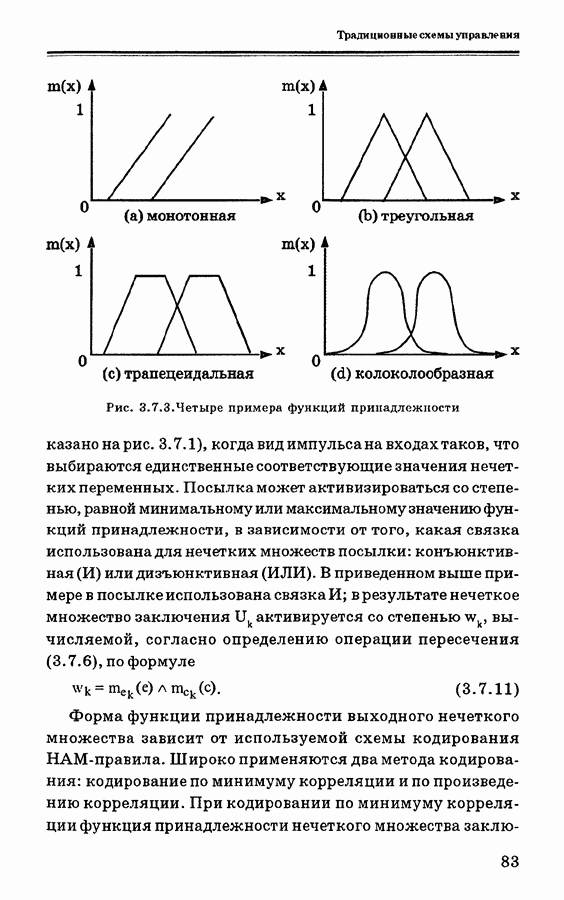
- 3.7.1. Краткие сведения по теории нечетких множеств и нечетких систем
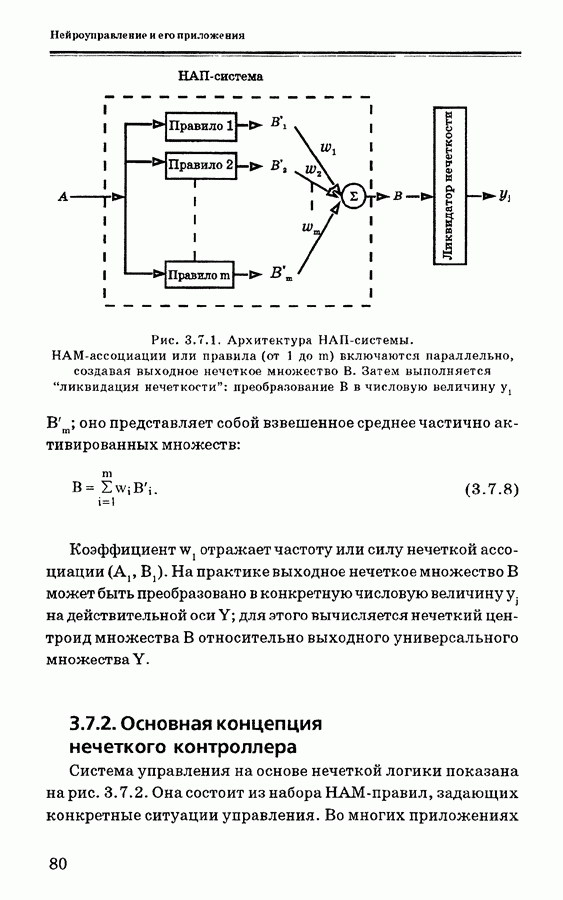
- 3.7.2. Основная концепция нечеткого контроллера
- 3.8. Заключение
- 4. ТЕХНОЛОГИИ НЕЙРОННОГО УПРАВЛЕНИЯ
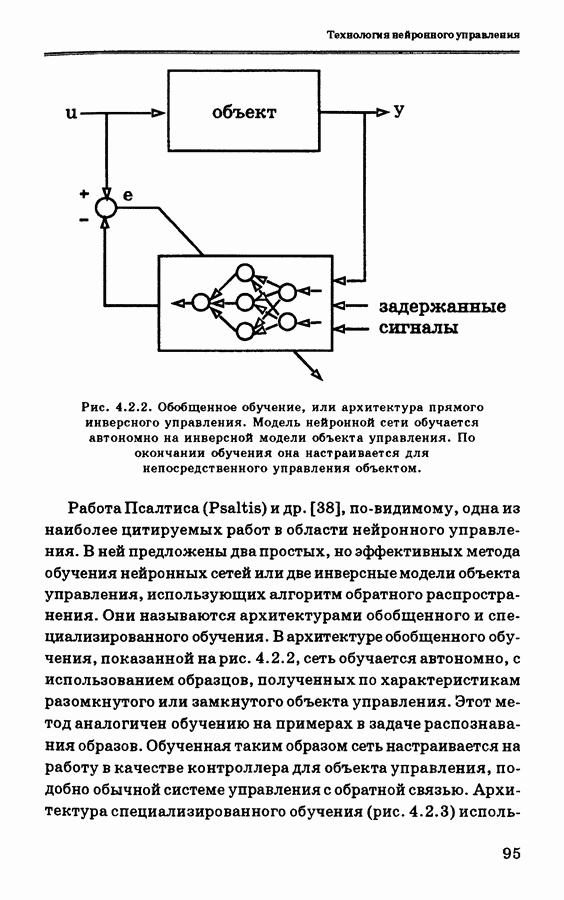
- 4.2. Общие сведения о нейронном управлении
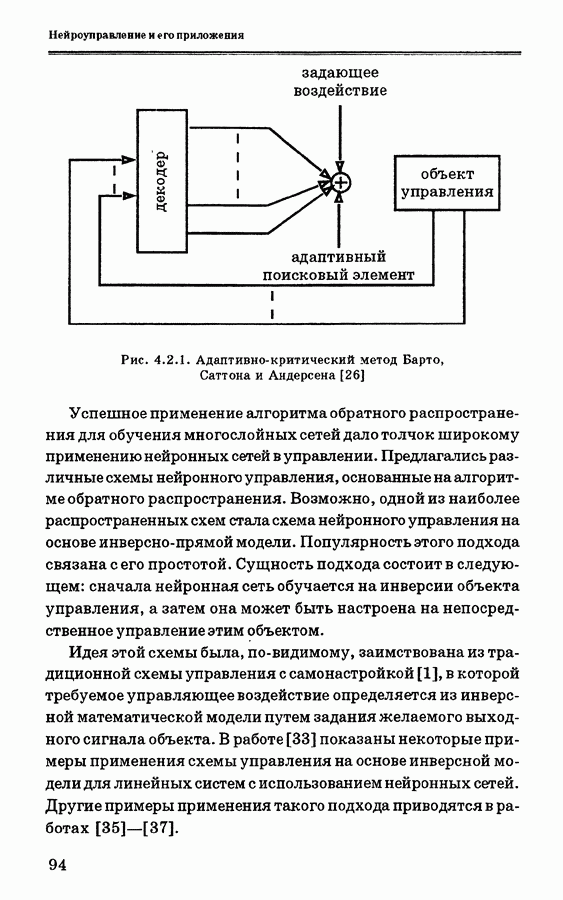
- 4.2.1. Подходы к нейронному управлению
- 4.2.2. Общая схема управления
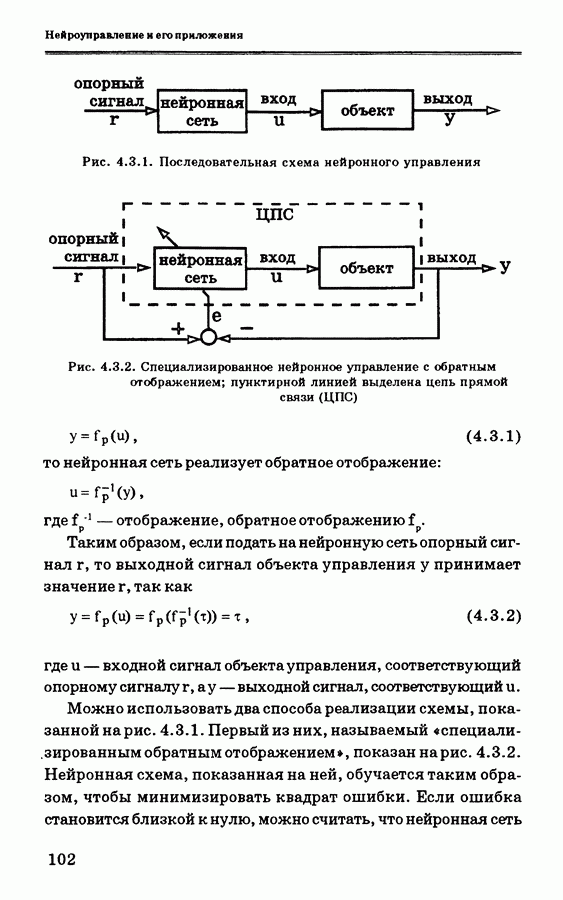
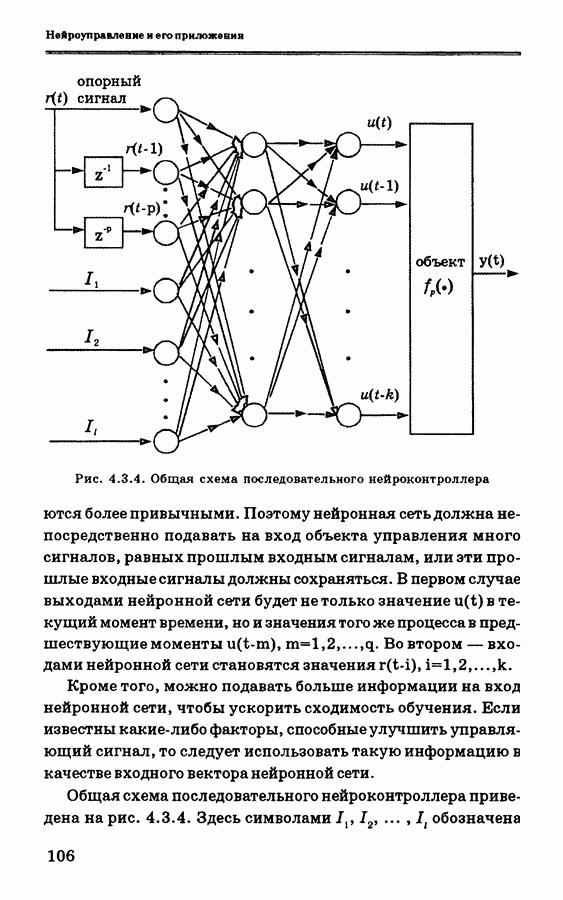
- 4.3. Последовательная схема нейронного управления
- 4.4. Расширение последовательной схемы нейронного управления
- 4.4.2. Нейроморфные структуры управления
- 4.4.3. Конфигурации обучения
- 4.4.4. Эффективное оперативное управление
- 4.4.5. Алгоритмы обучения
- 4.4.6. Оценка алгоритмов обучения на основе моделирования
- 4.5. Параллельная схема управления
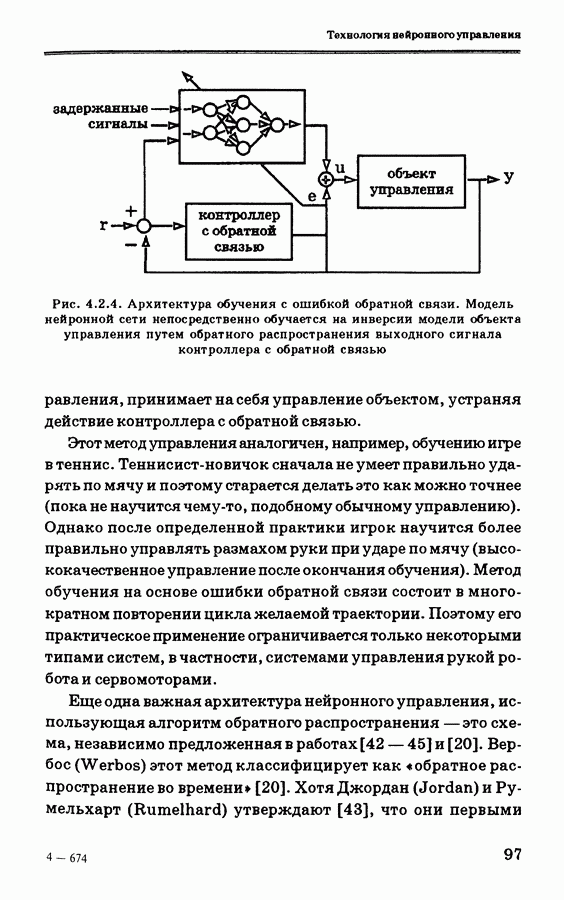
- 4.6. Алгоритм обучения по ошибке обратной связи
- 4.7. Расширение применения нейроконтроллеров параллельного типа
- 4.7.2. Линеаризованная система управления
- 4.7.3. Система управления с нейронными сетями
- 4.7.4. Нелинейный алгоритм наблюдения для нейронной сети
- 4.7.5. Нелинейный контроллер для нейронной сети
- 4.7.6. Численное моделирование
- 4.8. Схема нейронного управления с самонастройкой
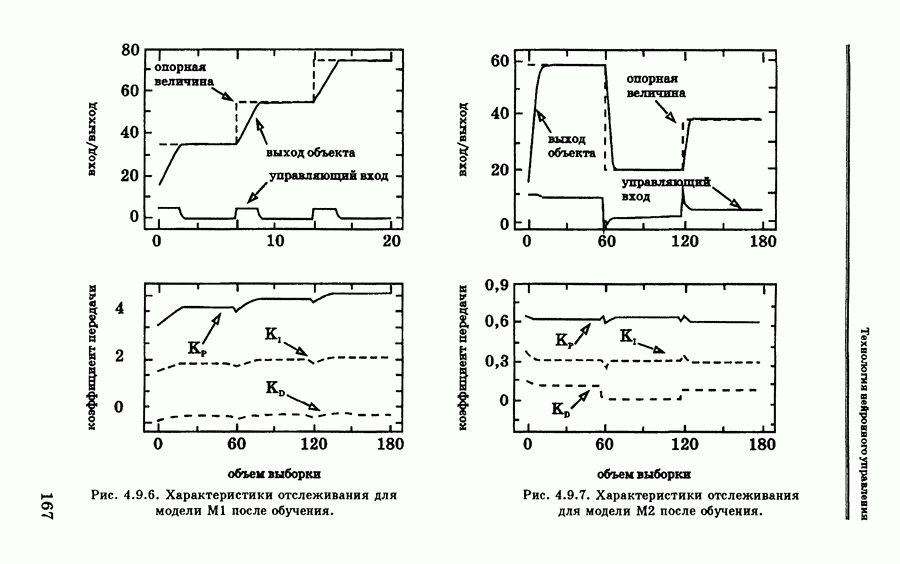
- 4.9. ПИД-нейроконтроллер с самонастройкой
- 4.9.1. Вывод уравнений ПИД-нейроконтроллера с самонастройкой
- 4.9.2. Примеры эмуляции
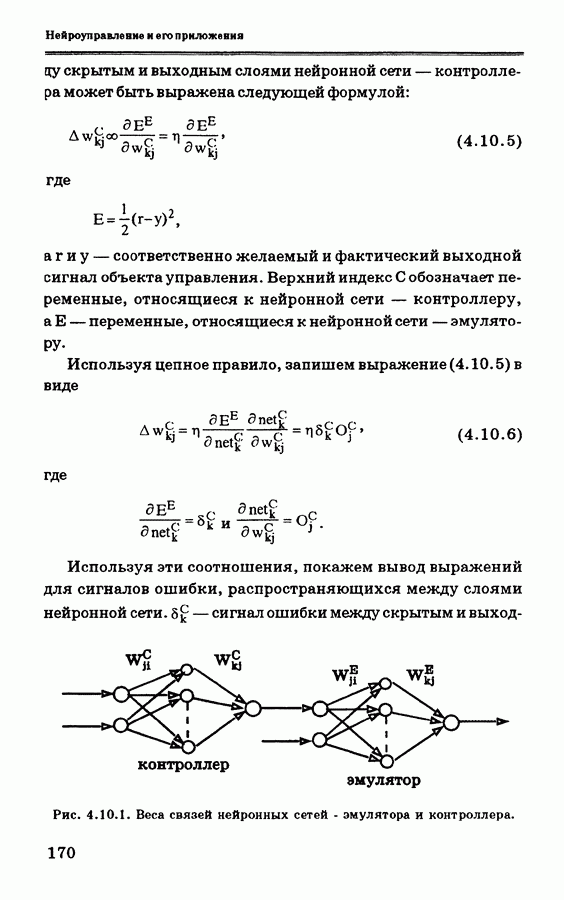
- 4.10. Схема нейронного управления с эмулятором и контроллером (схема обратного распространения во времени)
- 4.11. Заключение
- 5. ПРИЛОЖЕНИЯ НЕЙРОННОГО УПРАВЛЕНИЯ
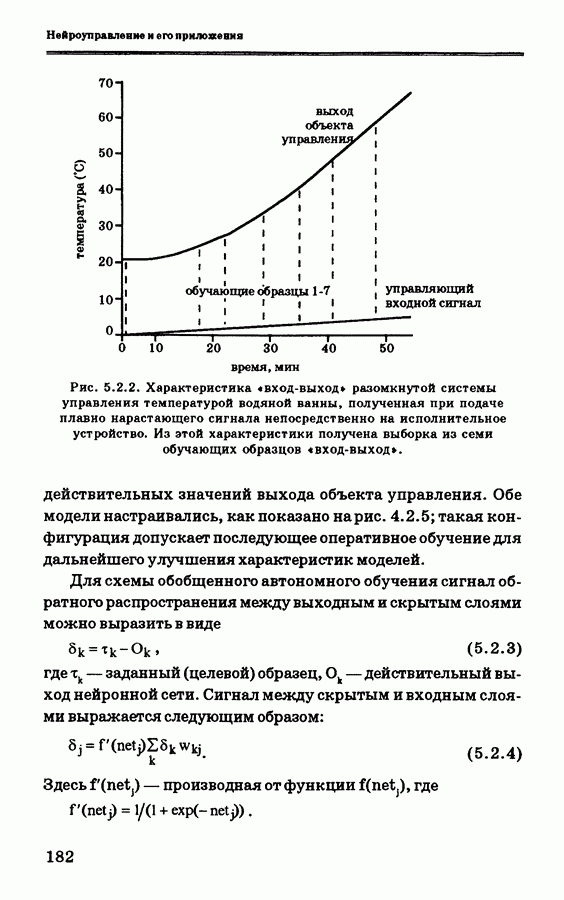
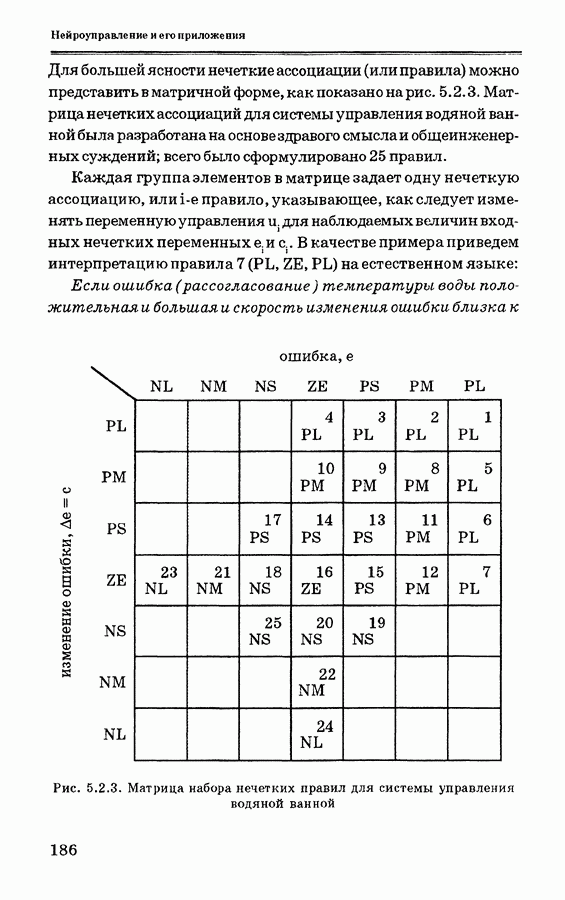
- 5.2. Применение нейронного управления в системе регулирования процессов в водяной ванне и сравнение его с другими схемами управления
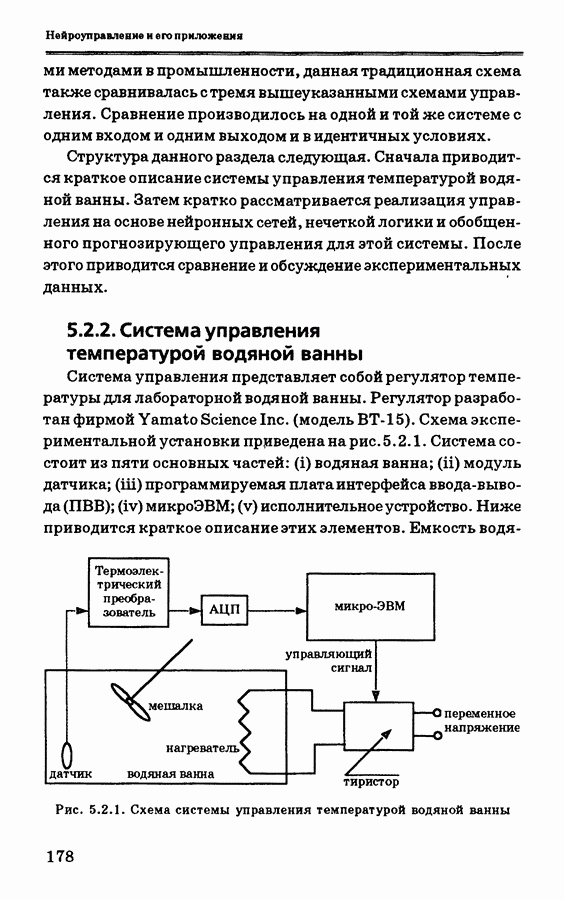
- 5.2.2. Система управления температурой водяной ванны
- 5.2.3. Схема нейронного управления
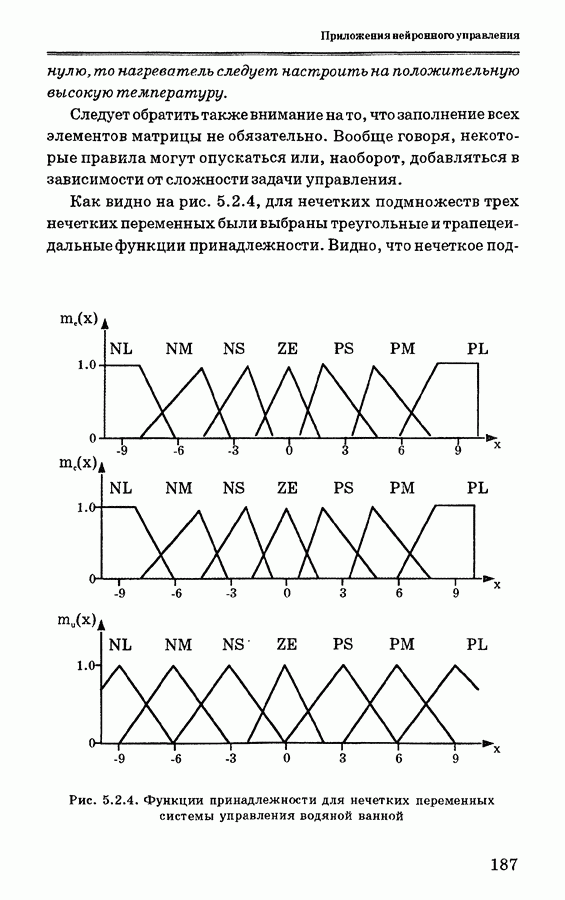
- 5.2.4. Схема управления на основе нечеткой логики
- 5.2.5. Схема обобщенного прогнозирующего управления
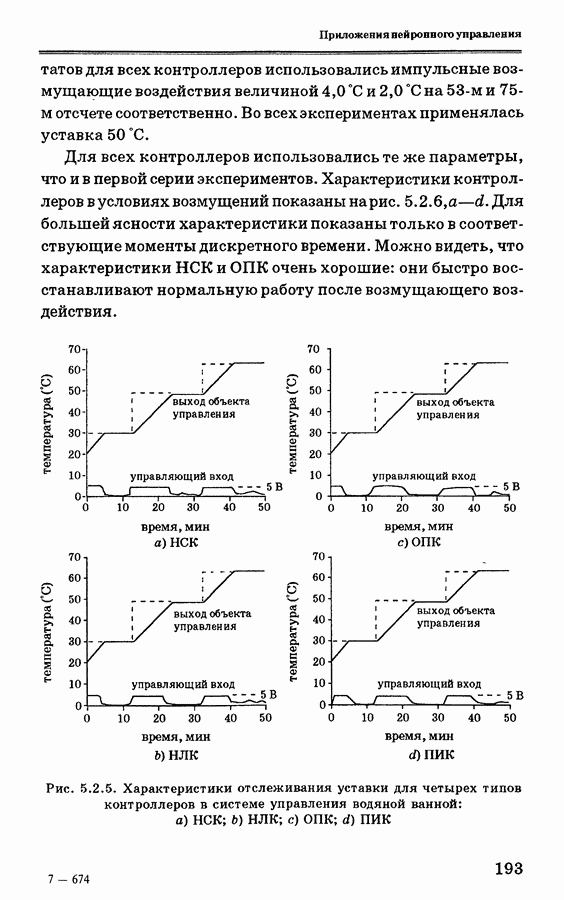
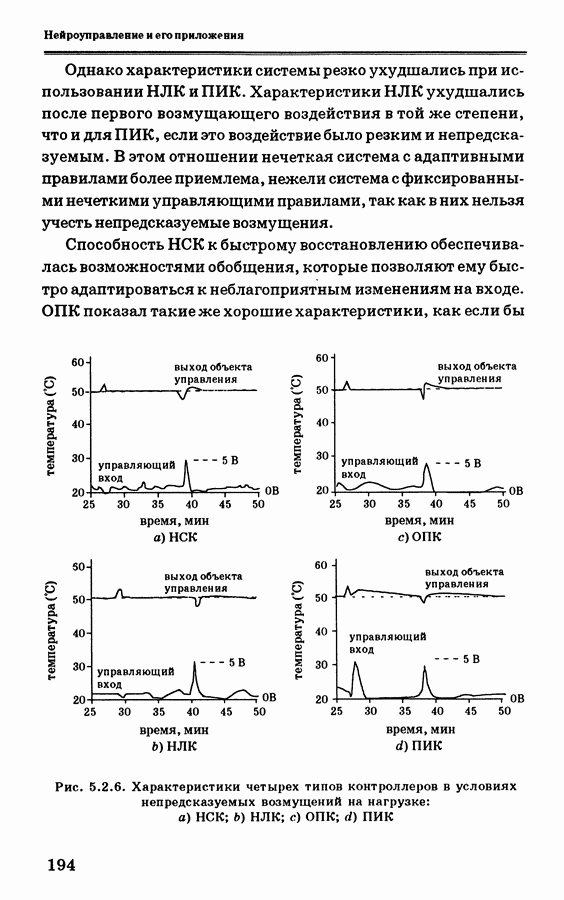
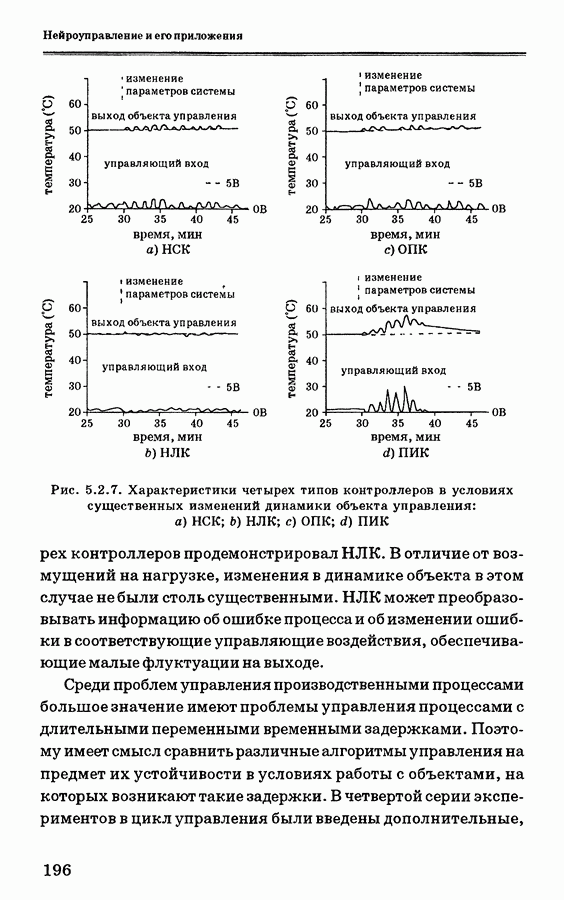
- 5.2.6. Экспериментальные данные и их анализ
- 5.2.7. Заключение
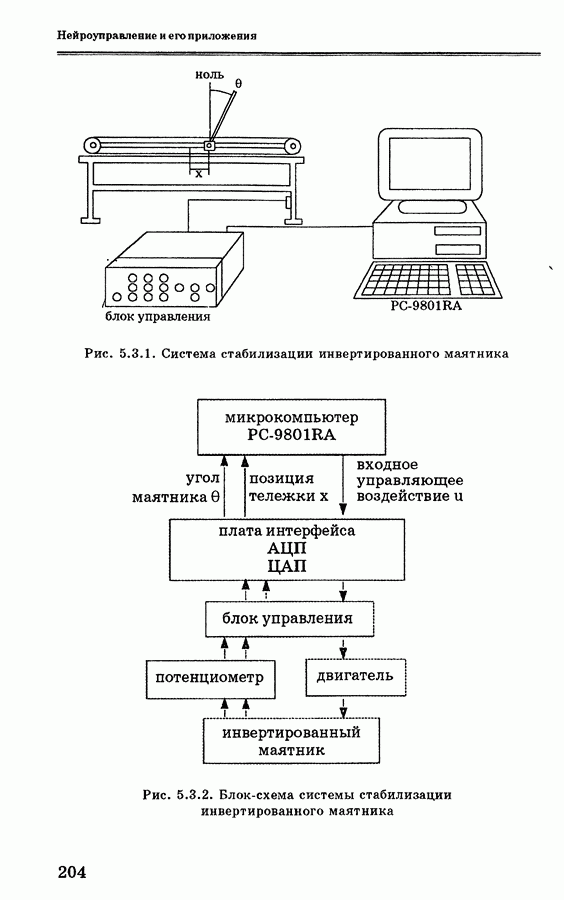
- 5.3. Система стабилизации инвертированного маятника на основе нейронных сетей
- 5.3.2. Система стабилизации инвертированного маятника
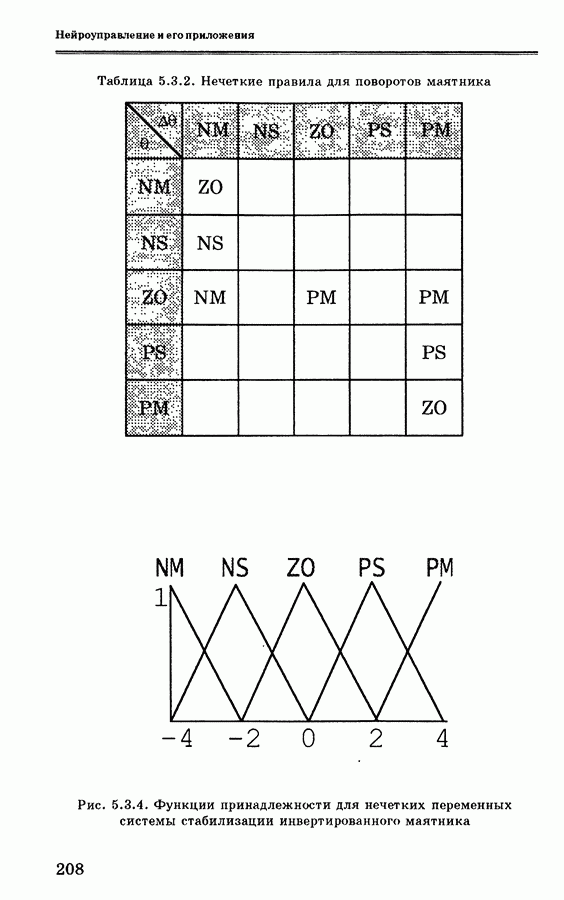
- 5.3.3. Инициализация поворотного управления с использованием нечеткой логики
- 5.3.4. Применение стратегии оптимального управления для стабилизации маятника
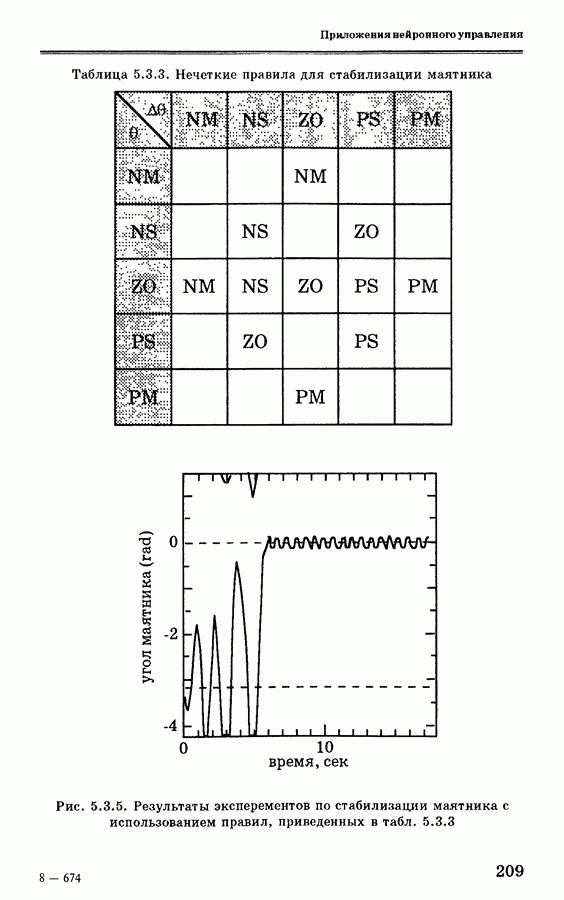
- 5.3.5. Точное управление на основе нейронных сетей
- 5.3.6. Заключение
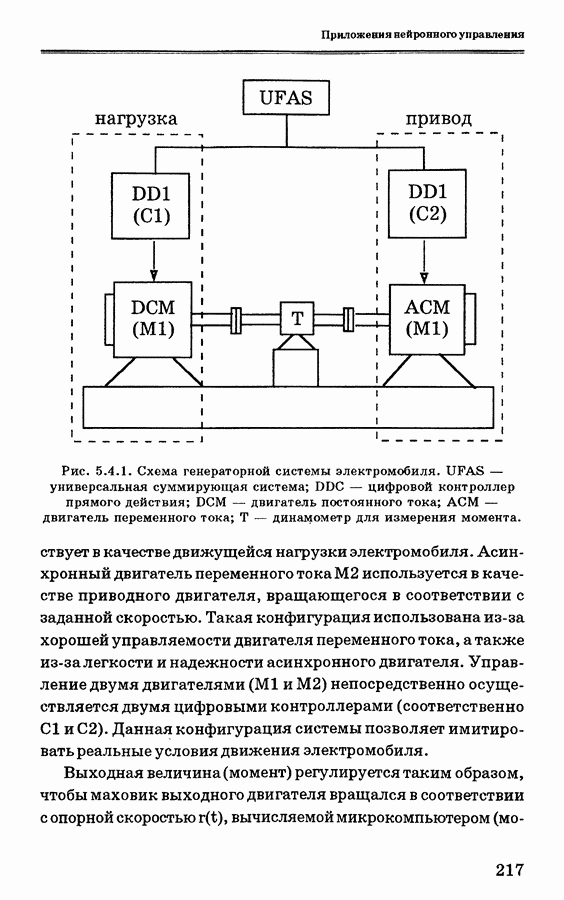
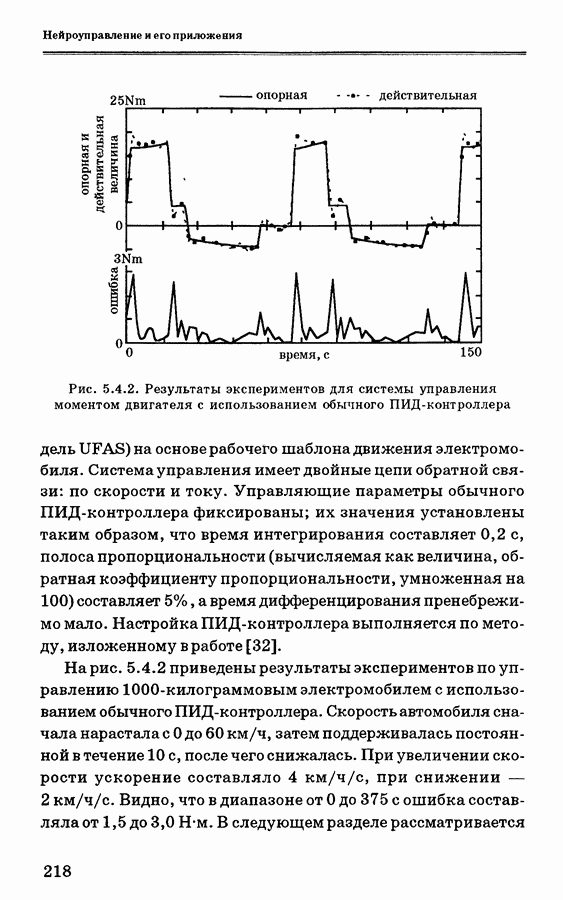
- 5.4. Применение ПИД-нейроконтроллера с самонастройкой для управления скоростью электромобиля
- 5.4.2. Система управления электромобилем
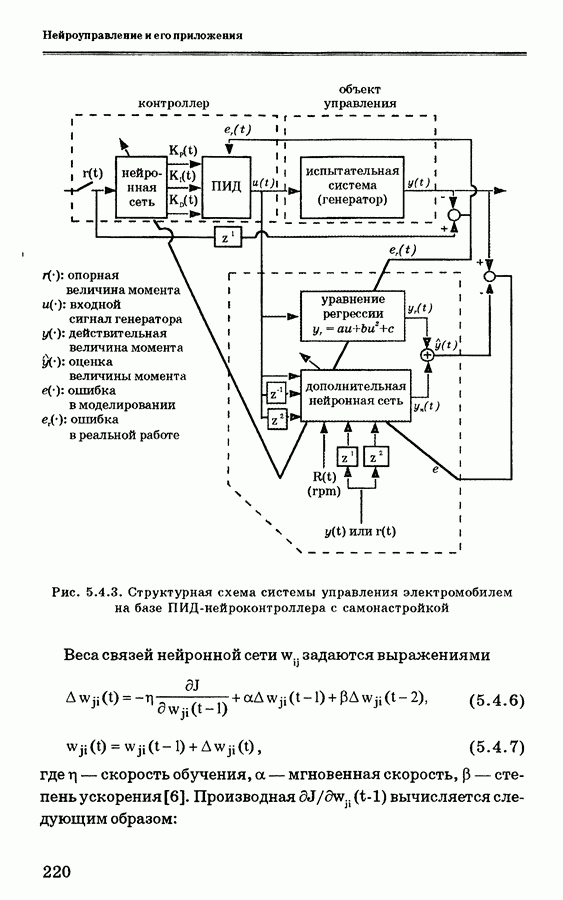
- 5.4.3. ПИД-нейроконтроллер с самонастройкой
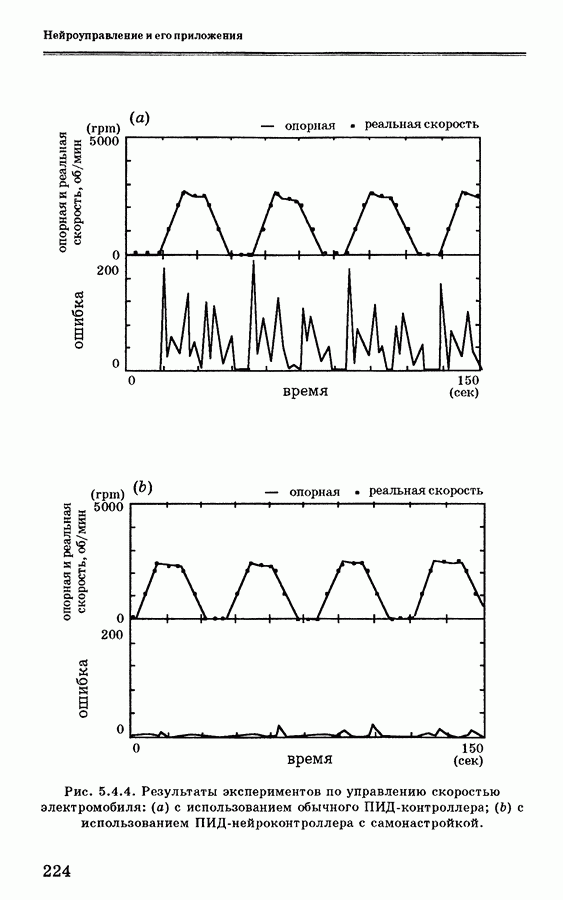
- 5.4.4. Применение нейронной сети для управления скоростью электромобиля
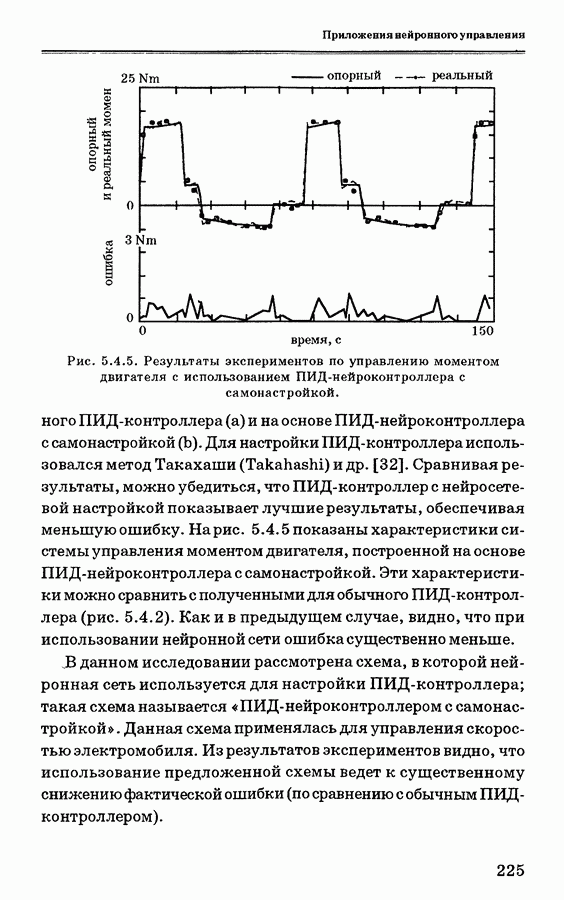
- 5.4.5. Заключение
- 5.5. Применение нейронных сетей для управления печью
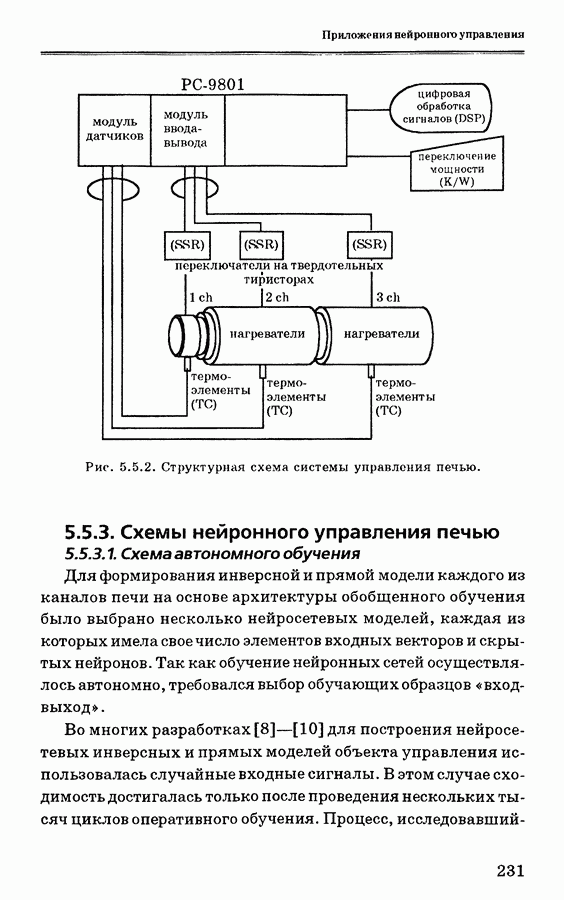
- 5.5.2. Система управления печью
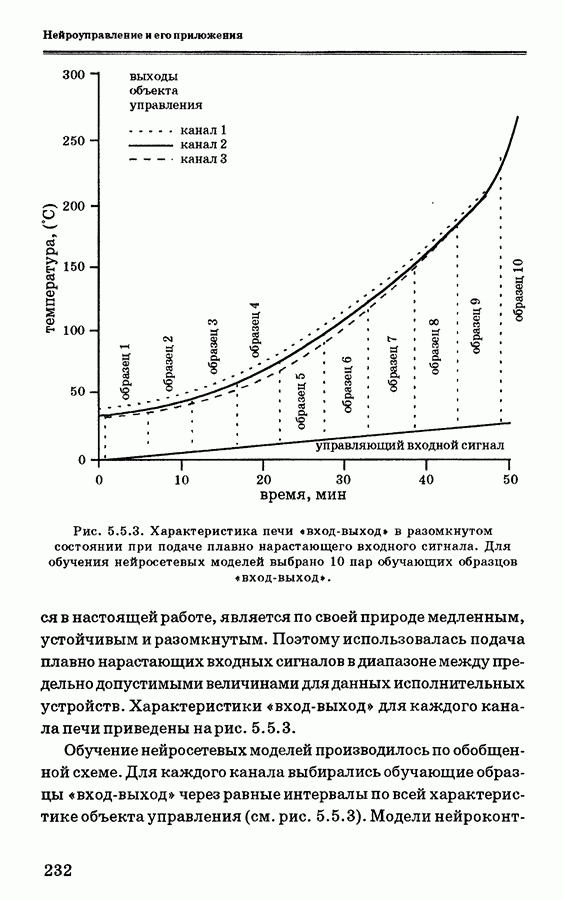
- 5.5.3. Схемы нейронного управления печью
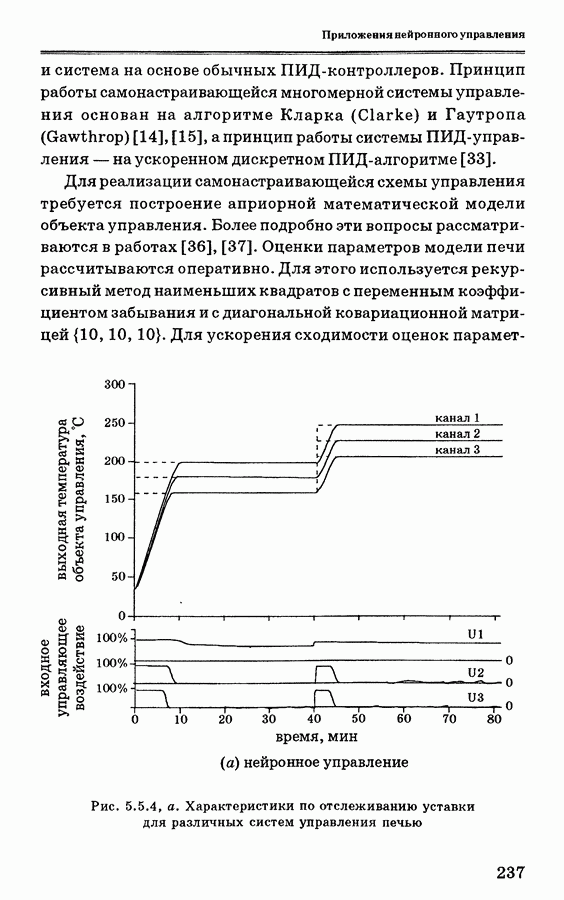
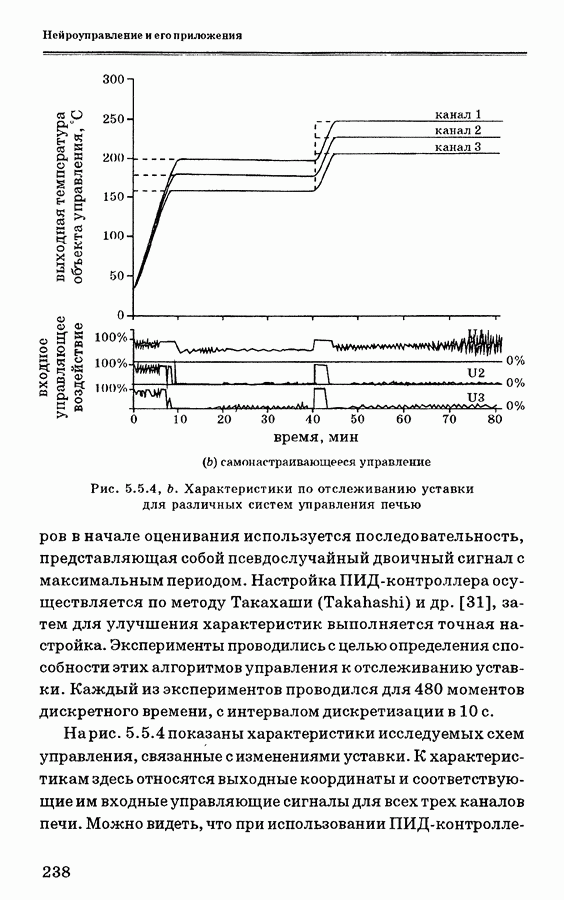
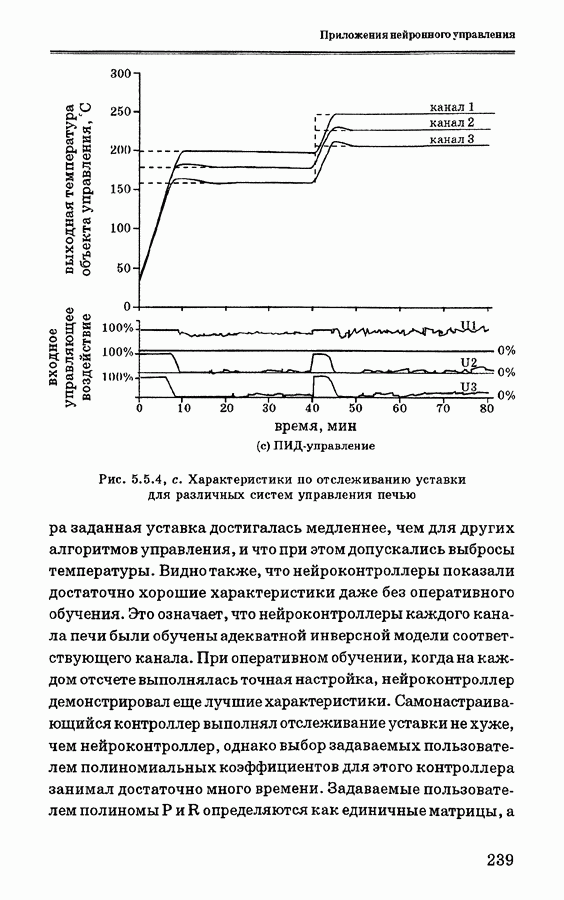
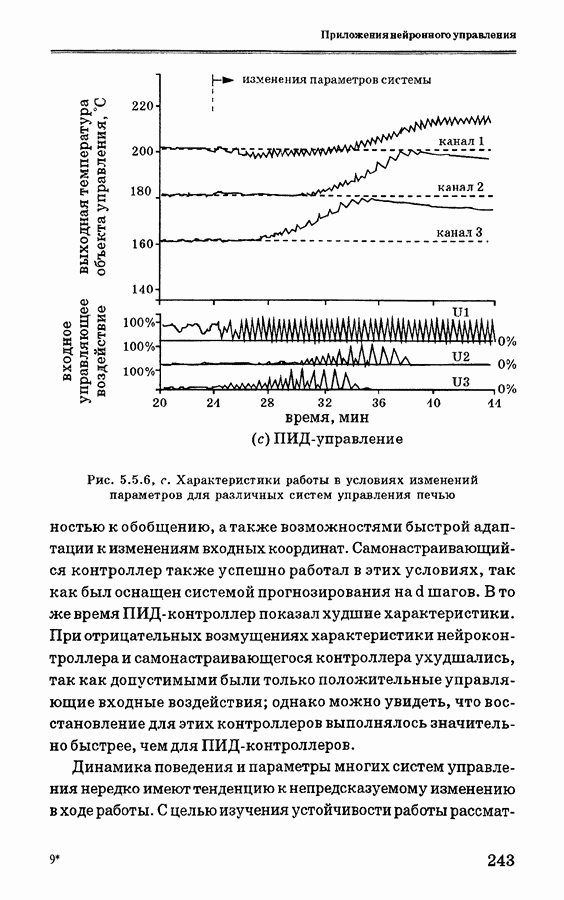
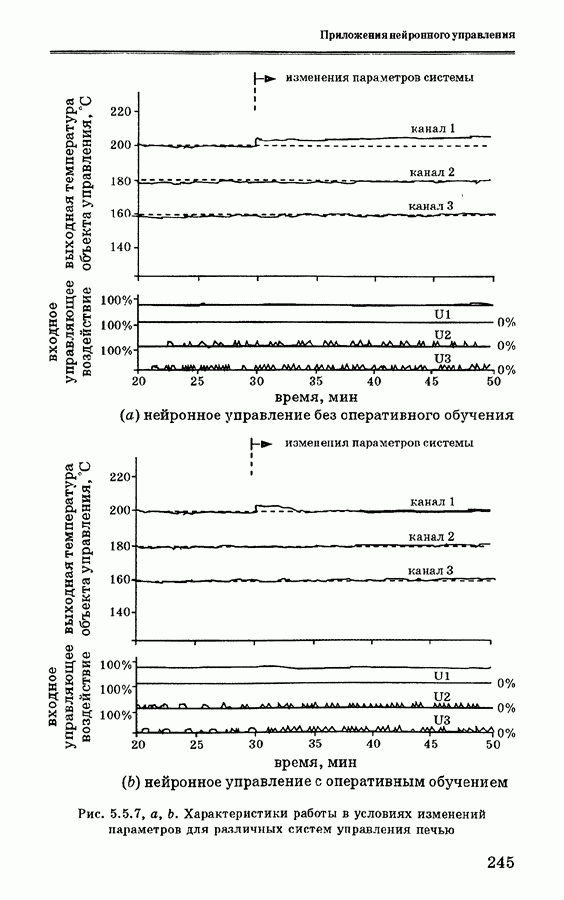
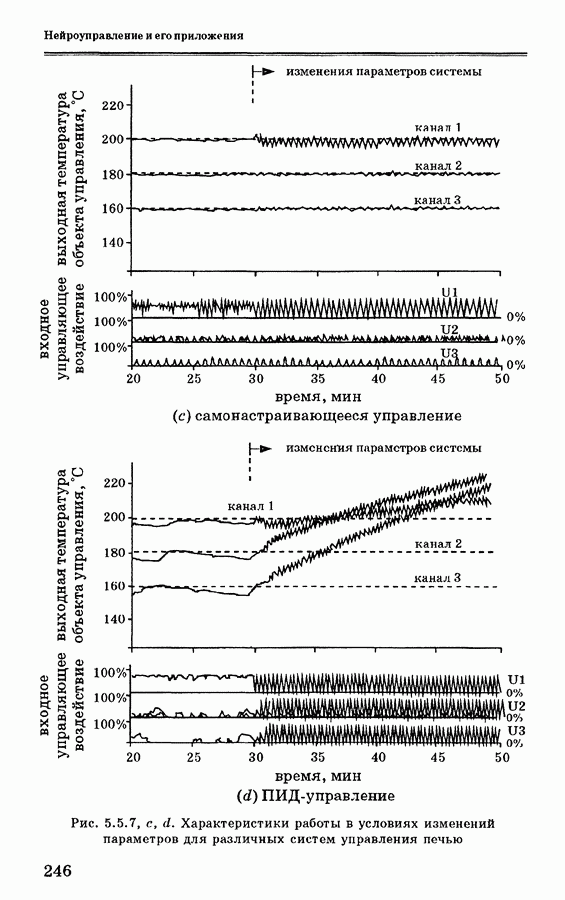
- 5.5.4. Анализ экспериментальных данных
- 5.6. Заключительные замечания и выводы
- Литература
- ЛИСТИНГ ПРОГРАММЫ