| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3.5. ПИД-управление с самонастройкой: многомерный подход
При выводе закона управления для СНПИ- или СНПИД-контроллера в многомерном случае будем использовать следующую модель:

где  —
—  -вектор выходного процесса,
-вектор выходного процесса,  —
—  -вектор управляющего воздействия,
-вектор управляющего воздействия,  —
—  -вектор некоррелированной последовательности случайных составляющих с нулевым математическим ожиданием и ковариацией
-вектор некоррелированной последовательности случайных составляющих с нулевым математическим ожиданием и ковариацией  Полиномиальные
Полиномиальные  -матрицы
-матрицы  выражаются с помощью оператора обратного сдвига
выражаются с помощью оператора обратного сдвига  в следующем виде:
в следующем виде:

Для реализации рассматриваемого алгоритма требуется ряд допущений. Они приводятся ниже:
А1. Шум, нарушающий работу системы, является стабильным в том смысле, что нули полинома  лежат внутри круга единичного радиуса на z-плоскости.
лежат внутри круга единичного радиуса на z-плоскости.
А2. Полиномы  являются взаимно простыми.
являются взаимно простыми.
А3. Структурные индексы системы равны, а верхние границы порядков всех скалярных полиномов, входящих в матрицы  известны.
известны.
А4. Связанное с каждым каналом передачи транспортное запаздывание, составляющее не менее  интервалов времени, предполагается известным и одинаковым для всех каналов.
интервалов времени, предполагается известным и одинаковым для всех каналов.
А5. Звенья  устойчивы, то есть система является минимально-фазовой.
устойчивы, то есть система является минимально-фазовой.
Как и для одномерных систем, вывод закона управления выполняется на основе минимизации дисперсии псевдовыхода  заданного в виде:
заданного в виде:

где  — полиномиальные
— полиномиальные  -матрицы,
-матрицы,  — вектор уставки.
— вектор уставки.  — рациональная матрица, которую можно представить следующим прямым матрично-дробным выражением:
— рациональная матрица, которую можно представить следующим прямым матрично-дробным выражением:

где  -матрицы числителя и знаменателя соответственно. Полиномы,
-матрицы числителя и знаменателя соответственно. Полиномы,  задаются пользователем, что позволяет получить достаточно общий случай замкнутой системы. Положим
задаются пользователем, что позволяет получить достаточно общий случай замкнутой системы. Положим  и введем (см. [40], [41], [42]) прямое матрично-дробное описание передаточной функции
и введем (см. [40], [41], [42]) прямое матрично-дробное описание передаточной функции  в виде:
в виде:

Будем считать, что  Тогда можно ввести тождество:
Тогда можно ввести тождество:

где  — полиномиальные
— полиномиальные  -матрицы вида:
-матрицы вида:

и

Здесь — степень полинома  Чтобы разрешить проблемы, связанные с некоммутативностью произведения
Чтобы разрешить проблемы, связанные с некоммутативностью произведения
матриц, введем полиномиальные матрицы  такие,что
такие,что

где

Используя (3.5.5), (3.5.6), (3.5.9) и (3.5.10), получим:

Умножив последнее уравнение на полином  и используя уравнения (3.3.1) и (3.5.11), получим:
и используя уравнения (3.3.1) и (3.5.11), получим:

Обозначим через  оптимальный прогноз значения
оптимальный прогноз значения  по измерениям до моменту времени
по измерениям до моменту времени  а через
а через  — ошибку прогноза. Таким образом, получим:
— ошибку прогноза. Таким образом, получим:

где

Заметим, что будущие ошибки  ,
, -рованы с текущими и прошлыми измерениями входного и выходного процессов. Управление по минимуму дисперсии
-рованы с текущими и прошлыми измерениями входного и выходного процессов. Управление по минимуму дисперсии  достигается путем выбора управляющего воздействия
достигается путем выбора управляющего воздействия  таким, чтобы величина
таким, чтобы величина  обращалась в ноль. На этом основании имеем:
обращалась в ноль. На этом основании имеем:

Здесь  — фильтрованный выход. Для
— фильтрованный выход. Для
непосредственного получения параметров контроллера  и шумовой компоненты
и шумовой компоненты  рассмотрим величину
рассмотрим величину  задаваемую выражением:
задаваемую выражением:

Используя (3.5.13), можно записать выражение в виде:

и

где  — оптимальный прогноз величины
— оптимальный прогноз величины  полученный на основе данных о выходном процессе до момента времени
полученный на основе данных о выходном процессе до момента времени  Положим
Положим  Тогда имеем:
Тогда имеем:

Для оценки параметров перепишем (3.5.17) в форме:

а вектор данных  зададим следующим образом:
зададим следующим образом:

Соответствующая матрица параметров  задается в виде:
задается в виде:

где вектор-столбец  имеет следующий вид:
имеет следующий вид:

Здесь  элементы первой строки
элементы первой строки  соответственно.
соответственно.
Если  — единичная матрица, то выражение (3.5.22) содержит только величины, известные к моменту времени
— единичная матрица, то выражение (3.5.22) содержит только величины, известные к моменту времени  и ошибка прогноза устраняется. Таким образом, параметры контроллера
и ошибка прогноза устраняется. Таким образом, параметры контроллера  могут быть получены на основе схемы оценивания параметров, например, рекурсивной оценки по методу наименьших квадратов. Если
могут быть получены на основе схемы оценивания параметров, например, рекурсивной оценки по методу наименьших квадратов. Если  — не единичная матрица, то оценка параметра будет смещена, так как величина
— не единичная матрица, то оценка параметра будет смещена, так как величина  неизвестна. Однако можно заменить
неизвестна. Однако можно заменить  ее оценкой
ее оценкой  , которую можно рассчитать, а затем для получения оценок параметров использовать обычный рекурсивный метод наименьших квадратов. Этот метод аналогичен расширенному методу наименьших квадратов [31], [32]. Вектор данных задается следующим образом:
, которую можно рассчитать, а затем для получения оценок параметров использовать обычный рекурсивный метод наименьших квадратов. Этот метод аналогичен расширенному методу наименьших квадратов [31], [32]. Вектор данных задается следующим образом:

Чтобы получить структуру многомерного ПИД-контроллера в выражении (3.5.17), необходимо, чтобы степень полинома  была равна двум. Поэтому
была равна двум. Поэтому

Следующее требование — введение интегрирующего управляющего воздействия в закон управления многомерного УОМД. Это можно сделать, положив

где

Устранение установившейся ошибки выполняется несколько по-другому:  где
где

Закон управления записывается в виде:

Выражения для параметров многомерного СНПИД-контроллера в терминах параметров многомерного ПИД-контроллера записываются следующим образом:

где

Для реализации структуры ПИ- или ПИД-контроллера степень  должна быть равна 1 или 2 соответственно. Предполагая взаимную простоту и несингулярность матриц
должна быть равна 1 или 2 соответственно. Предполагая взаимную простоту и несингулярность матриц  для случая, когда
для случая, когда  получим
получим  Степень полинома
Степень полинома  таким образом, определяется степенями полиномов
таким образом, определяется степенями полиномов  Отсюда следует, что если степень полинома
Отсюда следует, что если степень полинома  равна 1, то эффективным является ПИ- или ПИД-контроллер, в зависимости от того, равна степень полинома
равна 1, то эффективным является ПИ- или ПИД-контроллер, в зависимости от того, равна степень полинома  единице или двум. В некоторых случаях подходит управление системой первого порядка с помощью ПИ-контроллера. Преимущество такого варианта — в меньшем количестве параметров, которые требуется оценивать и предварительно выбирать. Однако для некоторых процессов требуются дифференцирующие воздействия с целью устранения осцилляций, возникающих вблизи уставки из-за медленного действия контроллеров. Диапазон процессов, управляемых с использованием данного алгоритма,
единице или двум. В некоторых случаях подходит управление системой первого порядка с помощью ПИ-контроллера. Преимущество такого варианта — в меньшем количестве параметров, которые требуется оценивать и предварительно выбирать. Однако для некоторых процессов требуются дифференцирующие воздействия с целью устранения осцилляций, возникающих вблизи уставки из-за медленного действия контроллеров. Диапазон процессов, управляемых с использованием данного алгоритма,
ограничивается третьим порядком. Однако можно доказать, что для процессов более высоких порядков может быть применена процедура редукции модели. Некоторые примеры редукции модели приводятся в [43—45]. Если  не единичная матрица, то для определения
не единичная матрица, то для определения  требуется сначала вычислить наибольший общий делитель
требуется сначала вычислить наибольший общий делитель  а затем воспользоваться формулами (3.5.7), (3.5.8), (3.5.12), (3.5.13). В этом случае степень полинома
а затем воспользоваться формулами (3.5.7), (3.5.8), (3.5.12), (3.5.13). В этом случае степень полинома  не обязана совпадать со степенью полинома
не обязана совпадать со степенью полинома 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРОВ ПЕРЕВОДА
- 1. ВВЕДЕНИЕ
- 1.1. Общие сведения об интеллектуальном управлении
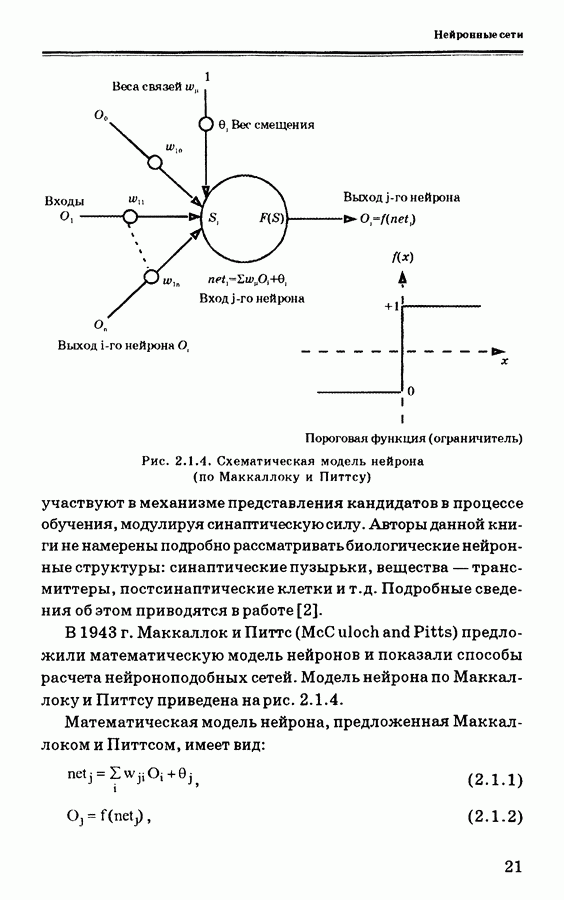
- 2. НЕЙРОННЫЕ СЕТИ
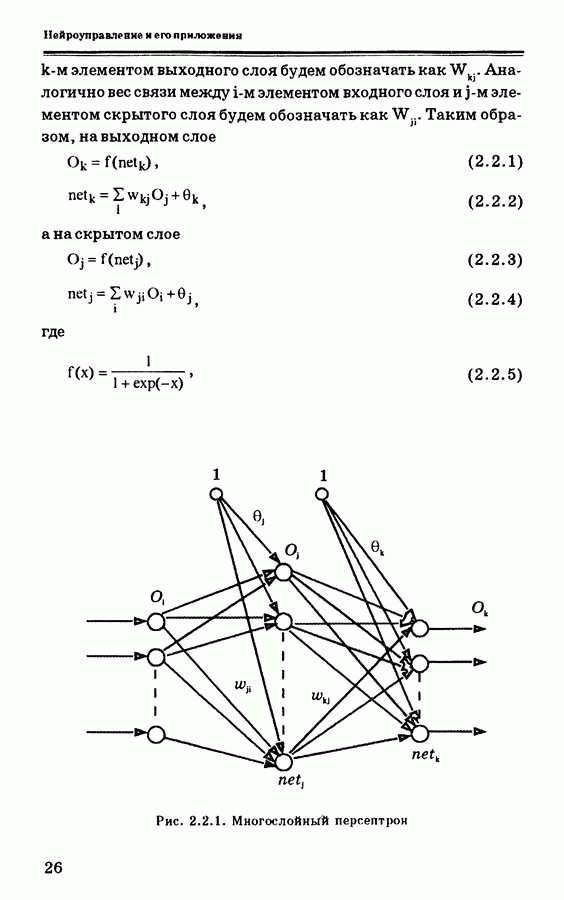
- 2.2. Алгоритм обратного распространения
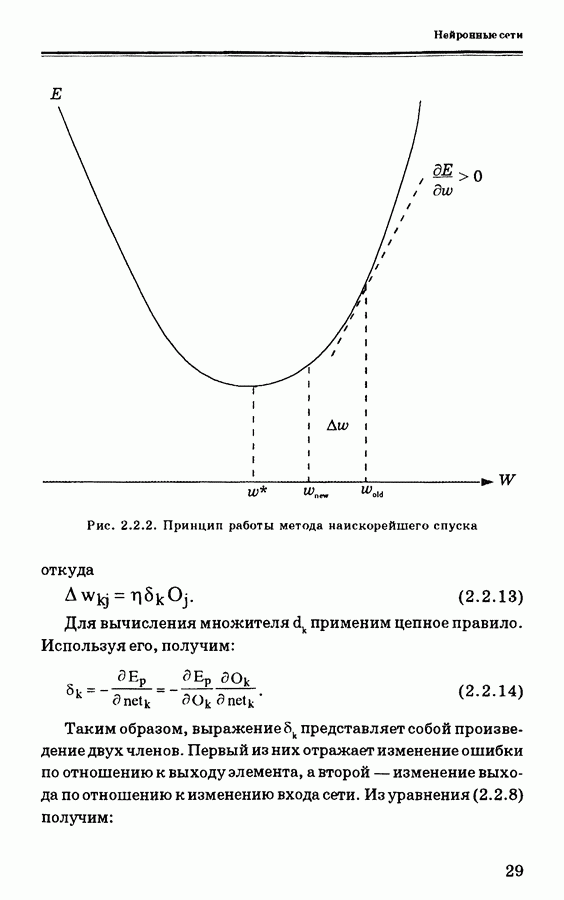
- 2.2.2. Вывод алгоритма обратного распространения
- 2.2.2.2. Правило для скрытого слоя
- 2.2.3. Алгоритм обратного распространения: порядок реализации
- 2.2.4. Обсуждение алгоритма обратного распространения
- 2.3. Заключение
- 3. ТРАДИЦИОННЫЕ СХЕМЫ УПРАВЛЕНИЯ
- 3.2. ПИ- и ПИД-контроллеры с дискретным временем
- 3.3. Управление с самонастройкой
- 3.4. Самонастраивающиеся ПИ- и ПИД- контроллеры
- 3.5. ПИД-управление с самонастройкой: многомерный подход
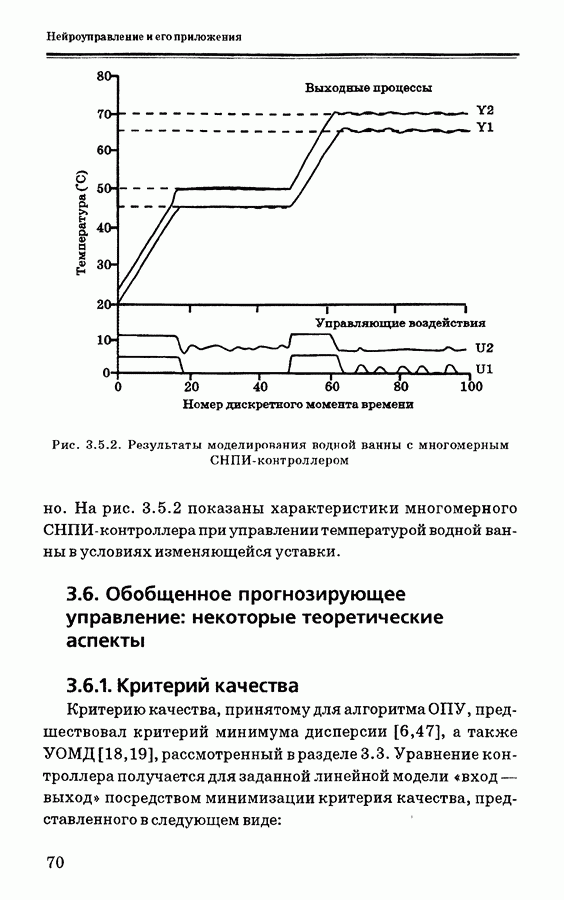
- 3.5.1. Пример моделирования
- 3.6. Обобщенное прогнозирующее управление: некоторые теоретические аспекты
- 3.6.2. Модель объекта управления и решение задачи оптимизации
- 3.7. Управление на основе нечеткой логики
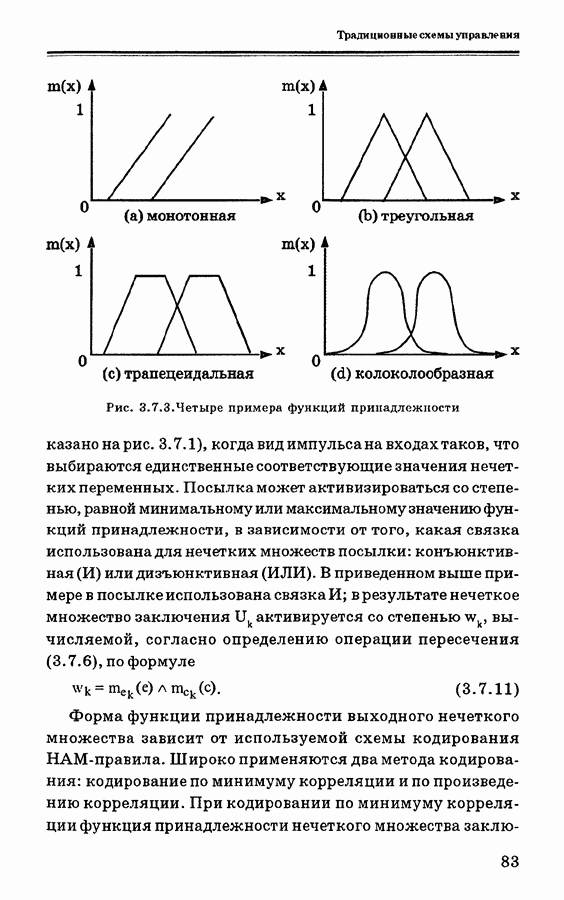
- 3.7.1. Краткие сведения по теории нечетких множеств и нечетких систем
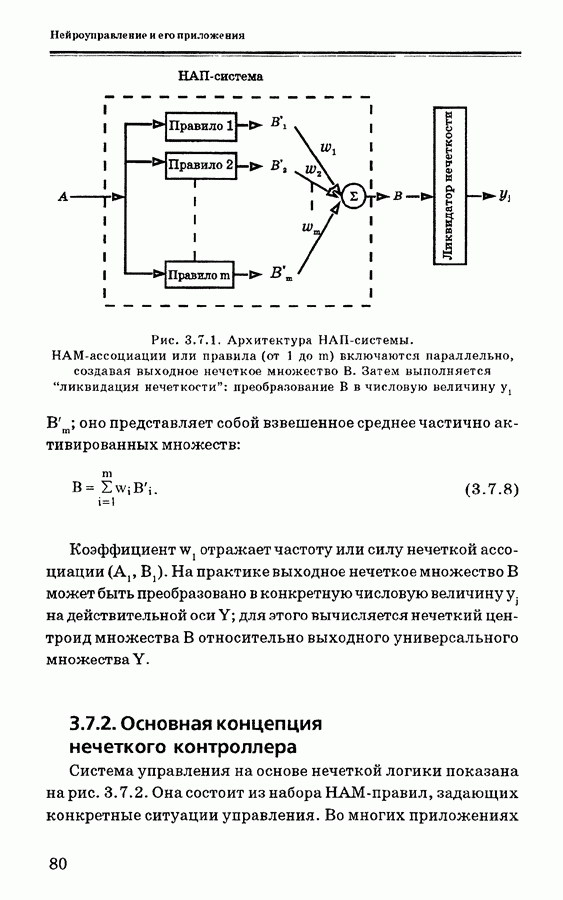
- 3.7.2. Основная концепция нечеткого контроллера
- 3.8. Заключение
- 4. ТЕХНОЛОГИИ НЕЙРОННОГО УПРАВЛЕНИЯ
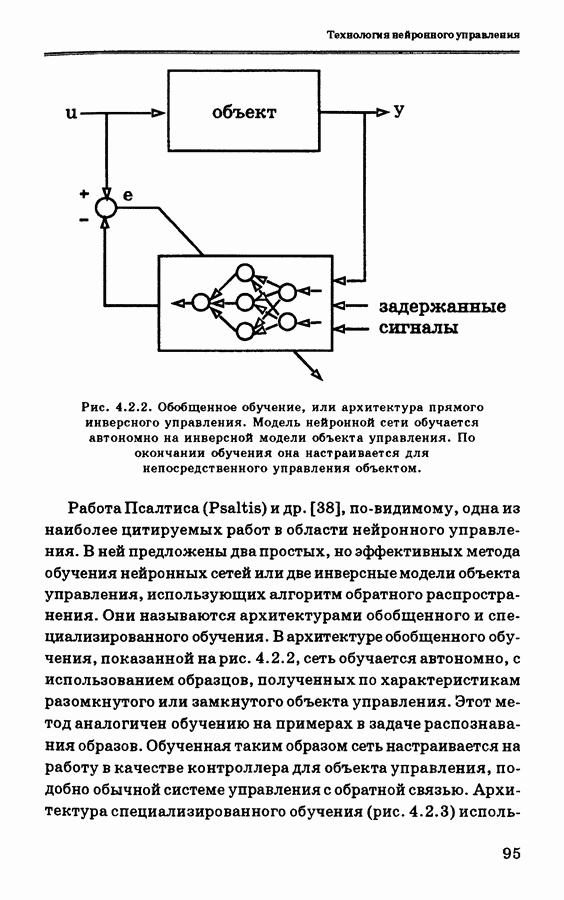
- 4.2. Общие сведения о нейронном управлении
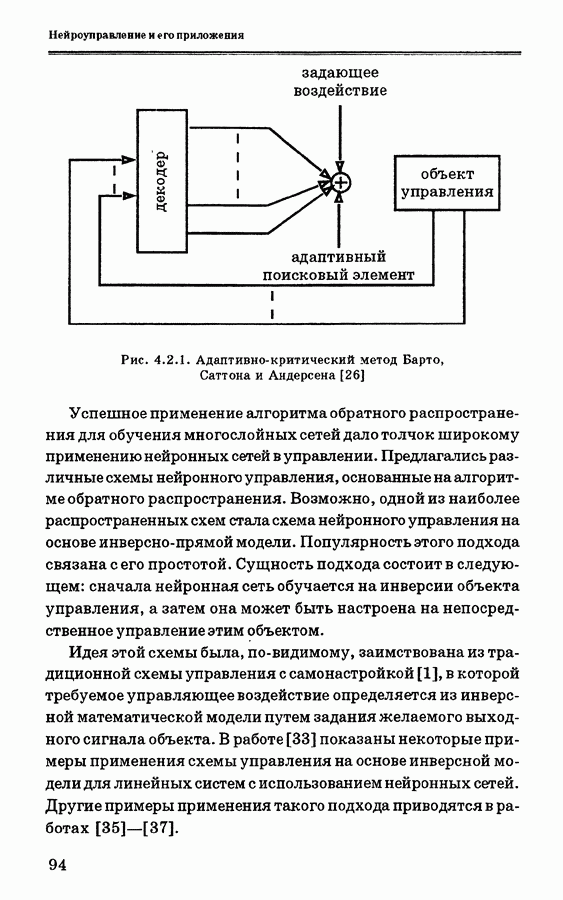
- 4.2.1. Подходы к нейронному управлению
- 4.2.2. Общая схема управления
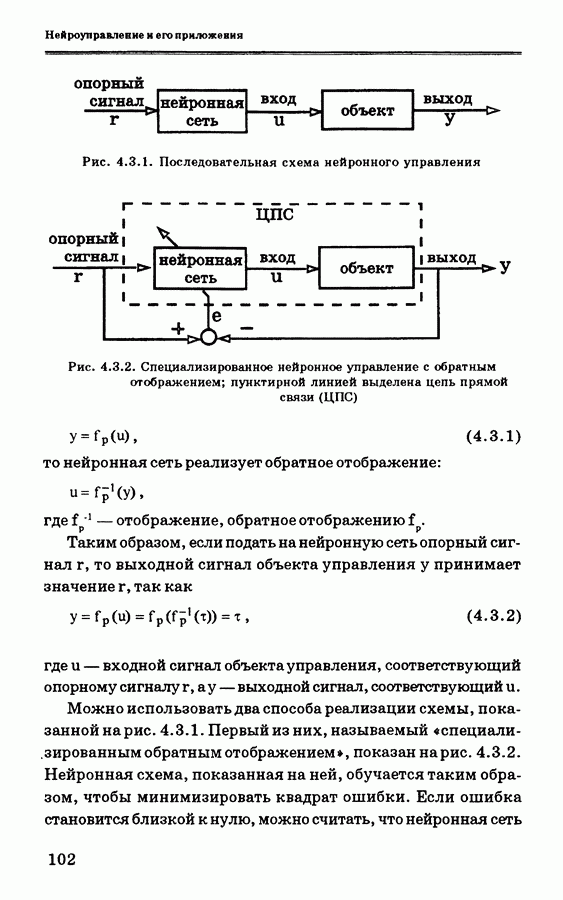
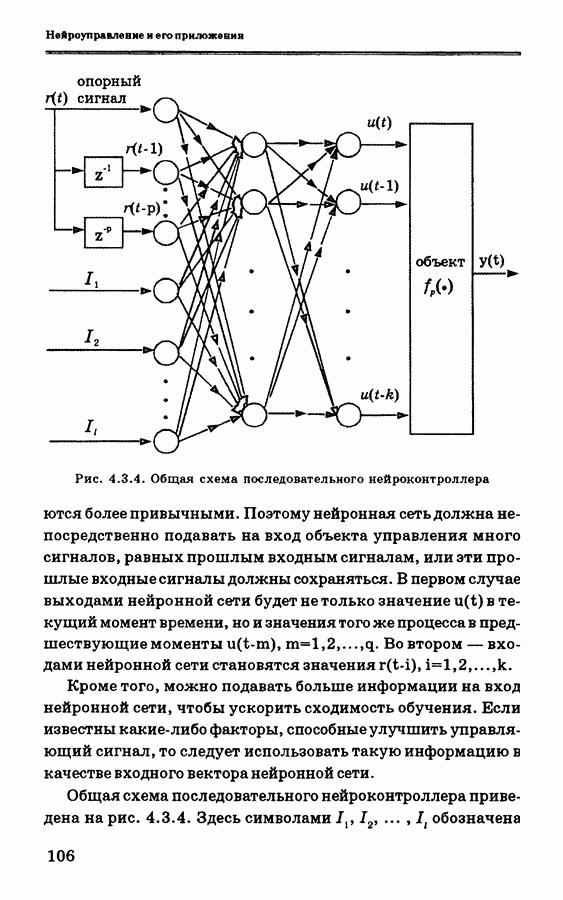
- 4.3. Последовательная схема нейронного управления
- 4.4. Расширение последовательной схемы нейронного управления
- 4.4.2. Нейроморфные структуры управления
- 4.4.3. Конфигурации обучения
- 4.4.4. Эффективное оперативное управление
- 4.4.5. Алгоритмы обучения
- 4.4.6. Оценка алгоритмов обучения на основе моделирования
- 4.5. Параллельная схема управления
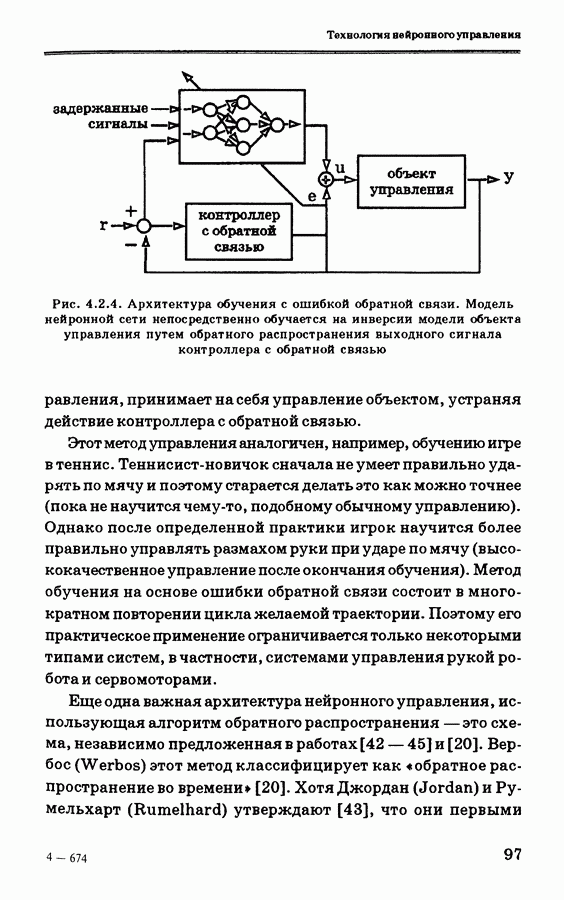
- 4.6. Алгоритм обучения по ошибке обратной связи
- 4.7. Расширение применения нейроконтроллеров параллельного типа
- 4.7.2. Линеаризованная система управления
- 4.7.3. Система управления с нейронными сетями
- 4.7.4. Нелинейный алгоритм наблюдения для нейронной сети
- 4.7.5. Нелинейный контроллер для нейронной сети
- 4.7.6. Численное моделирование
- 4.8. Схема нейронного управления с самонастройкой
- 4.9. ПИД-нейроконтроллер с самонастройкой
- 4.9.1. Вывод уравнений ПИД-нейроконтроллера с самонастройкой
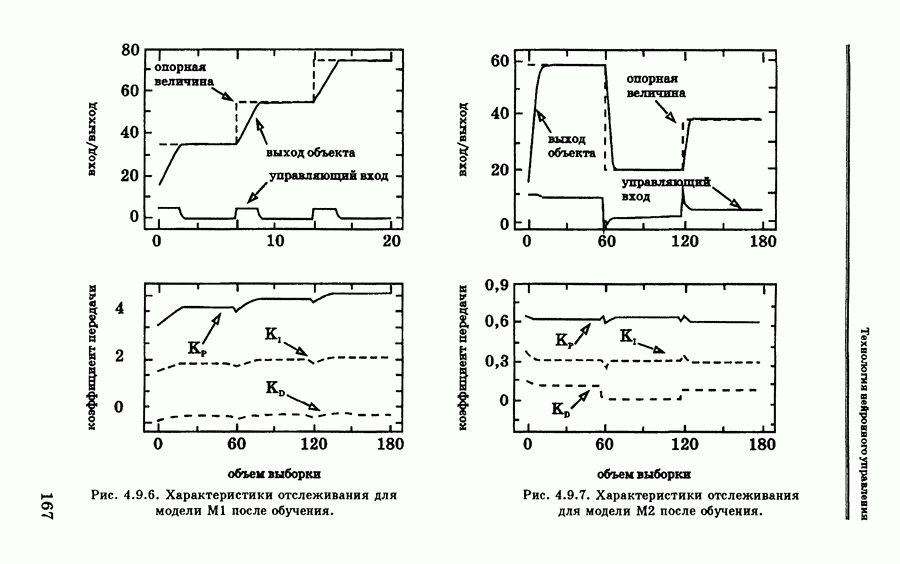
- 4.9.2. Примеры эмуляции
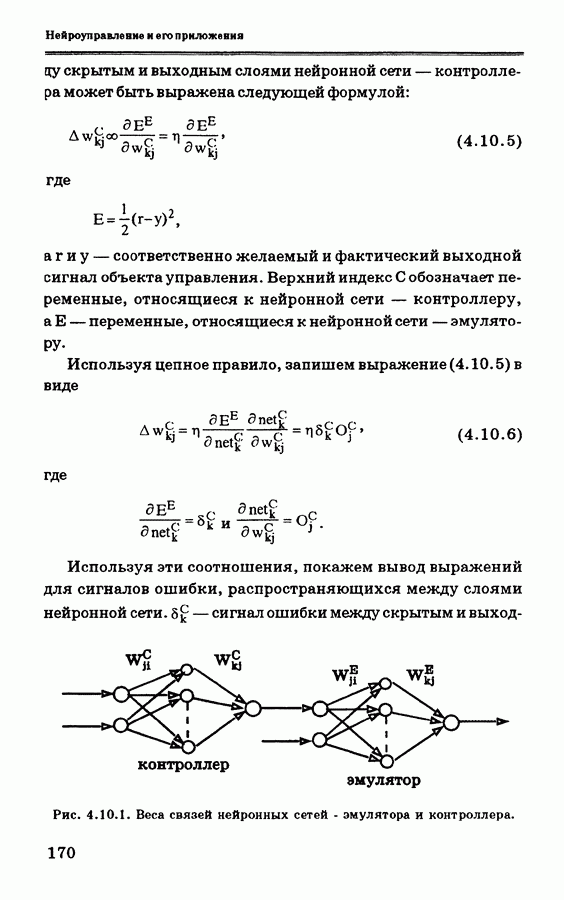
- 4.10. Схема нейронного управления с эмулятором и контроллером (схема обратного распространения во времени)
- 4.11. Заключение
- 5. ПРИЛОЖЕНИЯ НЕЙРОННОГО УПРАВЛЕНИЯ
- 5.2. Применение нейронного управления в системе регулирования процессов в водяной ванне и сравнение его с другими схемами управления
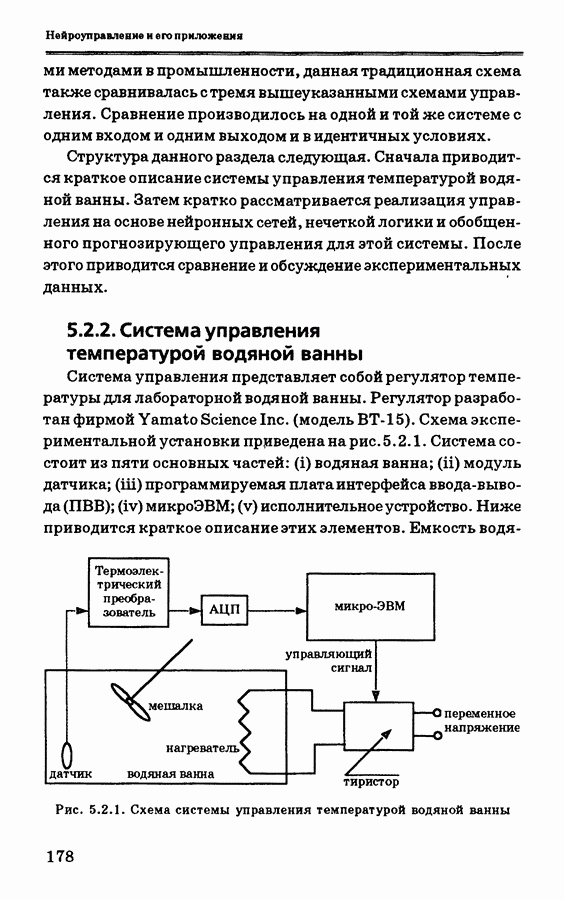
- 5.2.2. Система управления температурой водяной ванны
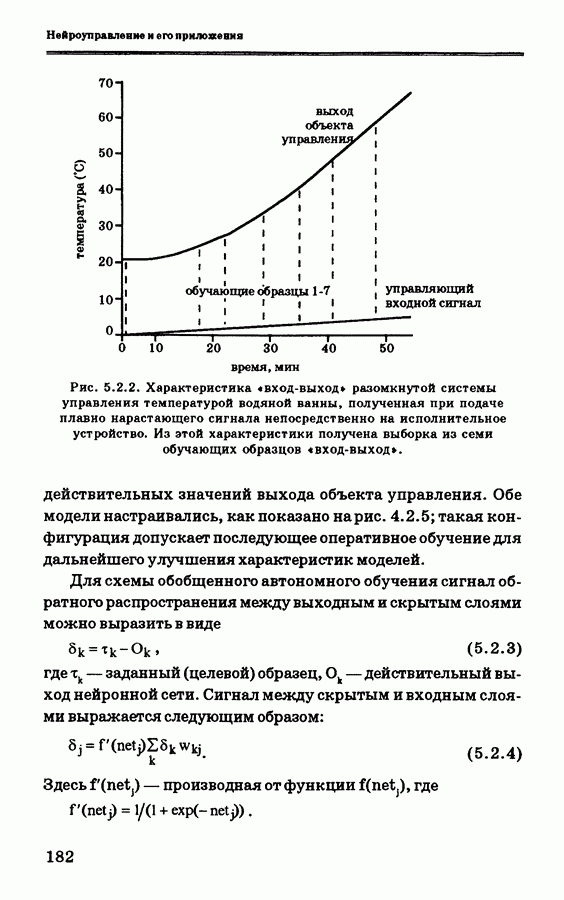
- 5.2.3. Схема нейронного управления
- 5.2.4. Схема управления на основе нечеткой логики
- 5.2.5. Схема обобщенного прогнозирующего управления
- 5.2.6. Экспериментальные данные и их анализ
- 5.2.7. Заключение
- 5.3. Система стабилизации инвертированного маятника на основе нейронных сетей
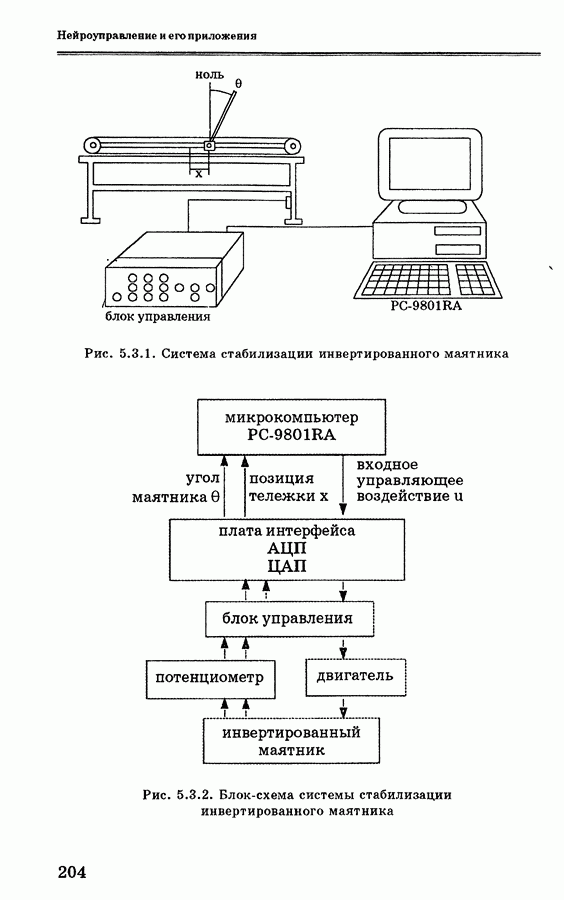
- 5.3.2. Система стабилизации инвертированного маятника
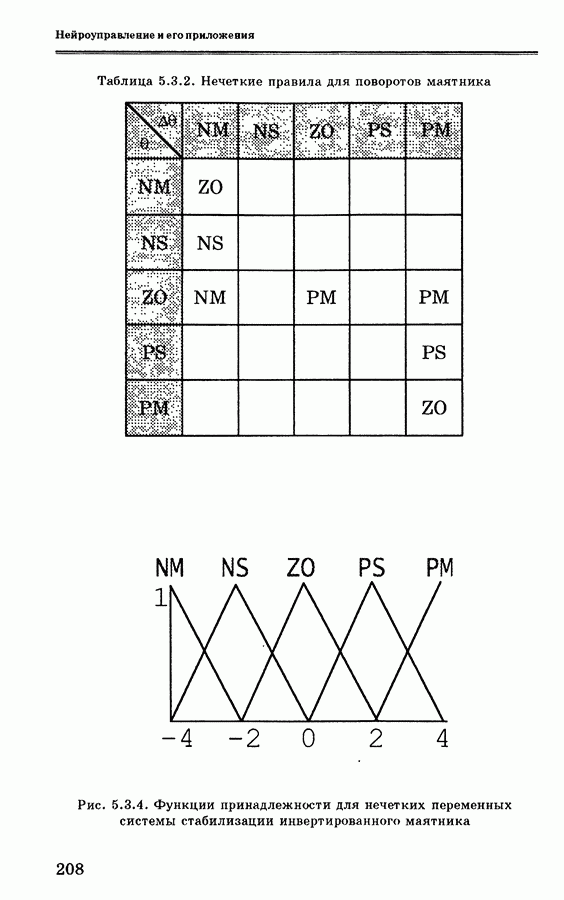
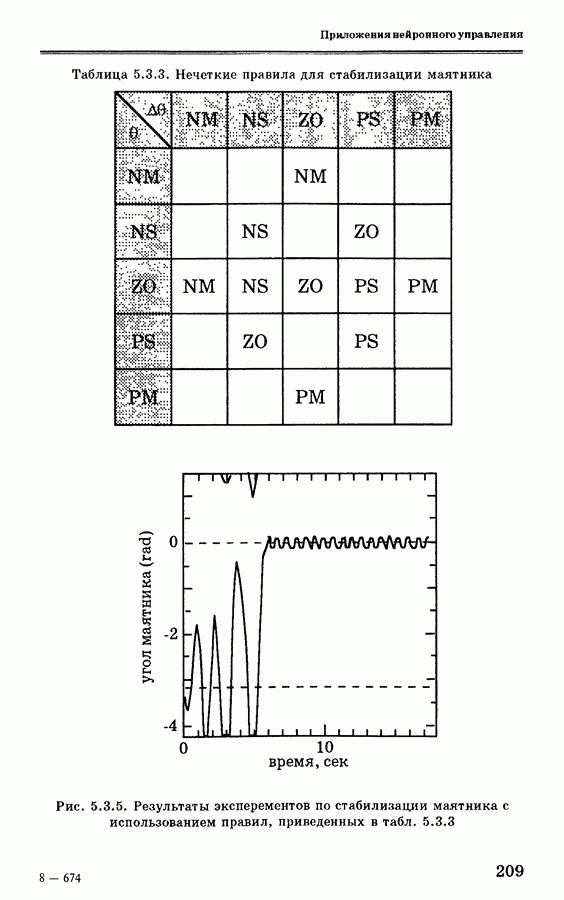
- 5.3.3. Инициализация поворотного управления с использованием нечеткой логики
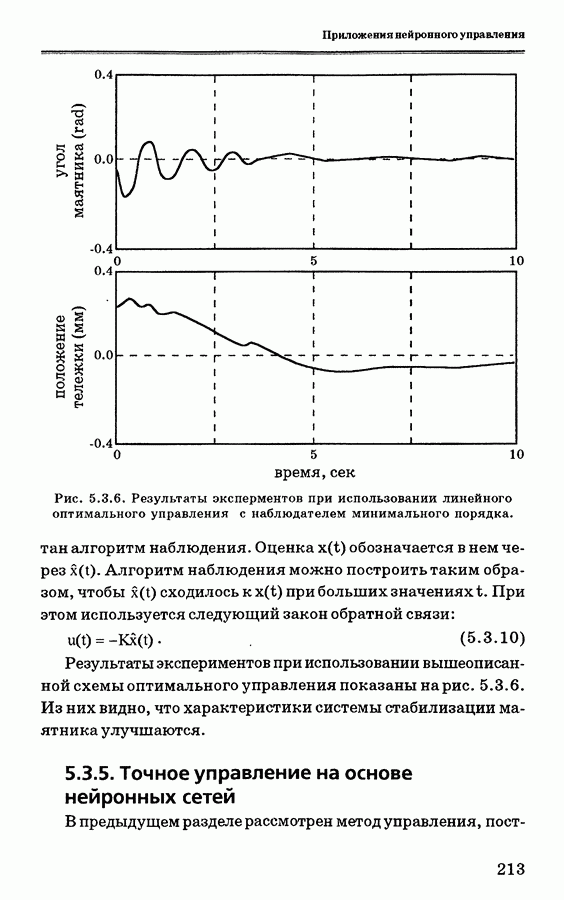
- 5.3.4. Применение стратегии оптимального управления для стабилизации маятника
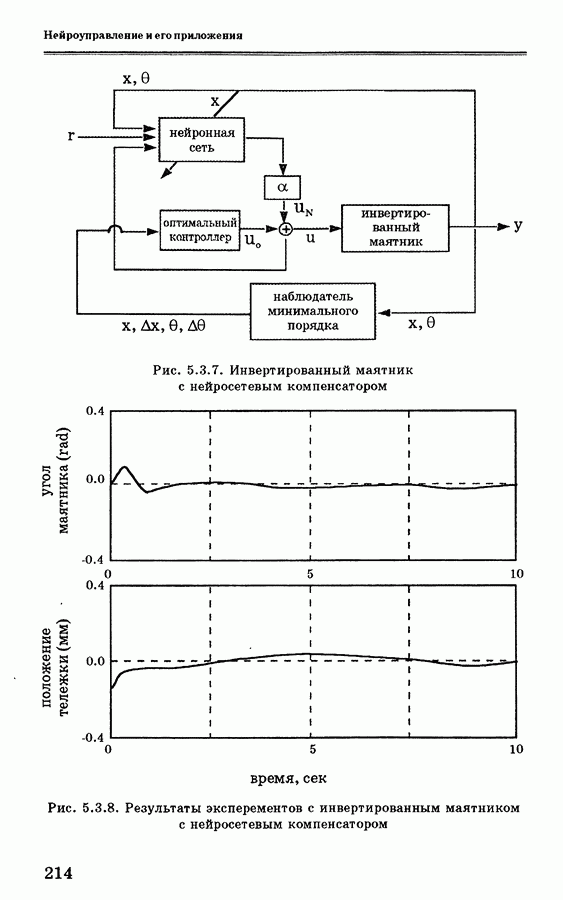
- 5.3.5. Точное управление на основе нейронных сетей
- 5.3.6. Заключение
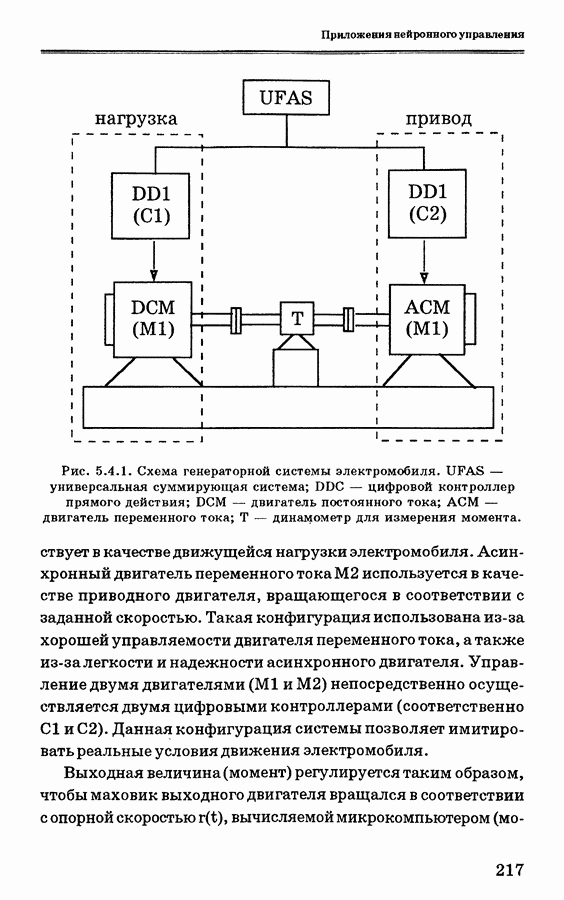
- 5.4. Применение ПИД-нейроконтроллера с самонастройкой для управления скоростью электромобиля
- 5.4.2. Система управления электромобилем
- 5.4.3. ПИД-нейроконтроллер с самонастройкой
- 5.4.4. Применение нейронной сети для управления скоростью электромобиля
- 5.4.5. Заключение
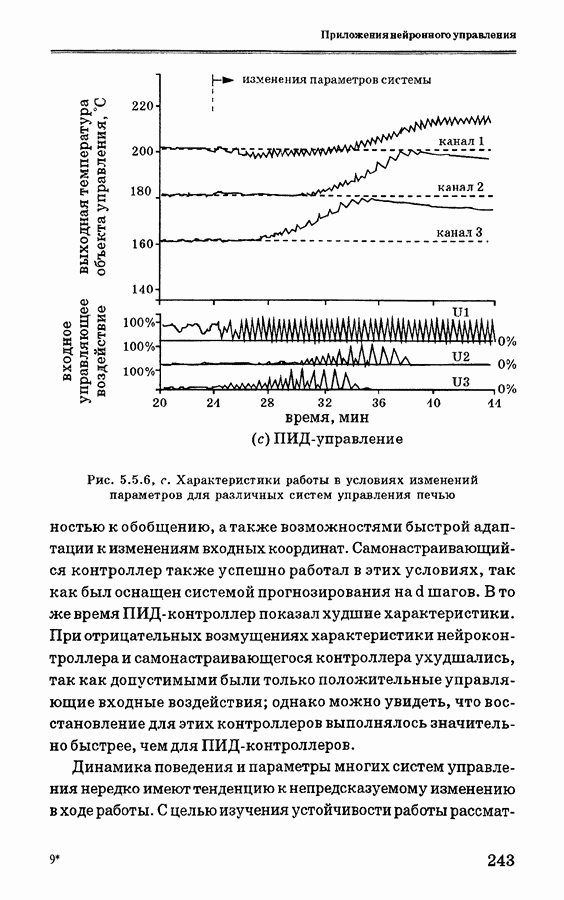
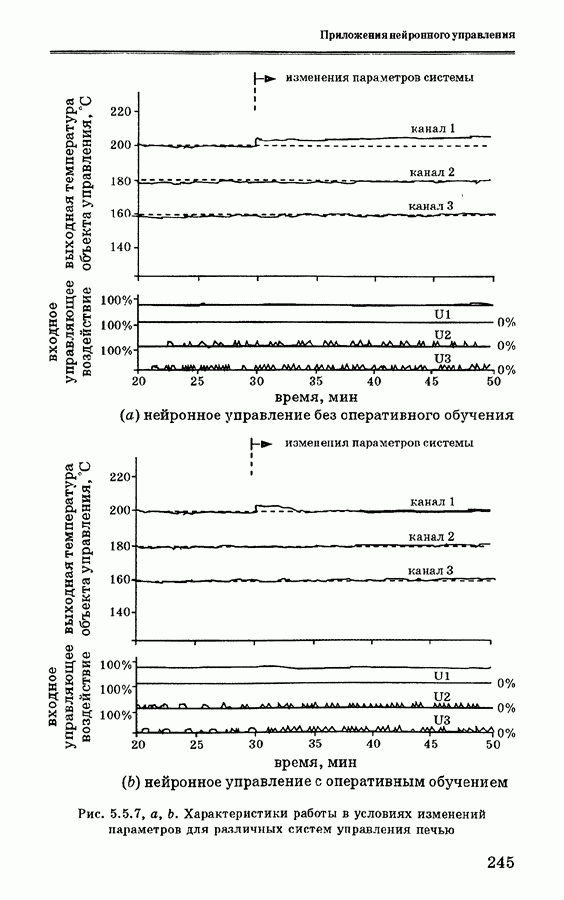
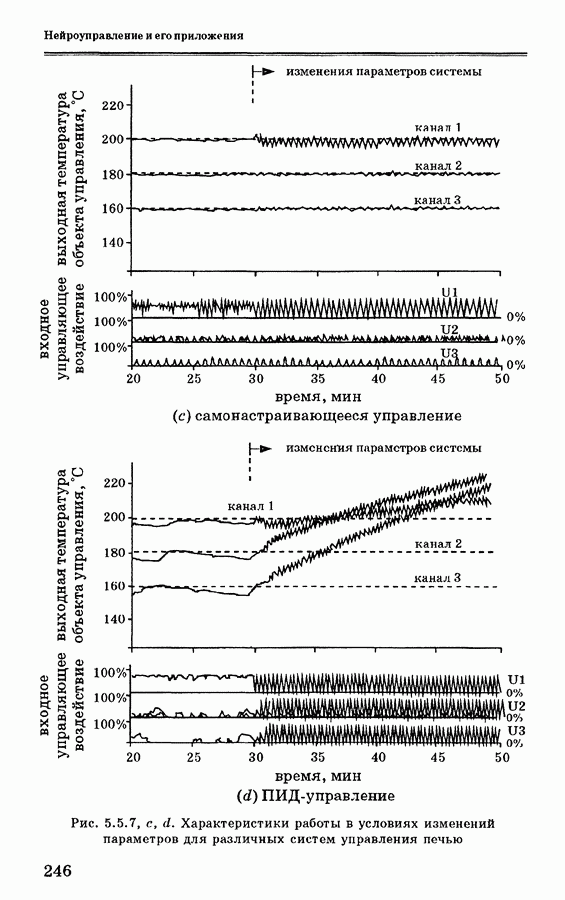
- 5.5. Применение нейронных сетей для управления печью
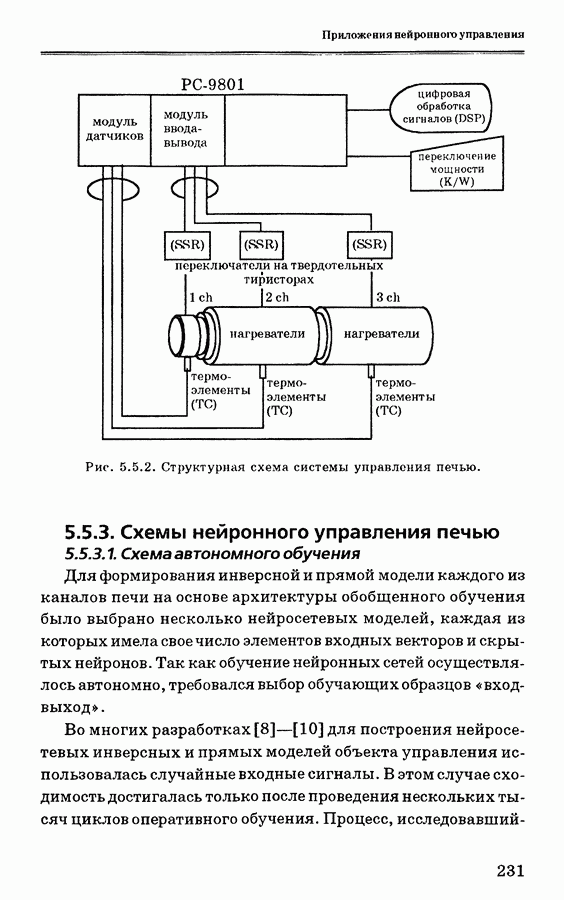
- 5.5.2. Система управления печью
- 5.5.3. Схемы нейронного управления печью
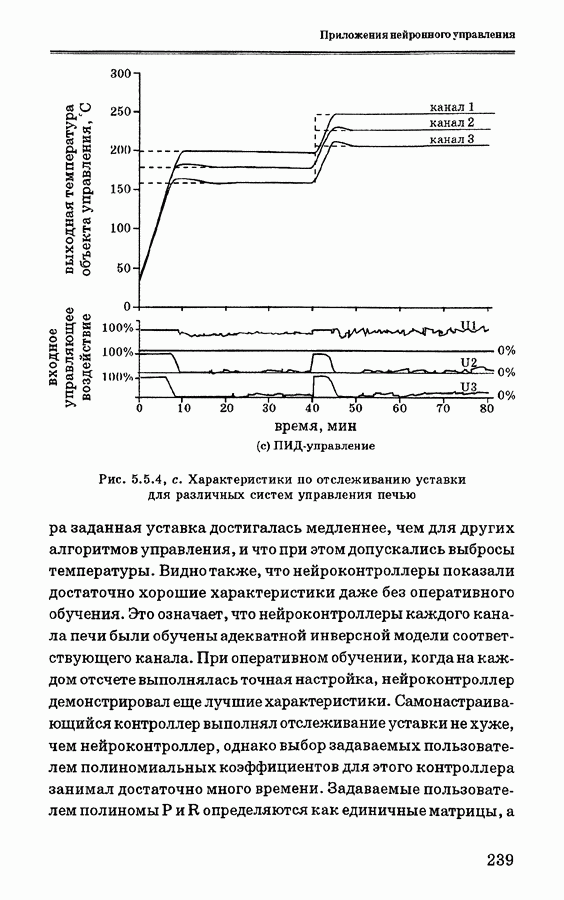
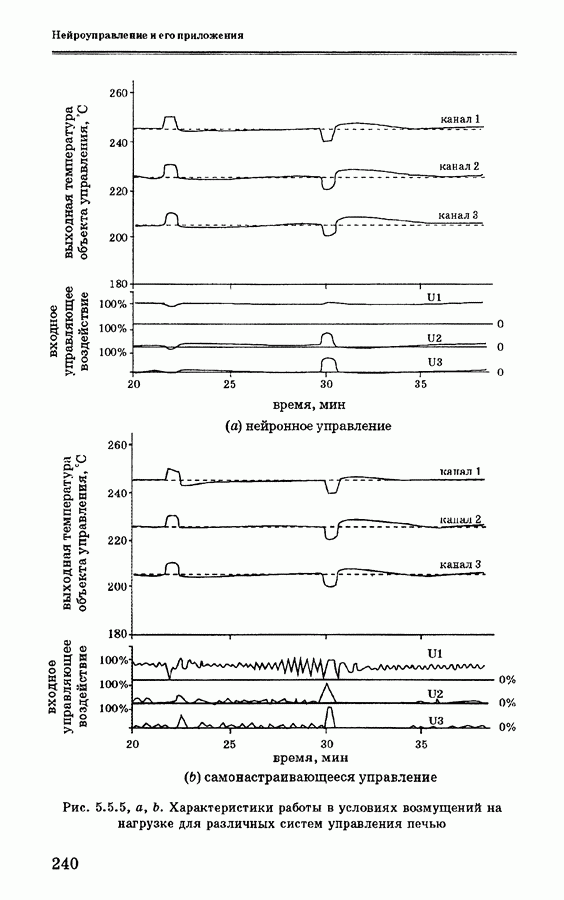
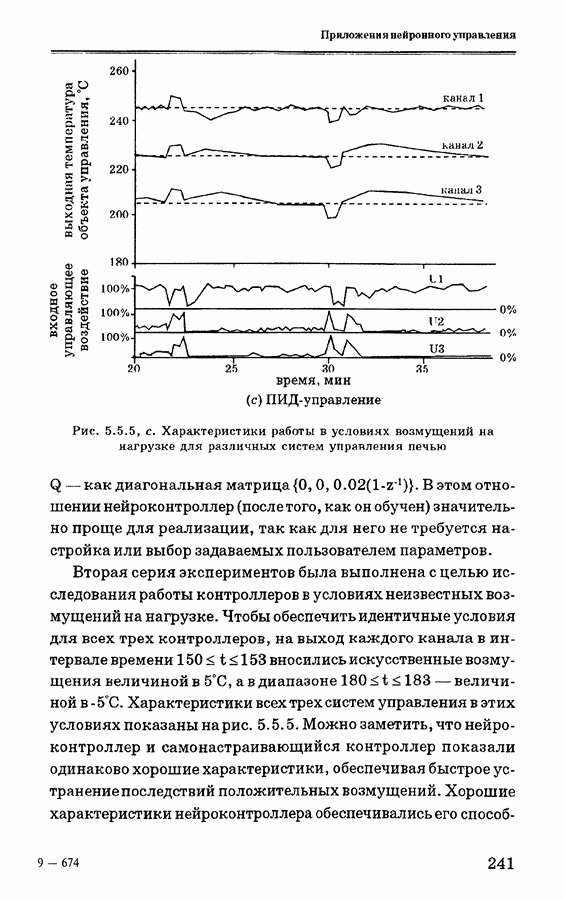
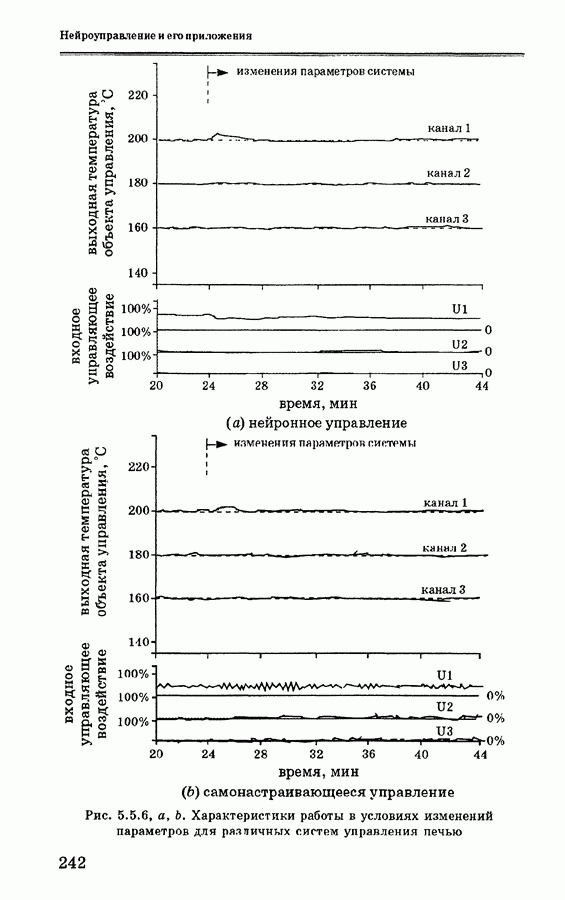
- 5.5.4. Анализ экспериментальных данных
- 5.6. Заключительные замечания и выводы
- Литература
- ЛИСТИНГ ПРОГРАММЫ