| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4.4.2. Нейроморфные структуры управления
4.4.2.1. Постановка задачи
Рассмотрим дискретный процесс с одним входом и с одним выходом:

где у — выход,  — вход,
— вход,  — дискретное целочисленное время,
— дискретное целочисленное время,  и
и  — неотрицательные целые числа,
— неотрицательные целые числа,  — некоторая функция. Во многих практических случаях входные координаты объекта управления ограничены по величине, т.е. существуют такие числа
— некоторая функция. Во многих практических случаях входные координаты объекта управления ограничены по величине, т.е. существуют такие числа  , что для любого момента времени
, что для любого момента времени  выполняется условие
выполняется условие

Итак, задача состоит в обучении управлению объектом, который описывается уравнением (4.4.1). Управление должно осуществляться таким образом, чтобы выходной сигнал соответствовал некоторому опорному сигналу  при этом должна минимизироваться некоторая норма ошибки
при этом должна минимизироваться некоторая норма ошибки  во времени. Единственные априорные количественные данные об объекте управления — величины
во времени. Единственные априорные количественные данные об объекте управления — величины  и
и  представляющие собой соответственно оценки величин
представляющие собой соответственно оценки величин  и
и  выражения (4.4.1) — предполагаются известными. Иными словами, предполагается известной приближенная оценка порядка дифференциального уравнения, описывающего объект управления.
выражения (4.4.1) — предполагаются известными. Иными словами, предполагается известной приближенная оценка порядка дифференциального уравнения, описывающего объект управления.
4.4.2.2. Многослойные нейронные сети для управления
Для управления роботами и различными технологическими процессами применяются различные архитектуры нейронных сетей. Однако большая часть литературы по нейронному управлению посвящена именно многослойным нейронным сетям. Этот вид нейронных сетей представляет особый интерес для специалистов по управлению по следующим причинам.
1. Такие сети представляют собой структуры с прямыми связями, в которых информация передается в прямом направлении, от входов к выходам, через скрытые слои. Это свойство особенно удобно для работы с системами, которые можно представить в виде блоков с входами и выходами, но не в виде рекуррентных сетей. В модели Хопфилда [53], например, используются двунаправленные узлы, и фактически отсутствуют входы и выходы.
2. Сети всего с одним скрытым слоем, использующие произвольную сигмоиднуюфункцию активации, могут выполнять любое нелинейное отображение между двумя пространствами конечной размерности с любой заданной точностью; для этого требуется лишь достаточное количество скрытых элементов (нейронов). Другими словами, многослойные нейронные сети обеспечивают самые разнообразные отображения с любой желаемой точностью. Обычно в системах управления многие блоки могут рассматриваться как отображающие элементы, поэтому для их эмуляции можно использовать многослойные нейронные сети с входами и выходами.
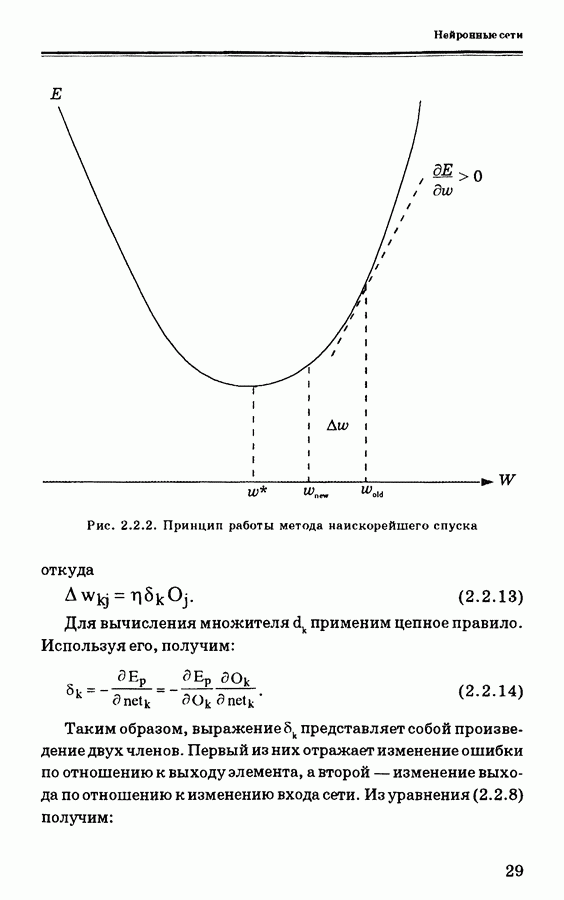
3. Основной алгоритм обучения многослойных нейронных сетей — алгоритм обратного распространения — относится к широкому классу градиентных методов наискорейшего спуска, широко применяемых в оптимальном управлении и поэтому известных специалистам по теории управления.
Указанные достоинства многослойных нейронных сетей свидетельствуют о том, что они могут рассматриваться как блоки, пригодные как для обучения, так и для отображения. На основе этой способности к отображению можно предложить две общие структуры нейронного управления: эмулятор объекта управления и контроллер.
4.4.2.3. Нейронный эмулятор объекта управления (НЭОУ)
При заданных оценках величин  и
и  многослойная нейронная сеть с
многослойная нейронная сеть с  входами и одним выходом может использоваться для эмуляции зависимости
входами и одним выходом может использоваться для эмуляции зависимости  выражения (4.4.1). Обозначив отображение, выполняемое эмулятором объекта управления, как
выражения (4.4.1). Обозначив отображение, выполняемое эмулятором объекта управления, как  а его выход — как
а его выход — как  получим
получим

где  -мерный вектор.
-мерный вектор.
Для случая, когда

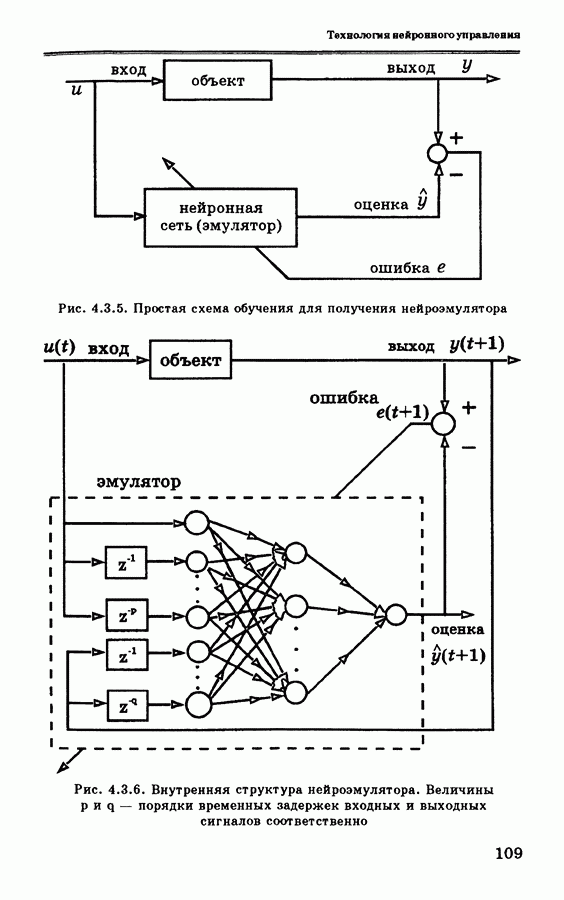
целью обучения эмулятора является минимизация нормы ошибки эмуляции  Схема НЭОУ показана на рис. 4.3.6.
Схема НЭОУ показана на рис. 4.3.6.
4.4.2.4. Нейроконтроллер
Предположим, что объект управления, описываемый уравнением (4.4.1), является обратимым, т.е. существует функция  такая, что
такая, что

Рассмотрим многослойную нейронную сеть с  -мерным вектором входов
-мерным вектором входов  одним выходом
одним выходом  и соотношением между входом и выходом, кратко описываемым следующим образом:
и соотношением между входом и выходом, кратко описываемым следующим образом:

где  — отображение «вход-выход» многослойной нейронной сети.
— отображение «вход-выход» многослойной нейронной сети.
Если выход  близок к выходу
близок к выходу  при соответствующих входах, то многослойная нейронная сеть может рассматриваться как контроллер в прямой цепи управления. В момент времени
при соответствующих входах, то многослойная нейронная сеть может рассматриваться как контроллер в прямой цепи управления. В момент времени  значение входа объекта управления можно получить с помощью выражения (4.4.5), подставив в него:
значение входа объекта управления можно получить с помощью выражения (4.4.5), подставив в него:

где вместо неизвестной величины  использовано значение опорного сигнала
использовано значение опорного сигнала  Если ошибка выхода
Если ошибка выхода  поддерживается на достаточно низком уровне после окончания процесса обучения, можно использовать выражение
поддерживается на достаточно низком уровне после окончания процесса обучения, можно использовать выражение

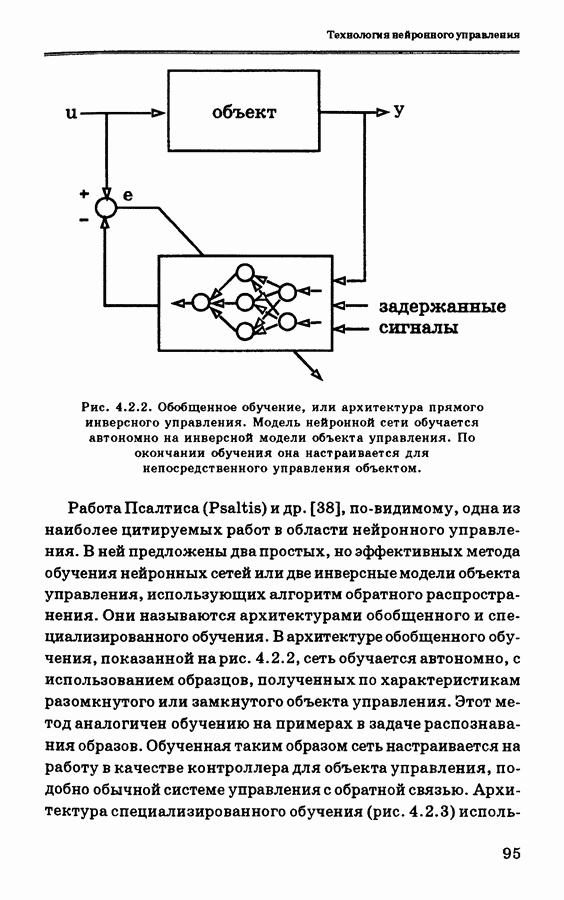
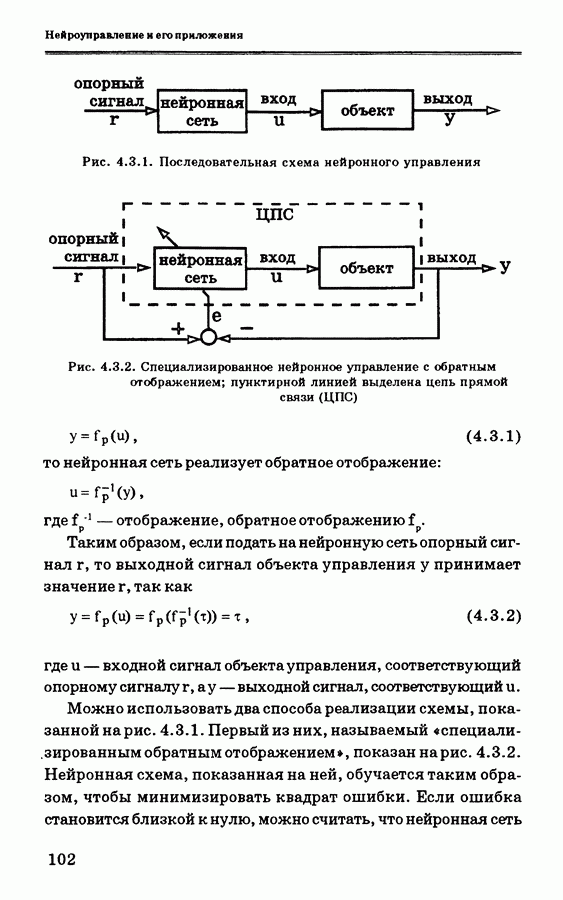
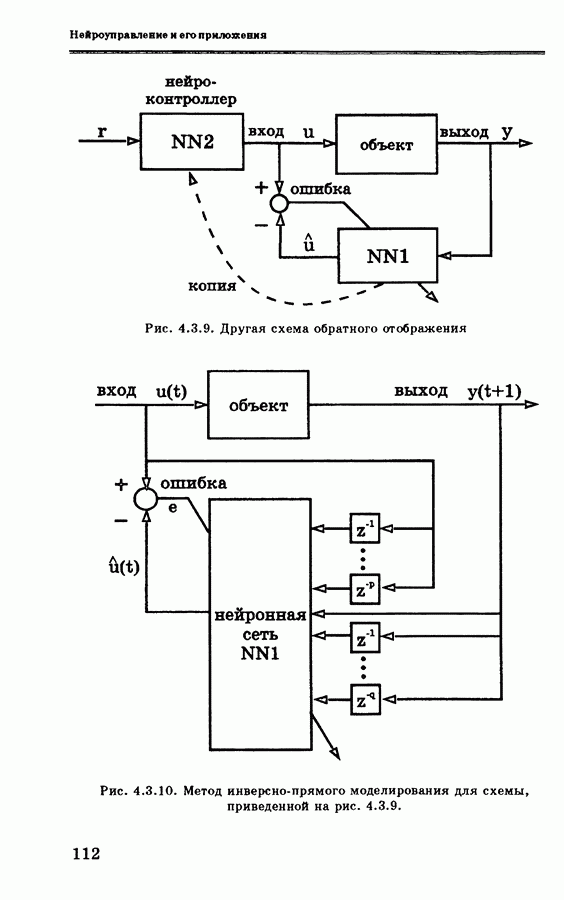
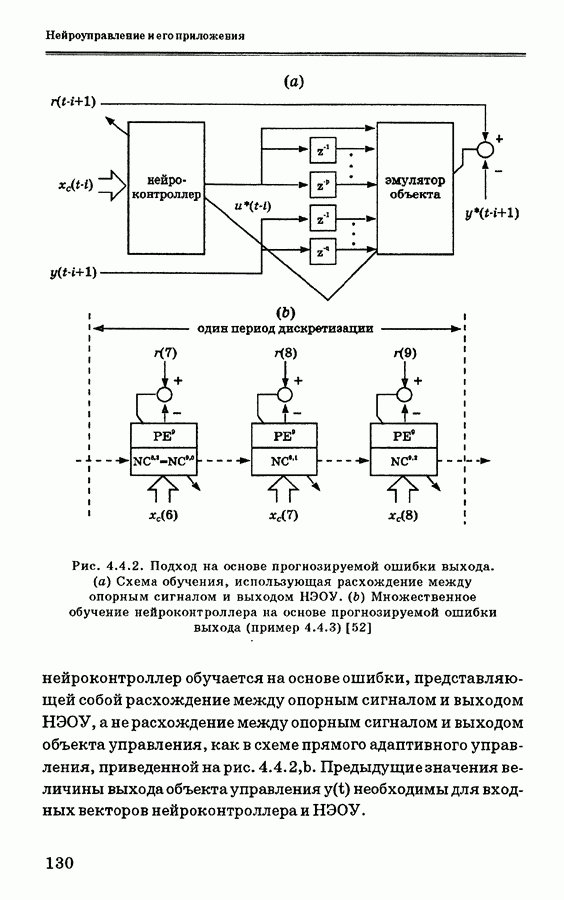
Отсюда видно, что нейроконтроллер не имеет обратных связей. Эта базовая конфигурация нейроконтроллера показана на рис. 4.3.1 под названием «последовательная схема нейронного управления».
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРОВ ПЕРЕВОДА
- 1. ВВЕДЕНИЕ
- 1.1. Общие сведения об интеллектуальном управлении
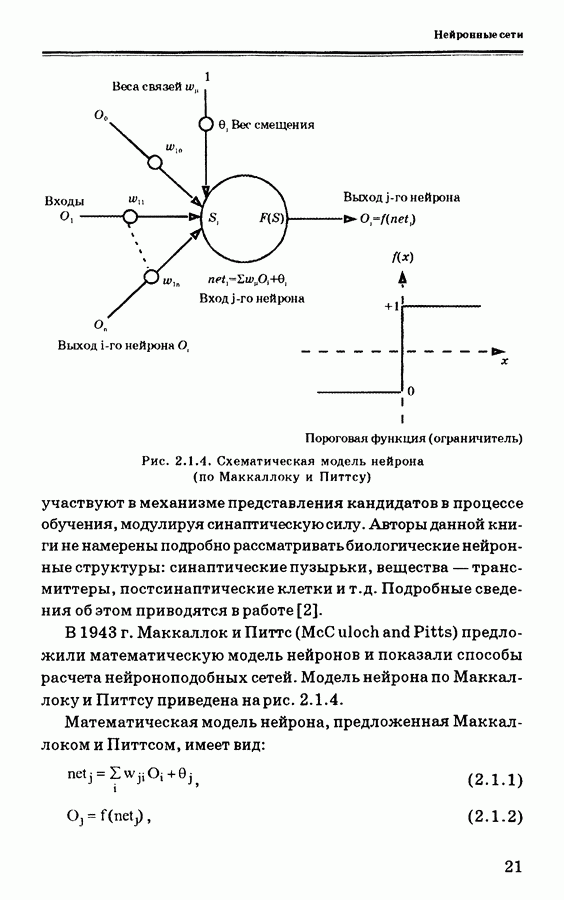
- 2. НЕЙРОННЫЕ СЕТИ
- 2.2. Алгоритм обратного распространения
- 2.2.2. Вывод алгоритма обратного распространения
- 2.2.2.2. Правило для скрытого слоя
- 2.2.3. Алгоритм обратного распространения: порядок реализации
- 2.2.4. Обсуждение алгоритма обратного распространения
- 2.3. Заключение
- 3. ТРАДИЦИОННЫЕ СХЕМЫ УПРАВЛЕНИЯ
- 3.2. ПИ- и ПИД-контроллеры с дискретным временем
- 3.3. Управление с самонастройкой
- 3.4. Самонастраивающиеся ПИ- и ПИД- контроллеры
- 3.5. ПИД-управление с самонастройкой: многомерный подход
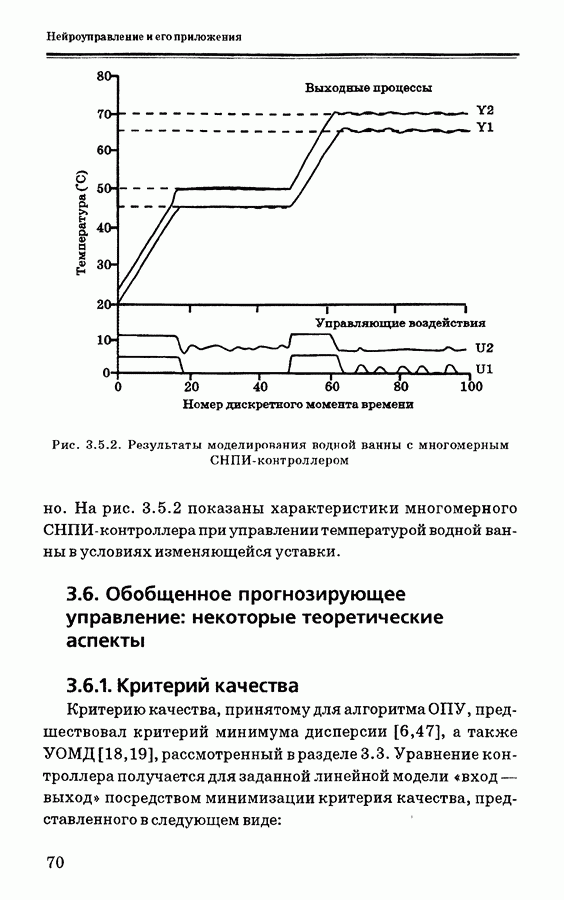
- 3.5.1. Пример моделирования
- 3.6. Обобщенное прогнозирующее управление: некоторые теоретические аспекты
- 3.6.2. Модель объекта управления и решение задачи оптимизации
- 3.7. Управление на основе нечеткой логики
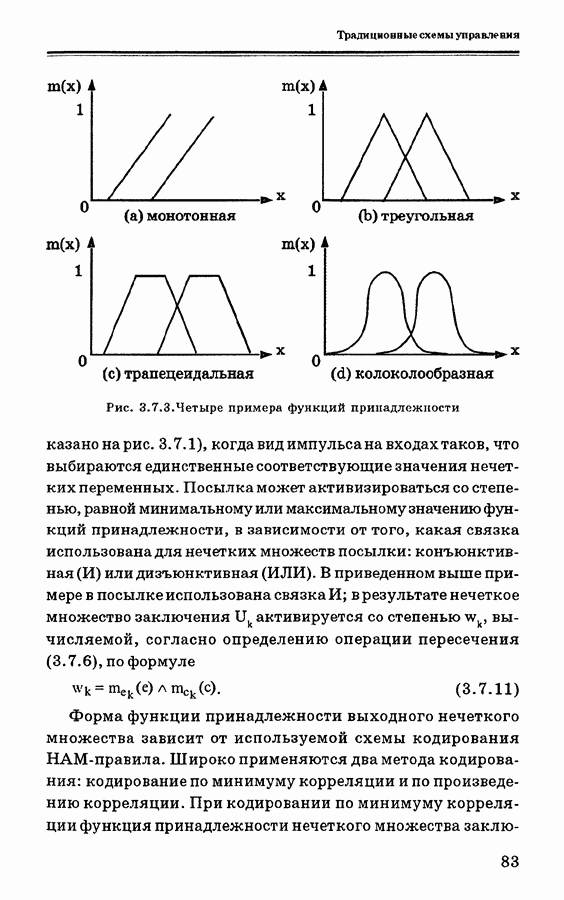
- 3.7.1. Краткие сведения по теории нечетких множеств и нечетких систем
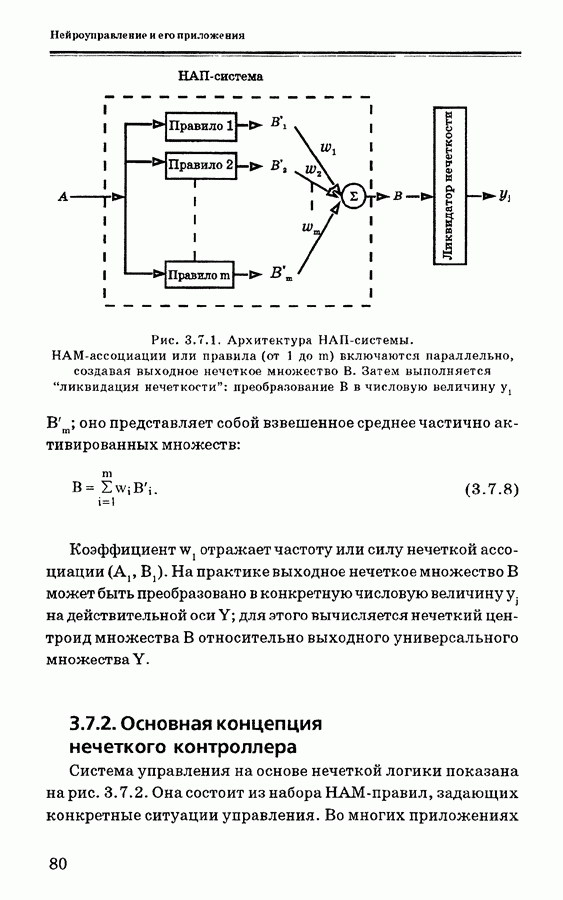
- 3.7.2. Основная концепция нечеткого контроллера
- 3.8. Заключение
- 4. ТЕХНОЛОГИИ НЕЙРОННОГО УПРАВЛЕНИЯ
- 4.2. Общие сведения о нейронном управлении
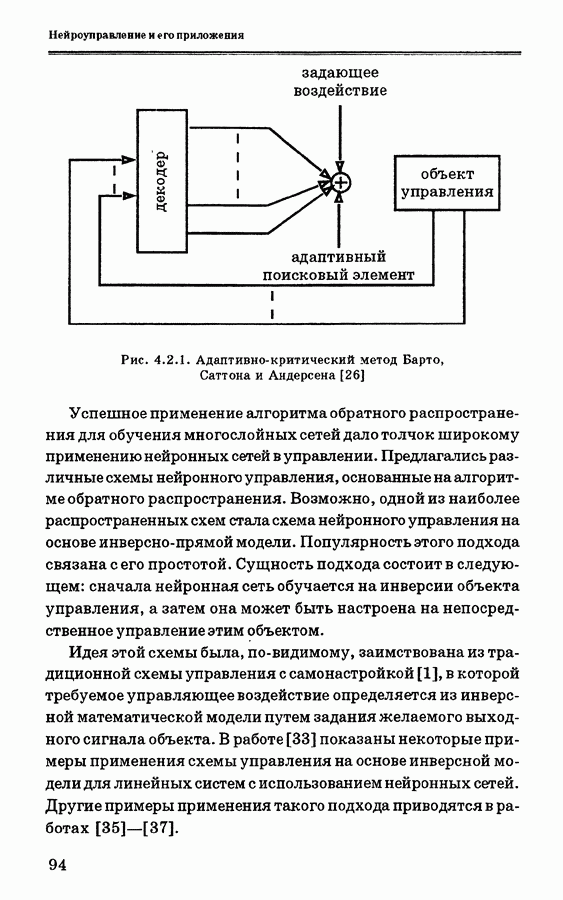
- 4.2.1. Подходы к нейронному управлению
- 4.2.2. Общая схема управления
- 4.3. Последовательная схема нейронного управления
- 4.4. Расширение последовательной схемы нейронного управления
- 4.4.2. Нейроморфные структуры управления
- 4.4.3. Конфигурации обучения
- 4.4.4. Эффективное оперативное управление
- 4.4.5. Алгоритмы обучения
- 4.4.6. Оценка алгоритмов обучения на основе моделирования
- 4.5. Параллельная схема управления
- 4.6. Алгоритм обучения по ошибке обратной связи
- 4.7. Расширение применения нейроконтроллеров параллельного типа
- 4.7.2. Линеаризованная система управления
- 4.7.3. Система управления с нейронными сетями
- 4.7.4. Нелинейный алгоритм наблюдения для нейронной сети
- 4.7.5. Нелинейный контроллер для нейронной сети
- 4.7.6. Численное моделирование
- 4.8. Схема нейронного управления с самонастройкой
- 4.9. ПИД-нейроконтроллер с самонастройкой
- 4.9.1. Вывод уравнений ПИД-нейроконтроллера с самонастройкой
- 4.9.2. Примеры эмуляции
- 4.10. Схема нейронного управления с эмулятором и контроллером (схема обратного распространения во времени)
- 4.11. Заключение
- 5. ПРИЛОЖЕНИЯ НЕЙРОННОГО УПРАВЛЕНИЯ
- 5.2. Применение нейронного управления в системе регулирования процессов в водяной ванне и сравнение его с другими схемами управления
- 5.2.2. Система управления температурой водяной ванны
- 5.2.3. Схема нейронного управления
- 5.2.4. Схема управления на основе нечеткой логики
- 5.2.5. Схема обобщенного прогнозирующего управления
- 5.2.6. Экспериментальные данные и их анализ
- 5.2.7. Заключение
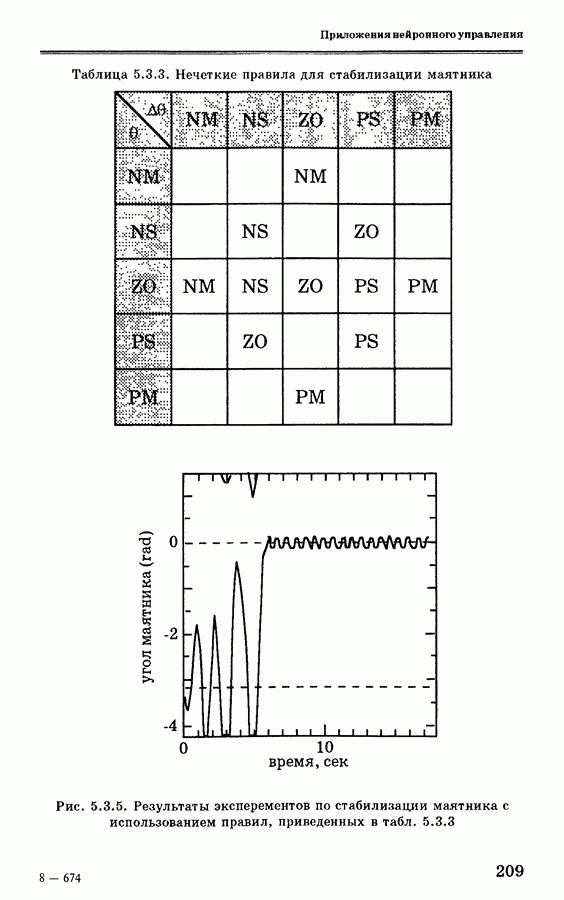
- 5.3. Система стабилизации инвертированного маятника на основе нейронных сетей
- 5.3.2. Система стабилизации инвертированного маятника
- 5.3.3. Инициализация поворотного управления с использованием нечеткой логики
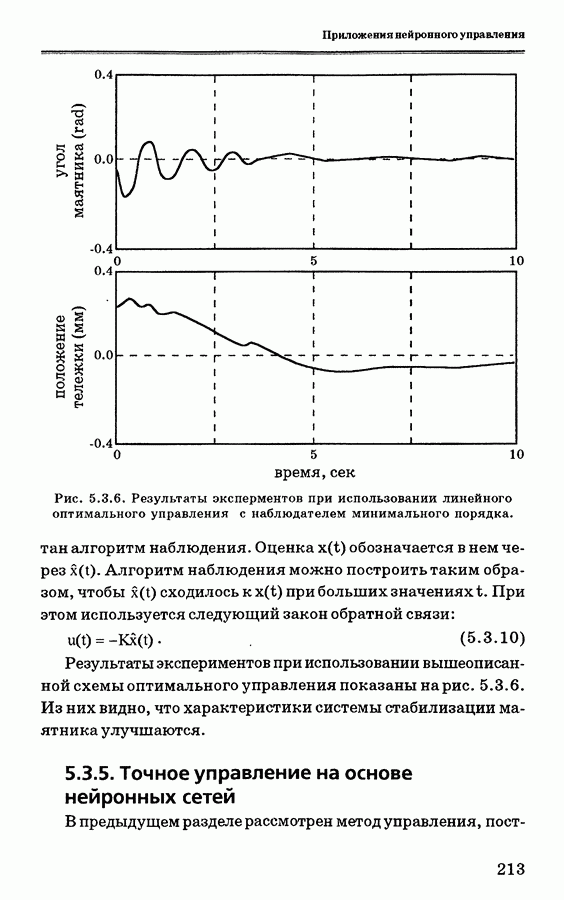
- 5.3.4. Применение стратегии оптимального управления для стабилизации маятника
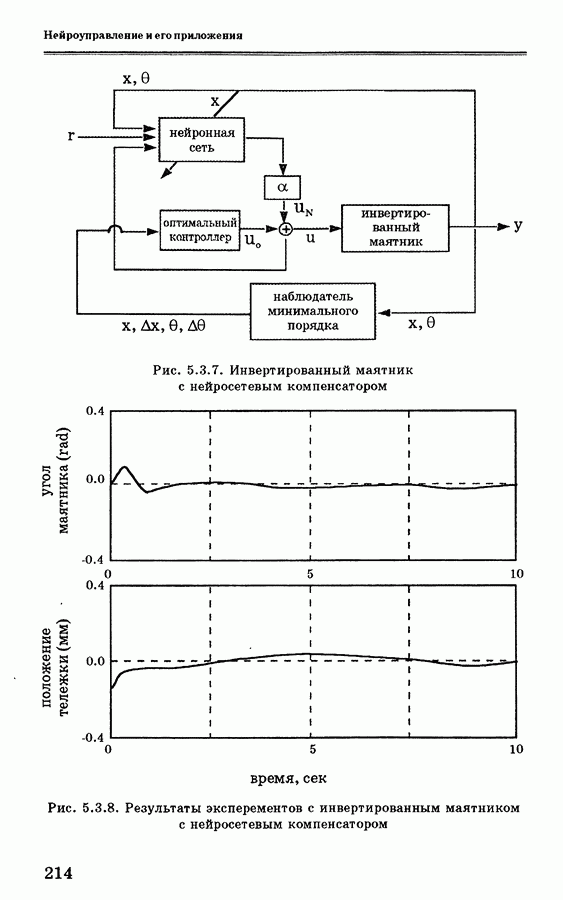
- 5.3.5. Точное управление на основе нейронных сетей
- 5.3.6. Заключение
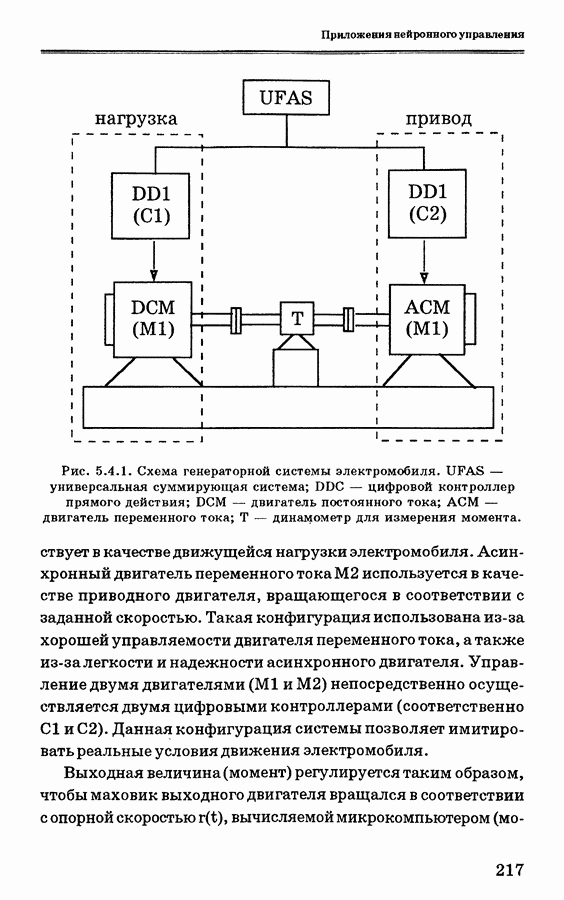
- 5.4. Применение ПИД-нейроконтроллера с самонастройкой для управления скоростью электромобиля
- 5.4.2. Система управления электромобилем
- 5.4.3. ПИД-нейроконтроллер с самонастройкой
- 5.4.4. Применение нейронной сети для управления скоростью электромобиля
- 5.4.5. Заключение
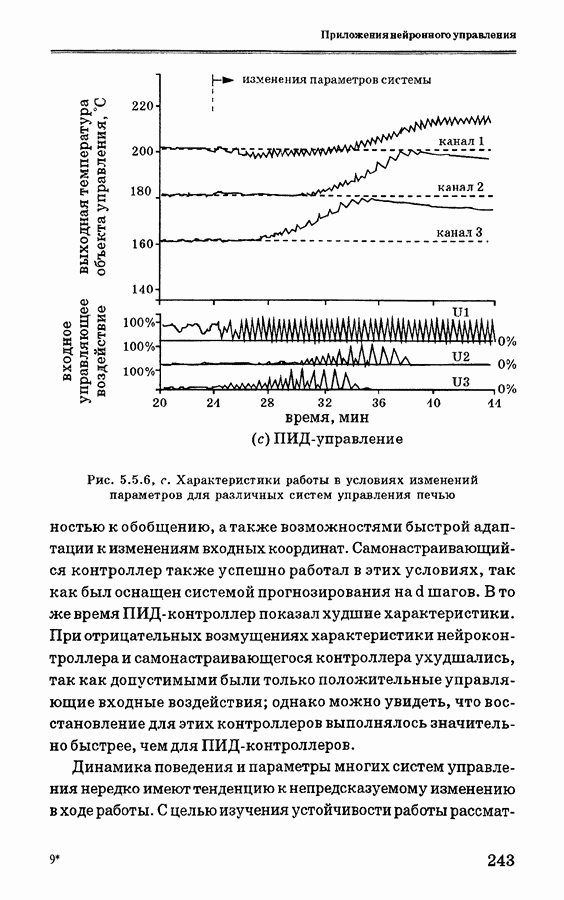
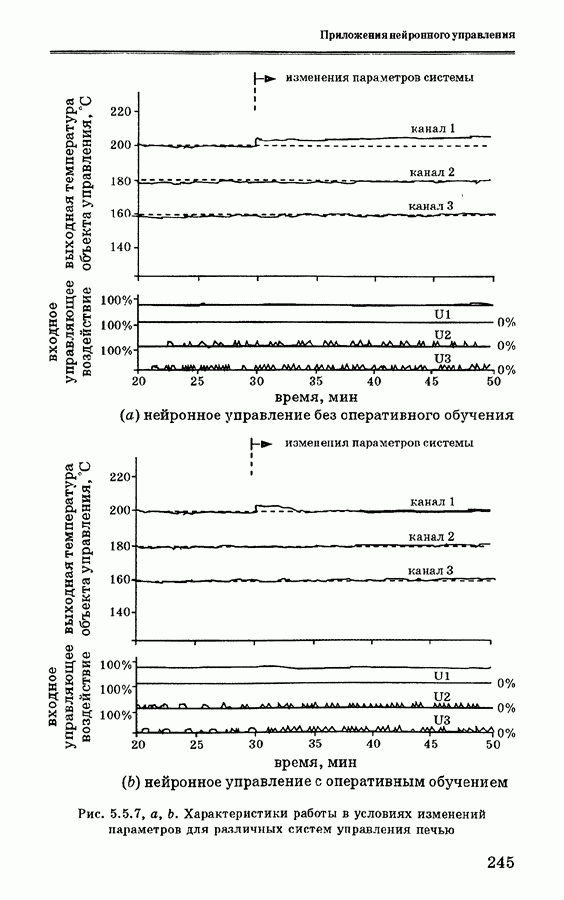
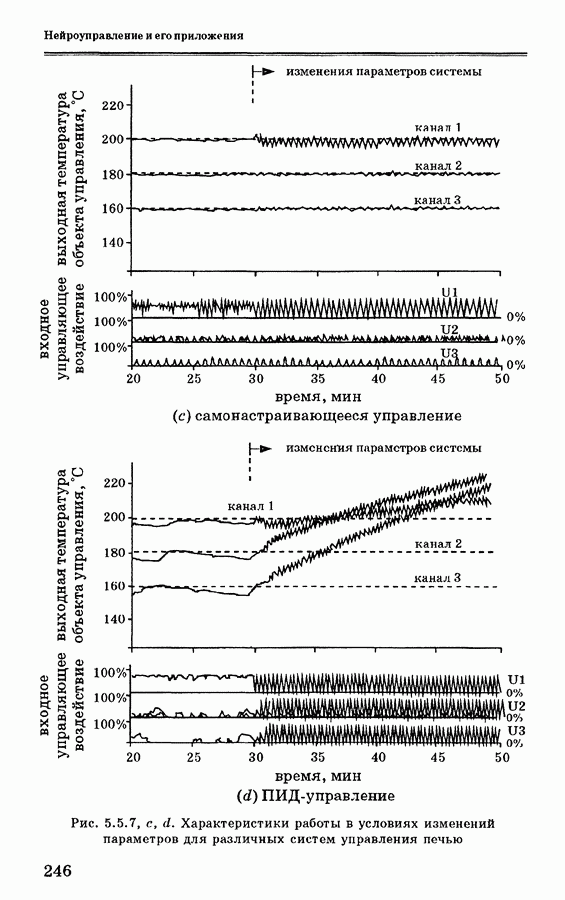
- 5.5. Применение нейронных сетей для управления печью
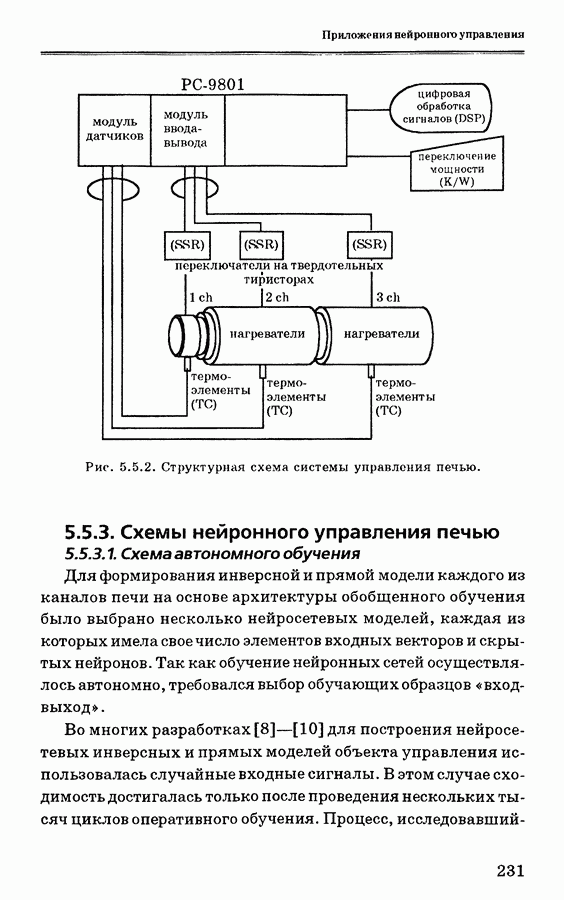
- 5.5.2. Система управления печью
- 5.5.3. Схемы нейронного управления печью
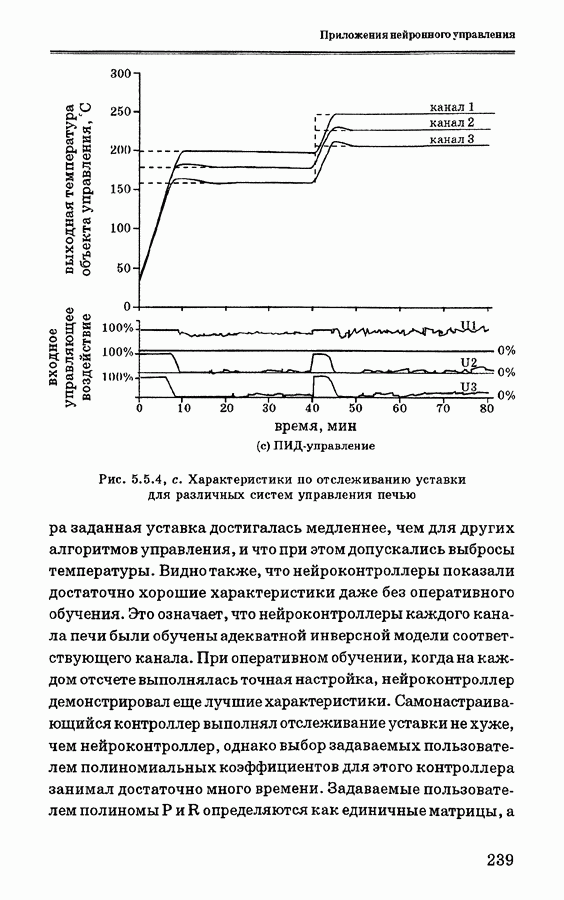
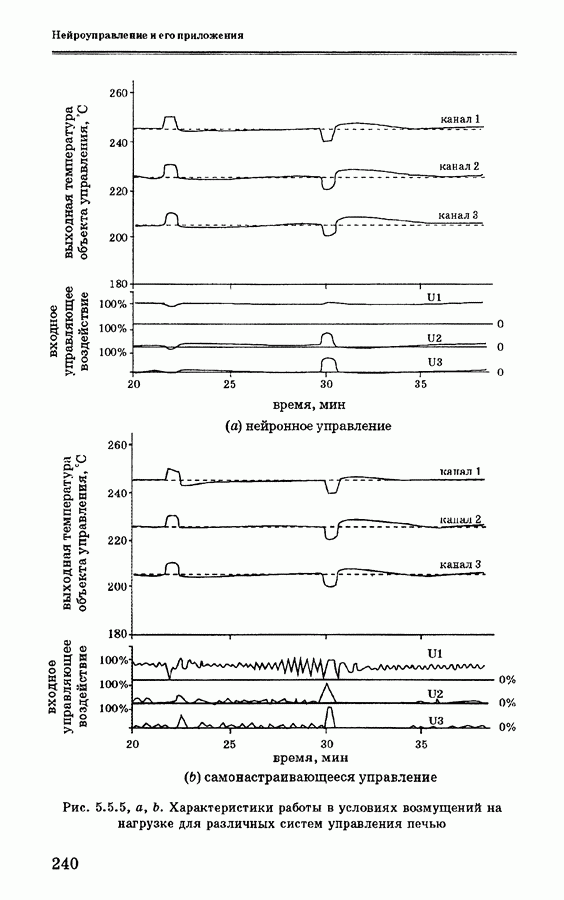
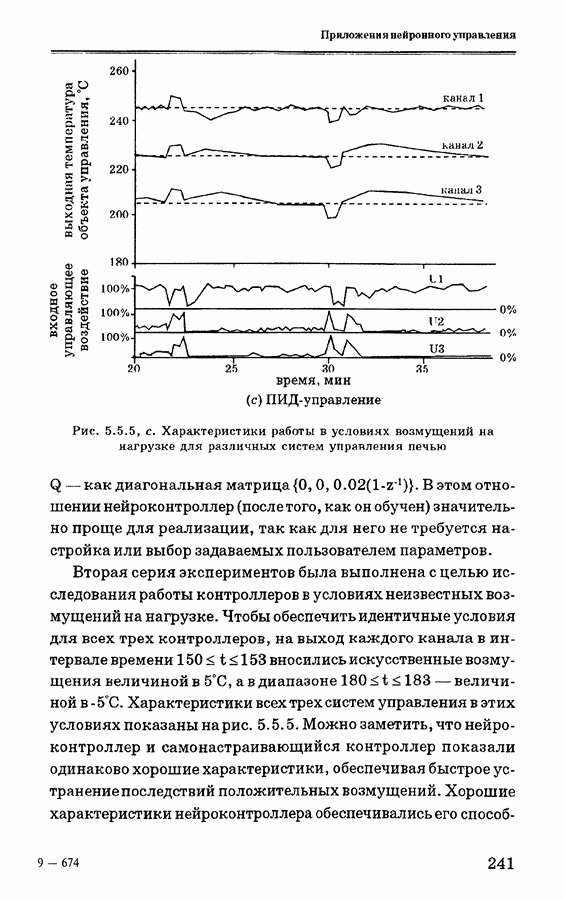
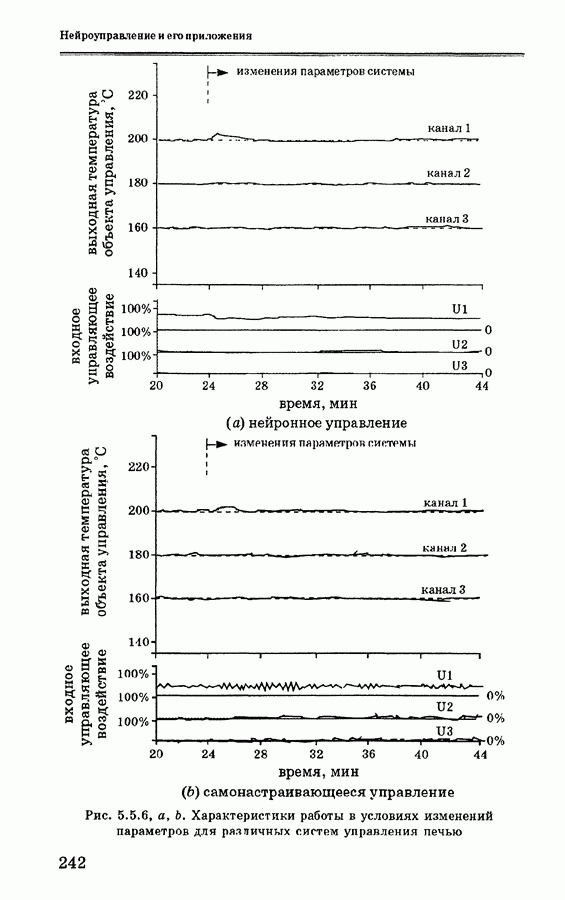
- 5.5.4. Анализ экспериментальных данных
- 5.6. Заключительные замечания и выводы
- Литература
- ЛИСТИНГ ПРОГРАММЫ