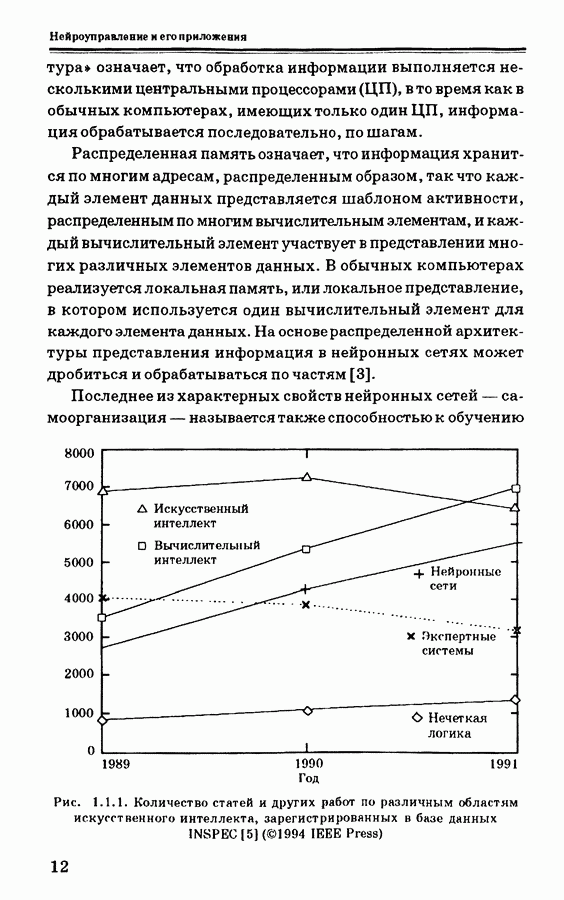
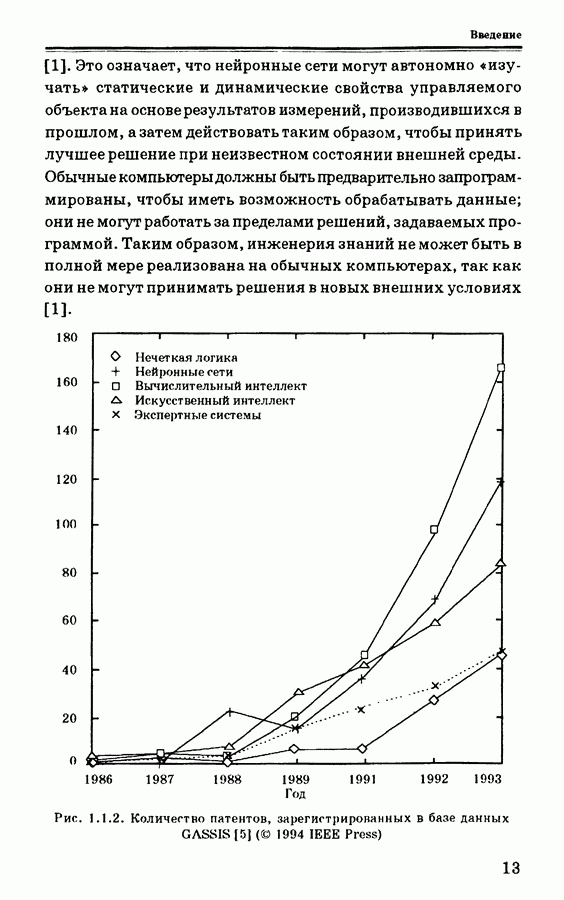
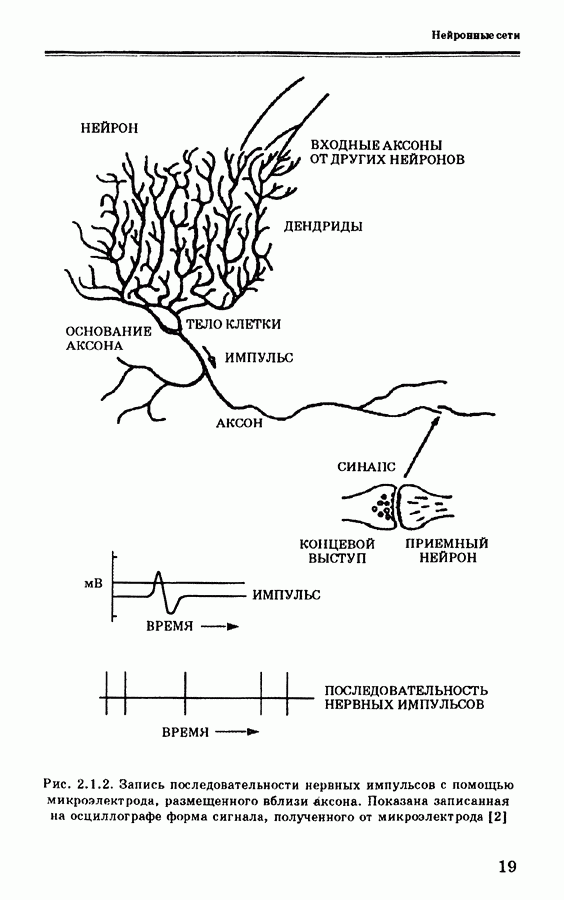
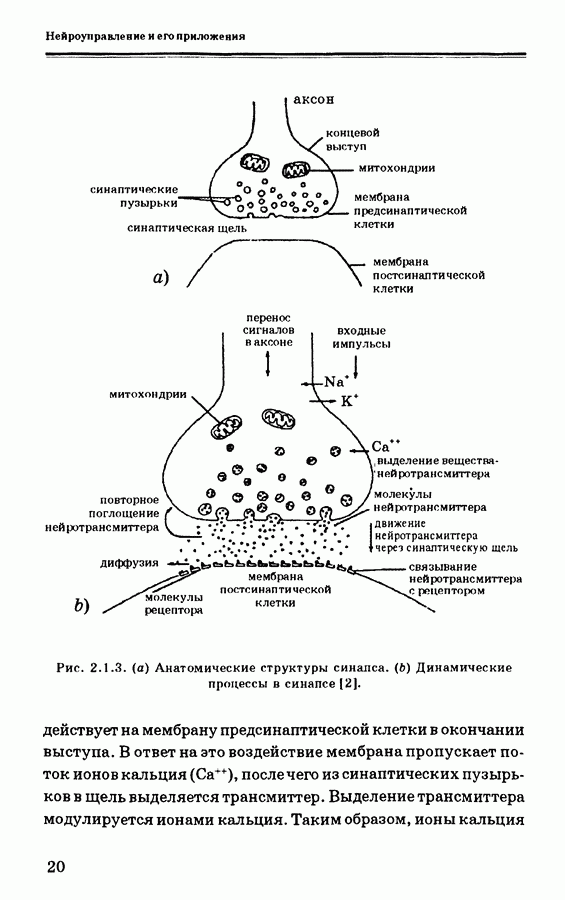
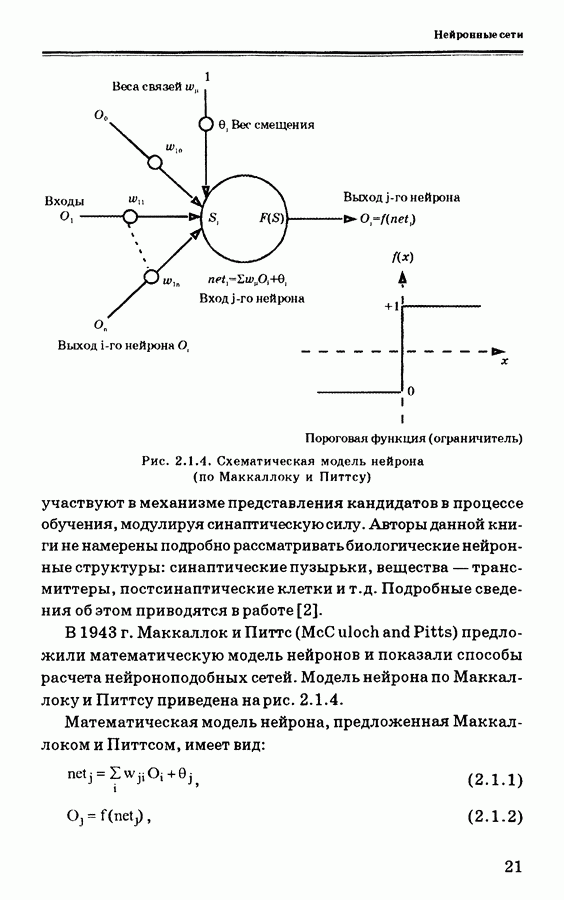
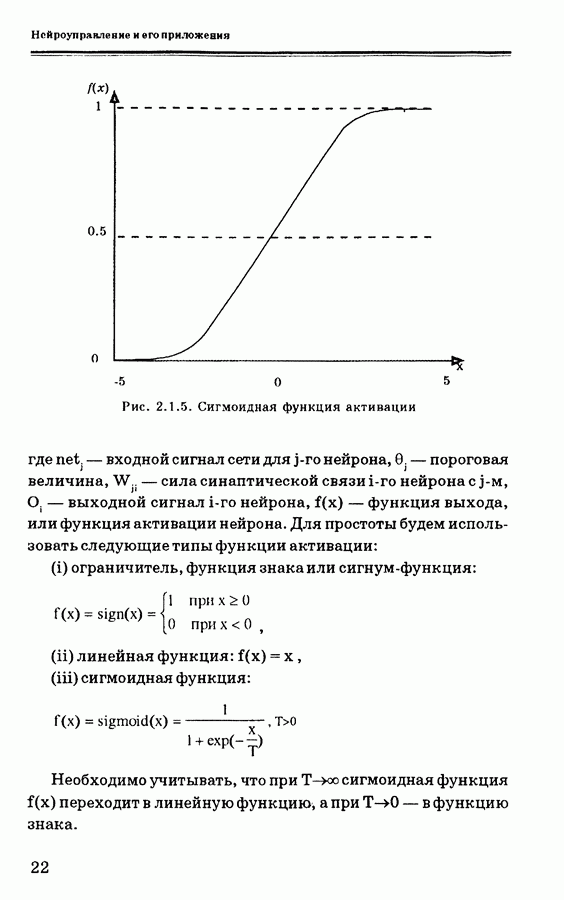
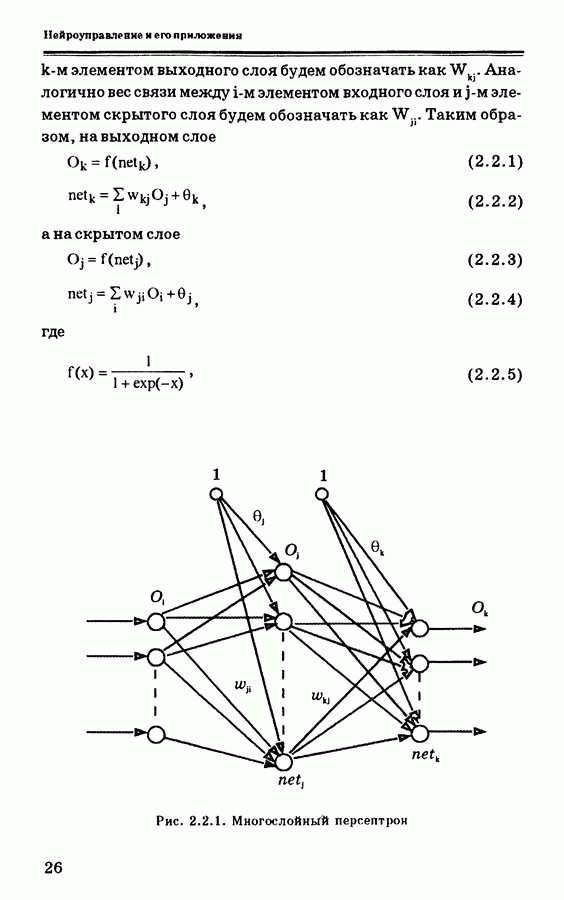
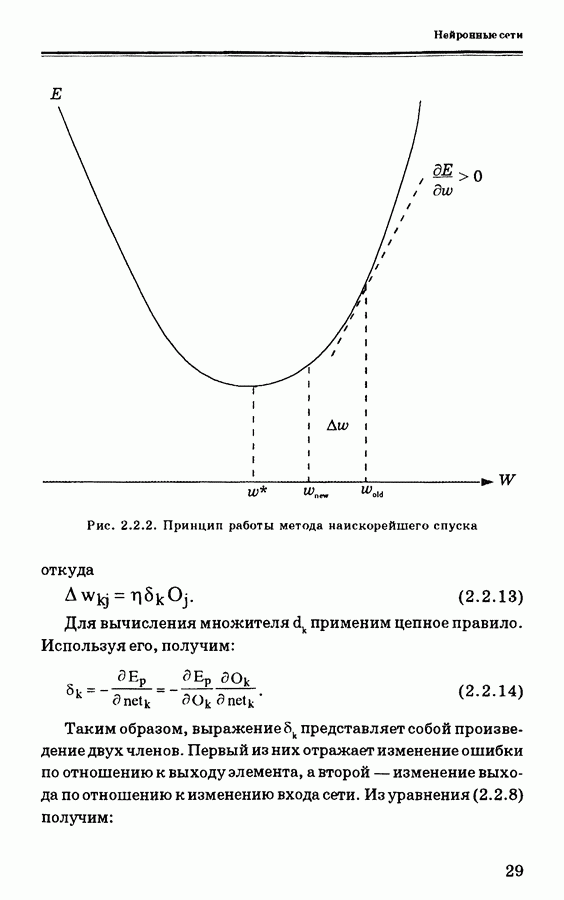
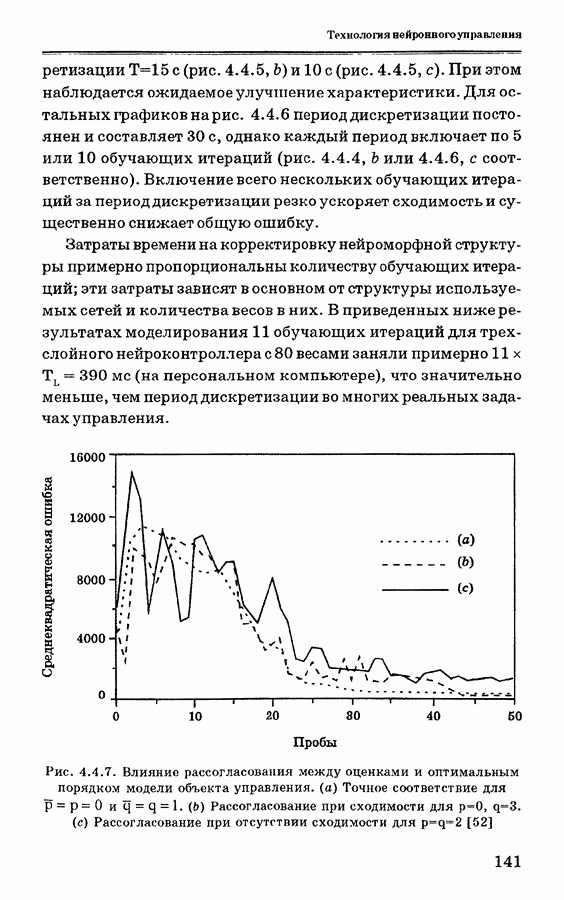
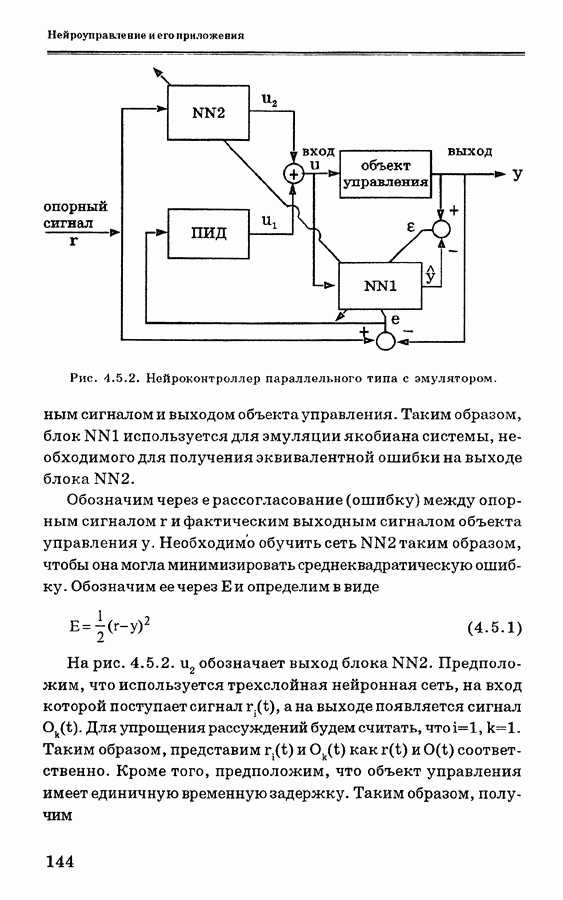
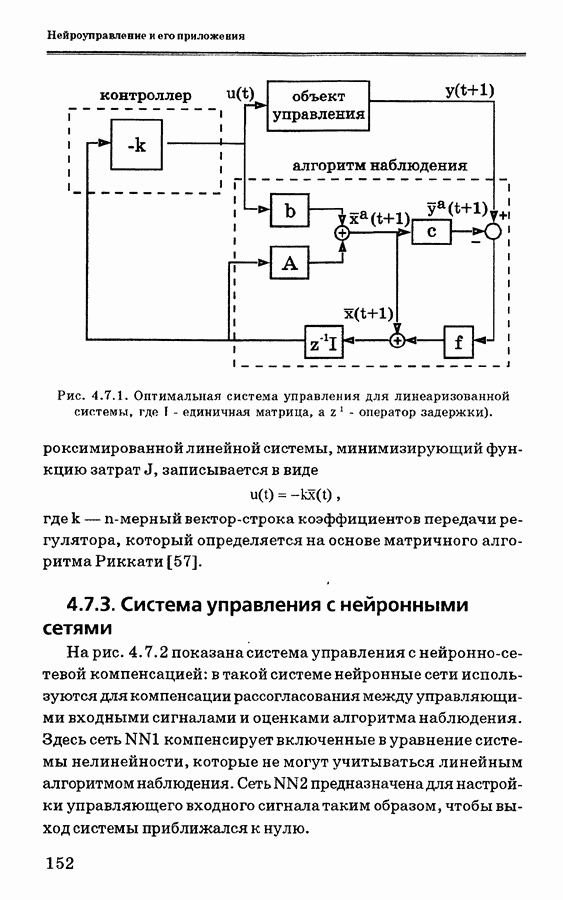
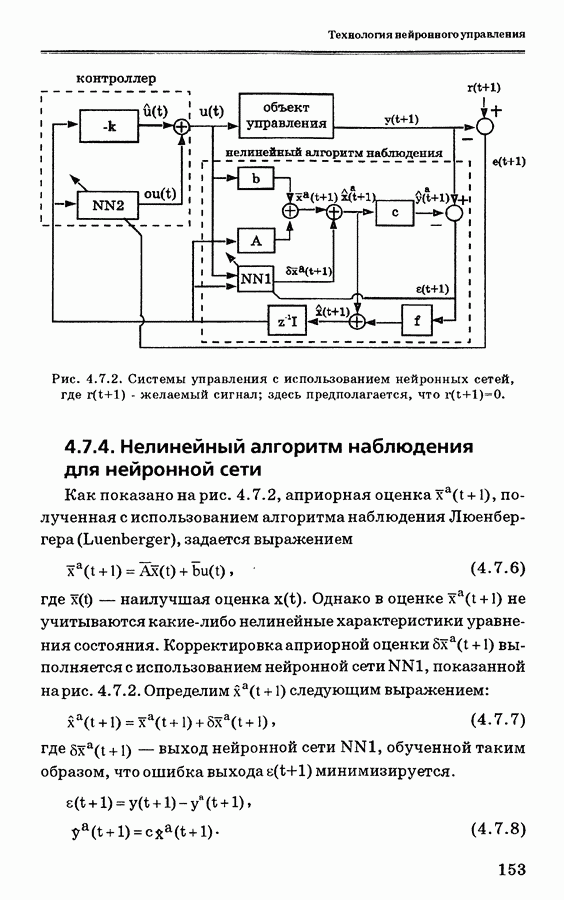
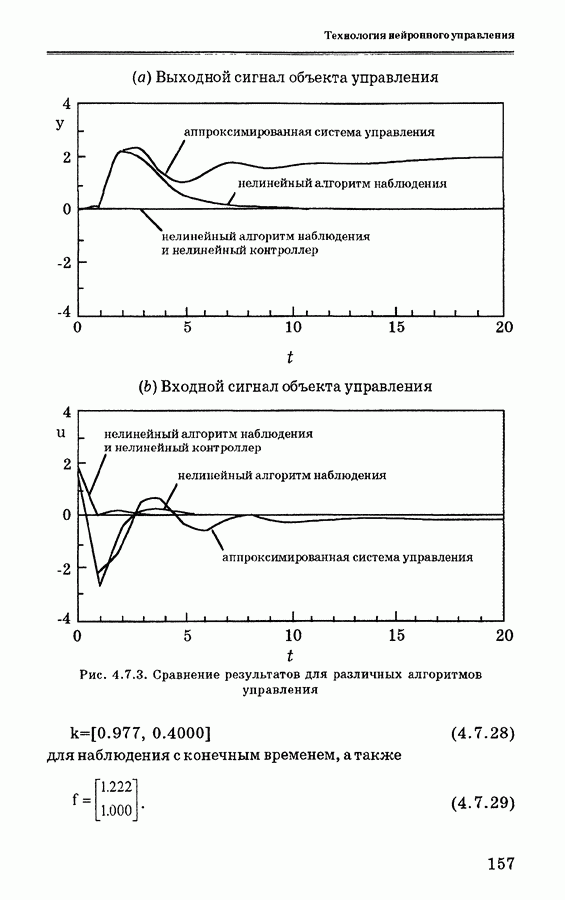
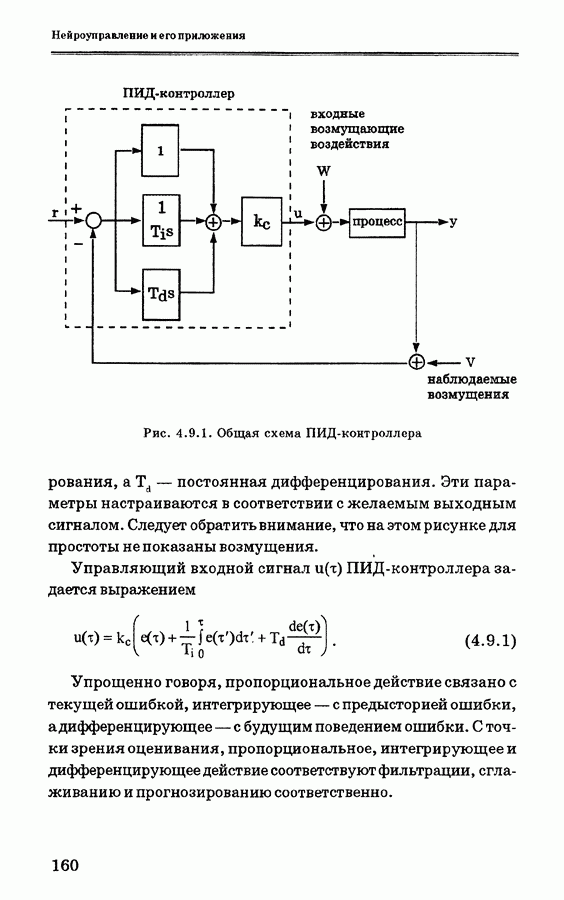
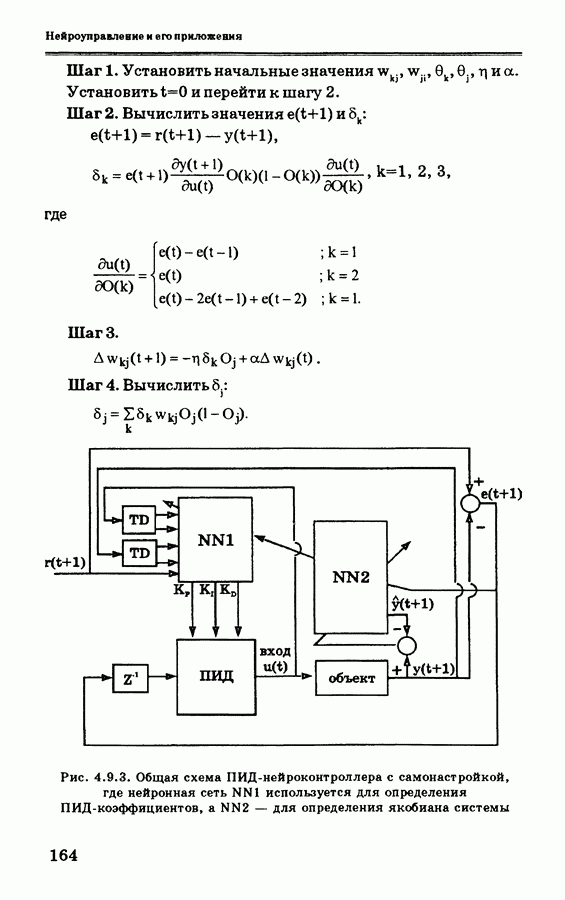
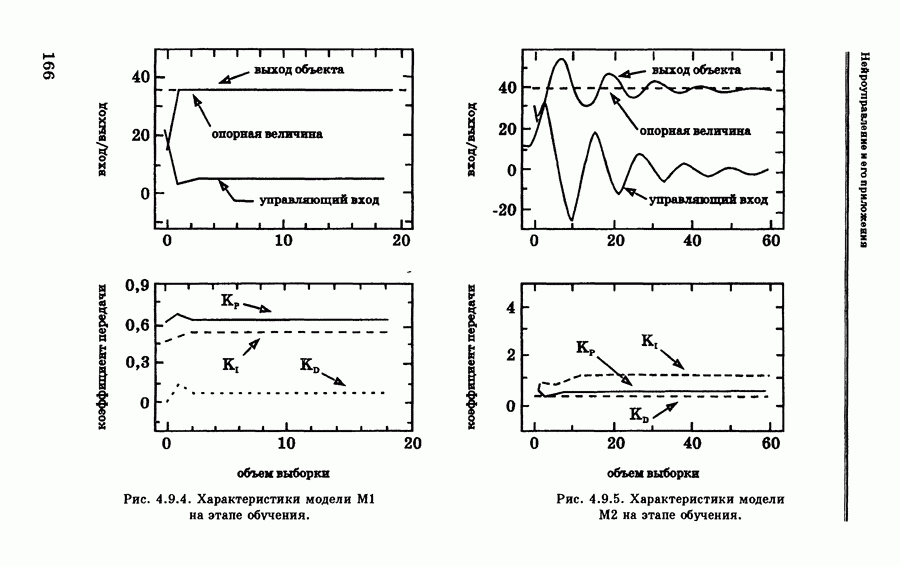
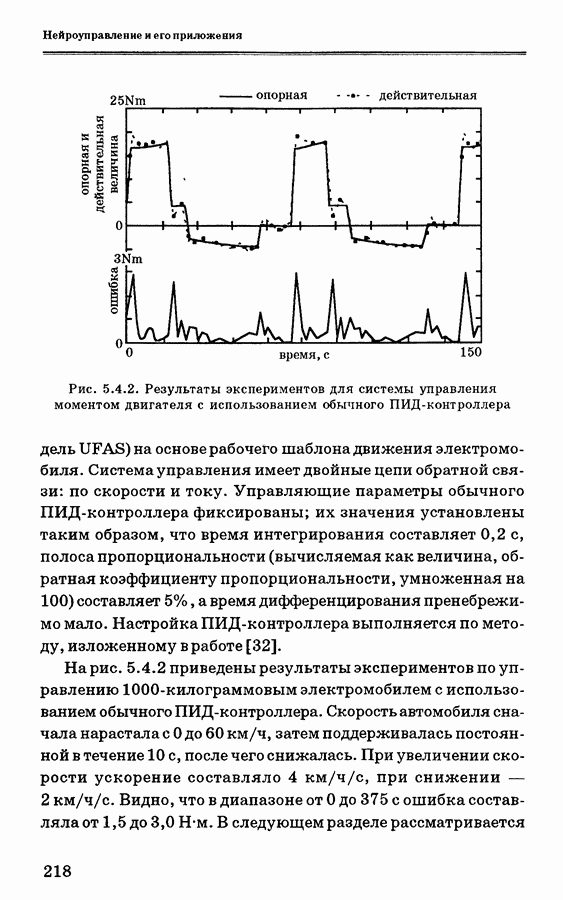
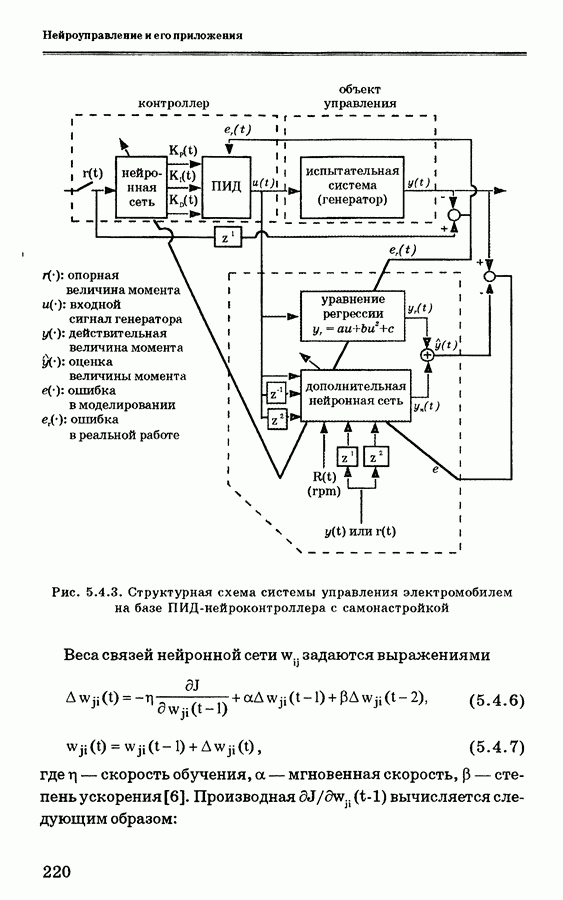
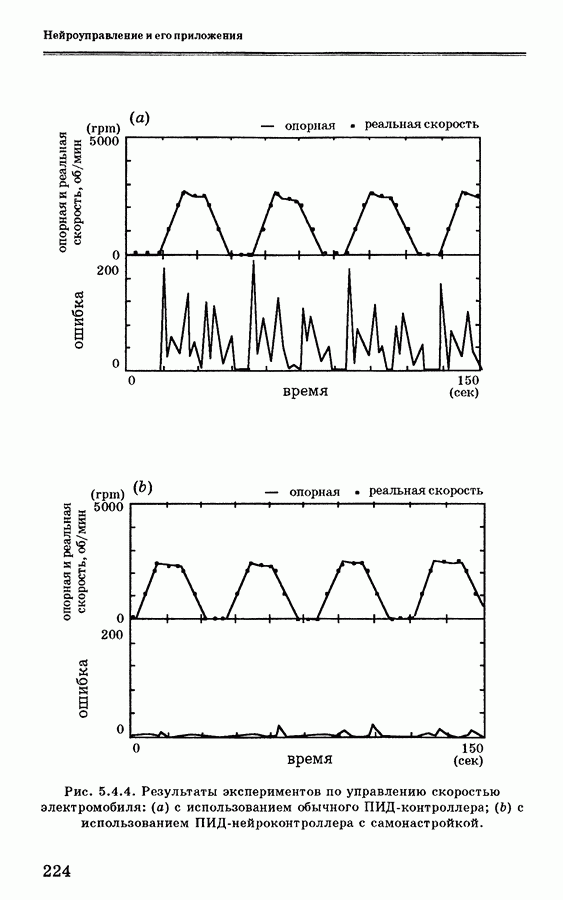
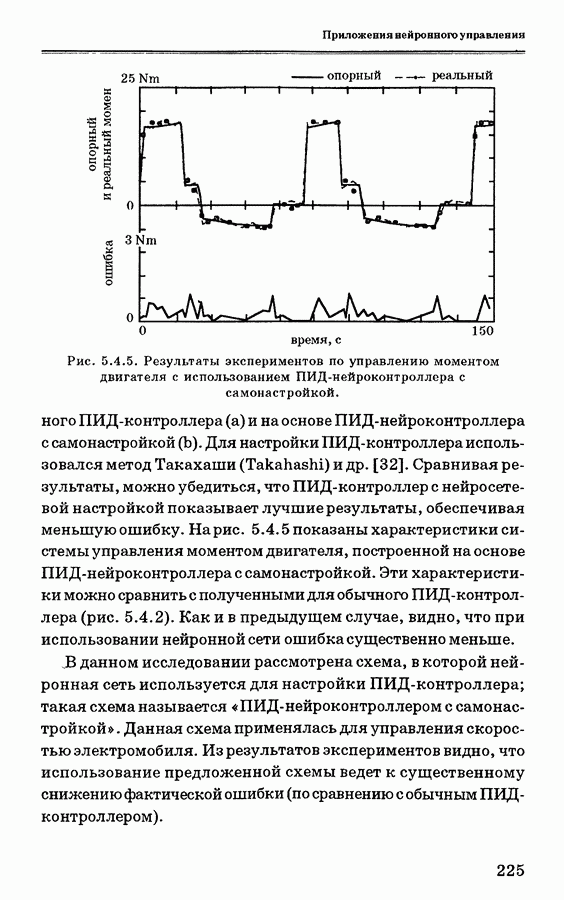
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
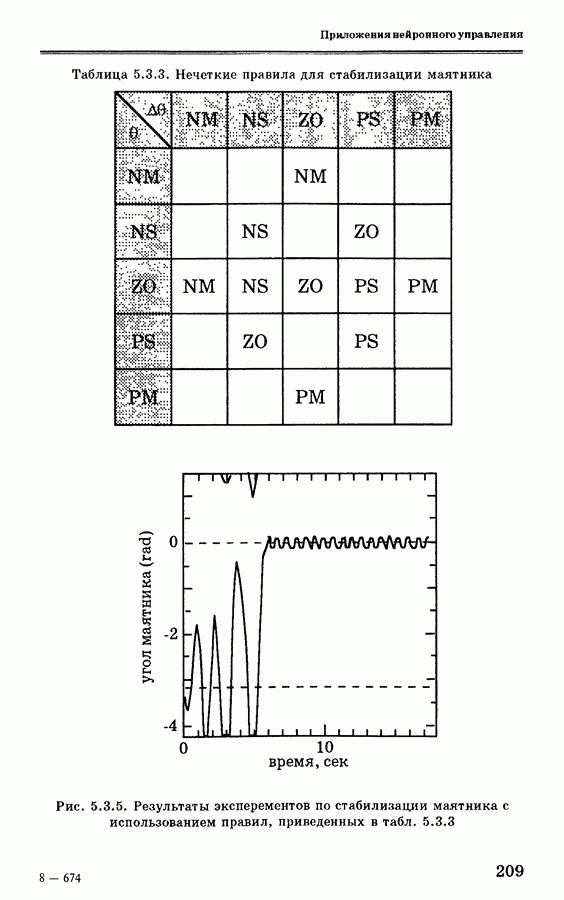
5.3.4. Применение стратегии оптимального управления для стабилизации маятника
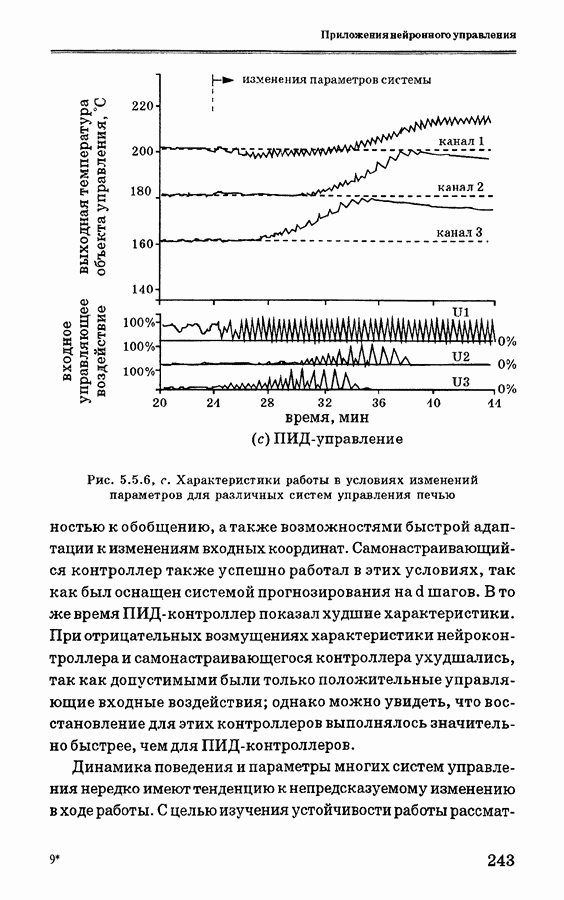
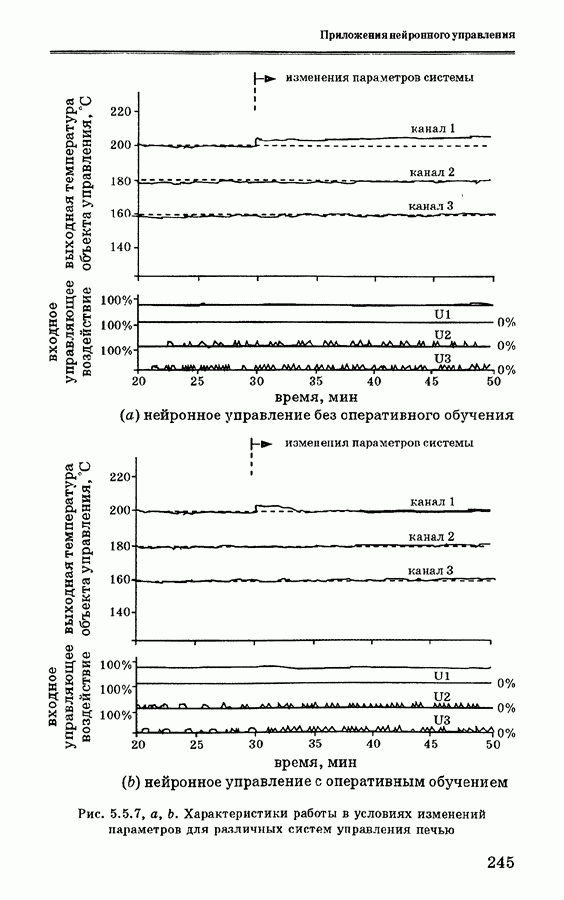
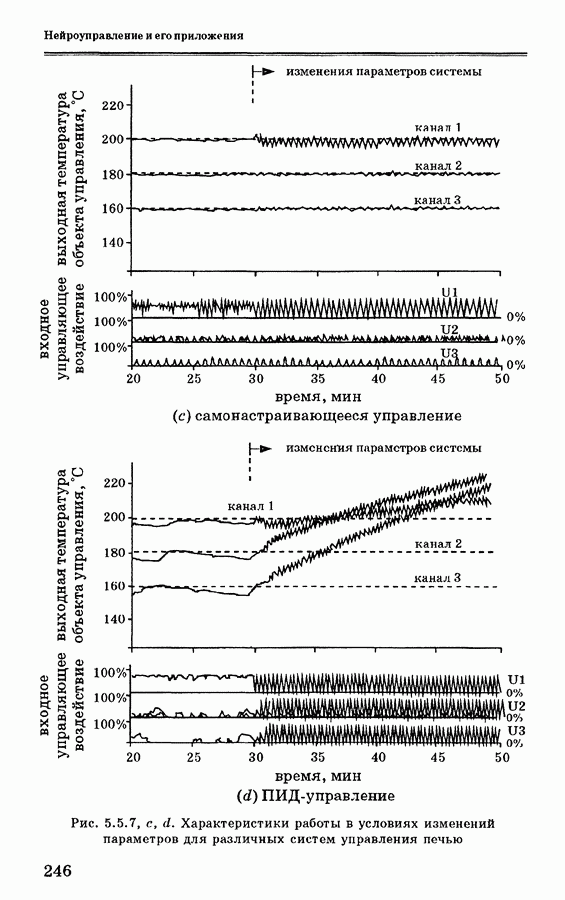
Нечеткий контроллер применяется в основном для начальной установки инвертированного маятника. Характеристики системы можно улучшить за счет добавления нечетких правил. Однако из-за ограниченности памяти и быстродействия персонального компьютера увеличение количества нечетких правил практически невозможно для систем реального времени, когда требуется быстрая реакция. Кроме того, достаточно сложно выбрать набор правил, обеспечивающий улучшение характеристик нечеткого контроллера. Обычно для грубой настройки применяется второй набор правил, предназначенный для стабилизационного управления.
Отметим, что в «диапазоне устойчивости» нелинейные уравнения динамики, описывающие инвертированный маятник, могут быть аппроксимированы линейными уравнениями. В этом случае для стабилизации инвертированного маятника можно использовать традиционные методы управления. В данном случае применяется теория линейного квадратичного оптимального управления [35]. Рассмотрим сначала уравнения движения маятника и тележки:

где  — эквивалентная масса тележки;
— эквивалентная масса тележки;  — масса инвертированного маятника;
— масса инвертированного маятника;  — эквивалентный коэффициент трения тележки;
— эквивалентный коэффициент трения тележки;  — расстояние от оси до центра тяжести маятника;
— расстояние от оси до центра тяжести маятника;  — момент инерции центра тяжести маятника; С — коэффициент вязкого трения оси;
— момент инерции центра тяжести маятника; С — коэффициент вязкого трения оси;  — ускорение силы тяжести.
— ускорение силы тяжести.
Если считать, что  и использовать приближенные равенства как точные, то нелинейная система уравнений (5.3.1), (5.3.2) становится линейной. В этом случае имеем
и использовать приближенные равенства как точные, то нелинейная система уравнений (5.3.1), (5.3.2) становится линейной. В этом случае имеем

где


В дискретном времени данные уравнения представляются следующим образом:

где  — интервал дискретизации. Стратегия оптимального управления состоит в минимизации функции затрат
— интервал дискретизации. Стратегия оптимального управления состоит в минимизации функции затрат  задаваемой выражением
задаваемой выражением

Оптимальный управляющий сигнал  задается в этом случае выражением:
задается в этом случае выражением:

где Н — устойчивое решение уравнения Риккати:

Используя приведенную выше линейную аппроксимацию системы, можно применить линейное квадратичное оптимальное управление для стабилизации маятника. Так как значение  неизвестно, необходимо найти его оценку по данным наблюдения
неизвестно, необходимо найти его оценку по данным наблюдения  Авторами данного исследования
Авторами данного исследования

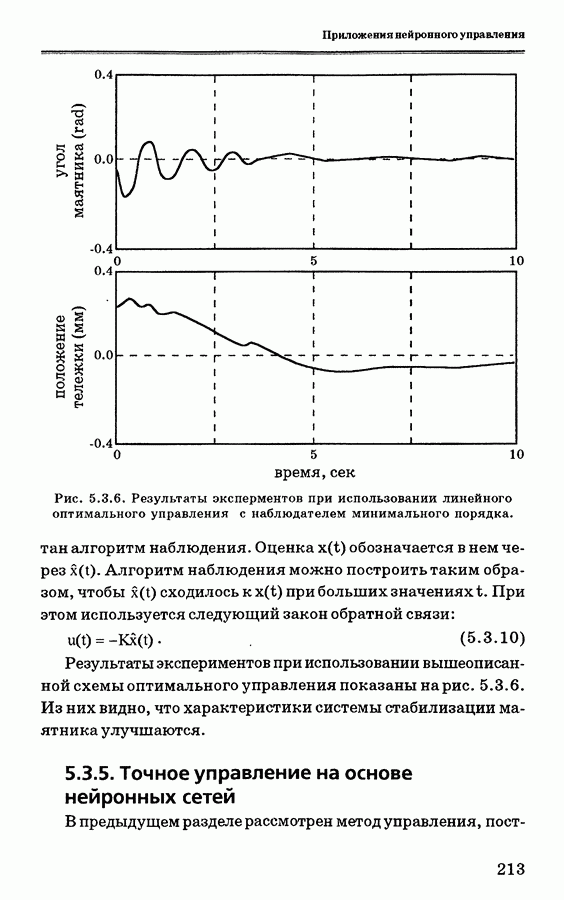
Рис. 5.3.6. Результаты эксперментов при использовании линейного оптимального управления с наблюдателем минимального порядка.
разработан алгоритм наблюдения. Оценка  обозначается в нем через
обозначается в нем через  Алгоритм наблюдения можно построить таким образом, чтобы
Алгоритм наблюдения можно построить таким образом, чтобы  сходилось к
сходилось к  при больших значениях
при больших значениях  При этом используется следующий закон обратной связи:
При этом используется следующий закон обратной связи:

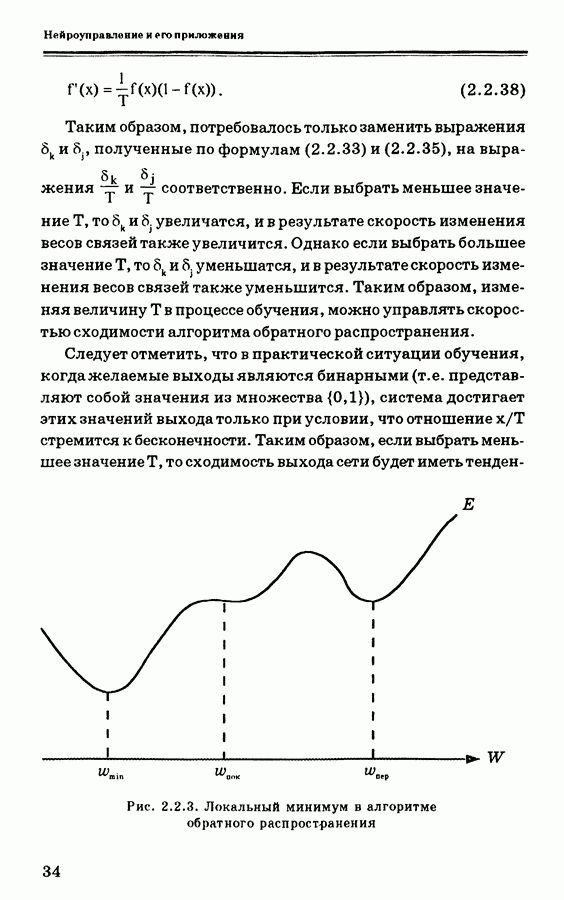
Результаты экспериментов при использовании вышеописанной схемы оптимального управления показаны на рис. 5.3.6. Из них видно, что характеристики системы стабилизации маятника улучшаются.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРОВ ПЕРЕВОДА
- 1. ВВЕДЕНИЕ
- 1.1. Общие сведения об интеллектуальном управлении
- 2. НЕЙРОННЫЕ СЕТИ
- 2.2. Алгоритм обратного распространения
- 2.2.2. Вывод алгоритма обратного распространения
- 2.2.2.2. Правило для скрытого слоя
- 2.2.3. Алгоритм обратного распространения: порядок реализации
- 2.2.4. Обсуждение алгоритма обратного распространения
- 2.3. Заключение
- 3. ТРАДИЦИОННЫЕ СХЕМЫ УПРАВЛЕНИЯ
- 3.2. ПИ- и ПИД-контроллеры с дискретным временем
- 3.3. Управление с самонастройкой
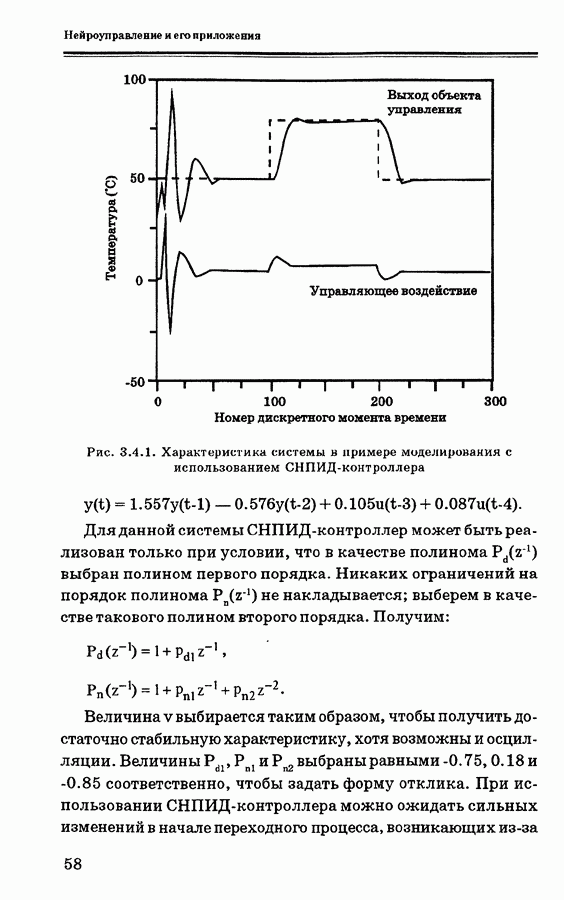
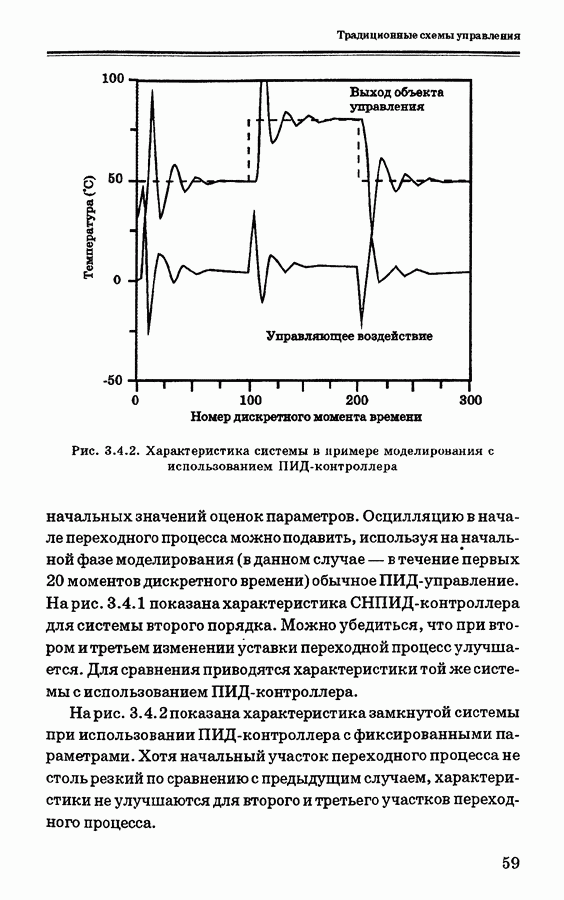
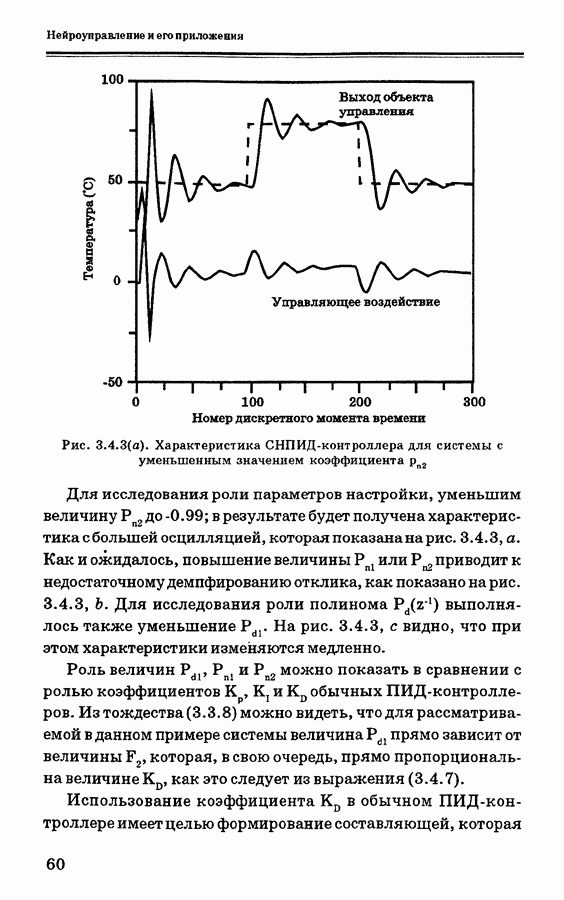
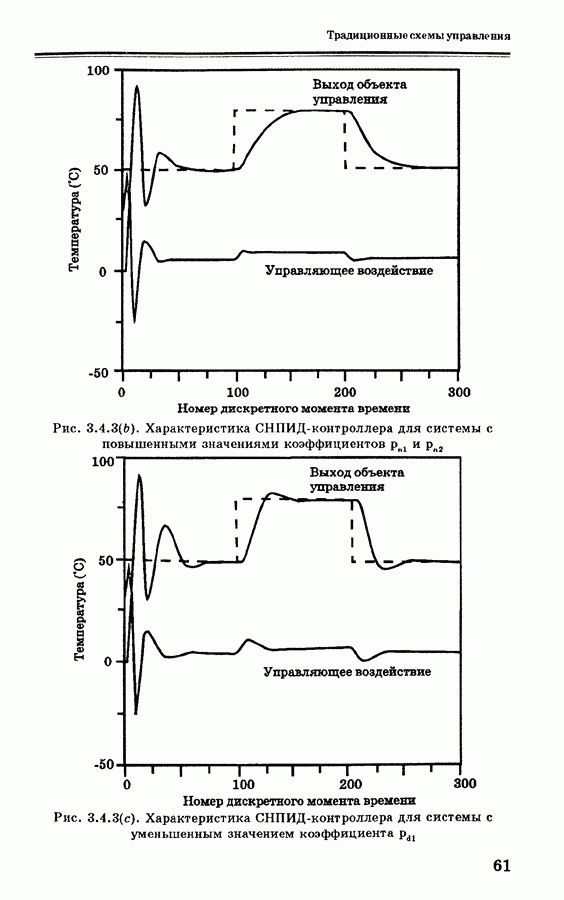
- 3.4. Самонастраивающиеся ПИ- и ПИД- контроллеры
- 3.5. ПИД-управление с самонастройкой: многомерный подход
- 3.5.1. Пример моделирования
- 3.6. Обобщенное прогнозирующее управление: некоторые теоретические аспекты
- 3.6.2. Модель объекта управления и решение задачи оптимизации
- 3.7. Управление на основе нечеткой логики
- 3.7.1. Краткие сведения по теории нечетких множеств и нечетких систем
- 3.7.2. Основная концепция нечеткого контроллера
- 3.8. Заключение
- 4. ТЕХНОЛОГИИ НЕЙРОННОГО УПРАВЛЕНИЯ
- 4.2. Общие сведения о нейронном управлении
- 4.2.1. Подходы к нейронному управлению
- 4.2.2. Общая схема управления
- 4.3. Последовательная схема нейронного управления
- 4.4. Расширение последовательной схемы нейронного управления
- 4.4.2. Нейроморфные структуры управления
- 4.4.3. Конфигурации обучения
- 4.4.4. Эффективное оперативное управление
- 4.4.5. Алгоритмы обучения
- 4.4.6. Оценка алгоритмов обучения на основе моделирования
- 4.5. Параллельная схема управления
- 4.6. Алгоритм обучения по ошибке обратной связи
- 4.7. Расширение применения нейроконтроллеров параллельного типа
- 4.7.2. Линеаризованная система управления
- 4.7.3. Система управления с нейронными сетями
- 4.7.4. Нелинейный алгоритм наблюдения для нейронной сети
- 4.7.5. Нелинейный контроллер для нейронной сети
- 4.7.6. Численное моделирование
- 4.8. Схема нейронного управления с самонастройкой
- 4.9. ПИД-нейроконтроллер с самонастройкой
- 4.9.1. Вывод уравнений ПИД-нейроконтроллера с самонастройкой
- 4.9.2. Примеры эмуляции
- 4.10. Схема нейронного управления с эмулятором и контроллером (схема обратного распространения во времени)
- 4.11. Заключение
- 5. ПРИЛОЖЕНИЯ НЕЙРОННОГО УПРАВЛЕНИЯ
- 5.2. Применение нейронного управления в системе регулирования процессов в водяной ванне и сравнение его с другими схемами управления
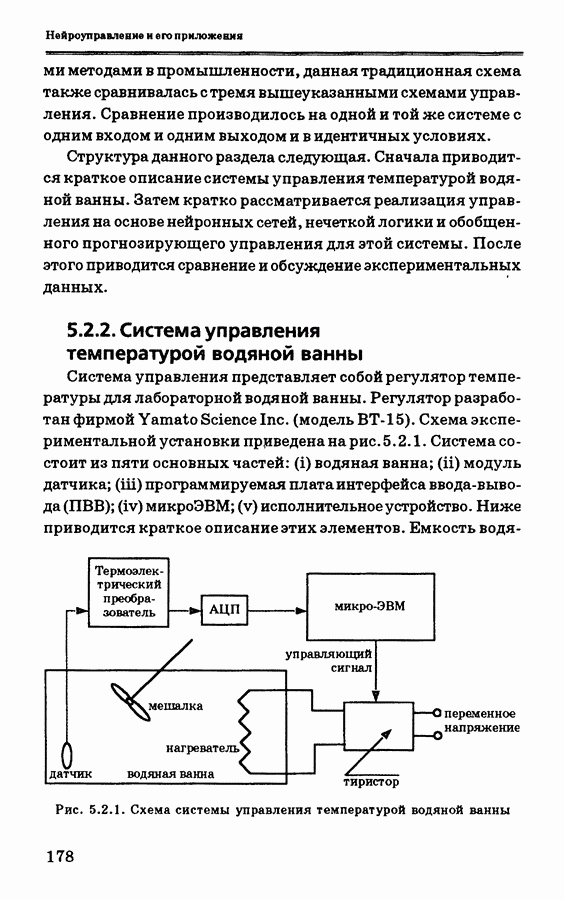
- 5.2.2. Система управления температурой водяной ванны
- 5.2.3. Схема нейронного управления
- 5.2.4. Схема управления на основе нечеткой логики
- 5.2.5. Схема обобщенного прогнозирующего управления
- 5.2.6. Экспериментальные данные и их анализ
- 5.2.7. Заключение
- 5.3. Система стабилизации инвертированного маятника на основе нейронных сетей
- 5.3.2. Система стабилизации инвертированного маятника
- 5.3.3. Инициализация поворотного управления с использованием нечеткой логики
- 5.3.4. Применение стратегии оптимального управления для стабилизации маятника
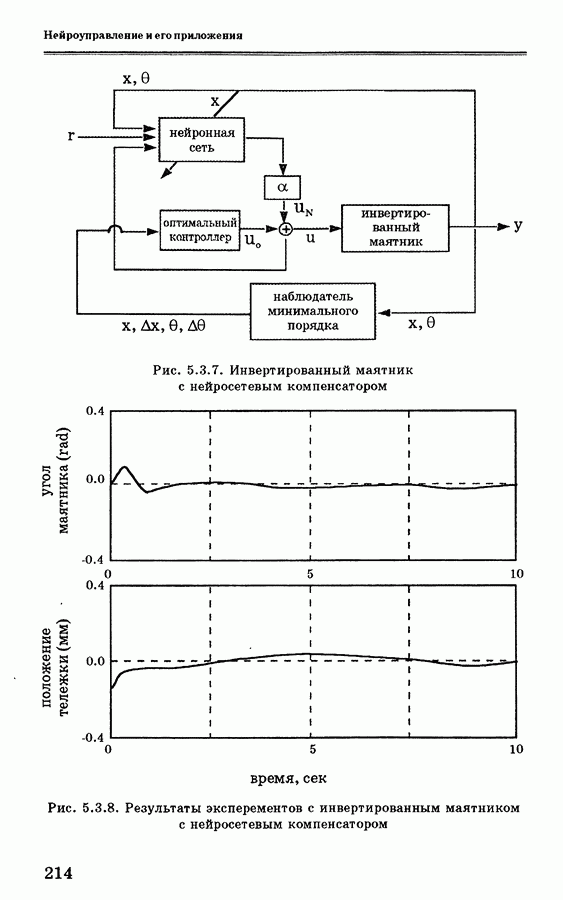
- 5.3.5. Точное управление на основе нейронных сетей
- 5.3.6. Заключение
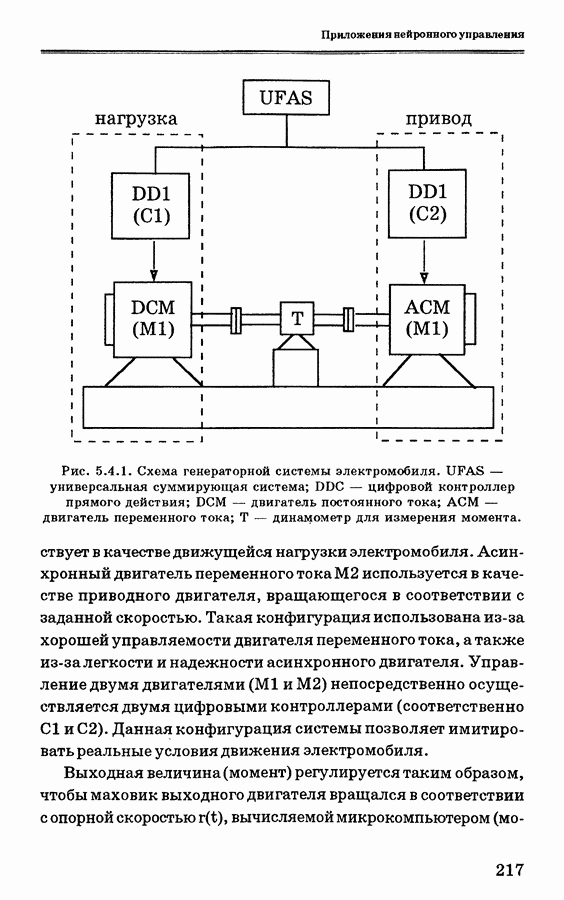
- 5.4. Применение ПИД-нейроконтроллера с самонастройкой для управления скоростью электромобиля
- 5.4.2. Система управления электромобилем
- 5.4.3. ПИД-нейроконтроллер с самонастройкой
- 5.4.4. Применение нейронной сети для управления скоростью электромобиля
- 5.4.5. Заключение
- 5.5. Применение нейронных сетей для управления печью
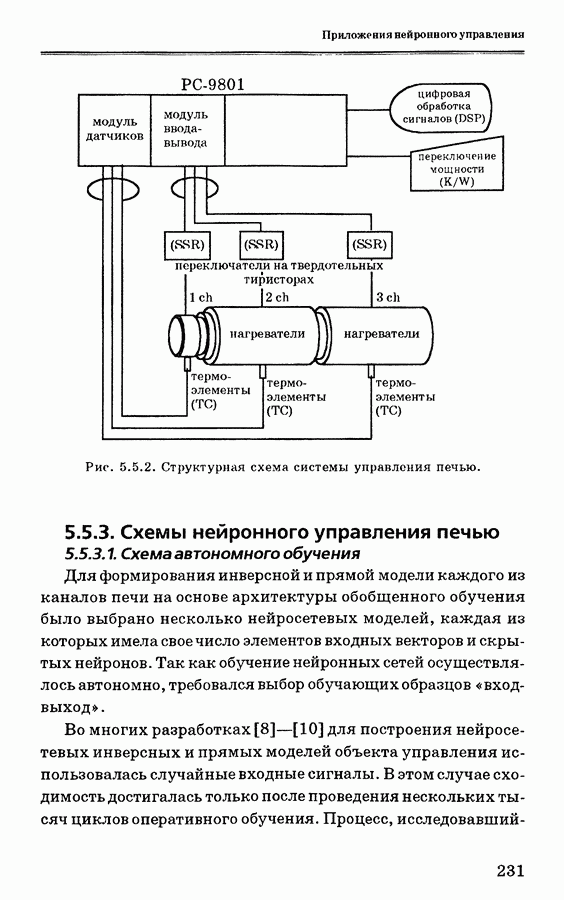
- 5.5.2. Система управления печью
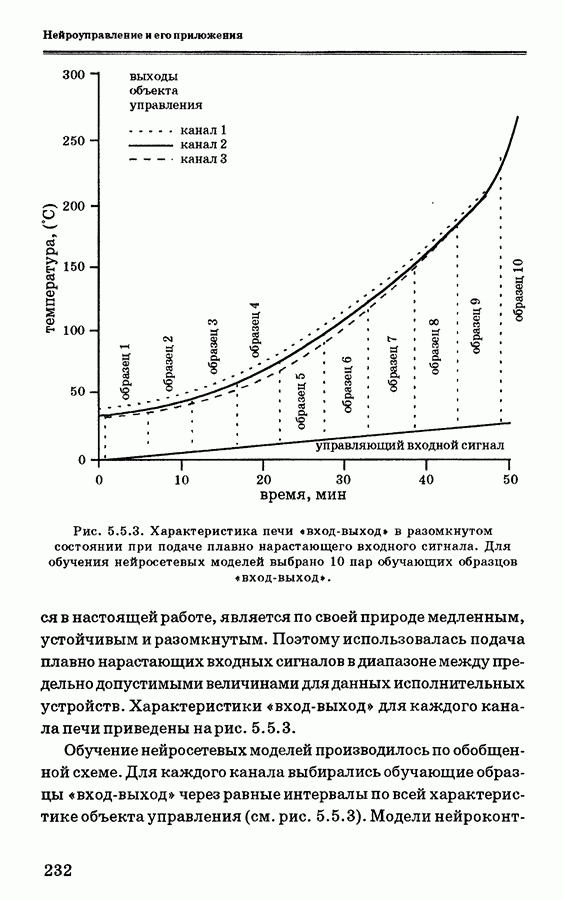
- 5.5.3. Схемы нейронного управления печью
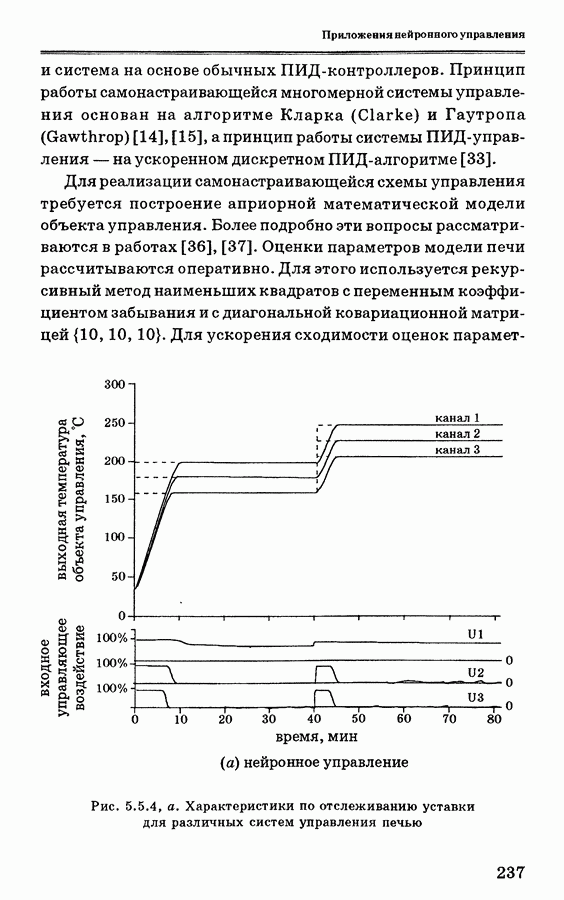
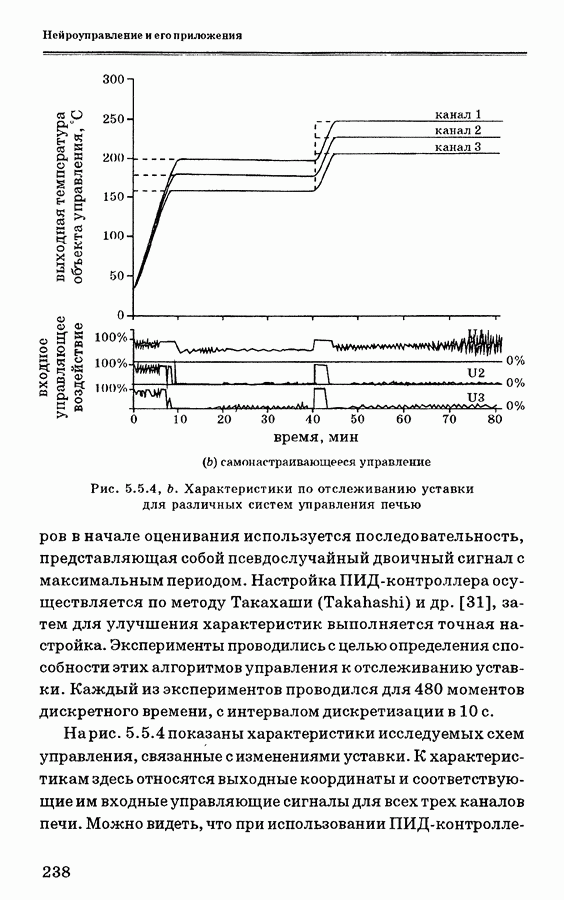
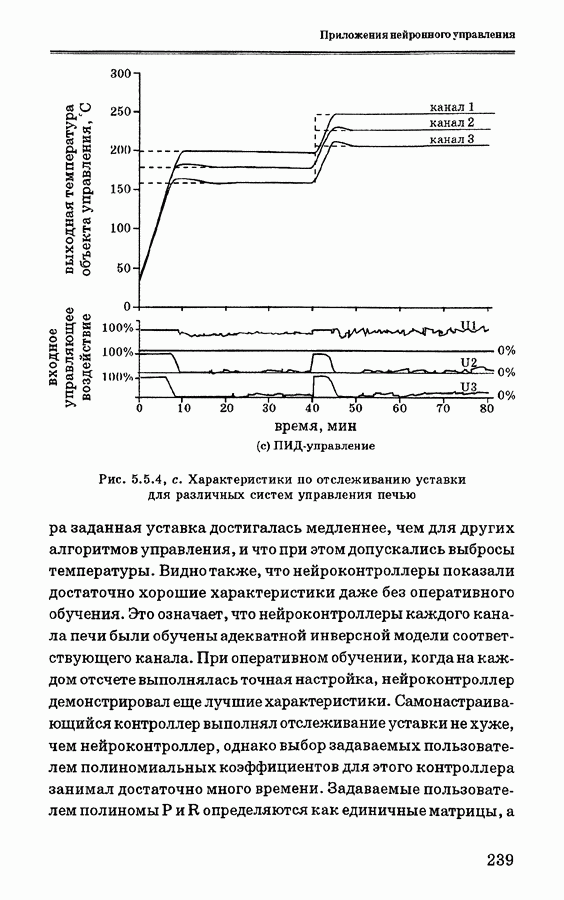
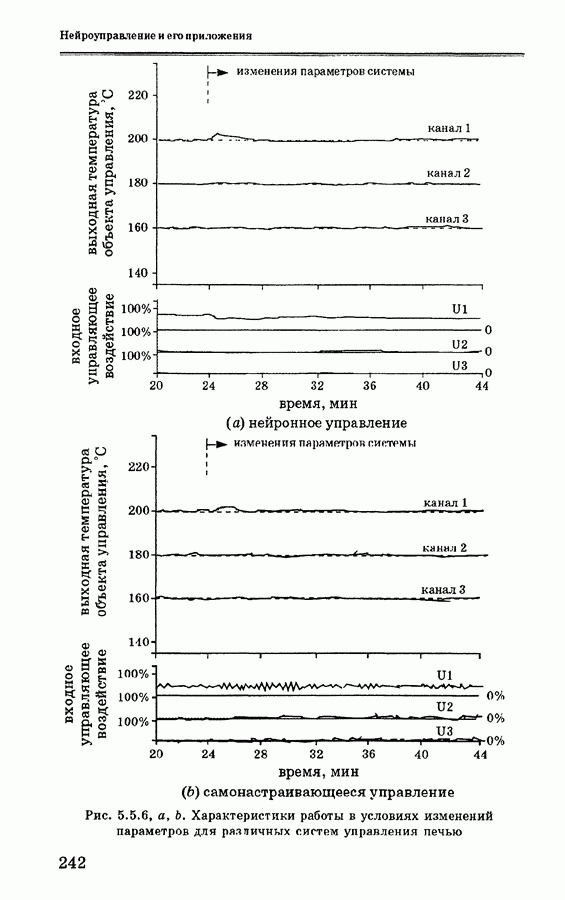
- 5.5.4. Анализ экспериментальных данных
- 5.6. Заключительные замечания и выводы
- Литература
- ЛИСТИНГ ПРОГРАММЫ