| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
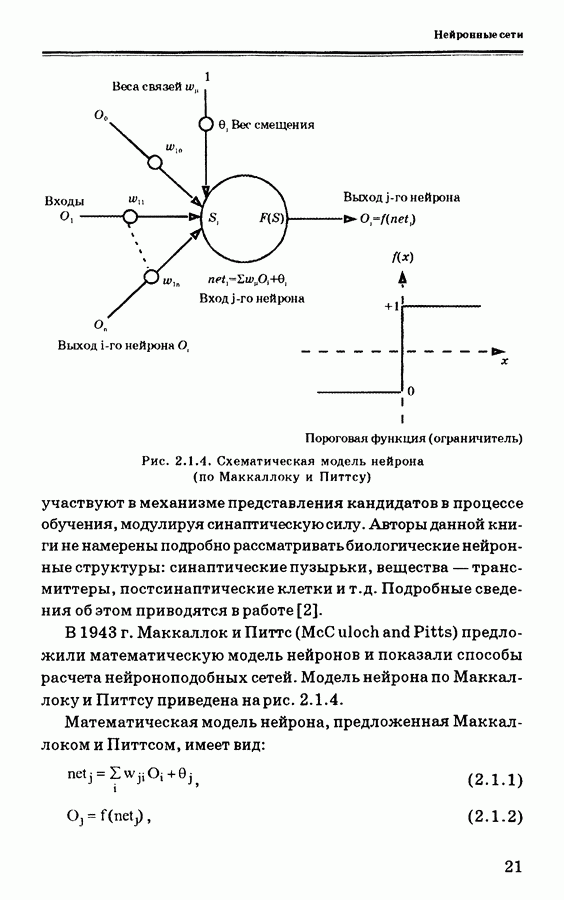
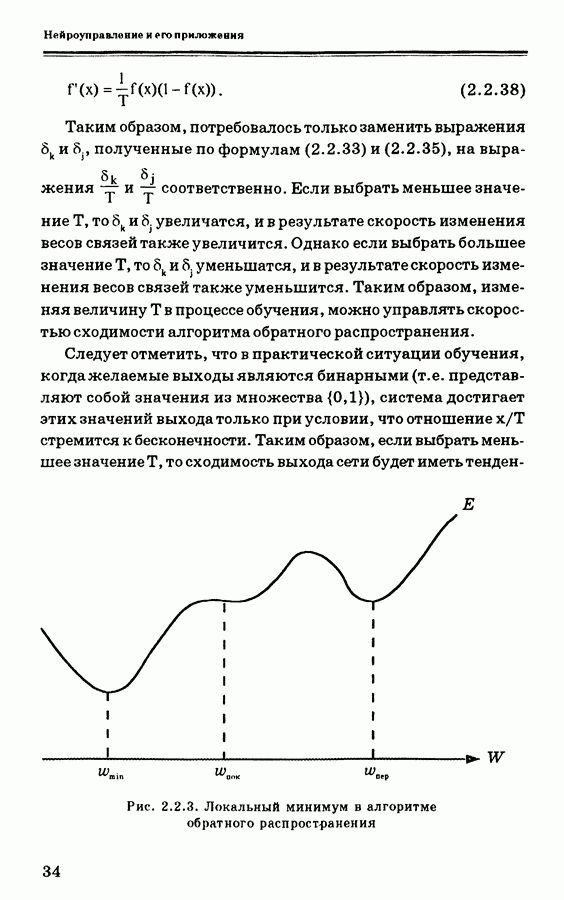
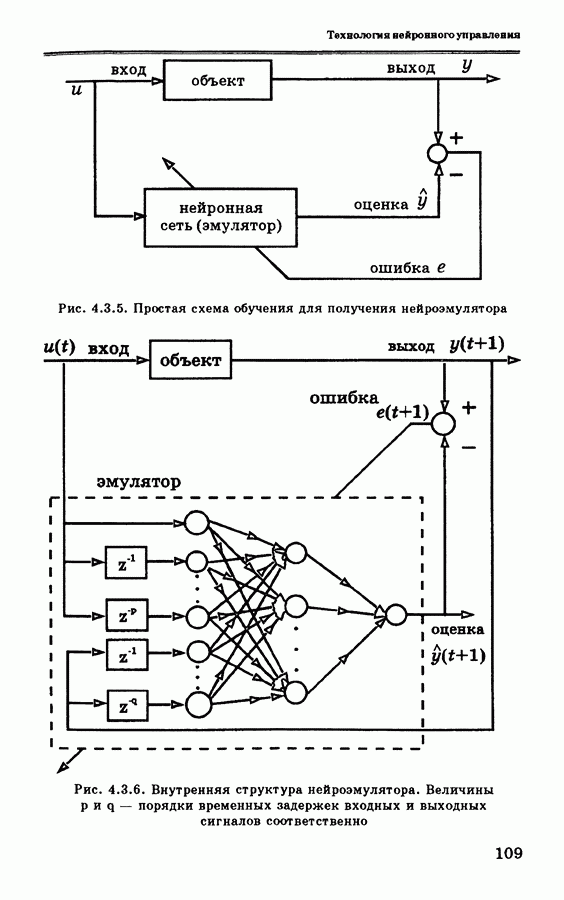
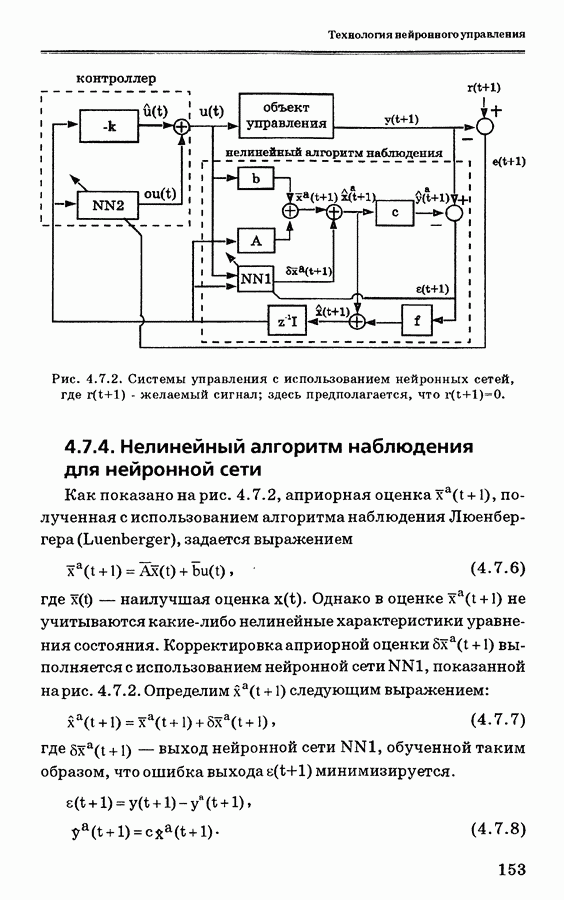
4.7.4. Нелинейный алгоритм наблюдения для нейронной сети
Как показано нарис. 4.7.2, априорная оценка  полученная с использованием алгоритма наблюдения Люенбергера (Luenberger), задается выражением
полученная с использованием алгоритма наблюдения Люенбергера (Luenberger), задается выражением

где  — наилучшая оценка
— наилучшая оценка  Однако в оценке
Однако в оценке  не учитываются какие-либо нелинейные характеристики уравнения состояния. Корректировка априорной оценки
не учитываются какие-либо нелинейные характеристики уравнения состояния. Корректировка априорной оценки  выполняется с использованием нейронной сети NN1, показанной нарис. 4.7.2. Определим
выполняется с использованием нейронной сети NN1, показанной нарис. 4.7.2. Определим  следующим выражением:
следующим выражением:

где  — выход нейронной сети NN1, обученной таким образом, что ошибка выхода
— выход нейронной сети NN1, обученной таким образом, что ошибка выхода  минимизируется.
минимизируется.

В этом случае оценка  величины
величины  задается следующим образом:
задается следующим образом:

где обучающее правило строится на основе алгоритма обратного распространения, что обеспечивает минимизацию квадратичной ошибки  , задаваемой выражением
, задаваемой выражением

Если определить  как
как

где

то величина  , задаваемая выражением (4.7.10), примет следующий вид:
, задаваемая выражением (4.7.10), примет следующий вид:

Таким образом, если рассматривать  как желаемый сигнал,
как желаемый сигнал,  — как часть выходного сигнала, задаваемую нейронной сетью NN1, то метод обратного распространения может применяться непосредственно для минимизации ошибки Здесь
— как часть выходного сигнала, задаваемую нейронной сетью NN1, то метод обратного распространения может применяться непосредственно для минимизации ошибки Здесь  — выходная часть нейронной сети
— выходная часть нейронной сети  — входы сети NN1.
— входы сети NN1.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРОВ ПЕРЕВОДА
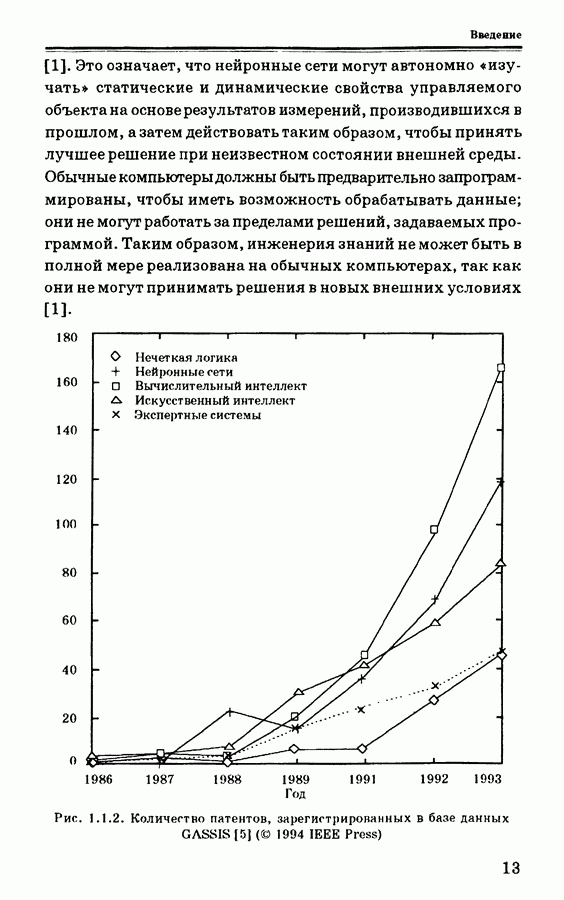
- 1. ВВЕДЕНИЕ
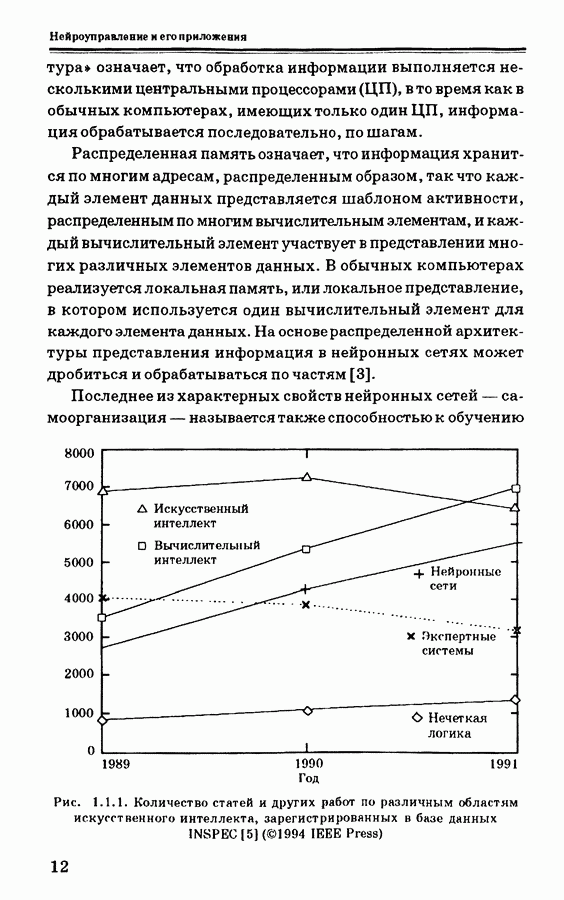
- 1.1. Общие сведения об интеллектуальном управлении
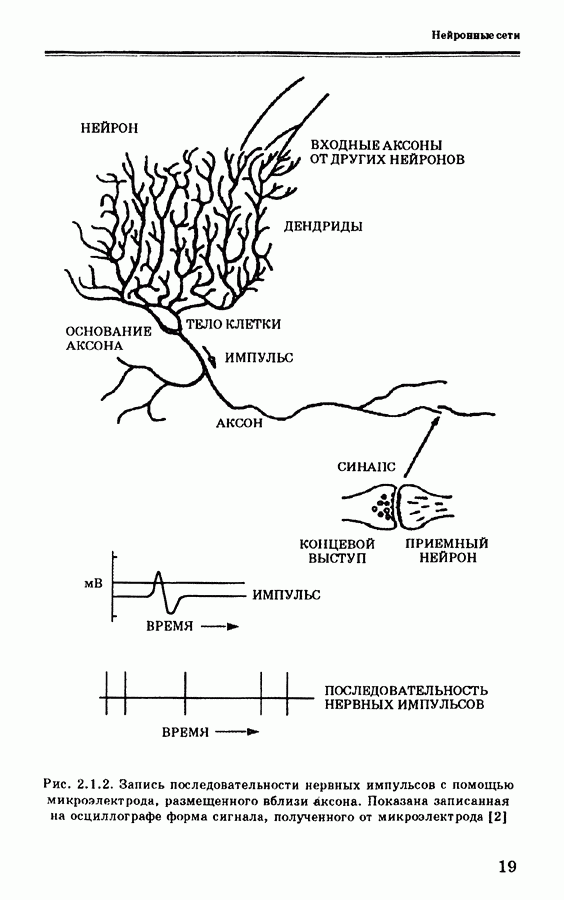
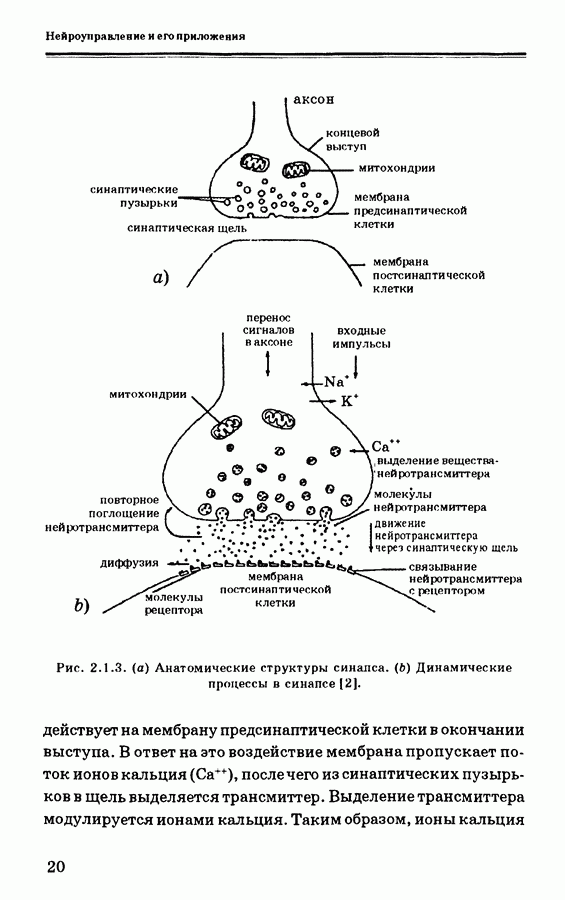
- 2. НЕЙРОННЫЕ СЕТИ
- 2.2. Алгоритм обратного распространения
- 2.2.2. Вывод алгоритма обратного распространения
- 2.2.2.2. Правило для скрытого слоя
- 2.2.3. Алгоритм обратного распространения: порядок реализации
- 2.2.4. Обсуждение алгоритма обратного распространения
- 2.3. Заключение
- 3. ТРАДИЦИОННЫЕ СХЕМЫ УПРАВЛЕНИЯ
- 3.2. ПИ- и ПИД-контроллеры с дискретным временем
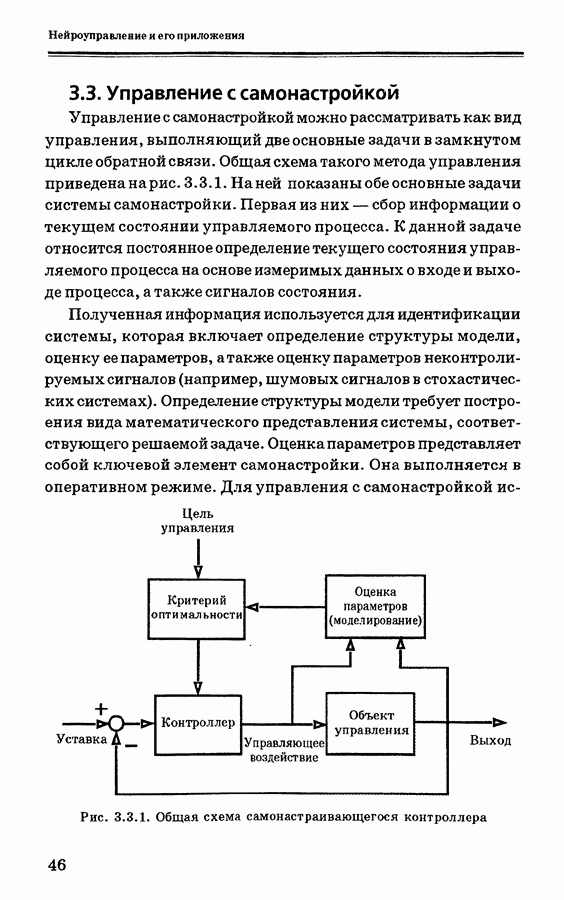
- 3.3. Управление с самонастройкой
- 3.4. Самонастраивающиеся ПИ- и ПИД- контроллеры
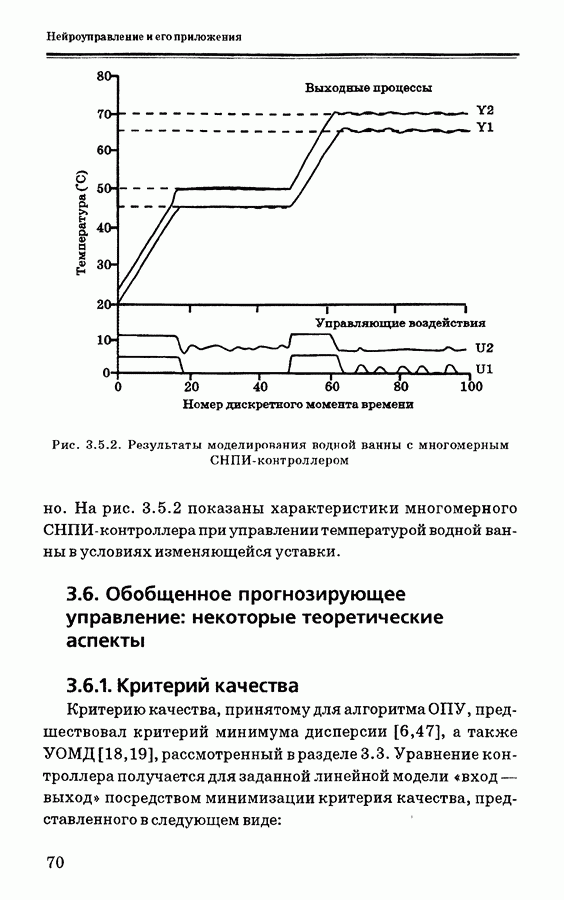
- 3.5. ПИД-управление с самонастройкой: многомерный подход
- 3.5.1. Пример моделирования
- 3.6. Обобщенное прогнозирующее управление: некоторые теоретические аспекты
- 3.6.2. Модель объекта управления и решение задачи оптимизации
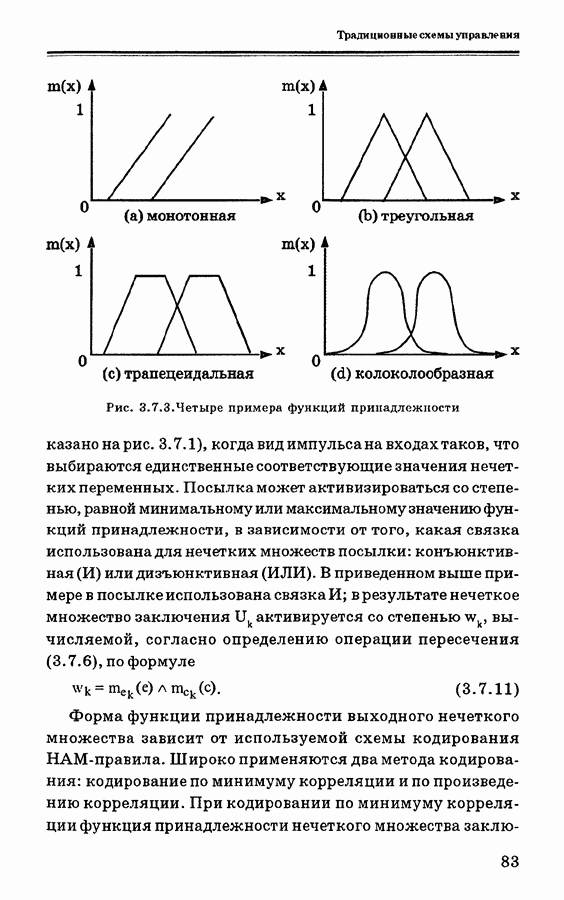
- 3.7. Управление на основе нечеткой логики
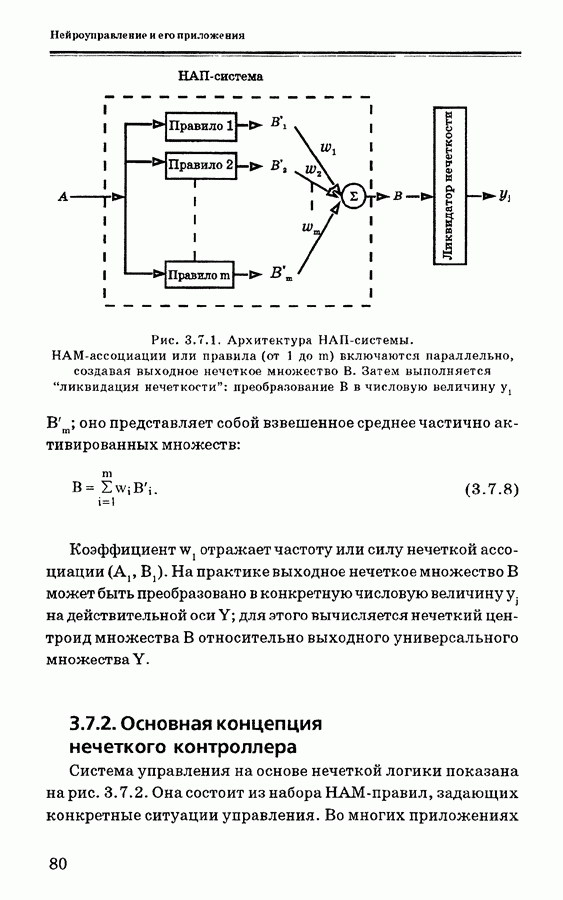
- 3.7.1. Краткие сведения по теории нечетких множеств и нечетких систем
- 3.7.2. Основная концепция нечеткого контроллера
- 3.8. Заключение
- 4. ТЕХНОЛОГИИ НЕЙРОННОГО УПРАВЛЕНИЯ
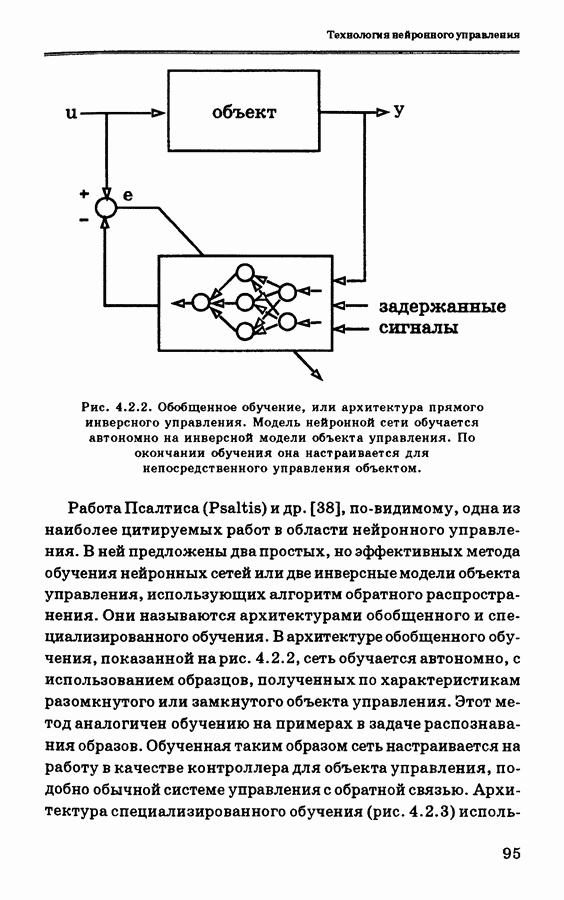
- 4.2. Общие сведения о нейронном управлении
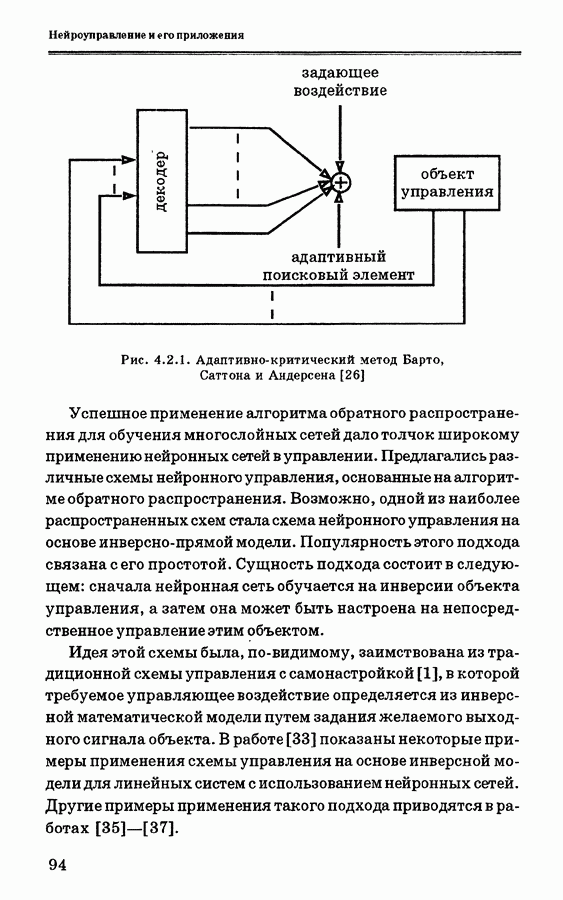
- 4.2.1. Подходы к нейронному управлению
- 4.2.2. Общая схема управления
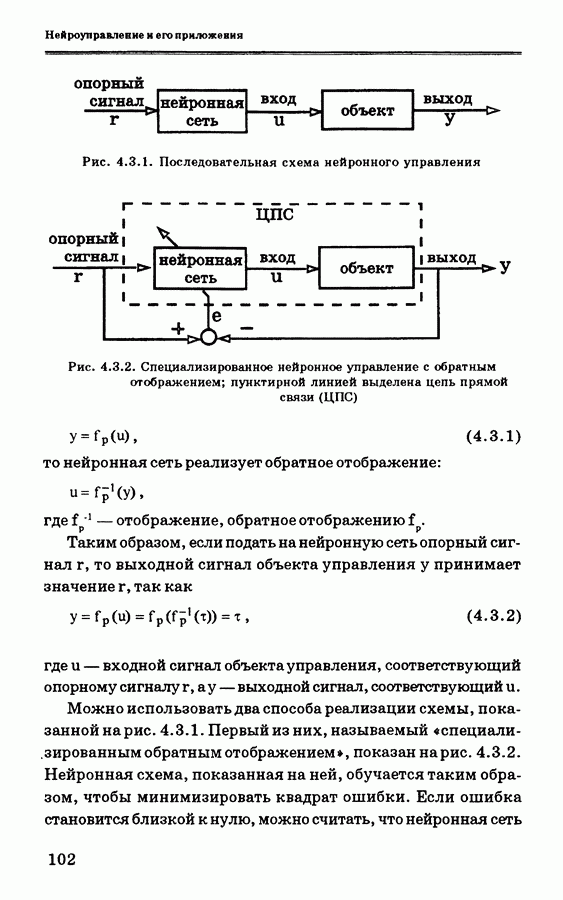
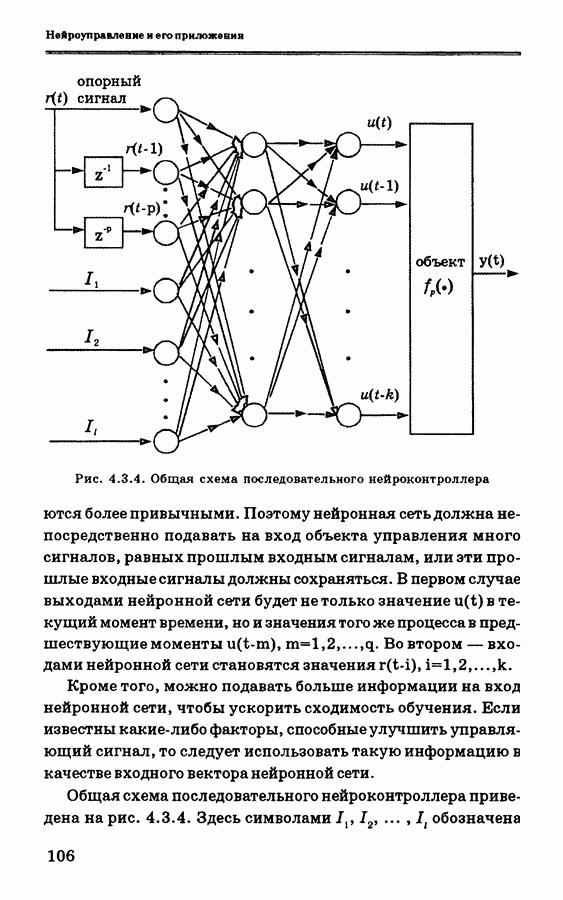
- 4.3. Последовательная схема нейронного управления
- 4.4. Расширение последовательной схемы нейронного управления
- 4.4.2. Нейроморфные структуры управления
- 4.4.3. Конфигурации обучения
- 4.4.4. Эффективное оперативное управление
- 4.4.5. Алгоритмы обучения
- 4.4.6. Оценка алгоритмов обучения на основе моделирования
- 4.5. Параллельная схема управления
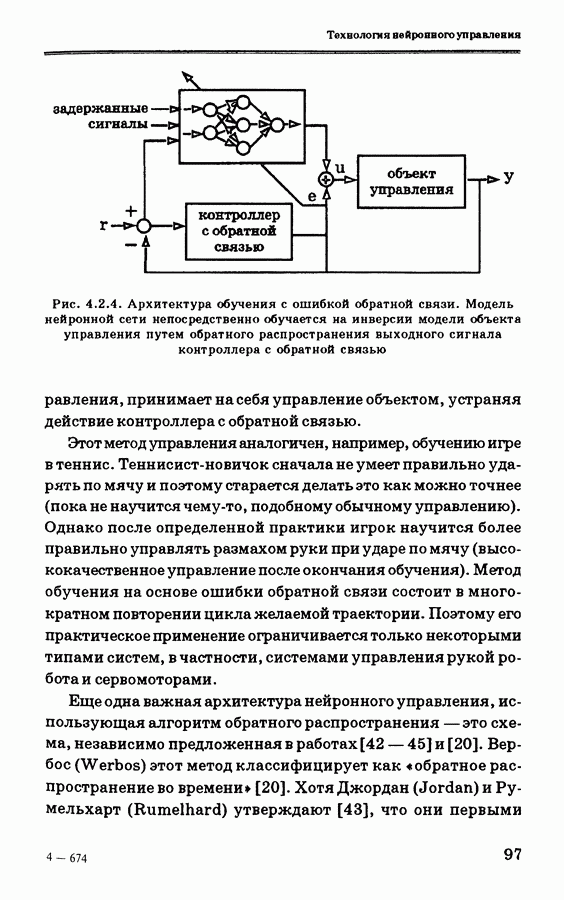
- 4.6. Алгоритм обучения по ошибке обратной связи
- 4.7. Расширение применения нейроконтроллеров параллельного типа
- 4.7.2. Линеаризованная система управления
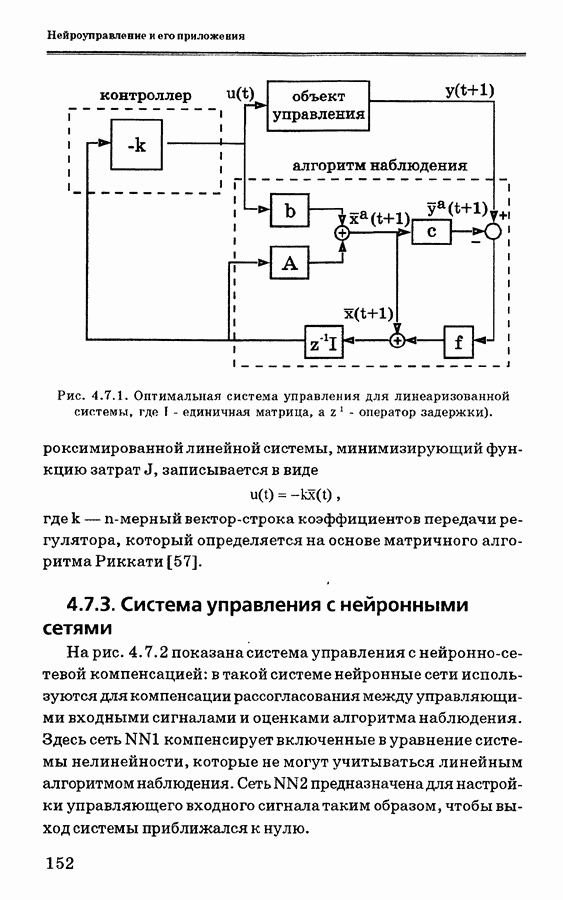
- 4.7.3. Система управления с нейронными сетями
- 4.7.4. Нелинейный алгоритм наблюдения для нейронной сети
- 4.7.5. Нелинейный контроллер для нейронной сети
- 4.7.6. Численное моделирование
- 4.8. Схема нейронного управления с самонастройкой
- 4.9. ПИД-нейроконтроллер с самонастройкой
- 4.9.1. Вывод уравнений ПИД-нейроконтроллера с самонастройкой
- 4.9.2. Примеры эмуляции
- 4.10. Схема нейронного управления с эмулятором и контроллером (схема обратного распространения во времени)
- 4.11. Заключение
- 5. ПРИЛОЖЕНИЯ НЕЙРОННОГО УПРАВЛЕНИЯ
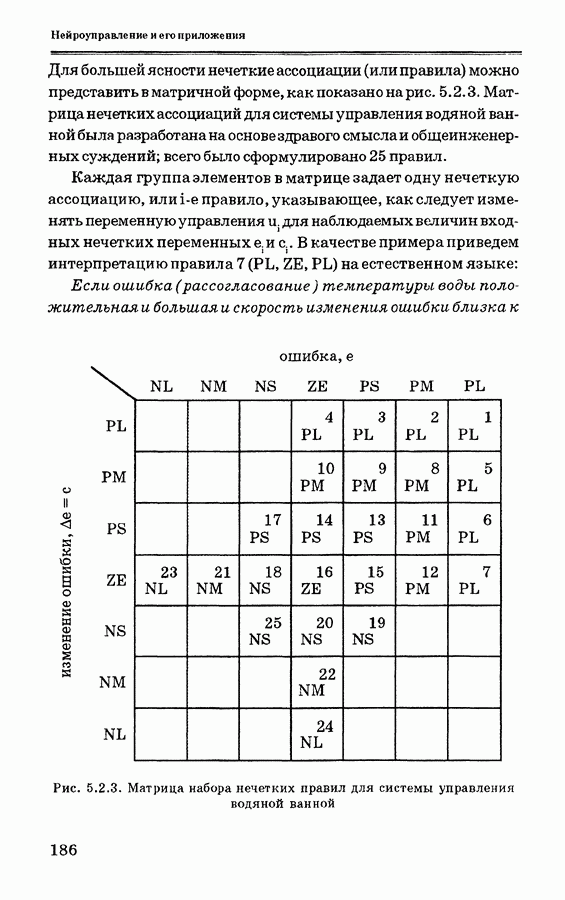
- 5.2. Применение нейронного управления в системе регулирования процессов в водяной ванне и сравнение его с другими схемами управления
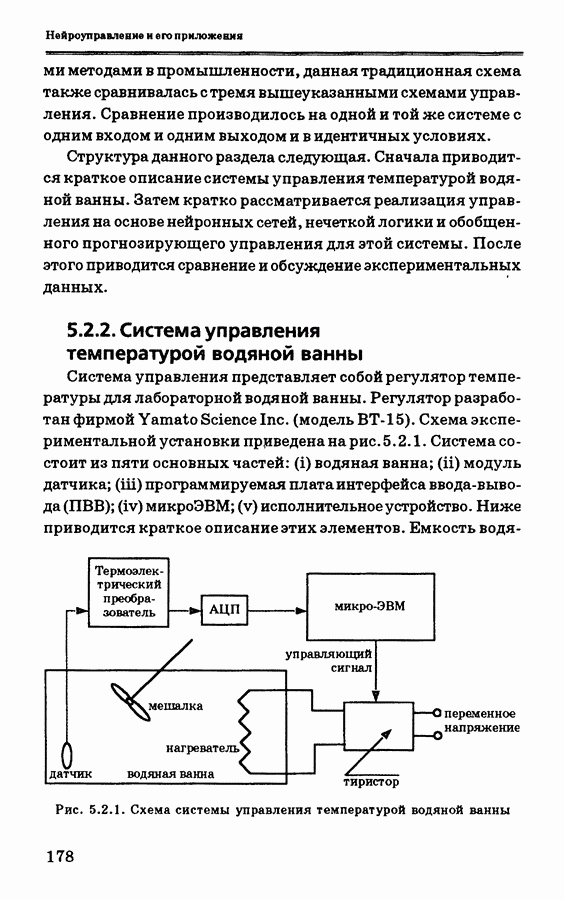
- 5.2.2. Система управления температурой водяной ванны
- 5.2.3. Схема нейронного управления
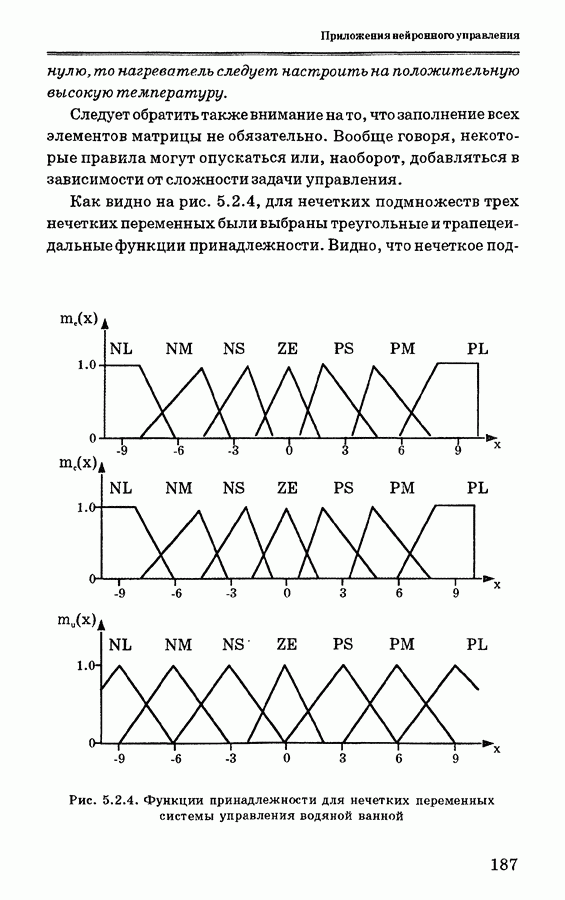
- 5.2.4. Схема управления на основе нечеткой логики
- 5.2.5. Схема обобщенного прогнозирующего управления
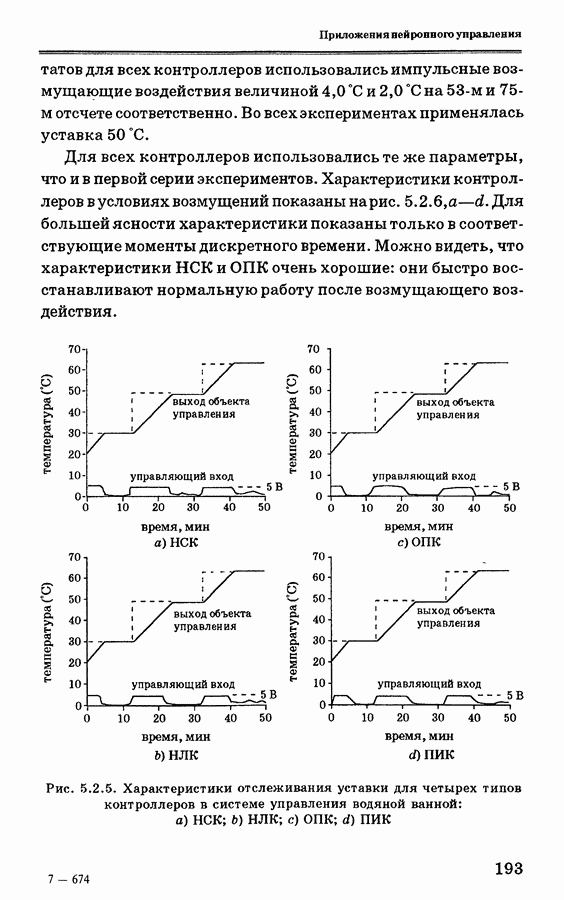
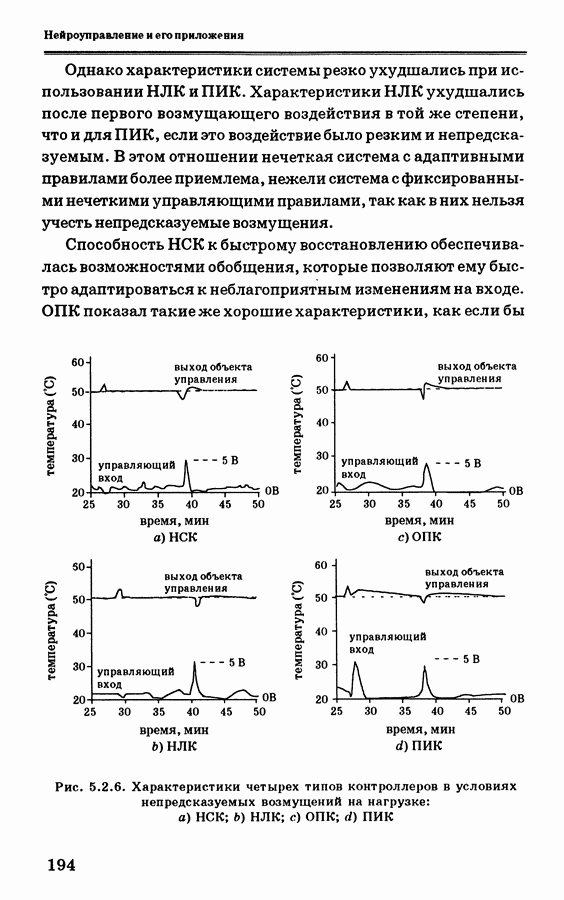
- 5.2.6. Экспериментальные данные и их анализ
- 5.2.7. Заключение
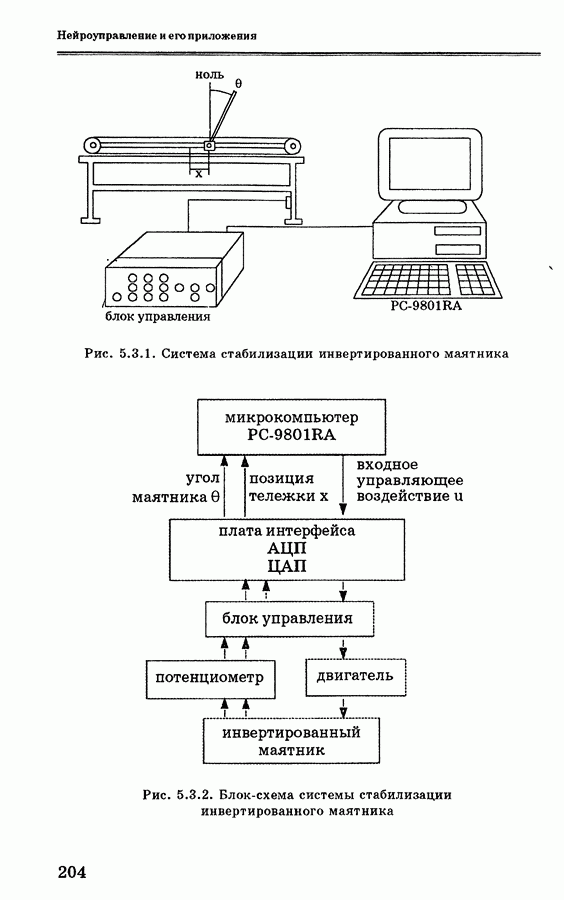
- 5.3. Система стабилизации инвертированного маятника на основе нейронных сетей
- 5.3.2. Система стабилизации инвертированного маятника
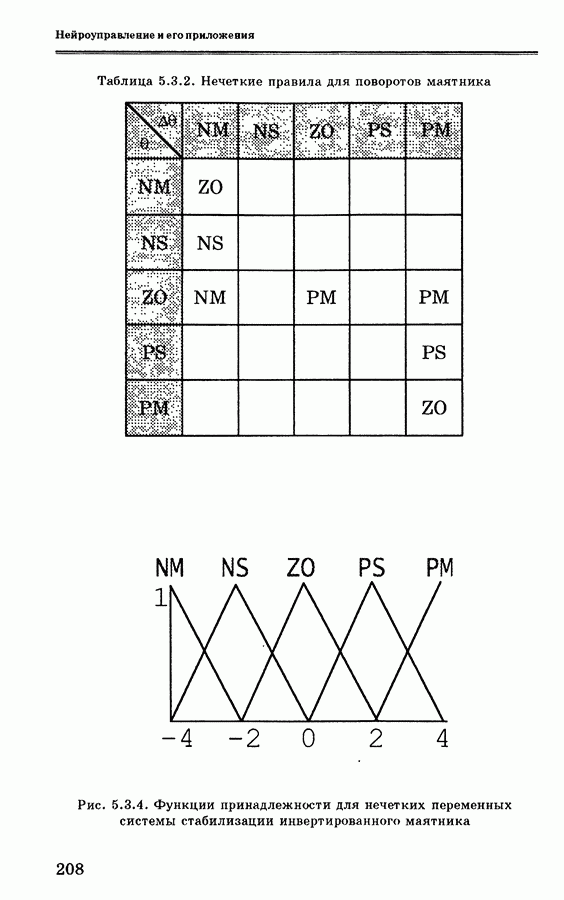
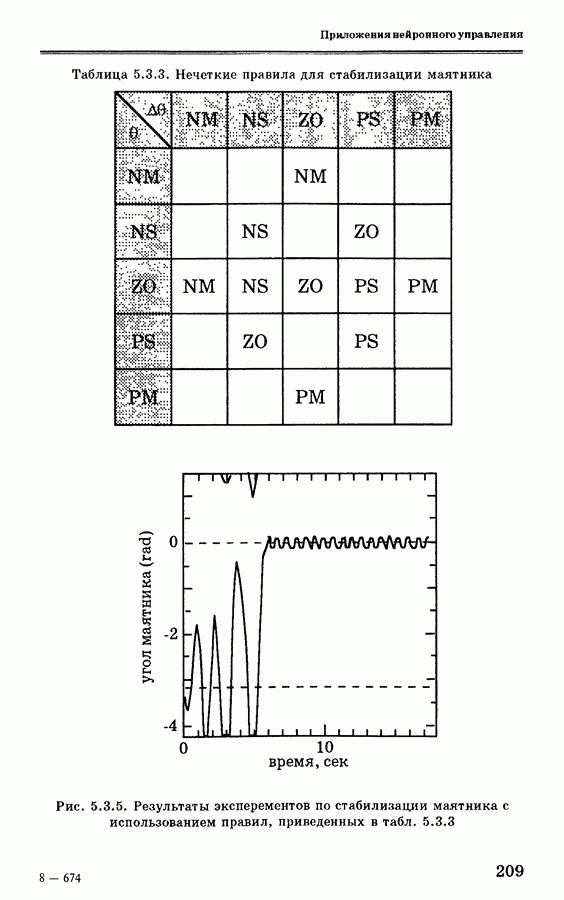
- 5.3.3. Инициализация поворотного управления с использованием нечеткой логики
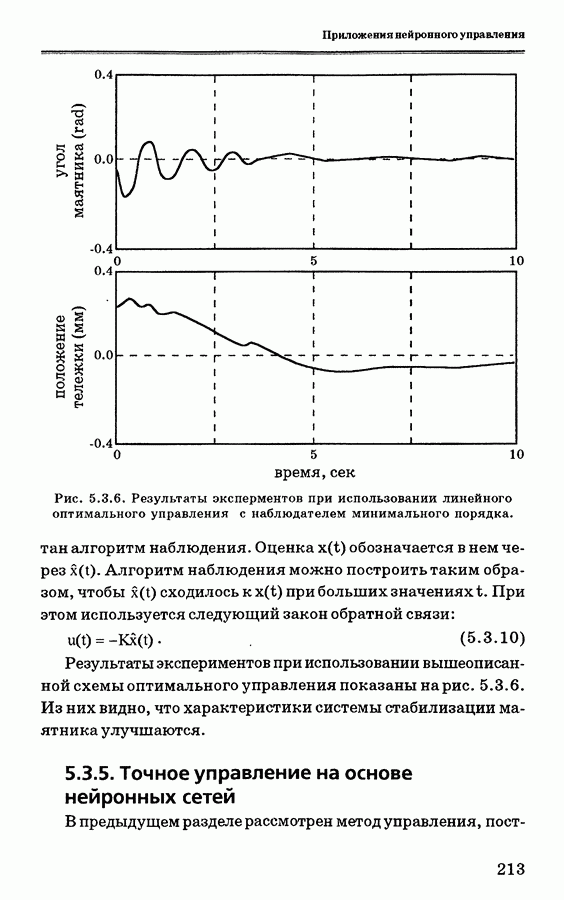
- 5.3.4. Применение стратегии оптимального управления для стабилизации маятника
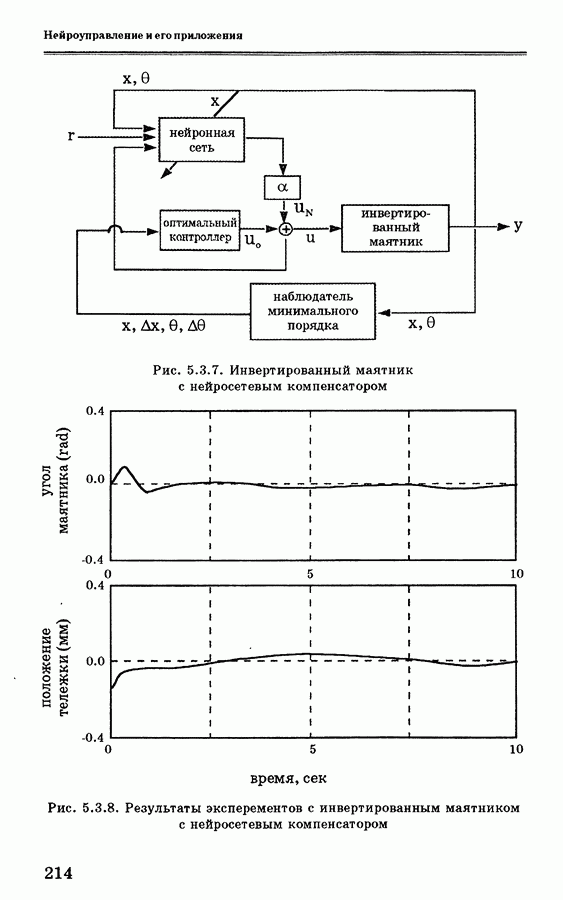
- 5.3.5. Точное управление на основе нейронных сетей
- 5.3.6. Заключение
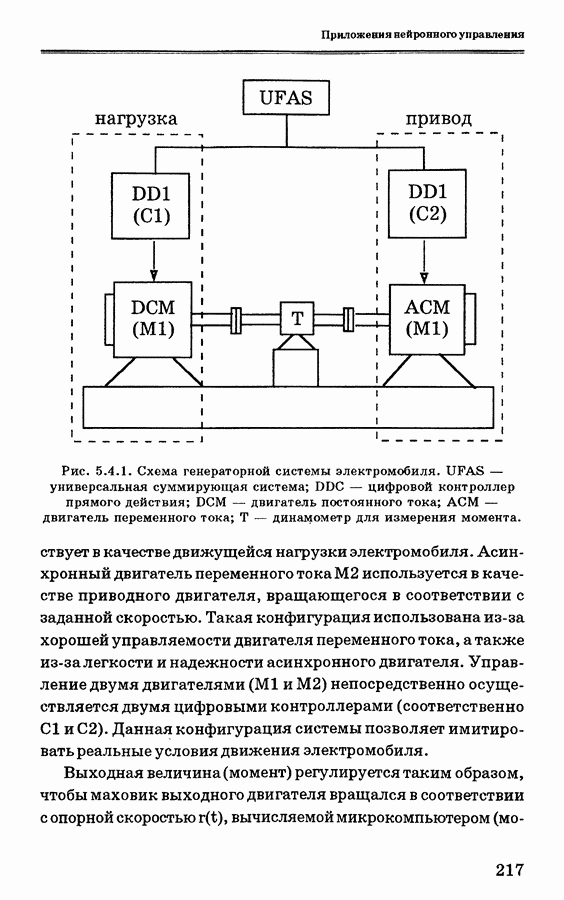
- 5.4. Применение ПИД-нейроконтроллера с самонастройкой для управления скоростью электромобиля
- 5.4.2. Система управления электромобилем
- 5.4.3. ПИД-нейроконтроллер с самонастройкой
- 5.4.4. Применение нейронной сети для управления скоростью электромобиля
- 5.4.5. Заключение
- 5.5. Применение нейронных сетей для управления печью
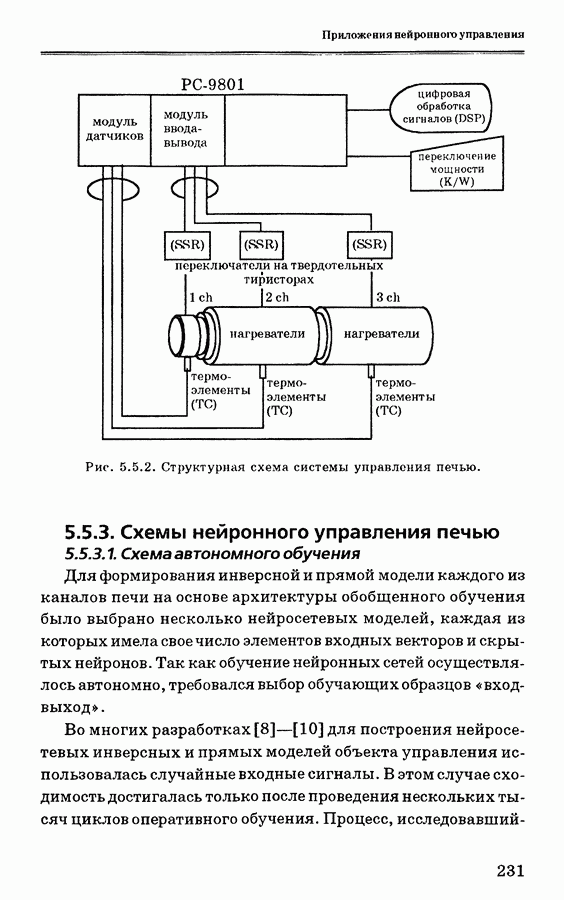
- 5.5.2. Система управления печью
- 5.5.3. Схемы нейронного управления печью
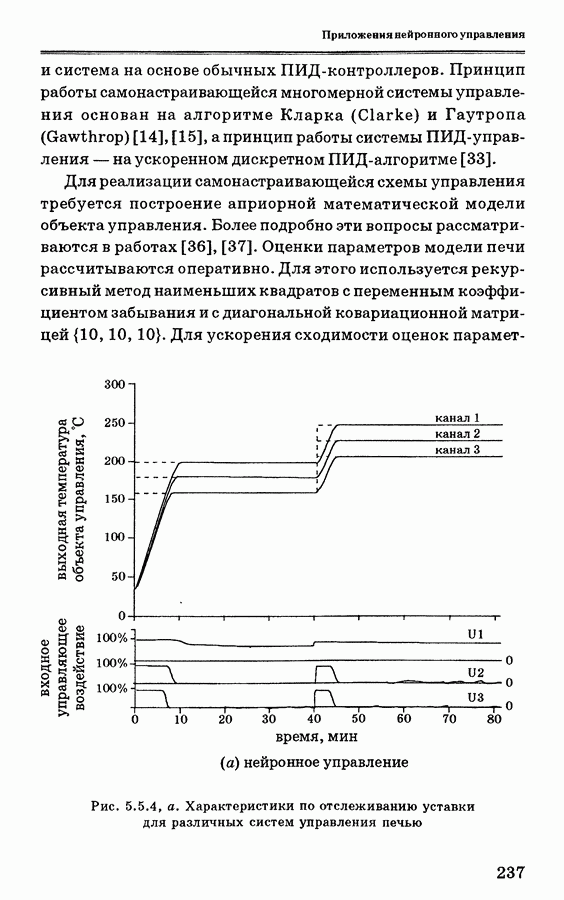
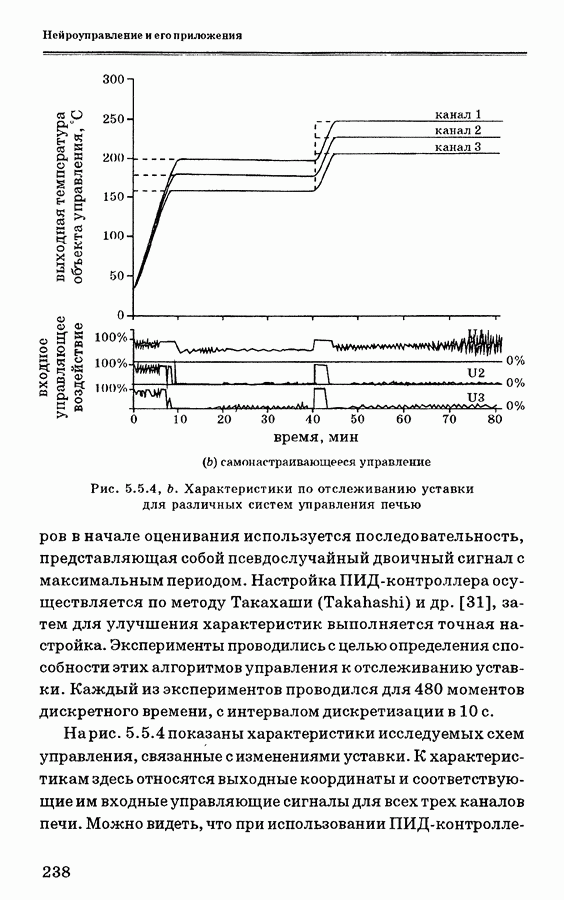
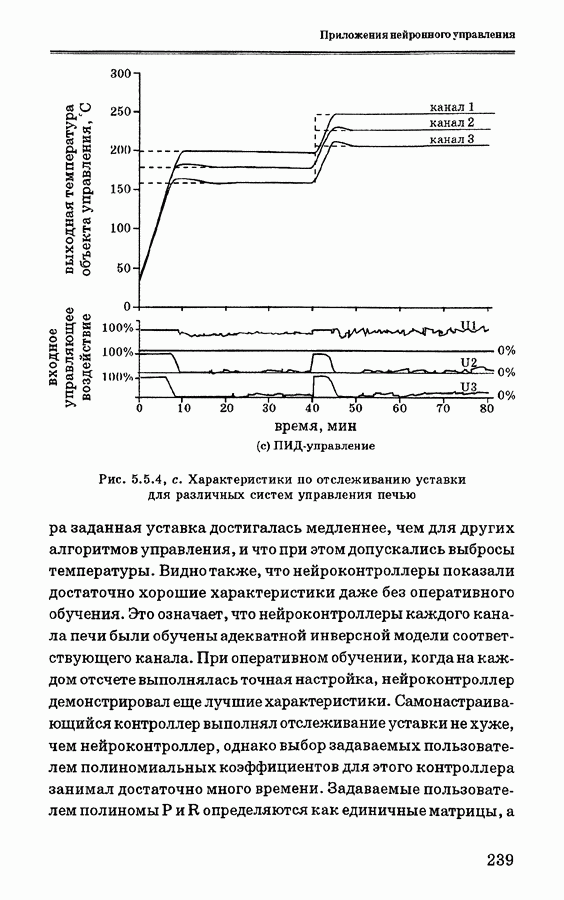
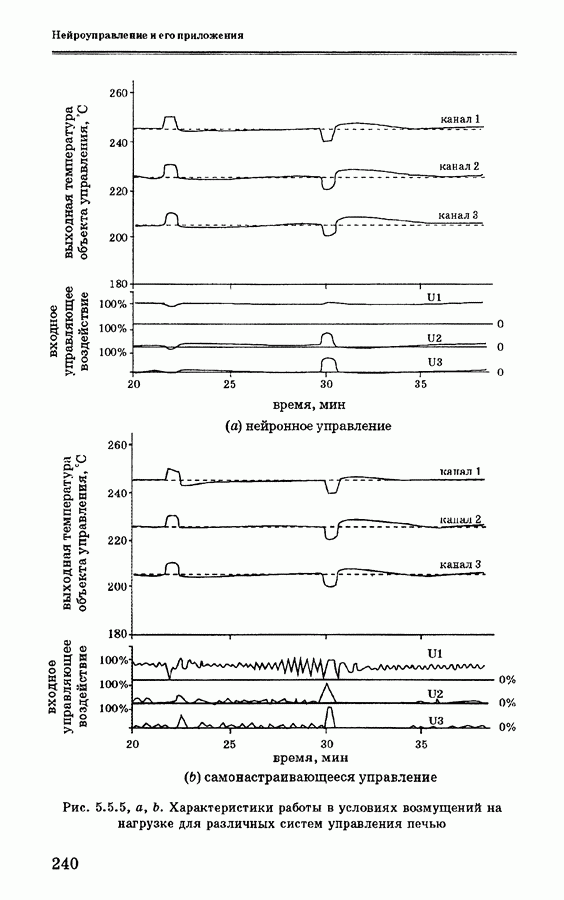
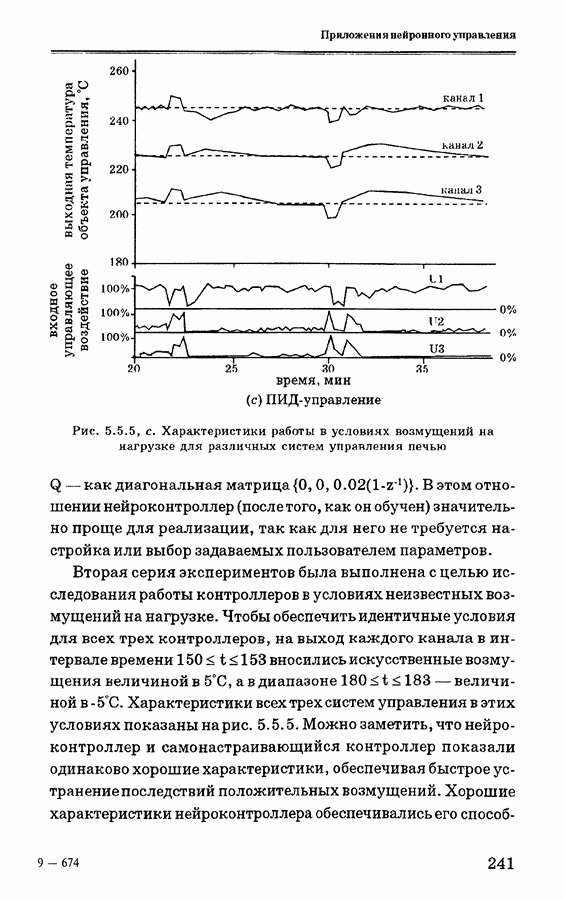
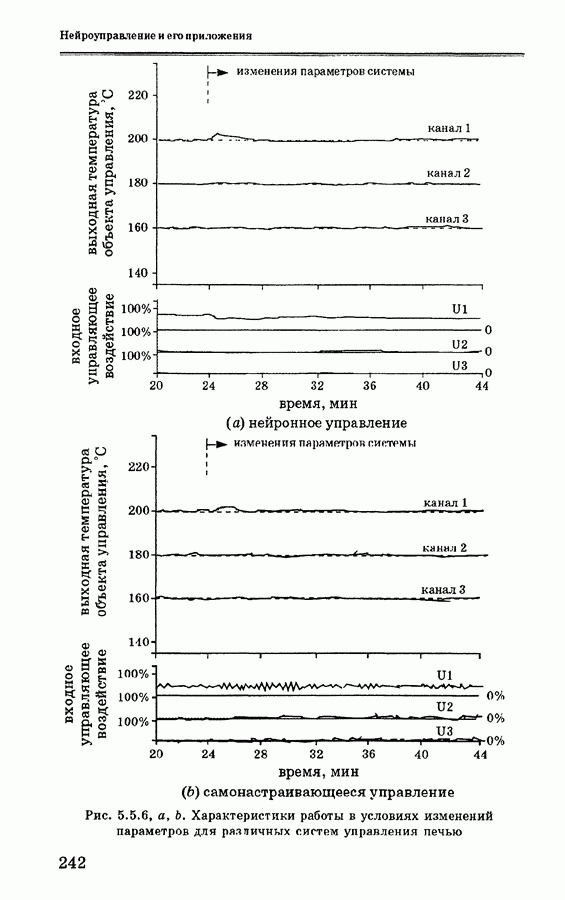
- 5.5.4. Анализ экспериментальных данных
- 5.6. Заключительные замечания и выводы
- Литература
- ЛИСТИНГ ПРОГРАММЫ