| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4.4.6. Оценка алгоритмов обучения на основе моделирования
Чтобы оценить характеристики предлагаемой системы управления и методов обучения, используются результаты моделирования для несложного объекта управления. Компьютерное моделирование особенно необходимо для оперативного обучения нейронных систем управления, так как натурные эксперименты для такого обучения во многих случаях занимают очень много времени. Рассмотрим систему управления температурой объекта, описываемую дифференциальным уравнением

где  — время;
— время;  — выходная температура;
— выходная температура;  — тепло, поступающее в систему;
— тепло, поступающее в систему;  — комнатная температура (для простоты будем считать ее постоянной); С — теплоемкость системы;
— комнатная температура (для простоты будем считать ее постоянной); С — теплоемкость системы;  — тепловое сопротивление между границами системы и
— тепловое сопротивление между границами системы и
окружающей средой. Считая величины  и С постоянными, по реакции на единичное ступенчатое воздействие выведем импульсную переходную функцию для системы, заданной уравнением (4.4.21). Это приводит к системе с дискретным временем, задаваемой уравнением
и С постоянными, по реакции на единичное ступенчатое воздействие выведем импульсную переходную функцию для системы, заданной уравнением (4.4.21). Это приводит к системе с дискретным временем, задаваемой уравнением

где  — дискретное целочисленное время, Т — интервал квантования,
— дискретное целочисленное время, Т — интервал квантования,  — вход и выход системы соответственно. Обозначив через
— вход и выход системы соответственно. Обозначив через  некоторые постоянные величины, зависящие от констант
некоторые постоянные величины, зависящие от констант  и С, остальные параметры можно выразить следующим образом:
и С, остальные параметры можно выразить следующим образом:

Приведенные ниже результаты моделирования были получены для системы, несколько отличающейся от заданной уравнениями (4.4.21) - (4.4.23). В системе была задана нелинейная характеристика с насыщением, чтобы исключить превышение выходной температуры некоторого граничного значения. Моделируемый объект управления описывался следующим уравнением:

При моделировании использовались следующие значения параметров:  Данные значения параметров были получены на реальном объекте (водяная ванна, рассматриваемая в
Данные значения параметров были получены на реальном объекте (водяная ванна, рассматриваемая в  Входной сигнал объекта
Входной сигнал объекта  мог принимать значения только в диапазоне от 0 до 5; кроме того, предполагалось, что на период дискретизации наложено ограничение
мог принимать значения только в диапазоне от 0 до 5; кроме того, предполагалось, что на период дискретизации наложено ограничение

При выбранных значениях параметров моделируемая система эквивалентна системе управления температурой водяной ванны с одним входом и одним выходом. Такая система имеет линейные характеристики при температуре примерно
до 70 °С, а при температуре около 80 °С она переходит в насыщение. Если сравнить (4.4.24) и (4.4.1), то можно заметить, 
В качестве ЭОУ и нейроконтроллера использовались трехслойные нейронные сети, содержащие от 10 до 20 скрытых нейронов с сигмоидной функцией активации. Сходимость была достигнута для нескольких пар  при значениях параметра
при значениях параметра  от 0 до 2, а параметра
от 0 до 2, а параметра  — от 1 до 3. Приведенные ниже графики соответствуют значениям
— от 1 до 3. Приведенные ниже графики соответствуют значениям  (точное согласование). Коррекция сетей производилась по следующему общему правилу:
(точное согласование). Коррекция сетей производилась по следующему общему правилу:

 — номер итерации обучения,
— номер итерации обучения,  — вес связи,
— вес связи,  — подлежащая минимизации функция ошибки,
— подлежащая минимизации функция ошибки,  — скорость обучения,
— скорость обучения,  - мгновенная составляющая.
- мгновенная составляющая.
До начала моделирования ЭОУ подвергался приближенному оперативному обучению, а первоначальные значения весов нейроконтроллера назначались случайным образом. В качестве начального состояния использовалось значение  Целью регулирования было поддержание температуры, равной
Целью регулирования было поддержание температуры, равной  для временного интервала
для временного интервала  — для интервала
— для интервала  мин. и
мин. и  для интервала 60 мин.
для интервала 60 мин.  мин. Каждый цикл имитации (для значений
мин. Каждый цикл имитации (для значений  от 0 до 90 мин) будем называть пробой. После каждой пробы веса фиксировались, и предпринималась новая проба. На рис.
от 0 до 90 мин) будем называть пробой. После каждой пробы веса фиксировались, и предпринималась новая проба. На рис.
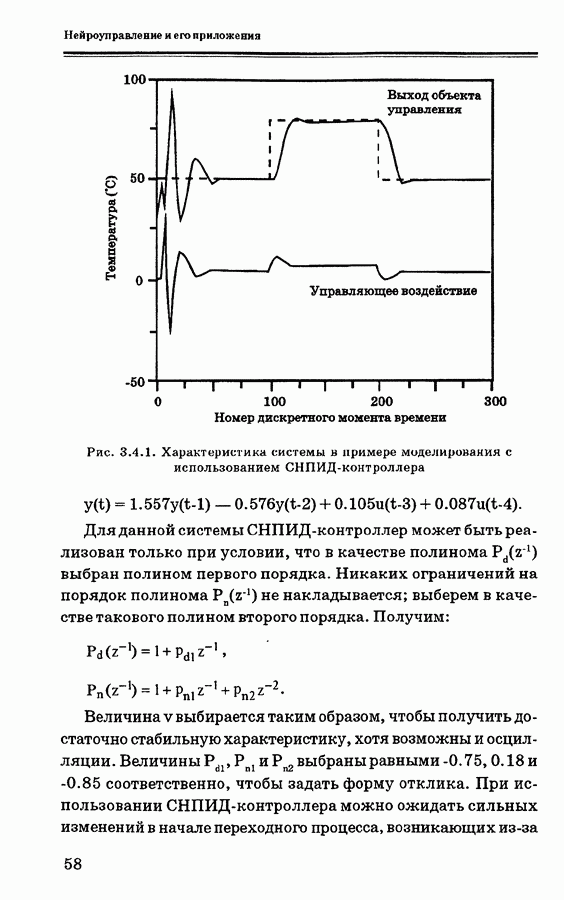
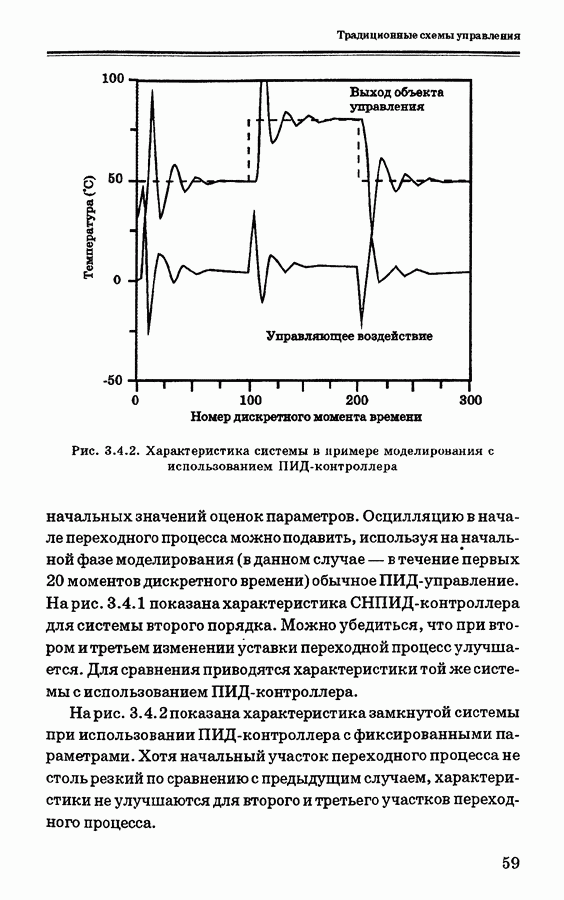
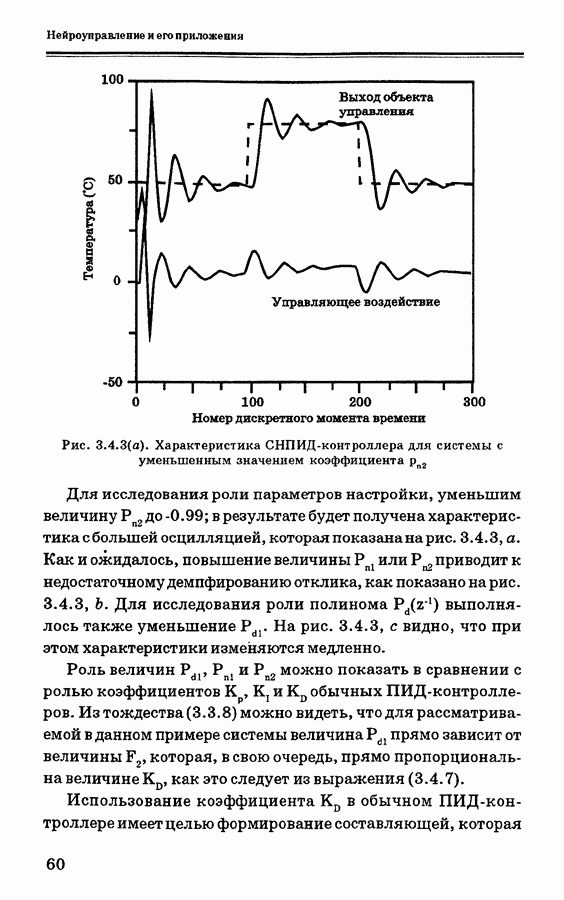
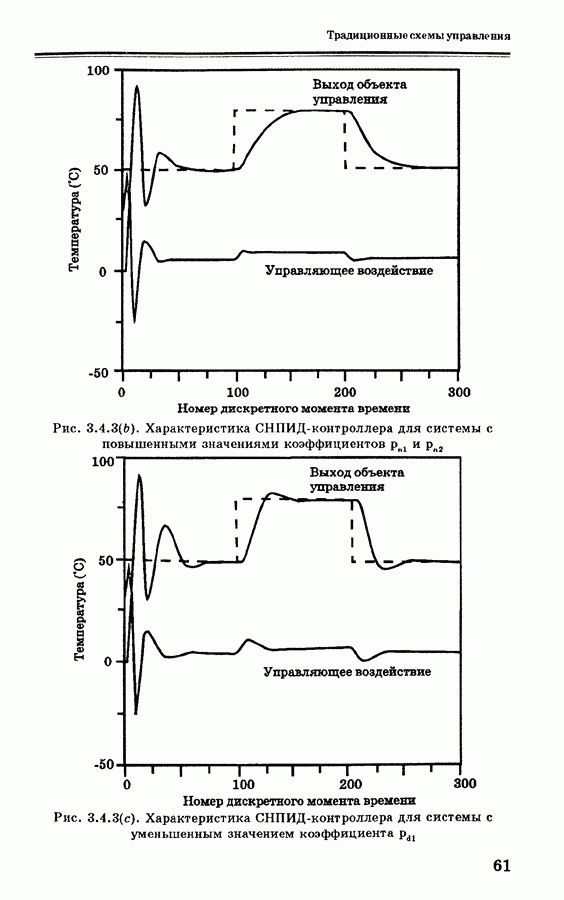
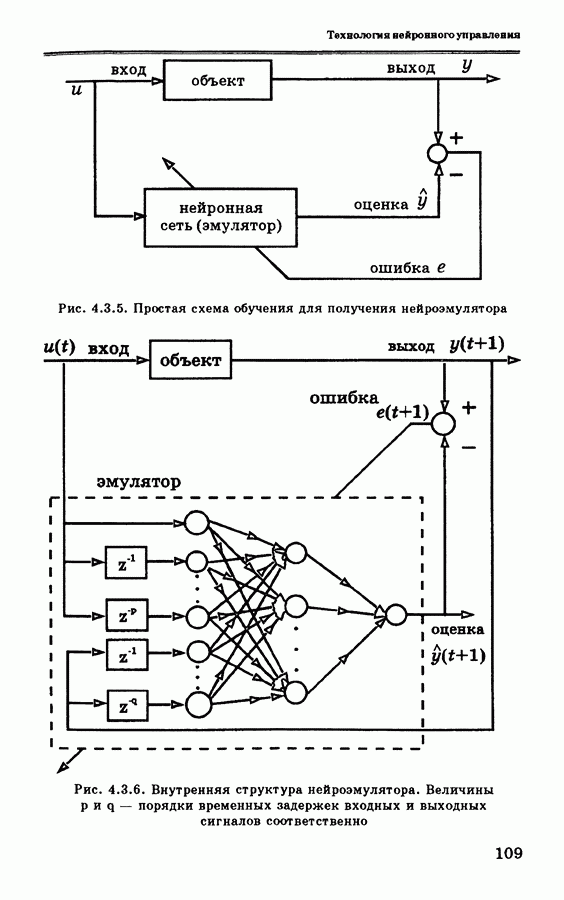
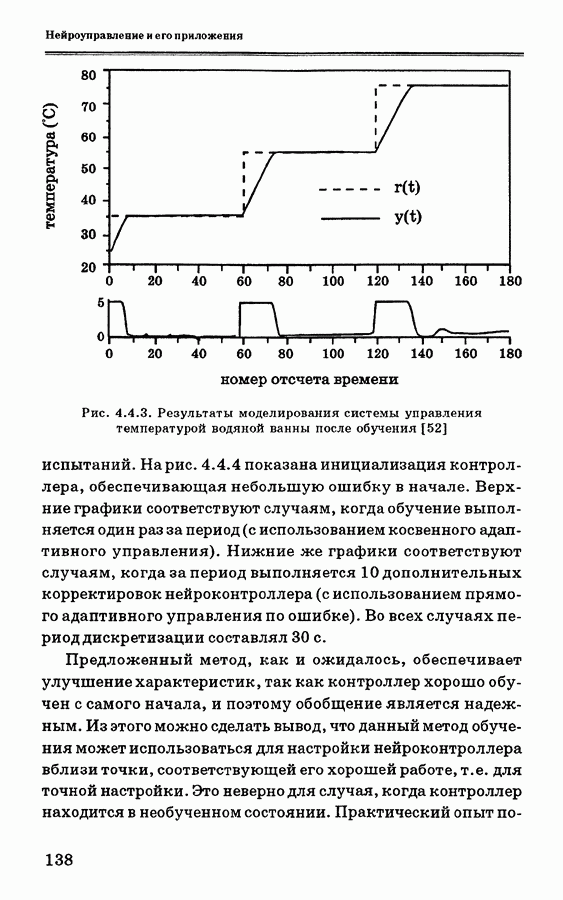
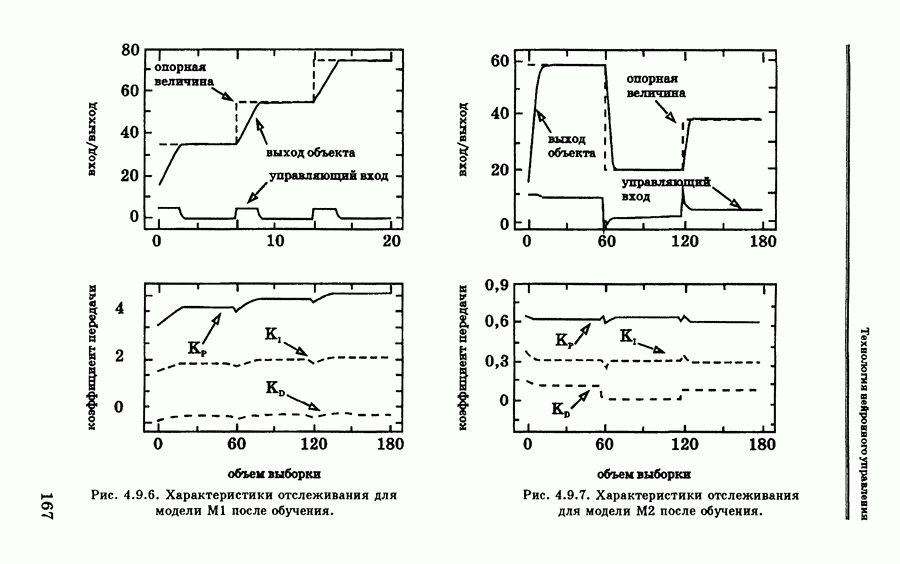
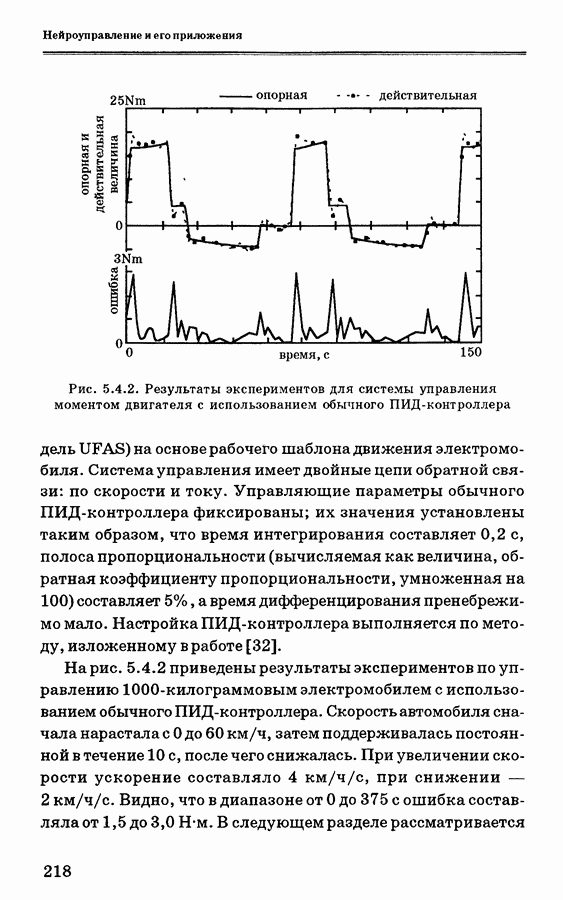
4.4.3 показан опорный сигнал, вход и выход объекта после достижения хорошей сходимости (для  ).
).
Характеристика нейроконтроллера, выполняющего одну обучающую итерацию за период дискретизации, сравнивается с характеристикой для множественного обучения на рис. 4.4.4-4.4.6. На графиках показана зависимость среднеквадратической ошибки в одном испытании от количества

Рис. 4.4.3. Результаты моделирования системы управления температурой водяной ванны после обучения [52]
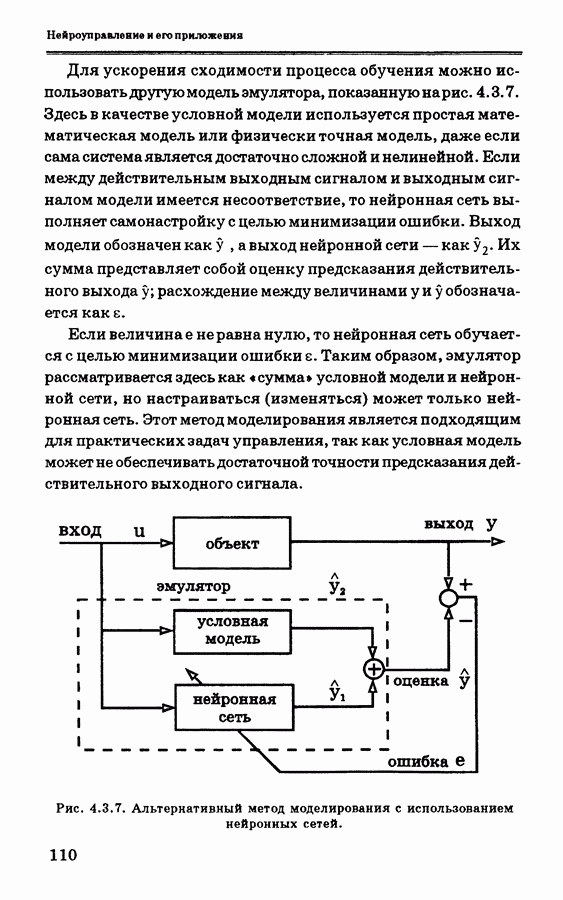
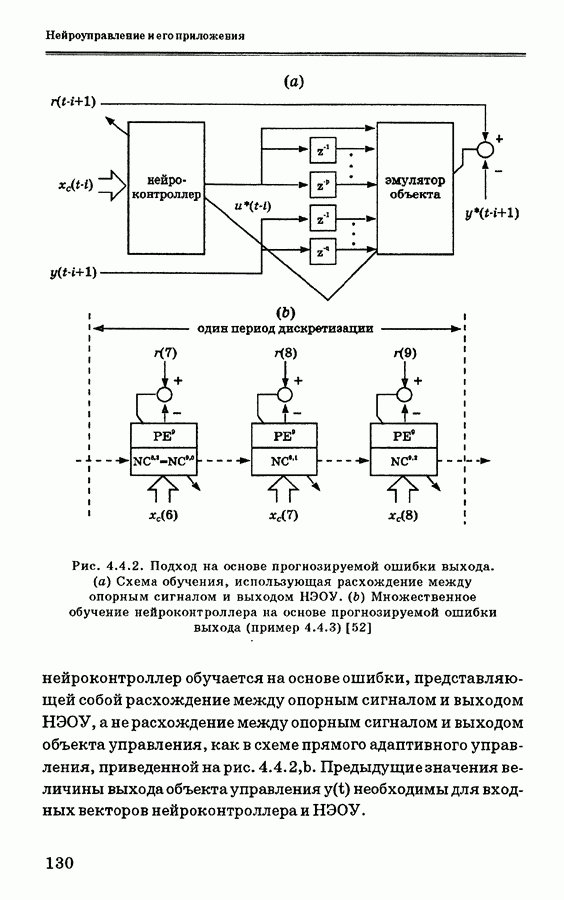
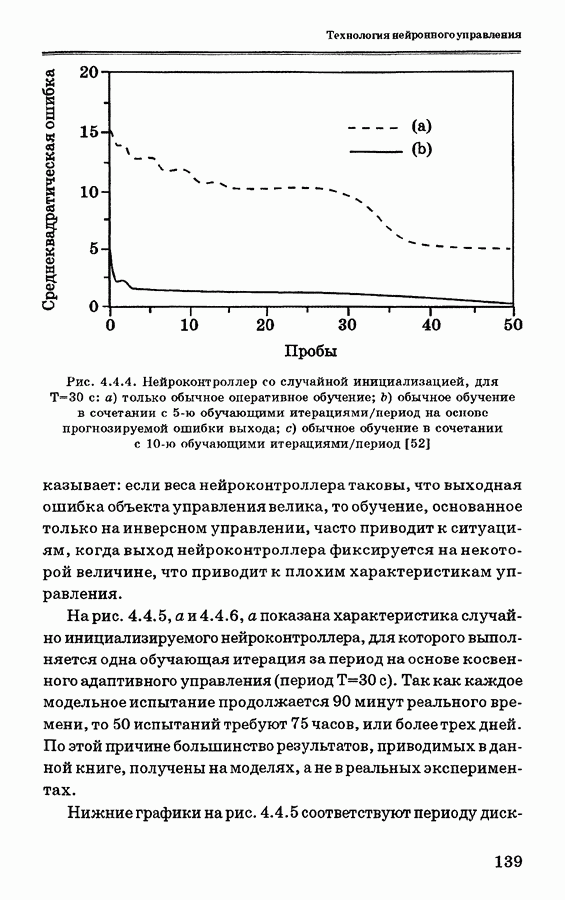
испытаний. Нарис. 4.4.4 показана инициализация контроллера, обеспечивающая небольшую ошибку в начале. Верхние графики соответствуют случаям, когда обучение выполняется один раз за период (с использованием косвенного адаптивного управления). Нижние же графики соответствуют случаям, когда за период выполняется 10 дополнительных корректировок нейроконтроллера (с использованием прямого адаптивного управления по ошибке). Во всех случаях период дискретизации составлял 30 с.
Предложенный метод, как и ожидалось, обеспечивает улучшение характеристик, так как контроллер хорошо обучен с самого начала, и поэтому обобщение является надежным. Из этого можно сделать вывод, что данный метод обучения может использоваться для настройки нейроконтроллера вблизи точки, соответствующей его хорошей работе, т.е. для точной настройки. Это неверно для случая, когда контроллер находится в необученном состоянии. Практический опыт

Рис. 4.4.4. Нейроконтроллер со случайной инициализацией, для  с: а) только обычное оперативное обучение; Ь) обычное обучение в сочетании с 5-ю обучающими итерациями/период на основе прогнозируемой ошибки выхода; с) обычное обучение в сочетании с 10-ю обучающими итерациями/период [52]
с: а) только обычное оперативное обучение; Ь) обычное обучение в сочетании с 5-ю обучающими итерациями/период на основе прогнозируемой ошибки выхода; с) обычное обучение в сочетании с 10-ю обучающими итерациями/период [52]
показывает: если веса нейроконтроллера таковы, что выходная ошибка объекта управления велика, то обучение, основанное только на инверсном управлении, часто приводит к ситуациям, когда выход нейроконтроллера фиксируется на некоторой величине, что приводит к плохим характеристикам управления.
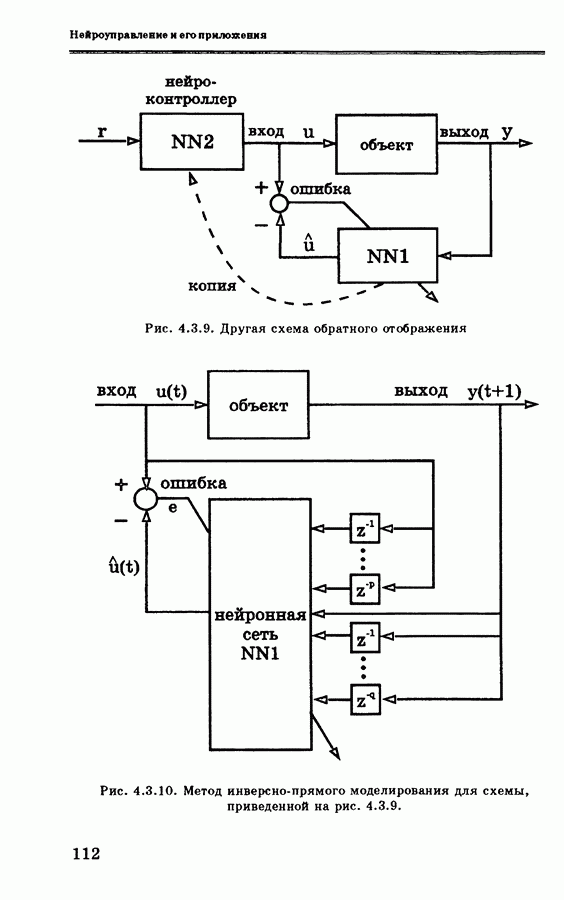
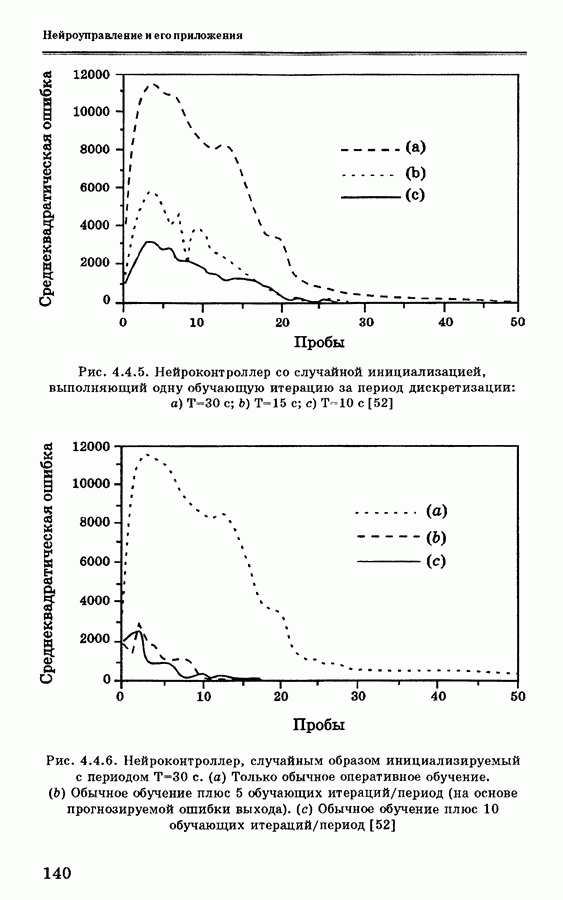
На рис. 4.4.5, а и 4.4.6, а показана характеристика случайно инициализируемого нейроконтроллера, для которого выполняется одна обучающая итерация за период на основе косвенного адаптивного управления (период  ). Так как каждое модельное испытание продолжается 90 минут реального времени, то 50 испытаний требуют 75 часов, или более трех дней. По этой причине большинство результатов, приводимых в данной книге, получены на моделях, а не в реальных экспериментах.
). Так как каждое модельное испытание продолжается 90 минут реального времени, то 50 испытаний требуют 75 часов, или более трех дней. По этой причине большинство результатов, приводимых в данной книге, получены на моделях, а не в реальных экспериментах.
Нижние графики на рис. 4.4.5 соответствуют периоду

(кликните для просмотра скана)
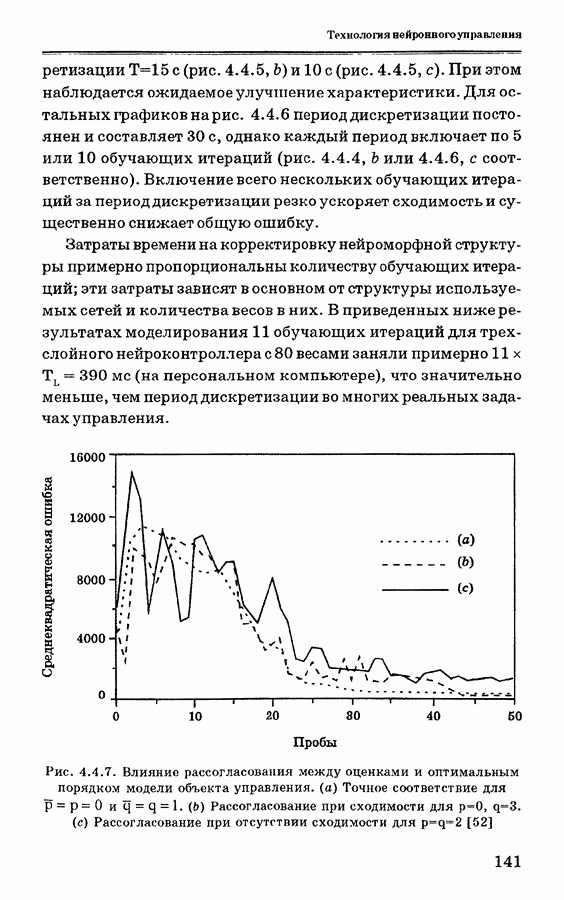
дискретизации  с (рис. 4.4.5, b) и 10 с (рис. 4.4.5, с). При этом наблюдается ожидаемое улучшение характеристики. Для остальных графиков нарис. 4.4.6 период дискретизации постоянен и составляет 30 с, однако каждый период включает по 5 или 10 обучающих итераций (рис. 4.4.4, b или 4.4.6, с соответственно). Включение всего нескольких обучающих итераций за период дискретизации резко ускоряет сходимость и существенно снижает общую ошибку.
с (рис. 4.4.5, b) и 10 с (рис. 4.4.5, с). При этом наблюдается ожидаемое улучшение характеристики. Для остальных графиков нарис. 4.4.6 период дискретизации постоянен и составляет 30 с, однако каждый период включает по 5 или 10 обучающих итераций (рис. 4.4.4, b или 4.4.6, с соответственно). Включение всего нескольких обучающих итераций за период дискретизации резко ускоряет сходимость и существенно снижает общую ошибку.
Затраты времени на корректировку нейроморфной структуры примерно пропорциональны количеству обучающих итераций; эти затраты зависят в основном от структуры используемых сетей и количества весов в них. В приведенных ниже результатах моделирования 11 обучающих итераций для трехслойного нейроконтроллера с 80 весами заняли примерно Их  (на персональном компьютере), что значительно меньше, чем период дискретизации во многих реальных задачах управления.
(на персональном компьютере), что значительно меньше, чем период дискретизации во многих реальных задачах управления.

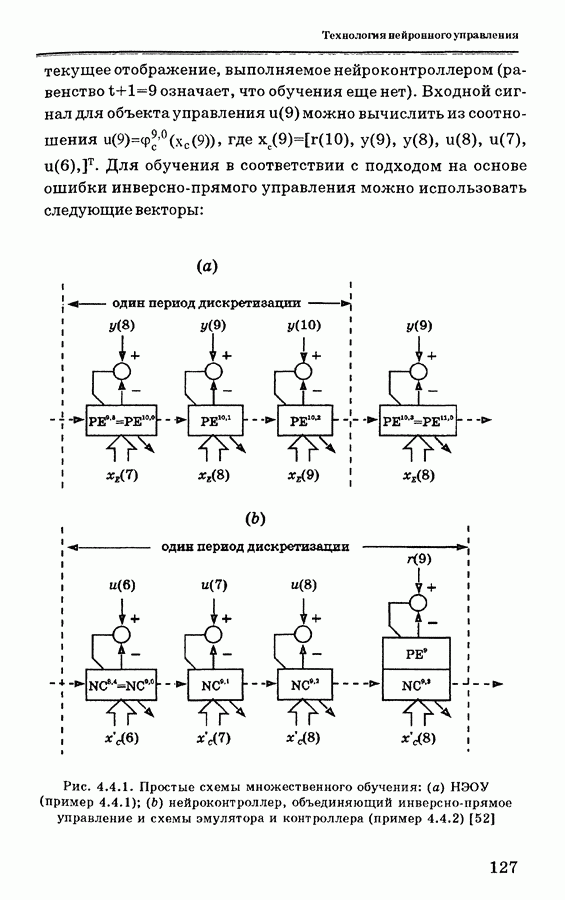
Рис. 4.4.7. Влияние рассогласования между оценками и оптимальным порядком модели объекта управления, (а) Точное соответствие для  . (b) Рассогласование при сходимости для
. (b) Рассогласование при сходимости для  . (с) Рассогласование при отсутствии сходимости для p=q=2 [52]
. (с) Рассогласование при отсутствии сходимости для p=q=2 [52]
Как уже отмечалось, показанные на рис. 4.4.3-4.4.6 результаты получены для случая, когда  Естественно возникает вопрос о том, что происходит, когда нет точных оценок порядка объекта управления. В проведенных модельных экспериментах обучение выполнялось для нескольких различных сочетаний значений параметров
Естественно возникает вопрос о том, что происходит, когда нет точных оценок порядка объекта управления. В проведенных модельных экспериментах обучение выполнялось для нескольких различных сочетаний значений параметров  и
и  однако при обобщении полученных результатов требуется соблюдать осторожность. Небольшие изменения в начальных условиях, опорных величинах, структурах нейронных сетей, функциях активации нейронов и т.п. часто приводят к резким изменениям характеристик. Испытания проводились в различных условиях и для разных комбинаций значений параметров
однако при обобщении полученных результатов требуется соблюдать осторожность. Небольшие изменения в начальных условиях, опорных величинах, структурах нейронных сетей, функциях активации нейронов и т.п. часто приводят к резким изменениям характеристик. Испытания проводились в различных условиях и для разных комбинаций значений параметров  и
и  некоторые результаты показаны на рис. 4.4.7. На рис. 4.4.7, а показан случай точного соответствия, а на рис. 4.4.7, b и 4.4.7, с — случаи рассогласования при
некоторые результаты показаны на рис. 4.4.7. На рис. 4.4.7, а показан случай точного соответствия, а на рис. 4.4.7, b и 4.4.7, с — случаи рассогласования при  соответственно. Хотя в некоторых случаях (как, например, на рис. 4.4.7, с), сходимость не была достигнута, для нескольких пар
соответственно. Хотя в некоторых случаях (как, например, на рис. 4.4.7, с), сходимость не была достигнута, для нескольких пар  вблизи действительных значений этих величин
вблизи действительных значений этих величин  и
и  были получены хорошие результаты.
были получены хорошие результаты.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРОВ ПЕРЕВОДА
- 1. ВВЕДЕНИЕ
- 1.1. Общие сведения об интеллектуальном управлении
- 2. НЕЙРОННЫЕ СЕТИ
- 2.2. Алгоритм обратного распространения
- 2.2.2. Вывод алгоритма обратного распространения
- 2.2.2.2. Правило для скрытого слоя
- 2.2.3. Алгоритм обратного распространения: порядок реализации
- 2.2.4. Обсуждение алгоритма обратного распространения
- 2.3. Заключение
- 3. ТРАДИЦИОННЫЕ СХЕМЫ УПРАВЛЕНИЯ
- 3.2. ПИ- и ПИД-контроллеры с дискретным временем
- 3.3. Управление с самонастройкой
- 3.4. Самонастраивающиеся ПИ- и ПИД- контроллеры
- 3.5. ПИД-управление с самонастройкой: многомерный подход
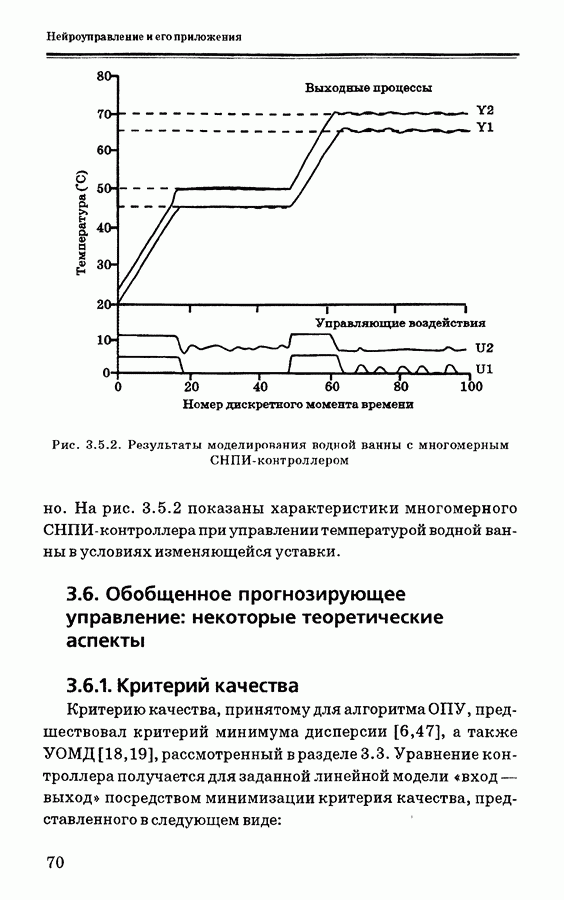
- 3.5.1. Пример моделирования
- 3.6. Обобщенное прогнозирующее управление: некоторые теоретические аспекты
- 3.6.2. Модель объекта управления и решение задачи оптимизации
- 3.7. Управление на основе нечеткой логики
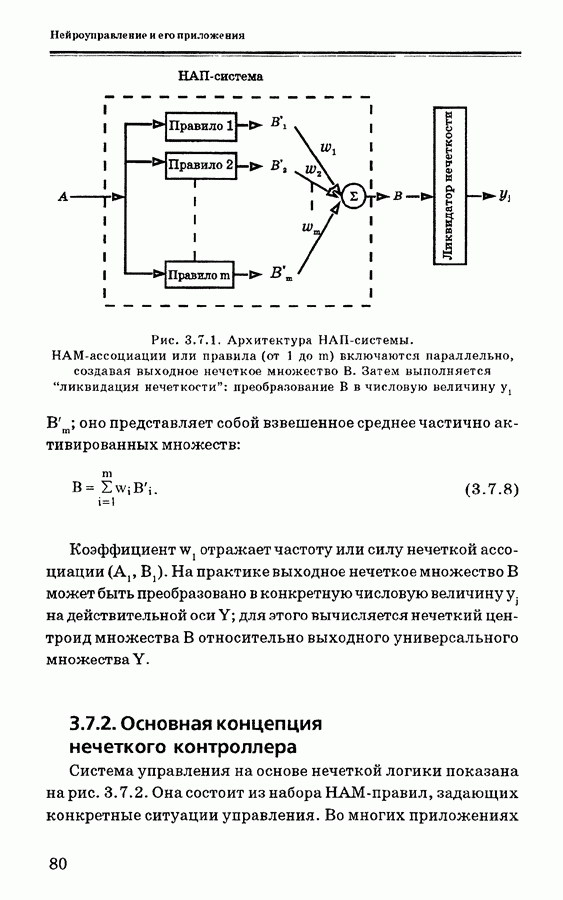
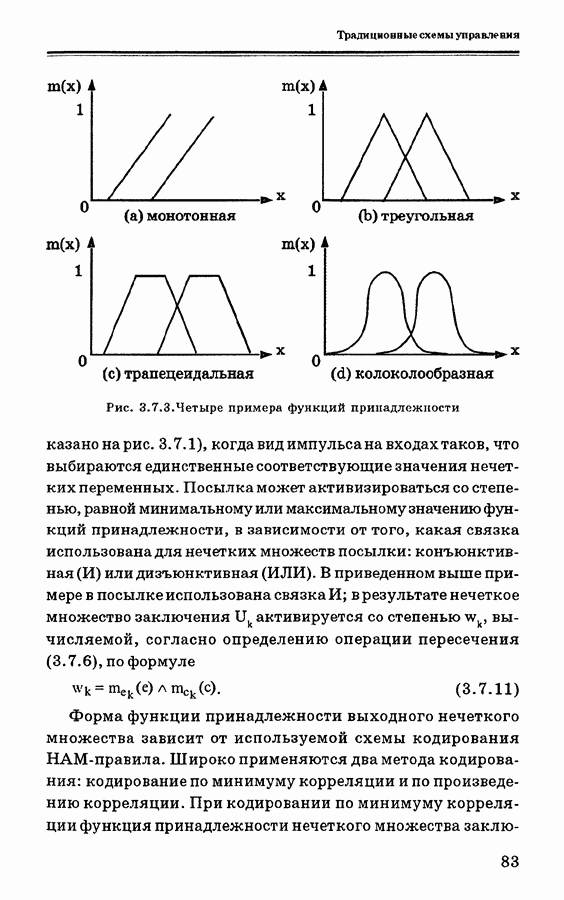
- 3.7.1. Краткие сведения по теории нечетких множеств и нечетких систем
- 3.7.2. Основная концепция нечеткого контроллера
- 3.8. Заключение
- 4. ТЕХНОЛОГИИ НЕЙРОННОГО УПРАВЛЕНИЯ
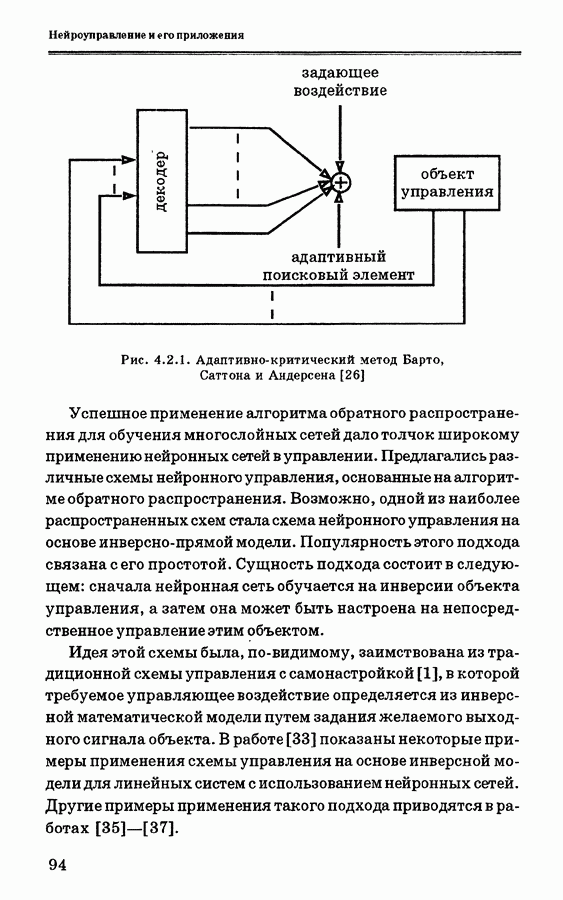
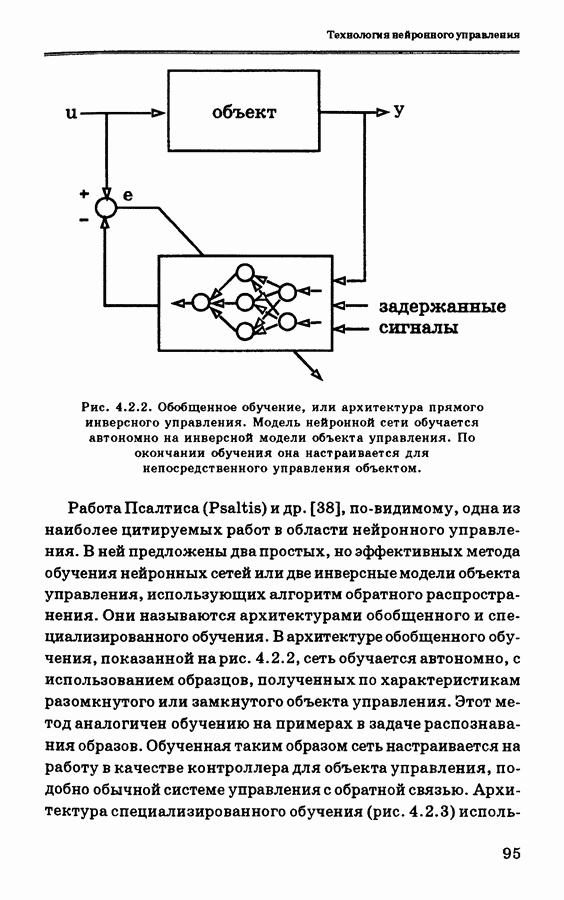
- 4.2. Общие сведения о нейронном управлении
- 4.2.1. Подходы к нейронному управлению
- 4.2.2. Общая схема управления
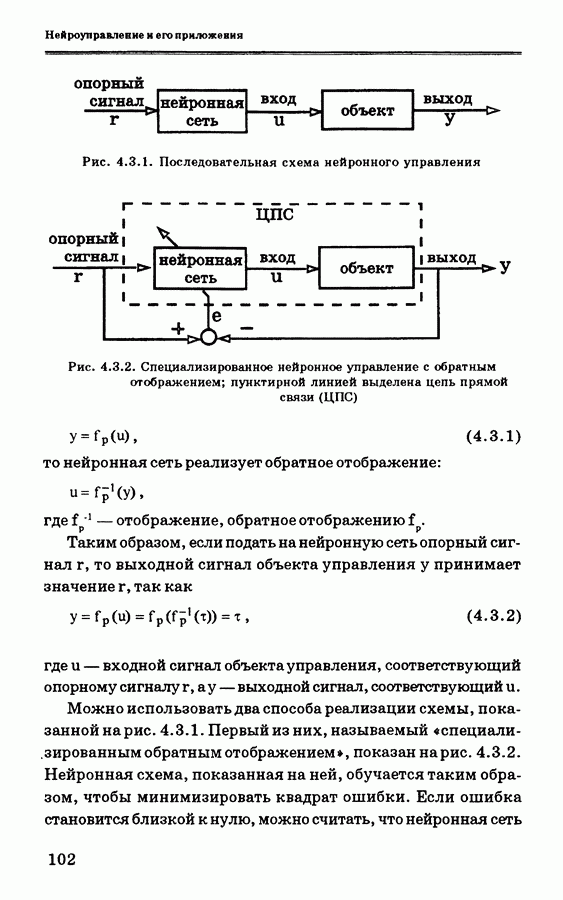
- 4.3. Последовательная схема нейронного управления
- 4.4. Расширение последовательной схемы нейронного управления
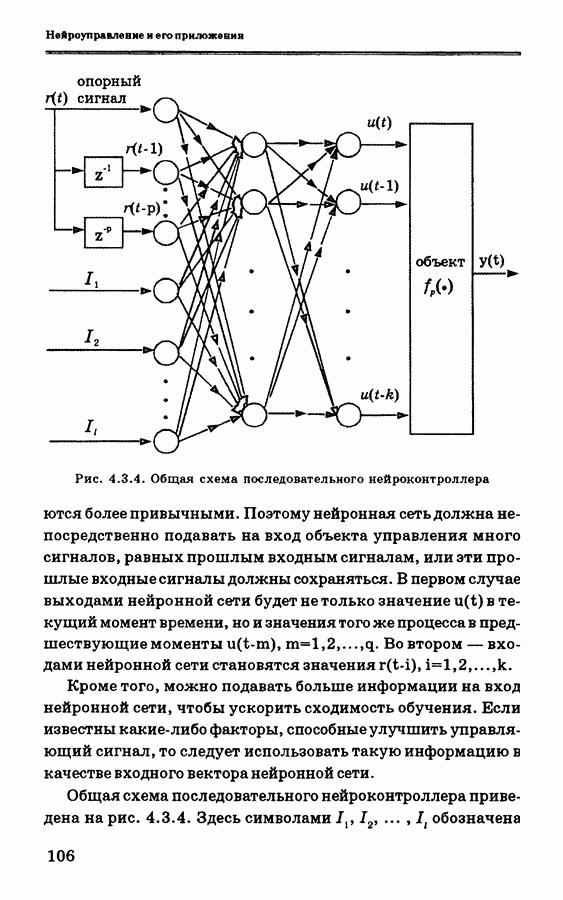
- 4.4.2. Нейроморфные структуры управления
- 4.4.3. Конфигурации обучения
- 4.4.4. Эффективное оперативное управление
- 4.4.5. Алгоритмы обучения
- 4.4.6. Оценка алгоритмов обучения на основе моделирования
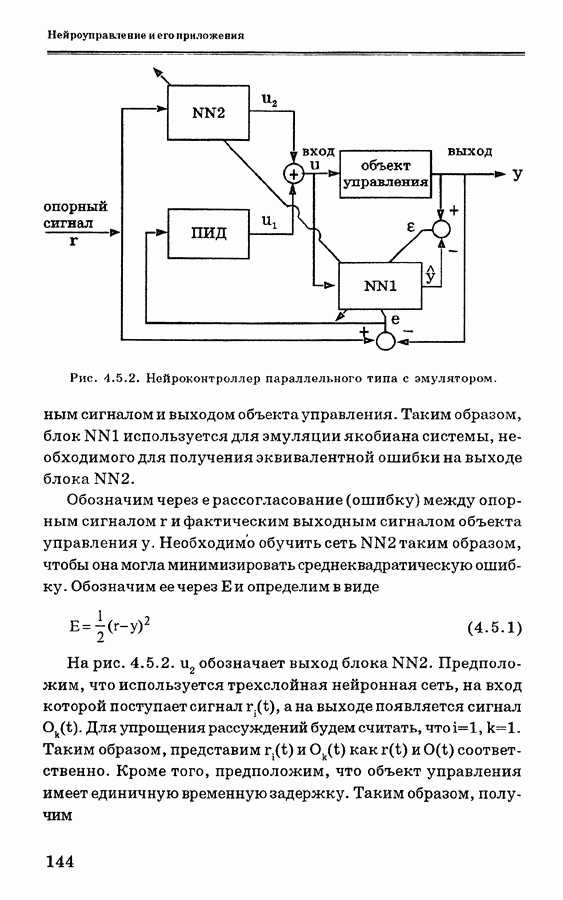
- 4.5. Параллельная схема управления
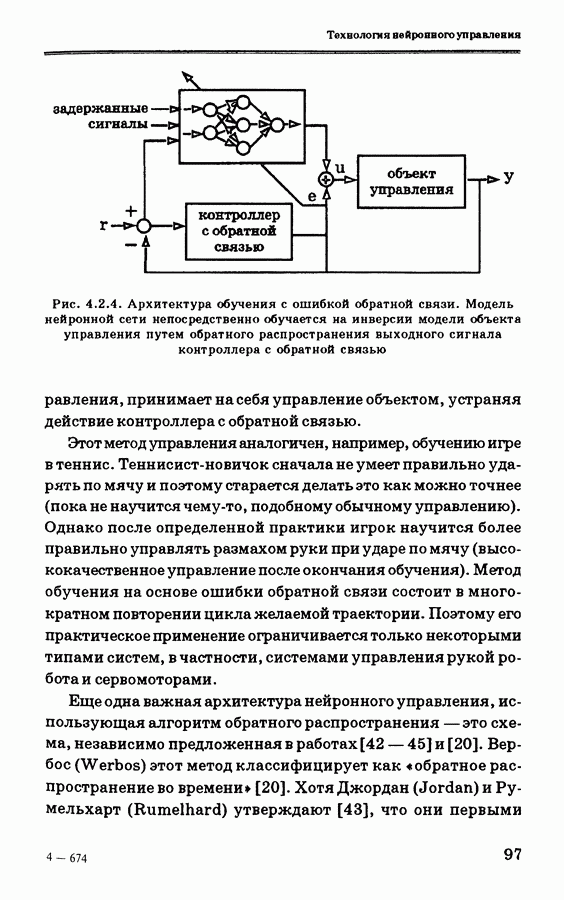
- 4.6. Алгоритм обучения по ошибке обратной связи
- 4.7. Расширение применения нейроконтроллеров параллельного типа
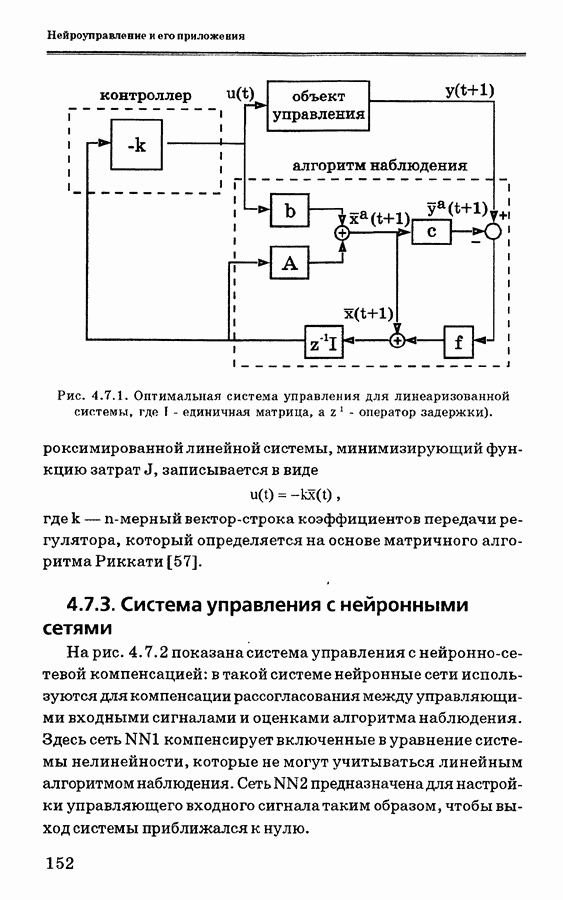
- 4.7.2. Линеаризованная система управления
- 4.7.3. Система управления с нейронными сетями
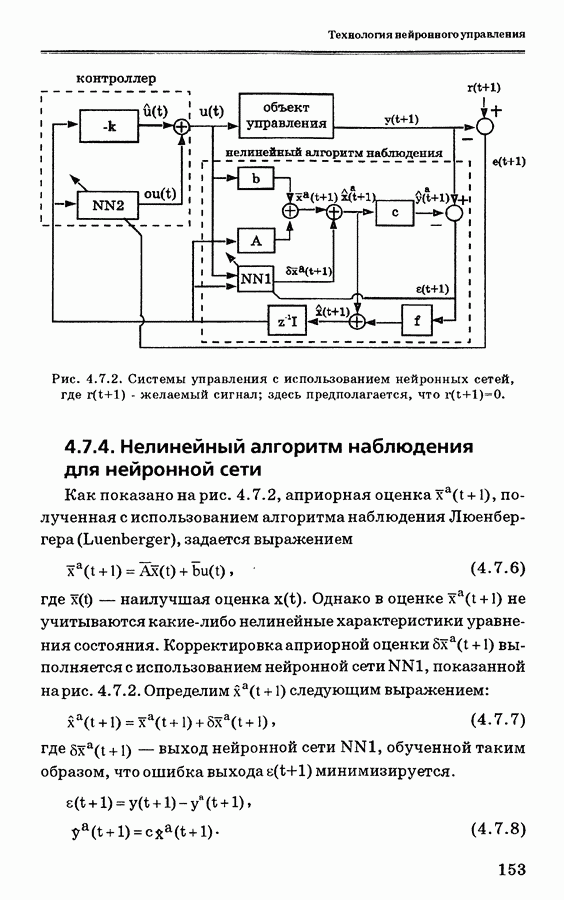
- 4.7.4. Нелинейный алгоритм наблюдения для нейронной сети
- 4.7.5. Нелинейный контроллер для нейронной сети
- 4.7.6. Численное моделирование
- 4.8. Схема нейронного управления с самонастройкой
- 4.9. ПИД-нейроконтроллер с самонастройкой
- 4.9.1. Вывод уравнений ПИД-нейроконтроллера с самонастройкой
- 4.9.2. Примеры эмуляции
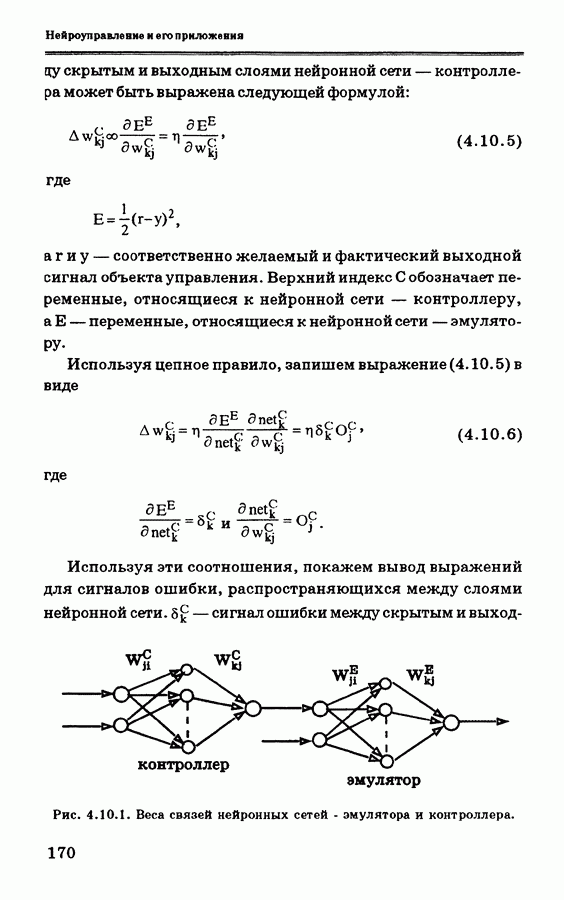
- 4.10. Схема нейронного управления с эмулятором и контроллером (схема обратного распространения во времени)
- 4.11. Заключение
- 5. ПРИЛОЖЕНИЯ НЕЙРОННОГО УПРАВЛЕНИЯ
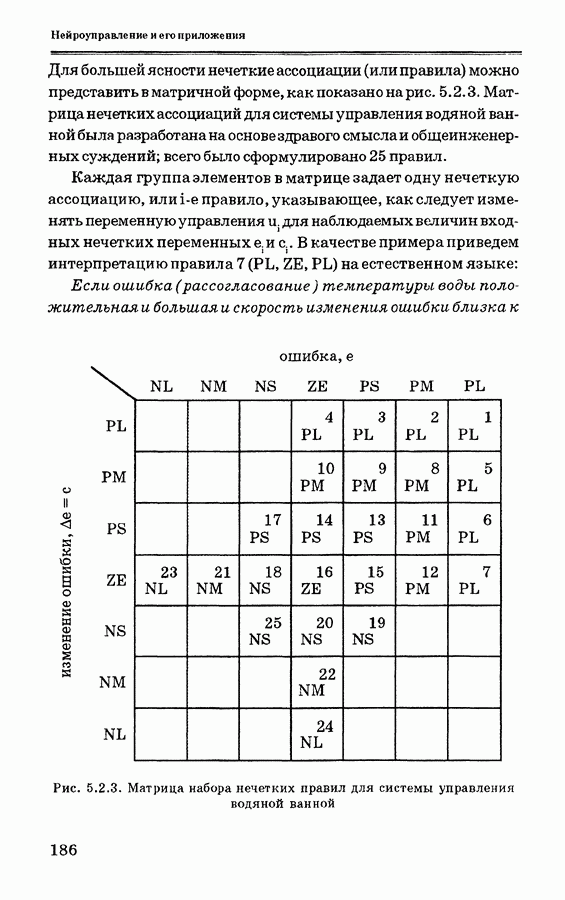
- 5.2. Применение нейронного управления в системе регулирования процессов в водяной ванне и сравнение его с другими схемами управления
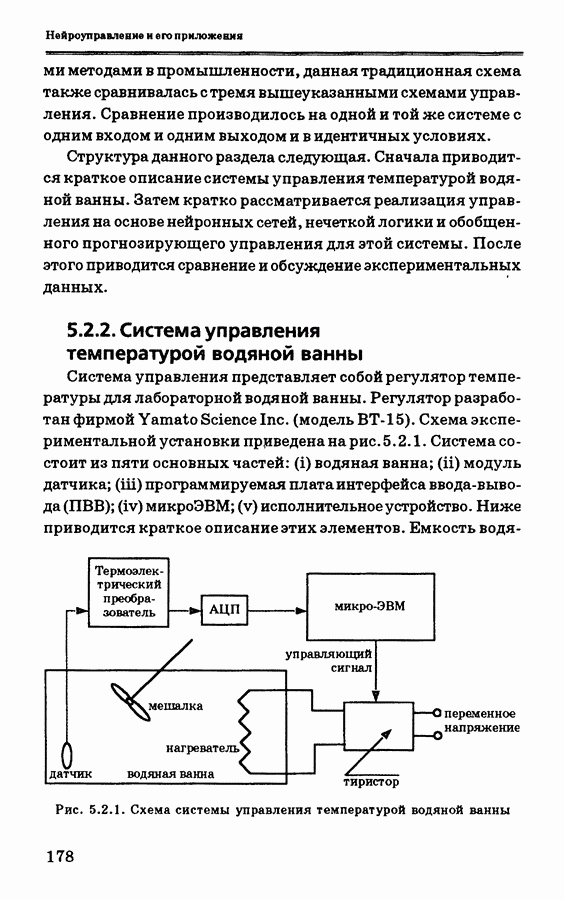
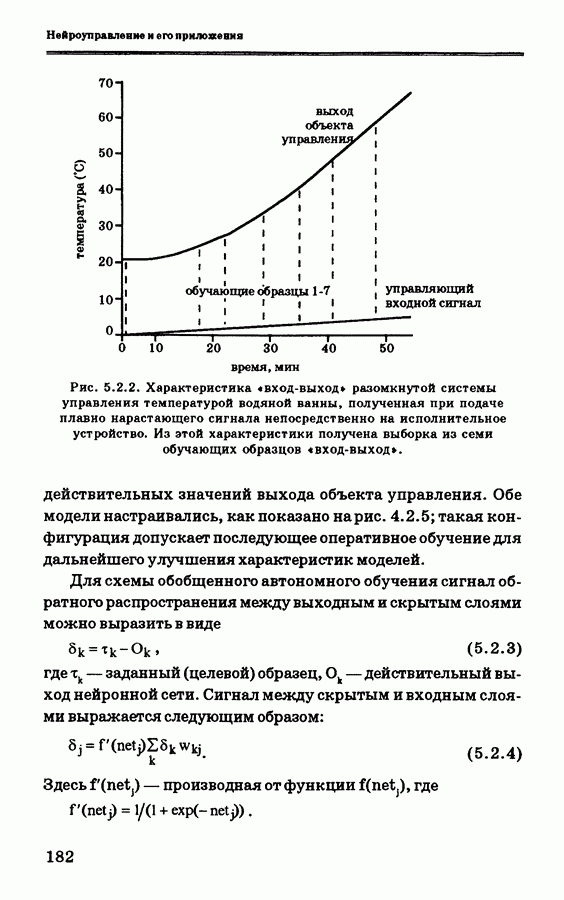
- 5.2.2. Система управления температурой водяной ванны
- 5.2.3. Схема нейронного управления
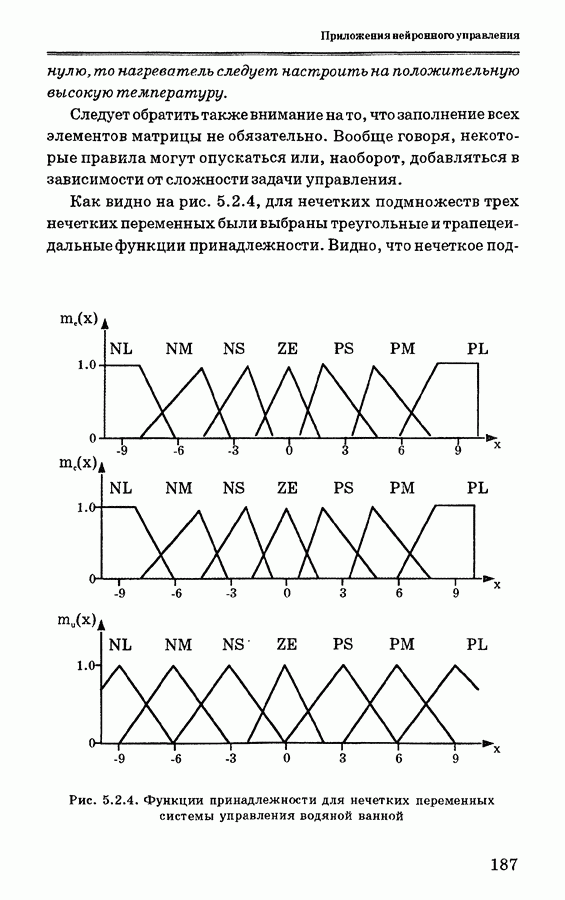
- 5.2.4. Схема управления на основе нечеткой логики
- 5.2.5. Схема обобщенного прогнозирующего управления
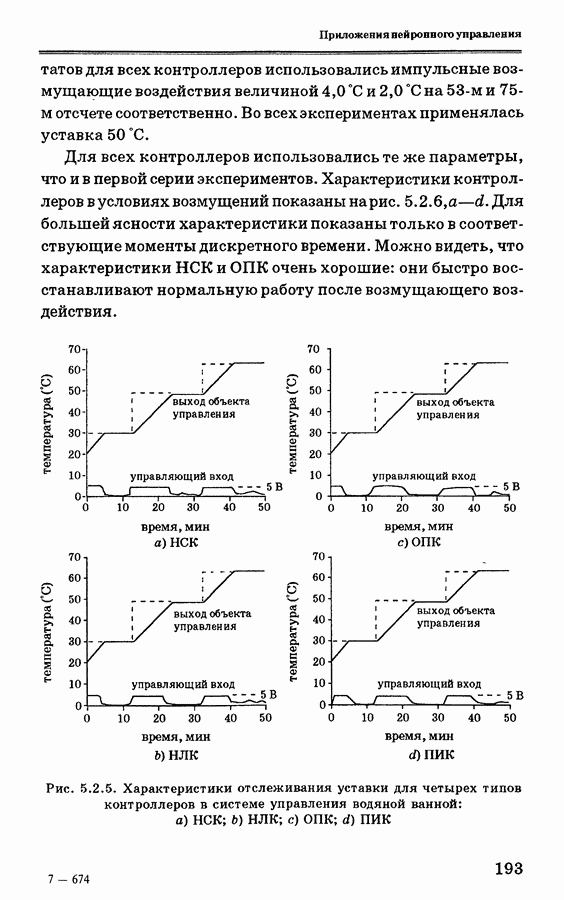
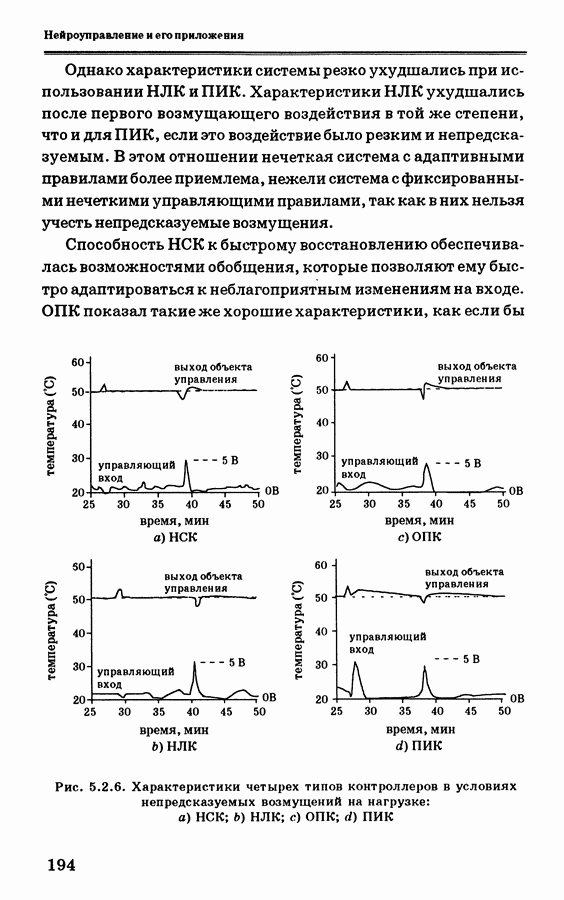
- 5.2.6. Экспериментальные данные и их анализ
- 5.2.7. Заключение
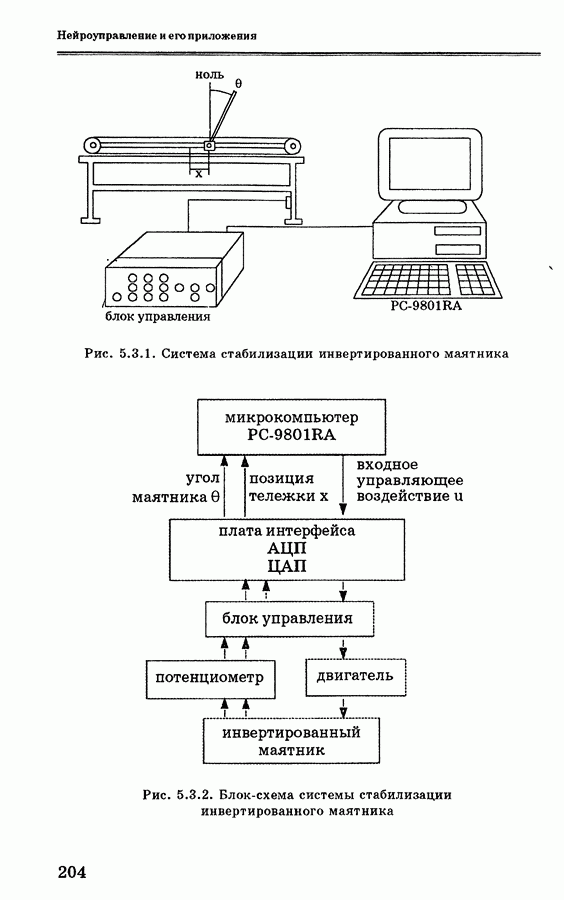
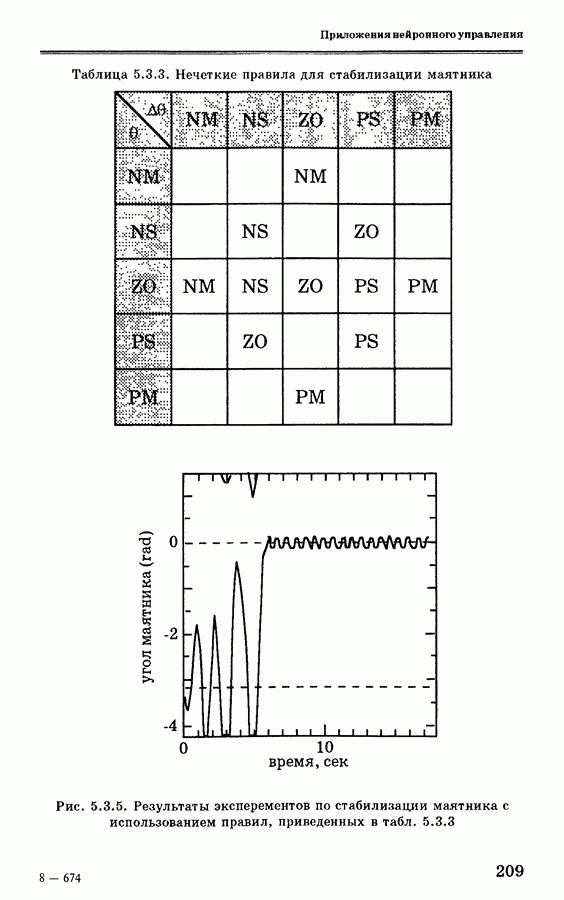
- 5.3. Система стабилизации инвертированного маятника на основе нейронных сетей
- 5.3.2. Система стабилизации инвертированного маятника
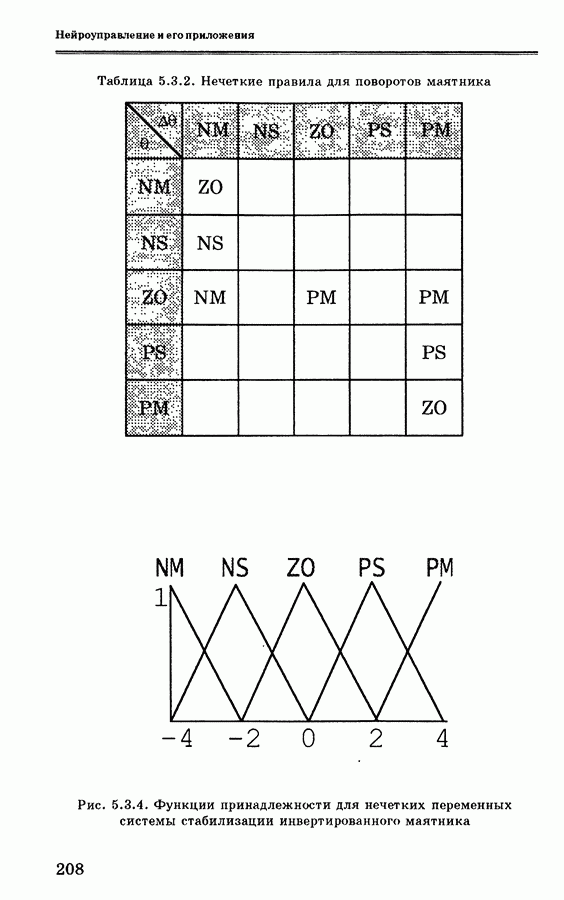
- 5.3.3. Инициализация поворотного управления с использованием нечеткой логики
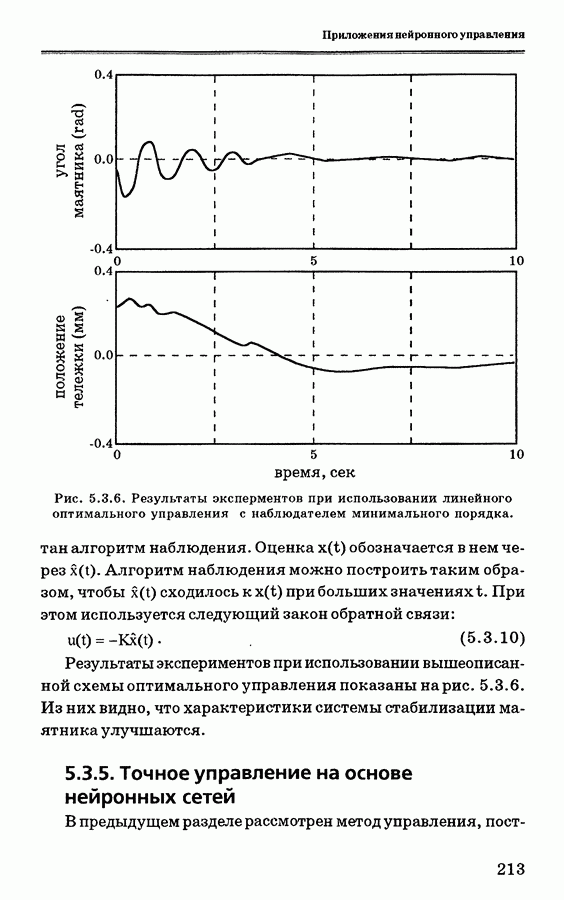
- 5.3.4. Применение стратегии оптимального управления для стабилизации маятника
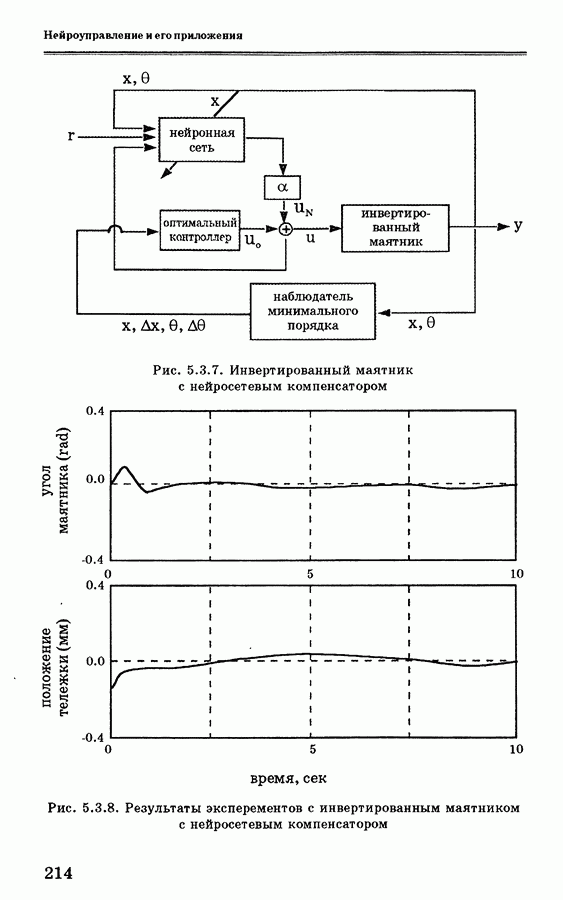
- 5.3.5. Точное управление на основе нейронных сетей
- 5.3.6. Заключение
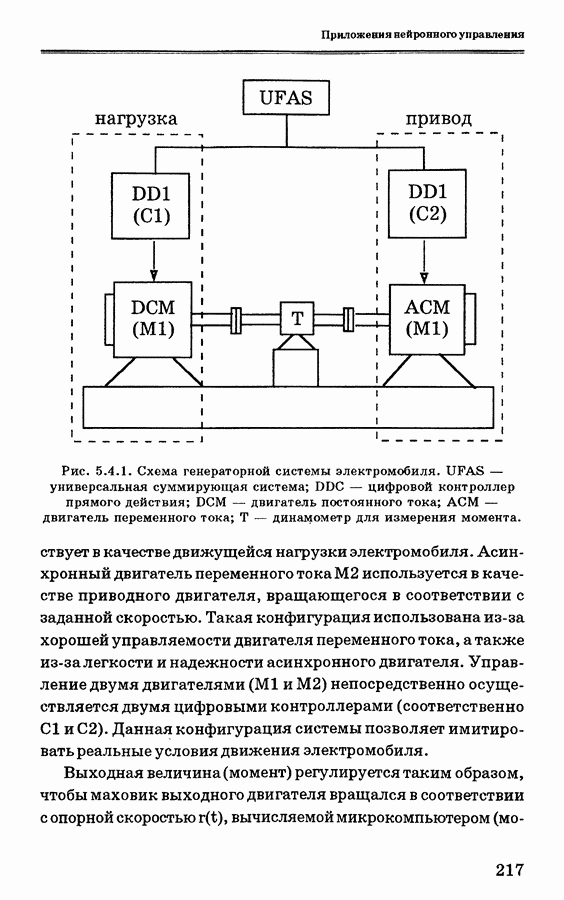
- 5.4. Применение ПИД-нейроконтроллера с самонастройкой для управления скоростью электромобиля
- 5.4.2. Система управления электромобилем
- 5.4.3. ПИД-нейроконтроллер с самонастройкой
- 5.4.4. Применение нейронной сети для управления скоростью электромобиля
- 5.4.5. Заключение
- 5.5. Применение нейронных сетей для управления печью
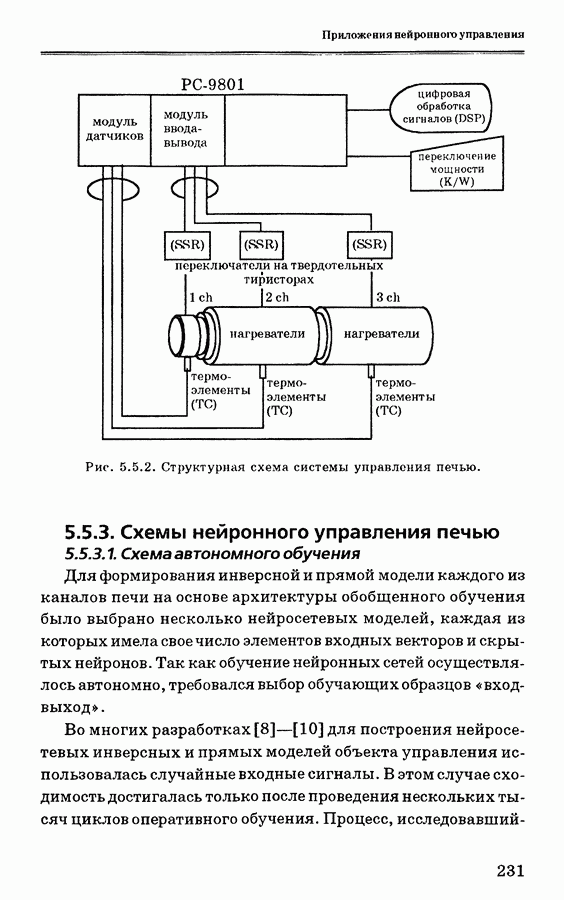
- 5.5.2. Система управления печью
- 5.5.3. Схемы нейронного управления печью
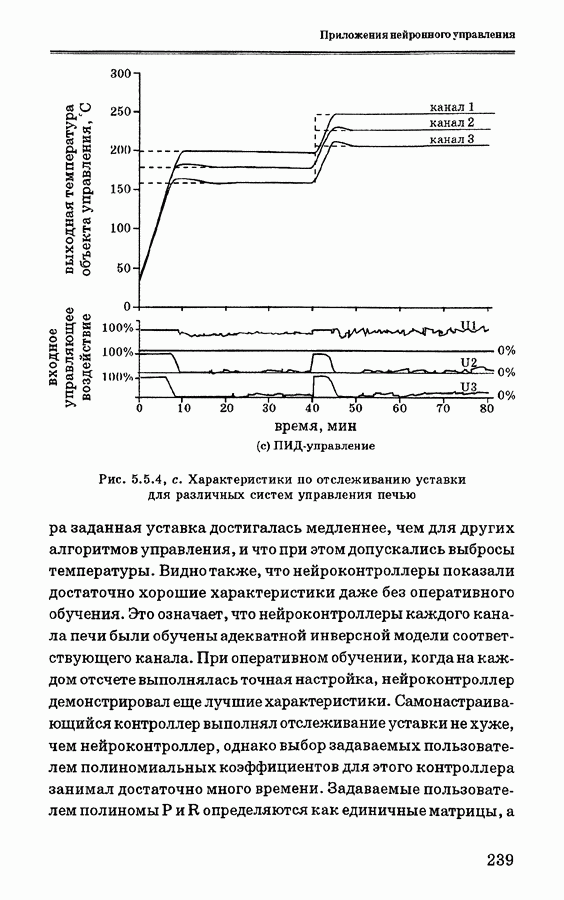
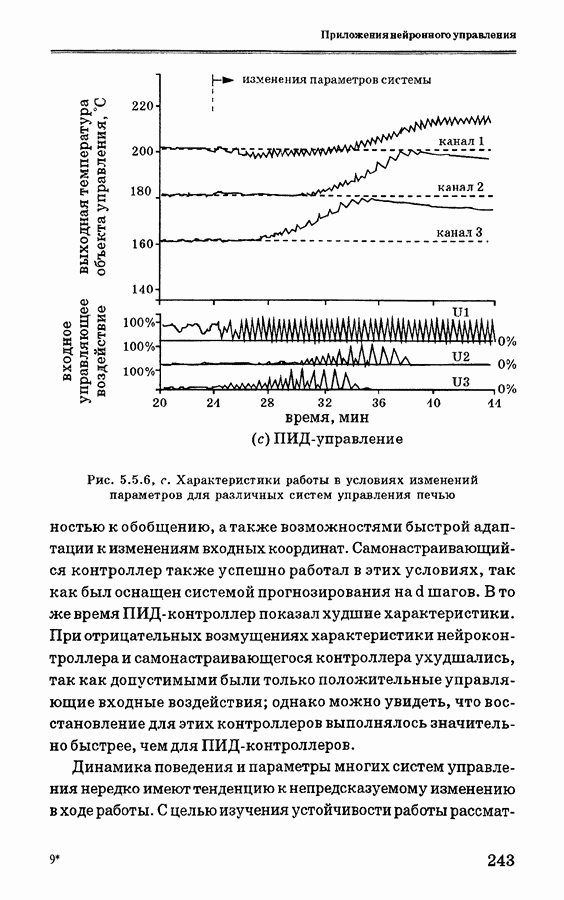
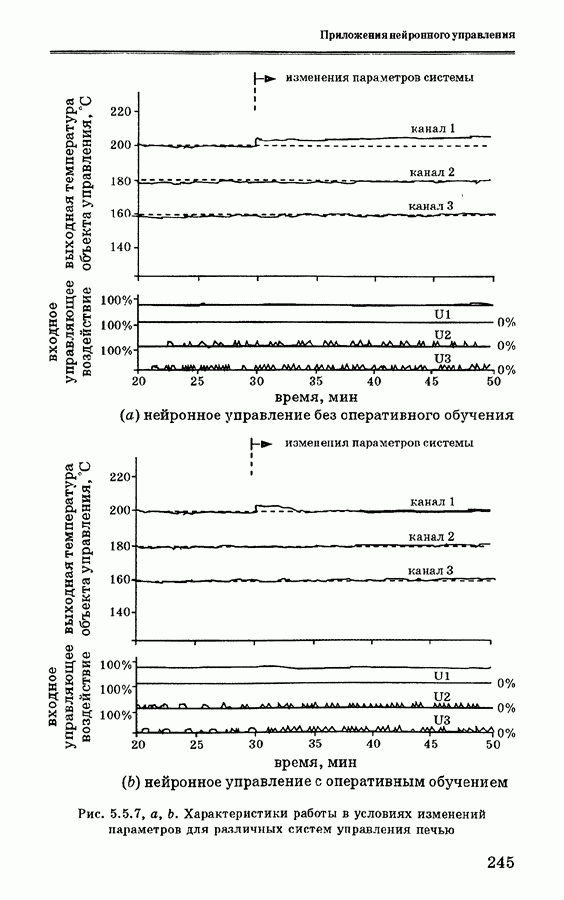
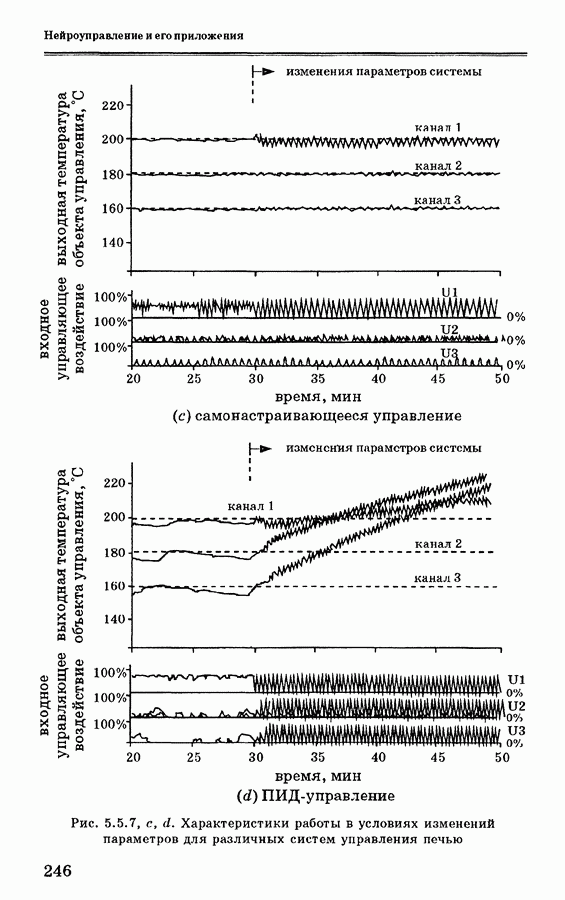
- 5.5.4. Анализ экспериментальных данных
- 5.6. Заключительные замечания и выводы
- Литература
- ЛИСТИНГ ПРОГРАММЫ