| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4.4.3. Конфигурации обучения
Обучающий сигнал для контроллера, показанный на рис. 4.3.8, передает информацию, необходимую для обучения нейроконтроллера инверсной динамике объекта управления. Обучение должно обеспечивать минимизацию функции ошибки  определенной для ошибки выхода объекта управления
определенной для ошибки выхода объекта управления  Для обучения на основе метода наискорейшего спуска необходимо вычислить производную функции ошибки
Для обучения на основе метода наискорейшего спуска необходимо вычислить производную функции ошибки  по выходной координате нейроконтроллера, т.е.
по выходной координате нейроконтроллера, т.е.  Знание величины
Знание величины  достаточно для корректировки весов нейроконтроллера в соответствии с алгоритмом обратного распространения. Для объяснения этой схемы обучения многослойных нейронных сетей в следующих разделах будут еще раз кратко описаны основные конфигурации нейронного управления.
достаточно для корректировки весов нейроконтроллера в соответствии с алгоритмом обратного распространения. Для объяснения этой схемы обучения многослойных нейронных сетей в следующих разделах будут еще раз кратко описаны основные конфигурации нейронного управления.
4.4.3.1. Инверсно-прямое управление
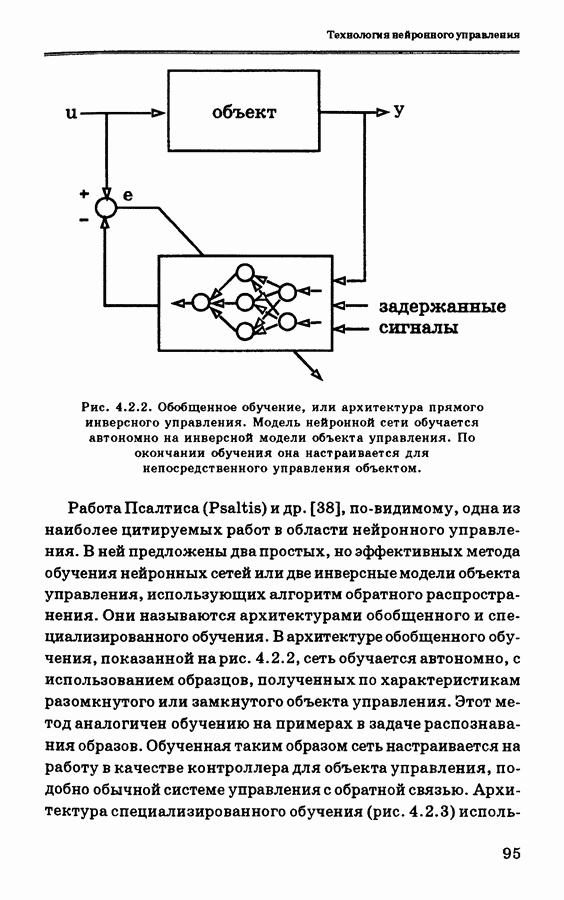
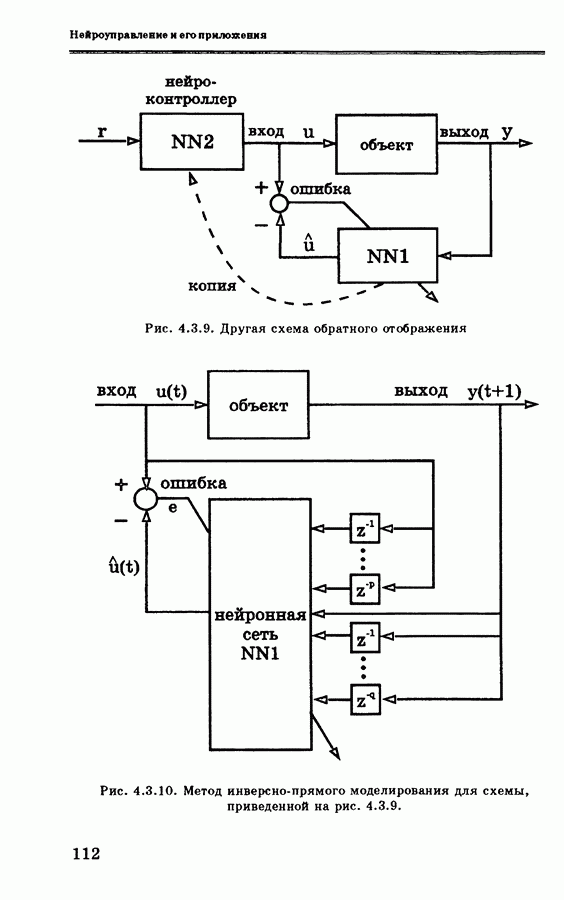
Инверсно-прямая конфигурация управления, или обобщенное обучение (см. рис. 4.3.10) — это схема автономного
обучения. Однако, поскольку эта схема управления строится на основе способности нейроконтроллеров к обобщению, ее не следует применять как единственную схему обучения. С другой стороны, обучающие данные для управляемого обучения могут быть получены достаточно просто. В момент времени  для вектора
для вектора

нейроконтроллер можно скорректировать с целью минимизации функции ошибки  определяемой как функция разности
определяемой как функция разности  где
где  таким образом, выражение
таким образом, выражение  можно легко вычислить, что делает возможным применение алгоритма обратного распространения. Например, если
можно легко вычислить, что делает возможным применение алгоритма обратного распространения. Например, если

то выражение для производной  принимает следующий вид:
принимает следующий вид:

где выражение  обозначает значение
обозначает значение  в момент времени t.
в момент времени t.
4.4.3.2. Оперативное специализированное обучение
Такая конфигурация показана на рис. 4.2.3. Обучение выполняется в оперативном режиме, а функция ошибки  определяется на основе ошибки выхода объекта управления, как и во многих стандартных задачах оптимизации управления. Сложность заключается в том, что для точного вычисления величины 5 (чувствительности показателя
определяется на основе ошибки выхода объекта управления, как и во многих стандартных задачах оптимизации управления. Сложность заключается в том, что для точного вычисления величины 5 (чувствительности показателя  относительно выхода нейроконтроллера) требуется знать якобиан объекта управления. Например, простая функция ошибки и соответствующее выражение 5 могут быть заданы следующим образом:
относительно выхода нейроконтроллера) требуется знать якобиан объекта управления. Например, простая функция ошибки и соответствующее выражение 5 могут быть заданы следующим образом:


где  а двоичный коэффициент
а двоичный коэффициент  вводится для учета ограничений на вход
вводится для учета ограничений на вход  Введя обозначение
Введя обозначение  приведем выражение для коэффициента в момент времени
приведем выражение для коэффициента в момент времени  для системы, описанной формулами (4.4.1) и (4.4.2):
для системы, описанной формулами (4.4.1) и (4.4.2):

Коэффициент  введен для того, чтобы исключить неправильное обучение нейроконтроллера по опорным сигналам, которые невозможно отслеживать. Включение коэффициента эквивалентно введению ограничителя между выходом нейроконтроллера и входом объекта управления. Когда из-за физических ограничений, заданных выражением (4.4.2), возникает ошибка выхода, ограничитель насыщается, и в выражение (4.4.11) включается нулевая производная
введен для того, чтобы исключить неправильное обучение нейроконтроллера по опорным сигналам, которые невозможно отслеживать. Включение коэффициента эквивалентно введению ограничителя между выходом нейроконтроллера и входом объекта управления. Когда из-за физических ограничений, заданных выражением (4.4.2), возникает ошибка выхода, ограничитель насыщается, и в выражение (4.4.11) включается нулевая производная  запрещающая обучение. В противоположном случае, когда работа в соответствии с опорным сигналом физически возможна, обучение выполняется обычным образом.
запрещающая обучение. В противоположном случае, когда работа в соответствии с опорным сигналом физически возможна, обучение выполняется обычным образом.
4.4.3.3. Схемы эмулятора и контроллера
Во многих практических ситуациях достаточно легко найти оценку производной, используемой в выражении (4.4.11). Иногда даже можно заменить ее значение  или -1, т.е. значением сигнум-функции от производной, так как алгебраического знака значения
или -1, т.е. значением сигнум-функции от производной, так как алгебраического знака значения  достаточно для определения направления градиента
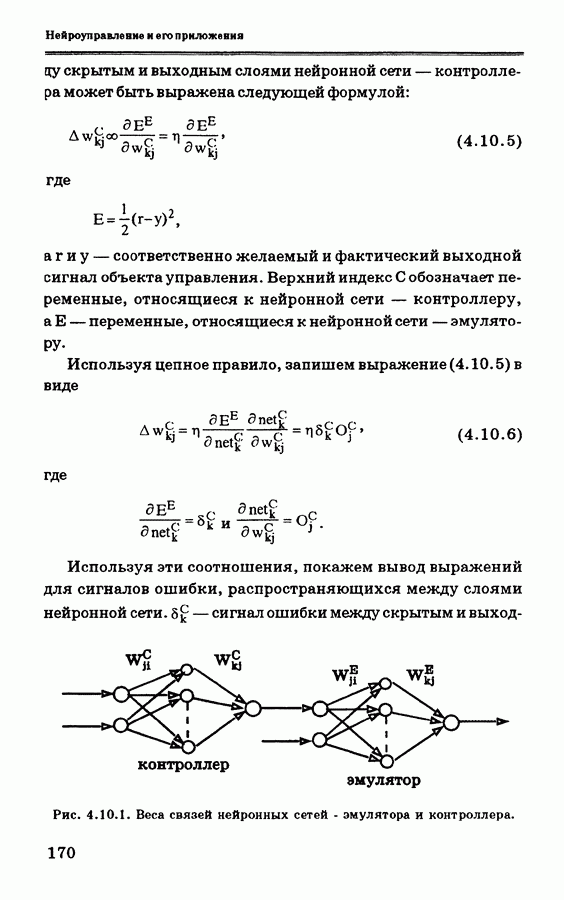
достаточно для определения направления градиента  . В общем случае, однако, все не так просто. В схеме эмулятора и контроллера, приведенной на рис. 4.2.5, для вычисления чувствительности функции ошибки
. В общем случае, однако, все не так просто. В схеме эмулятора и контроллера, приведенной на рис. 4.2.5, для вычисления чувствительности функции ошибки  относительно выхода контроллера используется НЭОУ. Так как НЭОУ представляет собой многослойную нейронную сеть,
относительно выхода контроллера используется НЭОУ. Так как НЭОУ представляет собой многослойную нейронную сеть,
желаемую чувствительность легко вычислить, используя обратное распространение. Кроме того, приведенная на рис. 4.2.5 конфигурация особенно полезна в случаях, когда инверсия объекта управления является плохо определенной, т.е. для функции  в уравнении (4.4.1) невозможно найти обратную функцию. Для коррекции контроллера, нейроконтроллер и НЭОУ рассматриваются соответственно как переменная и постоянная части многослойной нейронной сети с
в уравнении (4.4.1) невозможно найти обратную функцию. Для коррекции контроллера, нейроконтроллер и НЭОУ рассматриваются соответственно как переменная и постоянная части многослойной нейронной сети с  входами и одним выходом. Сначала НЭОУ подвергается автономному обучению; используемый при этом набор данных должен быть достаточно представительным, чтобы допускать идентификацию объекта управления. Затем и нейроконтроллер, и НЭОУ подвергаются оперативному обучению. В известном смысле НЭОУ выполняет здесь идентификацию системы; поэтому для быстро изменяющихся систем, по соображениям устойчивости, имеет смысл корректировать НЭОУ чаще, чем нейроконтроллер.
входами и одним выходом. Сначала НЭОУ подвергается автономному обучению; используемый при этом набор данных должен быть достаточно представительным, чтобы допускать идентификацию объекта управления. Затем и нейроконтроллер, и НЭОУ подвергаются оперативному обучению. В известном смысле НЭОУ выполняет здесь идентификацию системы; поэтому для быстро изменяющихся систем, по соображениям устойчивости, имеет смысл корректировать НЭОУ чаще, чем нейроконтроллер.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРОВ ПЕРЕВОДА
- 1. ВВЕДЕНИЕ
- 1.1. Общие сведения об интеллектуальном управлении
- 2. НЕЙРОННЫЕ СЕТИ
- 2.2. Алгоритм обратного распространения
- 2.2.2. Вывод алгоритма обратного распространения
- 2.2.2.2. Правило для скрытого слоя
- 2.2.3. Алгоритм обратного распространения: порядок реализации
- 2.2.4. Обсуждение алгоритма обратного распространения
- 2.3. Заключение
- 3. ТРАДИЦИОННЫЕ СХЕМЫ УПРАВЛЕНИЯ
- 3.2. ПИ- и ПИД-контроллеры с дискретным временем
- 3.3. Управление с самонастройкой
- 3.4. Самонастраивающиеся ПИ- и ПИД- контроллеры
- 3.5. ПИД-управление с самонастройкой: многомерный подход
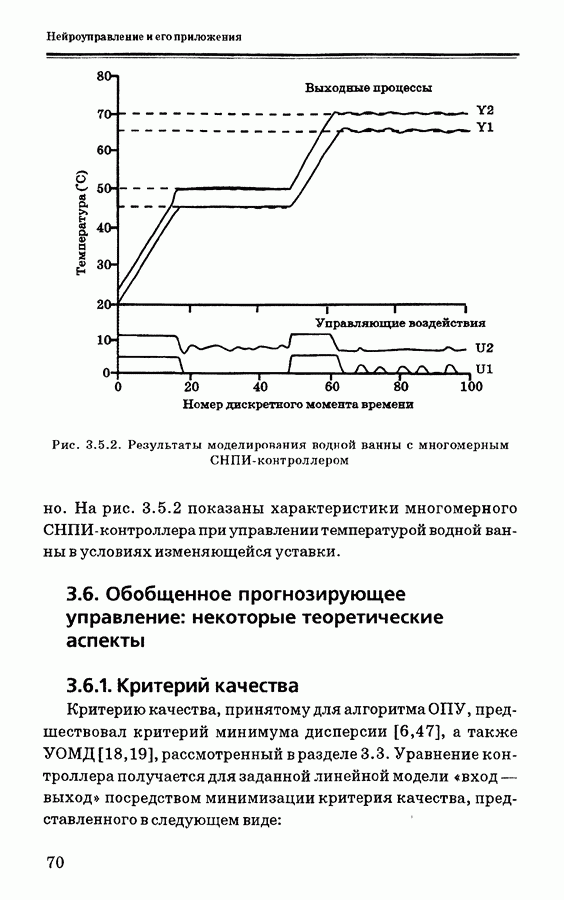
- 3.5.1. Пример моделирования
- 3.6. Обобщенное прогнозирующее управление: некоторые теоретические аспекты
- 3.6.2. Модель объекта управления и решение задачи оптимизации
- 3.7. Управление на основе нечеткой логики
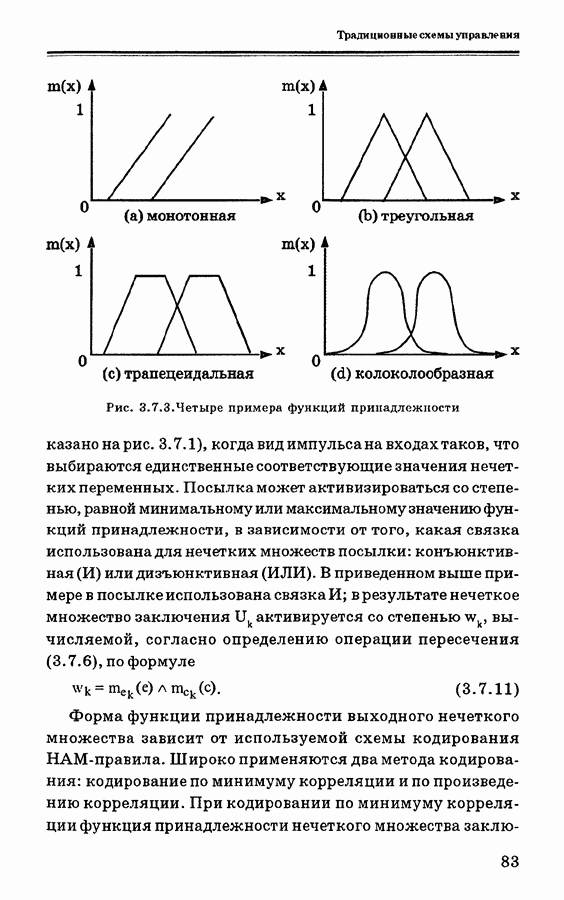
- 3.7.1. Краткие сведения по теории нечетких множеств и нечетких систем
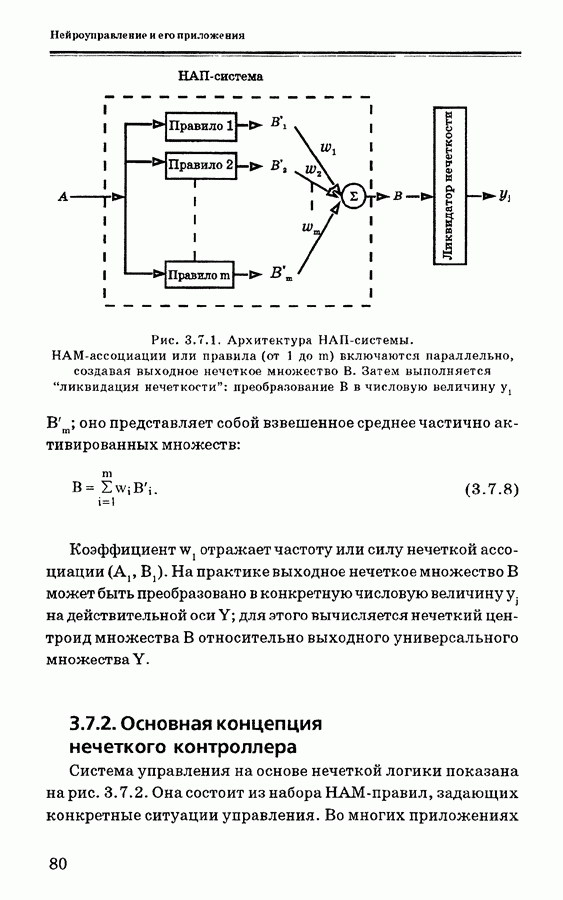
- 3.7.2. Основная концепция нечеткого контроллера
- 3.8. Заключение
- 4. ТЕХНОЛОГИИ НЕЙРОННОГО УПРАВЛЕНИЯ
- 4.2. Общие сведения о нейронном управлении
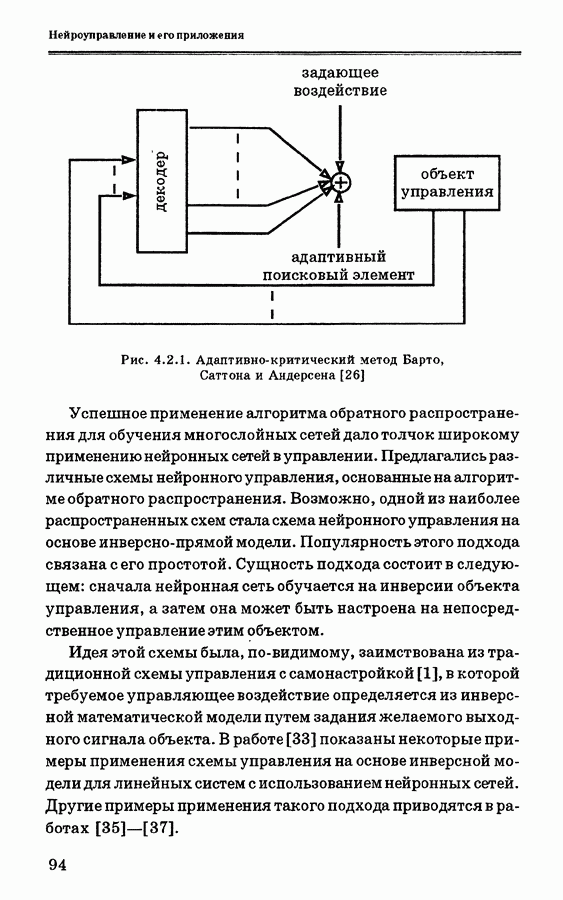
- 4.2.1. Подходы к нейронному управлению
- 4.2.2. Общая схема управления
- 4.3. Последовательная схема нейронного управления
- 4.4. Расширение последовательной схемы нейронного управления
- 4.4.2. Нейроморфные структуры управления
- 4.4.3. Конфигурации обучения
- 4.4.4. Эффективное оперативное управление
- 4.4.5. Алгоритмы обучения
- 4.4.6. Оценка алгоритмов обучения на основе моделирования
- 4.5. Параллельная схема управления
- 4.6. Алгоритм обучения по ошибке обратной связи
- 4.7. Расширение применения нейроконтроллеров параллельного типа
- 4.7.2. Линеаризованная система управления
- 4.7.3. Система управления с нейронными сетями
- 4.7.4. Нелинейный алгоритм наблюдения для нейронной сети
- 4.7.5. Нелинейный контроллер для нейронной сети
- 4.7.6. Численное моделирование
- 4.8. Схема нейронного управления с самонастройкой
- 4.9. ПИД-нейроконтроллер с самонастройкой
- 4.9.1. Вывод уравнений ПИД-нейроконтроллера с самонастройкой
- 4.9.2. Примеры эмуляции
- 4.10. Схема нейронного управления с эмулятором и контроллером (схема обратного распространения во времени)
- 4.11. Заключение
- 5. ПРИЛОЖЕНИЯ НЕЙРОННОГО УПРАВЛЕНИЯ
- 5.2. Применение нейронного управления в системе регулирования процессов в водяной ванне и сравнение его с другими схемами управления
- 5.2.2. Система управления температурой водяной ванны
- 5.2.3. Схема нейронного управления
- 5.2.4. Схема управления на основе нечеткой логики
- 5.2.5. Схема обобщенного прогнозирующего управления
- 5.2.6. Экспериментальные данные и их анализ
- 5.2.7. Заключение
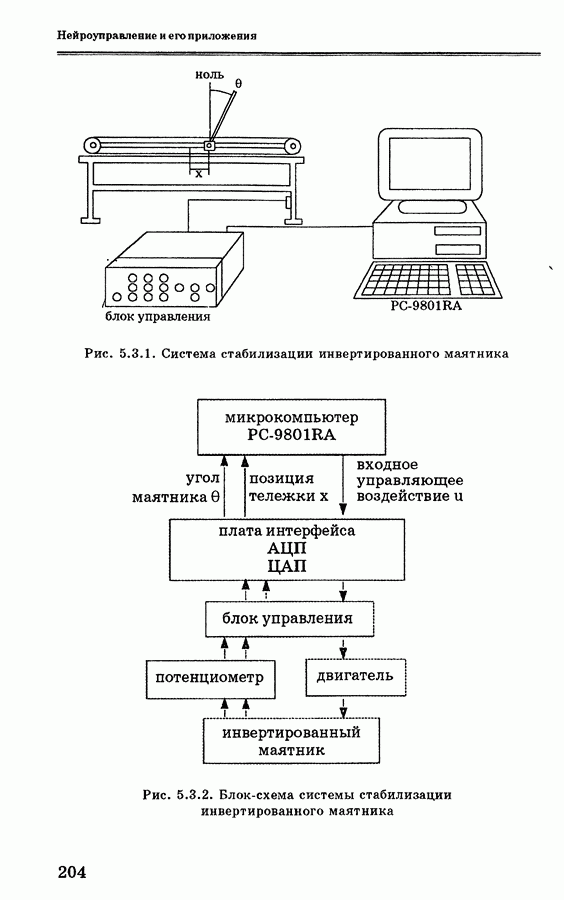
- 5.3. Система стабилизации инвертированного маятника на основе нейронных сетей
- 5.3.2. Система стабилизации инвертированного маятника
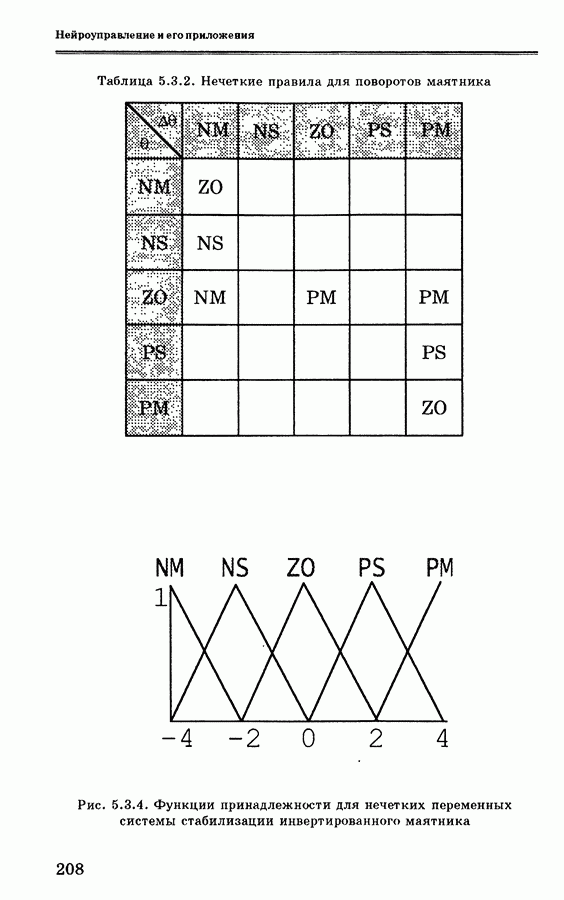
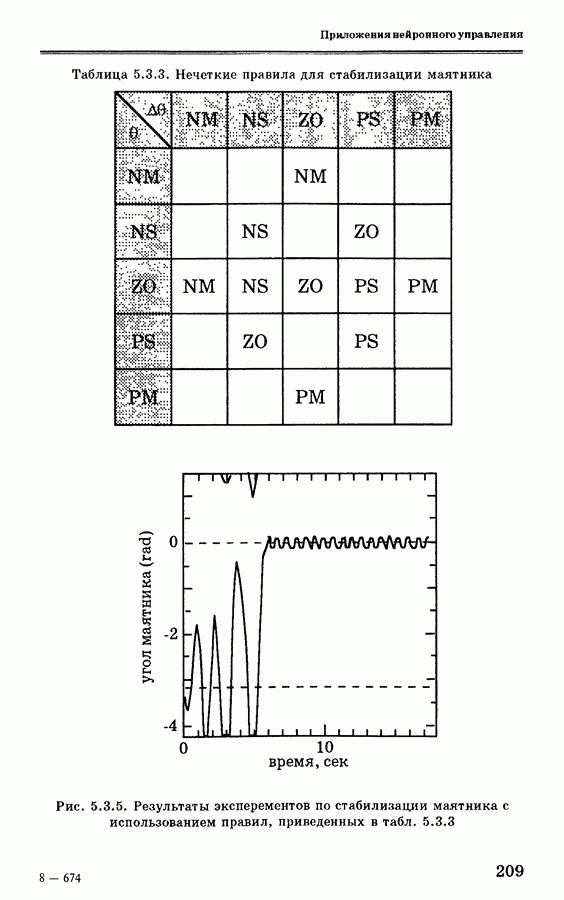
- 5.3.3. Инициализация поворотного управления с использованием нечеткой логики
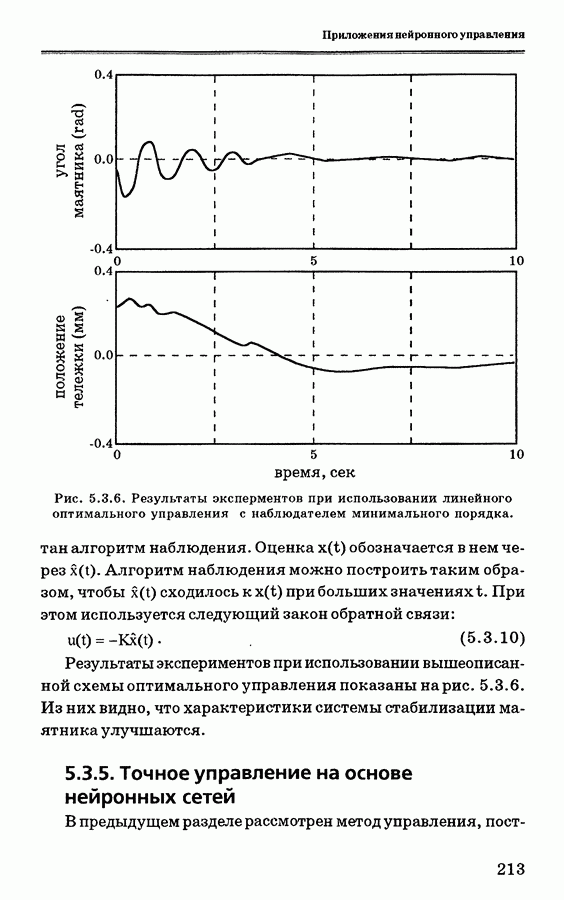
- 5.3.4. Применение стратегии оптимального управления для стабилизации маятника
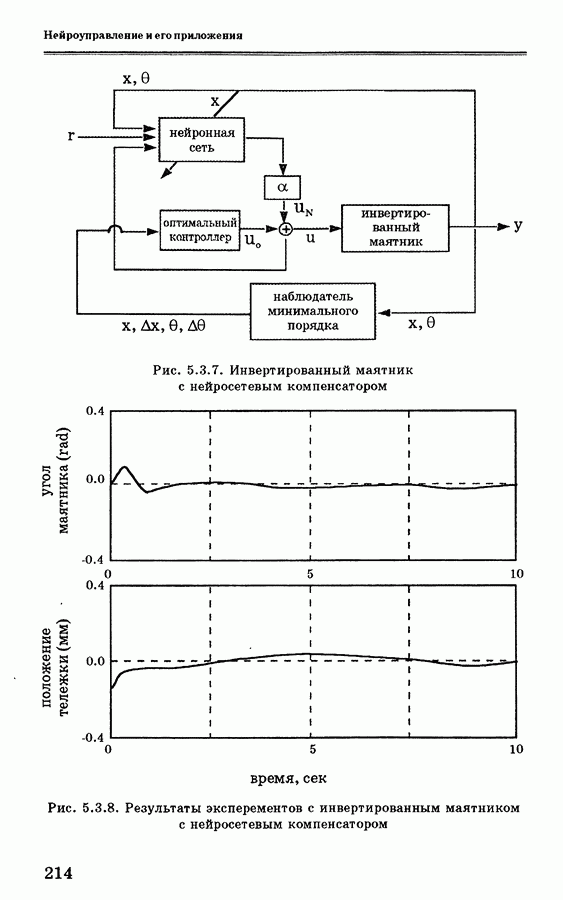
- 5.3.5. Точное управление на основе нейронных сетей
- 5.3.6. Заключение
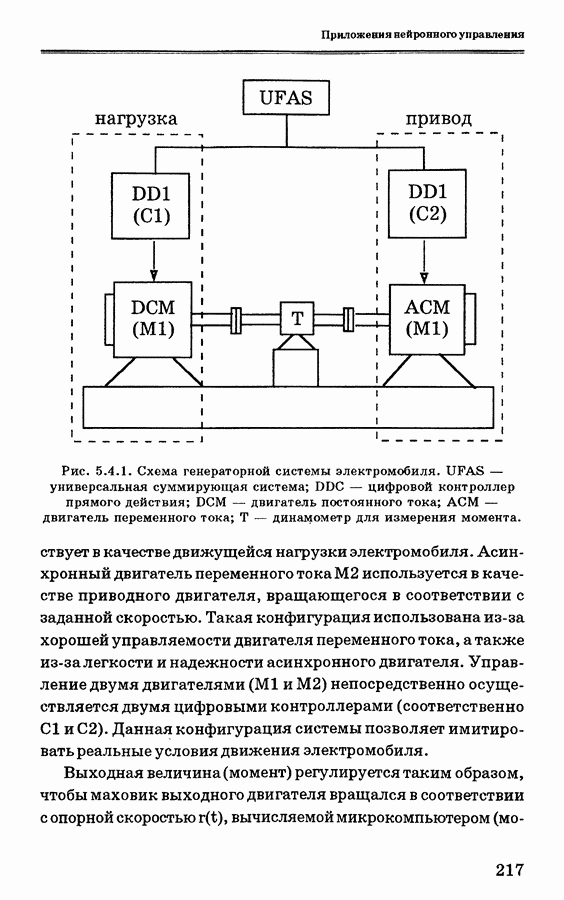
- 5.4. Применение ПИД-нейроконтроллера с самонастройкой для управления скоростью электромобиля
- 5.4.2. Система управления электромобилем
- 5.4.3. ПИД-нейроконтроллер с самонастройкой
- 5.4.4. Применение нейронной сети для управления скоростью электромобиля
- 5.4.5. Заключение
- 5.5. Применение нейронных сетей для управления печью
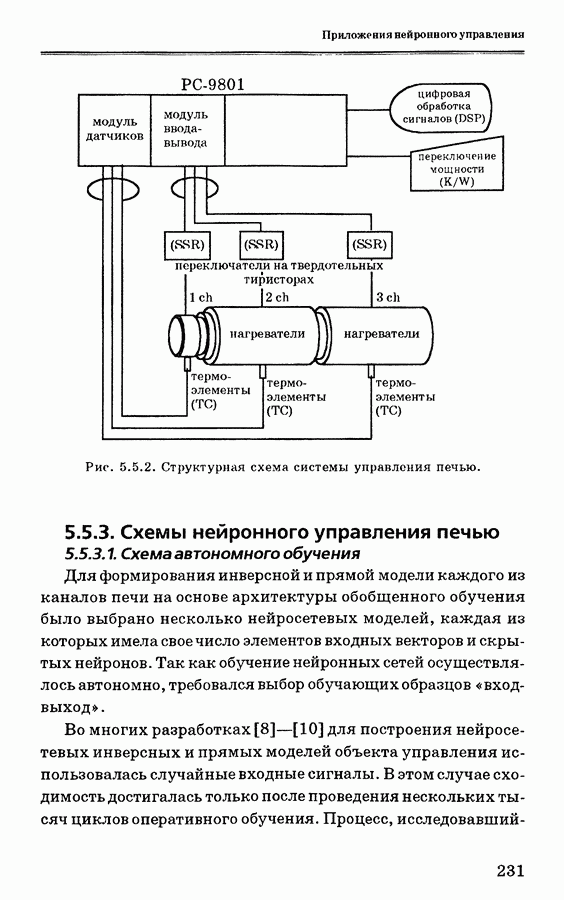
- 5.5.2. Система управления печью
- 5.5.3. Схемы нейронного управления печью
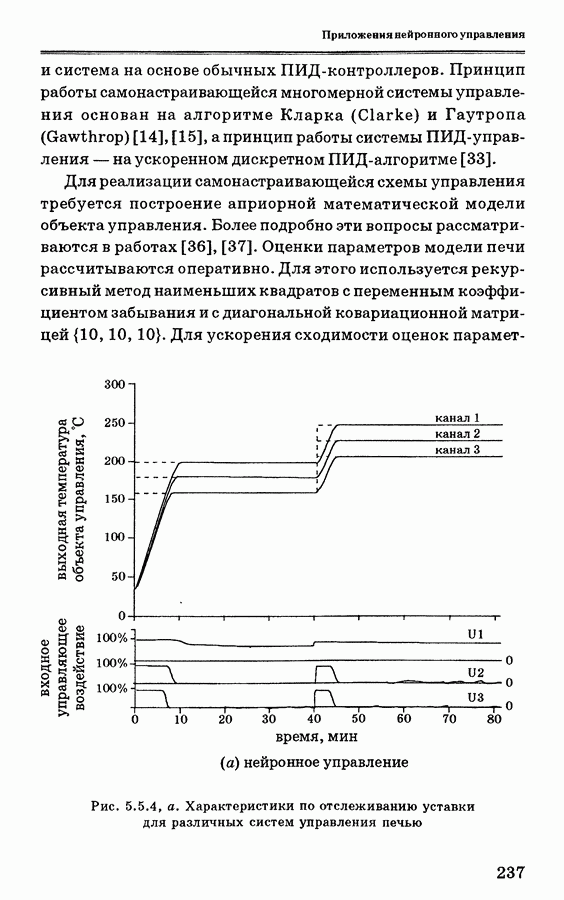
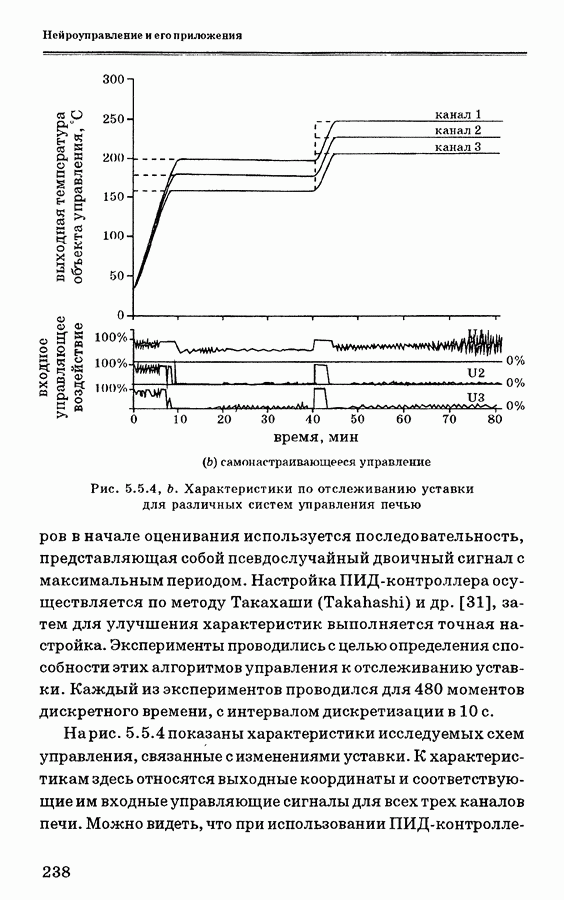
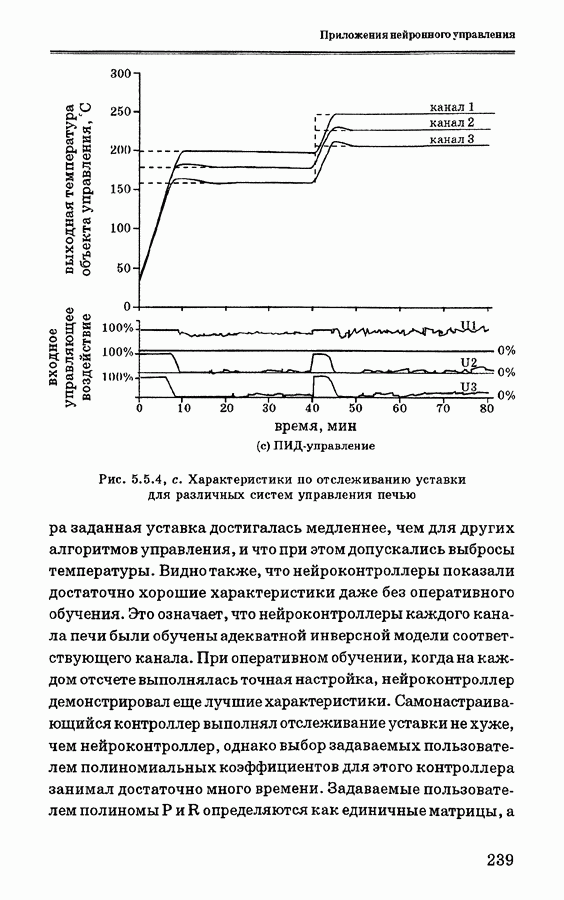
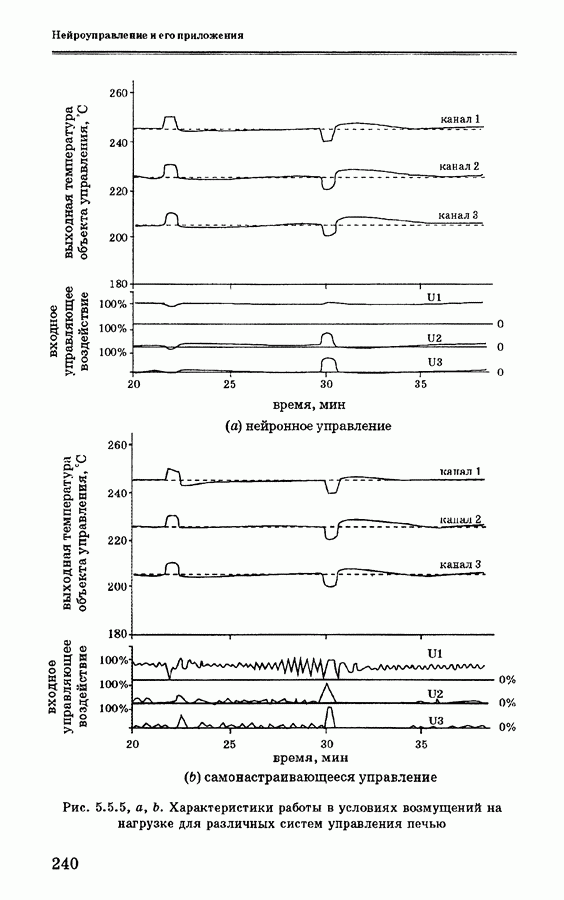
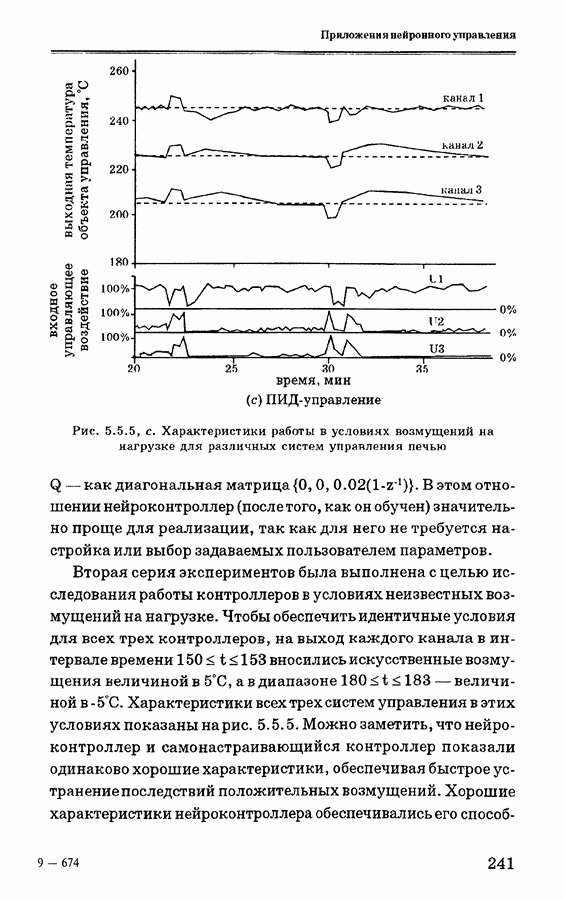
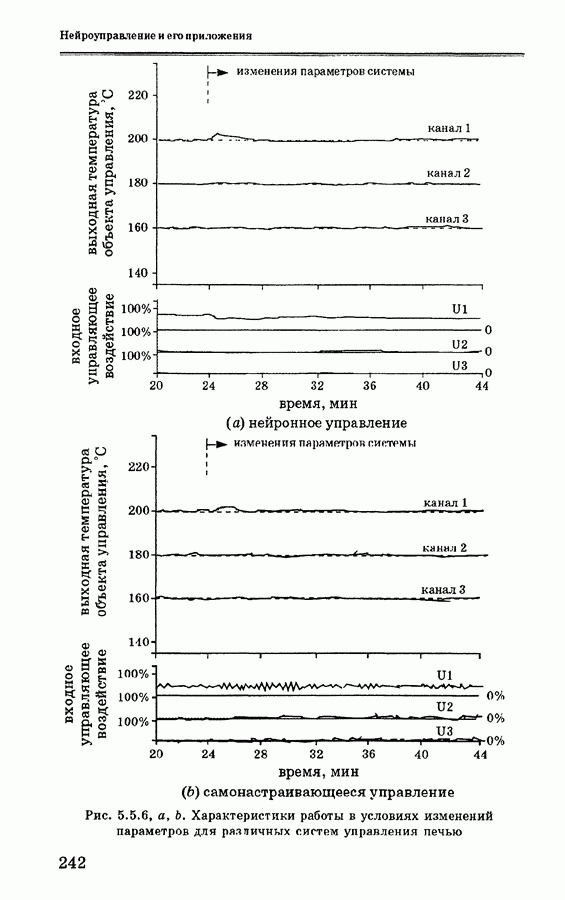
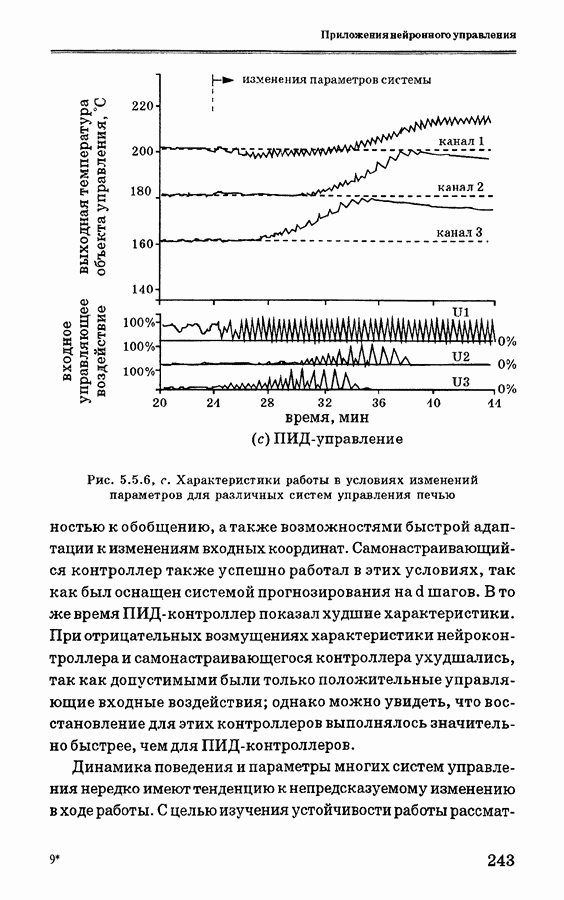
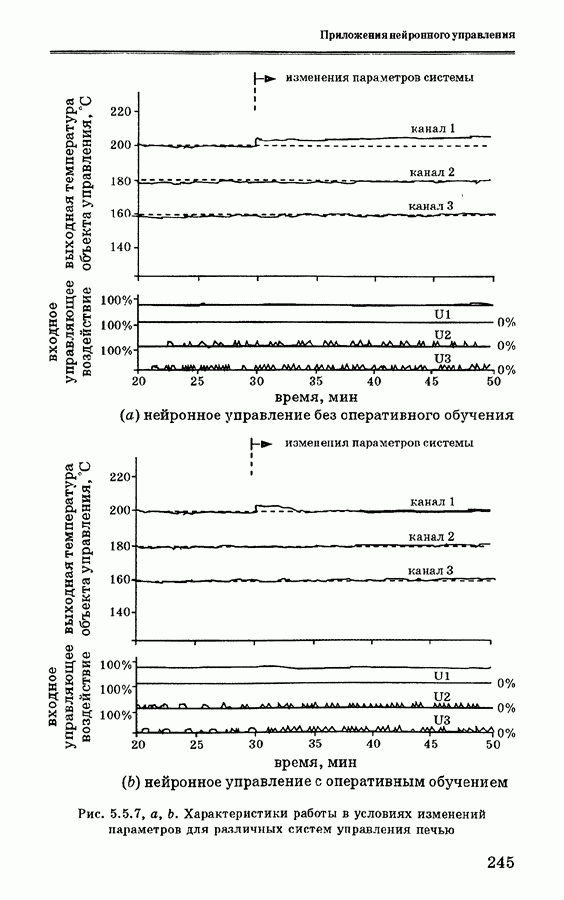
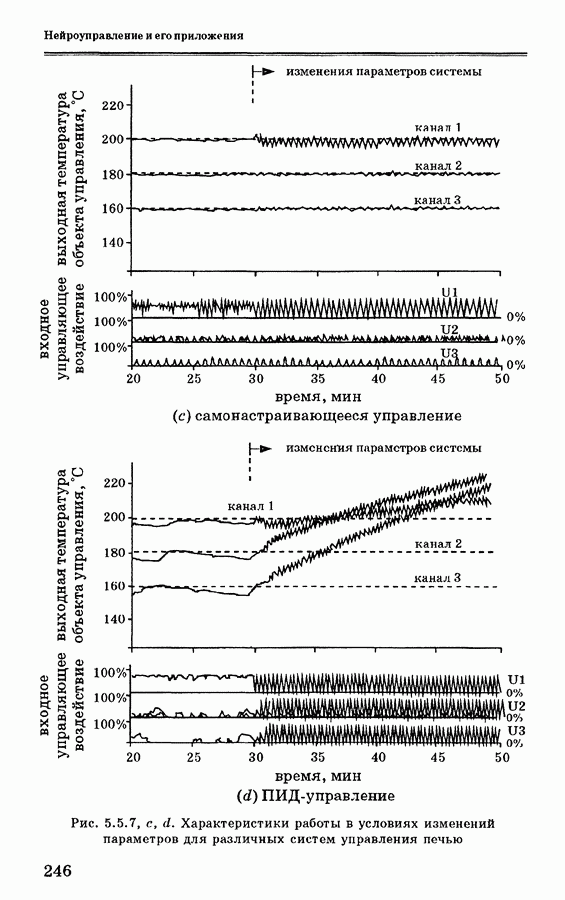
- 5.5.4. Анализ экспериментальных данных
- 5.6. Заключительные замечания и выводы
- Литература
- ЛИСТИНГ ПРОГРАММЫ