| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
5.2.3. Схема нейронного управления
Способность нейронных сетей к обучению и обобщению оказалась интересной для многих приложений. Одним из простейших подходов к реализации нейронного управления стал
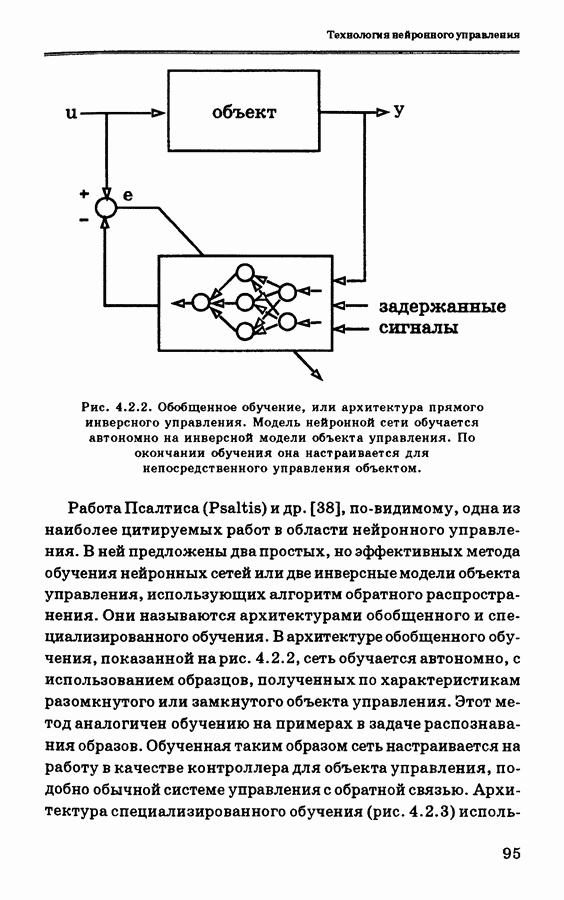
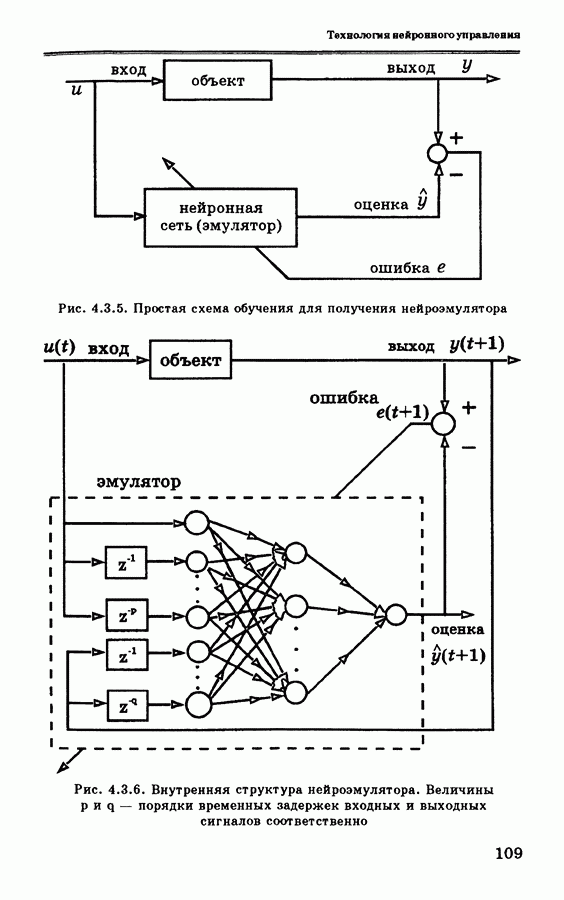
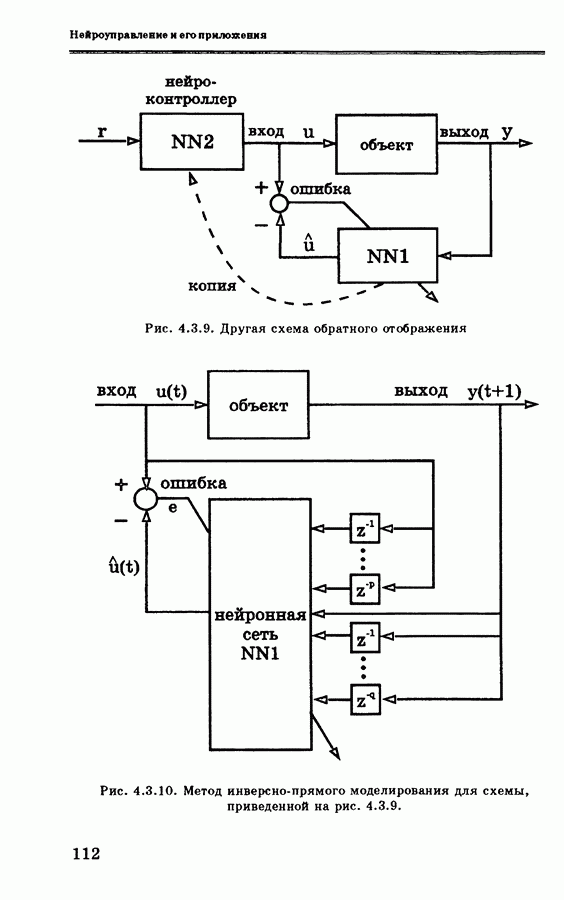
инверсно-прямой подход [16], [17]. В соответствии со схемой обобщенного обучения, рассмотренной в разделе 4.2.1, многослойная нейронная сеть сначала обучается автономно по алгоритму обратного распространения [18] для построения инверсной динамической модели объекта управления.
В исследовании [19], выполненном авторами данной работы, установлено, что количество задержанных сигналов от объекта управления, используемых на этапе обучения в качестве элементов входного вектора нейросетевой модели, влияет на процесс изучения контроллером инверсной модели объекта управления. Это, в свою очередь, влияет на характеристики нейроконтроллера в оперативном режиме. Теоретически эти процессы можно описать следующим образом.
Рассмотрим линейный динамический объект управления с одним входом и одним выходом, без помех. Предположим, что он описывается дискретным уравнением

где у и  — выходной и входной сигналы объекта управления соответственно. Здесь
— выходной и входной сигналы объекта управления соответственно. Здесь  — коэффициенты знаменателя,
— коэффициенты знаменателя,  — коэффициенты числителя,
— коэффициенты числителя,  — время запаздывания (или временная задержка),
— время запаздывания (или временная задержка),  — номер отсчета. Модель нейронной сети для инверсной динамической модели объекта управления представляет собой нелинейную функцию
— номер отсчета. Модель нейронной сети для инверсной динамической модели объекта управления представляет собой нелинейную функцию  содержащую задержанные входные и выходные сигналы объекта управления в соответствии с оценкой порядка и временной задержкой объекта управления:
содержащую задержанные входные и выходные сигналы объекта управления в соответствии с оценкой порядка и временной задержкой объекта управления:

где  — выходной сигнал нейронной сети, представляющий собой управляющий входной сигнал для объекта управления. При оперативной реализации системы нейронного управления действительный выходной сигнал объекта управления
— выходной сигнал нейронной сети, представляющий собой управляющий входной сигнал для объекта управления. При оперативной реализации системы нейронного управления действительный выходной сигнал объекта управления 
заменяется желаемым выходным сигналом  в качестве одного из элементов входного вектора нейронной сети.
в качестве одного из элементов входного вектора нейронной сети.
На данной основе разработаны нейросетевые модели объекта управления (инверсная и прямая); при этом использовалась математическая модель объекта управления пониженного порядка [20]. Хотя нейронные сети могут обучаться модели объекта управления, не используя предварительное математическое моделирование [8]-[10], тем не менее, было бы неправильно при разработке контроллеров игнорировать информацию об объекте управления, если такая информация есть. Более того, на основе такой информации можно избежать ненужных операций, выполняемых методом проб и ошибок [19].
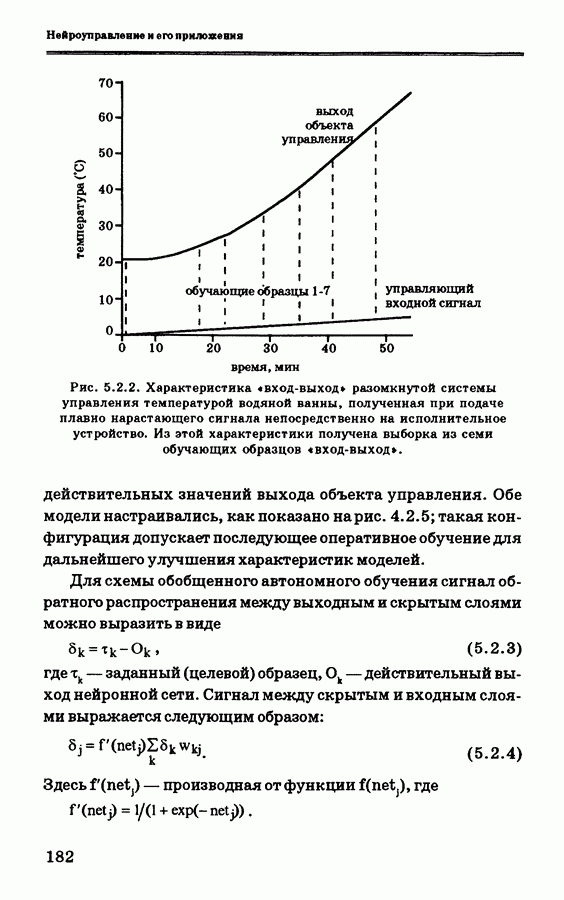
Обучение инверсной нейросетевой модели производилось с использованием выборки обучающих образцов, взятых из данных о реакции разомкнутой системы управления. В некоторых разработках [8]-[10], [21] обучающие образцы выбирались путем «зондирования» объекта управления случайными сигналами. В реальном времени такой метод нецелесообразен, так как изменения температуры происходят медленно. В связи с тем, что разомкнутая система является устойчивой, вместо случайных сигналов выполнялась подача плавно нарастающего сигнала непосредственно на исполнительное устройство (в пределах ограничений, установленных для входа этого устройства). Из данных о реакции системы был выбран набор обучающих образцов «вход-выход», как показано на рис. 5.2.2.
Было обнаружено, что нейросетевая модель, имеющая 8 скрытых нейронов, может изучать инверсную модель объекта управления. При этом используется два элемента входного вектора: текущего выхода объекта управления  и задержанного выхода
и задержанного выхода  полученных по математической модели объекта управления пониженного порядка. Прямая нейросетевая модель разрабатывалась аналогично, однако в этом случае входные обучающие образцы представляли собой выборку из входных сигналов объекта управления и задержанных выходных величин, а выходные образцы — из соответствующих
полученных по математической модели объекта управления пониженного порядка. Прямая нейросетевая модель разрабатывалась аналогично, однако в этом случае входные обучающие образцы представляли собой выборку из входных сигналов объекта управления и задержанных выходных величин, а выходные образцы — из соответствующих

Рис. 5.2.2. Характеристика «вход-выход» разомкнутой системы управления температурой водяной ванны, полученная при подаче плавно нарастающего сигнала непосредственно на исполнительное устройство. Из этой характеристики получена выборка из семи обучающих образцов «вход-выход».
действительных значений выхода объекта управления. Обе модели настраивались, как показано нарис. 4.2.5; такая конфигурация допускает последующее оперативное обучение для дальнейшего улучшения характеристик моделей.
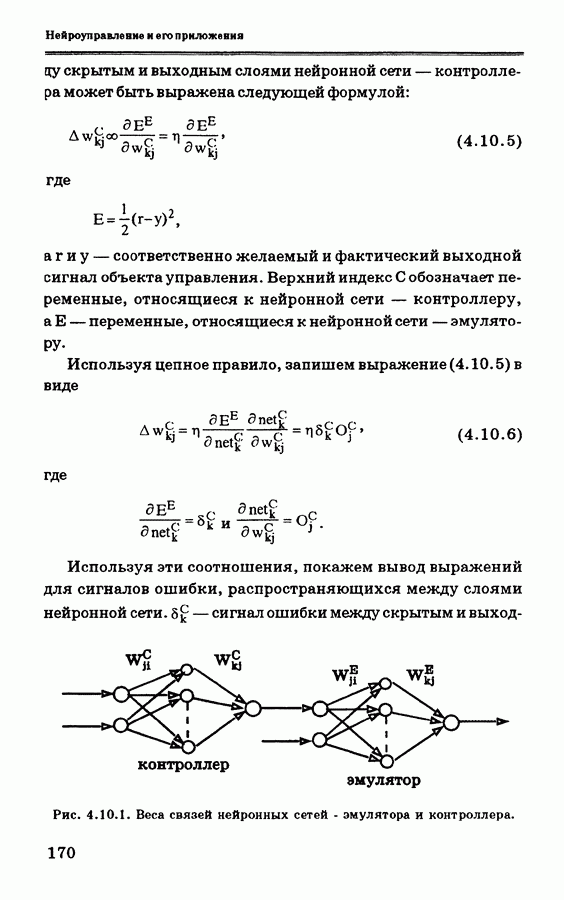
Для схемы обобщенного автономного обучения сигнал обратного распространения между выходным и скрытым слоями можно выразить в виде

где  — заданный (целевой) образец,
— заданный (целевой) образец,  — действительный выход нейронной сети. Сигнал между скрытым и входным слоями выражается следующим образом:
— действительный выход нейронной сети. Сигнал между скрытым и входным слоями выражается следующим образом:

Здесь  — производная от функции
— производная от функции  где
где

Веса связей между входным и скрытым слоями корректируются в соответствии с выражением

а между скрытым и выходным слоями — по формуле:

где  — скорость обучения,
— скорость обучения,  — коэффициент мгновенного значения и ускорения соответственно. Уравнения (5.2.5) и (5.2.6) представляют собой модифицированные формы обобщенного дельта-правила [22].
— коэффициент мгновенного значения и ускорения соответственно. Уравнения (5.2.5) и (5.2.6) представляют собой модифицированные формы обобщенного дельта-правила [22].
Для схемы оперативного обучения веса связей нейроконтроллера корректируются на основе ошибки, определяемой как

где  и у — заданный и фактический выход объекта управления соответственно. Эта ошибка распространяется через эмулятор. Таким образом, сигнал на выходе контроллера можно выразить следующим образом:
и у — заданный и фактический выход объекта управления соответственно. Эта ошибка распространяется через эмулятор. Таким образом, сигнал на выходе контроллера можно выразить следующим образом:

где  и
и  — соответственно входной и выходной сигналы нейронов выходного слоя контроллера. Верхний индекс Е обозначает эмулятор,
— соответственно входной и выходной сигналы нейронов выходного слоя контроллера. Верхний индекс Е обозначает эмулятор,  контроллер. Сигнал ошибки между скрытым и входным слоями контроллера выражается следующей формулой:
контроллер. Сигнал ошибки между скрытым и входным слоями контроллера выражается следующей формулой:

где  — выходной сигнал нейронов скрытого слоя контроллера. В данной схеме веса связей нейронного эмулятора не
— выходной сигнал нейронов скрытого слоя контроллера. В данной схеме веса связей нейронного эмулятора не
сохраняются постоянными, а корректируются в оперативном режиме. Это делается путем обратного распространения ошибки Е через эмулятор при каждом отсчете времени. Здесь ошибка Е определяется в виде

где у и у — выходы действительного объекта управления и эмулятора, соответственно.
Обратное распространение сигналов ошибки для эмулятора аналогично автономному обучению при использовании только одной сети. Схему оперативного обучения для нейронного управления можно представить в виде следующего алгоритма.
Шаг 1. Прочитать выход процесса у и сравнить его с желаемым опорным значением 
Шаг 2. Вычислить величину сигнала ошибки  между выходным и скрытым слоями нейроэмулятора.
между выходным и скрытым слоями нейроэмулятора.
Шаг 3. Вычислить величину сигнала ошибки  между скрытым и входным слоями нейроэмулятора.
между скрытым и входным слоями нейроэмулятора.
Шаг 4. Вычислить величину сигнала ошибки  между выходным и скрытым слоями нейроконтроллера.
между выходным и скрытым слоями нейроконтроллера.
Шаг 5. Вычислить величину сигнала ошибки 8 между скрытым и входным слоями нейроконтроллера.
Шаг 6. Скорректировать веса связей для нейроконтроллера (между выходным и скрытым и между скрытым и входным слоями).
Шаг 7. Сравнить выход нейроэмулятора у и фактический выход объекта управления у.
Шаг 8. Скорректировать веса связей для нейроэмулятора (между выходным и скрытым и между скрытым и входным слоями).
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРОВ ПЕРЕВОДА
- 1. ВВЕДЕНИЕ
- 1.1. Общие сведения об интеллектуальном управлении
- 2. НЕЙРОННЫЕ СЕТИ
- 2.2. Алгоритм обратного распространения
- 2.2.2. Вывод алгоритма обратного распространения
- 2.2.2.2. Правило для скрытого слоя
- 2.2.3. Алгоритм обратного распространения: порядок реализации
- 2.2.4. Обсуждение алгоритма обратного распространения
- 2.3. Заключение
- 3. ТРАДИЦИОННЫЕ СХЕМЫ УПРАВЛЕНИЯ
- 3.2. ПИ- и ПИД-контроллеры с дискретным временем
- 3.3. Управление с самонастройкой
- 3.4. Самонастраивающиеся ПИ- и ПИД- контроллеры
- 3.5. ПИД-управление с самонастройкой: многомерный подход
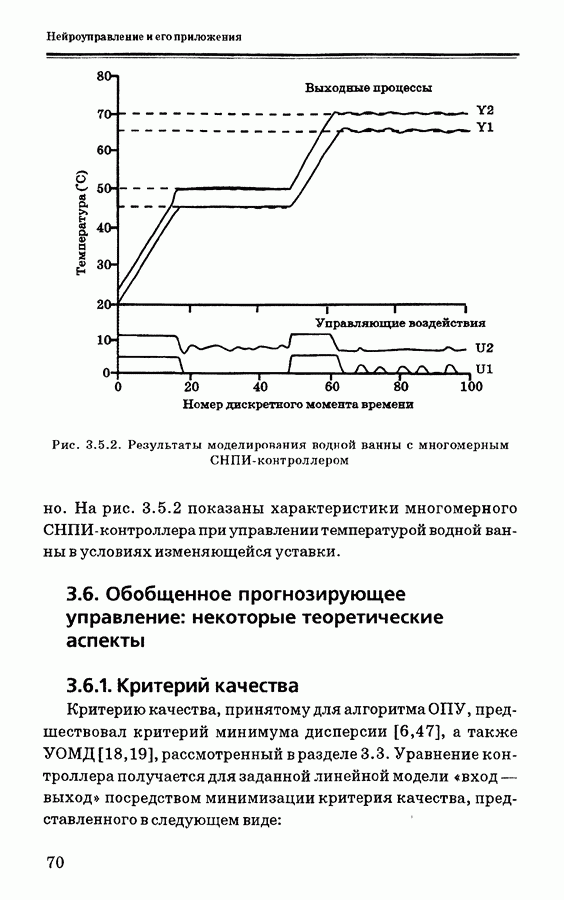
- 3.5.1. Пример моделирования
- 3.6. Обобщенное прогнозирующее управление: некоторые теоретические аспекты
- 3.6.2. Модель объекта управления и решение задачи оптимизации
- 3.7. Управление на основе нечеткой логики
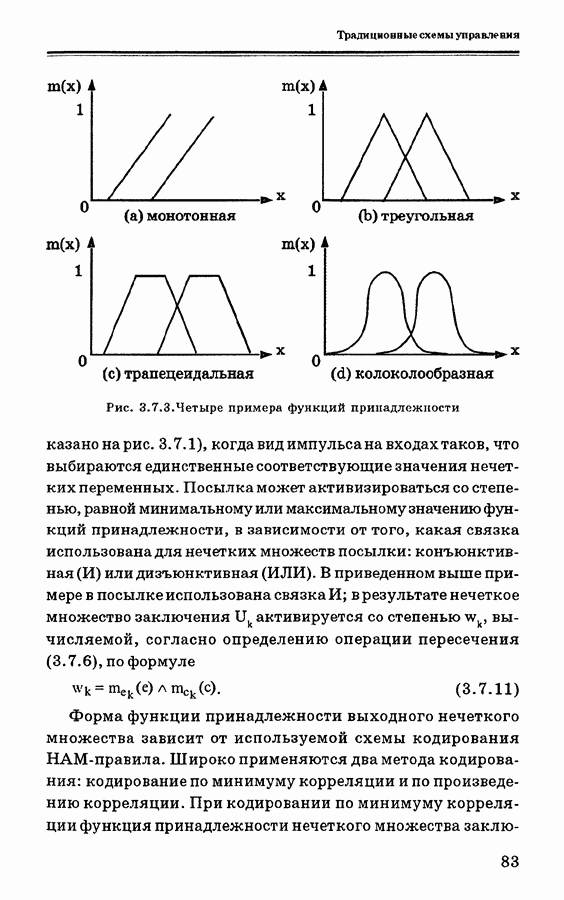
- 3.7.1. Краткие сведения по теории нечетких множеств и нечетких систем
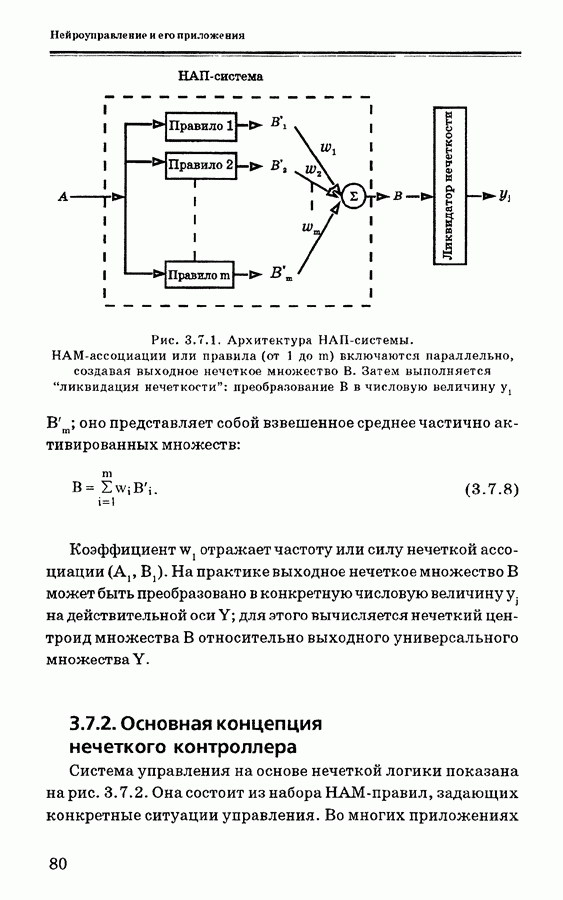
- 3.7.2. Основная концепция нечеткого контроллера
- 3.8. Заключение
- 4. ТЕХНОЛОГИИ НЕЙРОННОГО УПРАВЛЕНИЯ
- 4.2. Общие сведения о нейронном управлении
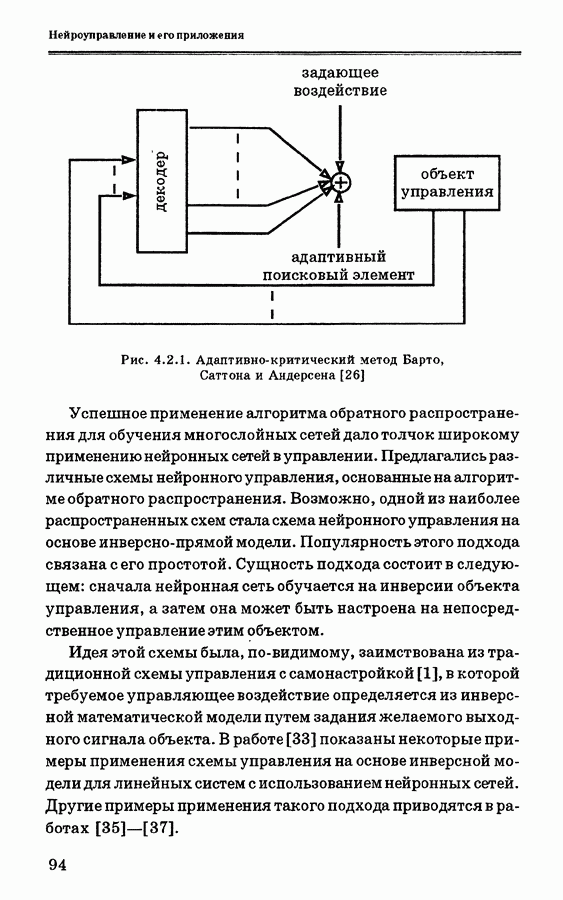
- 4.2.1. Подходы к нейронному управлению
- 4.2.2. Общая схема управления
- 4.3. Последовательная схема нейронного управления
- 4.4. Расширение последовательной схемы нейронного управления
- 4.4.2. Нейроморфные структуры управления
- 4.4.3. Конфигурации обучения
- 4.4.4. Эффективное оперативное управление
- 4.4.5. Алгоритмы обучения
- 4.4.6. Оценка алгоритмов обучения на основе моделирования
- 4.5. Параллельная схема управления
- 4.6. Алгоритм обучения по ошибке обратной связи
- 4.7. Расширение применения нейроконтроллеров параллельного типа
- 4.7.2. Линеаризованная система управления
- 4.7.3. Система управления с нейронными сетями
- 4.7.4. Нелинейный алгоритм наблюдения для нейронной сети
- 4.7.5. Нелинейный контроллер для нейронной сети
- 4.7.6. Численное моделирование
- 4.8. Схема нейронного управления с самонастройкой
- 4.9. ПИД-нейроконтроллер с самонастройкой
- 4.9.1. Вывод уравнений ПИД-нейроконтроллера с самонастройкой
- 4.9.2. Примеры эмуляции
- 4.10. Схема нейронного управления с эмулятором и контроллером (схема обратного распространения во времени)
- 4.11. Заключение
- 5. ПРИЛОЖЕНИЯ НЕЙРОННОГО УПРАВЛЕНИЯ
- 5.2. Применение нейронного управления в системе регулирования процессов в водяной ванне и сравнение его с другими схемами управления
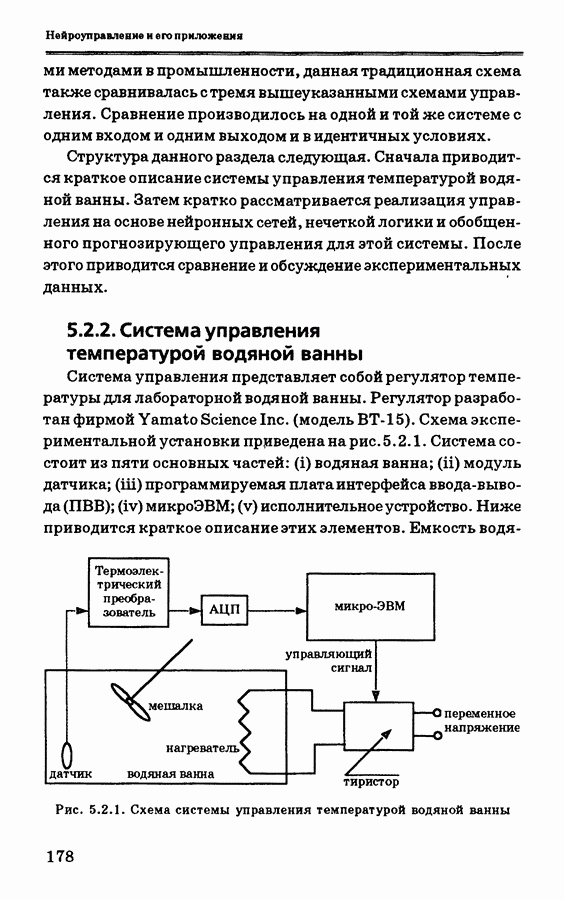
- 5.2.2. Система управления температурой водяной ванны
- 5.2.3. Схема нейронного управления
- 5.2.4. Схема управления на основе нечеткой логики
- 5.2.5. Схема обобщенного прогнозирующего управления
- 5.2.6. Экспериментальные данные и их анализ
- 5.2.7. Заключение
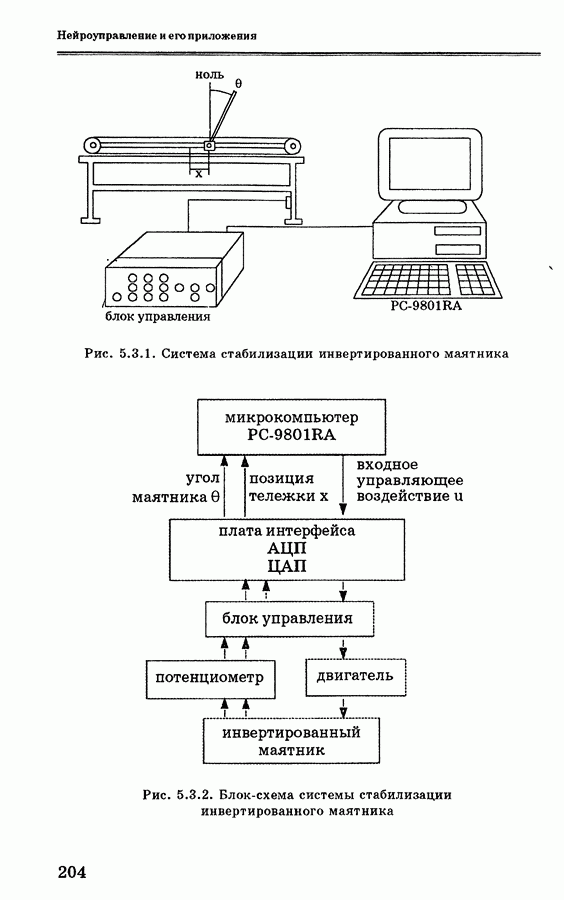
- 5.3. Система стабилизации инвертированного маятника на основе нейронных сетей
- 5.3.2. Система стабилизации инвертированного маятника
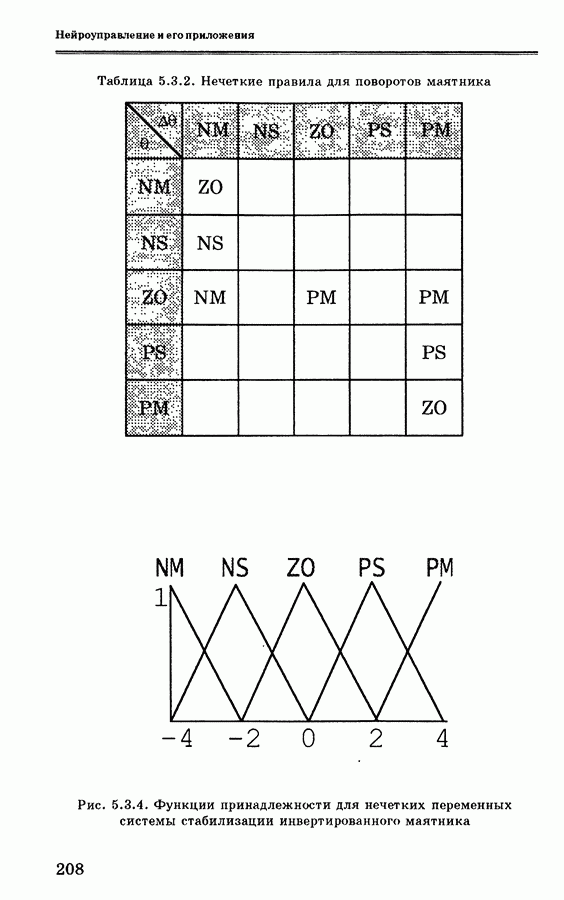
- 5.3.3. Инициализация поворотного управления с использованием нечеткой логики
- 5.3.4. Применение стратегии оптимального управления для стабилизации маятника
- 5.3.5. Точное управление на основе нейронных сетей
- 5.3.6. Заключение
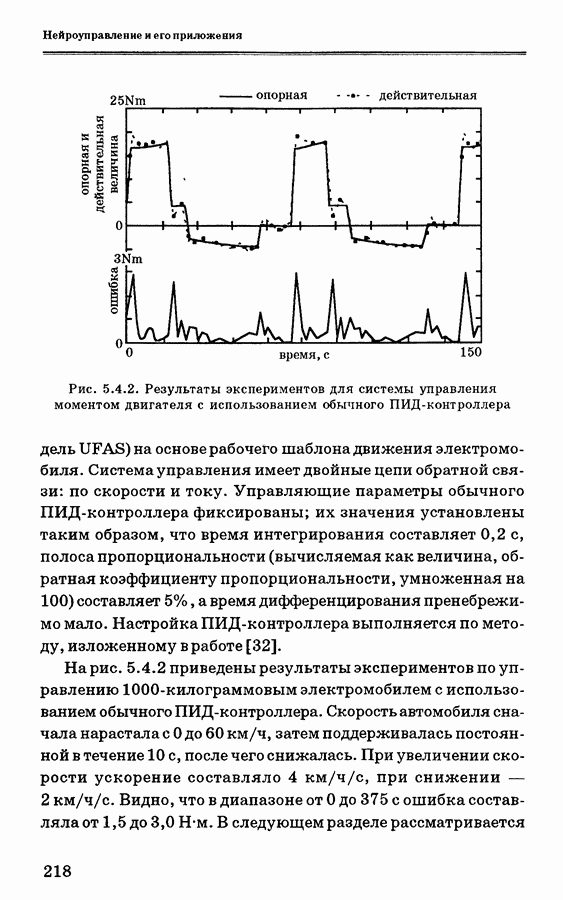
- 5.4. Применение ПИД-нейроконтроллера с самонастройкой для управления скоростью электромобиля
- 5.4.2. Система управления электромобилем
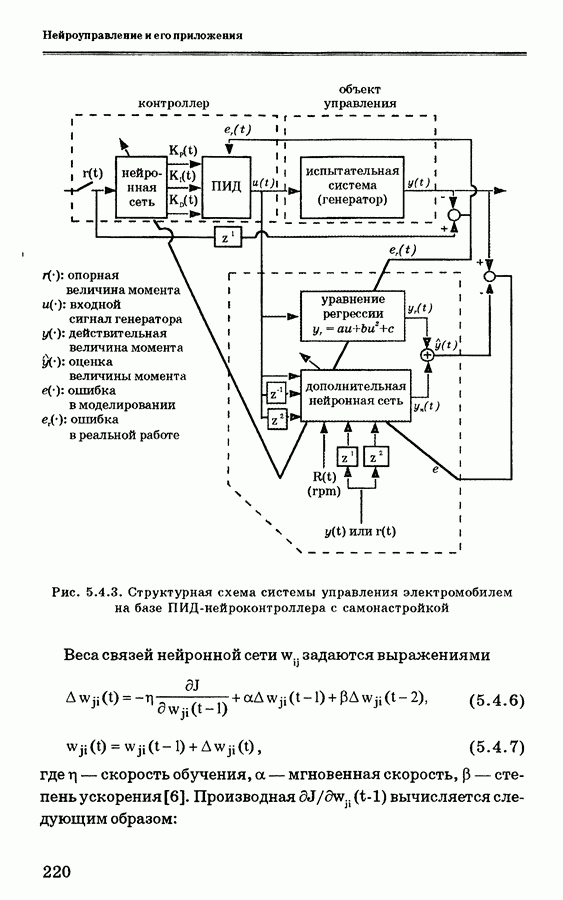
- 5.4.3. ПИД-нейроконтроллер с самонастройкой
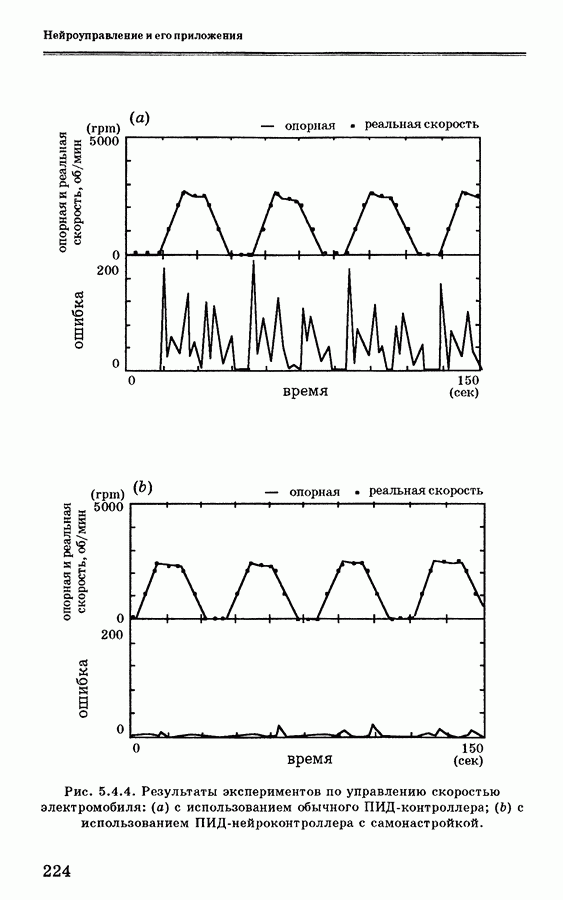
- 5.4.4. Применение нейронной сети для управления скоростью электромобиля
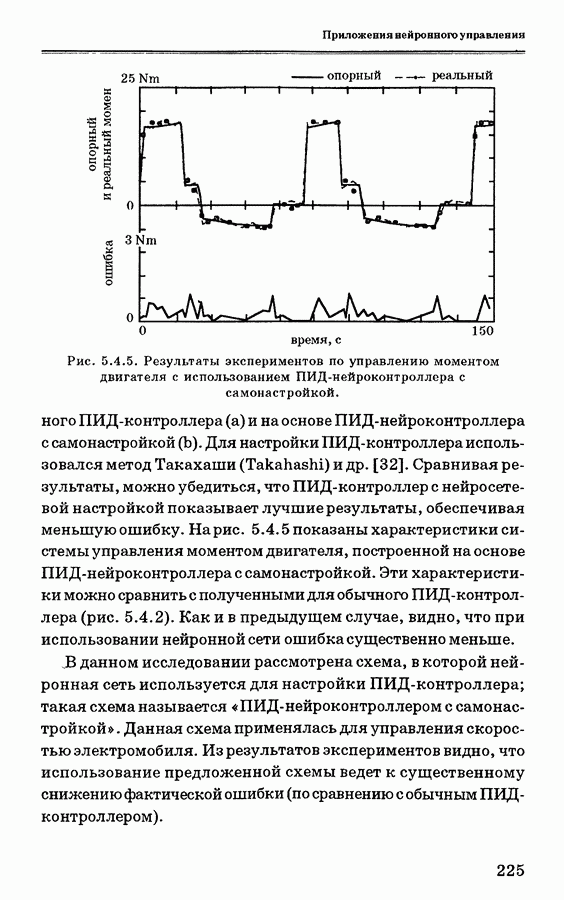
- 5.4.5. Заключение
- 5.5. Применение нейронных сетей для управления печью
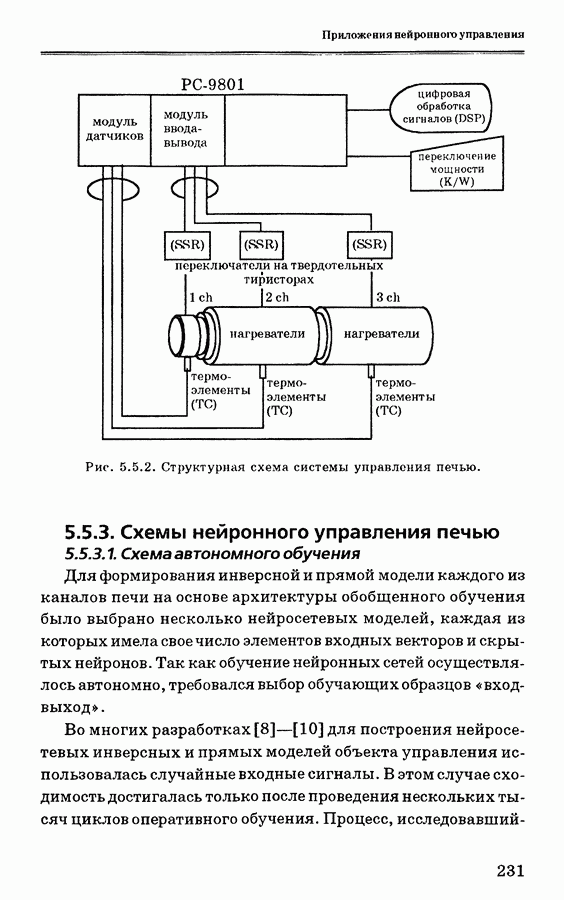
- 5.5.2. Система управления печью
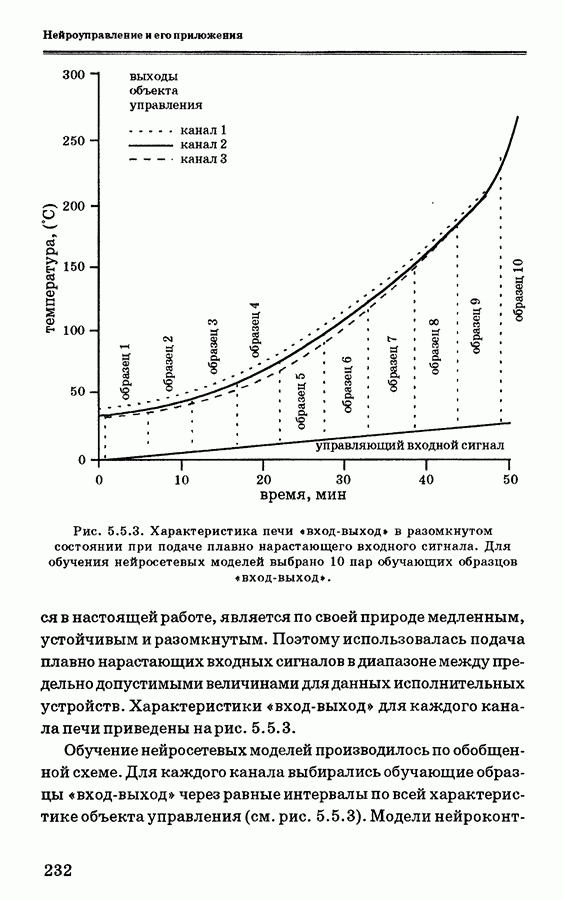
- 5.5.3. Схемы нейронного управления печью
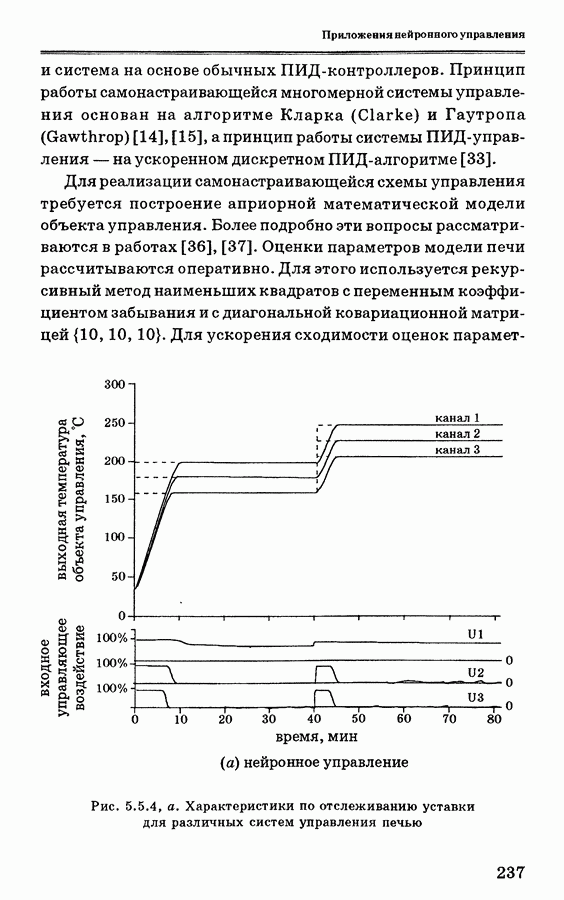
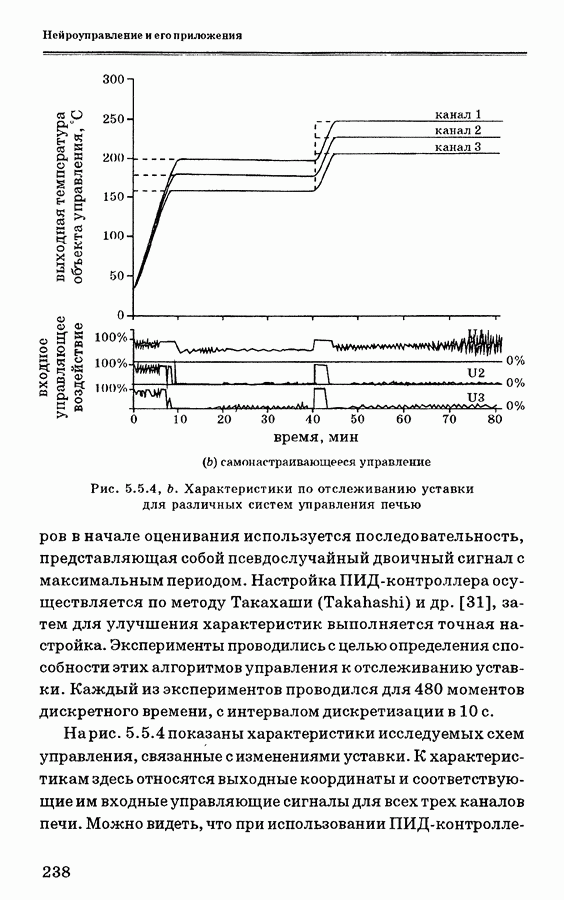
- 5.5.4. Анализ экспериментальных данных
- 5.6. Заключительные замечания и выводы
- Литература
- ЛИСТИНГ ПРОГРАММЫ