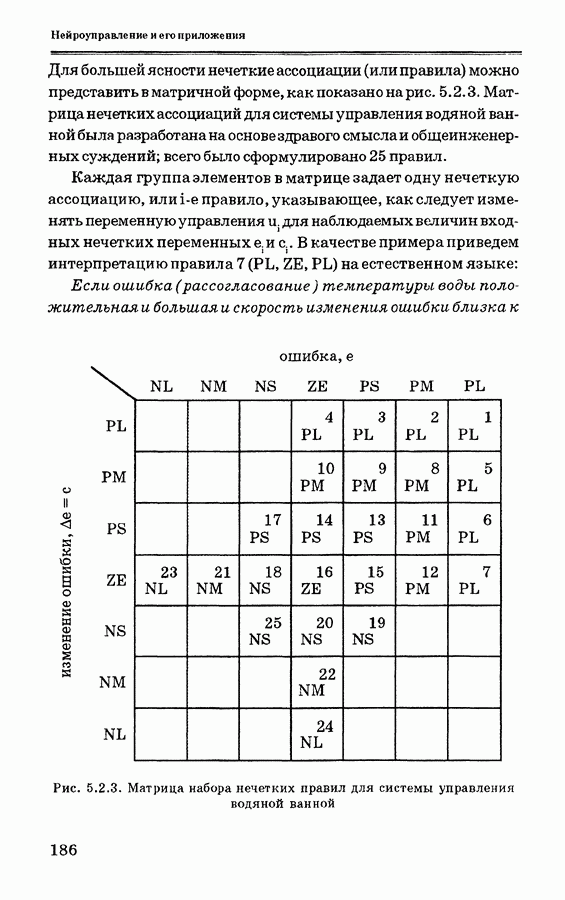
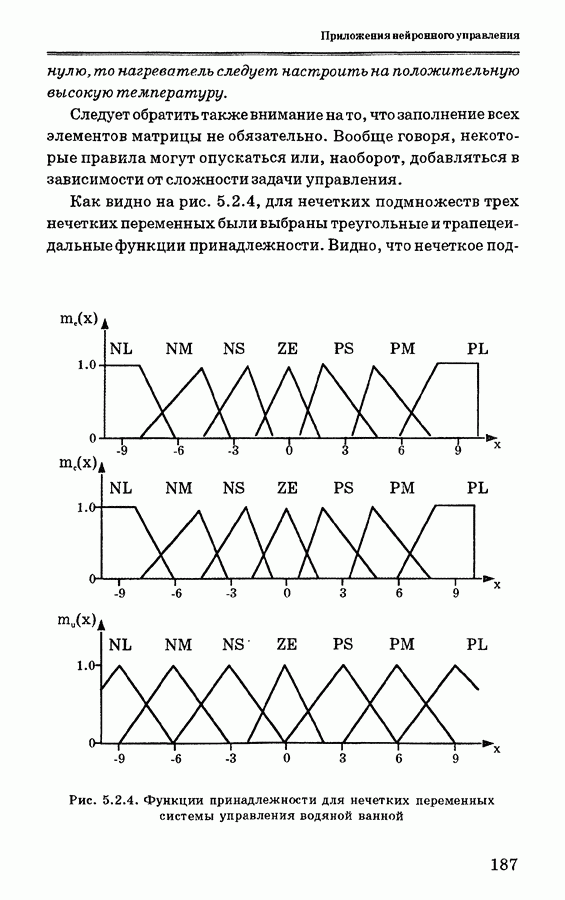
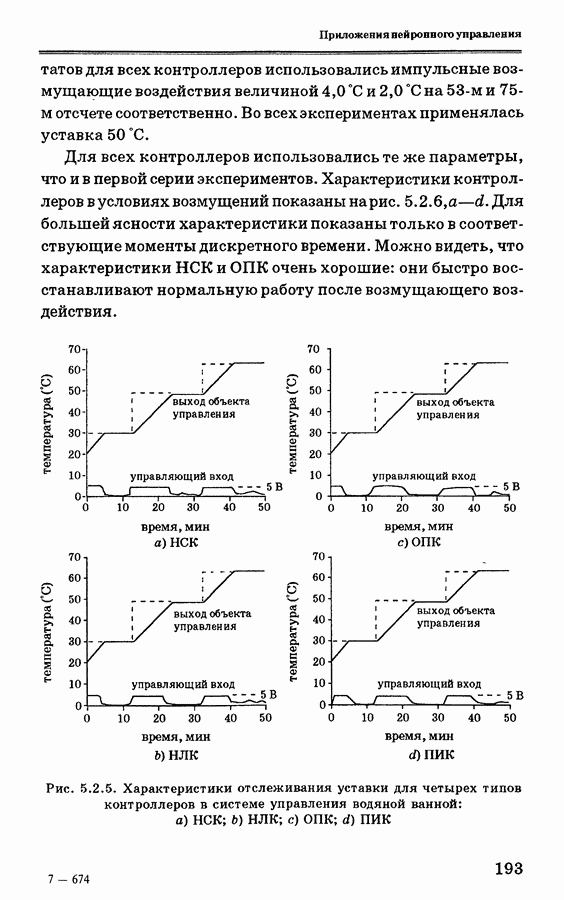
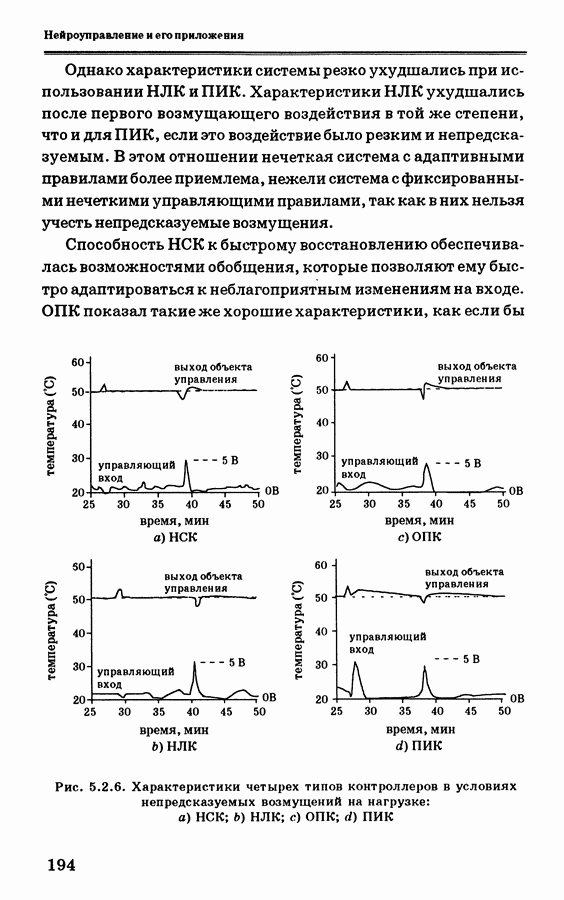
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
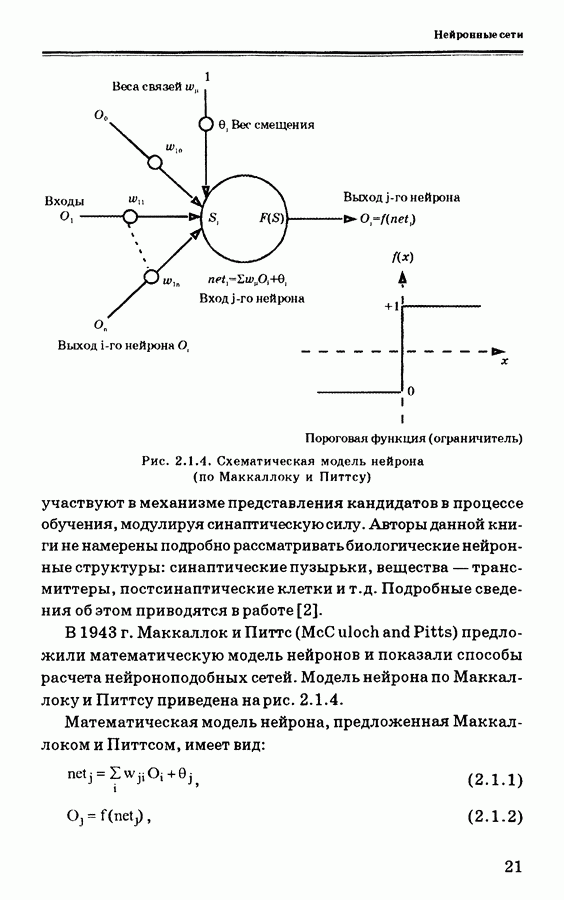
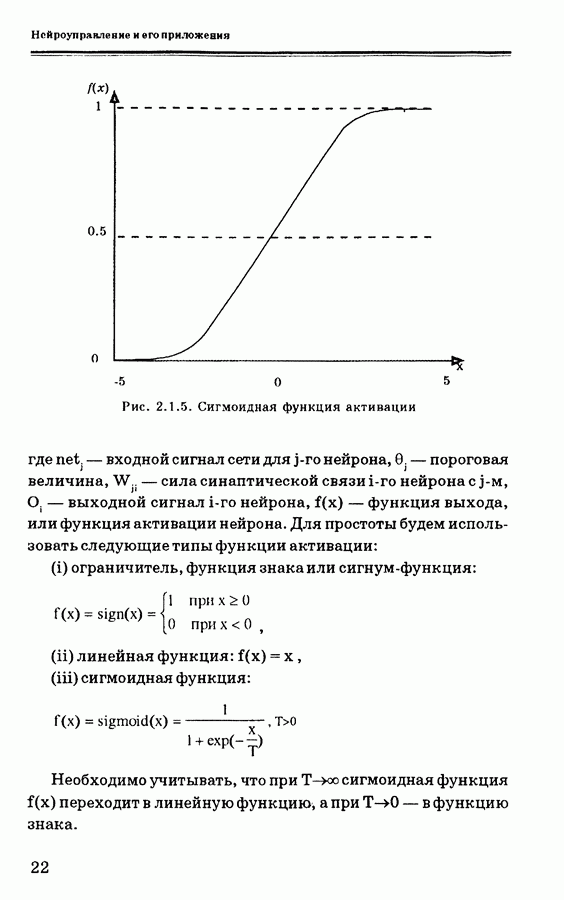
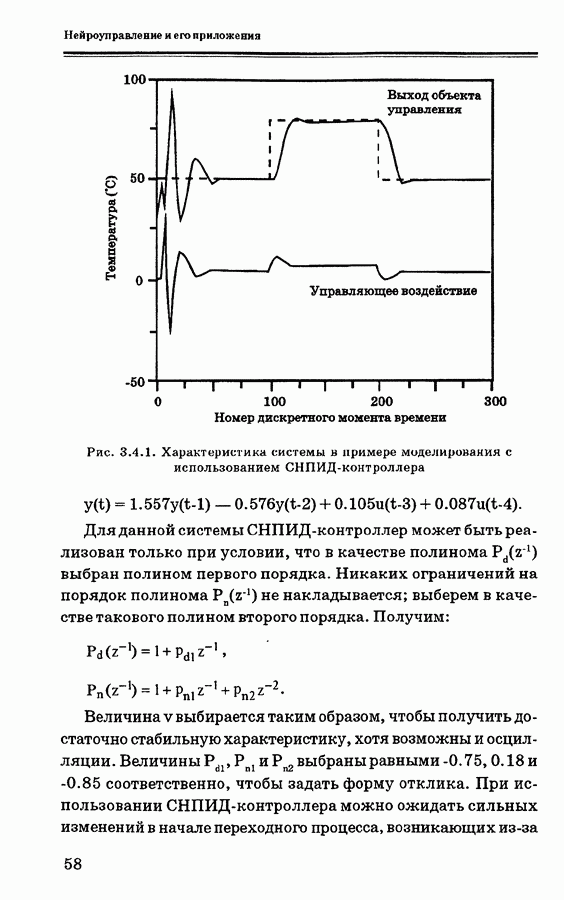
4.9.1. Вывод уравнений ПИД-нейроконтроллера с самонастройкой
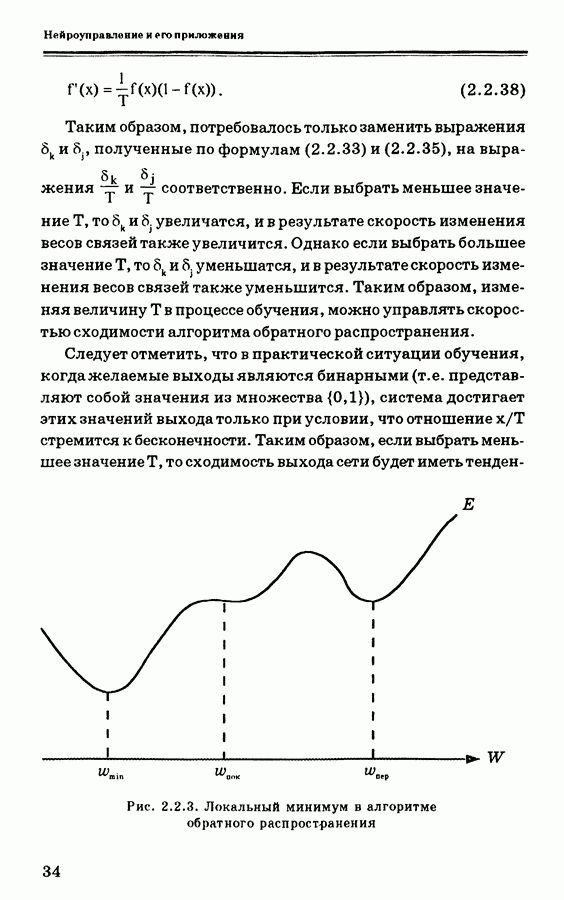
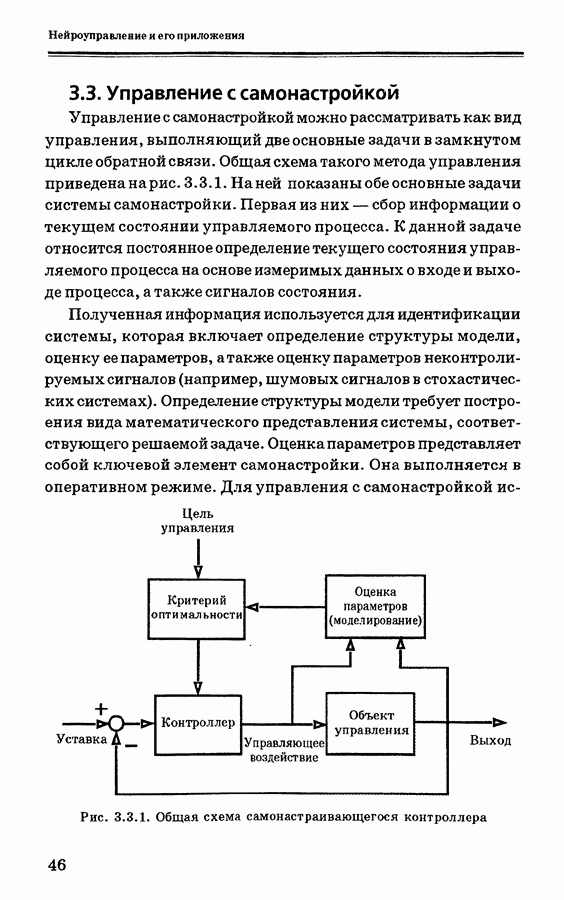
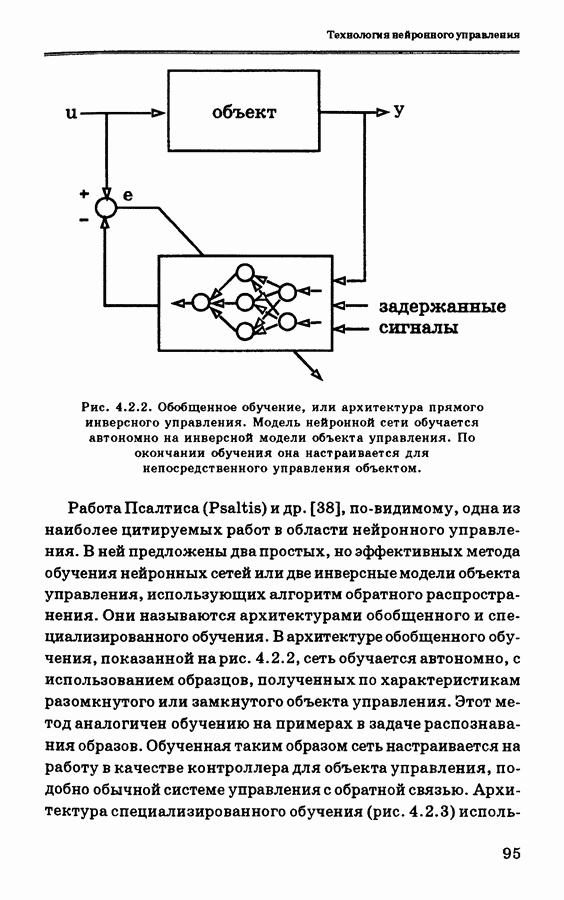
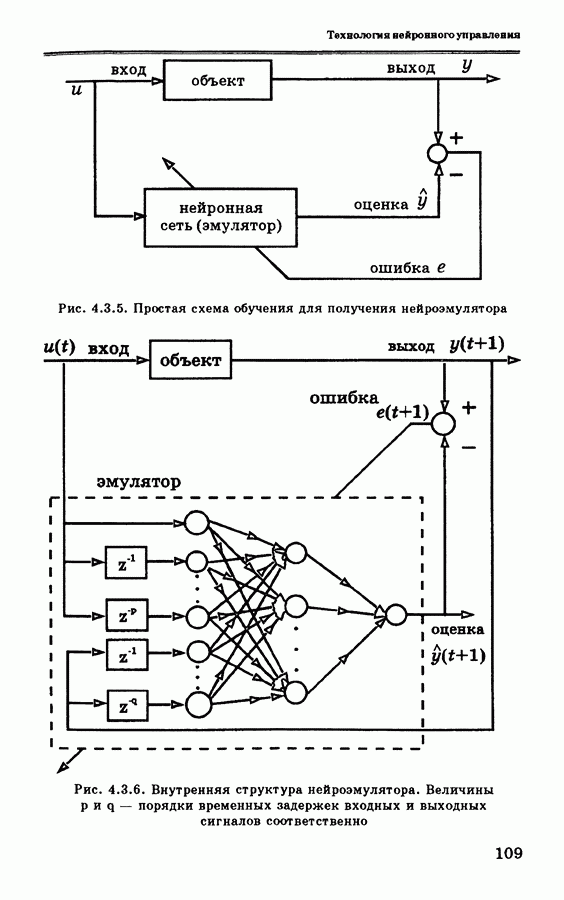
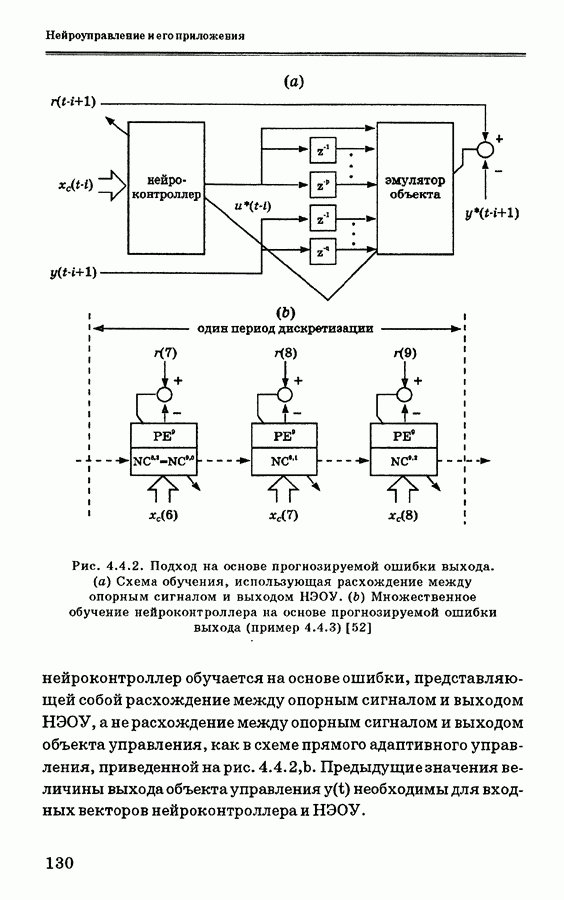
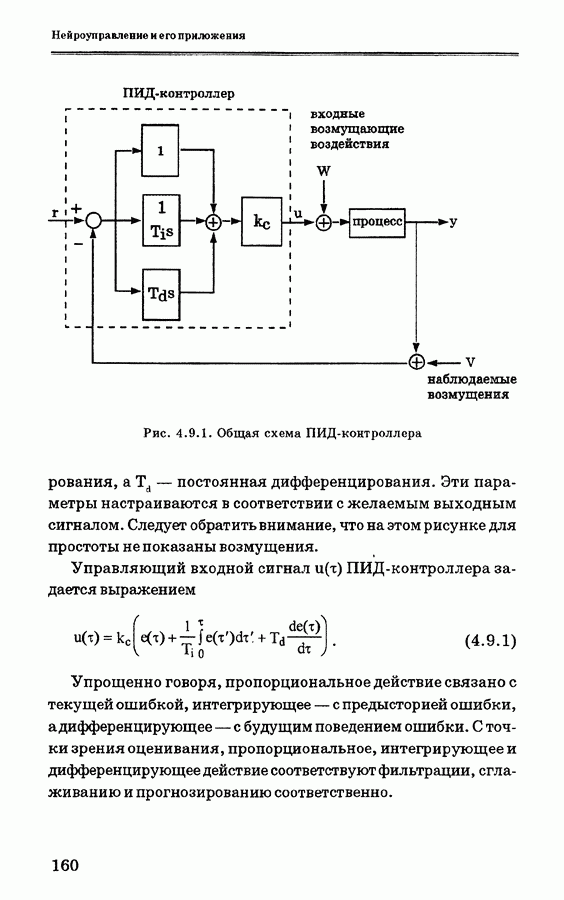
На рис. 4.9.2 показана общая структура управления для обучения ПИД-контроллера с самонастройкой. Нейронная сеть здесь используется вместо человека-оператора так, что обеспечивается минимизация ошибки путем настройки ПИД-коэффициентов [58]. ПИД-контроллер с дискретным временем описывается уравнениями

где  и
и  — ПИД-коэффициенты,
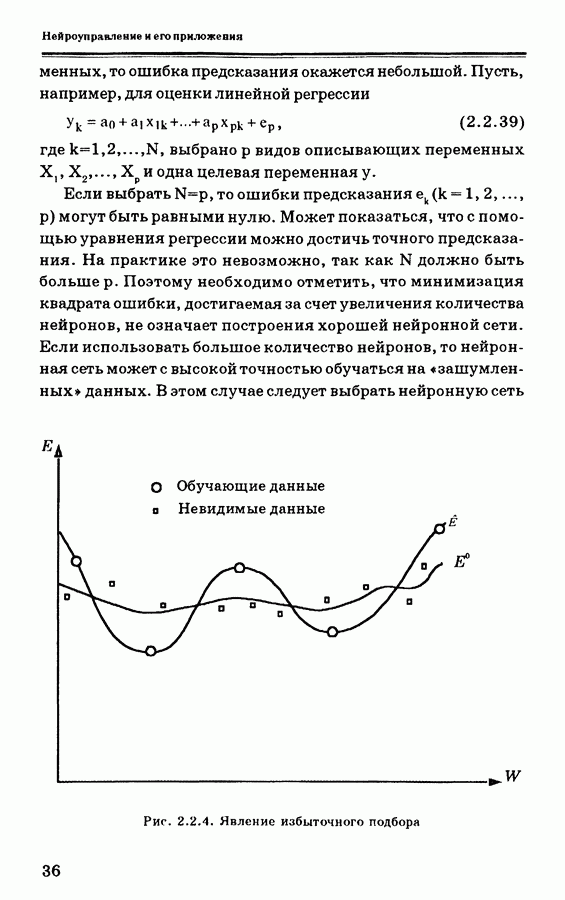
— ПИД-коэффициенты,  — заданная (желаемая) величина выходного сигнала объекта управления. Чтобы вывести алгоритм самонастройки ПИД-контроллера, зададим функцию стоимости Е, подлежащую минимизации, в виде
— заданная (желаемая) величина выходного сигнала объекта управления. Чтобы вывести алгоритм самонастройки ПИД-контроллера, зададим функцию стоимости Е, подлежащую минимизации, в виде

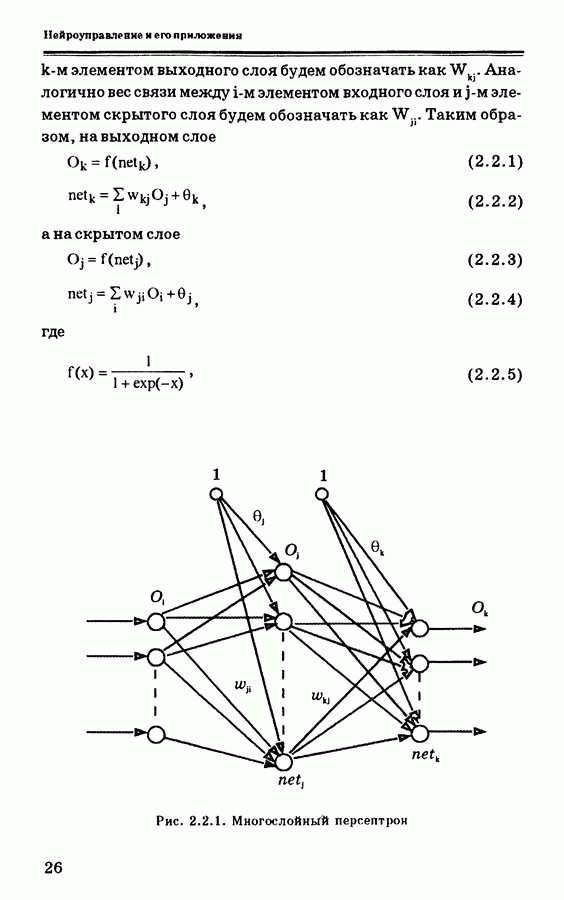
Используя трехслойную нейронную сеть, реализуем обучающее правило для поиска подходящих значений ПИД-коэффициентов. Таким образом, выходными сигналами выходного слоя будут величины  и
и  обозначенные через
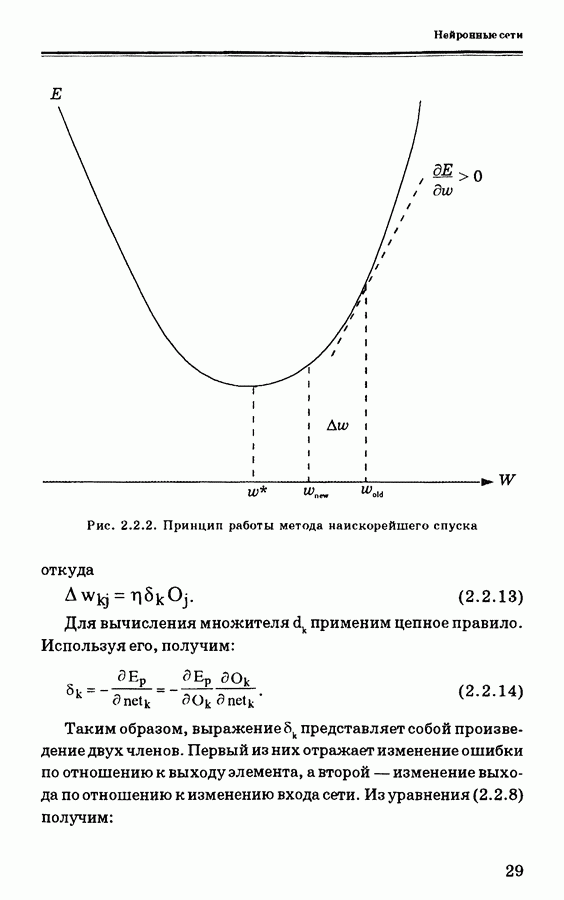
обозначенные через  соответственно. На основе алгоритма наискорейшего спуска получим для выходного слоя
соответственно. На основе алгоритма наискорейшего спуска получим для выходного слоя

Рис. 4.9.2. Схема обучения ПИД-контроллера с самонастройкой

а для скрытого слоя

Определим, что

где

Обозначим выход  нейрона выходного слоя через
нейрона выходного слоя через  Тогда имеем
Тогда имеем

Однако значения ПИД-коэффициентов не ограничены диапазоном от 0 до 1. Поэтому после выхода сети  можно использовать некоторый коэффициент передачи с, такой, что
можно использовать некоторый коэффициент передачи с, такой, что

Параметр с также можно определить путем обучения, увеличивая количество нейронов в скрытом слое. Для простоты положим  Используя цепное правило, получим
Используя цепное правило, получим

и

Однако


Последнее соотношение получено из (4.9.2) с учетом того, что 
Таким образом, имеем

где

Для скрытого слоя получим

Таким образом, имеем

Чтобы вычислить коэффициенты  по выражению (4.9.13), требуется знать якобиан системы
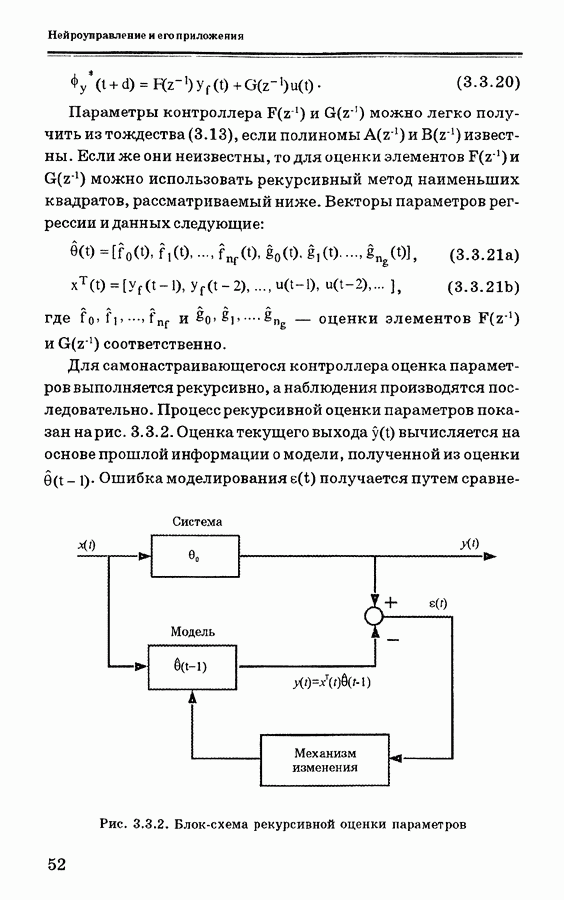
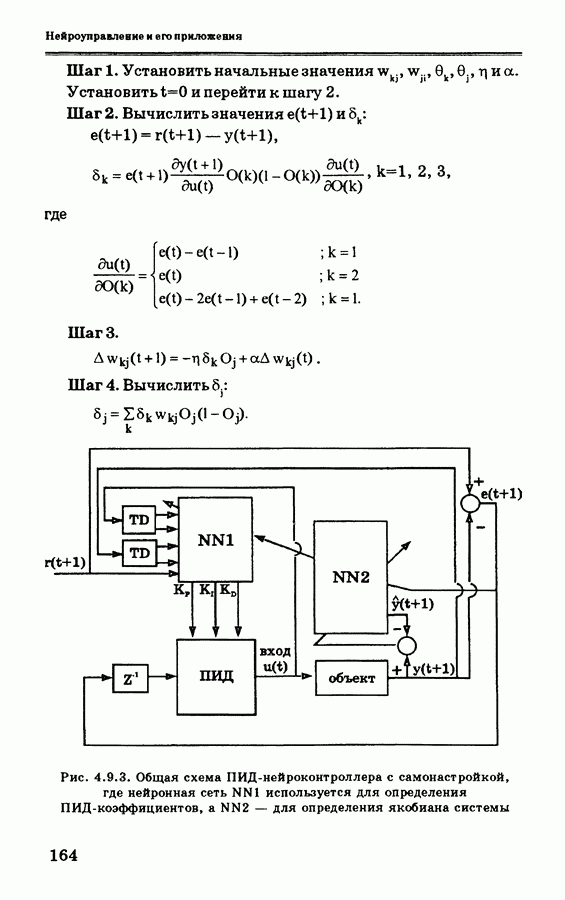
по выражению (4.9.13), требуется знать якобиан системы  и для получения его оценки используется эмулятор, как показано выше. Общая схема показана на рис. 4.9.3. Таким образом, алгоритм обучения ПИД-нейроконтроллера с самонастройкой можно представить в следующей форме.
и для получения его оценки используется эмулятор, как показано выше. Общая схема показана на рис. 4.9.3. Таким образом, алгоритм обучения ПИД-нейроконтроллера с самонастройкой можно представить в следующей форме.
Шаг 1. Установить начальные значения  и а. Установить
и а. Установить  и перейти к шагу 2.
и перейти к шагу 2.
Шаг 2. Вычислить значения 

где

Шаг 3.

Шаг 4. Вычислить 5.:


Рис. 4.9.3. Общая схема ПИД-нейроконтроллера с самонастройкой, где нейронная сеть NN1 используется для определения ПИД-коэффициентов, а NN2 — для определения якобиана системы
Шаг 5.

Шаг 6.  и перейти к шагу 2.
и перейти к шагу 2.
Следует отметить, что для вычисления якобиана системы  используется эмулятор NN2, как показано на рис. 4.9.3.
используется эмулятор NN2, как показано на рис. 4.9.3.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРОВ ПЕРЕВОДА
- 1. ВВЕДЕНИЕ
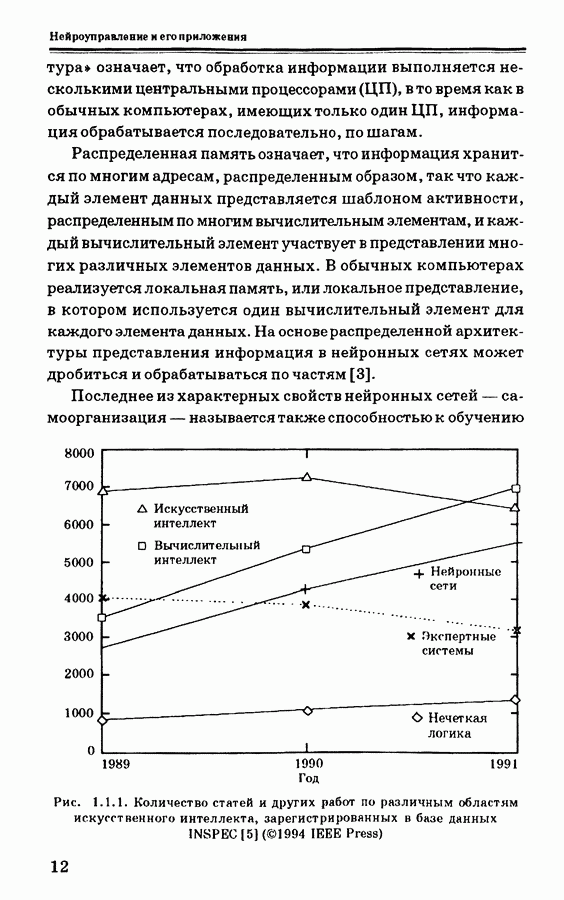
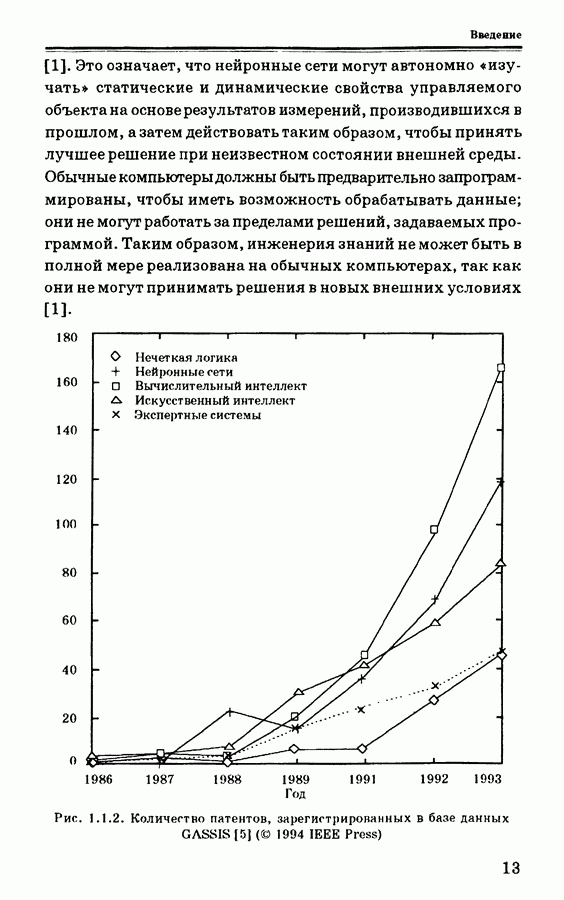
- 1.1. Общие сведения об интеллектуальном управлении
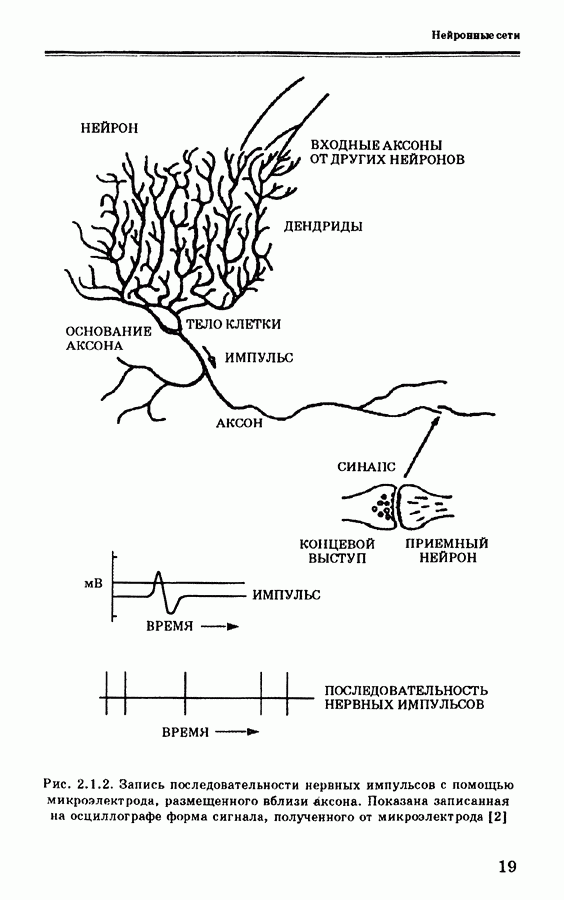
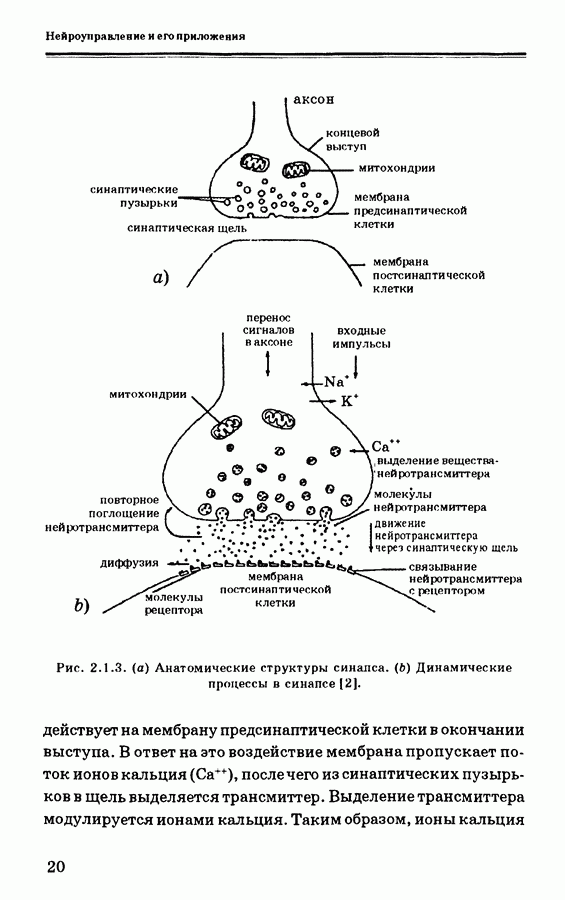
- 2. НЕЙРОННЫЕ СЕТИ
- 2.2. Алгоритм обратного распространения
- 2.2.2. Вывод алгоритма обратного распространения
- 2.2.2.2. Правило для скрытого слоя
- 2.2.3. Алгоритм обратного распространения: порядок реализации
- 2.2.4. Обсуждение алгоритма обратного распространения
- 2.3. Заключение
- 3. ТРАДИЦИОННЫЕ СХЕМЫ УПРАВЛЕНИЯ
- 3.2. ПИ- и ПИД-контроллеры с дискретным временем
- 3.3. Управление с самонастройкой
- 3.4. Самонастраивающиеся ПИ- и ПИД- контроллеры
- 3.5. ПИД-управление с самонастройкой: многомерный подход
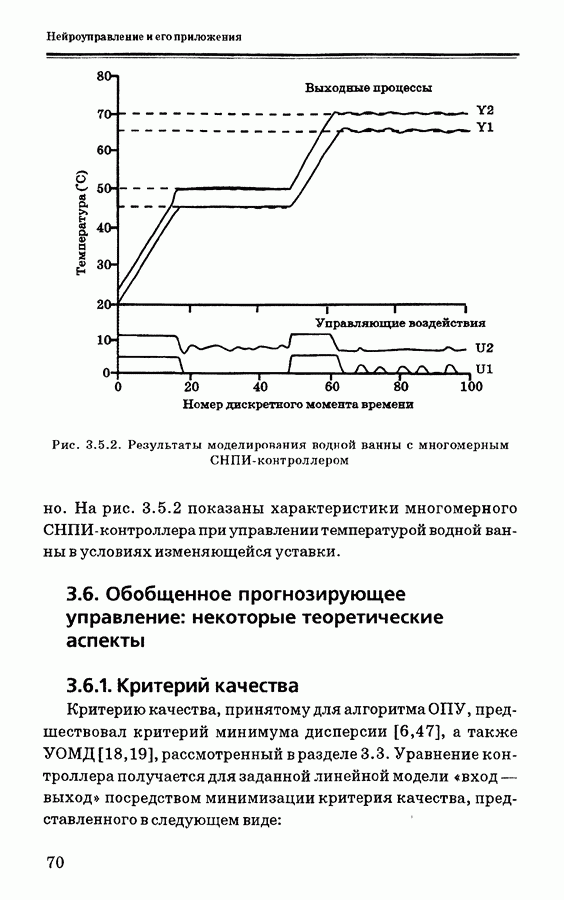
- 3.5.1. Пример моделирования
- 3.6. Обобщенное прогнозирующее управление: некоторые теоретические аспекты
- 3.6.2. Модель объекта управления и решение задачи оптимизации
- 3.7. Управление на основе нечеткой логики
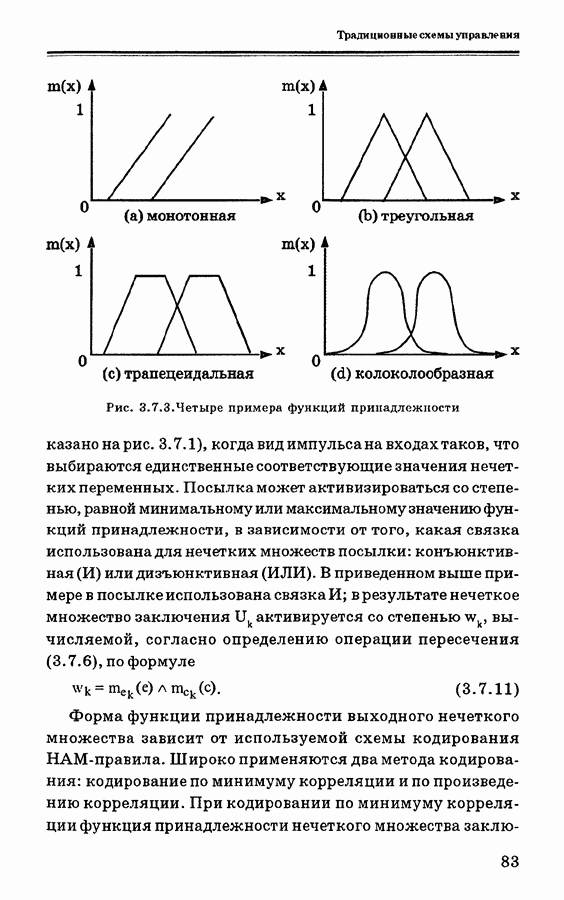
- 3.7.1. Краткие сведения по теории нечетких множеств и нечетких систем
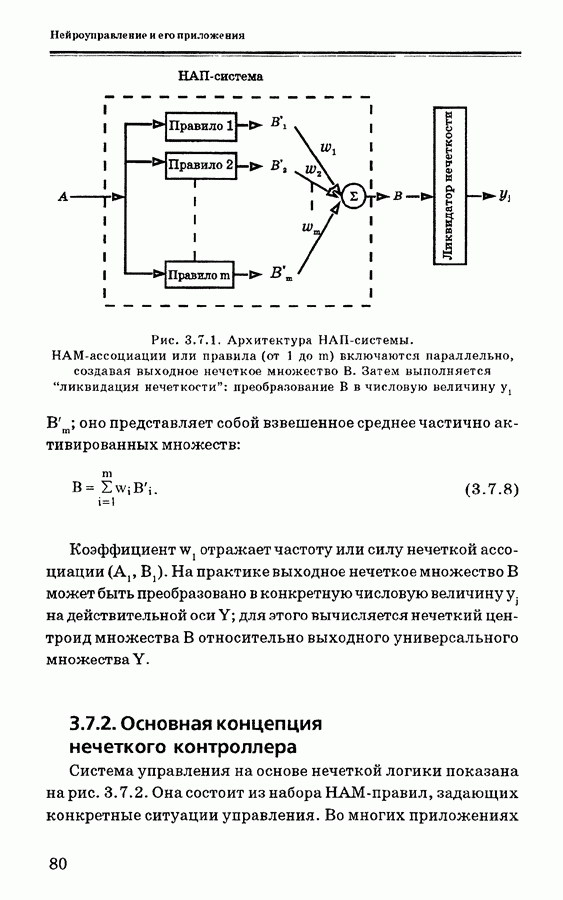
- 3.7.2. Основная концепция нечеткого контроллера
- 3.8. Заключение
- 4. ТЕХНОЛОГИИ НЕЙРОННОГО УПРАВЛЕНИЯ
- 4.2. Общие сведения о нейронном управлении
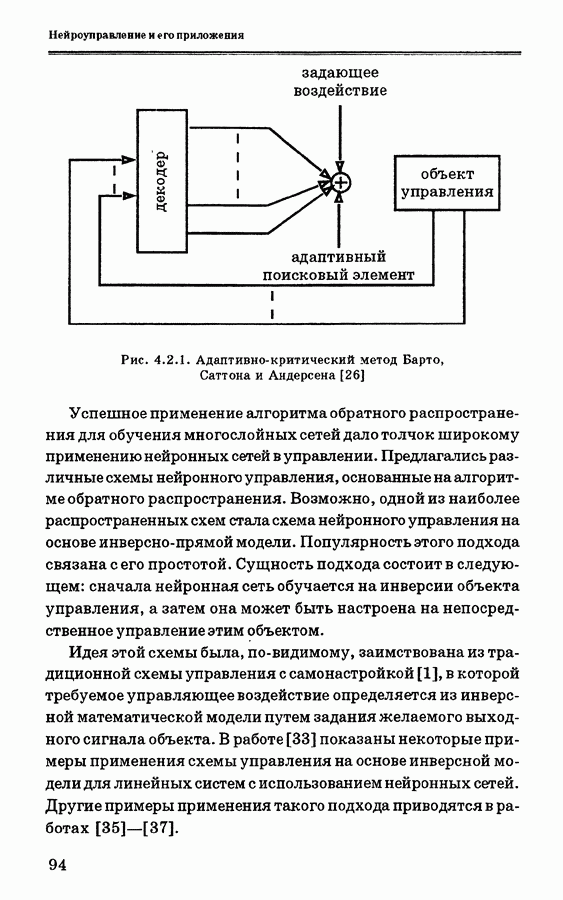
- 4.2.1. Подходы к нейронному управлению
- 4.2.2. Общая схема управления
- 4.3. Последовательная схема нейронного управления
- 4.4. Расширение последовательной схемы нейронного управления
- 4.4.2. Нейроморфные структуры управления
- 4.4.3. Конфигурации обучения
- 4.4.4. Эффективное оперативное управление
- 4.4.5. Алгоритмы обучения
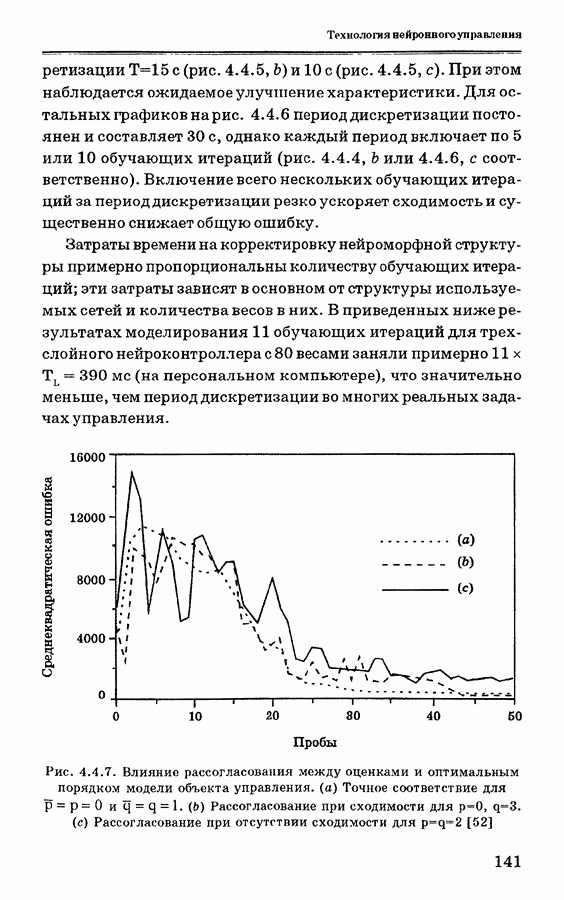
- 4.4.6. Оценка алгоритмов обучения на основе моделирования
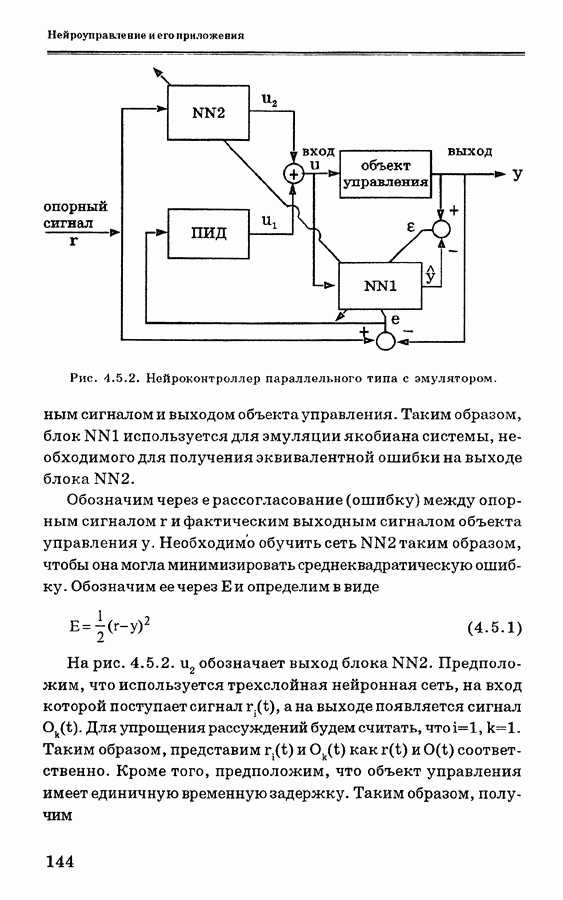
- 4.5. Параллельная схема управления
- 4.6. Алгоритм обучения по ошибке обратной связи
- 4.7. Расширение применения нейроконтроллеров параллельного типа
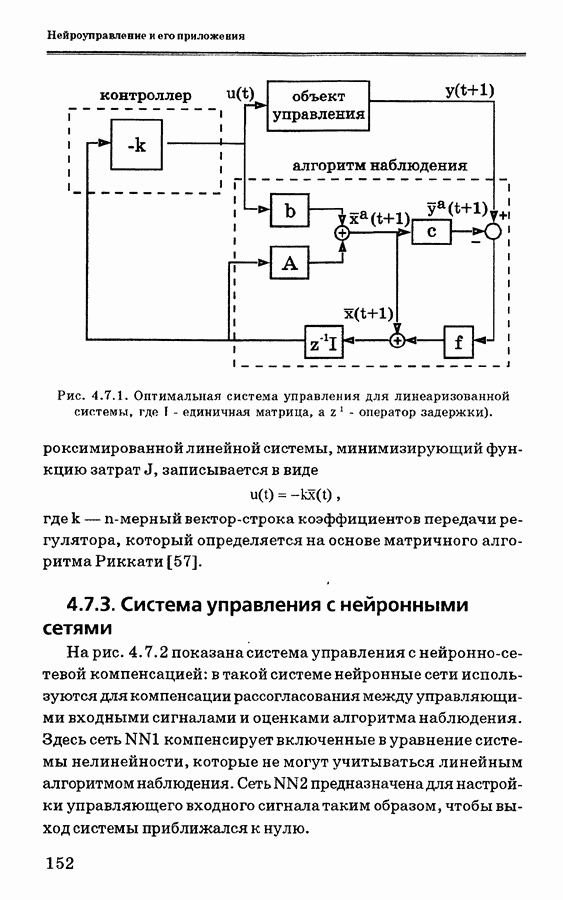
- 4.7.2. Линеаризованная система управления
- 4.7.3. Система управления с нейронными сетями
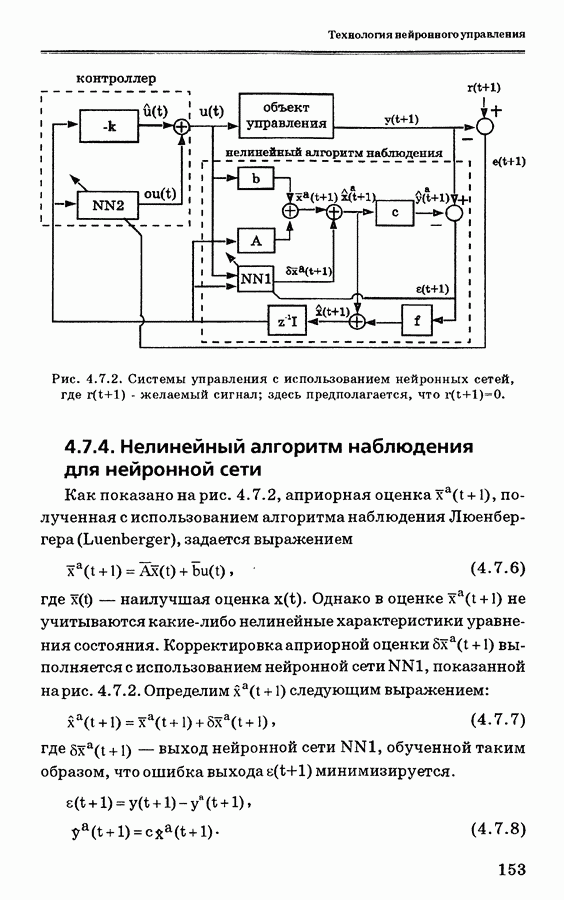
- 4.7.4. Нелинейный алгоритм наблюдения для нейронной сети
- 4.7.5. Нелинейный контроллер для нейронной сети
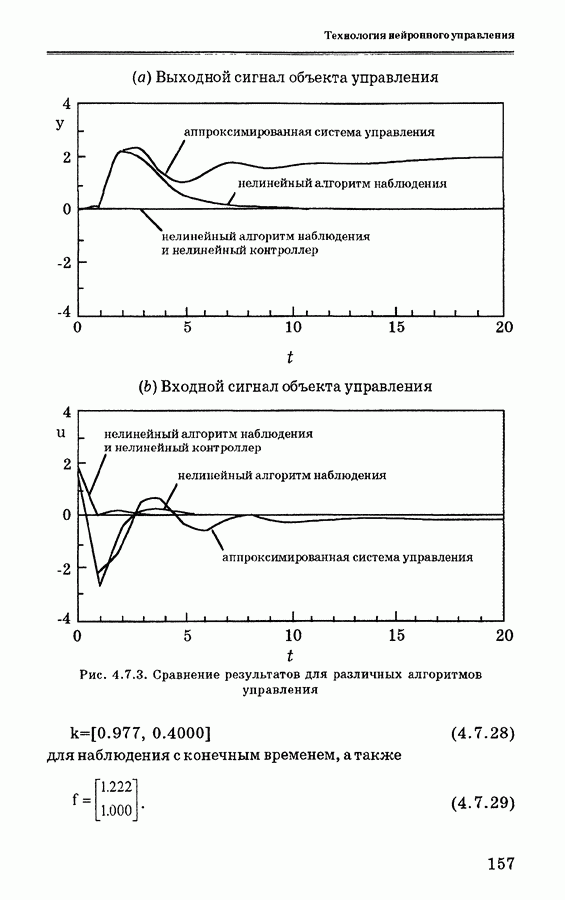
- 4.7.6. Численное моделирование
- 4.8. Схема нейронного управления с самонастройкой
- 4.9. ПИД-нейроконтроллер с самонастройкой
- 4.9.1. Вывод уравнений ПИД-нейроконтроллера с самонастройкой
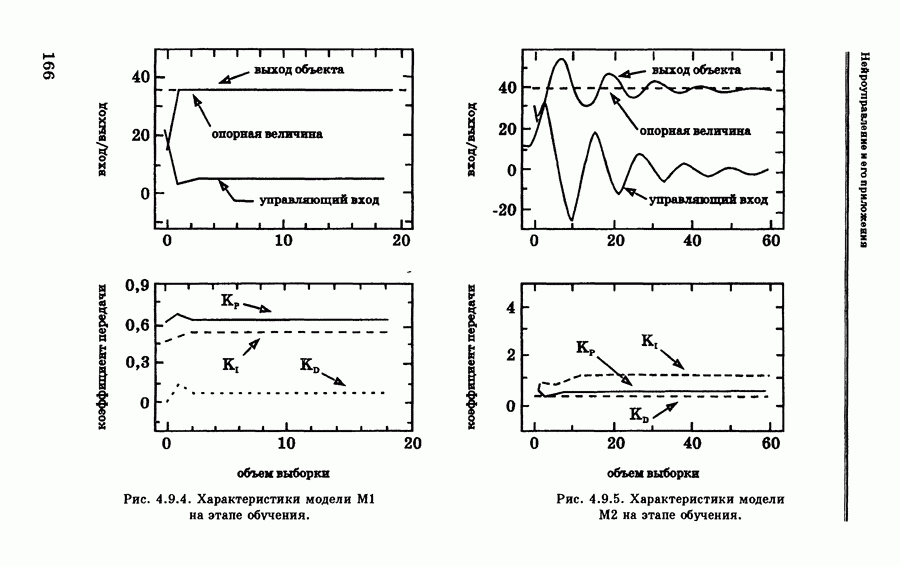
- 4.9.2. Примеры эмуляции
- 4.10. Схема нейронного управления с эмулятором и контроллером (схема обратного распространения во времени)
- 4.11. Заключение
- 5. ПРИЛОЖЕНИЯ НЕЙРОННОГО УПРАВЛЕНИЯ
- 5.2. Применение нейронного управления в системе регулирования процессов в водяной ванне и сравнение его с другими схемами управления
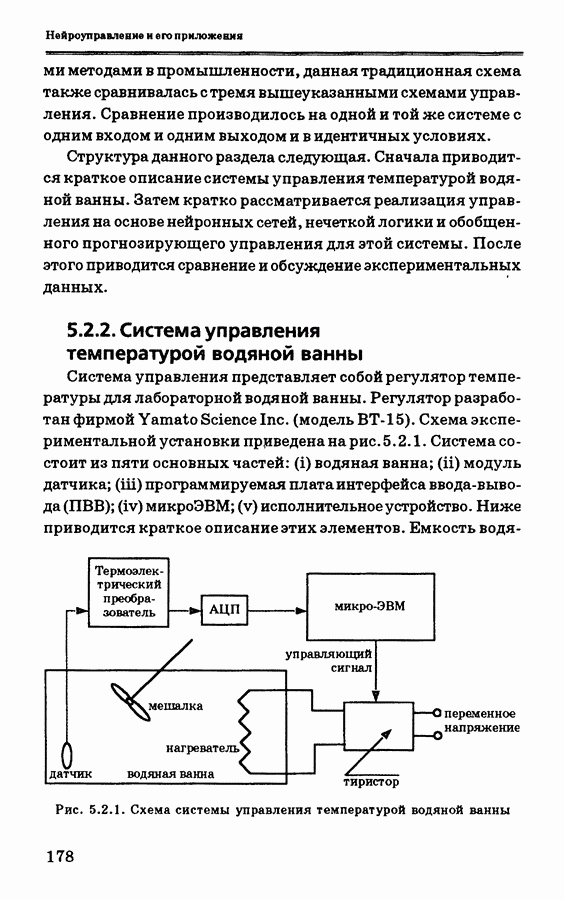
- 5.2.2. Система управления температурой водяной ванны
- 5.2.3. Схема нейронного управления
- 5.2.4. Схема управления на основе нечеткой логики
- 5.2.5. Схема обобщенного прогнозирующего управления
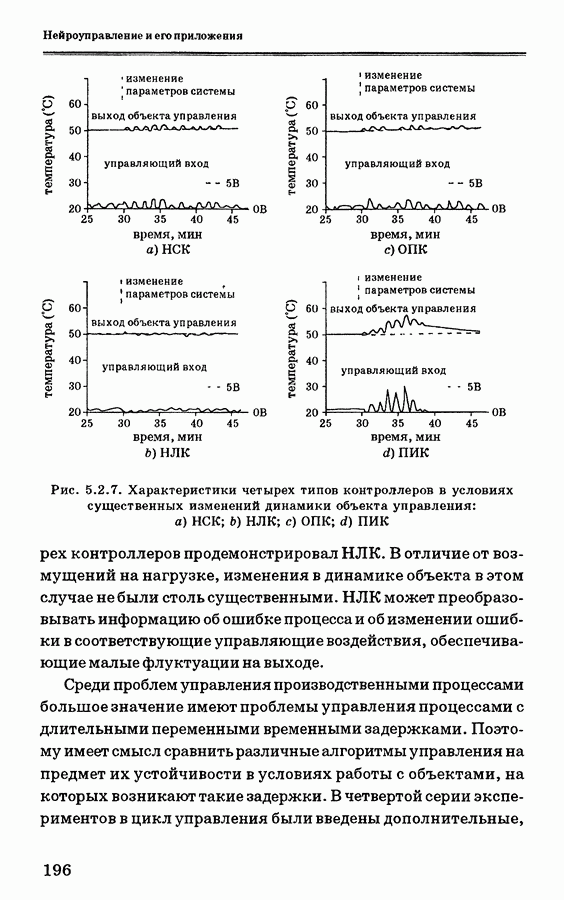
- 5.2.6. Экспериментальные данные и их анализ
- 5.2.7. Заключение
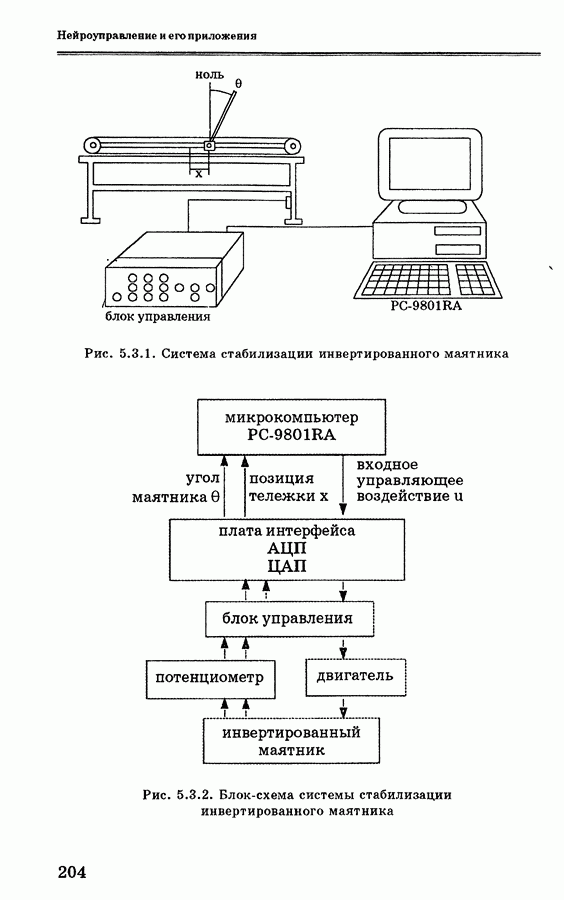
- 5.3. Система стабилизации инвертированного маятника на основе нейронных сетей
- 5.3.2. Система стабилизации инвертированного маятника
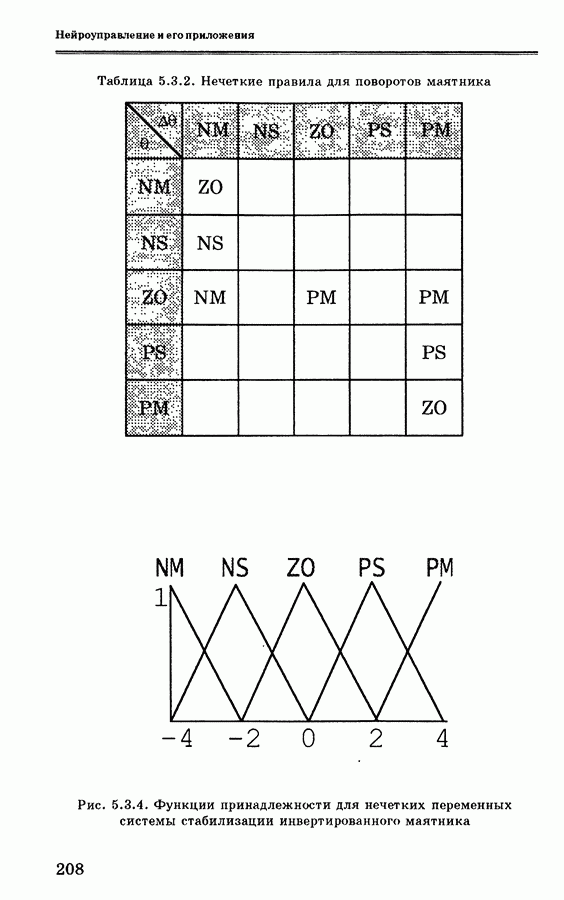
- 5.3.3. Инициализация поворотного управления с использованием нечеткой логики
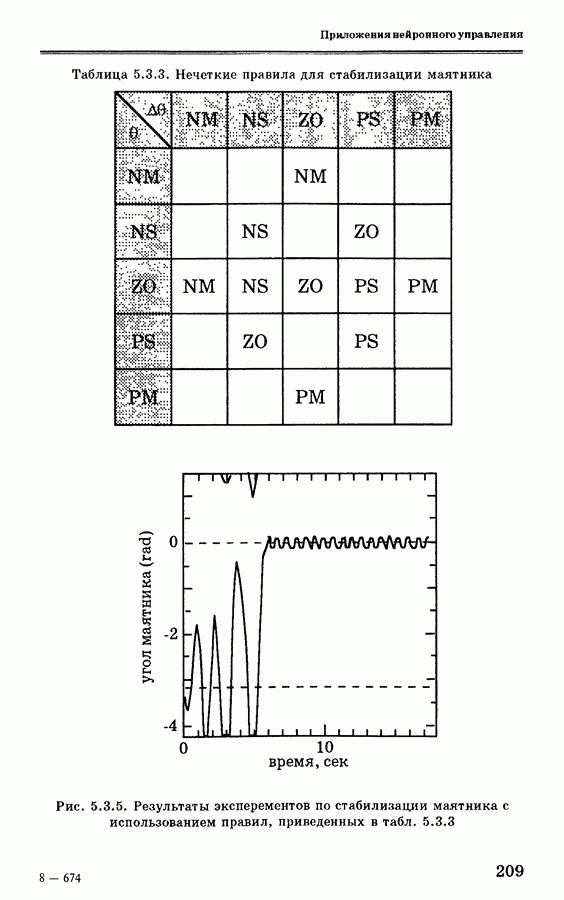
- 5.3.4. Применение стратегии оптимального управления для стабилизации маятника
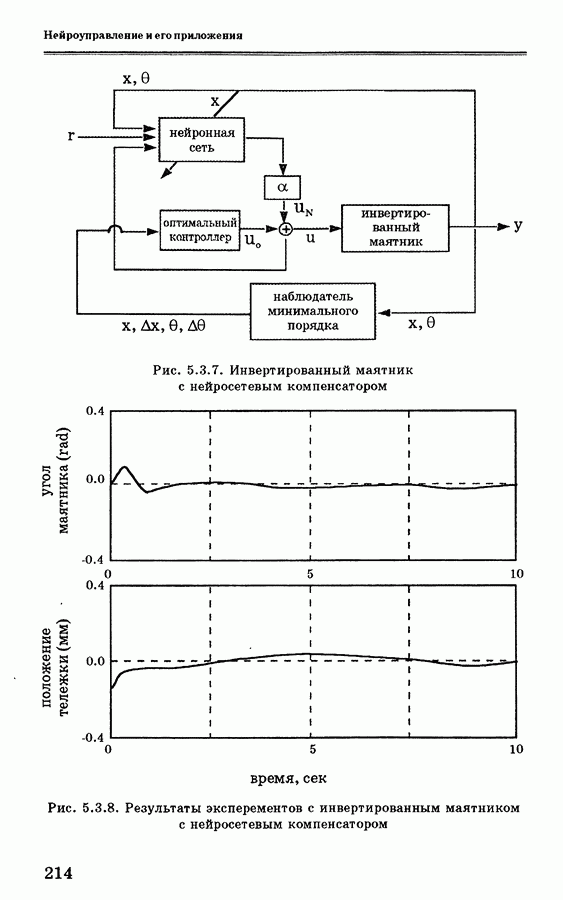
- 5.3.5. Точное управление на основе нейронных сетей
- 5.3.6. Заключение
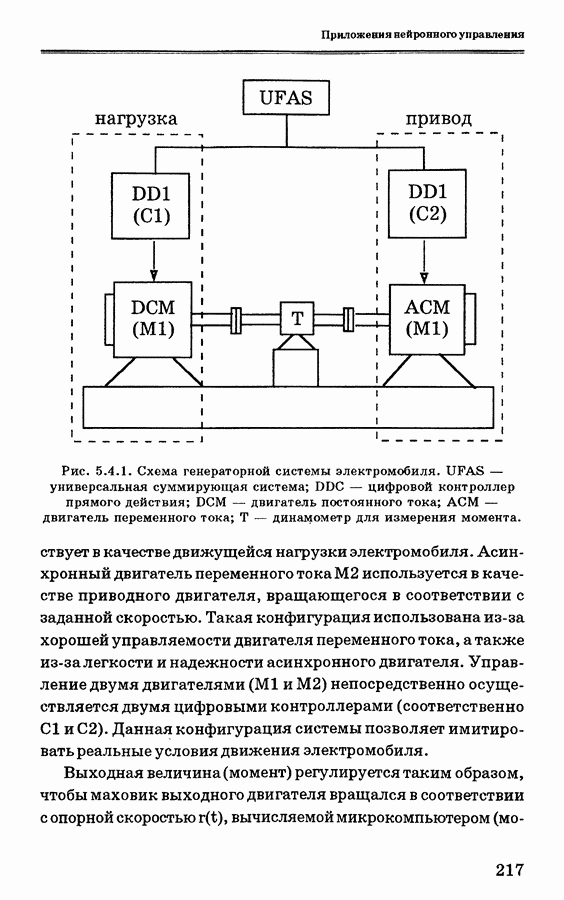
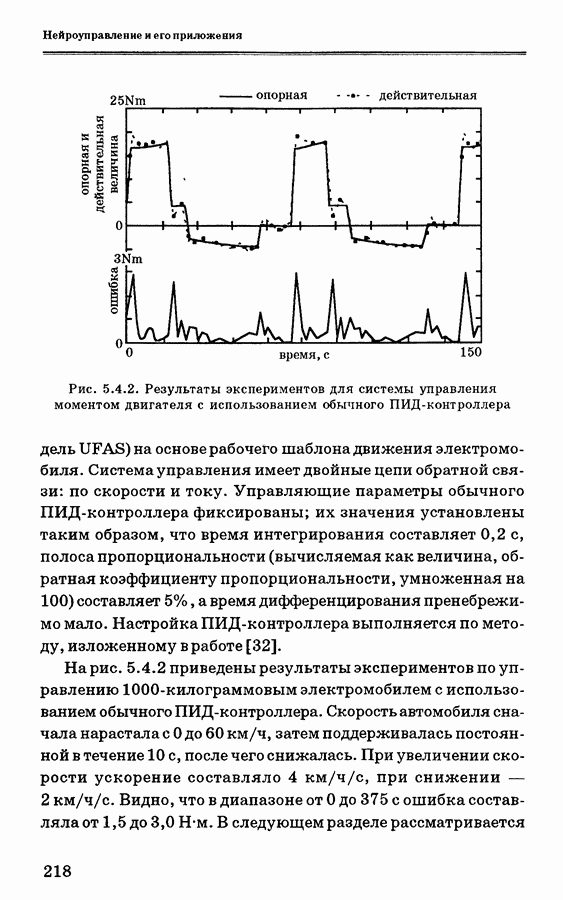
- 5.4. Применение ПИД-нейроконтроллера с самонастройкой для управления скоростью электромобиля
- 5.4.2. Система управления электромобилем
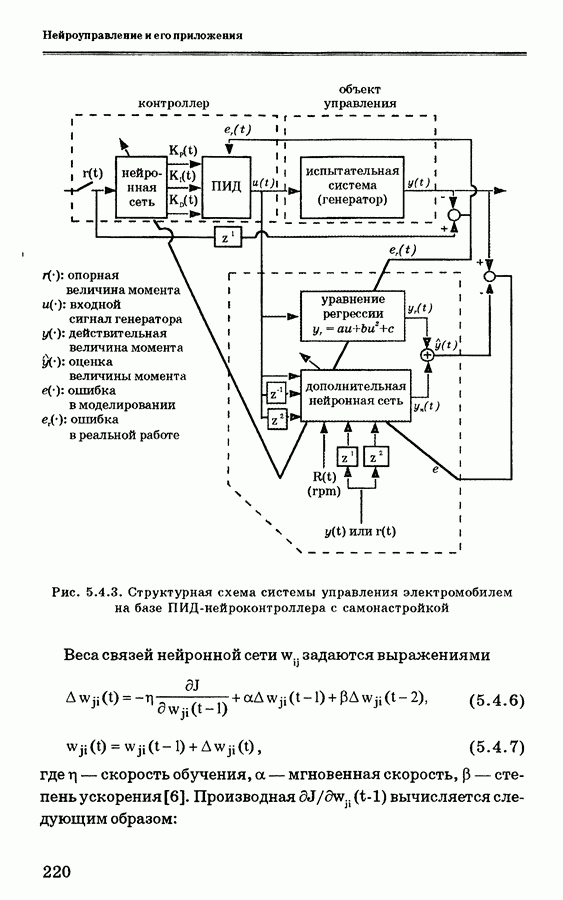
- 5.4.3. ПИД-нейроконтроллер с самонастройкой
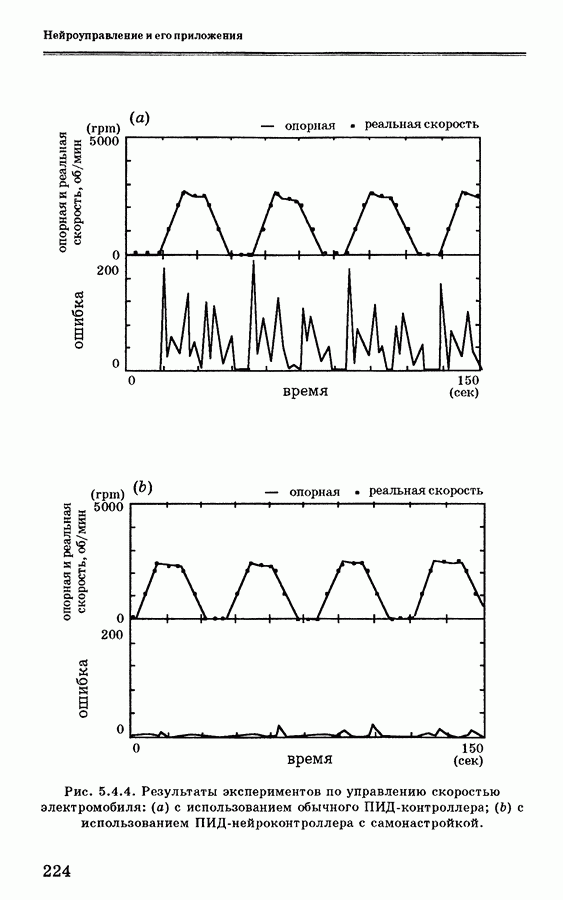
- 5.4.4. Применение нейронной сети для управления скоростью электромобиля
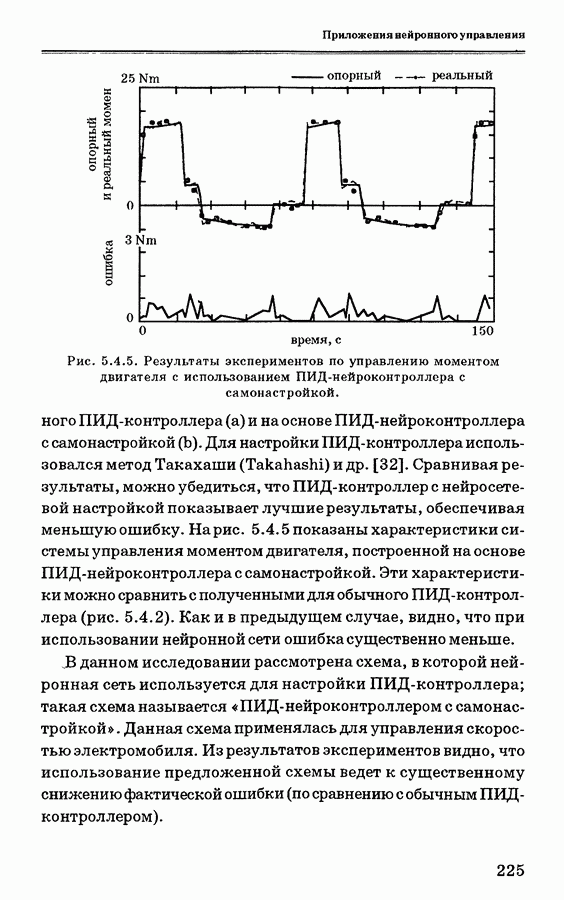
- 5.4.5. Заключение
- 5.5. Применение нейронных сетей для управления печью
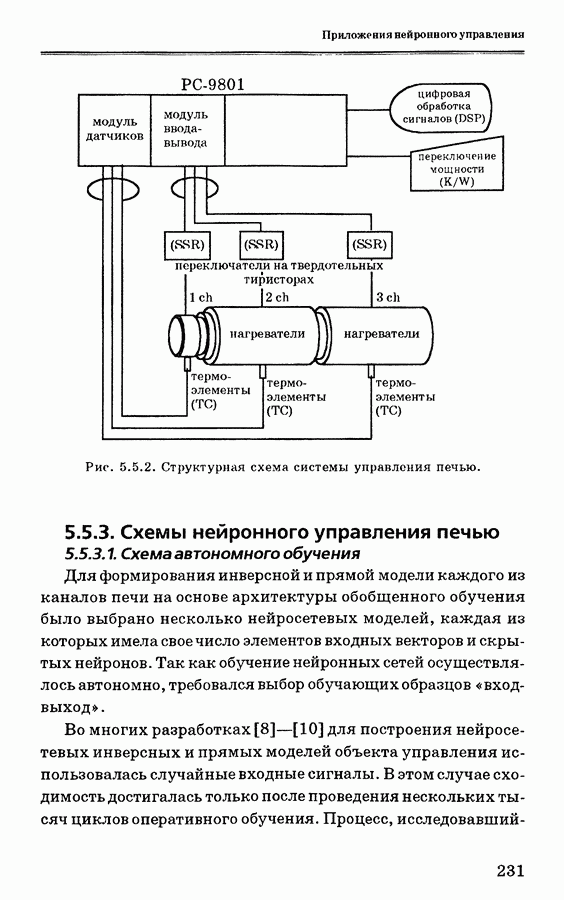
- 5.5.2. Система управления печью
- 5.5.3. Схемы нейронного управления печью
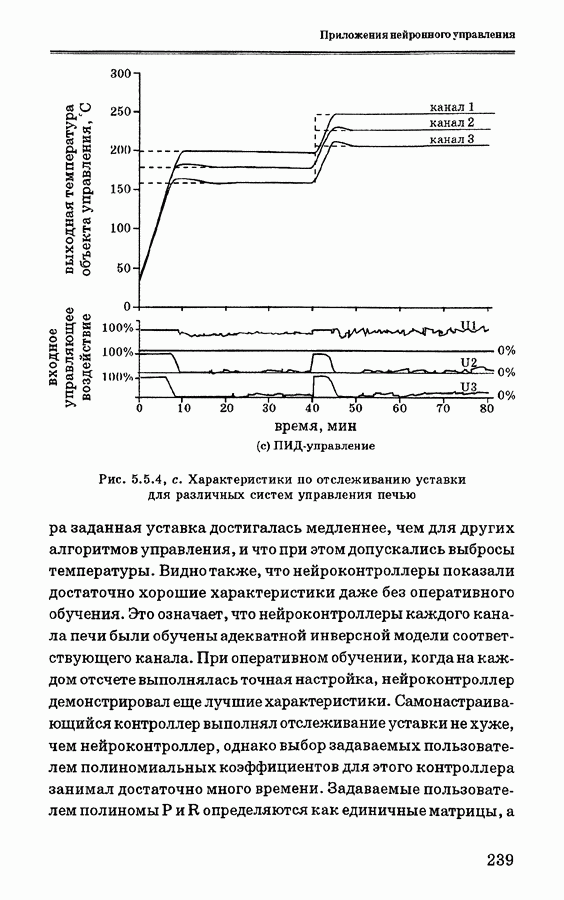
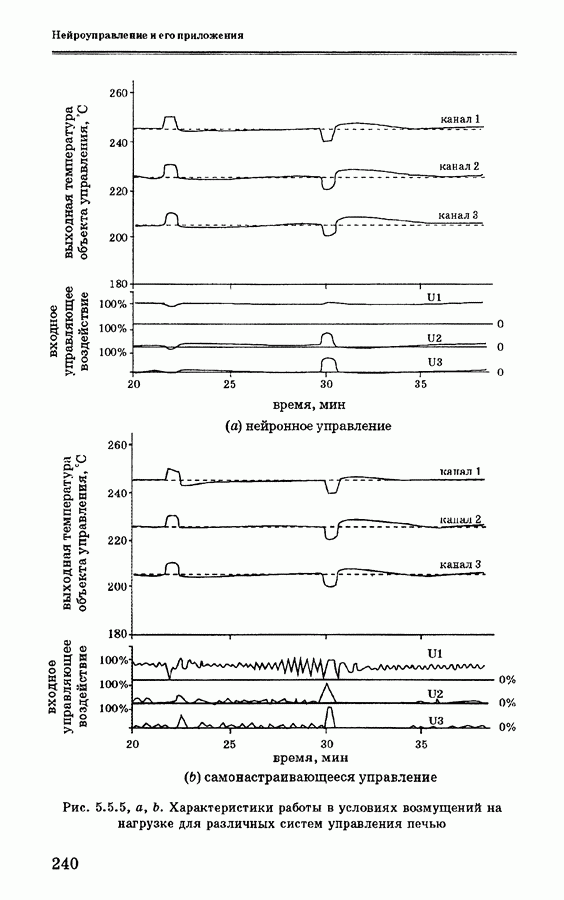
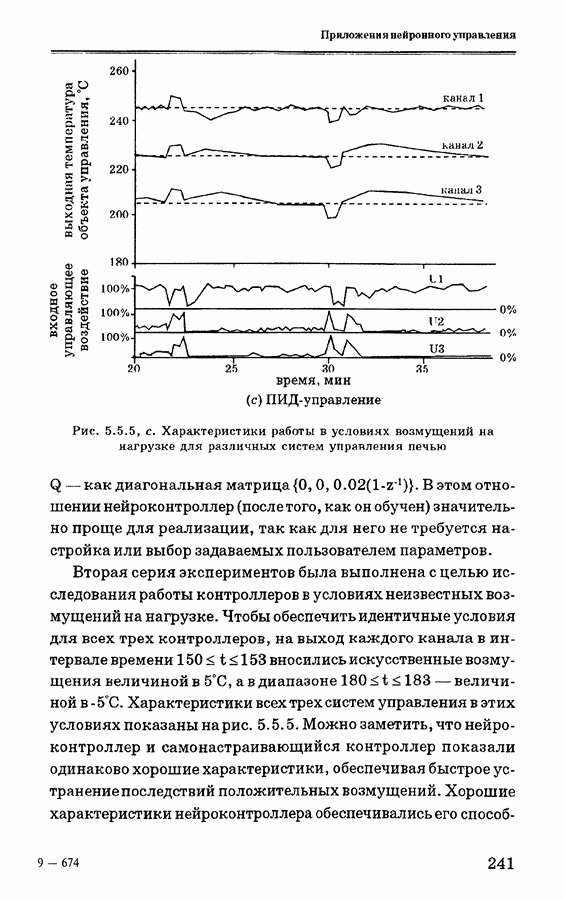
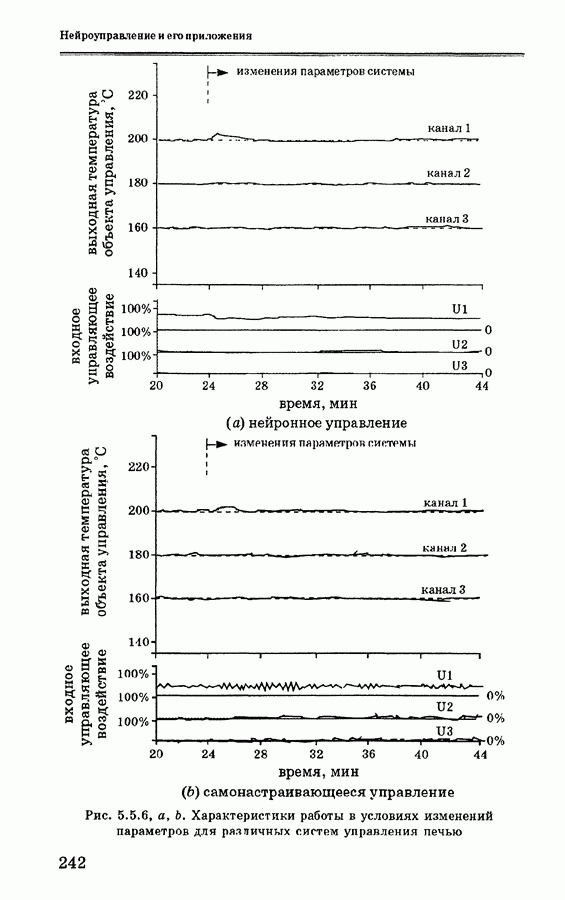
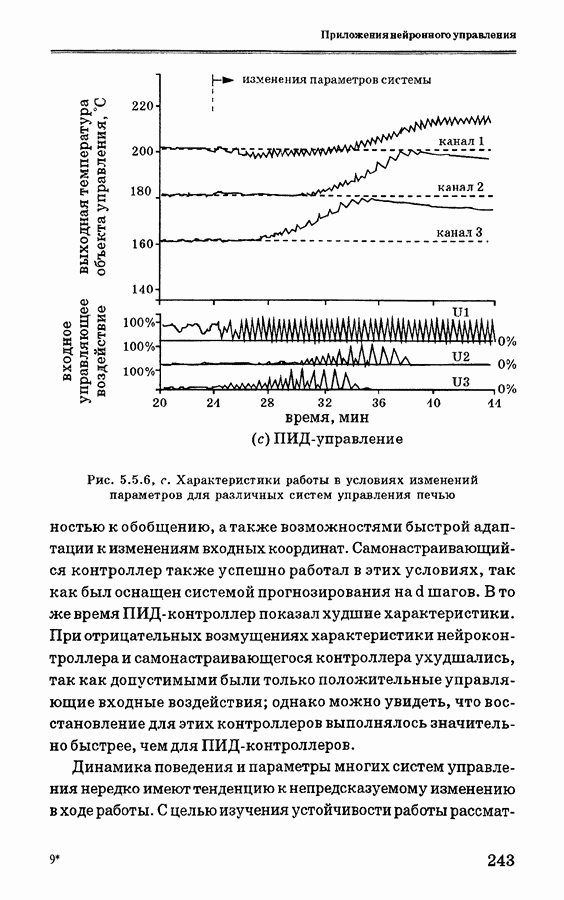
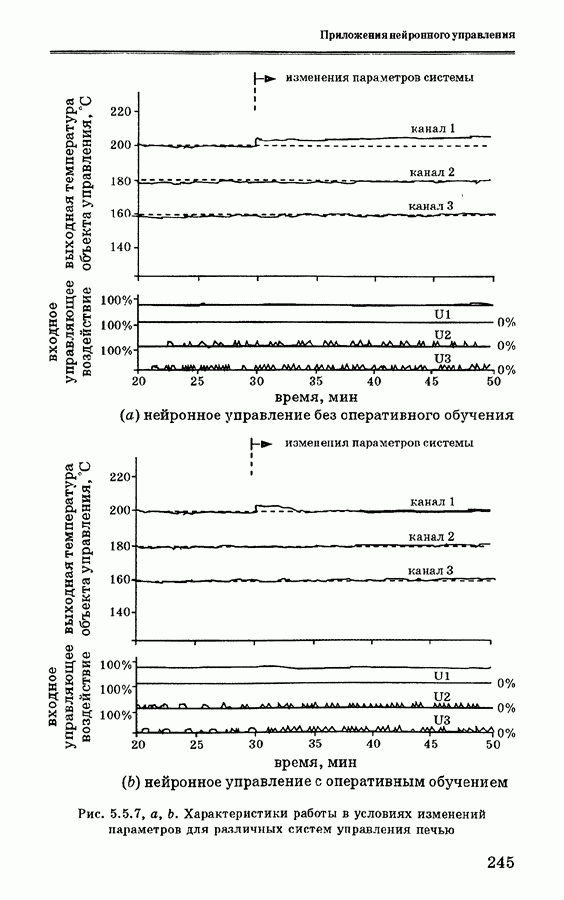
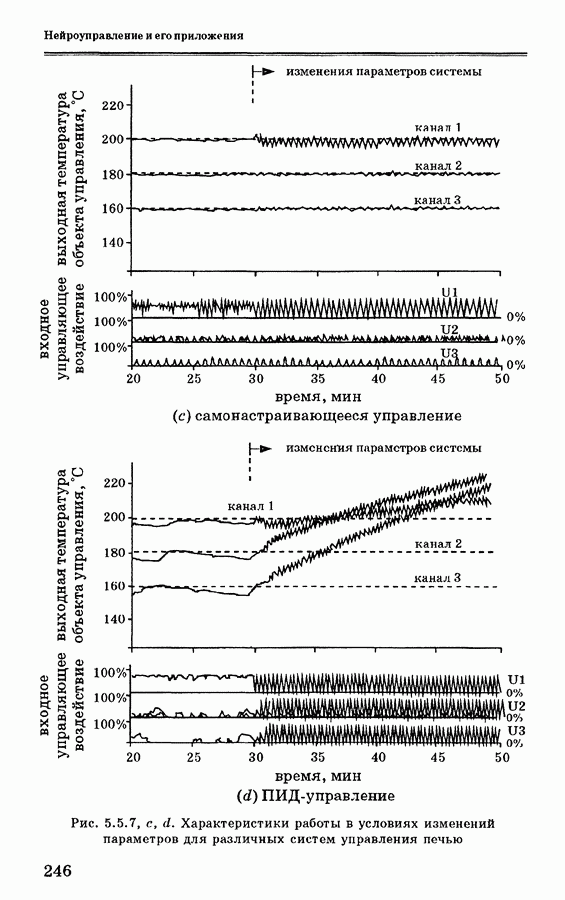
- 5.5.4. Анализ экспериментальных данных
- 5.6. Заключительные замечания и выводы
- Литература
- ЛИСТИНГ ПРОГРАММЫ