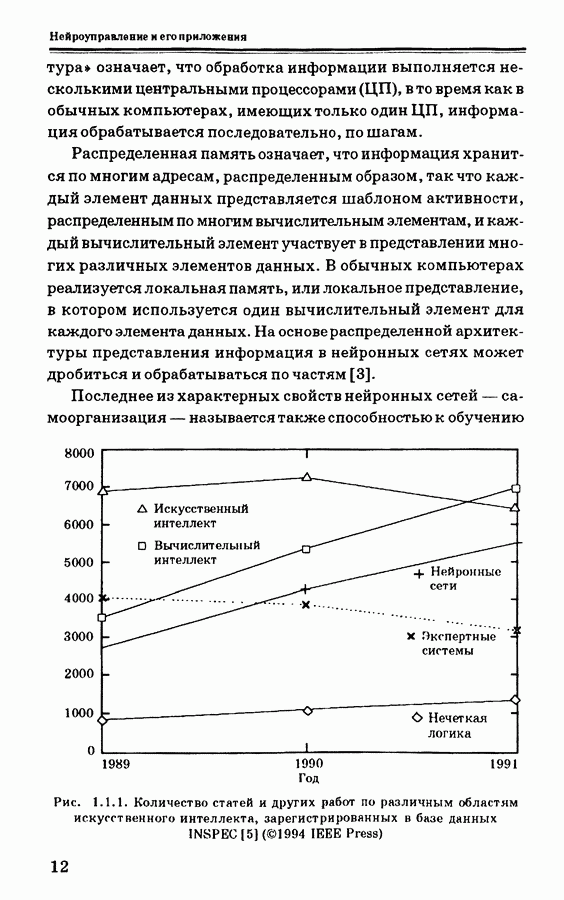
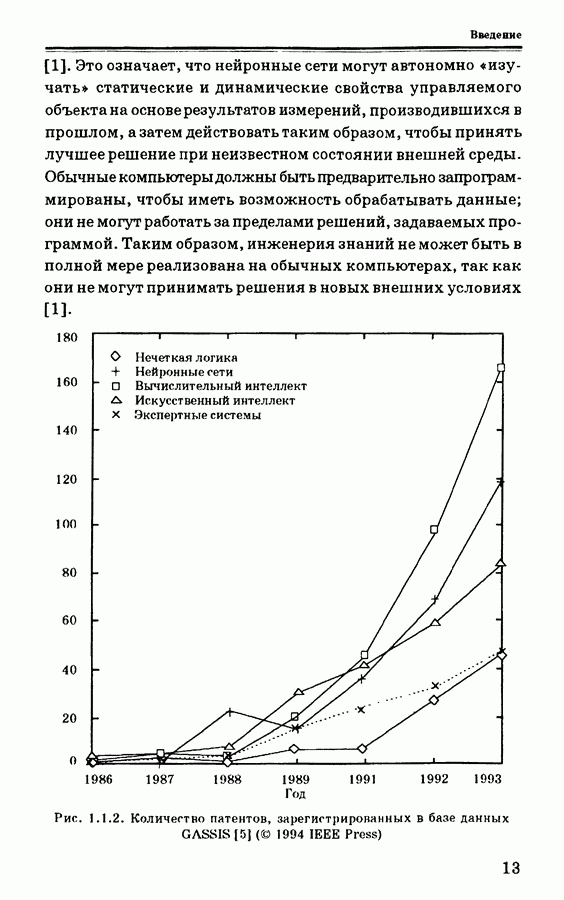
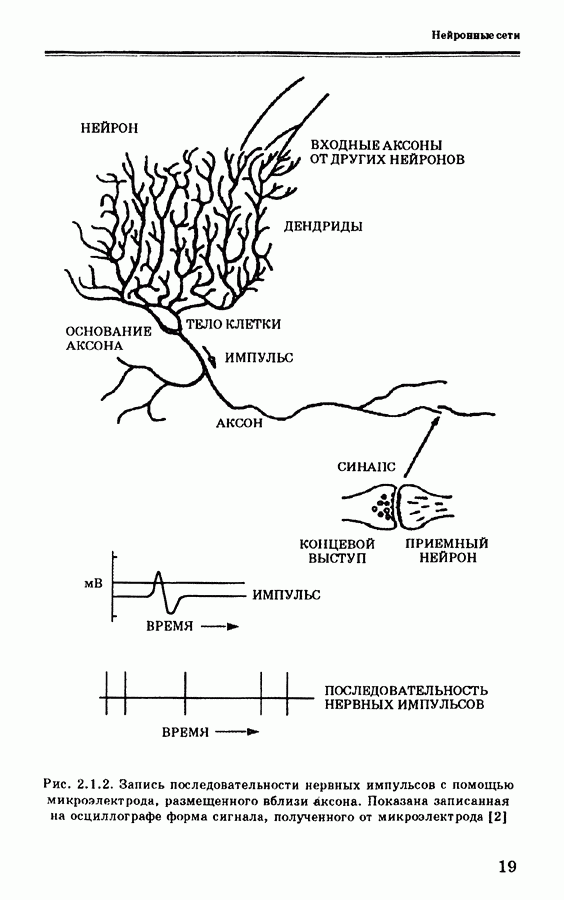
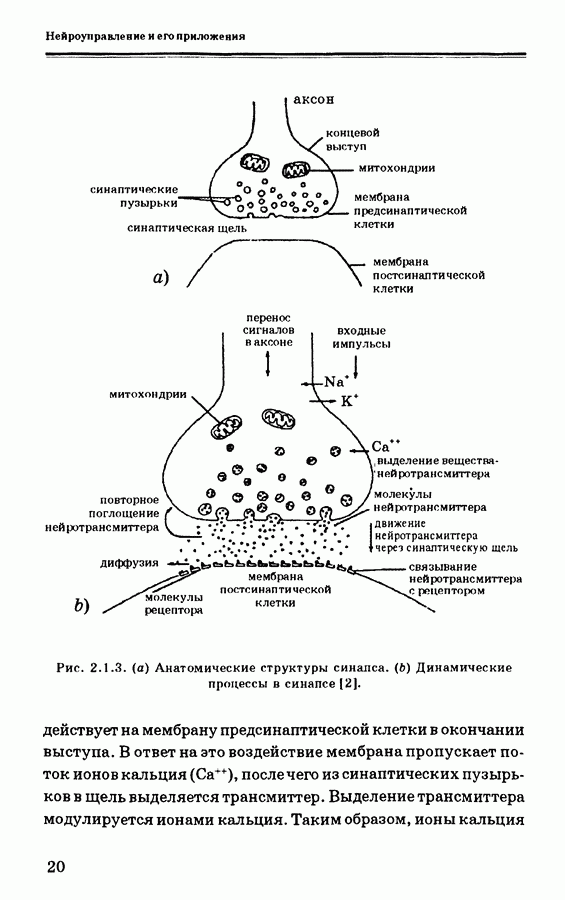
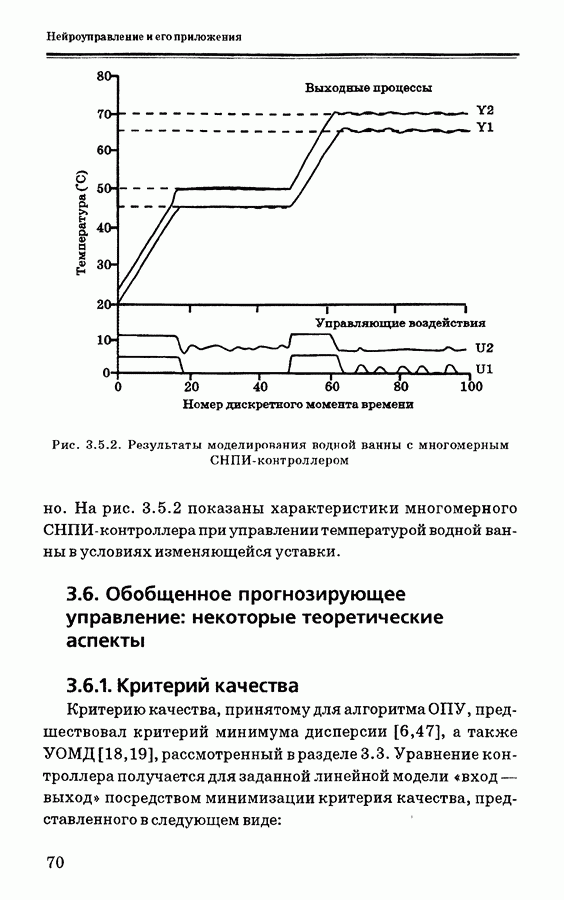
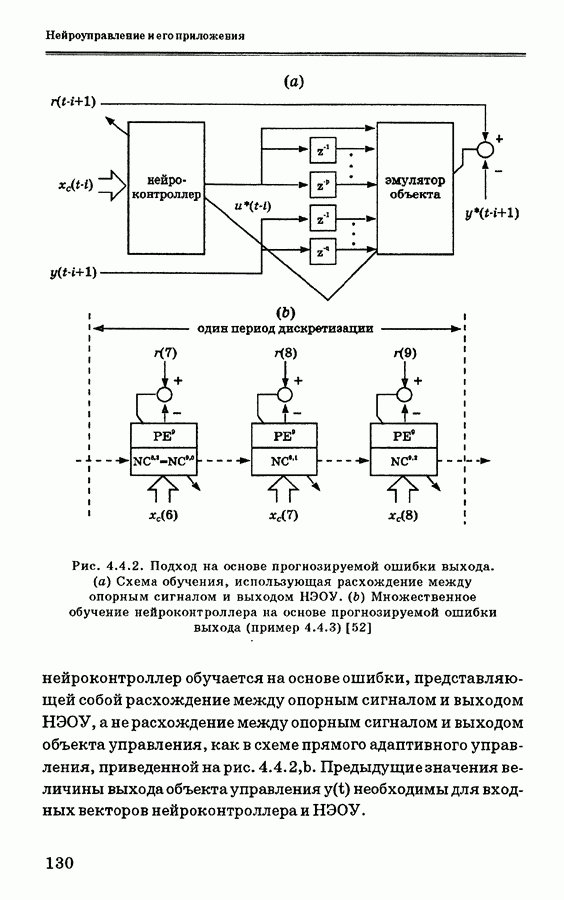
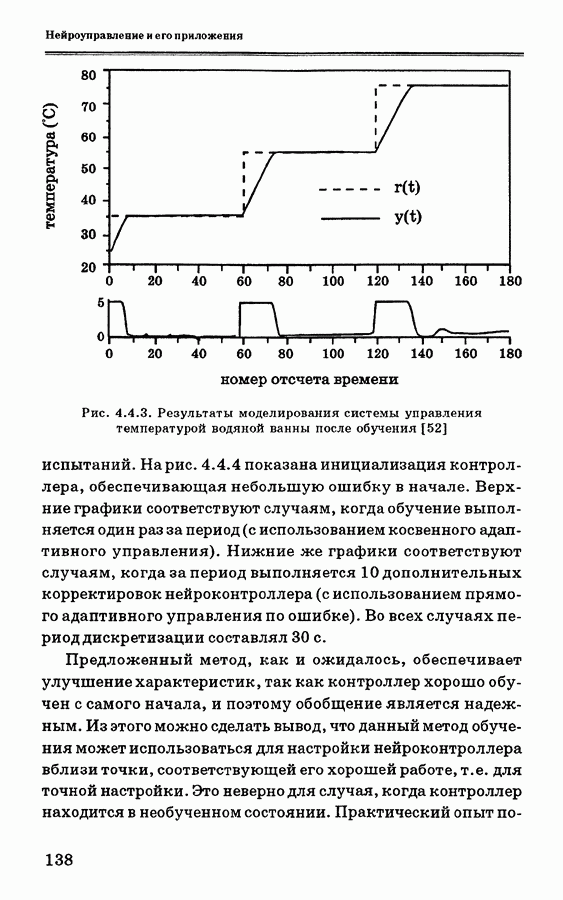
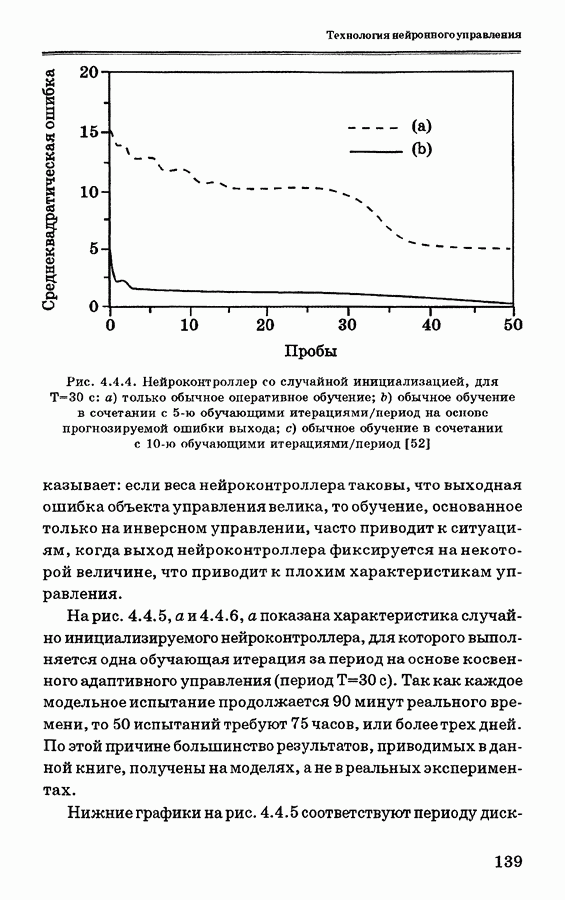
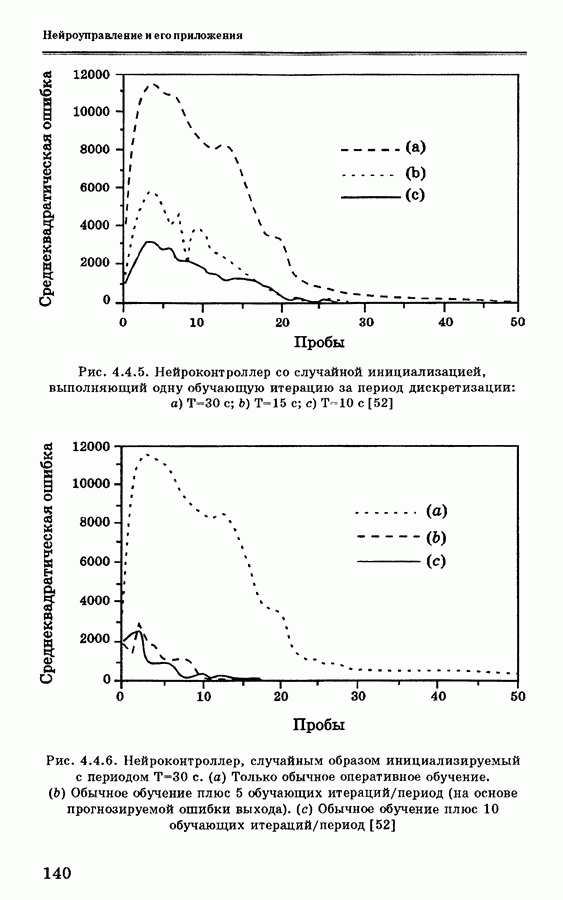
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3.7.1. Краткие сведения по теории нечетких множеств и нечетких систем
Теория нечетких множеств — активно развивающаяся сфера исследований. Некоторые ее аспекты рассмотрены в работах [61,62,63,64,65]. В данном разделе приводится краткий обзор теории нечетких множеств с точки зрения Коско (Kosko) [64]. Согласно этой теории [64], нечеткое множество можно определить как точку в кубе, а нечеткую систему — как отображение между такими кубами.  — нечеткая система, отображающая нечеткое множество в нечеткое множество. Таким образом, нечеткая система преобразует нечеткие множества из одного гиперкуба
— нечеткая система, отображающая нечеткое множество в нечеткое множество. Таким образом, нечеткая система преобразует нечеткие множества из одного гиперкуба  в другой гиперкуб
в другой гиперкуб 

где Р —  -мерный единичный гиперкуб, содержащий все нечеткие подмножества области определения, а
-мерный единичный гиперкуб, содержащий все нечеткие подмножества области определения, а  содержит все нечеткие подмножества области значений. Вообще говоря, нечеткая система
содержит все нечеткие подмножества области значений. Вообще говоря, нечеткая система  отображает семейства нечетких множеств друг на друга, т.е.
отображает семейства нечетких множеств друг на друга, т.е.

Такие нечеткие системы действуют как элементы ассоциативной памяти, когда они отображают замкнутые входы на замкнутые выходы; в этом смысле к ним применяется название «нечеткая ассоциативная память» (НАП). Простейшая НАП кодирует НАМ-правило, или ассоциацию  связывающую
связывающую  -мерное нечеткое множество В. с
-мерное нечеткое множество В. с  -мерным нечетким множеством А. Такие минимальные НАП отображают один элемент из гиперкуба 1° в один элемент гиперкуба
-мерным нечетким множеством А. Такие минимальные НАП отображают один элемент из гиперкуба 1° в один элемент гиперкуба 
В теории нечетких множеств [30] определены три основные операции: дополнение, объединение и пересечение нечетких множеств. Дополнение нечеткого множества А обозначается, как  и определяется выражением:
и определяется выражением:

где X — множество точек вещественной оси  — функция принадлежности нечеткого множества А, принимающая значения в диапазоне от 0 до 1. Объединение двух нечетких множеств А и В с соответствующими функциями принадлежности
— функция принадлежности нечеткого множества А, принимающая значения в диапазоне от 0 до 1. Объединение двух нечетких множеств А и В с соответствующими функциями принадлежности  — это нечеткое множество С, обозначаемое как
— это нечеткое множество С, обозначаемое как  Его функция принадлежности определяется по функциям принадлежности множеств А и В в соответствии с выражением:
Его функция принадлежности определяется по функциям принадлежности множеств А и В в соответствии с выражением:

или в сокращенной форме:

Пересечение двух нечетких множеств А и В с функциями принадлежности  — это нечеткое множество С, обозначаемое как
— это нечеткое множество С, обозначаемое как  Его функция принадлежности определяется выражением:
Его функция принадлежности определяется выражением:

или в сокращенной форме:

Проще говоря, объединение нечетких множеств А и В — это самое малое нечеткое множество, содержащее как А, так и В. Пересечение нечетких множеств А и В — это нечеткое множество, содержащееся как в А, так и в В.
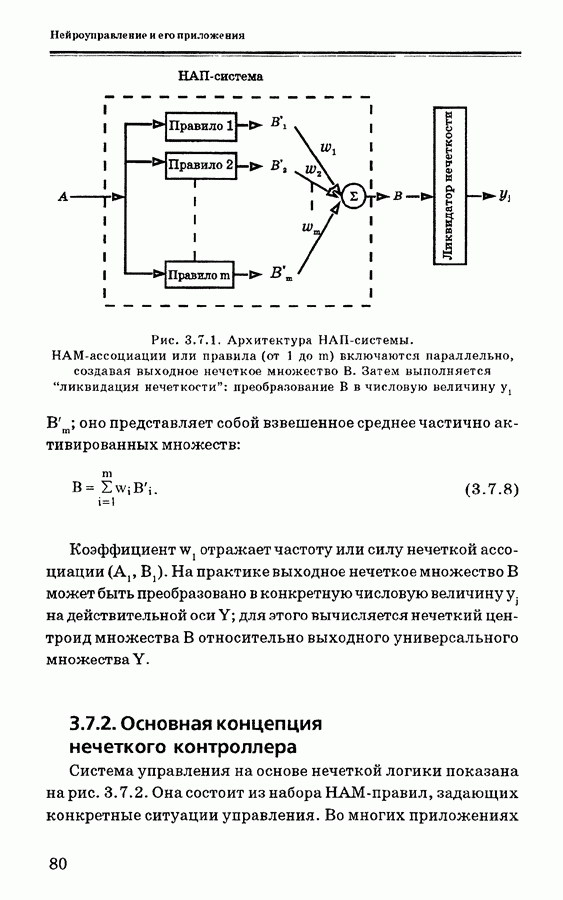
Вообще говоря, НАП-система  осуществляет кодирование и параллельную обработку набора из
осуществляет кодирование и параллельную обработку набора из  НАМ-правил
НАМ-правил  как показано нарис. 3.7.1. Каждый вход НАП-системы А активизирует каждое из хранимых НАМ-правил в различной степени. Минимальное НАМ-правило,
как показано нарис. 3.7.1. Каждый вход НАП-системы А активизирует каждое из хранимых НАМ-правил в различной степени. Минимальное НАМ-правило,  ассоциация, или правило
ассоциация, или правило  ) отображает вход А в выход В., представляющий собой частично активированный вариант В.. Чем больше вход А напоминает А., тем больше В, напоминает В.. Соответствующее выходное нечеткое множество В объединяет эти частично активированные нечеткие множества
) отображает вход А в выход В., представляющий собой частично активированный вариант В.. Чем больше вход А напоминает А., тем больше В, напоминает В.. Соответствующее выходное нечеткое множество В объединяет эти частично активированные нечеткие множества 

Рис. 3.7.1. Архитектура НАП-системы. НАМ-ассоциации или правила (от 1 до  ) включаются параллельно, создавая выходное нечеткое множество В. Затем выполняется “ликвидация нечеткости”: преобразование В в числовую величину
) включаются параллельно, создавая выходное нечеткое множество В. Затем выполняется “ликвидация нечеткости”: преобразование В в числовую величину 
 оно представляет собой взвешенное среднее частично активированных множеств:
оно представляет собой взвешенное среднее частично активированных множеств:

Коэффициент  отражает частоту или силу нечеткой ассоциации
отражает частоту или силу нечеткой ассоциации  На практике выходное нечеткое множество В может быть преобразовано в конкретную числовую величину у. на действительной оси
На практике выходное нечеткое множество В может быть преобразовано в конкретную числовую величину у. на действительной оси  для этого вычисляется нечеткий центроид множества В относительно выходного универсального множества У.
для этого вычисляется нечеткий центроид множества В относительно выходного универсального множества У.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРОВ ПЕРЕВОДА
- 1. ВВЕДЕНИЕ
- 1.1. Общие сведения об интеллектуальном управлении
- 2. НЕЙРОННЫЕ СЕТИ
- 2.2. Алгоритм обратного распространения
- 2.2.2. Вывод алгоритма обратного распространения
- 2.2.2.2. Правило для скрытого слоя
- 2.2.3. Алгоритм обратного распространения: порядок реализации
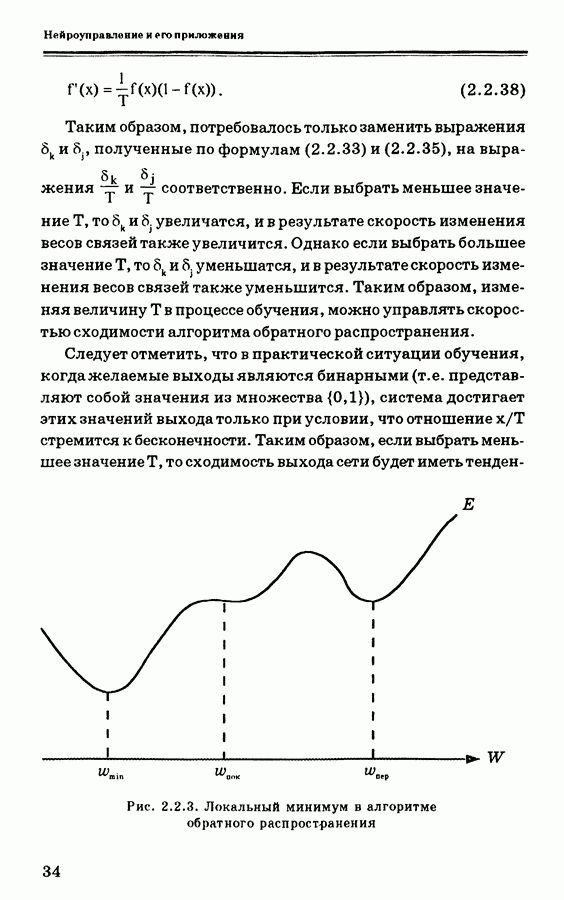
- 2.2.4. Обсуждение алгоритма обратного распространения
- 2.3. Заключение
- 3. ТРАДИЦИОННЫЕ СХЕМЫ УПРАВЛЕНИЯ
- 3.2. ПИ- и ПИД-контроллеры с дискретным временем
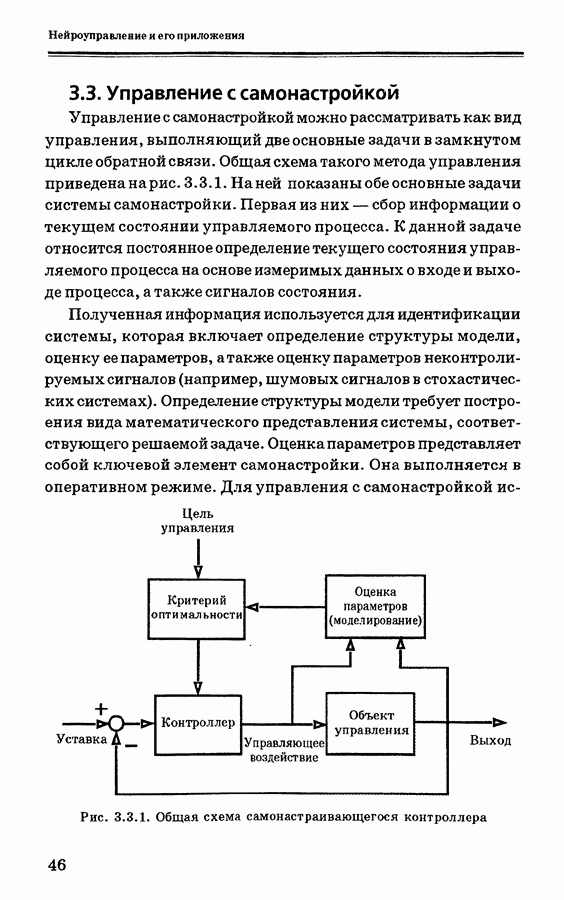
- 3.3. Управление с самонастройкой
- 3.4. Самонастраивающиеся ПИ- и ПИД- контроллеры
- 3.5. ПИД-управление с самонастройкой: многомерный подход
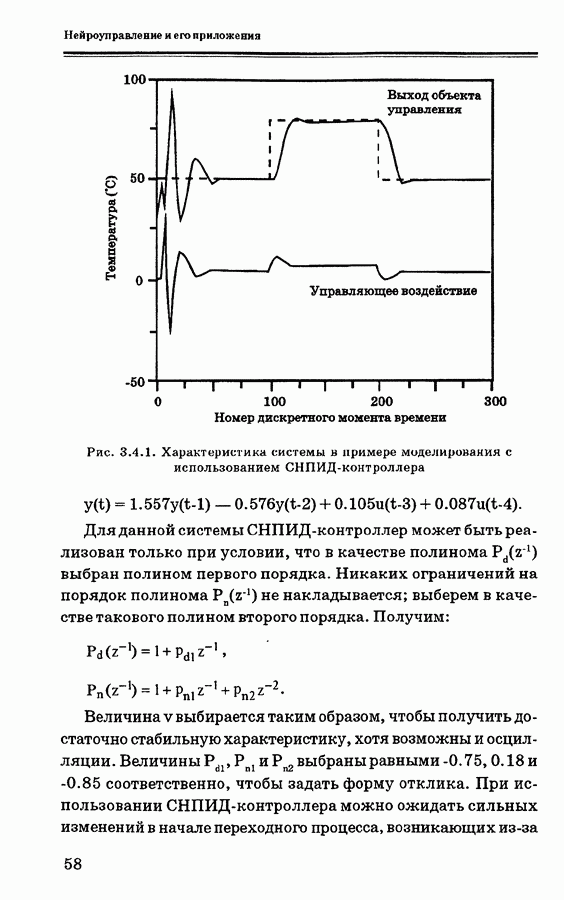
- 3.5.1. Пример моделирования
- 3.6. Обобщенное прогнозирующее управление: некоторые теоретические аспекты
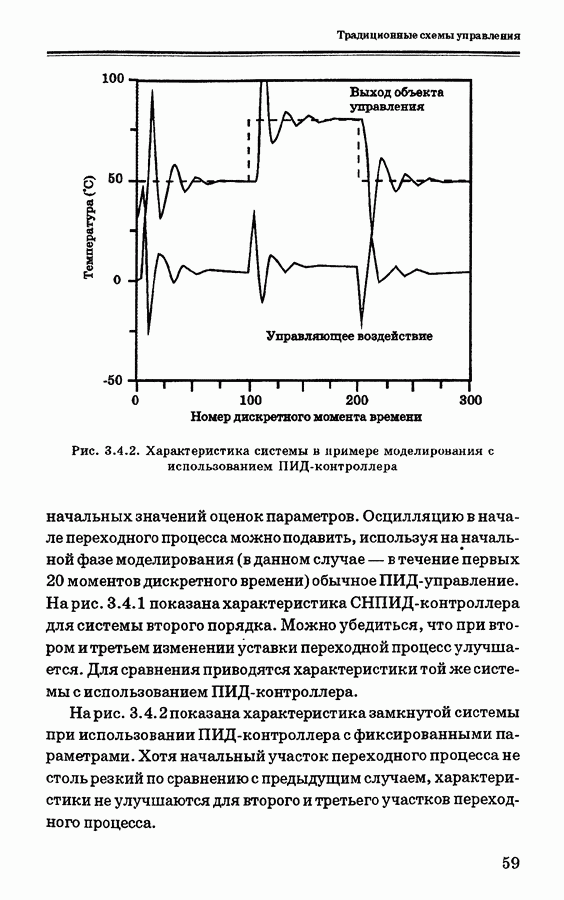
- 3.6.2. Модель объекта управления и решение задачи оптимизации
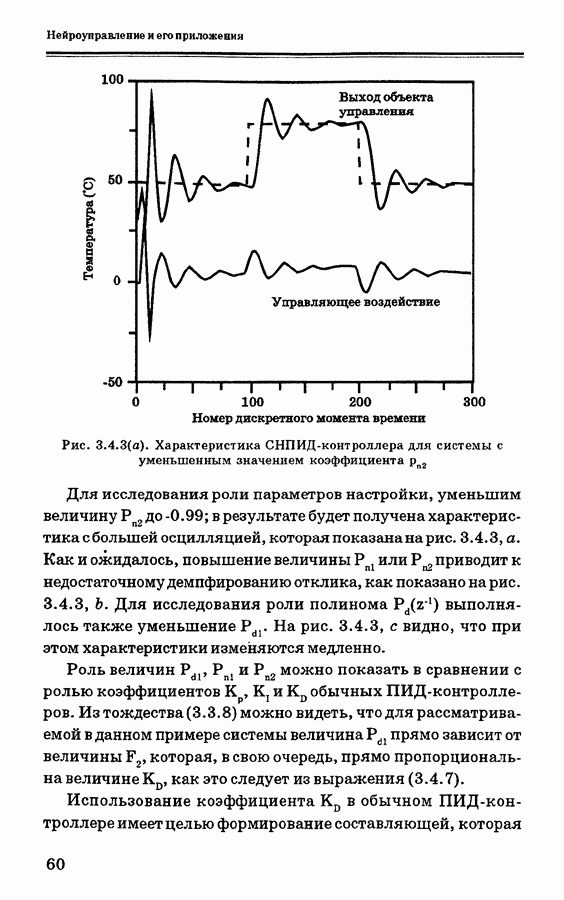
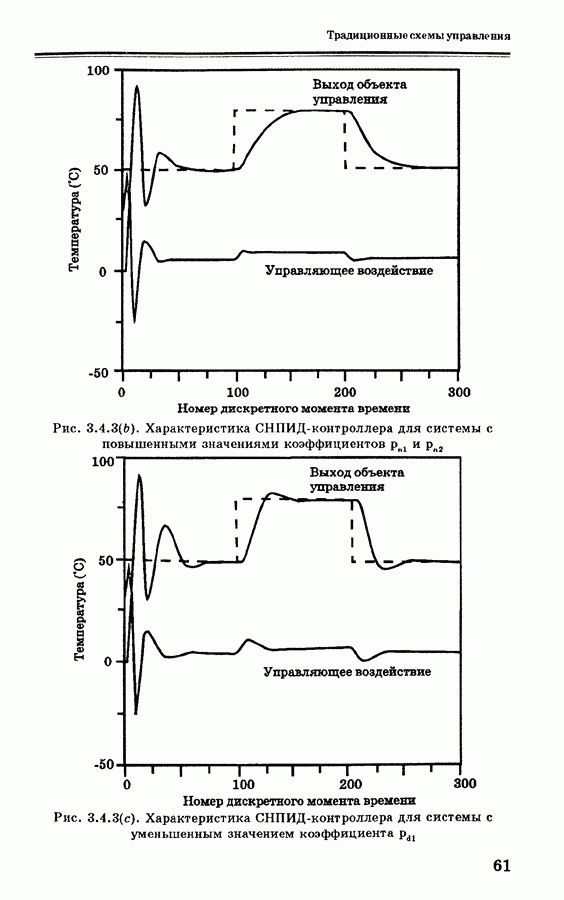
- 3.7. Управление на основе нечеткой логики
- 3.7.1. Краткие сведения по теории нечетких множеств и нечетких систем
- 3.7.2. Основная концепция нечеткого контроллера
- 3.8. Заключение
- 4. ТЕХНОЛОГИИ НЕЙРОННОГО УПРАВЛЕНИЯ
- 4.2. Общие сведения о нейронном управлении
- 4.2.1. Подходы к нейронному управлению
- 4.2.2. Общая схема управления
- 4.3. Последовательная схема нейронного управления
- 4.4. Расширение последовательной схемы нейронного управления
- 4.4.2. Нейроморфные структуры управления
- 4.4.3. Конфигурации обучения
- 4.4.4. Эффективное оперативное управление
- 4.4.5. Алгоритмы обучения
- 4.4.6. Оценка алгоритмов обучения на основе моделирования
- 4.5. Параллельная схема управления
- 4.6. Алгоритм обучения по ошибке обратной связи
- 4.7. Расширение применения нейроконтроллеров параллельного типа
- 4.7.2. Линеаризованная система управления
- 4.7.3. Система управления с нейронными сетями
- 4.7.4. Нелинейный алгоритм наблюдения для нейронной сети
- 4.7.5. Нелинейный контроллер для нейронной сети
- 4.7.6. Численное моделирование
- 4.8. Схема нейронного управления с самонастройкой
- 4.9. ПИД-нейроконтроллер с самонастройкой
- 4.9.1. Вывод уравнений ПИД-нейроконтроллера с самонастройкой
- 4.9.2. Примеры эмуляции
- 4.10. Схема нейронного управления с эмулятором и контроллером (схема обратного распространения во времени)
- 4.11. Заключение
- 5. ПРИЛОЖЕНИЯ НЕЙРОННОГО УПРАВЛЕНИЯ
- 5.2. Применение нейронного управления в системе регулирования процессов в водяной ванне и сравнение его с другими схемами управления
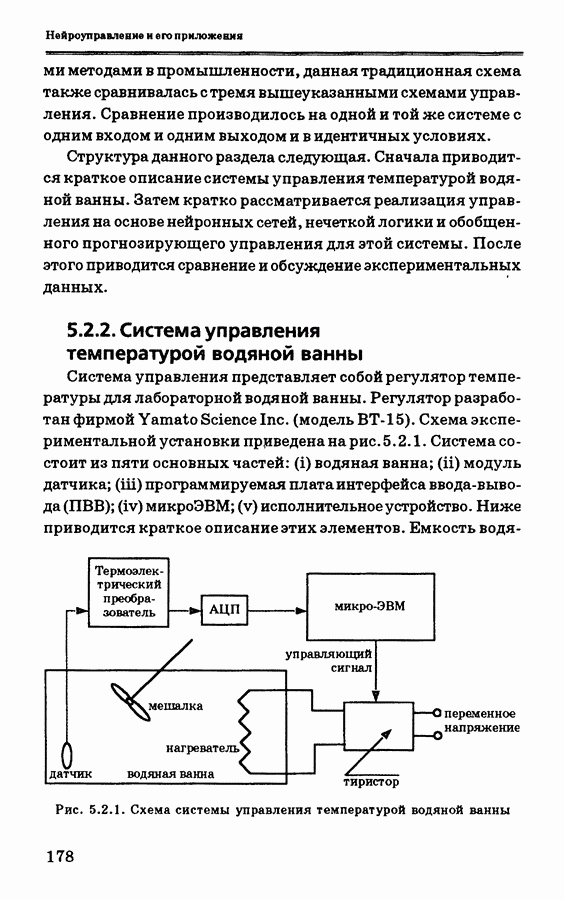
- 5.2.2. Система управления температурой водяной ванны
- 5.2.3. Схема нейронного управления
- 5.2.4. Схема управления на основе нечеткой логики
- 5.2.5. Схема обобщенного прогнозирующего управления
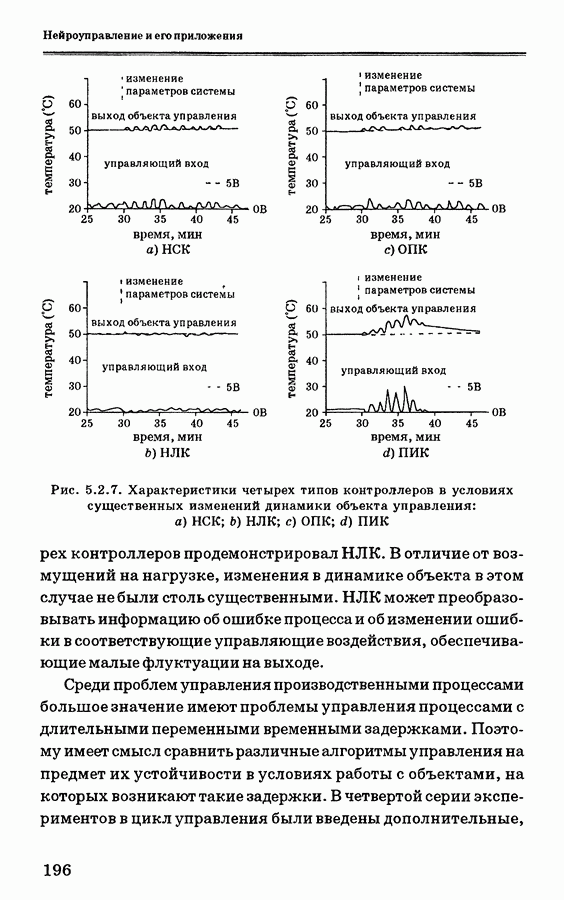
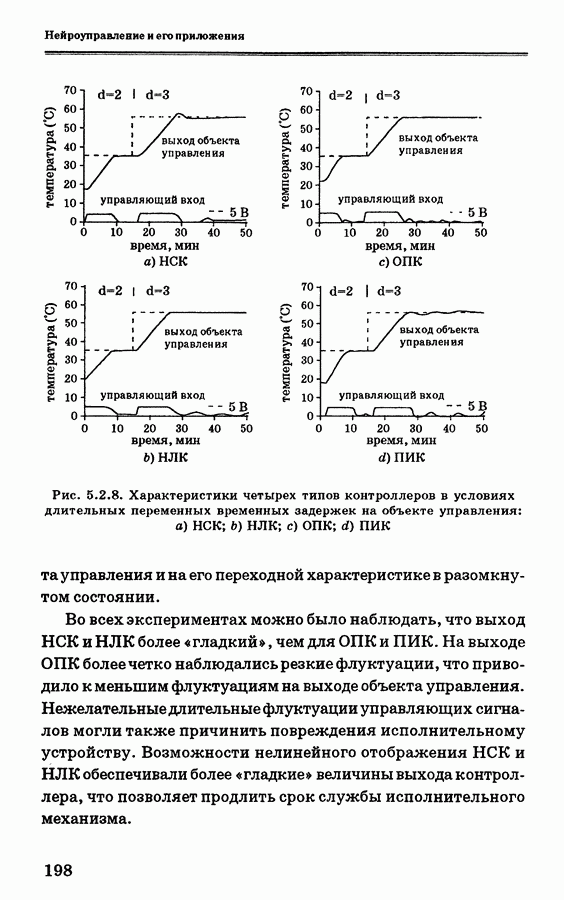
- 5.2.6. Экспериментальные данные и их анализ
- 5.2.7. Заключение
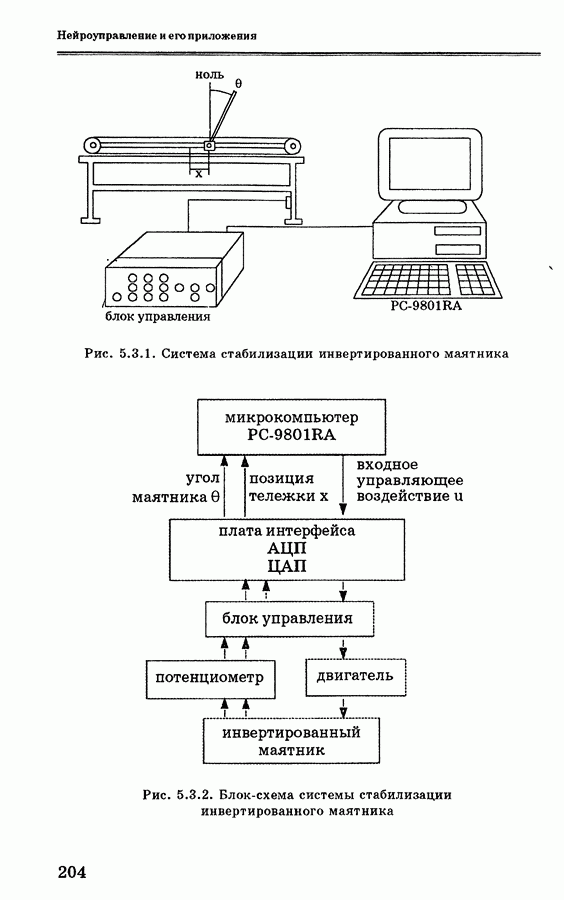
- 5.3. Система стабилизации инвертированного маятника на основе нейронных сетей
- 5.3.2. Система стабилизации инвертированного маятника
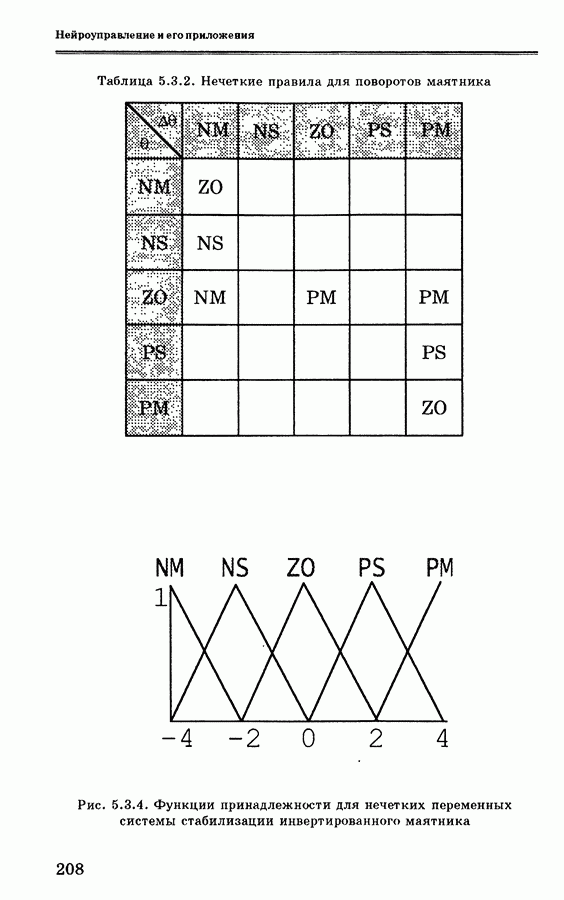
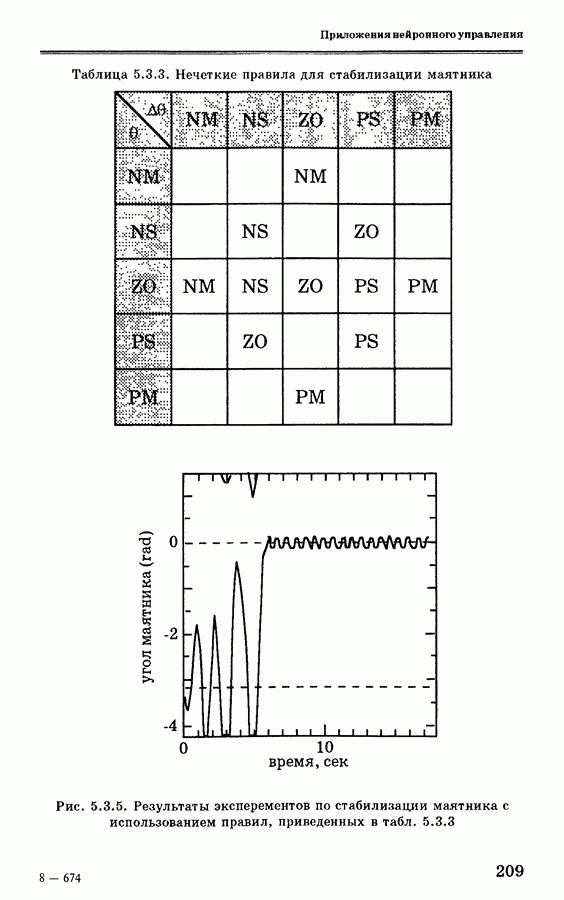
- 5.3.3. Инициализация поворотного управления с использованием нечеткой логики
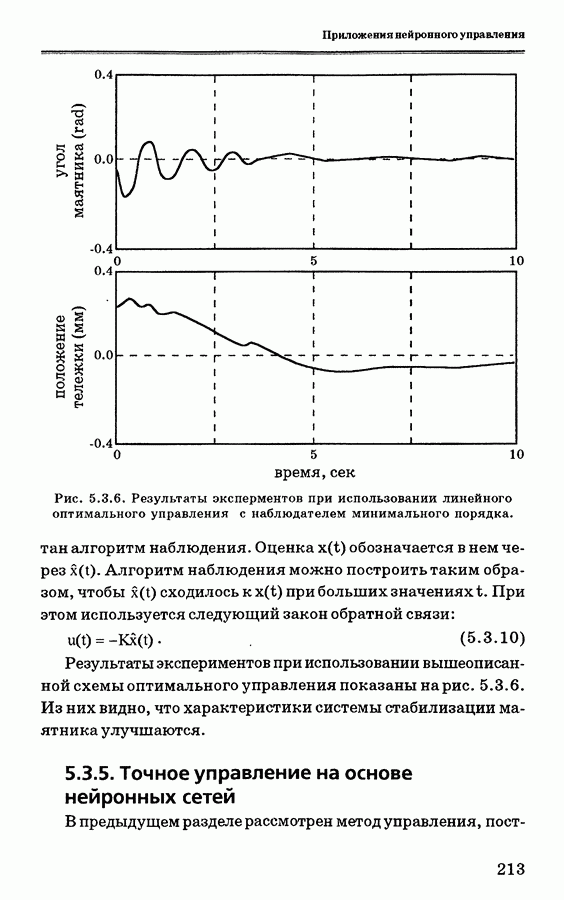
- 5.3.4. Применение стратегии оптимального управления для стабилизации маятника
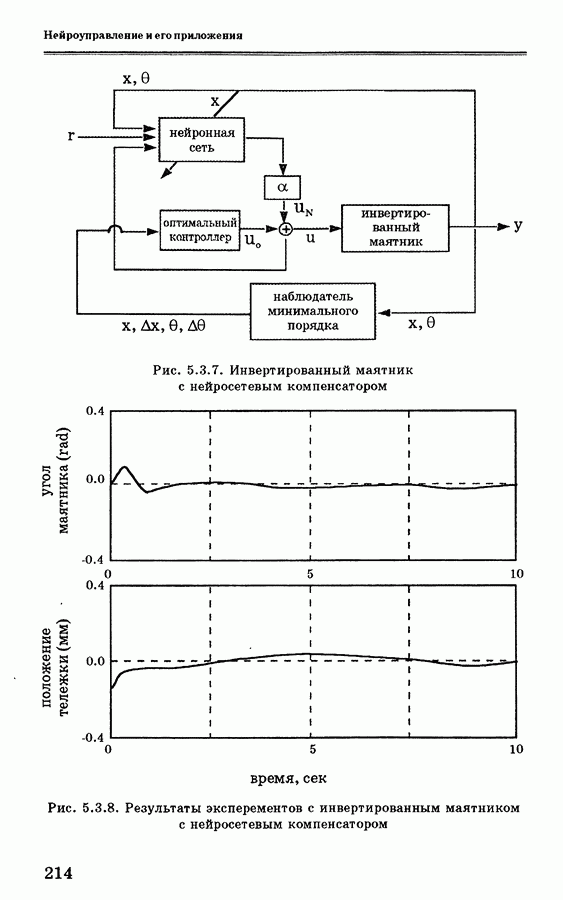
- 5.3.5. Точное управление на основе нейронных сетей
- 5.3.6. Заключение
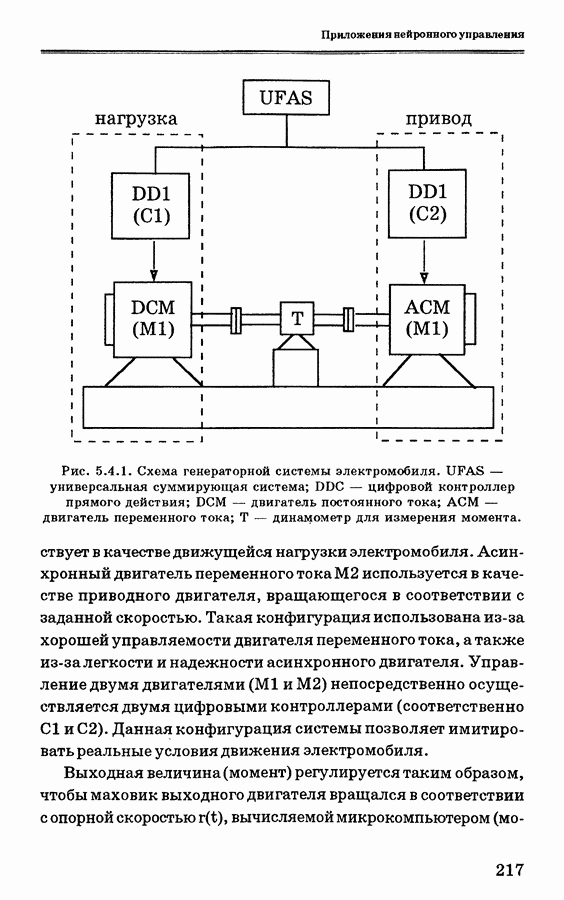
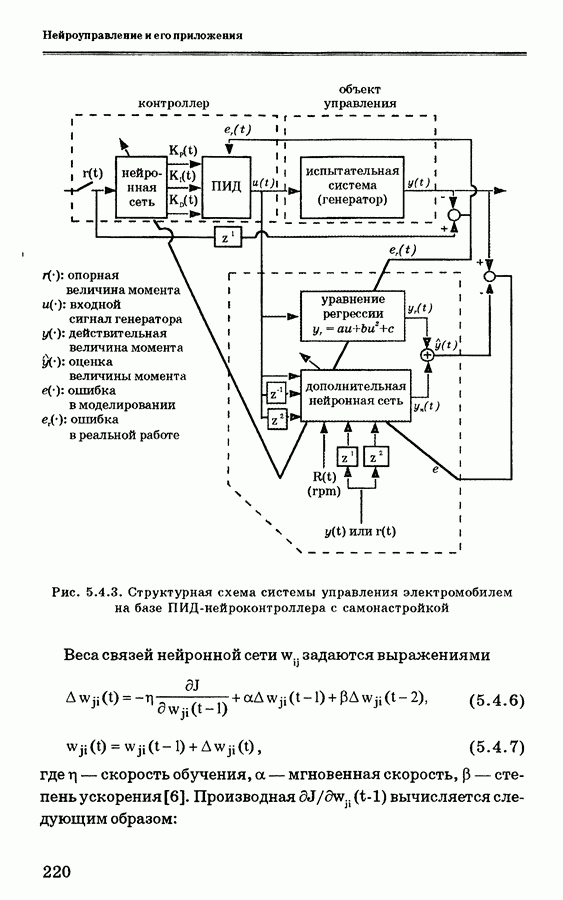
- 5.4. Применение ПИД-нейроконтроллера с самонастройкой для управления скоростью электромобиля
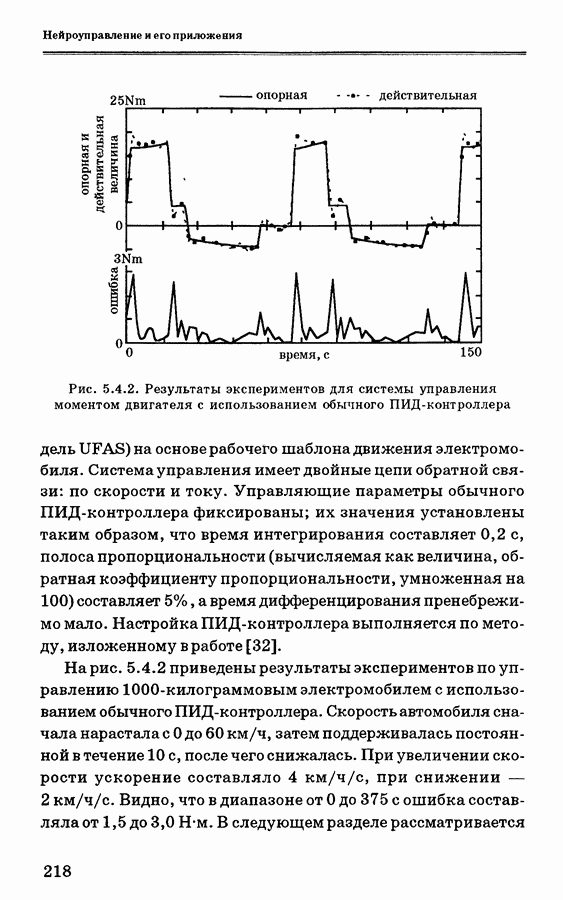
- 5.4.2. Система управления электромобилем
- 5.4.3. ПИД-нейроконтроллер с самонастройкой
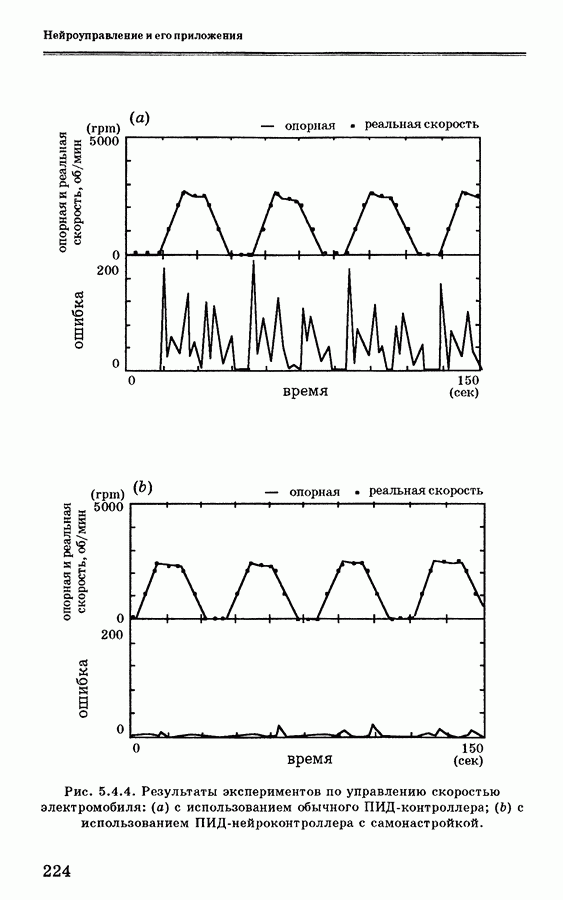
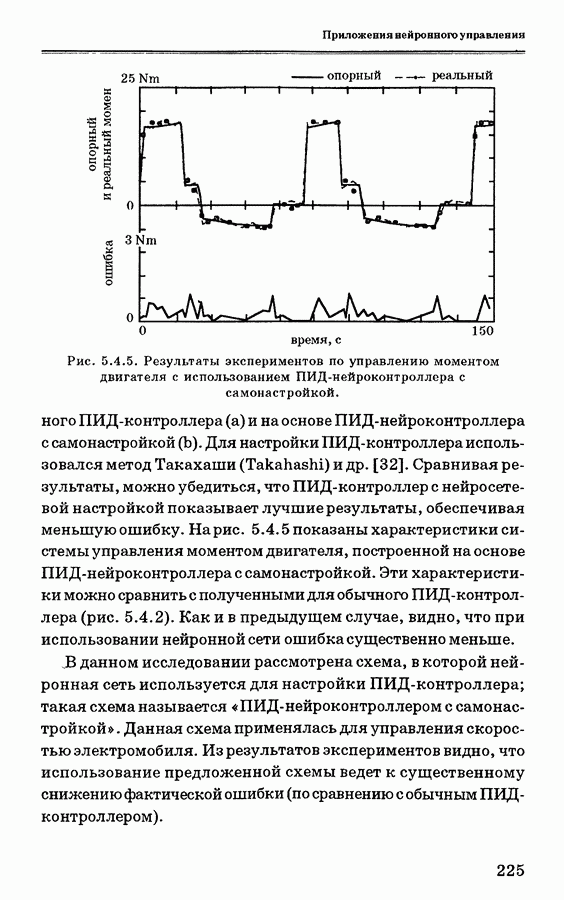
- 5.4.4. Применение нейронной сети для управления скоростью электромобиля
- 5.4.5. Заключение
- 5.5. Применение нейронных сетей для управления печью
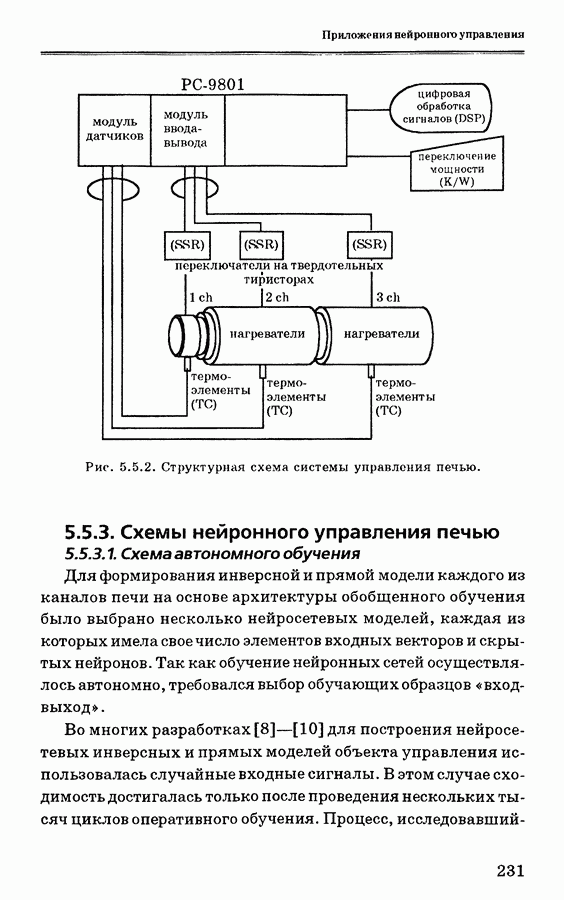
- 5.5.2. Система управления печью
- 5.5.3. Схемы нейронного управления печью
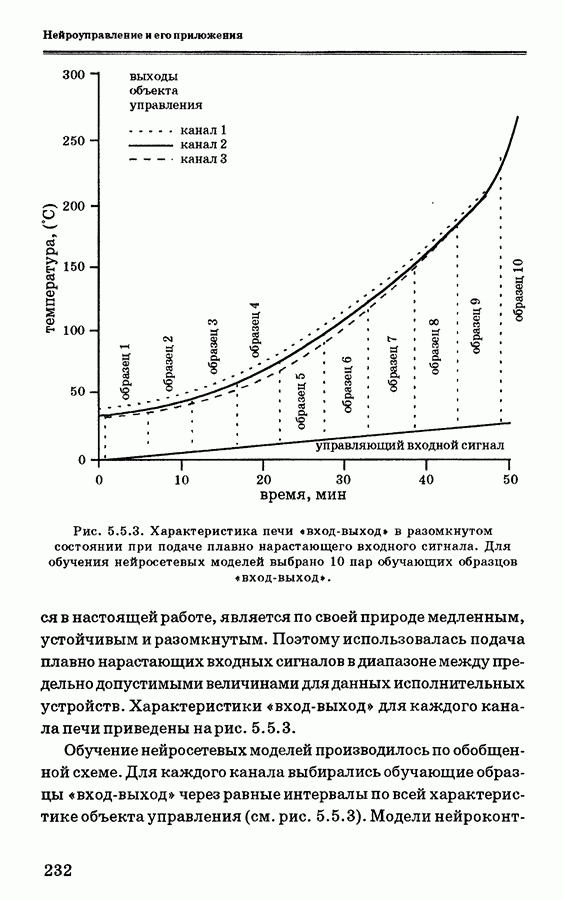
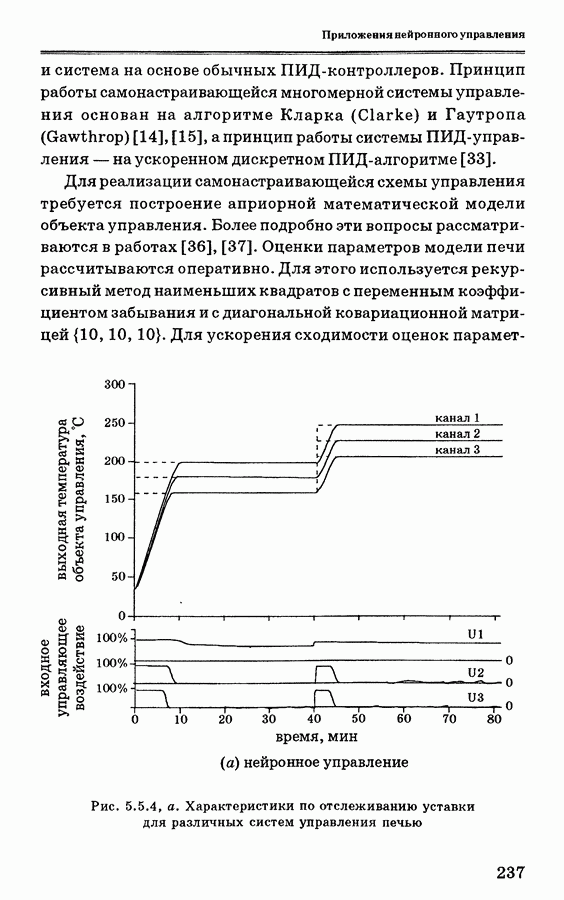
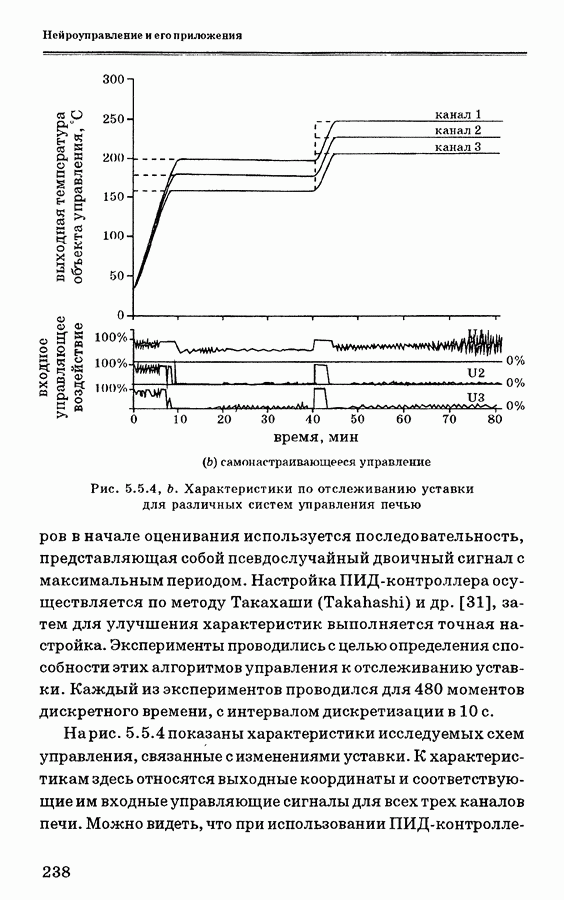
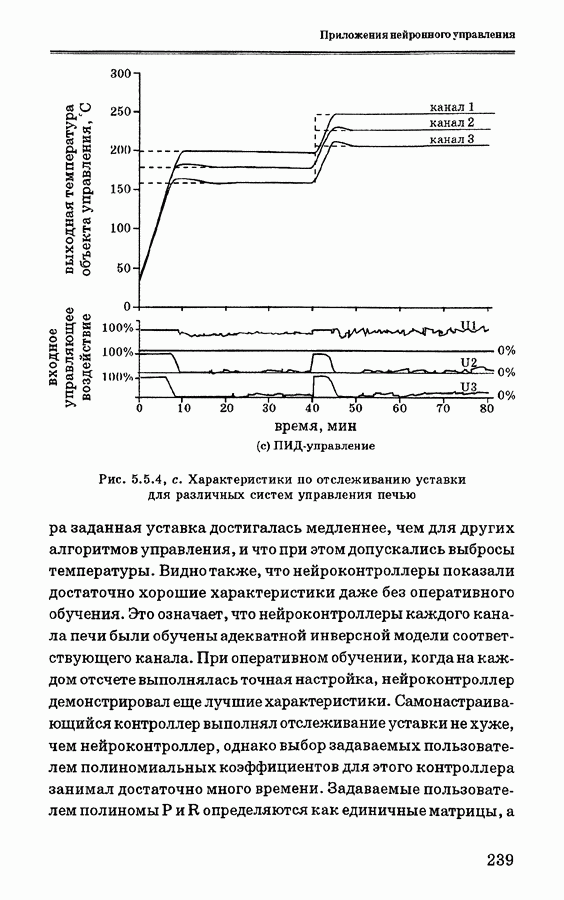
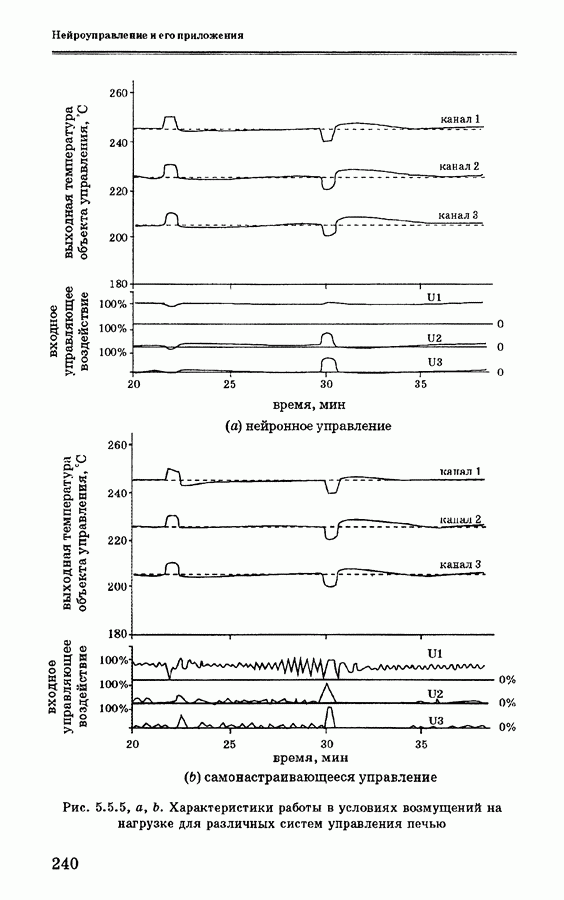
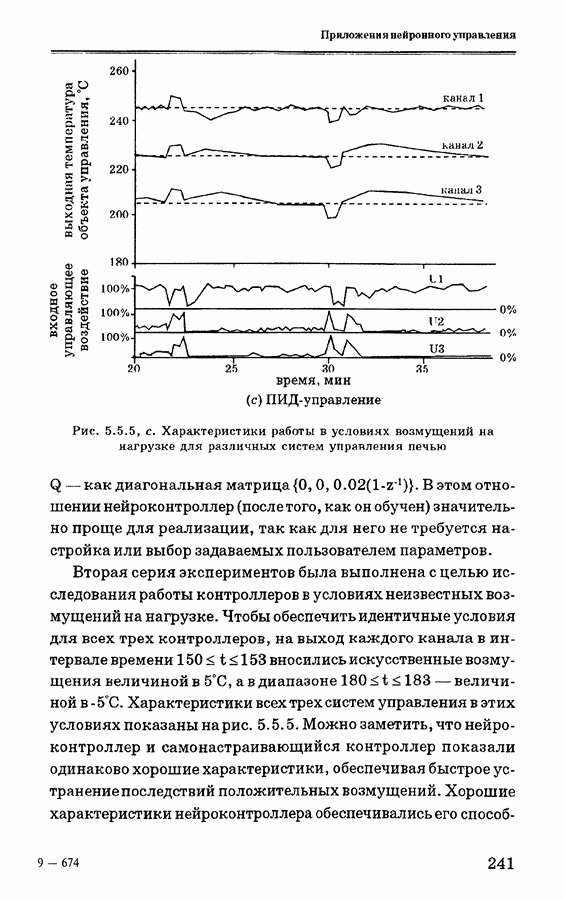
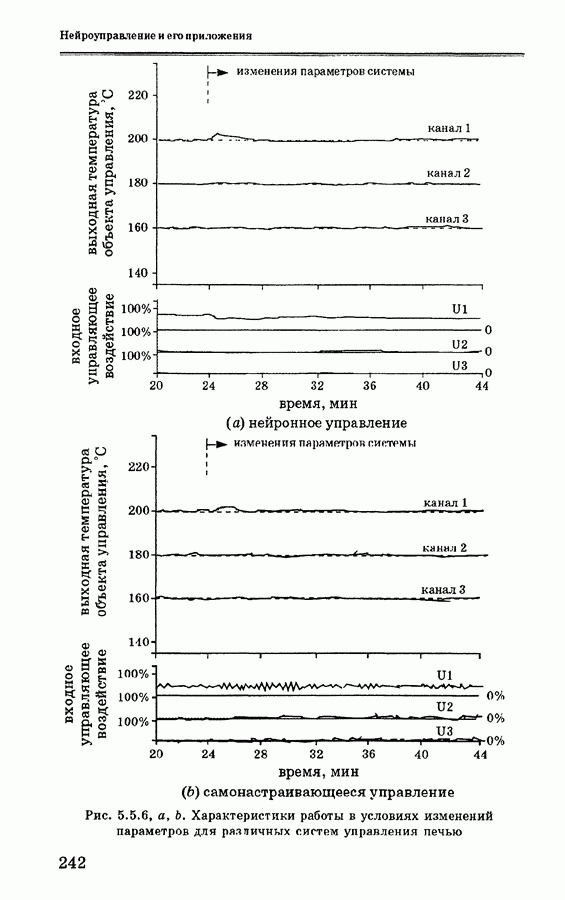
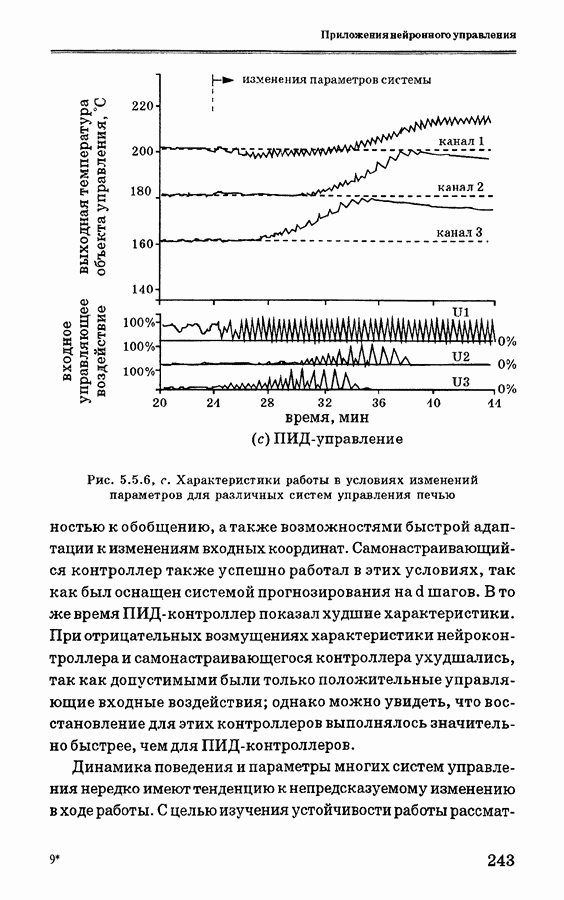
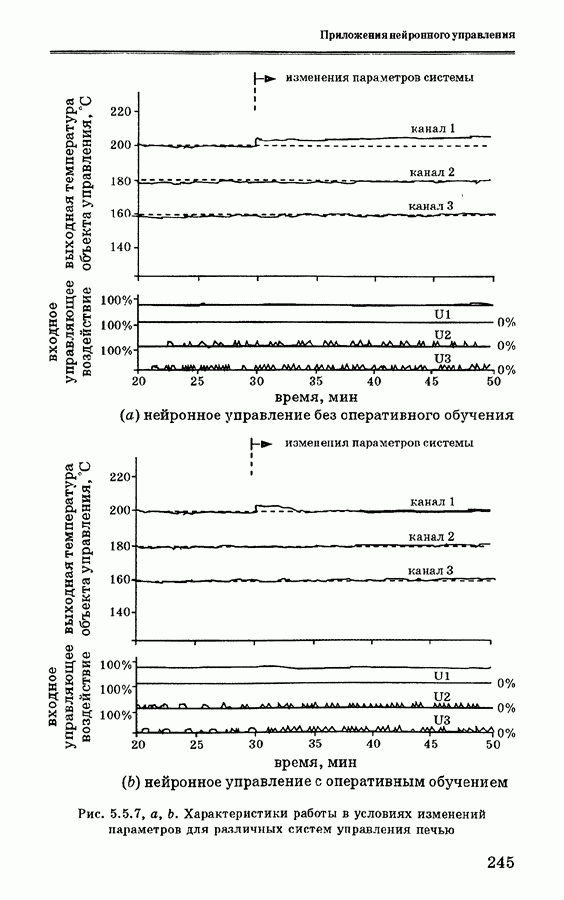
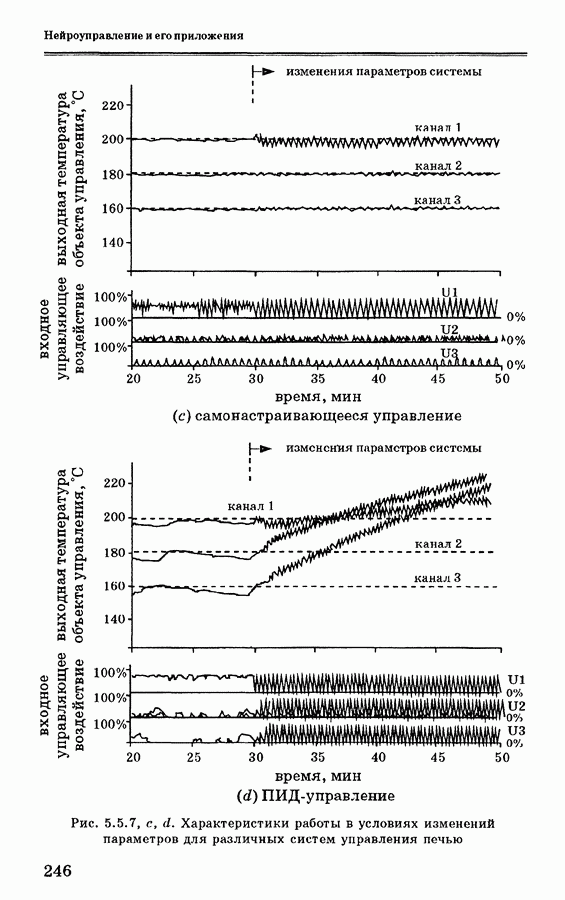
- 5.5.4. Анализ экспериментальных данных
- 5.6. Заключительные замечания и выводы
- Литература
- ЛИСТИНГ ПРОГРАММЫ