| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3.4. Самонастраивающиеся ПИ- и ПИД- контроллеры
Доминирование ПИ- и ПИД-контроллеров среди промышленных регуляторов — основная движущая сила в развитии теории и практики самонастраивающихся ПИ- и ПИД-контроллеров (СНПИ- и СНПИД-контроллеров). Хотя самонастраивающиеся контроллеры обладают большей гибкостью и более приспособлены для управления объектами с переменными параметрами, нелинейностями и неопределенностями, их практическое применение пока не выглядит особенно перспективным.
Самонастраивающиеся регуляторы ориентированы на характеристики: характеристика замкнутой системы задается пользователем и алгоритм настраивается таким образом, чтобы достичь заданной характеристики, даже если параметры объекта управления или величины дрейфа неизвестны. Здесь подразумевается, что желаемая характеристика замкнутой системы управления может быть достигнута при определенных характеристиках исполнительного механизма; критически важным при этом является опыт инженерного персонала объекта управления. В этих условиях для упомянутого персонала крайне желательным является обеспечение как
можно большего интуитивного понимания предельной характеристики замкнутой системы в условиях самонастраивающегося управления. В связи с этим теория самонастраивающихся контроллеров быстро продвигается в направлении расширения диапазона возможных целей управления и их интерпретации в терминах классической теории управления, что упрощает понимание, как целей, так и методов их достижения.
Вывод выражений для СНПИ- и СНПИД-контроллеров [17] может быть получен из комбинации выражений (3.2.5) и (3.3.19). Чтобы закон управления (3.3.19) имел ПИД-струк-туру, аналогичную закону (3.2.5), передаточная функция  должна быть представленаполином второго порядка. Таким образом, порядок полинома
должна быть представленаполином второго порядка. Таким образом, порядок полинома  определяется равенством:
определяется равенством:

считая,что  . Для системы первого порядка ПИД-структура получается, если знаменатель
. Для системы первого порядка ПИД-структура получается, если знаменатель  передаточной функции корректирующего фильтра выбирать в виде полинома второго порядка. Так как полином
передаточной функции корректирующего фильтра выбирать в виде полинома второго порядка. Так как полином  может выбираться пользователем, интегрирующее действие может быть введено следующим выражением:
может выбираться пользователем, интегрирующее действие может быть введено следующим выражением:

где  — константа.
— константа.
Установившуюся ошибку можно устранить, положив:

Используя уравнения (3.4.2) и (3.4.3), выражение (3.3.18) можно записать в форме:

что представляет собой закон управления для самонастраивающегося контроллера с ПИД-структурой. Выражения для соответствующих параметров ПИД-контроллера имеют следующий вид:

и

Интересно заметить, что, исходя из соответствующих выражений для ПИД-контроллера, можно ожидать, что коэффициент  будет иметь то же влияние для СНПИД-контроллеров, что и коэффициент
будет иметь то же влияние для СНПИД-контроллеров, что и коэффициент  для ПИД-контроллеров. При небольшой величине
для ПИД-контроллеров. При небольшой величине  управление будет колебательным (осциллирующим). Целесообразно в качестве фильтра
управление будет колебательным (осциллирующим). Целесообразно в качестве фильтра  использовать дифференцирующее звено. Здесь подразумевается, что замкнутая система представляет собой фильтр нижних частот. Величины
использовать дифференцирующее звено. Здесь подразумевается, что замкнутая система представляет собой фильтр нижних частот. Величины  выбираются в основном методом проб и ошибок. Обоснованный подход к выбору этих параметров состоит в следующем: выбрать величину
выбираются в основном методом проб и ошибок. Обоснованный подход к выбору этих параметров состоит в следующем: выбрать величину  таким образом, чтобы характеристика замкнутой системы была стабильной и не слишком осциллирующей, а затем варьировать величины
таким образом, чтобы характеристика замкнутой системы была стабильной и не слишком осциллирующей, а затем варьировать величины  так, чтобы добиться достаточной эффективности системы.
так, чтобы добиться достаточной эффективности системы.
Программная реализация СНПИД-контроллера для каждого момента дискретизации может быть представлена следующим образом.
Вычисления СНПИД-контроллера:
Шаг 1, Установить опорный входной сигнал.
Шаг 2. Прочитать входные и выходные данные.
Шаг 3. Задать начальные значения коэффициентов  и
и
Шаг 4. Выполнить вычисления по формулам (3.3.22), (3.3.23), (3.3.24).
Шаг 5. Определить управляющее воздействие по формуле (3.4.4).
Шаг 6. Рассчитать ПИД-параметры по выражениям 
3.4.1. Замкнутая система
Замкнутая система с СНПИ- или СНПИД-контроллером описывается уравнением

где  — возмущающее воздействие на процесс. Очевидно, что полиномы корректирующего фильтра
— возмущающее воздействие на процесс. Очевидно, что полиномы корректирующего фильтра  будут оказывать некоторое влияние на замкнутую систему. Можно также видеть, что для постоянного опорного сигнала достигается точное асимптотическое отслеживание, если выполняется условие:
будут оказывать некоторое влияние на замкнутую систему. Можно также видеть, что для постоянного опорного сигнала достигается точное асимптотическое отслеживание, если выполняется условие:

что соответствует условию (3.4.3). Отметим также, что в установившемся режиме слагаемое, соответствующее возмущению, равно нулю. Это означает, что замкнутая система может парировать действие возмущения.
3.4.2. Пример моделирования
В большинстве систем управления требуется задавать предварительно некоторые параметры настройки. Для СНПИ- и СНПИД-контроллеров параметрами настройки являются  Они играют важную роль в регулировке
Они играют важную роль в регулировке
характеристик замкнутой системы, поскольку относятся к контролируемым параметрам. Для ПИ- и ПИД-контроллеров параметры  и
и  также требуется выбирать, хотя они и остаются неизменными до тех пор, пока на управляемом объекте не произойдут какие-либо существенные изменения, что может потребовать перенастройки параметров.
также требуется выбирать, хотя они и остаются неизменными до тех пор, пока на управляемом объекте не произойдут какие-либо существенные изменения, что может потребовать перенастройки параметров.
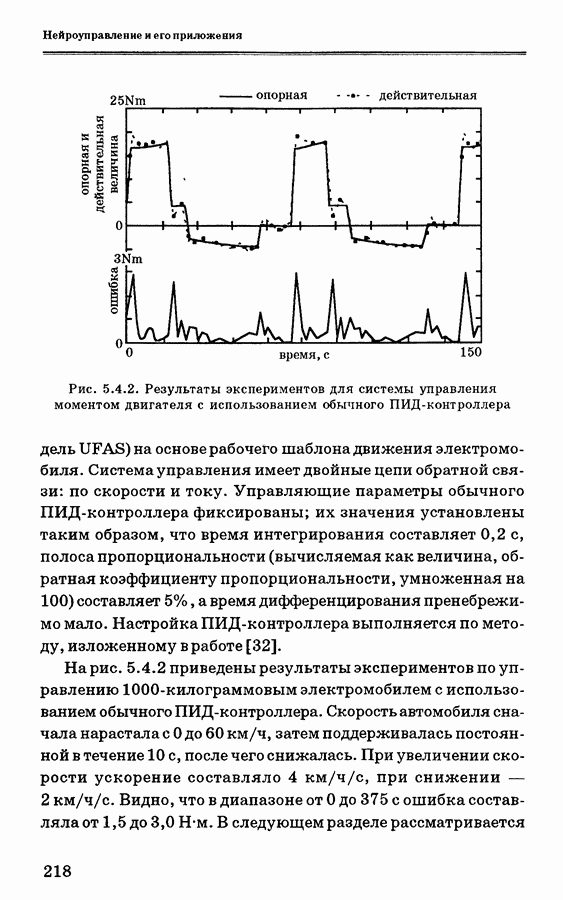
В данном разделе приводятся результаты имитационного моделирования, которые предназначены помочь в выборе параметров настройки СНПИ- и СНПИД-контроллеров. В этих примерах проводятся некоторые исследования свойств и роли параметров настройки. Для сравнения сданными, полученными для СНПИ- и СНПИД-контроллеров, приводится также несколько примеров моделирования с использованием ПИ- и ПИД-контроллеров с постоянными параметрами. Примеры моделирования получены для 300 дискретных моментов времени. Для оценки параметров использовался метод наименьших квадратов; в качестве ковариационной матрицы была выбрана единичная матрица, умноженная на число 10. Значение коэффициента отсутствия последействия было выбрано равным единице.
В данном примере рассматривается непрерывная система второго порядка с запаздывающим звеном. Передаточная функция системы задается выражением:

Проведя дискретизацию соответствующего дифференциального уравнения с интервалом квантования в 0.5 с. и применив z-преобразование для полученного уравнения, получим z-передаточную функцию в виде:

Во временной области данной передаточной функции соответствует уравнение:

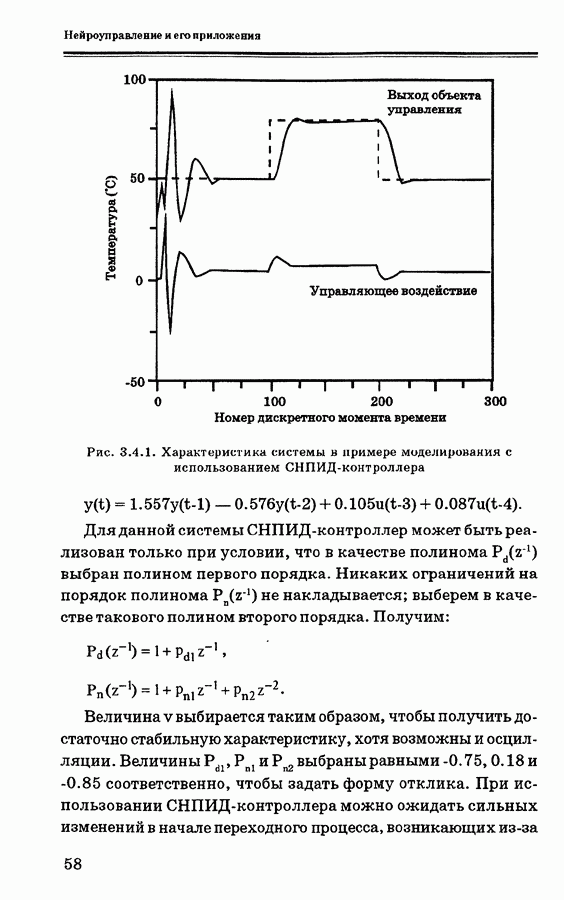
Рис. 3.4.1. Характеристика системы в иримере моделирования с использованием СНПИД-контроллера

Для данной системы СНПИД-контроллер может быть реализован только при условии, что в качестве полинома  выбран полином первого порядка. Никаких ограничений на порядок полинома
выбран полином первого порядка. Никаких ограничений на порядок полинома  не накладывается; выберем в качестве такового полином второго порядка. Получим:
не накладывается; выберем в качестве такового полином второго порядка. Получим:

Величина  выбирается таким образом, чтобы получить достаточно стабильную характеристику, хотя возможны и осцилляции. Величины
выбирается таким образом, чтобы получить достаточно стабильную характеристику, хотя возможны и осцилляции. Величины  выбраны равными
выбраны равными  соответственно, чтобы задать форму отклика. При использовании СНПИД-контроллера можно ожидать сильных изменений в начале переходного процесса, возникающих из-за
соответственно, чтобы задать форму отклика. При использовании СНПИД-контроллера можно ожидать сильных изменений в начале переходного процесса, возникающих из-за

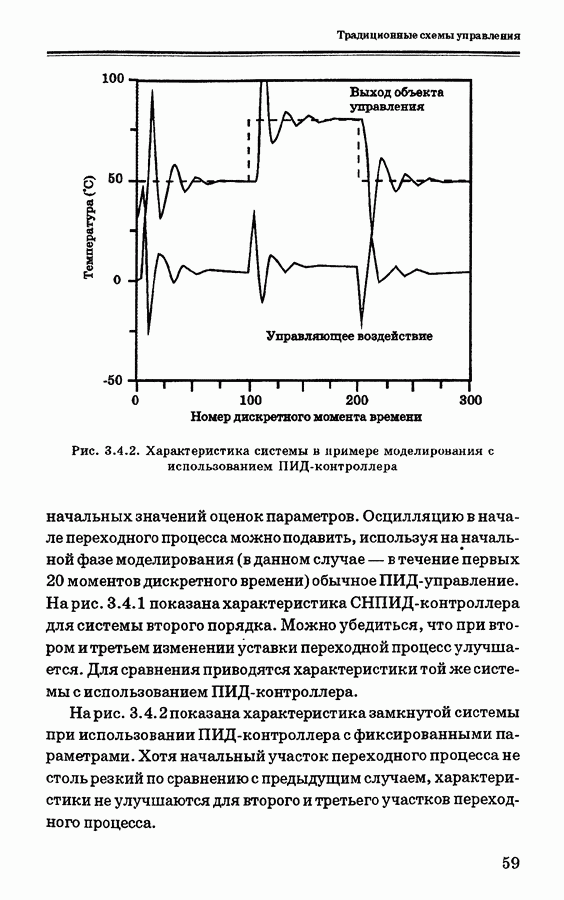
Рис. 3.4.2. Характеристика системы в примере моделирования с использованием ПИД-контроллера
начальных значений оценок параметров. Осцилляцию в начале переходного процесса можно подавить, используя на начальной фазе моделирования (в данном случае — в течение первых
20 моментов дискретного времени) обычное ПИД-управление. На рис. 3.4.1 показана характеристика СНПИД-контроллера для системы второго порядка. Можно убедиться, что при втором и третьем изменении уставки переходной процесс улучшается. Для сравнения приводятся характеристики той же системы с использованием ПИД-контроллера.
На рис. 3.4.2 показана характеристика замкнутой системы при использовании ПИД-контроллера с фиксированными параметрами. Хотя начальный участок переходного процесса не столь резкий по сравнению с предыдущим случаем, характеристики не улучшаются для второго и третьего участков переходного процесса.

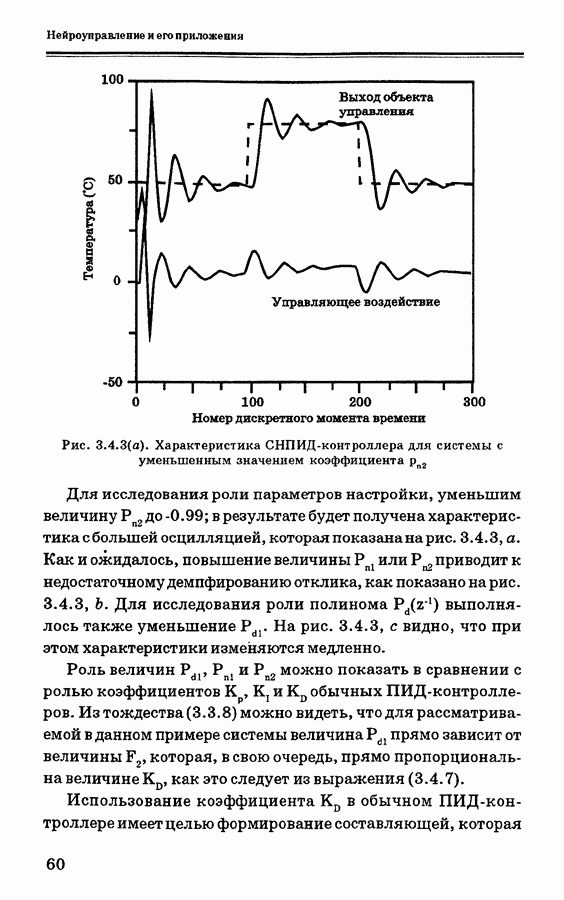
Рис. 3.4.3(a). Характеристика СНПИД-контроллера для системы с уменьшенным значением коэффициента 
Для исследования роли параметров настройки, уменьшим величину  до -0.99; в результате будет получена характеристика с большей осцилляцией, которая показана на рис. 3.4.3, а. Как и ожидалось, повышение величины
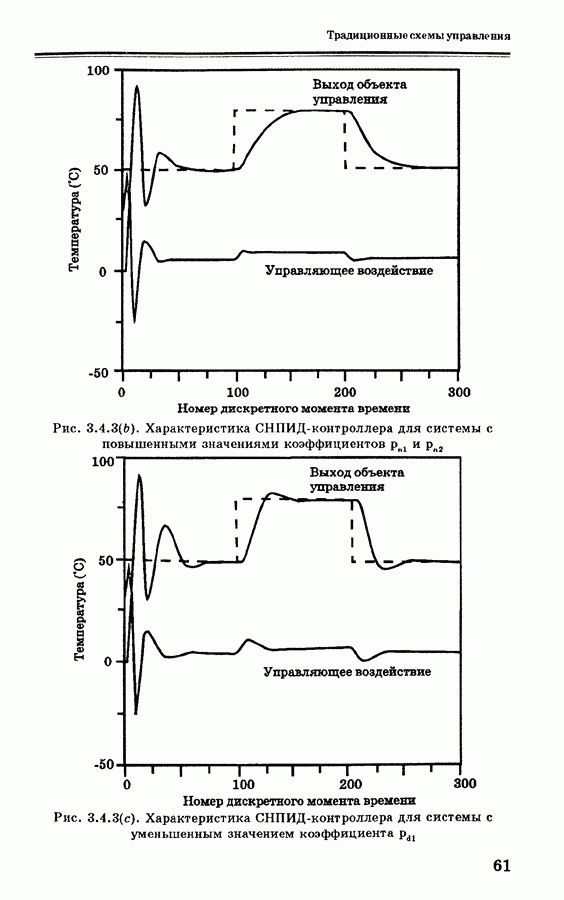
до -0.99; в результате будет получена характеристика с большей осцилляцией, которая показана на рис. 3.4.3, а. Как и ожидалось, повышение величины  или Р приводит к недостаточному демпфированию отклика, как показано на рис. 3.4.3, b. Для исследования роли полинома
или Р приводит к недостаточному демпфированию отклика, как показано на рис. 3.4.3, b. Для исследования роли полинома  выполнялось также уменьшение
выполнялось также уменьшение  На рис. 3.4.3, с видно, что при этом характеристики изменяются медленно.
На рис. 3.4.3, с видно, что при этом характеристики изменяются медленно.
Роль величин  можно показать в сравнении с ролью коэффициентов
можно показать в сравнении с ролью коэффициентов  и
и  обычных ПИД-контроллеров. Из тождества (3.3.8) можно видеть, что для рассматриваемой в данном примере системы величина
обычных ПИД-контроллеров. Из тождества (3.3.8) можно видеть, что для рассматриваемой в данном примере системы величина  прямо зависит от величины
прямо зависит от величины  которая, в свою очередь, прямо пропорциональна величине
которая, в свою очередь, прямо пропорциональна величине  как это следует из выражения (3.4.7).
как это следует из выражения (3.4.7).
Использование коэффициента  в обычном ПИД-контроллере имеет целью формирование составляющей, которая
в обычном ПИД-контроллере имеет целью формирование составляющей, которая

(кликните для просмотра скана)
содержит информацию о направлении развития процесса. Из приведенных выше результатов моделирования видно, что действия коэффициентов  и
и  аналогичны. Параметры настройки
аналогичны. Параметры настройки  оказывают некоторое влияние на параметры
оказывают некоторое влияние на параметры  как это следует из выражений (3.3.8), (3.4.5) и (3.4.6).
как это следует из выражений (3.3.8), (3.4.5) и (3.4.6).
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРОВ ПЕРЕВОДА
- 1. ВВЕДЕНИЕ
- 1.1. Общие сведения об интеллектуальном управлении
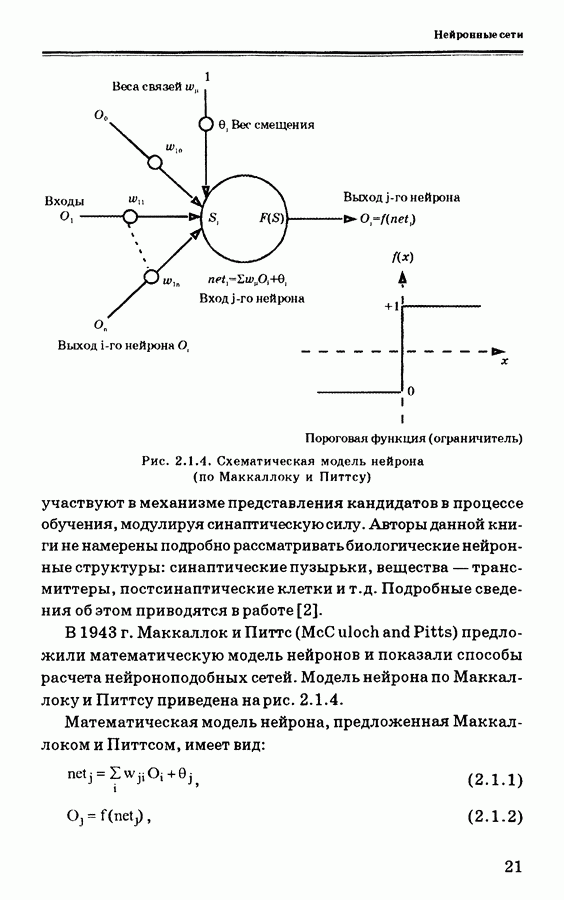
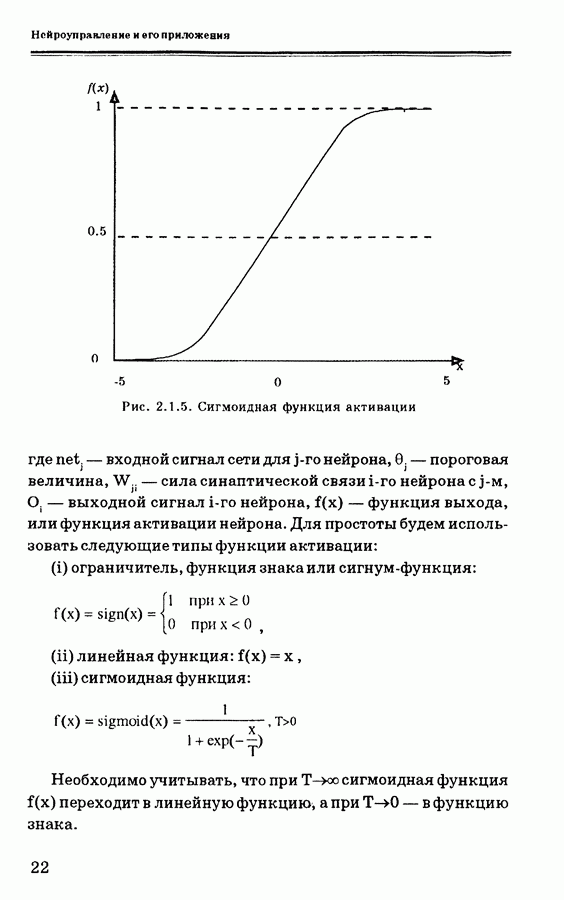
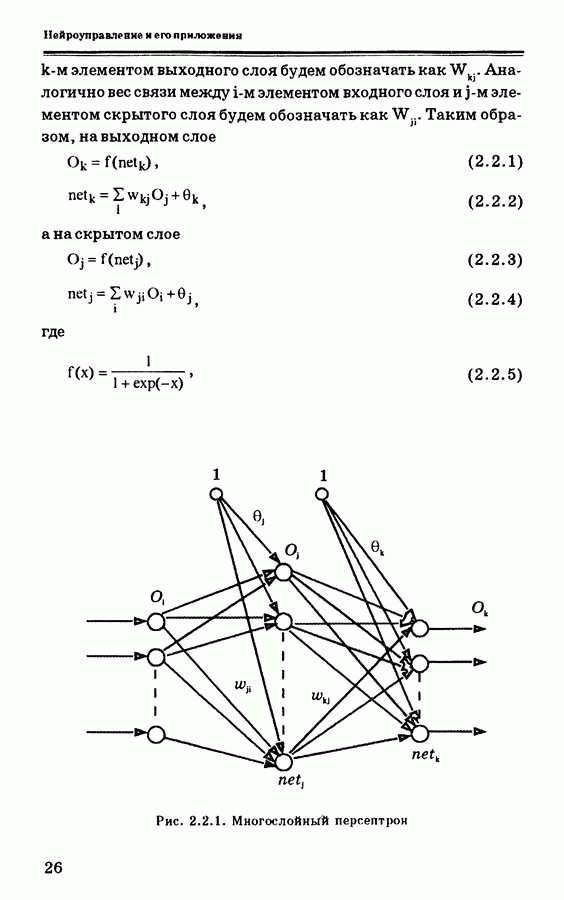
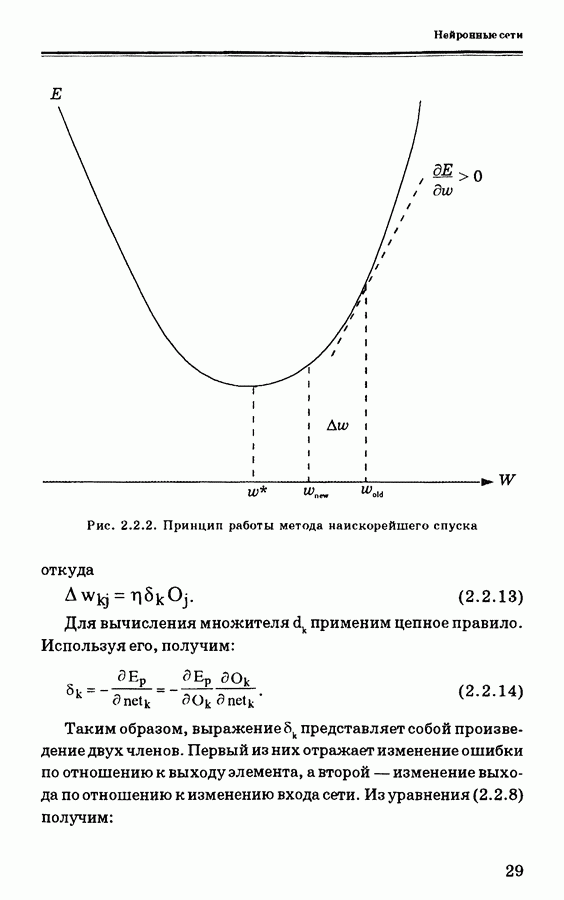
- 2. НЕЙРОННЫЕ СЕТИ
- 2.2. Алгоритм обратного распространения
- 2.2.2. Вывод алгоритма обратного распространения
- 2.2.2.2. Правило для скрытого слоя
- 2.2.3. Алгоритм обратного распространения: порядок реализации
- 2.2.4. Обсуждение алгоритма обратного распространения
- 2.3. Заключение
- 3. ТРАДИЦИОННЫЕ СХЕМЫ УПРАВЛЕНИЯ
- 3.2. ПИ- и ПИД-контроллеры с дискретным временем
- 3.3. Управление с самонастройкой
- 3.4. Самонастраивающиеся ПИ- и ПИД- контроллеры
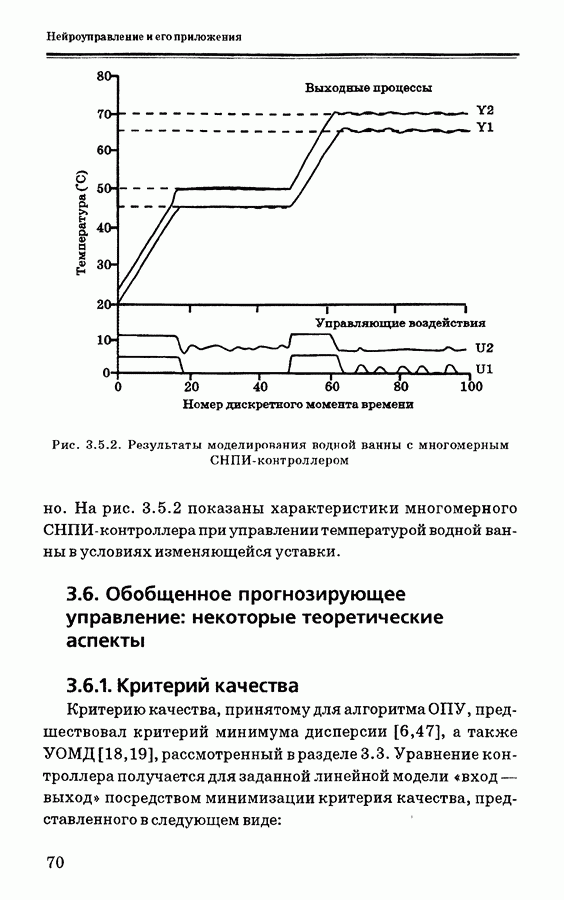
- 3.5. ПИД-управление с самонастройкой: многомерный подход
- 3.5.1. Пример моделирования
- 3.6. Обобщенное прогнозирующее управление: некоторые теоретические аспекты
- 3.6.2. Модель объекта управления и решение задачи оптимизации
- 3.7. Управление на основе нечеткой логики
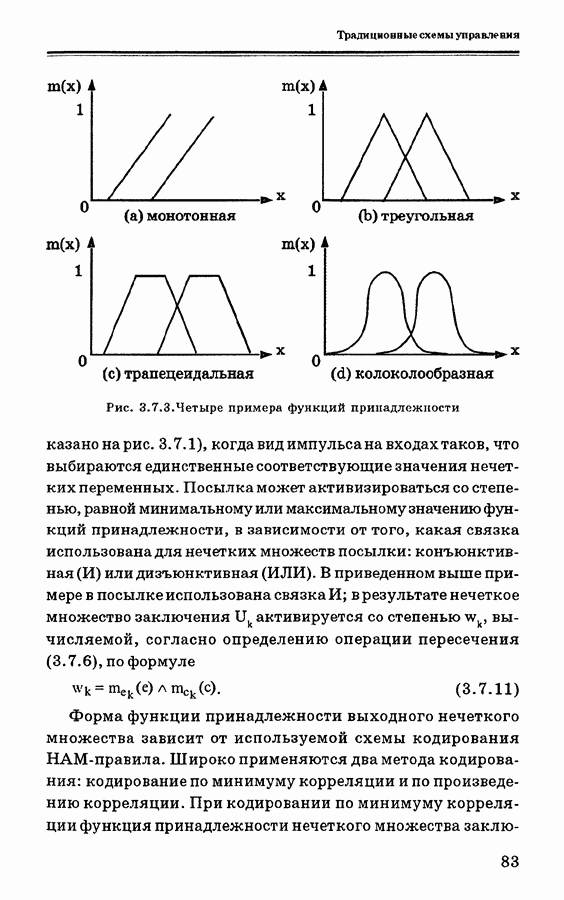
- 3.7.1. Краткие сведения по теории нечетких множеств и нечетких систем
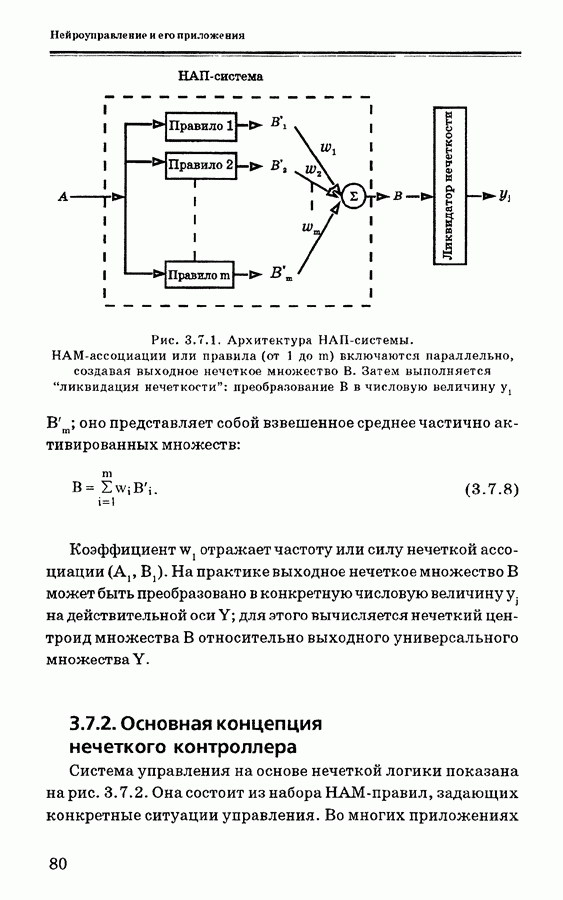
- 3.7.2. Основная концепция нечеткого контроллера
- 3.8. Заключение
- 4. ТЕХНОЛОГИИ НЕЙРОННОГО УПРАВЛЕНИЯ
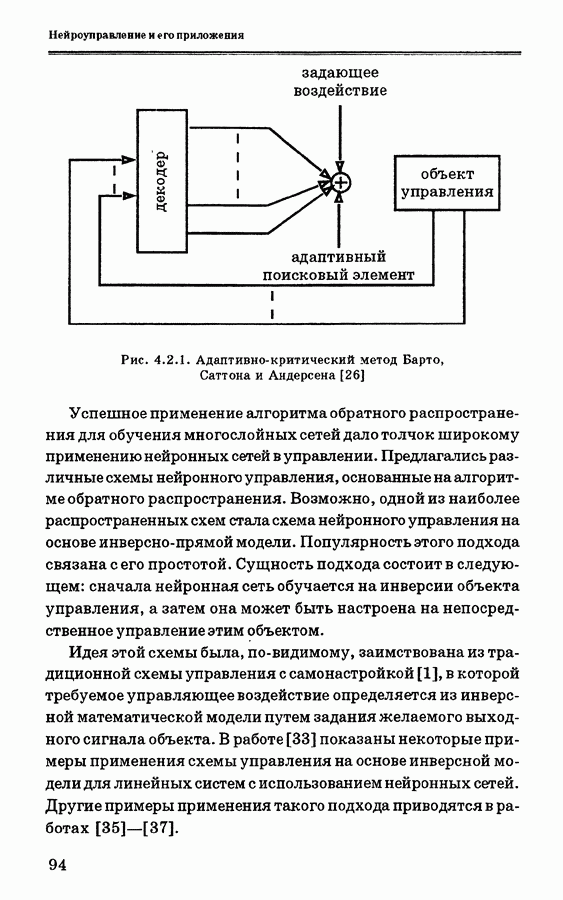
- 4.2. Общие сведения о нейронном управлении
- 4.2.1. Подходы к нейронному управлению
- 4.2.2. Общая схема управления
- 4.3. Последовательная схема нейронного управления
- 4.4. Расширение последовательной схемы нейронного управления
- 4.4.2. Нейроморфные структуры управления
- 4.4.3. Конфигурации обучения
- 4.4.4. Эффективное оперативное управление
- 4.4.5. Алгоритмы обучения
- 4.4.6. Оценка алгоритмов обучения на основе моделирования
- 4.5. Параллельная схема управления
- 4.6. Алгоритм обучения по ошибке обратной связи
- 4.7. Расширение применения нейроконтроллеров параллельного типа
- 4.7.2. Линеаризованная система управления
- 4.7.3. Система управления с нейронными сетями
- 4.7.4. Нелинейный алгоритм наблюдения для нейронной сети
- 4.7.5. Нелинейный контроллер для нейронной сети
- 4.7.6. Численное моделирование
- 4.8. Схема нейронного управления с самонастройкой
- 4.9. ПИД-нейроконтроллер с самонастройкой
- 4.9.1. Вывод уравнений ПИД-нейроконтроллера с самонастройкой
- 4.9.2. Примеры эмуляции
- 4.10. Схема нейронного управления с эмулятором и контроллером (схема обратного распространения во времени)
- 4.11. Заключение
- 5. ПРИЛОЖЕНИЯ НЕЙРОННОГО УПРАВЛЕНИЯ
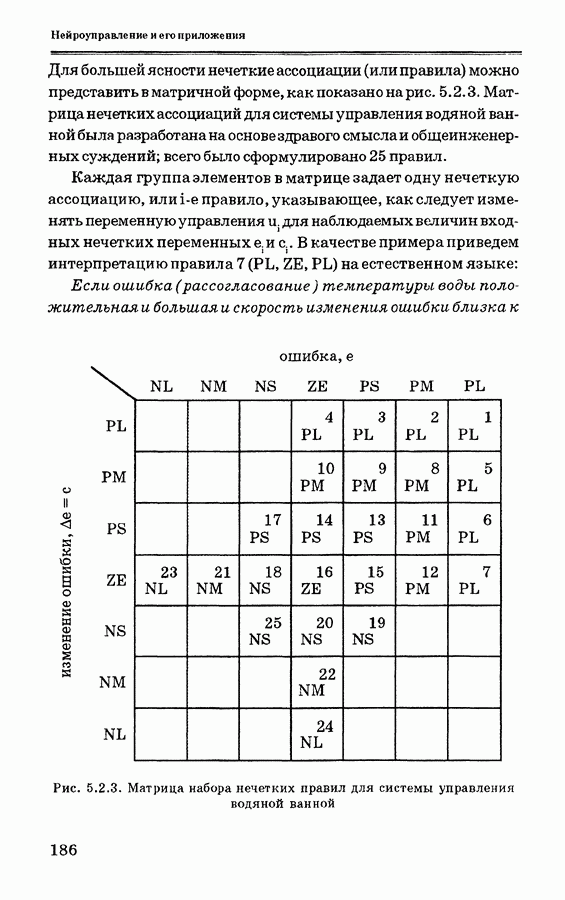
- 5.2. Применение нейронного управления в системе регулирования процессов в водяной ванне и сравнение его с другими схемами управления
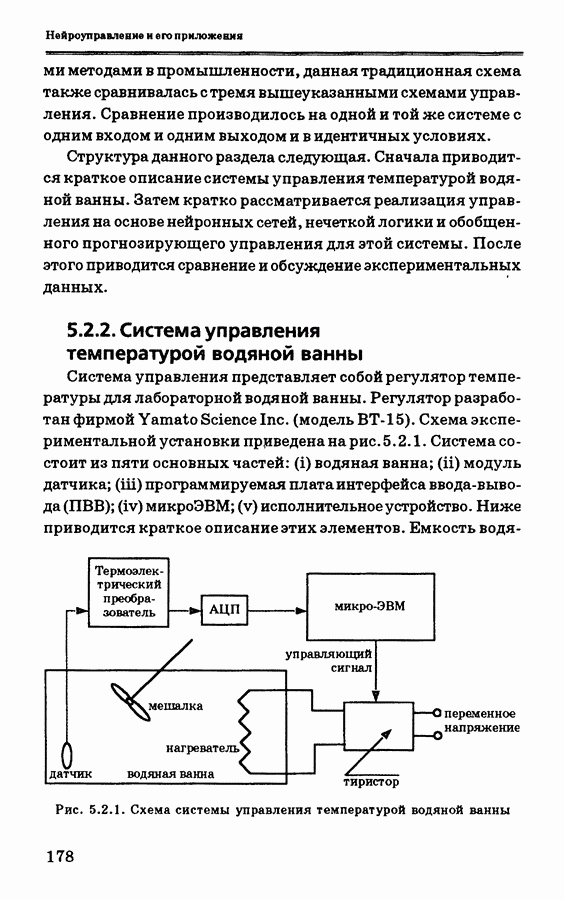
- 5.2.2. Система управления температурой водяной ванны
- 5.2.3. Схема нейронного управления
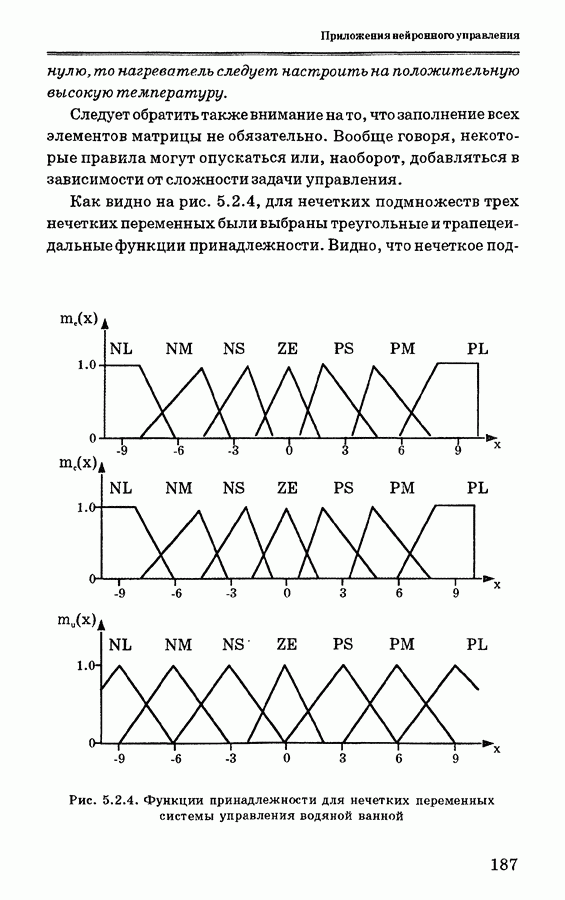
- 5.2.4. Схема управления на основе нечеткой логики
- 5.2.5. Схема обобщенного прогнозирующего управления
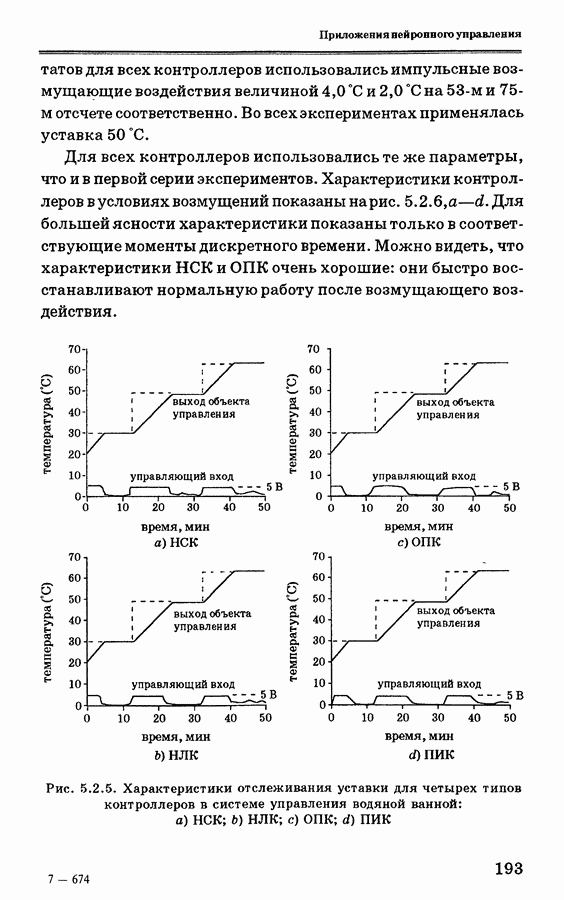
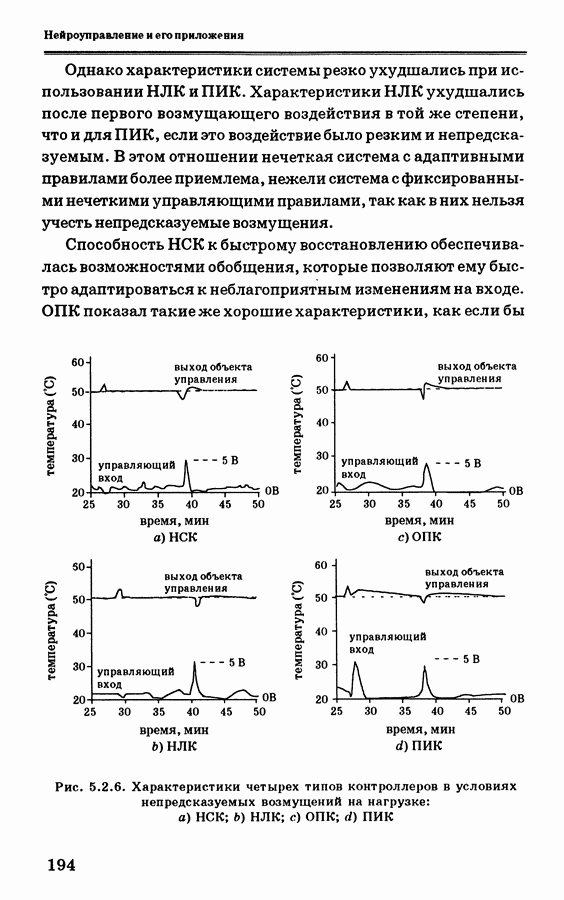
- 5.2.6. Экспериментальные данные и их анализ
- 5.2.7. Заключение
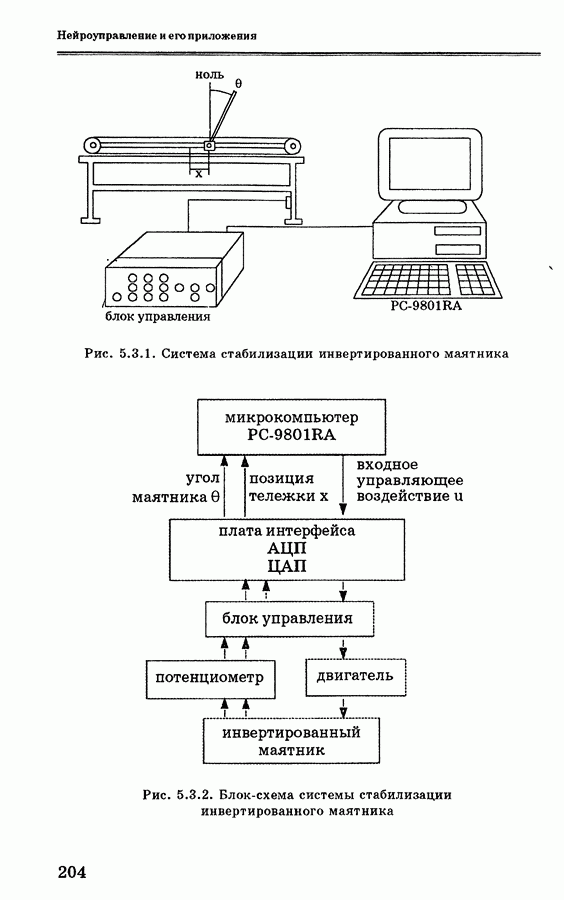
- 5.3. Система стабилизации инвертированного маятника на основе нейронных сетей
- 5.3.2. Система стабилизации инвертированного маятника
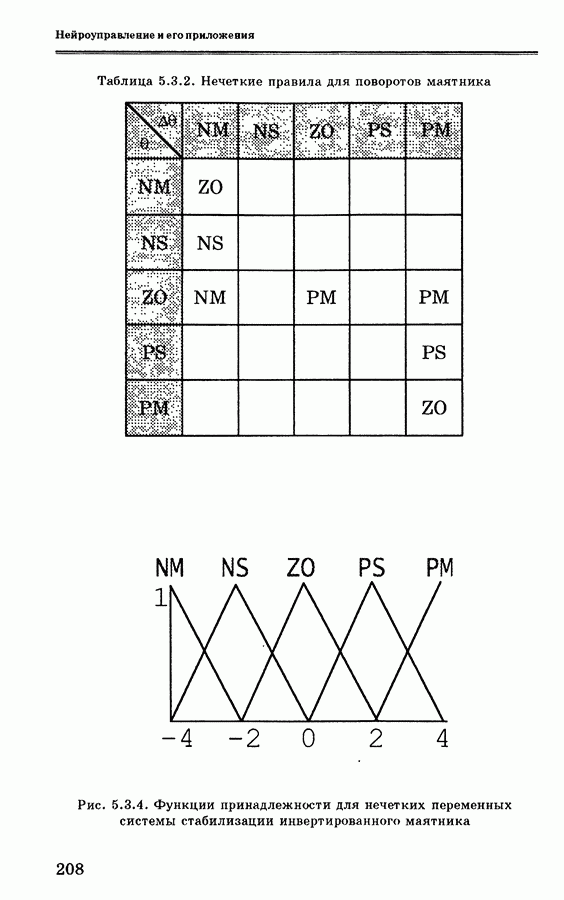
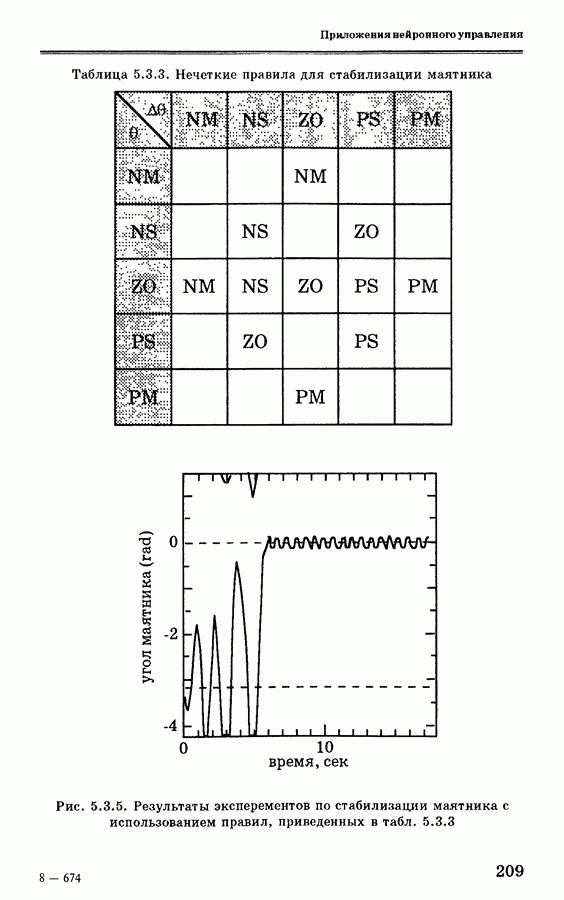
- 5.3.3. Инициализация поворотного управления с использованием нечеткой логики
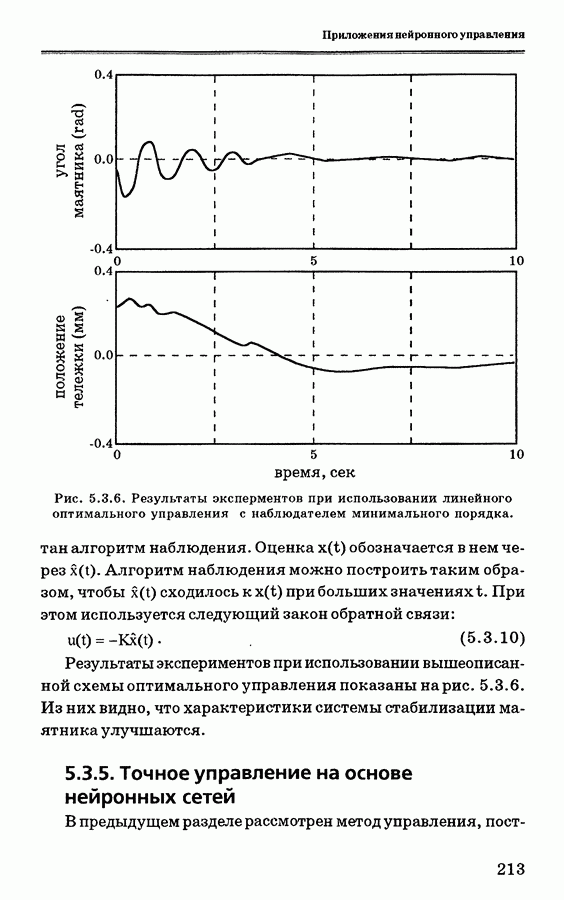
- 5.3.4. Применение стратегии оптимального управления для стабилизации маятника
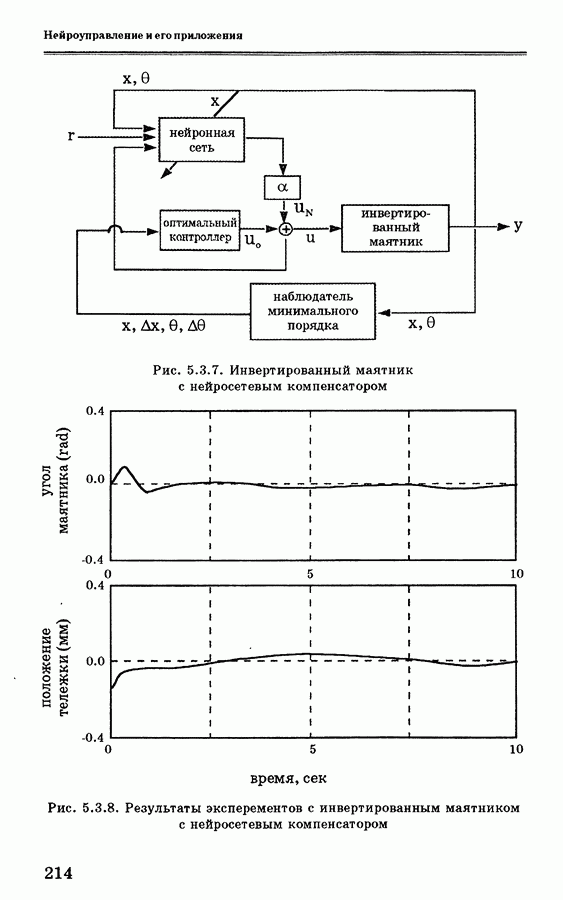
- 5.3.5. Точное управление на основе нейронных сетей
- 5.3.6. Заключение
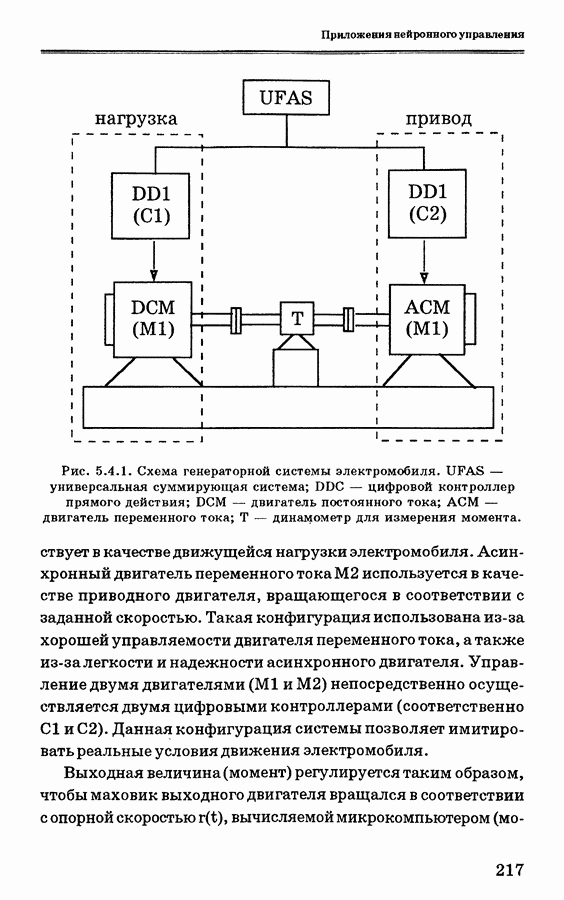
- 5.4. Применение ПИД-нейроконтроллера с самонастройкой для управления скоростью электромобиля
- 5.4.2. Система управления электромобилем
- 5.4.3. ПИД-нейроконтроллер с самонастройкой
- 5.4.4. Применение нейронной сети для управления скоростью электромобиля
- 5.4.5. Заключение
- 5.5. Применение нейронных сетей для управления печью
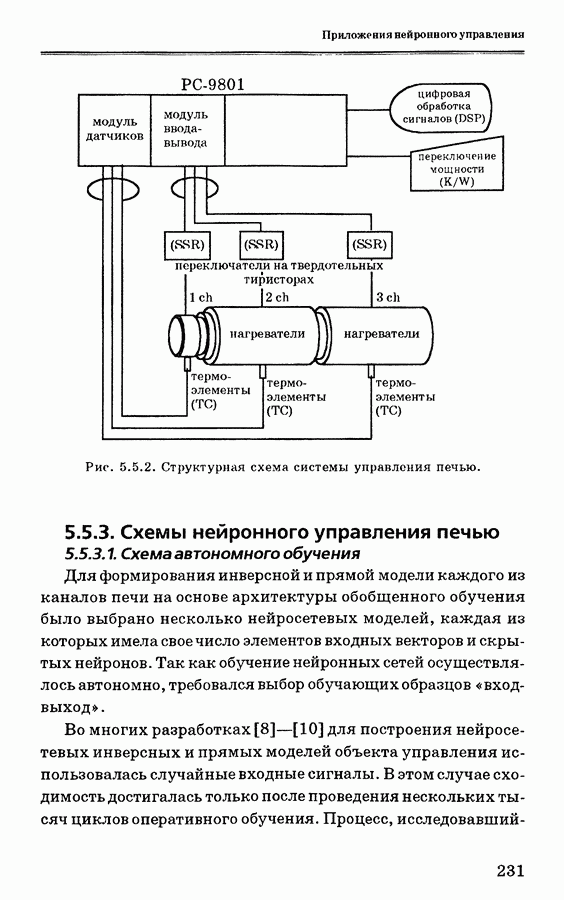
- 5.5.2. Система управления печью
- 5.5.3. Схемы нейронного управления печью
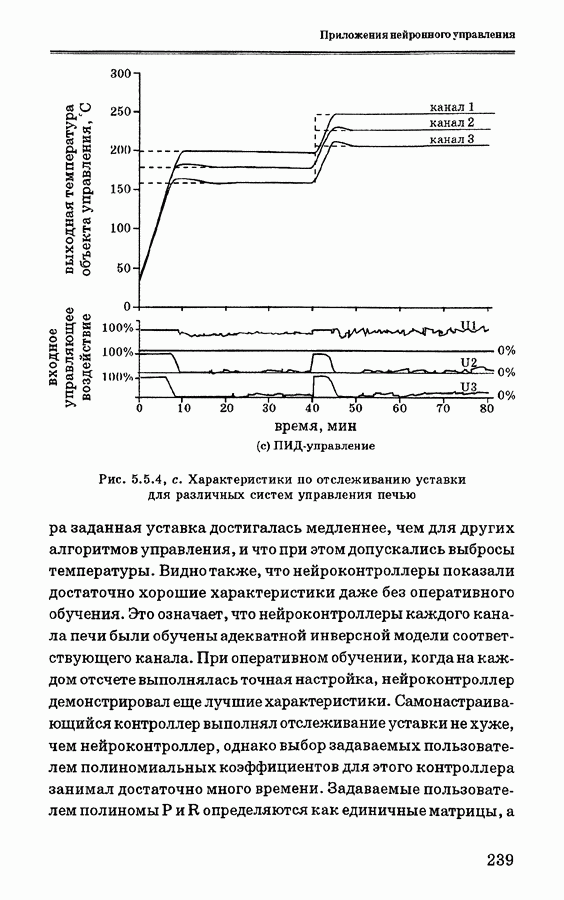
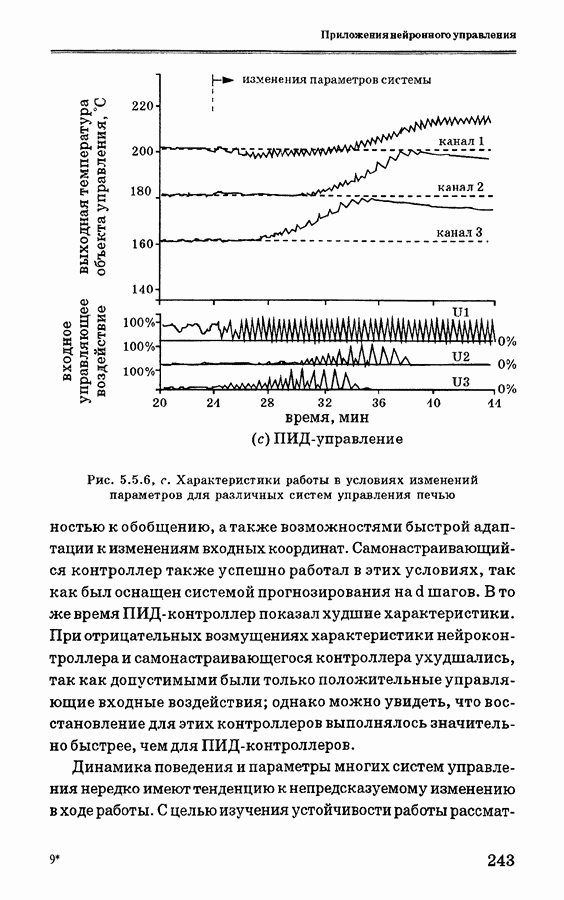
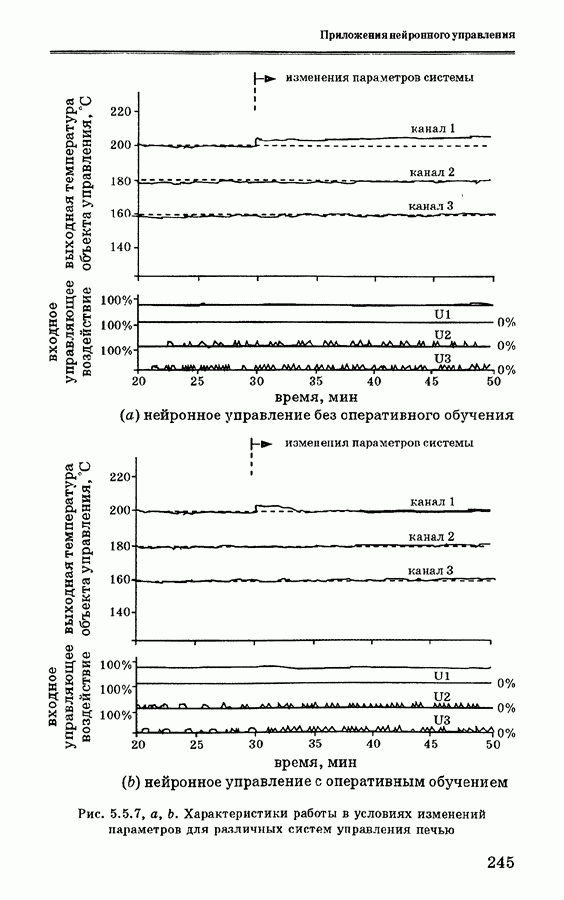
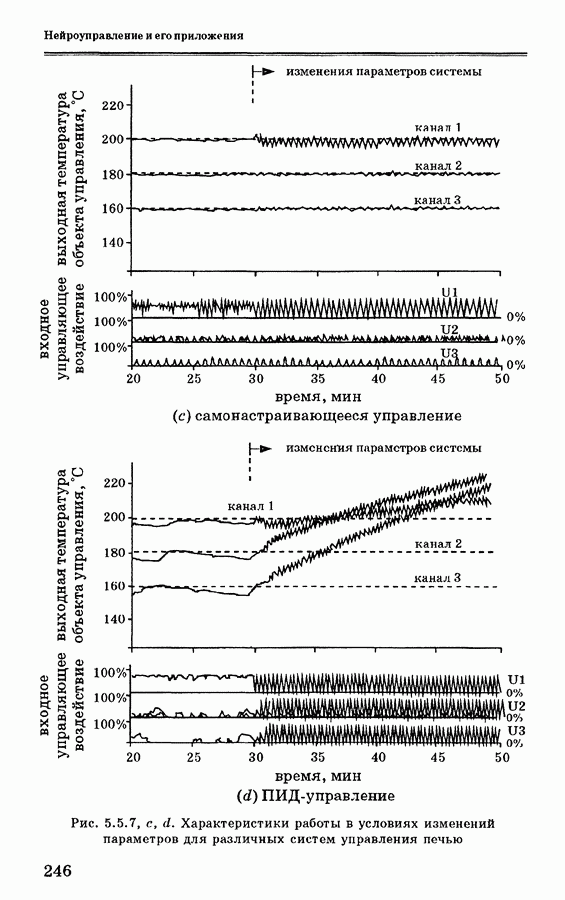
- 5.5.4. Анализ экспериментальных данных
- 5.6. Заключительные замечания и выводы
- Литература
- ЛИСТИНГ ПРОГРАММЫ