| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
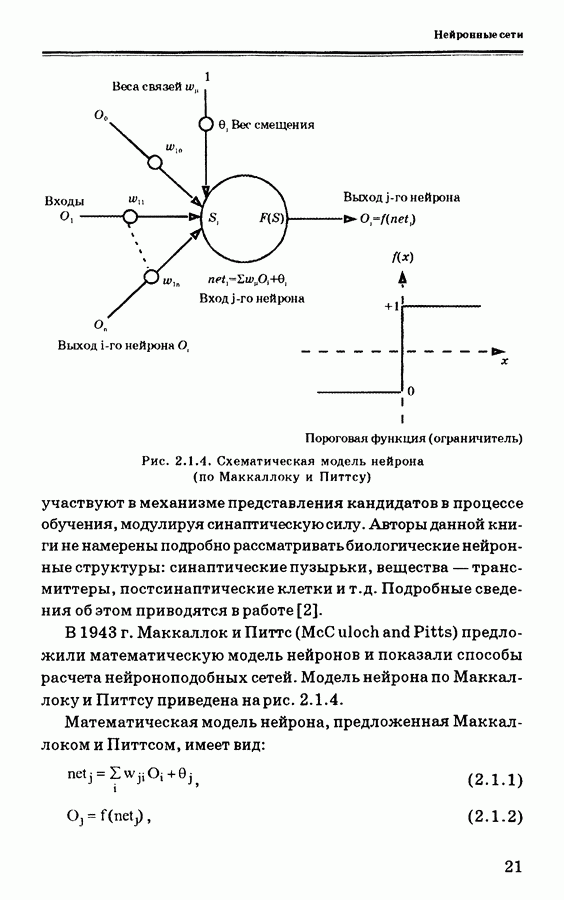
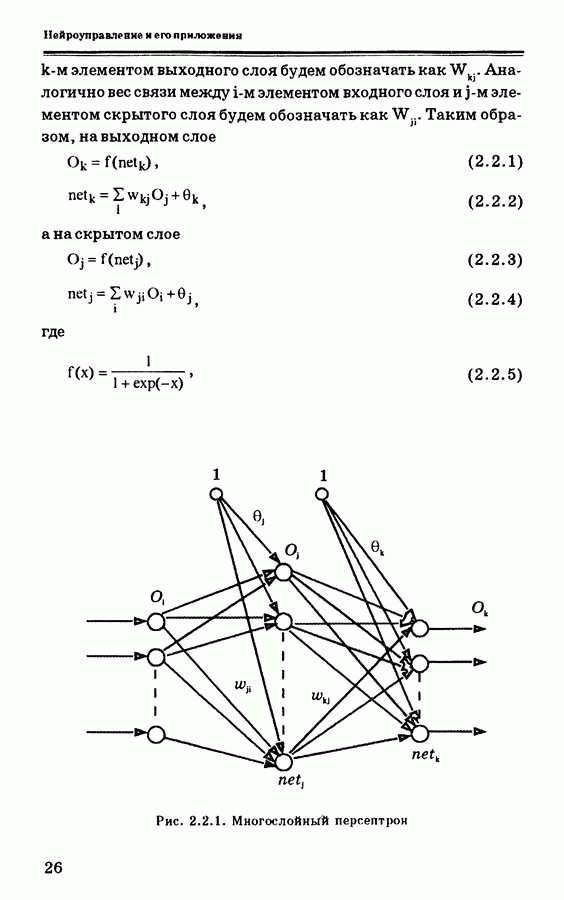
2.2.4. Обсуждение алгоритма обратного распространения
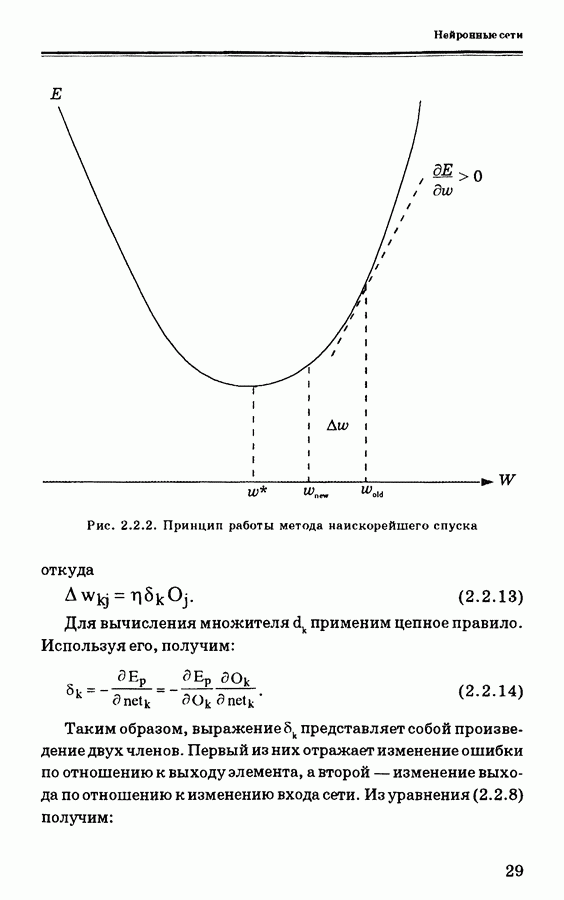
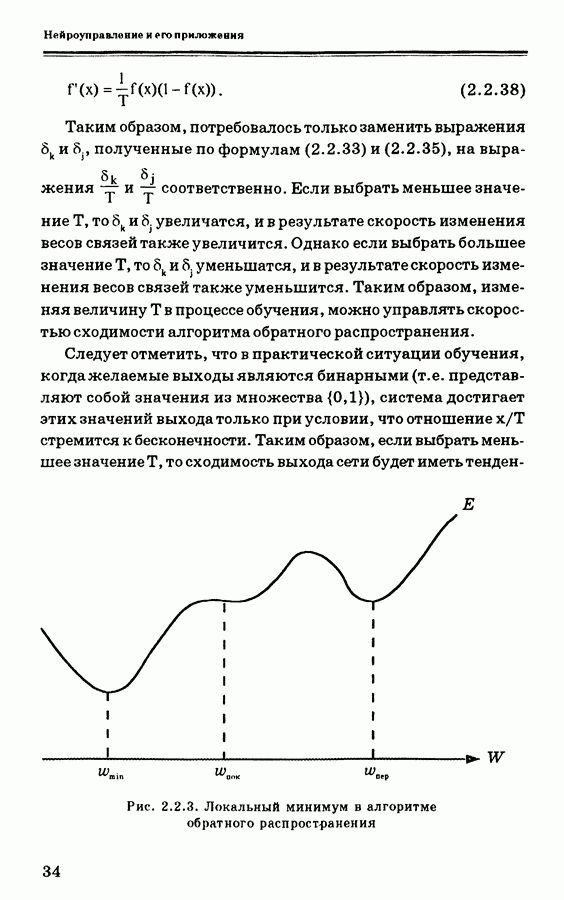
Алгоритм обратного распространения, полученный на основе градиентного метода наискорейшего спуска, предназначен для поиска минимума ошибки, что приводит, однако, к поиску локального минимума или точки перегиба (плато), как показано на рис. 2.2.3. В идеальном случае должен отыскиваться глобальный минимум, представляющий собой нижнюю точку на всей области определения. Так как локальный минимум окружен более высокими точками, стандартный алгоритм обратного распространения обычно не пропускает локальных минимумов.
Вид локального минимума не всегда представляет существенный интерес. Можно ожидать, что в ходе обучения в соответствии с алгоритмом обратного распространения ошибка сети будет сходиться к приемлемому значению, если обучающие образцы четко различимы. Чтобы избежать «ловушек» на локальных минимумах, можно изменять параметры обучения, количество скрытых слоев, начальные значения весов связей. Обычно эти методы разрабатываются так, чтобы попытаться изменить сценарий перемещения по участку, содержащему локальные минимумы и максимумы. Для поиска достаточно приемлемых значений параметров алгоритма обратного распространения в последнее время используется генетический алгоритм.
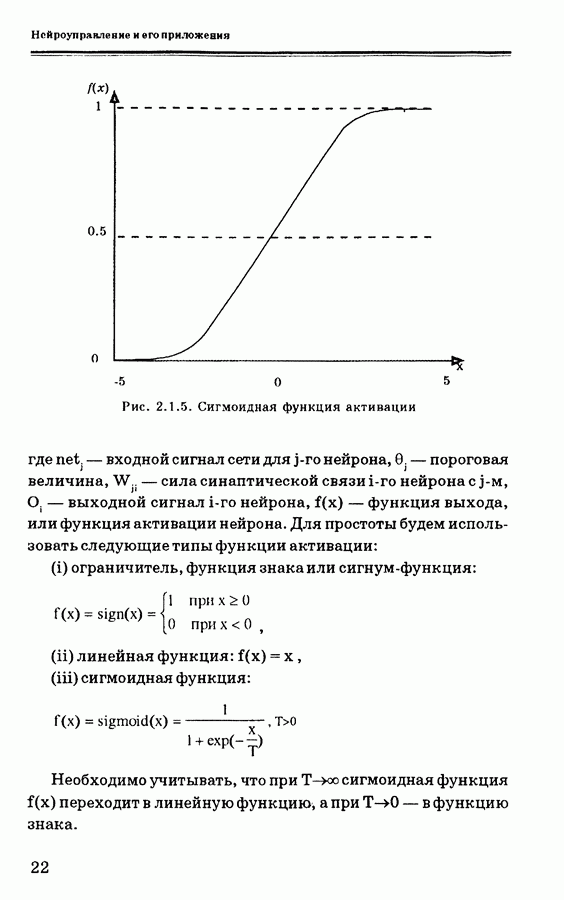
Для вывода алгоритма обратного распространения, представленного в разделе 2.2.2, использована сигмоидная функция (2.2.5). Могут использоваться и другие функции активации. Если, например, использовать функцию вида:

то получим:

Таким образом, потребовалось только заменить выражения  и
и  , полученные по формулам (2.2.33) и (2.2.35), на выражения
, полученные по формулам (2.2.33) и (2.2.35), на выражения  и
и  соответственно. Если выбрать меньшее значение Т, то
соответственно. Если выбрать меньшее значение Т, то  . увеличатся, и в результате скорость изменения весов связей также увеличится. Однако если выбрать большее значение Т, то
. увеличатся, и в результате скорость изменения весов связей также увеличится. Однако если выбрать большее значение Т, то  уменьшатся, и в результате скорость изменения весов связей также уменьшится. Таким образом, изменяя величину Т в процессе обучения, можно управлять скоростью сходимости алгоритма обратного распространения.
уменьшатся, и в результате скорость изменения весов связей также уменьшится. Таким образом, изменяя величину Т в процессе обучения, можно управлять скоростью сходимости алгоритма обратного распространения.
Следует отметить, что в практической ситуации обучения, когда желаемые выходы являются бинарными (т.е. представляют собой значения из множества  система достигает этих значений выхода только при условии, что отношение
система достигает этих значений выхода только при условии, что отношение  стремится к бесконечности. Таким образом, если выбрать меньшее значение Т, то сходимость выхода сети будет иметь
стремится к бесконечности. Таким образом, если выбрать меньшее значение Т, то сходимость выхода сети будет иметь

Рис. 2.2.3. Локальный минимум в алгоритме обратного распространения
тенденцию к ускорению. При  производные
производные  достигают максимальных значений при
достигают максимальных значений при  . В связи с тем, что
. В связи с тем, что  минимумы производных достигаются при приближении этих величин к нулевому или единичному значениям. Так как величина изменения конкретного веса связи пропорциональна производной, эти веса будут изменяться в основном для этих значений.
минимумы производных достигаются при приближении этих величин к нулевому или единичному значениям. Так как величина изменения конкретного веса связи пропорциональна производной, эти веса будут изменяться в основном для этих значений.
Другое свойство функции активации состоит в том, что нейронная сеть не может достигать предельных значений 0 и 1, если веса связей не являются бесконечно большими. Таким образом, в практической ситуации обучения, когда желаемые выходы являются бинарными  нейронная сеть никогда не достигнет этих значений. Поэтому в качестве желаемых величин можно рассматривать 0,1 и 0,9, даже если в действительности желаемыми величинами являются 0 и 1.
нейронная сеть никогда не достигнет этих значений. Поэтому в качестве желаемых величин можно рассматривать 0,1 и 0,9, даже если в действительности желаемыми величинами являются 0 и 1.
Скорость обучения  — это константа, представляющая собой коэффициент пропорциональности между изменением веса связи и градиентом ошибки Е относительно веса. Чем больше данная константа, тем больше изменения в весах связей. Обычно скорость обучения выбирается как можно большей, но такой, чтобы не возникало осцилляции. Так как для исключения осцилляции в формулы был введен момент времени, требуется выбрать подходящее значение а. Введение момента времени «отфильтровывает» высокочастотные изменения поверхности ошибки в пространстве весов связей. Это полезно в случаях, когда пространство весов связей содержит длинные овраги с острыми искривлениями. В связи с тем, что такое искривление вызывает резкие расходящиеся колебания в долине, необходимо выбирать небольшой размер шага, для чего требуется небольшая скорость обучения. В книге Румельхарта (Rumelhart) и др. [11] рекомендуется использовать величину а, приблизительно равную 0,9.
— это константа, представляющая собой коэффициент пропорциональности между изменением веса связи и градиентом ошибки Е относительно веса. Чем больше данная константа, тем больше изменения в весах связей. Обычно скорость обучения выбирается как можно большей, но такой, чтобы не возникало осцилляции. Так как для исключения осцилляции в формулы был введен момент времени, требуется выбрать подходящее значение а. Введение момента времени «отфильтровывает» высокочастотные изменения поверхности ошибки в пространстве весов связей. Это полезно в случаях, когда пространство весов связей содержит длинные овраги с острыми искривлениями. В связи с тем, что такое искривление вызывает резкие расходящиеся колебания в долине, необходимо выбирать небольшой размер шага, для чего требуется небольшая скорость обучения. В книге Румельхарта (Rumelhart) и др. [11] рекомендуется использовать величину а, приблизительно равную 0,9.
Другой проблемой является выбор количества скрытых узлов или скрытых слоев. Из регрессионного анализа известно, что если выбрать достаточно много видов описывающих
переменных, то ошибка предсказания окажется небольшой. Пусть, например, для оценки линейной регрессии

где  выбрано
выбрано  видов описывающих переменных
видов описывающих переменных  и одна целевая переменная у.
и одна целевая переменная у.
Если выбрать  то ошибки предсказания
то ошибки предсказания  могут быть равными нулю. Может показаться, что с помощью уравнения регрессии можно достичь точного предсказания. На практике это невозможно, так как
могут быть равными нулю. Может показаться, что с помощью уравнения регрессии можно достичь точного предсказания. На практике это невозможно, так как  должно быть больше
должно быть больше  Поэтому необходимо отметить, что минимизация квадрата ошибки, достигаемая за счет увеличения количества нейронов, не означает построения хорошей нейронной сети. Если использовать большое количество нейронов, то нейронная сеть может с высокой точностью обучаться на «зашумленных» данных. В этом случае следует выбрать нейронную сеть
Поэтому необходимо отметить, что минимизация квадрата ошибки, достигаемая за счет увеличения количества нейронов, не означает построения хорошей нейронной сети. Если использовать большое количество нейронов, то нейронная сеть может с высокой точностью обучаться на «зашумленных» данных. В этом случае следует выбрать нейронную сеть

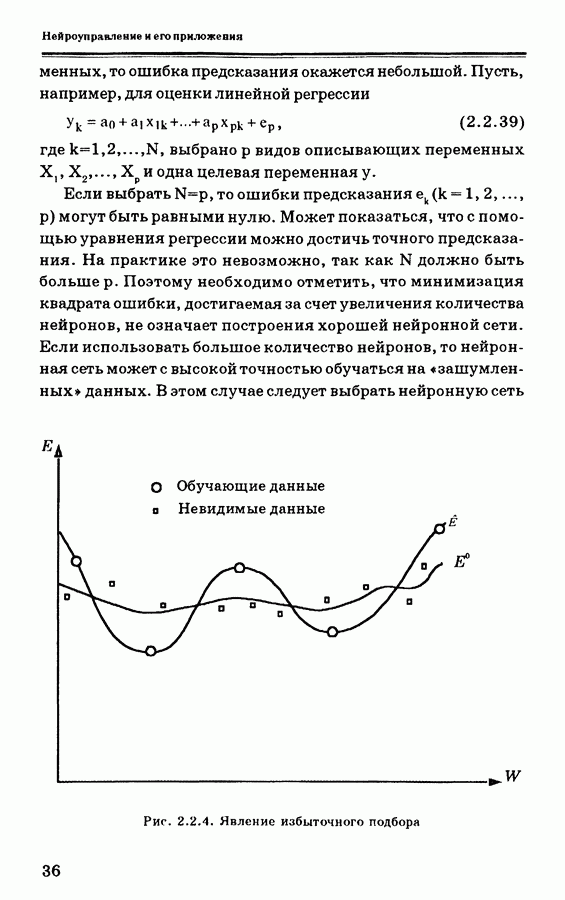
Рис. 2.2.4. Явление избыточного подбора
меньшего размера, даже если ошибка при этом оказывается не такой малой, как показано на рис. 2.2.4. На этом рисунке Е представляет кривую ошибки, полученную приточном обучении на наблюдаемых данных, а  — кривую ошибки, обеспечивающую наименьшую ошибку предсказания для невидимых данных. Это явление называется проблемой избыточного подбора. Для ее решения предложено несколько методов, которые позволяют уменьшить размер нейронной сети.
— кривую ошибки, обеспечивающую наименьшую ошибку предсказания для невидимых данных. Это явление называется проблемой избыточного подбора. Для ее решения предложено несколько методов, которые позволяют уменьшить размер нейронной сети.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРОВ ПЕРЕВОДА
- 1. ВВЕДЕНИЕ
- 1.1. Общие сведения об интеллектуальном управлении
- 2. НЕЙРОННЫЕ СЕТИ
- 2.2. Алгоритм обратного распространения
- 2.2.2. Вывод алгоритма обратного распространения
- 2.2.2.2. Правило для скрытого слоя
- 2.2.3. Алгоритм обратного распространения: порядок реализации
- 2.2.4. Обсуждение алгоритма обратного распространения
- 2.3. Заключение
- 3. ТРАДИЦИОННЫЕ СХЕМЫ УПРАВЛЕНИЯ
- 3.2. ПИ- и ПИД-контроллеры с дискретным временем
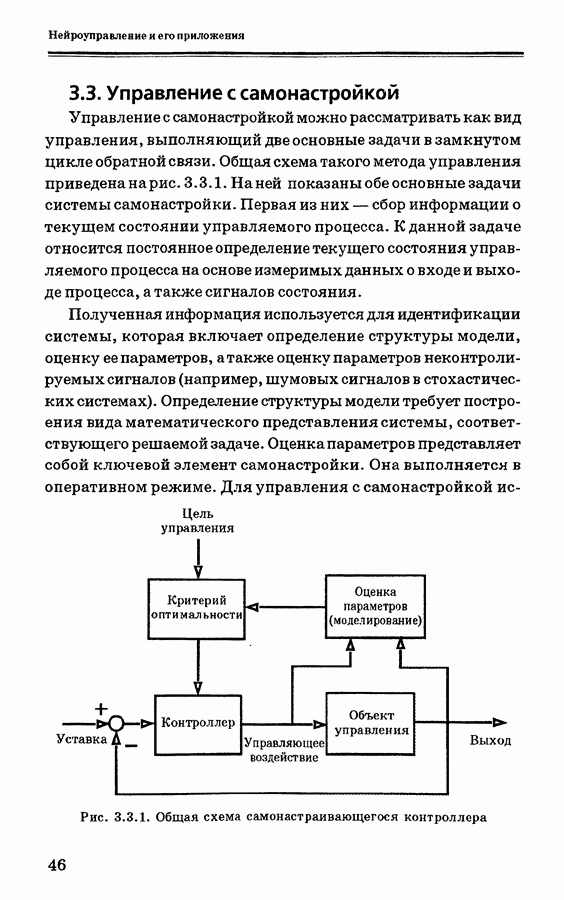
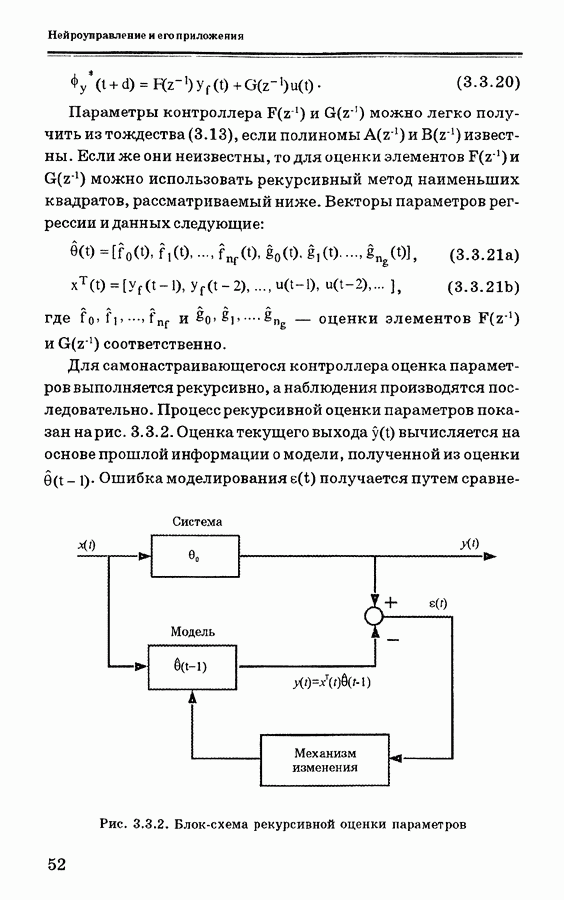
- 3.3. Управление с самонастройкой
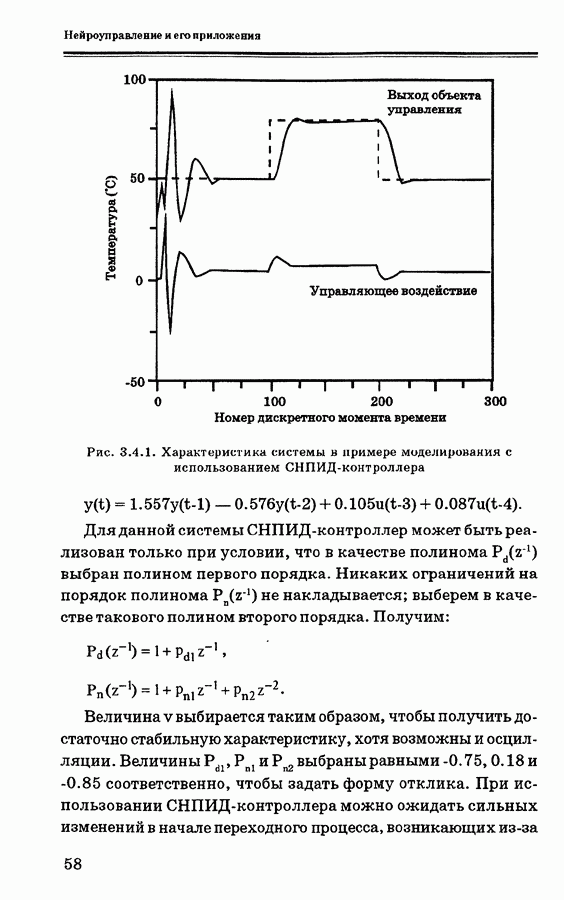
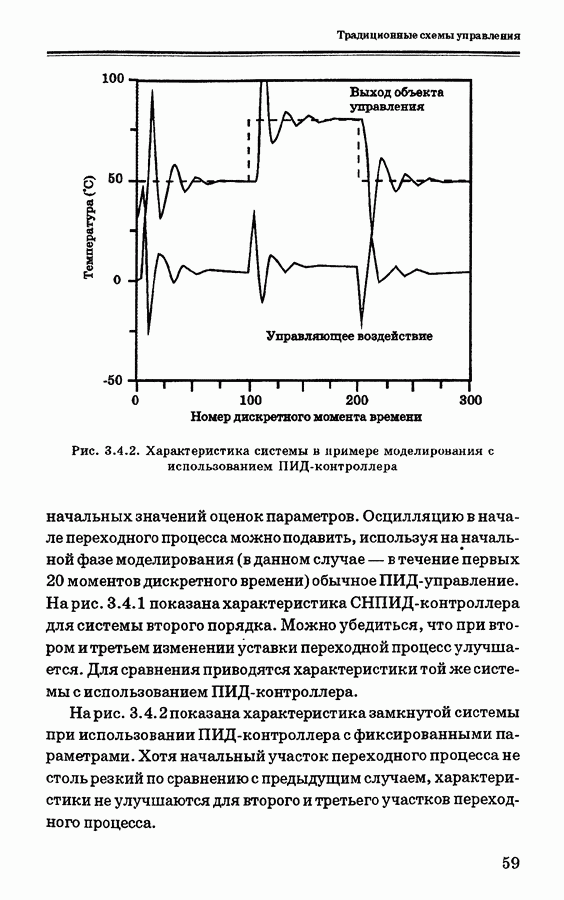
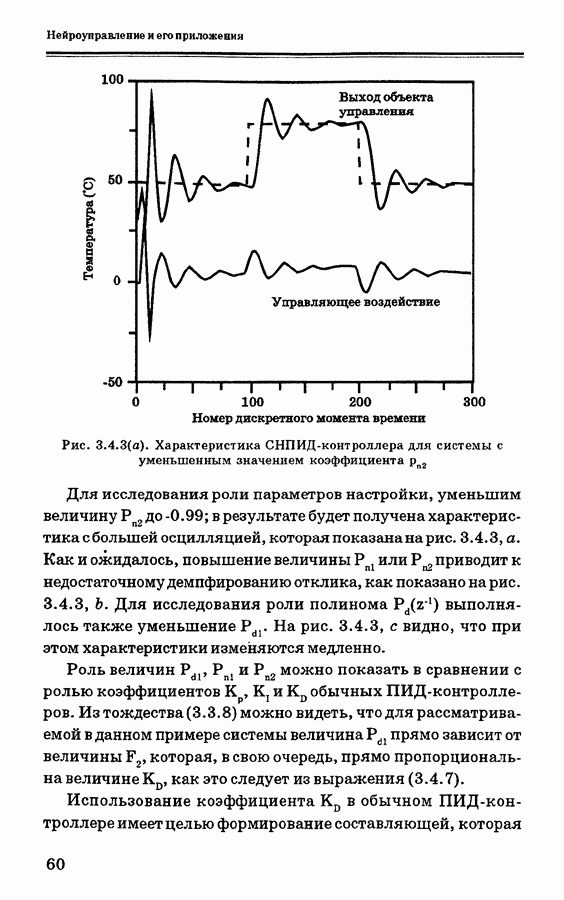
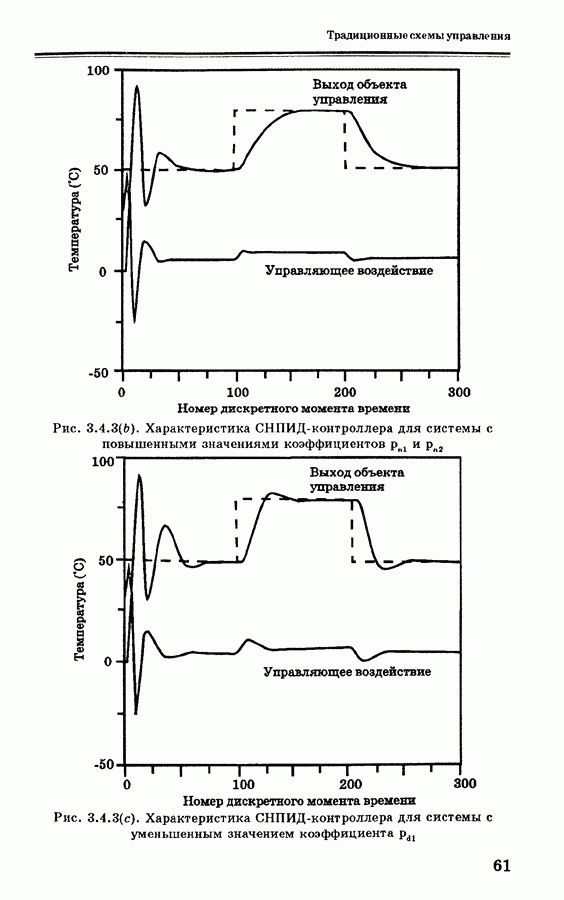
- 3.4. Самонастраивающиеся ПИ- и ПИД- контроллеры
- 3.5. ПИД-управление с самонастройкой: многомерный подход
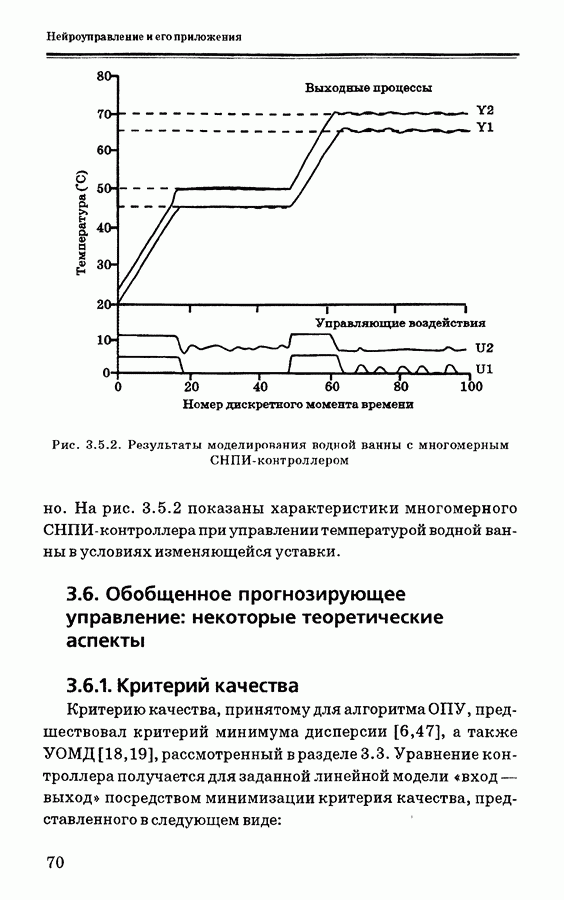
- 3.5.1. Пример моделирования
- 3.6. Обобщенное прогнозирующее управление: некоторые теоретические аспекты
- 3.6.2. Модель объекта управления и решение задачи оптимизации
- 3.7. Управление на основе нечеткой логики
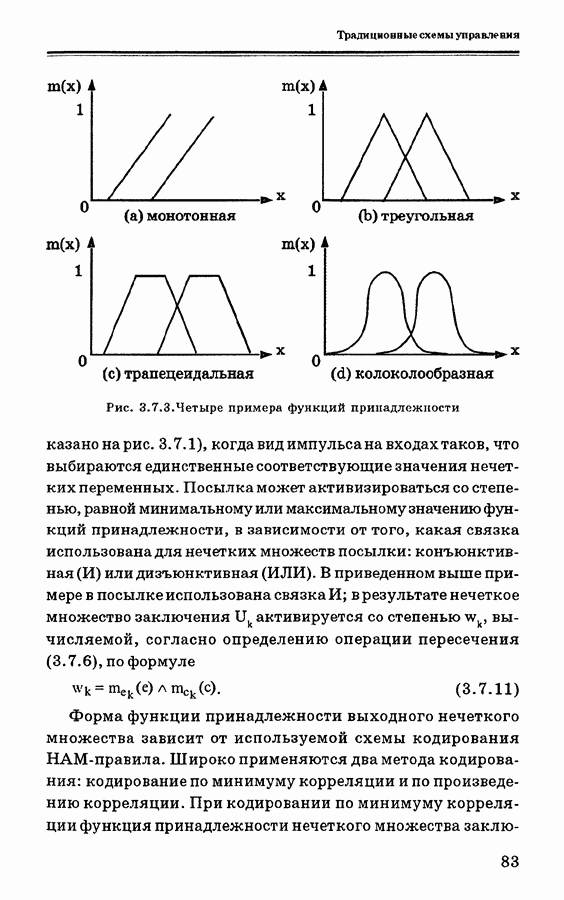
- 3.7.1. Краткие сведения по теории нечетких множеств и нечетких систем
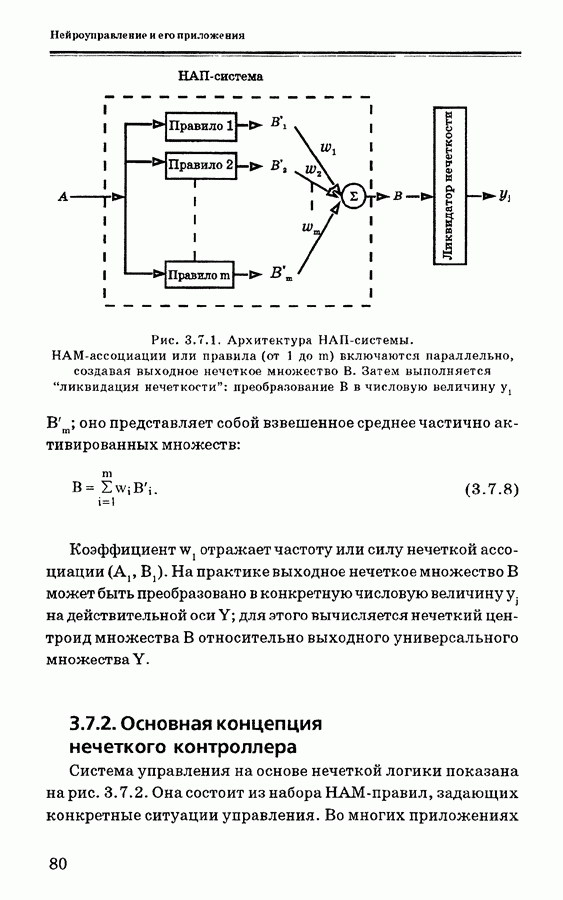
- 3.7.2. Основная концепция нечеткого контроллера
- 3.8. Заключение
- 4. ТЕХНОЛОГИИ НЕЙРОННОГО УПРАВЛЕНИЯ
- 4.2. Общие сведения о нейронном управлении
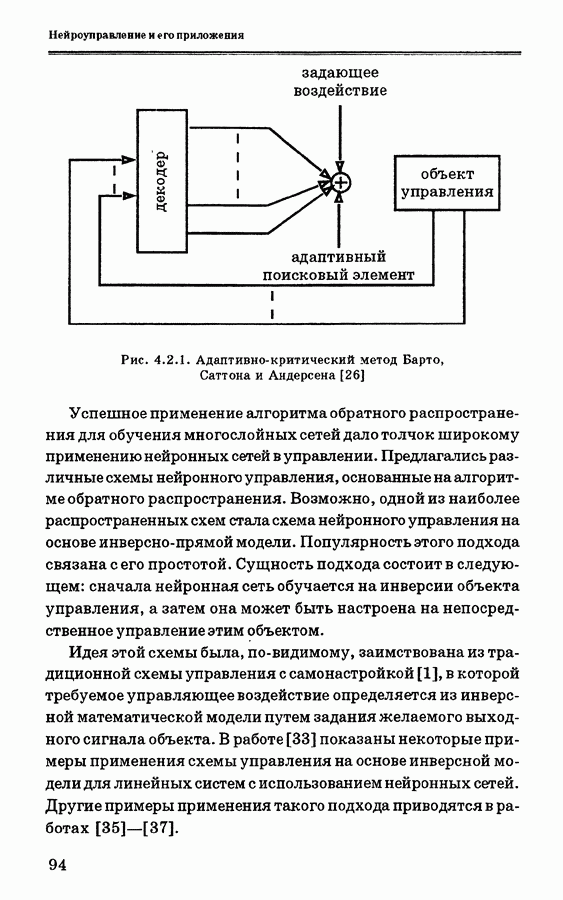
- 4.2.1. Подходы к нейронному управлению
- 4.2.2. Общая схема управления
- 4.3. Последовательная схема нейронного управления
- 4.4. Расширение последовательной схемы нейронного управления
- 4.4.2. Нейроморфные структуры управления
- 4.4.3. Конфигурации обучения
- 4.4.4. Эффективное оперативное управление
- 4.4.5. Алгоритмы обучения
- 4.4.6. Оценка алгоритмов обучения на основе моделирования
- 4.5. Параллельная схема управления
- 4.6. Алгоритм обучения по ошибке обратной связи
- 4.7. Расширение применения нейроконтроллеров параллельного типа
- 4.7.2. Линеаризованная система управления
- 4.7.3. Система управления с нейронными сетями
- 4.7.4. Нелинейный алгоритм наблюдения для нейронной сети
- 4.7.5. Нелинейный контроллер для нейронной сети
- 4.7.6. Численное моделирование
- 4.8. Схема нейронного управления с самонастройкой
- 4.9. ПИД-нейроконтроллер с самонастройкой
- 4.9.1. Вывод уравнений ПИД-нейроконтроллера с самонастройкой
- 4.9.2. Примеры эмуляции
- 4.10. Схема нейронного управления с эмулятором и контроллером (схема обратного распространения во времени)
- 4.11. Заключение
- 5. ПРИЛОЖЕНИЯ НЕЙРОННОГО УПРАВЛЕНИЯ
- 5.2. Применение нейронного управления в системе регулирования процессов в водяной ванне и сравнение его с другими схемами управления
- 5.2.2. Система управления температурой водяной ванны
- 5.2.3. Схема нейронного управления
- 5.2.4. Схема управления на основе нечеткой логики
- 5.2.5. Схема обобщенного прогнозирующего управления
- 5.2.6. Экспериментальные данные и их анализ
- 5.2.7. Заключение
- 5.3. Система стабилизации инвертированного маятника на основе нейронных сетей
- 5.3.2. Система стабилизации инвертированного маятника
- 5.3.3. Инициализация поворотного управления с использованием нечеткой логики
- 5.3.4. Применение стратегии оптимального управления для стабилизации маятника
- 5.3.5. Точное управление на основе нейронных сетей
- 5.3.6. Заключение
- 5.4. Применение ПИД-нейроконтроллера с самонастройкой для управления скоростью электромобиля
- 5.4.2. Система управления электромобилем
- 5.4.3. ПИД-нейроконтроллер с самонастройкой
- 5.4.4. Применение нейронной сети для управления скоростью электромобиля
- 5.4.5. Заключение
- 5.5. Применение нейронных сетей для управления печью
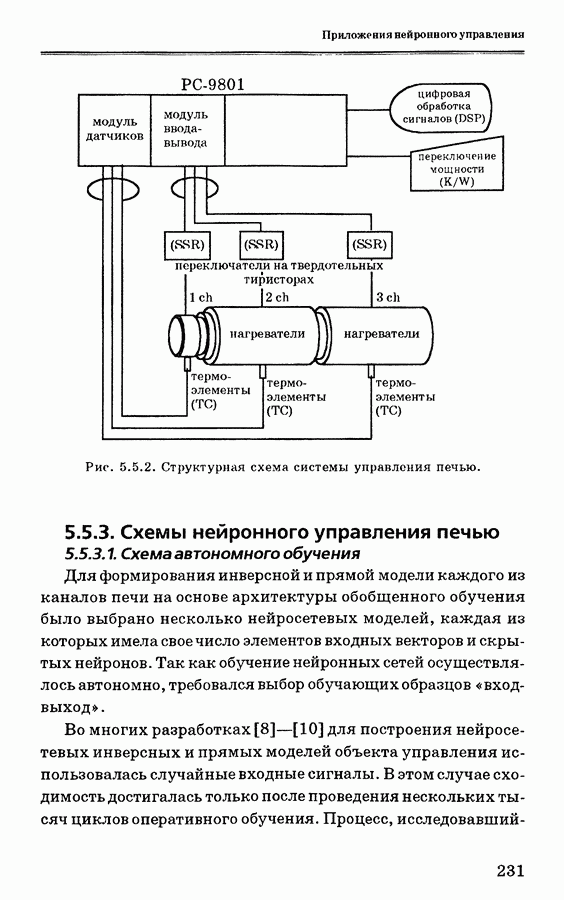
- 5.5.2. Система управления печью
- 5.5.3. Схемы нейронного управления печью
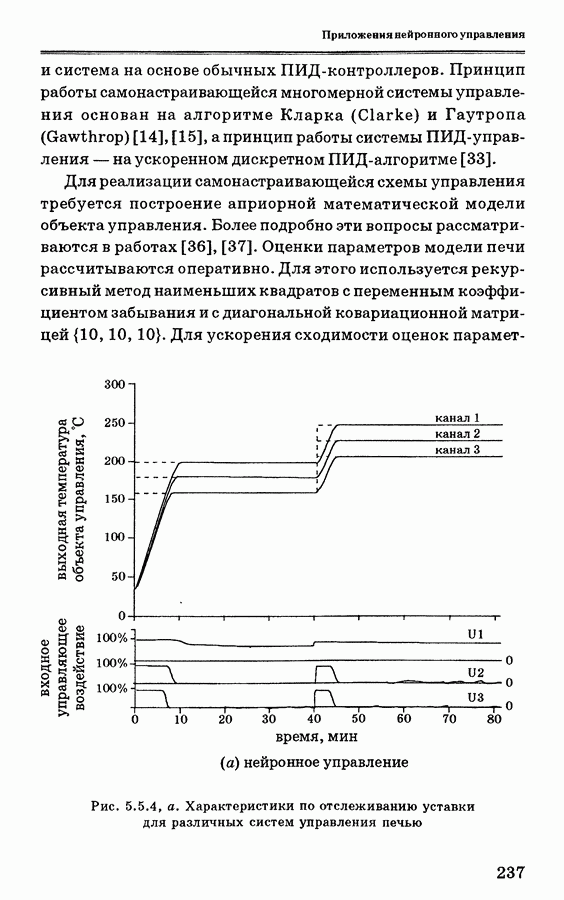
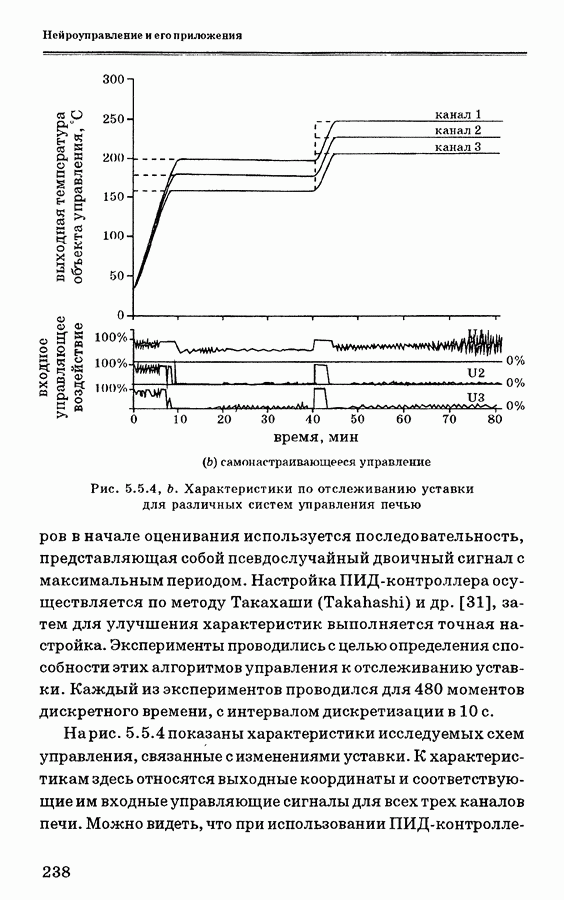
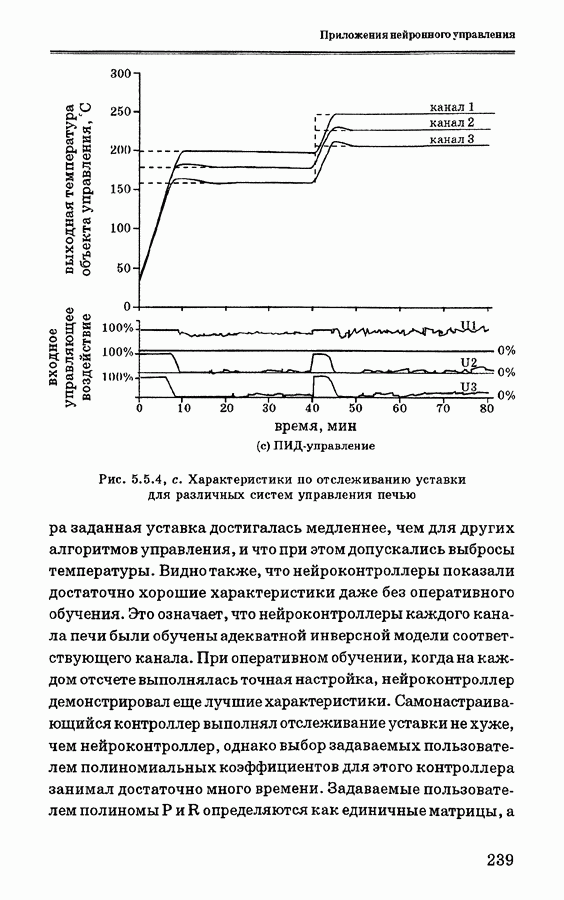
- 5.5.4. Анализ экспериментальных данных
- 5.6. Заключительные замечания и выводы
- Литература
- ЛИСТИНГ ПРОГРАММЫ