| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3.7.2. Основная концепция нечеткого контроллера
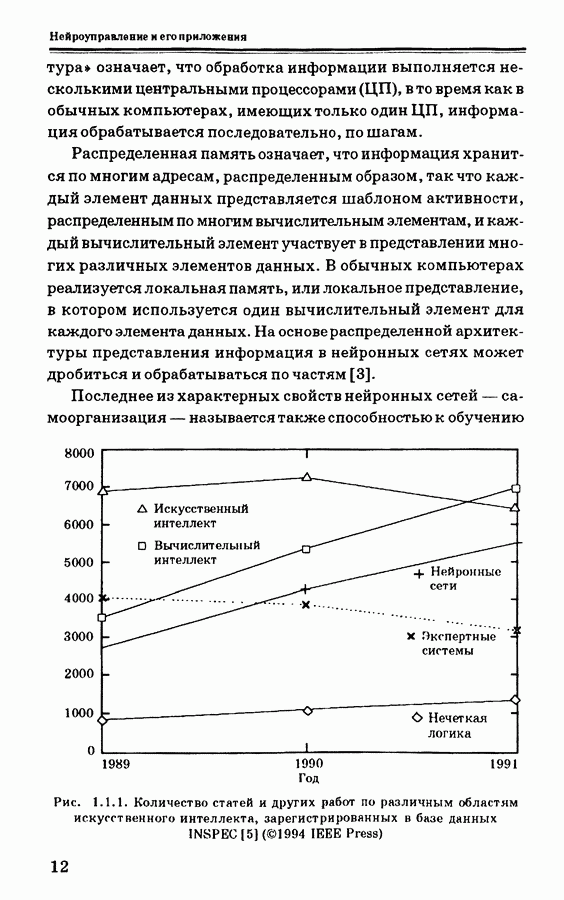
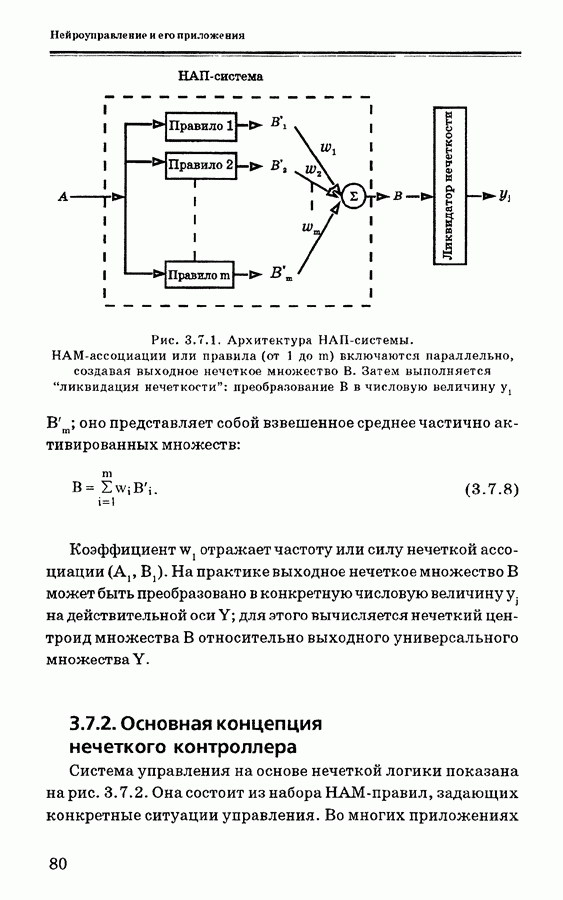
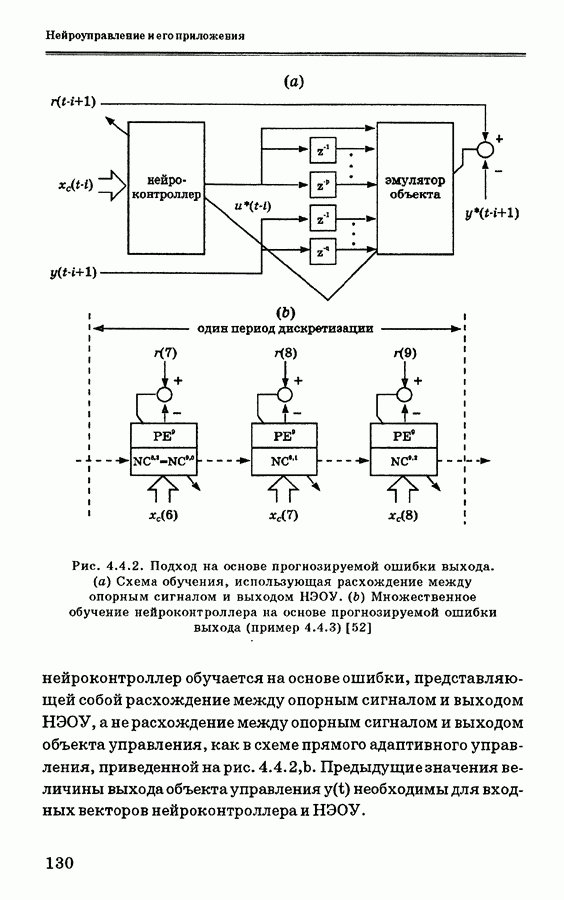
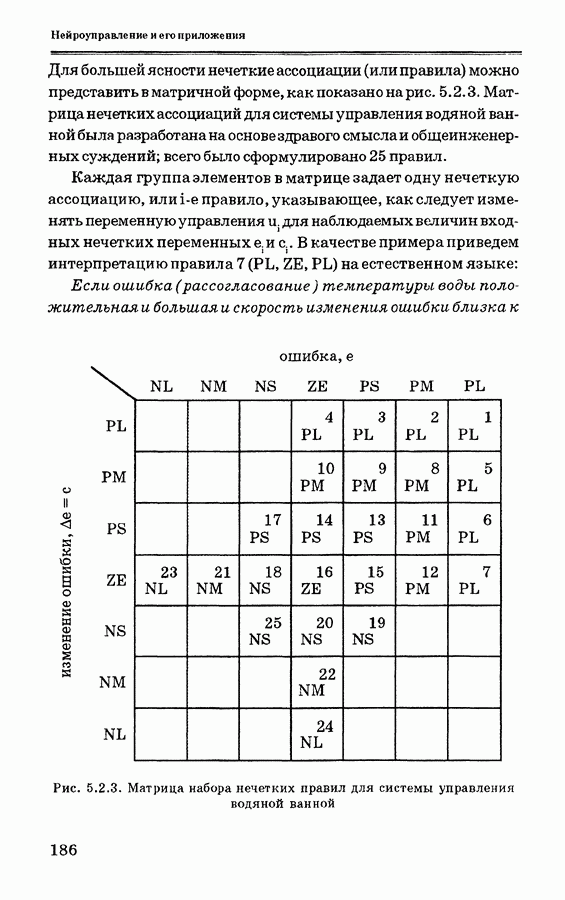
Система управления на основе нечеткой логики показана на рис. 3.7.2. Она состоит из набора НАМ-правил, задающих конкретные ситуации управления. Во многих приложениях

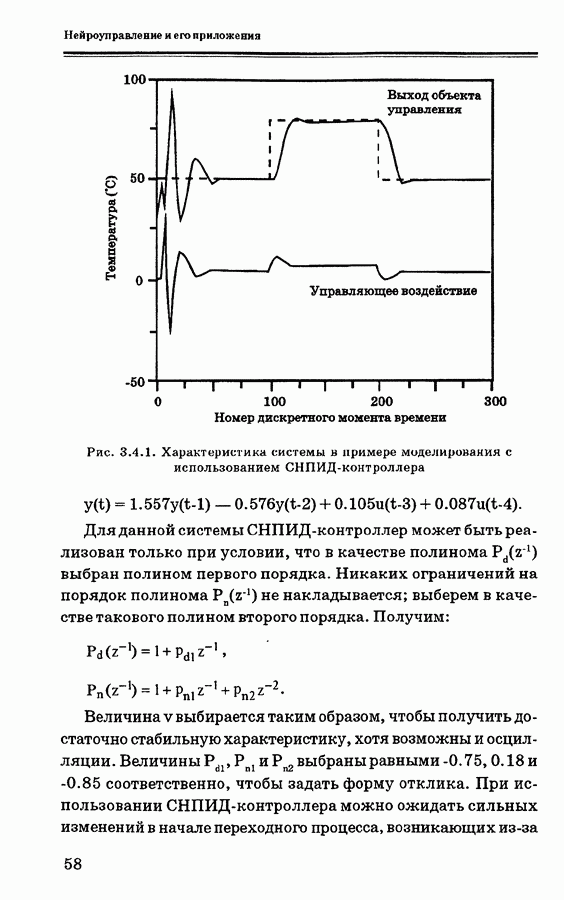
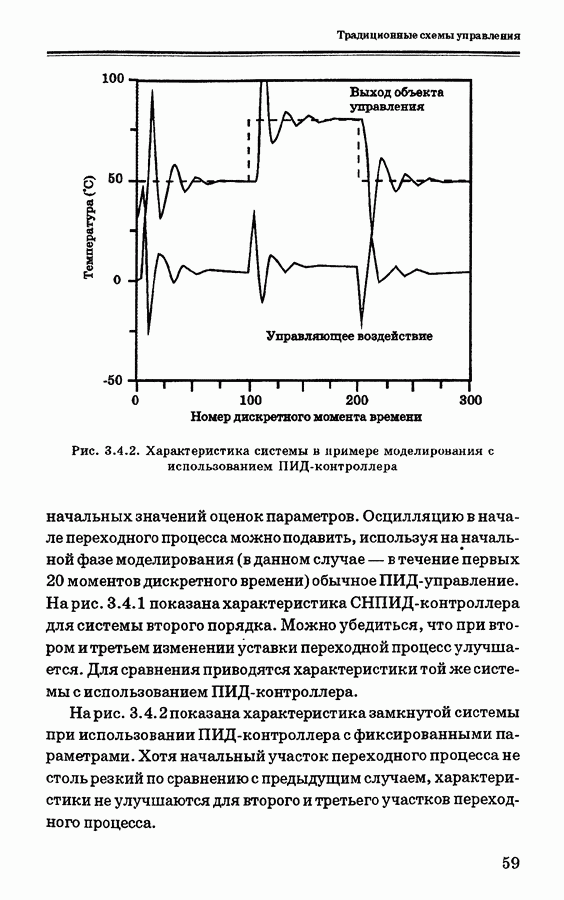
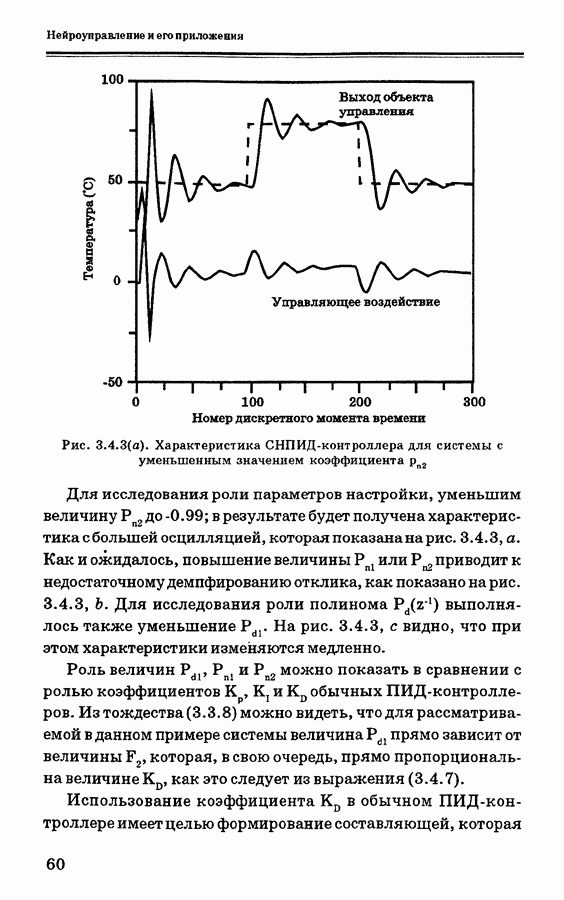
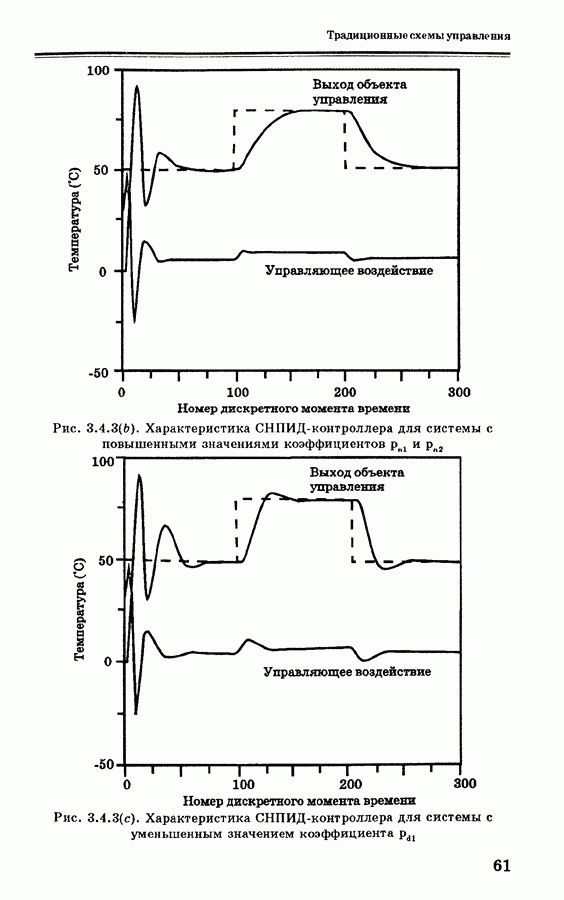
Рис. 3.7.2. Система управления на основе нечеткой логики
достаточно найти соотношение между ошибкой и скоростью изменения ошибки в процессе, чтобы изменить управляющее воздействие на величину, обеспечивающую удовлетворительное управление системой. В этом отношении могут быть сформулированы простые лингвистические правила, основанные на наблюдениях или на простом изучении хода процесса. Приведем пример лингвистического правила на естественном языке, которое эксперт может использовать для описания действия системы управления:
Если ошибка является положительной и большой, а скорость изменения ошибки — отрицательная и малая, то изменение на входе процесса — положительное и большое.
В правиле использованы три переменных: ошибка (Е), скорость изменения ошибки (С) и изменение управляющего воздействия (U). Они задаются фиксированными универсальными множествами, определяющими диапазоны измерений величин, возможные в данной системе управления. В некоторых приложениях [66,67] в качестве посылки НАМ-правила, с целью улучшения характеристик системы, может быть добавлена еще какая-либо переменная, например, величина предыдущего управляющего воздействия, однако это приводит к усложнению в разработке системы управления.
Каждая из нечетких переменных может быть преобразована в нечеткие подмножества в соответствии со сложностью процесса. Лингвистические термины (положительное большое, отрицательное малое, нулевое и т.д.), которыми эксперт
может воспользоваться для описания действий системы управления, используются для обозначения нечетких подмножеств, которые в действительности представляют числовые величины. Каждое из этих нечетких подмножеств содержит элементы вместе со своими степенями принадлежности. Функция принадлежности нечеткого множества ставит в соответствие каждому элементу из универсального множества некоторое вещественное число (обычно — из диапазона от 0 до 1); это число обозначает степень, с которой конкретный объект или элемент данных принадлежит нечеткому множеству.
Например,  НАМ-правило может быть записано в виде оператора следующей формы:
НАМ-правило может быть записано в виде оператора следующей формы:

Нечеткие подмножества  задаются набором упорядоченных пар вида:
задаются набором упорядоченных пар вида:

где  — элементы дискретных универсальных множеств, а
— элементы дискретных универсальных множеств, а  и
и  — соответствующие значения функции принадлежности, указывающие степень, с которой соответствующий элемент является членом нечеткого подмножества.
— соответствующие значения функции принадлежности, указывающие степень, с которой соответствующий элемент является членом нечеткого подмножества.
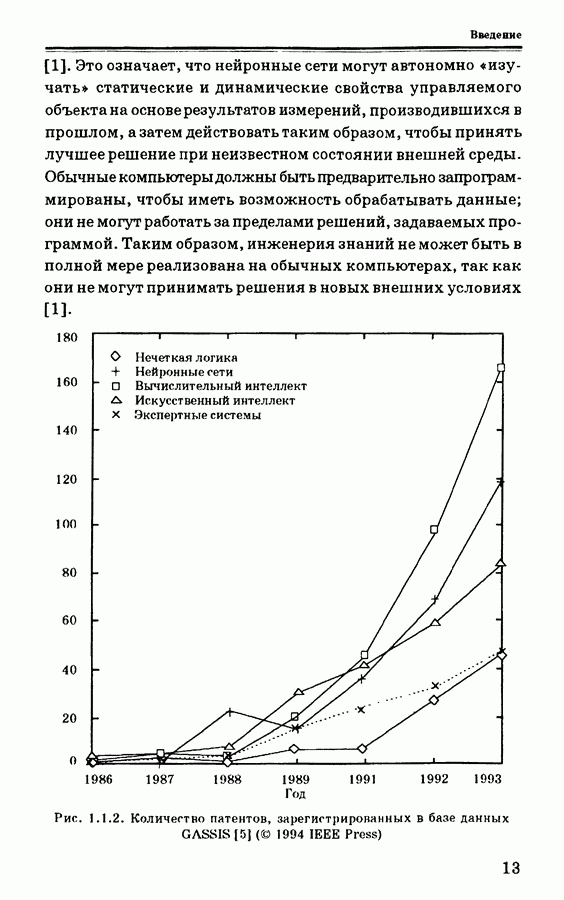
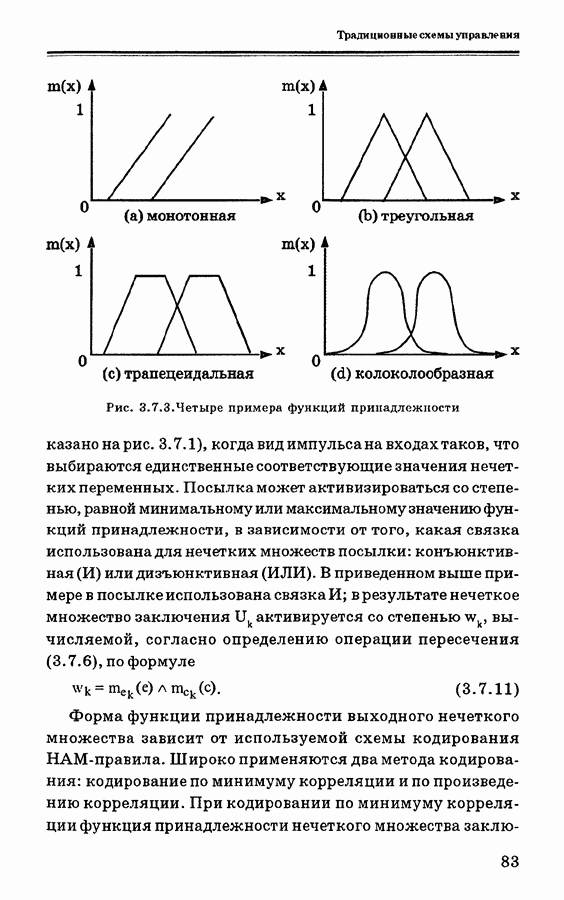
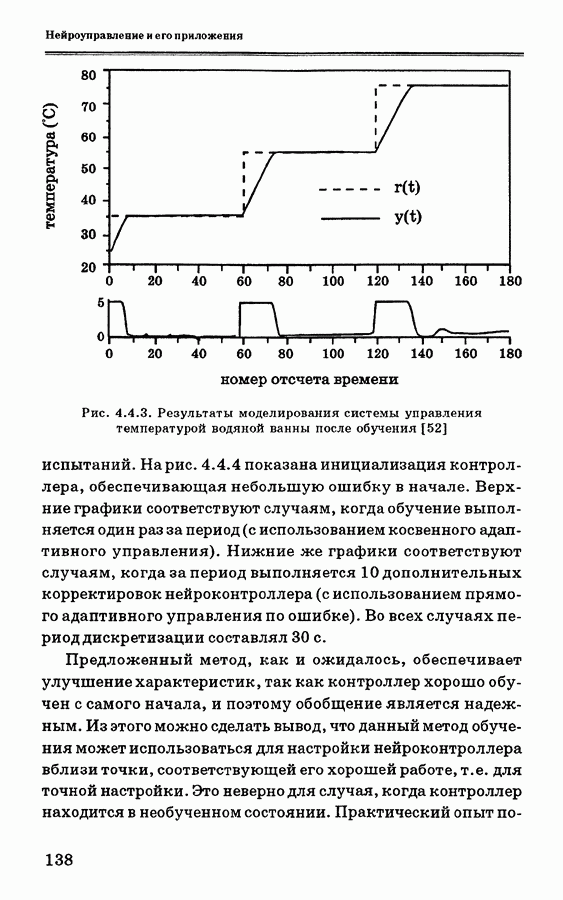
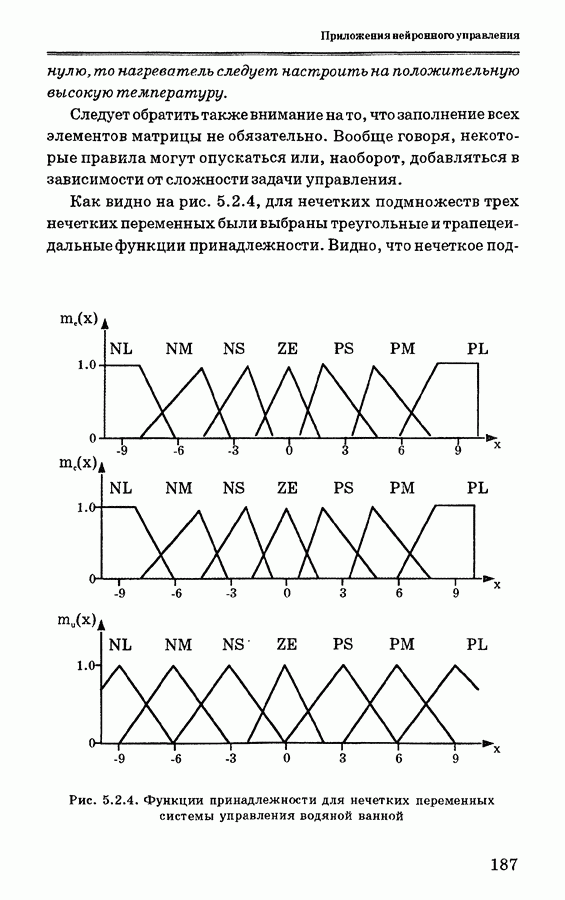
Графики функций принадлежности нечетких множеств могут иметь различную форму: монотонную, треугольную, трапецеидальную, колоколообразную (форму нормального распределения), в зависимости от предпочтений и опыта разработчика. Примеры основных форм функций принадлежности приведены нарис. 3.7.3. Выбор типафункции принадлежности влияет на используемый тип вывода [68]. На практике широко применяются трапецеидальные и треугольные функции принадлежности, обеспечивающие упрощение вычислений.
Посылки всех НАМ-правил, описывающих управляющее воздействие на процесс, активизируются параллельно (как

Рис. 3.7.3. Четыре примера функций принадлежности
показано на рис. 3.7.1), когда вид импульса на входах таков, что выбираются единственные соответствующие значения нечетких переменных. Посылка может активизироваться со степенью, равной миниматьному или максимальному значению функций принадлежности, в зависимости от того, какая связка использована для нечетких множеств посылки: конъюнктивная  или дизъюнктивная
или дизъюнктивная  . В приведенном выше примере в посылке использована связка И; в результате нечеткое множество заключения
. В приведенном выше примере в посылке использована связка И; в результате нечеткое множество заключения  активируется со степенью
активируется со степенью  вычисляемой, согласно определению операции пересечения (3.7.6), по формуле
вычисляемой, согласно определению операции пересечения (3.7.6), по формуле

Форма функции принадлежности выходного нечеткого множества зависит от используемой схемы кодирования НАМ-правила. Широко применяются два метода кодирования: кодирование по минимуму корреляции и по произведению корреляции. При кодировании по минимуму корреляции функция принадлежности нечеткого множества
заключения  усекается до степени
усекается до степени  с минимумом по всем точкам, так, что
с минимумом по всем точкам, так, что

а при кодировании по произведению корреляции  умножается на величину
умножается на величину 

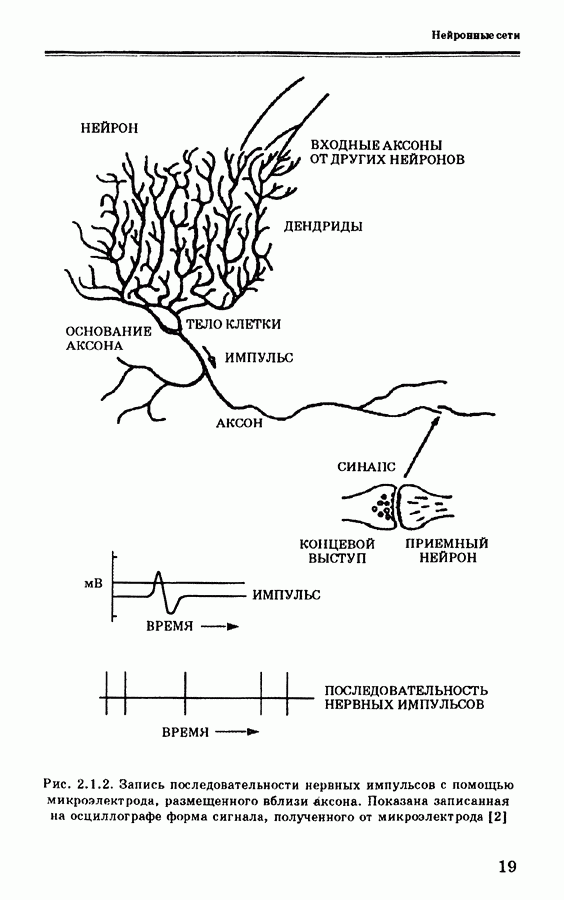
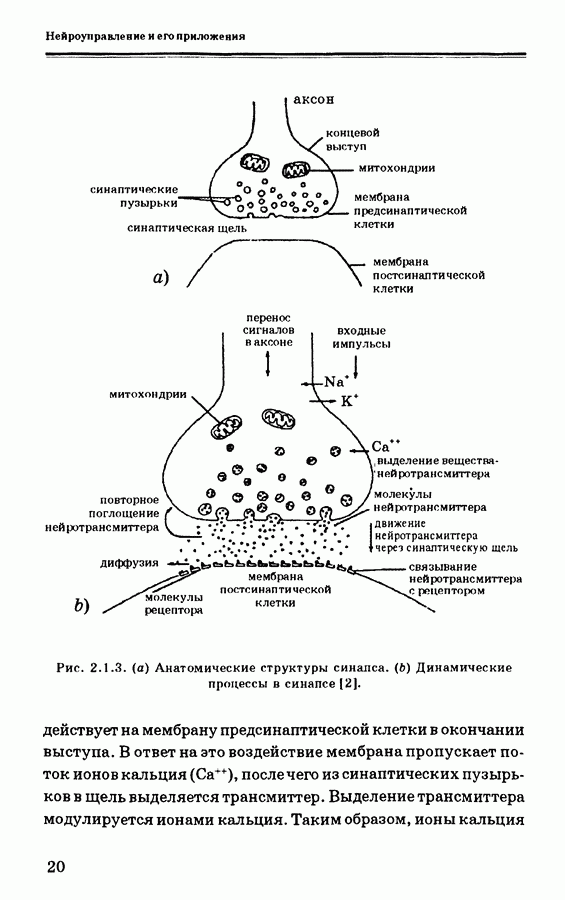
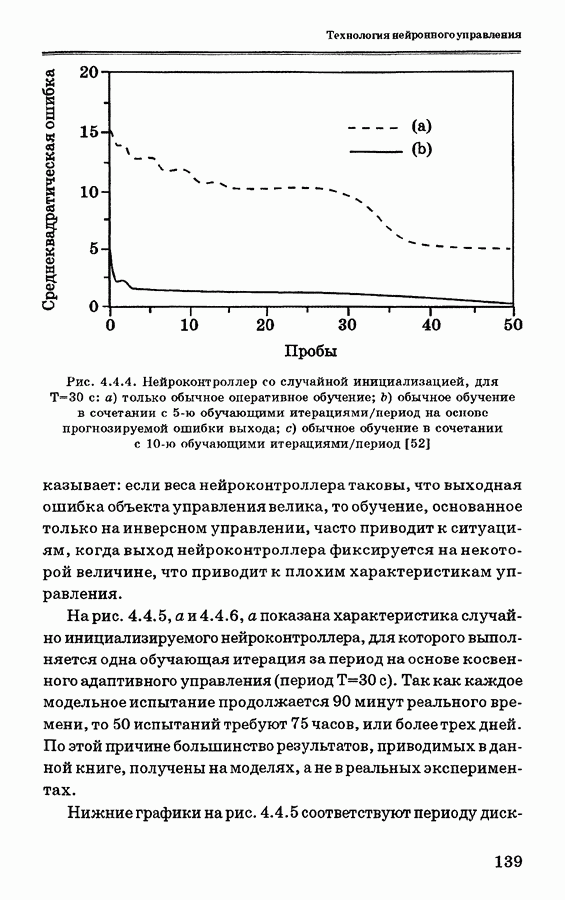
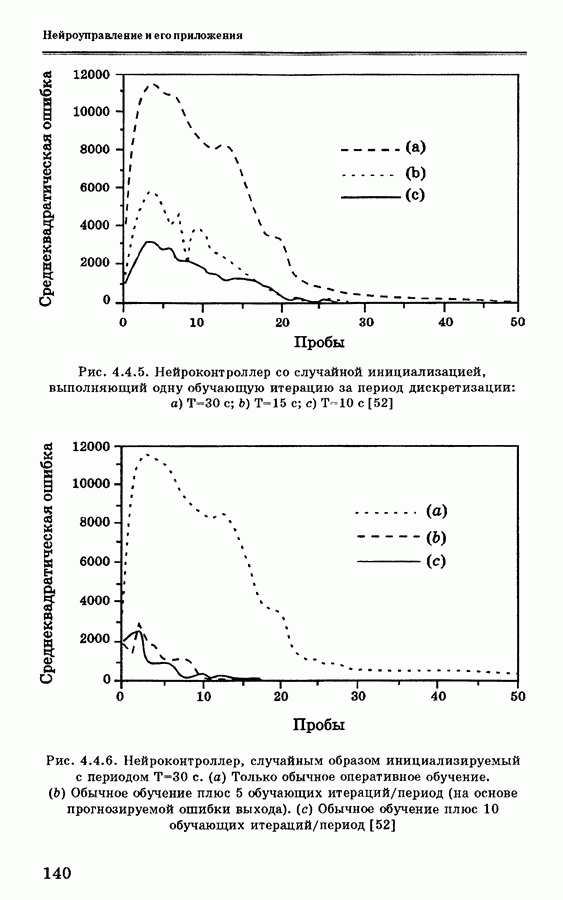
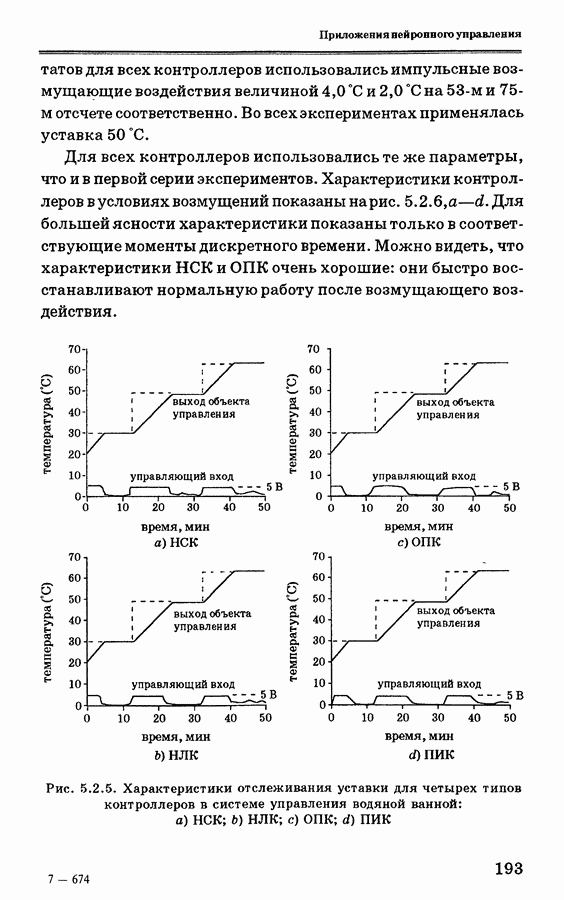
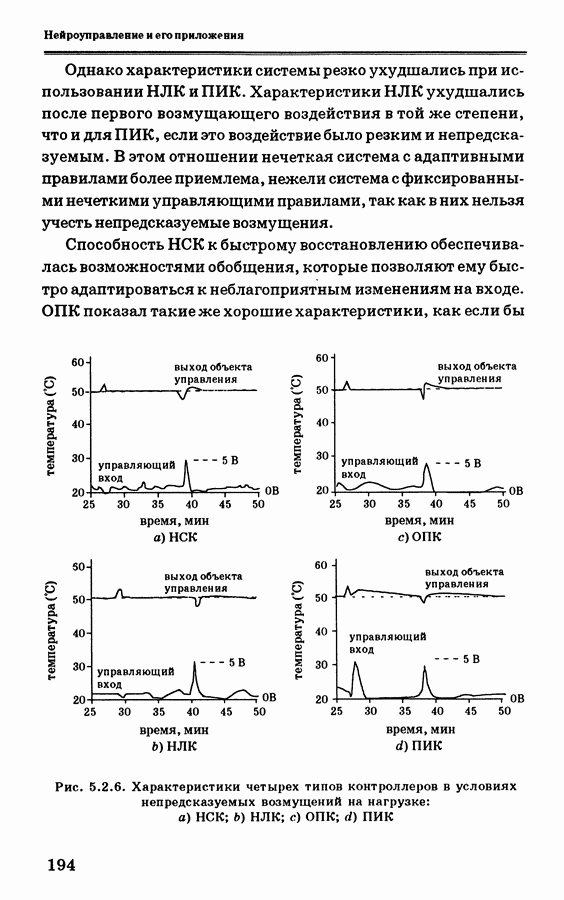
где  — степень принадлежности для выходного нечеткого множества в интервале у выходного множества. На рис. 3.7.4 показаны примеры изменения выходного нечеткого множества при использовании кодирования по минимуму корреляции (а) и по произведению корреляции
— степень принадлежности для выходного нечеткого множества в интервале у выходного множества. На рис. 3.7.4 показаны примеры изменения выходного нечеткого множества при использовании кодирования по минимуму корреляции (а) и по произведению корреляции 
На практике величина  не является единственной; в этом случае для получения функции принадлежности выходного нечеткого множества выполняется объединение всех функций согласно определению нечеткой операции объединения (3.7.4):
не является единственной; в этом случае для получения функции принадлежности выходного нечеткого множества выполняется объединение всех функций согласно определению нечеткой операции объединения (3.7.4):

Обратите внимание, что здесь  — не количество правил, а индекс квантования выходного нечеткого множества на подмножества.
— не количество правил, а индекс квантования выходного нечеткого множества на подмножества.
Выходной ликвидатор нечеткости, т.е. величина изменения выходного сигнала управления и, равен нечеткому центроиду:

где пределы интегрирования соответствуют всему универсальному множеству 
Для упрощения вычислений  может подвергаться дискретизации на
может подвергаться дискретизации на  значений через постоянные интервалы
значений через постоянные интервалы  Используя дискретное представление
Используя дискретное представление  получим дискретный вариант нечеткого центроида:
получим дискретный вариант нечеткого центроида:

Нечеткий контроллер имеет ряд параметров, которые должны выбираться разработчиком заранее. В рассматриваемом примере к ним относятся коэффициенты масштабирования  для ошибки процесса, изменения ошибки и выхода контроллера соответственно. Величины ошибки и изменения ошибки, используемые контроллером, представляют собой элементы соответствующих универсальных множеств дискурса, которые можно представить во времени функциями
для ошибки процесса, изменения ошибки и выхода контроллера соответственно. Величины ошибки и изменения ошибки, используемые контроллером, представляют собой элементы соответствующих универсальных множеств дискурса, которые можно представить во времени функциями  где
где  — момент дискретизации. Так как эти величины требуется перевести в количественную величину, соответствующую ближайшему элементу универсального множества дискурса, их сначала требуется масштабировать путем умножения на подходящую величину. Если в момент
— момент дискретизации. Так как эти величины требуется перевести в количественную величину, соответствующую ближайшему элементу универсального множества дискурса, их сначала требуется масштабировать путем умножения на подходящую величину. Если в момент  выход процесса и уставка имеют значения
выход процесса и уставка имеют значения  соответственно, то
соответственно, то  находятся из следующих уравнений:
находятся из следующих уравнений:

Аналогично результат преобразования нечеткого центроида в числовую (четкую) форму требуется умножить на соответствующую величину  чтобы вычислить действительное изменение входа процесса. Таким образом, если
чтобы вычислить действительное изменение входа процесса. Таким образом, если  — новая величина входа процесса, то она задается выражением:
— новая величина входа процесса, то она задается выражением:

Выбор рассмотренных коэффициентов масштабирования выполняется аналогично выбору параметров ПИД-контроллера или задаваемых пользователем полиномов для некоторых адаптивных контроллеров. Некоторыми исследователями предложены систематические подходы к выбору этих коэффициентов [69,70,71].

Рис. 3.7.4. Примеры процедур вывода из НАМ-правил, показывающие влияние на выход: (а) кодирование по минимуму корреляции; (b) кодирование по произведению корреляции
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРОВ ПЕРЕВОДА
- 1. ВВЕДЕНИЕ
- 1.1. Общие сведения об интеллектуальном управлении
- 2. НЕЙРОННЫЕ СЕТИ
- 2.2. Алгоритм обратного распространения
- 2.2.2. Вывод алгоритма обратного распространения
- 2.2.2.2. Правило для скрытого слоя
- 2.2.3. Алгоритм обратного распространения: порядок реализации
- 2.2.4. Обсуждение алгоритма обратного распространения
- 2.3. Заключение
- 3. ТРАДИЦИОННЫЕ СХЕМЫ УПРАВЛЕНИЯ
- 3.2. ПИ- и ПИД-контроллеры с дискретным временем
- 3.3. Управление с самонастройкой
- 3.4. Самонастраивающиеся ПИ- и ПИД- контроллеры
- 3.5. ПИД-управление с самонастройкой: многомерный подход
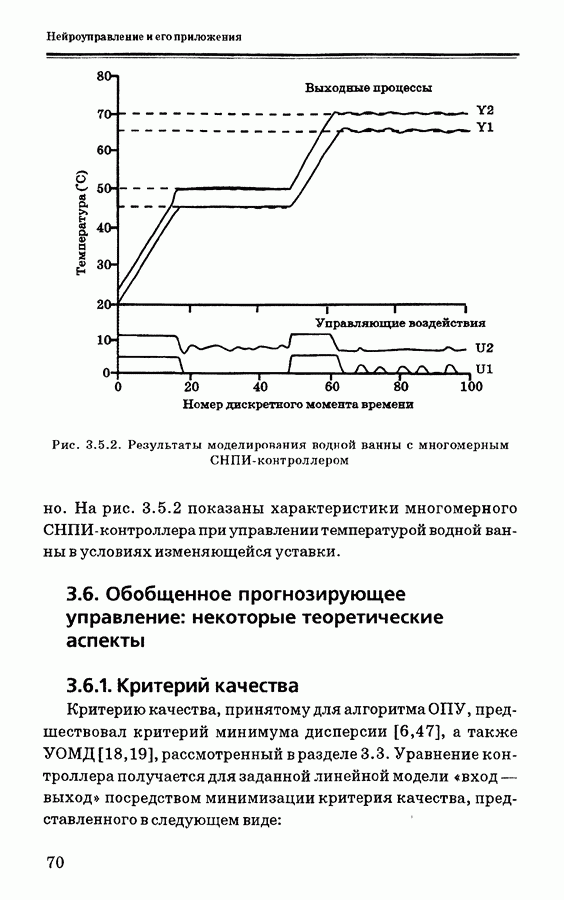
- 3.5.1. Пример моделирования
- 3.6. Обобщенное прогнозирующее управление: некоторые теоретические аспекты
- 3.6.2. Модель объекта управления и решение задачи оптимизации
- 3.7. Управление на основе нечеткой логики
- 3.7.1. Краткие сведения по теории нечетких множеств и нечетких систем
- 3.7.2. Основная концепция нечеткого контроллера
- 3.8. Заключение
- 4. ТЕХНОЛОГИИ НЕЙРОННОГО УПРАВЛЕНИЯ
- 4.2. Общие сведения о нейронном управлении
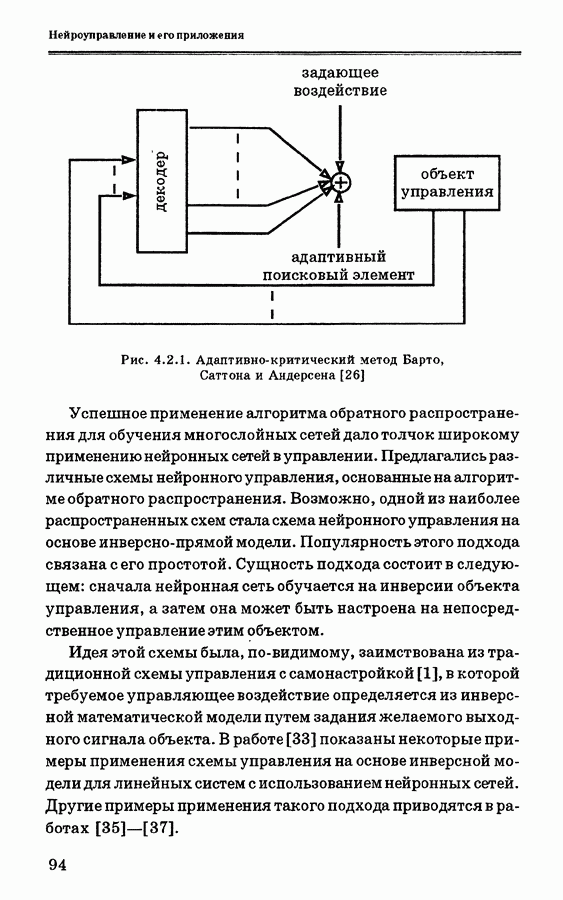
- 4.2.1. Подходы к нейронному управлению
- 4.2.2. Общая схема управления
- 4.3. Последовательная схема нейронного управления
- 4.4. Расширение последовательной схемы нейронного управления
- 4.4.2. Нейроморфные структуры управления
- 4.4.3. Конфигурации обучения
- 4.4.4. Эффективное оперативное управление
- 4.4.5. Алгоритмы обучения
- 4.4.6. Оценка алгоритмов обучения на основе моделирования
- 4.5. Параллельная схема управления
- 4.6. Алгоритм обучения по ошибке обратной связи
- 4.7. Расширение применения нейроконтроллеров параллельного типа
- 4.7.2. Линеаризованная система управления
- 4.7.3. Система управления с нейронными сетями
- 4.7.4. Нелинейный алгоритм наблюдения для нейронной сети
- 4.7.5. Нелинейный контроллер для нейронной сети
- 4.7.6. Численное моделирование
- 4.8. Схема нейронного управления с самонастройкой
- 4.9. ПИД-нейроконтроллер с самонастройкой
- 4.9.1. Вывод уравнений ПИД-нейроконтроллера с самонастройкой
- 4.9.2. Примеры эмуляции
- 4.10. Схема нейронного управления с эмулятором и контроллером (схема обратного распространения во времени)
- 4.11. Заключение
- 5. ПРИЛОЖЕНИЯ НЕЙРОННОГО УПРАВЛЕНИЯ
- 5.2. Применение нейронного управления в системе регулирования процессов в водяной ванне и сравнение его с другими схемами управления
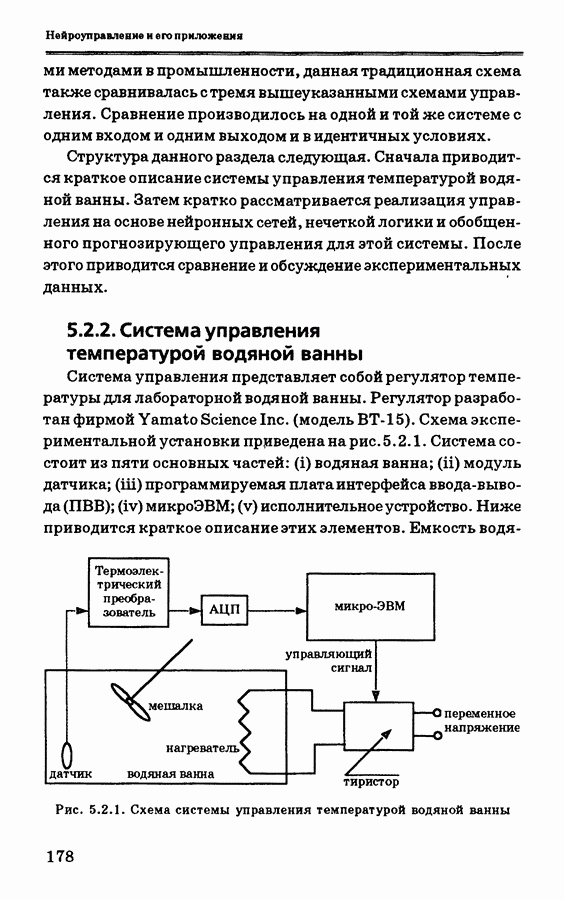
- 5.2.2. Система управления температурой водяной ванны
- 5.2.3. Схема нейронного управления
- 5.2.4. Схема управления на основе нечеткой логики
- 5.2.5. Схема обобщенного прогнозирующего управления
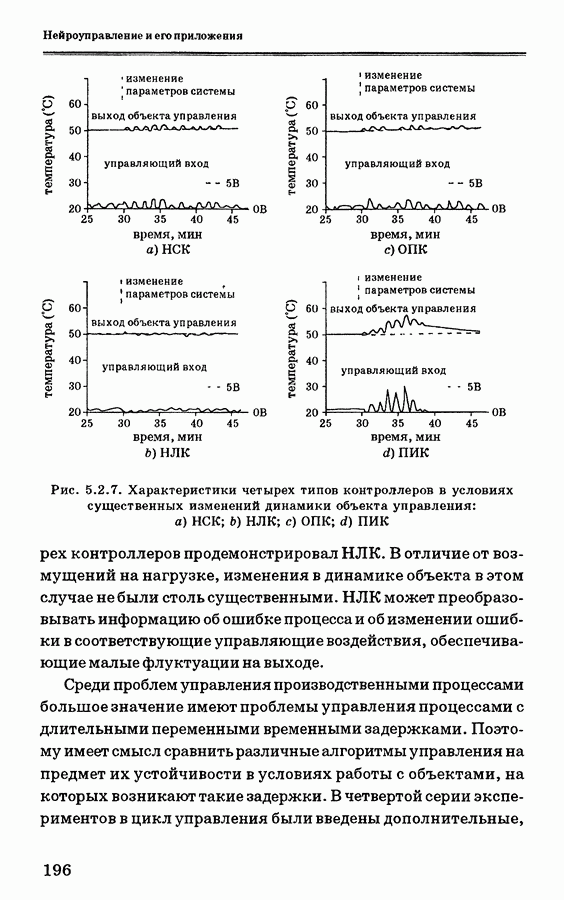
- 5.2.6. Экспериментальные данные и их анализ
- 5.2.7. Заключение
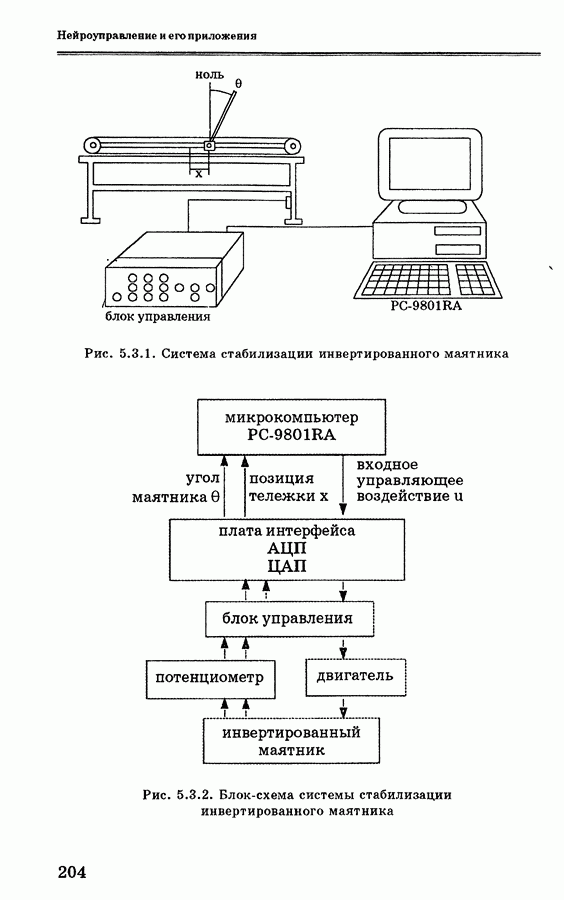
- 5.3. Система стабилизации инвертированного маятника на основе нейронных сетей
- 5.3.2. Система стабилизации инвертированного маятника
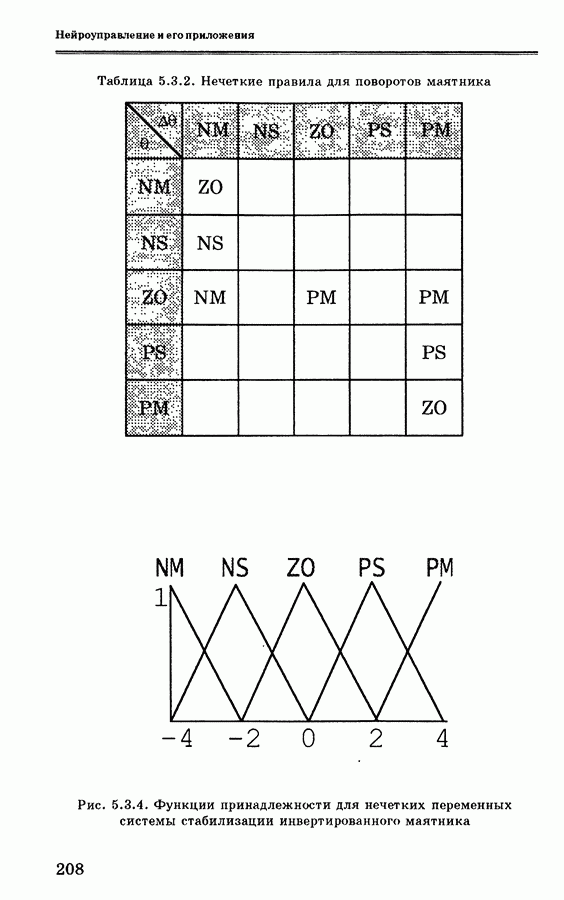
- 5.3.3. Инициализация поворотного управления с использованием нечеткой логики
- 5.3.4. Применение стратегии оптимального управления для стабилизации маятника
- 5.3.5. Точное управление на основе нейронных сетей
- 5.3.6. Заключение
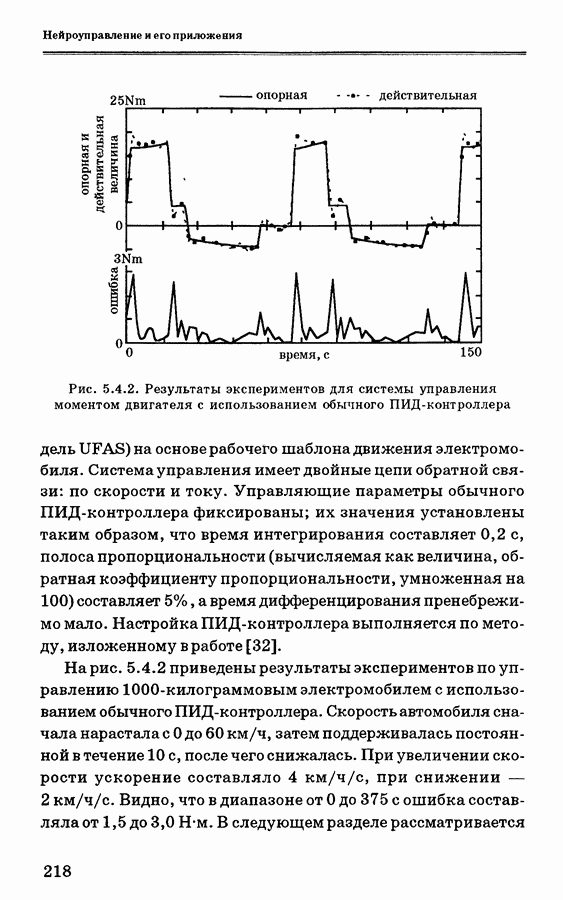
- 5.4. Применение ПИД-нейроконтроллера с самонастройкой для управления скоростью электромобиля
- 5.4.2. Система управления электромобилем
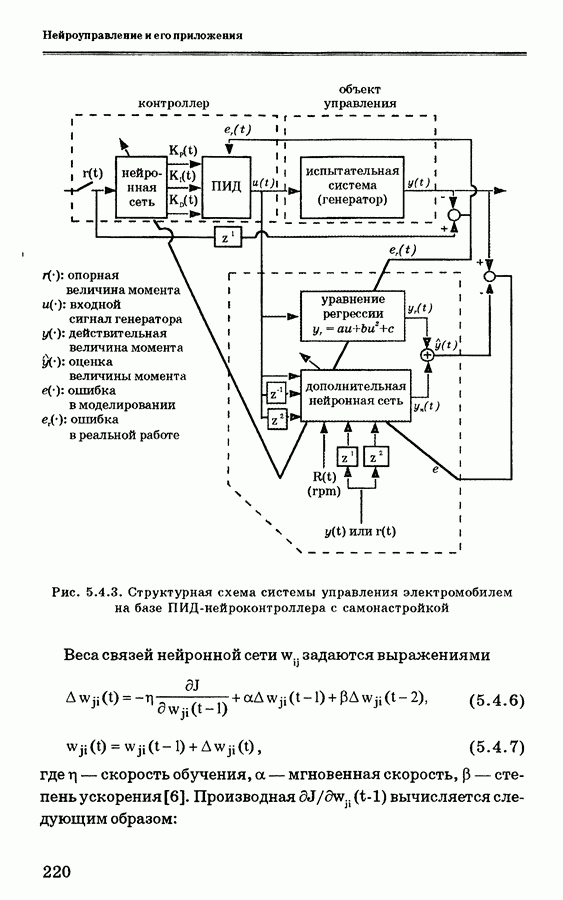
- 5.4.3. ПИД-нейроконтроллер с самонастройкой
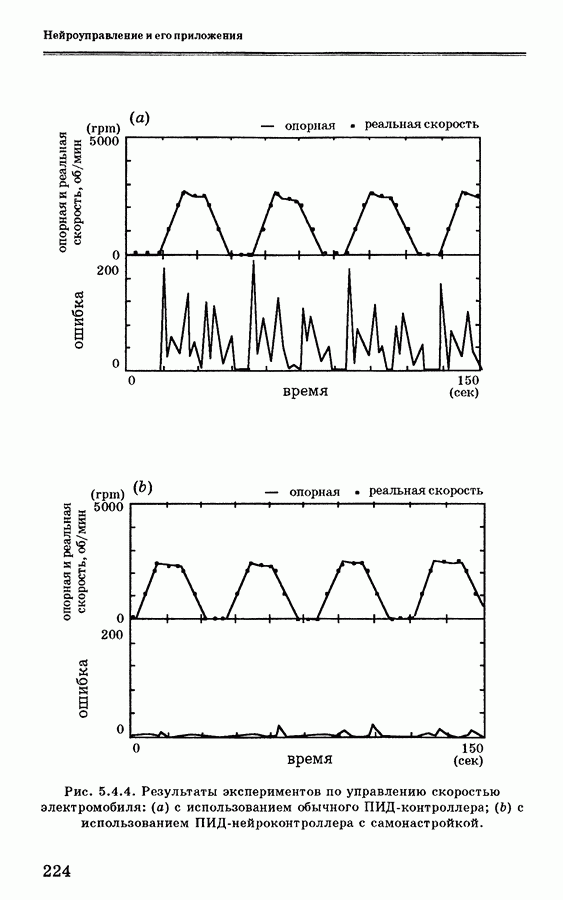
- 5.4.4. Применение нейронной сети для управления скоростью электромобиля
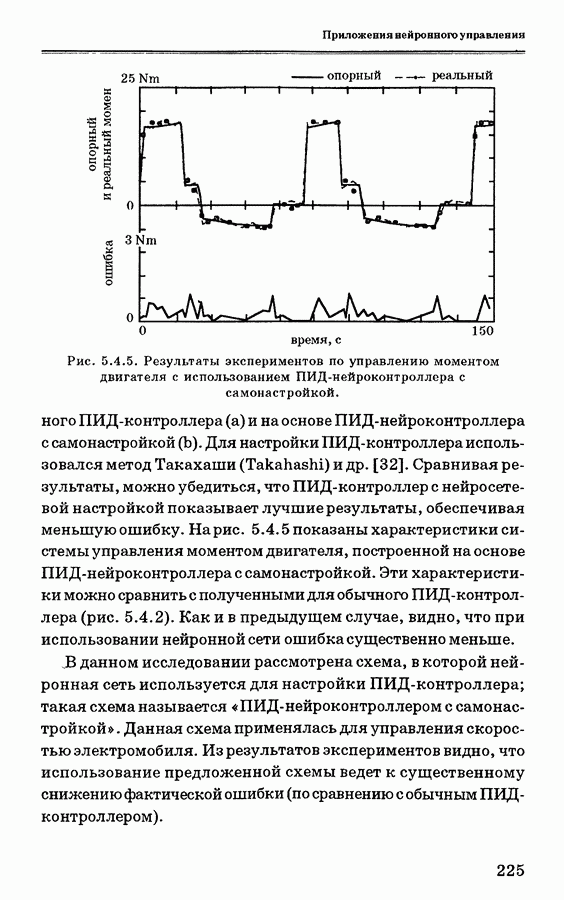
- 5.4.5. Заключение
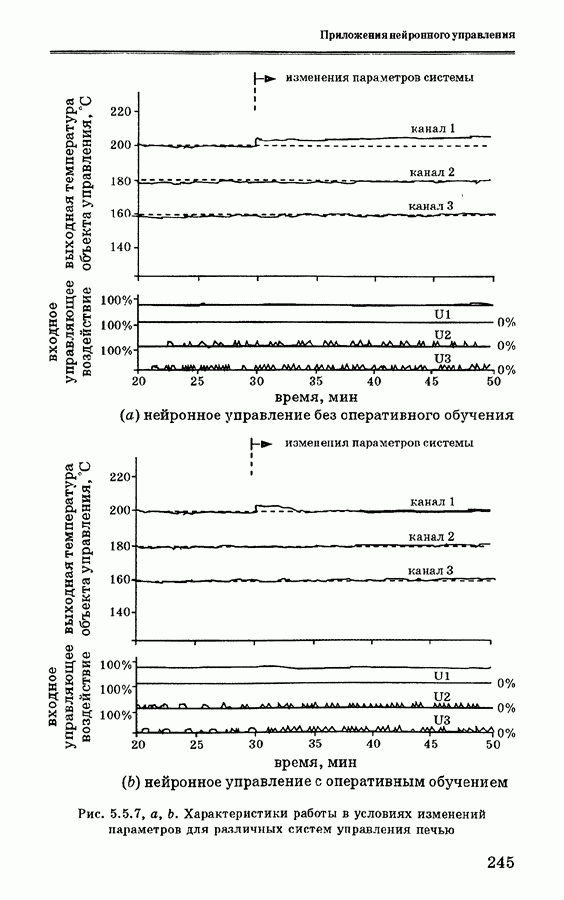
- 5.5. Применение нейронных сетей для управления печью
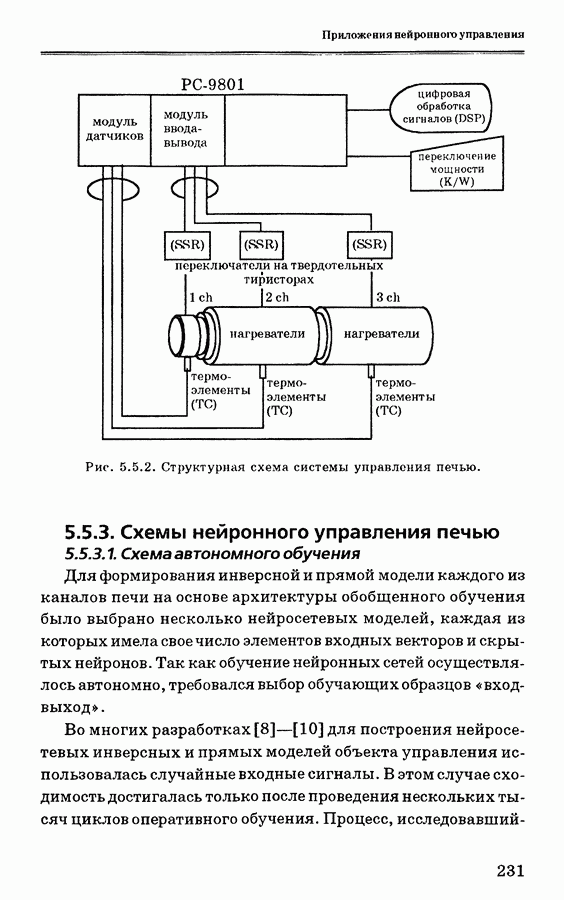
- 5.5.2. Система управления печью
- 5.5.3. Схемы нейронного управления печью
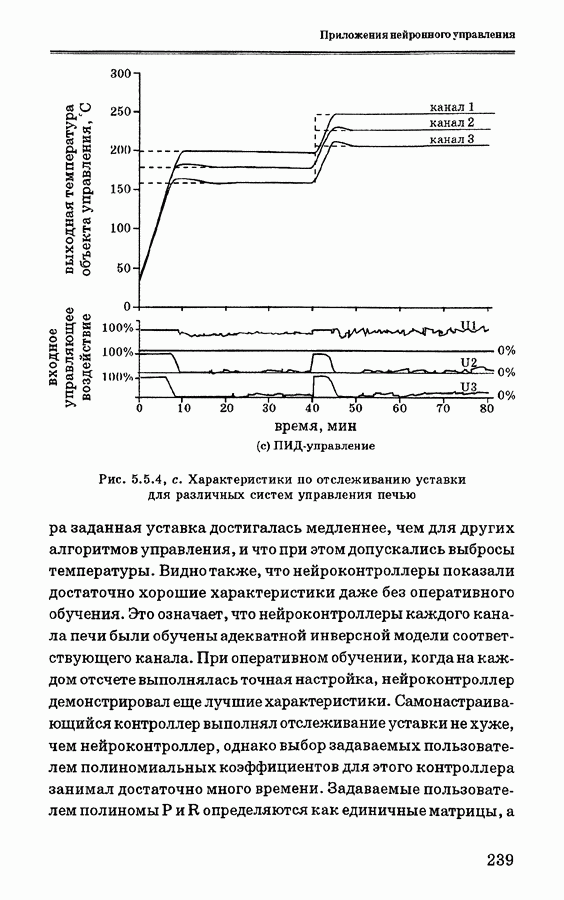
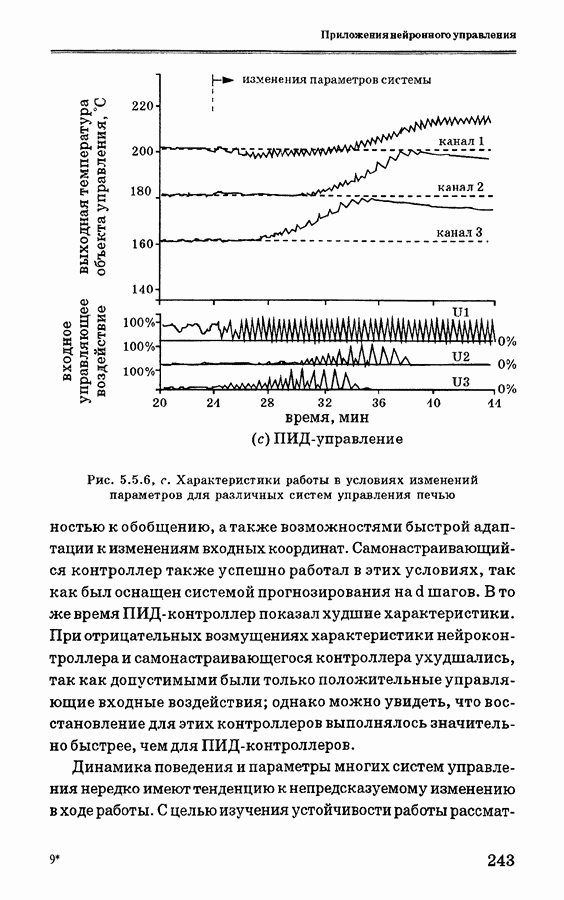
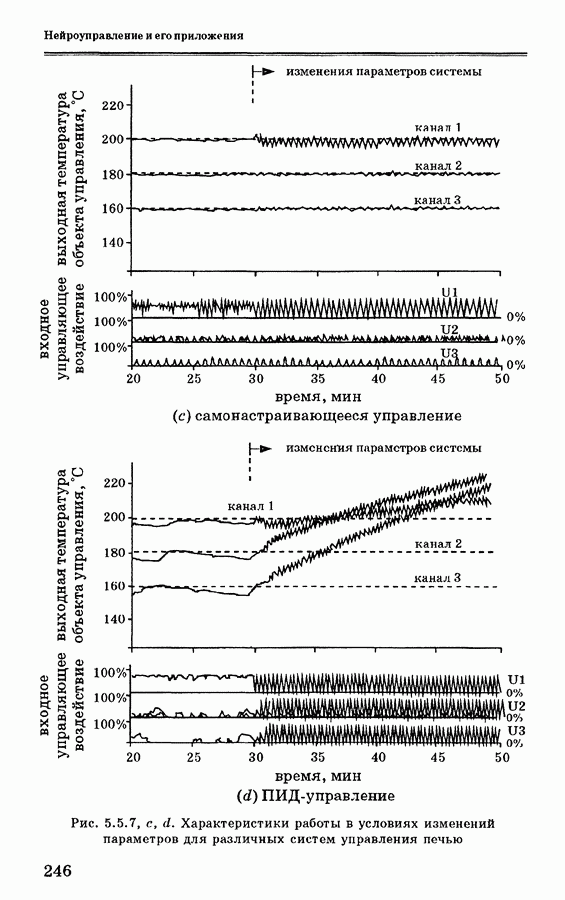
- 5.5.4. Анализ экспериментальных данных
- 5.6. Заключительные замечания и выводы
- Литература
- ЛИСТИНГ ПРОГРАММЫ