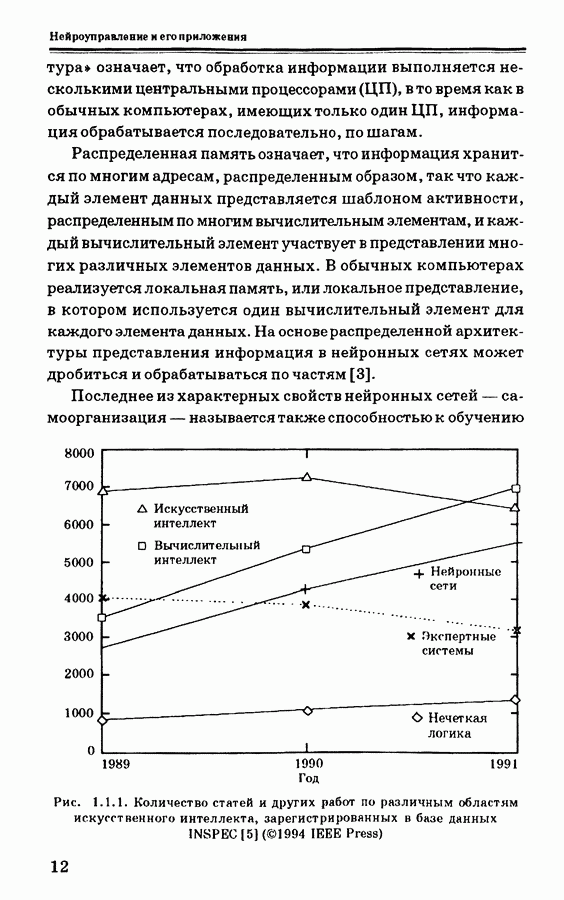
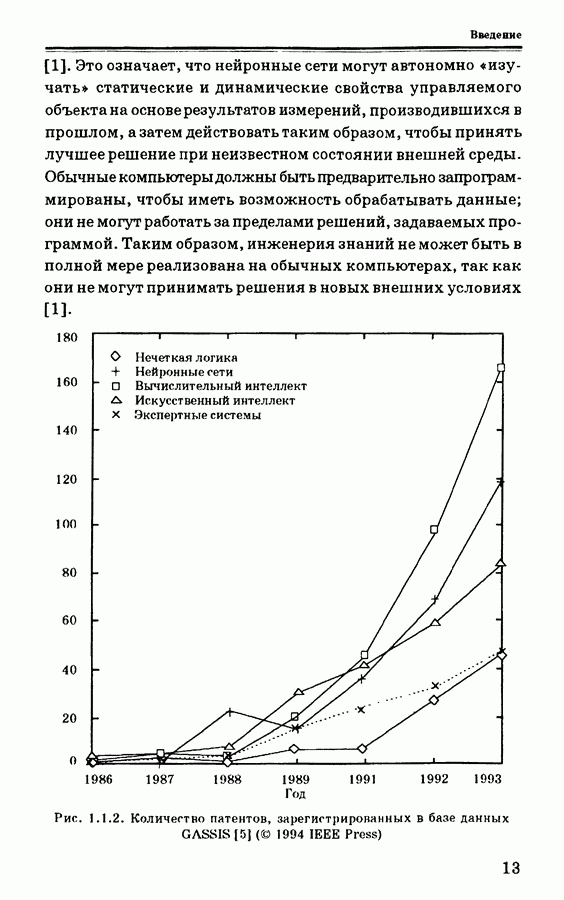
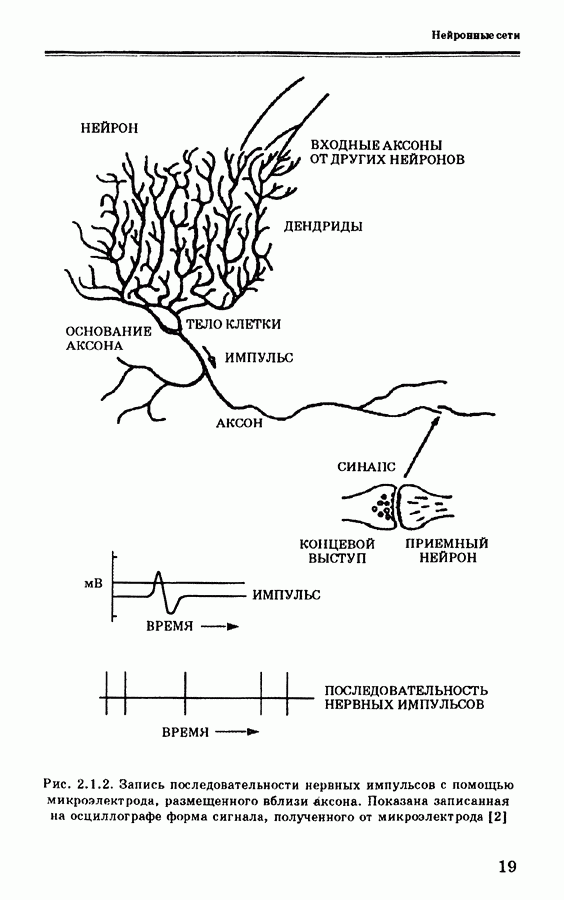
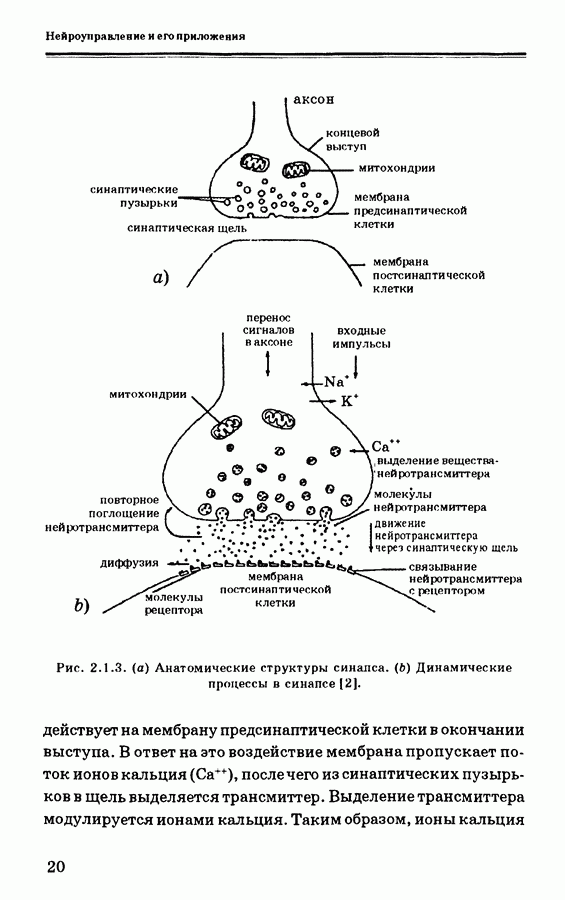
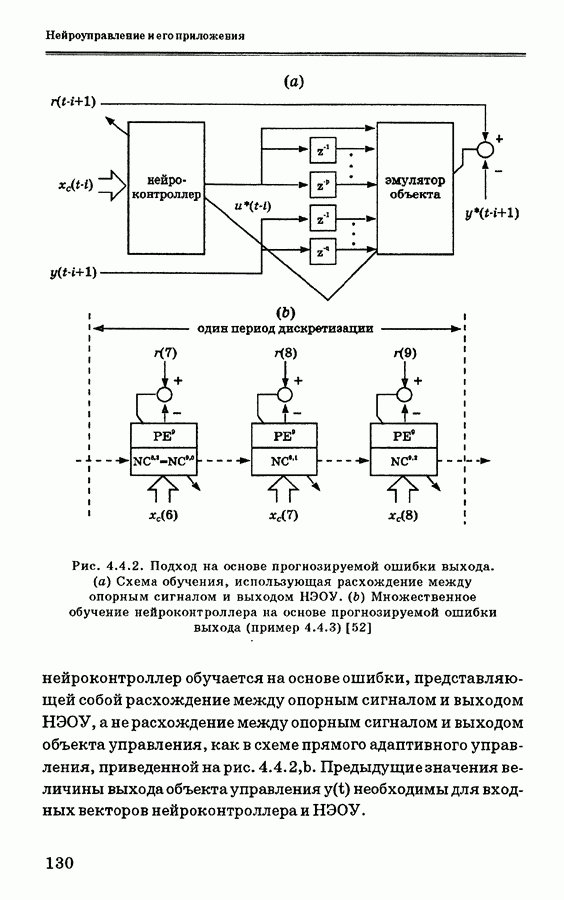
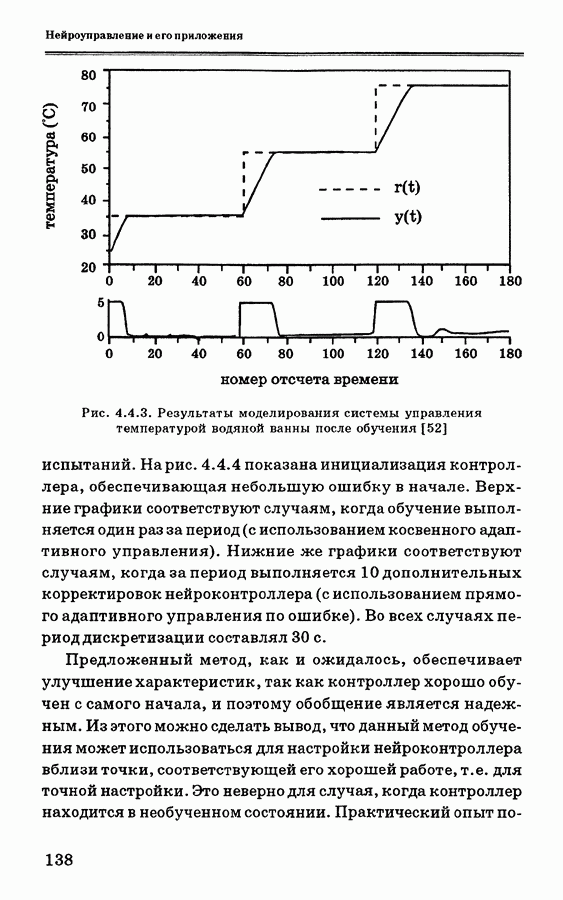
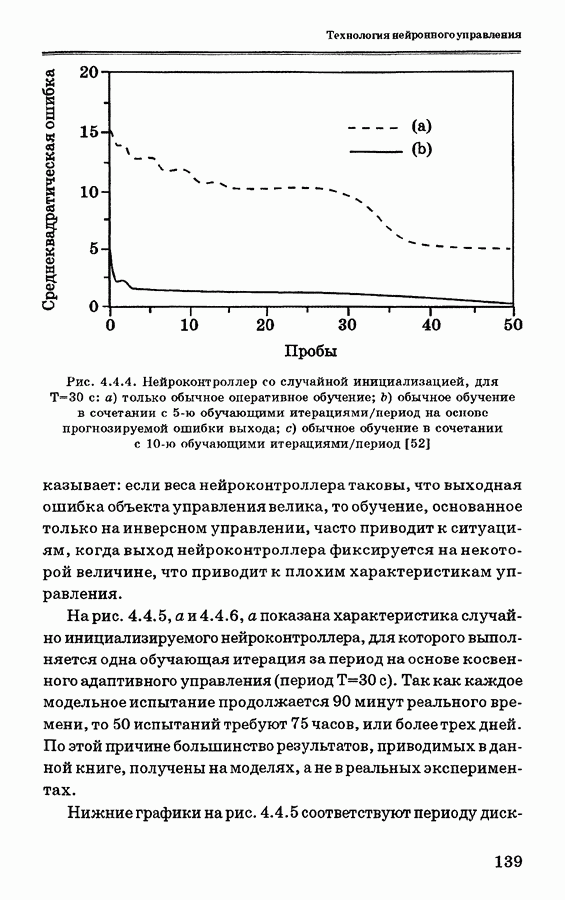
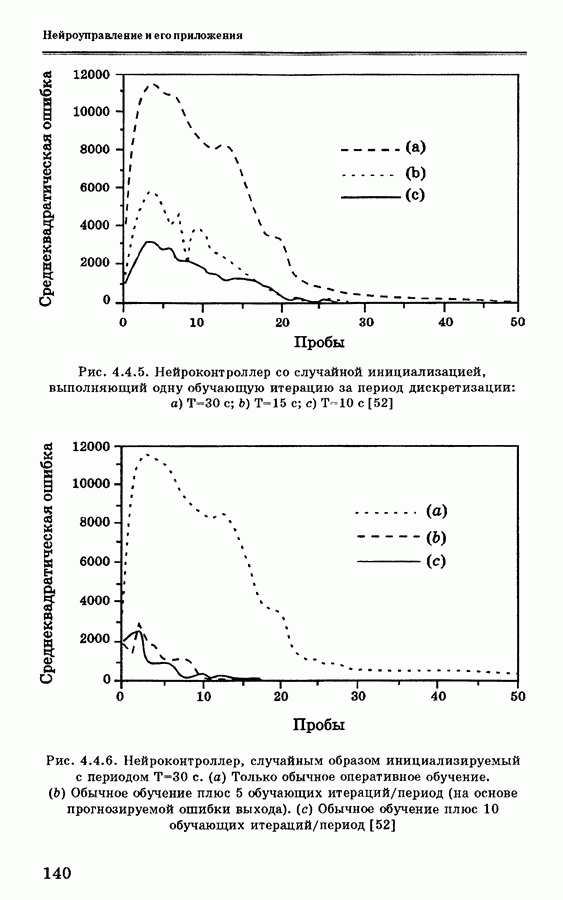
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
4.7. Расширение применения нейроконтроллеров параллельного типа
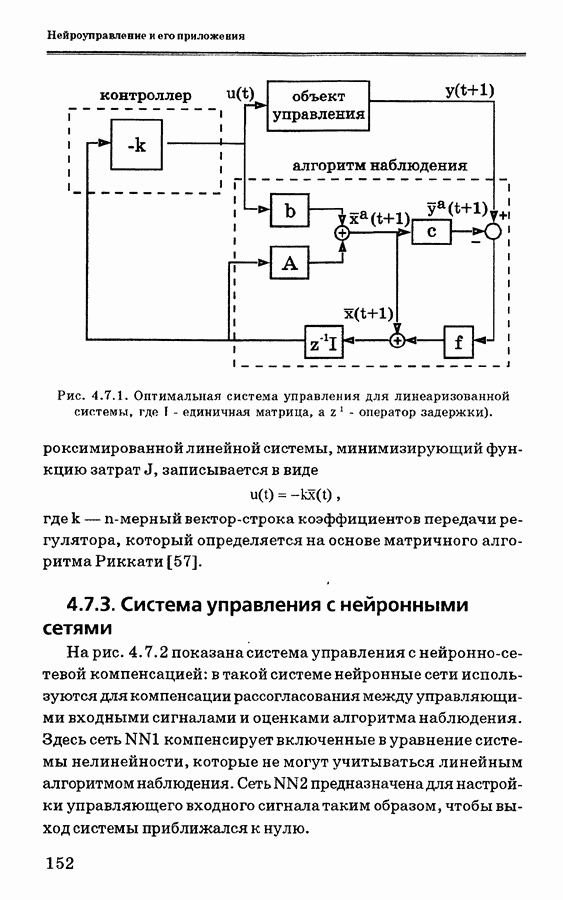
Еще одно применение таких нейроконтроллеров состоит в решении задач управления нелинейными системами. Такой подход предложен в работе [13] и расширен в работе [57]. Основная его идея состоит в том, чтобы в качестве аппроксимации первого порядка создать линейную математическую модель нелинейной динамической системы, а затем применить нейронную сеть для уменьшения расхождения между выходом модели и фактическим выходом системы. Используя линейную модель, можно определить закон оптимального управления для квадратичной функции затрат. Однако он не должен быть действительным законом управления, так как выведен на основе линеаризованной математической модели. С целью настройки управляющего входного сигнала, обеспечивающей минимизацию квадратичной функции затрат для реального объекта управления, вводится нейронная сеть. Соответствующий алгоритм рассматривается ниже.
4.7.1. Описание системы управления
Рассмотрим обобщенный объект управления, который описывается системой уравнений

где  — скалярные функции, обозначающие соответственно вход и выход системы;
— скалярные функции, обозначающие соответственно вход и выход системы;  -мерный вектор состояния;
-мерный вектор состояния;  — параметры системы; А — обозначение нелинейной части системы. Эта составляющая необходима в качестве дополнительного члена, когда выполняется подстройка линейной модели в качестве модели объекта управления. Задача управления состоит в том, чтобы найти оптимальное решение, минимизирующее следующую функцию затрат
— параметры системы; А — обозначение нелинейной части системы. Эта составляющая необходима в качестве дополнительного члена, когда выполняется подстройка линейной модели в качестве модели объекта управления. Задача управления состоит в том, чтобы найти оптимальное решение, минимизирующее следующую функцию затрат 

где у — положительная константа.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРОВ ПЕРЕВОДА
- 1. ВВЕДЕНИЕ
- 1.1. Общие сведения об интеллектуальном управлении
- 2. НЕЙРОННЫЕ СЕТИ
- 2.2. Алгоритм обратного распространения
- 2.2.2. Вывод алгоритма обратного распространения
- 2.2.2.2. Правило для скрытого слоя
- 2.2.3. Алгоритм обратного распространения: порядок реализации
- 2.2.4. Обсуждение алгоритма обратного распространения
- 2.3. Заключение
- 3. ТРАДИЦИОННЫЕ СХЕМЫ УПРАВЛЕНИЯ
- 3.2. ПИ- и ПИД-контроллеры с дискретным временем
- 3.3. Управление с самонастройкой
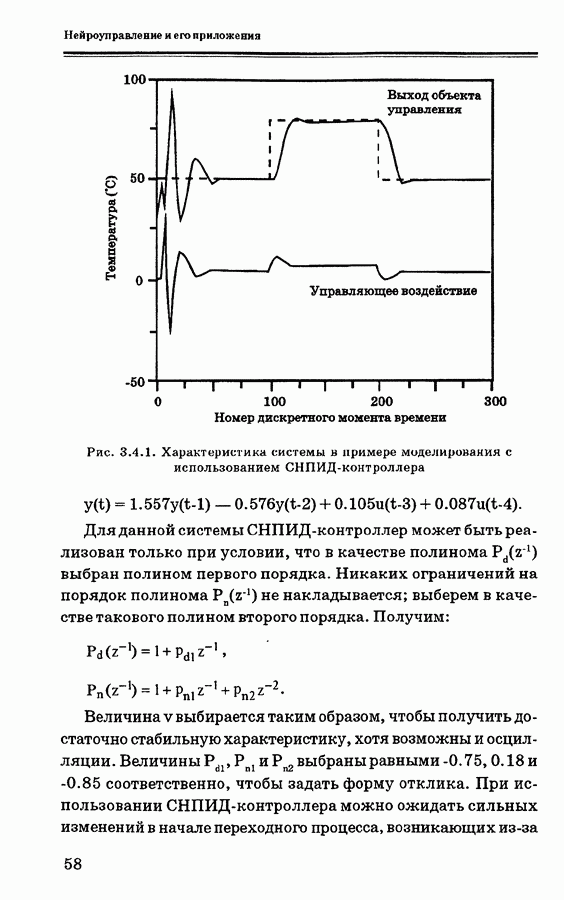
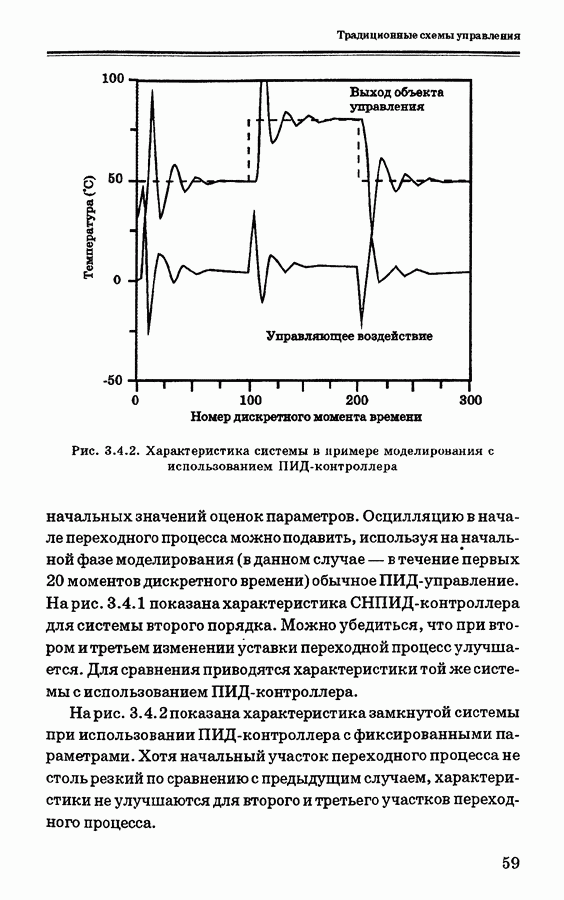
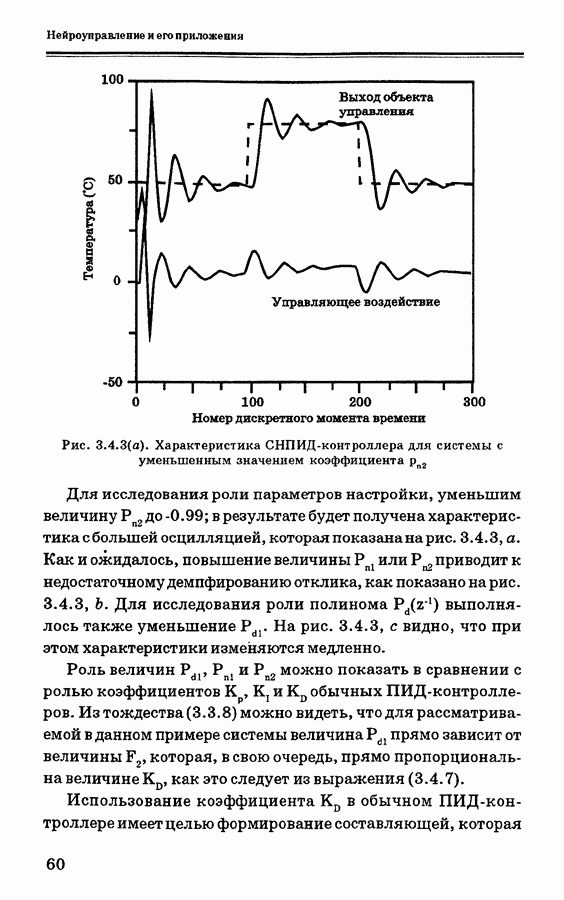
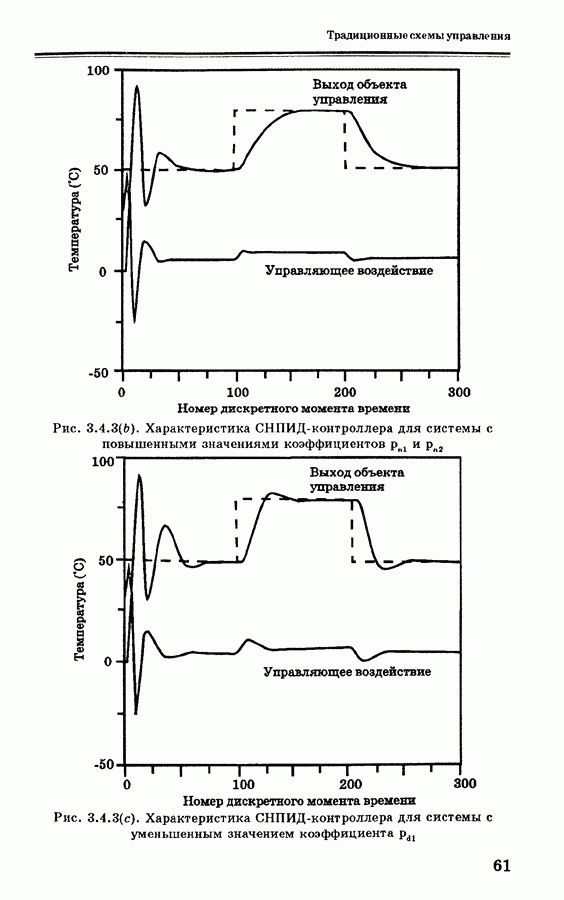
- 3.4. Самонастраивающиеся ПИ- и ПИД- контроллеры
- 3.5. ПИД-управление с самонастройкой: многомерный подход
- 3.5.1. Пример моделирования
- 3.6. Обобщенное прогнозирующее управление: некоторые теоретические аспекты
- 3.6.2. Модель объекта управления и решение задачи оптимизации
- 3.7. Управление на основе нечеткой логики
- 3.7.1. Краткие сведения по теории нечетких множеств и нечетких систем
- 3.7.2. Основная концепция нечеткого контроллера
- 3.8. Заключение
- 4. ТЕХНОЛОГИИ НЕЙРОННОГО УПРАВЛЕНИЯ
- 4.2. Общие сведения о нейронном управлении
- 4.2.1. Подходы к нейронному управлению
- 4.2.2. Общая схема управления
- 4.3. Последовательная схема нейронного управления
- 4.4. Расширение последовательной схемы нейронного управления
- 4.4.2. Нейроморфные структуры управления
- 4.4.3. Конфигурации обучения
- 4.4.4. Эффективное оперативное управление
- 4.4.5. Алгоритмы обучения
- 4.4.6. Оценка алгоритмов обучения на основе моделирования
- 4.5. Параллельная схема управления
- 4.6. Алгоритм обучения по ошибке обратной связи
- 4.7. Расширение применения нейроконтроллеров параллельного типа
- 4.7.2. Линеаризованная система управления
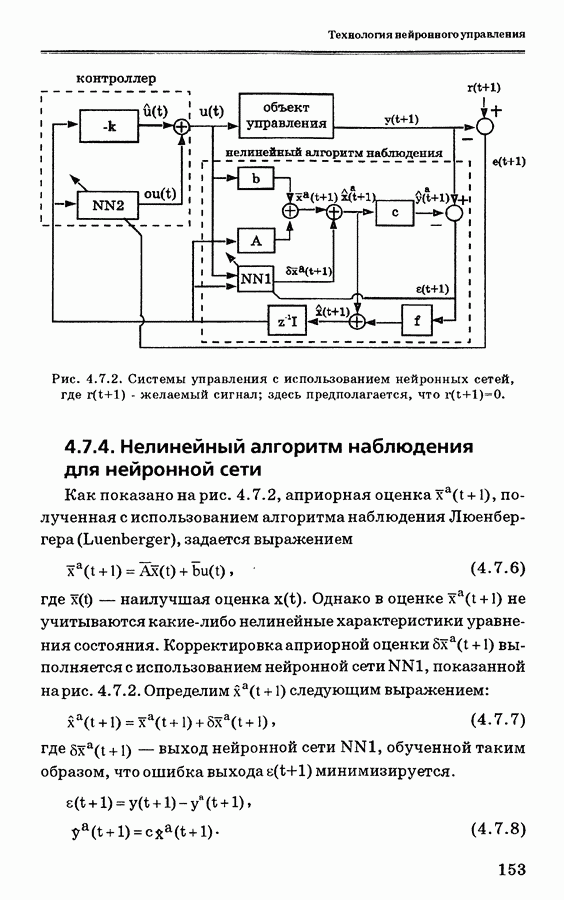
- 4.7.3. Система управления с нейронными сетями
- 4.7.4. Нелинейный алгоритм наблюдения для нейронной сети
- 4.7.5. Нелинейный контроллер для нейронной сети
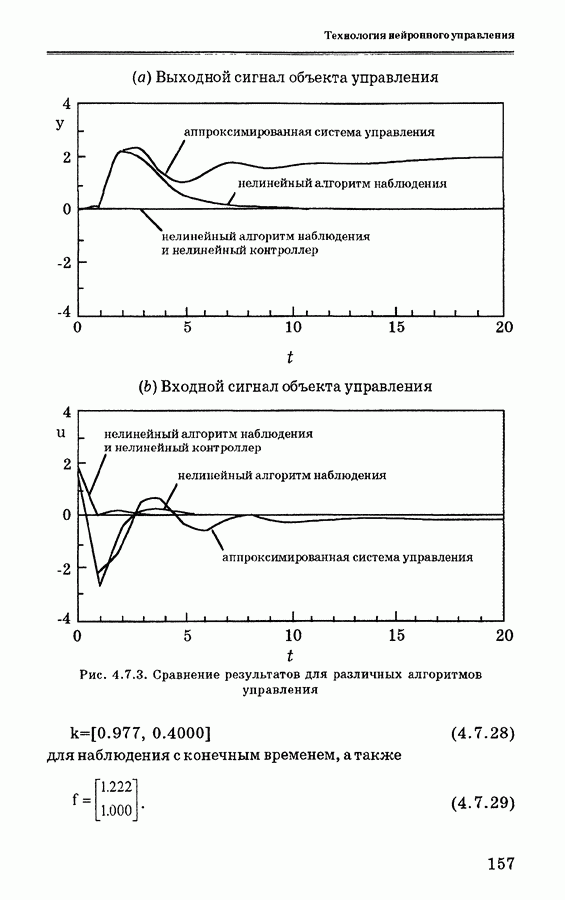
- 4.7.6. Численное моделирование
- 4.8. Схема нейронного управления с самонастройкой
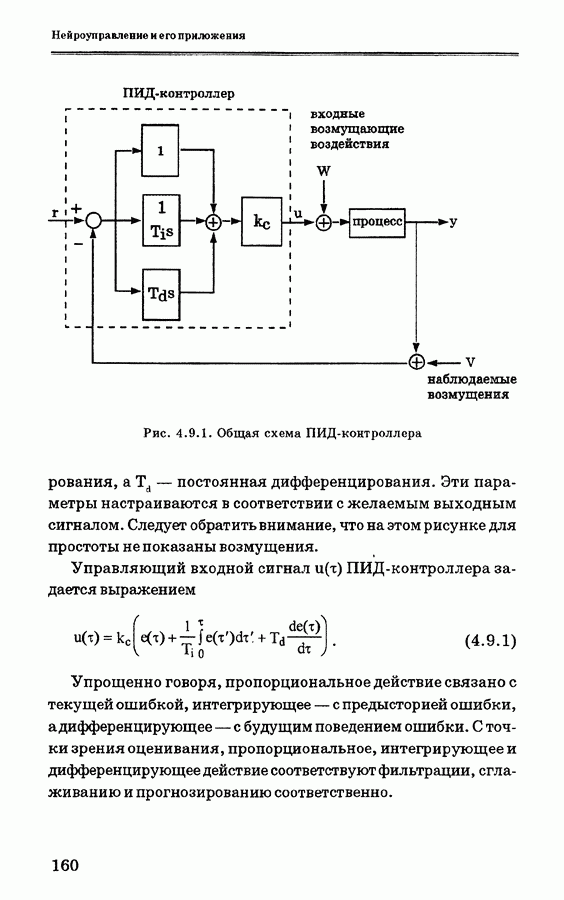
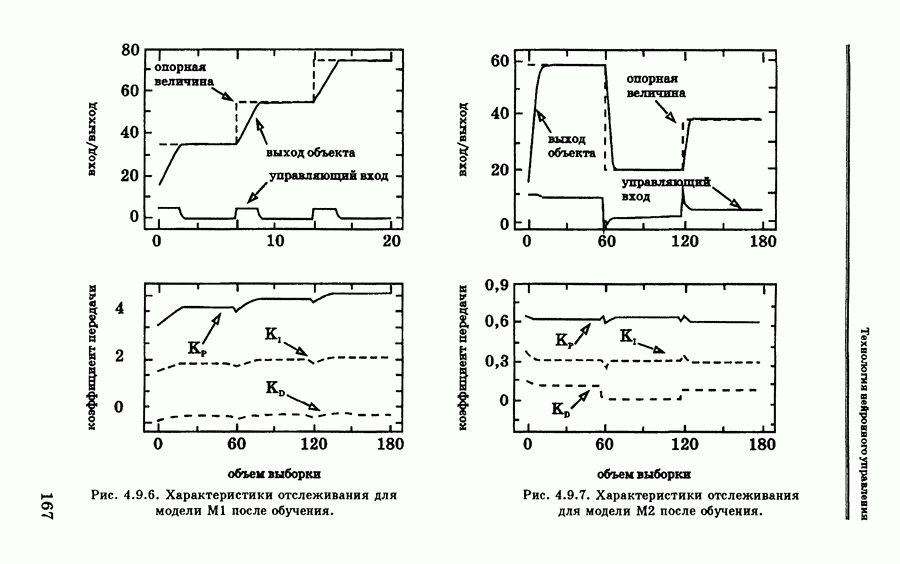
- 4.9. ПИД-нейроконтроллер с самонастройкой
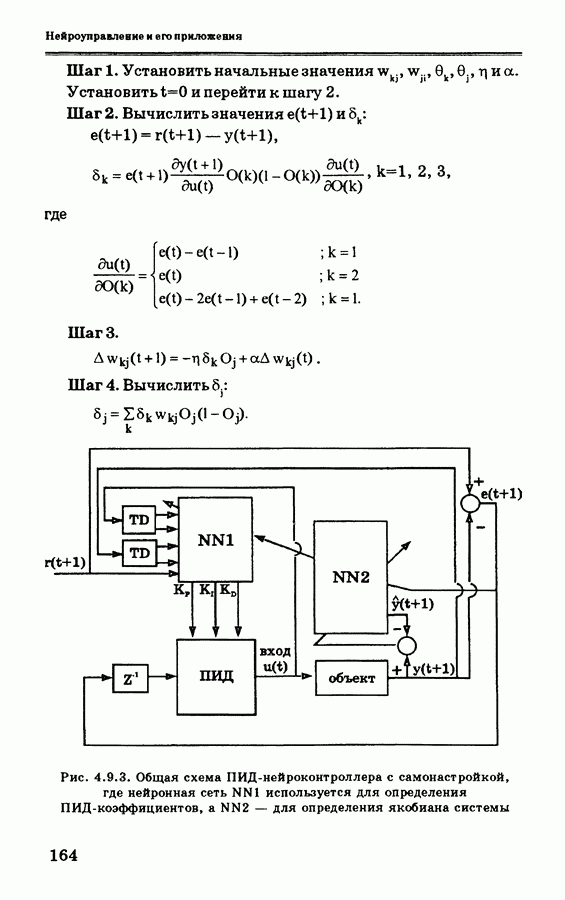
- 4.9.1. Вывод уравнений ПИД-нейроконтроллера с самонастройкой
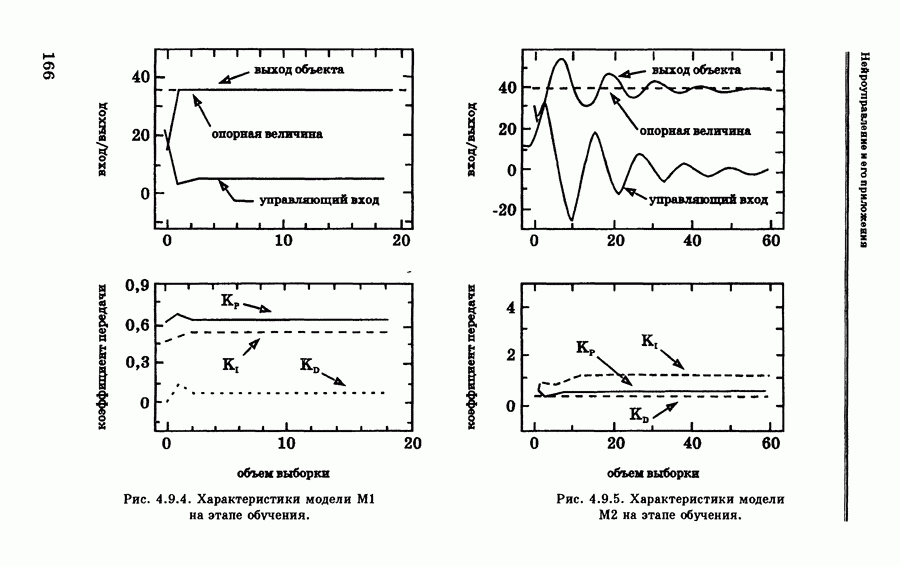
- 4.9.2. Примеры эмуляции
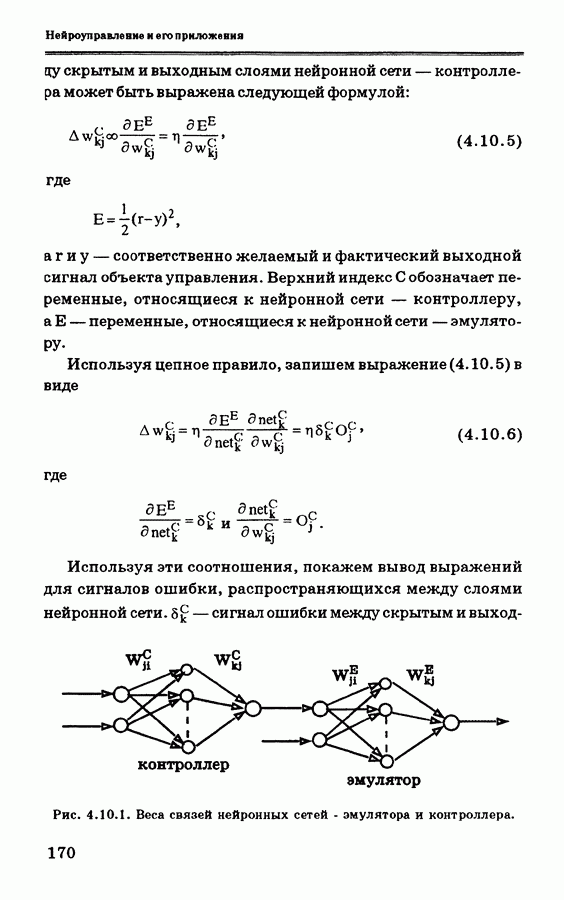
- 4.10. Схема нейронного управления с эмулятором и контроллером (схема обратного распространения во времени)
- 4.11. Заключение
- 5. ПРИЛОЖЕНИЯ НЕЙРОННОГО УПРАВЛЕНИЯ
- 5.2. Применение нейронного управления в системе регулирования процессов в водяной ванне и сравнение его с другими схемами управления
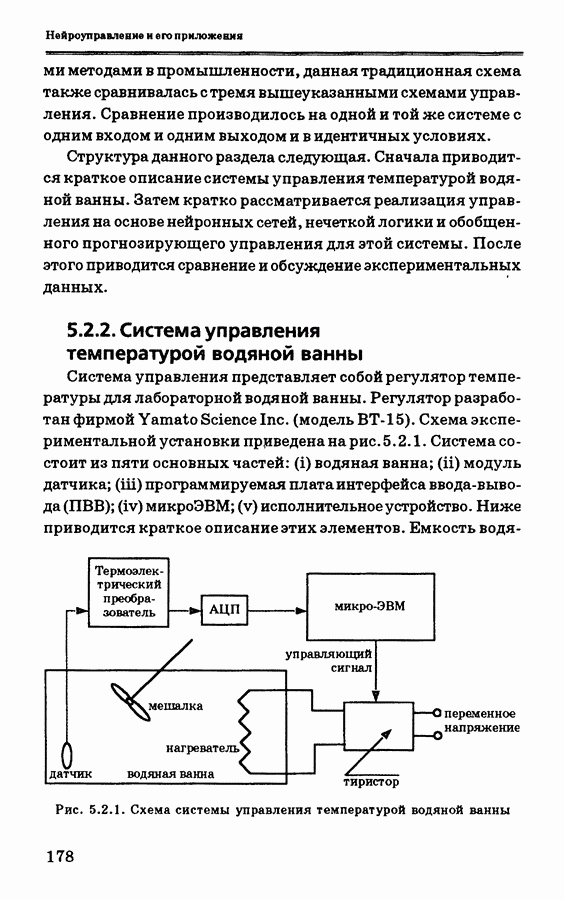
- 5.2.2. Система управления температурой водяной ванны
- 5.2.3. Схема нейронного управления
- 5.2.4. Схема управления на основе нечеткой логики
- 5.2.5. Схема обобщенного прогнозирующего управления
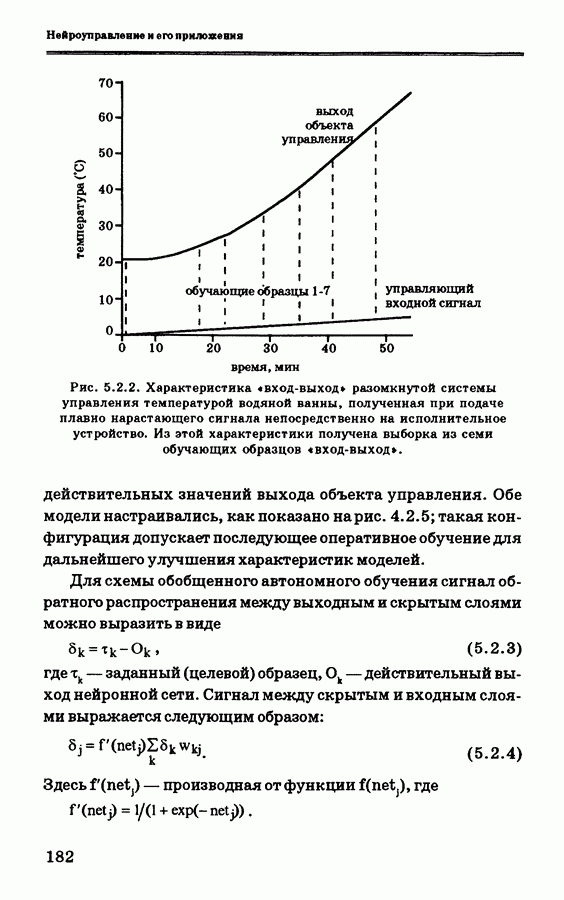
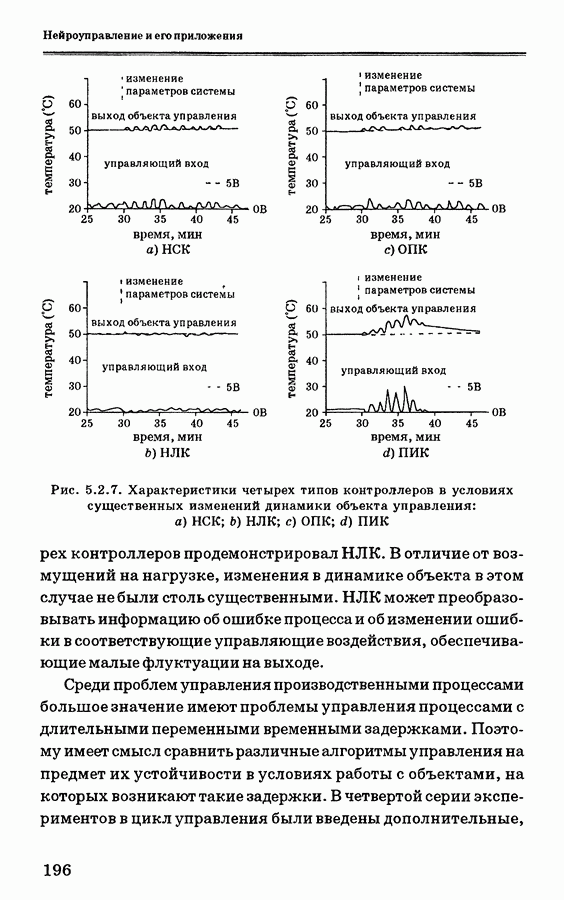
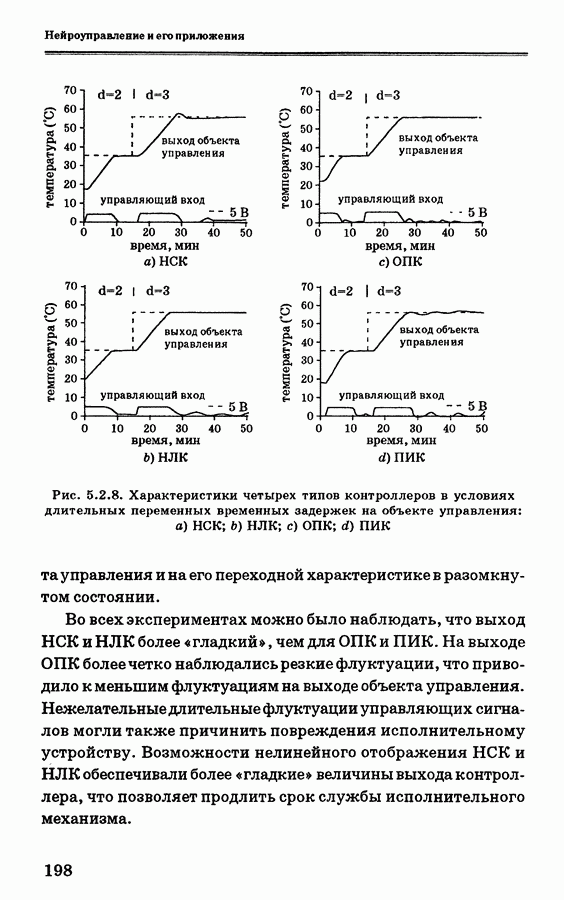
- 5.2.6. Экспериментальные данные и их анализ
- 5.2.7. Заключение
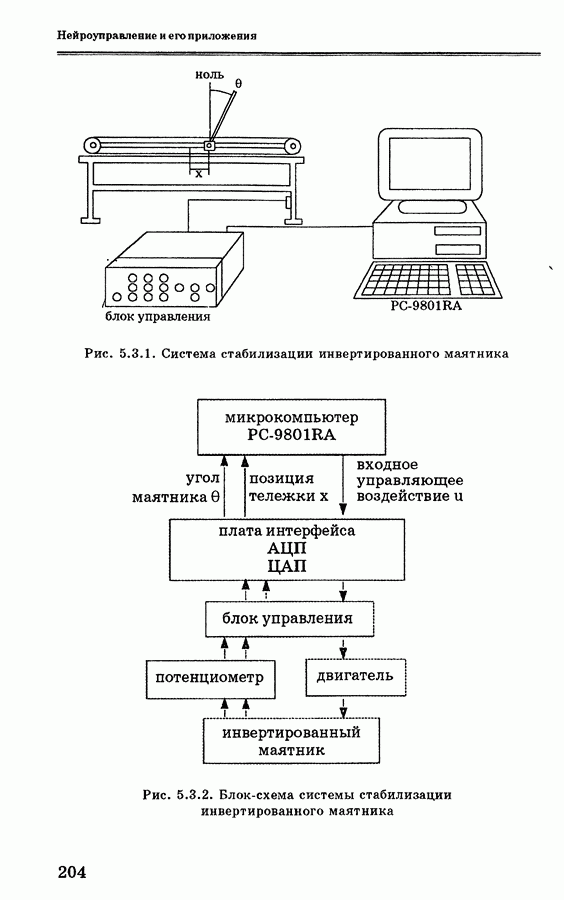
- 5.3. Система стабилизации инвертированного маятника на основе нейронных сетей
- 5.3.2. Система стабилизации инвертированного маятника
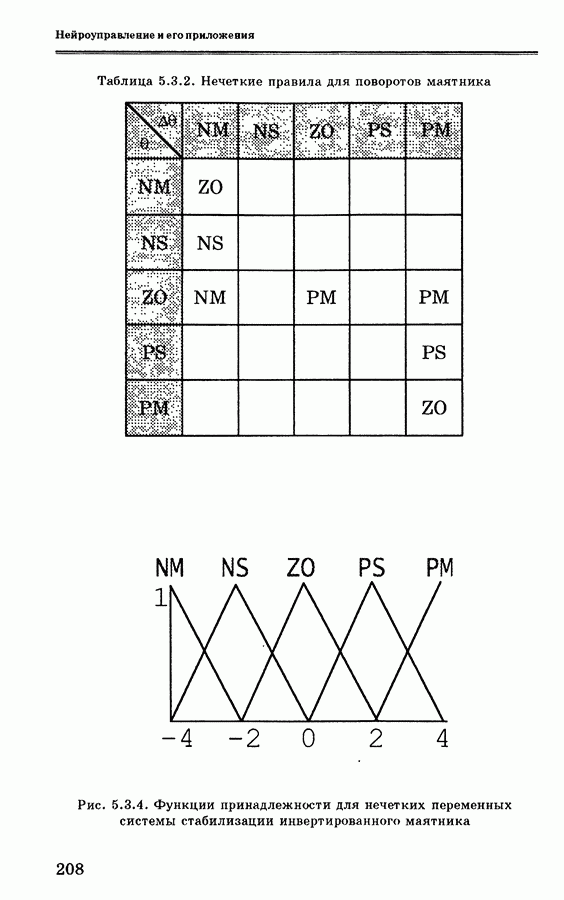
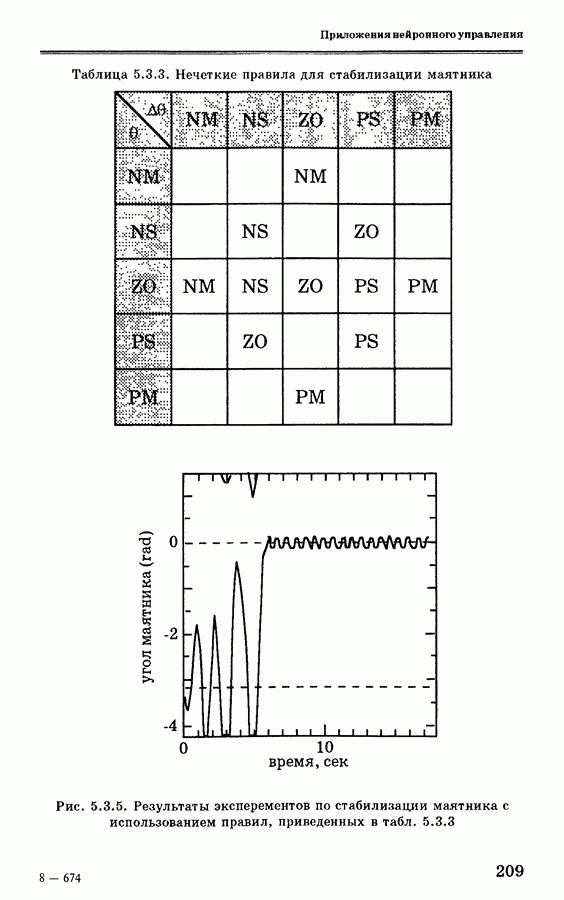
- 5.3.3. Инициализация поворотного управления с использованием нечеткой логики
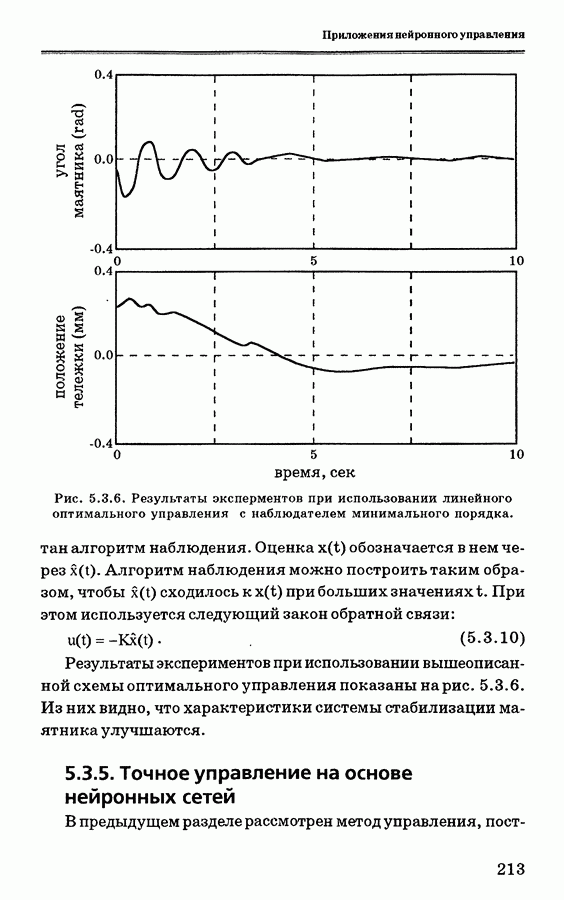
- 5.3.4. Применение стратегии оптимального управления для стабилизации маятника
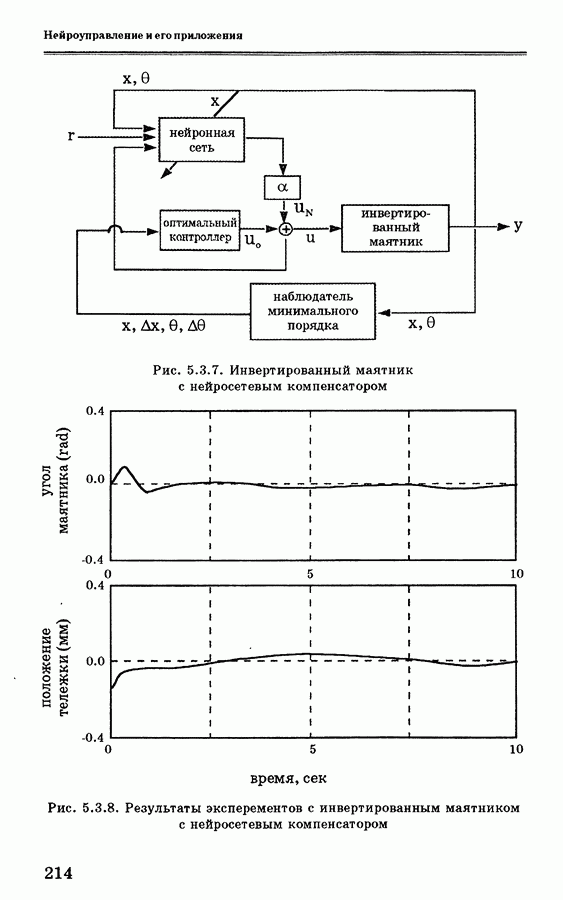
- 5.3.5. Точное управление на основе нейронных сетей
- 5.3.6. Заключение
- 5.4. Применение ПИД-нейроконтроллера с самонастройкой для управления скоростью электромобиля
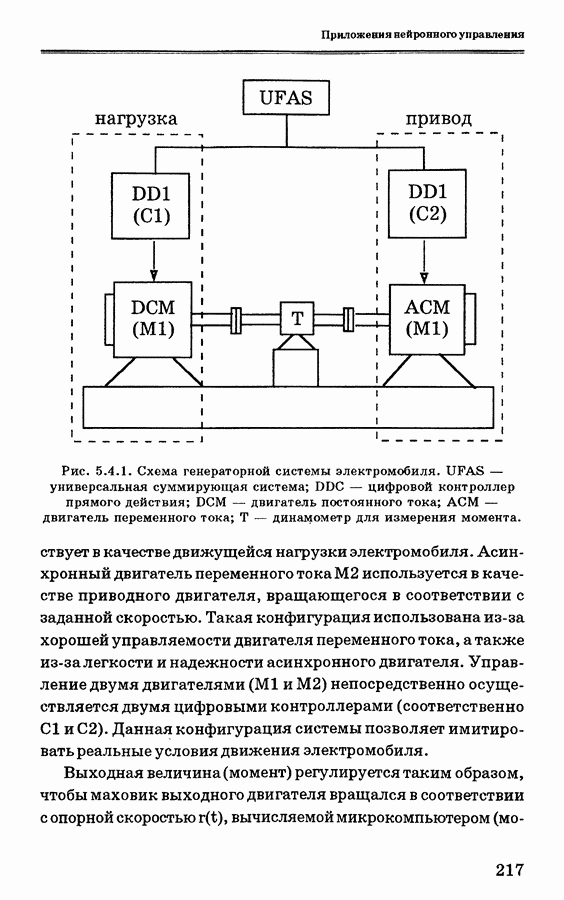
- 5.4.2. Система управления электромобилем
- 5.4.3. ПИД-нейроконтроллер с самонастройкой
- 5.4.4. Применение нейронной сети для управления скоростью электромобиля
- 5.4.5. Заключение
- 5.5. Применение нейронных сетей для управления печью
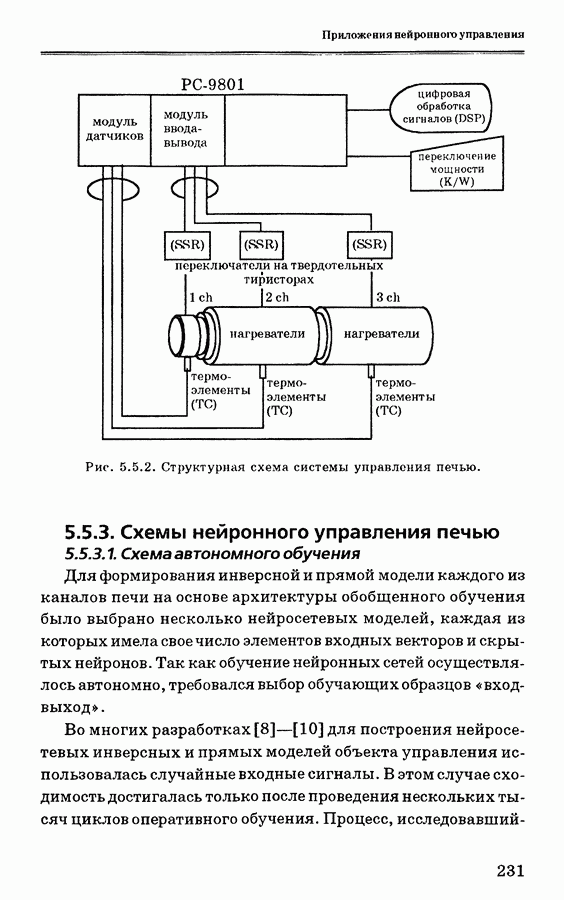
- 5.5.2. Система управления печью
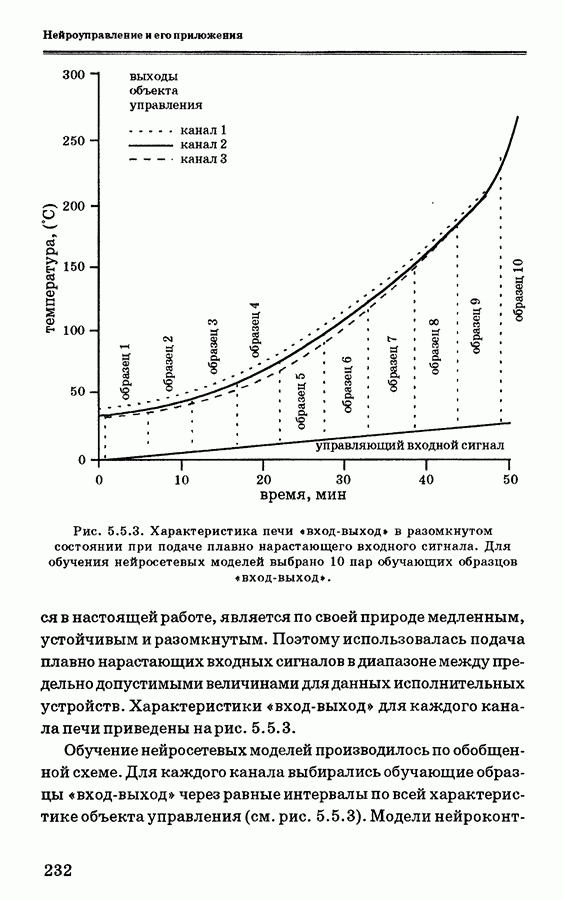
- 5.5.3. Схемы нейронного управления печью
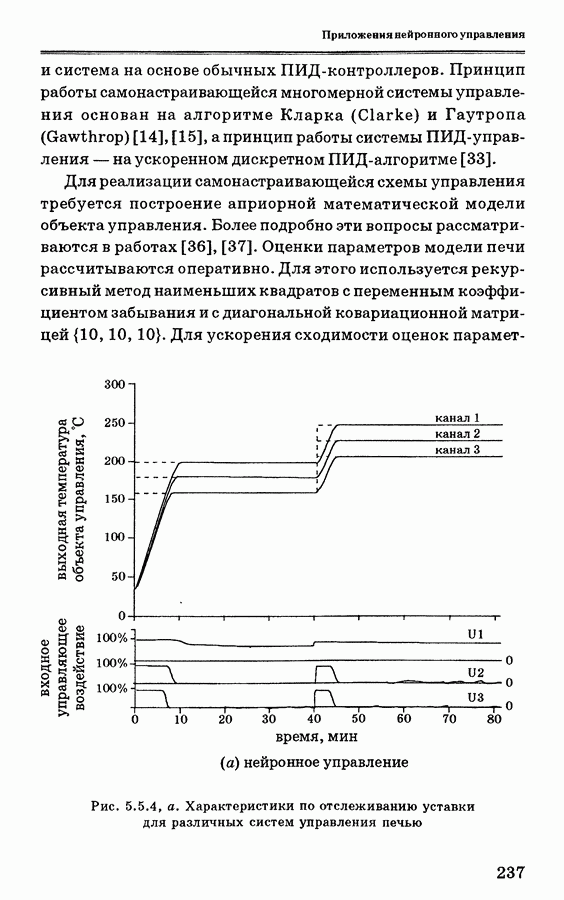
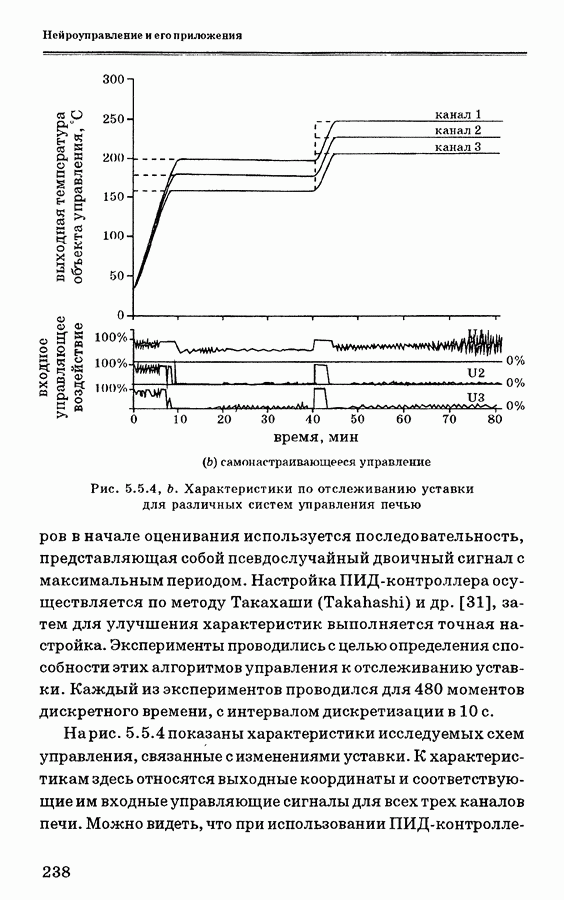
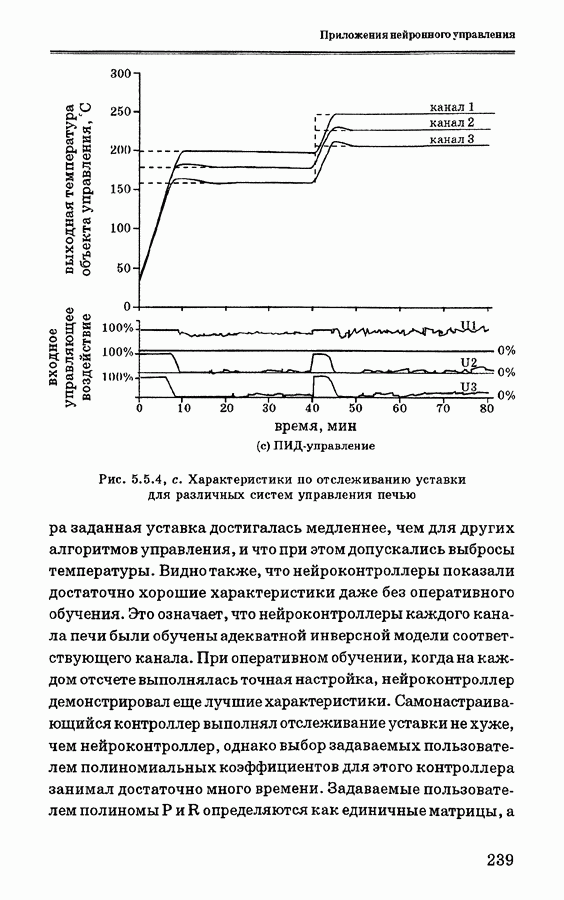
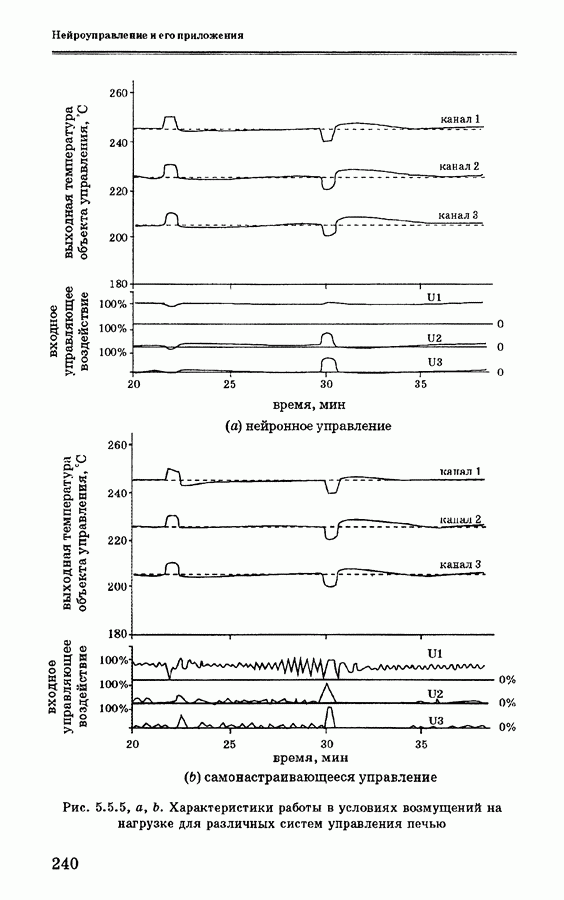
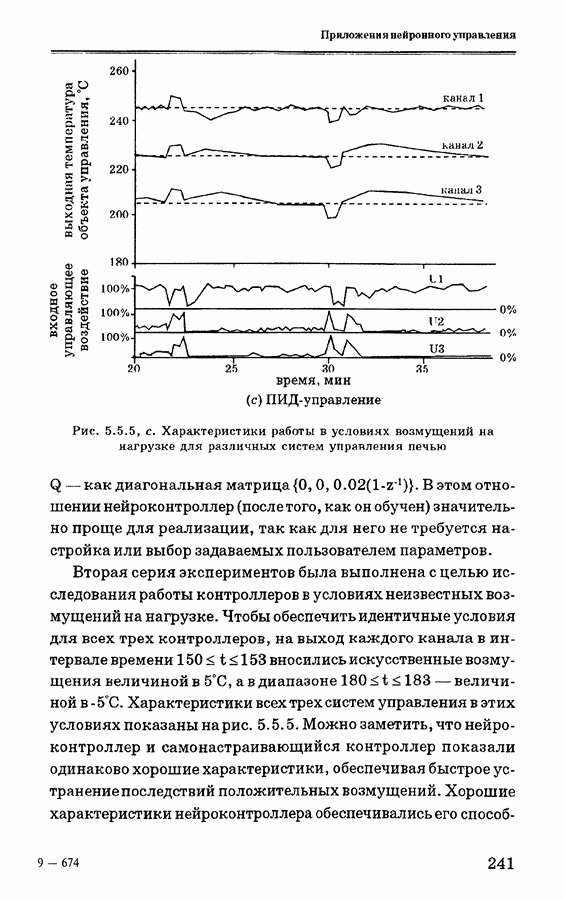
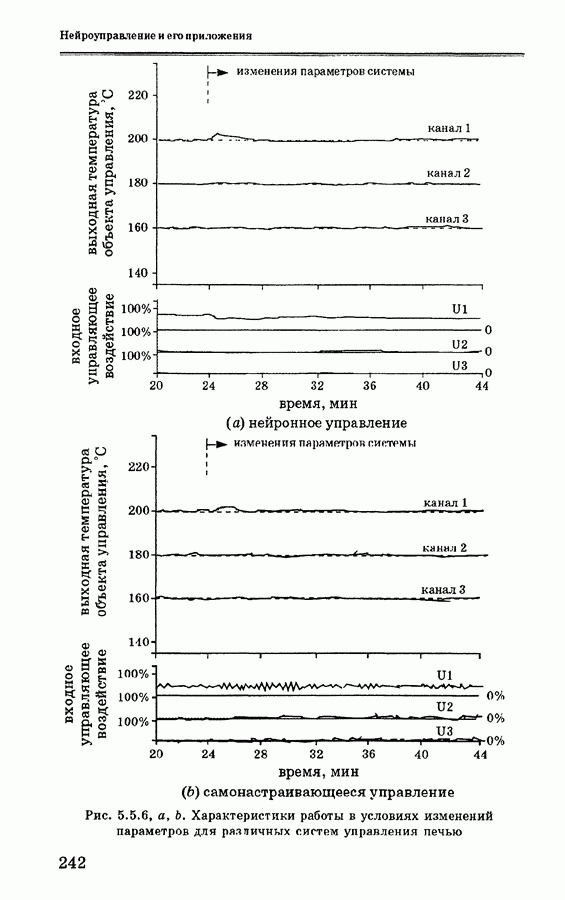
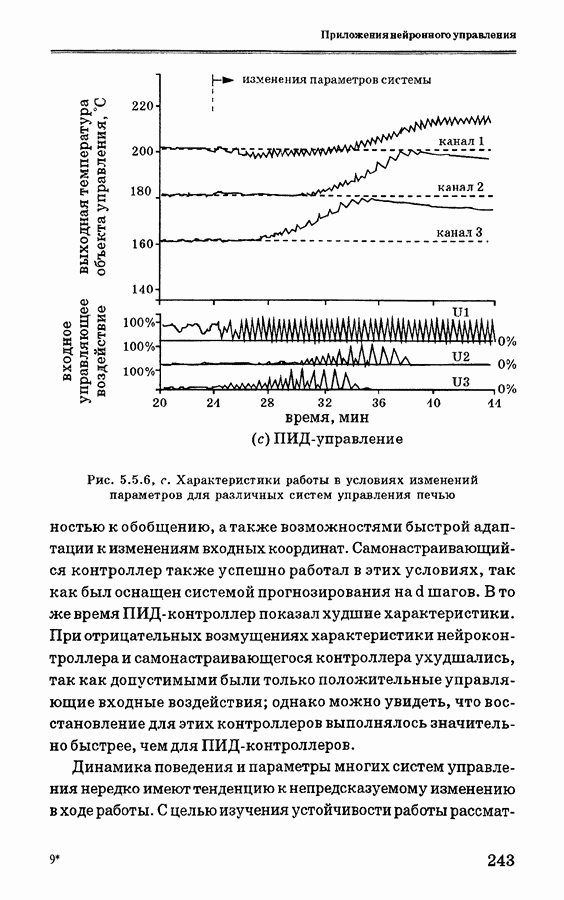
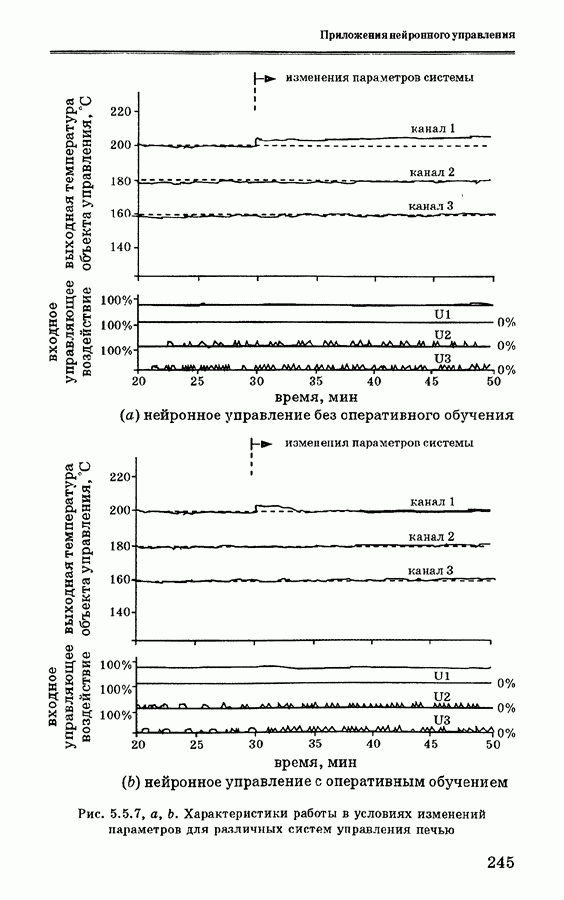
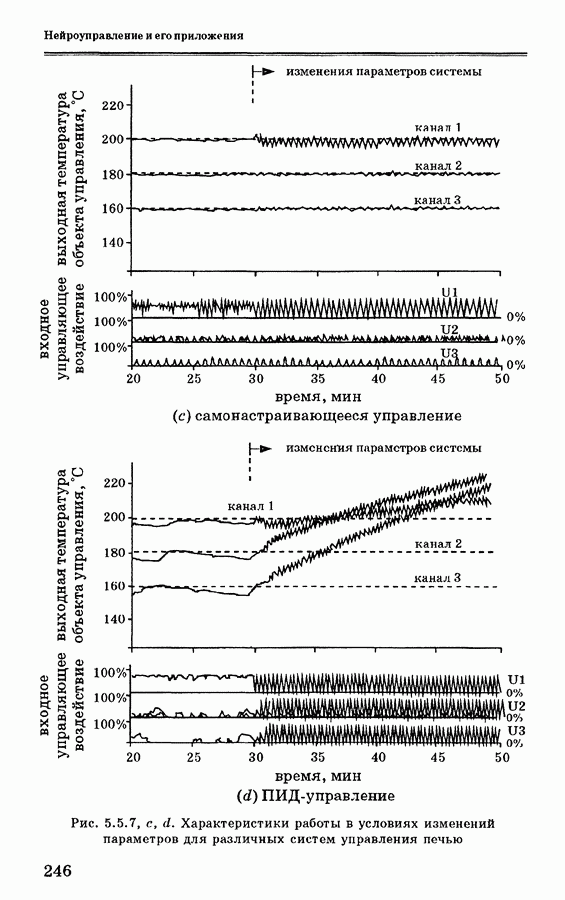
- 5.5.4. Анализ экспериментальных данных
- 5.6. Заключительные замечания и выводы
- Литература
- ЛИСТИНГ ПРОГРАММЫ