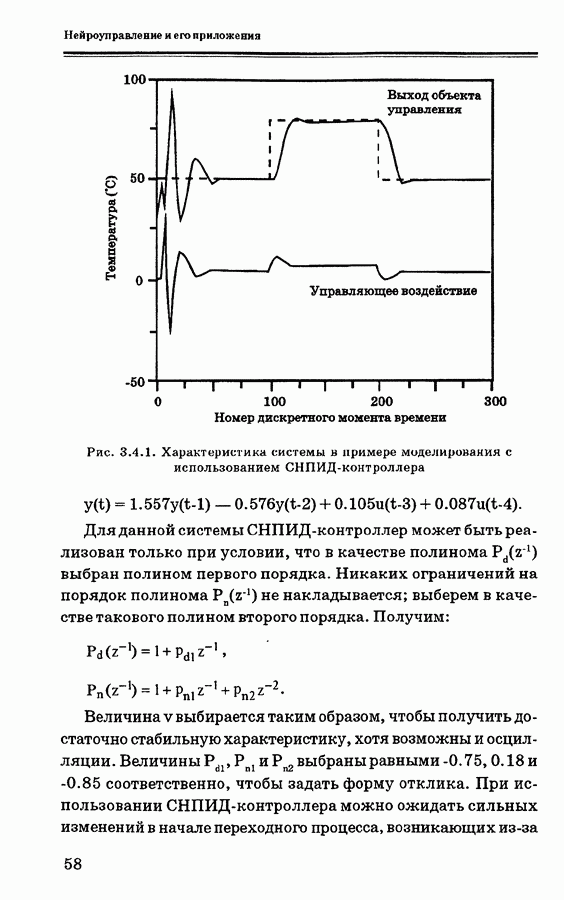
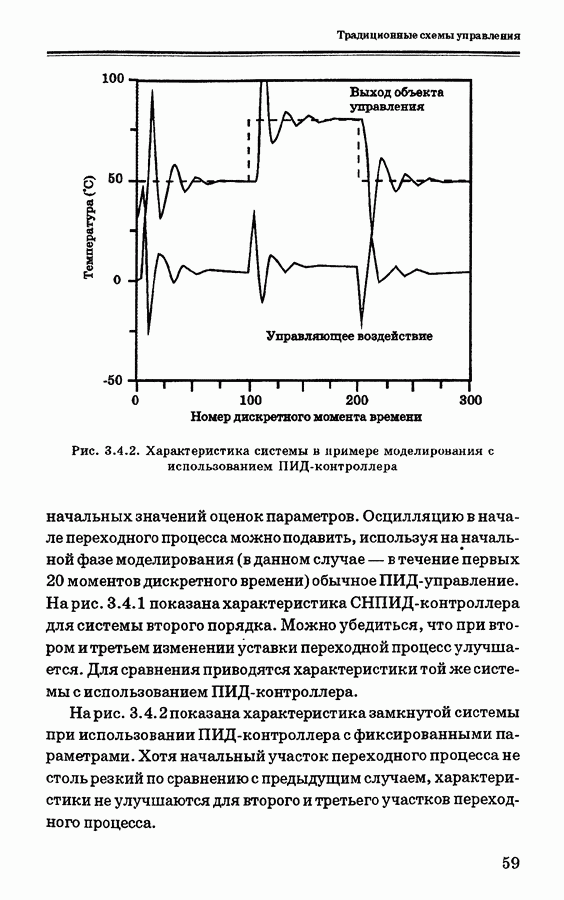
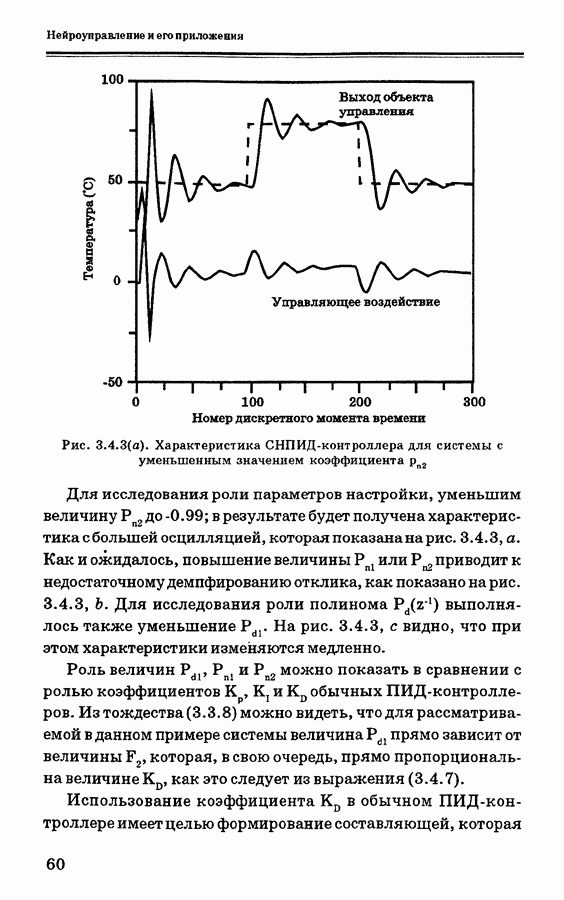
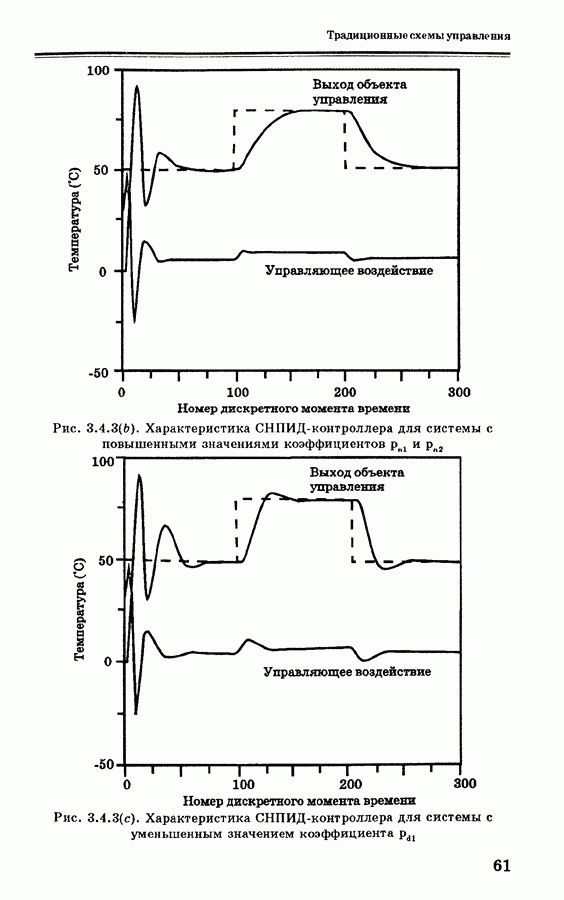
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3. ТРАДИЦИОННЫЕ СХЕМЫ УПРАВЛЕНИЯ
3.1. Введение
В данной главе рассматриваются некоторые другие методы управления: ПИД-управление (пропорционально-интег-рально-дифференциальное), управление с самонастройкой, ПИД-управление с самонастройкой, обобщенное прогнозирующее управление, управление на основе нечеткой логики. Одними из первых систем управления были ПИ- и ПИД-контроллеры. Они доказали свою эффективность в управлении разнообразными процессами. Использование ПИ- и ПИД-контроллеров не требует знания точной модели процесса, поэтому они эффективны в управлении промышленными процессами, математические модели которых достаточно сложно определить. ПИ- и ПИД-контроллеры строятся на основе классической теории управления и просты для понимания. Установление связей между параметрами и управление действиями системы могут осуществляться инженерами-практиками и операторами.
Крометого, за последние десятилетия разработано несколько методов настройки ПИ- и ПИД-контроллеров. Зиглер (Ziegler) и Никольс (Nichols) [1] предложили метод настройки, основанный на данных о реакции на единичное ступенчатое воздействие. Он широко использовался в течение многих лет и оказался достаточно эффективным. На его основе Такахаши (Takahashi) и др. [2] предложили метод настройки для ПИ- и ПИД-контроллеров с дискретным временем. Более современный метод автоматической настройки ПИ- и ПИД-контроллеров был предложен Нишикавой (Nishikawa) и др. [3]. Он требует подачи входного испытательного сигнала для оценки параметров процесса. Оптимальные значения ПИ- и
ПИД-параметров достигаются путем минимизации взвешенного интеграла квадратичной ошибки. Другой метод автоматической настройки ПИД-контроллеров был предложен Хаглундом (Hagglund) и Остремом (Astrom) [4]. Он базируется на формуле замкнутого цикла, приведенной в [1].
Однако, наряду с вышеуказанными достоинствами, ПИ- и ПИД- контроллеры имеют и ряд недостатков. Так, если рабочая точка процесса изменяется из-за возмущений, параметры контроллера требуется перенастраивать вручную, чтобы получить новую оптимальную настройку. Настройка должна выполняться опытным оператором. Для систем с взаимодействующими контурами эта процедура может быть сложной и занимать много времени. Кроме того, для процессов с переменными параметрами, временными задержками, существенными нелинейностями и значительными помехами использование ПИ- и ПИД-контроллеров может не обеспечить оптимальных характеристик. Методы настройки ПИ- и ПИД-контроллеров также имеют ряд недостатков. Например, метод Зиглера-Никольса (Ziegler - Nichols) [1] чувствителен к возмущениям, так как разработан на основе экспериментов с разомкнутыми системами. В методе настройки, предложенном Нишикавой (Nishikawa) и др. [3], требуется человеко-машинное взаимодействие, в ходе которого оператор должен генерировать входные сигналы каждый раз, когда требуется изменение параметров с целью адаптации к изменению динамики процесса.
По этим причинам Калман (Kalman) [5] выдвинул идею управления с самонастройкой, в котором параметры контроллера настраивались бы в оперативном режиме. Калман предложил концепцию машины, которая автоматически выполняла бы самонастройку в целях управления произвольным динамическим процессом. Эта идея была важной в общем ходе развития самонастраивающихся средств управления, однако она не получила активной поддержки из-за неадекватности теории и технологии. «Вторым рождением» данной теории,
вызвавшим большой интерес среди инженеров и исследователей в области управления, стало появление работы Острема (Astrom) и Виттенмарка (Wittenmark) [б]. Они обнаружили неожиданное явление: в ряде случаев комбинация оценок, полученных по обычному методу наименьших квадратов, и управления по минимальной дисперсии обеспечивает свойство самонастраиваемости. За этой работой последовал ряд практических приложений, которые, в свою очередь, породили новые теоретические разработки, так как проблемы, связанные с реализацией управления с самонастройкой, требовали разъяснения. Быстрое развитие цифровых ЭВМ в 70-е и 80-е годы сыграло важную роль в повышении интереса к управлению с самонастройкой, как в теоретическом, так и в практическом плане.
Исследования и разработки в области самонастраивающихся алгоритмов проводились по двум направлениям: распространение существующих схем управления на новые области применения и выдвижение новых подходов к задачам автоматического регулирования, для которых уже применялись имеющиеся виды контроллеров. Еще одной сферой исследований в этом направлении стали самонастраивающиеся ПИ- и ПИД-контроллеры (СНПИ- и СНПИД-контроллеры). Основная идея разработки контроллеров такого типа состоит в объединении возможностей самонастраивающихся контроллеров, способных в оперативном режиме приспосабливаться к изменениям параметров объекта управления, и простоты структур ПИД-контроллеров.
Предложено несколько схем СНПИД-контроллеров. Так, Виттенмарк (Wittenmark) [7] предложил схему СНПИД-контроллера на основе схемы размещения полюсов. При этом ПИД-алгоритм встраивается в структуру управления, которая рассчитывается на основе схемы размещения полюсов. Этот метод пригоден только для управления процессами ограниченных порядков. Модификация этого метода, позволяющая управлять процессами более общего вида, была предложена
Савелли (Savelli) и др. [8]. Позднее Гаутроп (Gawthrop) [9] предложил схему СНПИ- и СНПИ Д-контроллера для систем с непрерывным временем. В этой схеме ПИ- или ПИД-алгоритм автоматически выводится из обоснованных предположений о динамике управляемого процесса, а также из результатов моделирования возмущений с ненулевым математическим ожиданием. Иные формы СНПИД-контроллеров приводятся в работах [10—16].
Другая концепция управления, рассматриваемая в данной главе, была предложена Камероном (Cameron) и Себоргом (Seborg) [17]. Предложенный ими алгоритм основан на обобщенном управлении по минимальной дисперсии [18,19]. Закон управления с самонастройкой ориентируется на получение ПИ- или ПИД-структуры. Для этого делаются некоторые обоснованные допущения в отношении полиномиальных функций управления с самонастройкой, задаваемых пользователем. Способ ввода в алгоритм интегрирующего действия, необходимого для устранения ступенчатых возмущений и установившейся ошибки, отличается от используемого в СНПИ- и СНПИД-контроллерах. Параметры контроллеров определяются на основе схемы оценки параметров. Для ПИ-структуры требуются два параметра контроллера, для ПИД-структуры — три. Эти требования налагают некоторые ограничения на порядок полюсов разомкнутых систем управления, однако не на порядок нулей. В то же время можно показать, что для систем высоких порядков может быть осуществлено понижение порядка модели.
Рассматриваются также СНПИД-контроллеры со многими переменными (в разделе 3.3). При построении таких СНПИД-контроллеров учитываются те же проблемы управления, что и для контроллеров с одним входом и одним выходом. К ним относятся нелинейности, переменная динамика объекта управления, детерминированные и стохастические возмущения, временные задержки. Для многомерного случая имеются также некоторые технические сложности, которые не возникают для
контроллеров с одним входом и одним выходом. К ним относятся, в частности, проблемы, вытекающие из хорошо известных разделов теории управления многомерными системами. Например, для контроллеров со многими переменными соотношение «вход-выход» должно представляться в виде левого или правого дробно-матричного описания. Кроме того, полиномиальные матрицы не переставляются; для разрешения этой проблемы требуется вводить некоторые дополнительные матрицы. В результате всего этого усложняются формулировки и вычисления, которые становятся по своему характеру алгебраическими [20]. В разработке СНПИ- и СНПИД-контроллеров со многими переменными имеются и другие проблемы, например, связанные с параметризацией, неравными временными задержками и устойчивостью.
Другой современной разработкой в области адаптивного управления является управление на основе долгосрочного прогнозирования. Принцип этого метода управления показан на рис. 3.1.1. Стратегия метода состоит в том, что в каждый конкретный

Рис. 3.1.1. Стратегия управления на основе долгосрочного прог нозирования
момент  делается прогноз выхода процесса на длительный временной горизонт. Этот прогноз, основанный на математической модели динамики процесса, делается явно или подразумевается в алгоритме управления.
делается прогноз выхода процесса на длительный временной горизонт. Этот прогноз, основанный на математической модели динамики процесса, делается явно или подразумевается в алгоритме управления.
Кроме всего прочего, прогноз зависит от сценария управления в будущем, которое предполагается постоянным на все время прогнозирования. Из нескольких сценариев управления выбирается стратегия, обеспечивающая сходимость выходного процессак уставке наилучшим образом. Стратегия, выбранная в качестве наилучшей, применяется затем в качестве управляющего воздействия к реальному процессу, однако только на заданное время. В следующий момент дискретного времени вся процедура повторяется, в результате чего обеспечивается уточненное управляющее действие. Такая стратегия известна под названием стратегии управления по удаляющемуся горизонту.
Предложено несколько методов управления, основывающихся на долгосрочном прогнозировании: модельно-алгоритмическое управление (МАУ) (Model Algorithmic Control) [21], динамическое матричное управление (ДМУ) (Dynamic Matrix Control) [22], расширенное прогнозирующее самоадаптирую-щееся управление (РПСАУ) (Extended Predictive Self Adaptive Control) [23], адаптивное управление по расширенному горизонту (АУРГ) (Extended Horizon Adaptive Control) [24], система самонастройки на основе прогнозирования [25], обобщенное прогнозирующее управление (ОПУ) (Generalized Predictive Control) [26-28]. В [29] приведен достаточно исчерпывающий сравнительный анализ различных методов управления на основе долгосрочного прогнозирования, с рассмотрением достоинств каждого из них.
В первых методах прогнозирующего управления (МАУ, ДМУ) использовались математические модели объектов управления, получаемые по реакции на единичное ступенчатое или импульсное воздействие. Для этих моделей требуется графическое представление реакции или экспериментальные данные
о ней, что достаточно сложно реализовать. В алгоритме ОПУ используется модель управляемой авторегрессии — проинтегрированного скользящего среднего (УАРПСС) (Controlled Auto-Regressive and Integrated Moving Average (CARIMA) model), параметры которой можно получить, используя методы оценки параметров (например, рекуррентный метод наименьших квадратов). Диапазон параметров настройки для алгоритма ОПУ является более общим, что обеспечивает большую гибкость в разработке разомкнутых систем по сравнению с методами РПСАУ и АУРГ; эти методы могут рассматриваться как частные случаи ОПУ.
Один из новейших и наиболее эффективных методов управления — управление на основе нечеткой логики. Теория нечеткой логики была впервые разработана Заде (Zadeh) [30] в начале 60-х годов и сейчас успешно применяется во многих промышленных системах и бытовых изделиях. Теория нечетких множеств и управление на основе нечеткой логики рассматриваются в последнем разделе данной главы.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРОВ ПЕРЕВОДА
- 1. ВВЕДЕНИЕ
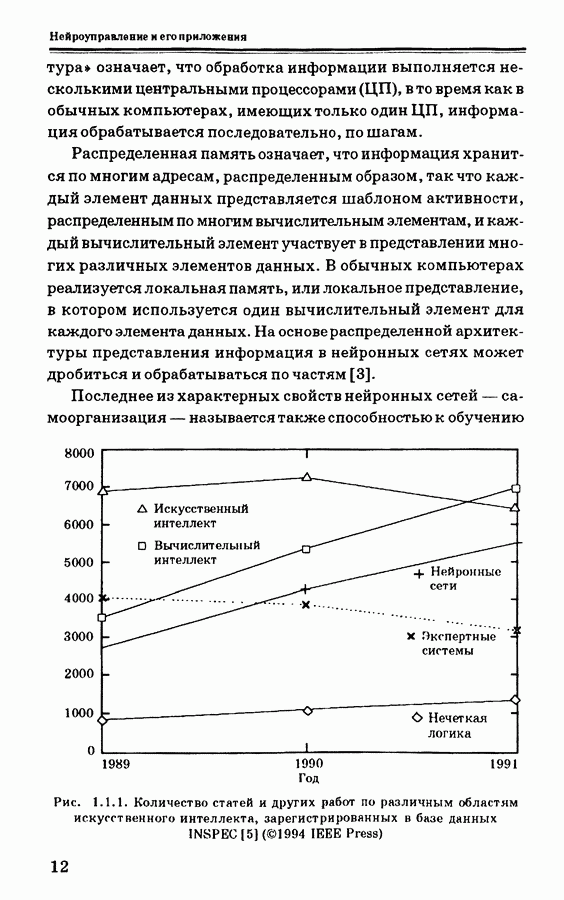
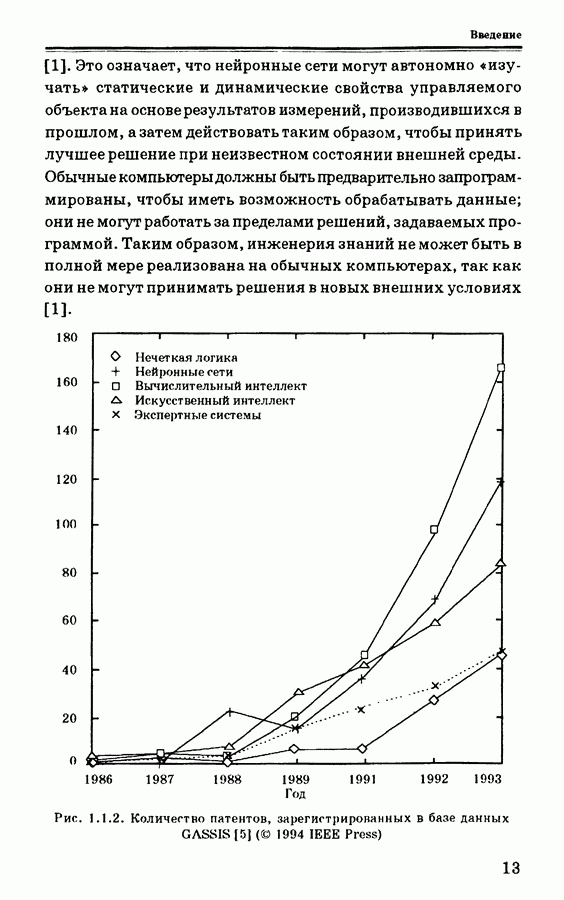
- 1.1. Общие сведения об интеллектуальном управлении
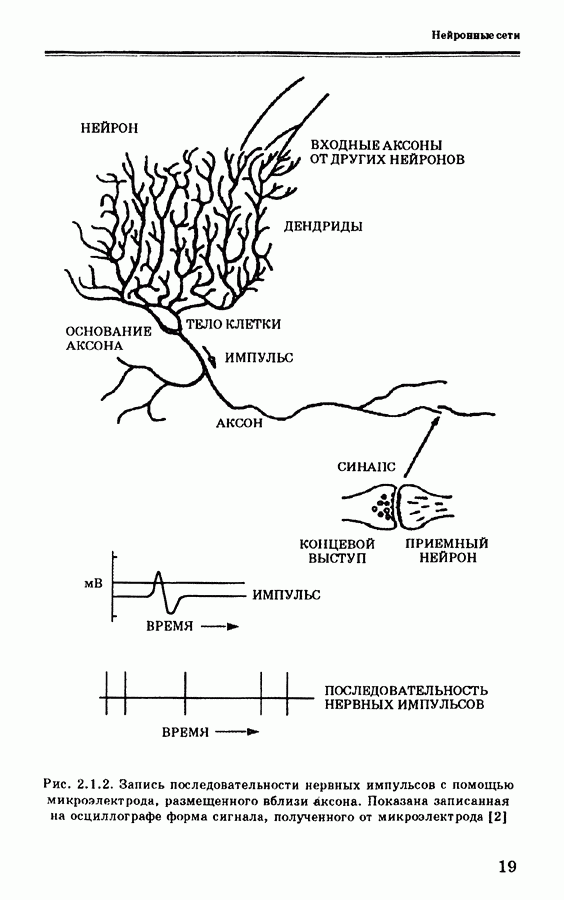
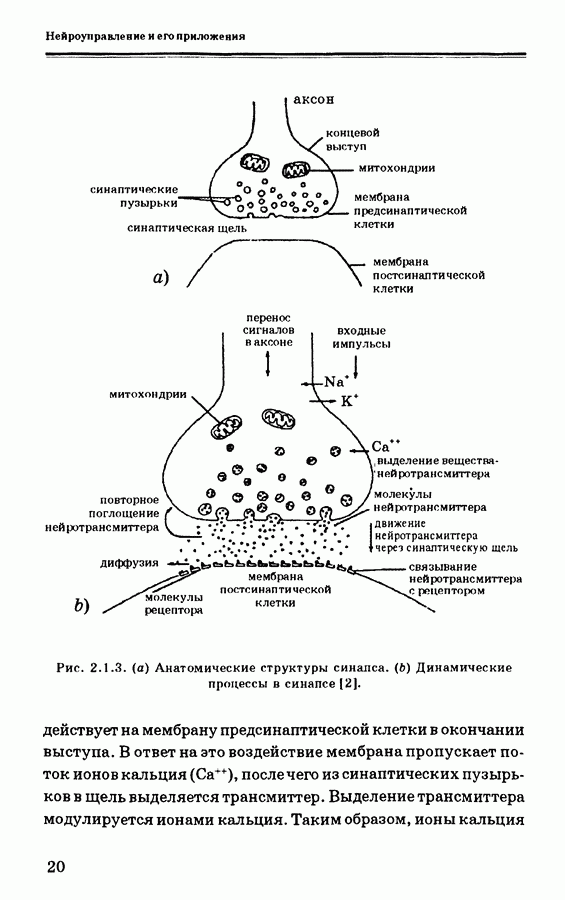
- 2. НЕЙРОННЫЕ СЕТИ
- 2.2. Алгоритм обратного распространения
- 2.2.2. Вывод алгоритма обратного распространения
- 2.2.2.2. Правило для скрытого слоя
- 2.2.3. Алгоритм обратного распространения: порядок реализации
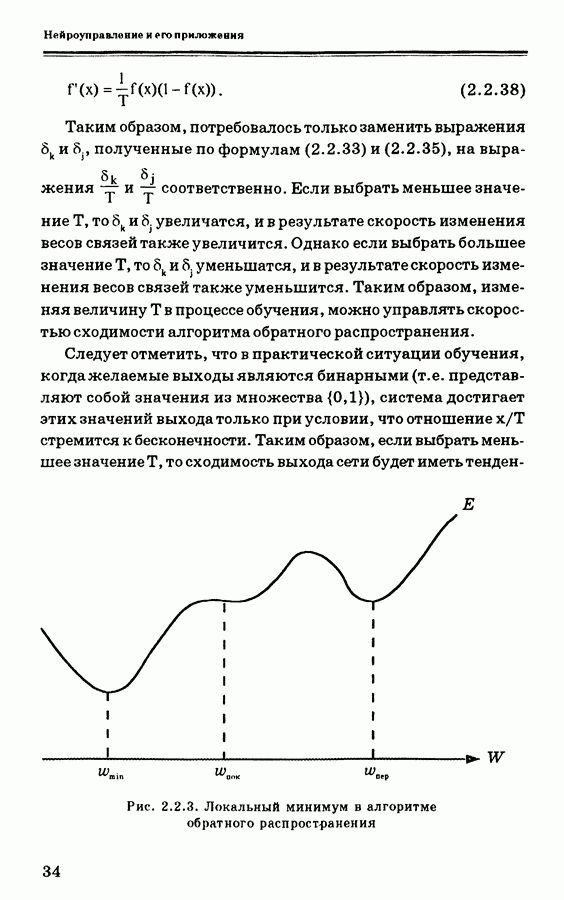
- 2.2.4. Обсуждение алгоритма обратного распространения
- 2.3. Заключение
- 3. ТРАДИЦИОННЫЕ СХЕМЫ УПРАВЛЕНИЯ
- 3.2. ПИ- и ПИД-контроллеры с дискретным временем
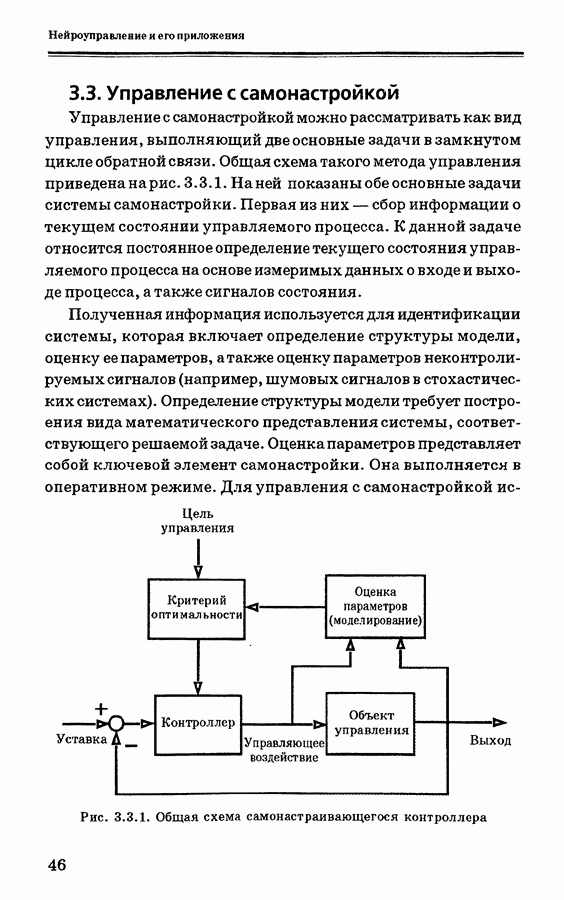
- 3.3. Управление с самонастройкой
- 3.4. Самонастраивающиеся ПИ- и ПИД- контроллеры
- 3.5. ПИД-управление с самонастройкой: многомерный подход
- 3.5.1. Пример моделирования
- 3.6. Обобщенное прогнозирующее управление: некоторые теоретические аспекты
- 3.6.2. Модель объекта управления и решение задачи оптимизации
- 3.7. Управление на основе нечеткой логики
- 3.7.1. Краткие сведения по теории нечетких множеств и нечетких систем
- 3.7.2. Основная концепция нечеткого контроллера
- 3.8. Заключение
- 4. ТЕХНОЛОГИИ НЕЙРОННОГО УПРАВЛЕНИЯ
- 4.2. Общие сведения о нейронном управлении
- 4.2.1. Подходы к нейронному управлению
- 4.2.2. Общая схема управления
- 4.3. Последовательная схема нейронного управления
- 4.4. Расширение последовательной схемы нейронного управления
- 4.4.2. Нейроморфные структуры управления
- 4.4.3. Конфигурации обучения
- 4.4.4. Эффективное оперативное управление
- 4.4.5. Алгоритмы обучения
- 4.4.6. Оценка алгоритмов обучения на основе моделирования
- 4.5. Параллельная схема управления
- 4.6. Алгоритм обучения по ошибке обратной связи
- 4.7. Расширение применения нейроконтроллеров параллельного типа
- 4.7.2. Линеаризованная система управления
- 4.7.3. Система управления с нейронными сетями
- 4.7.4. Нелинейный алгоритм наблюдения для нейронной сети
- 4.7.5. Нелинейный контроллер для нейронной сети
- 4.7.6. Численное моделирование
- 4.8. Схема нейронного управления с самонастройкой
- 4.9. ПИД-нейроконтроллер с самонастройкой
- 4.9.1. Вывод уравнений ПИД-нейроконтроллера с самонастройкой
- 4.9.2. Примеры эмуляции
- 4.10. Схема нейронного управления с эмулятором и контроллером (схема обратного распространения во времени)
- 4.11. Заключение
- 5. ПРИЛОЖЕНИЯ НЕЙРОННОГО УПРАВЛЕНИЯ
- 5.2. Применение нейронного управления в системе регулирования процессов в водяной ванне и сравнение его с другими схемами управления
- 5.2.2. Система управления температурой водяной ванны
- 5.2.3. Схема нейронного управления
- 5.2.4. Схема управления на основе нечеткой логики
- 5.2.5. Схема обобщенного прогнозирующего управления
- 5.2.6. Экспериментальные данные и их анализ
- 5.2.7. Заключение
- 5.3. Система стабилизации инвертированного маятника на основе нейронных сетей
- 5.3.2. Система стабилизации инвертированного маятника
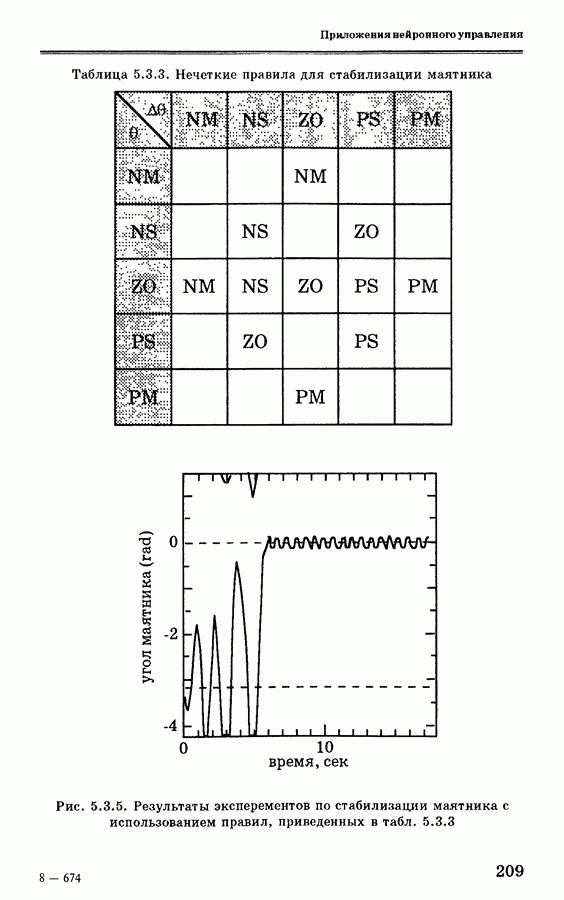
- 5.3.3. Инициализация поворотного управления с использованием нечеткой логики
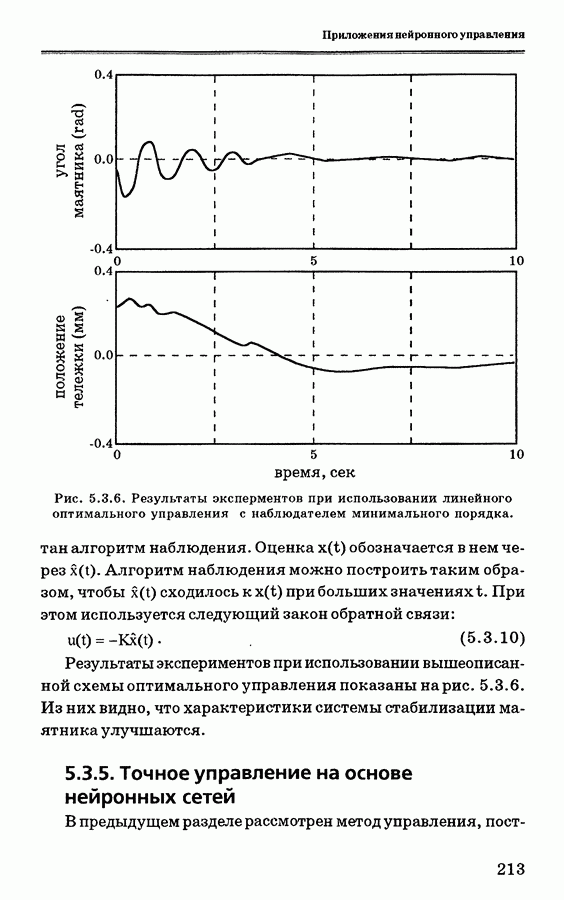
- 5.3.4. Применение стратегии оптимального управления для стабилизации маятника
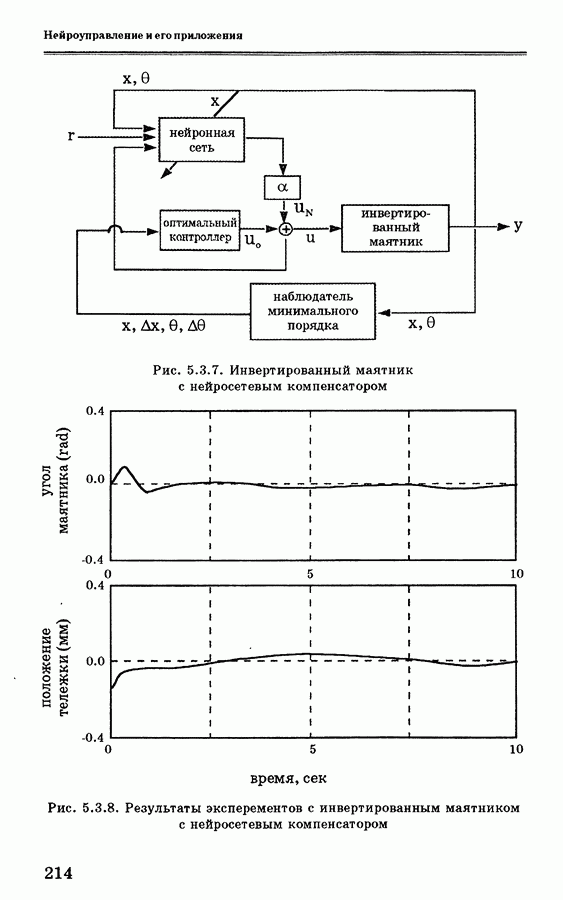
- 5.3.5. Точное управление на основе нейронных сетей
- 5.3.6. Заключение
- 5.4. Применение ПИД-нейроконтроллера с самонастройкой для управления скоростью электромобиля
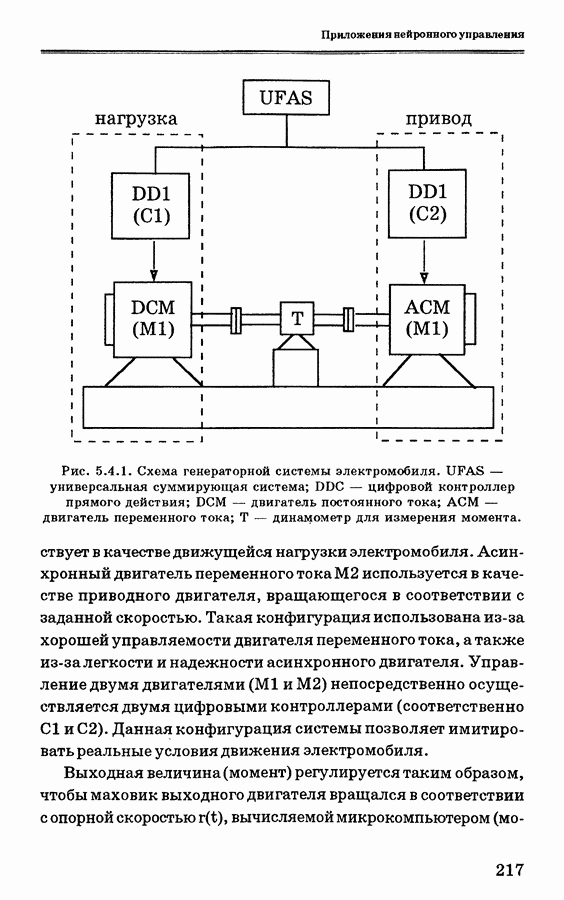
- 5.4.2. Система управления электромобилем
- 5.4.3. ПИД-нейроконтроллер с самонастройкой
- 5.4.4. Применение нейронной сети для управления скоростью электромобиля
- 5.4.5. Заключение
- 5.5. Применение нейронных сетей для управления печью
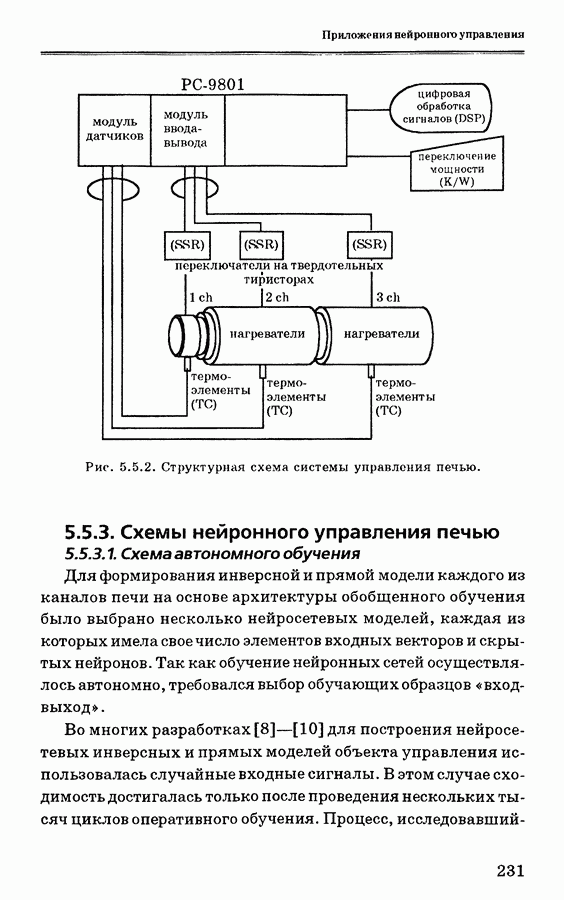
- 5.5.2. Система управления печью
- 5.5.3. Схемы нейронного управления печью
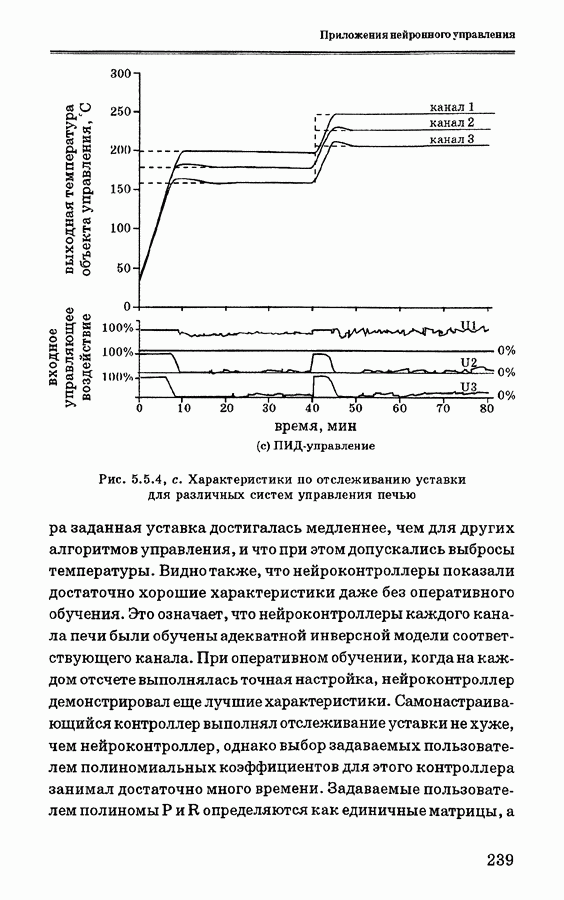
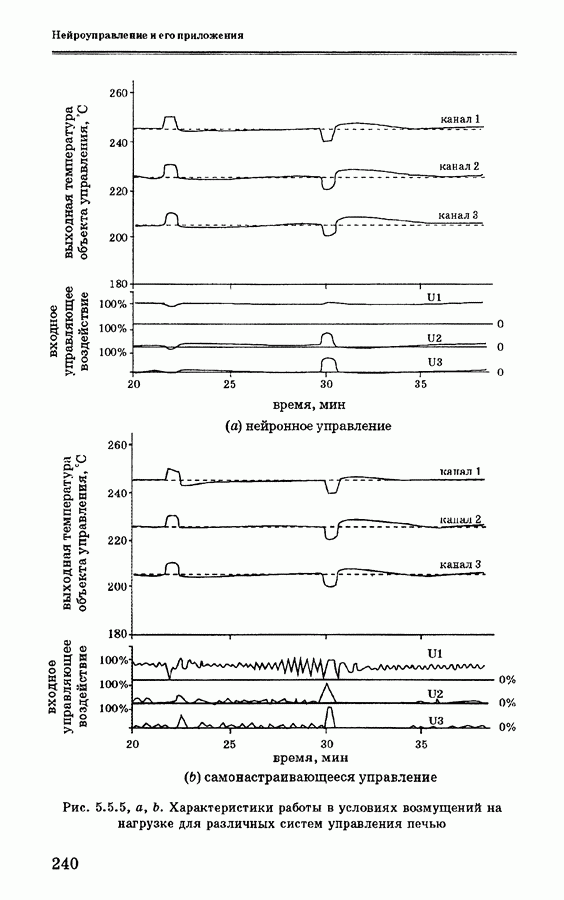
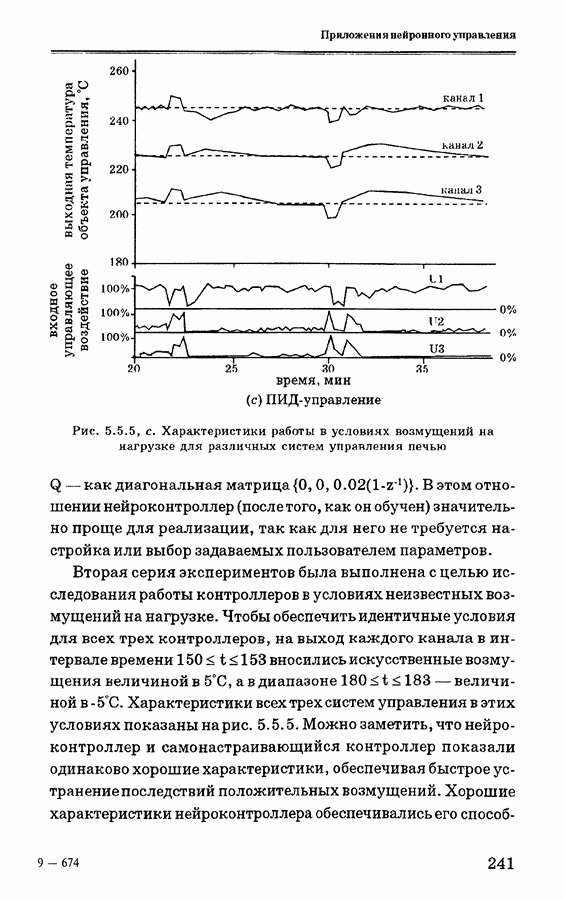
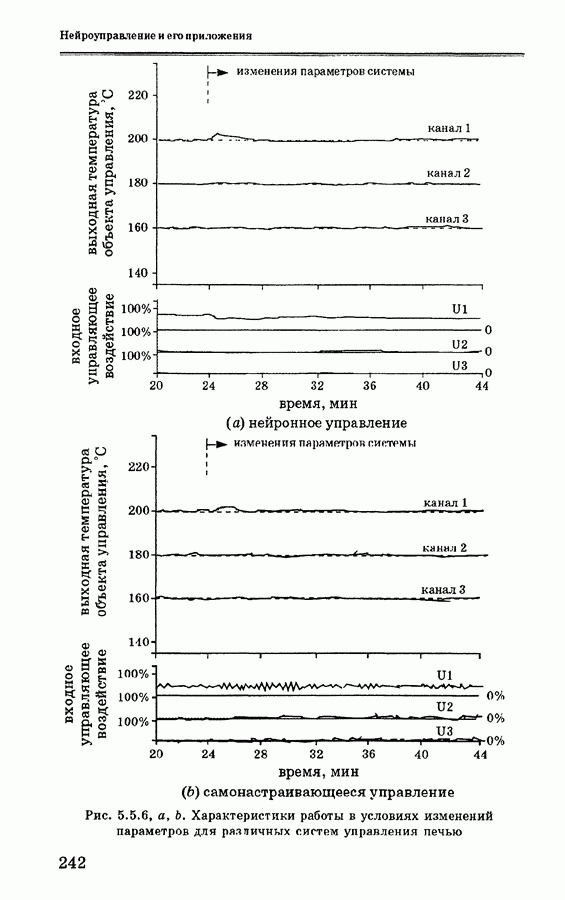
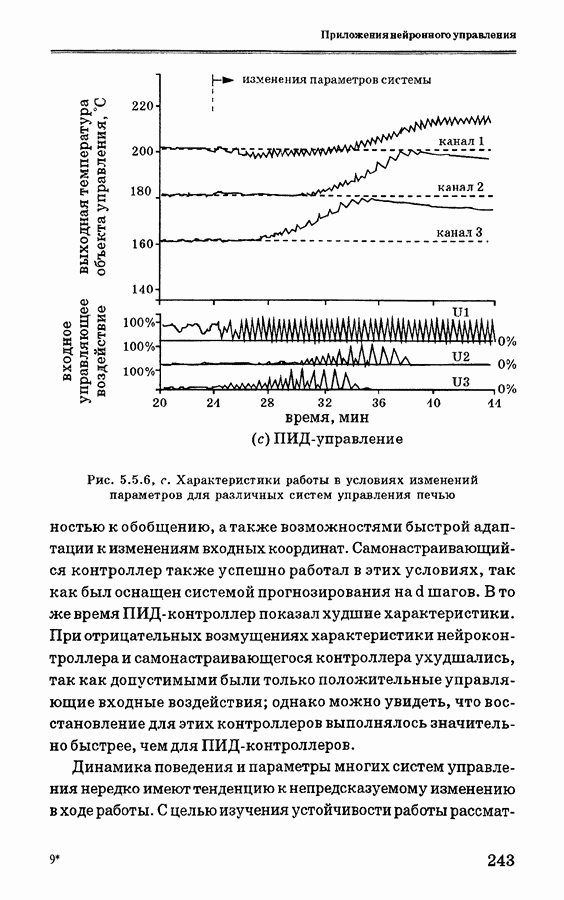
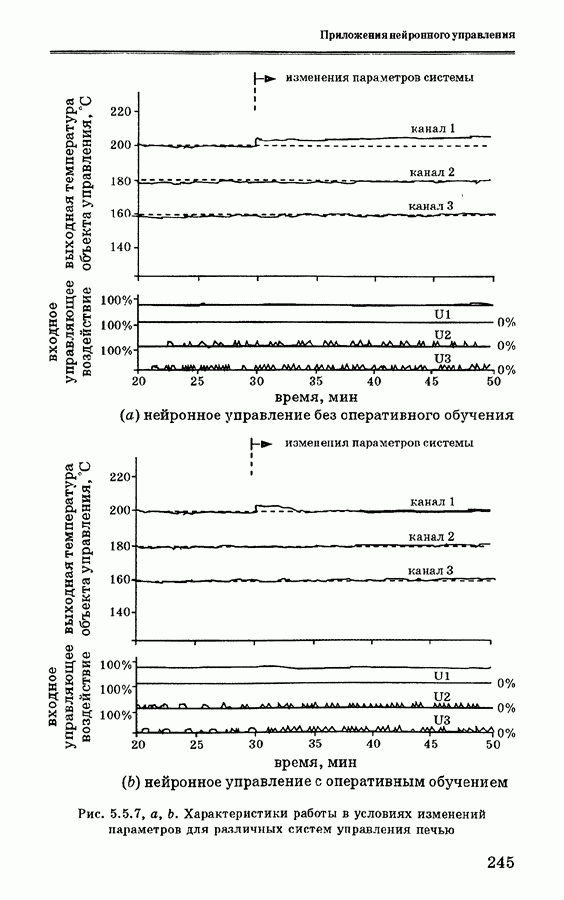
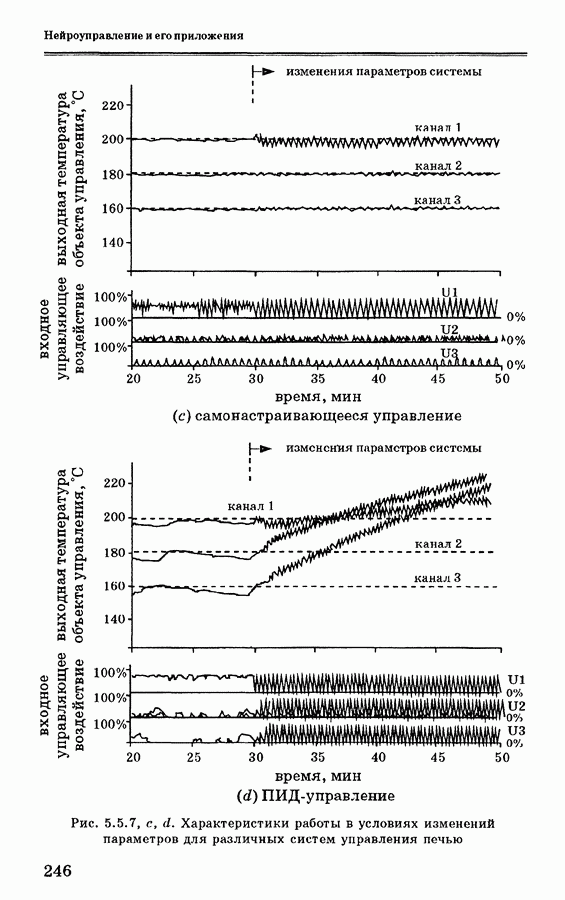
- 5.5.4. Анализ экспериментальных данных
- 5.6. Заключительные замечания и выводы
- Литература
- ЛИСТИНГ ПРОГРАММЫ