| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2. НЕЙРОННЫЕ СЕТИ
2.1. Исторические сведения
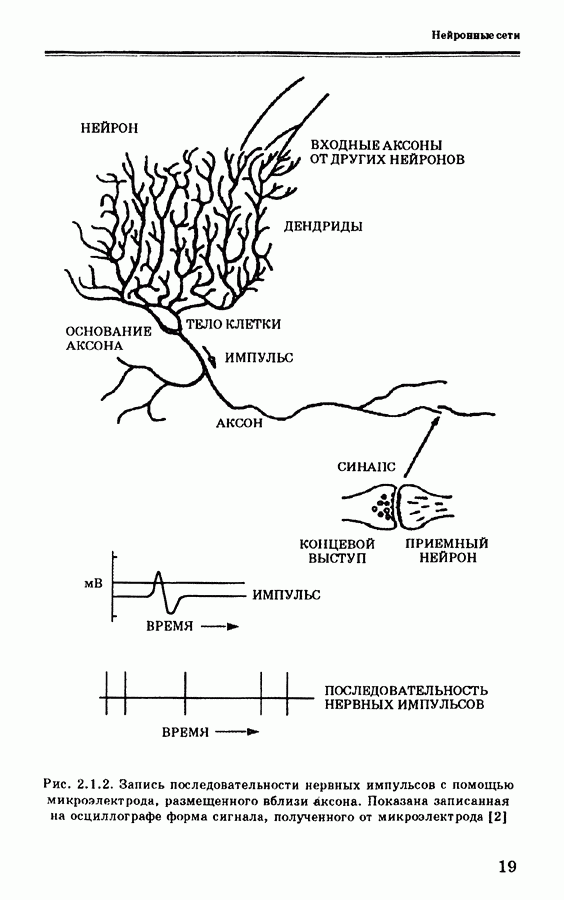
Нейронные сети — это сети нервных клеток (нейронов) в мозге. Человеческий мозг содержит миллиарды нейронов и триллионы связей меясдуними. Нейроны непрерывно обрабатывают информацию и обмениваются ею друг с другом. В 1909 г. Кайял (Cajal) [1], [2] обнаружил, что мозг состоит из огромного количества нейронов, сильно связанных друг с другом, способных обмениваться очень простыми возбуждающими и тормозящими сигналами и изменять свое состояние под действиемэтих сигналов. На рис. 2.1.1 показана клетка Пуркинье (Purkinje) с закрашенным дендритом [2]. Нейрон состоит из трех основных частей: тела клетки (сомы), аксона и дендритов (рис. 2.1.2 [2]).
Сома выполняет опорные функции и создает структуру клетки. Аксон представляет собой разветвленное волокно, передающее сигналы от нейрона. Дендриты также состоят из разветвленных волокон, принимающих сигналы от других нервных клеток. Исходящие сигналы представляют собой импульсы, инициируемые в бугре аксона, там, где аксон соединяется с сомой. На рис. 2.1.3 [2] показана схема синапса, включающая предсинаптическую клетку, ее синаптические пузырьки, синаптическую щель и постсинаптическую клетку.
Конечный выступ находится на конце ветви аксона, как показано на рис. 2.1.2, и имеет сложную структуру. Она выделяет химические трансмиттеры (передатчики), которые, пересекая синаптическую щель, достигают нейрона-приемника. Химические трансмиттеры действуют на мембрану нейрона-приемника, усиливая или ослабляя его тенденцию к возбуждению собственного импульса в зависимости от того, каким был входной сигнал: возбуждающим или тормозящим. Так как «синапс» — основное понятие для
искусственных нейронных сетей, рассмотрим его подробнее. На рис. 2.1.3 показана схема синапса, включающая предсинаптическую клетку, синаптические пузырьки, синаптическую щель и постсинаптическую клетку. В предсинаптической клетке входные сигналы действуют на мембрану в предсинаптической области, вызывая выделение трансмиттера из синаптических пузырьков. Трансмиттер пересекает синаптическую щель и достигает постсинаптической клетки, создающей мембранные свойства клетки-приемника. Интенсивность возбуждения постсинаптической клетки усиливается или ослабевает.
На конце аксонного отростка предсинаптической клетки имеется выступ. Поступление действующего потенциала

Рис. 2.1.1. Клетка Пуркинье (из мозжечка). Дендриты, образующие плоскую веерную структуру, показаны закрашенными [2]

(кликните для просмотра скана)
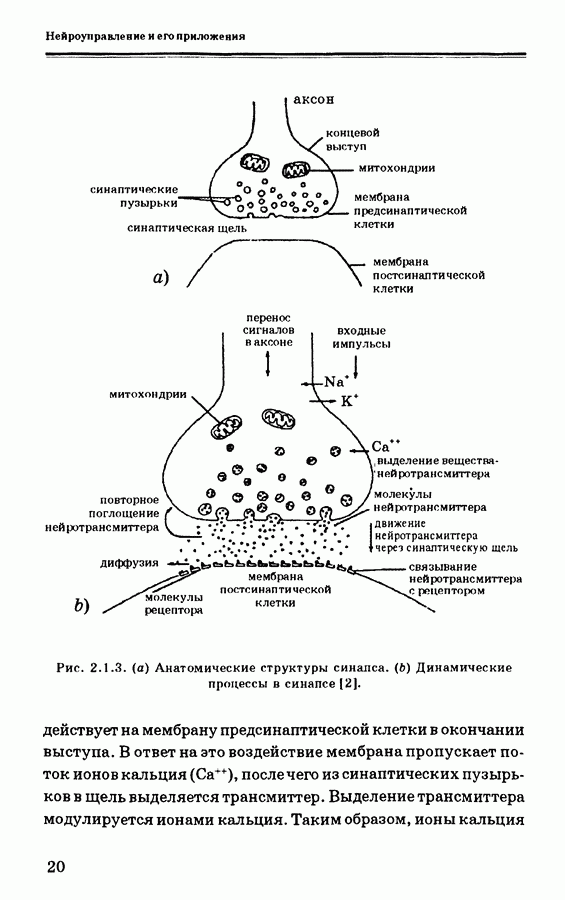
Рис. 2.1.3. (см. скан) (а) Анатомические структуры синапса. (b) Динамические процессы в синапсе [2].
воздействует на мембрану предсинаптической клетки в окончании выступа. В ответ на это воздействие мембрана пропускает поток ионов кальция (Са++), после чего из синаптических пузырьков в щель выделяется трансмиттер. Выделение трансмиттера модулируется ионами кальция. Таким образом, ионы кальция

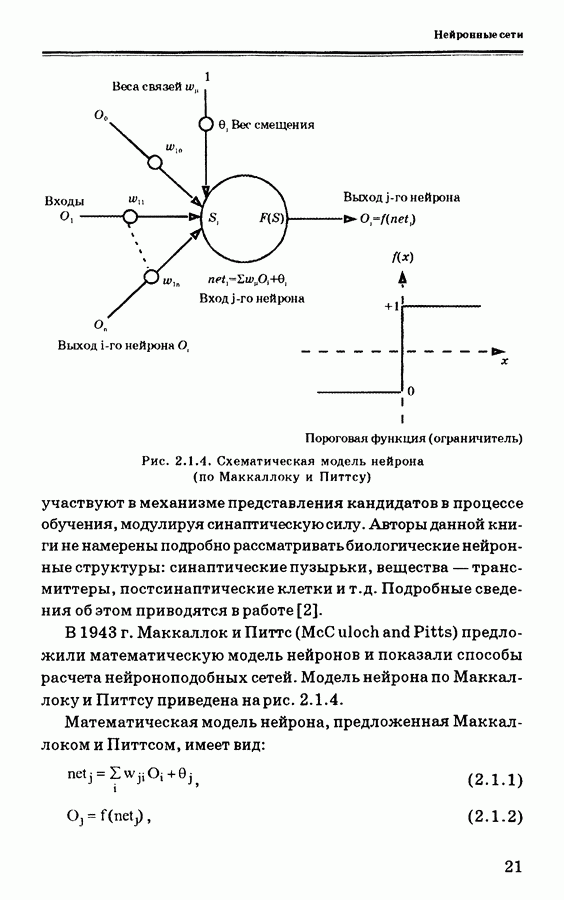
Рис. 2.1.4. Схематическая модель нейрона (по Маккаллоку и Питтсу)
участвуют в механизме представления кандидатов в процессе обучения, модулируя синаптическую силу. Авторы данной книги не намерены подробно рассматривать биологические нейронные структуры: синаптические пузырьки, вещества — трансмиттеры, постсинаптические клетки и т.д. Подробные сведения об этом приводятся в работе [2].
В 1943 г. Маккаллок и Питтс (McC uloch and Pitts) предложили математическую модель нейронов и показали способы расчета нейроноподобных сетей. Модель нейрона по Маккаллоку и Питтсу приведена на рис. 2.1.4.
Математическая модель нейрона, предложенная Маккал-локом и Питтсом, имеет вид:


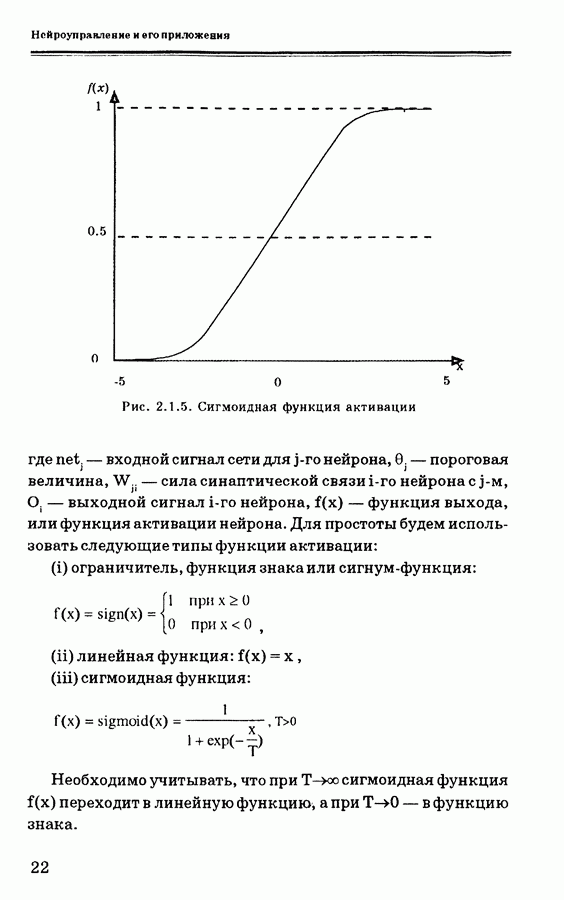
Рис. 2.1.5. Сигмоидная функция активации
где  — входной сигнал сети для
— входной сигнал сети для  нейрона,
нейрона,  — пороговая величина,
— пороговая величина,  — сила синаптической связи
— сила синаптической связи  нейрона
нейрона  — выходной сигнал
— выходной сигнал  нейрона,
нейрона,  — функция выхода, или функция активации нейрона. Для простоты будем использовать следующие типы функции активации:
— функция выхода, или функция активации нейрона. Для простоты будем использовать следующие типы функции активации:
(i) ограничитель, функция знака или сигнум-функция:

(ii) линейная функция:  ,
,
(iii) сигмоидная функция:

Необходимо учитывать, что при  сигмоидная функция
сигмоидная функция  переходит в линейную функцию, а при
переходит в линейную функцию, а при  — в функцию знака.
— в функцию знака.
Впервые идея обучения в нейронных сетях нашла отражение в книге Хебба(Hebb) [4] «Организация поведения», вышедшей в 1949 г. До этой работы считалось, что для обеспечения обучения в нейронной сети должны происходить какие-то физические изменения, однако было неизвестно, какие именно. Хебб предположил, что существенное биологическое изменение потребуется для укрепления связей между элементами нейронной сети только в том случае, если предсинапти-ческая и постсинаптическая мембраны активизируются одновременно.
Сущность идей Хебба проявляется в различных парадигмах обучения. Хотя отдельные детали правил изменения весов могут быть разными, основное утверждение Хебба о том, что сила связей между элементами должна изменяться в определенной зависимости от коррелированной активности связанных элементов, была принята во многих моделях обучения.
В 1951 г. Эдмондс (Edmonds) и Минский (Minsky) разработали свою обучающуюся машину на основе идеи Хебба [5]. Хотя Минский первым предложил идею обучающейся машины, фактическим началом разработок в области обучения нейроноподобных сетей стала работа Розенблатта (Rosenblatt), вышедшая в 1962 г. [5]. Розенблатт предложил класс простых нейроноподобных сетей, названный им персептроном. Персептрон, действительно, представлял собой целый класс структур, состоящий из обрабатывающих элементов, способных передавать сигналы и изменять веса своих связей. Исследования Розенблатта были направлены прежде всего на моделирование мозга в попытке понять механизмы работы памяти, обучения, когнитивные процессы. Работы Розенблатта были продолжены и развиты многими учеными и инженерами; был создан ряд машин на основе архитектуры персептрона. Выполнялись работы по математическому анализу вычислительной мощности персептронов (с целью выявления пределов их возможностей). Ослабление интереса к
использованию нейроноподобных сетей в качестве вычислительных устройств наступило после выхода книги Минского и Пейперта (Papert) [7].
В 1982 г. Хопфилд (Hopfield) выдвинул идею архитектуры нейронной сети, получившей название сети Хопфилда [8]. Им было показано, как могут строиться вычислительные средства на основе нейронных сетей. Хопфилдом была показана также реализация ассоциативной памяти на основе нейронной сети, а позднее — продемонстрирована возможность использования нейронных сетей для решения задач оптимизации, например, задачи о коммивояжере [9].
Другой подход, широко применявшийся в парадигмах нейронных сетей — обратное распространение ошибок, или обратное распространение (backpropagation). Концептуальные основы этого подхода были предложены Вербосом (Werbos) в 1974 г. [10], а затем, независимо от него — Румельхартом (Rumelhart) и др. в 1986 г. [11]. В книге последнего «Параллельные распределенные процессы» были показаны широкие перспективы для подходов, основанных на нейронных сетях.
Из других разработок, выполненных в последнее время, следует назвать машину Больцмана, конкурентное обучение и карту характеристик Кохонена (Kohonen). Машина Больцмана разработана Хинтоном (Hinton) и Сейновски (Sejnowski) на основе термодинамических моделей [11]. В этих моделях используются бинарные элементы, принимающие значения 0 и
1. Эти значения определяются стохастической функцией входов. При предположениях, применявшихся к сети Хопфилда, можно доказать, что сеть переходит в состояния, в наибольшей степени соответствующие входам и внутренним ограничениям, задаваемым весами.
Парадигма конкурентного обучения использует слой обрабатывающих элементов, конкурирующих друг с другом, в результате чего образуется нейронная сеть, применимая для решения задач распознавания образов. Такой подход был рассмотрен Румельхартом (Rumelhart) и Зипсером (Zipser) [12] и
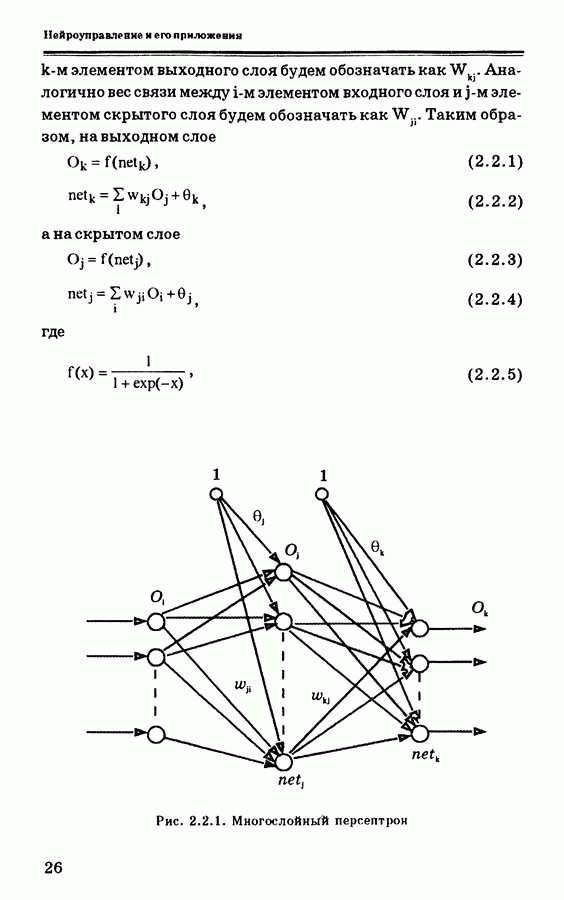
Гроссбергом (Grossberg) [13]. Самоорганизующаяся матрица характеристик Кохонена представляет собой двухслойную сеть, которая может организовать топологическую карту из случайной начальной точки. Полученная таким образом карта отражает естественные отношения между образами, предъявленными сети. Эта парадигма предложена Кохоненом [14]. Результаты, предложенные в данной книге, основываются главным образом на алгоритме обратного распространения. Рассмотрим его в следующем разделе.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРОВ ПЕРЕВОДА
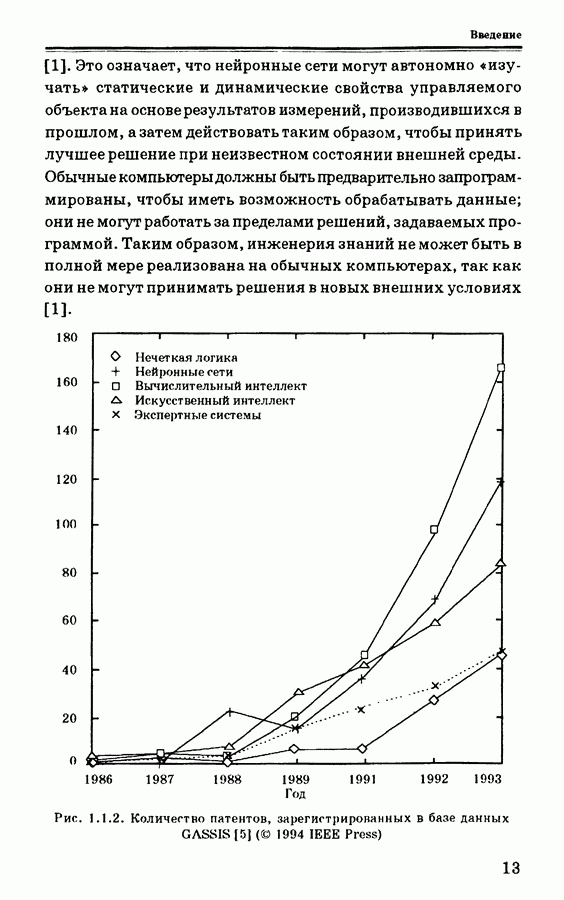
- 1. ВВЕДЕНИЕ
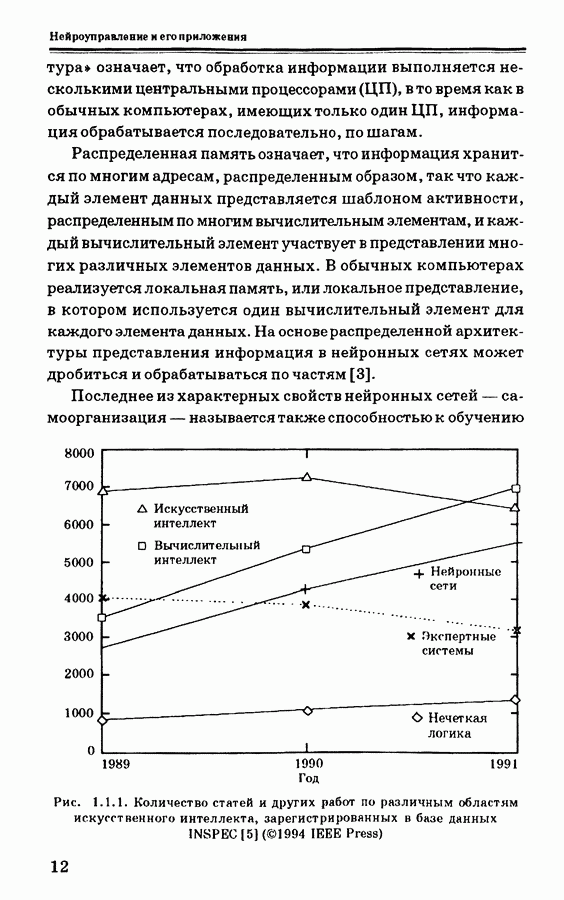
- 1.1. Общие сведения об интеллектуальном управлении
- 2. НЕЙРОННЫЕ СЕТИ
- 2.2. Алгоритм обратного распространения
- 2.2.2. Вывод алгоритма обратного распространения
- 2.2.2.2. Правило для скрытого слоя
- 2.2.3. Алгоритм обратного распространения: порядок реализации
- 2.2.4. Обсуждение алгоритма обратного распространения
- 2.3. Заключение
- 3. ТРАДИЦИОННЫЕ СХЕМЫ УПРАВЛЕНИЯ
- 3.2. ПИ- и ПИД-контроллеры с дискретным временем
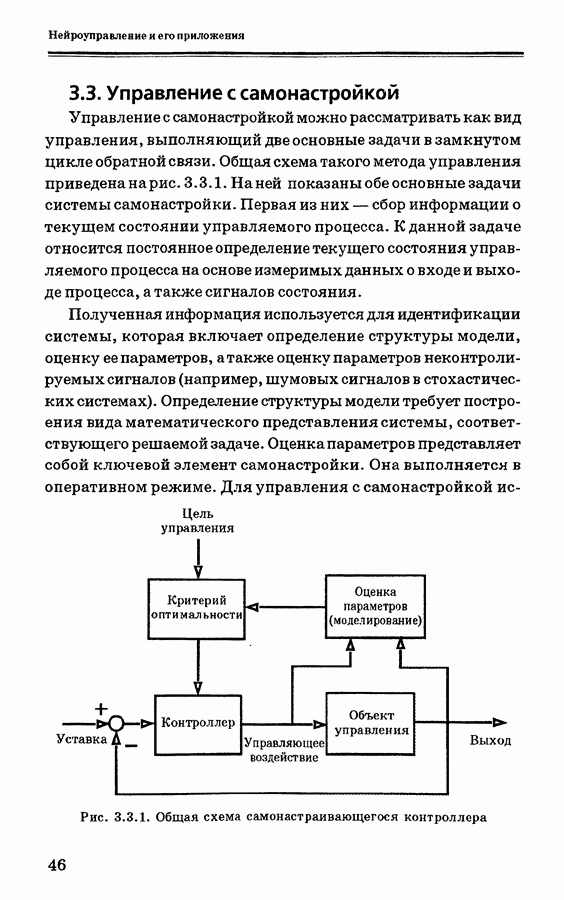
- 3.3. Управление с самонастройкой
- 3.4. Самонастраивающиеся ПИ- и ПИД- контроллеры
- 3.5. ПИД-управление с самонастройкой: многомерный подход
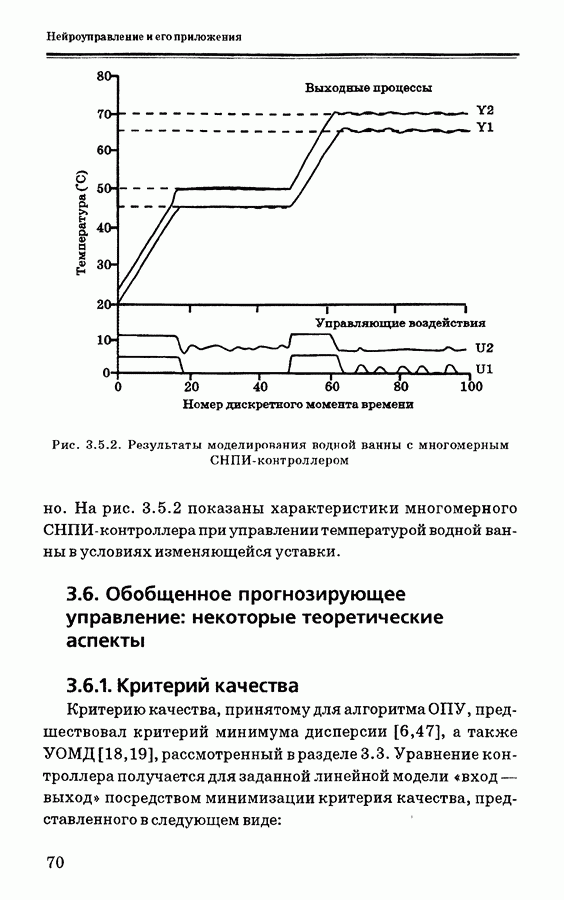
- 3.5.1. Пример моделирования
- 3.6. Обобщенное прогнозирующее управление: некоторые теоретические аспекты
- 3.6.2. Модель объекта управления и решение задачи оптимизации
- 3.7. Управление на основе нечеткой логики
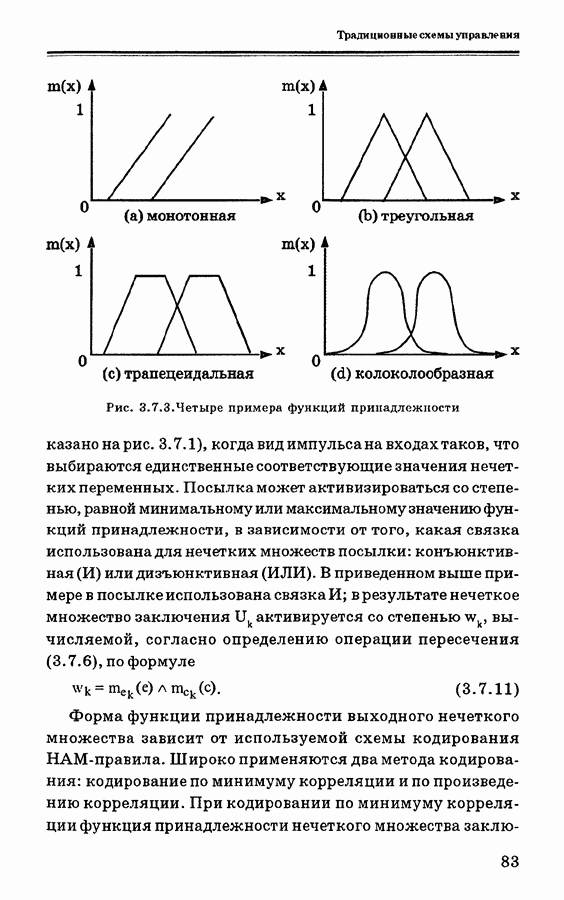
- 3.7.1. Краткие сведения по теории нечетких множеств и нечетких систем
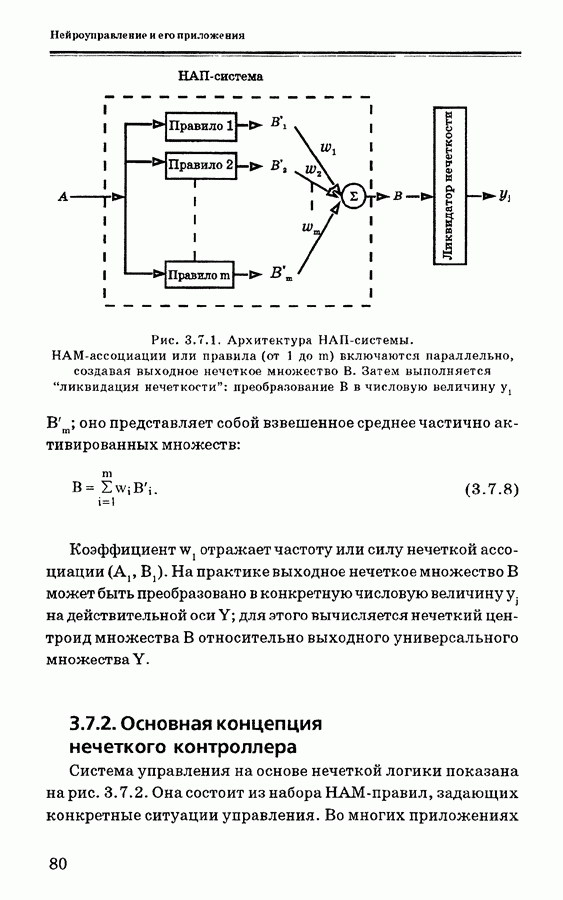
- 3.7.2. Основная концепция нечеткого контроллера
- 3.8. Заключение
- 4. ТЕХНОЛОГИИ НЕЙРОННОГО УПРАВЛЕНИЯ
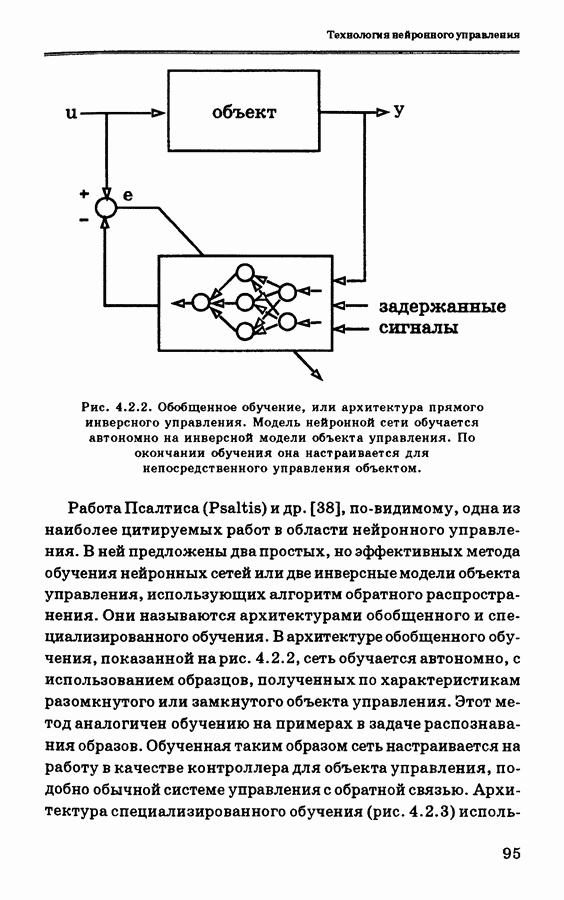
- 4.2. Общие сведения о нейронном управлении
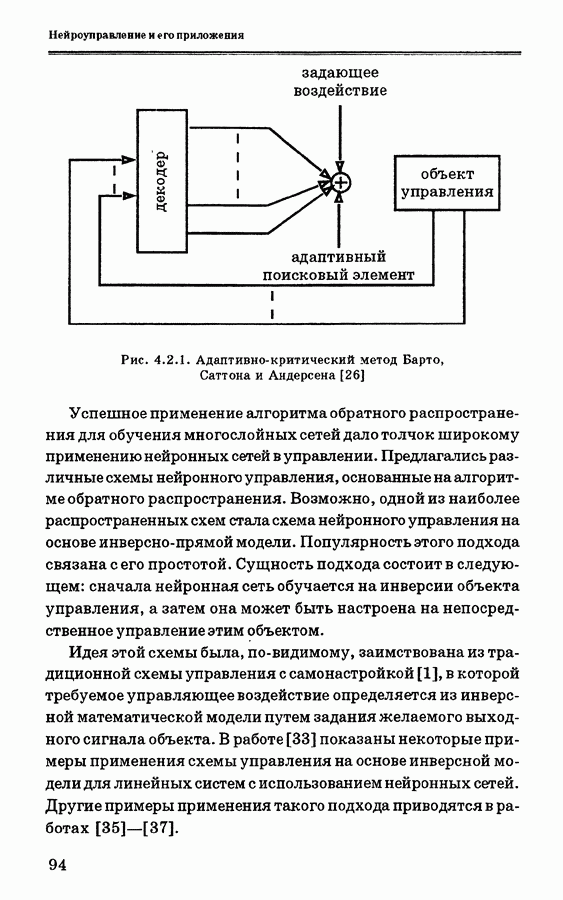
- 4.2.1. Подходы к нейронному управлению
- 4.2.2. Общая схема управления
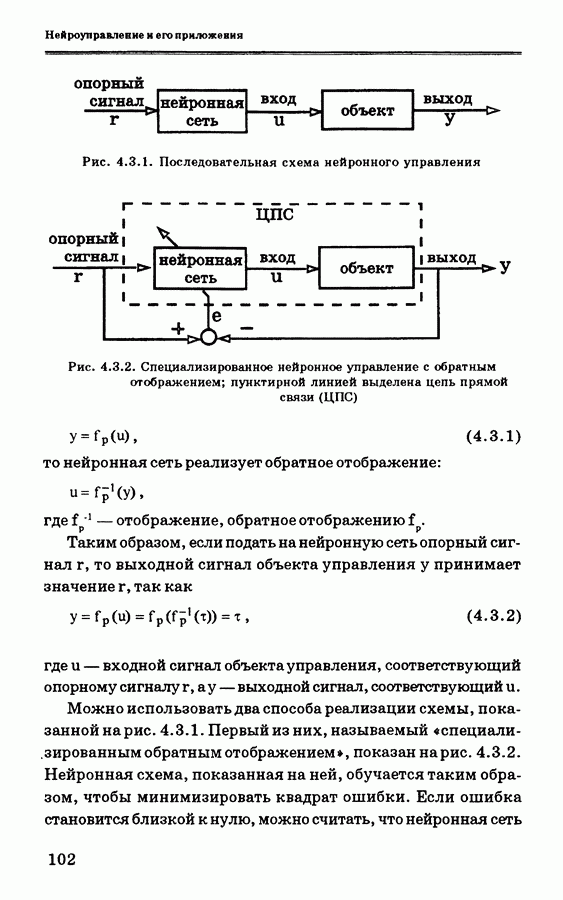
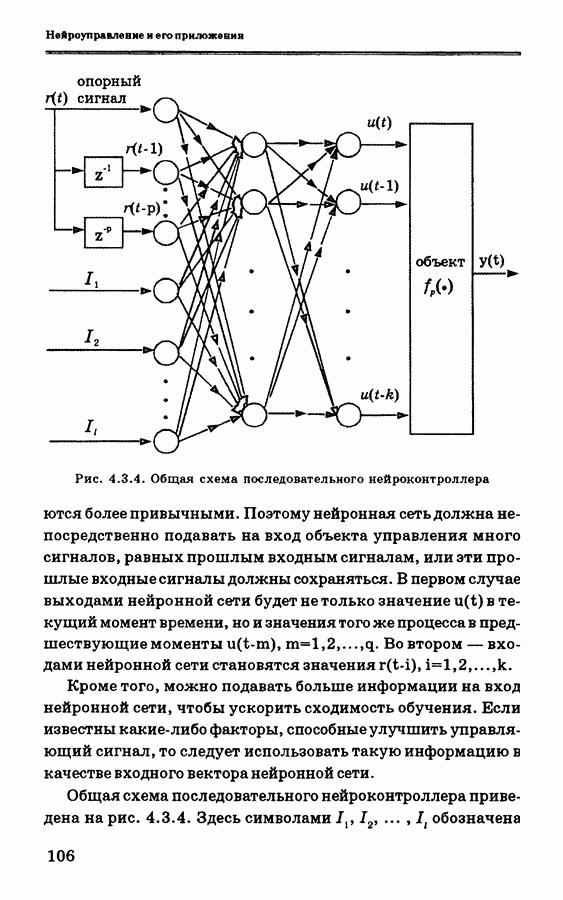
- 4.3. Последовательная схема нейронного управления
- 4.4. Расширение последовательной схемы нейронного управления
- 4.4.2. Нейроморфные структуры управления
- 4.4.3. Конфигурации обучения
- 4.4.4. Эффективное оперативное управление
- 4.4.5. Алгоритмы обучения
- 4.4.6. Оценка алгоритмов обучения на основе моделирования
- 4.5. Параллельная схема управления
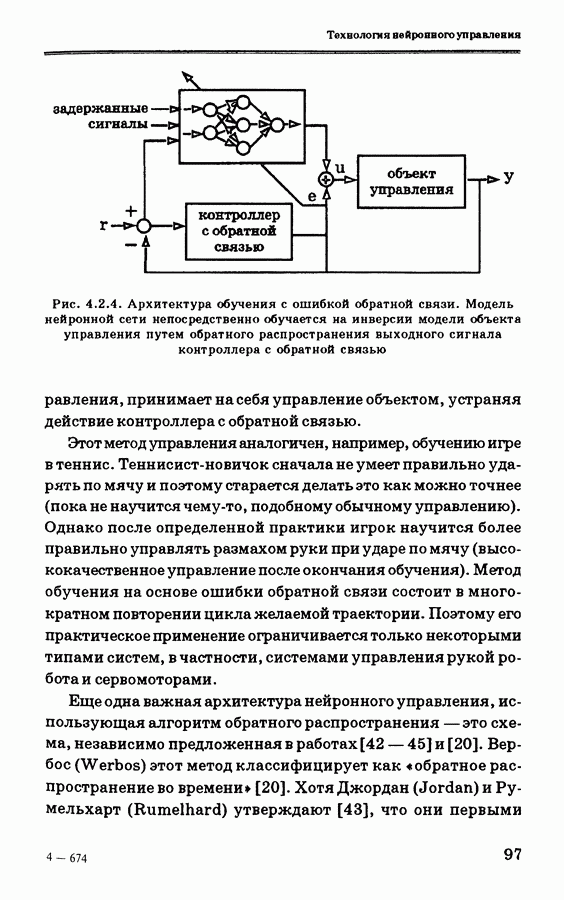
- 4.6. Алгоритм обучения по ошибке обратной связи
- 4.7. Расширение применения нейроконтроллеров параллельного типа
- 4.7.2. Линеаризованная система управления
- 4.7.3. Система управления с нейронными сетями
- 4.7.4. Нелинейный алгоритм наблюдения для нейронной сети
- 4.7.5. Нелинейный контроллер для нейронной сети
- 4.7.6. Численное моделирование
- 4.8. Схема нейронного управления с самонастройкой
- 4.9. ПИД-нейроконтроллер с самонастройкой
- 4.9.1. Вывод уравнений ПИД-нейроконтроллера с самонастройкой
- 4.9.2. Примеры эмуляции
- 4.10. Схема нейронного управления с эмулятором и контроллером (схема обратного распространения во времени)
- 4.11. Заключение
- 5. ПРИЛОЖЕНИЯ НЕЙРОННОГО УПРАВЛЕНИЯ
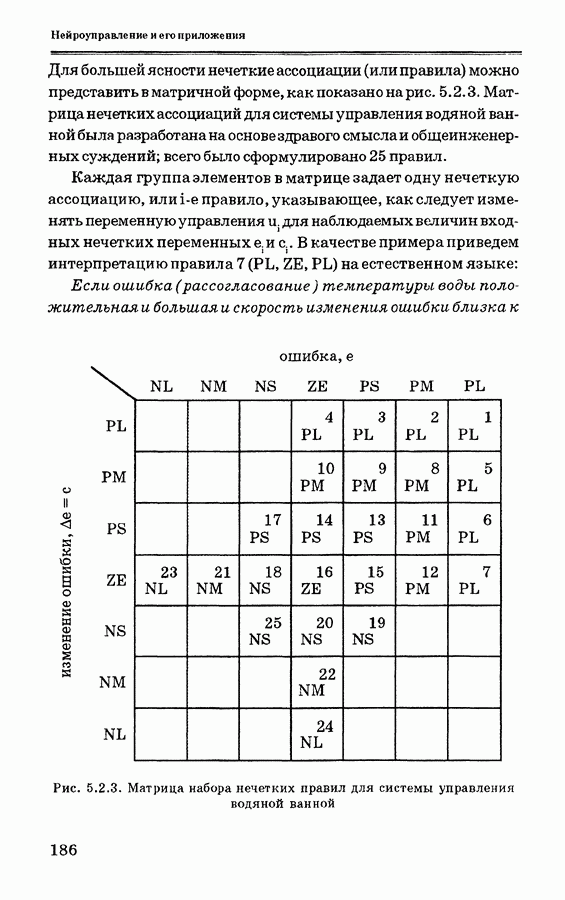
- 5.2. Применение нейронного управления в системе регулирования процессов в водяной ванне и сравнение его с другими схемами управления
- 5.2.2. Система управления температурой водяной ванны
- 5.2.3. Схема нейронного управления
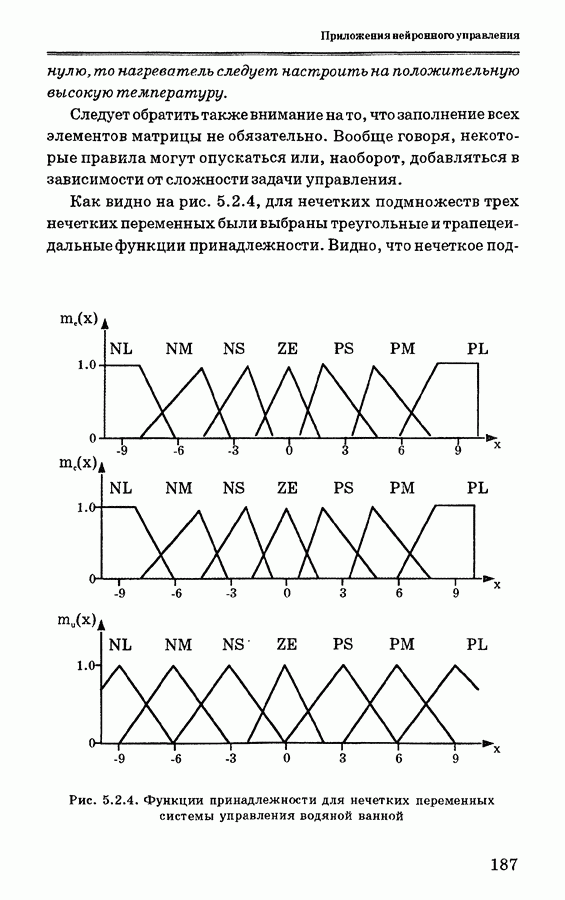
- 5.2.4. Схема управления на основе нечеткой логики
- 5.2.5. Схема обобщенного прогнозирующего управления
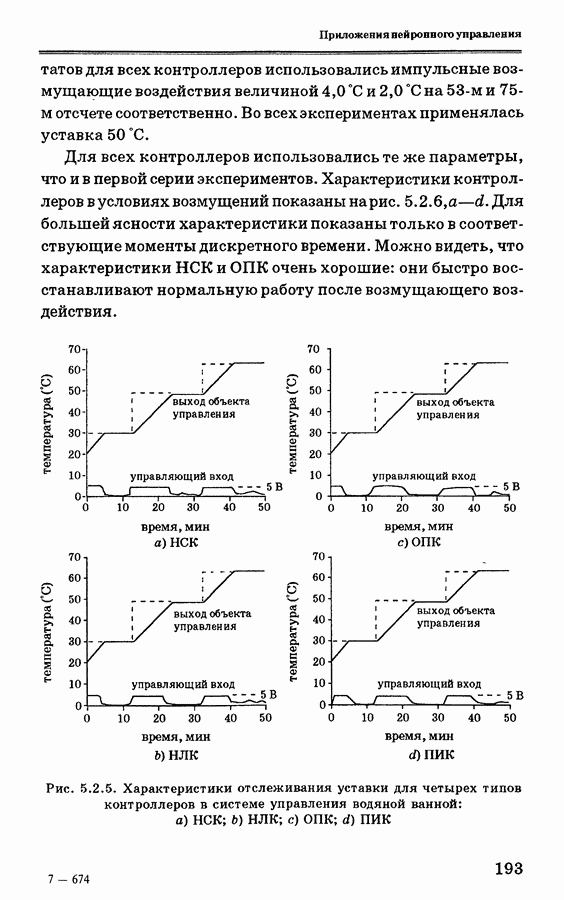
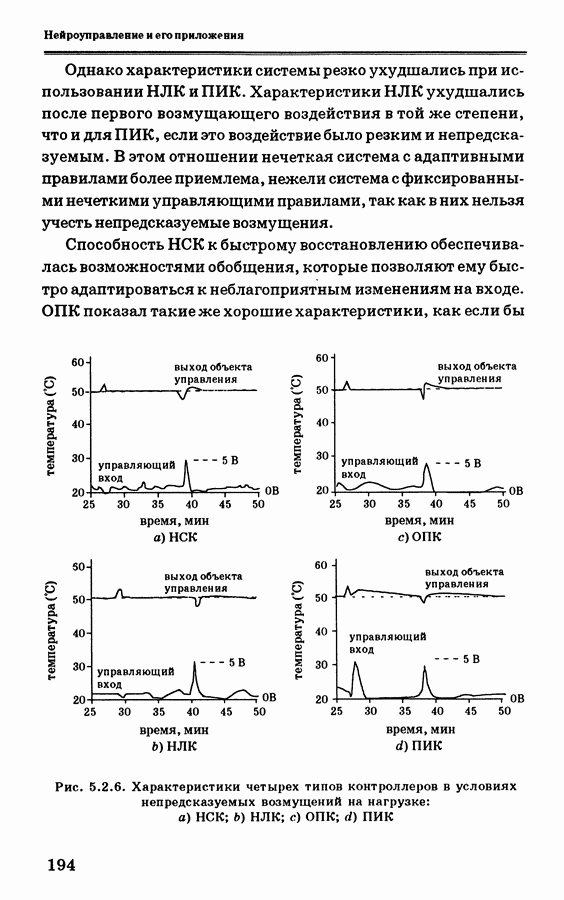
- 5.2.6. Экспериментальные данные и их анализ
- 5.2.7. Заключение
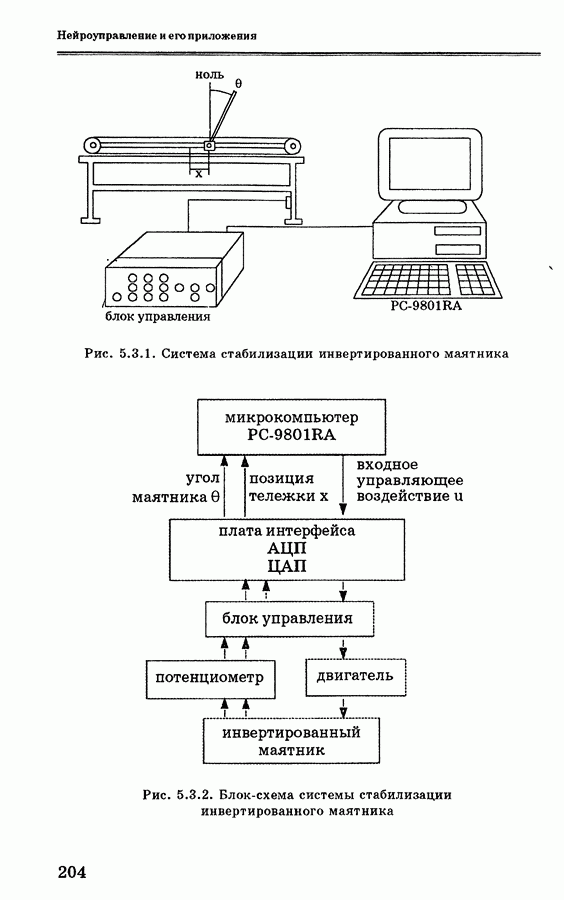
- 5.3. Система стабилизации инвертированного маятника на основе нейронных сетей
- 5.3.2. Система стабилизации инвертированного маятника
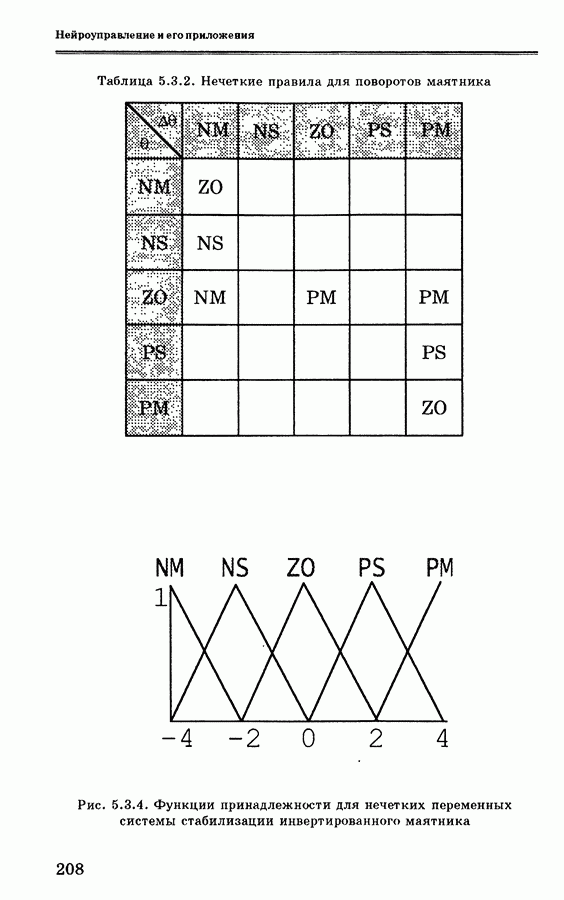
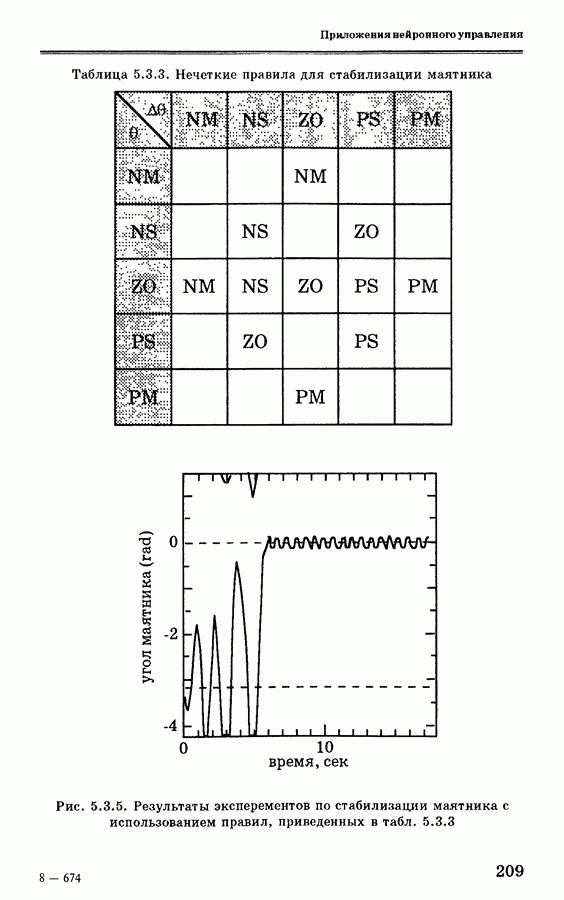
- 5.3.3. Инициализация поворотного управления с использованием нечеткой логики
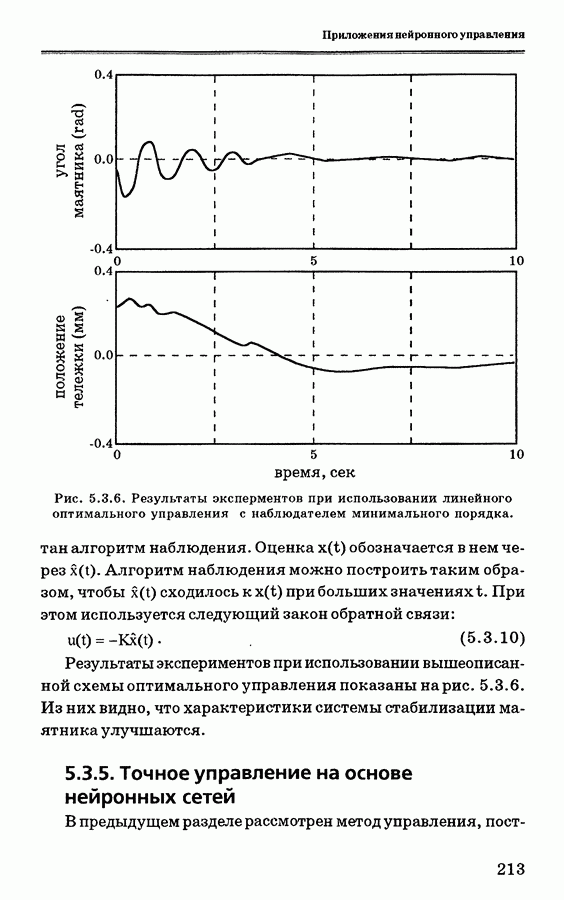
- 5.3.4. Применение стратегии оптимального управления для стабилизации маятника
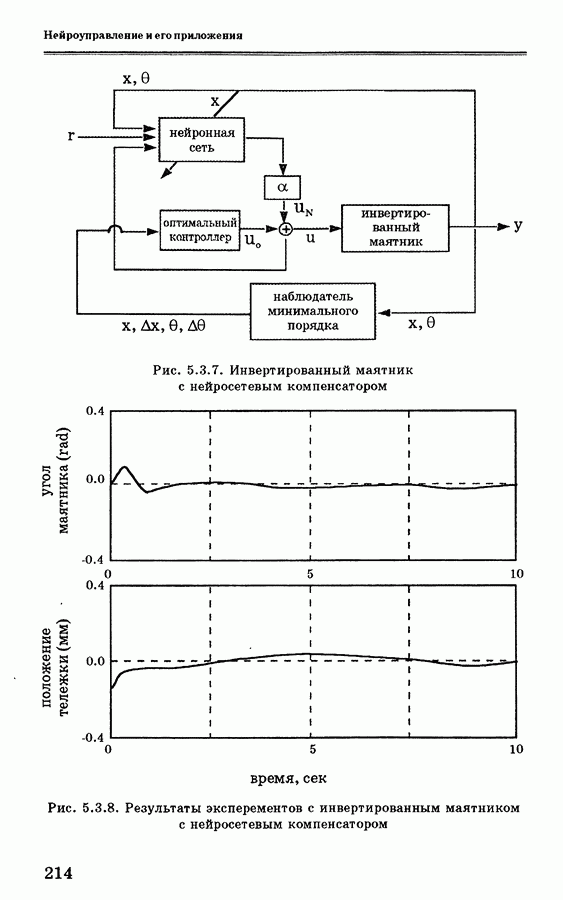
- 5.3.5. Точное управление на основе нейронных сетей
- 5.3.6. Заключение
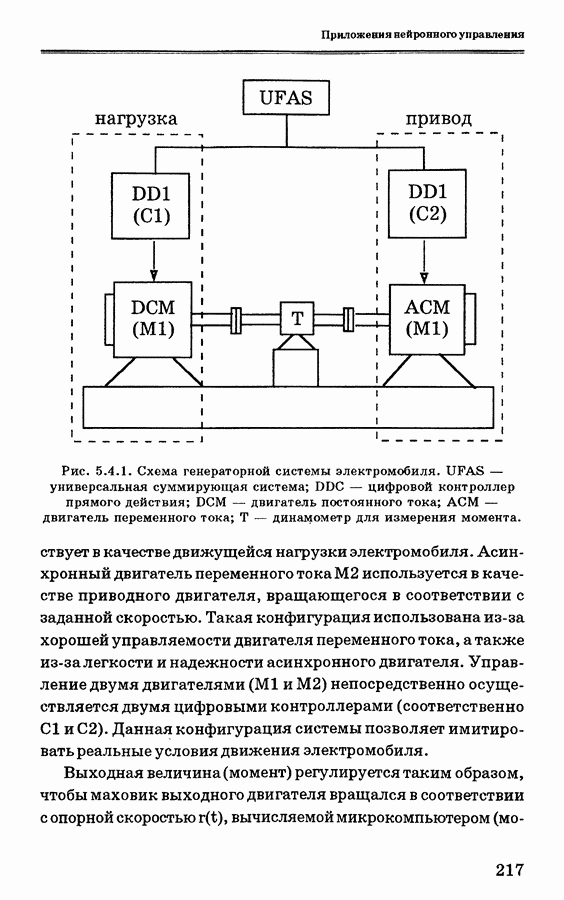
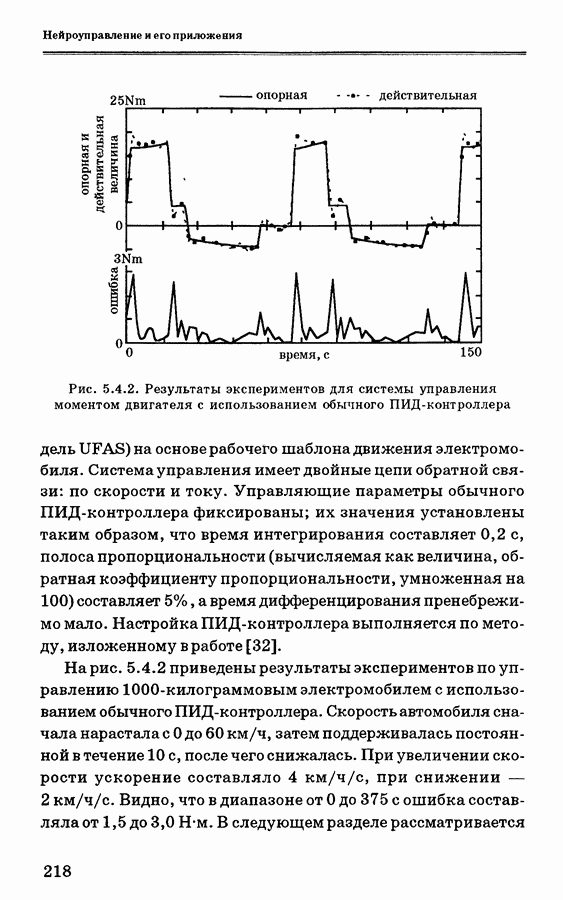
- 5.4. Применение ПИД-нейроконтроллера с самонастройкой для управления скоростью электромобиля
- 5.4.2. Система управления электромобилем
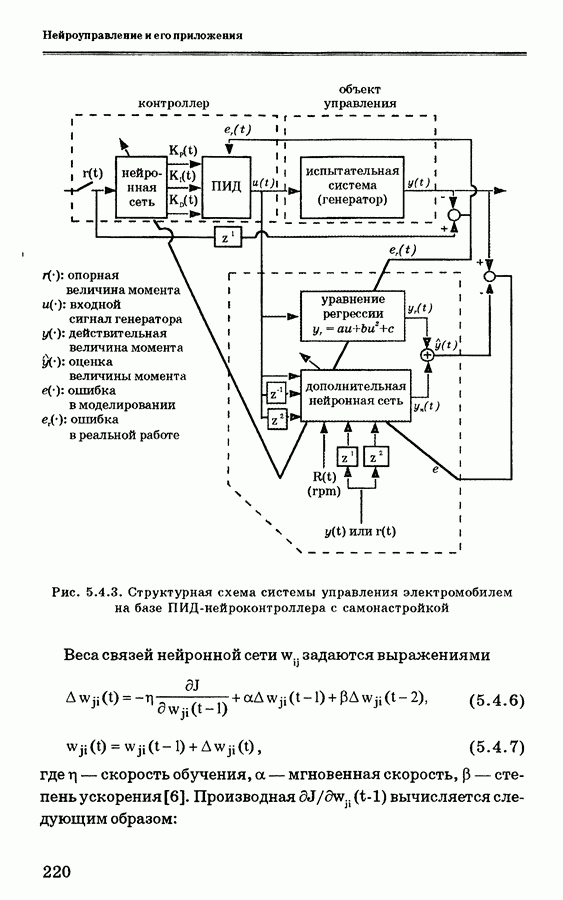
- 5.4.3. ПИД-нейроконтроллер с самонастройкой
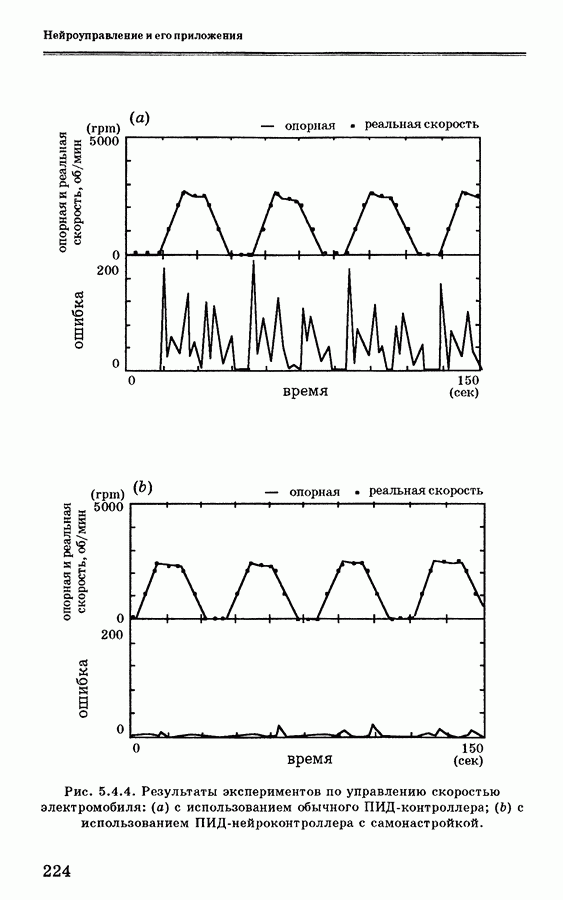
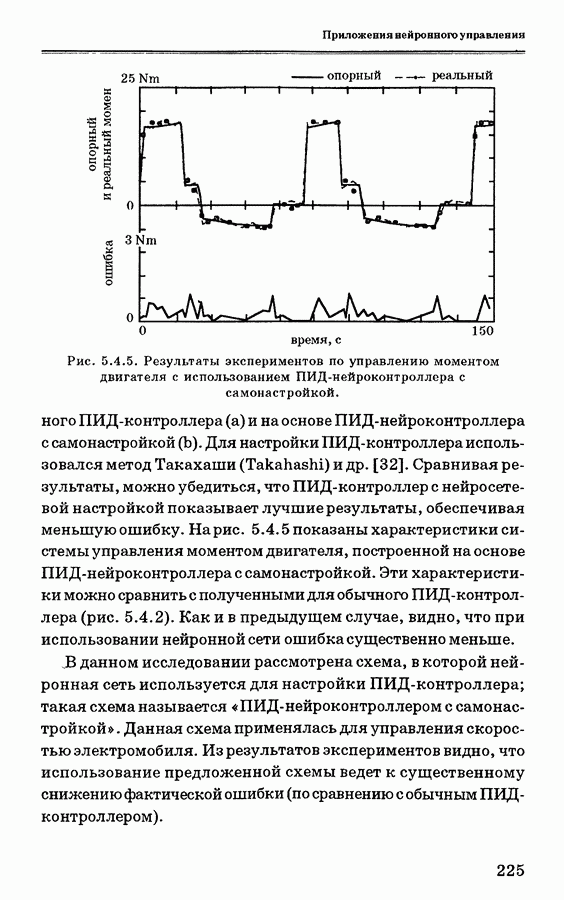
- 5.4.4. Применение нейронной сети для управления скоростью электромобиля
- 5.4.5. Заключение
- 5.5. Применение нейронных сетей для управления печью
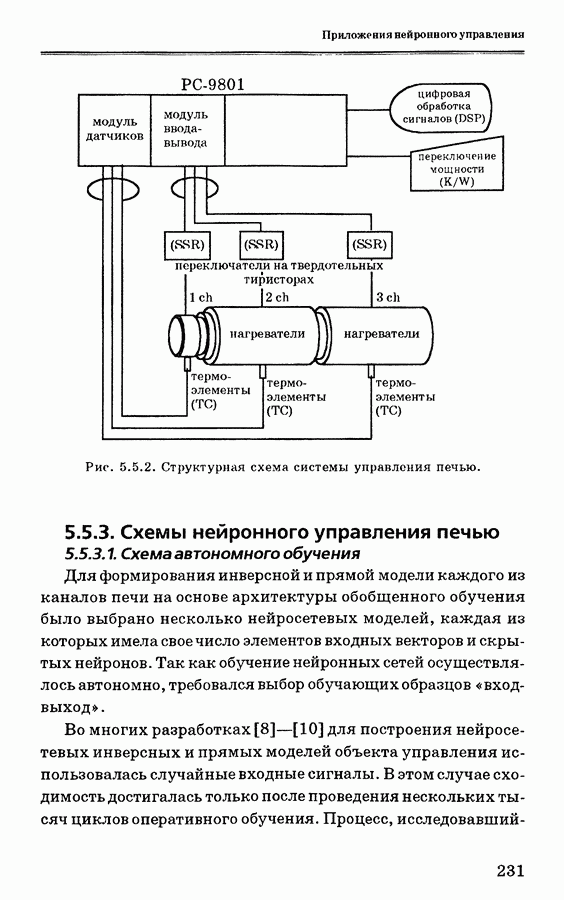
- 5.5.2. Система управления печью
- 5.5.3. Схемы нейронного управления печью
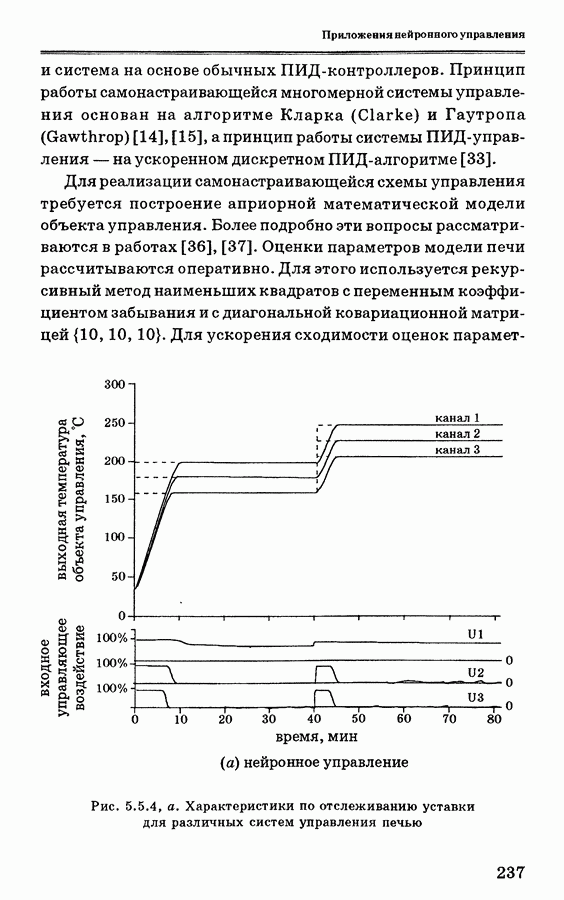
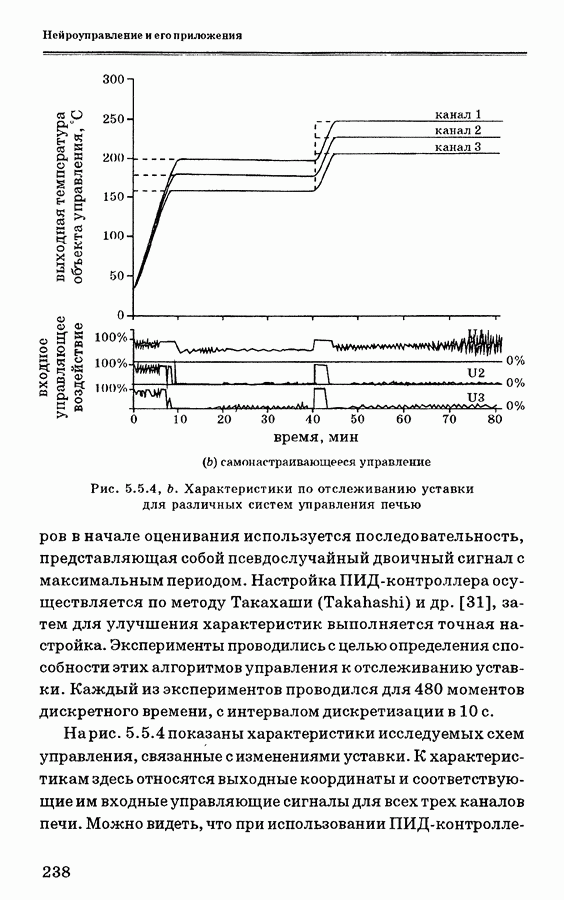
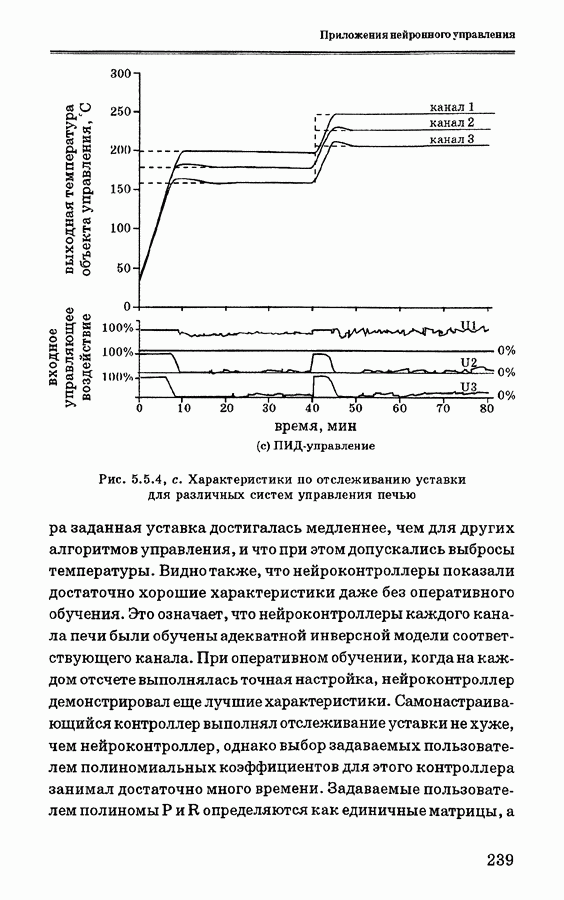
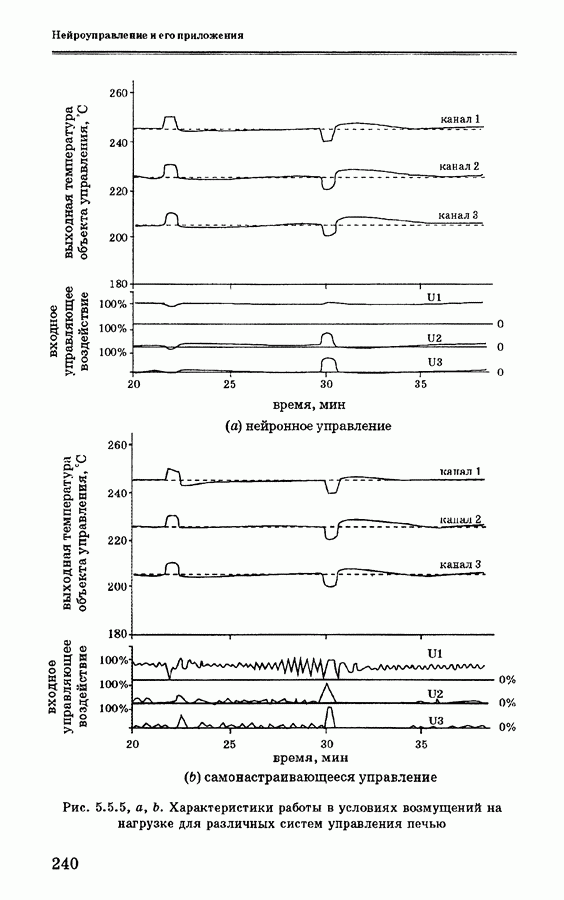
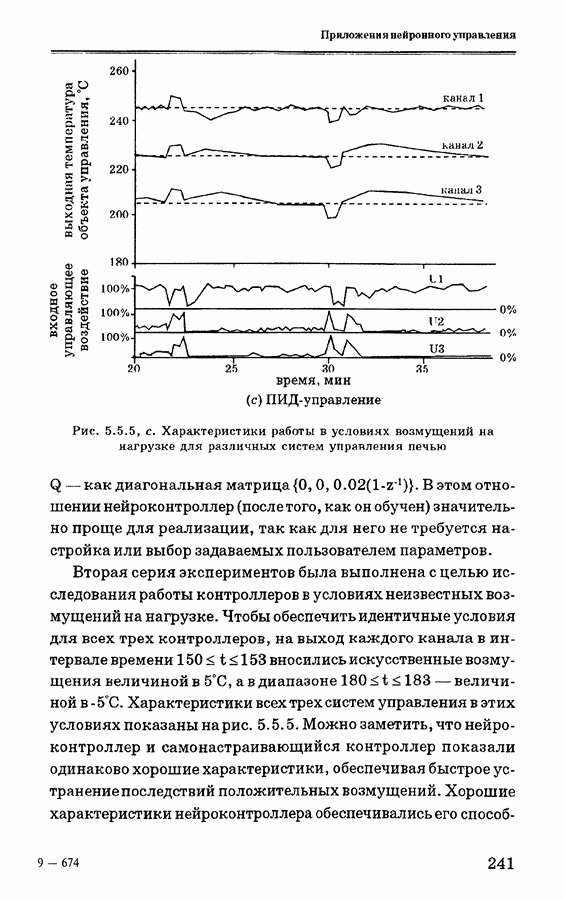
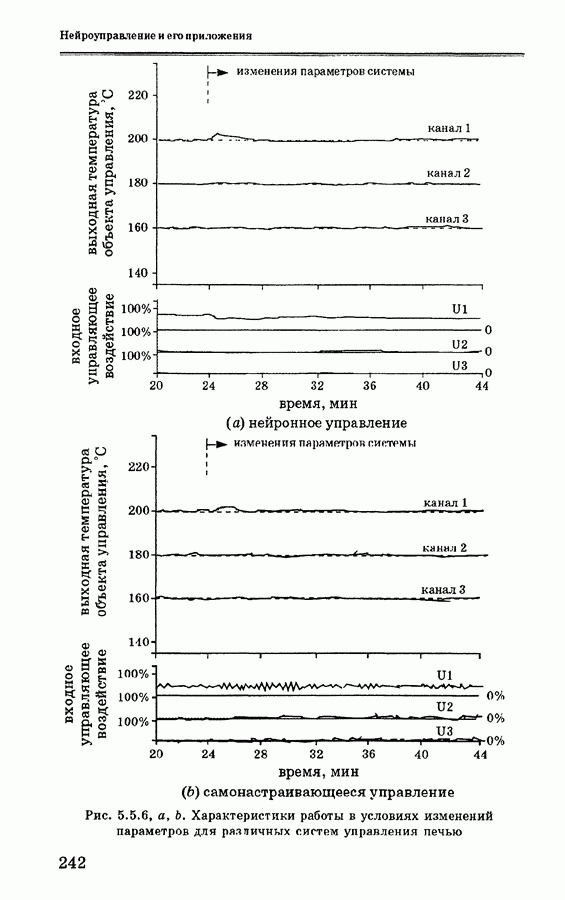
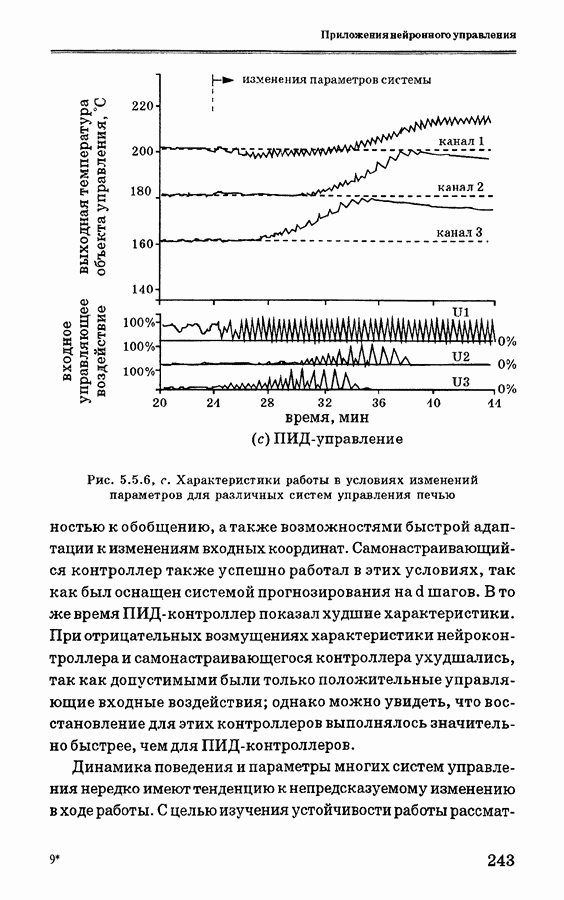
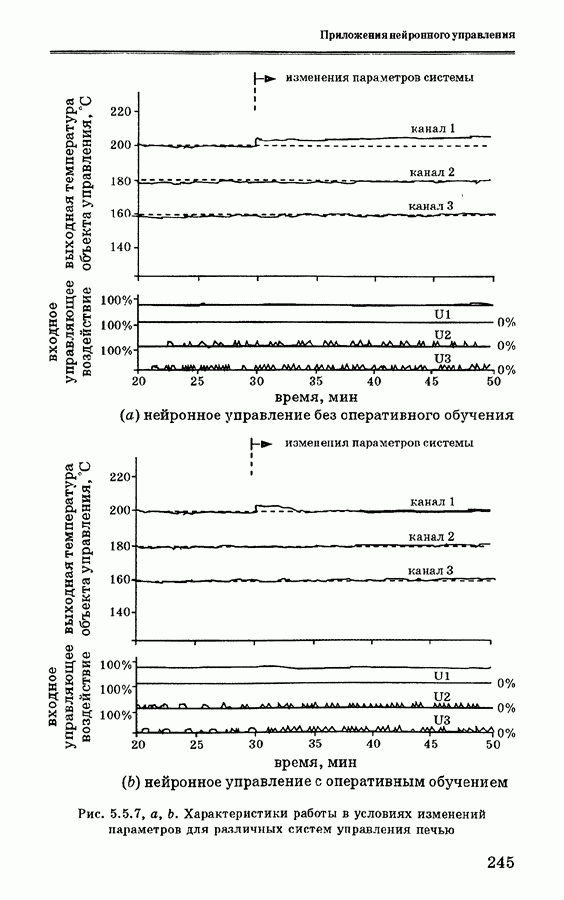
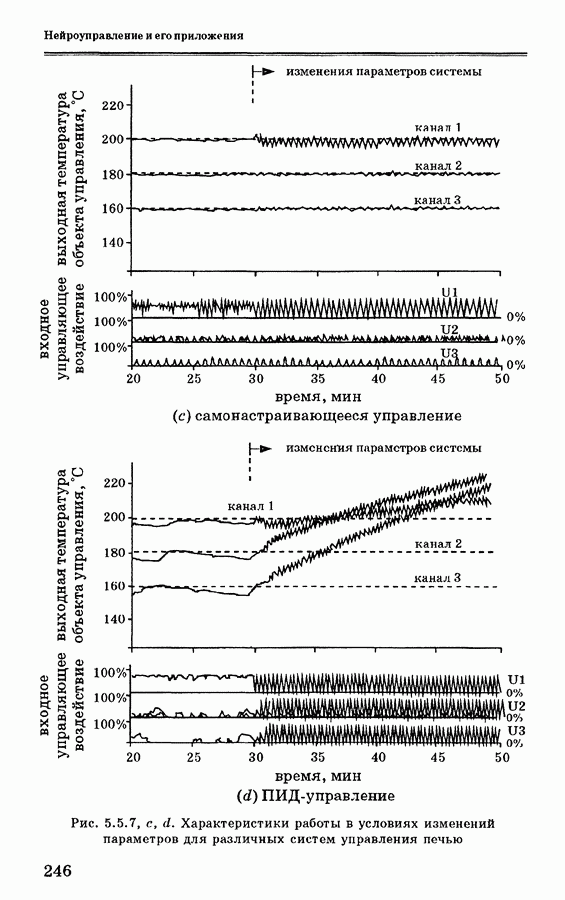
- 5.5.4. Анализ экспериментальных данных
- 5.6. Заключительные замечания и выводы
- Литература
- ЛИСТИНГ ПРОГРАММЫ