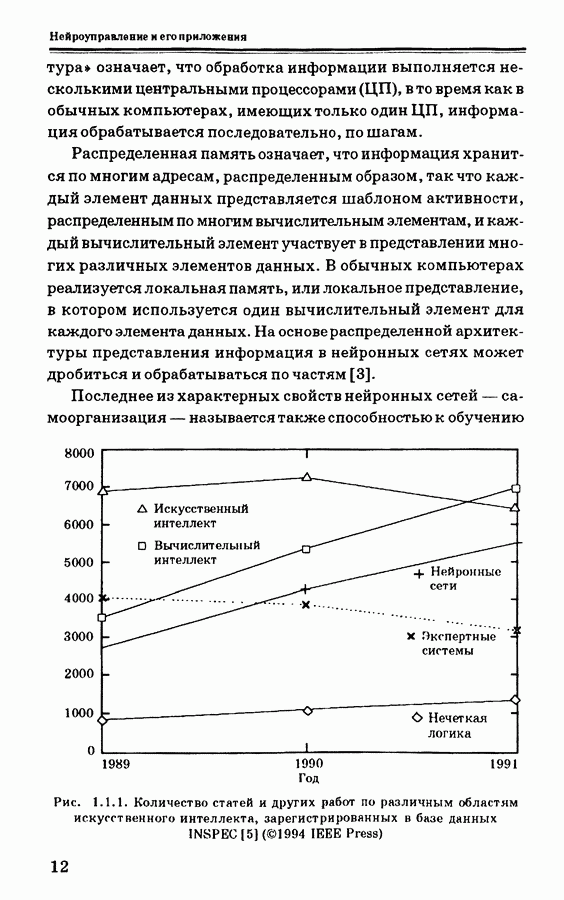
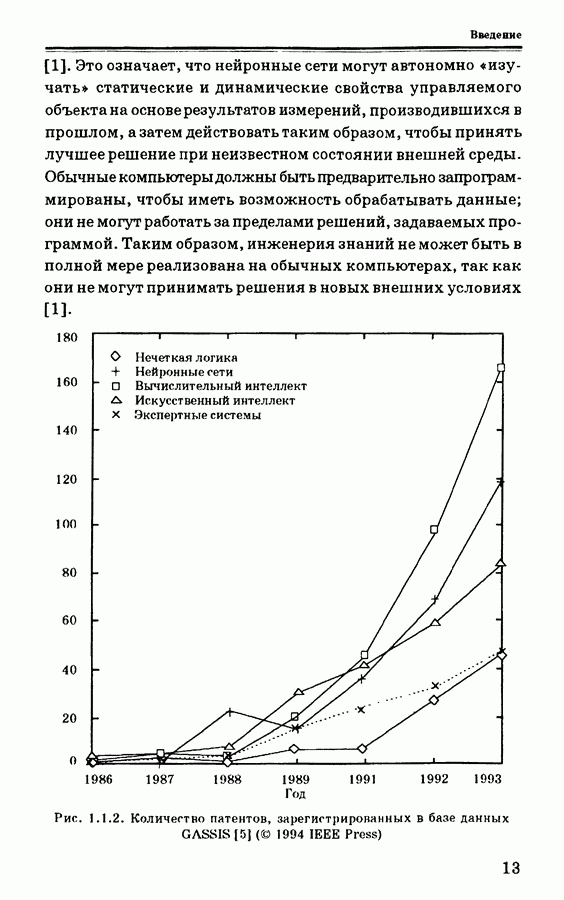
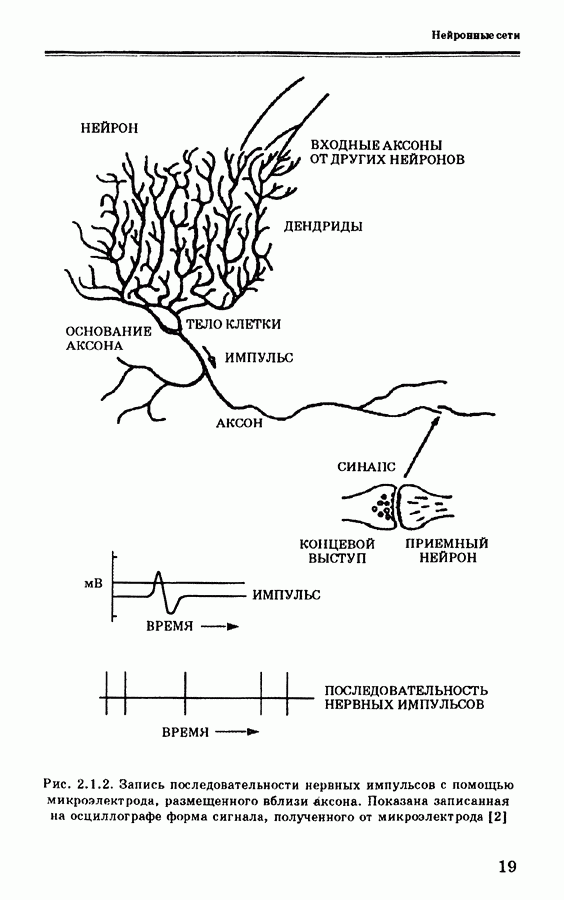
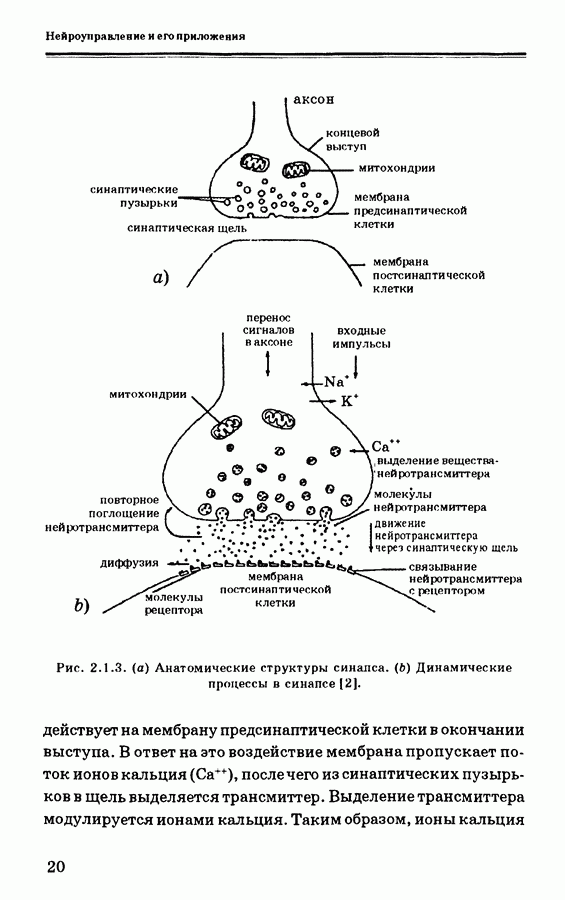
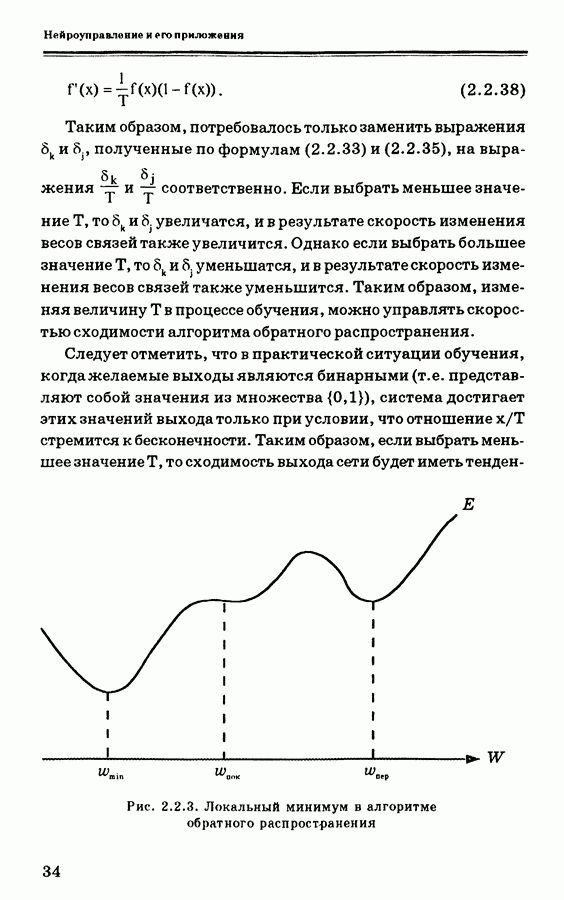
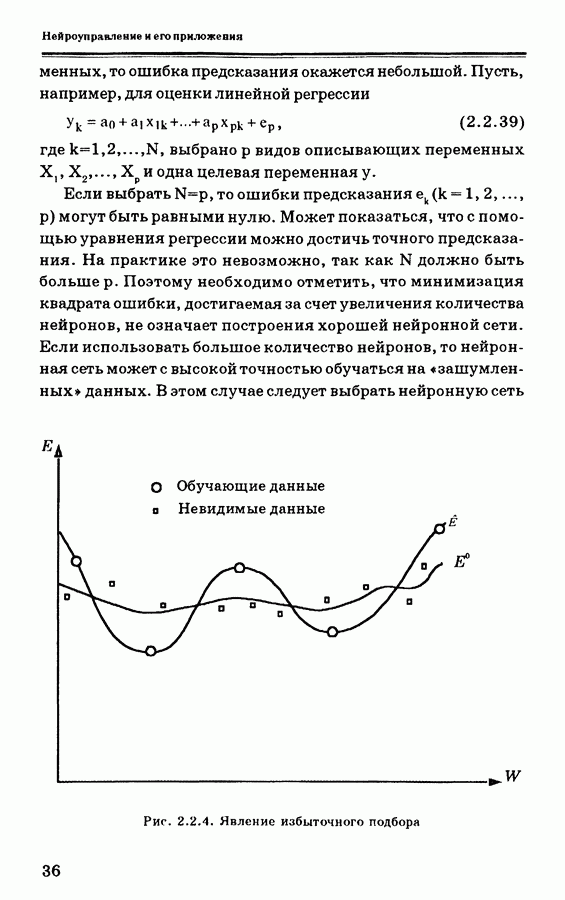
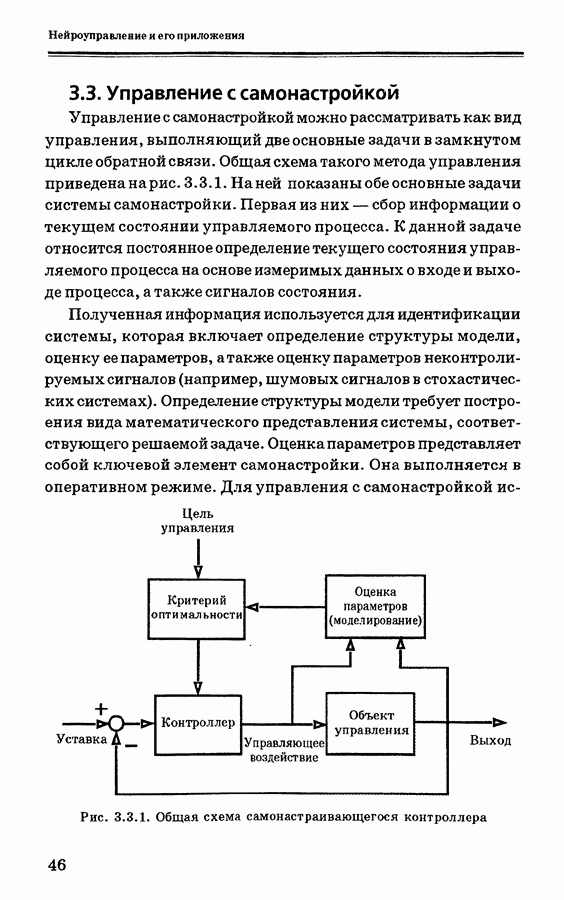
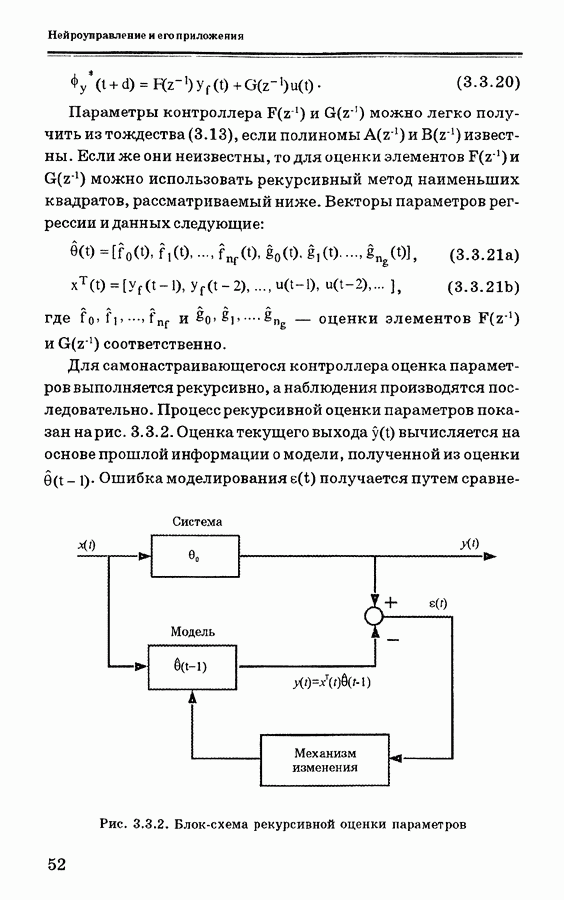
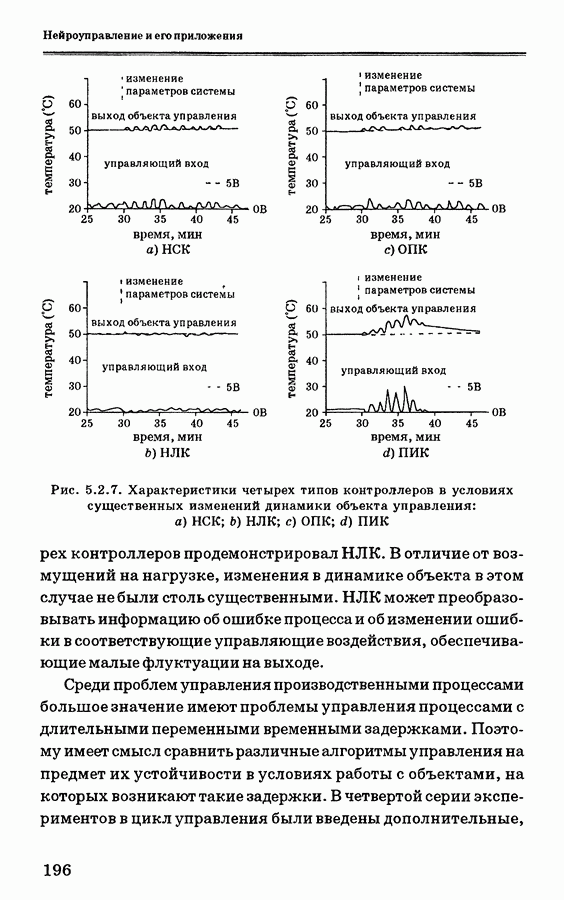
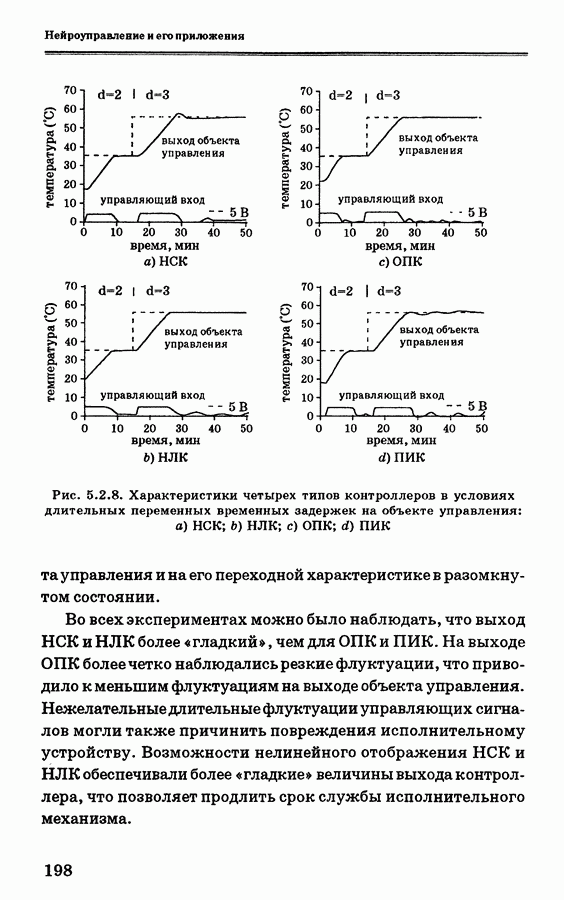
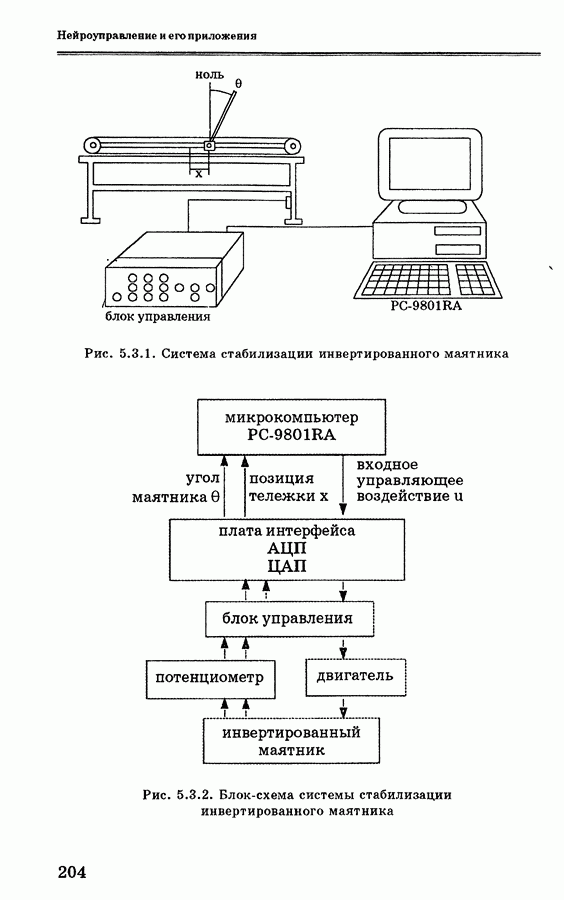
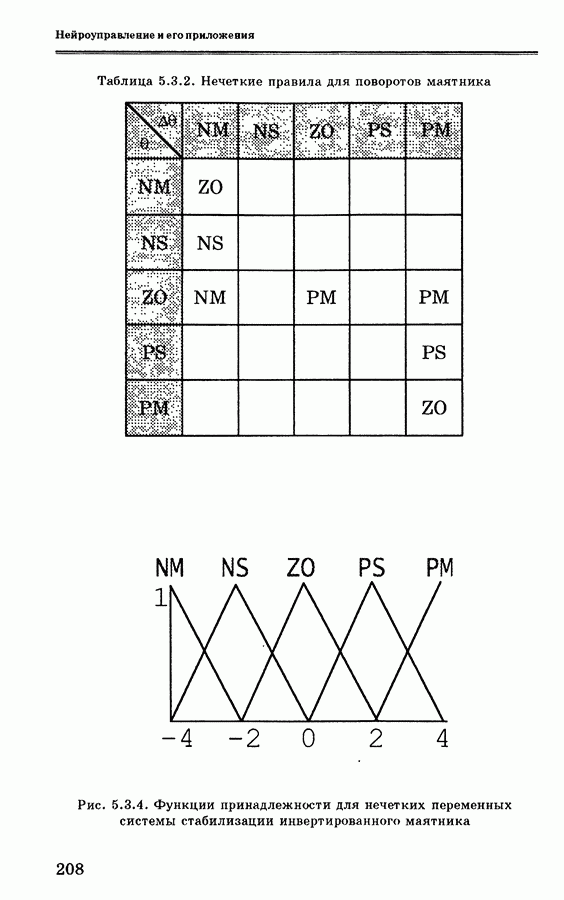
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
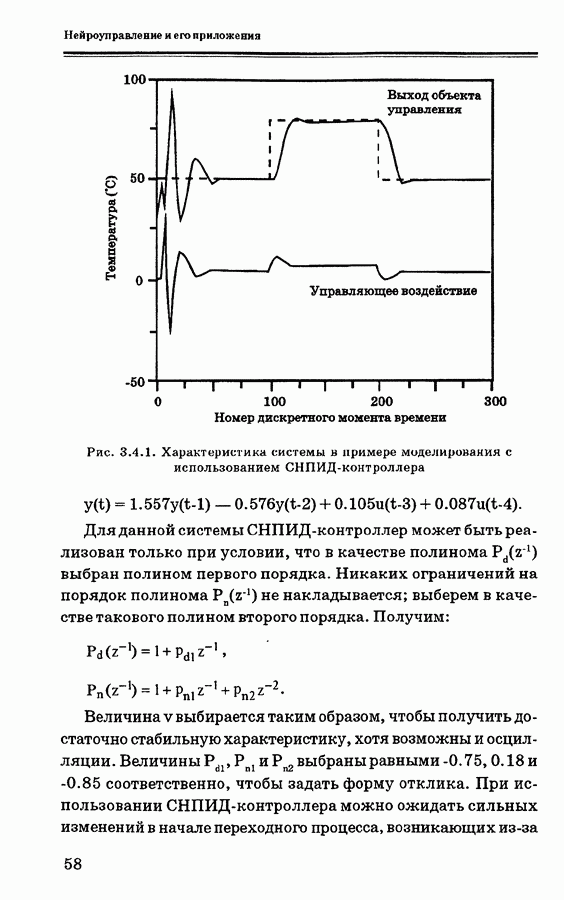
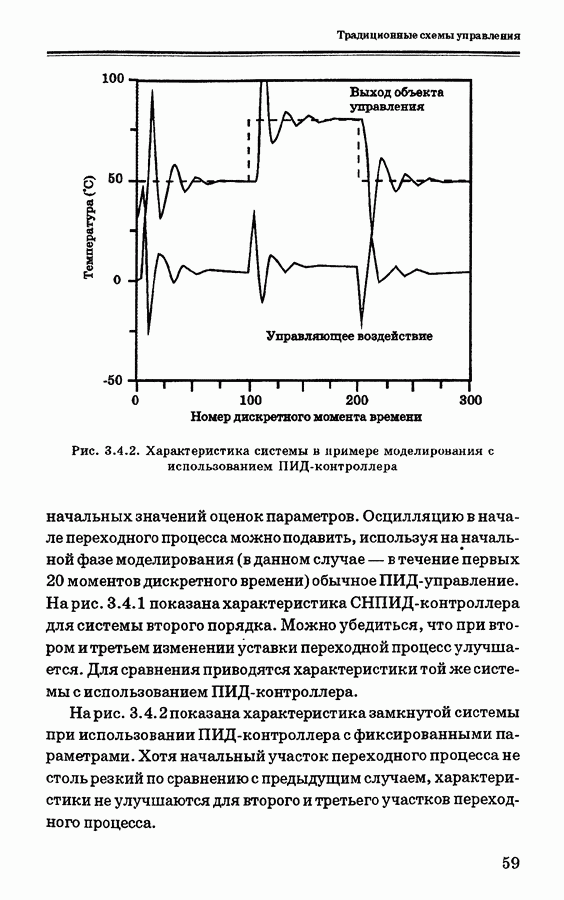
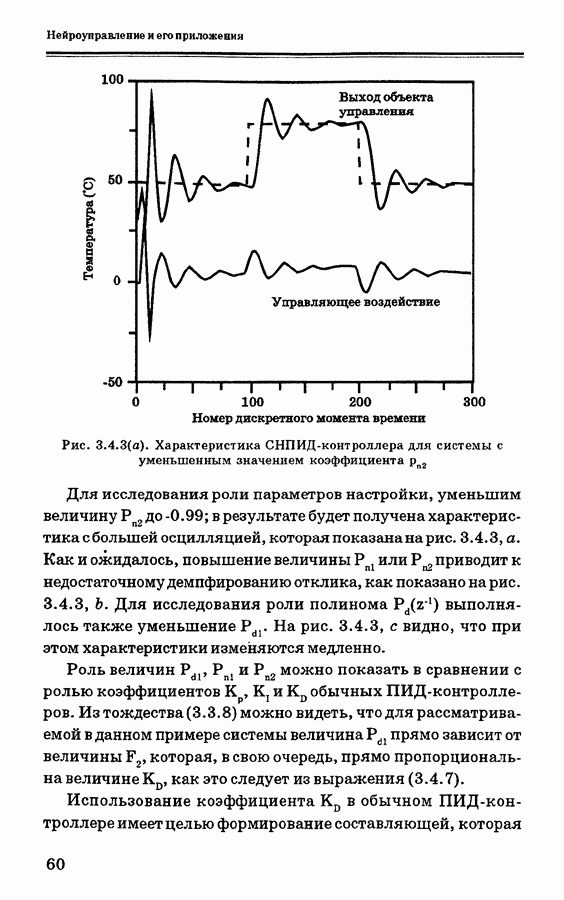
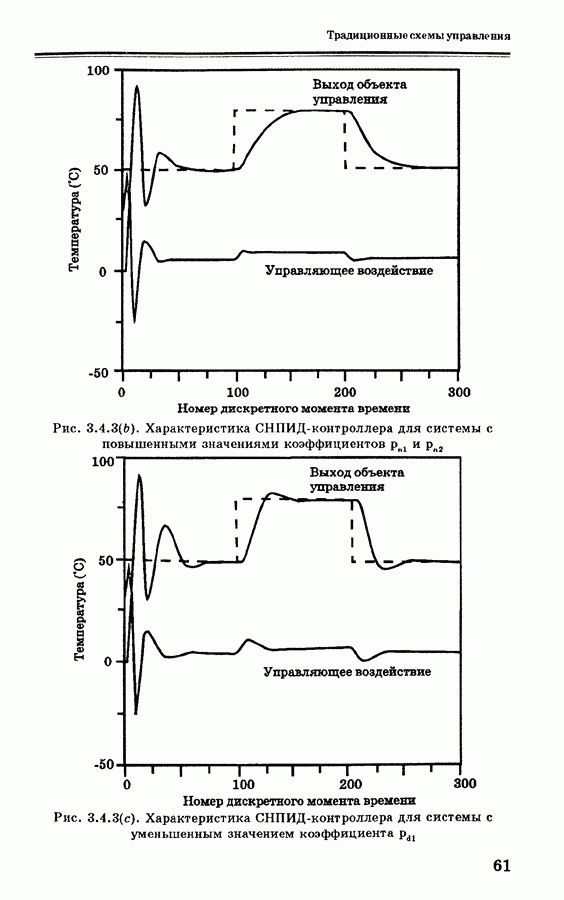
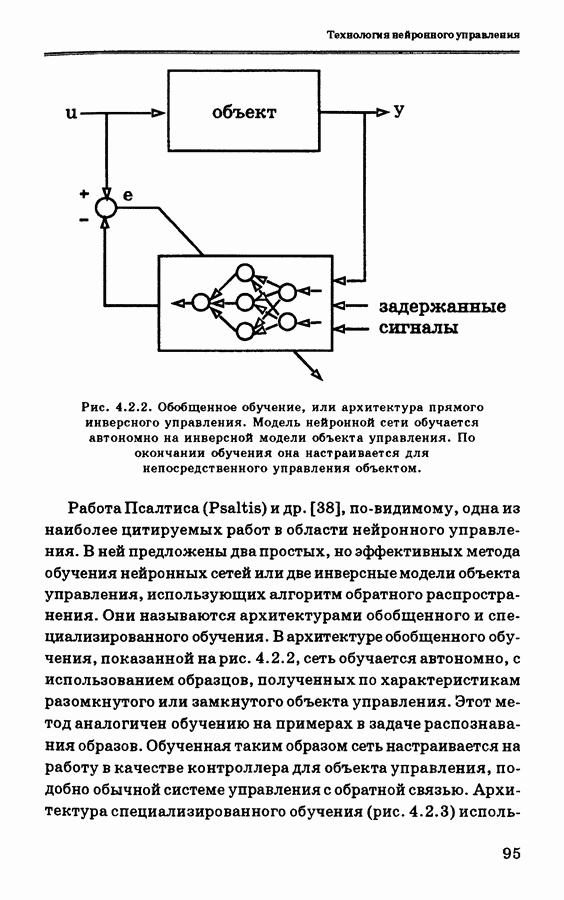
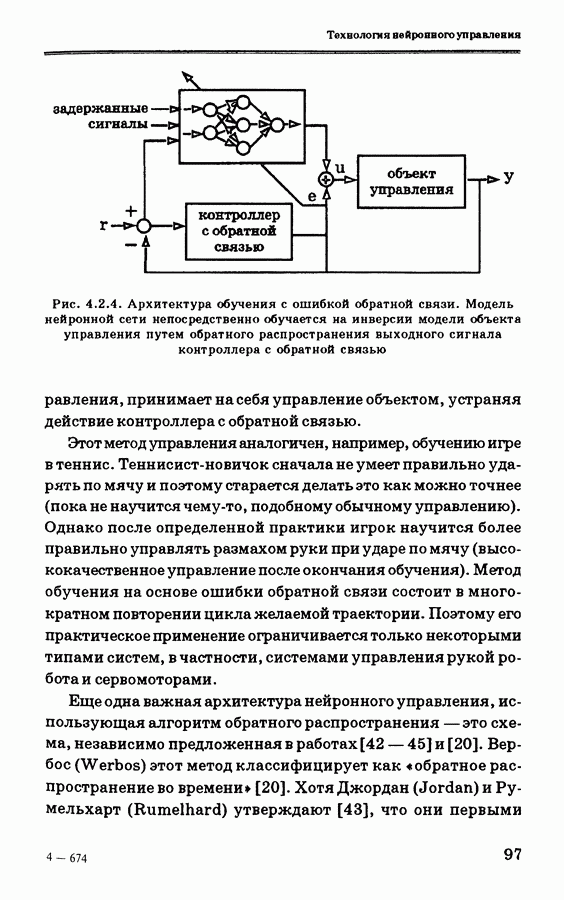
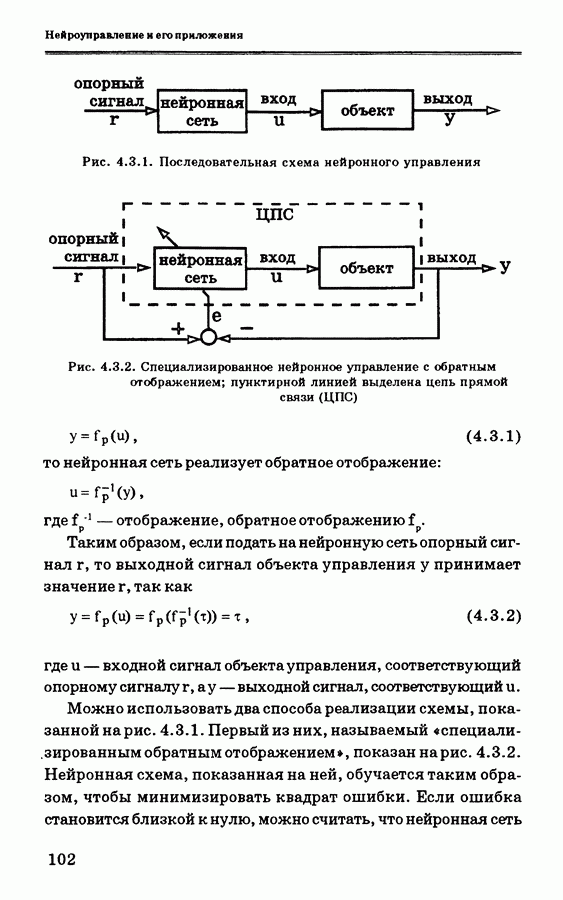
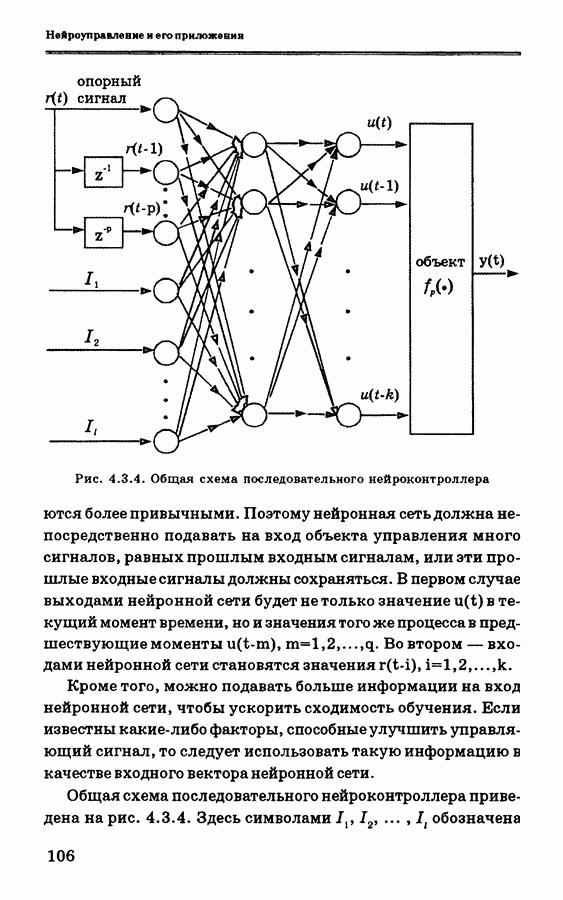
3.6.2. Модель объекта управления и решение задачи оптимизации
Рассмотрим сначала алгоритм ОПУ для систем с одним входом и одним выходом. При выводе алгоритма ОПУ Кларк и др. ввели модель УАРПСС (управляемая авторегрессия — проинтегрированное скользящее среднее); эта модель является более подходящей для использования в управлении процессами с целью устранения смещения, вызываемого возмущениями. Эти возмущения можно смоделировать как дрейф (броуновское
движение) или как ступенчатую случайную величину, изменяющуюся в случайные моменты времени. Модель УАРПСС с временной задержкой  равной 1, может быть записана в следующей форме:
равной 1, может быть записана в следующей форме:

Возмущающее воздействие может быть как детерминированным, так и стохастическим, однако за счет оператора А его математическое ожидание принимается равным нулю. В подходе на основе ОПУ процесс  предполагается стохастическим, а полином
предполагается стохастическим, а полином  — устойчивым и равным 1.
— устойчивым и равным 1.
Для решения задачи оптимизации (3.6.2) требуется вычислить прогноз на  шагов вперед для выходного процесса
шагов вперед для выходного процесса  при
при  Вычисления выполняются на основе информации, известной в момент времени
Вычисления выполняются на основе информации, известной в момент времени  а также информации о будущих значениях инкремента управления, которые требуется выбирать таким образом, чтобы оптимизировать критерий (3.6.2). Прогноз выходного процесса на
а также информации о будущих значениях инкремента управления, которые требуется выбирать таким образом, чтобы оптимизировать критерий (3.6.2). Прогноз выходного процесса на  шагов можно описать в следующей форме:
шагов можно описать в следующей форме:

где  и
и  получены путем рекурсивного решения диофантова уравнения:
получены путем рекурсивного решения диофантова уравнения:

где 
Вычитая уравнение (3.6.5) из уравнения (3.6.6), получим

Таким образом,

Полагая  получим
получим

Из уравнения (3.6.7) получим:

Так как слагаемое  содержит члены
содержит члены  значит, первый
значит, первый  член выражения
член выражения  нулевой. Отсюда следует, что
нулевой. Отсюда следует, что  Таким образом, имеем
Таким образом, имеем

и

Приравнивая члены при одинаковых степенях  получим:
получим:

где индекс! изменяется от 0 до степени полинома.
Прогноз выходного значения можно разбить на две компоненты:  которая известна в момент
которая известна в момент  и
и  — компонента, соответствующая управляющему воздействию. Таким образом,
— компонента, соответствующая управляющему воздействию. Таким образом,

где

Здесь Г — нижняя треугольная  -матрица. Ее элементы представляют собой величины реакции объекта управления на соответствующих шагах.
-матрица. Ее элементы представляют собой величины реакции объекта управления на соответствующих шагах.

Отличительная особенность алгоритма ОПУ состоит в том, что выбор параметров  , является гибким и не влияет на устойчивость управляемой системы. Однако правильный выбор величин
, является гибким и не влияет на устойчивость управляемой системы. Однако правильный выбор величин  обеспечивает сокращение времени вычислений.
обеспечивает сокращение времени вычислений.
Квадратичной показатель качества (3.6.2) теперь можно представить в виде

где  — вектор заранее заданных уставок. Получение инкрементного вектора управления
— вектор заранее заданных уставок. Получение инкрементного вектора управления  для будущих моментов времени достигается посредством дифференцирования показателя качества по
для будущих моментов времени достигается посредством дифференцирования показателя качества по  Таким образом, получим:
Таким образом, получим:

Так как требуется только первое управляющее воздействие, имеем

где  — первая строка матрицы
— первая строка матрицы 
Чтобы сделать алгоритм самонастраивающимся,
выполняется оценка параметров объекта управления на основе рекурсивного метода наименьших квадратов, рассмотренного в разделе 3.2. Векторы данных и параметров для модели объекта управления записываются в следующем виде:

| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРОВ ПЕРЕВОДА
- 1. ВВЕДЕНИЕ
- 1.1. Общие сведения об интеллектуальном управлении
- 2. НЕЙРОННЫЕ СЕТИ
- 2.2. Алгоритм обратного распространения
- 2.2.2. Вывод алгоритма обратного распространения
- 2.2.2.2. Правило для скрытого слоя
- 2.2.3. Алгоритм обратного распространения: порядок реализации
- 2.2.4. Обсуждение алгоритма обратного распространения
- 2.3. Заключение
- 3. ТРАДИЦИОННЫЕ СХЕМЫ УПРАВЛЕНИЯ
- 3.2. ПИ- и ПИД-контроллеры с дискретным временем
- 3.3. Управление с самонастройкой
- 3.4. Самонастраивающиеся ПИ- и ПИД- контроллеры
- 3.5. ПИД-управление с самонастройкой: многомерный подход
- 3.5.1. Пример моделирования
- 3.6. Обобщенное прогнозирующее управление: некоторые теоретические аспекты
- 3.6.2. Модель объекта управления и решение задачи оптимизации
- 3.7. Управление на основе нечеткой логики
- 3.7.1. Краткие сведения по теории нечетких множеств и нечетких систем
- 3.7.2. Основная концепция нечеткого контроллера
- 3.8. Заключение
- 4. ТЕХНОЛОГИИ НЕЙРОННОГО УПРАВЛЕНИЯ
- 4.2. Общие сведения о нейронном управлении
- 4.2.1. Подходы к нейронному управлению
- 4.2.2. Общая схема управления
- 4.3. Последовательная схема нейронного управления
- 4.4. Расширение последовательной схемы нейронного управления
- 4.4.2. Нейроморфные структуры управления
- 4.4.3. Конфигурации обучения
- 4.4.4. Эффективное оперативное управление
- 4.4.5. Алгоритмы обучения
- 4.4.6. Оценка алгоритмов обучения на основе моделирования
- 4.5. Параллельная схема управления
- 4.6. Алгоритм обучения по ошибке обратной связи
- 4.7. Расширение применения нейроконтроллеров параллельного типа
- 4.7.2. Линеаризованная система управления
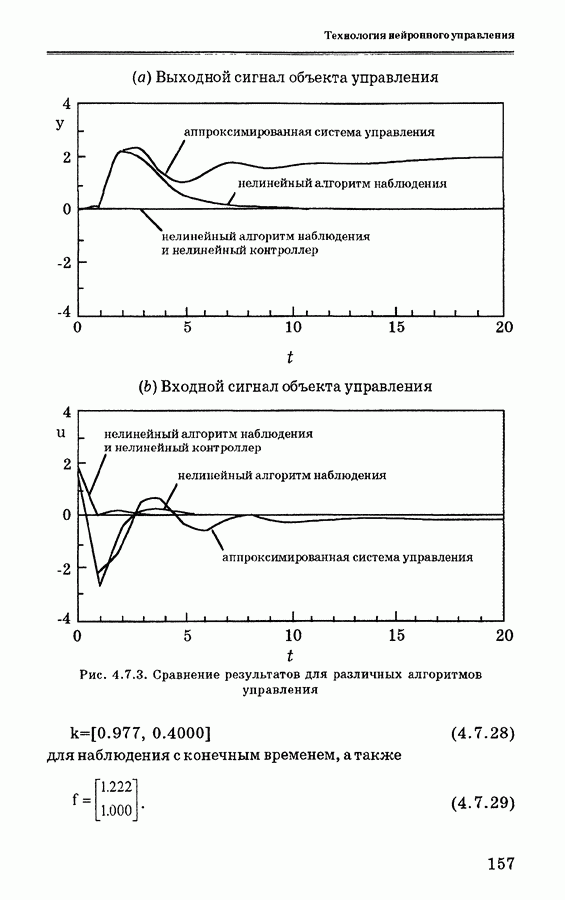
- 4.7.3. Система управления с нейронными сетями
- 4.7.4. Нелинейный алгоритм наблюдения для нейронной сети
- 4.7.5. Нелинейный контроллер для нейронной сети
- 4.7.6. Численное моделирование
- 4.8. Схема нейронного управления с самонастройкой
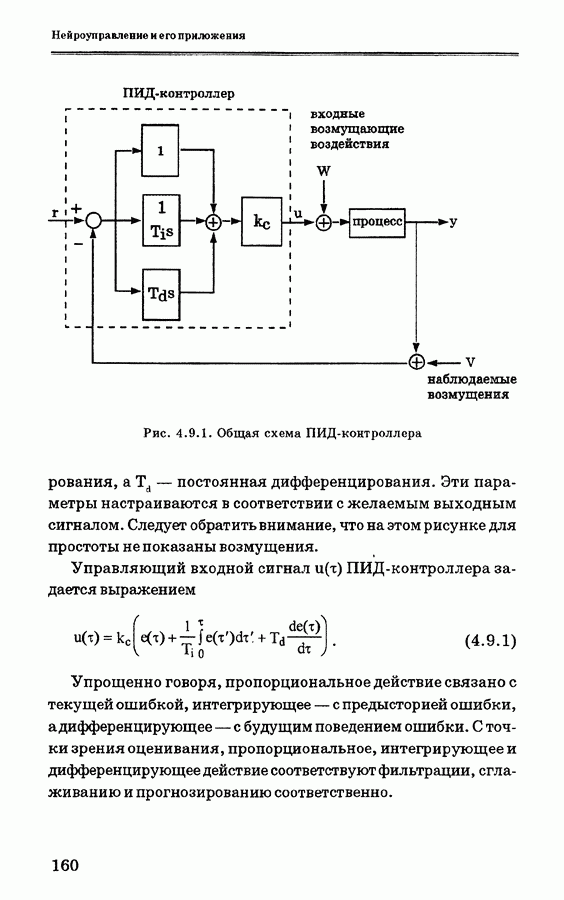
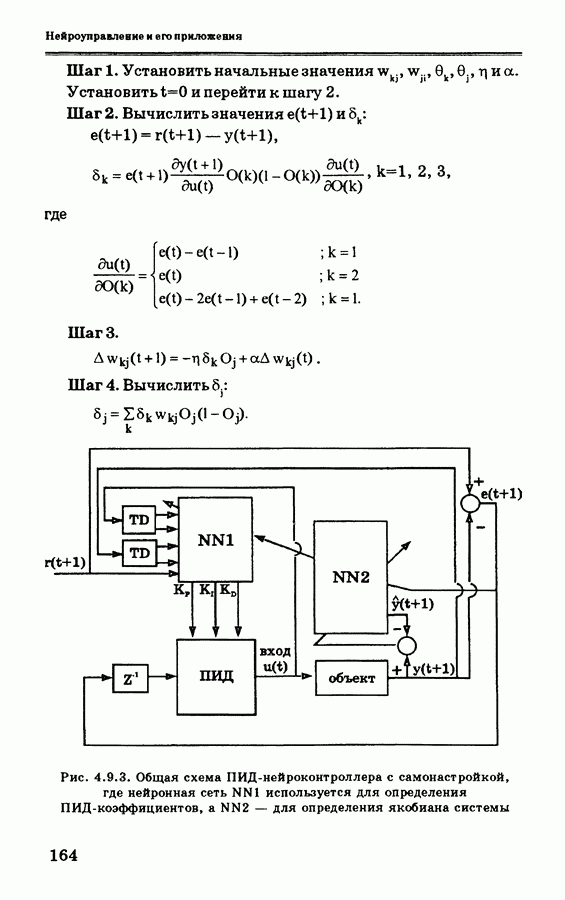
- 4.9. ПИД-нейроконтроллер с самонастройкой
- 4.9.1. Вывод уравнений ПИД-нейроконтроллера с самонастройкой
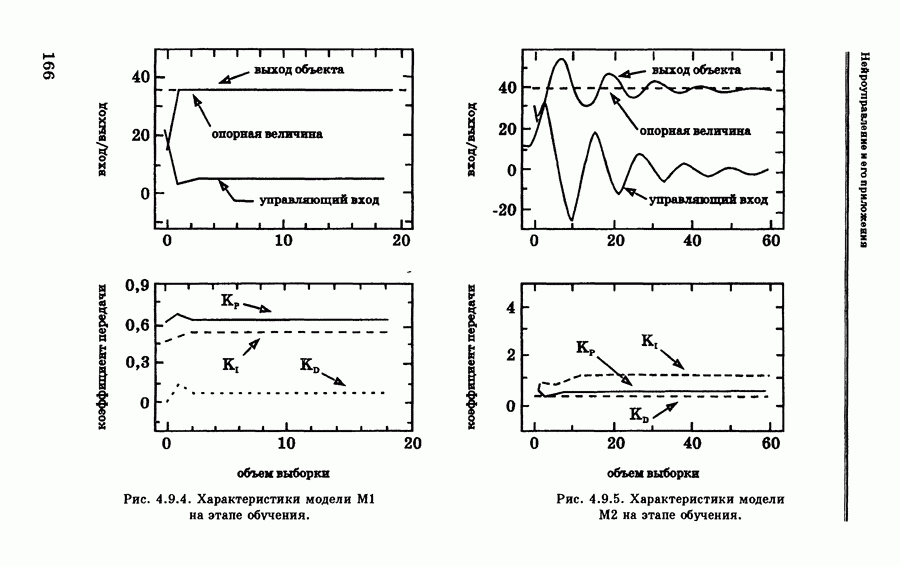
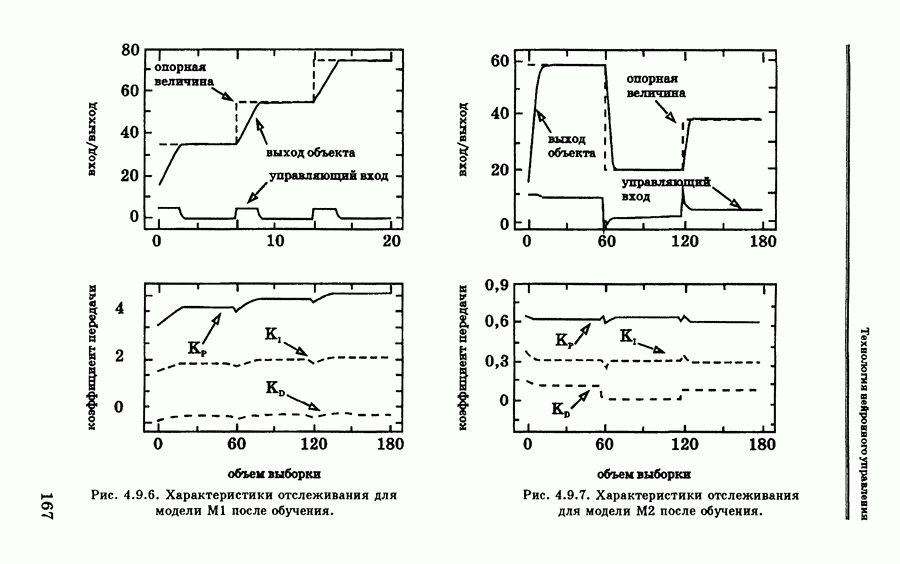
- 4.9.2. Примеры эмуляции
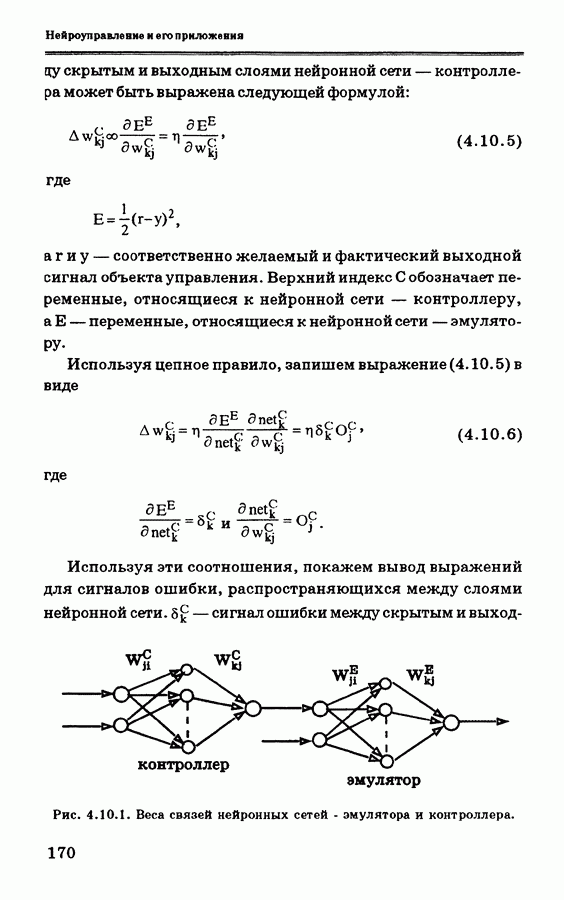
- 4.10. Схема нейронного управления с эмулятором и контроллером (схема обратного распространения во времени)
- 4.11. Заключение
- 5. ПРИЛОЖЕНИЯ НЕЙРОННОГО УПРАВЛЕНИЯ
- 5.2. Применение нейронного управления в системе регулирования процессов в водяной ванне и сравнение его с другими схемами управления
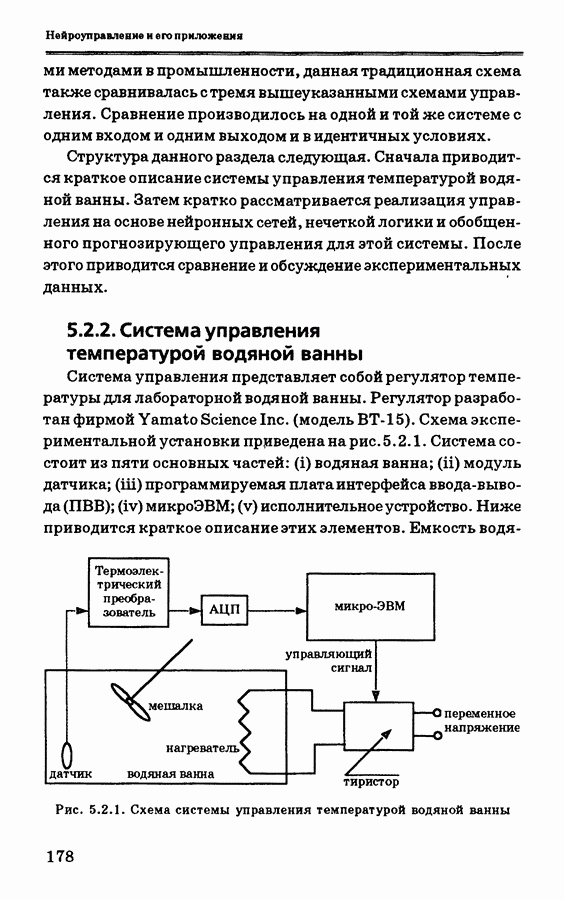
- 5.2.2. Система управления температурой водяной ванны
- 5.2.3. Схема нейронного управления
- 5.2.4. Схема управления на основе нечеткой логики
- 5.2.5. Схема обобщенного прогнозирующего управления
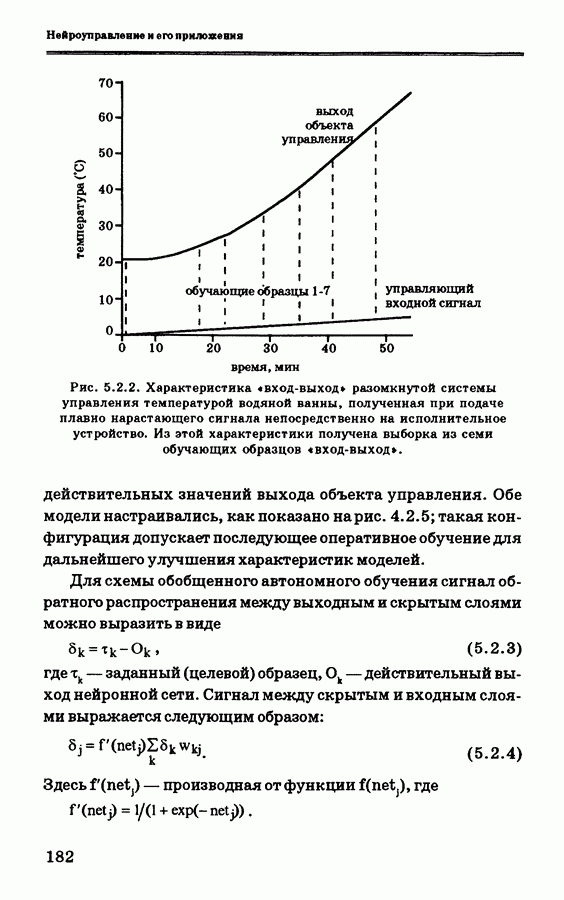
- 5.2.6. Экспериментальные данные и их анализ
- 5.2.7. Заключение
- 5.3. Система стабилизации инвертированного маятника на основе нейронных сетей
- 5.3.2. Система стабилизации инвертированного маятника
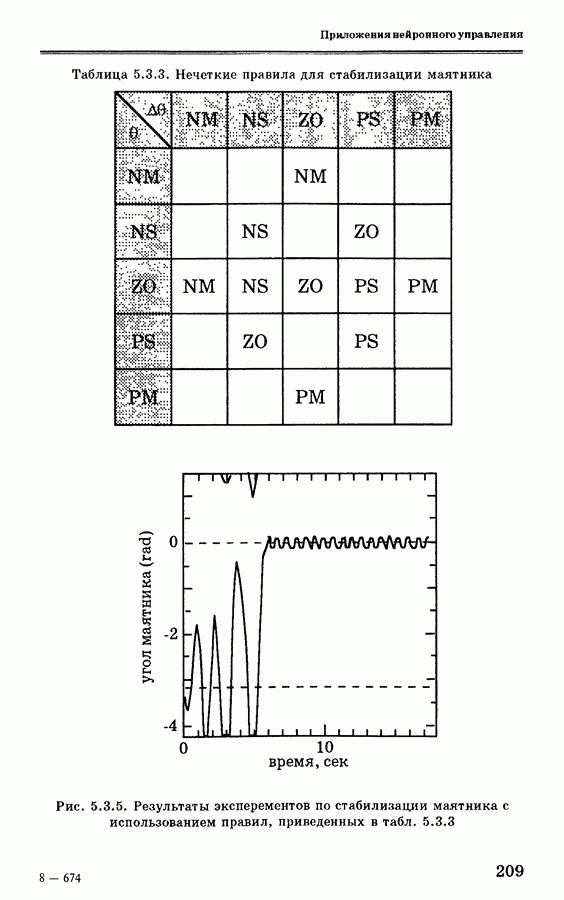
- 5.3.3. Инициализация поворотного управления с использованием нечеткой логики
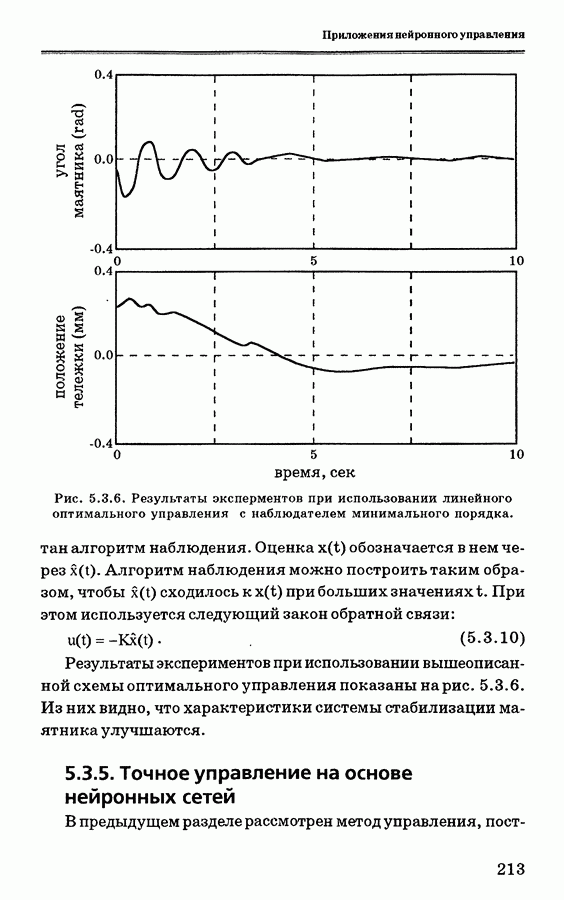
- 5.3.4. Применение стратегии оптимального управления для стабилизации маятника
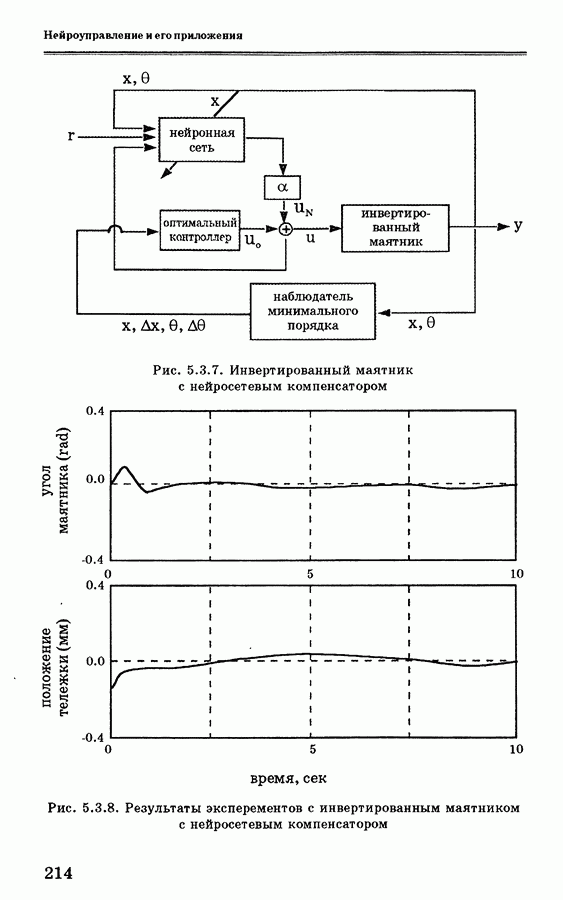
- 5.3.5. Точное управление на основе нейронных сетей
- 5.3.6. Заключение
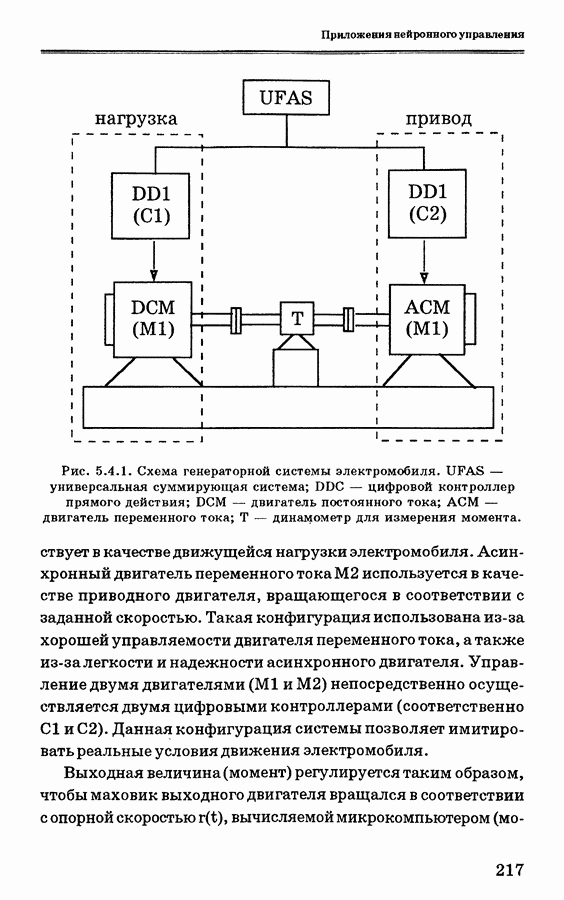
- 5.4. Применение ПИД-нейроконтроллера с самонастройкой для управления скоростью электромобиля
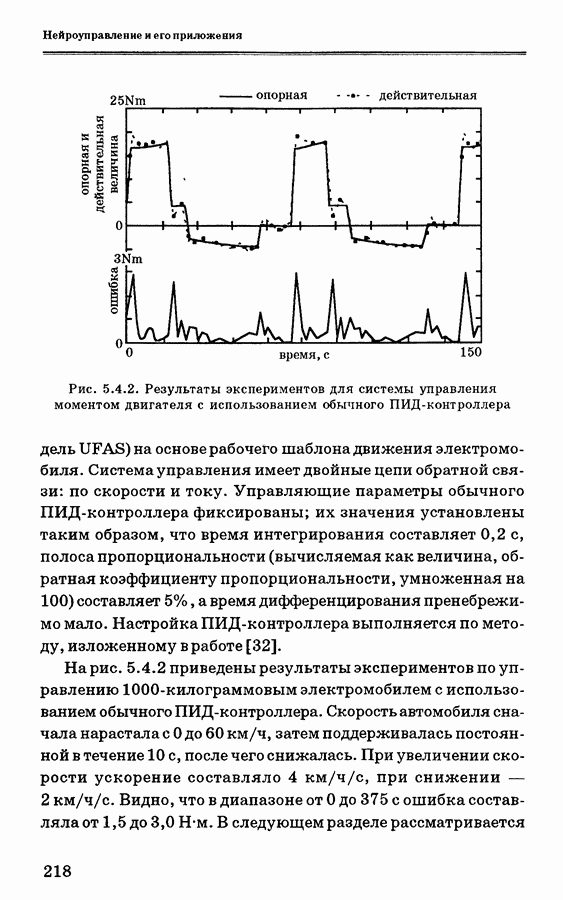
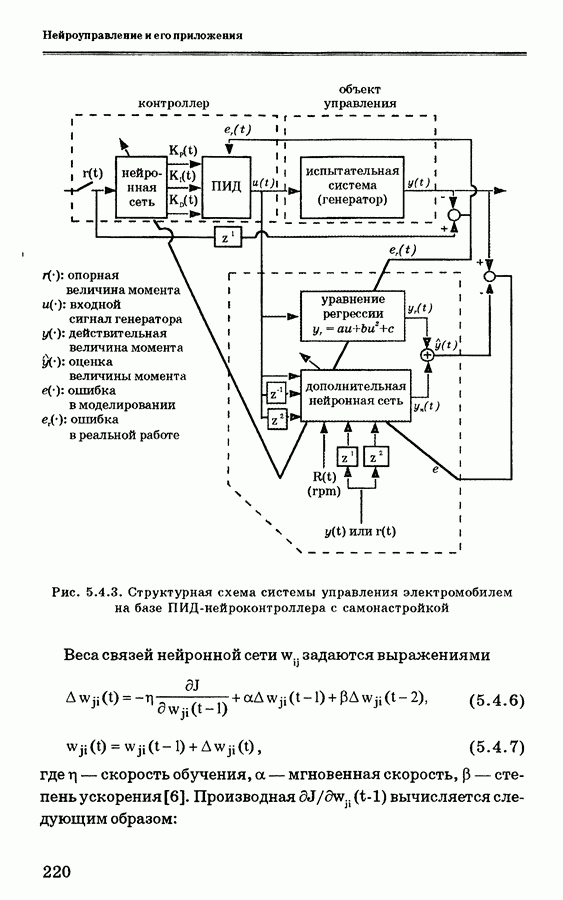
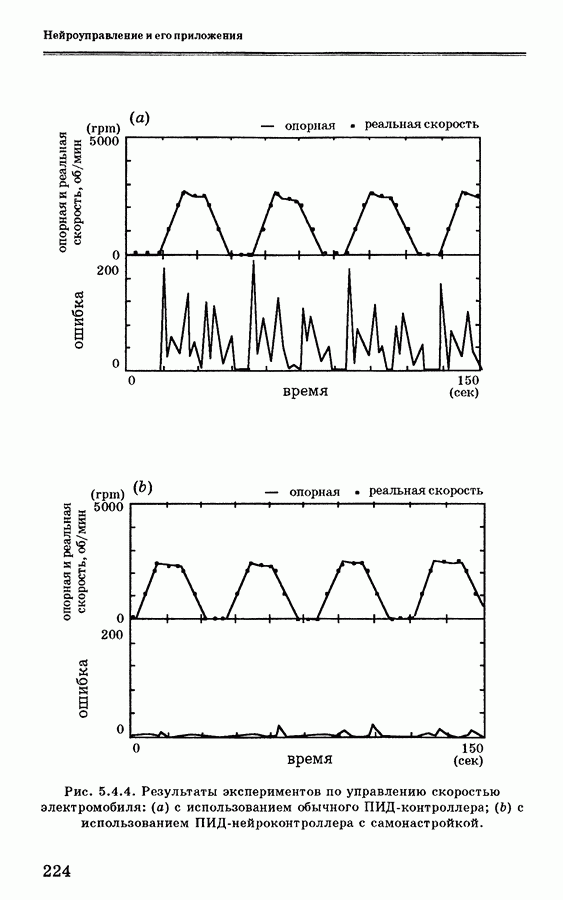
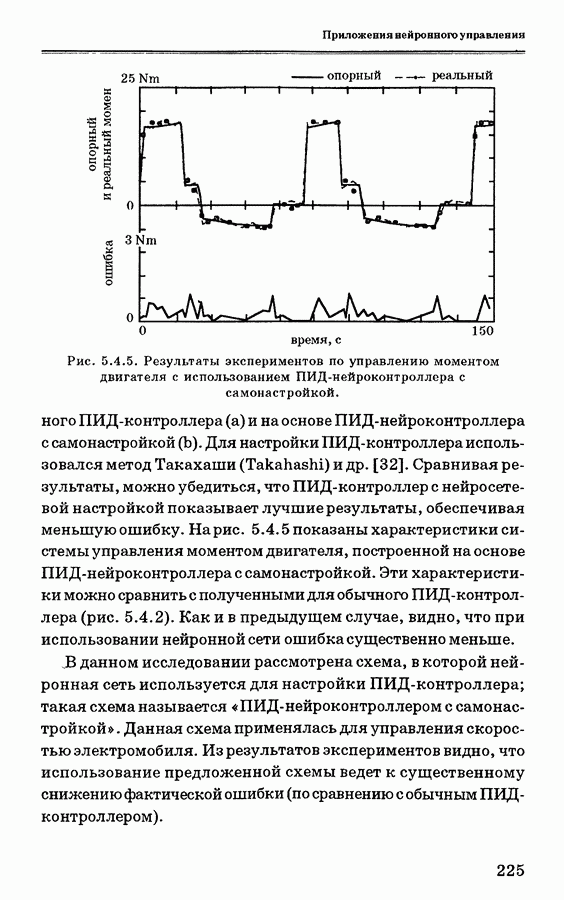
- 5.4.2. Система управления электромобилем
- 5.4.3. ПИД-нейроконтроллер с самонастройкой
- 5.4.4. Применение нейронной сети для управления скоростью электромобиля
- 5.4.5. Заключение
- 5.5. Применение нейронных сетей для управления печью
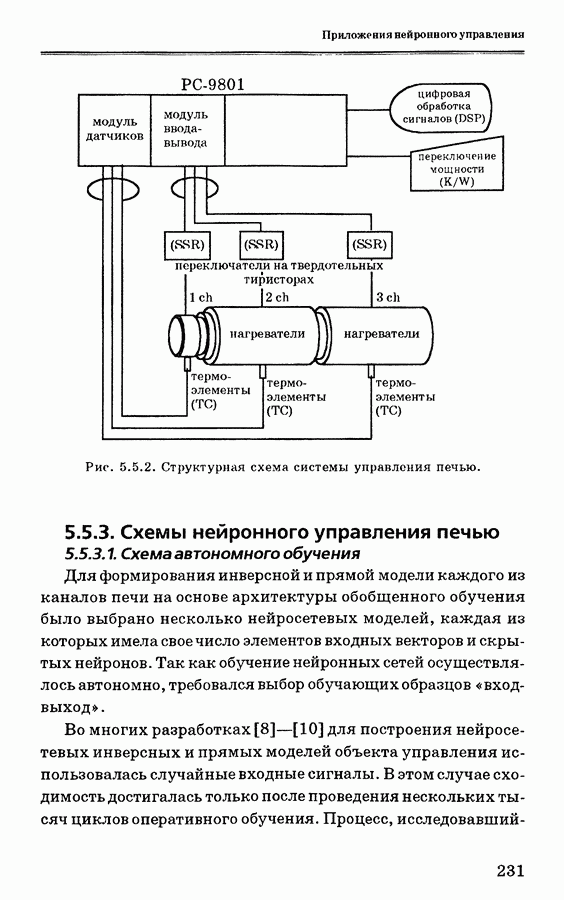
- 5.5.2. Система управления печью
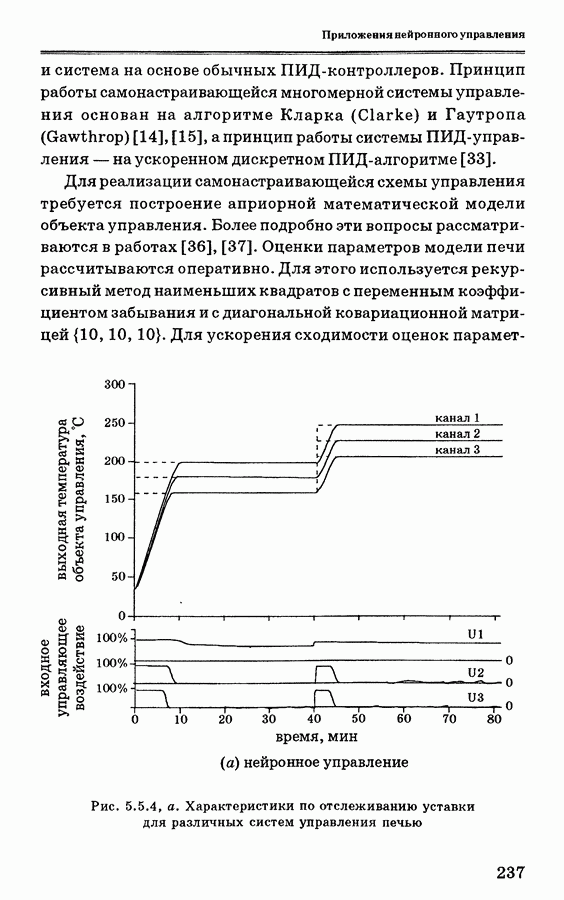
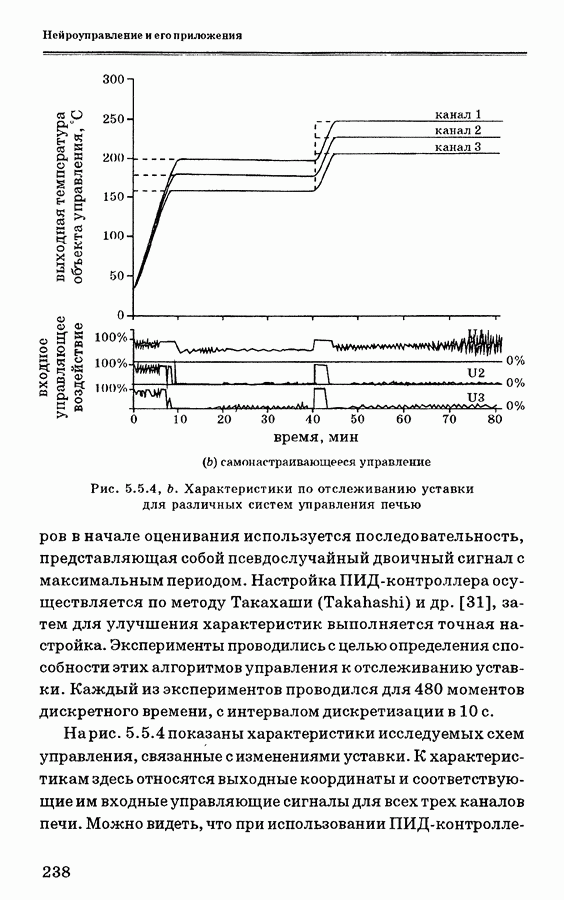
- 5.5.3. Схемы нейронного управления печью
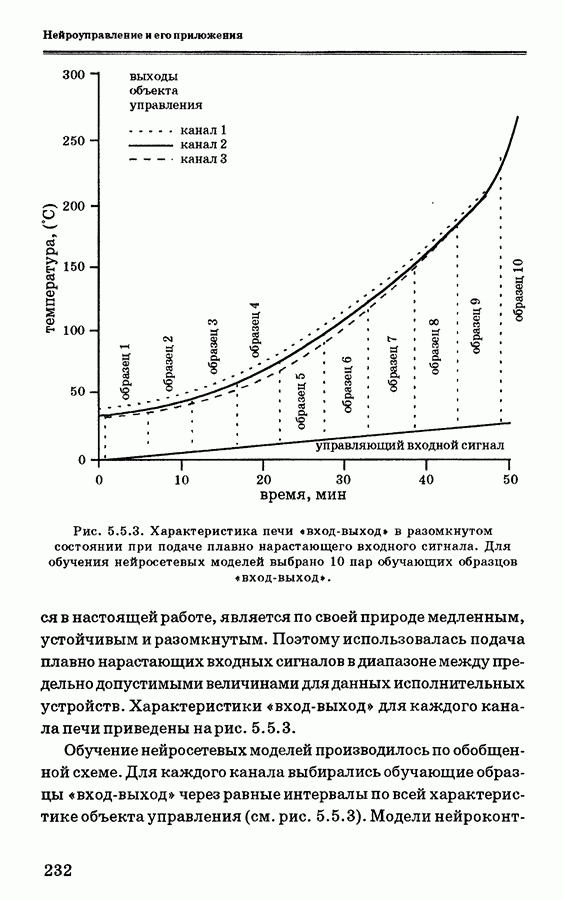
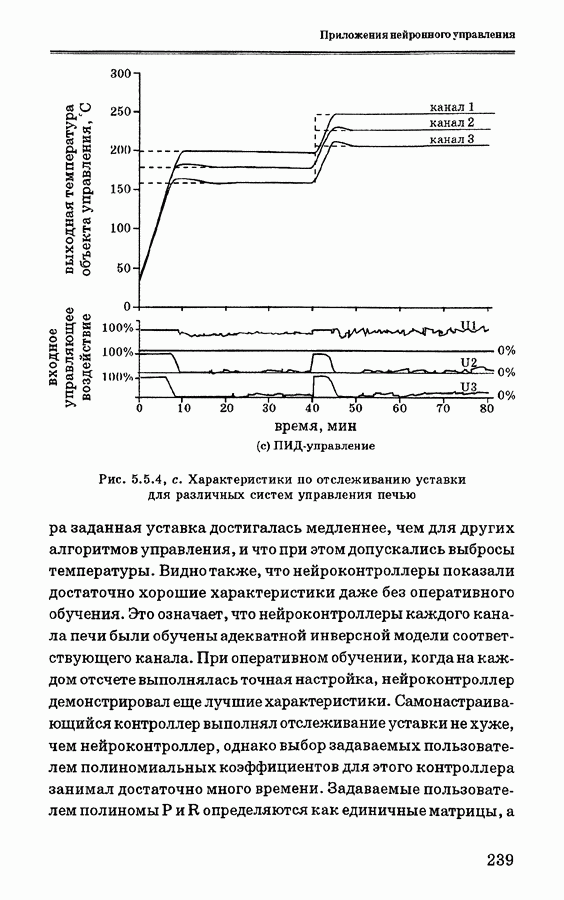
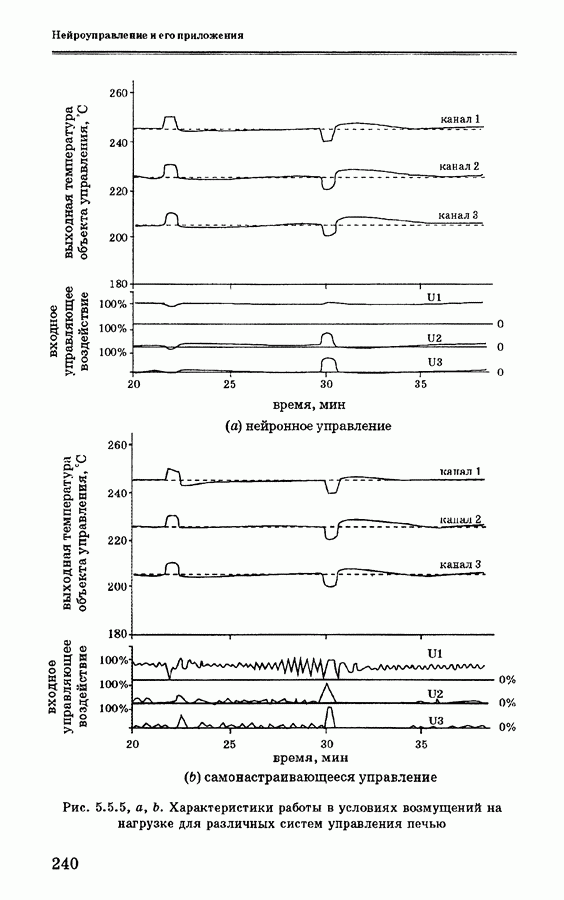
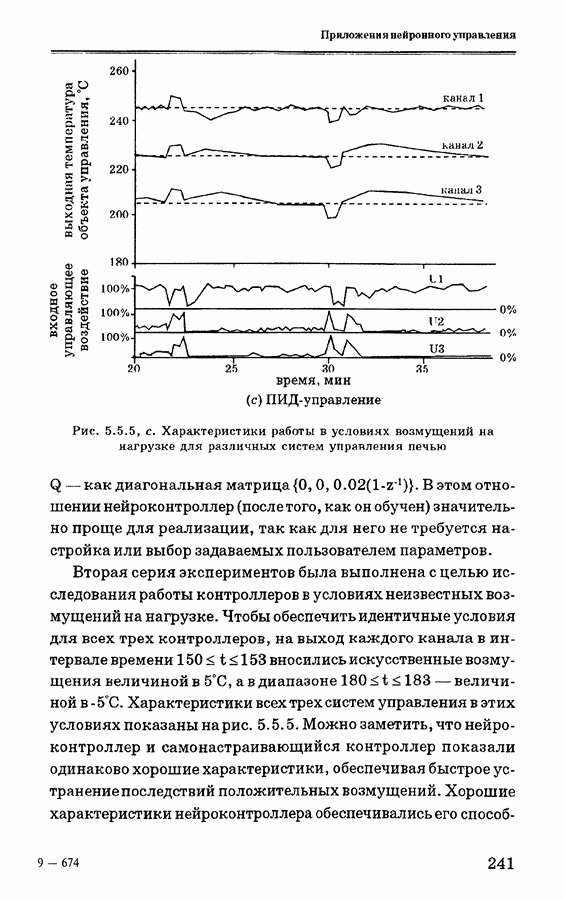
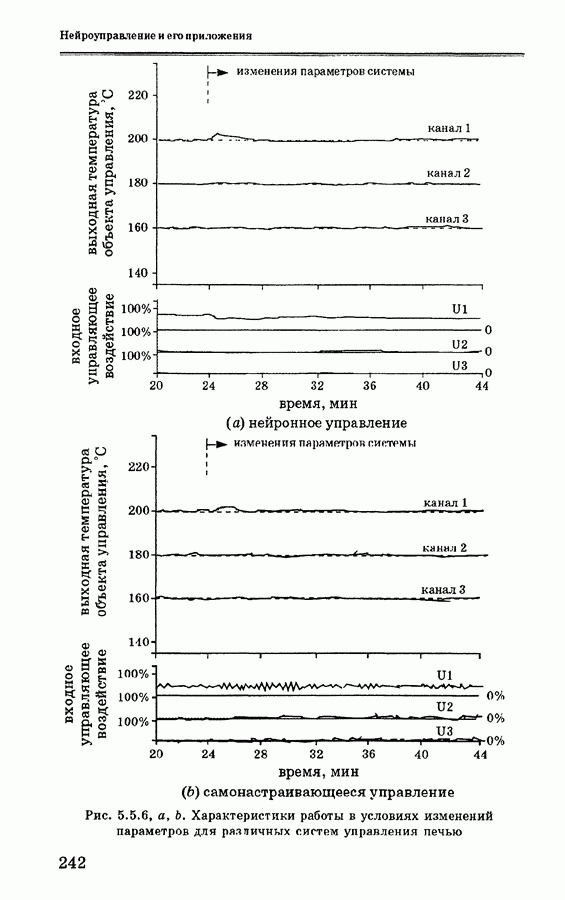
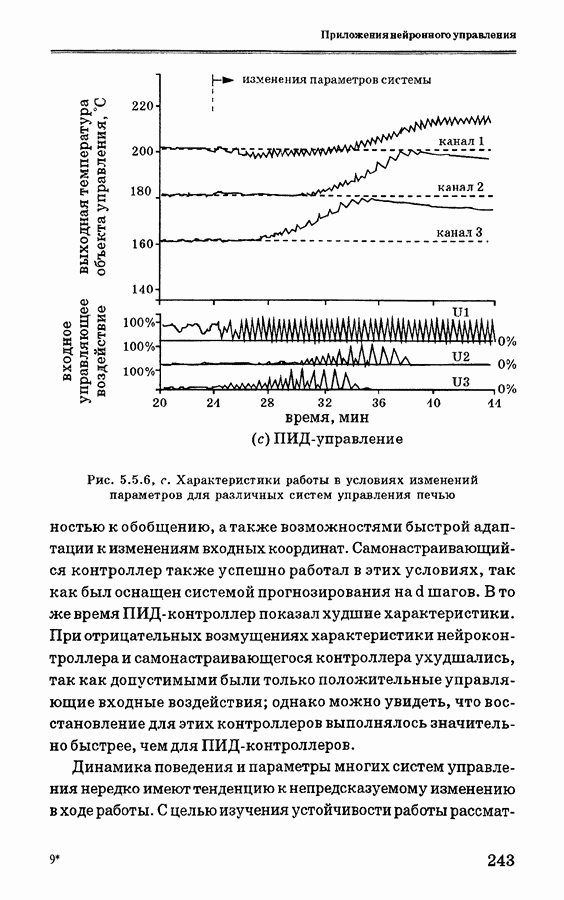
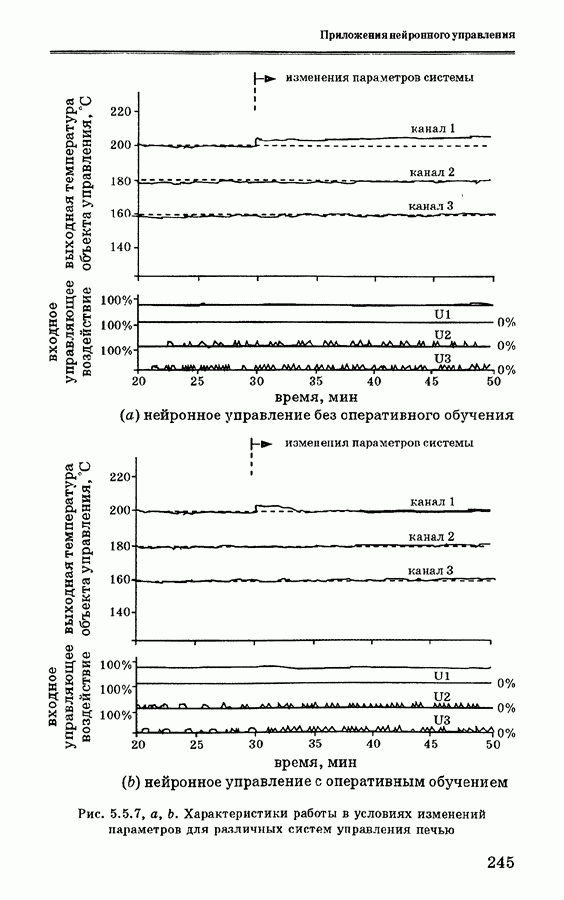
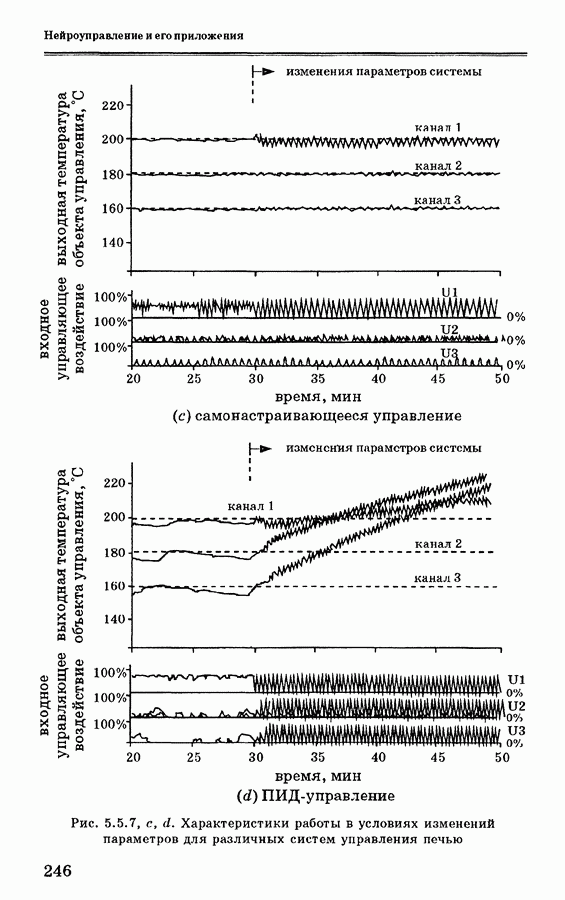
- 5.5.4. Анализ экспериментальных данных
- 5.6. Заключительные замечания и выводы
- Литература
- ЛИСТИНГ ПРОГРАММЫ