| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4.3. Последовательная схема нейронного управления
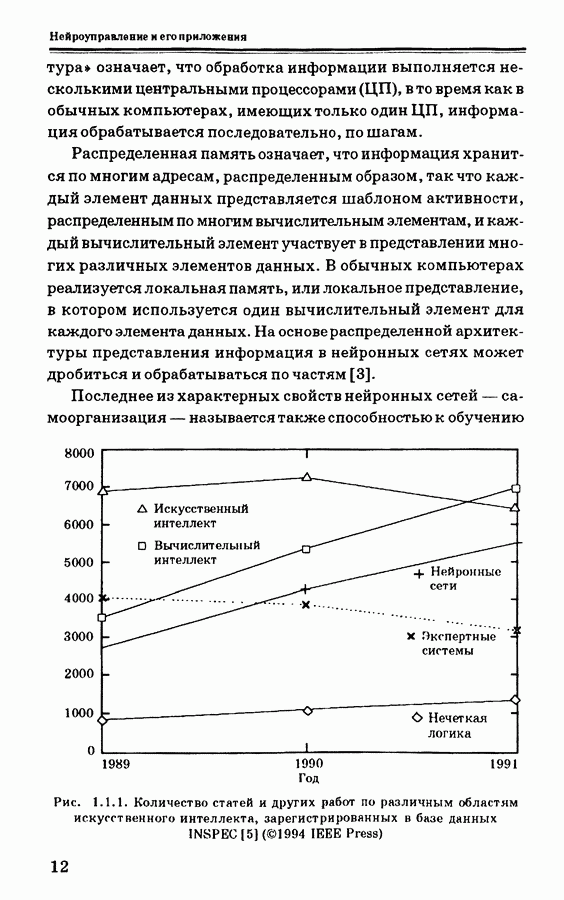
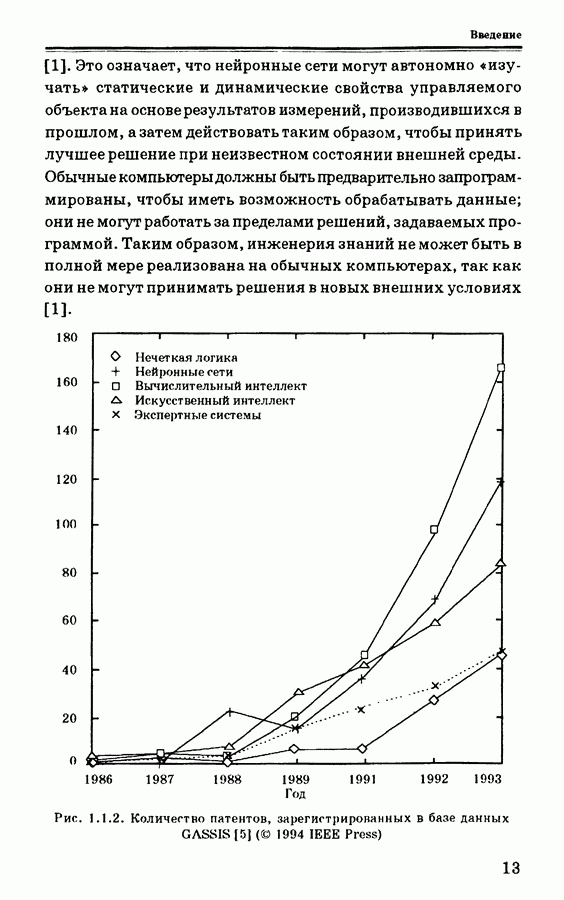
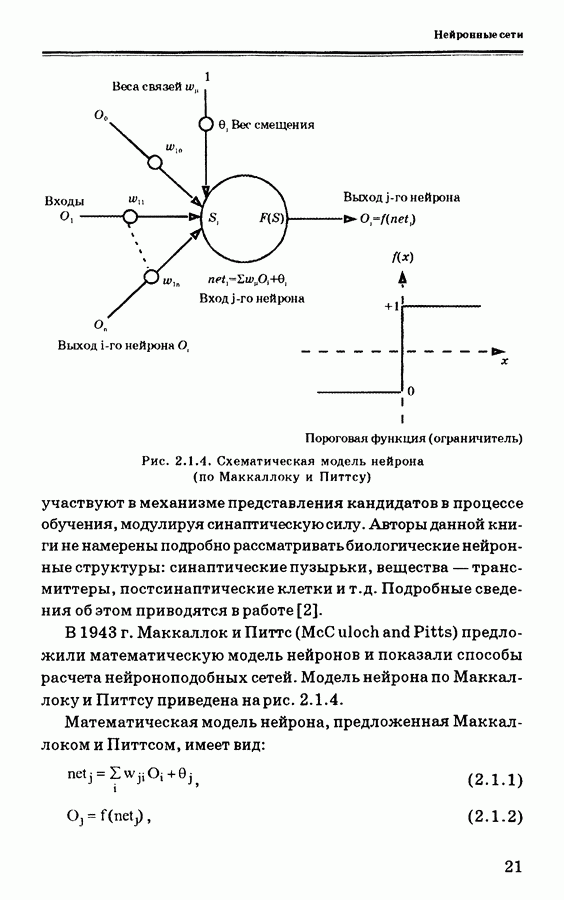
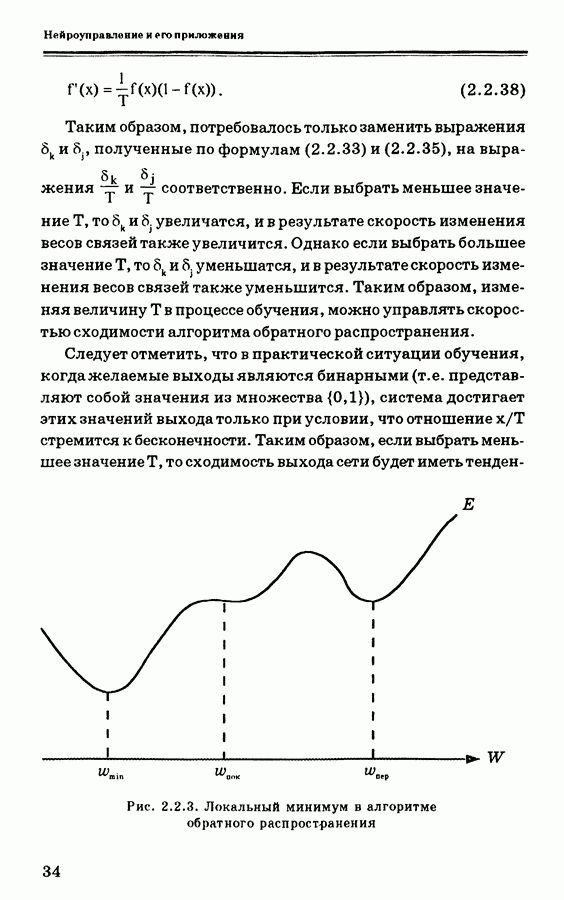
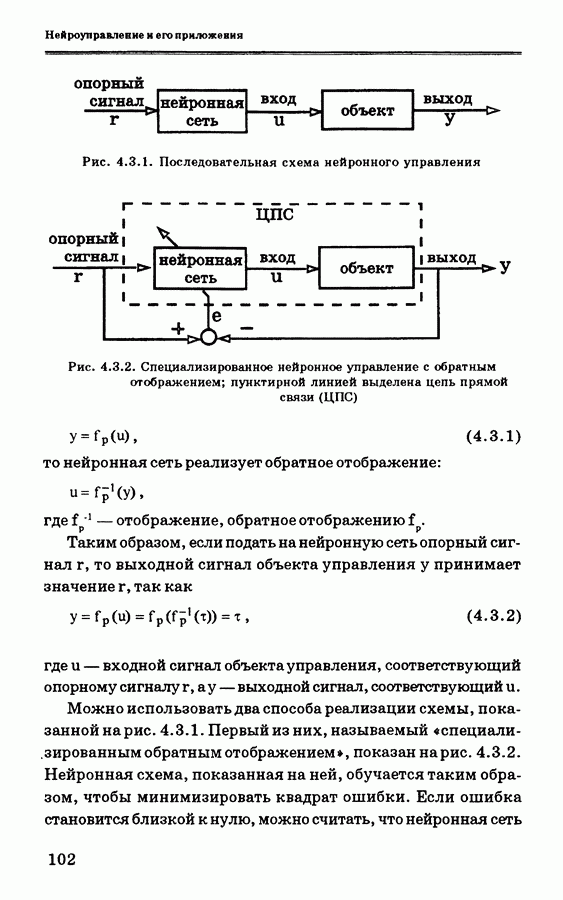
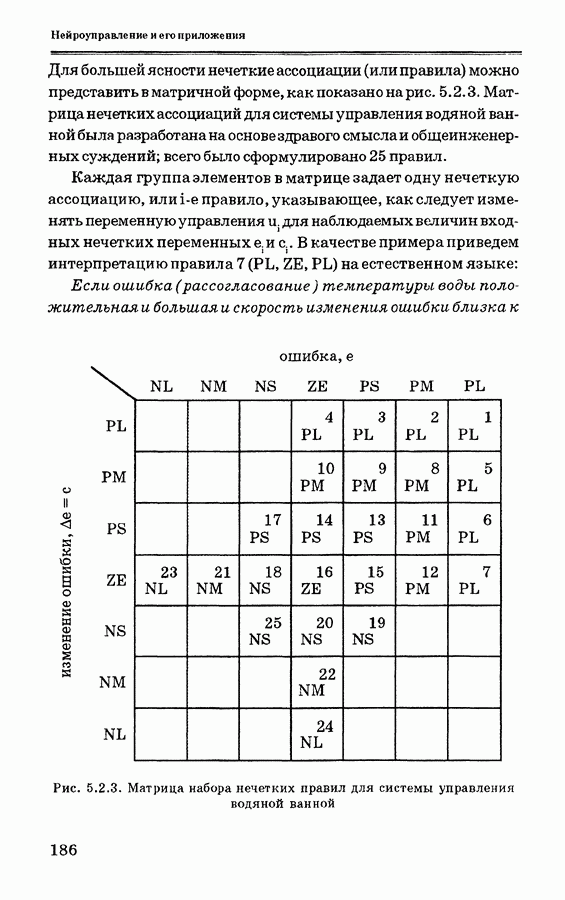
Последовательная схема нейронного управления показана нарис. 4.3.1. Для такого типа нейронного управления используется также название «инверсно-прямое управление»; это означает, что нейронная сеть может реализовывать обратную динамику объекта управления.
Если обозначить соответствие между входом и выходом как  т.е.
т.е.

Рис. 4.3.1. Последовательная схема нейронного управления

Рис. 4.3.2. Специализированное нейронное управление с обратным отображением; пунктирной линией выделена цепь прямой связи (ЦПС)

то нейронная сеть реализует обратное отображение:

где  — отображение, обратное отображению
— отображение, обратное отображению 
Таким образом, если подать на нейронную сеть опорный сигнал  то выходной сигнал объекта управления у принимает значение
то выходной сигнал объекта управления у принимает значение  так как
так как

где  — входной сигнал объекта управления, соответствующий опорному сигналу
— входной сигнал объекта управления, соответствующий опорному сигналу  — выходной сигнал, соответствующий и.
— выходной сигнал, соответствующий и.
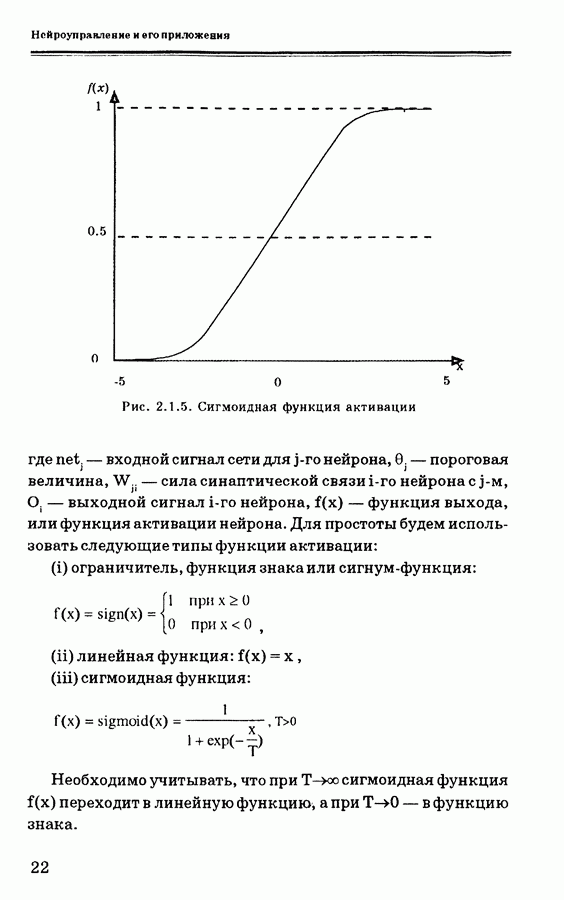
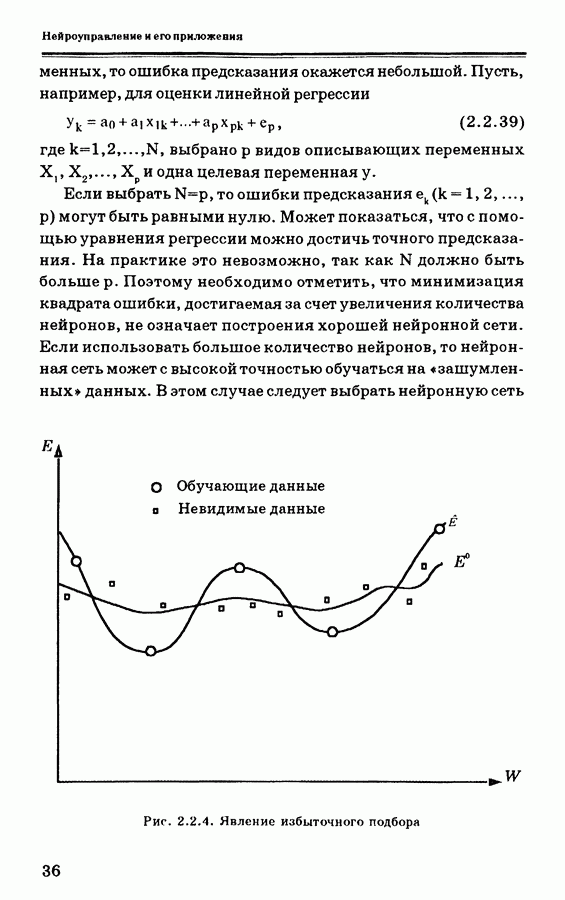
Можно использовать два способа реализации схемы, показанной на рис. 4.3.1. Первый из них, называемый «специализированным обратным отображением», показан на рис. 4.3.2. Нейронная схема, показанная на ней, обучается таким образом, чтобы минимизировать квадрат ошибки. Если ошибка становится близкой к нулю, можно считать, что нейронная сеть

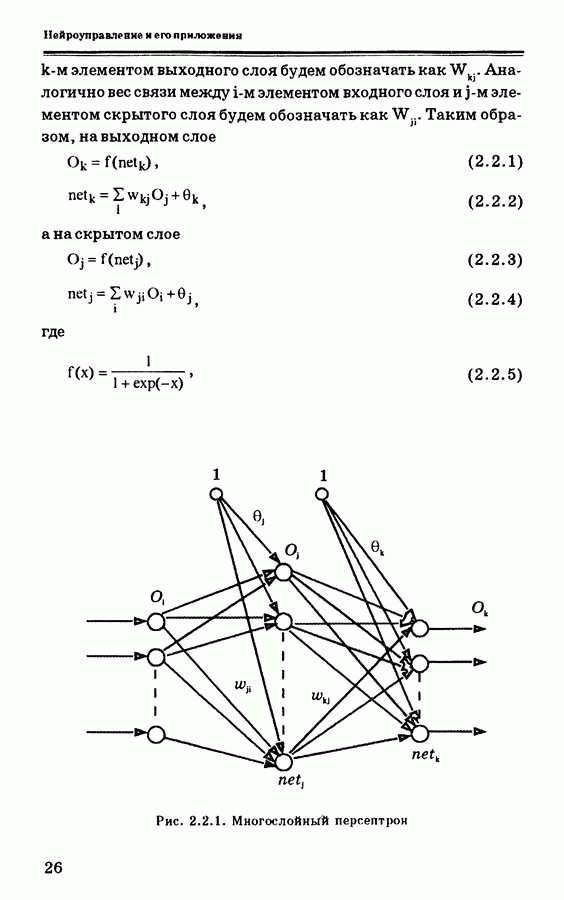
Рис. 4.3.3. Внутренняя структура нейроконтроллера, используемого в схеме, показанной на рис. 4.3.2. Величины  и
и  соответствуют коэффициентам и в разделе 2.2.1.
соответствуют коэффициентам и в разделе 2.2.1.
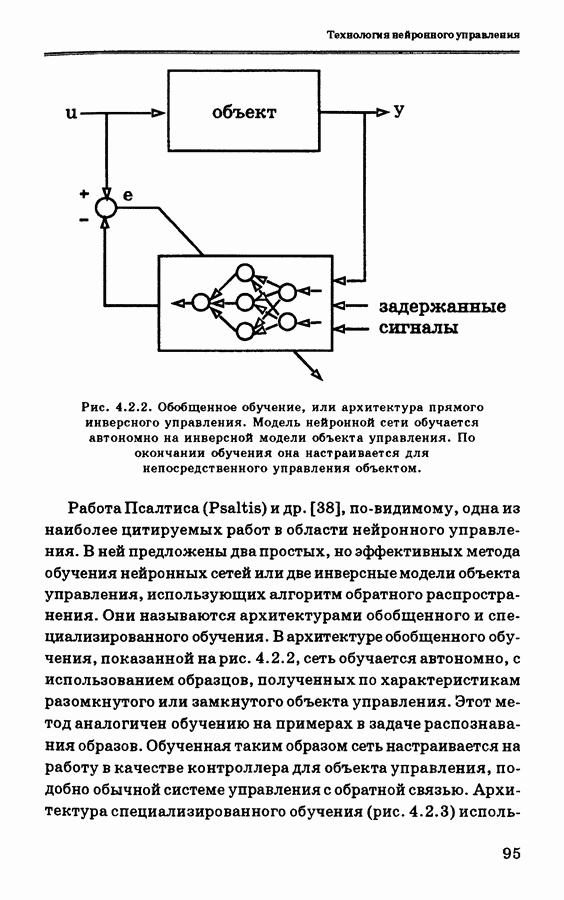
реализует инверсную динамику объекта управления. Заключенная в пунктирную линию часть схемы, называемая цепью прямой связи (ЦПС), может рассматриваться как разновидность нейронной сети, у которой выходной слой жестко задан. Ниже будет показано, что в этом случае для использования алгоритма обратного распространения необходимо знать якобиан системы.
Для схемы, показанной на рис. 4.3.2, простейшая внутренняя структура нейронной сети показана на рис. 4.3.3, где используется один нейрон во входном и один в выходном слоях. На рис. 4.3.3 входным сигналом для нейронной сети является только сигнал  а выходным — только сигнал и. Для простоты обозначим отношение «вход/выход» для объекта управления как
а выходным — только сигнал и. Для простоты обозначим отношение «вход/выход» для объекта управления как  При этом желательно, чтобы по результатам обучения выходной сигнал имел значение как можно ближе к
При этом желательно, чтобы по результатам обучения выходной сигнал имел значение как можно ближе к  Таким образом, подлежащая минимизации функция ошибки записывается в следующей форме:
Таким образом, подлежащая минимизации функция ошибки записывается в следующей форме:

Входной сигнал объекта управления задается следующим образом:

где  — веса связей и пороговая величина соответственно для выходного слоя,
— веса связей и пороговая величина соответственно для выходного слоя,  — вес связи для скрытого слоя. Используя принцип наискорейшего спуска, получим
— вес связи для скрытого слоя. Используя принцип наискорейшего спуска, получим

Используя цепное правило получения частных производных, правило дифференцирования сложных функций, получим:

Из (4.3.7) получим

Определяя  как
как

и снова используя цепное правило для 8., получим:

Таким образом, имеем следующее соотношение:


Аналогично для  получим:
получим:

и

Таким образом, получен следующий алгоритм.
Шаг 1. Установить начальные значения  .
.
Положить  и перейти к шагу 2.
и перейти к шагу 2.
Шаг 2. Подать на вход нейронной сети сигнал, равный желаемому выходному сигналу  и вычислить значения сигналов
и вычислить значения сигналов  Затем вычислить 5. по формуле:
Затем вычислить 5. по формуле:

Шаг 3. Изменить веса связей в соответствии с выражением:

Шаг 4. Вычислить значение 5.:

Шаг 5. Изменить веса связей в соответствии с выражением:

Шаг 6. Заменить  и перейти к шагу 2.
и перейти к шагу 2.
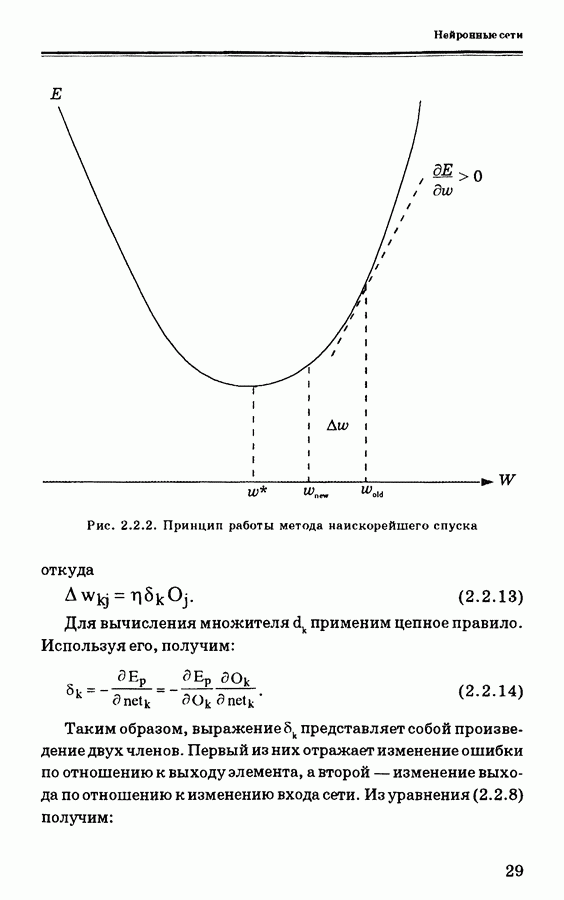
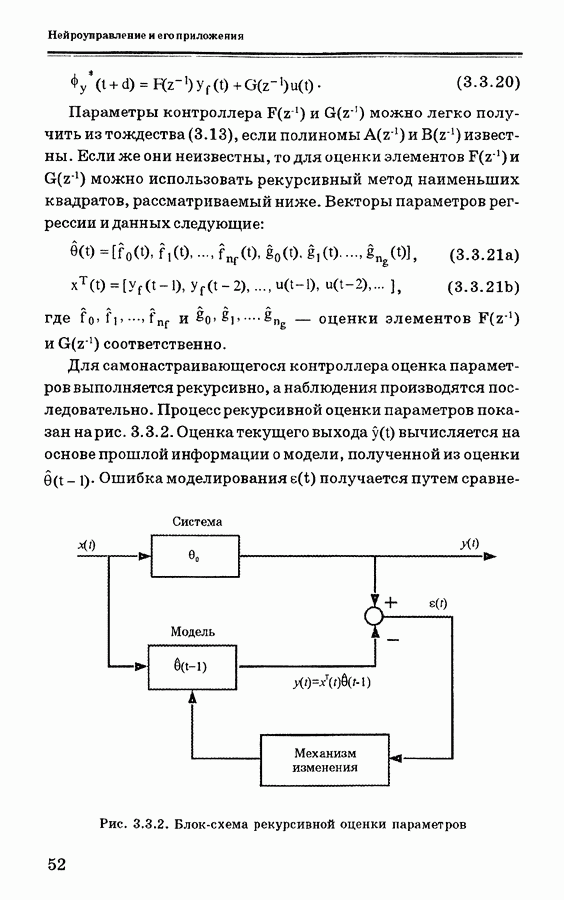
При практическом применении этого алгоритма возникают, однако, некоторые трудности. Одна из них состоит в том, что соответствие «вход — выход», задаваемое нейронной сетью, показанной на рис. 4.3.3, является нединамическим, а скорее статическим отображением координат и на у. В практических задачах управления динамические отображения

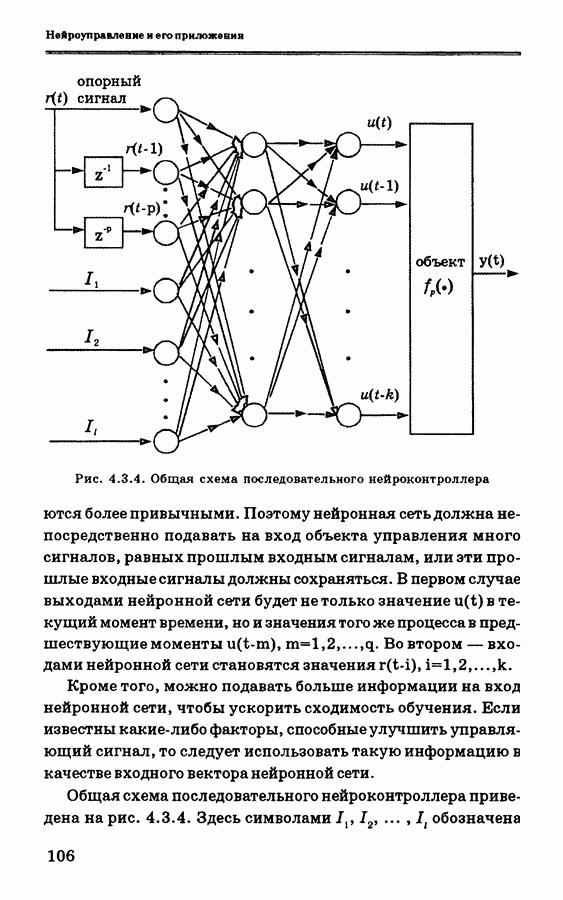
Рис. 4.3.4. Общая схема последовательного нейроконтроллера
являются более привычными. Поэтому нейронная сеть должна непосредственно подавать на вход объекта управления много сигналов, равных прошлым входным сигналам, или эти прошлые входные сигналы должны сохраняться. В первом случае выходами нейронной сети будет не только значение  в текущий момент времени, но и значения того же процесса в предшествующие моменты
в текущий момент времени, но и значения того же процесса в предшествующие моменты  Во втором — входами нейронной сети становятся значения
Во втором — входами нейронной сети становятся значения 
Кроме того, можно подавать больше информации на вход нейронной сети, чтобы ускорить сходимость обучения. Если известны какие-либо факторы, способные улучшить управляющий сигнал, то следует использовать такую информацию в качестве входного вектора нейронной сети.
Общая схема последовательного нейроконтроллера приведена на рис. 4.3.4. Здесь символами  обозначена
обозначена
дополнительная информация, которая может влиять на управляющий сигнал. Однако если величины временной задержки  и
и  точно не известны, то использовать такую структуру нельзя. В этом случае можно использовать оценки величин
точно не известны, то использовать такую структуру нельзя. В этом случае можно использовать оценки величин 
При использовании схемы управления, показанной на рис. 4.3.4, для обучения нейронной сети можно применить методику, которая аналогична описанной выше. Таким образом, если приравнять соответствующие величины:

то для обучения нейроконтроллера можно применить вышеописанный алгоритм (шаги 
Необходимо отметить, что данный алгоритм основан на алгоритме обратного распространения, в котором в качестве функции активации используется сигмоидная функция; причем в данном случае все входные управляющие сигналы могут принимать значения между 0 и 1. Если в качестве управляющих входных сигналов используются только положительные величины, то управляющий сигнал и необходимо умножить на некоторую положительную константу С, а если в качестве управляющих входных сигналов используются только отрицательные величины, то управляющие сигналы требуется умножать на отрицательную константу С. Для определения величины С можно включить дополнительный слой. В более простом случае, если в качестве функции активации для выходного слоя используется функция идентичности, то можно выбрать любую величину (положительную или отрицательную).
В этом случае шаг 2 принимает следующий вид.
Шаг 2. Подать на вход нейронной сети сигнал, равный желаемому выходному сигналу  и вычислить
и вычислить  Затем вычислить
Затем вычислить  по формулам:
по формулам:

В рассмотренном выше алгоритме единственная сложность состоит в вычислении якобиана системы  на шаге 2. Как правило, выражение
на шаге 2. Как правило, выражение  неизвестно, и требуется искать его аппроксимацию. Один из способов состоит в использовании численной аппроксимации:
неизвестно, и требуется искать его аппроксимацию. Один из способов состоит в использовании численной аппроксимации:

где

Другой подход состоит в том, чтобы выполнить имитационное моделирование объекта управления, используя другую нейронную сеть, реализующую отображение «вход — выход для объекта управления. В этом случае данная нейронная сеть используется в качестве идентификатора системы. Для нейронных сетей вместо термина  идентификатор системы
идентификатор системы  применяется термин «эмулятор. Таким образом, используя эмулятор, можно вычислить якобиан системы, как если бы эмулятор представлял собой действительный объект управления.
применяется термин «эмулятор. Таким образом, используя эмулятор, можно вычислить якобиан системы, как если бы эмулятор представлял собой действительный объект управления.

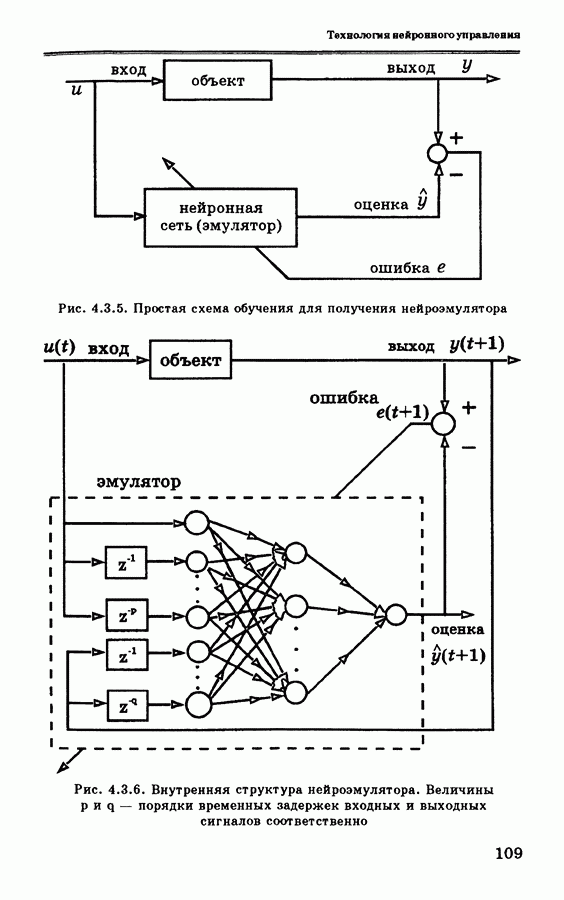
где  — отображение «вход/выход для эмулятора. Простая процедура обучения для эмулятора показана на рис. 4.3.5.
— отображение «вход/выход для эмулятора. Простая процедура обучения для эмулятора показана на рис. 4.3.5.
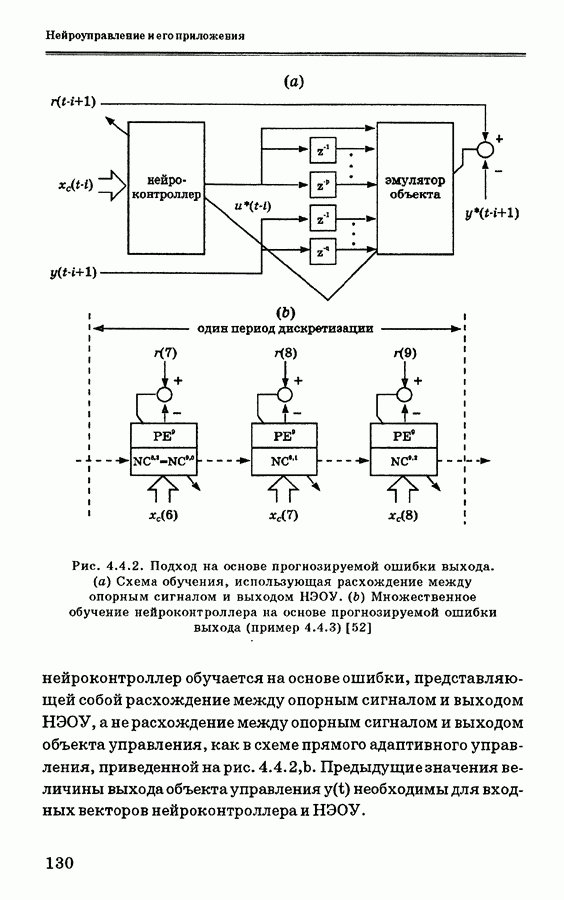
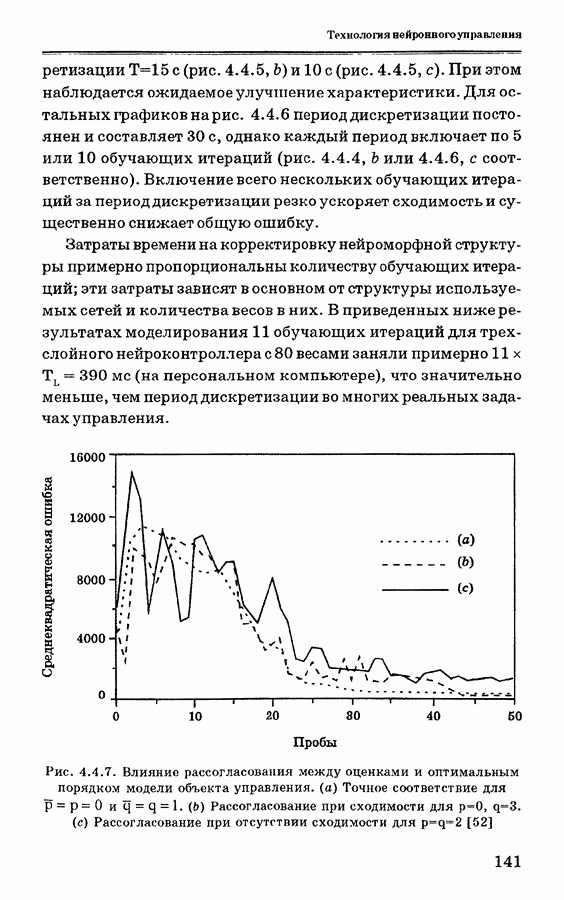
На рис. 4.3.5 показана схема обучения нейронной сети, при котором минимизируется ошибка предсказания  где у — выходной сигнал эмулятора, обозначающий предсказанную оценку величины у. Более подробно эта схема обучения показана на рис. 4.3.6. Если известны порядки временных задержек входных и выходных сигналов, то они используются для определения величин р и q (рис. 4.3.6).
где у — выходной сигнал эмулятора, обозначающий предсказанную оценку величины у. Более подробно эта схема обучения показана на рис. 4.3.6. Если известны порядки временных задержек входных и выходных сигналов, то они используются для определения величин р и q (рис. 4.3.6).

(кликните для просмотра скана)
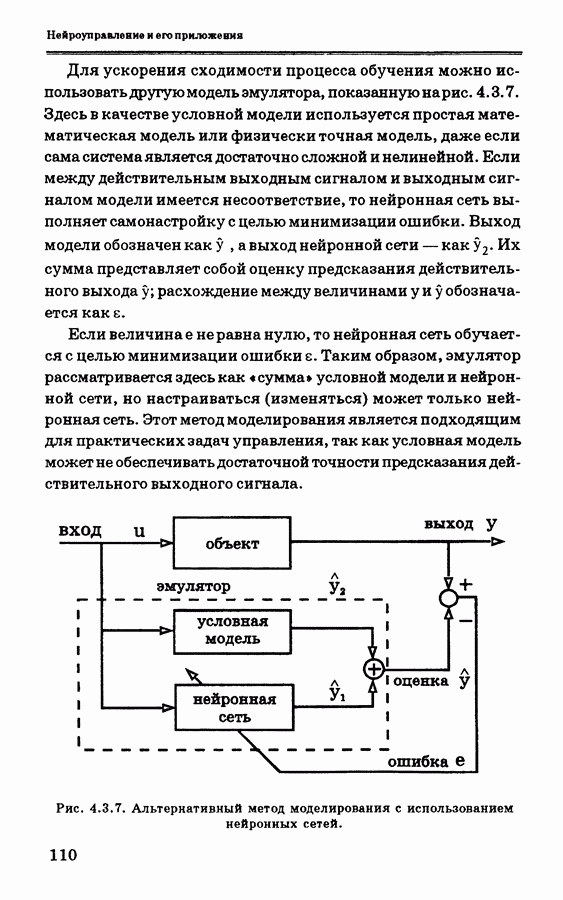
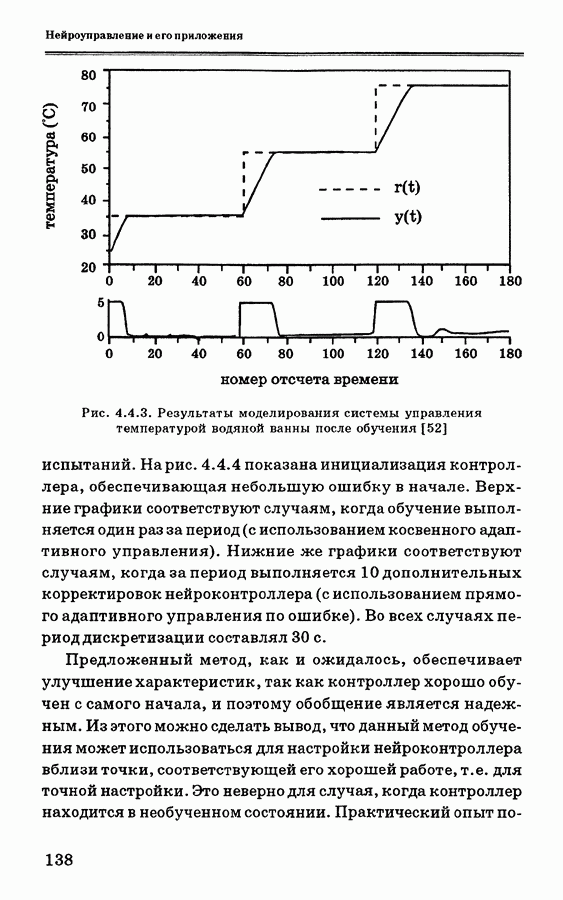
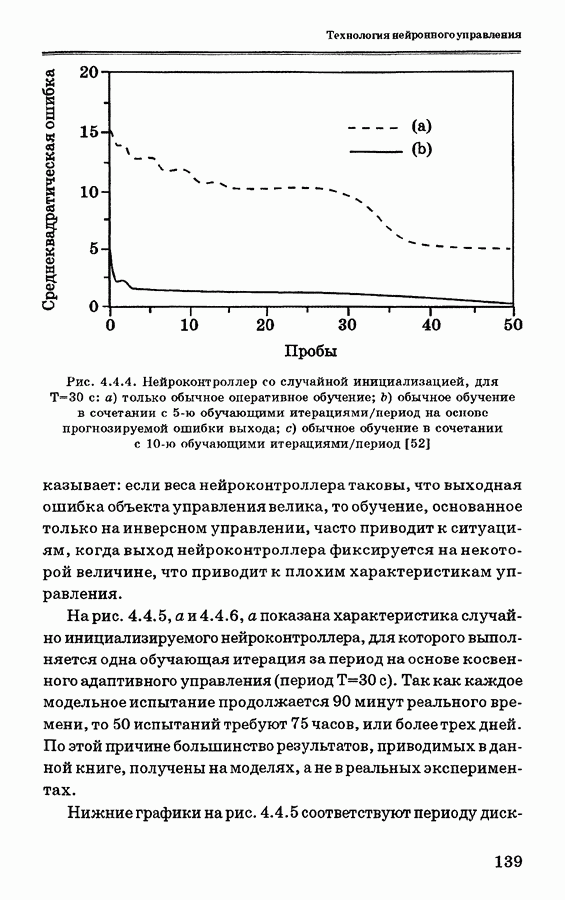
Для ускорения сходимости процесса обучения можно использовать другую модель эмулятора, показанную нарис. 4.3.7. Здесь в качестве условной модели используется простая математическая модель или физически точная модель, даже если сама система является достаточно сложной и нелинейной. Если между действительным выходным сигналом и выходным сигналом модели имеется несоответствие, то нейронная сеть выполняет самонастройку с целью минимизации ошибки. Выход модели обозначен как  а выход нейронной сети — как у. Их сумма представляет собой оценку предсказания действительного выхода у; расхождение меясду величинами
а выход нейронной сети — как у. Их сумма представляет собой оценку предсказания действительного выхода у; расхождение меясду величинами  обозначается как е.
обозначается как е.
Если величина  не равна нулю, то нейронная сеть обучается с целью минимизации ошибки е. Таким образом, эмулятор рассматривается здесь как
не равна нулю, то нейронная сеть обучается с целью минимизации ошибки е. Таким образом, эмулятор рассматривается здесь как  сумма» условной модели и нейронной сети, но настраиваться (изменяться) может только нейронная сеть. Этот метод моделирования является подходящим для практических задач управления, так как условная модель может не обеспечивать достаточной точности предсказания действительного выходного сигнала.
сумма» условной модели и нейронной сети, но настраиваться (изменяться) может только нейронная сеть. Этот метод моделирования является подходящим для практических задач управления, так как условная модель может не обеспечивать достаточной точности предсказания действительного выходного сигнала.

Рис. 4.3.7. Альтернативный метод моделирования с использованием нейронных сетей.

Рис. 4.3.8. Общая схема инверсно-динамического нейроконтроллера. Эмулятор NN1 реализован по схеме, показанной на рис. 4.3.6 и 4.3.7, а нейроконтроллер NN2 - по схеме рис. 4.3.4.
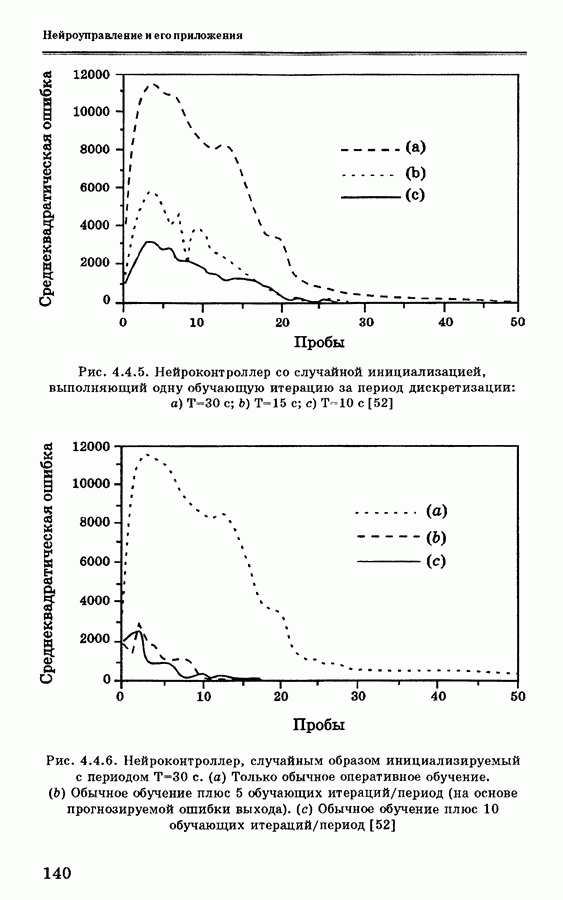
Основываясь на собственном опыте, в качестве условных моделей авторы могут рекомендовать использование статической модели, модели авторегрессии (АР), модель авторегрессии — скользящего среднего (АРСС), линейных векторных уравнений и т.п., так как они позволяют выявить долгосрочные тенденции. В свою очередь, нейронная сеть позволяет реализовать нелинейные соотношения. Таким образом, общая конфигурация схемы управления на основе нейронной сети показана нарис. 4.3.8, где NN1 — нейросетевой эмулятор (или просто — нейроэмулятор), a NN2 — нейроконтроллер, реализующий инверсно-динамическое отображение.
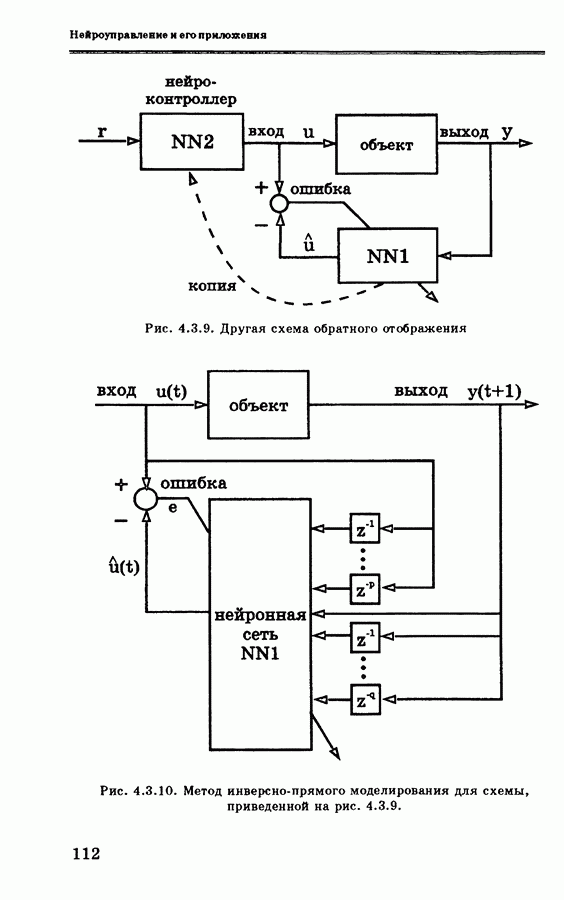
Другая схема реализации инверсной динамики с помощью нейронной сети показана на рис. 4.3.9, где нейронная сеть NN1 используется для обучения инверсному отображению, а математическая модель NN2 копируется с модели NN1 после того, как заканчивается обучение последней. Эта архитектура, предложенная в [38], описана в разделе 4.2.1. Реализация нейронной сети NN1 показана на рис. 4.3.10, где  и
и  — временные задержки входных и выходных сигналов соответственно.
— временные задержки входных и выходных сигналов соответственно.

(кликните для просмотра скана)
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРОВ ПЕРЕВОДА
- 1. ВВЕДЕНИЕ
- 1.1. Общие сведения об интеллектуальном управлении
- 2. НЕЙРОННЫЕ СЕТИ
- 2.2. Алгоритм обратного распространения
- 2.2.2. Вывод алгоритма обратного распространения
- 2.2.2.2. Правило для скрытого слоя
- 2.2.3. Алгоритм обратного распространения: порядок реализации
- 2.2.4. Обсуждение алгоритма обратного распространения
- 2.3. Заключение
- 3. ТРАДИЦИОННЫЕ СХЕМЫ УПРАВЛЕНИЯ
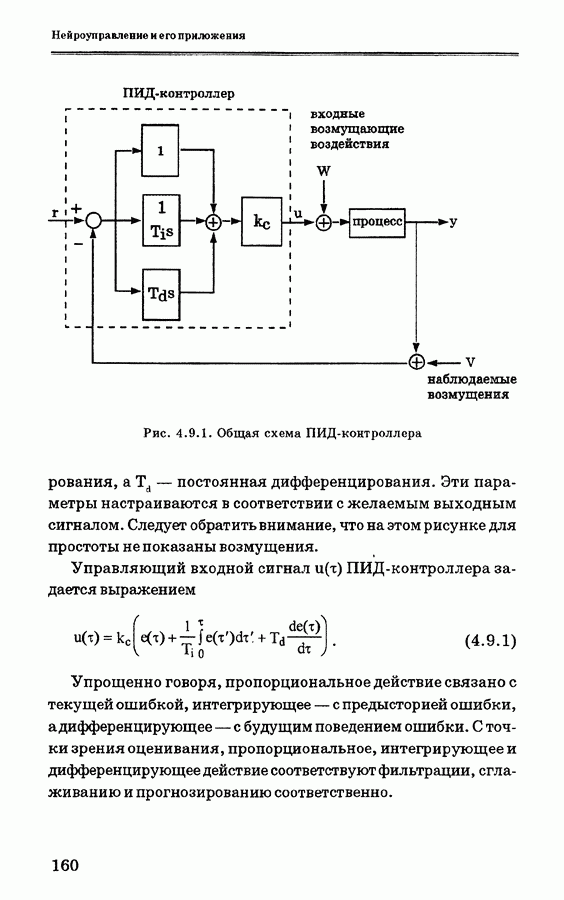
- 3.2. ПИ- и ПИД-контроллеры с дискретным временем
- 3.3. Управление с самонастройкой
- 3.4. Самонастраивающиеся ПИ- и ПИД- контроллеры
- 3.5. ПИД-управление с самонастройкой: многомерный подход
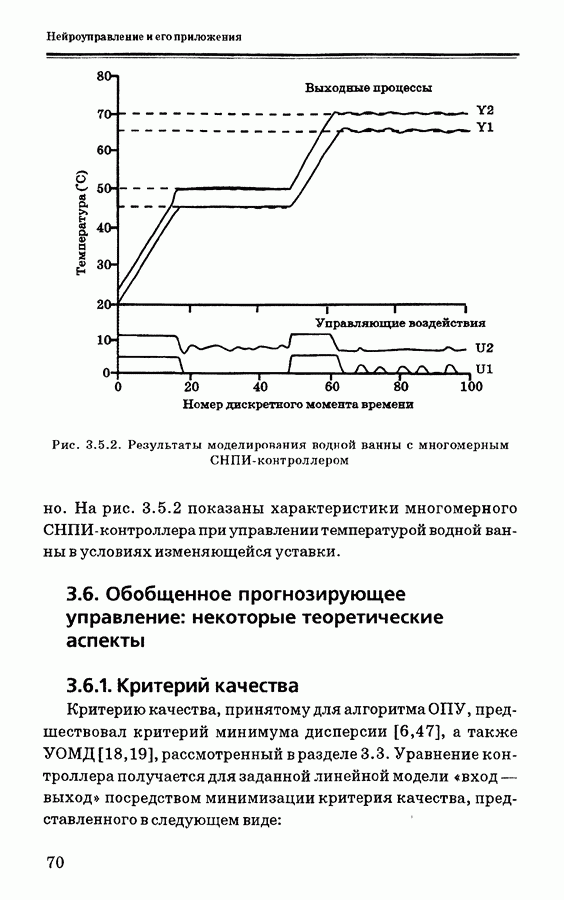
- 3.5.1. Пример моделирования
- 3.6. Обобщенное прогнозирующее управление: некоторые теоретические аспекты
- 3.6.2. Модель объекта управления и решение задачи оптимизации
- 3.7. Управление на основе нечеткой логики
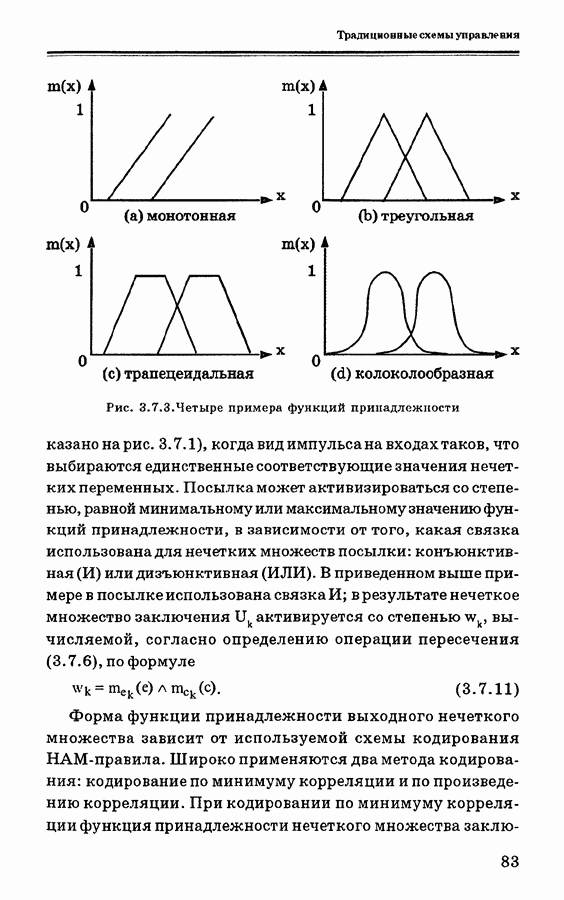
- 3.7.1. Краткие сведения по теории нечетких множеств и нечетких систем
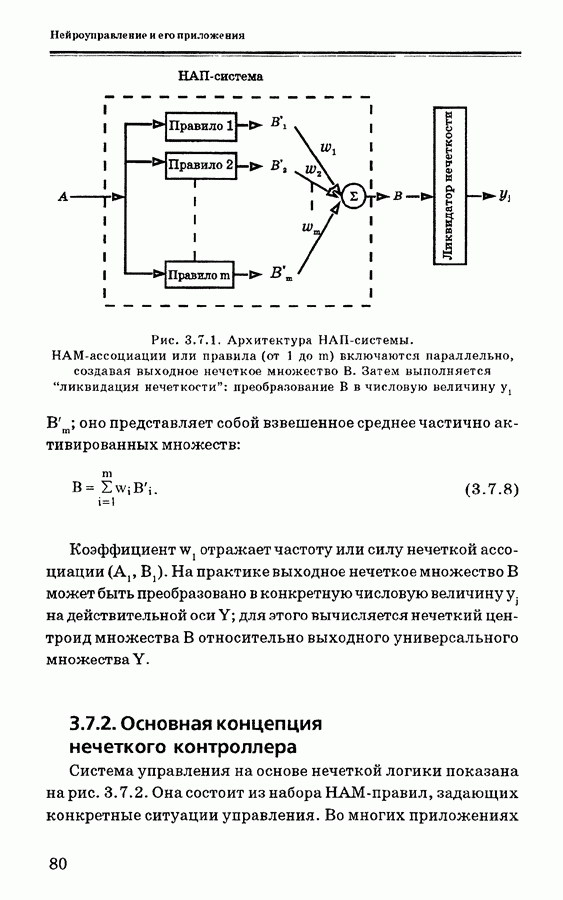
- 3.7.2. Основная концепция нечеткого контроллера
- 3.8. Заключение
- 4. ТЕХНОЛОГИИ НЕЙРОННОГО УПРАВЛЕНИЯ
- 4.2. Общие сведения о нейронном управлении
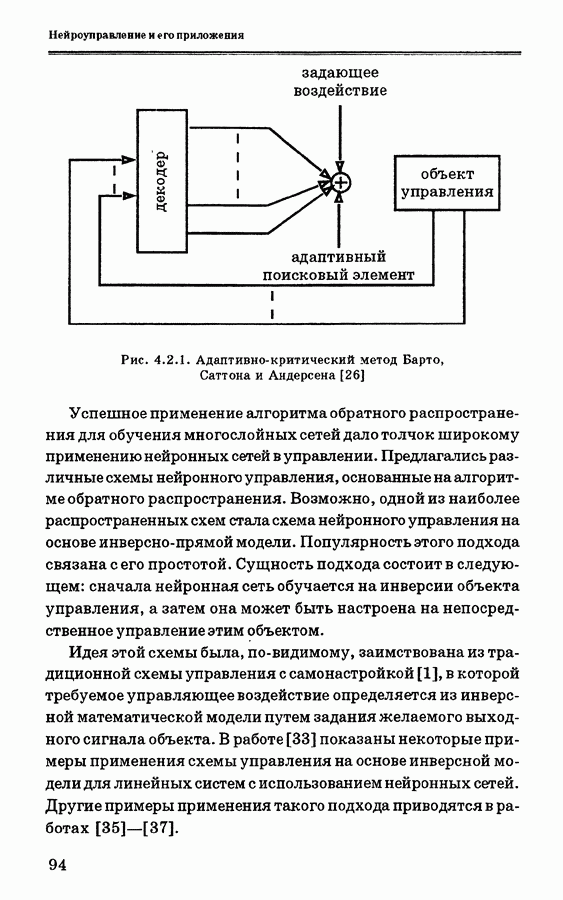
- 4.2.1. Подходы к нейронному управлению
- 4.2.2. Общая схема управления
- 4.3. Последовательная схема нейронного управления
- 4.4. Расширение последовательной схемы нейронного управления
- 4.4.2. Нейроморфные структуры управления
- 4.4.3. Конфигурации обучения
- 4.4.4. Эффективное оперативное управление
- 4.4.5. Алгоритмы обучения
- 4.4.6. Оценка алгоритмов обучения на основе моделирования
- 4.5. Параллельная схема управления
- 4.6. Алгоритм обучения по ошибке обратной связи
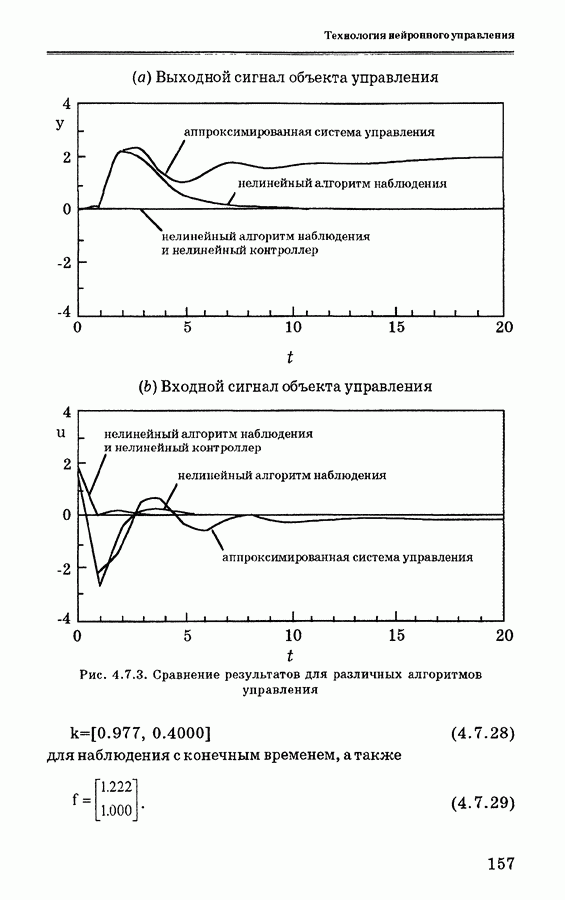
- 4.7. Расширение применения нейроконтроллеров параллельного типа
- 4.7.2. Линеаризованная система управления
- 4.7.3. Система управления с нейронными сетями
- 4.7.4. Нелинейный алгоритм наблюдения для нейронной сети
- 4.7.5. Нелинейный контроллер для нейронной сети
- 4.7.6. Численное моделирование
- 4.8. Схема нейронного управления с самонастройкой
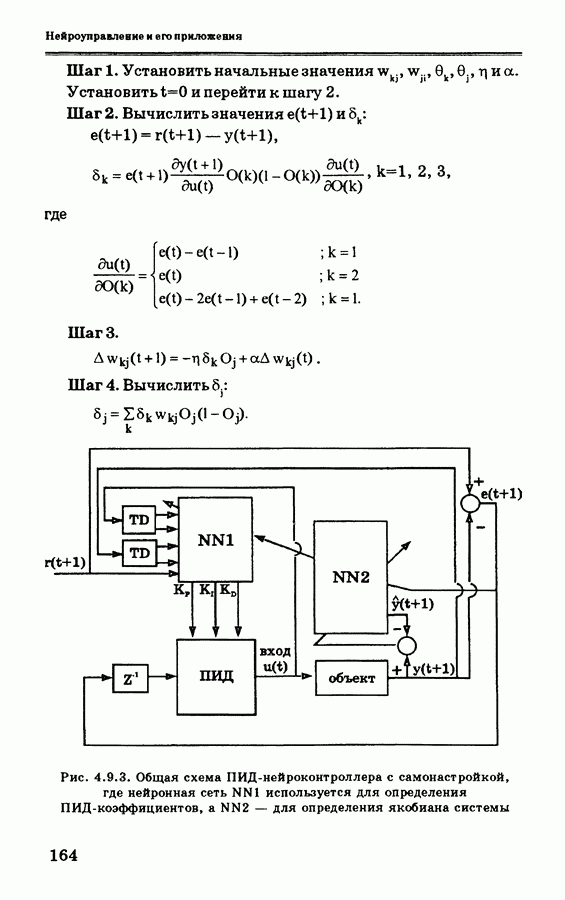
- 4.9. ПИД-нейроконтроллер с самонастройкой
- 4.9.1. Вывод уравнений ПИД-нейроконтроллера с самонастройкой
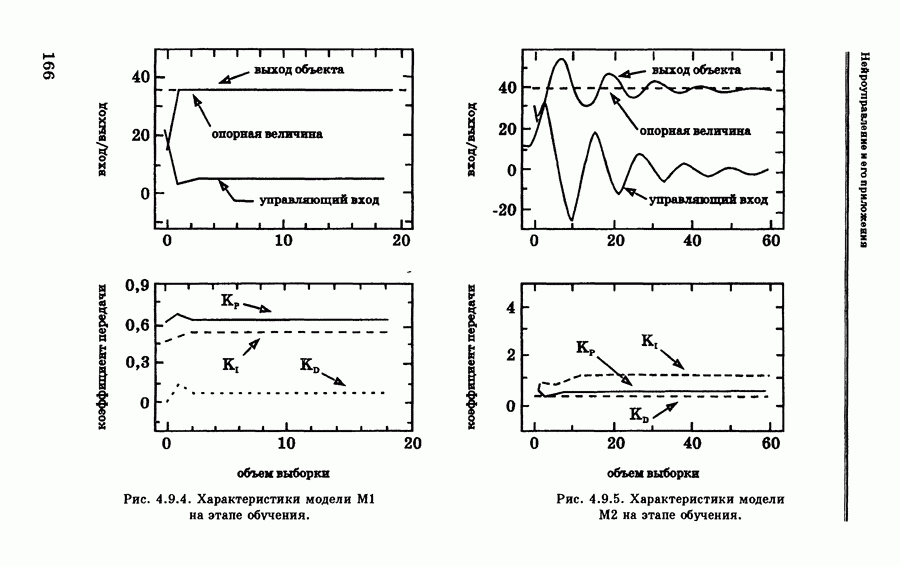
- 4.9.2. Примеры эмуляции
- 4.10. Схема нейронного управления с эмулятором и контроллером (схема обратного распространения во времени)
- 4.11. Заключение
- 5. ПРИЛОЖЕНИЯ НЕЙРОННОГО УПРАВЛЕНИЯ
- 5.2. Применение нейронного управления в системе регулирования процессов в водяной ванне и сравнение его с другими схемами управления
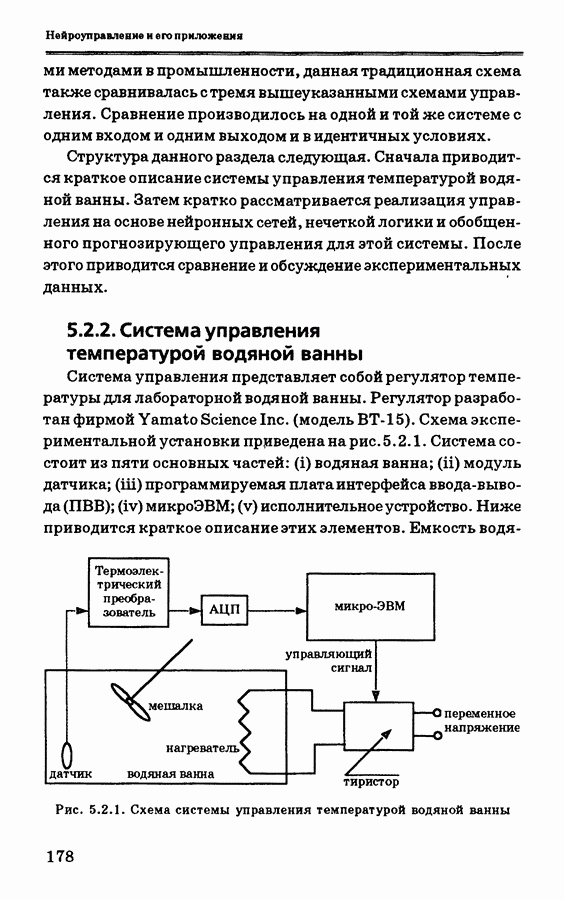
- 5.2.2. Система управления температурой водяной ванны
- 5.2.3. Схема нейронного управления
- 5.2.4. Схема управления на основе нечеткой логики
- 5.2.5. Схема обобщенного прогнозирующего управления
- 5.2.6. Экспериментальные данные и их анализ
- 5.2.7. Заключение
- 5.3. Система стабилизации инвертированного маятника на основе нейронных сетей
- 5.3.2. Система стабилизации инвертированного маятника
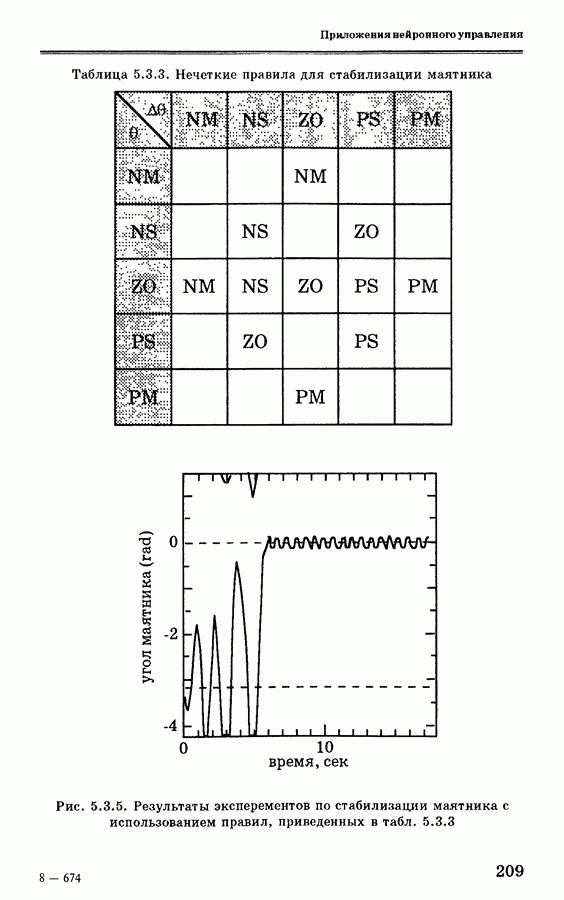
- 5.3.3. Инициализация поворотного управления с использованием нечеткой логики
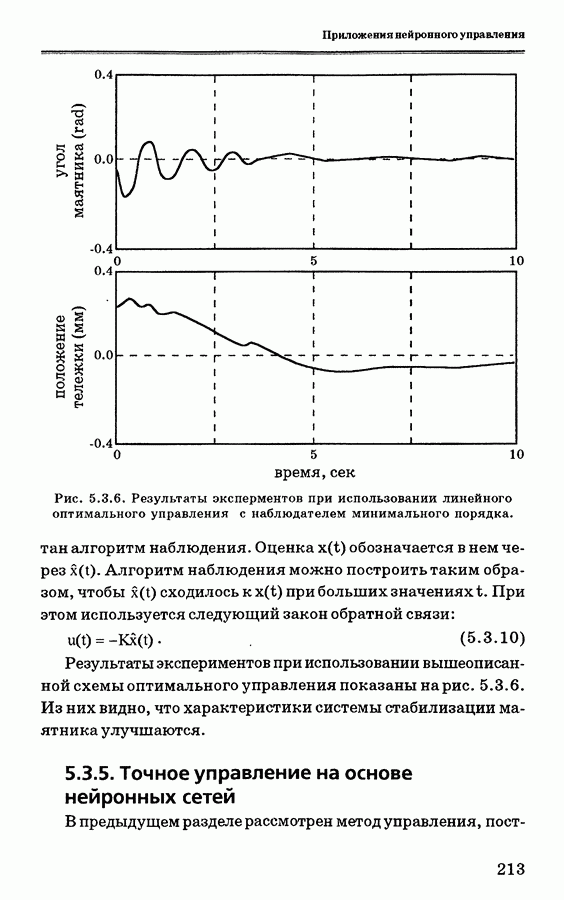
- 5.3.4. Применение стратегии оптимального управления для стабилизации маятника
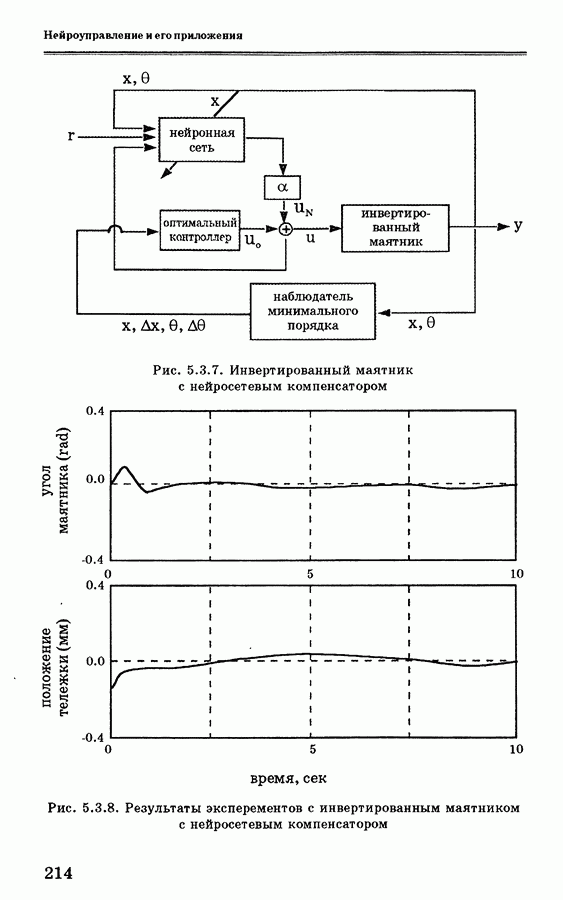
- 5.3.5. Точное управление на основе нейронных сетей
- 5.3.6. Заключение
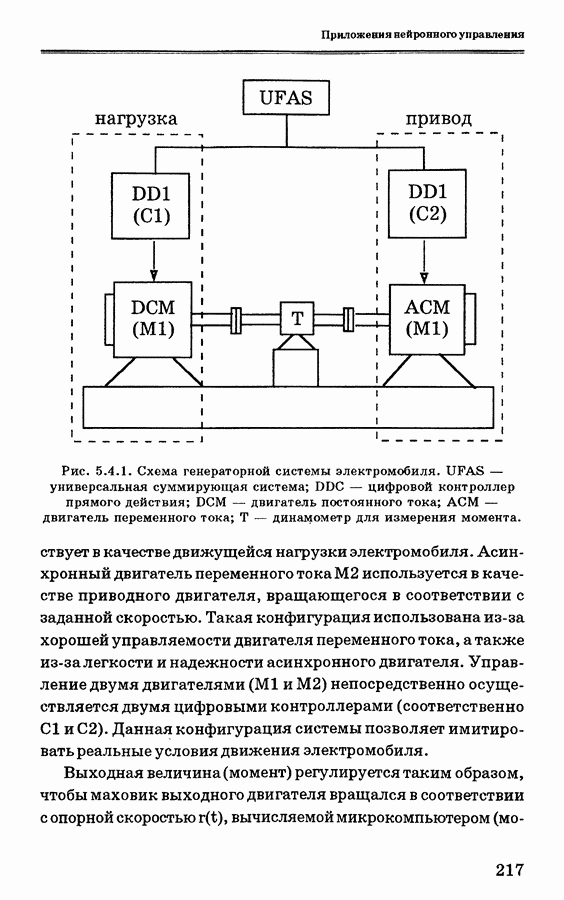
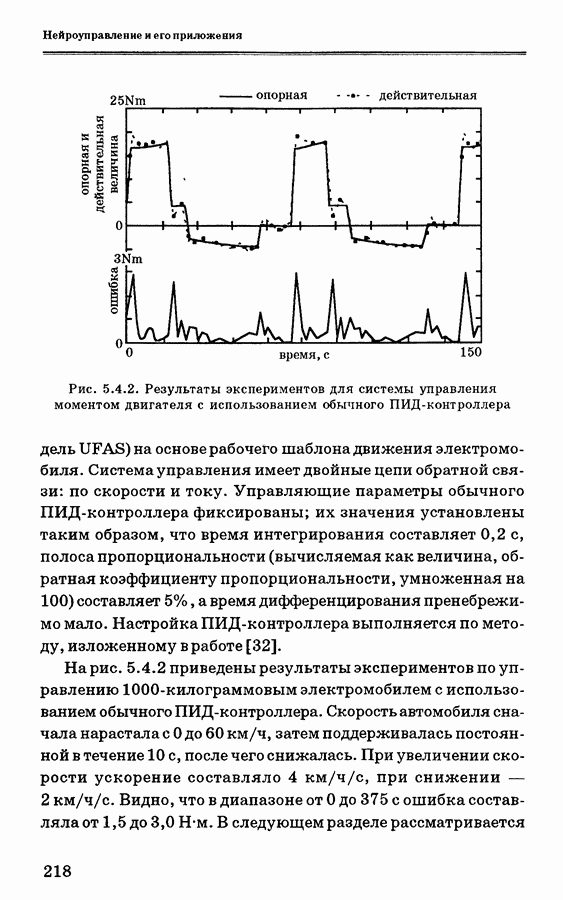
- 5.4. Применение ПИД-нейроконтроллера с самонастройкой для управления скоростью электромобиля
- 5.4.2. Система управления электромобилем
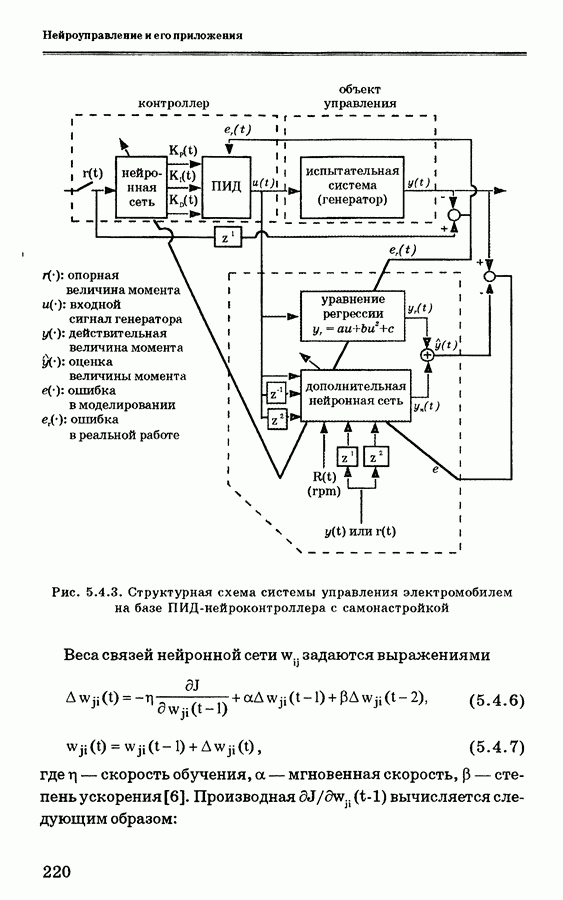
- 5.4.3. ПИД-нейроконтроллер с самонастройкой
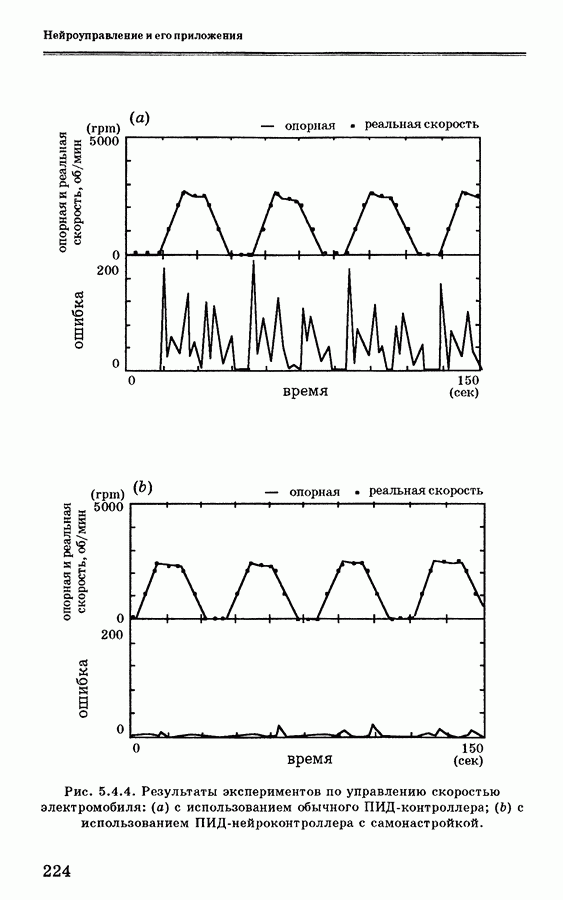
- 5.4.4. Применение нейронной сети для управления скоростью электромобиля
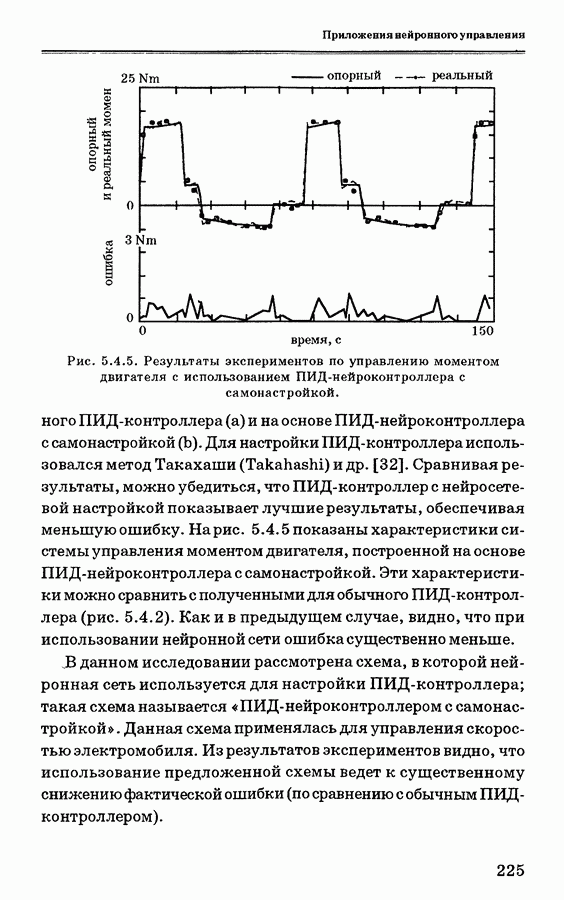
- 5.4.5. Заключение
- 5.5. Применение нейронных сетей для управления печью
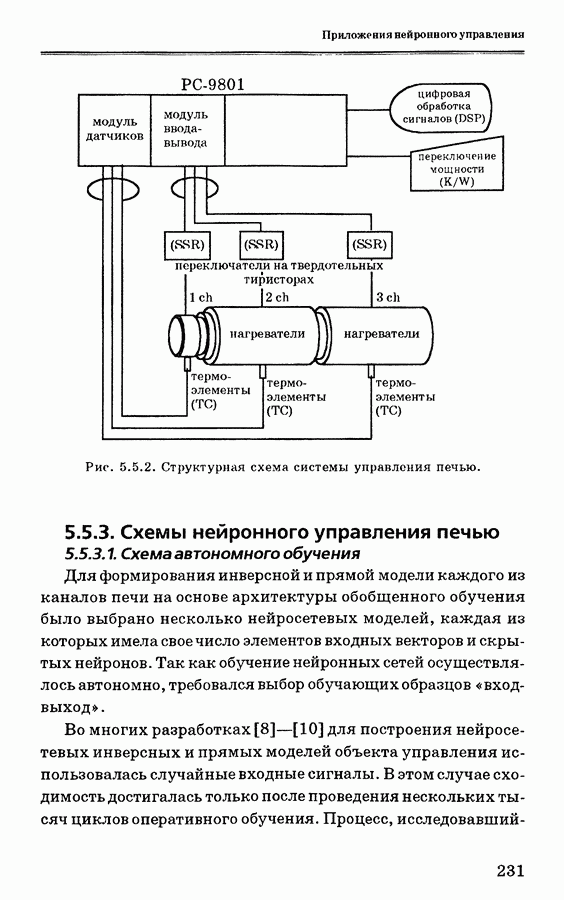
- 5.5.2. Система управления печью
- 5.5.3. Схемы нейронного управления печью
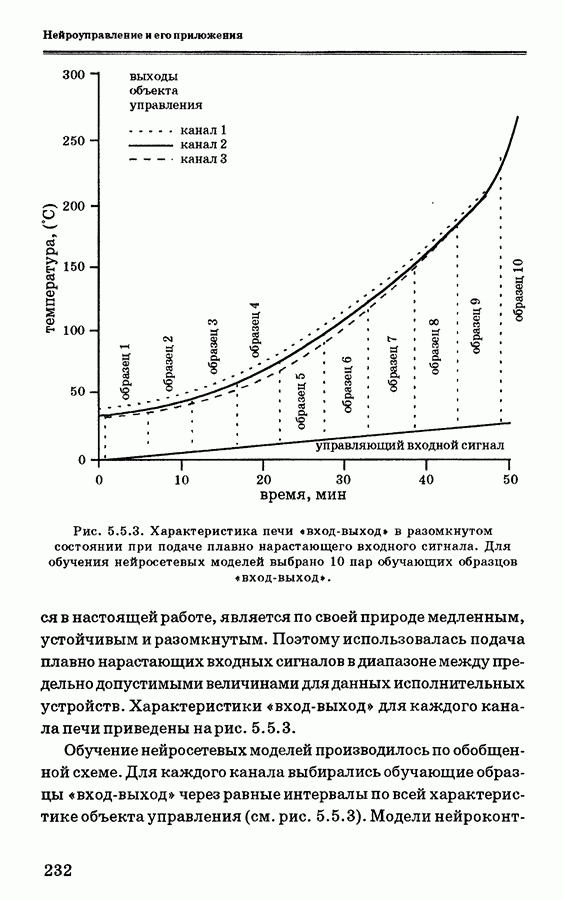
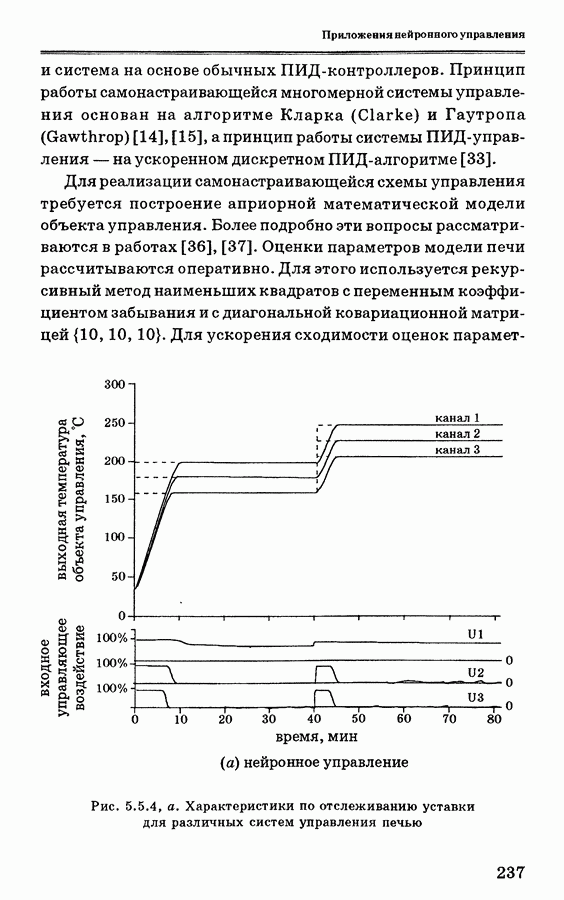
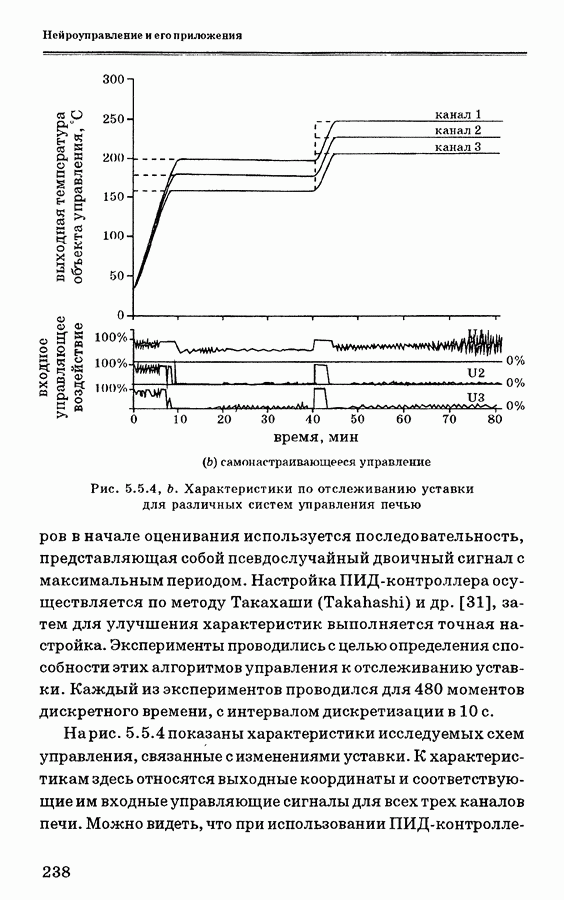
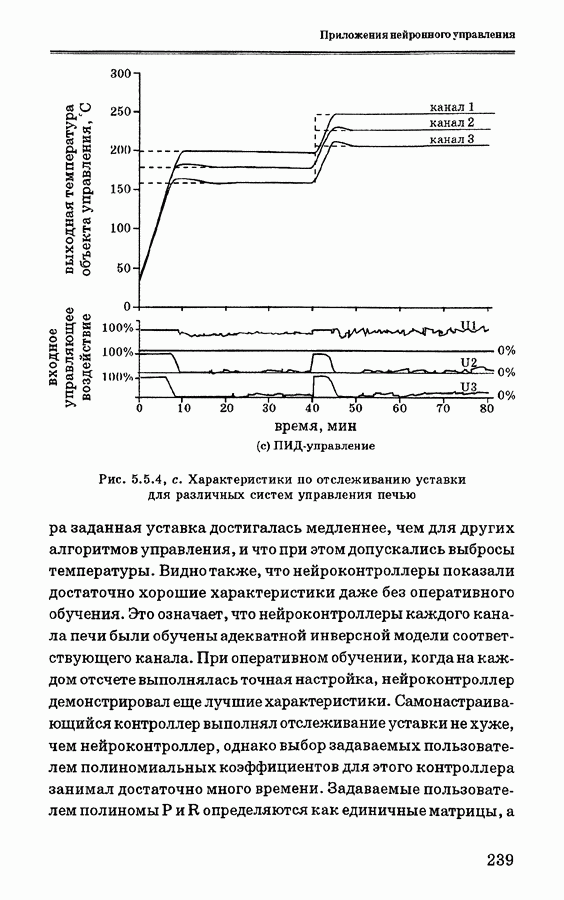
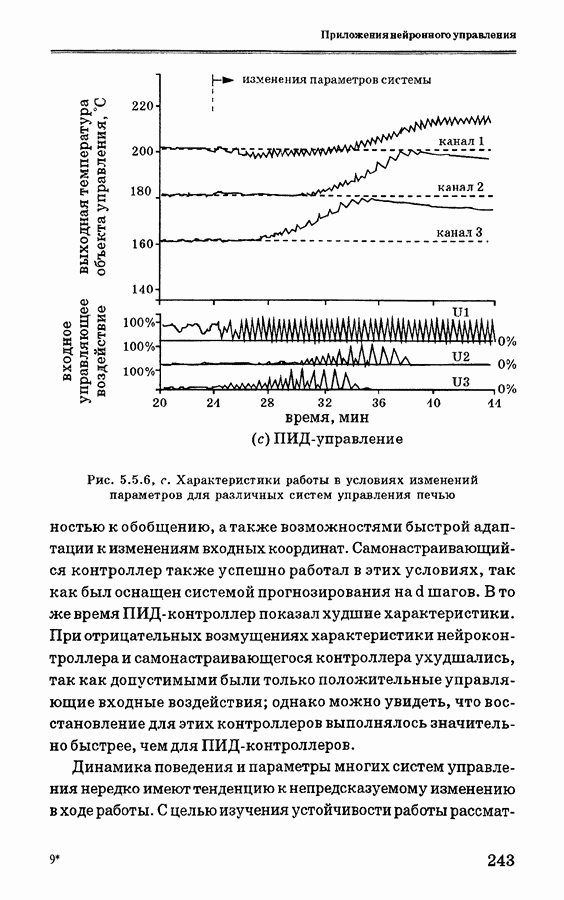
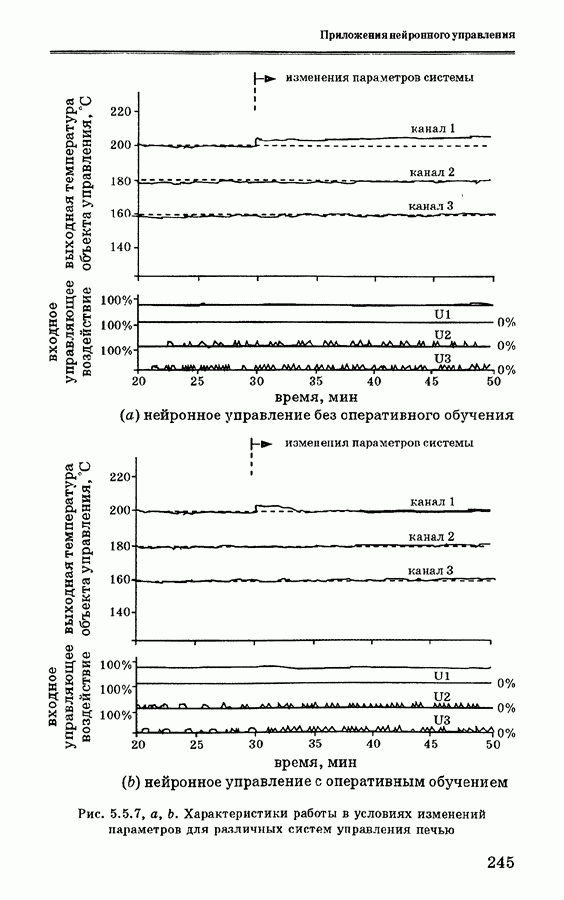
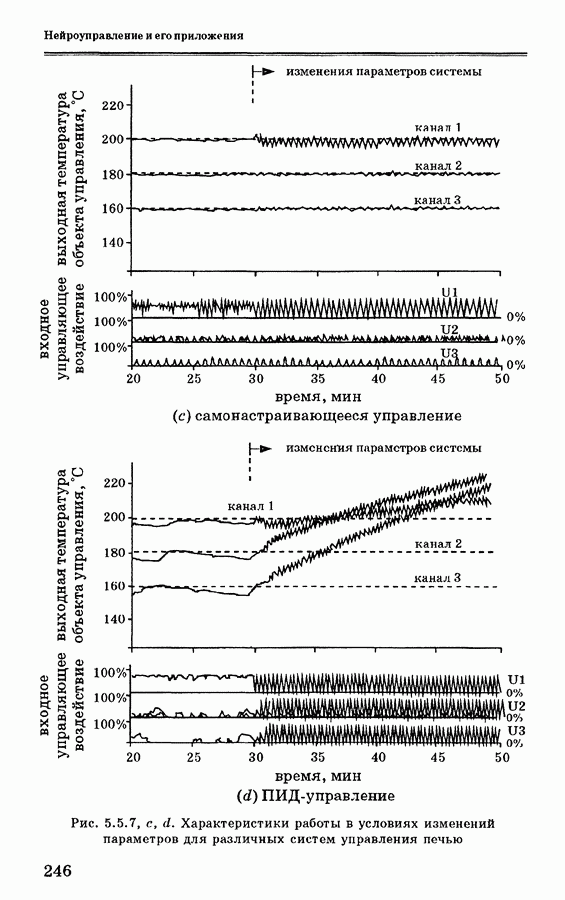
- 5.5.4. Анализ экспериментальных данных
- 5.6. Заключительные замечания и выводы
- Литература
- ЛИСТИНГ ПРОГРАММЫ