| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
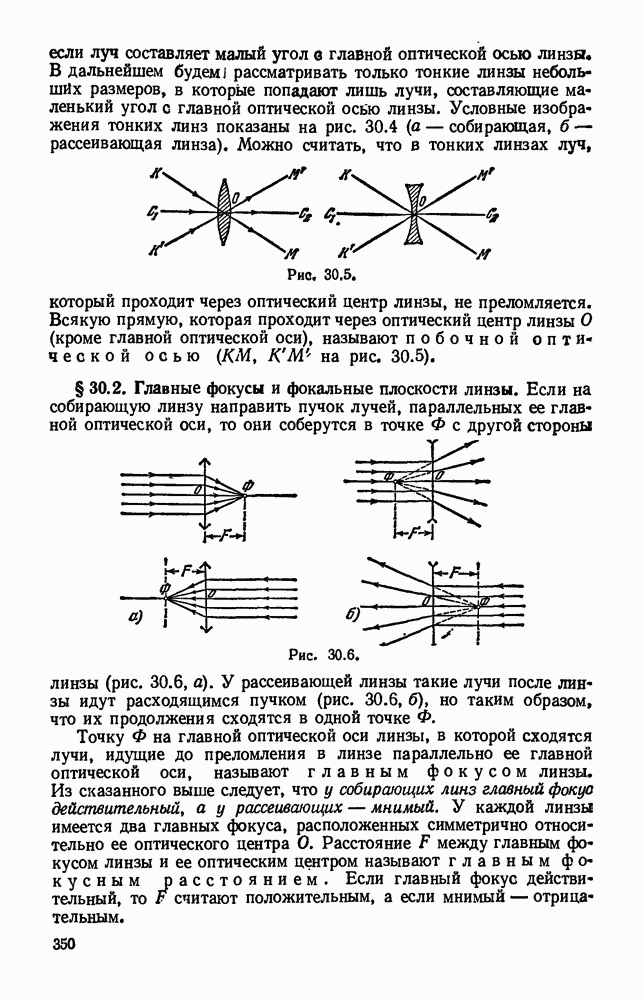
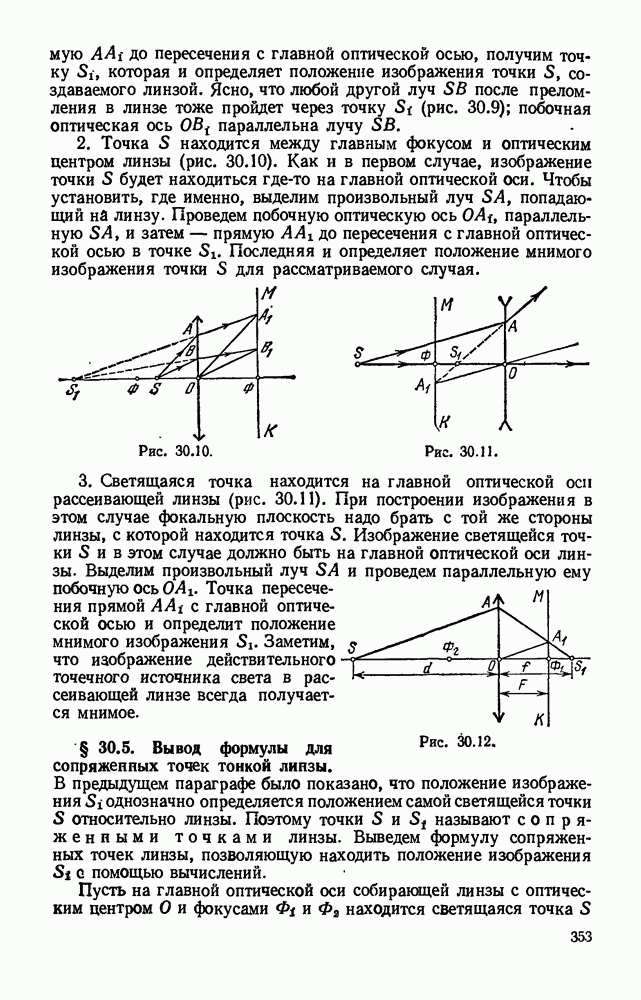
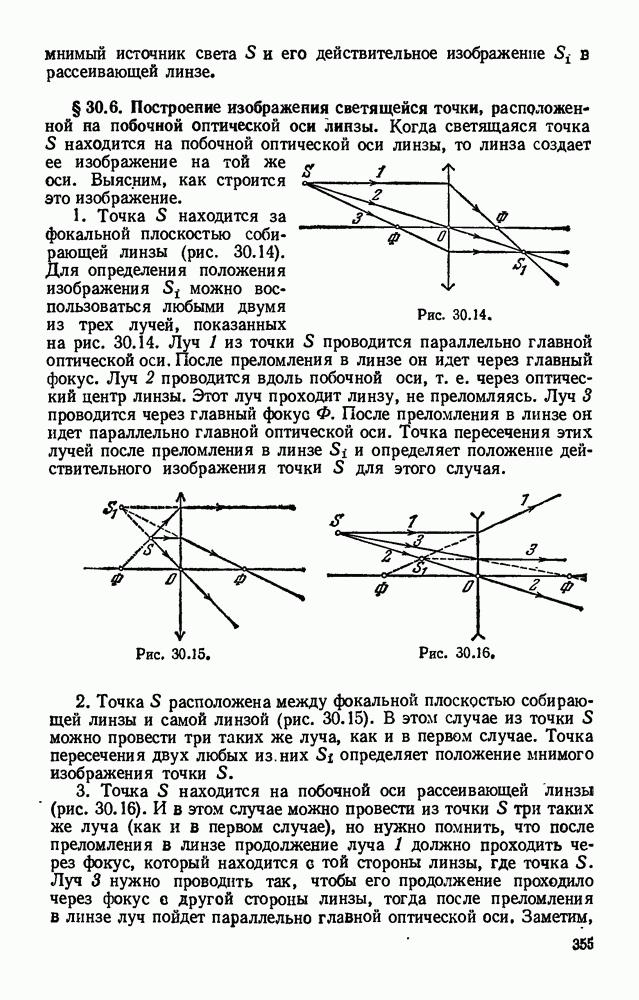
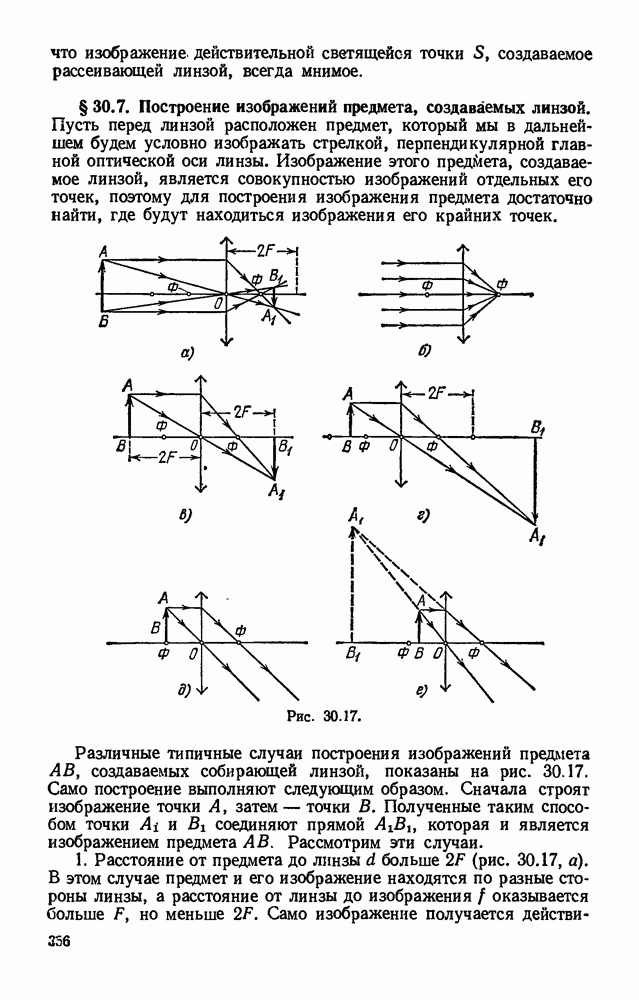
§ 16.15. Закон Ома для участка цепи с э. д. с. и для всей цепи при нескольких э. д. с.
Сторонние силы могут действовать одновременно во многих участках замкнутой цепи, в том числе и у потребителя. Поэтому э. д. в. имеется не только в генераторе, но и во всех тех участках цепи, в которых действуют сторонние силы.
Когда заряды на участке цепи движутся по направлению действия на них сторонних сил, э. д. с. участка считается положительной. На этом участке обязательно происходит превращение в электрическую энергию других видов энергии. Если же заряды движутся в сторону, противоположную направлению действия на них сторонних сил, а. д. с. считается отрицательной. В этом случае электрические заряды теряют свою энергию, преодолевая противодействие сторонних сил. Электродвижущую силу на таком участке цепи принято называть противо-э. д. с.
Вспомним, что, преодолевая сопротивление, заряды теряют свою энергию, которая превращается во внутреннюю энергию проводника, т. е. идет на его нагревание. Аналогично, преодолевая противодействие сторонних сил На участке цепи с отрицательной
э. д. с., заряды теряют свою энергию, которая превращается в другие виды энергии, отличные от внутренней энергии. Итак, наличие
э. д. с. на участке цепи обеспечивает либо превращение в электрическую энергию других видов энергии (в генераторе), либо превращение электрической энергии в другие виды (кроме внутренней энергии) при отрицательной э. д. с. Например, при работе электродвигателя наличие противо-э. д. с. обусловливает превращение электрической энергии в механическую.
Обобщим все изложенное. Когда на участке цепи действуют посторонние силы, то возможны три различных случая:
1) электрические и сторонние силы действуют на заряды в противоположные стороны, а э. д. с. больше напряжения;
2) электрические и сторонние силы действуют на заряды в противоположные стороны, а напряжение больше э. д. с.;
3) электрические и сторонние силы действуют на заряды в одну сторону.
Первый случай относится к генератору, т. е. к участку цепи, который снабжает электрической энергией другие участки цепи. Его э. д. с.  численно равна электрической энергии, приобретенной единичным зарядом. Если
численно равна электрической энергии, приобретенной единичным зарядом. Если  есть сопротивление всего этого участка (включая сюда и внутреннее сопротивление генератора
есть сопротивление всего этого участка (включая сюда и внутреннее сопротивление генератора  ), a U - напряжение на нем, то, когда по нему течет ток I,
), a U - напряжение на нем, то, когда по нему течет ток I,

Действительно, на основании закона сохранения энергии можно утверждать, что если единичный заряд получил на участке энергию  и потерял на нем же энергию
и потерял на нем же энергию  на тепловое действие, то у него остается энергия
на тепловое действие, то у него остается энергия  Эту энергию заряд передает в цепь, присоединенную к генератору. Определив I из (16.37), получим закон Ома для участка цепи, являющегося генер атором:
Эту энергию заряд передает в цепь, присоединенную к генератору. Определив I из (16.37), получим закон Ома для участка цепи, являющегося генер атором:

Заметим, что эта формула применима при любой присоединенной к генератору цепи.
Второй случай наблюдают при зарядке аккумулятора и при работе электродвигателя. Электрическая энергия, израсходованная единичным зарядом на таком участке, определяется напряжением  (рис. 16.15). Если сопротивление всего этого участка
(рис. 16.15). Если сопротивление всего этого участка  , а ток в нем
, а ток в нем  то энергия, израсходованная в нем единичным зарядом на тепловое действие, равна
то энергия, израсходованная в нем единичным зарядом на тепловое действие, равна  , а энергия, превратившаяся в другие виды, равна
, а энергия, превратившаяся в другие виды, равна  . Таким образом, на основании закона сохранения энергии имеем
. Таким образом, на основании закона сохранения энергии имеем

откуда получаем закон Ома для участка цепи с противо-э.д. с.:


Рис. 16.15.
В третьем случае электрические и сторонние силы направлены в одну сторону. Поэтому заряды будут двигаться в ту же сторону. Это означает, что такой участок обязательно будет потребителем энергии, полученной из остальной цепи. Кроме того, под действием сторонних сил он получает дополнительную энергию. Итак, единичный заряд, получив энергию  от остальной цепи, на таком участке цепи получает еще энергию и всю эту энергию
от остальной цепи, на таком участке цепи получает еще энергию и всю эту энергию  расходует на тепловое действие, которое оценивается падением напряжения
расходует на тепловое действие, которое оценивается падением напряжения  Таким образом,
Таким образом,

Определив  получим закон Ома для такого участка цепи:
получим закон Ома для такого участка цепи:

Объединяя все три случая, можно следующим образом сформулировать закон Ома для участка цепи с э. д. с.: сила тот на участке цепи с э. д. с. прямо пропорциональна алгебраической сумме напряжения и э. д. с. на этом участке и обратно пропорциональна его сопротивлению.
При расчетах, когда знак  или
или  не известен, следует пользоваться формулой (16.39). Если в результате решения найденная величина
не известен, следует пользоваться формулой (16.39). Если в результате решения найденная величина  или
или  окажется отрицательной, то это будет означать, что ее действие на заряды в действительности обратно принятому при решении.
окажется отрицательной, то это будет означать, что ее действие на заряды в действительности обратно принятому при решении.
Заметим, что для неразветвленной цепи с несколькими источниками э. д. с. закон Ома для всей цепи имеет вид

где  — число э. д. с., а
— число э. д. с., а  — число сопротивлений во всей цепи. Здесь в числителе — алгебраическая сумма всех э. д. с., причем э. д. с. на участке цепи положительна, если по направлению тока потенциал на этом участке возрастает; если же потенциал в этом направлении убывает, то значение э. д. с. берется с минусом.
— число сопротивлений во всей цепи. Здесь в числителе — алгебраическая сумма всех э. д. с., причем э. д. с. на участке цепи положительна, если по направлению тока потенциал на этом участке возрастает; если же потенциал в этом направлении убывает, то значение э. д. с. берется с минусом.

Рис. 16.16,
Для схемы рис. 16.16 формула (16.40) имеет вид

| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ВВЕДЕНИЕ
- § 1.2. Физика и техника.
- § 1.3. Понятие о величине и измерении. Физические величины.
- § 1.4. Прямое и косвенное измерения.
- § 1.5. Звездное небо и его видимое вращение.
- § 1.6. Угловые измерения на небе.
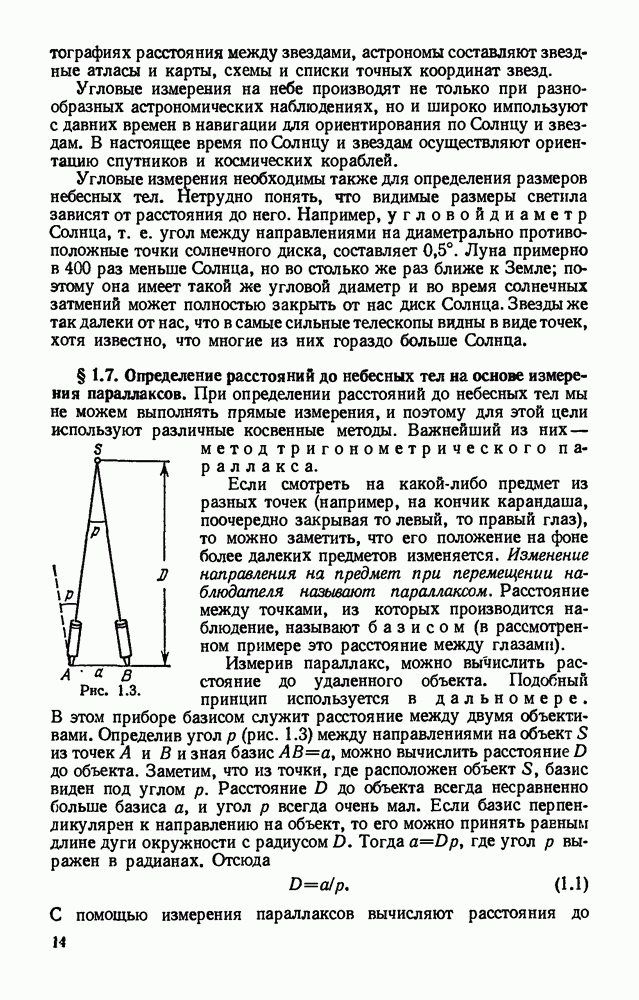
- § 1.7. Определение расстояний до небесных тел на основе измерения параллаксов.
- § 1.8. Основные единицы времени и их связь с движением Земли.
- § 1.9. Правило вывода единиц физических величин из формул. Международная система единиц СИ.
- § 1.10. Плотность вещества.
- Раздел I. МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕПЛОТА
- Глава 2. ОСНОВЫ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ СТРОЕНИЯ ВЕЩЕСТВА
- § 2.2. Диффузия.
- § 2.3. Силы молекулярного взаимодействия.
- § 2.4. Кинетическая и потенциальная энергия молекул.
- § 2.5. Агрегатное состояние вещества.
- § 2.6. Понятие о температуре и внутренней энергии тела.
- Глава 3. МОЛЕКУЛЯРНО-КИНЕТИЧЕСКАЯ ТЕОРИЯ ГАЗООБРАЗНОГО СОСТОЯНИЯ ВЕЩЕСТВА
- § 3.2. Броуновское движение.
- § 3.3. Измерение скорости движения молекул газа. Опыт Штерна.
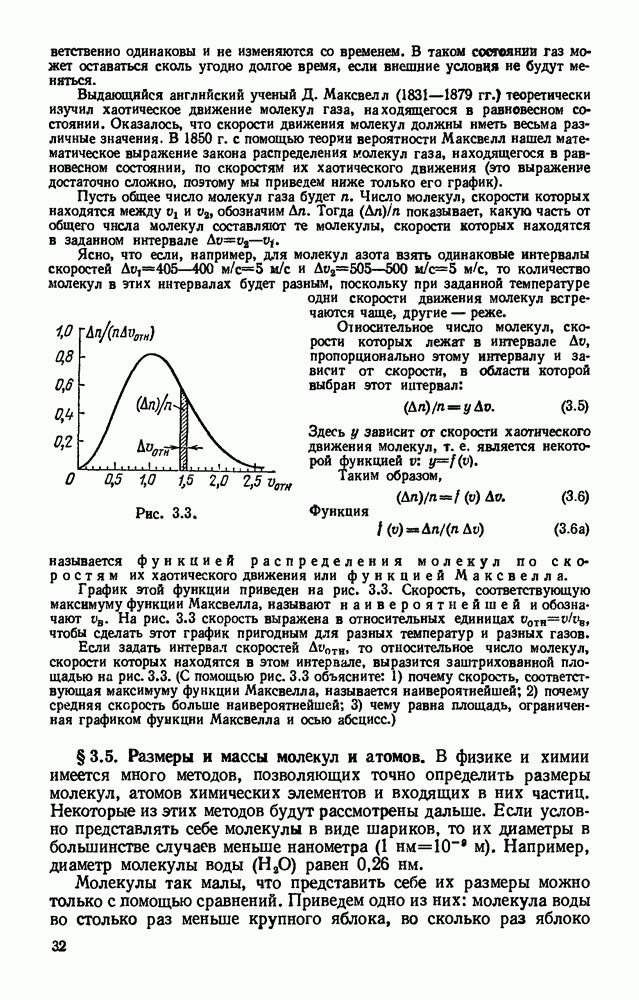
- § 3.4. Распределение молекул по скоростям их хаотического движения.
- § 3.5. Размеры и массы молекул и атомов.
- § 3.6. Постоянная Авогадро и постоянная Лошмидта.
- § 3.7. Число столкновений и длина свободного пробега молекул в газе.
- § 3.8. Давление газа. Манометры.
- § 3.9. Понятие вакуума.
- § 3.10. Межзвездный газ.
- Глава 4. ИДЕАЛЬНЫЙ ГАЗ. АБСОЛЮТНАЯ ТЕМПЕРАТУРА И ЕЕ СВЯЗЬ С ЭНЕРГИЕЙ МОЛЕКУЛ ГАЗА
- § 4.2. Основное уравнение молекулярно-кинетической теории газов.
- § 4.3. Зависимость давления газа от температуры при постоянном объеме.
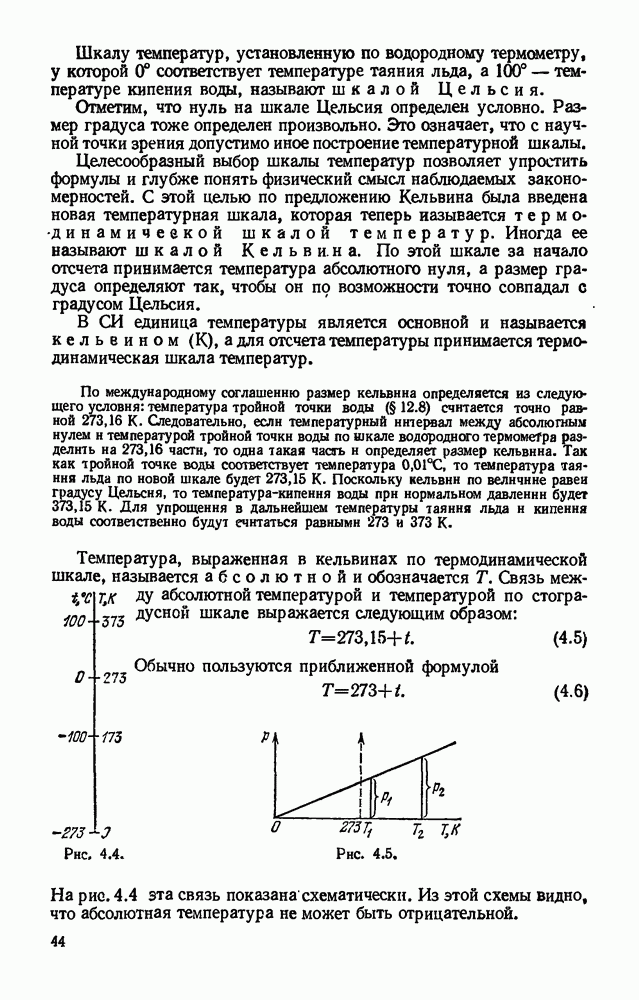
- § 4.4. Абсолютный нуль.
- § 4.5. Термодинамическая шкала температур. Абсолютная температура.
- § 4.6. Связь между температурой и кинетической энергией молекул газа. Постоянная Больцмана.
- Глава 5. УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА
- § 5.2. Объединенный газовый закон. Приведение объема газа к нормальным условиям.
- § 5.3. Молярная газовая постоянная. Определение числового значения постоянной Больцмана.
- § 5.4. Уравнение Клапейрона — Менделеева. Плотность газа.
- § 5.5. Зависимость средней квадратичной скорости молекул газа от температуры.
- § 5.6. Изохорический процесс.
- § 5.7. Изобарический процесс.
- § 5.8. Изотермический процесс.
- § 5.9. Внутренняя энергия идеального газа.
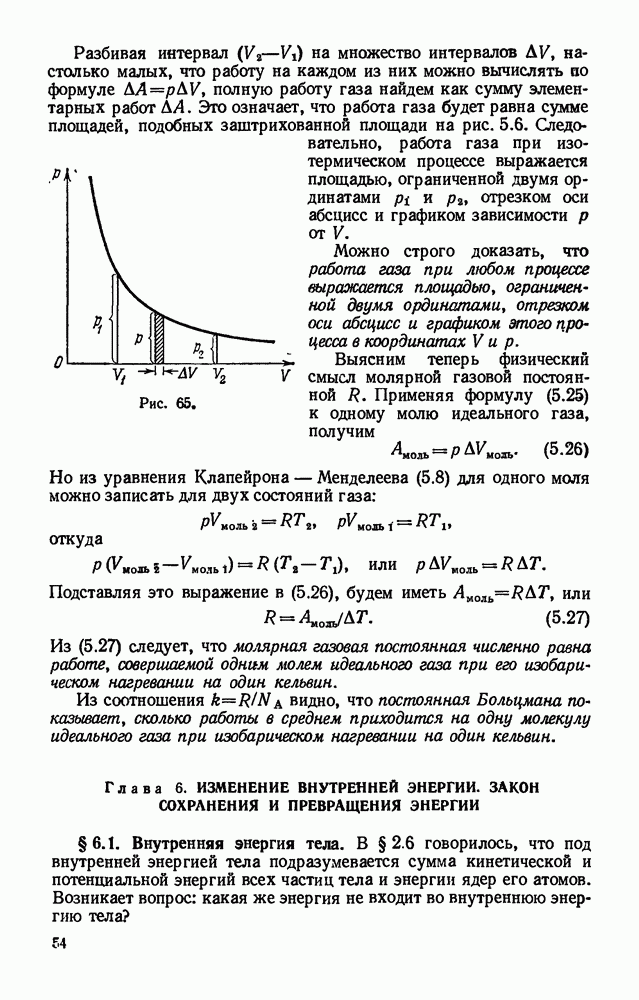
- § 5.10. Работа газа при изменении его объема. Физический смысл молярной газовой постоянной.
- Глава 6. ИЗМЕНЕНИЕ ВНУТРЕННЕЙ ЭНЕРГИИ. ЗАКОН СОХРАНЕНИЯ И ПРЕВРАЩЕНИЯ ЭНЕРГИИ
- § 6.2. Теплообмен.
- § 6.3. Виды теплообмена.
- § 6.4. Изменение внутренней энергии при нагревании и охлаждении.
- § 6.5. Уравнение теплового баланса при теплообмене.
- § 6.6. Подсчет теплоты, выделяемой при сжигании топлива. К. п. д. нагревателя.
- § 6.7. Изменение внутренней энергии при выполнении механической работы. Опыт Джоуля.
- § 6.8. Закон сохранения и превращения энергии в механике.
- § 6.9. Закон сохранения и превращения энергии в механических и тепловых процессах.
- § 6.10. Первое начало термодинамики.
- § 6.11. Применение первого начала термодинамики к изопроцессам в идеальном газе.
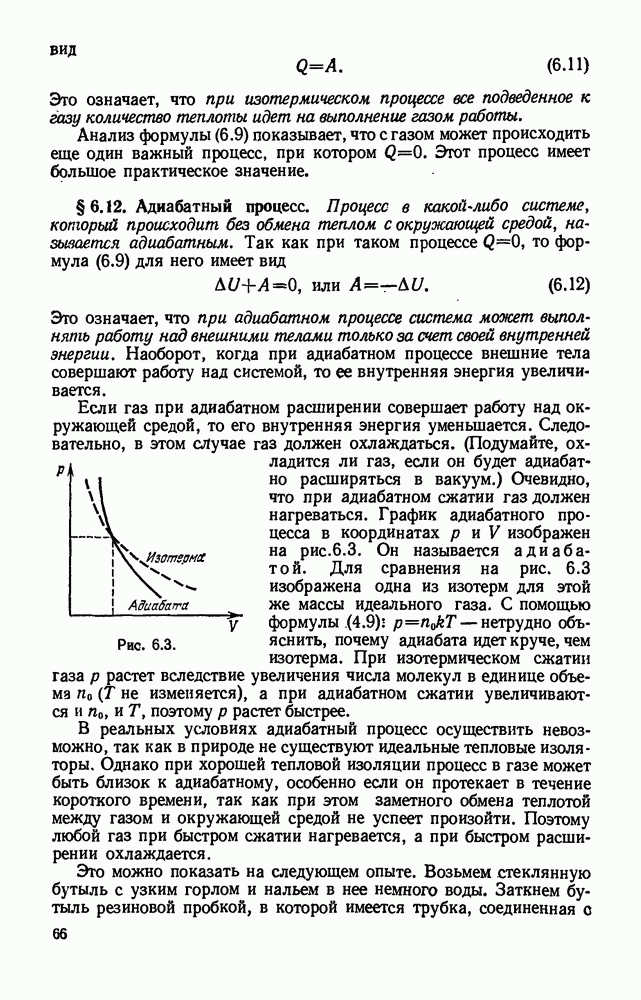
- § 6.12. Адиабатный процесс.
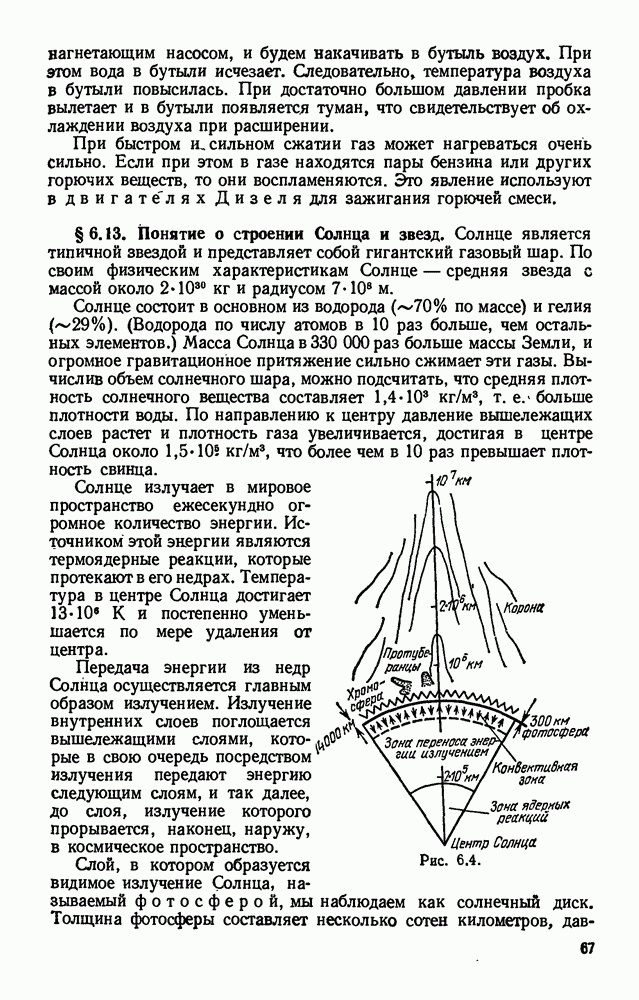
- § 6.13. Понятие о строении Солнца и звезд.
- Глава 7. ПЕРЕХОД ВЕЩЕСТВА ИЗ ЖИДКОГО СОСТОЯНИЯ В ГАЗООБРАЗНОЕ И ОБРАТНО
- § 7.2. Испарение.
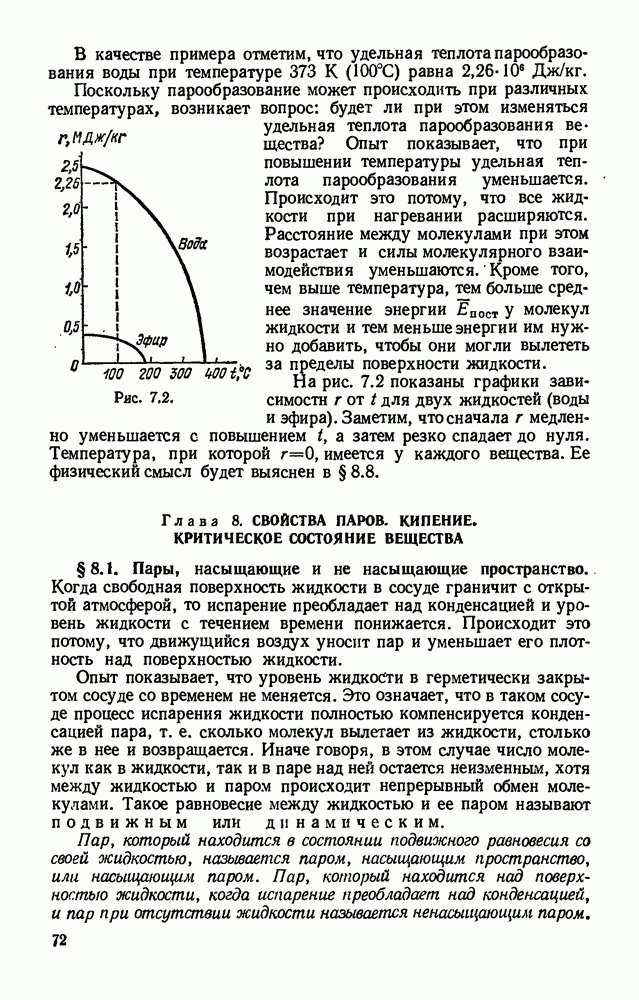
- § 7.3. Теплота парообразования.
- Глава 8. СВОЙСТВА ПАРОВ. КИПЕНИЕ. КРИТИЧЕСКОЕ СОСТОЯНИЕ ВЕЩЕСТВА
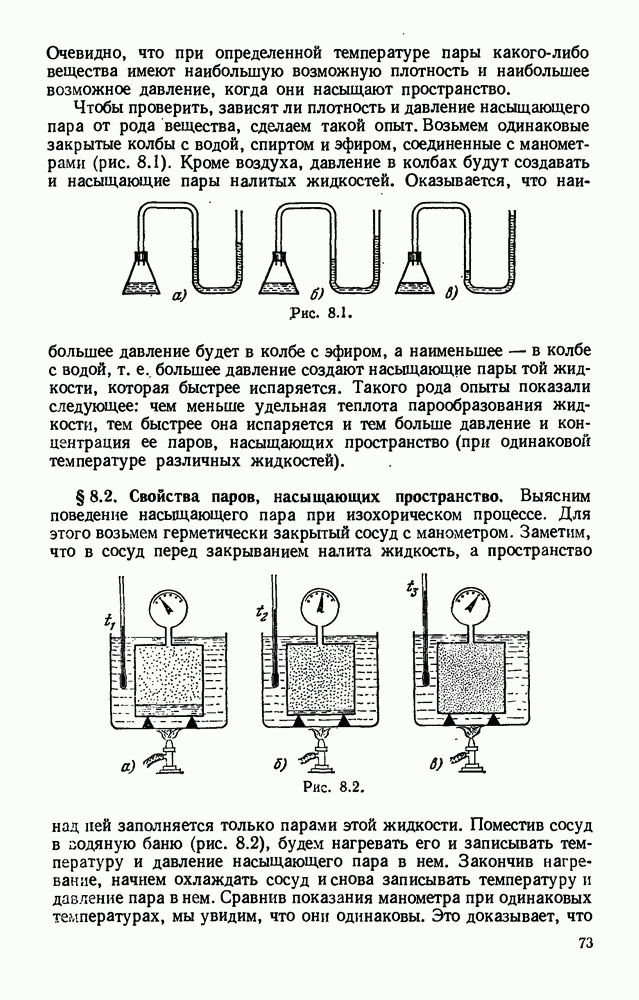
- § 8.2. Свойства паров, насыщающих пространство.
- § 8.3. Свойства паров, не насыщающих пространство.
- § 8.4. Процесс кипения жидкости.
- § 8.5. Зависимость температуры кипения жидкости от внешнего давления. Точка кипения.
- § 8.6. Уравнение теплового баланса при парообразовании и конденсации.
- § 8.7. Перегретый пар и его использование в технике.
- § 8.8. Критическое состояние вещества.
- § 8.9. Сжижение газов и использование жидких газов в технике.
- Глава 9. ВОДЯНОЙ ПАР В АТМОСФЕРЕ
- § 9.2. Абсолютная и относительная влажность воздуха. Точка росы.
- § 9.3. Приборы для определения влажности воздуха.
- § 9.4. Понятие об атмосферах планет.
- Глава 10. СВОЙСТВА ЖИДКОСТЕЙ
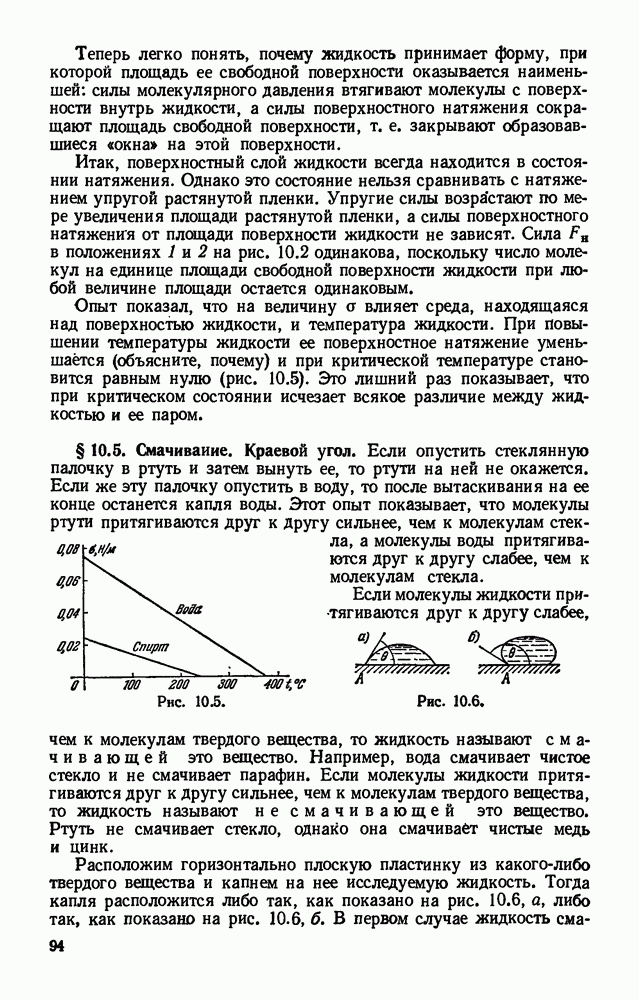
- § 10.2. Поверхностный слой жидкости.
- § 10.3. Энергия поверхностного слоя жидкости. Поверхностное натяжение.
- § 10.4. Сила поверхностного натяжения.
- § 10.5. Смачивание. Краевой угол.
- § 10.6. Мениск. Давление, создаваемое искривленной поверхностью жидкости.
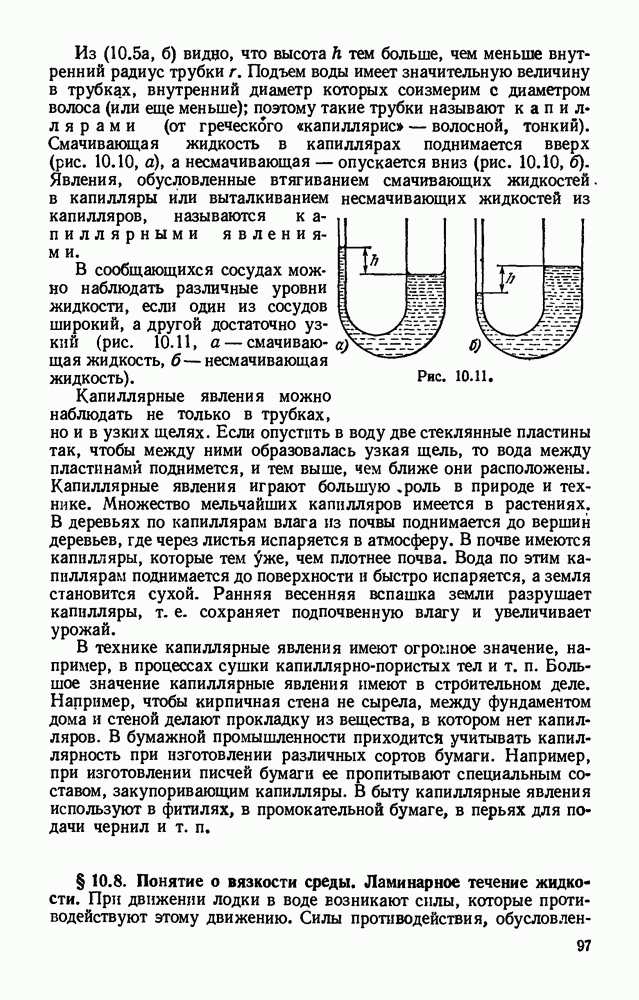
- § 10.7. Капиллярность. Капиллярные явления в природе и технике.
- § 10.8. Понятие о вязкости среды. Ламинарное течение жидкости.
- § 10.9. Закон Ньютона для внутреннего трения. Динамическая вязкость.
- § 10.10. Аморфные вещества.
- Глава 11. СВОЙСТВА ТВЕРДЫХ ТЕЛ. ДЕФОРМАЦИИ
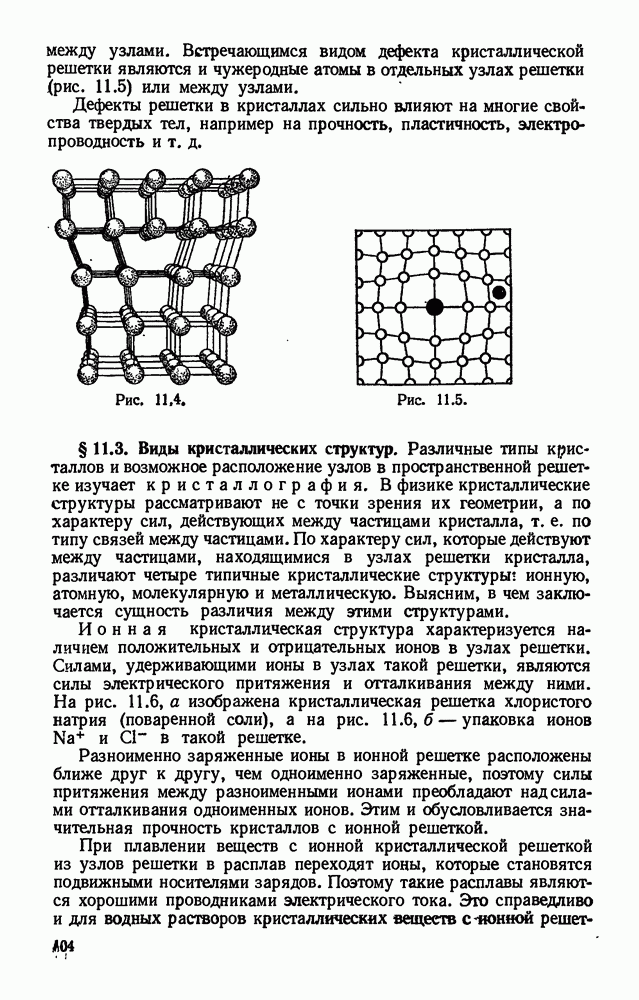
- § 11.2. Анизотропия кристаллов. Пространственная решетка и ее дефекты.
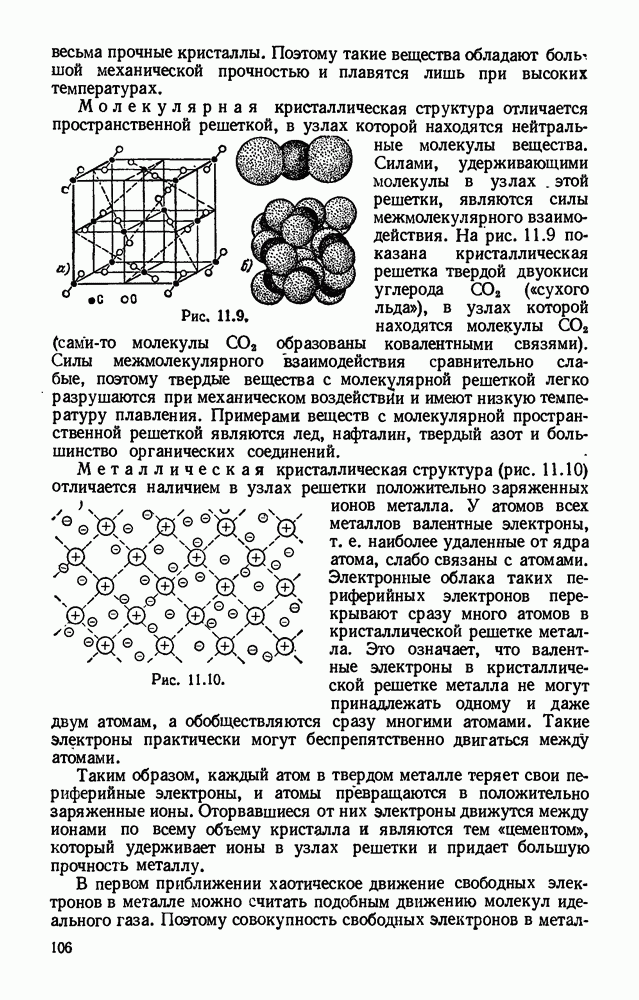
- § 11.3. Виды кристаллических структур.
- § 11.4. Виды деформаций.
- § 11.5. Механическое напряжение.
- § 11.6. Упругость, пластичность, хрупкость и твердость.
- § 11.7. Закон Гука. Модуль упругости.
- § 11.8. Энергия упруго деформированного тела.
- Глава 12. ПЛАВЛЕНИЕ И КРИСТАЛЛИЗАЦИЯ. СУБЛИМАЦИЯ. ДИАГРАММА СОСТОЯНИЙ ВЕЩЕСТВА
- § 12.2. Удельная теплота плавления.
- § 12.3. Изменение объема и плотности вещества при плавлении и отвердевании.
- § 12.4. Зависимость температуры и теплоты плавления от давления. Точка плавления.
- § 12.5. Уравнение теплового баланса при плавлении и кристаллизации.
- § 12.6. Растворы и сплавы. Охлаждающие смеси.
- § 12.7. Испарение твердых тел (сублимация).
- § 12.8. Диаграмма состоянии вещества. Тройная точка.
- Глава 13. ТЕПЛОВОЕ РАСШИРЕНИЕ ТЕЛ
- § 13.2. Линейное расширение твердых тел при нагревании.
- § 13.3. Объемное расширение тел при нагревании. Зависимость плотности вещества от температуры.
- § 13.4. Особенности теплового расширения твердых тел.
- § 13.5. Некоторые особенности теплового расширения жидкостей.
- § 13.6. Значение теплового расширения тел в природе и технике.
- Раздел II. ОСНОВЫ ЭЛЕКТРОДИНАМИКИ
- Глава 14. ЭЛЕКТРИЧЕСКИЕ ЗАРЯДЫ. ЗАКОН КУЛОНА
- § 14.2. Явления, подтверждающие сложное строение атома.
- § 14.3. Опыты Резерфорда. Ядерная модель строения атома.
- § 14.4. Понятие о строении атомов различных химических элементов.
- § 14.5. Электризация при соприкосновении незаряженных тел.
- § 14.6. Сила взаимодействия электрических зарядов. Закон Кулона.
- § 14.7. Диэлектрическая проницаемость среды.
- § 14.8. Международная система единиц СИ в электричестве. Электрическая постоянная.
- § 14.9. Электроскоп.
- Глава 15. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
- § 15.2. Напряженность электрического поля.
- § 15.3. Линии напряженности электрического поля.
- § 15.4. Однородное поле. Поверхностная плотность заряда.
- § 15.5. Работа электрического поля при перемещении заряда. Потенциальная энергия заряда.
- § 15.6. Потенциал. Разность потенциалов и напряжение. Эквипотенциальные поверхности.
- § 15.7. Связь между напряженностью поля и напряжением. Градиент потенциала.
- § 15.8. Проводник в электрическом поле.
- § 15.9. Электрометр.
- § 15.10. Диэлектрик в электрическом поле. Поляризация диэлектрика.
- § 15.11. Понятие о сегнетоэлектриках.
- § 15.12. Пьезоэлектрический эффект.
- § 15.13. Электроемкость проводника.
- § 15.14. Условия, от которых зависит электроемкость проводника.
- § 15.15. Конденсаторы.
- § 15.16. Соединение конденсаторов в батарею.
- § 15.17. Энергия заряженного конденсатора. Плотность энергии электрического поля.
- § 15.18. Опыт Милликена.
- Глава 16. ЭЛЕКТРИЧЕСКИЙ ТОК В МЕТАЛЛАХ. ЗАКОНЫ ПОСТОЯННОГО ТОКА
- § 16.2. Сила тока и плотность тока в проводнике.
- § 16.3. Замкнутая электрическая цепь.
- § 16.4. Электродвижущая сила источника электрической энергии.
- § 16.5. Внешняя и внутренняя части цепи.
- § 16.6. Закон Ома для участка цепи без э. д. с. Сопротивление проводника. Падение напряжения.
- § 16.7. Зависимость сопротивления от материала, длины и площади поперечного сечения проводника.
- § 16.8. Зависимость сопротивления от температуры.
- § 16.9. Сверхпроводимость.
- § 16.10. Эквивалентное сопротивление.
- § 16.11. Последовательное соединение потребителей энергии тока.
- § 16.12. Параллельное соединение потребителей энергии тока
- § 16.13. Закон Ома для всей цепи.
- § 16.14. Соединение одинаковых источников электрической энергии в батарею.
- § 16.15. Закон Ома для участка цепи с э. д. с. и для всей цепи при нескольких э. д. с.
- Глава 17. РАБОТА, МОЩНОСТЬ И ТЕПЛОВОЕ ДЕЙСТВИЕ ЭЛЕКТРИЧЕСКОГО ТОКА
- § 17.2. Мощность электрического тока.
- § 17.3. Тепловое действие электрического тока. Закон Джоуля — Ленца.
- § 17.4. Короткое замыкание. Практическое применение теплового действия тока.
- Глава 18. ТЕРМОЭЛЕКТРИЧЕСКИЕ ЯВЛЕНИЯ
- § 18.2. Контактная разность потенциалов.
- § 18.3. Термоэлектродвижущая сила.
- § 18.4. Явление Пельтье.
- § 18.5. Применение термоэлектрических явлений в науке и технике.
- Глава 19. ЭЛЕКТРИЧЕСКИЙ ТОК В ЭЛЕКТРОЛИТАХ
- § 19.2. Электролиз.
- § 19.3. Электролиз, сопровождающийся растворением анода.
- § 19.4. Количество вещества, выделяющегося при электролизе. Первый закон Фарадея.
- § 19.5. Второй закон Фарадея. Определение заряда иона.
- § 19.6. Использование электролиза в технике.
- § 19.7. Гальванические элементы.
- § 19.8. Аккумуляторы.
- § 19.9. Применение гальванических элементов и аккумуляторов в технике. Явление электрокоррозии.
- Глава 20. ЭЛЕКТРИЧЕСКИЙ ТОК В ГАЗАХ И В ВАКУУМЕ
- § 20.2. Зависимость силы тока в газе от напряжения.
- § 20.3. Электрический разряд в газе при атмосферном давлении.
- § 20.4. Электрический разряд в разреженных газах. Газосветные трубки и лампы дневного света.
- § 20.5. Излучение и поглощение энергии атомом.
- § 20.6. Катодные лучи.
- § 20.7. Понятие о плазме.
- § 20.8. Электрический ток в вакууме.
- § 20.9. Двухэлектродная лампа (диод).
- § 20.10. Трехэлектродная лампа (триод).
- § 20.11. Электронно-лучевая трубка.
- Глава 21. ЭЛЕКТРИЧЕСКИЙ ТОК В ПОЛУПРОВОДНИКАХ
- § 21.2. Чистые (беспримесные) полупроводники. Термисторы.
- § 21.3. Примесные полупроводники.
- § 21.4. Электронно-дырочный переход.
- § 21.5. Полупроводниковый диод.
- § 21.6. Полупроводниковый триод (транзистор).
- Глава 22. ЭЛЕКТРОМАГНЕТИЗМ
- § 22.2. Магнитное поле как особый вид материи.
- § 22.3. Магниты.
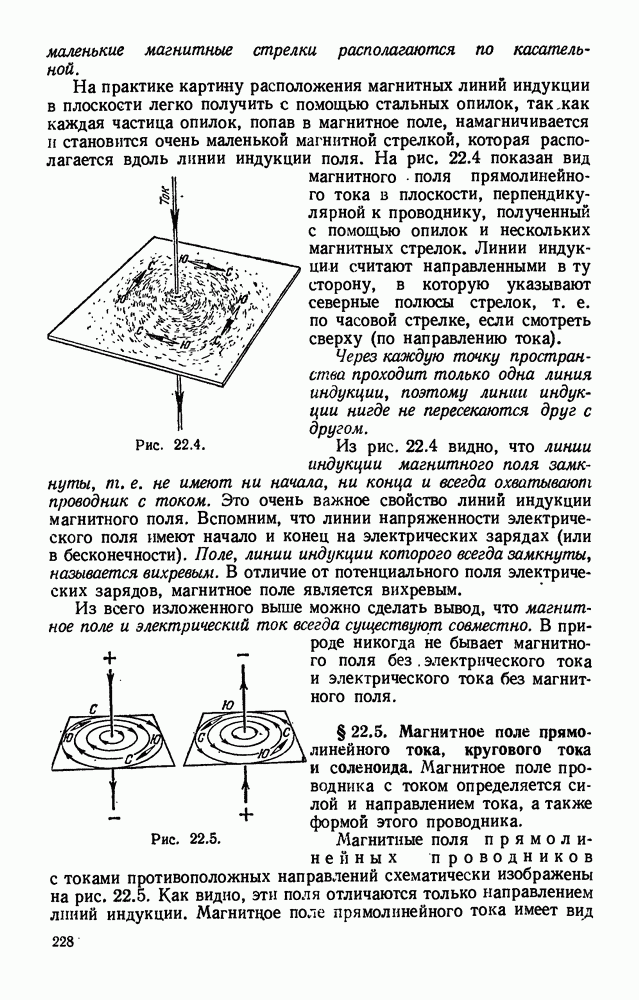
- § 22.4. Линии магнитной индукции. Понятие о вихревом поле.
- § 22.5. Магнитное поле прямолинейного тока, кругового тока и соленоида.
- § 22.6. Сравнение магнитных свойств соленоида и постоянного магнита.
- § 22.7. Сила взаимодействия параллельных токов. Магнитная проницаемость среды.
- § 22.8. Определение ампера. Магнитная постоянная.
- § 22.9. Действие магнитного поля на прямолинейный проводник с током.
- § 22.10. Однородное магнитное поле.
- § 22.11. Магнитный момент контура с током.
- § 22.12. Работа при перемещении проводника с током в магнитном поле. Магнитный поток.
- § 22.13. Индукция магнитного поля, создаваемая в веществе проводниками с током различной формы.
- § 22.14. Напряженность магнитного поля и ее связь с индукцией и магнитной проницаемостью среды.
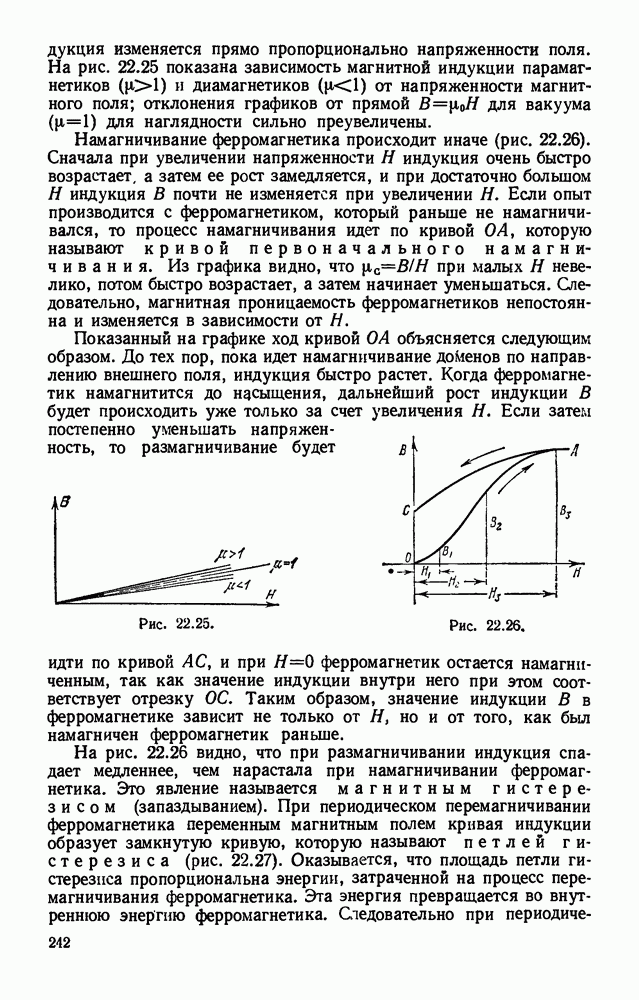
- § 22.15. Парамагнитные, диамагнитные и ферромагнитные вещества.
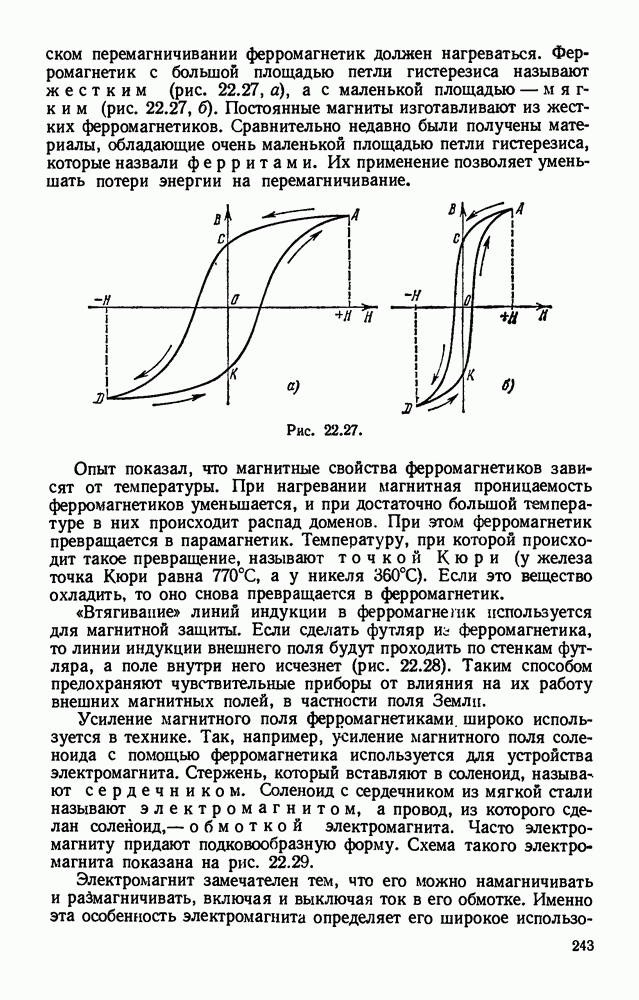
- § 22.16. Намагничивание ферромагнетиков. Электромагнит.
- § 22.17. Работа и устройство амперметра и вольтметра.
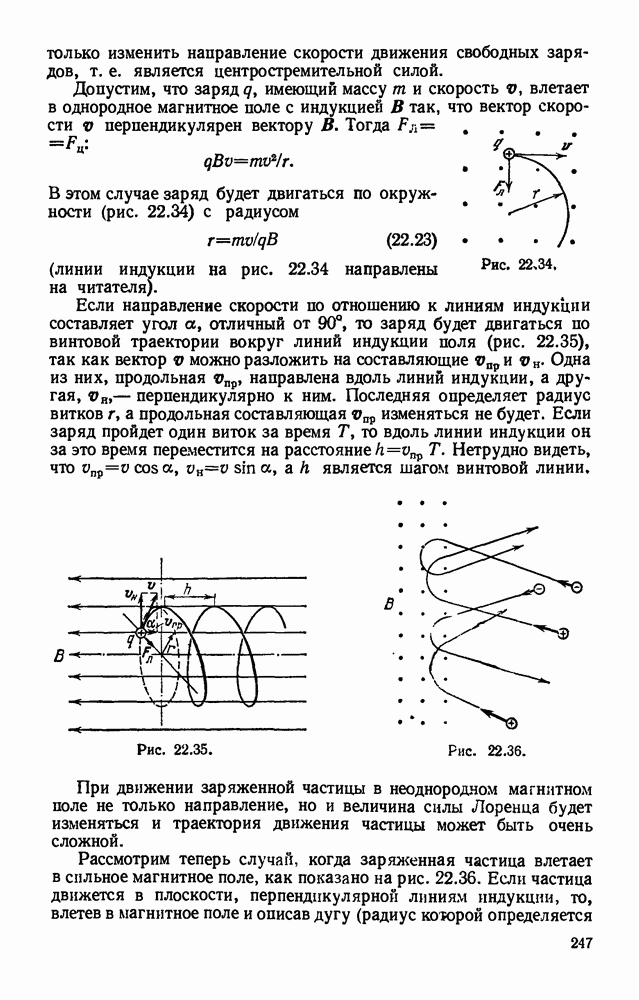
- § 22.18. Сила Лоренца. Движение заряда в магнитном поле.
- § 22.19. Постоянное и переменное магнитные поля.
- Глава 23. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ
- § 23.2. Явление электромагнитной индукции.
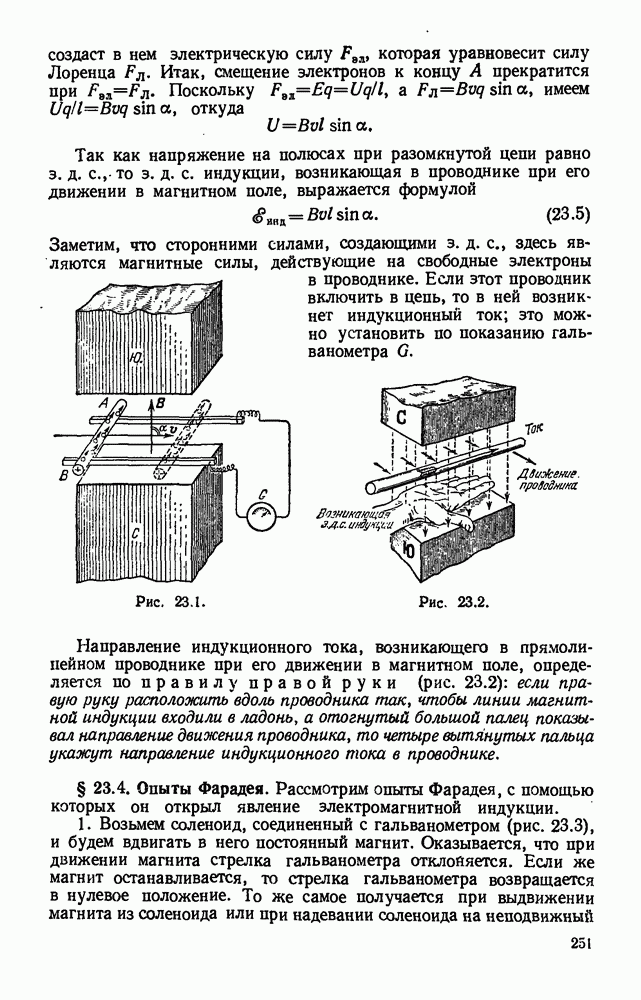
- § 23.3. Э. д. с. индукции, возникающая в прямолинейном проводнике при его движении в магнитном поле. Правило правой руки.
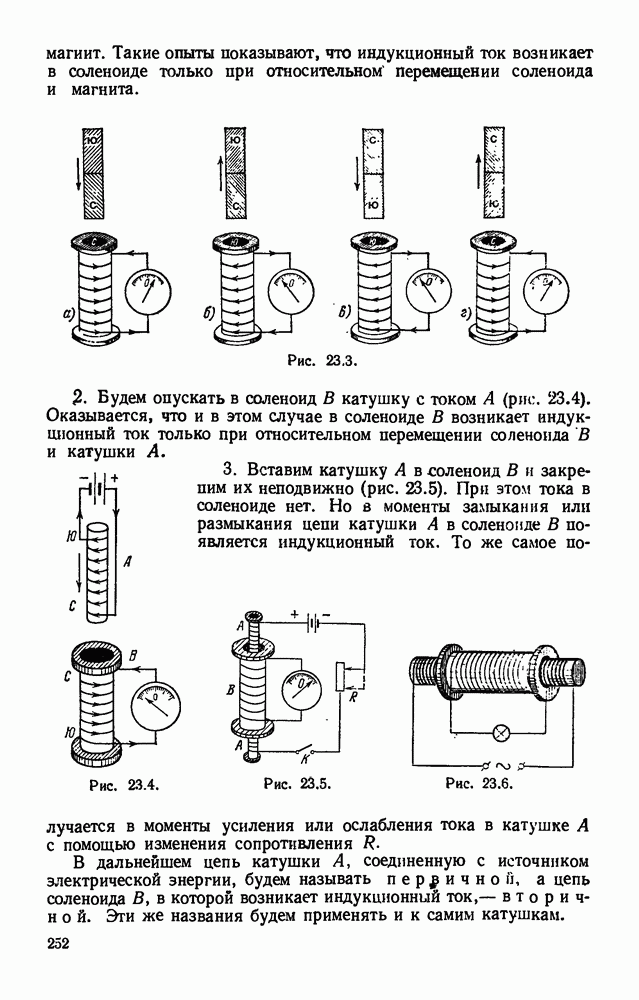
- § 23.4. Опыты Фарадея.
- § 23.5. Закон Ленца для электромагнитной индукции. Объяснение диамагнитных явлений.
- § 23.6. Величина э. д. с. индукции.
- § 23.7. Вихревое электрическое поле и его связь с магнитным полем.
- § 23.8. Вихревые токи.
- § 23.9. Роль магнитных полей в явлениях, происходящих на Солнце и в космосе.
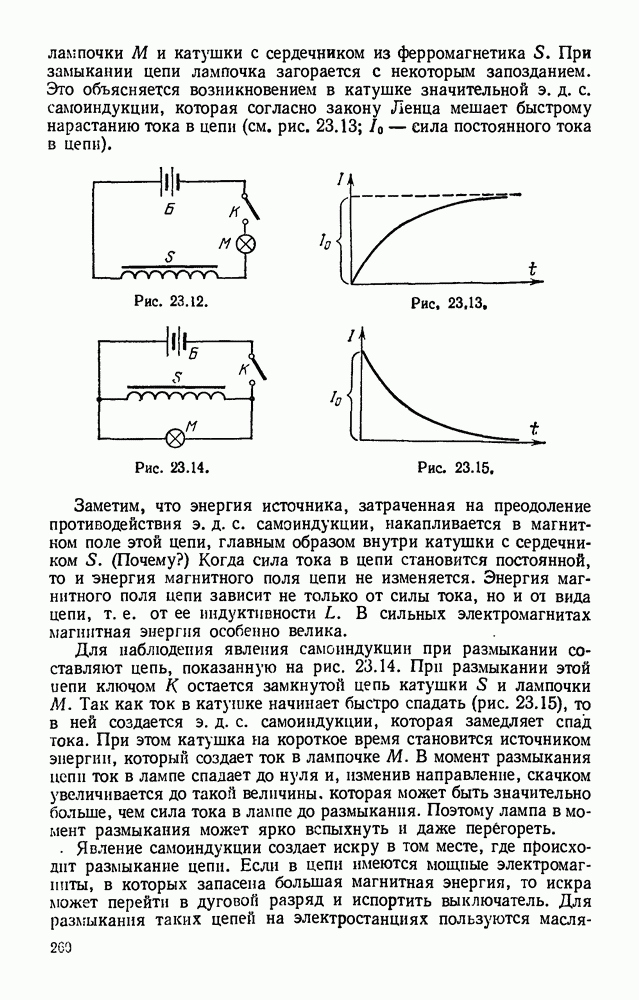
- § 23.10. Явление самоиндукции. Э. д. с. самоиндукции.
- § 23.11. Энергия магнитного поля.
- Раздел III. КОЛЕБАНИЯ И ВОЛНЫ
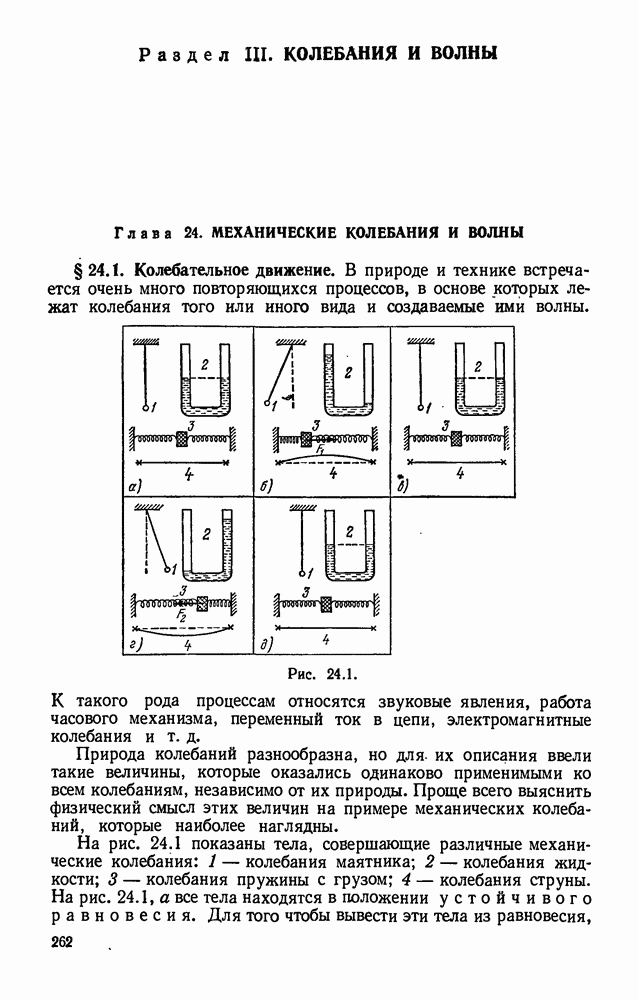
- Глава 24. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ
- § 24.2. Условия возникновения колебаний.
- § 24.3. Классификация колебательных движений тела в зависимости от действующей на него силы.
- § 24.4. Параметры колебательного движения.
- § 24.5. Величины, характеризующие мгновенное состояние колеблющейся точки.
- § 24.6. Гармоническое колебание.
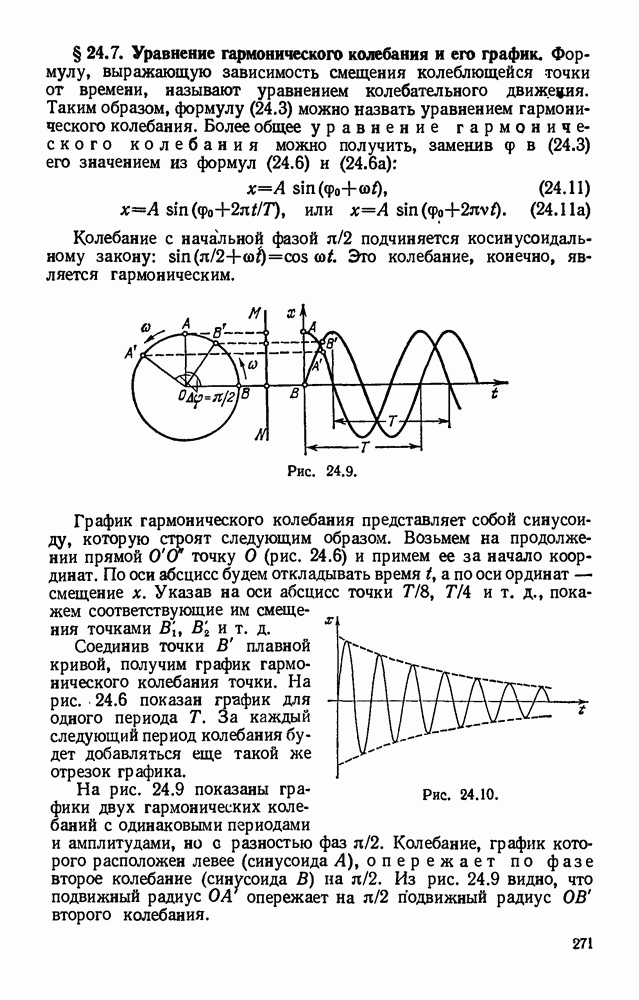
- § 24.7. Уравнение гармонического колебания и его график.
- § 24.8. Математический маятник.
- § 24.9. Законы колебания математического маятника. Формула маятника.
- § 24.10. Физический маятник.
- § 24.11. Практические применения маятников.
- § 24.12. Упругие колебания. Превращение энергии при колебательном движении.
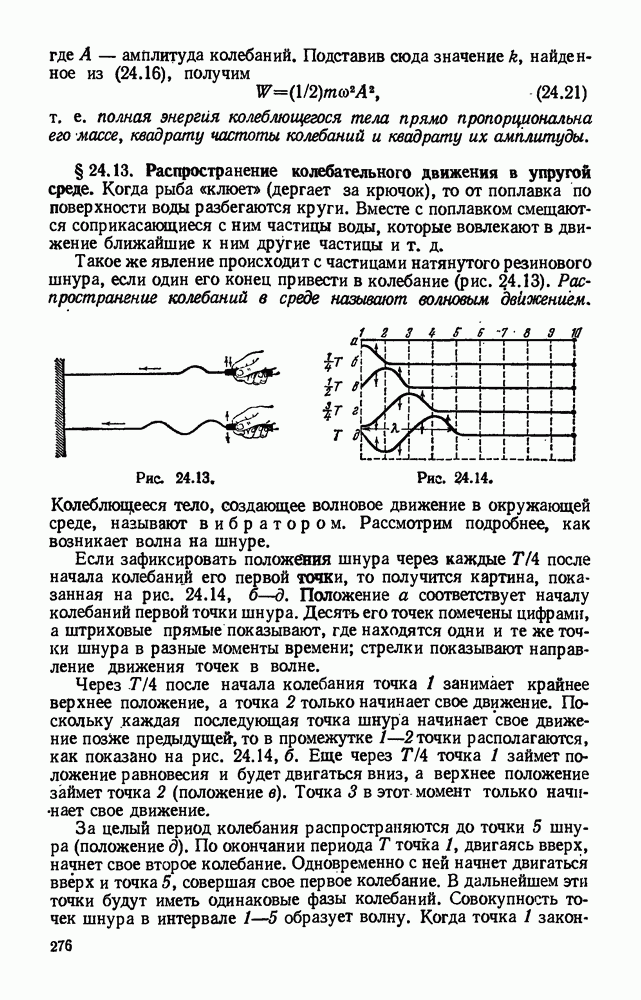
- § 24.13. Распространение колебательного движения в упругой среде.
- § 24.14. Перенос энергии бегущей волной.
- § 24.15. Поперечные и продольные волны.
- § 24.16. Волна и луч. Длина волны.
- § 24.17. Скорость распространения волн и ее связь с длиной волны и периодом (частотой) колебаний.
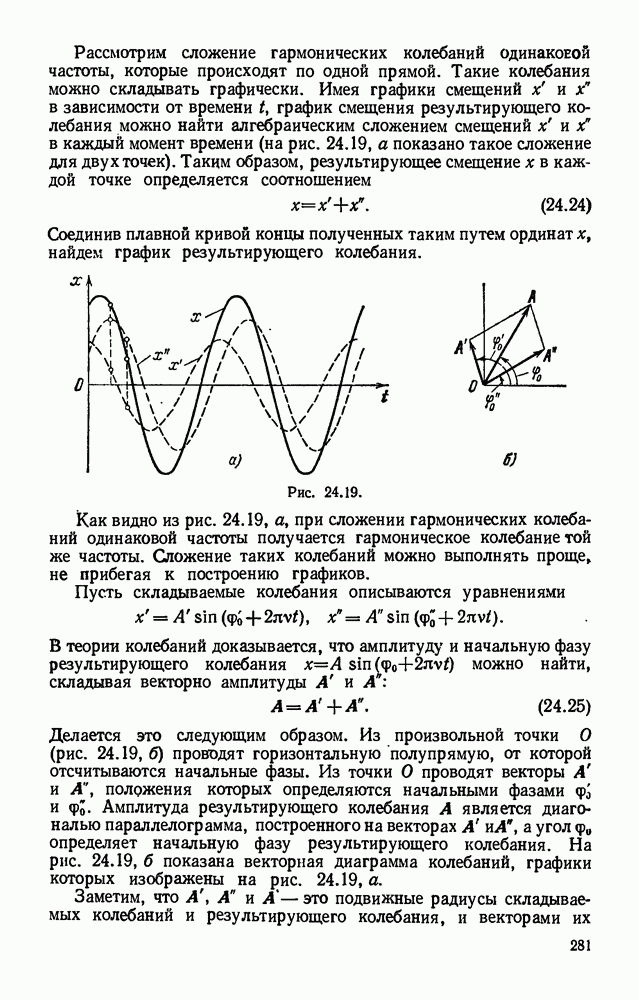
- § 24.18. Сложение колебаний, происходящих по одной прямой.
- § 24.19. Отражение волн.
- § 24.20. Стоячие волны.
- § 24.21. Интерференция волн.
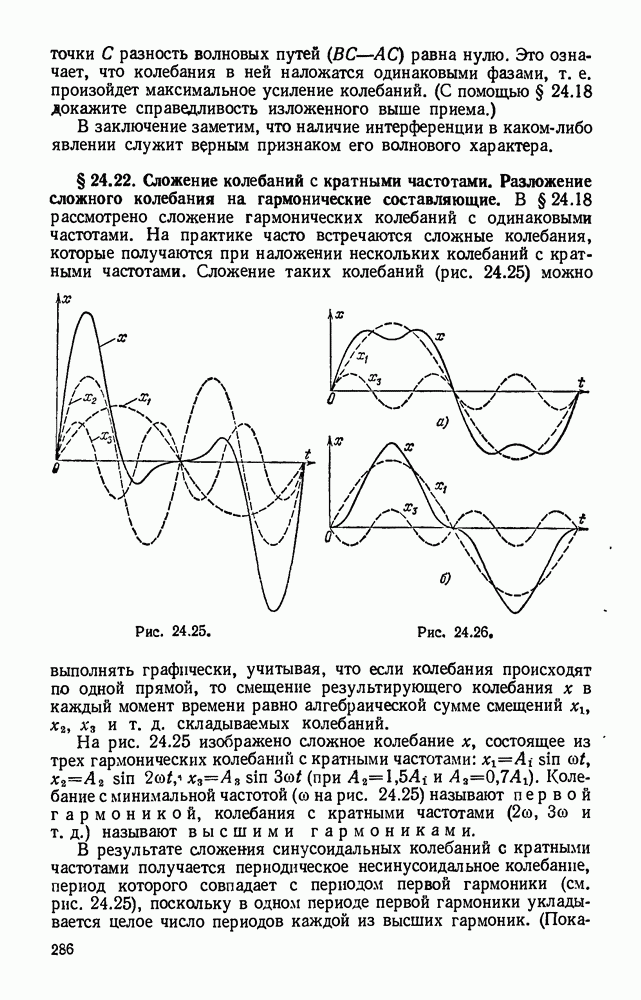
- § 24.22. Сложение колебаний с кратными частотами. Разложение сложного колебания на гармонические составляющие.
- § 24.23. Вынужденные колебания. Механический резонанс и его роль в технике.
- Глава 25. ЗВУК И УЛЬТРАЗВУК
- § 25.3. Громкость и интенсивность звука.
- § 25.4. Высота тона и тембр звука.
- § 25.5. Интерференция звуковых волн.
- § 25.6. Отражение и поглощение звука.
- § 25.7. Звуковой резонанс.
- § 25.8. Ультразвук и его применение в технике.
- Глава 26. ПЕРЕМЕННЫЙ ТОК
- § 26.2. Понятие об устройстве индукционных генераторов.
- § 26.3. Действующие значения э. д. с., напряжения и силы переменного тока.
- § 26.4. Индуктивность и емкость в цепи переменного тока.
- § 26.5. Преобразование переменного тока. Трансформатор.
- § 26.6. Индукционная катушка.
- § 26.7. Трехфазный ток.
- § 26.8. Получение, передача и распределение электрической энергии в народном хозяйстве СССР.
- Глава 27. ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ И ВОЛНЫ
- § 27.2. Затухающие электромагнитные колебания. Электрический резонанс.
- § 27.3. Получение незатухающих колебаний с помощью лампового генератора.
- § 27.4. Токи высокой частоты и их применение.
- § 27.5. Электромагнитное поле как особый вид материи.
- § 27.6. Открытый колебательный контур. Излучение.
- § 27.7. Электромагнитные волны. Скорость их распространения.
- § 27.8. Опыты Герца.
- § 27.9. Изобретение радио А С. Поповым. Радиотелеграфная связь.
- § 27.10. Радиотелефонная связь. Амплитудная модуляция.
- § 27.11. Устройство простейшего лампового радиоприемника с усилителем низкой частоты.
- § 27.12. Понятие о радиолокации.
- Раздел IV. ОПТИКА. ОСНОВЫ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Глава 28. ПРИРОДА СВЕТА. РАСПРОСТРАНЕНИЕ СВЕТА
- § 28.2. Понятие об электромагнитной теории света. Диапазон световых волн.
- § 28.3. Понятие о квантовой теории света. Постоянная Планка.
- § 28.4. Источники света.
- § 28.5. Принцип Гюйгенса. Световые лучи.
- § 28.6. Скорость распространения света в вакууме. Опыт Майкельсона.
- § 28.7. Скорость распространения света в различных средах.
- Глава 29. ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ СВЕТА
- § 29.2. Законы отражения света.
- § 29.3. Зеркальное и диффузное отражение. Плоское зеркало.
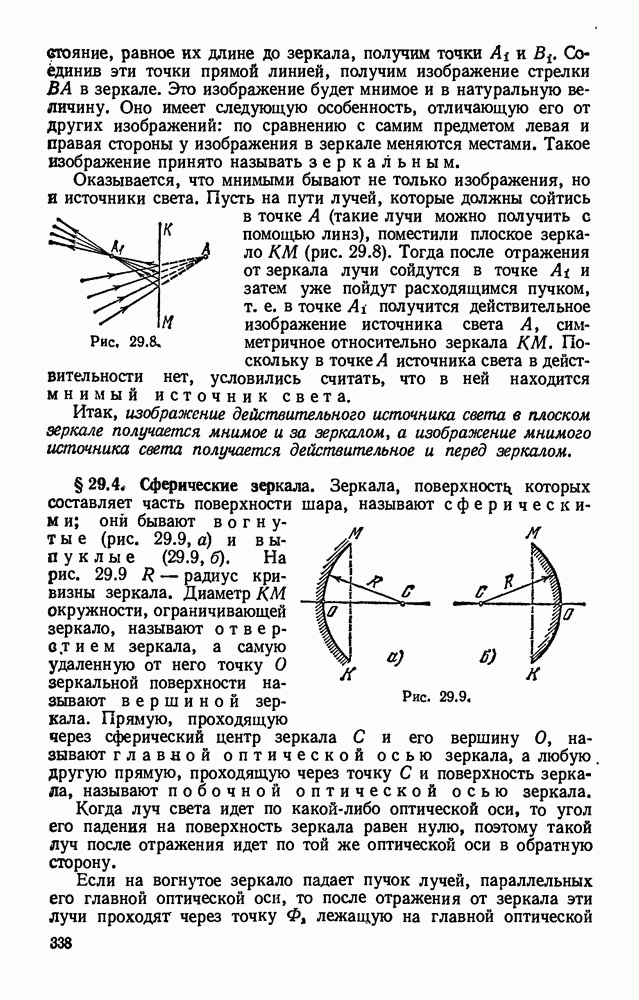
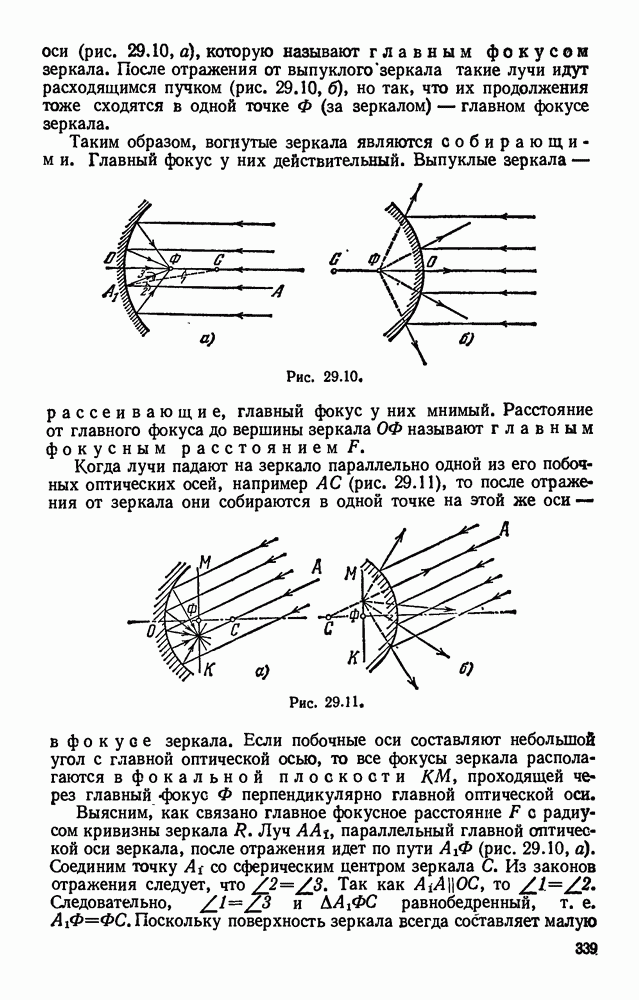
- § 29.4. Сферические зеркала.
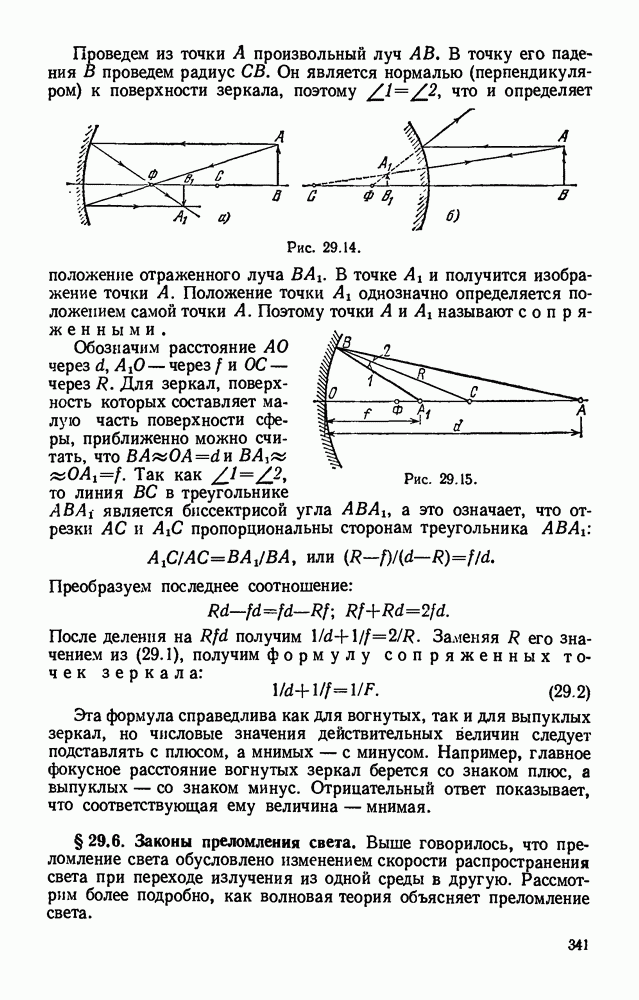
- § 29.5. Построение изображений, получаемых с помощью сферических зеркал. Формула сферического зеркала.
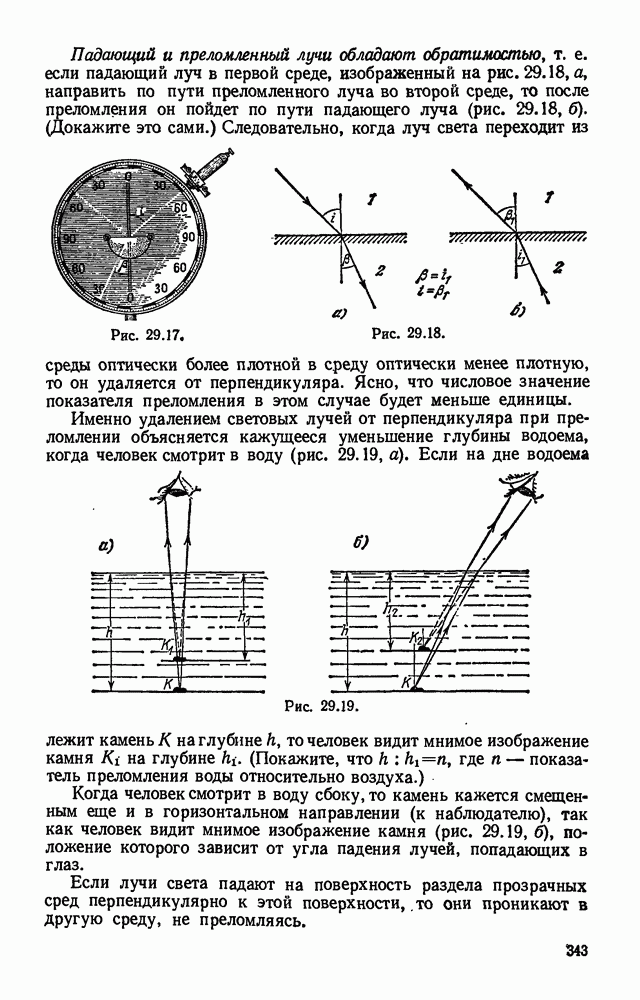
- § 29.6. Законы преломления света.
- § 29.7. Абсолютный показатель преломления и его связь с относительным показателем преломления.
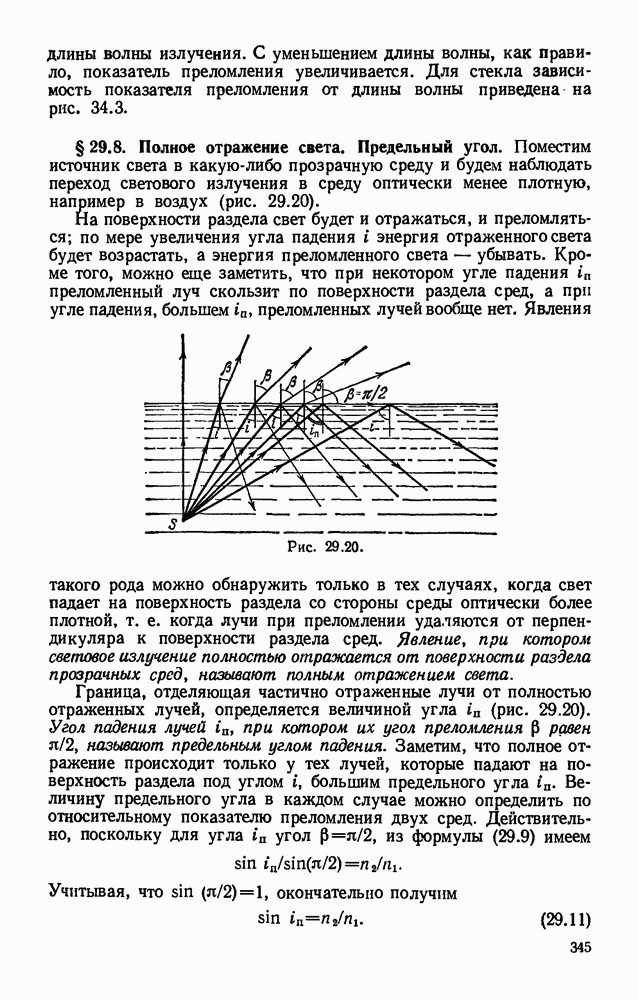
- § 29.8. Полное отражение света. Предельный угол.
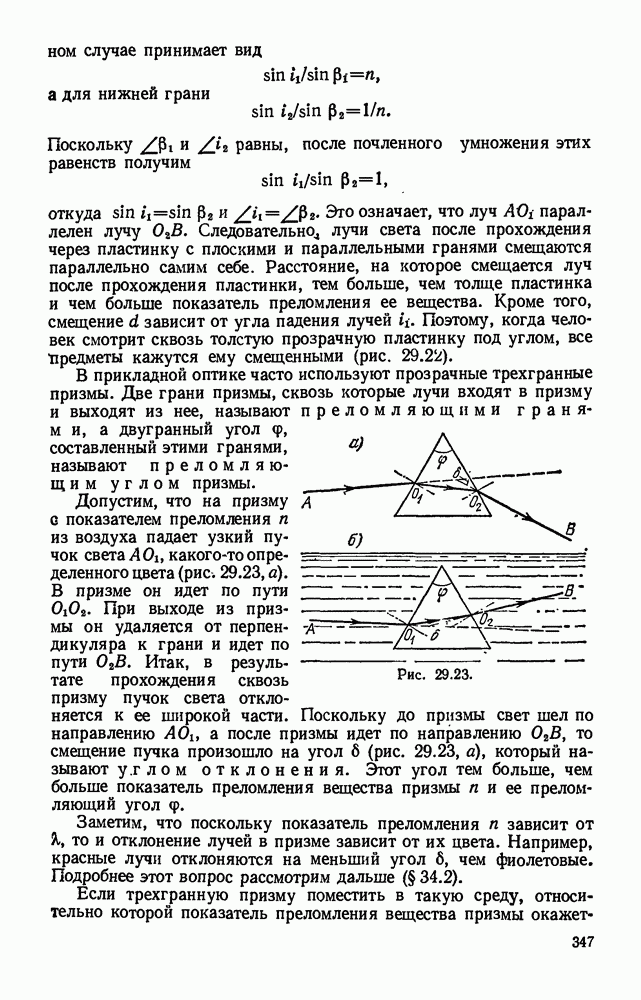
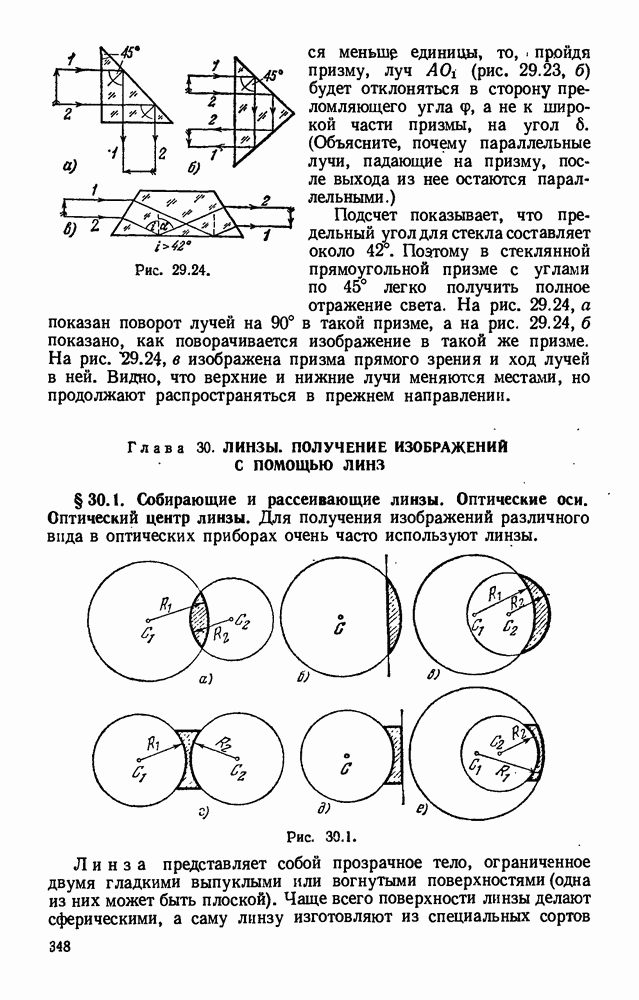
- § 29.9. Прохождение света через пластинку с параллельными гранями и через трехгранную призму. Призма с полным отражением.
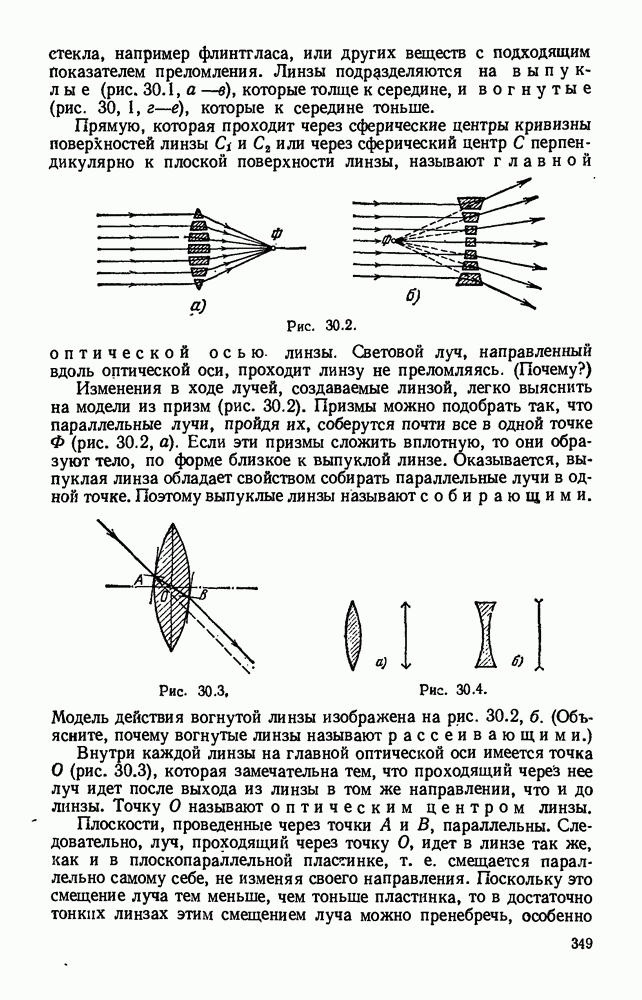
- Глава 30. ЛИНЗЫ. ПОЛУЧЕНИЕ ИЗОБРАЖЕНИЙ С ПОМОЩЬЮ ЛИНЗ
- § 30.2. Главные фокусы и фокальные плоскости линзы.
- § 30.3. Оптическая сила линзы.
- § 30.4. Построение изображения светящейся точки, расположенной на главной оптической оси линзы.
- § 30.5. Вывод формулы для сопряжеппых точек тонкой линзы.
- § 30.6. Построение изображения светящейся точки, расположенной на побочной оптической оси линзы.
- § 30.7. Построение изображений предмета, создаваемых линзой.
- § 30.8. Линейное увеличение, полученное с помощью линзы.
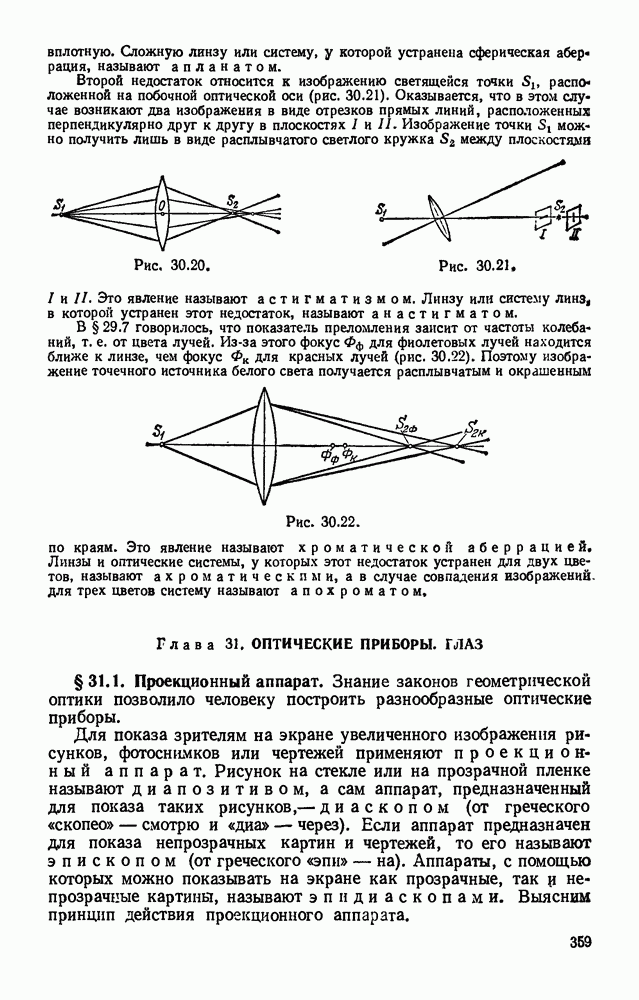
- § 30.9. Недостатки линз. Выясним, какие существенные недостатки встречаются у линз.
- Глава 31. ОПТИЧЕСКИЕ ПРИБОРЫ. ГЛАЗ
- § 31.2. Фотографический аппарат.
- § 31.3. Глаз как оптическая система.
- § 31.4, Длительность зрительного ощущения.
- § 31.5. Угол зрения.
- § 31.6. Расстояние наилучшего зрения. Оптические дефекты глаза.
- § 31.7. Увеличение оптического прибора. Лупа.
- § 31.8. Микроскоп.
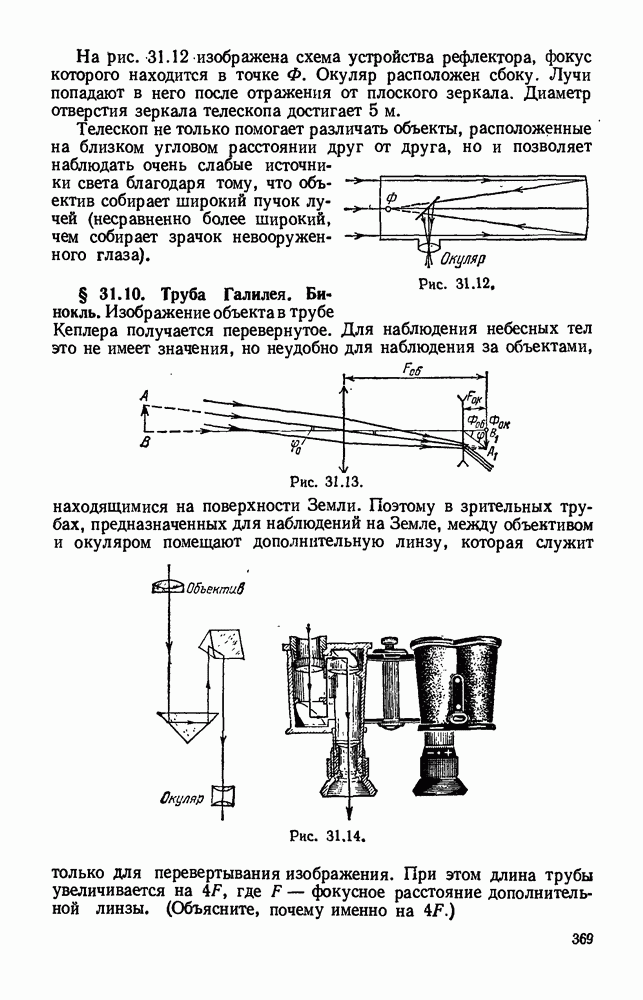
- § 31.9. Труба Кеплера. Телескопы.
- § 31.10. Труба Галилея. Бинокль.
- Глава 32. ЯВЛЕНИЯ, ОБЪЯСНЯЕМЫЕ ВОЛНОВЫМИ СВОЙСТВАМИ СВЕТА
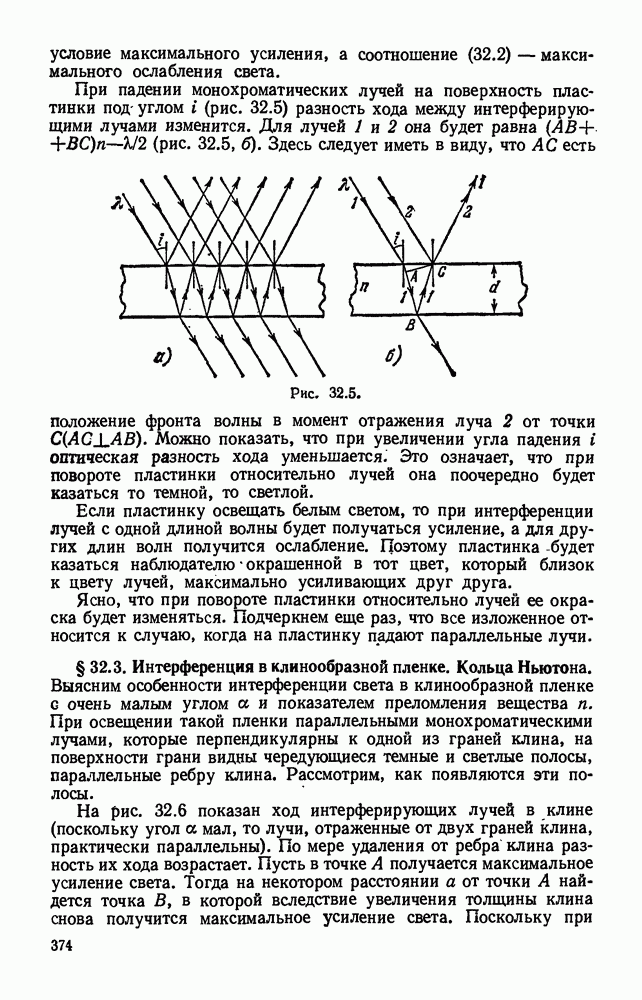
- § 32.2. Цвета тонких пленок.
- § 32.3. Интерференция в клинообразной пленке. Кольца Ньютона.
- § 32.4. Интерференция света в природе и технике.
- § 32.5. Дифракция света.
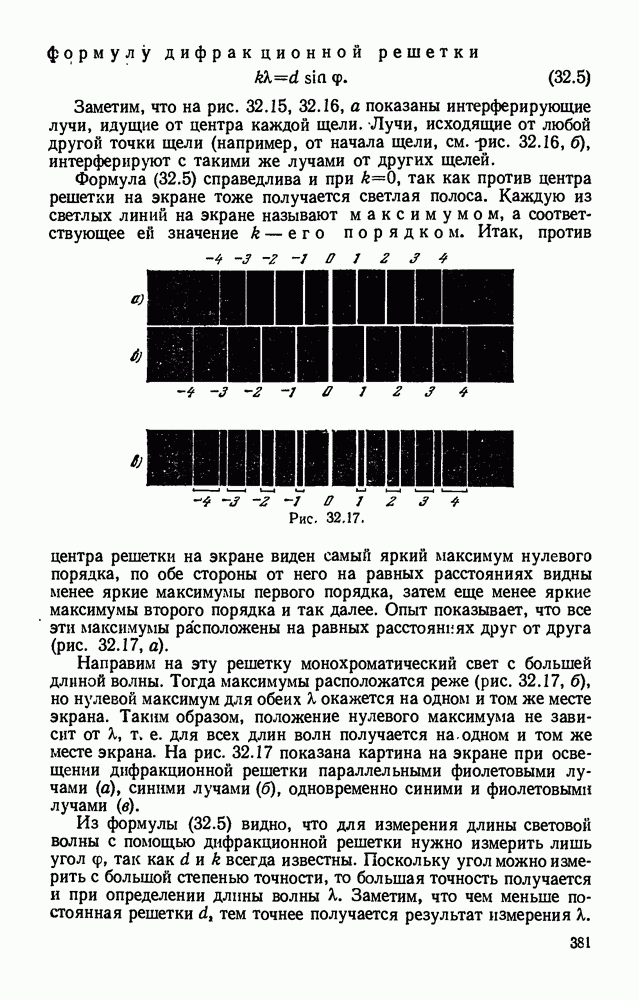
- § 32.6. Дифракционная решетка и дифракционный спектр. Измерение длины световой волны.
- § 32.7. Поляризация волн.
- § 32.8. Поляризация света. Поляроиды.
- § 32.9. Поляризация при отражении и преломлении света.
- Глава 33. ФОТОМЕТРИЯ
- § 33.2. Световой поток.
- § 33.3. Сила света. Единицы силы света и светового потока.
- § 33.4. Освещенность.
- § 33.5. Яркость.
- § 33.6. Законы освещенности.
- § 33.7. Сравнение силы света двух источников. Фотометр. Люксметр.
- Глава 34. ИЗЛУЧЕНИЕ И СПЕКТРЫ. РЕНТГЕНОВСКИЕ ЛУЧИ
- § 34.2. Разложение белого света призмой. Сплошной спектр.
- § 34.3. Сложение спектральных цветов. Дополнительные цвета.
- § 34.4. Цвета тел.
- § 34.5. Ультрафиолетовая и инфракрасная части спектра.
- § 34.6. Роль ультрафиолетовых и инфракрасных лучей в природе. Их применение в технике.
- § 34.7. Приборы для получения и исследования спектров.
- § 34.8. Виды спектров.
- § 34.9. Спектры поглощения газов. Опыты Кирхгофа.
- § 34.10. Закон теплового излучения Кирхгофа.
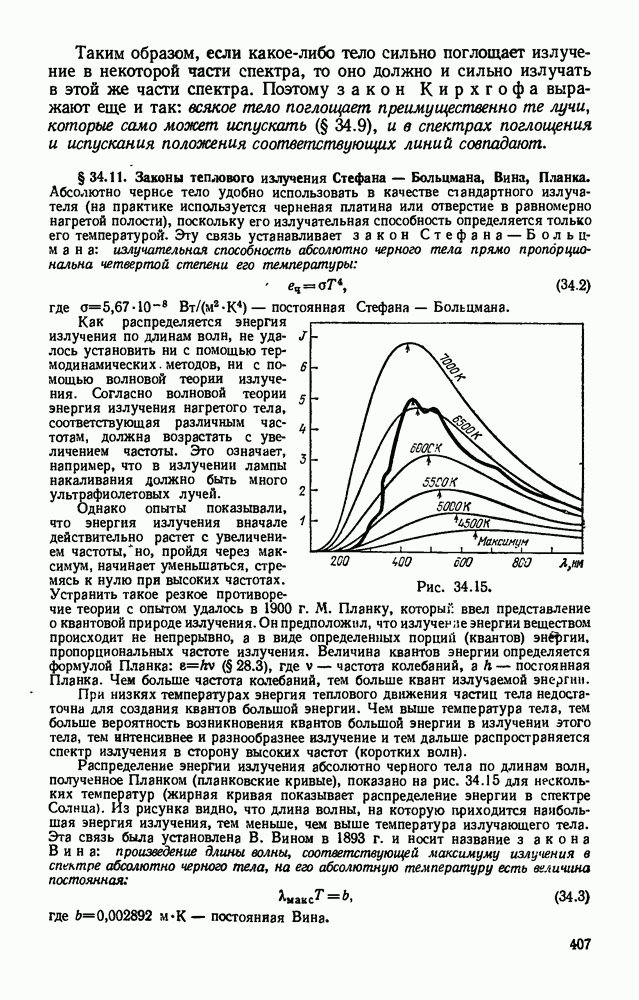
- § 34.11. Законы теплового излучения Стефана — Больцмана, Вина, Планка.
- § 34.12. Спектры Солнца и звезд. Их связь с температурой.
- § 34.13. Спектральный анализ.
- § 34.14. Понятие о принципе Доплера.
- § 34.15. Рентгеновские лучи и их практическое применение.
- § 34.16. Шкала электромагнитных волн.
- § 34.17. Виды космического излучения.
- Глава 35. ЯВЛЕНИЯ, ОБЪЯСНЯЕМЫЕ КВАНТОВЫМИ СВОЙСТВАМИ ИЗЛУЧЕНИЯ
- § 35.2. Давление световых лучей. Опыты П. Н. Лебедева.
- § 35.3. Тепловое действие света.
- § 35.4. Химическое действие света.
- § 35.5. Использование химического действия света при фотографировании. Понятие о квантовой природе химического действия излучения.
- § 35.6. Внешний фотоэлектрический эффект. Опыты Столетова.
- § 35.7. Законы внешнего фотоэффекта.
- § 35.8. Объяснение фотоэффекта на основе квантовой теории.
- § 35.9. Фотоэлементы с внешним фотоэффектом.
- § 35.10. Внутренний фотоэффект.
- § 35.11. Фотосопротивления.
- § 35.12. Фотоэлементы с внутренним фотоэффектом.
- § 35.13. Использование фотоэлементов в науке и технике.
- § 35.14. Понятие о телевидении.
- § 35.15. Понятие о теории Бора. Строение атома водорода.
- § 35.16. Излучение и поглощение энергии атомами.
- § 35.17. Явление люминесценции.
- § 35.18. Понятие о квантовых генераторах.
- Глава 36. ОСНОВЫ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- § 36.2. Экспериментальные основы специальной теории относительности Эйнштейна. Постулаты Эйнштейна.
- § 36.3. Понятие одновременности.
- § 36.4. Относительность понятий длины и промежутка времени
- § 36.5. Теорема сложения скоростей Эйнштейна.
- § 36.6. Масса и импульс в специальной теории относительности.
- § 36.7. Связь между массой и энергией. Уравнение Эйнштейна.
- § 36.8. Связь между импульсом и энергией. Импульс и энергия фотонов.
- Раздел V. ФИЗИКА АТОМНОГО ЯДРА
- Глава 37. СТРОЕНИЕ АТОМНОГО ЯДРА
- § 37.2. Радиоактивность.
- § 37.3. Понятие о превращении химических элементов.
- § 37.4. Понятие об энергии и проникающей способности радиоактивного излучения.
- § 37.5. Эффект Вавилова — Черенкова.
- § 37.6. Открытие искусственного превращения атомных ядер.
- § 37.7. Открытие нейтрона.
- § 37.8. Состав атомного ядра. Запись ядерных реакций.
- § 37.9. Изотопы.
- § 37.10. Понятие о ядерных силах.
- § 37.11. Дефект массы атомных ядер. Энергия связи.
- Глава 38. КОСМИЧЕСКИЕ ЛУЧИ. ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
- § 38.2. Открытие позитрона.
- § 38.3. Нейтрино.
- § 38.4. Открытие новых элементарных частиц.
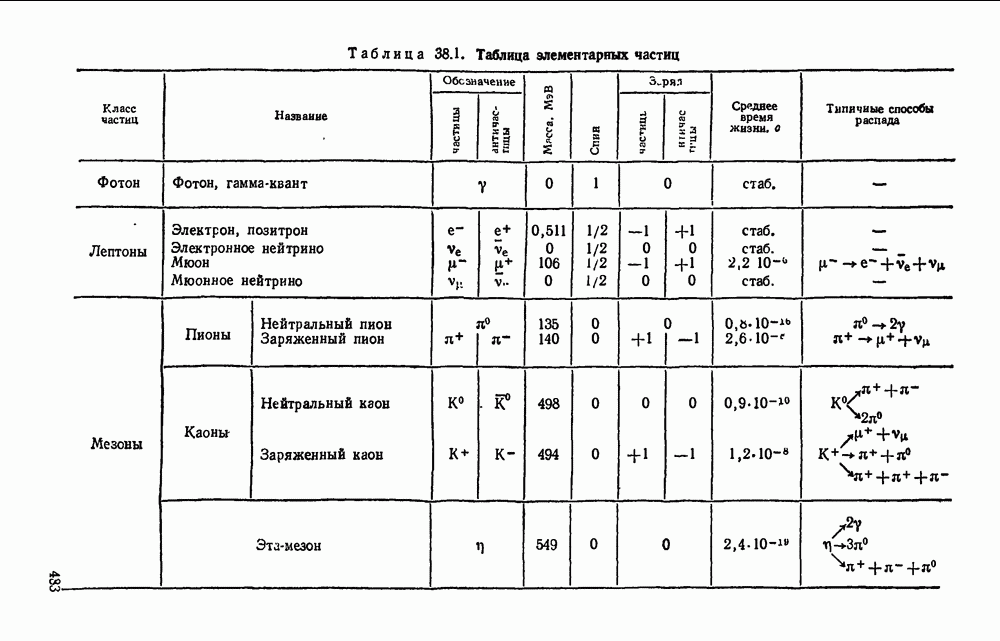
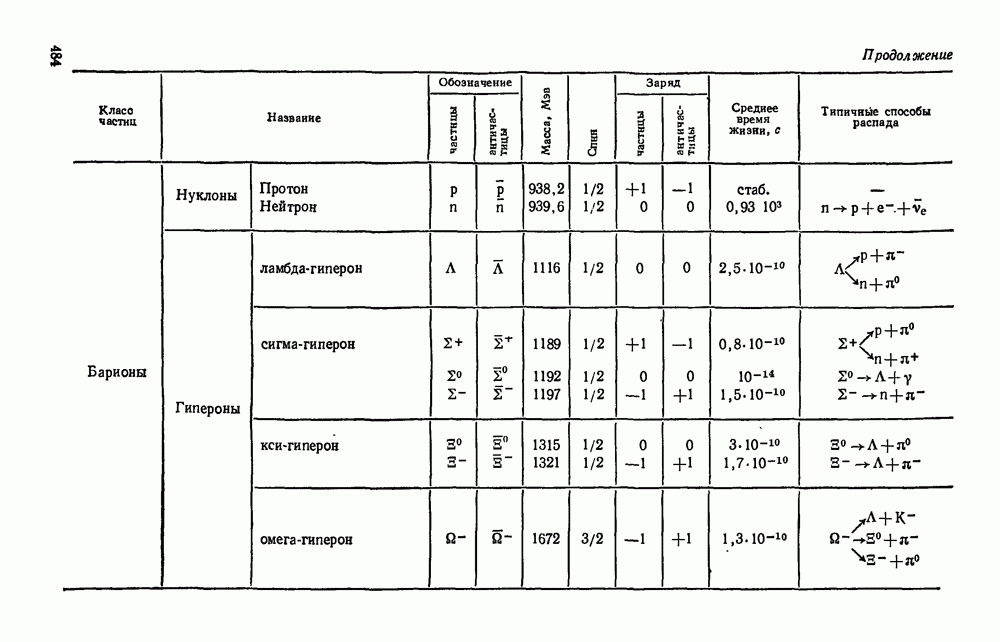
- § 38.5. Классификация элементарных частиц.
- § 38.6. Античастицы. Взаимные превращения вещества и поля.
- § 38.7. Гипотеза кварков.
- Глава 39. АТОМНАЯ ЭНЕРГИЯ И ЕЕ ИСПОЛЬЗОВАНИЕ
- § 39.2. Деление тяжелых атомных ядер.
- § 39.3. Цепная реакция деления. Ядерный взрыв.
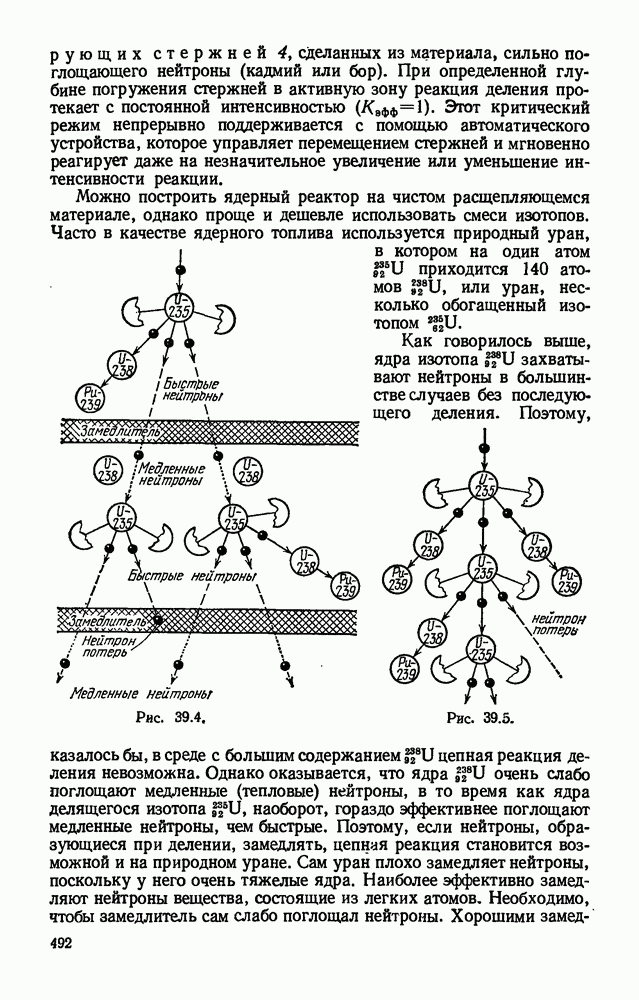
- § 39.4. Ядерный реактор.
- § 39.5. Развитие ядерной энергетики в СССР.
- § 39.6. Понятие о термоядерной реакции. Энергия Солнца и звезд.
- § 39.7. Понятие об управляемой термоядерной реакции.
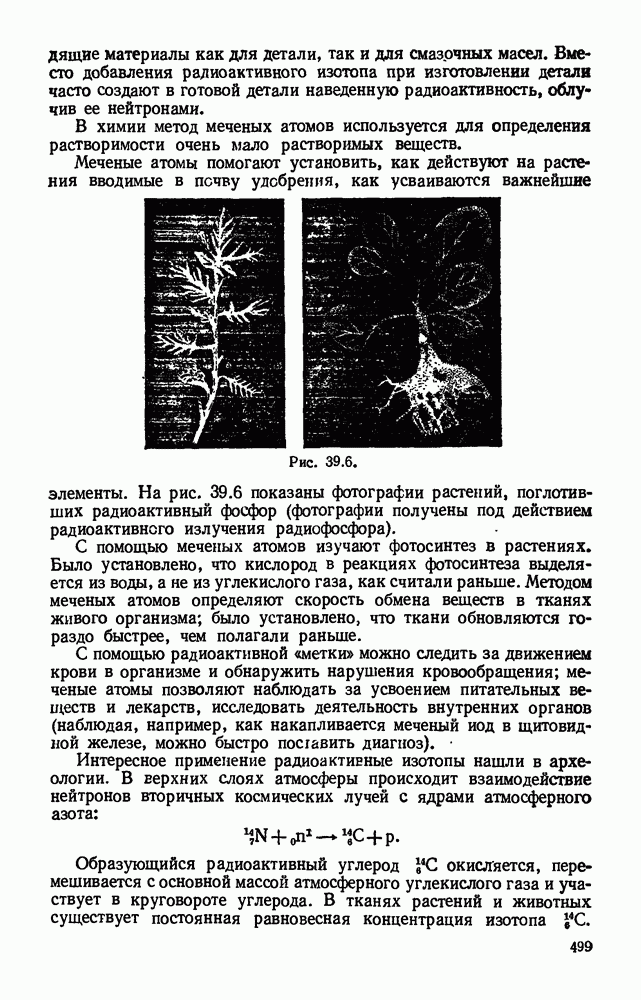
- § 39.8. Получение радиоактивных изотопов и их применение.
- Раздел VI. ОСНОВНЫЕ СВЕДЕНИЯ ПО АСТРОНОМИИ
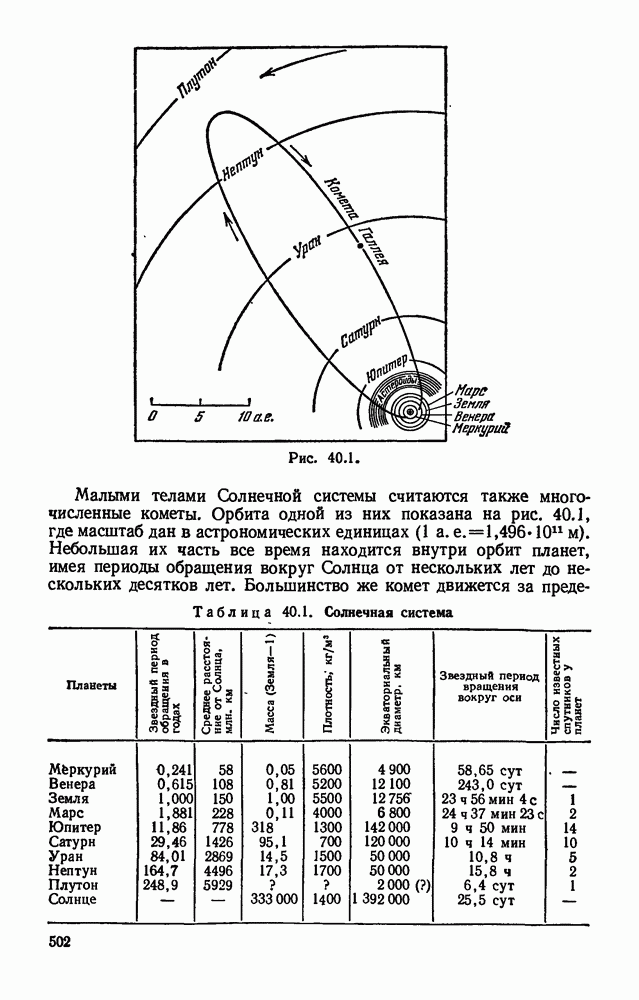
- Глава 40. СТРОЕНИЕ И РАЗВИТИЕ ВСЕЛЕННОЙ
- § 40.2. Происхождение и развитие небесных тел.
- § 40.3. Понятие о космологии.