| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 24.12. Упругие колебания. Превращение энергии при колебательном движении.
Колебания, при которых возвращающая  создается силами упругости, называются упругими.
создается силами упругости, называются упругими.
Примером упругих колебаний может служить колебание пружины с грузом  рис. 24.8. Поскольку сила упругости пропорциональна абсолютной деформации (§§ 11.7 и 11.8), то сила упругости пружины выражается формулой (24.7):
рис. 24.8. Поскольку сила упругости пропорциональна абсолютной деформации (§§ 11.7 и 11.8), то сила упругости пружины выражается формулой (24.7):  , где х — смещение груза, закрепленного на пружине, и ее абсолютная деформация,
, где х — смещение груза, закрепленного на пружине, и ее абсолютная деформация,  жесткость пружины. Следовательно, собственные упругие колебания системы являются гармоническими (см. § 24.6). Можно показать (§ 24.6), что круговая частота упругих колебаний равна
жесткость пружины. Следовательно, собственные упругие колебания системы являются гармоническими (см. § 24.6). Можно показать (§ 24.6), что круговая частота упругих колебаний равна

Учитывая (24.4), для периода упругих колебаний получаем

При колебаниях груза на пружине в любом положении груза его полная механическая энергия  равна сумме потенциальной энергии П (§ 11.8) и кинетической энергии
равна сумме потенциальной энергии П (§ 11.8) и кинетической энергии 

где х — смещение и  — скорость в точке, в которой определяют энергию тела,
— скорость в точке, в которой определяют энергию тела,  — масса груза.
— масса груза.
При колебаниях груза наглядно виден переход кинетической энергии груза в потенциальную и обратно. При собственных колебаниях силы сопротивления отсутствуют, поэтому полная механическая энергия колеблющегося тела  остается постоянной (§ 6.8). В положении равновесия тело обладает только кинетической энергией, поэтому полную энергию можно выразить формулой
остается постоянной (§ 6.8). В положении равновесия тело обладает только кинетической энергией, поэтому полную энергию можно выразить формулой

Так как в крайнем положении колеблющееся на пружине тело обладает только потенциальной энергией, то его полную избыточную энергию при колебаниях можно выразить и формулой

где А — амплитуда колебаний. Подставив сюда значение  найденное из (24.16), получим
найденное из (24.16), получим

т. е. полная энергия колеблющегося тела прямо пропорциональна его массе, квадрату частоты колебаний и квадрату их амплитуды.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ВВЕДЕНИЕ
- § 1.2. Физика и техника.
- § 1.3. Понятие о величине и измерении. Физические величины.
- § 1.4. Прямое и косвенное измерения.
- § 1.5. Звездное небо и его видимое вращение.
- § 1.6. Угловые измерения на небе.
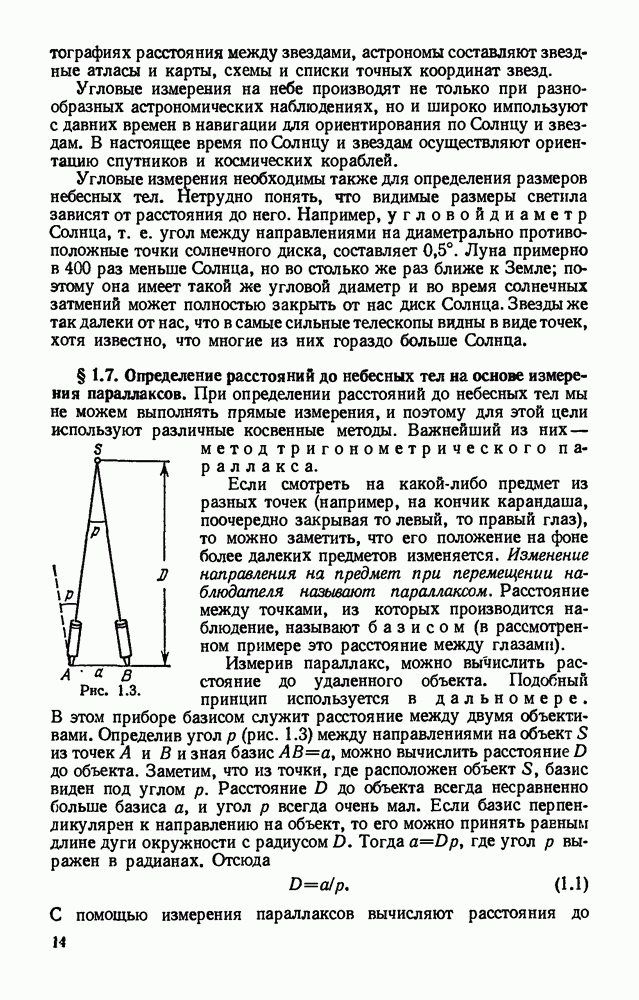
- § 1.7. Определение расстояний до небесных тел на основе измерения параллаксов.
- § 1.8. Основные единицы времени и их связь с движением Земли.
- § 1.9. Правило вывода единиц физических величин из формул. Международная система единиц СИ.
- § 1.10. Плотность вещества.
- Раздел I. МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕПЛОТА
- Глава 2. ОСНОВЫ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ СТРОЕНИЯ ВЕЩЕСТВА
- § 2.2. Диффузия.
- § 2.3. Силы молекулярного взаимодействия.
- § 2.4. Кинетическая и потенциальная энергия молекул.
- § 2.5. Агрегатное состояние вещества.
- § 2.6. Понятие о температуре и внутренней энергии тела.
- Глава 3. МОЛЕКУЛЯРНО-КИНЕТИЧЕСКАЯ ТЕОРИЯ ГАЗООБРАЗНОГО СОСТОЯНИЯ ВЕЩЕСТВА
- § 3.2. Броуновское движение.
- § 3.3. Измерение скорости движения молекул газа. Опыт Штерна.
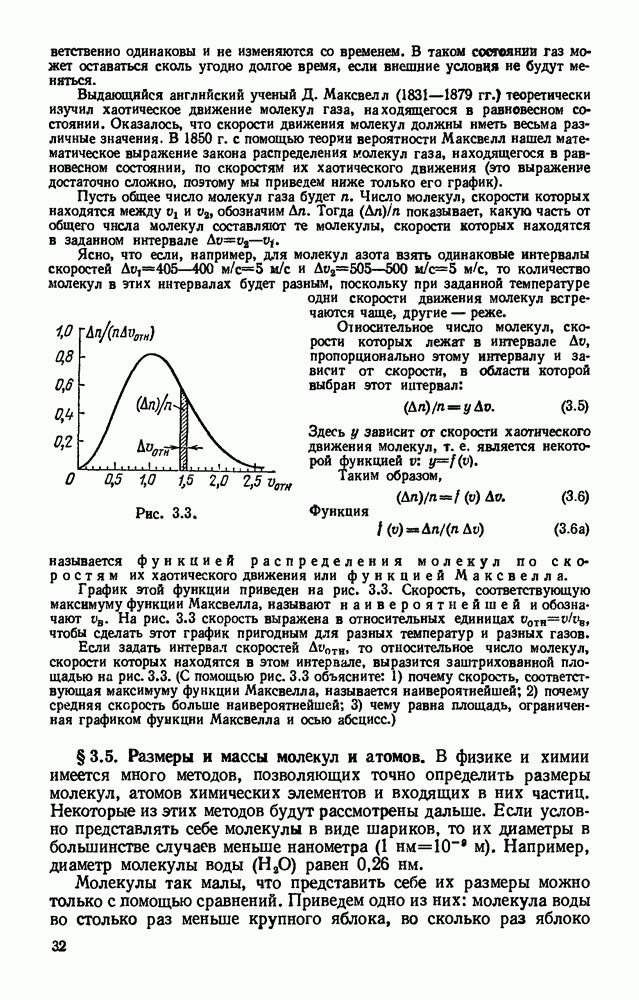
- § 3.4. Распределение молекул по скоростям их хаотического движения.
- § 3.5. Размеры и массы молекул и атомов.
- § 3.6. Постоянная Авогадро и постоянная Лошмидта.
- § 3.7. Число столкновений и длина свободного пробега молекул в газе.
- § 3.8. Давление газа. Манометры.
- § 3.9. Понятие вакуума.
- § 3.10. Межзвездный газ.
- Глава 4. ИДЕАЛЬНЫЙ ГАЗ. АБСОЛЮТНАЯ ТЕМПЕРАТУРА И ЕЕ СВЯЗЬ С ЭНЕРГИЕЙ МОЛЕКУЛ ГАЗА
- § 4.2. Основное уравнение молекулярно-кинетической теории газов.
- § 4.3. Зависимость давления газа от температуры при постоянном объеме.
- § 4.4. Абсолютный нуль.
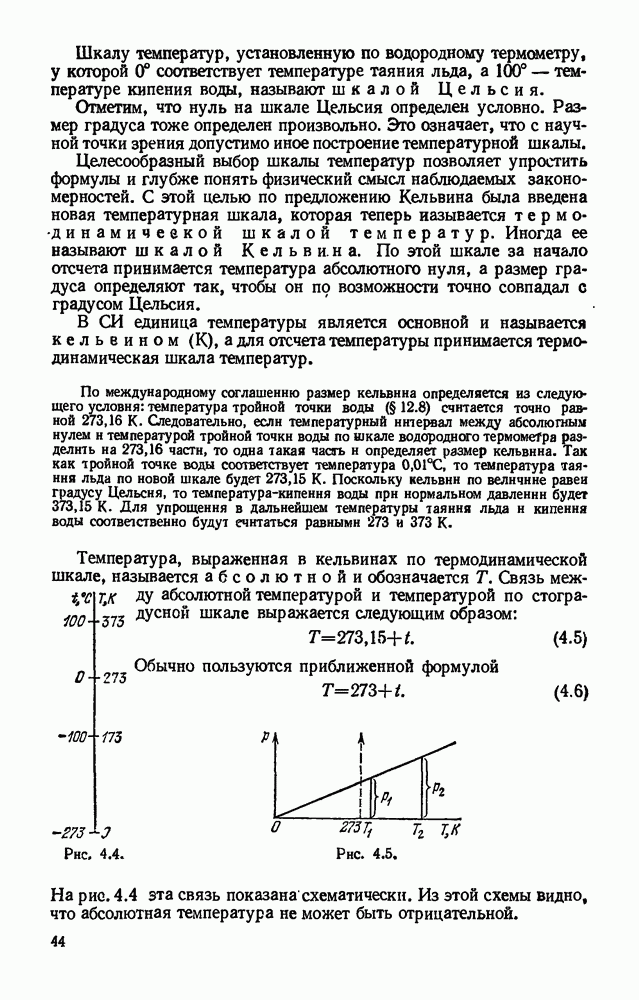
- § 4.5. Термодинамическая шкала температур. Абсолютная температура.
- § 4.6. Связь между температурой и кинетической энергией молекул газа. Постоянная Больцмана.
- Глава 5. УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА
- § 5.2. Объединенный газовый закон. Приведение объема газа к нормальным условиям.
- § 5.3. Молярная газовая постоянная. Определение числового значения постоянной Больцмана.
- § 5.4. Уравнение Клапейрона — Менделеева. Плотность газа.
- § 5.5. Зависимость средней квадратичной скорости молекул газа от температуры.
- § 5.6. Изохорический процесс.
- § 5.7. Изобарический процесс.
- § 5.8. Изотермический процесс.
- § 5.9. Внутренняя энергия идеального газа.
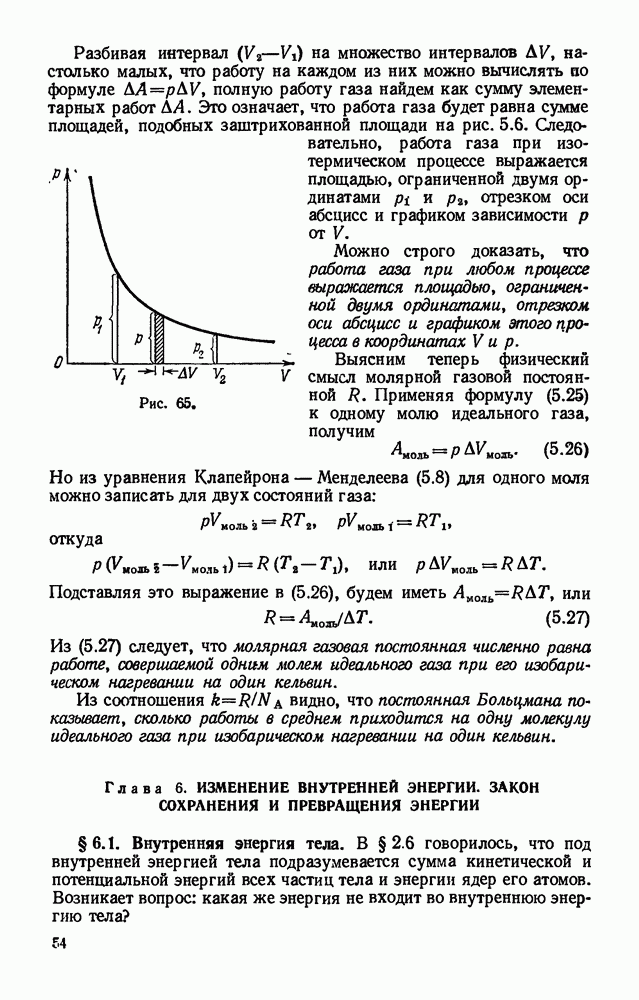
- § 5.10. Работа газа при изменении его объема. Физический смысл молярной газовой постоянной.
- Глава 6. ИЗМЕНЕНИЕ ВНУТРЕННЕЙ ЭНЕРГИИ. ЗАКОН СОХРАНЕНИЯ И ПРЕВРАЩЕНИЯ ЭНЕРГИИ
- § 6.2. Теплообмен.
- § 6.3. Виды теплообмена.
- § 6.4. Изменение внутренней энергии при нагревании и охлаждении.
- § 6.5. Уравнение теплового баланса при теплообмене.
- § 6.6. Подсчет теплоты, выделяемой при сжигании топлива. К. п. д. нагревателя.
- § 6.7. Изменение внутренней энергии при выполнении механической работы. Опыт Джоуля.
- § 6.8. Закон сохранения и превращения энергии в механике.
- § 6.9. Закон сохранения и превращения энергии в механических и тепловых процессах.
- § 6.10. Первое начало термодинамики.
- § 6.11. Применение первого начала термодинамики к изопроцессам в идеальном газе.
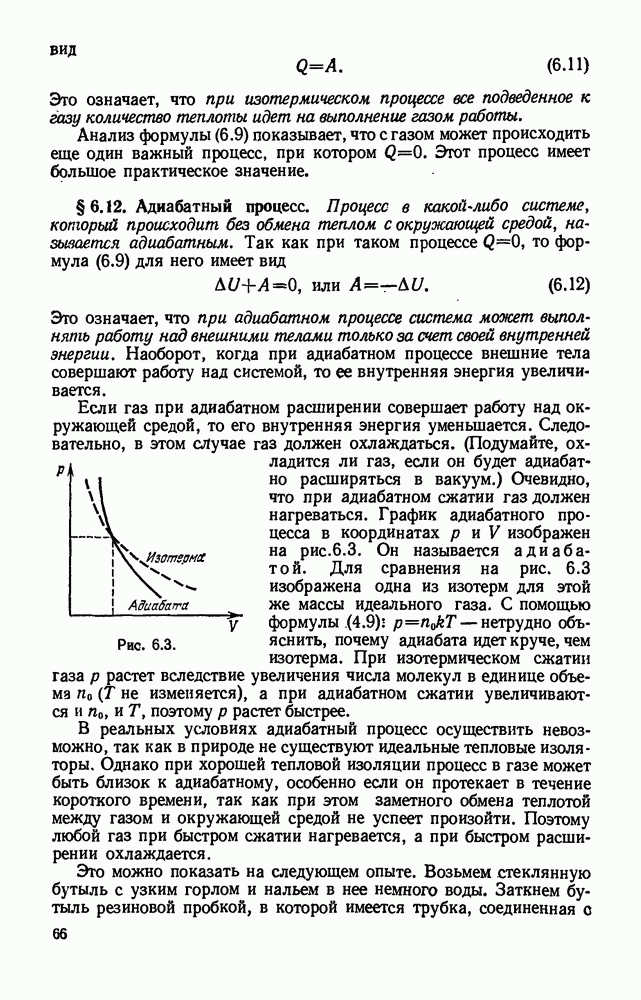
- § 6.12. Адиабатный процесс.
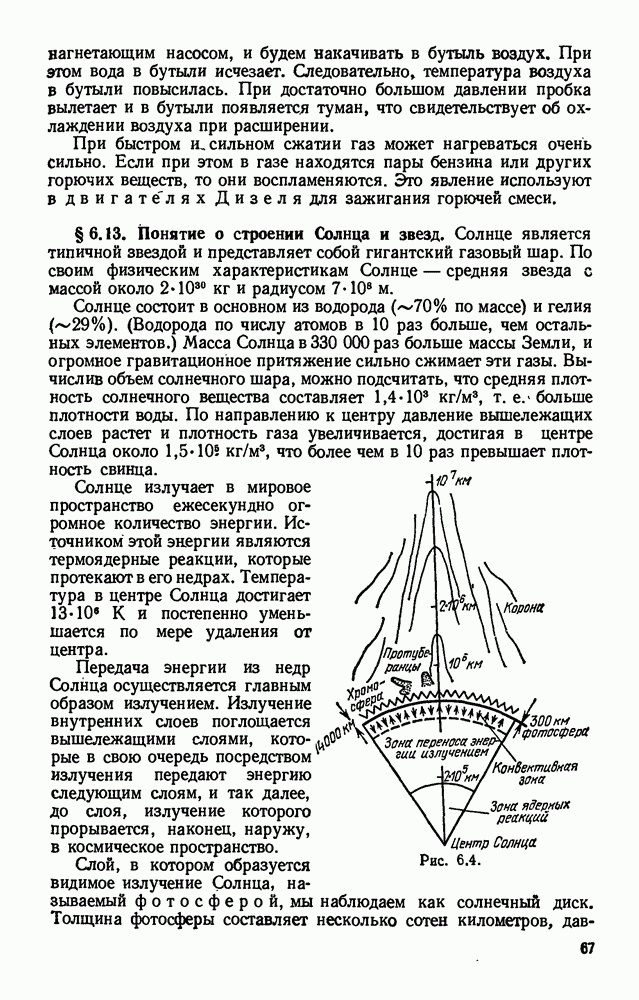
- § 6.13. Понятие о строении Солнца и звезд.
- Глава 7. ПЕРЕХОД ВЕЩЕСТВА ИЗ ЖИДКОГО СОСТОЯНИЯ В ГАЗООБРАЗНОЕ И ОБРАТНО
- § 7.2. Испарение.
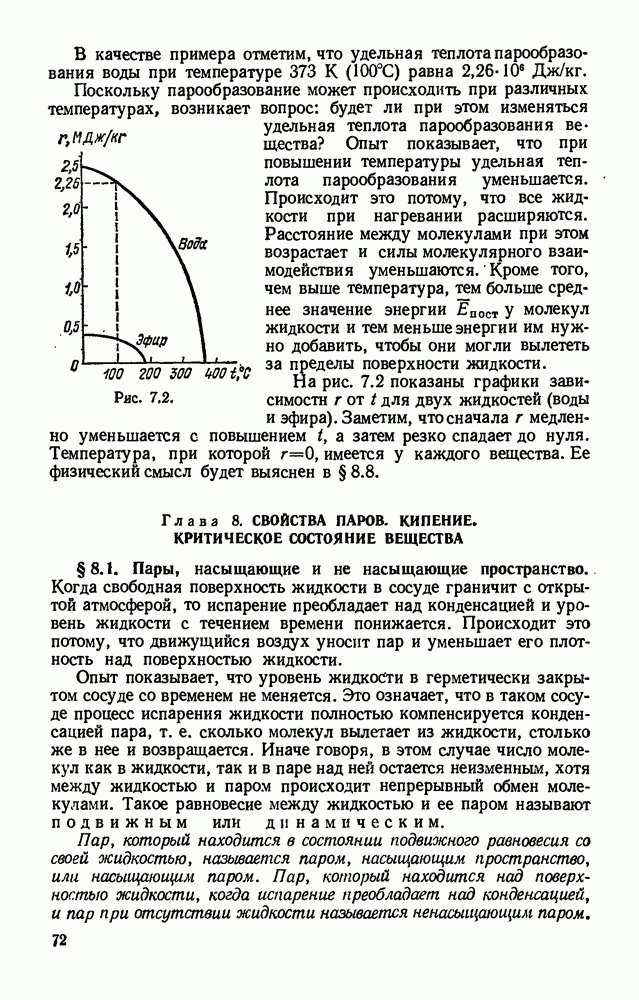
- § 7.3. Теплота парообразования.
- Глава 8. СВОЙСТВА ПАРОВ. КИПЕНИЕ. КРИТИЧЕСКОЕ СОСТОЯНИЕ ВЕЩЕСТВА
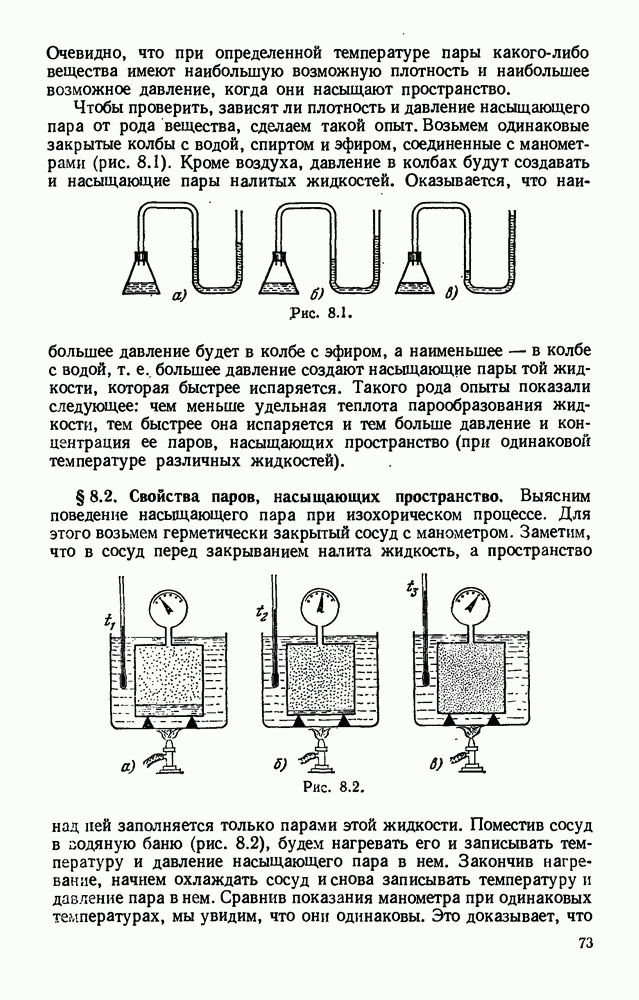
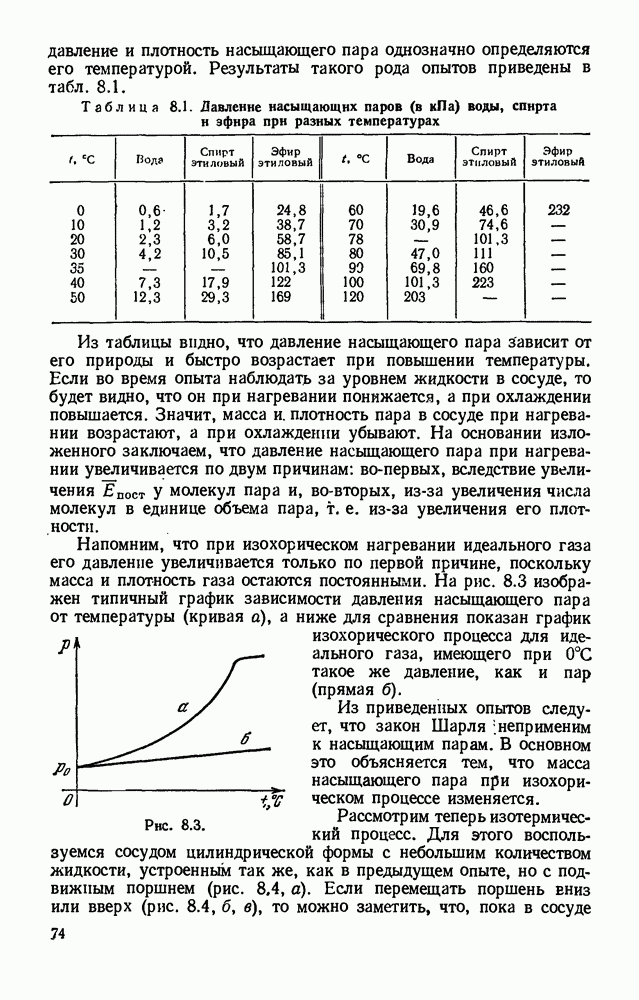
- § 8.2. Свойства паров, насыщающих пространство.
- § 8.3. Свойства паров, не насыщающих пространство.
- § 8.4. Процесс кипения жидкости.
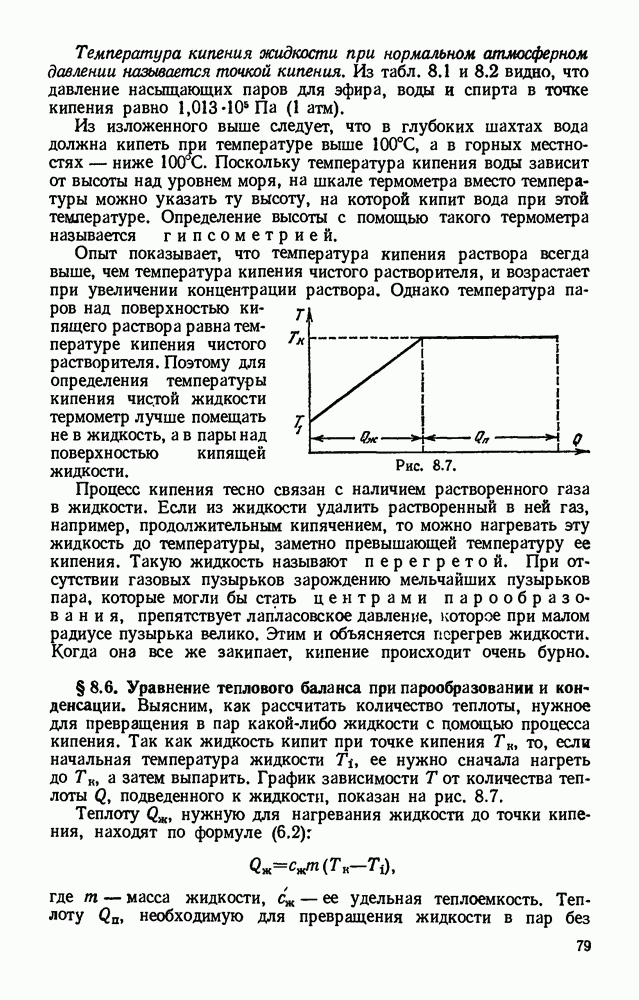
- § 8.5. Зависимость температуры кипения жидкости от внешнего давления. Точка кипения.
- § 8.6. Уравнение теплового баланса при парообразовании и конденсации.
- § 8.7. Перегретый пар и его использование в технике.
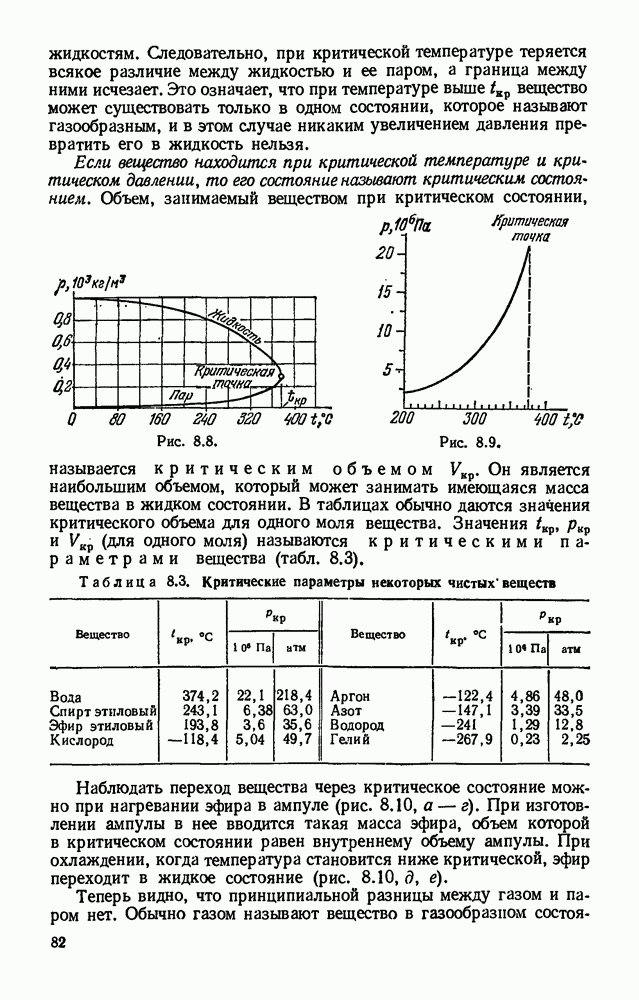
- § 8.8. Критическое состояние вещества.
- § 8.9. Сжижение газов и использование жидких газов в технике.
- Глава 9. ВОДЯНОЙ ПАР В АТМОСФЕРЕ
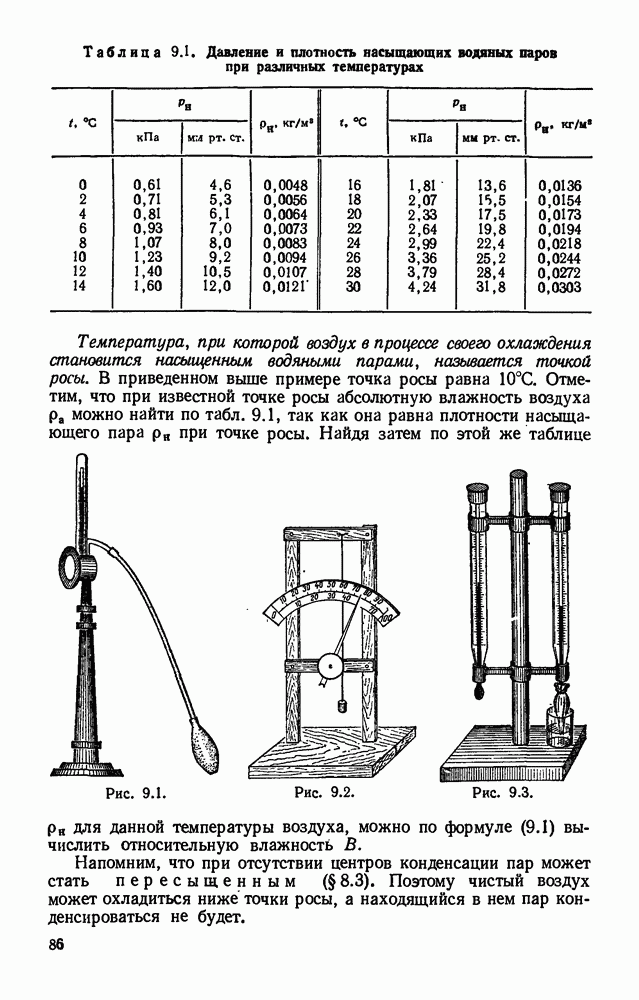
- § 9.2. Абсолютная и относительная влажность воздуха. Точка росы.
- § 9.3. Приборы для определения влажности воздуха.
- § 9.4. Понятие об атмосферах планет.
- Глава 10. СВОЙСТВА ЖИДКОСТЕЙ
- § 10.2. Поверхностный слой жидкости.
- § 10.3. Энергия поверхностного слоя жидкости. Поверхностное натяжение.
- § 10.4. Сила поверхностного натяжения.
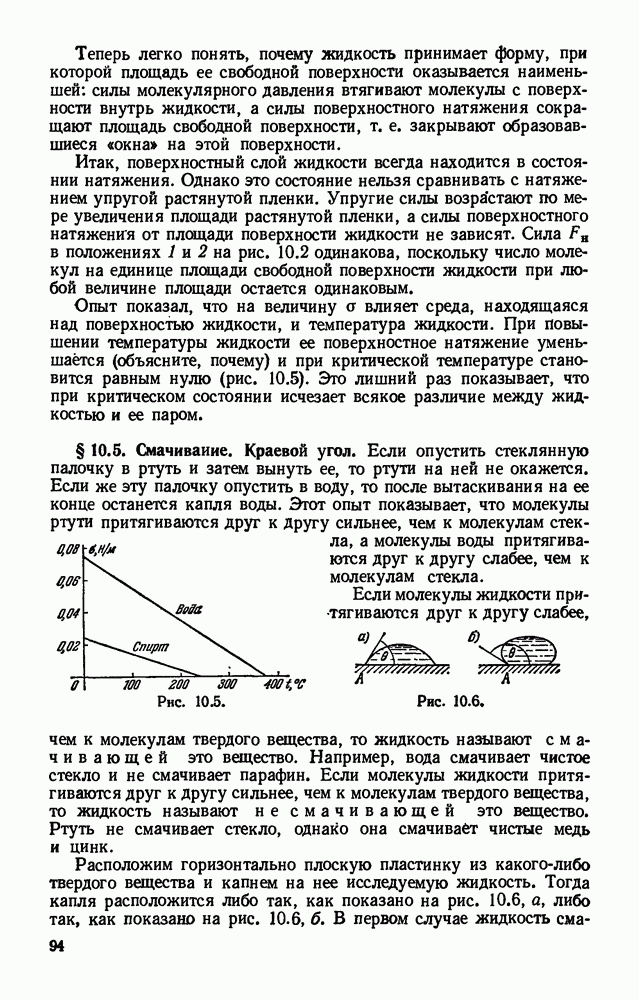
- § 10.5. Смачивание. Краевой угол.
- § 10.6. Мениск. Давление, создаваемое искривленной поверхностью жидкости.
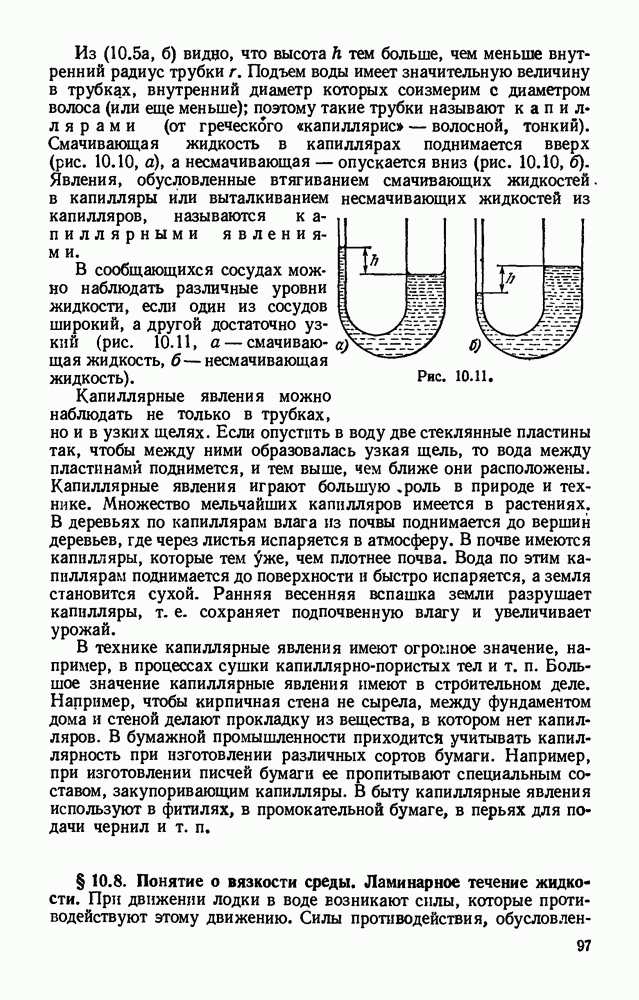
- § 10.7. Капиллярность. Капиллярные явления в природе и технике.
- § 10.8. Понятие о вязкости среды. Ламинарное течение жидкости.
- § 10.9. Закон Ньютона для внутреннего трения. Динамическая вязкость.
- § 10.10. Аморфные вещества.
- Глава 11. СВОЙСТВА ТВЕРДЫХ ТЕЛ. ДЕФОРМАЦИИ
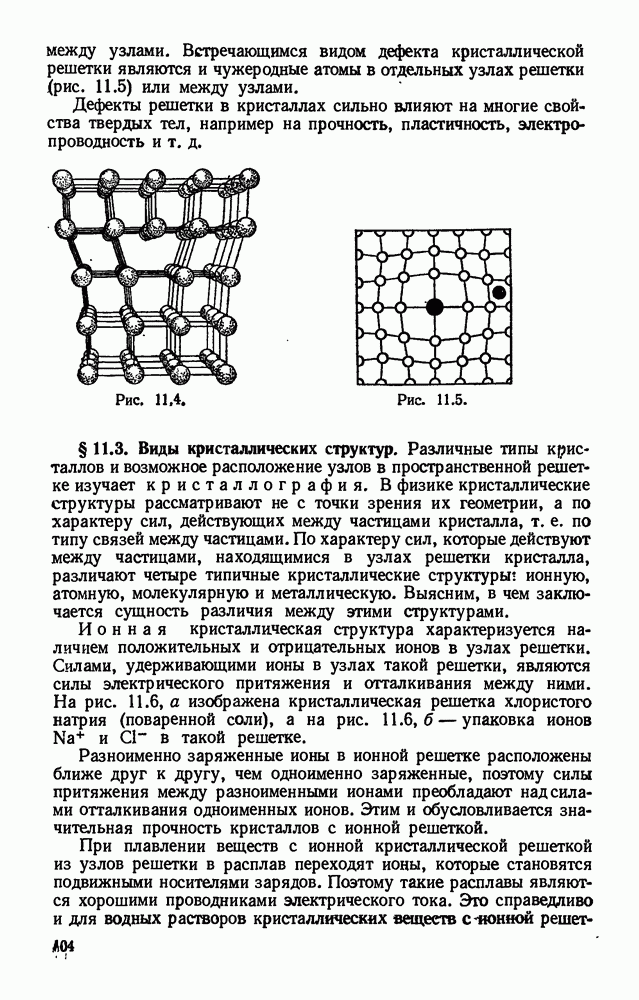
- § 11.2. Анизотропия кристаллов. Пространственная решетка и ее дефекты.
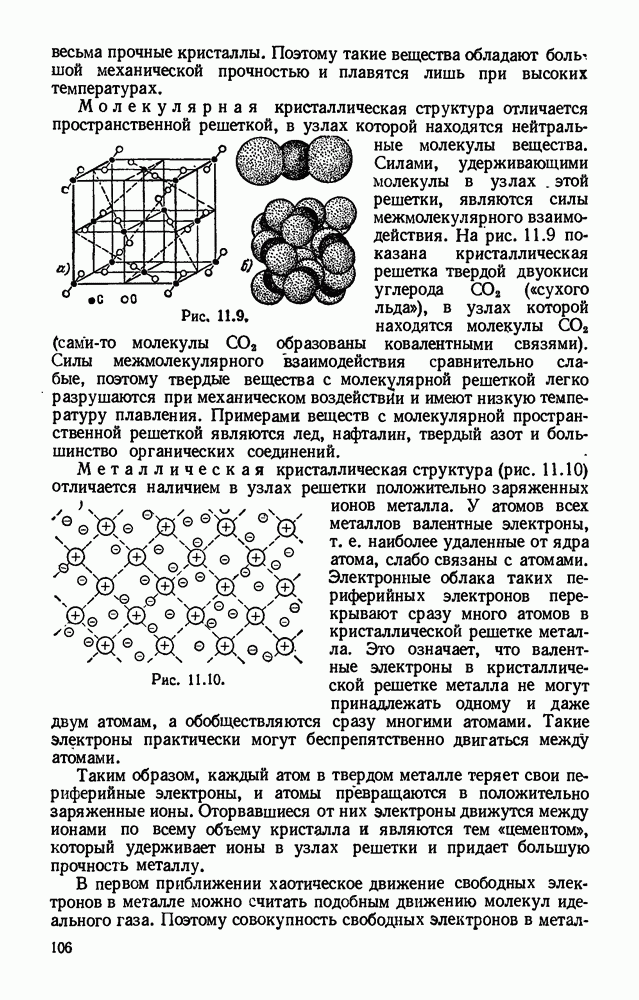
- § 11.3. Виды кристаллических структур.
- § 11.4. Виды деформаций.
- § 11.5. Механическое напряжение.
- § 11.6. Упругость, пластичность, хрупкость и твердость.
- § 11.7. Закон Гука. Модуль упругости.
- § 11.8. Энергия упруго деформированного тела.
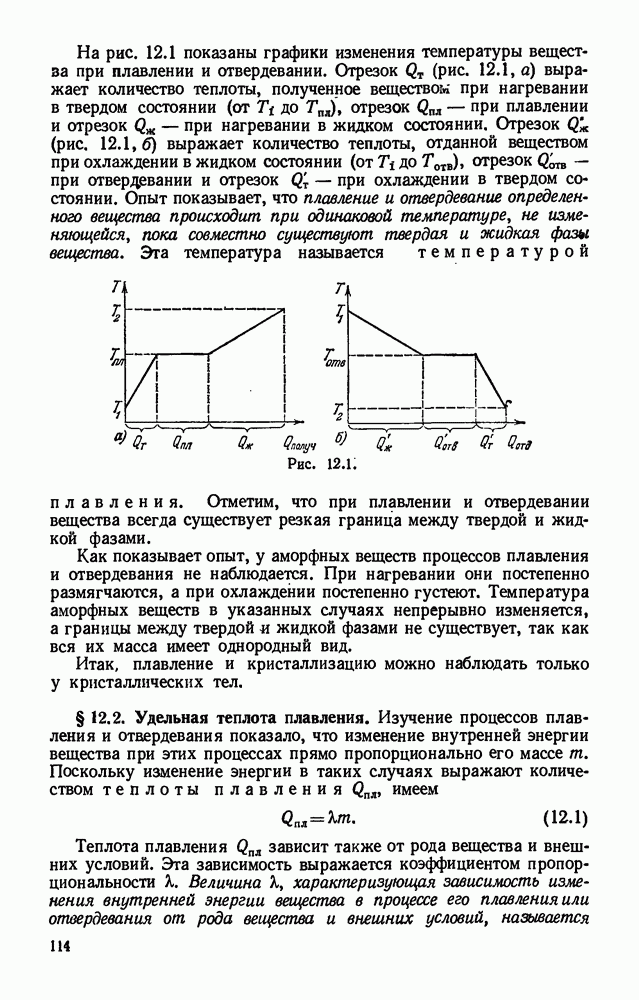
- Глава 12. ПЛАВЛЕНИЕ И КРИСТАЛЛИЗАЦИЯ. СУБЛИМАЦИЯ. ДИАГРАММА СОСТОЯНИЙ ВЕЩЕСТВА
- § 12.2. Удельная теплота плавления.
- § 12.3. Изменение объема и плотности вещества при плавлении и отвердевании.
- § 12.4. Зависимость температуры и теплоты плавления от давления. Точка плавления.
- § 12.5. Уравнение теплового баланса при плавлении и кристаллизации.
- § 12.6. Растворы и сплавы. Охлаждающие смеси.
- § 12.7. Испарение твердых тел (сублимация).
- § 12.8. Диаграмма состоянии вещества. Тройная точка.
- Глава 13. ТЕПЛОВОЕ РАСШИРЕНИЕ ТЕЛ
- § 13.2. Линейное расширение твердых тел при нагревании.
- § 13.3. Объемное расширение тел при нагревании. Зависимость плотности вещества от температуры.
- § 13.4. Особенности теплового расширения твердых тел.
- § 13.5. Некоторые особенности теплового расширения жидкостей.
- § 13.6. Значение теплового расширения тел в природе и технике.
- Раздел II. ОСНОВЫ ЭЛЕКТРОДИНАМИКИ
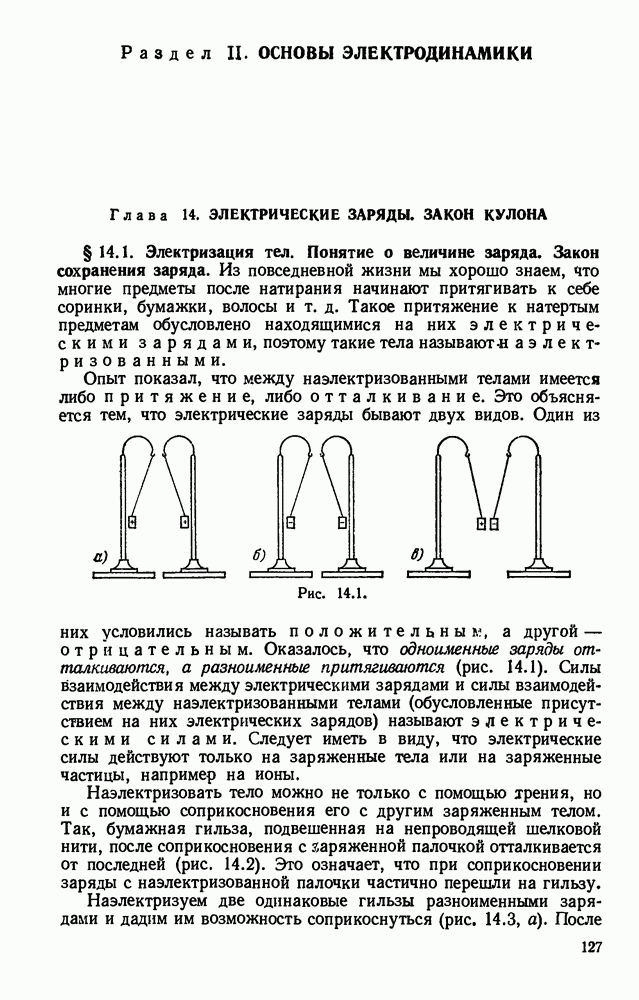
- Глава 14. ЭЛЕКТРИЧЕСКИЕ ЗАРЯДЫ. ЗАКОН КУЛОНА
- § 14.2. Явления, подтверждающие сложное строение атома.
- § 14.3. Опыты Резерфорда. Ядерная модель строения атома.
- § 14.4. Понятие о строении атомов различных химических элементов.
- § 14.5. Электризация при соприкосновении незаряженных тел.
- § 14.6. Сила взаимодействия электрических зарядов. Закон Кулона.
- § 14.7. Диэлектрическая проницаемость среды.
- § 14.8. Международная система единиц СИ в электричестве. Электрическая постоянная.
- § 14.9. Электроскоп.
- Глава 15. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
- § 15.2. Напряженность электрического поля.
- § 15.3. Линии напряженности электрического поля.
- § 15.4. Однородное поле. Поверхностная плотность заряда.
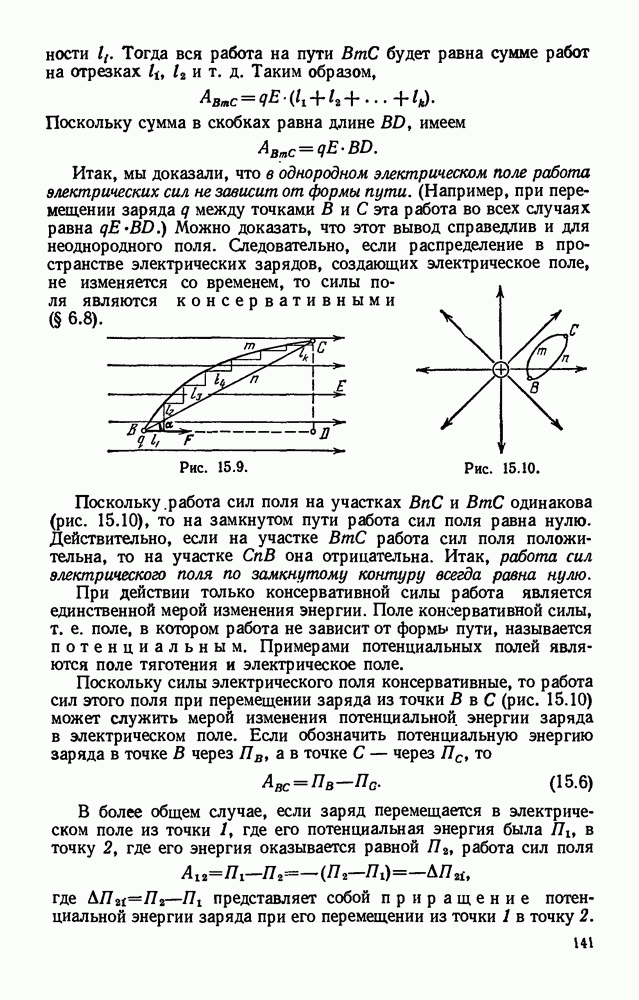
- § 15.5. Работа электрического поля при перемещении заряда. Потенциальная энергия заряда.
- § 15.6. Потенциал. Разность потенциалов и напряжение. Эквипотенциальные поверхности.
- § 15.7. Связь между напряженностью поля и напряжением. Градиент потенциала.
- § 15.8. Проводник в электрическом поле.
- § 15.9. Электрометр.
- § 15.10. Диэлектрик в электрическом поле. Поляризация диэлектрика.
- § 15.11. Понятие о сегнетоэлектриках.
- § 15.12. Пьезоэлектрический эффект.
- § 15.13. Электроемкость проводника.
- § 15.14. Условия, от которых зависит электроемкость проводника.
- § 15.15. Конденсаторы.
- § 15.16. Соединение конденсаторов в батарею.
- § 15.17. Энергия заряженного конденсатора. Плотность энергии электрического поля.
- § 15.18. Опыт Милликена.
- Глава 16. ЭЛЕКТРИЧЕСКИЙ ТОК В МЕТАЛЛАХ. ЗАКОНЫ ПОСТОЯННОГО ТОКА
- § 16.2. Сила тока и плотность тока в проводнике.
- § 16.3. Замкнутая электрическая цепь.
- § 16.4. Электродвижущая сила источника электрической энергии.
- § 16.5. Внешняя и внутренняя части цепи.
- § 16.6. Закон Ома для участка цепи без э. д. с. Сопротивление проводника. Падение напряжения.
- § 16.7. Зависимость сопротивления от материала, длины и площади поперечного сечения проводника.
- § 16.8. Зависимость сопротивления от температуры.
- § 16.9. Сверхпроводимость.
- § 16.10. Эквивалентное сопротивление.
- § 16.11. Последовательное соединение потребителей энергии тока.
- § 16.12. Параллельное соединение потребителей энергии тока
- § 16.13. Закон Ома для всей цепи.
- § 16.14. Соединение одинаковых источников электрической энергии в батарею.
- § 16.15. Закон Ома для участка цепи с э. д. с. и для всей цепи при нескольких э. д. с.
- Глава 17. РАБОТА, МОЩНОСТЬ И ТЕПЛОВОЕ ДЕЙСТВИЕ ЭЛЕКТРИЧЕСКОГО ТОКА
- § 17.2. Мощность электрического тока.
- § 17.3. Тепловое действие электрического тока. Закон Джоуля — Ленца.
- § 17.4. Короткое замыкание. Практическое применение теплового действия тока.
- Глава 18. ТЕРМОЭЛЕКТРИЧЕСКИЕ ЯВЛЕНИЯ
- § 18.2. Контактная разность потенциалов.
- § 18.3. Термоэлектродвижущая сила.
- § 18.4. Явление Пельтье.
- § 18.5. Применение термоэлектрических явлений в науке и технике.
- Глава 19. ЭЛЕКТРИЧЕСКИЙ ТОК В ЭЛЕКТРОЛИТАХ
- § 19.2. Электролиз.
- § 19.3. Электролиз, сопровождающийся растворением анода.
- § 19.4. Количество вещества, выделяющегося при электролизе. Первый закон Фарадея.
- § 19.5. Второй закон Фарадея. Определение заряда иона.
- § 19.6. Использование электролиза в технике.
- § 19.7. Гальванические элементы.
- § 19.8. Аккумуляторы.
- § 19.9. Применение гальванических элементов и аккумуляторов в технике. Явление электрокоррозии.
- Глава 20. ЭЛЕКТРИЧЕСКИЙ ТОК В ГАЗАХ И В ВАКУУМЕ
- § 20.2. Зависимость силы тока в газе от напряжения.
- § 20.3. Электрический разряд в газе при атмосферном давлении.
- § 20.4. Электрический разряд в разреженных газах. Газосветные трубки и лампы дневного света.
- § 20.5. Излучение и поглощение энергии атомом.
- § 20.6. Катодные лучи.
- § 20.7. Понятие о плазме.
- § 20.8. Электрический ток в вакууме.
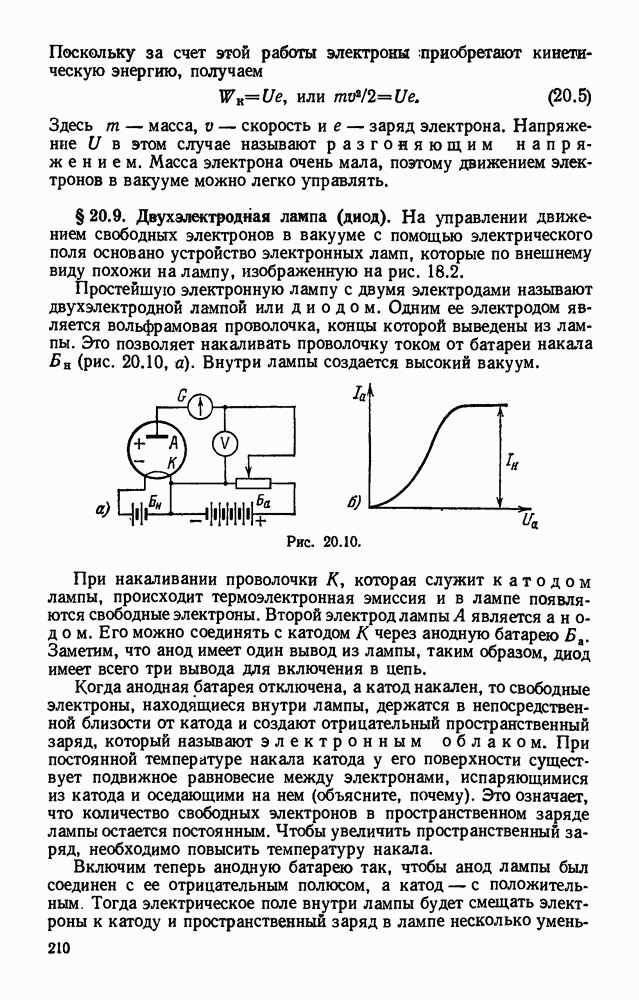
- § 20.9. Двухэлектродная лампа (диод).
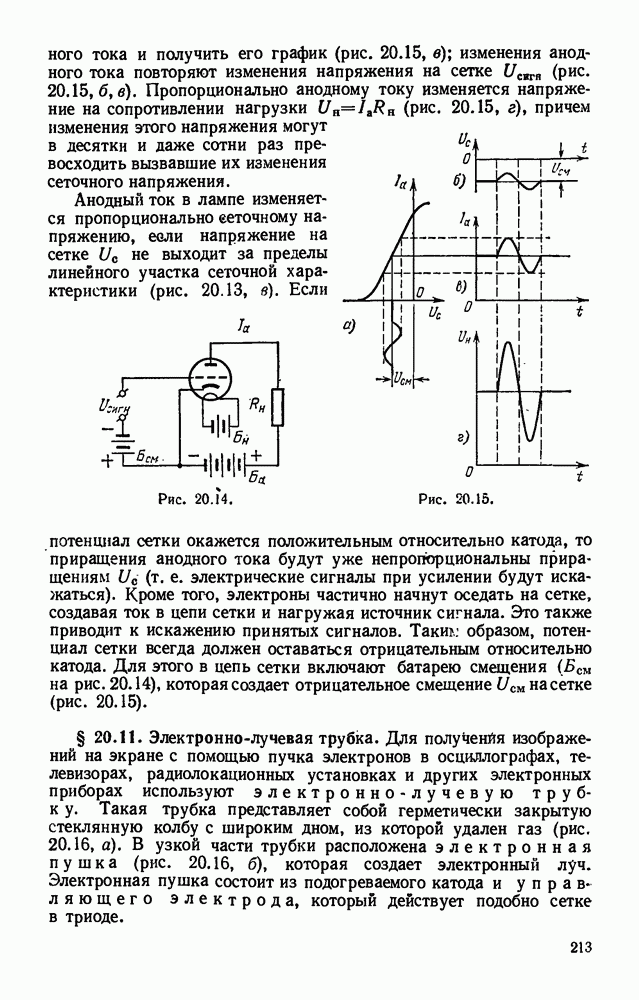
- § 20.10. Трехэлектродная лампа (триод).
- § 20.11. Электронно-лучевая трубка.
- Глава 21. ЭЛЕКТРИЧЕСКИЙ ТОК В ПОЛУПРОВОДНИКАХ
- § 21.2. Чистые (беспримесные) полупроводники. Термисторы.
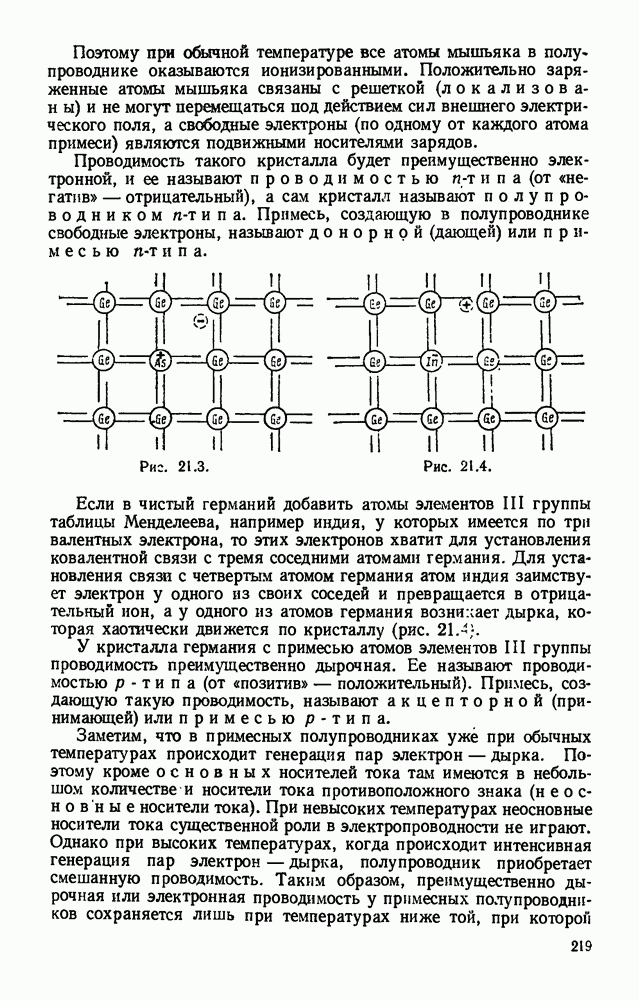
- § 21.3. Примесные полупроводники.
- § 21.4. Электронно-дырочный переход.
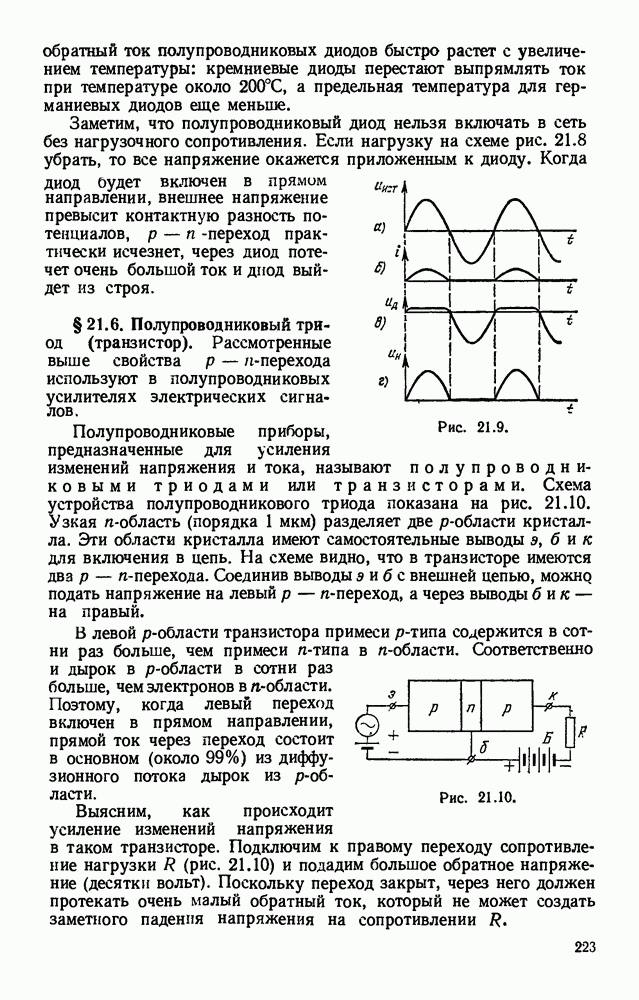
- § 21.5. Полупроводниковый диод.
- § 21.6. Полупроводниковый триод (транзистор).
- Глава 22. ЭЛЕКТРОМАГНЕТИЗМ
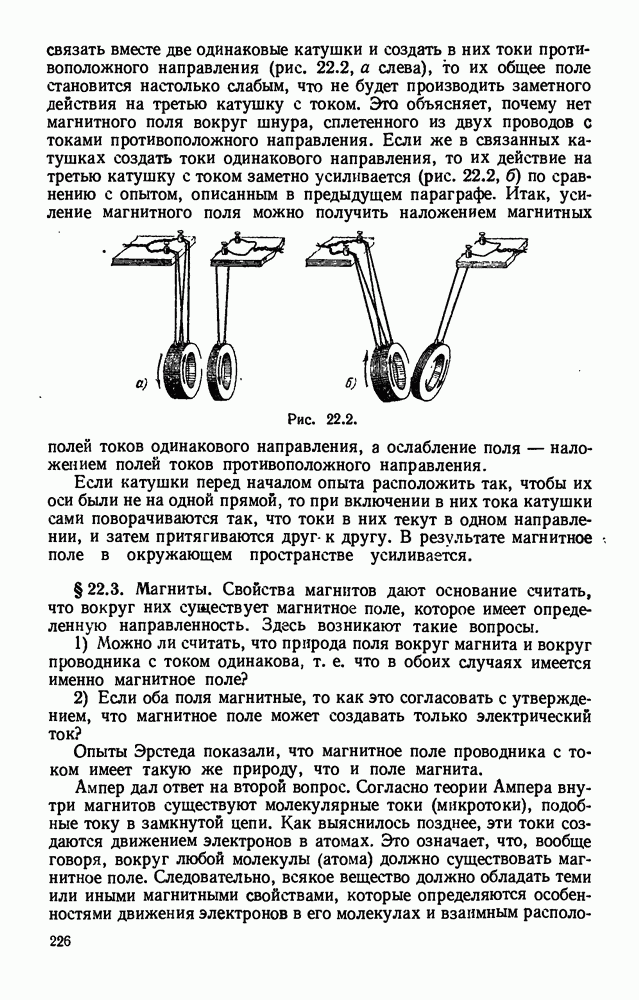
- § 22.2. Магнитное поле как особый вид материи.
- § 22.3. Магниты.
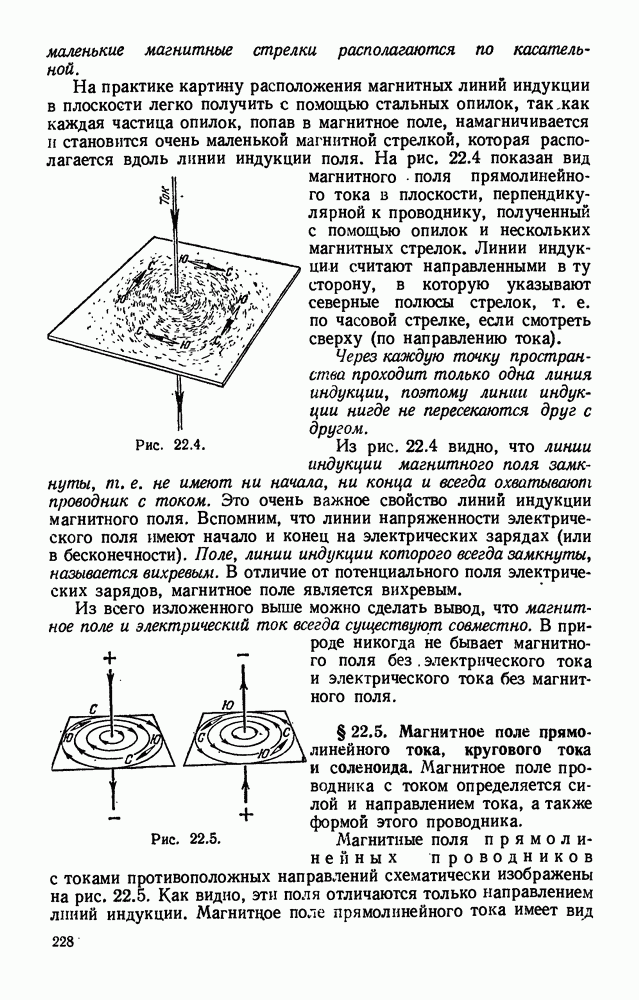
- § 22.4. Линии магнитной индукции. Понятие о вихревом поле.
- § 22.5. Магнитное поле прямолинейного тока, кругового тока и соленоида.
- § 22.6. Сравнение магнитных свойств соленоида и постоянного магнита.
- § 22.7. Сила взаимодействия параллельных токов. Магнитная проницаемость среды.
- § 22.8. Определение ампера. Магнитная постоянная.
- § 22.9. Действие магнитного поля на прямолинейный проводник с током.
- § 22.10. Однородное магнитное поле.
- § 22.11. Магнитный момент контура с током.
- § 22.12. Работа при перемещении проводника с током в магнитном поле. Магнитный поток.
- § 22.13. Индукция магнитного поля, создаваемая в веществе проводниками с током различной формы.
- § 22.14. Напряженность магнитного поля и ее связь с индукцией и магнитной проницаемостью среды.
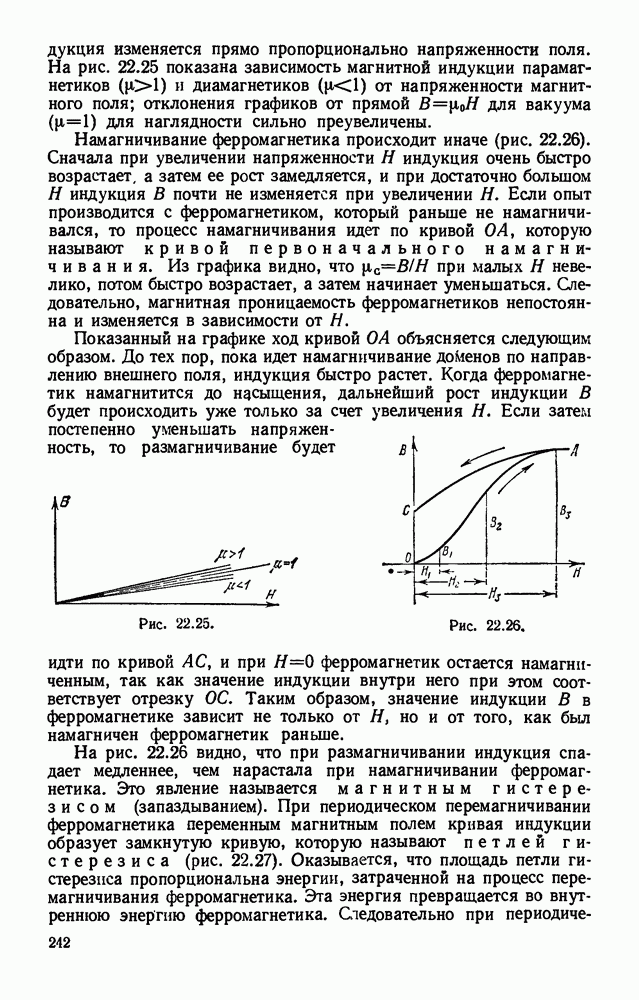
- § 22.15. Парамагнитные, диамагнитные и ферромагнитные вещества.
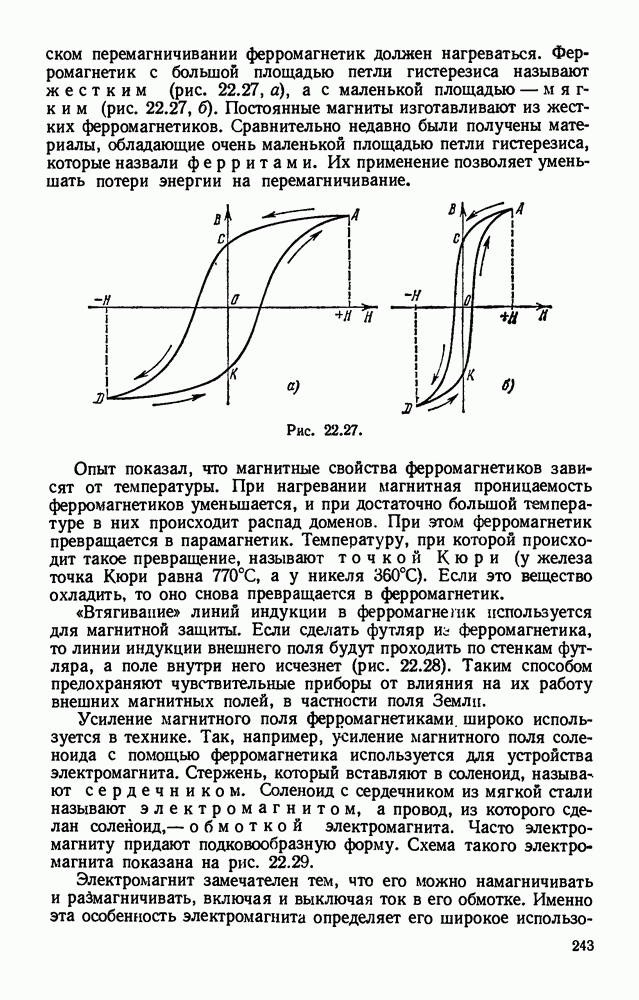
- § 22.16. Намагничивание ферромагнетиков. Электромагнит.
- § 22.17. Работа и устройство амперметра и вольтметра.
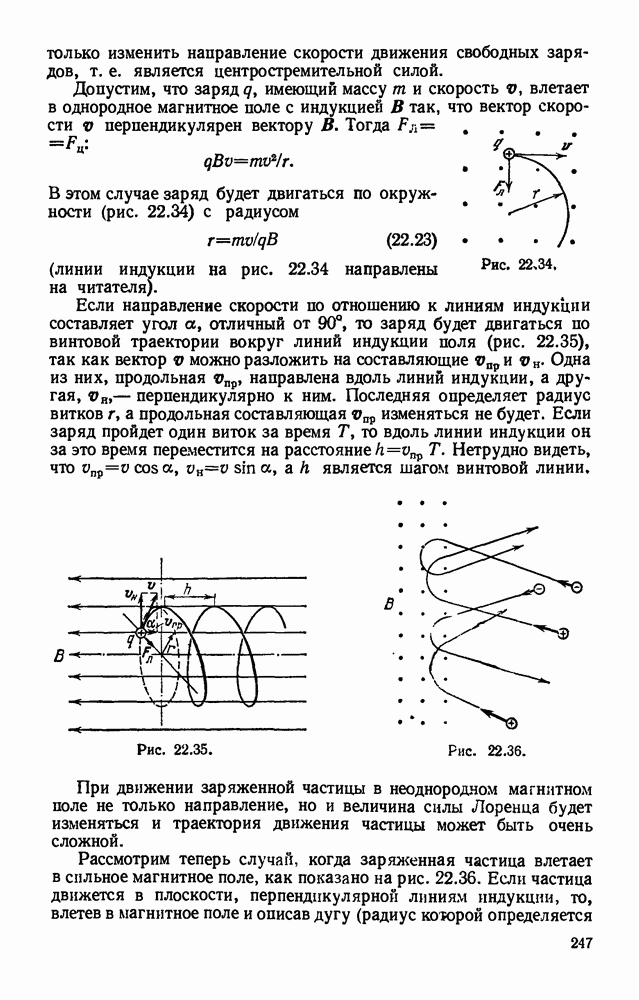
- § 22.18. Сила Лоренца. Движение заряда в магнитном поле.
- § 22.19. Постоянное и переменное магнитные поля.
- Глава 23. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ
- § 23.2. Явление электромагнитной индукции.
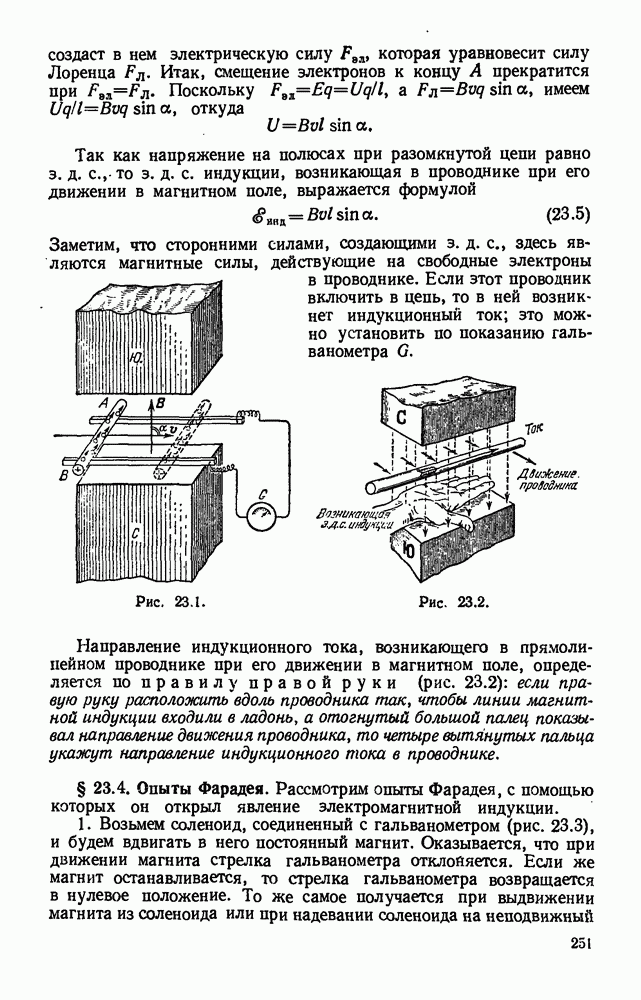
- § 23.3. Э. д. с. индукции, возникающая в прямолинейном проводнике при его движении в магнитном поле. Правило правой руки.
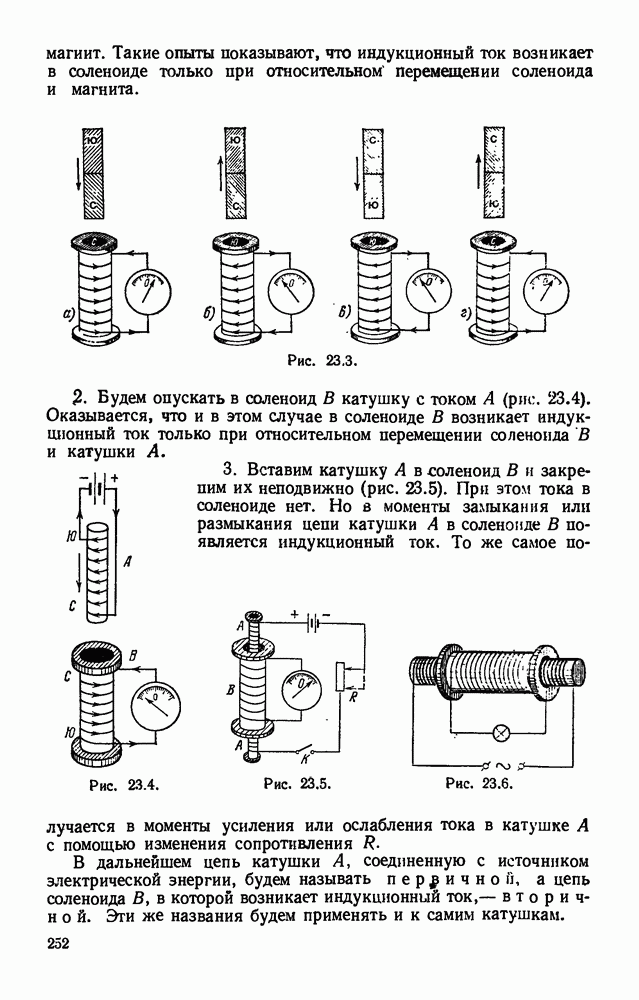
- § 23.4. Опыты Фарадея.
- § 23.5. Закон Ленца для электромагнитной индукции. Объяснение диамагнитных явлений.
- § 23.6. Величина э. д. с. индукции.
- § 23.7. Вихревое электрическое поле и его связь с магнитным полем.
- § 23.8. Вихревые токи.
- § 23.9. Роль магнитных полей в явлениях, происходящих на Солнце и в космосе.
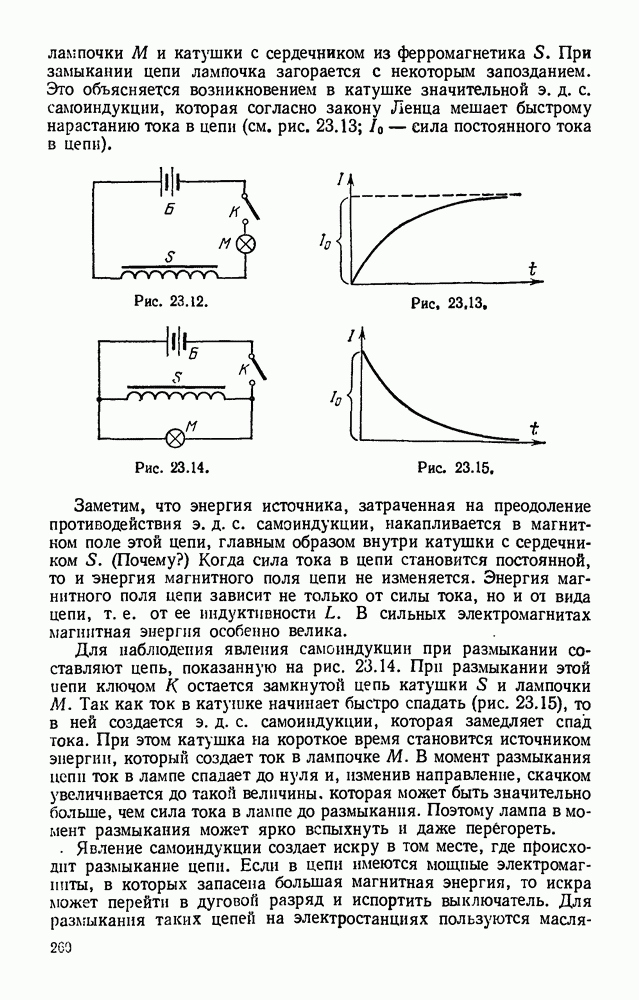
- § 23.10. Явление самоиндукции. Э. д. с. самоиндукции.
- § 23.11. Энергия магнитного поля.
- Раздел III. КОЛЕБАНИЯ И ВОЛНЫ
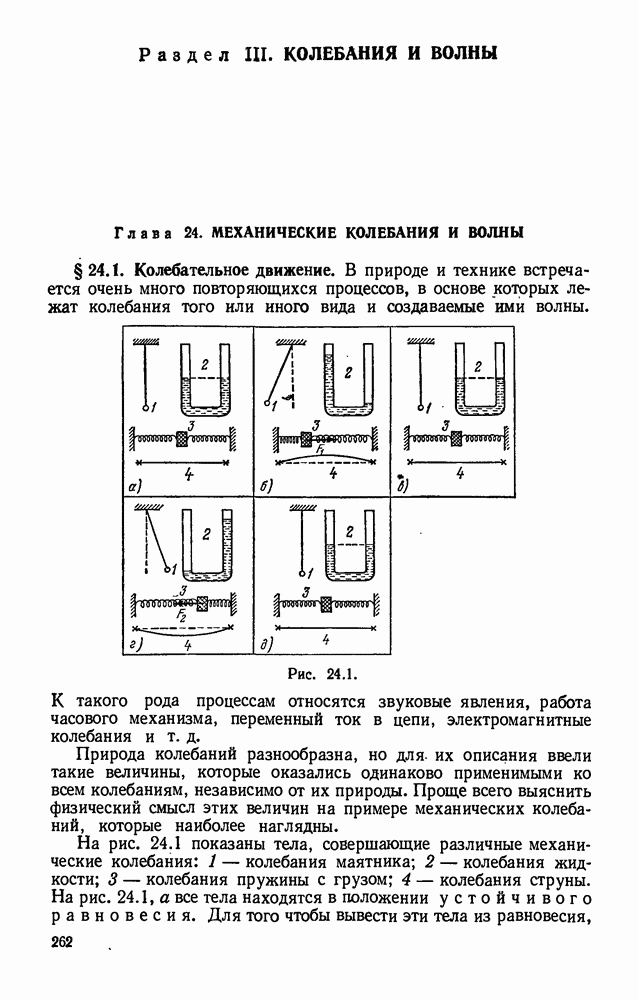
- Глава 24. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ
- § 24.2. Условия возникновения колебаний.
- § 24.3. Классификация колебательных движений тела в зависимости от действующей на него силы.
- § 24.4. Параметры колебательного движения.
- § 24.5. Величины, характеризующие мгновенное состояние колеблющейся точки.
- § 24.6. Гармоническое колебание.
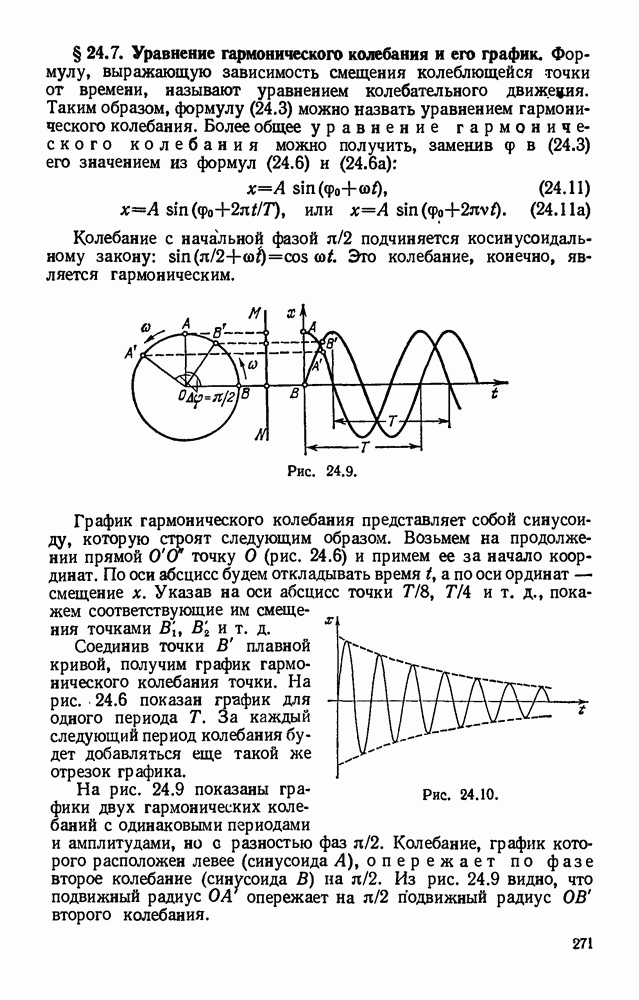
- § 24.7. Уравнение гармонического колебания и его график.
- § 24.8. Математический маятник.
- § 24.9. Законы колебания математического маятника. Формула маятника.
- § 24.10. Физический маятник.
- § 24.11. Практические применения маятников.
- § 24.12. Упругие колебания. Превращение энергии при колебательном движении.
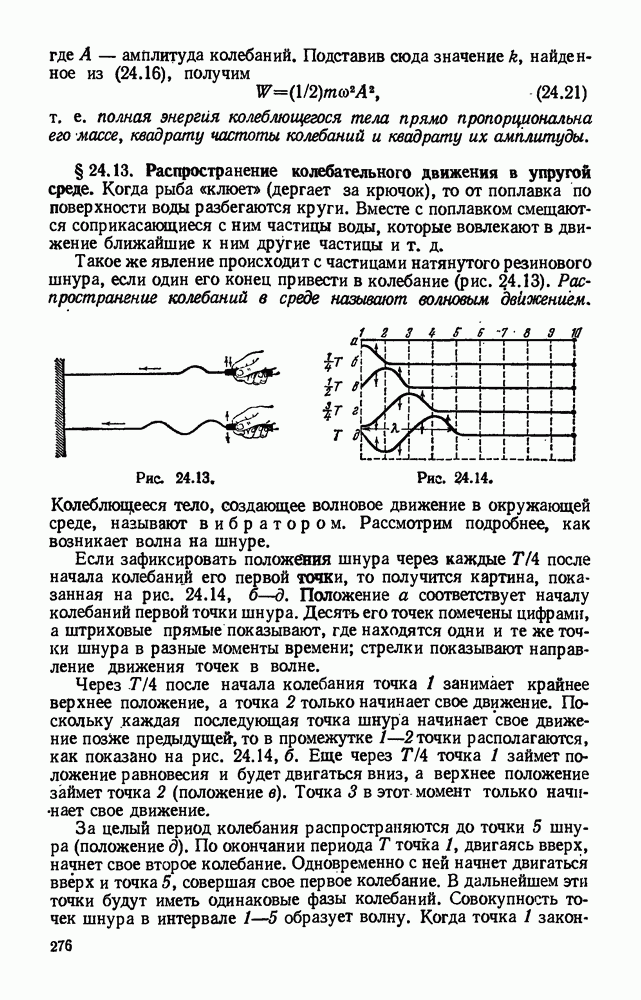
- § 24.13. Распространение колебательного движения в упругой среде.
- § 24.14. Перенос энергии бегущей волной.
- § 24.15. Поперечные и продольные волны.
- § 24.16. Волна и луч. Длина волны.
- § 24.17. Скорость распространения волн и ее связь с длиной волны и периодом (частотой) колебаний.
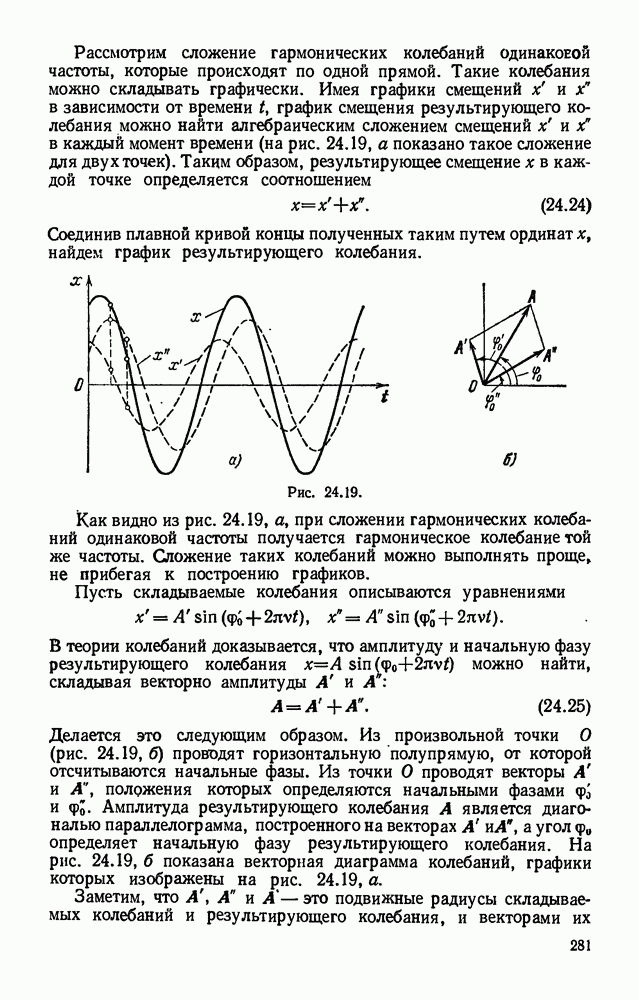
- § 24.18. Сложение колебаний, происходящих по одной прямой.
- § 24.19. Отражение волн.
- § 24.20. Стоячие волны.
- § 24.21. Интерференция волн.
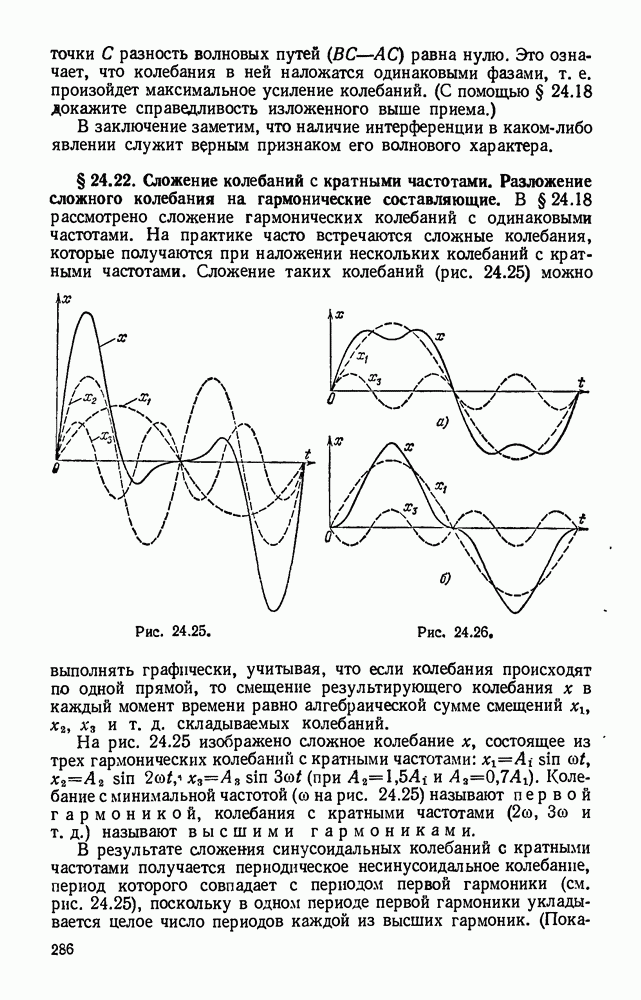
- § 24.22. Сложение колебаний с кратными частотами. Разложение сложного колебания на гармонические составляющие.
- § 24.23. Вынужденные колебания. Механический резонанс и его роль в технике.
- Глава 25. ЗВУК И УЛЬТРАЗВУК
- § 25.3. Громкость и интенсивность звука.
- § 25.4. Высота тона и тембр звука.
- § 25.5. Интерференция звуковых волн.
- § 25.6. Отражение и поглощение звука.
- § 25.7. Звуковой резонанс.
- § 25.8. Ультразвук и его применение в технике.
- Глава 26. ПЕРЕМЕННЫЙ ТОК
- § 26.2. Понятие об устройстве индукционных генераторов.
- § 26.3. Действующие значения э. д. с., напряжения и силы переменного тока.
- § 26.4. Индуктивность и емкость в цепи переменного тока.
- § 26.5. Преобразование переменного тока. Трансформатор.
- § 26.6. Индукционная катушка.
- § 26.7. Трехфазный ток.
- § 26.8. Получение, передача и распределение электрической энергии в народном хозяйстве СССР.
- Глава 27. ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ И ВОЛНЫ
- § 27.2. Затухающие электромагнитные колебания. Электрический резонанс.
- § 27.3. Получение незатухающих колебаний с помощью лампового генератора.
- § 27.4. Токи высокой частоты и их применение.
- § 27.5. Электромагнитное поле как особый вид материи.
- § 27.6. Открытый колебательный контур. Излучение.
- § 27.7. Электромагнитные волны. Скорость их распространения.
- § 27.8. Опыты Герца.
- § 27.9. Изобретение радио А С. Поповым. Радиотелеграфная связь.
- § 27.10. Радиотелефонная связь. Амплитудная модуляция.
- § 27.11. Устройство простейшего лампового радиоприемника с усилителем низкой частоты.
- § 27.12. Понятие о радиолокации.
- Раздел IV. ОПТИКА. ОСНОВЫ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- Глава 28. ПРИРОДА СВЕТА. РАСПРОСТРАНЕНИЕ СВЕТА
- § 28.2. Понятие об электромагнитной теории света. Диапазон световых волн.
- § 28.3. Понятие о квантовой теории света. Постоянная Планка.
- § 28.4. Источники света.
- § 28.5. Принцип Гюйгенса. Световые лучи.
- § 28.6. Скорость распространения света в вакууме. Опыт Майкельсона.
- § 28.7. Скорость распространения света в различных средах.
- Глава 29. ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ СВЕТА
- § 29.2. Законы отражения света.
- § 29.3. Зеркальное и диффузное отражение. Плоское зеркало.
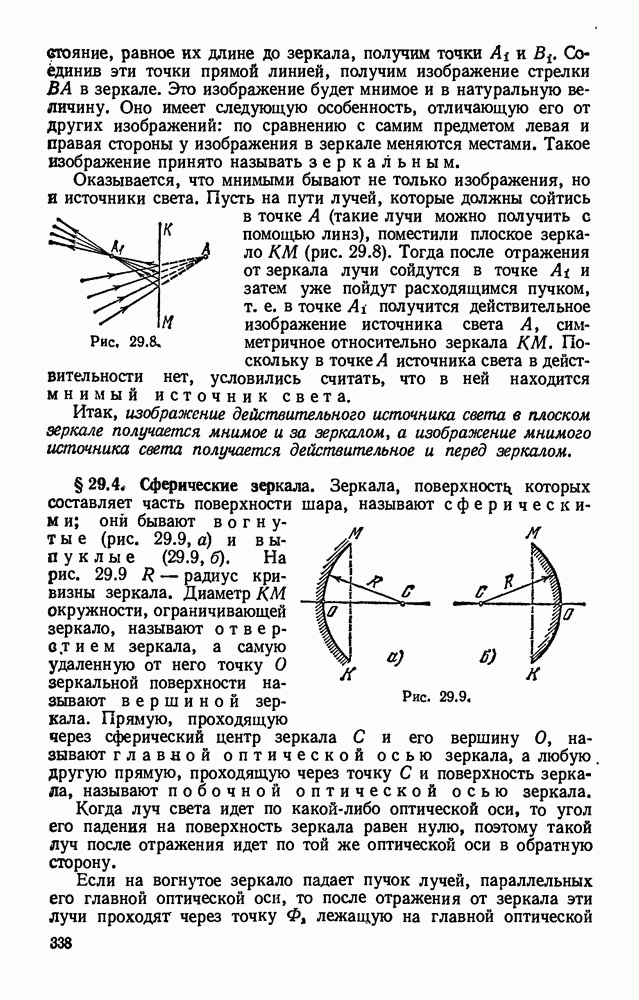
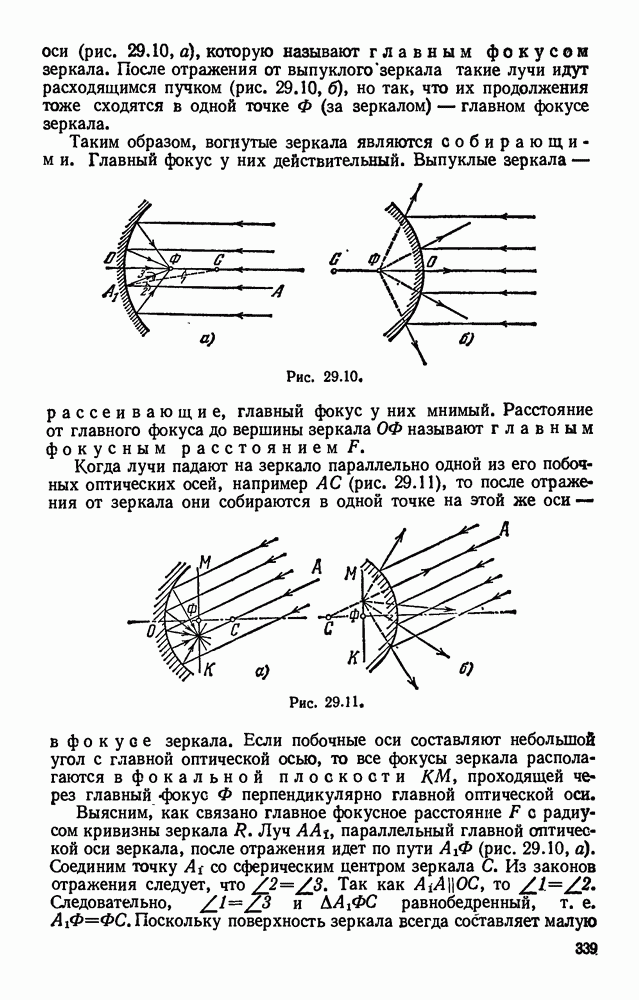
- § 29.4. Сферические зеркала.
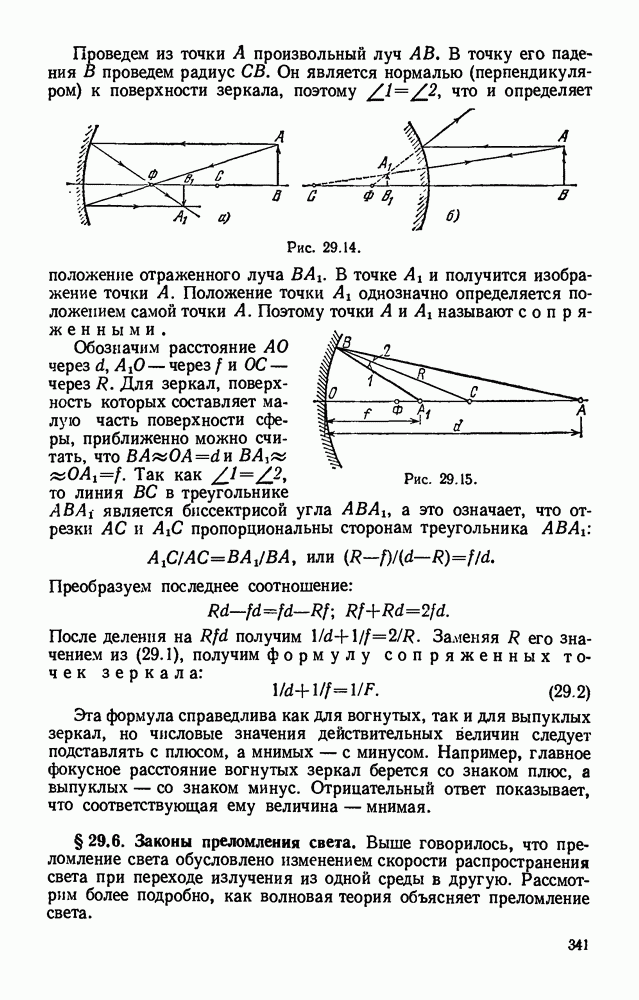
- § 29.5. Построение изображений, получаемых с помощью сферических зеркал. Формула сферического зеркала.
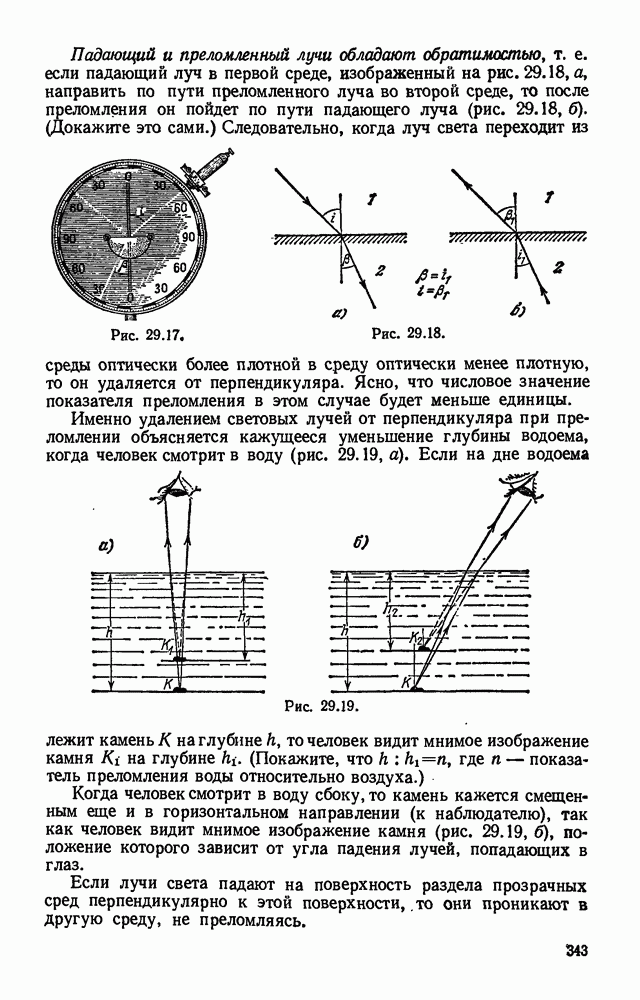
- § 29.6. Законы преломления света.
- § 29.7. Абсолютный показатель преломления и его связь с относительным показателем преломления.
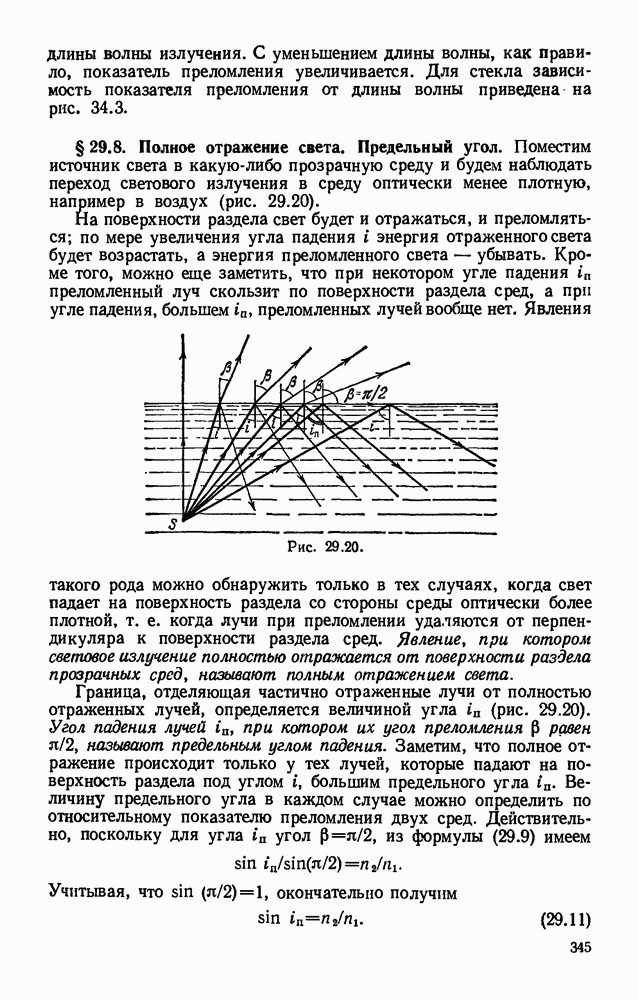
- § 29.8. Полное отражение света. Предельный угол.
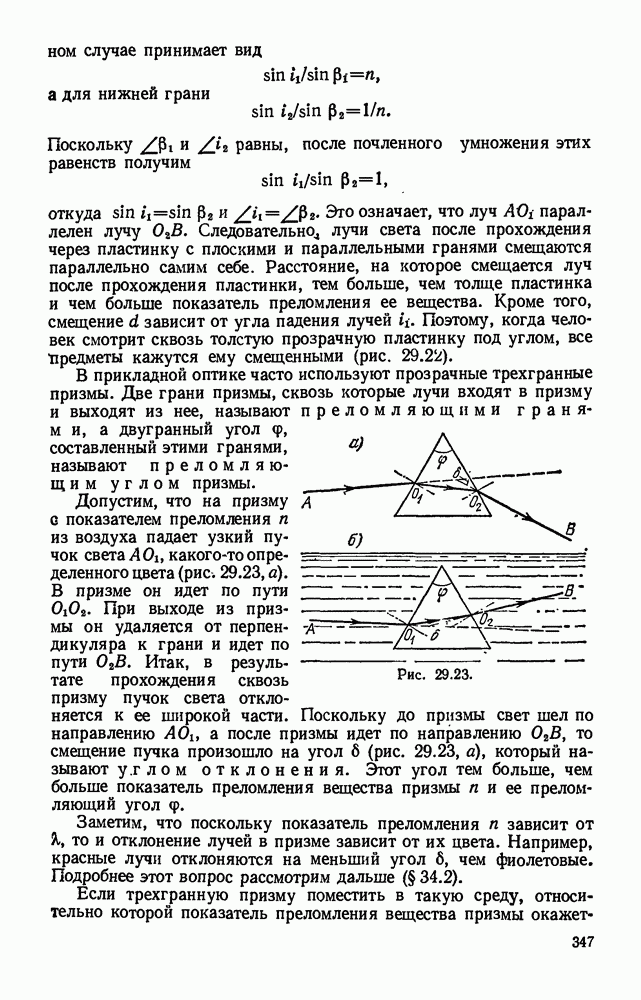
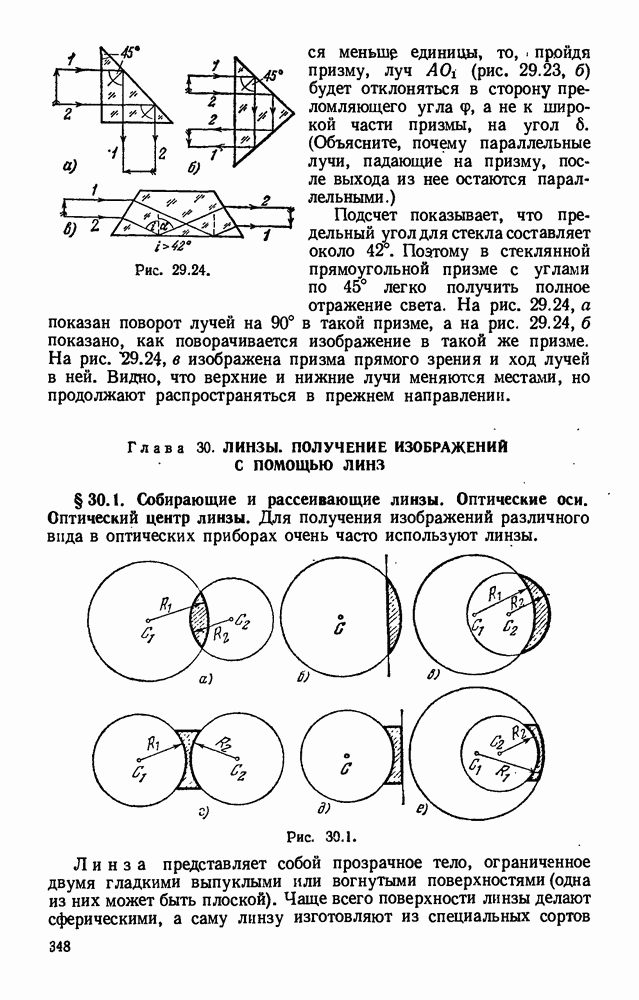
- § 29.9. Прохождение света через пластинку с параллельными гранями и через трехгранную призму. Призма с полным отражением.
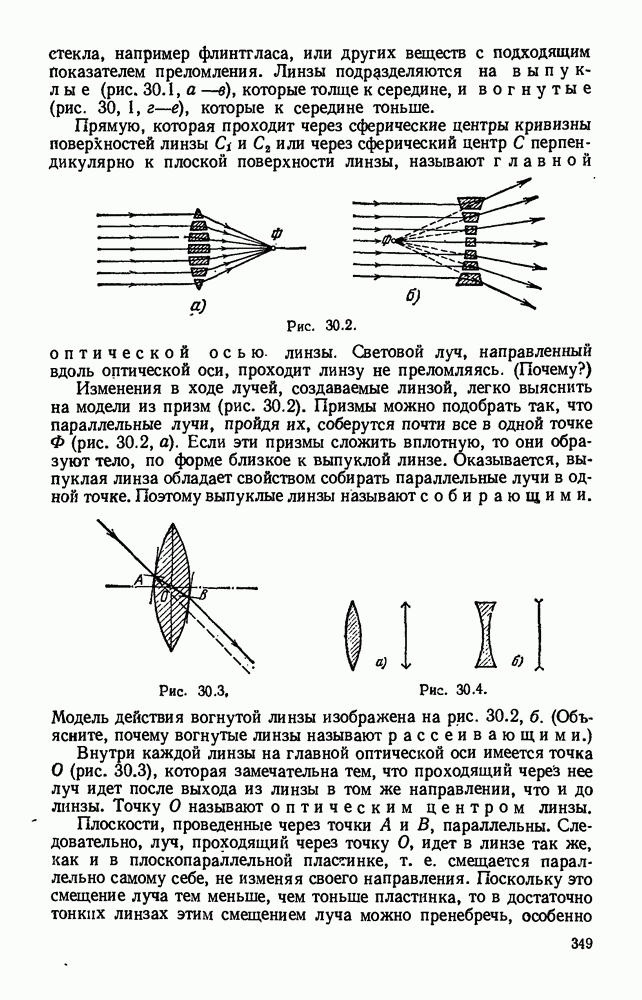
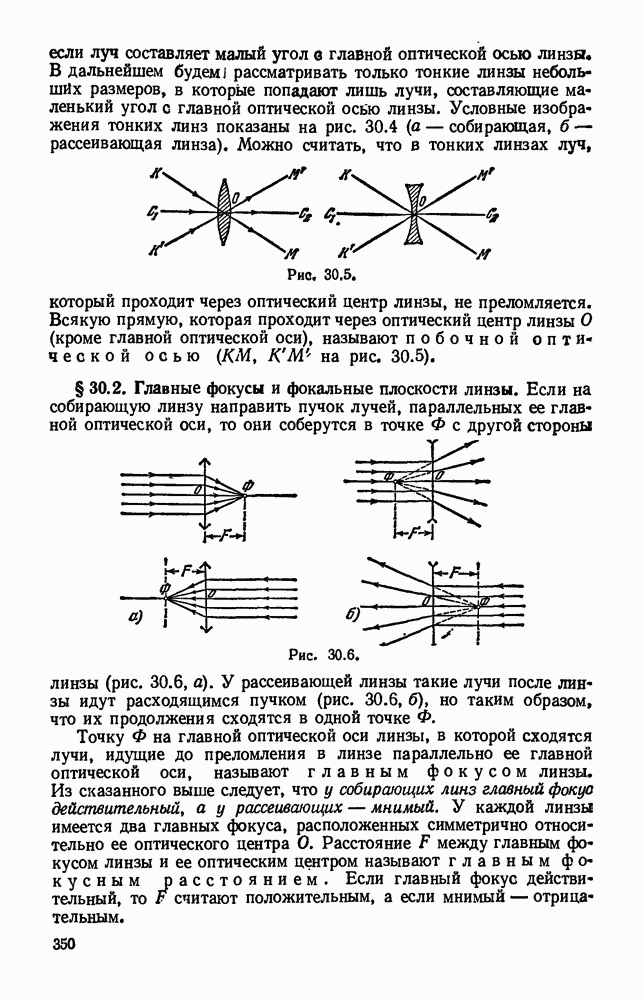
- Глава 30. ЛИНЗЫ. ПОЛУЧЕНИЕ ИЗОБРАЖЕНИЙ С ПОМОЩЬЮ ЛИНЗ
- § 30.2. Главные фокусы и фокальные плоскости линзы.
- § 30.3. Оптическая сила линзы.
- § 30.4. Построение изображения светящейся точки, расположенной на главной оптической оси линзы.
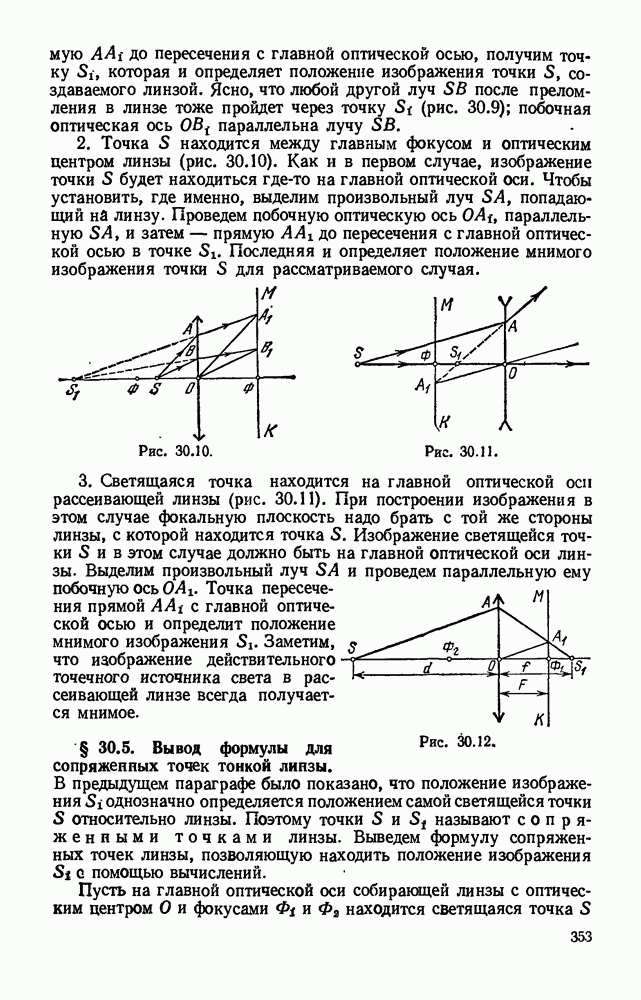
- § 30.5. Вывод формулы для сопряжеппых точек тонкой линзы.
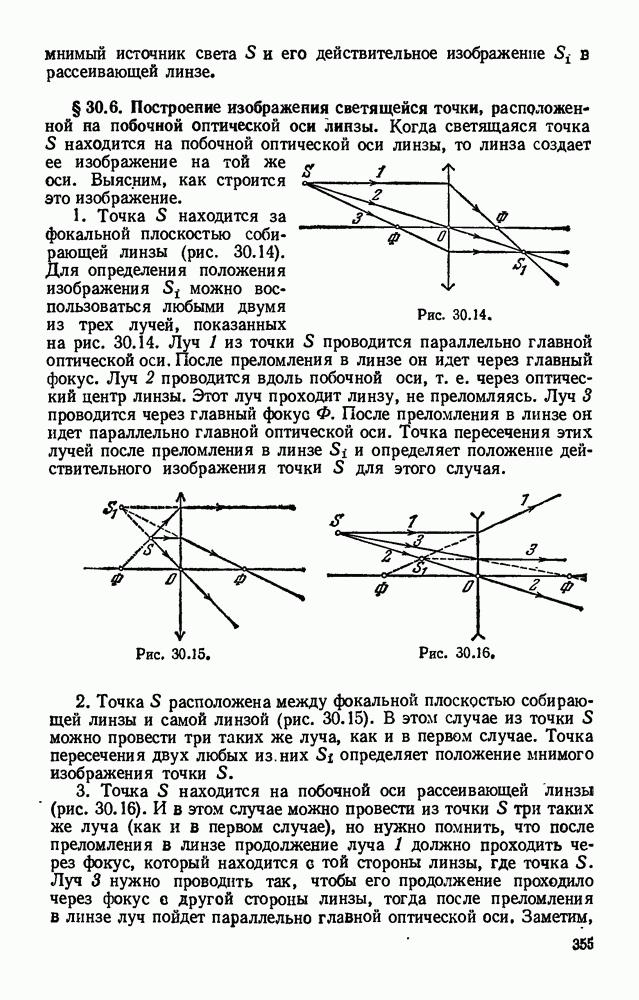
- § 30.6. Построение изображения светящейся точки, расположенной на побочной оптической оси линзы.
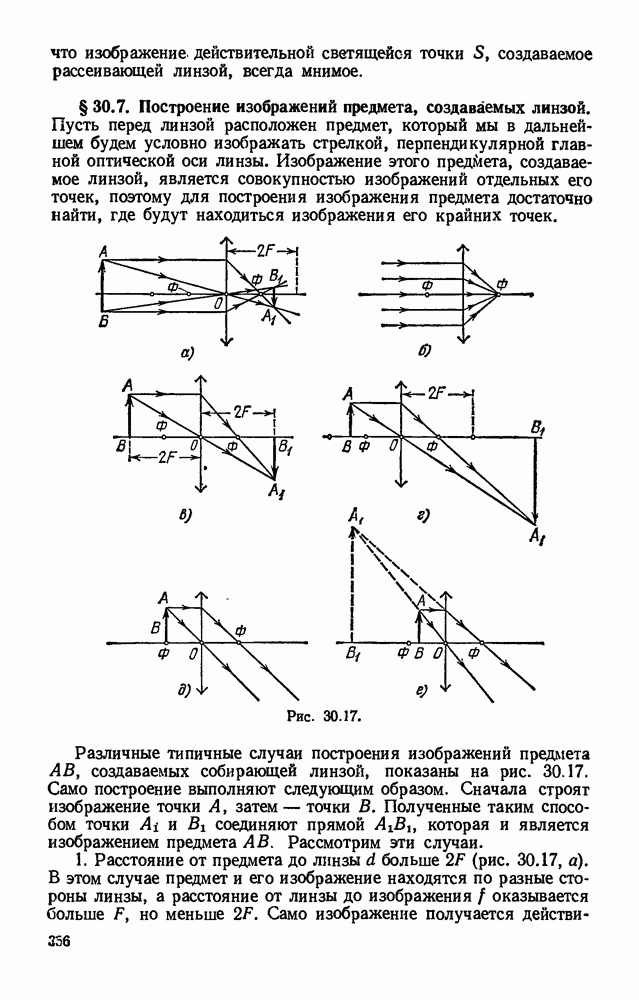
- § 30.7. Построение изображений предмета, создаваемых линзой.
- § 30.8. Линейное увеличение, полученное с помощью линзы.
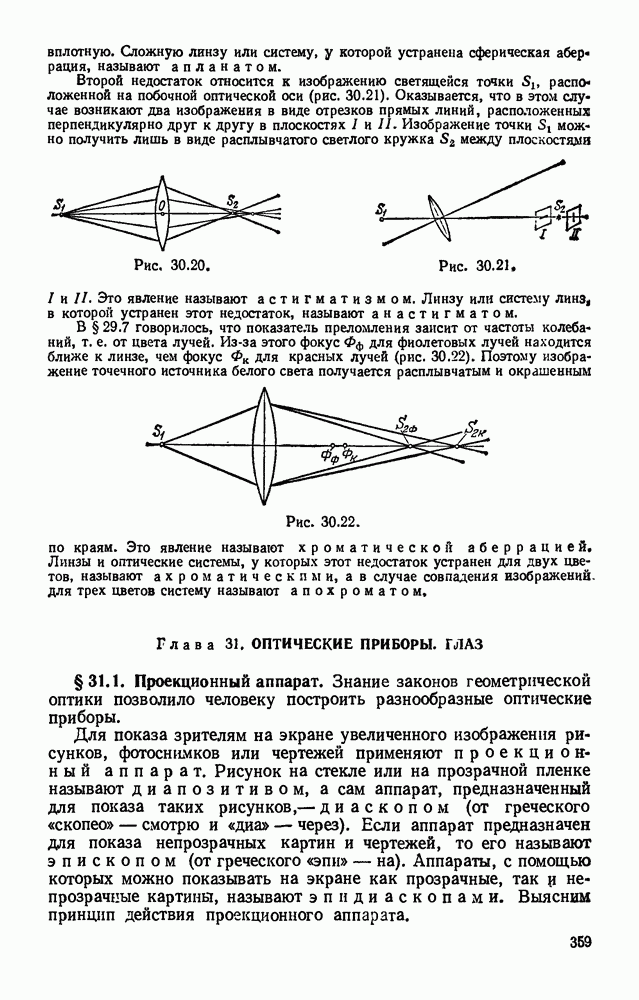
- § 30.9. Недостатки линз. Выясним, какие существенные недостатки встречаются у линз.
- Глава 31. ОПТИЧЕСКИЕ ПРИБОРЫ. ГЛАЗ
- § 31.2. Фотографический аппарат.
- § 31.3. Глаз как оптическая система.
- § 31.4, Длительность зрительного ощущения.
- § 31.5. Угол зрения.
- § 31.6. Расстояние наилучшего зрения. Оптические дефекты глаза.
- § 31.7. Увеличение оптического прибора. Лупа.
- § 31.8. Микроскоп.
- § 31.9. Труба Кеплера. Телескопы.
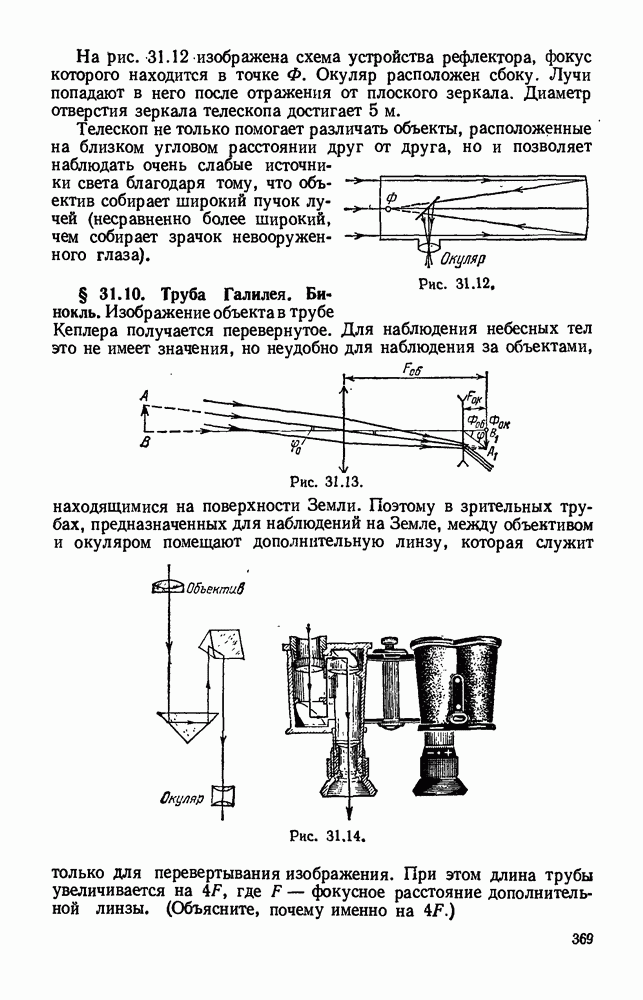
- § 31.10. Труба Галилея. Бинокль.
- Глава 32. ЯВЛЕНИЯ, ОБЪЯСНЯЕМЫЕ ВОЛНОВЫМИ СВОЙСТВАМИ СВЕТА
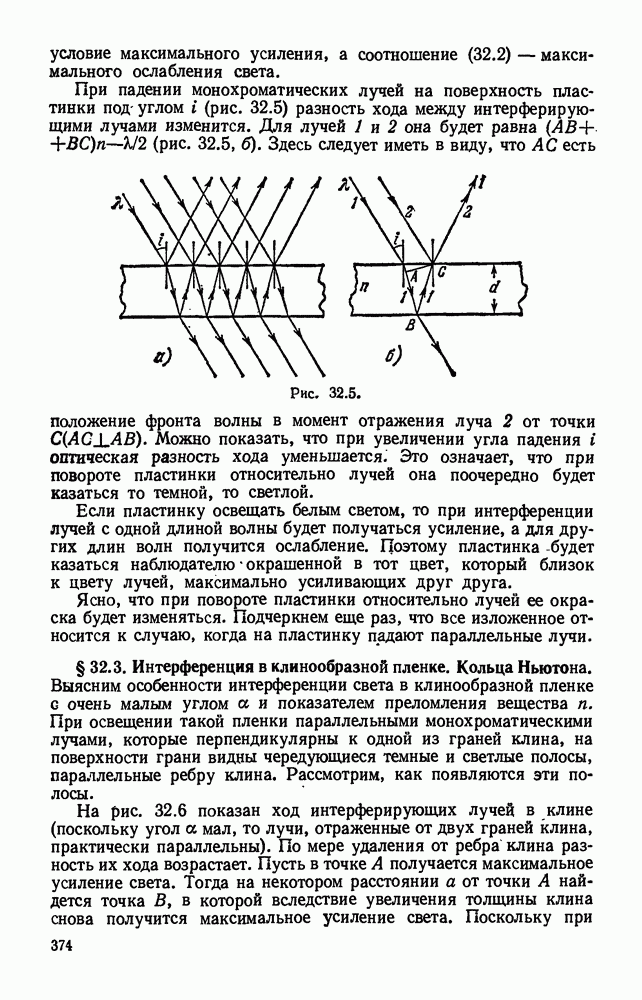
- § 32.2. Цвета тонких пленок.
- § 32.3. Интерференция в клинообразной пленке. Кольца Ньютона.
- § 32.4. Интерференция света в природе и технике.
- § 32.5. Дифракция света.
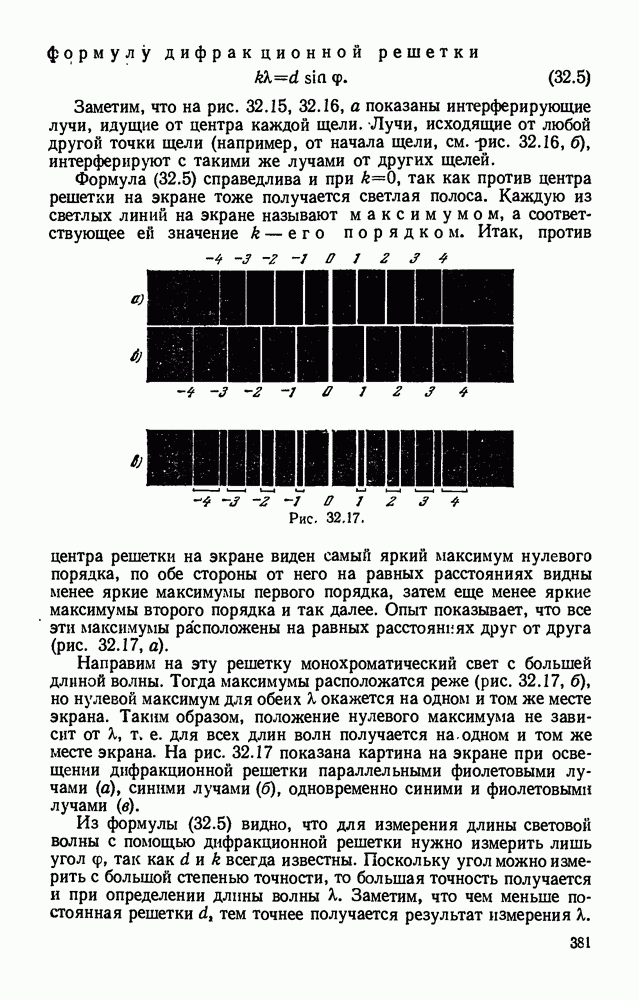
- § 32.6. Дифракционная решетка и дифракционный спектр. Измерение длины световой волны.
- § 32.7. Поляризация волн.
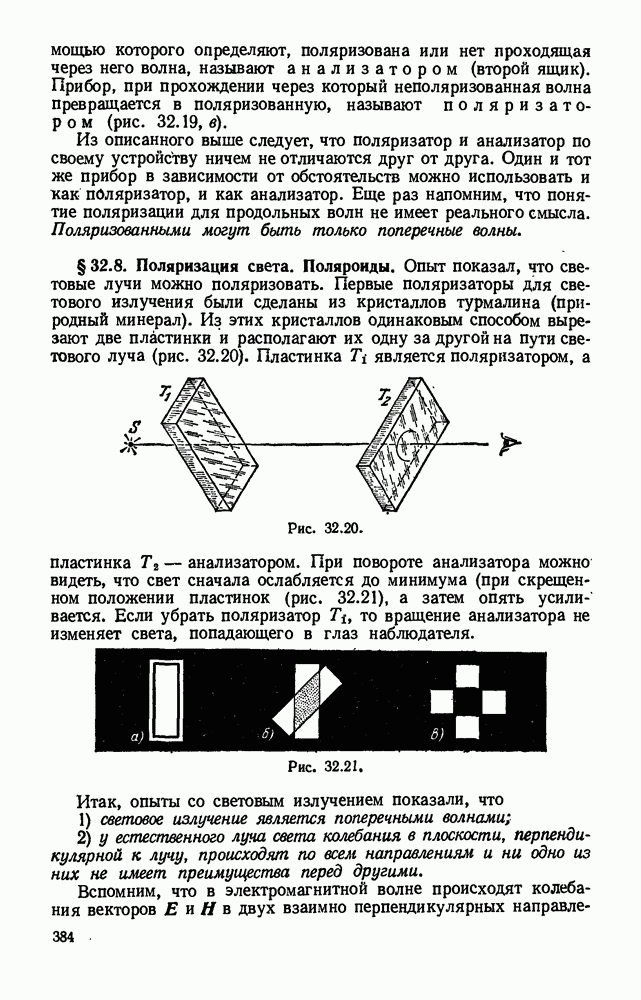
- § 32.8. Поляризация света. Поляроиды.
- § 32.9. Поляризация при отражении и преломлении света.
- Глава 33. ФОТОМЕТРИЯ
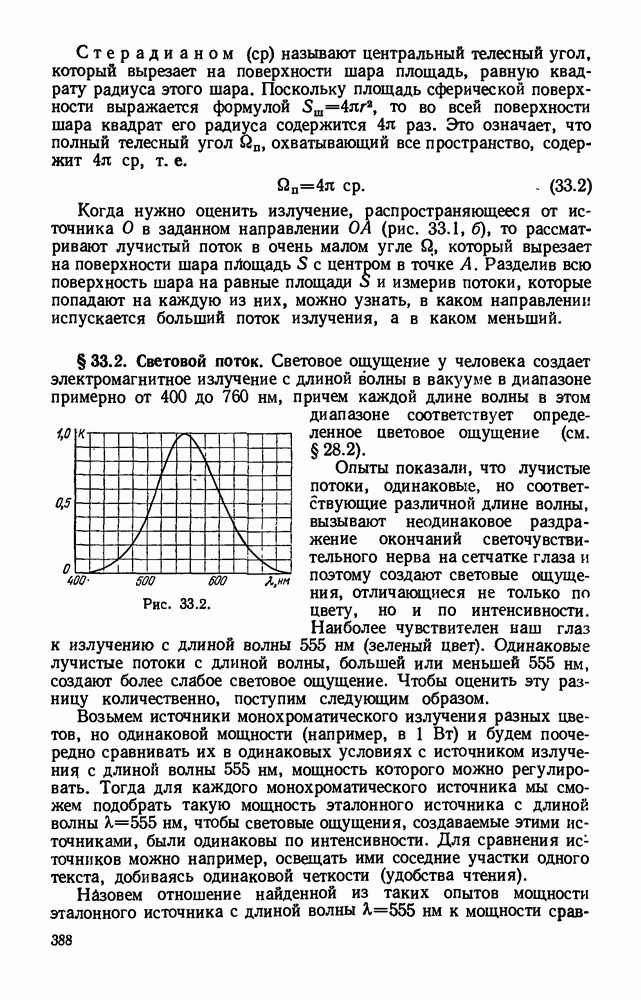
- § 33.2. Световой поток.
- § 33.3. Сила света. Единицы силы света и светового потока.
- § 33.4. Освещенность.
- § 33.5. Яркость.
- § 33.6. Законы освещенности.
- § 33.7. Сравнение силы света двух источников. Фотометр. Люксметр.
- Глава 34. ИЗЛУЧЕНИЕ И СПЕКТРЫ. РЕНТГЕНОВСКИЕ ЛУЧИ
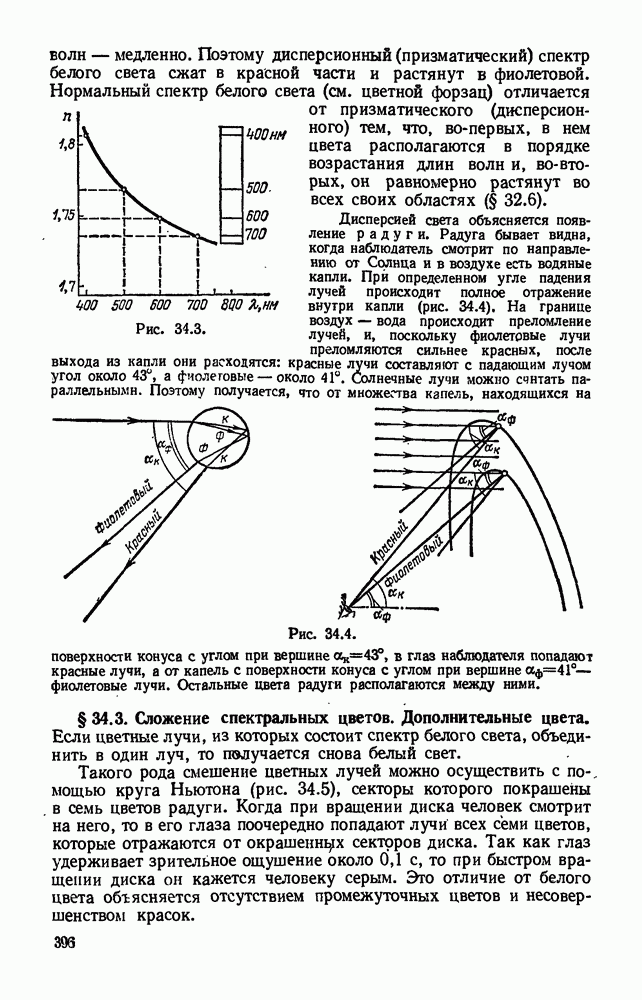
- § 34.2. Разложение белого света призмой. Сплошной спектр.
- § 34.3. Сложение спектральных цветов. Дополнительные цвета.
- § 34.4. Цвета тел.
- § 34.5. Ультрафиолетовая и инфракрасная части спектра.
- § 34.6. Роль ультрафиолетовых и инфракрасных лучей в природе. Их применение в технике.
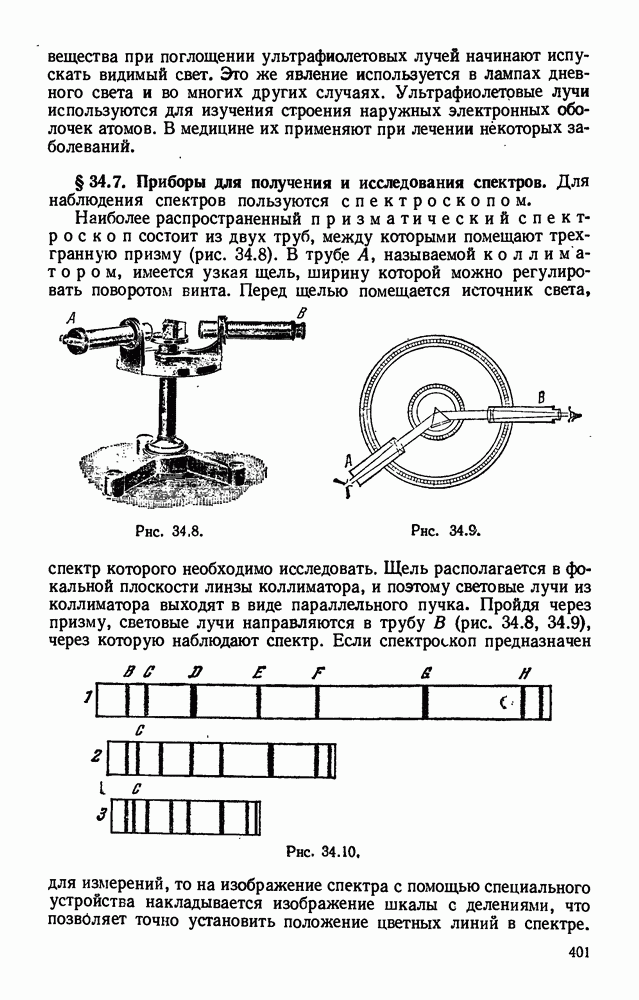
- § 34.7. Приборы для получения и исследования спектров.
- § 34.8. Виды спектров.
- § 34.9. Спектры поглощения газов. Опыты Кирхгофа.
- § 34.10. Закон теплового излучения Кирхгофа.
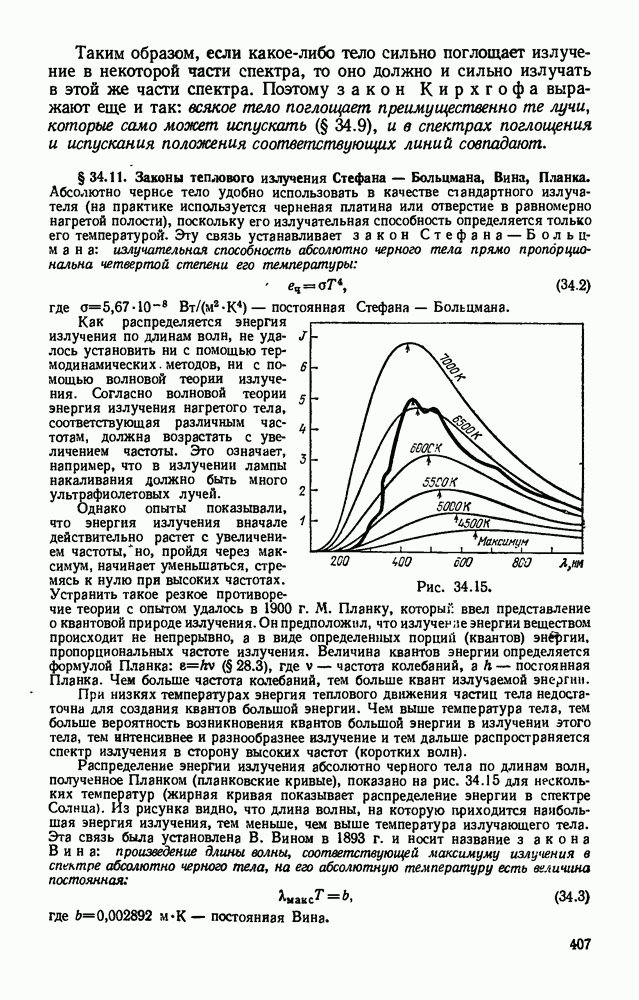
- § 34.11. Законы теплового излучения Стефана — Больцмана, Вина, Планка.
- § 34.12. Спектры Солнца и звезд. Их связь с температурой.
- § 34.13. Спектральный анализ.
- § 34.14. Понятие о принципе Доплера.
- § 34.15. Рентгеновские лучи и их практическое применение.
- § 34.16. Шкала электромагнитных волн.
- § 34.17. Виды космического излучения.
- Глава 35. ЯВЛЕНИЯ, ОБЪЯСНЯЕМЫЕ КВАНТОВЫМИ СВОЙСТВАМИ ИЗЛУЧЕНИЯ
- § 35.2. Давление световых лучей. Опыты П. Н. Лебедева.
- § 35.3. Тепловое действие света.
- § 35.4. Химическое действие света.
- § 35.5. Использование химического действия света при фотографировании. Понятие о квантовой природе химического действия излучения.
- § 35.6. Внешний фотоэлектрический эффект. Опыты Столетова.
- § 35.7. Законы внешнего фотоэффекта.
- § 35.8. Объяснение фотоэффекта на основе квантовой теории.
- § 35.9. Фотоэлементы с внешним фотоэффектом.
- § 35.10. Внутренний фотоэффект.
- § 35.11. Фотосопротивления.
- § 35.12. Фотоэлементы с внутренним фотоэффектом.
- § 35.13. Использование фотоэлементов в науке и технике.
- § 35.14. Понятие о телевидении.
- § 35.15. Понятие о теории Бора. Строение атома водорода.
- § 35.16. Излучение и поглощение энергии атомами.
- § 35.17. Явление люминесценции.
- § 35.18. Понятие о квантовых генераторах.
- Глава 36. ОСНОВЫ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- § 36.2. Экспериментальные основы специальной теории относительности Эйнштейна. Постулаты Эйнштейна.
- § 36.3. Понятие одновременности.
- § 36.4. Относительность понятий длины и промежутка времени
- § 36.5. Теорема сложения скоростей Эйнштейна.
- § 36.6. Масса и импульс в специальной теории относительности.
- § 36.7. Связь между массой и энергией. Уравнение Эйнштейна.
- § 36.8. Связь между импульсом и энергией. Импульс и энергия фотонов.
- Раздел V. ФИЗИКА АТОМНОГО ЯДРА
- Глава 37. СТРОЕНИЕ АТОМНОГО ЯДРА
- § 37.2. Радиоактивность.
- § 37.3. Понятие о превращении химических элементов.
- § 37.4. Понятие об энергии и проникающей способности радиоактивного излучения.
- § 37.5. Эффект Вавилова — Черенкова.
- § 37.6. Открытие искусственного превращения атомных ядер.
- § 37.7. Открытие нейтрона.
- § 37.8. Состав атомного ядра. Запись ядерных реакций.
- § 37.9. Изотопы.
- § 37.10. Понятие о ядерных силах.
- § 37.11. Дефект массы атомных ядер. Энергия связи.
- Глава 38. КОСМИЧЕСКИЕ ЛУЧИ. ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
- § 38.2. Открытие позитрона.
- § 38.3. Нейтрино.
- § 38.4. Открытие новых элементарных частиц.
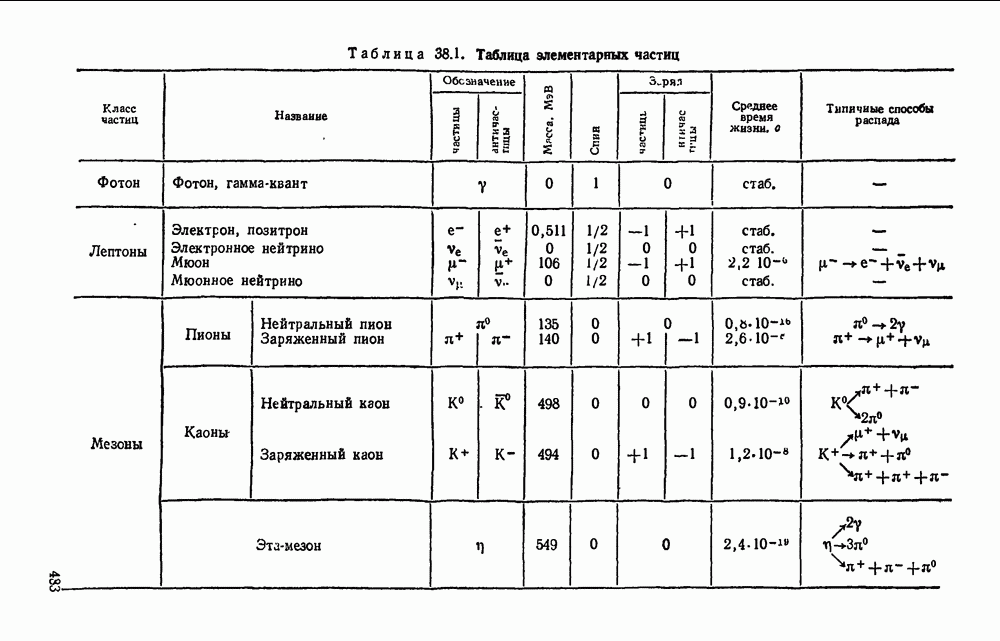
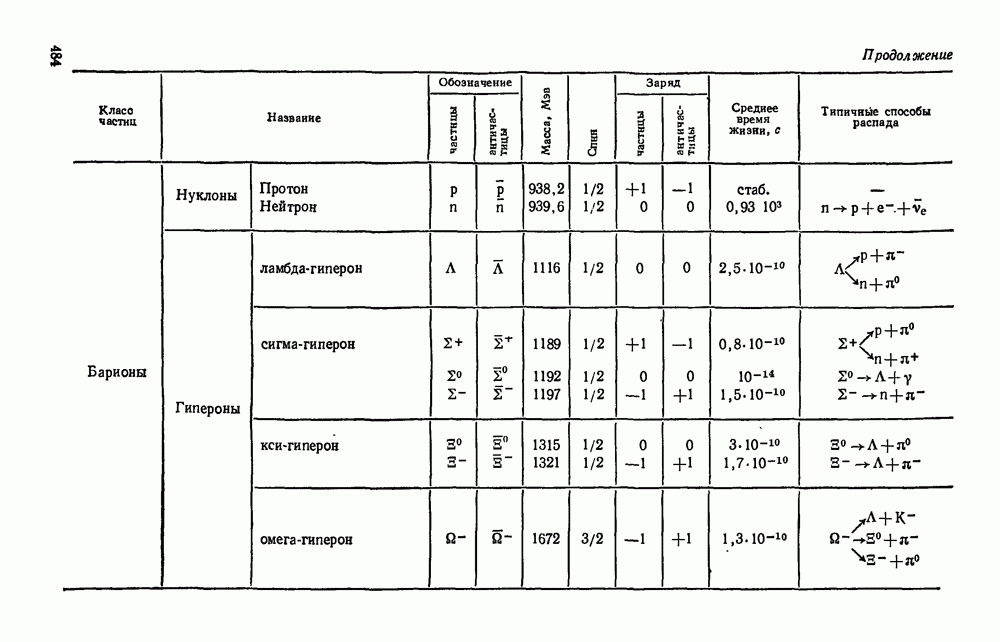
- § 38.5. Классификация элементарных частиц.
- § 38.6. Античастицы. Взаимные превращения вещества и поля.
- § 38.7. Гипотеза кварков.
- Глава 39. АТОМНАЯ ЭНЕРГИЯ И ЕЕ ИСПОЛЬЗОВАНИЕ
- § 39.2. Деление тяжелых атомных ядер.
- § 39.3. Цепная реакция деления. Ядерный взрыв.
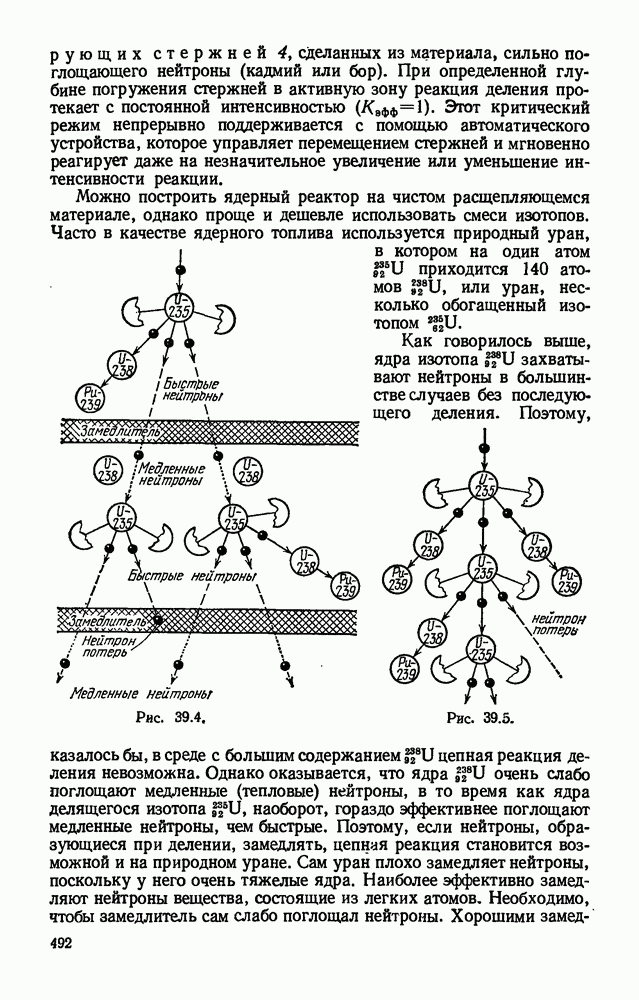
- § 39.4. Ядерный реактор.
- § 39.5. Развитие ядерной энергетики в СССР.
- § 39.6. Понятие о термоядерной реакции. Энергия Солнца и звезд.
- § 39.7. Понятие об управляемой термоядерной реакции.
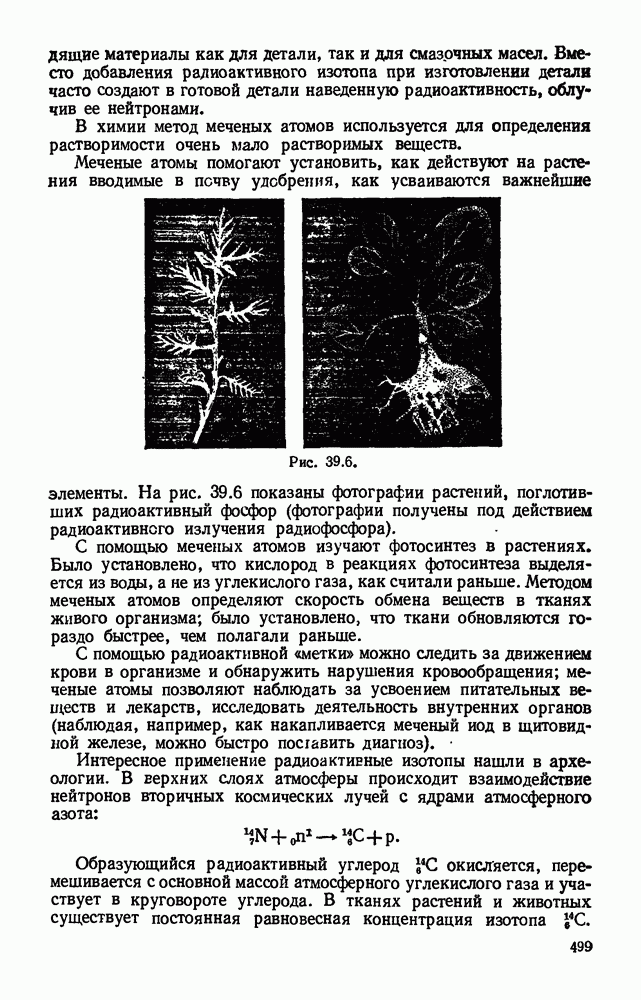
- § 39.8. Получение радиоактивных изотопов и их применение.
- Раздел VI. ОСНОВНЫЕ СВЕДЕНИЯ ПО АСТРОНОМИИ
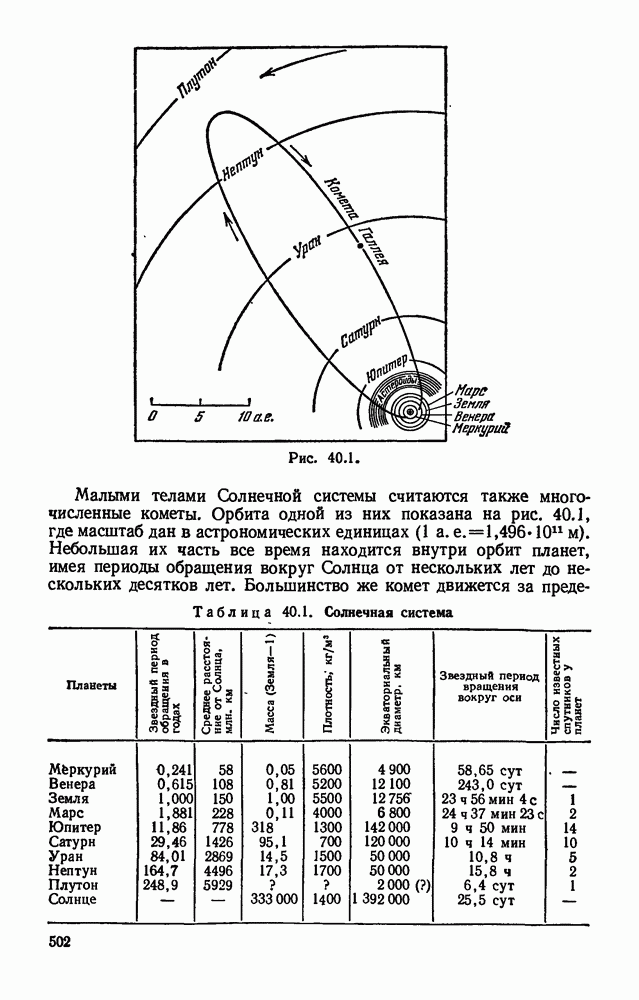
- Глава 40. СТРОЕНИЕ И РАЗВИТИЕ ВСЕЛЕННОЙ
- § 40.2. Происхождение и развитие небесных тел.
- § 40.3. Понятие о космологии.