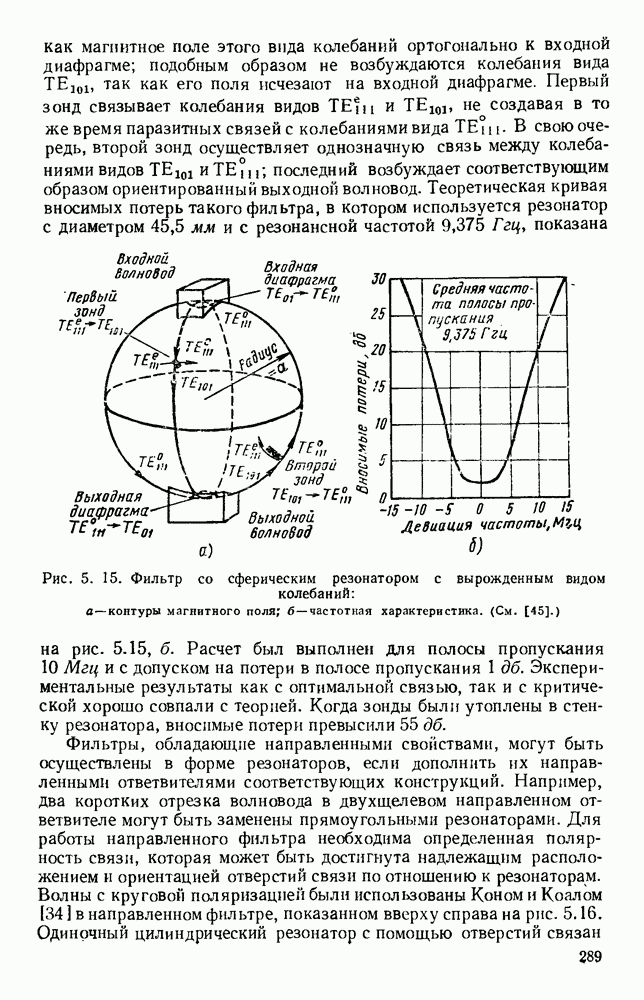
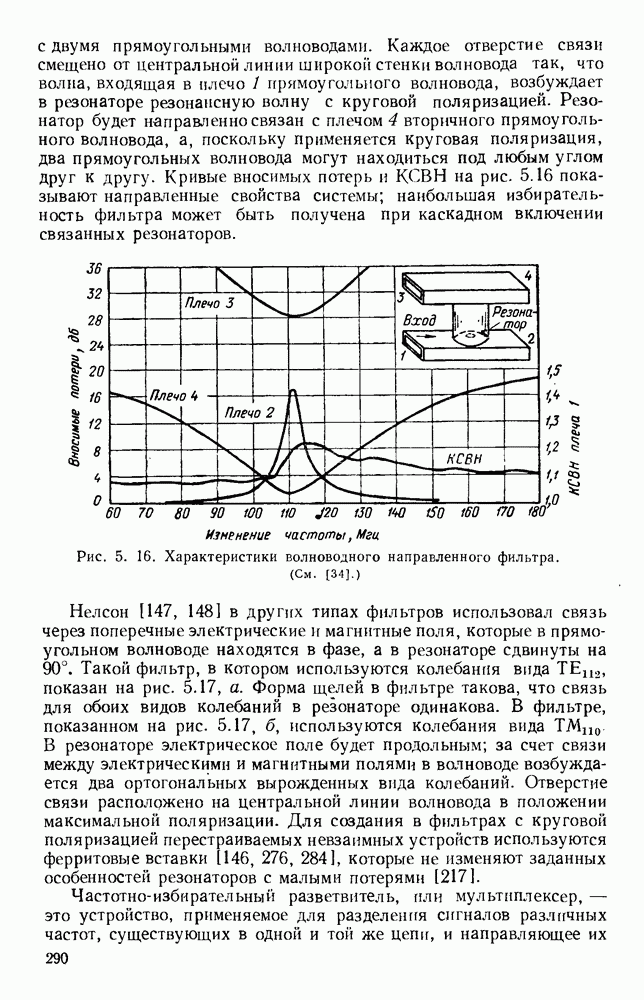
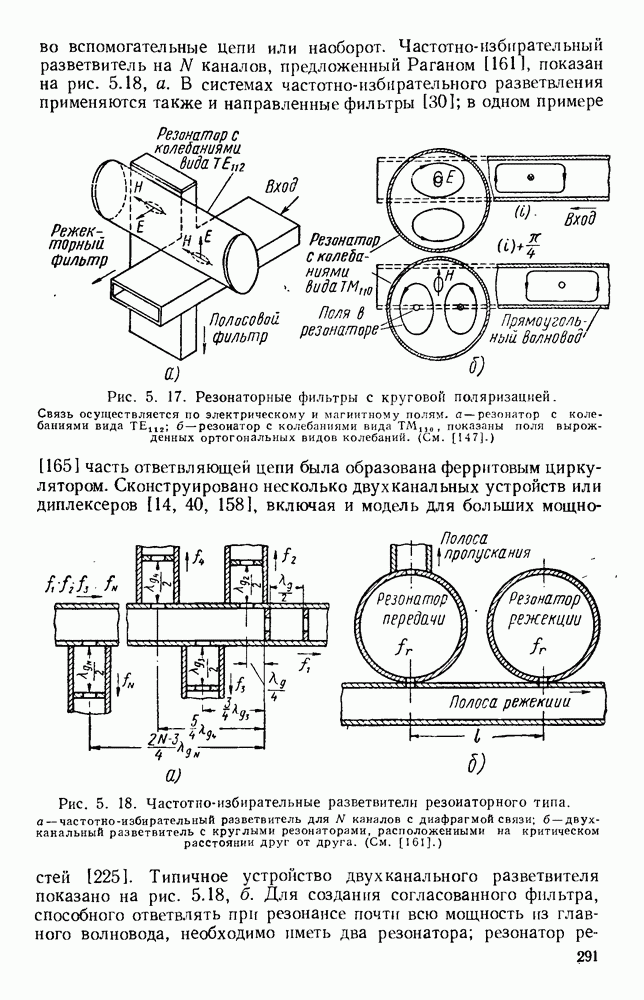
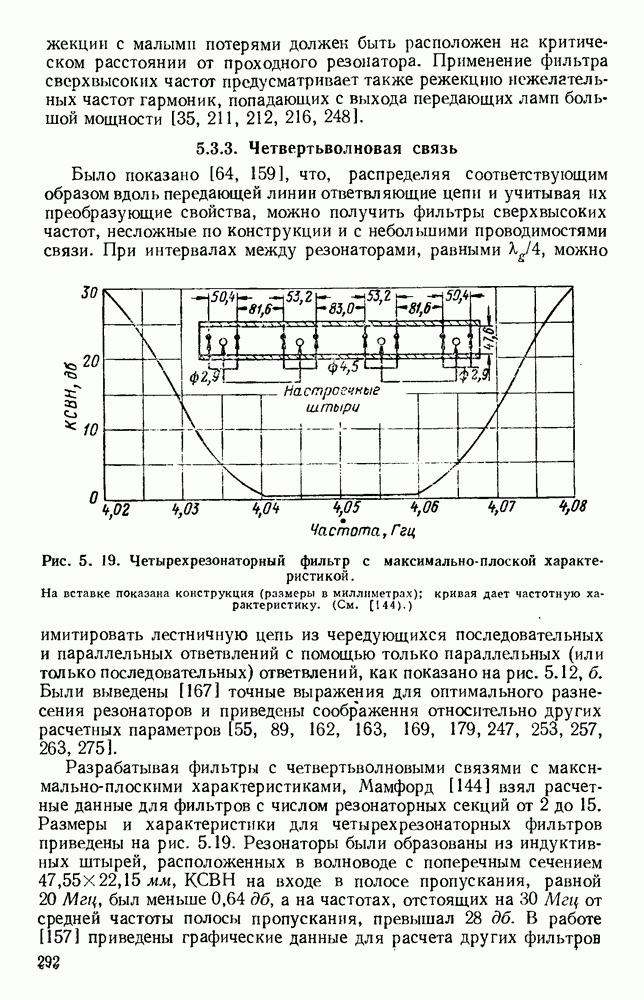
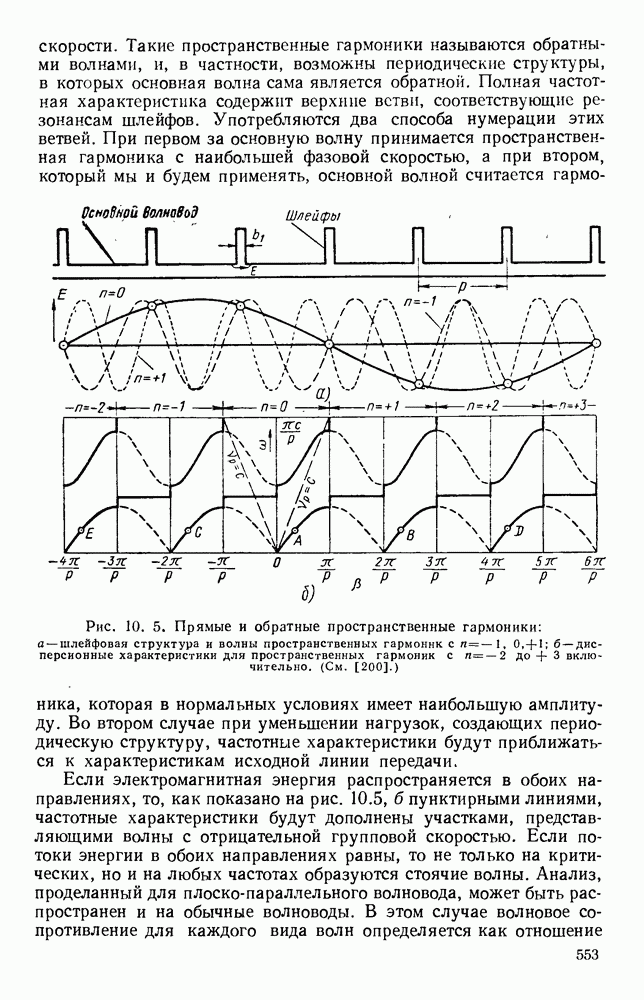
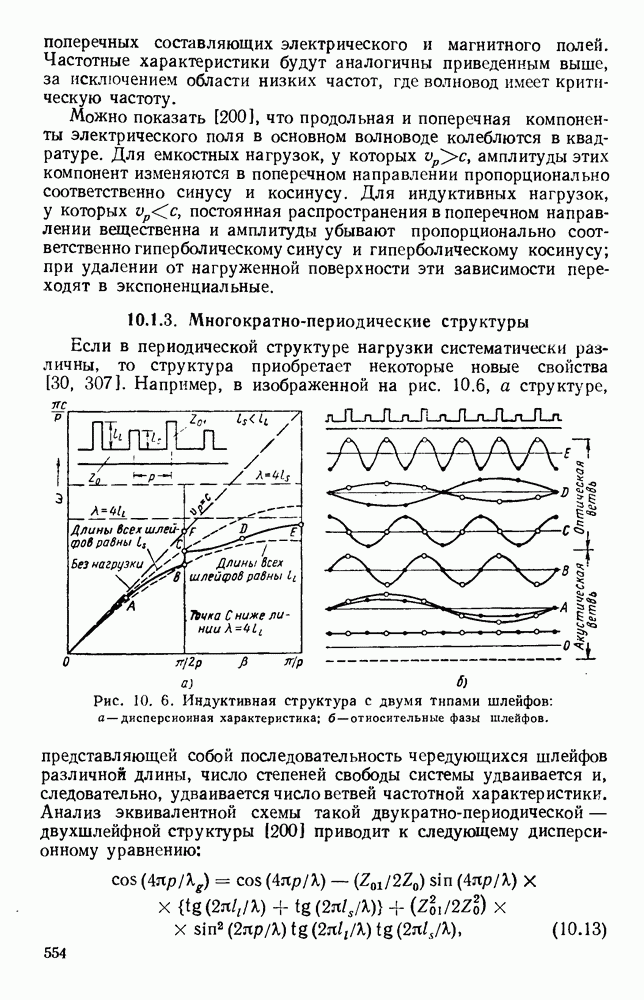
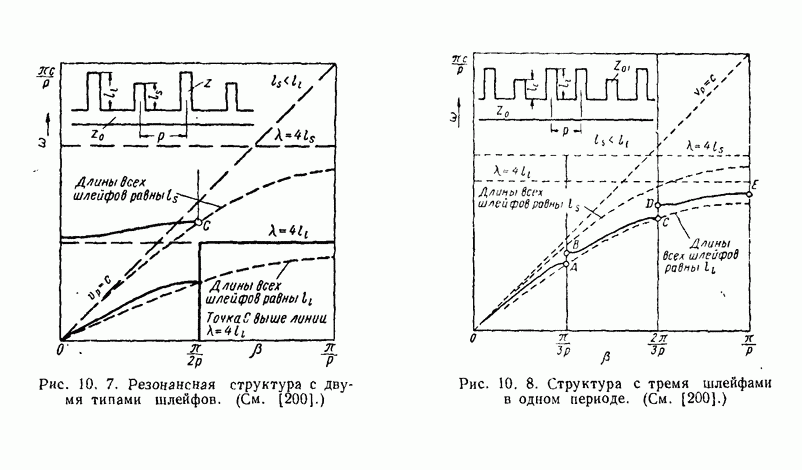
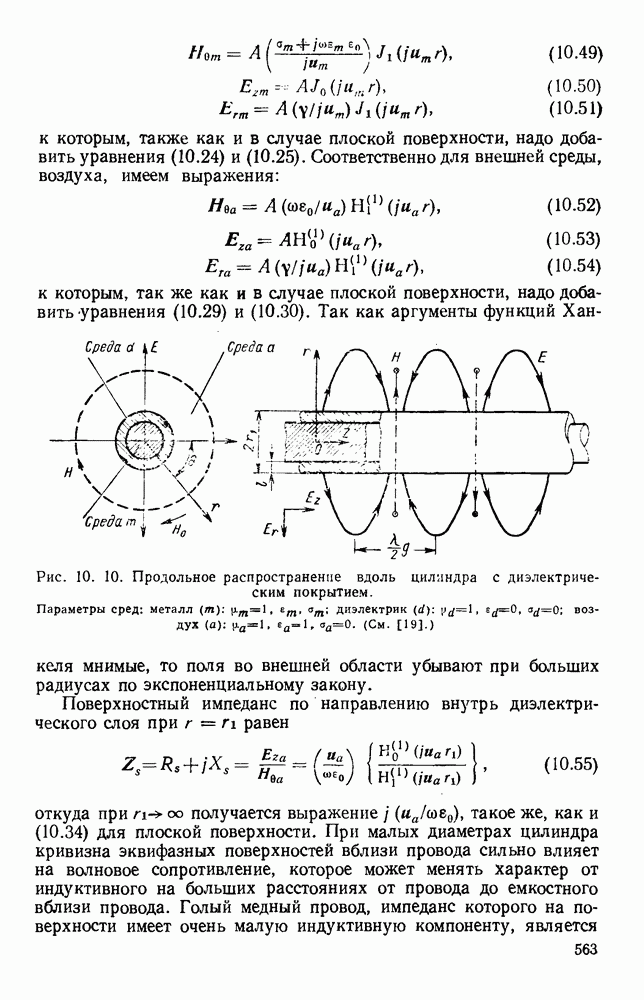
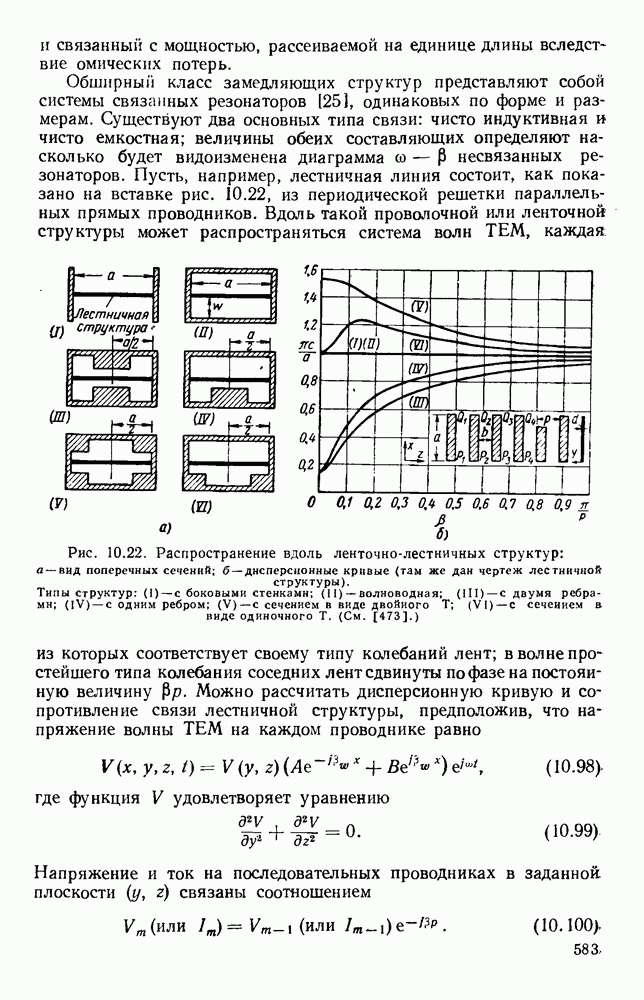
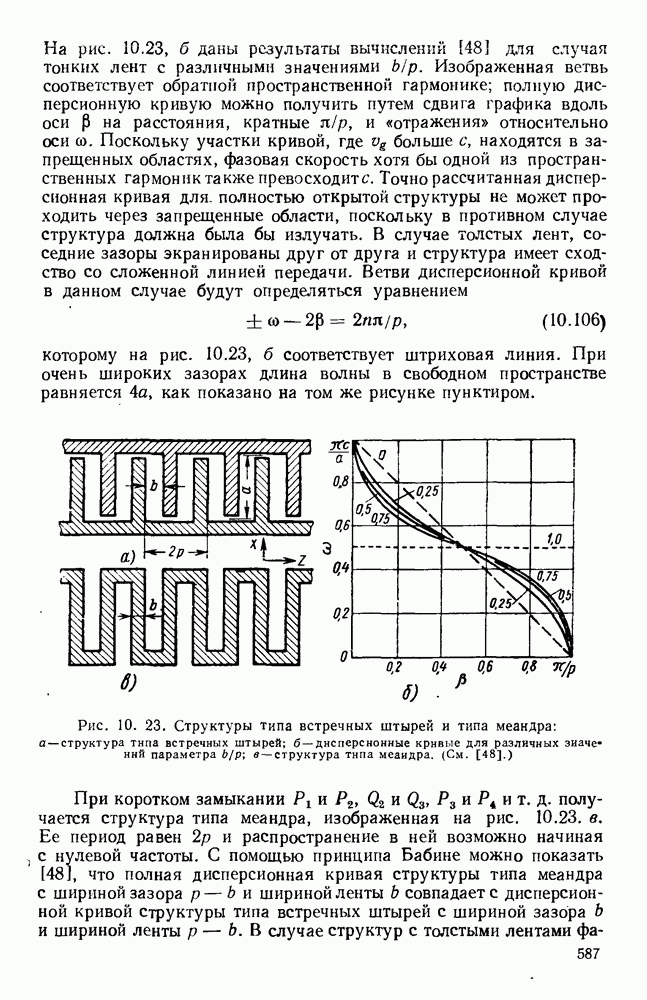
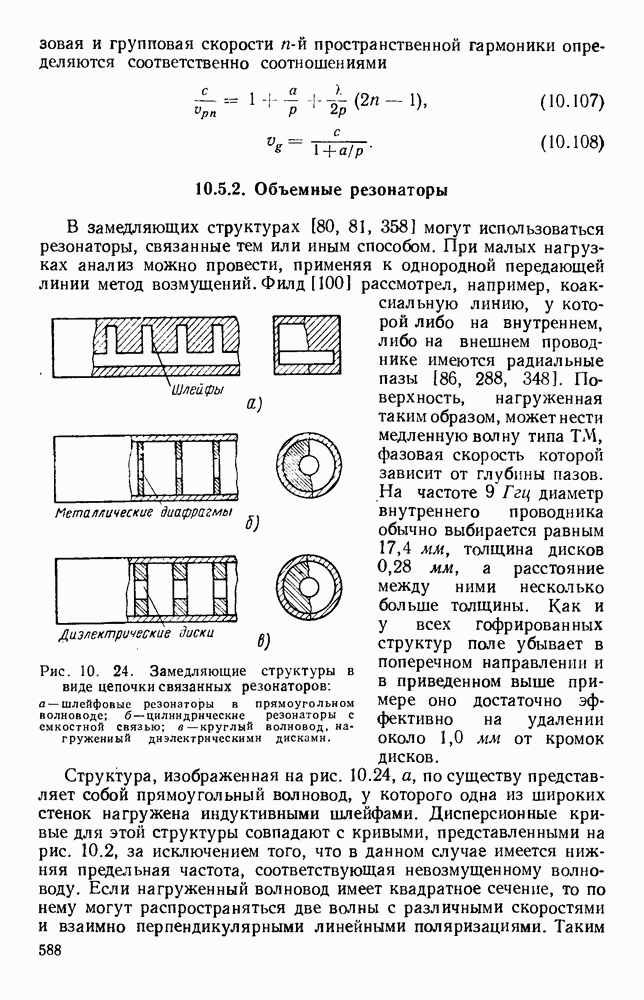
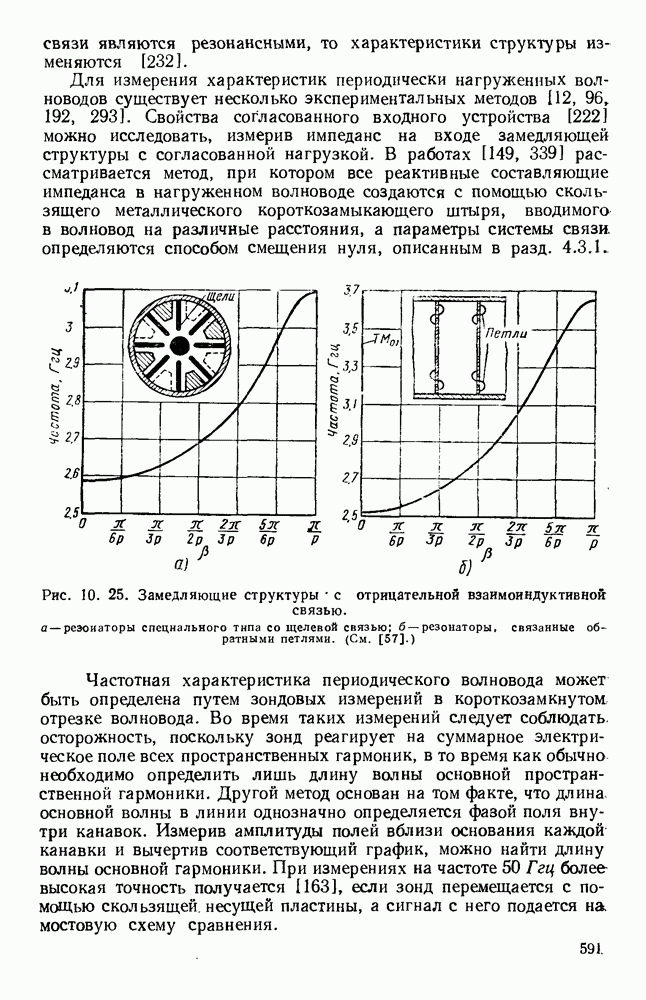
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
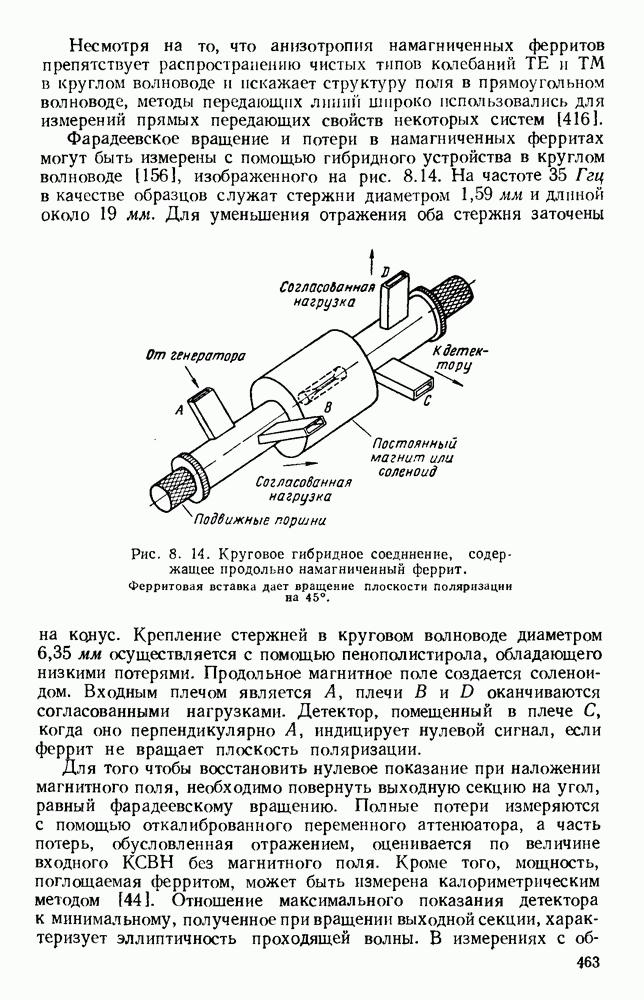
1.4. ВОЛНЫ В ПОЛЫХ ПРОВОДЯЩИХ ТРУБАХ
1.4.1. Прямоугольные волноводы
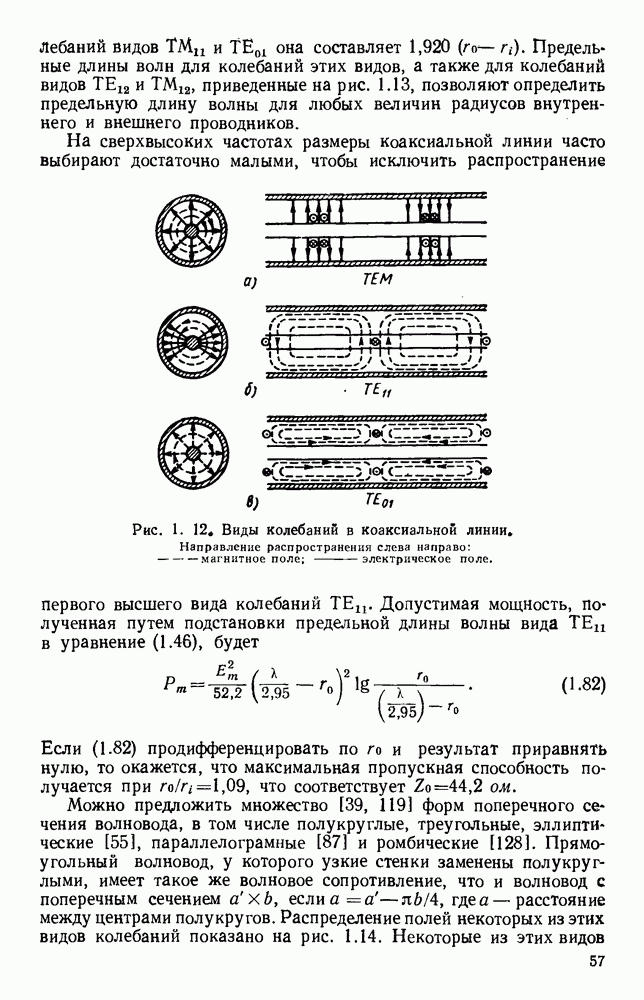
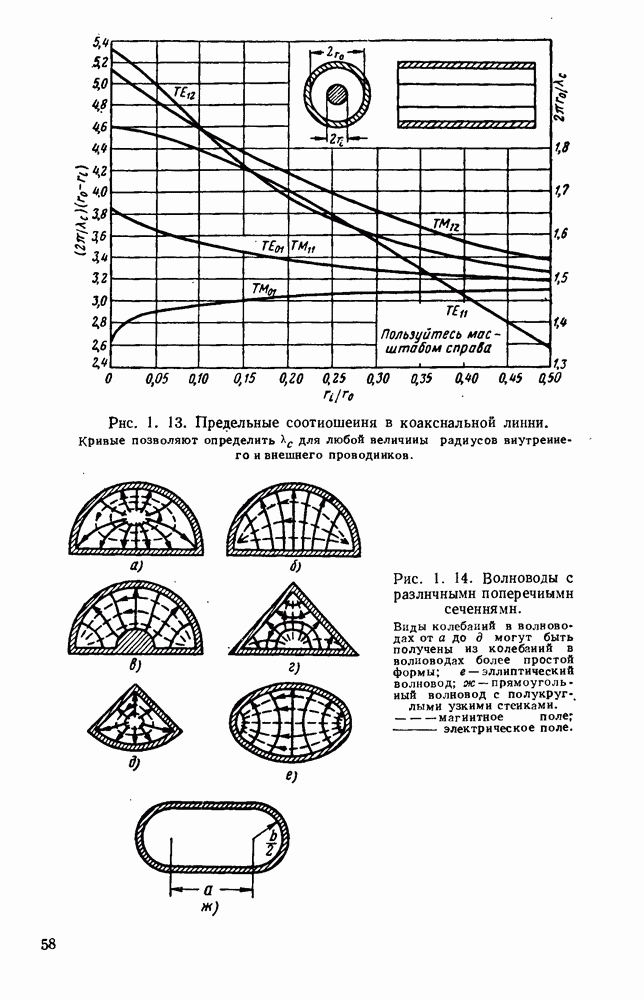
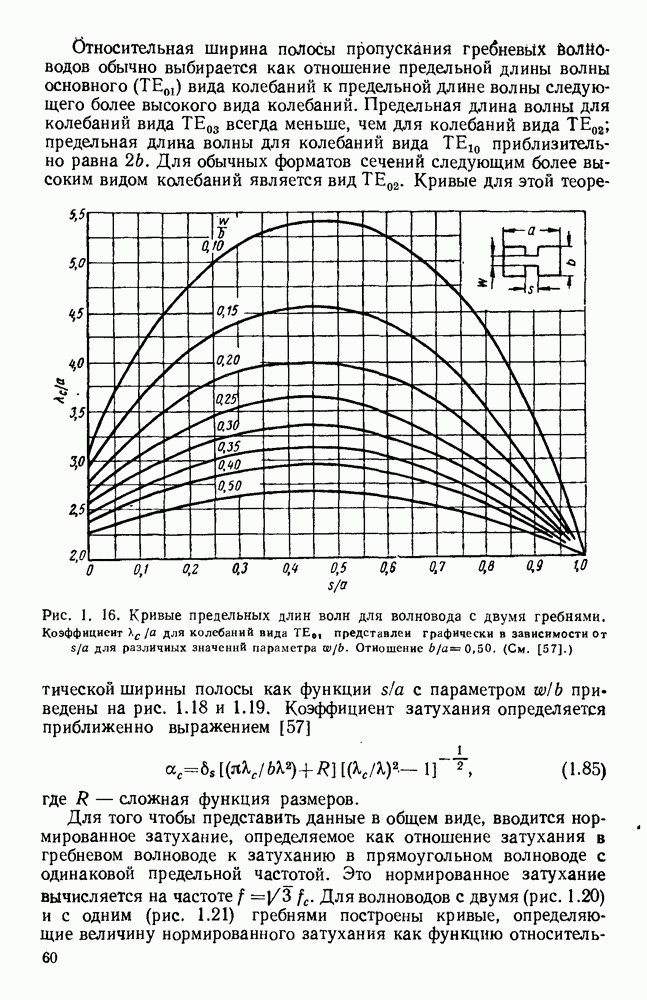
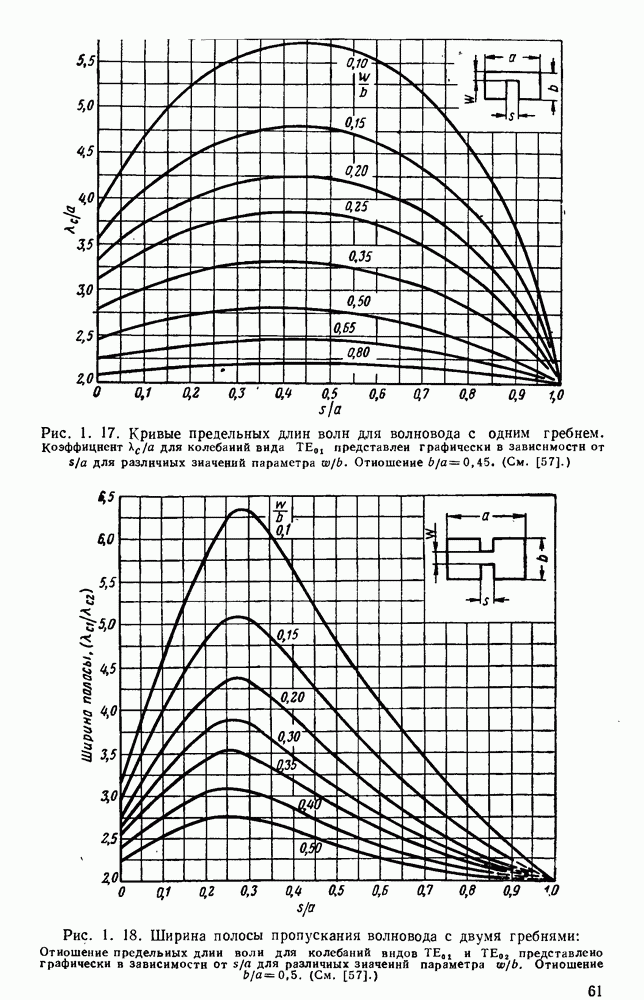
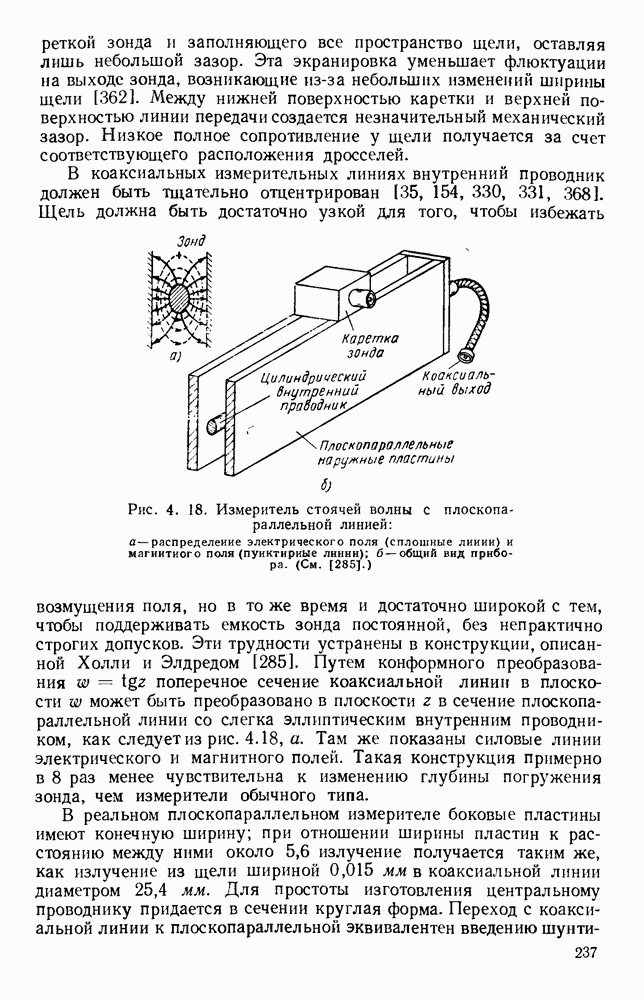
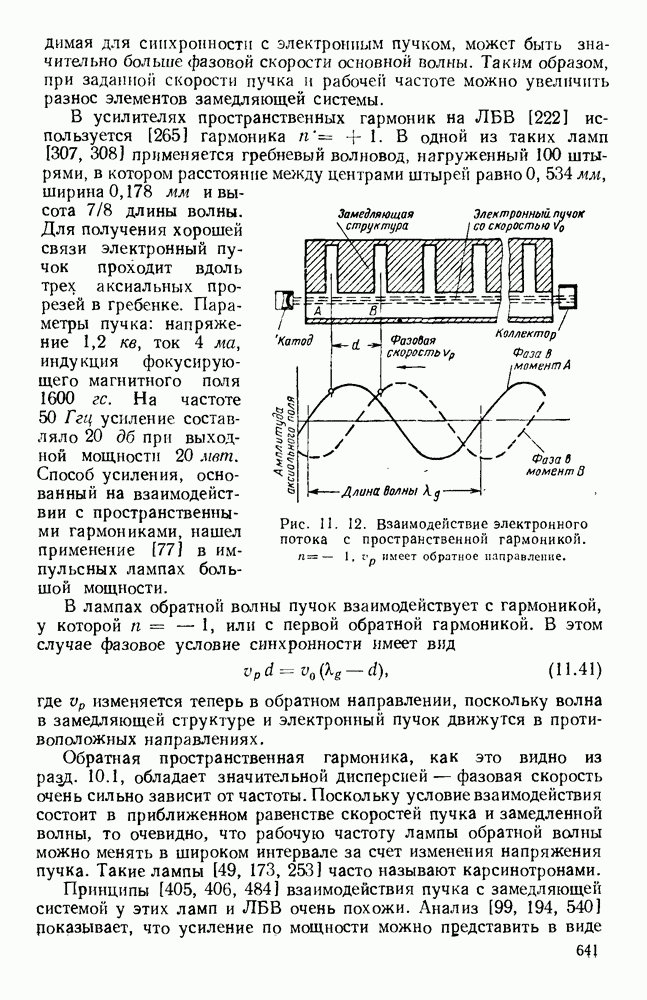
Давно известно [114, 168—180, 185—211, 217—222], что электромагнитные волны распространяются внутри полых проводников и что в этом случае электрическое или магнитное поля могут иметь
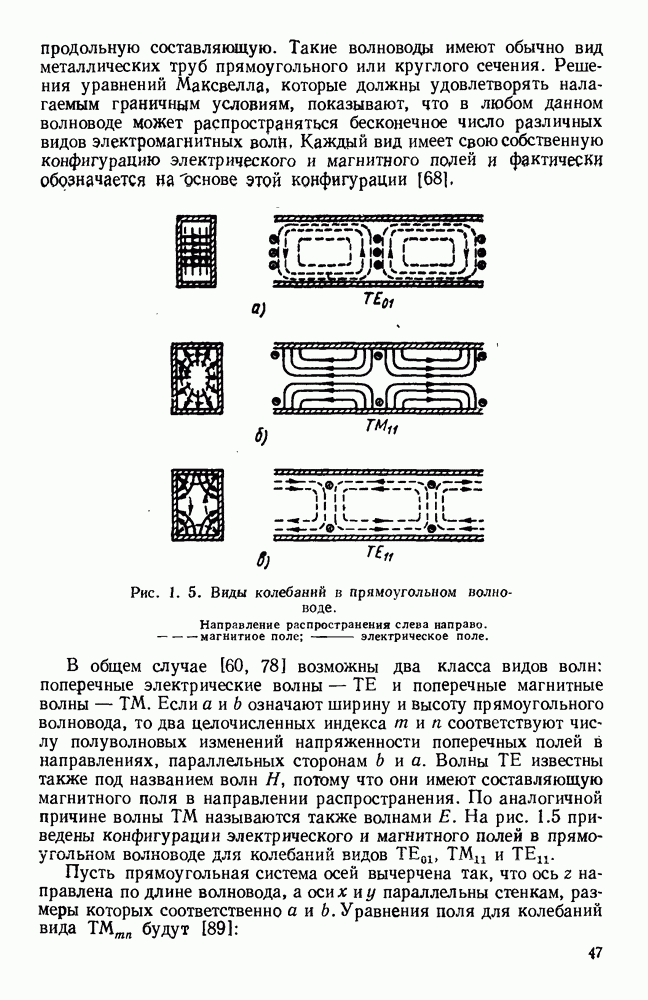
продольную составляющую. Такие волновода имеют обычно вид металлических труб прямоугольного или круглого сечения. Решения уравнений Максвелла, которые должны удовлетворять налагаемым граничным условиям, показывают, что в любом данном волноводе может распространяться бесконечное число различных видов электромагнитных волй, Каждый вид имеет свою собственную конфигурацию электрического и магнитного полей и фактически обозначается на основе этой конфигурации [681,

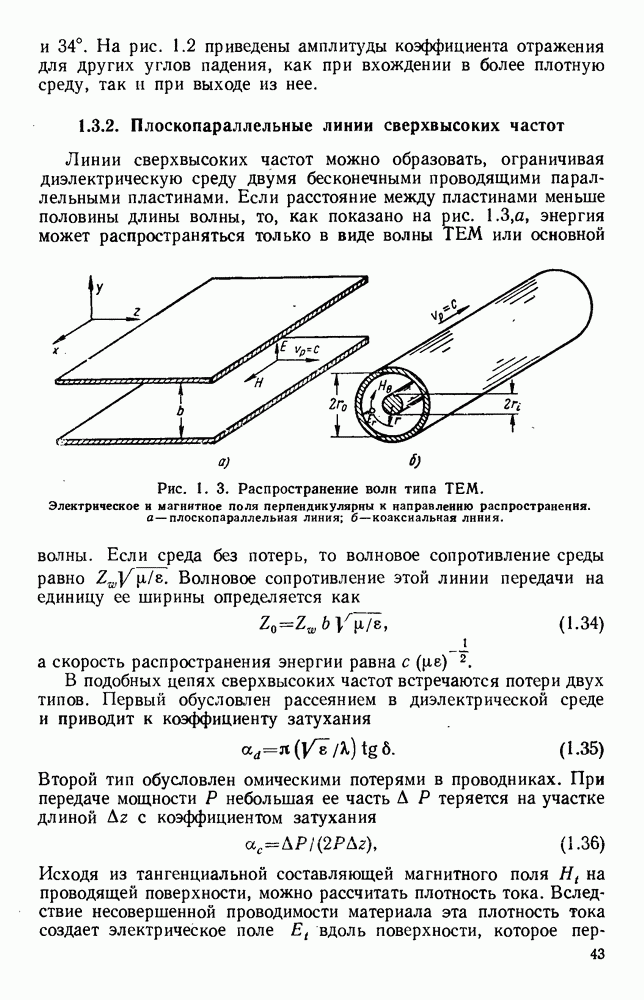
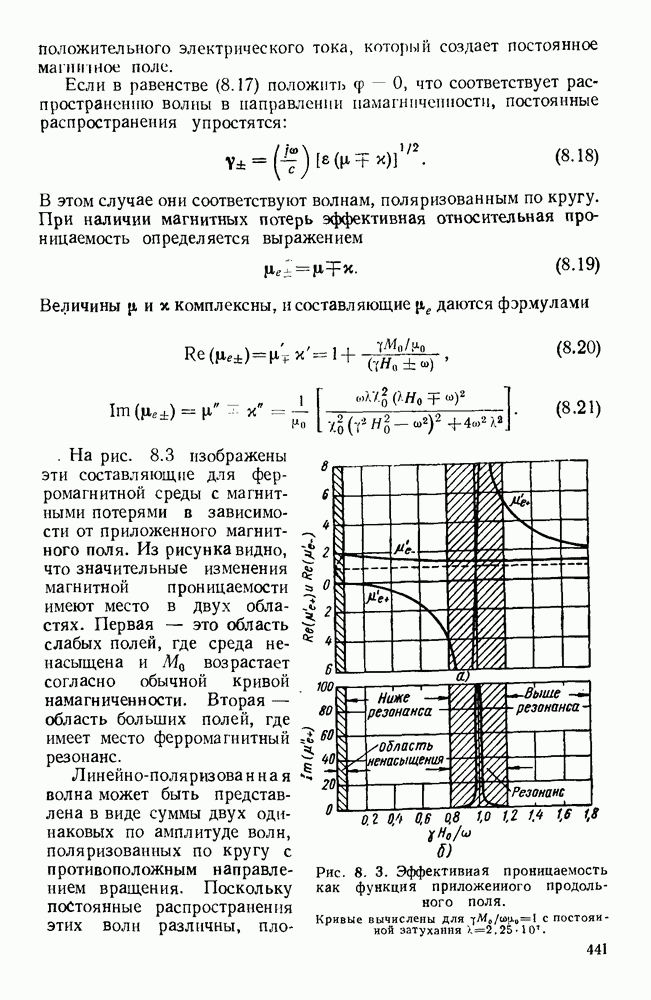
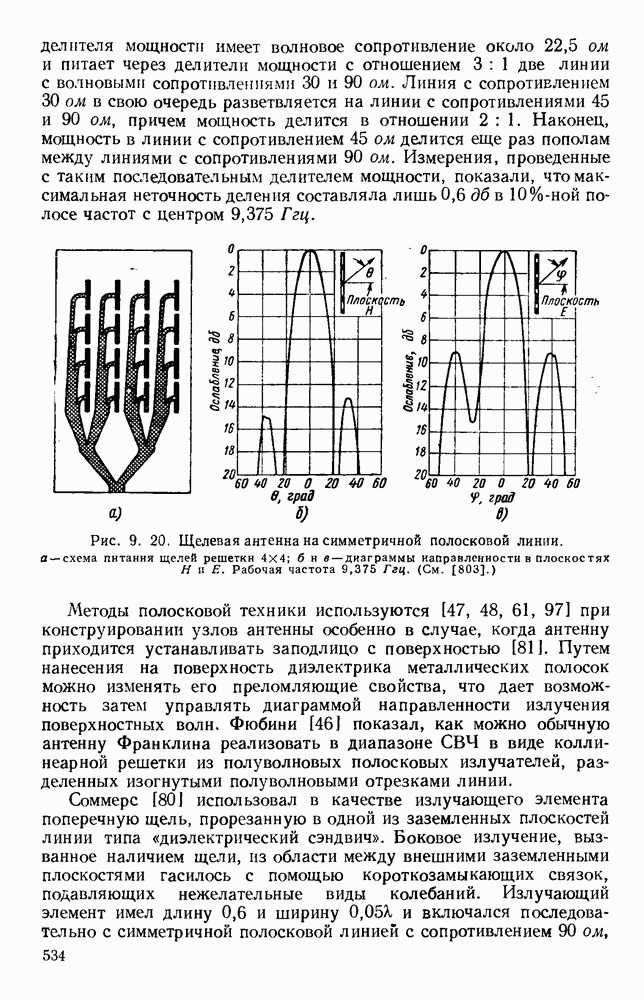
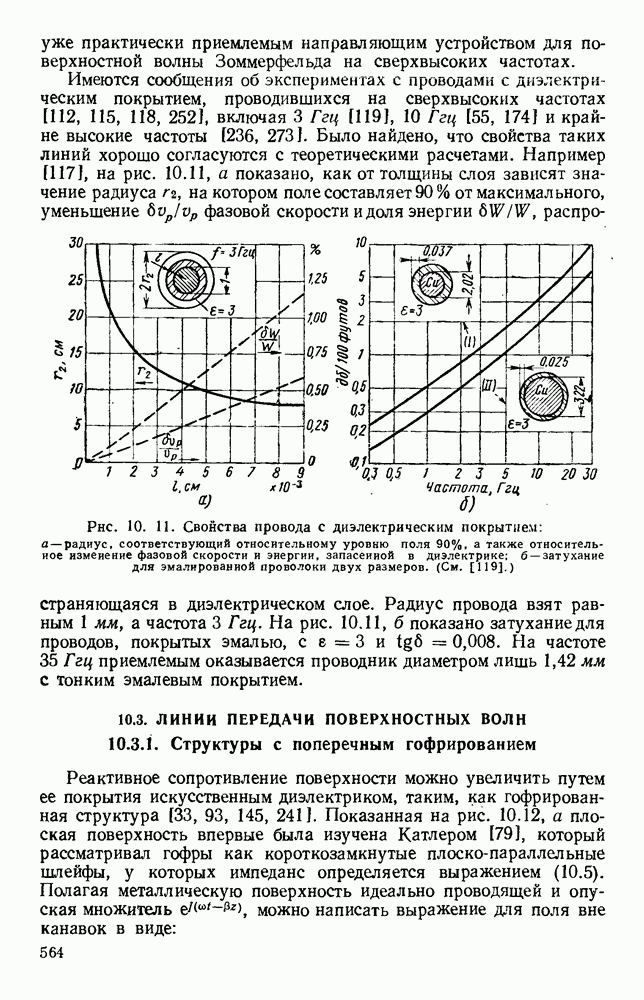
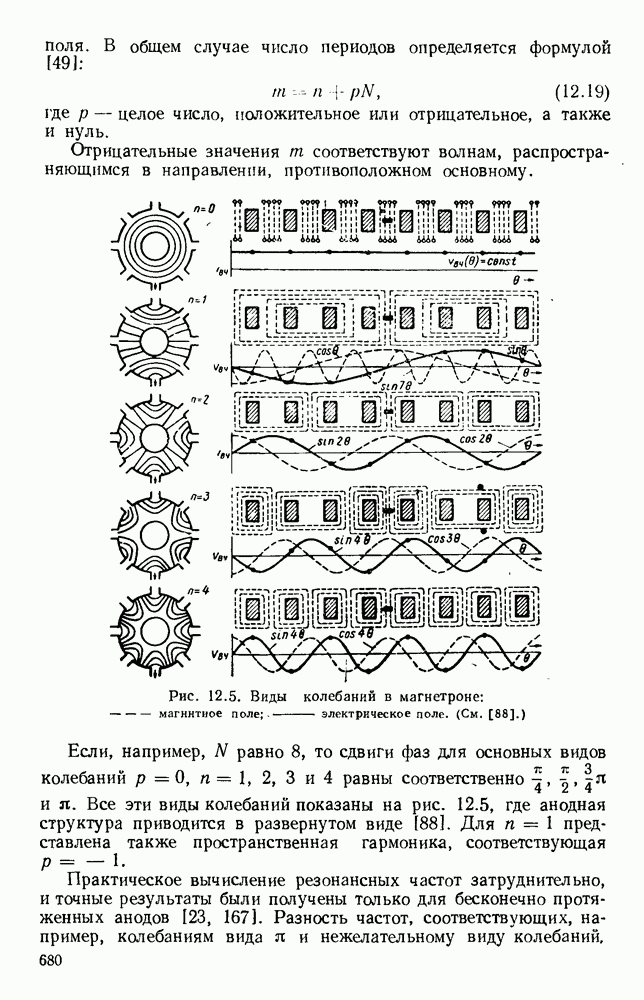
Рис. 1. 5. Виды колебаний в прямоугольном волноводе. Направление распространения слева направо.  магнитное поле;
магнитное поле;  электрическое поле.
электрическое поле.
В общем случае [60, 78] возможны два класса видов волн: поперечные электрические волны — ТЕ и поперечные магнитные волны — ТМ. Если а и  означают ширину и высоту прямоугольного волновода, то два целочисленных индекса тип соответствуют числу полуволновых изменений напряженности поперечных полей в направлениях, параллельных сторонам
означают ширину и высоту прямоугольного волновода, то два целочисленных индекса тип соответствуют числу полуволновых изменений напряженности поперечных полей в направлениях, параллельных сторонам  и а. Волны ТЕ известны также под названием волн Н, потому что они имеют составляющую магнитного поля в направлении распространения. По аналогичной причине волны ТМ называются также волнами Е. На рис. 1.5 приведены конфигурации электрического и магнитного полей в прямоугольном волноводе для колебаний видов
и а. Волны ТЕ известны также под названием волн Н, потому что они имеют составляющую магнитного поля в направлении распространения. По аналогичной причине волны ТМ называются также волнами Е. На рис. 1.5 приведены конфигурации электрического и магнитного полей в прямоугольном волноводе для колебаний видов  и ТЕ.
и ТЕ.
Пусть прямоугольная система осей вычерчена так, что ось  направлена по длине волновода, а осих и у параллельны стенкам, размеры которых соответственно а и 6. Уравнения поля для колебаний вида
направлена по длине волновода, а осих и у параллельны стенкам, размеры которых соответственно а и 6. Уравнения поля для колебаний вида  будут [89]:
будут [89]:

Для колебаний вида  уравнения имеют вид:
уравнения имеют вид:

В уравнениях (1.51)-(1.54)  - произвольные постоянные амплитуды, а
- произвольные постоянные амплитуды, а

Уравнение (1.55) показывает, что для угловой частоты существует предельное или критическое значение:

ниже которого распространение энергии прекращается. Это соотношение можно переписать, используя предельную длину волны:

Подставляя уравнение (1.58) в (1.55) и полагая  получаем выражение для длины волны в волноводе:
получаем выражение для длины волны в волноводе:

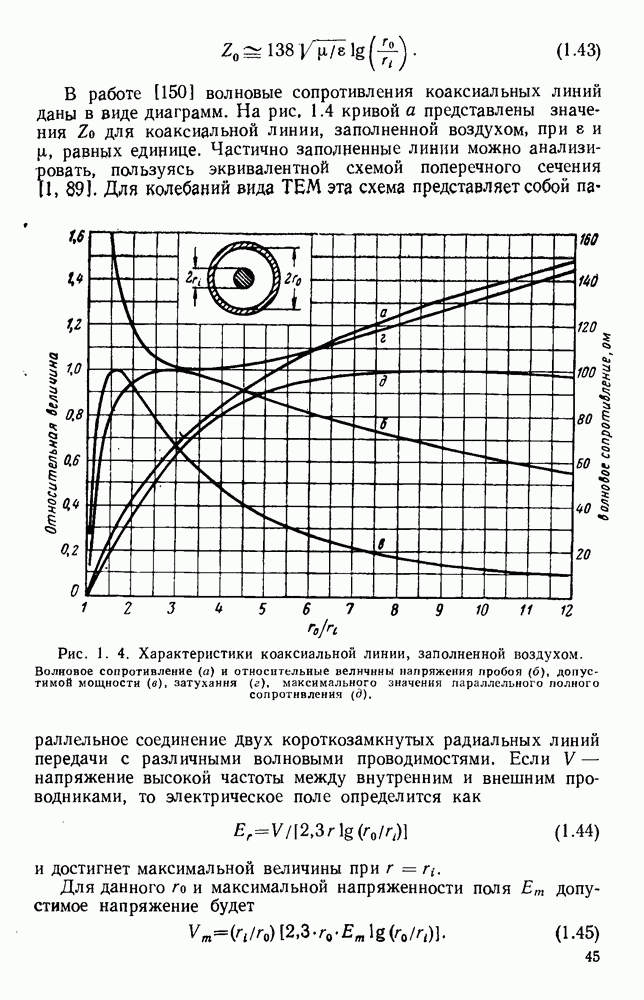
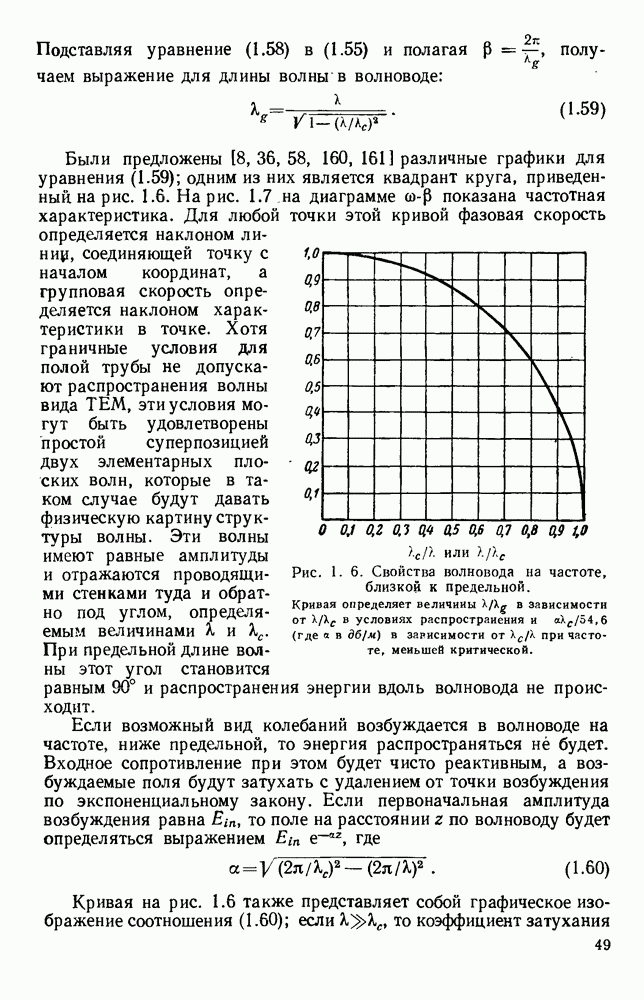
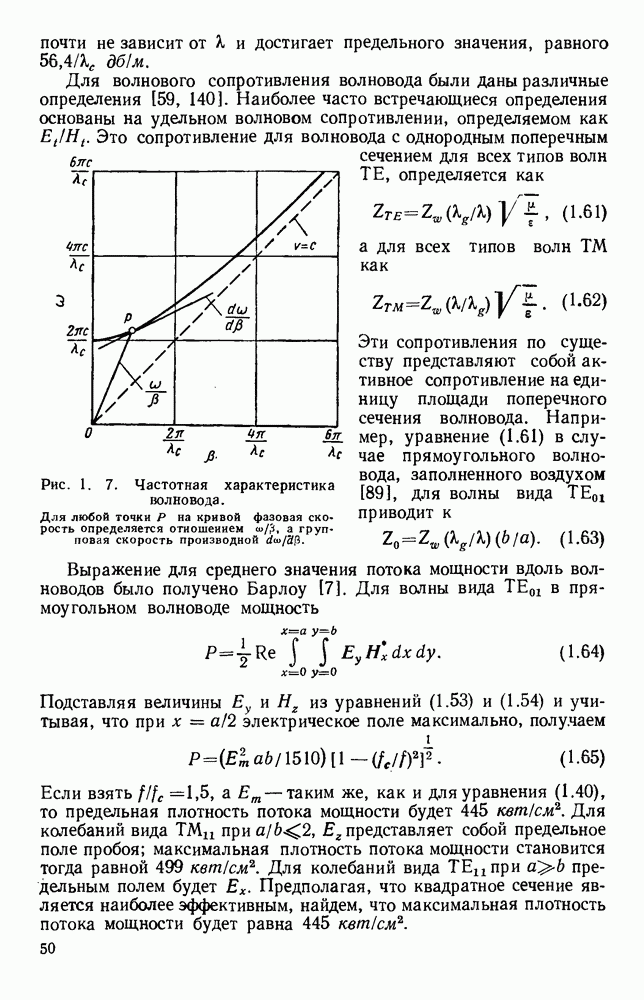
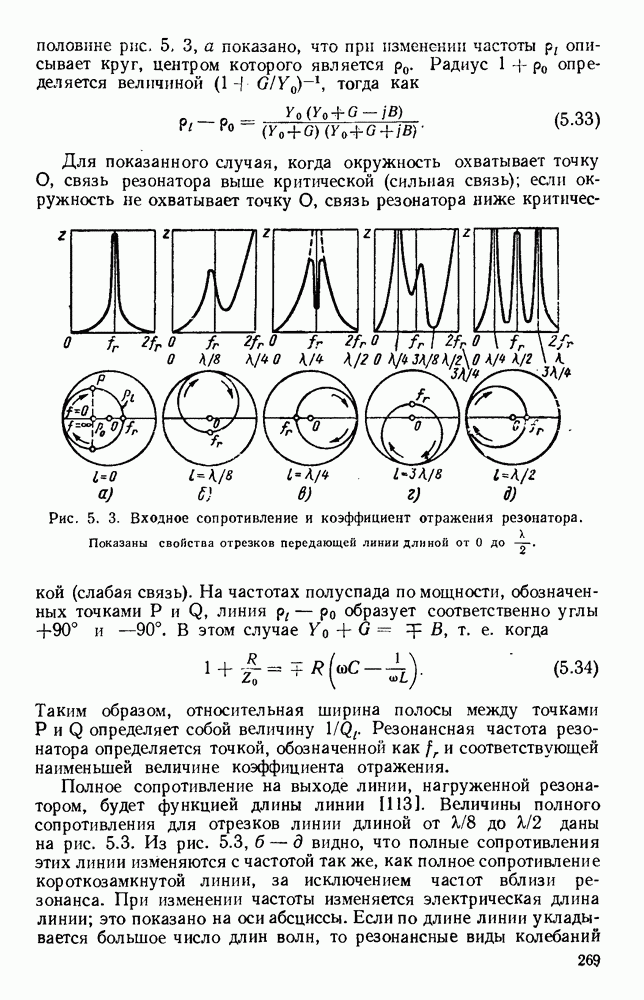
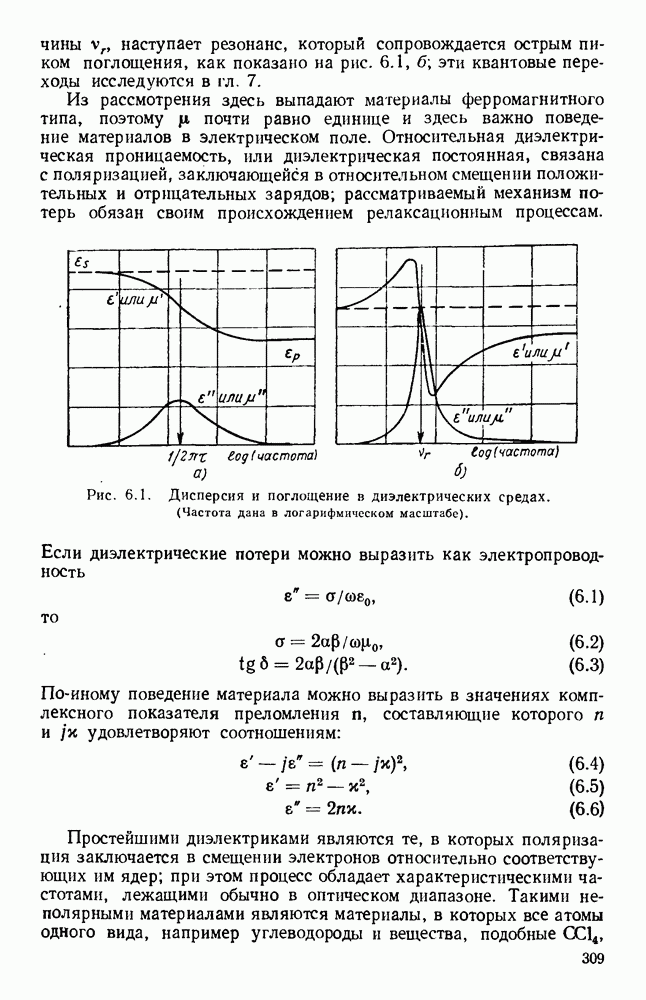
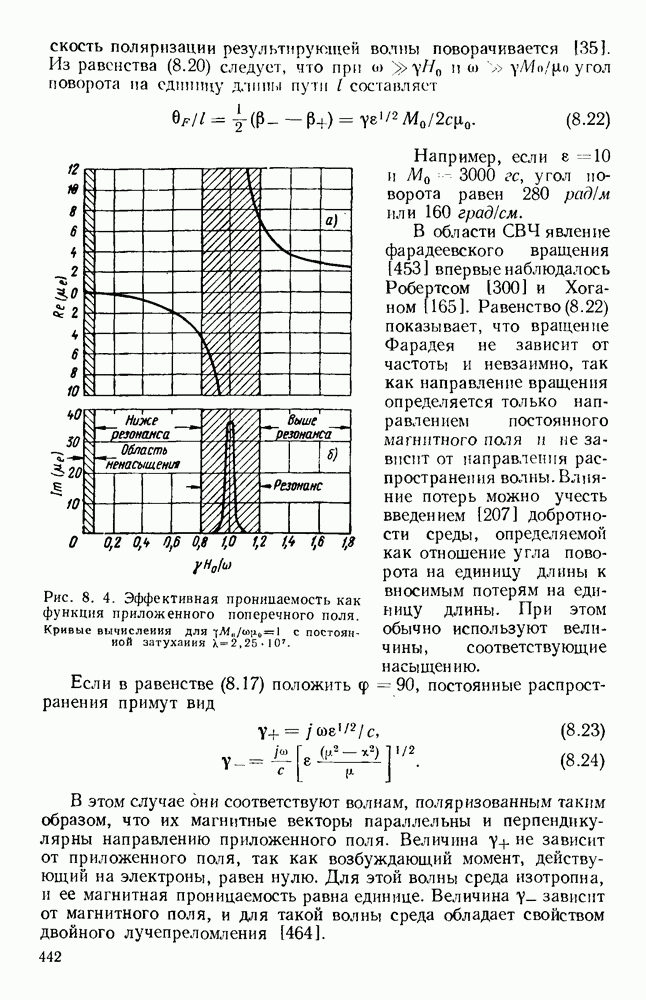
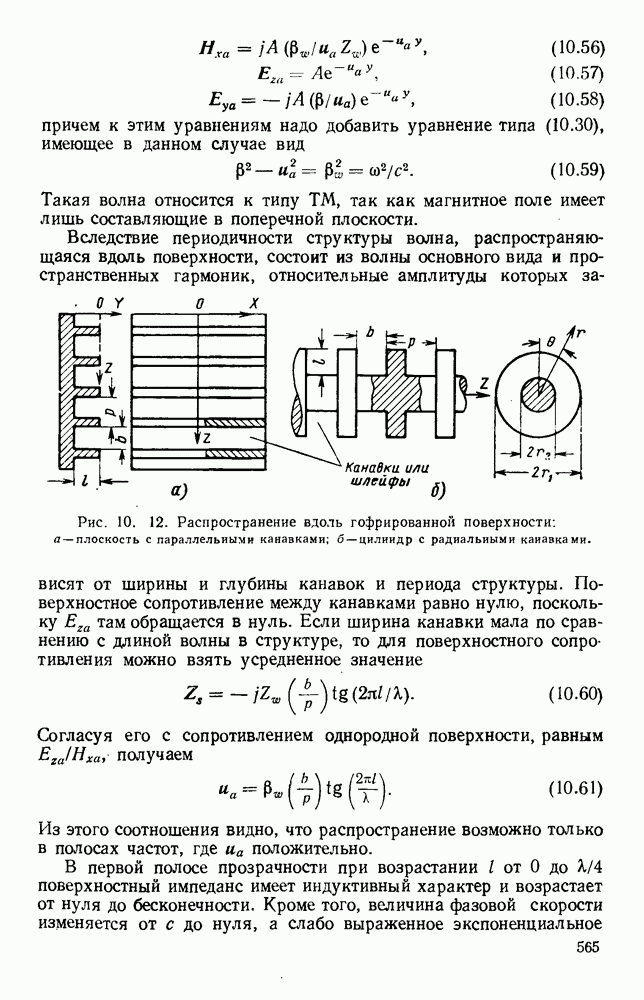
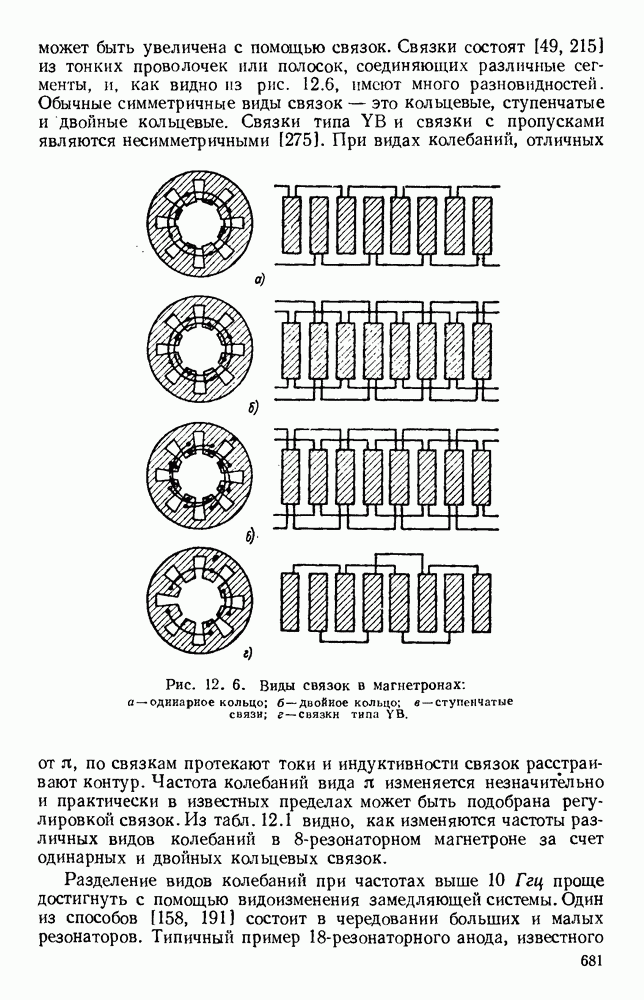
Были предложены [8, 36, 58, 160, 161] различные графики для уравнения (1.59); одним из них является квадрант круга, приведенный, на рис. 1.6. На рис. 1.7 на диаграмме  показана частотная характеристика. Для любой точки этой кривой фазовая скорость определяется наклоном линии, соединяющей точку с началом координат, а групповая скорость определяется наклоном характеристики в точке. Хотя граничные условия для полой трубы не допускают распространения волны вида ТЕМ, эти условия могут быть удовлетворены простой суперпозицией двух элементарных плоских волн, которые в таком случае будут давать физическую картину структуры волны. Эти волны имеют равные амплитуды и отражаются проводящими стенками туда и обратно под углом, определяемым величинами а, и
показана частотная характеристика. Для любой точки этой кривой фазовая скорость определяется наклоном линии, соединяющей точку с началом координат, а групповая скорость определяется наклоном характеристики в точке. Хотя граничные условия для полой трубы не допускают распространения волны вида ТЕМ, эти условия могут быть удовлетворены простой суперпозицией двух элементарных плоских волн, которые в таком случае будут давать физическую картину структуры волны. Эти волны имеют равные амплитуды и отражаются проводящими стенками туда и обратно под углом, определяемым величинами а, и 

Рис. 1. 6. Свойства волновода на частоте, близкой к предельной.
Кривая определяет величины  в зависимости от
в зависимости от  в условиях распространения и
в условиях распространения и  (где
(где  ) в зарисимости от
) в зарисимости от  при частоте, меньшей критической.
при частоте, меньшей критической.
При предельной длине волны этот угол становится равным 90° и распространения энергии вдоль волновода не происходит.
Если возможный вид колебаний возбуждается в волноводе на частоте, ниже предельной, то энергия распространяться не будет. Входное сопротивление при этом будет чисто реактивным, а возбуждаемые поля будут затухать с удалением от точки возбуждения по экспоненциальному закону. Если первоначальная амплитуда возбуждения равна  то поле на расстоянии
то поле на расстоянии  по волноводу будет определяться выражением
по волноводу будет определяться выражением  где
где

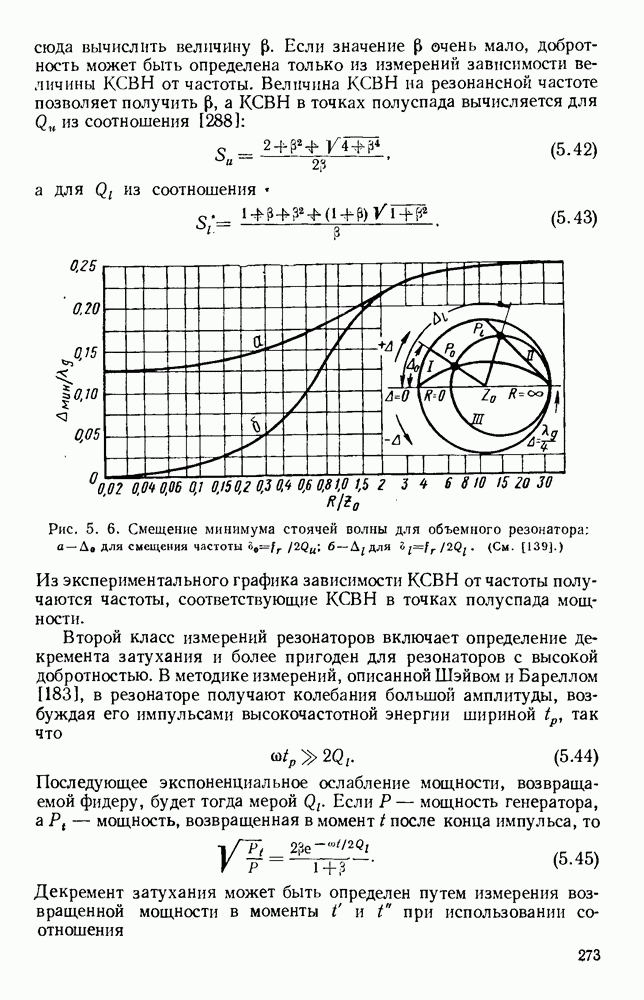
Кривая на рис. 1.6 также представляет собой графическое изображение соотношения (1.60); если то коэффициент затухания
почти не зависит от А, и достигает предельного значения, равного 
Для волнового сопротивления волновода были даны различные определения [59, 140]. Наиболее часто встречающиеся определения основаны на удельном волновом сопротивлении, определяемом как  Это сопротивление для волновода с однородным поперечным сечением для всех типов волн ТЕ, определяется как
Это сопротивление для волновода с однородным поперечным сечением для всех типов волн ТЕ, определяется как

а для всех типов волн ТМ как


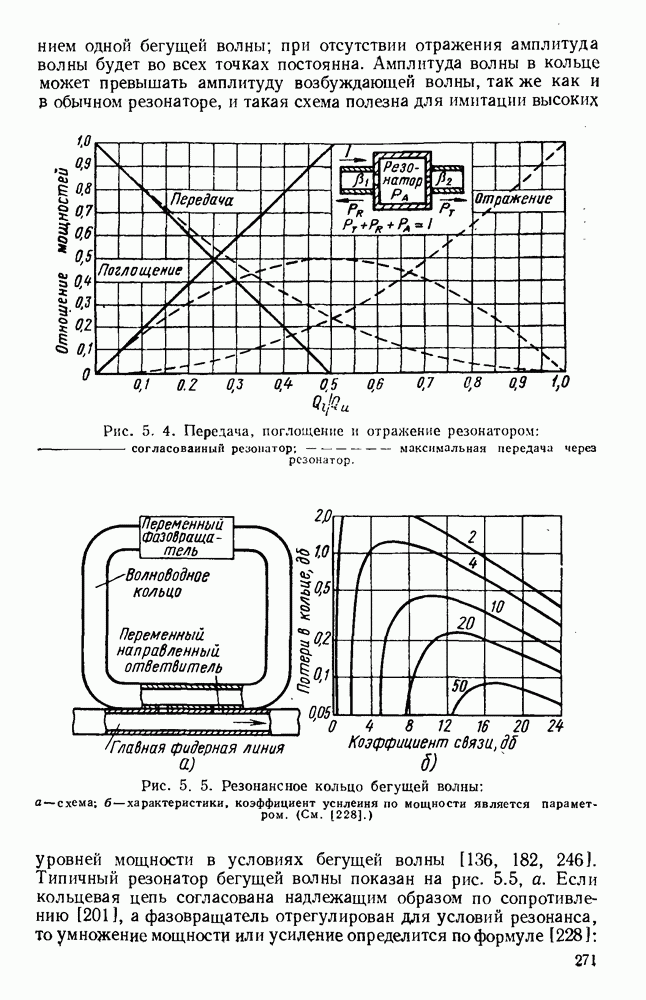
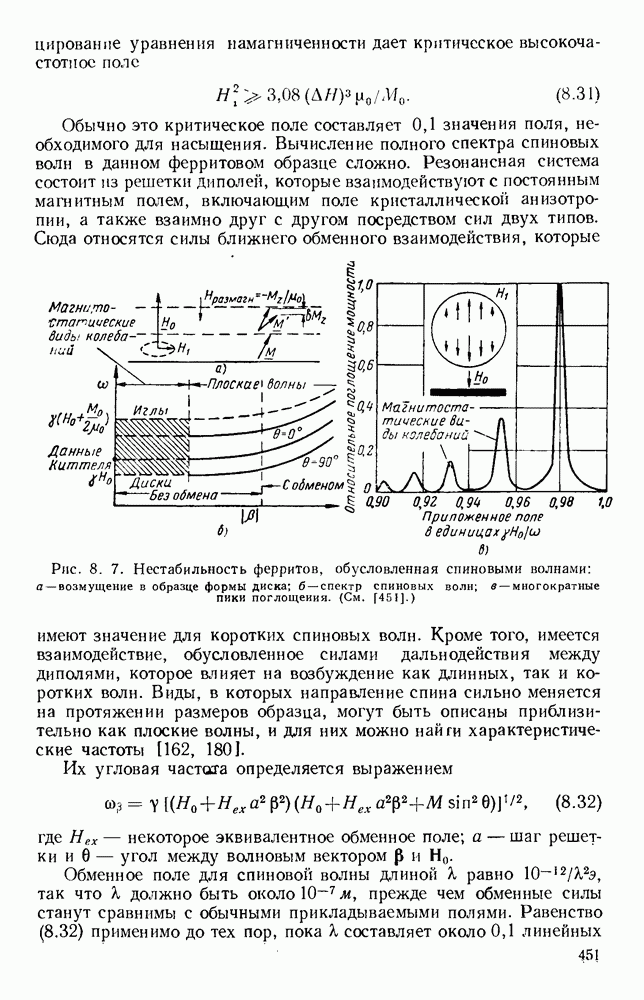
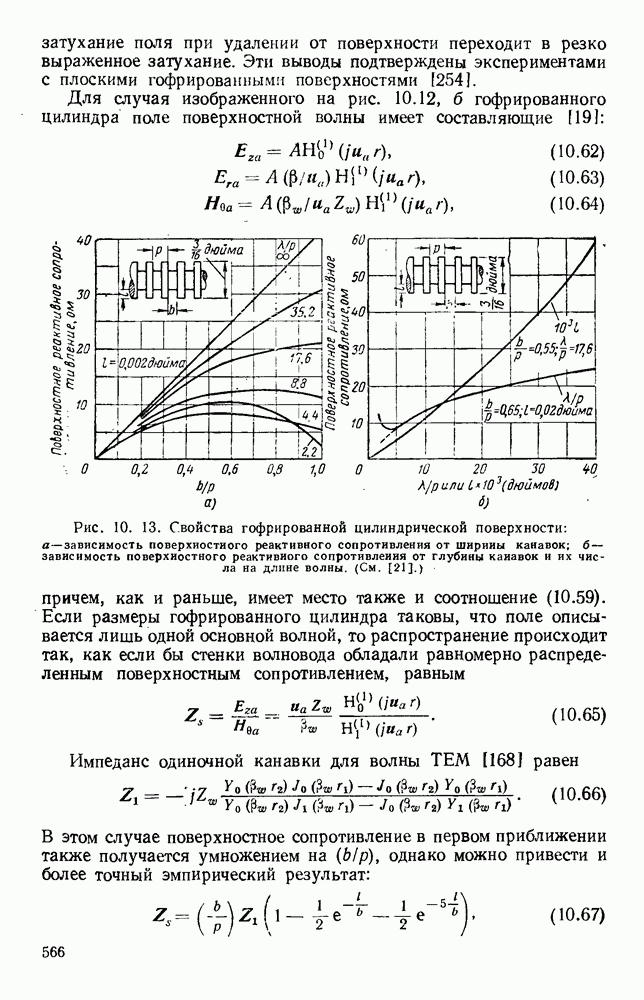
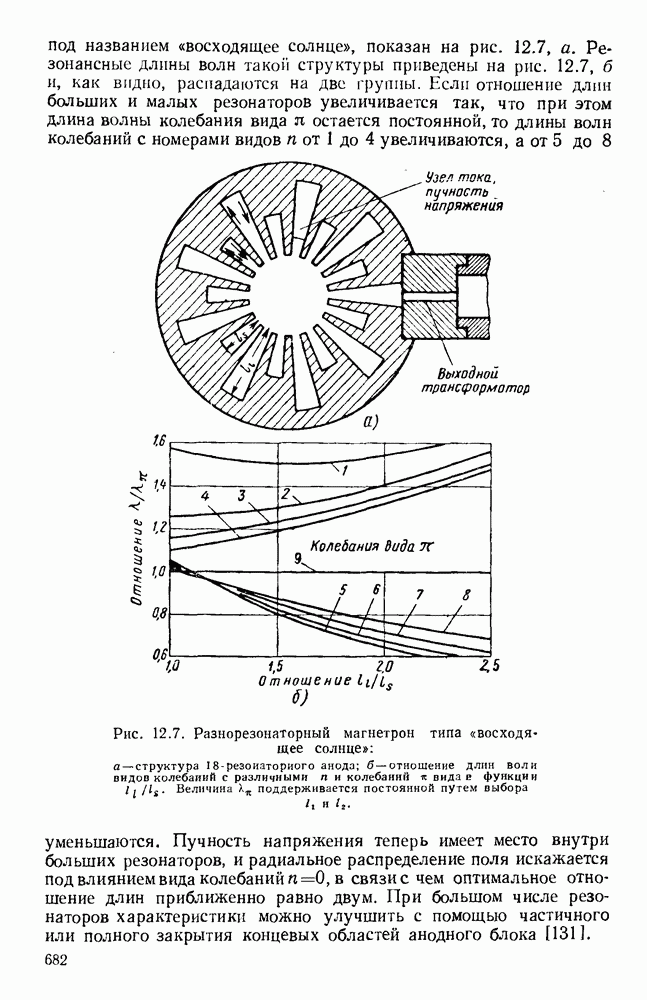
Рис. 1. 7. Частотная характеристика волновода.
Для любой точки Р на кривой фазовая ско рость определяется отношением  а груп повая скорость производной
а груп повая скорость производной 
Эти сопротивления по существу представляют собой активное сопротивление на единицу площади поперечного сечения волновода. Например, уравнение (1.61) в случае прямоугольного волновода, заполненного воздухом [89], для волны вида  приводит к
приводит к

Выражение для среднего значения потока мощности вдоль волноводов было получено Барлоу [7]. Для волны вида  в прямоугольном волноводе мощность
в прямоугольном волноводе мощность

Подставляя величины  из уравнений (1.53) и (1.54) и учитывая, что при
из уравнений (1.53) и (1.54) и учитывая, что при  электрическое поле максимально,
электрическое поле максимально, 

Если взять  таким же, как и для уравнения (1.40), то предельная плотность потока мощности будет
таким же, как и для уравнения (1.40), то предельная плотность потока мощности будет  Для колебаний вида
Для колебаний вида  представляет собой предельное поле пробоя; максимальная плотность потока мощности становится тогда равной
представляет собой предельное поле пробоя; максимальная плотность потока мощности становится тогда равной  Для колебаний вида
Для колебаний вида  предельным полем будет
предельным полем будет  Предполагая, что квадратное сечение является наиболее эффективным, найдем, что максимальная плотность потока мощности будет равна
Предполагая, что квадратное сечение является наиболее эффективным, найдем, что максимальная плотность потока мощности будет равна 
Потери в волноводе, обусловленные конечной проводимостью материала стенок, зависят [77] от формы поперечного сечения, вида колебаний и отношения  Для прямоугольных медных волноводов, заполненных воздухом и работающих в режиме колебаний вида
Для прямоугольных медных волноводов, заполненных воздухом и работающих в режиме колебаний вида  коэффициент затухания в децибелах на метр [97] равен
коэффициент затухания в децибелах на метр [97] равен

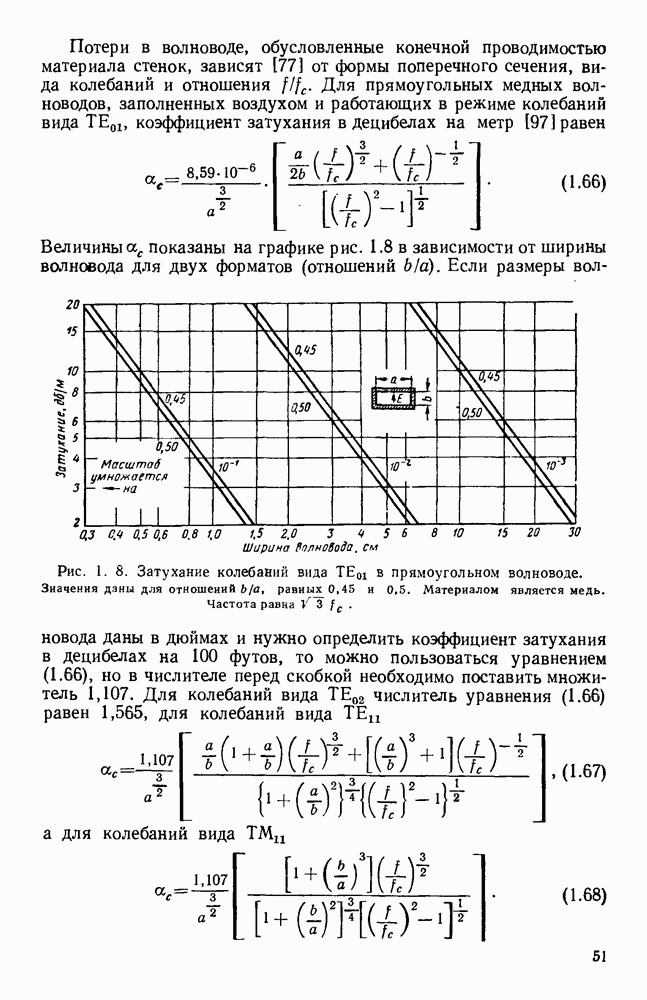
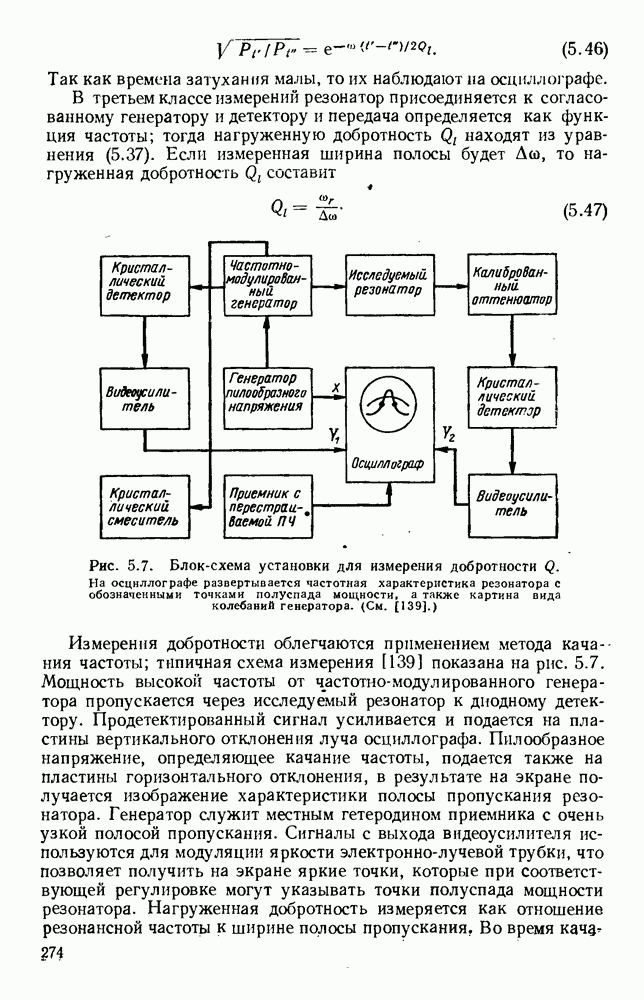
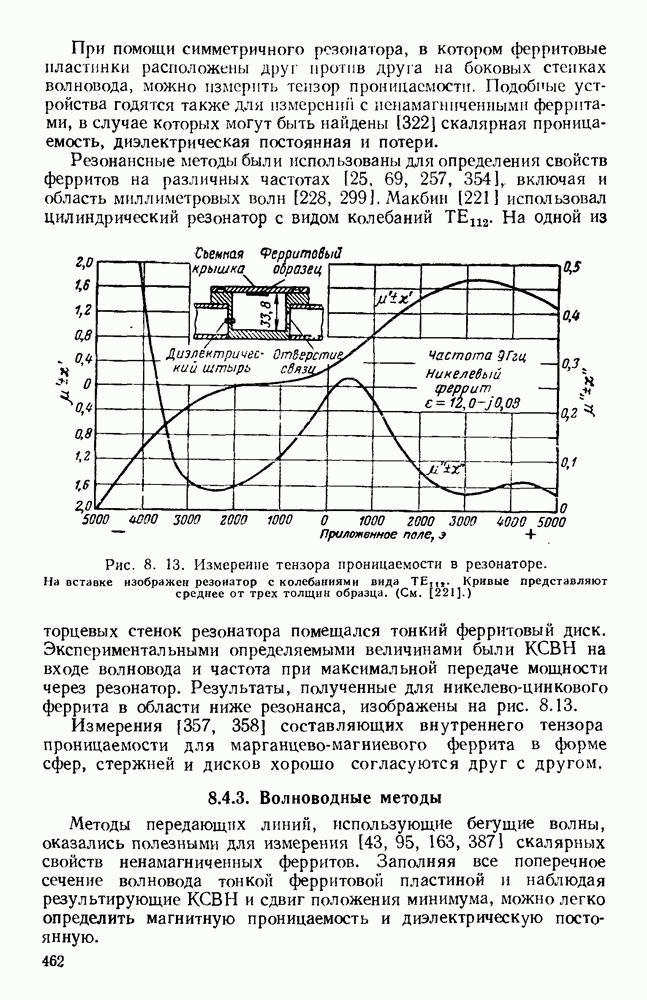
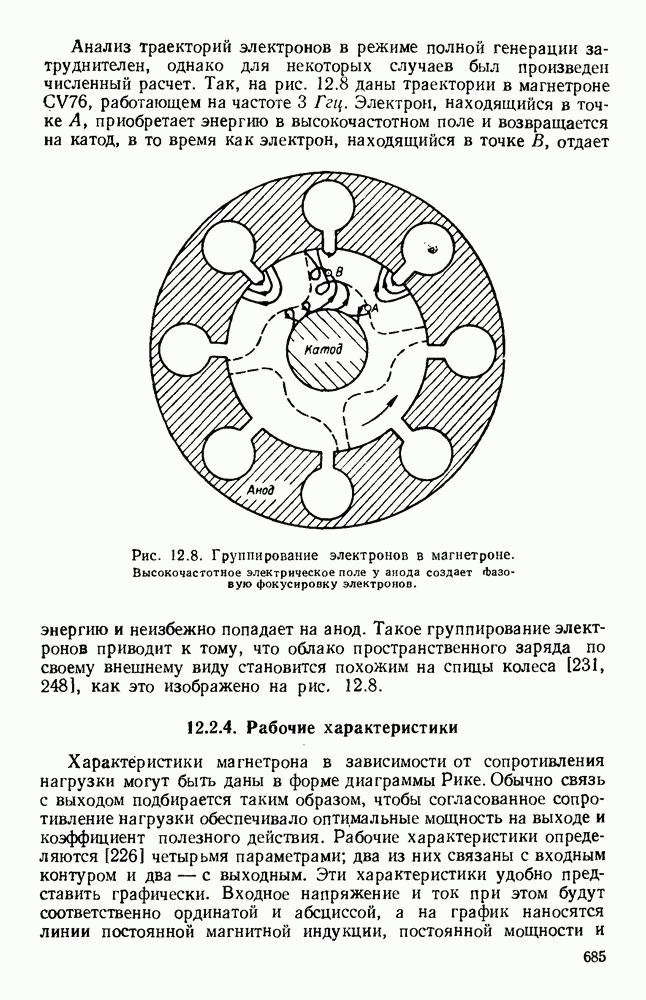
Величины показаны на графике рис. 1.8 в зависимости от ширины волновода для двух форматов (отношений 

Рис. 1. 8. Затухание колебаний вида  в прямоугольном волноводе. Значения даны для отношений
в прямоугольном волноводе. Значения даны для отношений  равных 0,45 и 0,5. Материалом является медь. Частота равна
равных 0,45 и 0,5. Материалом является медь. Частота равна 
Если размеры волновода даны в дюймах и нужно определить коэффициент затухания в децибелах на 100 футов, то можно пользоваться уравнением (1.66), но в числителе перед скобкой необходимо поставить множитель 1,107. Для колебаний вида  числитель уравнения (1.66) равен 1,565, для колебаний вида
числитель уравнения (1.66) равен 1,565, для колебаний вида 

а для колебаний вида 

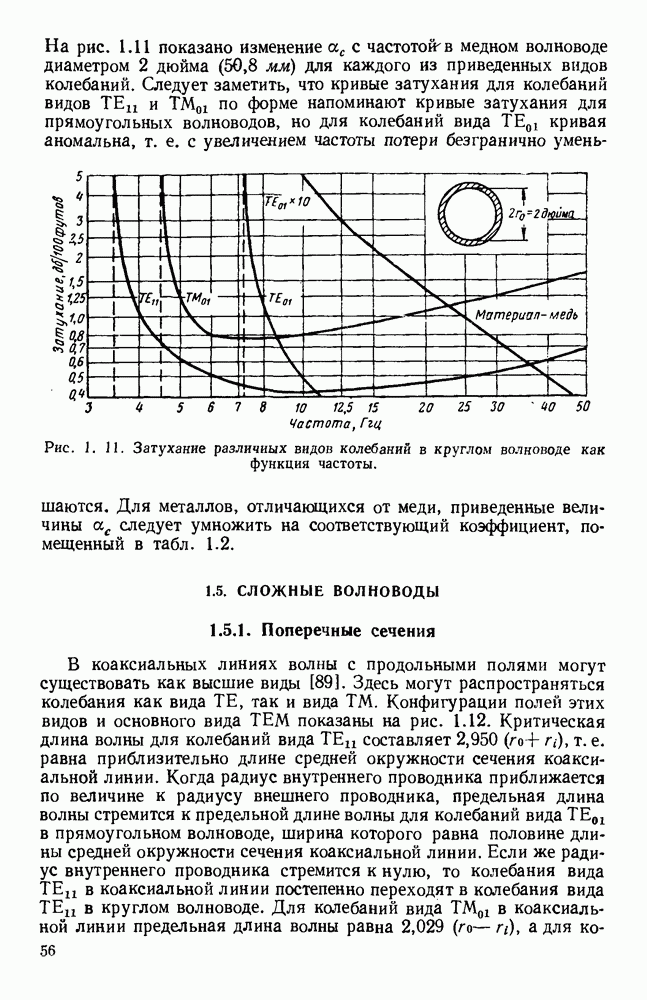
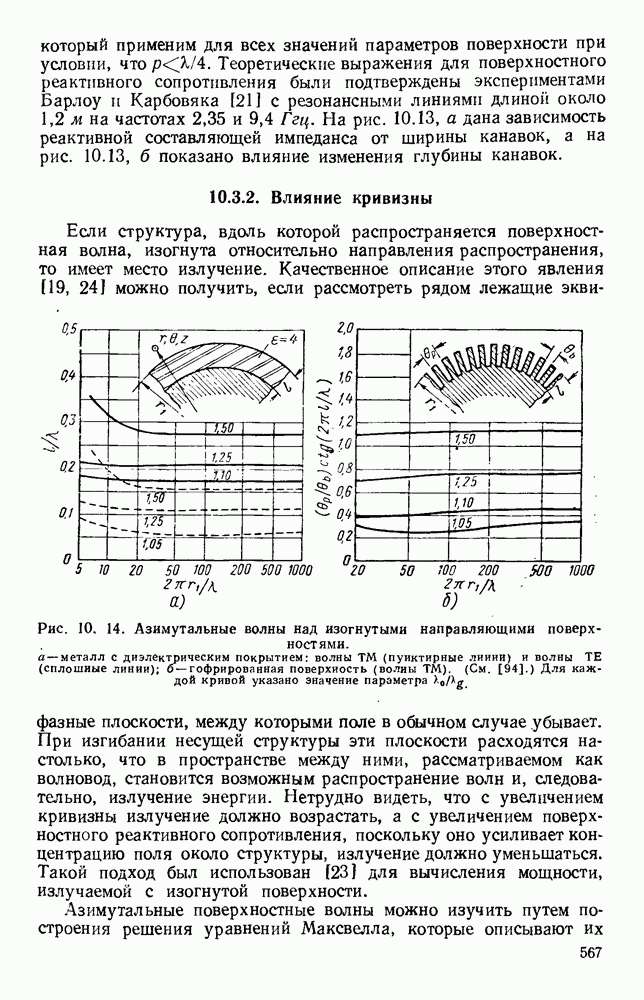
Эти величины  приведены на графике рис. 1.9 в функции частоты для волновода с размерами поперечного сечения
приведены на графике рис. 1.9 в функции частоты для волновода с размерами поперечного сечения  дюйма
дюйма  Из графика видно, что коэффициент затухания велик на высоких частотах, а также вблизи предельной частоты и падает до минимума между этими частотами.
Из графика видно, что коэффициент затухания велик на высоких частотах, а также вблизи предельной частоты и падает до минимума между этими частотами.

Рис. 1. 9. Затухание различных лидов колебаний в прямоугольном волноводе как функция частоты.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА
- ОБОЗНАЧЕНИЯ
- ГЛАВА 1. РАСПРОСТРАНЕНИЕ ВОЛН В ЦЕПЯХ
- 1.1. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ СВЕРХВЫСОКИХ ЧАСТОТ КАК ЭЛЕКТРОМАГНИТНОЕ ИЗЛУЧЕНИЕ
- 1.2. СВОЙСТВА МАТЕРИАЛОВ
- 1.2.2. Металлические проводники
- 1.2.3. Полупроводники
- 1.3. ВОЛНЫ С ЧИСТО ПОПЕРЕЧНЫМИ ПОЛЯМИ
- 1.3.2. Плоскопараллельные линии сверхвысоких частот
- 1.3.3. Коаксиальные линии
- 1.4. ВОЛНЫ В ПОЛЫХ ПРОВОДЯЩИХ ТРУБАХ
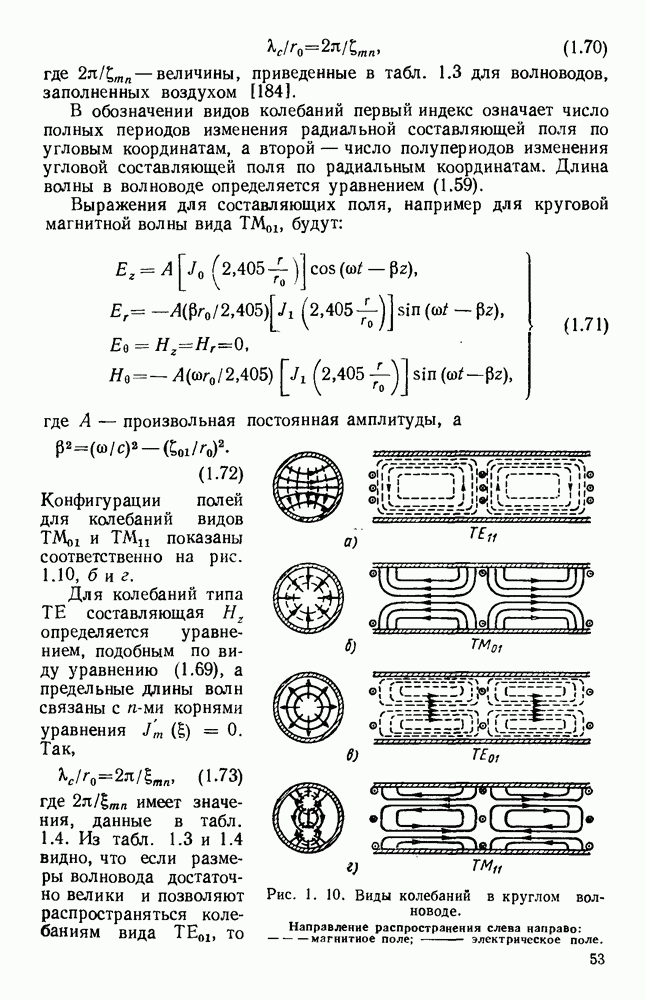
- 1.4.2. Круглые волноводы
- 1.5. СЛОЖНЫЕ ВОЛНОВОДЫ
- 1.5.2. Гребневые волноводы
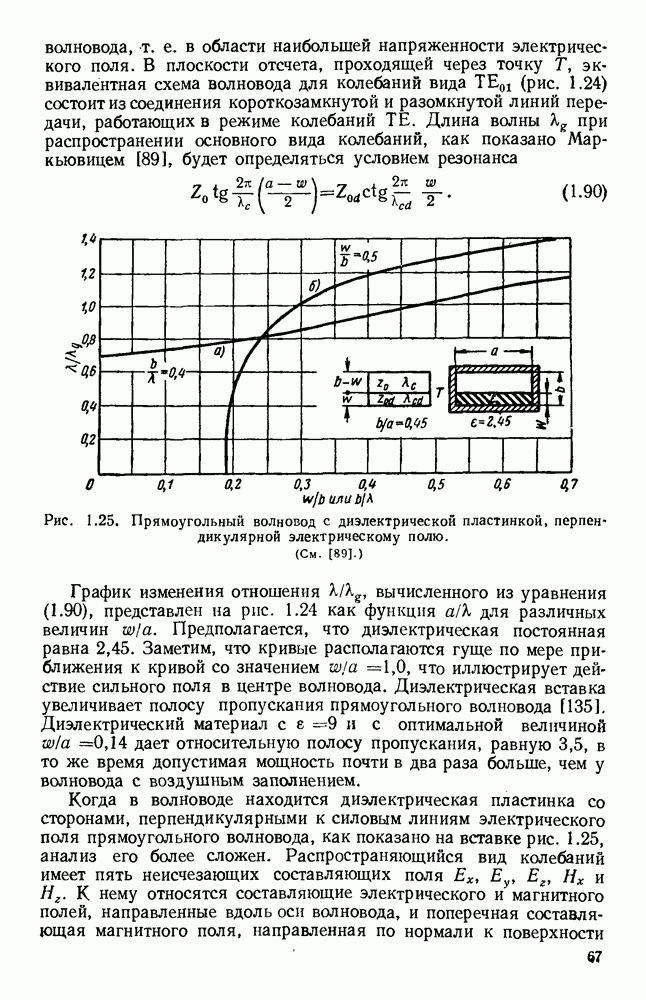
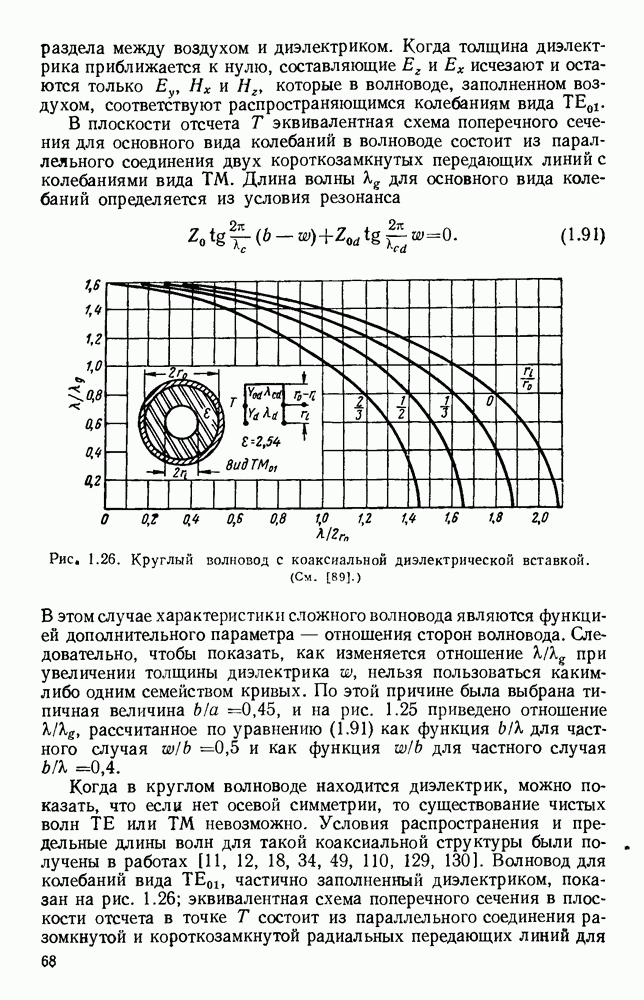
- 1.5.3. Волноводы, содержащие диэлектрик
- ГЛАВА 2. ПРАКТИЧЕСКИЕ ЛИНИИ ПЕРЕДАЧИ
- 2.1. ТЕОРИЯ ЛИНИИ ПЕРЕДАЧИ
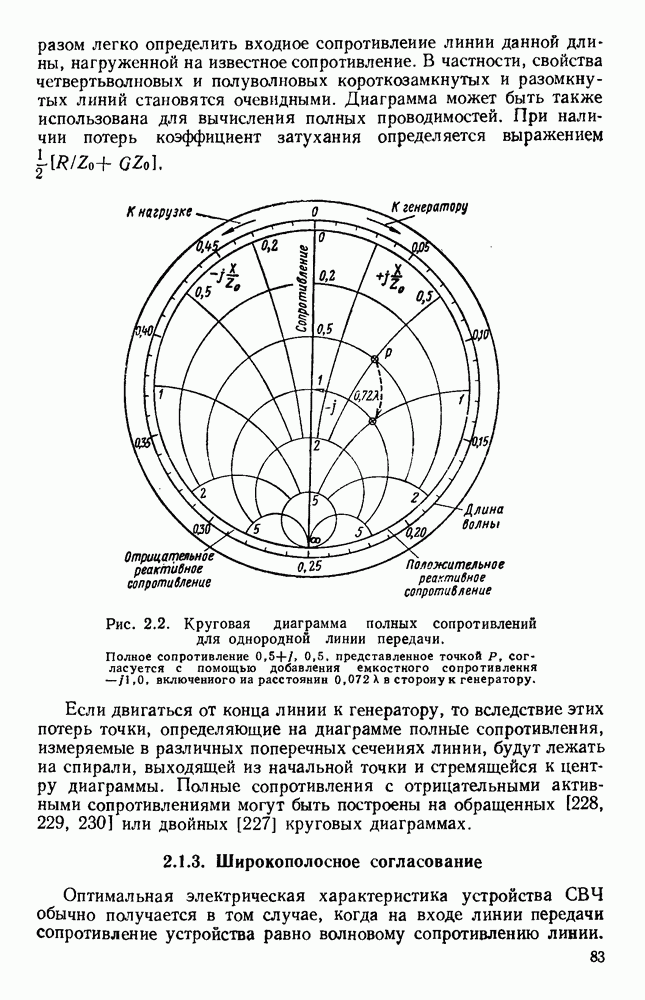
- 2.1.2. Круговая диаграмма
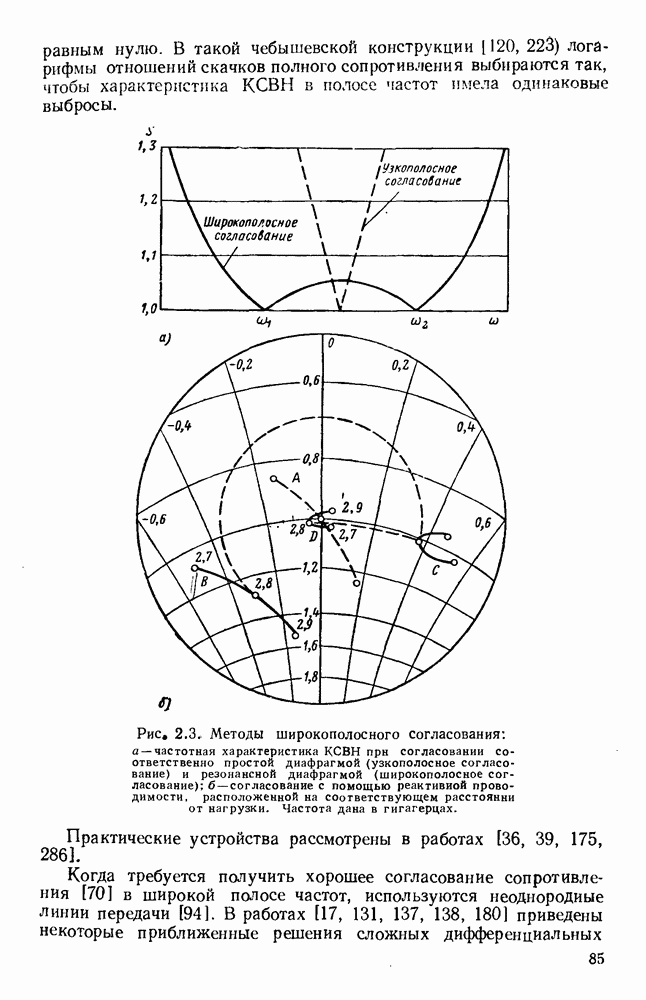
- 2.1.3. Широкополосное согласование
- 2.2. РАБОЧИЕ ПАРАМЕТРЫ
- 2.2.1. Перекрытие по частоте
- 2.2.2. Затухание
- 2.2.3. Допустимая мощность
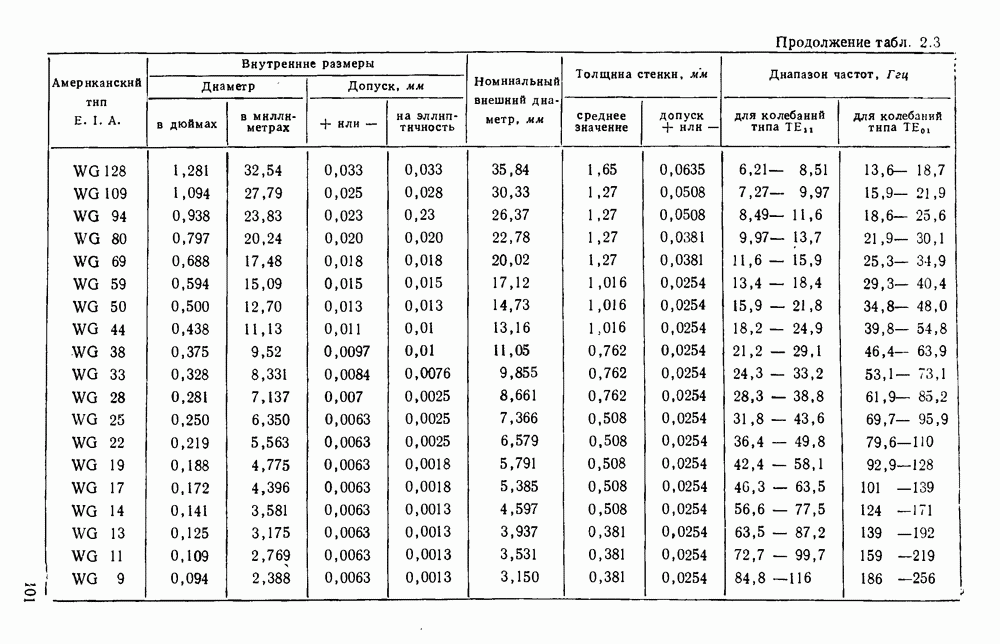
- 2.3. СТАНДАРТНЫЕ ВОЛНОВОДЫ
- 2.3.1. Прямоугольные волноводы
- 2.3.2. Круглые волноводы
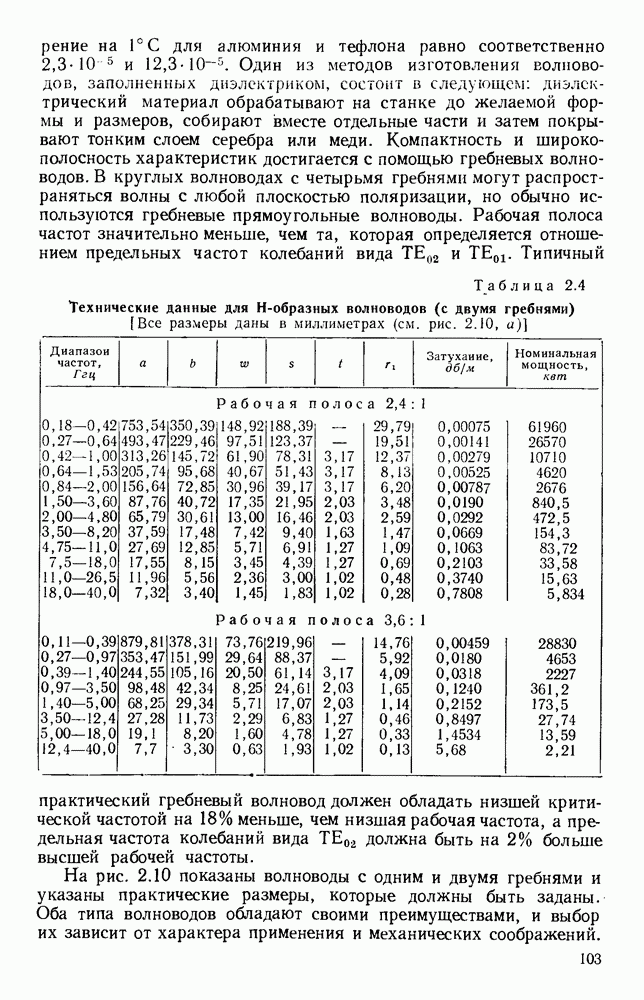
- 2.3.3. Широкополосные и компактные волноводы
- 2.4. МЕТОДЫ СОЕДИНЕНИЯ
- 2.4.1. Выравнивание волноводов
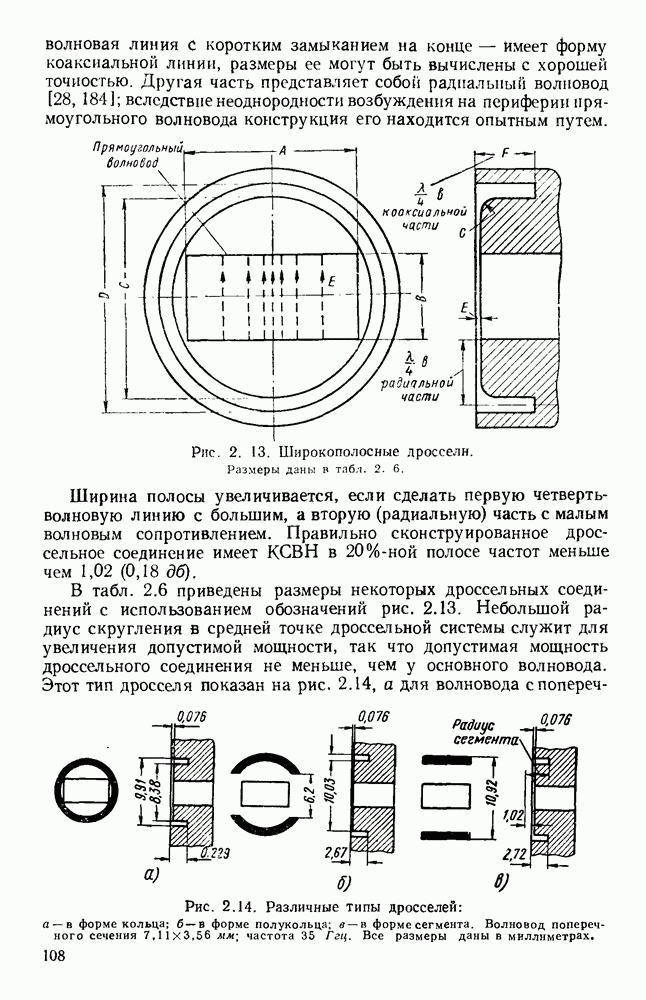
- 2.4.2. Контактные прокладки и дроссели
- 2.4.3. Крепежные и зажимные устройства
- 2.5. УПЛОТНЕНИЕ И ГЕРМЕТИЗАЦИЯ
- 2.5.1. Волноводные системы
- 2.5.2. Соединители и сочленения
- 2.6. ПРОСТЫЕ ПЕРЕХОДЫ
- 2.6.1. Изгибы, уголки и скрутки
- 2.6.2. Переходы и преобразователи
- 2.7. ГИБКИЕ ВОЛНОВОДЫ
- 2.7.2. Позвонковая модель
- ГЛАВА 3. ЭЛЕМЕНТЫ ЦЕПЕЙ И УЗЛЫ
- 3.1.2. Отверстия связи
- 3.1.3. Параллельные и последовательные тройники
- 3.2. ПРЕОБРАЗОВАТЕЛИ ВИДОВ КОЛЕБАНИЙ
- 3.2.1. Коаксиально-волноводные переходы
- 3.2.2. Переходы с прямоугольного волновода на круглый
- 3.2.3. Переход от линейной поляризации к круговой
- 3.3. НАПРАВЛЕННЫЕ ОТВЕТВИТЕЛИ
- 3.3.2. Распределенная связь
- 3.3.3. Системы с полной передачей мощности
- 3.4. ГИБРИДНЫЕ СОЕДИНЕНИЯ
- 3.4.1. Тип соединения с фазами, находящимися в квадратуре
- 3.4.2. Синфазные гибридные соединения
- 3.4.3. Различные гибридные соединения
- 3.5. РЕГУЛИРУЕМЫЕ ПОЛНЫЕ СОПРОТИВЛЕНИЯ
- 3.5.2. Подвижные вставки
- 3.5.3. Фазовращатели
- 3.6. ВРАЩАЮЩИЕСЯ СОЧЛЕНЕНИЯ
- 3.6.1. Вращающиеся сочленения с колебаниями кругового магнитного вида
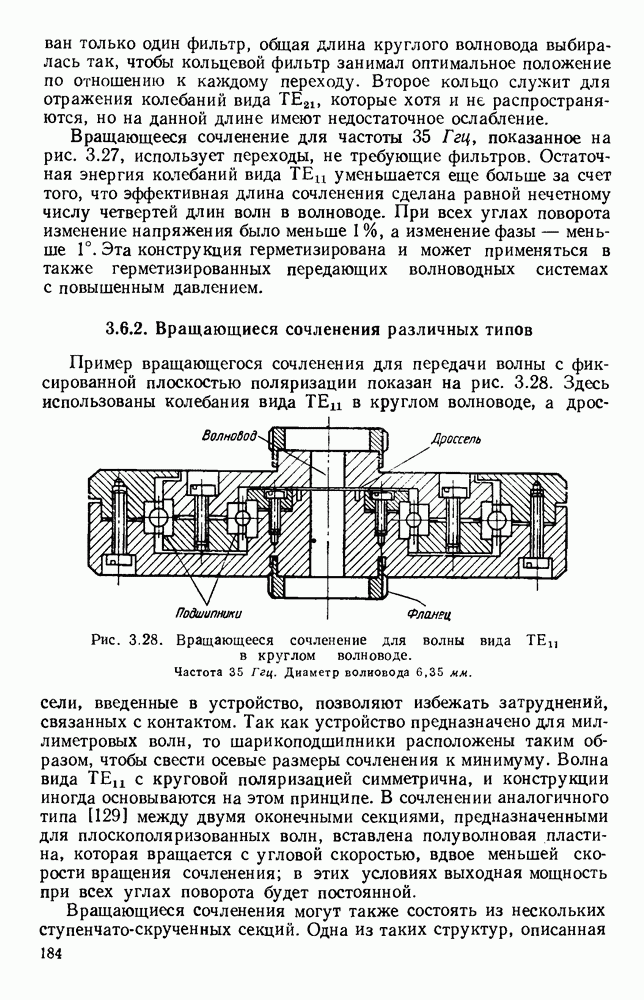
- 3.6.2. Вращающиеся сочленения различных типов
- 3.7. МЕХАНИЧЕСКИЕ ПЕРЕКЛЮЧАТЕЛИ
- 3.7.1. Механические переключатели с ручным управлением
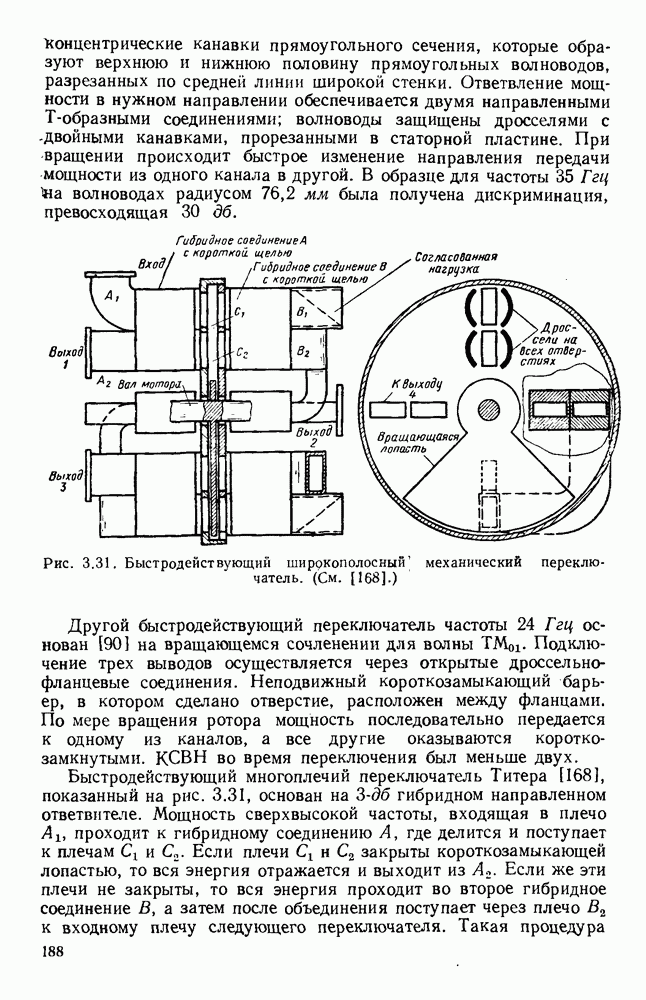
- 3.7.2. Быстродействующие переключатели
- ГЛАВА 4. МЕТОДЫ ИЗМЕРЕНИЙ И ПРИБОРЫ
- 4.1. ИЗМЕРЕНИЕ МОЩНОСТИ
- 4.1.2. Методы измерений, основанные на преобразовании мощности в тепловую энергию
- 4.1.3. Эффект Холла и давление излучения
- 4.2. ИЗМЕРЕНИЕ ЗАТУХАНИЯ
- 4.2.2. Фиксированные аттенюаторы и оконечные нагрузки
- 4.2.3. Переменные аттенюаторы
- 4.3. ИЗМЕРЕНИЕ ПОЛНЫХ СОПРОТИВЛЕНИЙ
- 4.3.2. Картина стоячей волны
- 4.3.3. Мостовые методы
- ГЛАВА 5. РЕЗОНАТОРЫ И ФИЛЬТРЫ
- 5.1.2. Свойства цепей
- 5.1.3. Измерения характеристик
- 5.2. ИЗМЕРЕНИЕ ДЛИНЫ ВОЛНЫ
- 5.2.1. Волномеры с объемными резонаторами
- 5.2.2. Волноводные интерферометры
- 5.3. ФИЛЬТРУЮЩИЕ ЦЕПИ
- 5.3.2. Связанные резонаторы
- 5.3.3. Четвертьволновая связь
- ГЛАВА 6. ХАРАКТЕРИСТИКИ МАТЕРИАЛОВ И МЕТОДЫ ИХ ИЗМЕРЕНИЙ
- 6.1.2. Методы измерений в свободном пространстве и в линии передачи
- 6.1.3. Методы измерений в объемном резонаторе
- 6.2. ЭКСПЕРИМЕНТЫ И РЕЗУЛЬТАТЫ
- 6.2.2. Жидкости
- 6.2.3. Твердые тела
- 6.3. ПРОВОДИМОСТЬ МЕТАЛЛОВ
- 6.3.2. Аномальное поведение
- 6.3.3. Сверхпроводимость
- ГЛАВА 7. СПЕКТРОМЕТРИЯ ДИЭЛЕКТРИКОВ
- 7.1.2. Форма линии и интенсивность
- 7.1.3. Сверхтонкая структура
- 7.1.4. Явления Штарка и Зеемана
- 7.2. СПЕКТРОМЕТРЫ
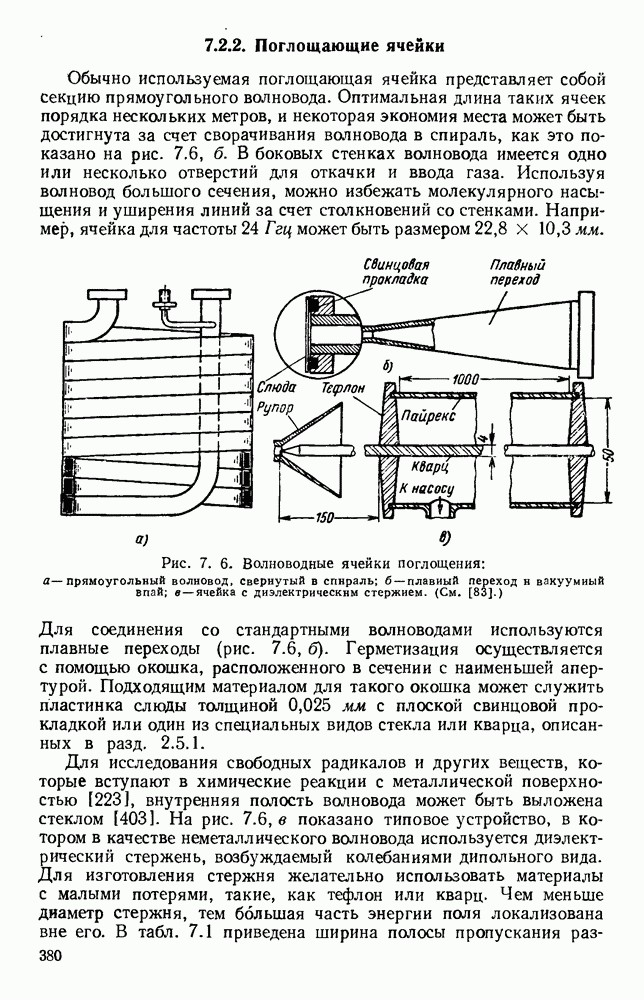
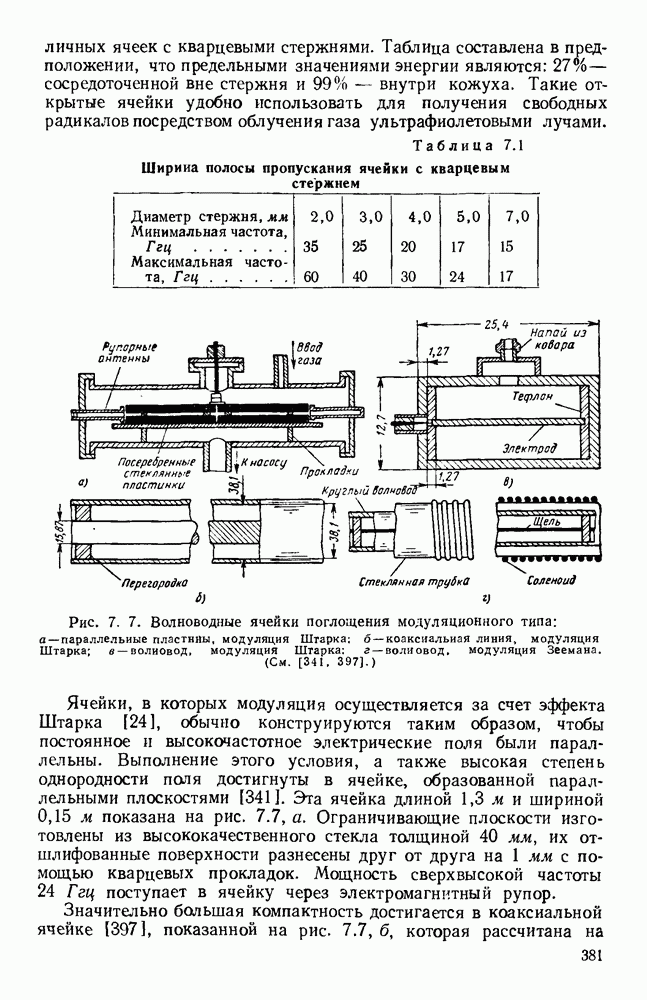
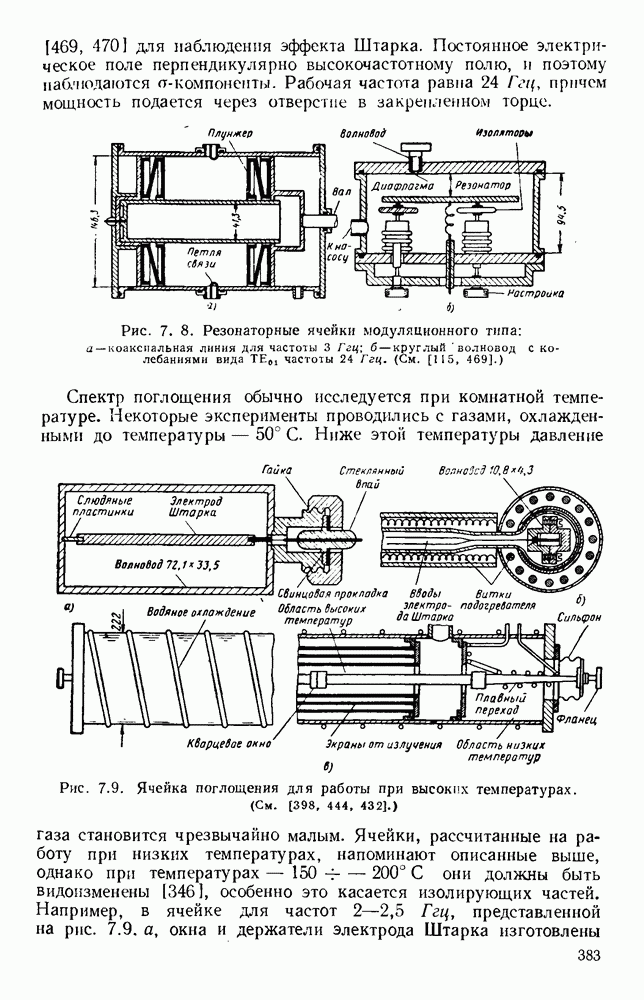
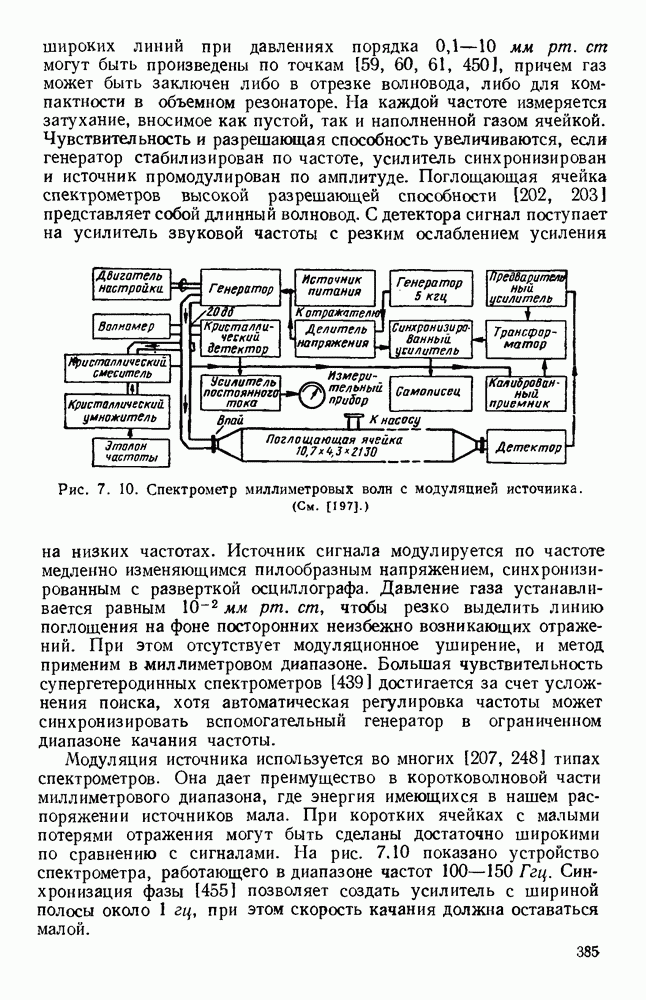
- 7.2.2. Поглощающие ячейки
- 7.2.3. Типы спектрометров
- 7.3. ПАРАМАГНИТНЫЙ РЕЗОНАНС В ТВЕРДЫХ ТЕЛАХ
- 7.3.2. Техника измерения
- 7.3.3. Типичные материалы
- 7.3.4. Времена релаксации
- 7.4. ЦИКЛОТРОННЫЙ РЕЗОНАНС
- 7.4.2. Определение эффективной массы носителей
- ГЛАВА 8. СВОЙСТВА И ПРИМЕНЕНИЕ ГИРОМАГНИТНЫХ СРЕД
- 8.1.2. Распространение электромагнитных волн в неограниченной среде
- 8.2. СВОЙСТВА МАГНИТНЫХ МАТЕРИАЛОВ
- 8.2.2. Ферромагнитный резонанс
- 8.2.3. Нелинейные эффекты и нестабильность
- 8.3. РАСПРОСТРАНЕНИЕ В НАПРАВЛЯЮЩИХ СИСТЕМАХ
- 8.3.2. Прямоугольный волновод
- 8.3.3. Ферритовые устройства в качестве элементов схем
- 8.4. ИЗМЕРЕНИЯ ПАРАМЕТРОВ ФЕРРИТОВЫХ МАТЕРИАЛОВ
- 8.4.2. Резонансные методы
- 8.4.3. Волноводные методы
- 8.5. РЕЗОНАНСНЫЕ ВЕНТИЛИ
- 8.6. УСТРОЙСТВА, РАБОТАЮЩИЕ СО СЛАБЫМИ ПОЛЯМИ
- 8.6.2. Устройства с поперечным полем
- 8.6.3. Прочие узлы
- ГЛАВА 9. ПЛОСКОПАРАЛЛЕЛЬНЫЕ СИСТЕМЫ
- 9.2. СИММЕТРИЧНЫЕ ПОЛОСКОВЫЕ ЛИНИИ
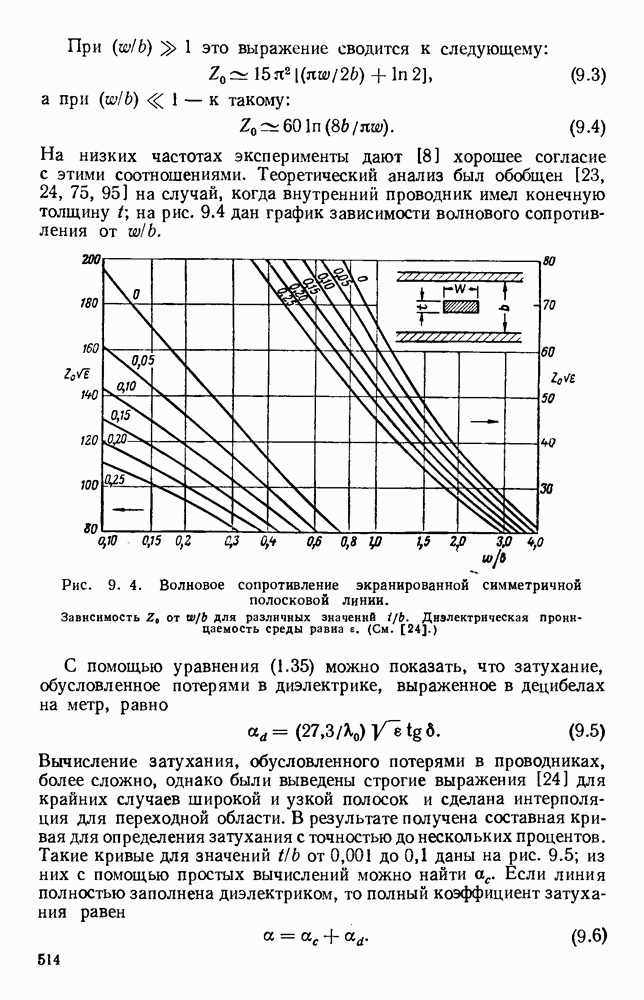
- 9.2.1. Линии типа «диэлектрических сэндвичей»
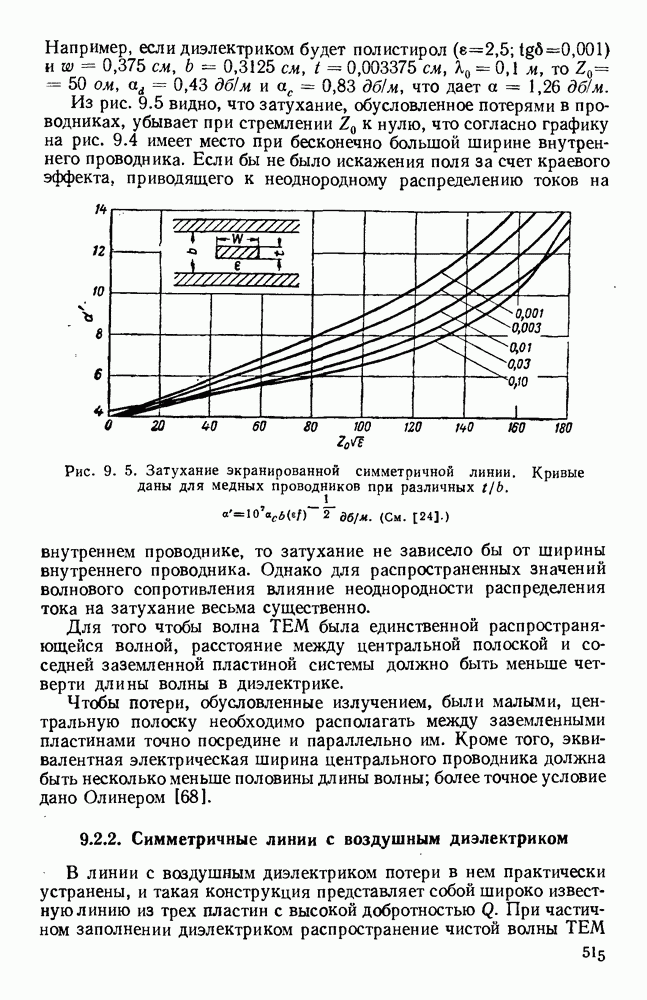
- 9.2.2. Симметричные линии с воздушным диэлектриком
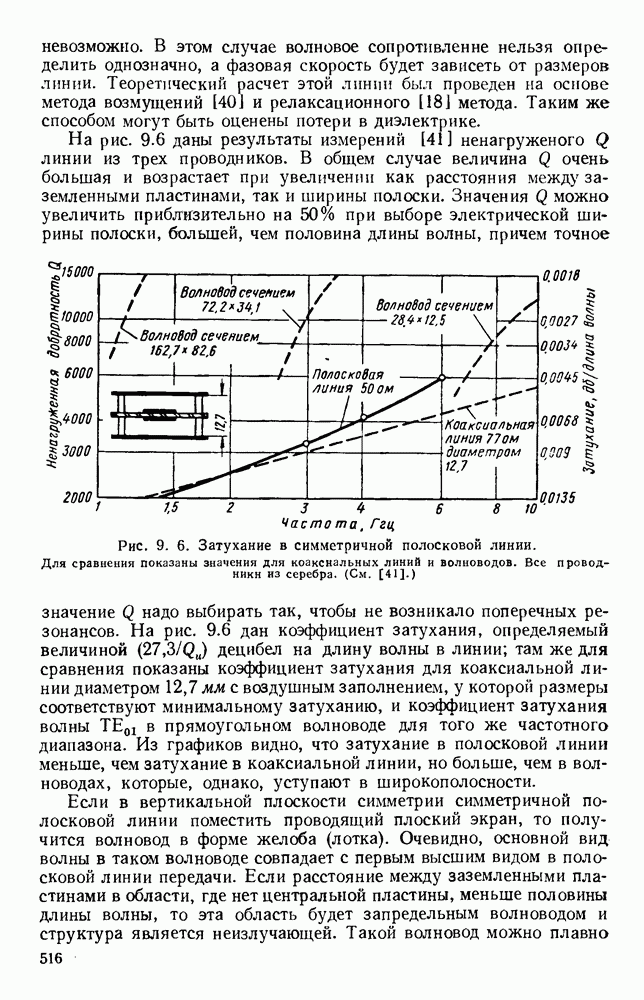
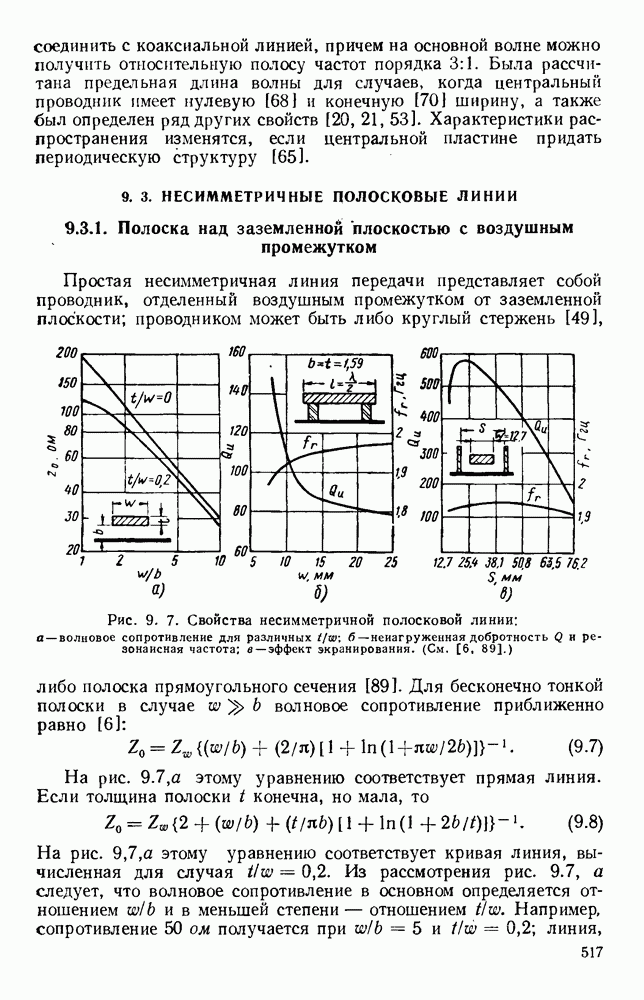
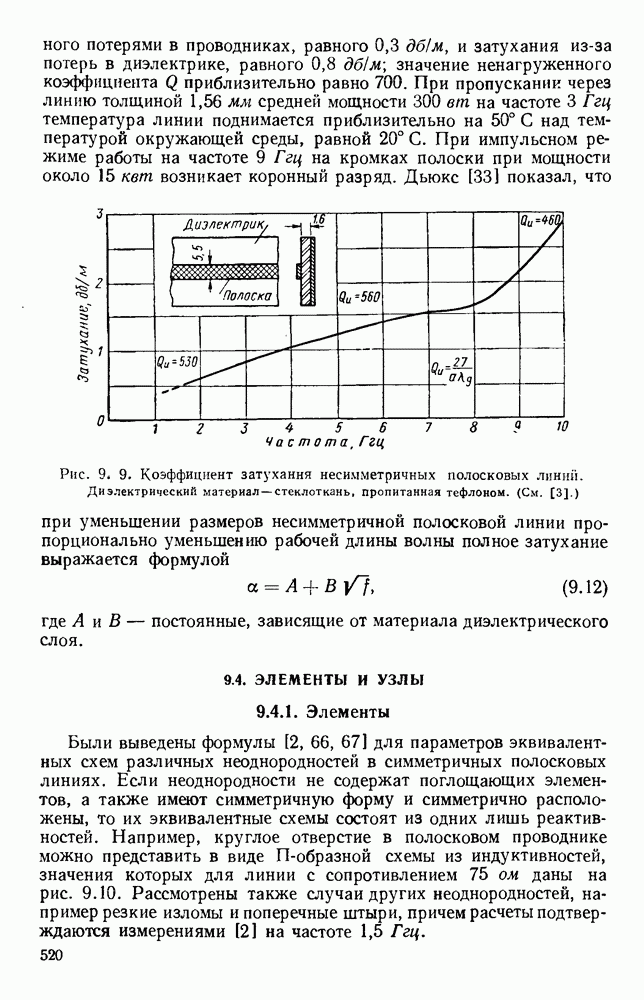
- 9.3. НЕСИММЕТРИЧНЫЕ ПОЛОСКОВЫЕ ЛИНИИ
- 9.3.2. Несимметричная полосковая линия с твердым диэлектриком
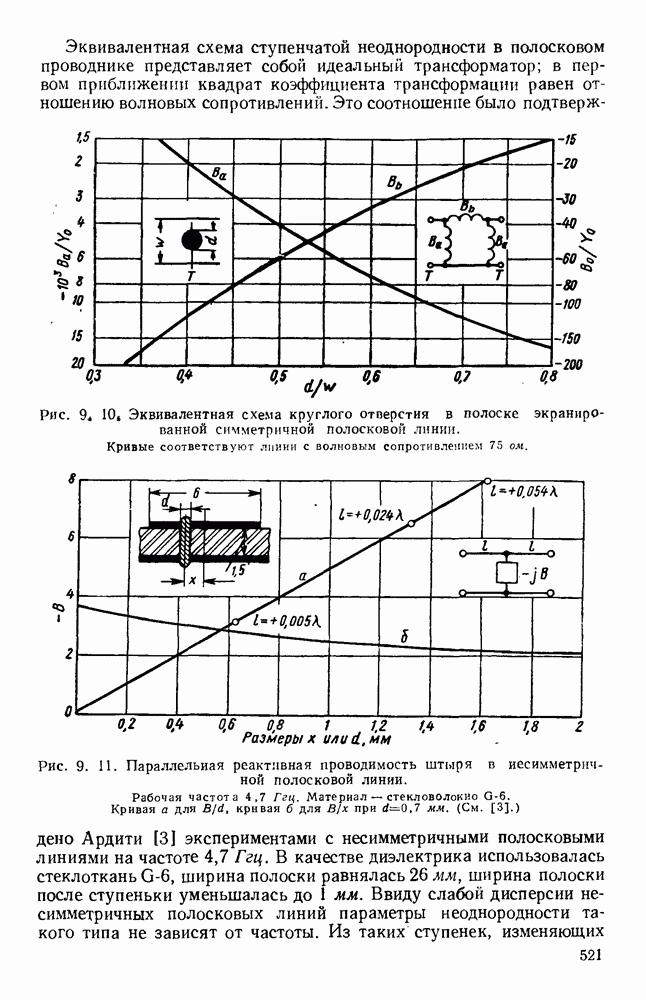
- 9.4. ЭЛЕМЕНТЫ И УЗЛЫ
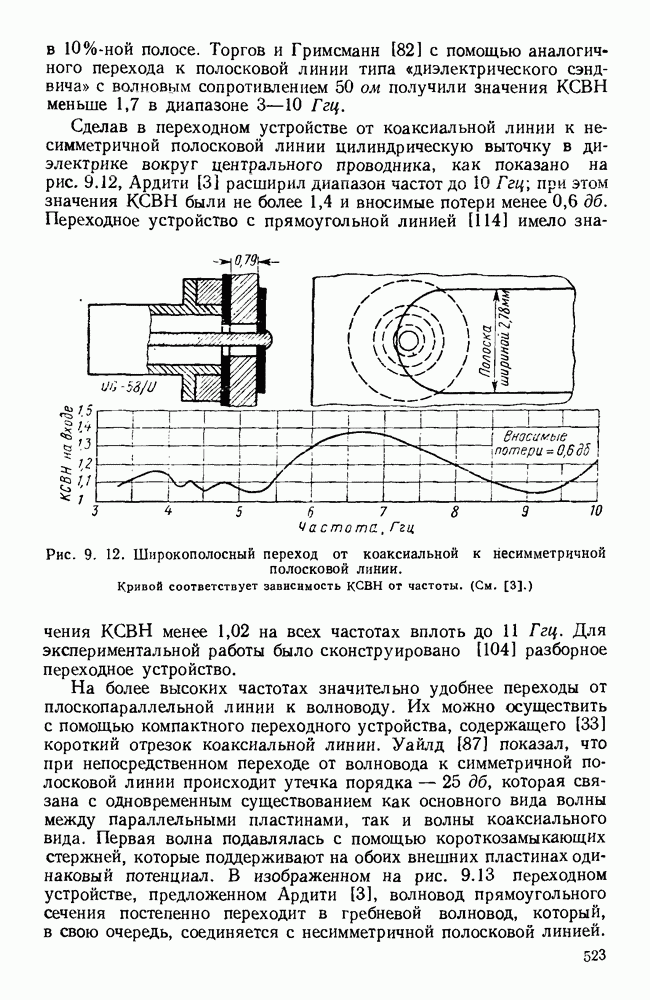
- 9.4.2. Переходные устройства
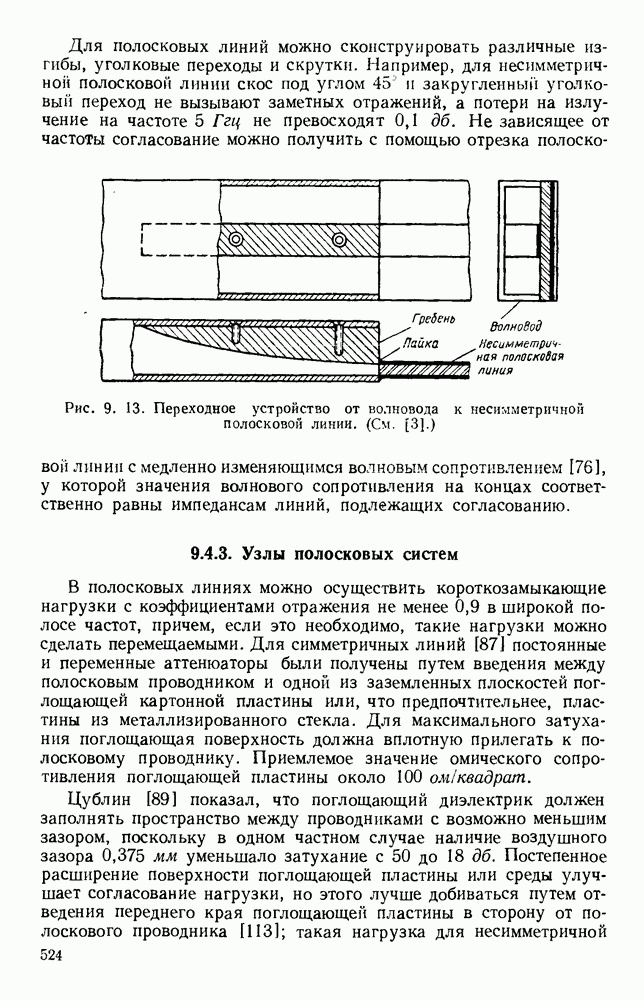
- 9.4.3. Узлы полосковых систем
- 9.5. ЦЕПИ И СИСТЕМЫ
- 9.5.3. Частотные фильтры
- 9.5.4. Цепи питания антенн
- 9.6. МАТЕРИАЛЫ И МЕТОДЫ ПРОИЗВОДСТВА
- 9.6.2. Техника изготовления печатных схем
- ГЛАВА 10. ПЕРИОДИЧЕСКИЕ И НАПРАВЛЯЮЩИЕ СТРУКТУРЫ
- 10.1. ВОЛНЫ В ПЕРИОДИЧЕСКИ НАГРУЖЕННЫХ ЛИНИЯХ
- 10.1.2. Пространственные гармоники
- 10.1.3. Многократно-периодические структуры
- 10.2. МЕТАЛЛИЧЕСКИЕ СТРУКТУРЫ С ДИЭЛЕКТРИЧЕСКИМ ПОКРЫТИЕМ
- 10.2.2. Радиальные волны над плоскими поверхностями
- 10.2.3. Продольные цилиндрические волны
- 10.3. ЛИНИИ ПЕРЕДАЧИ ПОВЕРХНОСТНЫХ ВОЛН
- 10.3.2. Влияние кривизны
- 10.3.3. Возбудители и другие устройства
- 10.4. ВОЛНЫ В ДИЭЛЕКТРИЧЕСКИХ ЛИНИЯХ
- 10.4.2. Цилиндрические стержни
- 10.4.3. Многослойные среды
- 10.4.4. Линии с зеркальным изображением
- 10.5. СТРУКТУРЫ ИЗ СВЯЗАННЫХ РЕЗОНАТОРОВ
- 10.5.2. Объемные резонаторы
- 10.6. СПИРАЛЬНЫЕ СТРУКТУРЫ
- 10.6.2. Практические варианты
- ГЛАВА 11. ЛАМПЫ С СЕТОЧНЫМ УПРАВЛЕНИЕМ И ЛАМПЫ С ПРОСТРАНСТВЕННЫМ ЗАРЯДОМ
- 11.1.2. Лампы с сеточным управлением
- 11.2. ВЗАИМОДЕЙСТВИЕ ПУЧКА И РЕЗОНАТОРА
- 11.2.2. Усилительные клистроны
- 11.2.3. Отражательные клистроны
- 11.3. ВЗАИМОДЕЙСТВИЕ ПУЧКА И КОНТУРА
- 11.3.1. Электронно-волновые лампы
- 11.3.2. Лампы с бегущей волной
- 11.3.3. Лампы обратной волны
- ГЛАВА 12. ЛАМПЫ СО СКРЕЩЕННЫМИ ПОЛЯМИ И ГЕНЕРАЦИЯ ВОЛН МИЛЛИМЕТРОВОГО ДИАПАЗОНА
- 12.1.2 Карсинотрон типа М
- 12.2. МАГНЕТРОНЫ
- 12.2.2. Резонаторные системы
- 12.2.3. Взаимодействие между электронным потоком и резонансной системой
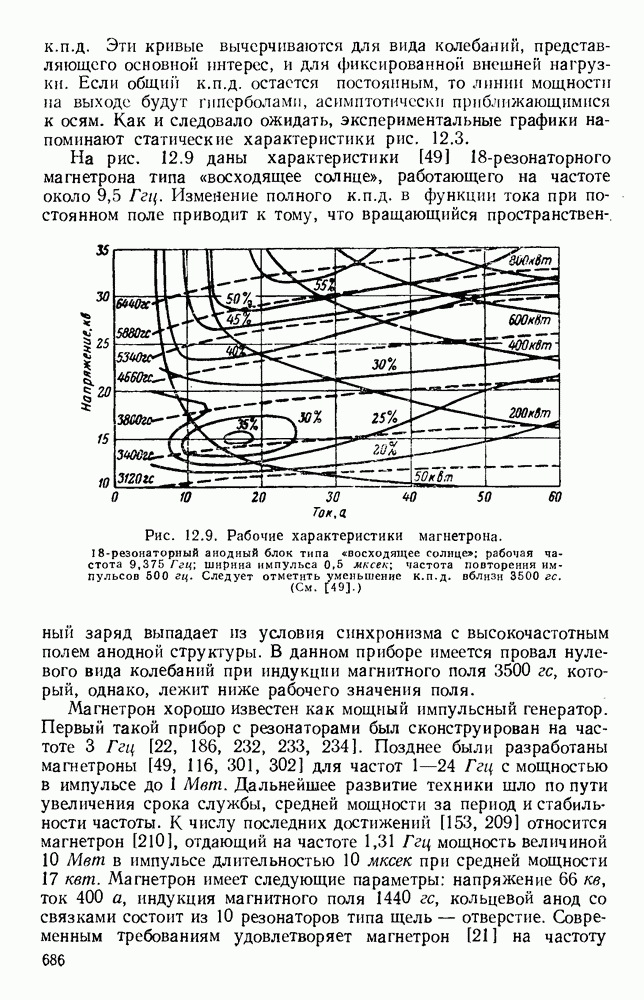
- 12.2.4. Рабочие характеристики
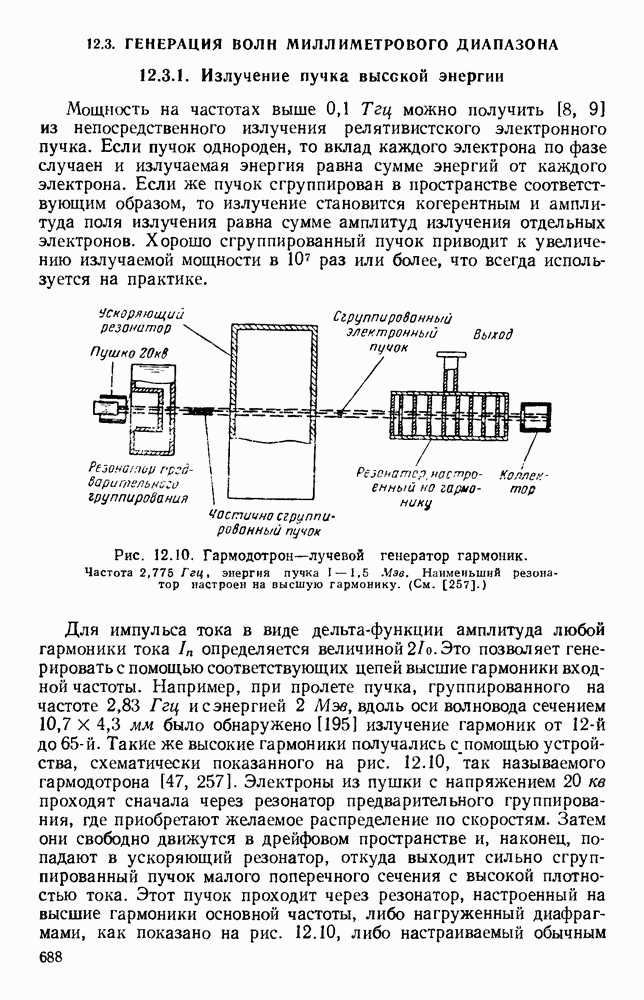
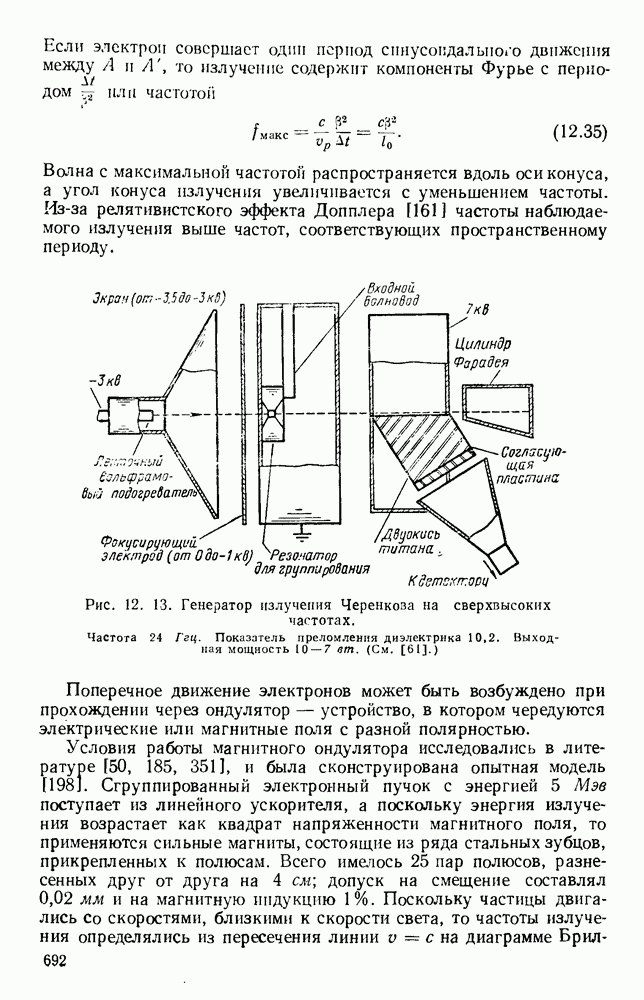
- 12.3. ГЕНЕРАЦИЯ ВОЛН МИЛЛИМЕТРОВОГО ДИАПАЗОНА
- 12.3.2. Высокочастотный предел когерентного излучения
- 12.4. ИСТОЧНИКИ ЭЛЕКТРОНОВ
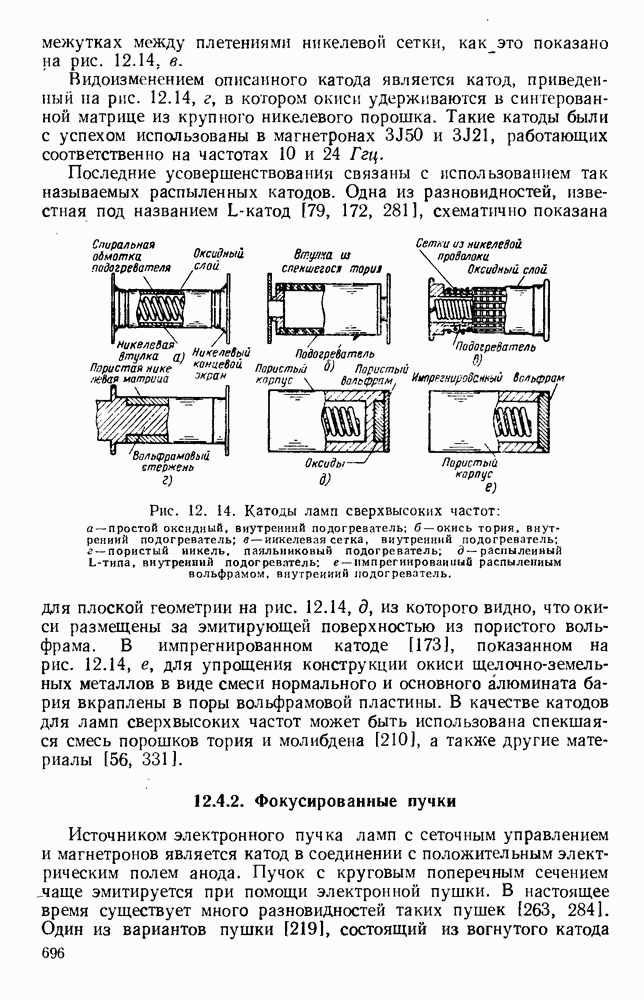
- 12.4.1. Термоэлектронные катоды
- 12.4.2. Фокусированные пучки
- ГЛАВА 13. ТЕХНИКА ОПТИЧЕСКОГО ТИПА
- 13.1.2. Типы дифракции
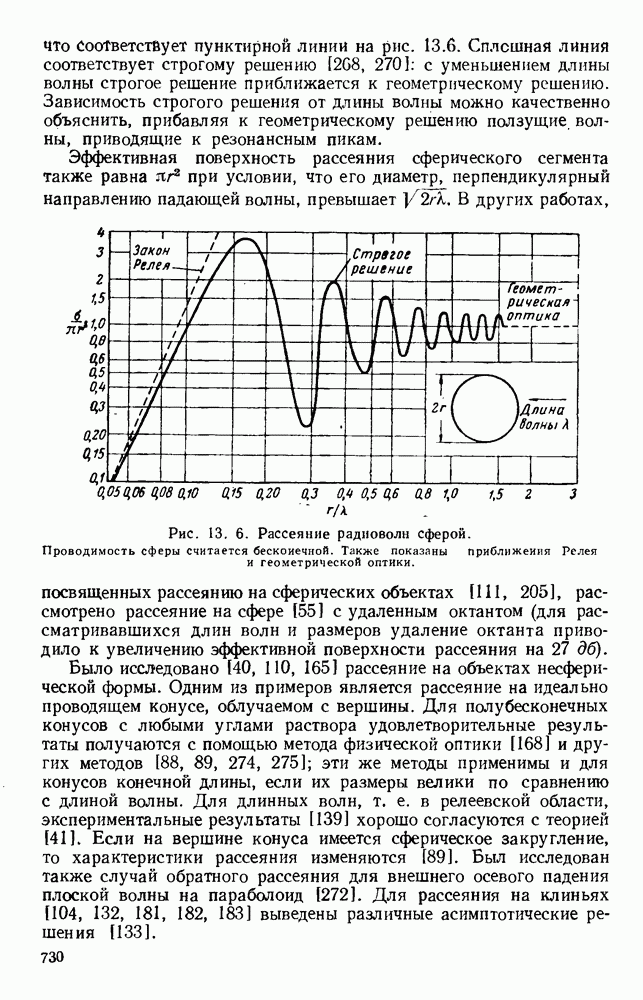
- 13.1.3. Рассеяние
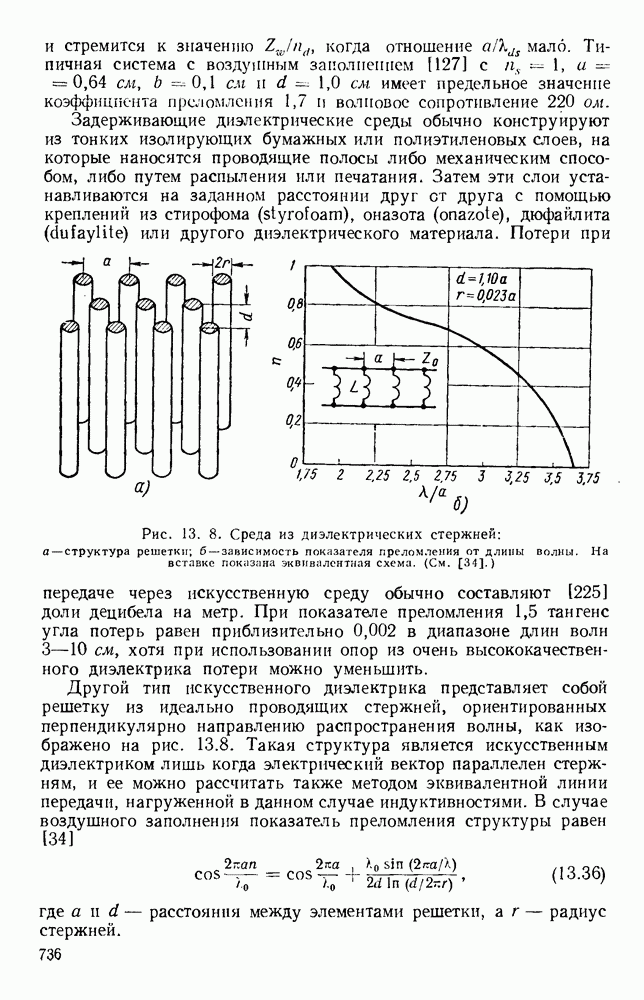
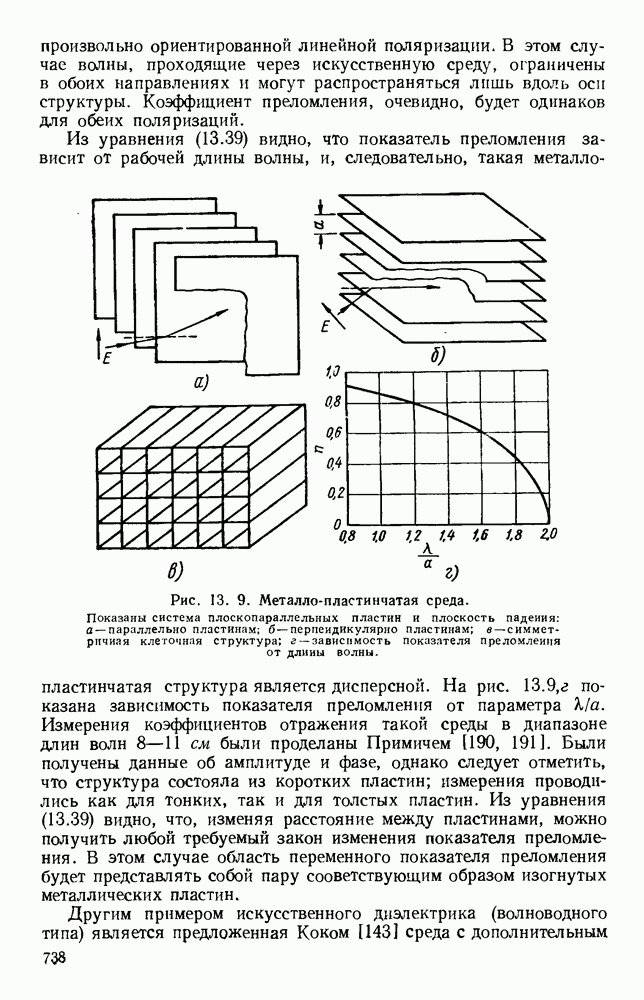
- 13.2. ИСКУССТВЕННЫЕ ДИЭЛЕКТРИКИ
- 13.2.2. Структуры волноводного типа
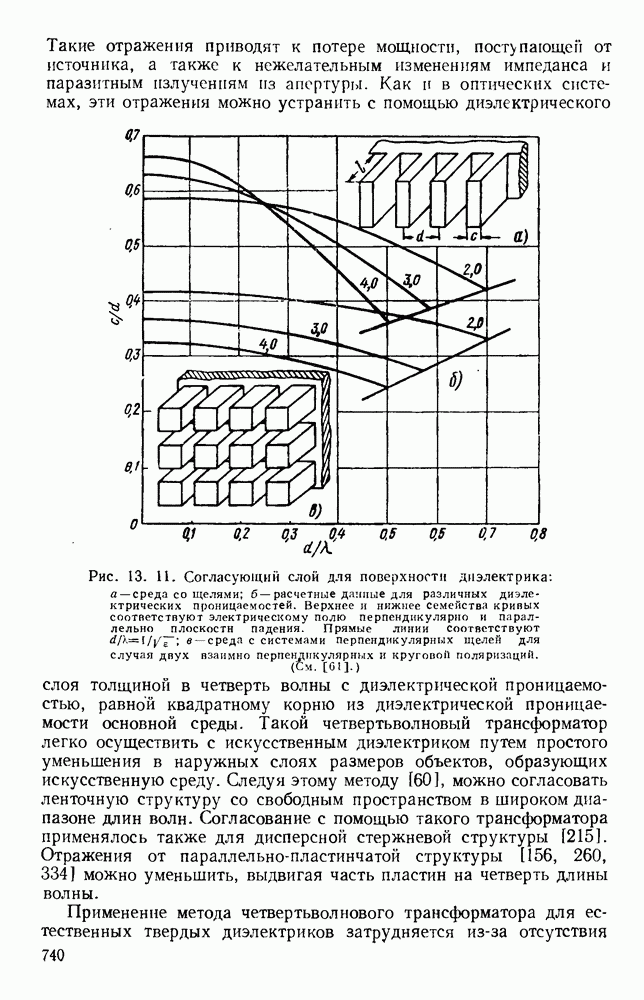
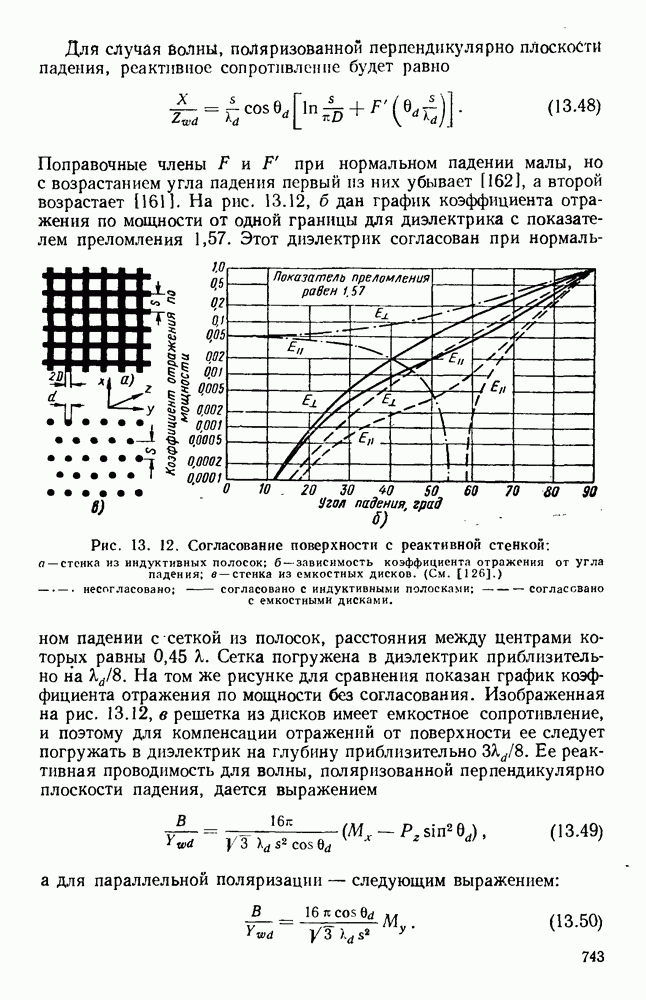
- 13.3. КОНТРОЛЬ ОТРАЖЕНИЙ ОТ ПОВЕРХНОСТИ
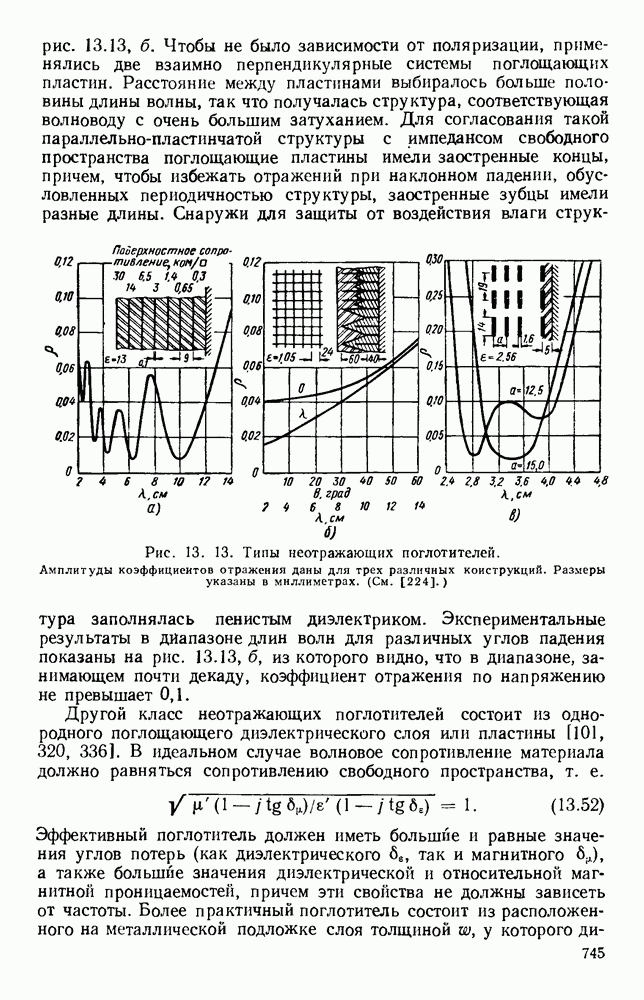
- 13.3.2. Неотражающие поглотители
- 13.3.3. Увеличение отражающей способности
- 13.4. ПРИБОРЫ И СИСТЕМЫ
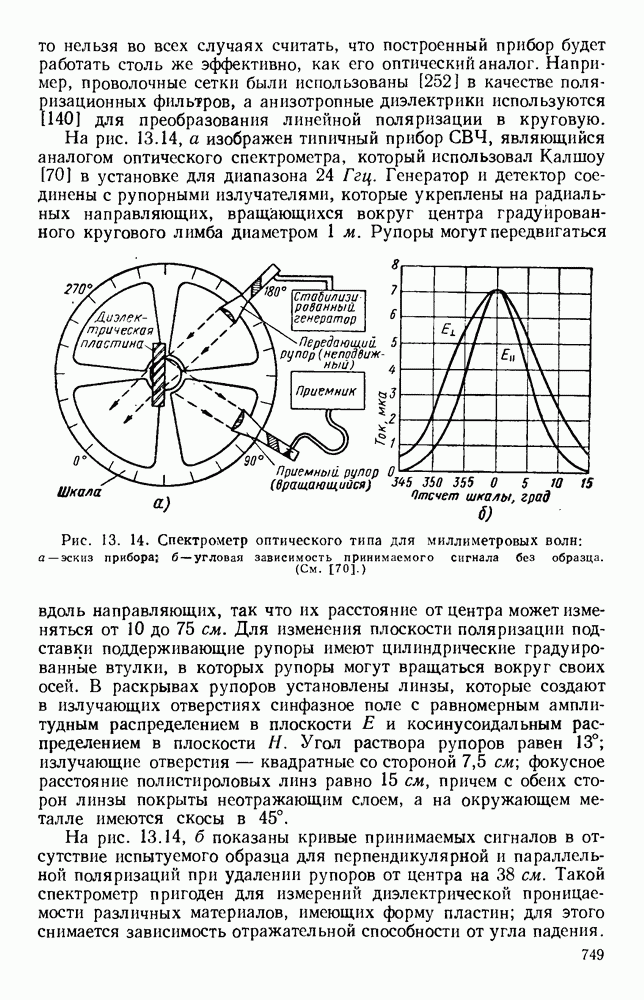
- 13.4.1. Спектрометры
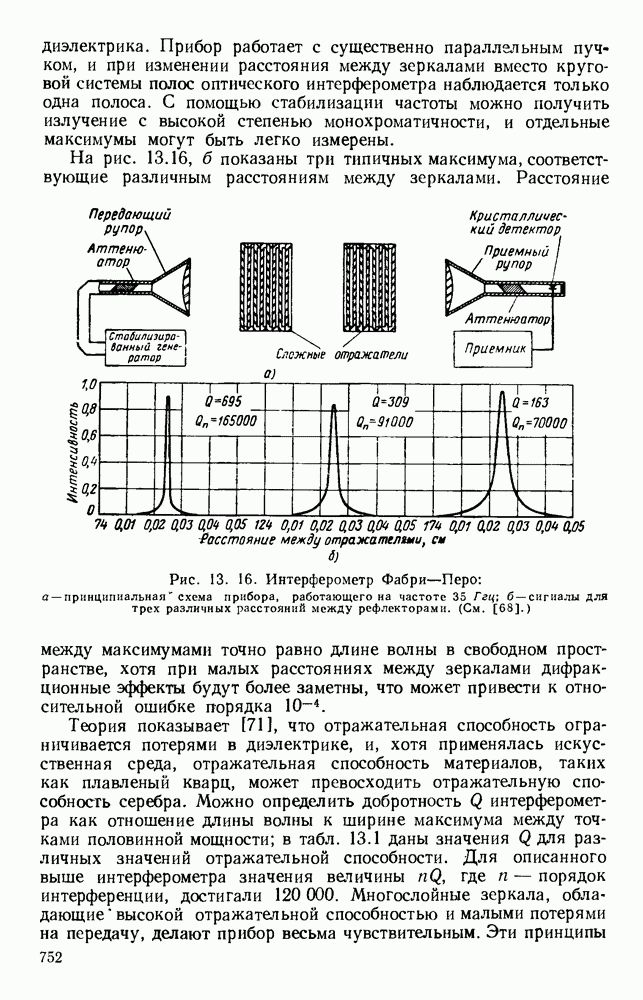
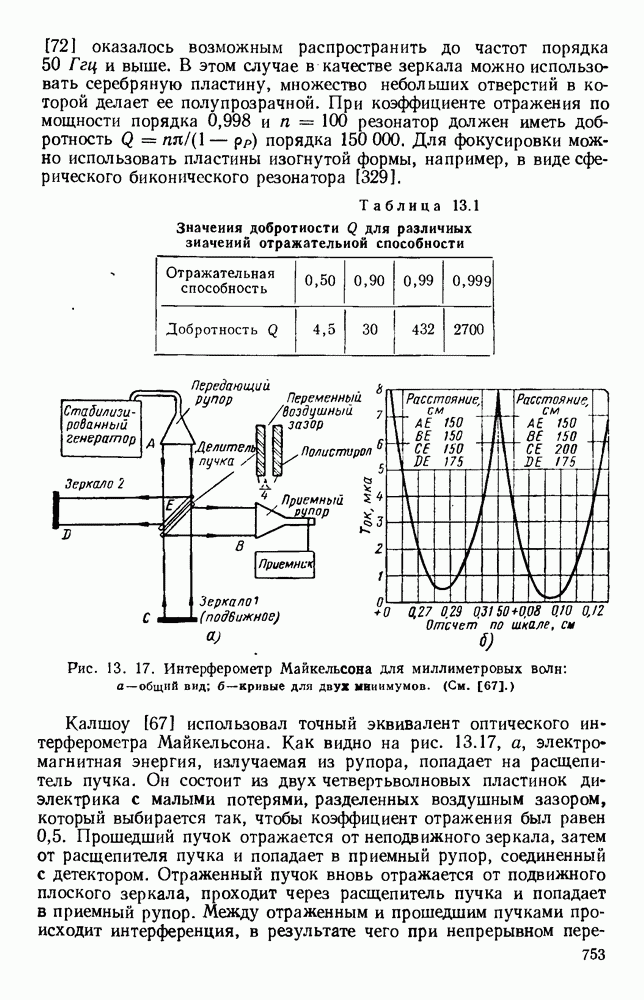
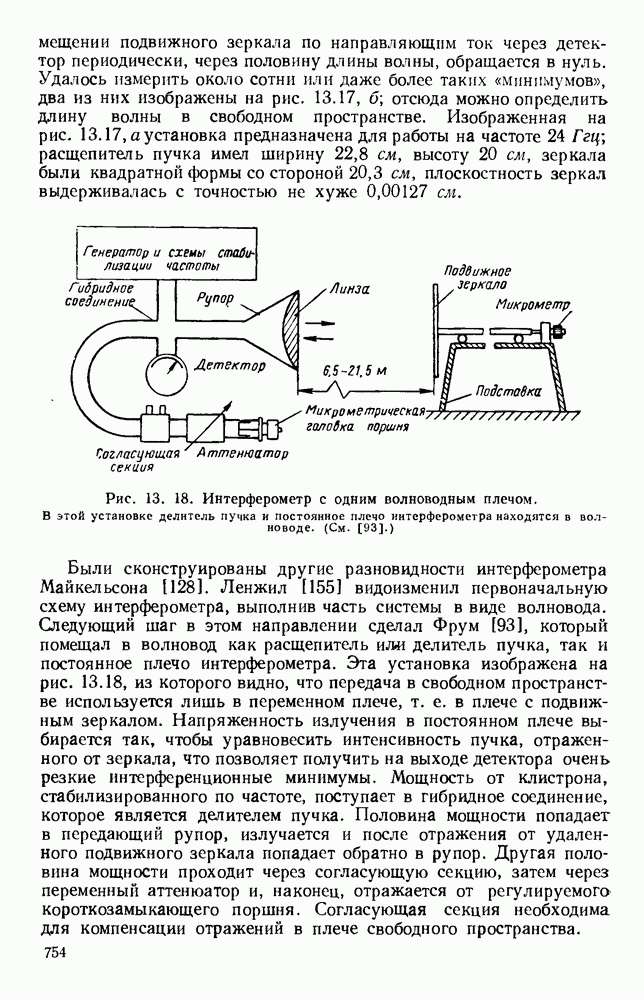
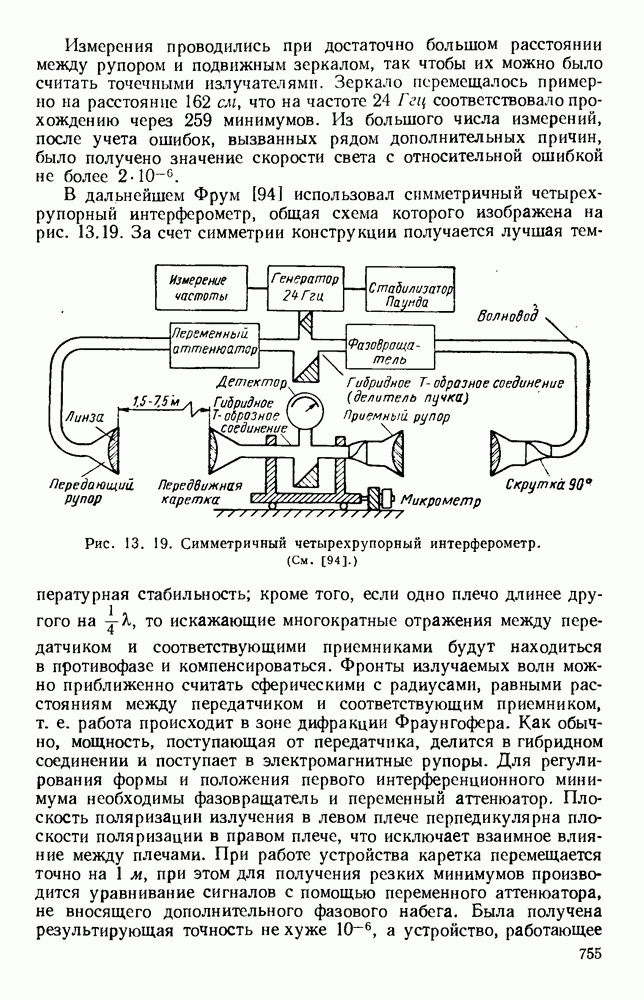
- 13.4.2. Интерферометры
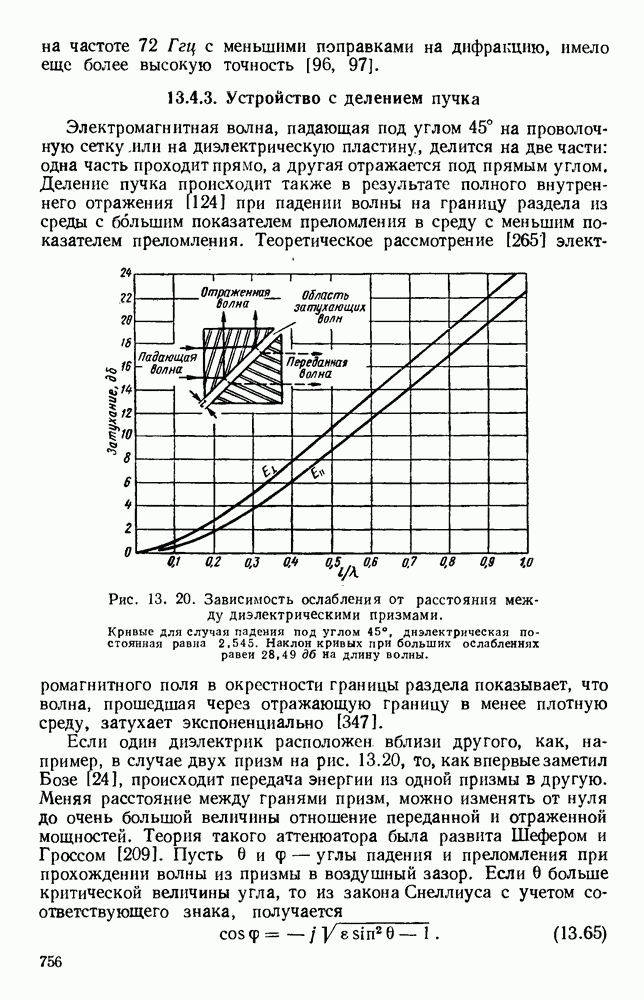
- 13.4.3. Устройство с делением пучка