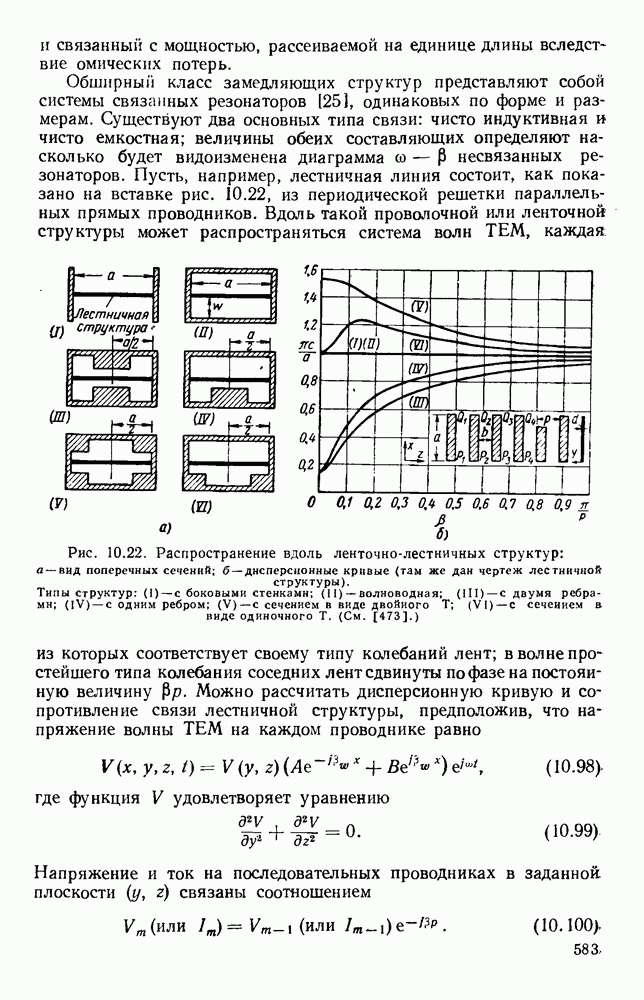
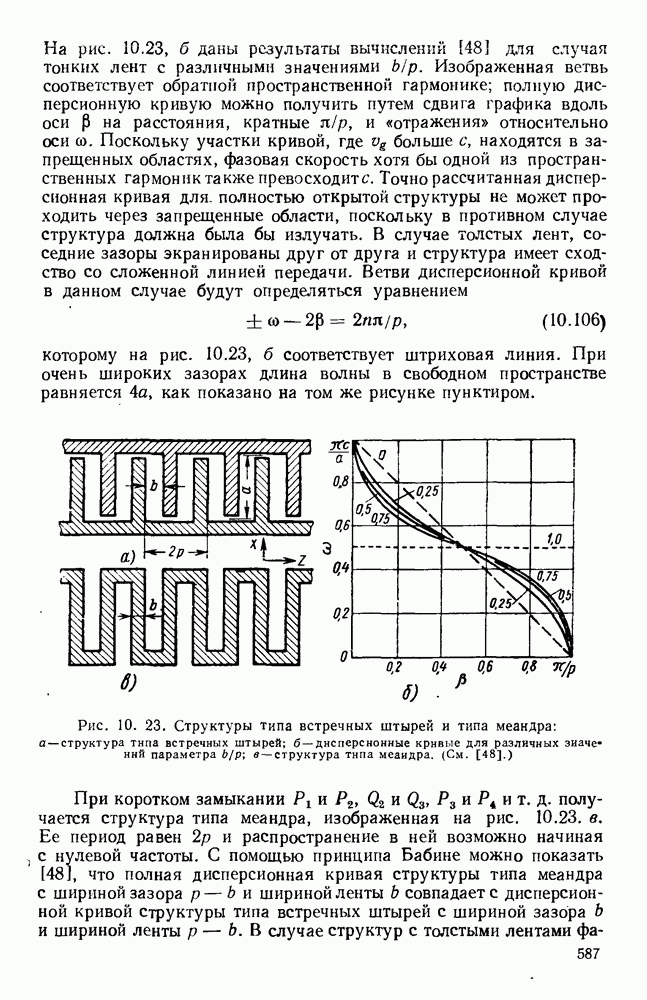
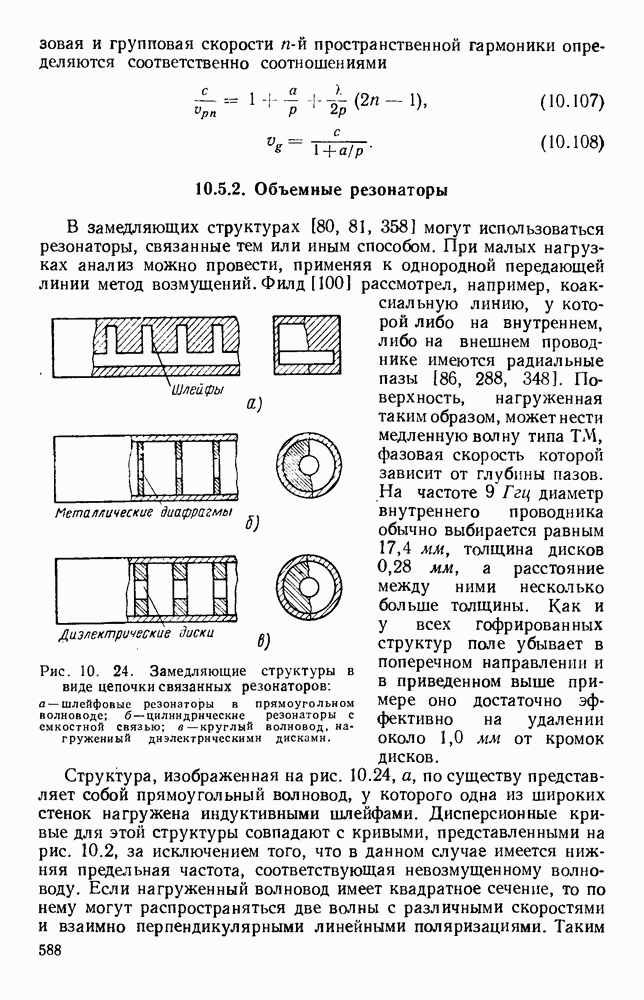
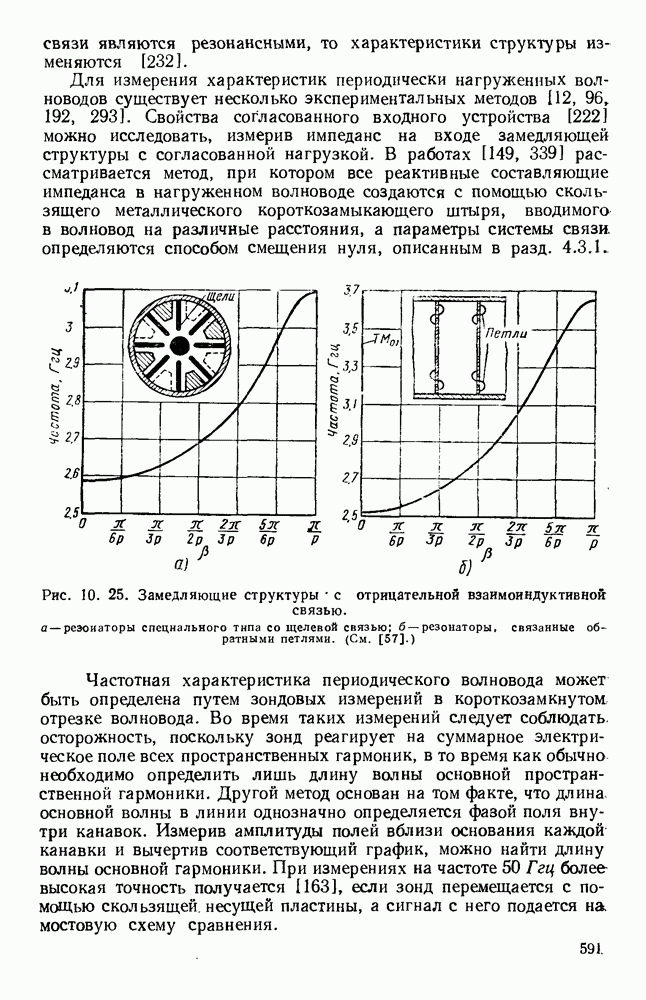
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
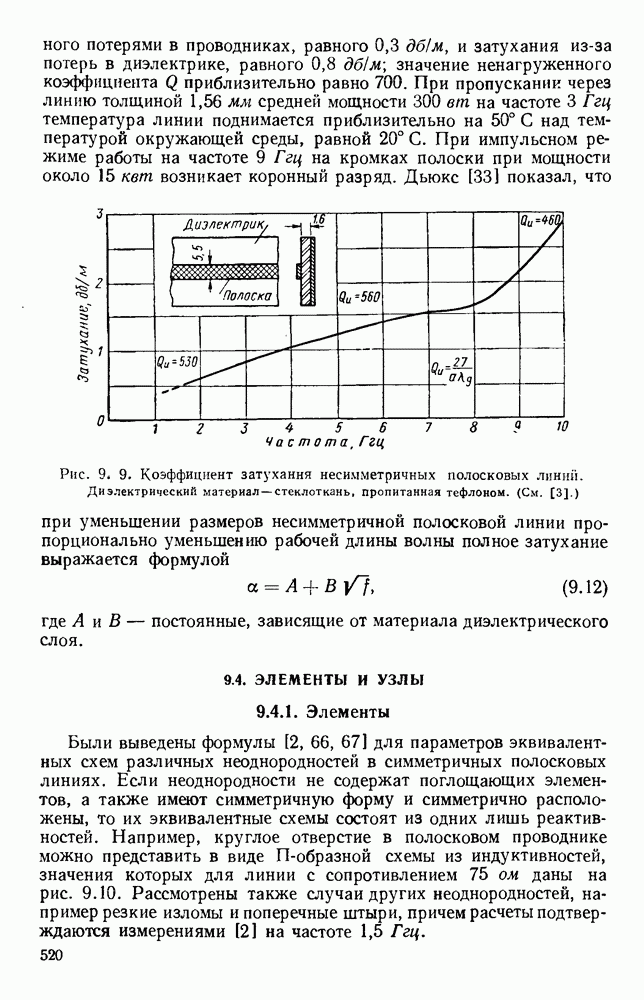
10.2. МЕТАЛЛИЧЕСКИЕ СТРУКТУРЫ С ДИЭЛЕКТРИЧЕСКИМ ПОКРЫТИЕМ
10.2.1. Плоские волны над плоскими поверхностями
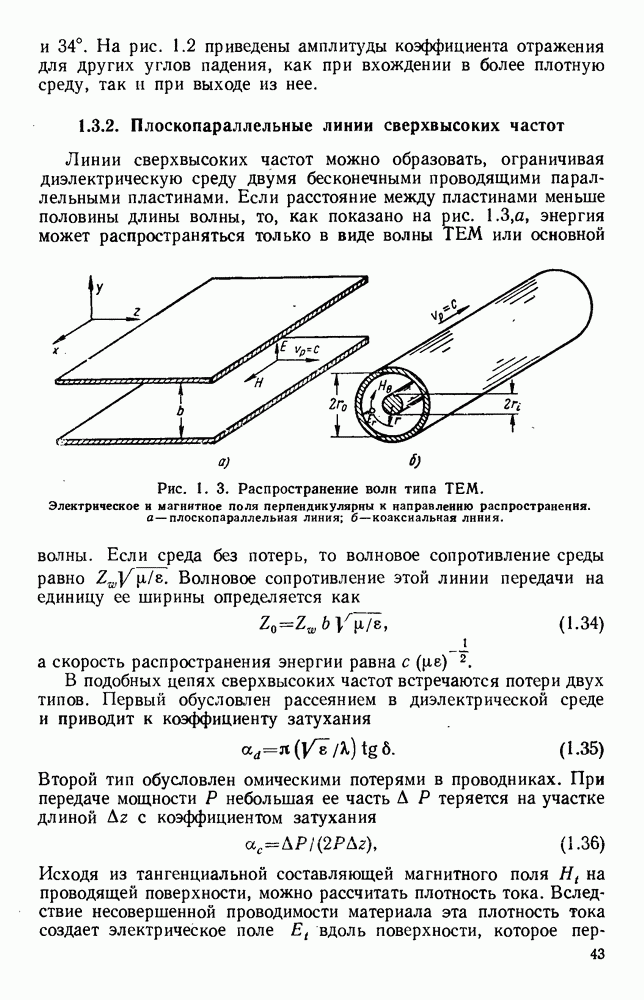
В обычных линиях передачи, которые были рассмотрены в гл. 1, электромагнитная энергия сосредоточена внутри замкнутого пространства, ограниченного проводящими поверхностями. При некоторых условиях могут существовать другие типы передачи, в которых нет резкого ограничения поля, а оно скорее связано с поверхностью или структурой [172]. У таких направляющих структур возможны три класса волн [38]:
— непрерывный спектр распространяющихся волн,
— непрерывный спектр быстро затухающих волн, которые экспоненциально убывают в направлении распространения,
— одна или более поверхностных волн, которые при специальных способах возбуждения могут быть преобладающими.
Поверхностные волны [24, 228, 346, 347, 377] представляют собой электромагнитные колебания, которые распространяются без излучения вдоль границы раздела между двумя средами с различными физическими свойствами. В поперечном направлении электромагнитное поле простирается до бесконечности, но при этом плотность энергии убывает, так что практически основная часть энергии волны сосредоточена вблизи структуры. Составляющая потока энергии, направленная от поверхности, возникает лишь из-за потерь в окружающей среде. Свойства поверхностных волн зависят от поверхностного импеданса  определяемого как отношение тангенциальных составляющих электрического и магнитного векторов. Поверхностный импеданс обычно является комплексной величиной, т. е. имеет как активную, так и реактивную составляющие (см. разд. 6.3).
определяемого как отношение тангенциальных составляющих электрического и магнитного векторов. Поверхностный импеданс обычно является комплексной величиной, т. е. имеет как активную, так и реактивную составляющие (см. разд. 6.3).
Распространение поверхностных волн, строго говоря, возможно вдоль поверхности, которая прямолинейна в направлении распространения. В поперечном направлении форма поверхности может быть произвольной. Внешней средой обычно является воздух, а структура может состоять либо из диэлектрика, либо из комбинации диэлектрика и металла, либо из гофрированной металлической поверхности. Например, Ценек [345] показал, что уравнения Максвелла имеют частное решение, представляющее волну, которая распространяется без изменения формы над плоской границей раздела [9] двух однородных сред с различными проводимостями и диэлектрическими проницаемостями. Такая волна является волной типа ТМ и имеет продольную составляющую электрического вектора [113].
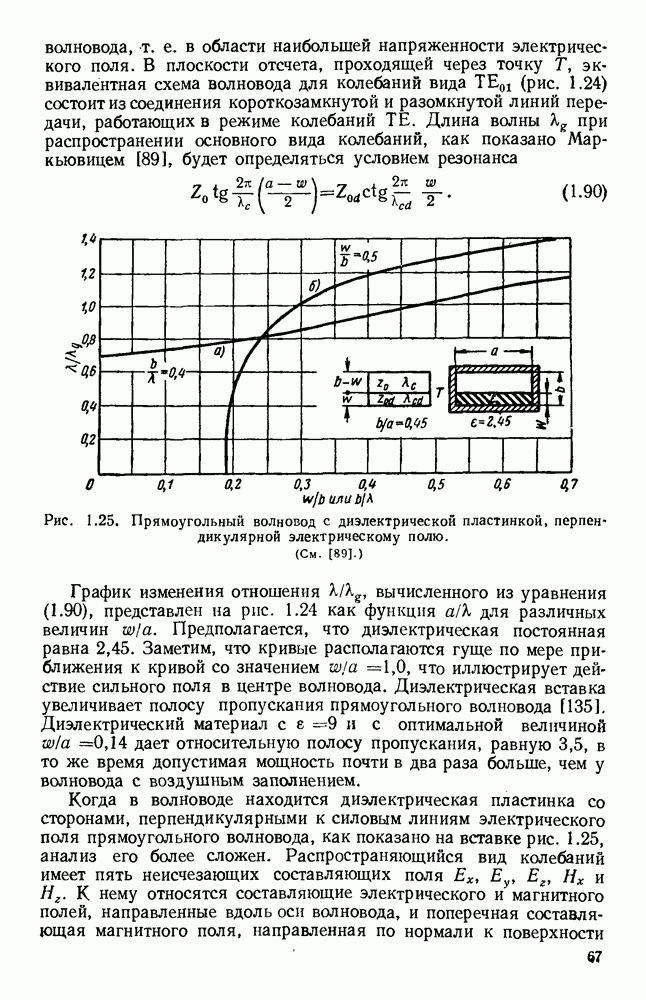
Вдоль плоскости, покрытой диэлектриком, могут распространяться как плоские, так и радиально-цилиндрические поверхностные волны, а вдоль цилиндрической поверхности — осевые поверхностные волны [54, 285, 308]. Волны, распространяющиеся вдоль
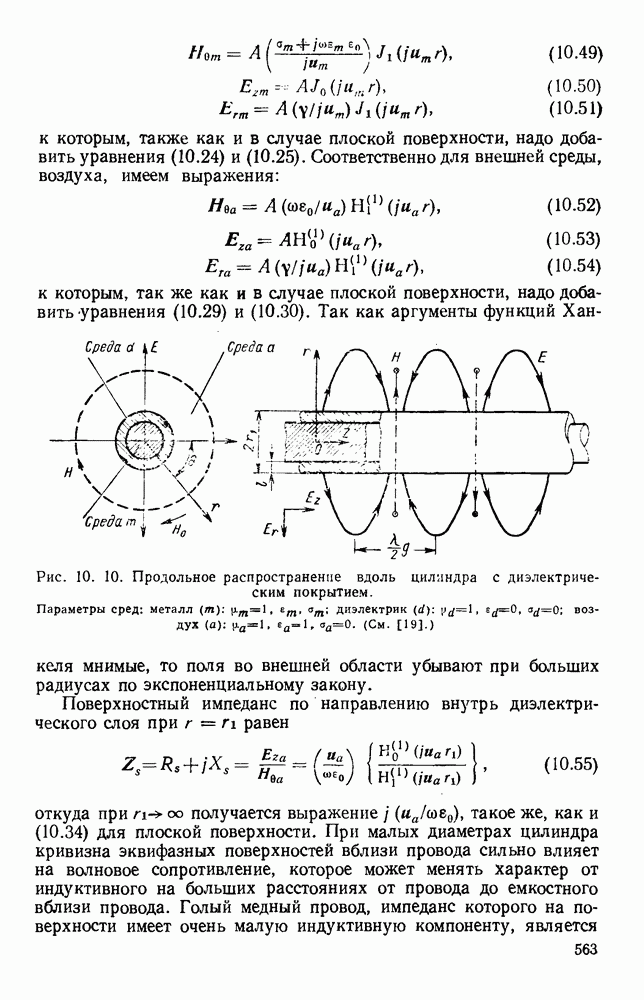
образующих конической поверхности, являются промежуточным случаем между осевыми и радиальными. На рис. 10.9, а изображена типичная плоская направляющая поверхностная структура. Через  здесь обозначен металл, через
здесь обозначен металл, через  диэлектрическая пластина и через а — воздух. Рассмотрим основную плоскую поверхностную волну типа ТМ, распространяющуюся вдоль структуры параллельно оси z с коэффициентом распространения
диэлектрическая пластина и через а — воздух. Рассмотрим основную плоскую поверхностную волну типа ТМ, распространяющуюся вдоль структуры параллельно оси z с коэффициентом распространения 

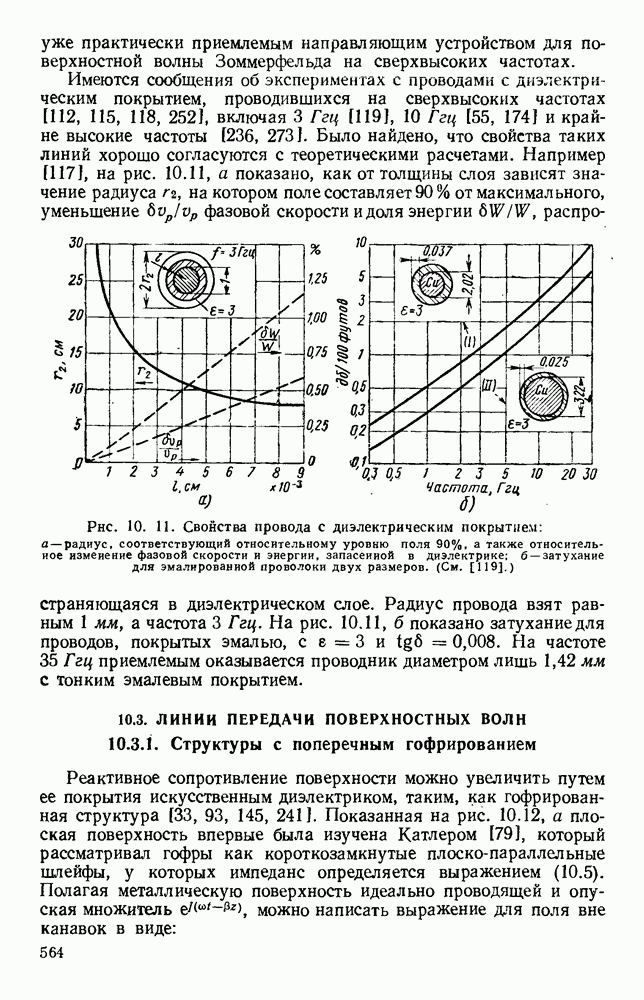
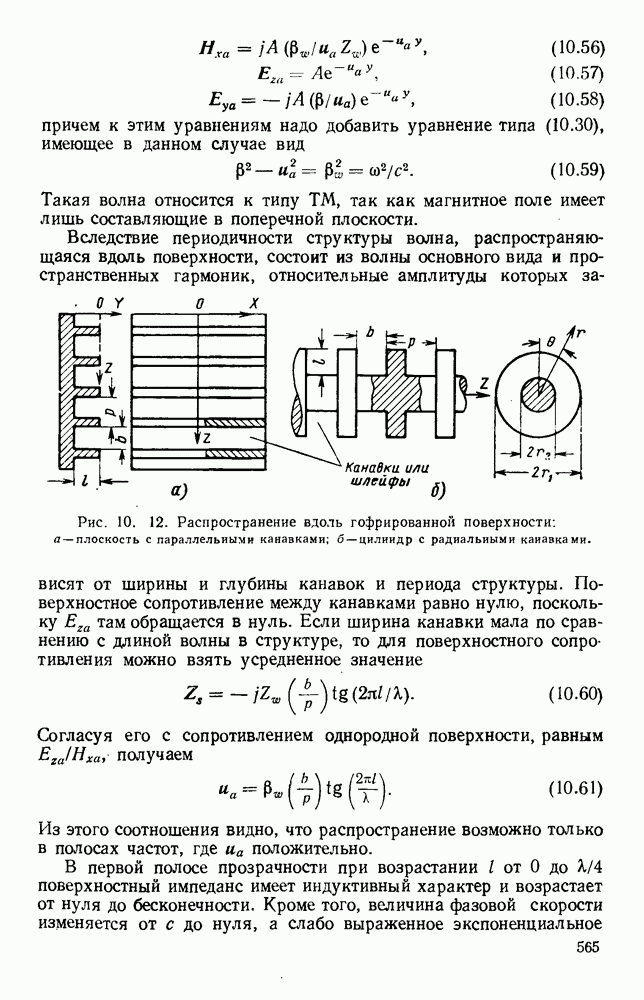
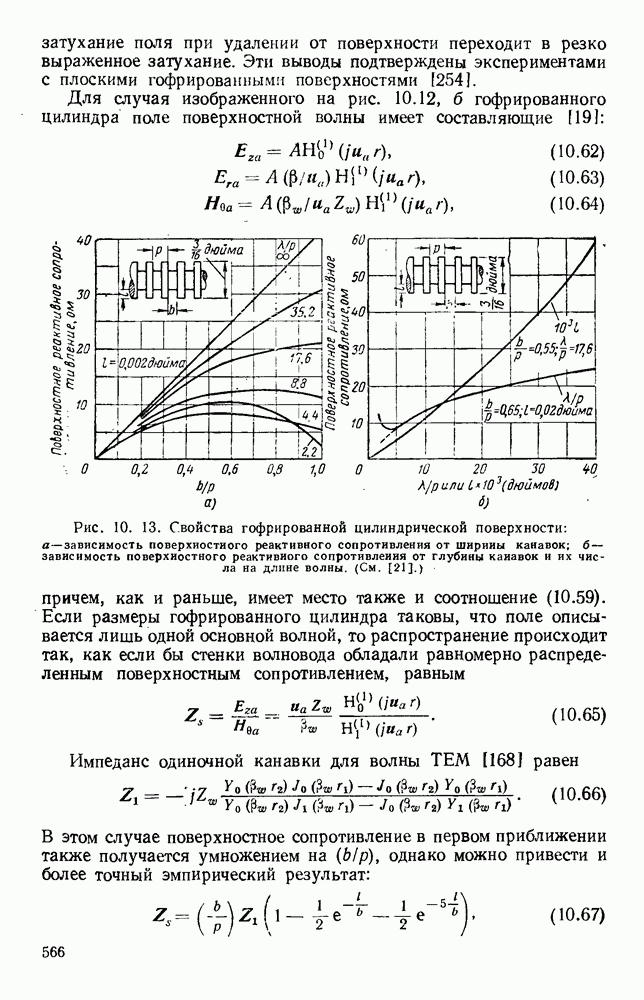
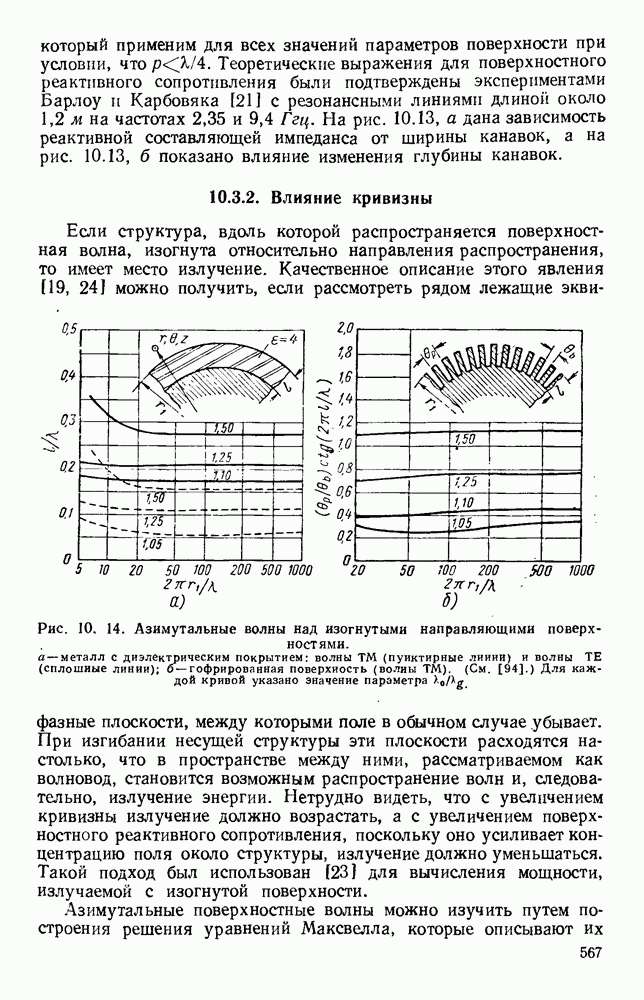
Рис. 10. 9. Распространение над плоскостью, покрытой диэлектрическим слоем: а — плоская волна; б - радиальная волна. (См. [19].) Параметры сред: металл  воздух
воздух 
Следуя Барлоу и Каллену [19], для области, занятой металлом  берется решение волнового уравнения, имеющее три компоненты, отличные от нуля:
берется решение волнового уравнения, имеющее три компоненты, отличные от нуля:

Здесь для краткости опущен множитель  а величина А постоянная. В коэффициент распространения вдоль оси у.
а величина А постоянная. В коэффициент распространения вдоль оси у.

входят коэффициент затухания  и коэффициент распространения
и коэффициент распространения  волны, уходящей от поверхности
волны, уходящей от поверхности  в глубь металла. Величины у и а должны удовлетворять соотношению
в глубь металла. Величины у и а должны удовлетворять соотношению

Аналогично для области, занятой воздухом  решение берется в виде:
решение берется в виде:


Здесь на имеет вид

где  соответствует экспоненциальному затуханию в поперечном направлении, а
соответствует экспоненциальному затуханию в поперечном направлении, а  описывает фазовый набег для волны, распространяющейся по направлению к поверхности раздела.
описывает фазовый набег для волны, распространяющейся по направлению к поверхности раздела.
Коэффициенты распространения должны удовлетворять уравнению

Внутри диэлектрической пластины поле имеет вид стоячей волны, у которой магнитное поле равно

причем

Из условий сопряжения полей на границах раздела между различными средами получается соотношение

Поверхностный импеданс структуры по направлению внутрь диэлектрика равен

Поверхностный импеданс металлической поверхности для хорошо проводящих металлов имеет почти равные вещественную и мнимую части и дается выражением

Если диэлектрик имеет потери, то активная составляющая поверхностного импеданса структуры будет выглядеть как

Если потерь в диэлектрике нет, то активная составляющая поверхностного импеданса структуры определяется проводимостью металла. Реактивная составляющая поверхностного импеданса структуры  слагается из двух частей: одна связана с металлом, а другая, равная
слагается из двух частей: одна связана с металлом, а другая, равная

связана с диэлектрическим слоем. Если толщина диэлектрического слоя приблизительно равна толщине поверхностного слоя в металле  то величины обеих частей реактивной составляющей будут одного порядка.
то величины обеих частей реактивной составляющей будут одного порядка.
Если I мало и можно считать, что  и
и  , то из уравнения (10.33) получается
, то из уравнения (10.33) получается

В общем случае, чем больше поверхностное реактивное сопротивление структуры и чем выше частота, тем больше значение показателя затухания  а это приводит к более сильной концентрации поля около поверхности структуры. Возрастание
а это приводит к более сильной концентрации поля около поверхности структуры. Возрастание  вызывает увеличение наклона волнового фронта относительно нормали в пространстве около структуры, что в свою очередь увеличивает фазовую скорость вдоль структуры. С другой стороны, по аналогии с электрическими линиями можно ожидать, что индуктивное поверхностное реактивное сопротивление будет уменьшать соответствующую фазовую скорость, а емкостное сопротивление будет ее увеличивать.
вызывает увеличение наклона волнового фронта относительно нормали в пространстве около структуры, что в свою очередь увеличивает фазовую скорость вдоль структуры. С другой стороны, по аналогии с электрическими линиями можно ожидать, что индуктивное поверхностное реактивное сопротивление будет уменьшать соответствующую фазовую скорость, а емкостное сопротивление будет ее увеличивать.
Чтобы вычислить постоянные затухания и распространения вдоль структуры, надо уравнения (10.29) и (10.30) подставить в выражение

Если то для скорости распространения получается следующее выражение:

Из уравнения (10.39) видно, что величина а пропорциональна  а уравнение (10.41) показывает, что если
а уравнение (10.41) показывает, что если  значительно больше, чем
значительно больше, чем  то
то  и наоборот. Численные значения затухания и фазовой скорости вычислены [16] в диапазоне частот
и наоборот. Численные значения затухания и фазовой скорости вычислены [16] в диапазоне частот  для диэлектрического слоя с
для диэлектрического слоя с  и толщинами от 0,1 до
и толщинами от 0,1 до  На частоте
На частоте  слой толщиной
слой толщиной  дает потери порядка
дает потери порядка  и фазовую скорость порядка 0,65 с.
и фазовую скорость порядка 0,65 с.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА
- ОБОЗНАЧЕНИЯ
- ГЛАВА 1. РАСПРОСТРАНЕНИЕ ВОЛН В ЦЕПЯХ
- 1.1. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ СВЕРХВЫСОКИХ ЧАСТОТ КАК ЭЛЕКТРОМАГНИТНОЕ ИЗЛУЧЕНИЕ
- 1.2. СВОЙСТВА МАТЕРИАЛОВ
- 1.2.2. Металлические проводники
- 1.2.3. Полупроводники
- 1.3. ВОЛНЫ С ЧИСТО ПОПЕРЕЧНЫМИ ПОЛЯМИ
- 1.3.2. Плоскопараллельные линии сверхвысоких частот
- 1.3.3. Коаксиальные линии
- 1.4. ВОЛНЫ В ПОЛЫХ ПРОВОДЯЩИХ ТРУБАХ
- 1.4.2. Круглые волноводы
- 1.5. СЛОЖНЫЕ ВОЛНОВОДЫ
- 1.5.2. Гребневые волноводы
- 1.5.3. Волноводы, содержащие диэлектрик
- ГЛАВА 2. ПРАКТИЧЕСКИЕ ЛИНИИ ПЕРЕДАЧИ
- 2.1. ТЕОРИЯ ЛИНИИ ПЕРЕДАЧИ
- 2.1.2. Круговая диаграмма
- 2.1.3. Широкополосное согласование
- 2.2. РАБОЧИЕ ПАРАМЕТРЫ
- 2.2.1. Перекрытие по частоте
- 2.2.2. Затухание
- 2.2.3. Допустимая мощность
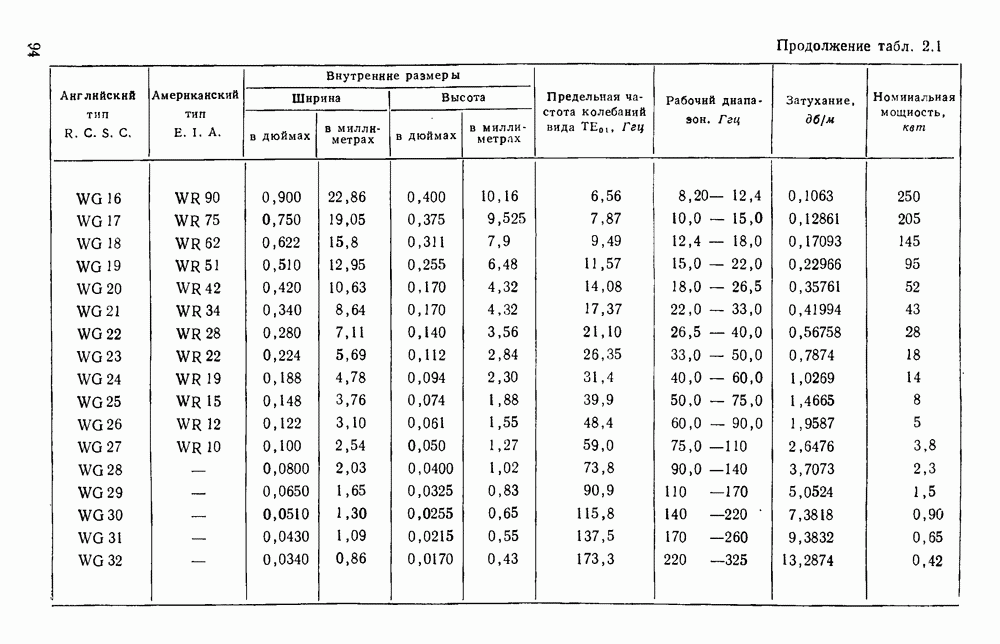
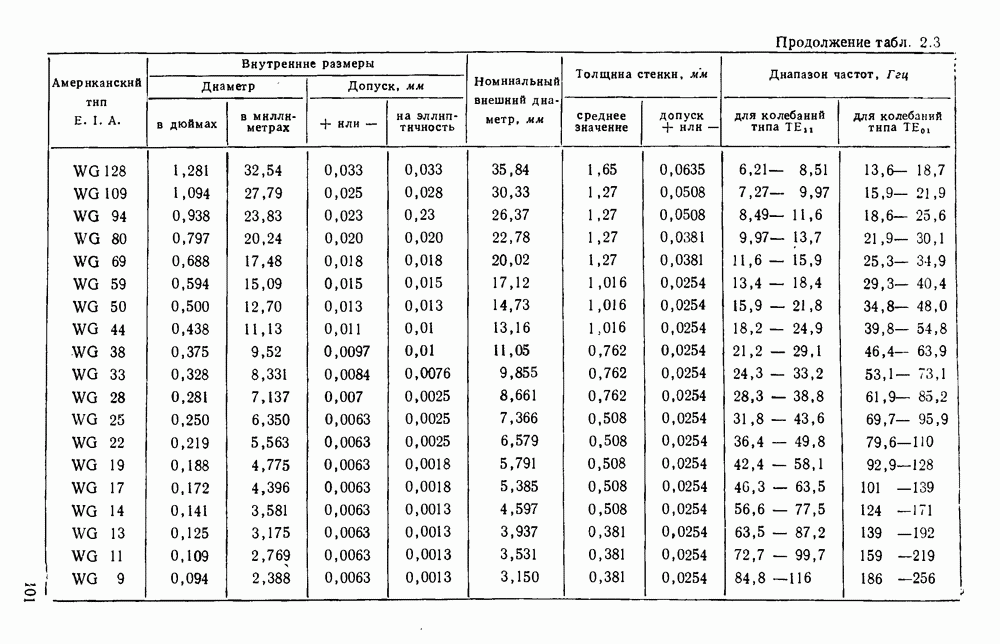
- 2.3. СТАНДАРТНЫЕ ВОЛНОВОДЫ
- 2.3.1. Прямоугольные волноводы
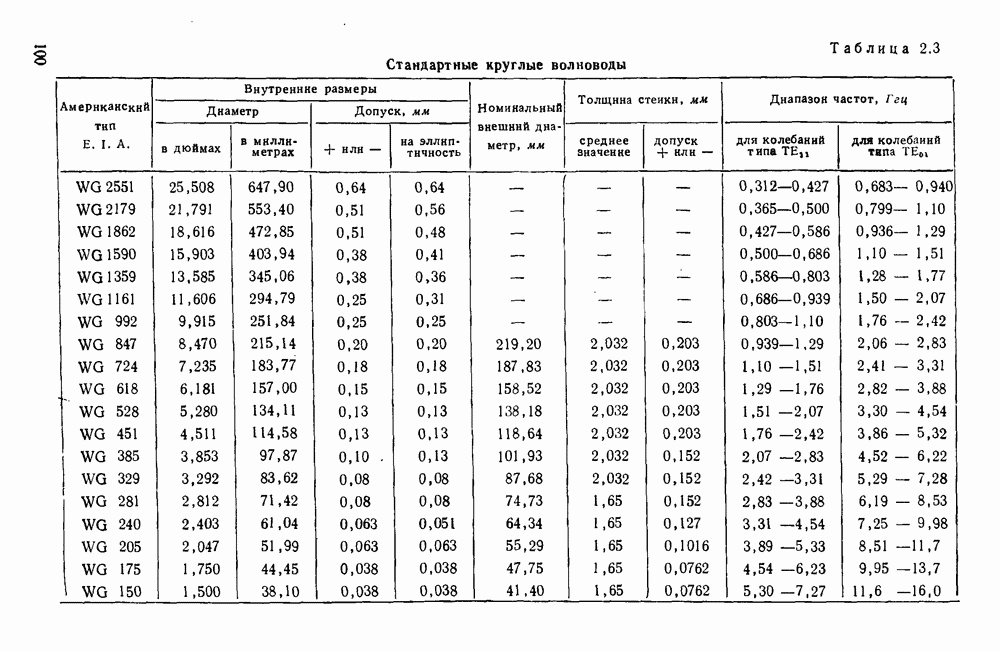
- 2.3.2. Круглые волноводы
- 2.3.3. Широкополосные и компактные волноводы
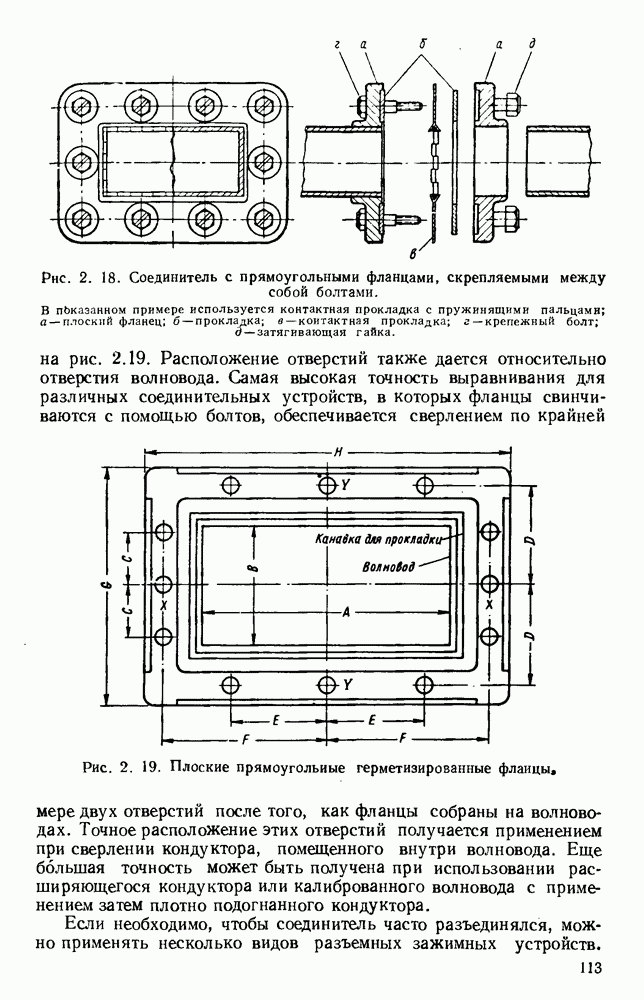
- 2.4. МЕТОДЫ СОЕДИНЕНИЯ
- 2.4.1. Выравнивание волноводов
- 2.4.2. Контактные прокладки и дроссели
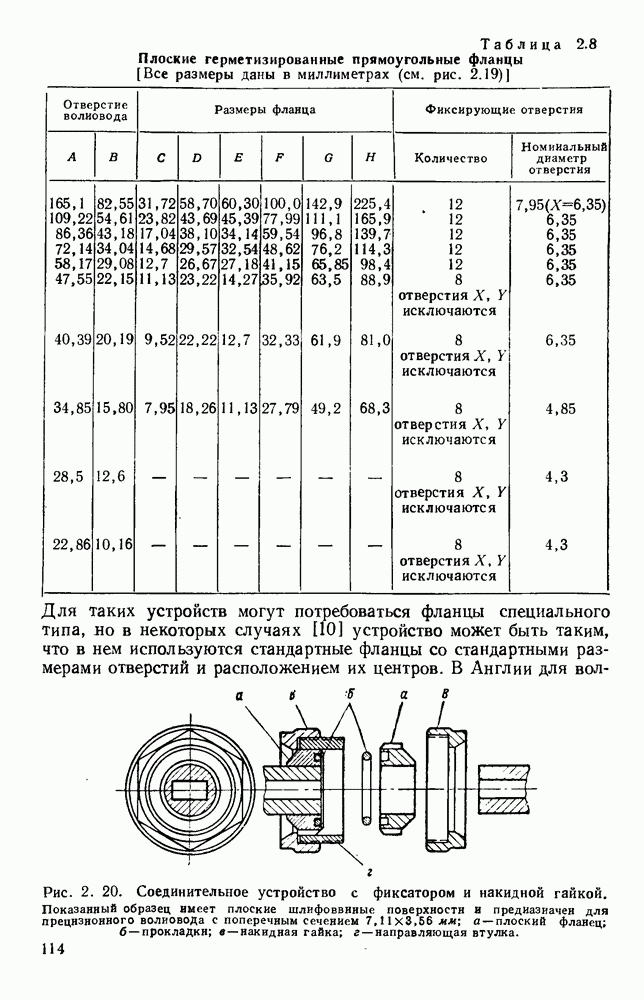
- 2.4.3. Крепежные и зажимные устройства
- 2.5. УПЛОТНЕНИЕ И ГЕРМЕТИЗАЦИЯ
- 2.5.1. Волноводные системы
- 2.5.2. Соединители и сочленения
- 2.6. ПРОСТЫЕ ПЕРЕХОДЫ
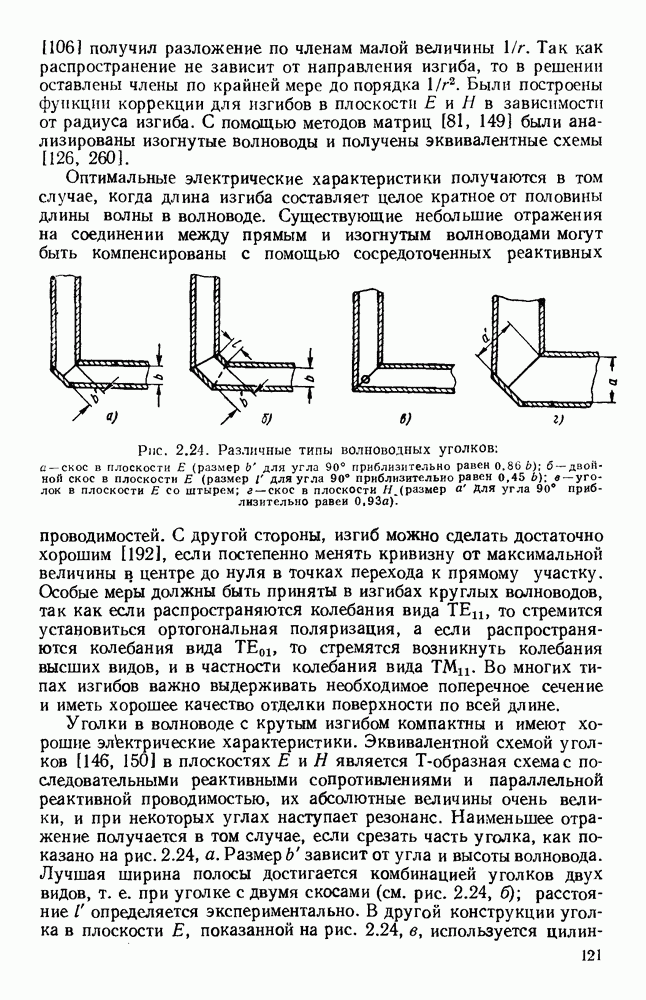
- 2.6.1. Изгибы, уголки и скрутки
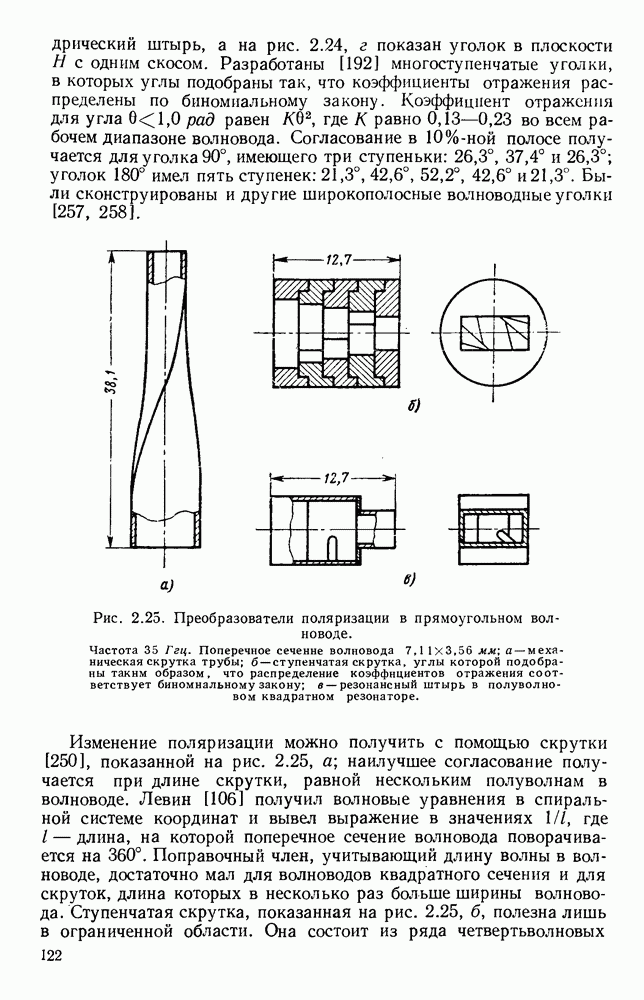
- 2.6.2. Переходы и преобразователи
- 2.7. ГИБКИЕ ВОЛНОВОДЫ
- 2.7.2. Позвонковая модель
- ГЛАВА 3. ЭЛЕМЕНТЫ ЦЕПЕЙ И УЗЛЫ
- 3.1.2. Отверстия связи
- 3.1.3. Параллельные и последовательные тройники
- 3.2. ПРЕОБРАЗОВАТЕЛИ ВИДОВ КОЛЕБАНИЙ
- 3.2.1. Коаксиально-волноводные переходы
- 3.2.2. Переходы с прямоугольного волновода на круглый
- 3.2.3. Переход от линейной поляризации к круговой
- 3.3. НАПРАВЛЕННЫЕ ОТВЕТВИТЕЛИ
- 3.3.2. Распределенная связь
- 3.3.3. Системы с полной передачей мощности
- 3.4. ГИБРИДНЫЕ СОЕДИНЕНИЯ
- 3.4.1. Тип соединения с фазами, находящимися в квадратуре
- 3.4.2. Синфазные гибридные соединения
- 3.4.3. Различные гибридные соединения
- 3.5. РЕГУЛИРУЕМЫЕ ПОЛНЫЕ СОПРОТИВЛЕНИЯ
- 3.5.2. Подвижные вставки
- 3.5.3. Фазовращатели
- 3.6. ВРАЩАЮЩИЕСЯ СОЧЛЕНЕНИЯ
- 3.6.1. Вращающиеся сочленения с колебаниями кругового магнитного вида
- 3.6.2. Вращающиеся сочленения различных типов
- 3.7. МЕХАНИЧЕСКИЕ ПЕРЕКЛЮЧАТЕЛИ
- 3.7.1. Механические переключатели с ручным управлением
- 3.7.2. Быстродействующие переключатели
- ГЛАВА 4. МЕТОДЫ ИЗМЕРЕНИЙ И ПРИБОРЫ
- 4.1. ИЗМЕРЕНИЕ МОЩНОСТИ
- 4.1.2. Методы измерений, основанные на преобразовании мощности в тепловую энергию
- 4.1.3. Эффект Холла и давление излучения
- 4.2. ИЗМЕРЕНИЕ ЗАТУХАНИЯ
- 4.2.2. Фиксированные аттенюаторы и оконечные нагрузки
- 4.2.3. Переменные аттенюаторы
- 4.3. ИЗМЕРЕНИЕ ПОЛНЫХ СОПРОТИВЛЕНИЙ
- 4.3.2. Картина стоячей волны
- 4.3.3. Мостовые методы
- ГЛАВА 5. РЕЗОНАТОРЫ И ФИЛЬТРЫ
- 5.1.2. Свойства цепей
- 5.1.3. Измерения характеристик
- 5.2. ИЗМЕРЕНИЕ ДЛИНЫ ВОЛНЫ
- 5.2.1. Волномеры с объемными резонаторами
- 5.2.2. Волноводные интерферометры
- 5.3. ФИЛЬТРУЮЩИЕ ЦЕПИ
- 5.3.2. Связанные резонаторы
- 5.3.3. Четвертьволновая связь
- ГЛАВА 6. ХАРАКТЕРИСТИКИ МАТЕРИАЛОВ И МЕТОДЫ ИХ ИЗМЕРЕНИЙ
- 6.1.2. Методы измерений в свободном пространстве и в линии передачи
- 6.1.3. Методы измерений в объемном резонаторе
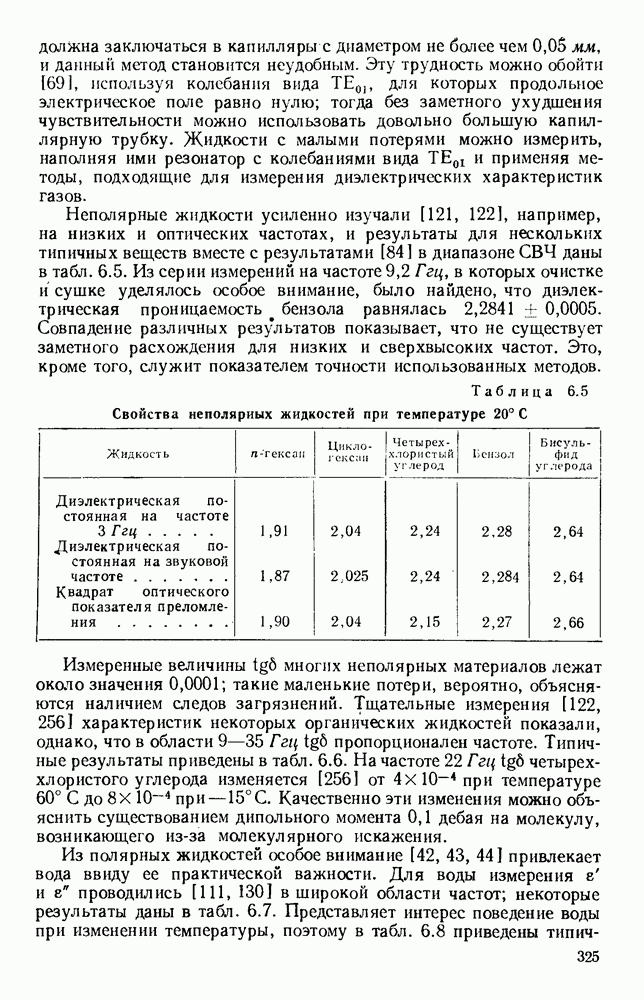
- 6.2. ЭКСПЕРИМЕНТЫ И РЕЗУЛЬТАТЫ
- 6.2.2. Жидкости
- 6.2.3. Твердые тела
- 6.3. ПРОВОДИМОСТЬ МЕТАЛЛОВ
- 6.3.2. Аномальное поведение
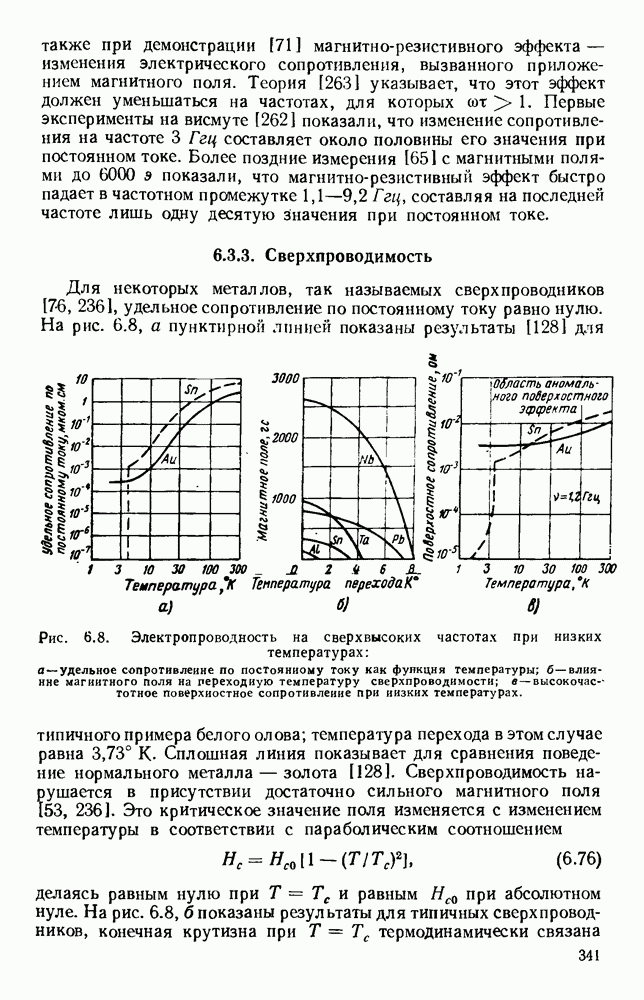
- 6.3.3. Сверхпроводимость
- ГЛАВА 7. СПЕКТРОМЕТРИЯ ДИЭЛЕКТРИКОВ
- 7.1.2. Форма линии и интенсивность
- 7.1.3. Сверхтонкая структура
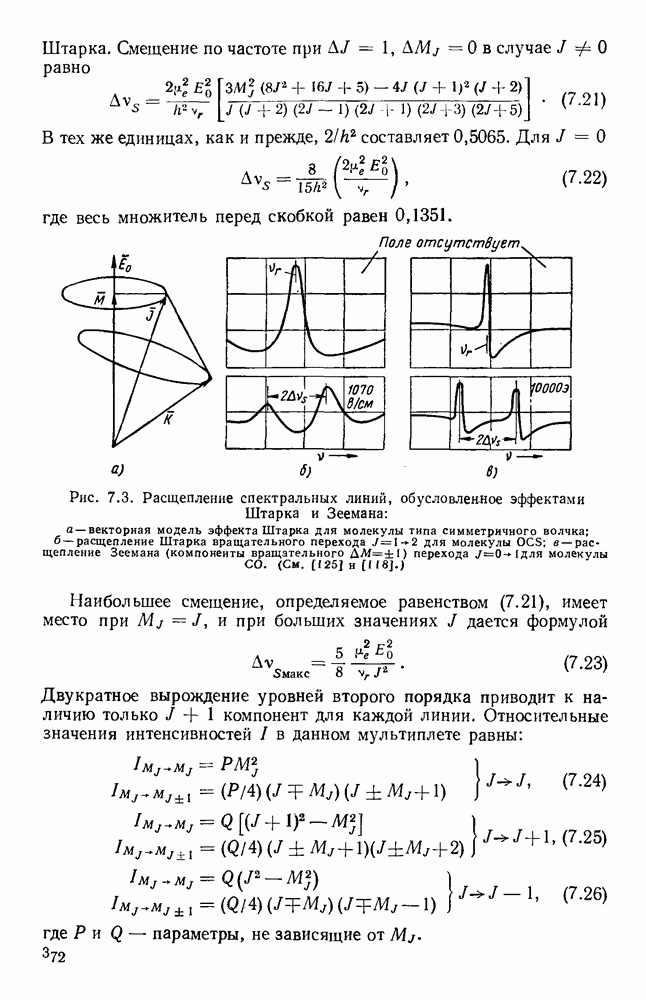
- 7.1.4. Явления Штарка и Зеемана
- 7.2. СПЕКТРОМЕТРЫ
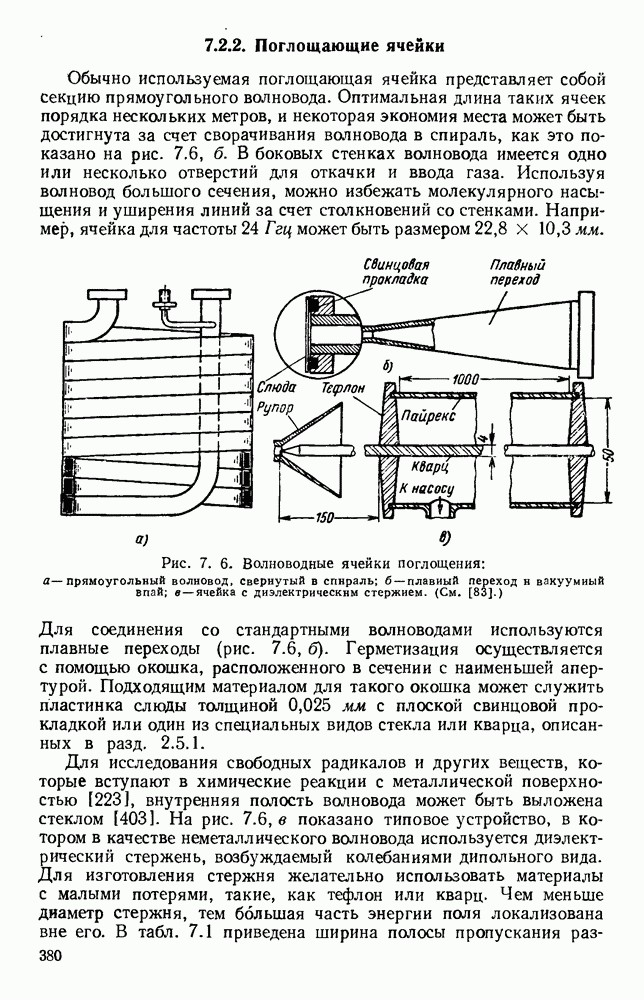
- 7.2.2. Поглощающие ячейки
- 7.2.3. Типы спектрометров
- 7.3. ПАРАМАГНИТНЫЙ РЕЗОНАНС В ТВЕРДЫХ ТЕЛАХ
- 7.3.2. Техника измерения
- 7.3.3. Типичные материалы
- 7.3.4. Времена релаксации
- 7.4. ЦИКЛОТРОННЫЙ РЕЗОНАНС
- 7.4.2. Определение эффективной массы носителей
- ГЛАВА 8. СВОЙСТВА И ПРИМЕНЕНИЕ ГИРОМАГНИТНЫХ СРЕД
- 8.1.2. Распространение электромагнитных волн в неограниченной среде
- 8.2. СВОЙСТВА МАГНИТНЫХ МАТЕРИАЛОВ
- 8.2.2. Ферромагнитный резонанс
- 8.2.3. Нелинейные эффекты и нестабильность
- 8.3. РАСПРОСТРАНЕНИЕ В НАПРАВЛЯЮЩИХ СИСТЕМАХ
- 8.3.2. Прямоугольный волновод
- 8.3.3. Ферритовые устройства в качестве элементов схем
- 8.4. ИЗМЕРЕНИЯ ПАРАМЕТРОВ ФЕРРИТОВЫХ МАТЕРИАЛОВ
- 8.4.2. Резонансные методы
- 8.4.3. Волноводные методы
- 8.5. РЕЗОНАНСНЫЕ ВЕНТИЛИ
- 8.6. УСТРОЙСТВА, РАБОТАЮЩИЕ СО СЛАБЫМИ ПОЛЯМИ
- 8.6.2. Устройства с поперечным полем
- 8.6.3. Прочие узлы
- ГЛАВА 9. ПЛОСКОПАРАЛЛЕЛЬНЫЕ СИСТЕМЫ
- 9.2. СИММЕТРИЧНЫЕ ПОЛОСКОВЫЕ ЛИНИИ
- 9.2.1. Линии типа «диэлектрических сэндвичей»
- 9.2.2. Симметричные линии с воздушным диэлектриком
- 9.3. НЕСИММЕТРИЧНЫЕ ПОЛОСКОВЫЕ ЛИНИИ
- 9.3.2. Несимметричная полосковая линия с твердым диэлектриком
- 9.4. ЭЛЕМЕНТЫ И УЗЛЫ
- 9.4.2. Переходные устройства
- 9.4.3. Узлы полосковых систем
- 9.5. ЦЕПИ И СИСТЕМЫ
- 9.5.3. Частотные фильтры
- 9.5.4. Цепи питания антенн
- 9.6. МАТЕРИАЛЫ И МЕТОДЫ ПРОИЗВОДСТВА
- 9.6.2. Техника изготовления печатных схем
- ГЛАВА 10. ПЕРИОДИЧЕСКИЕ И НАПРАВЛЯЮЩИЕ СТРУКТУРЫ
- 10.1. ВОЛНЫ В ПЕРИОДИЧЕСКИ НАГРУЖЕННЫХ ЛИНИЯХ
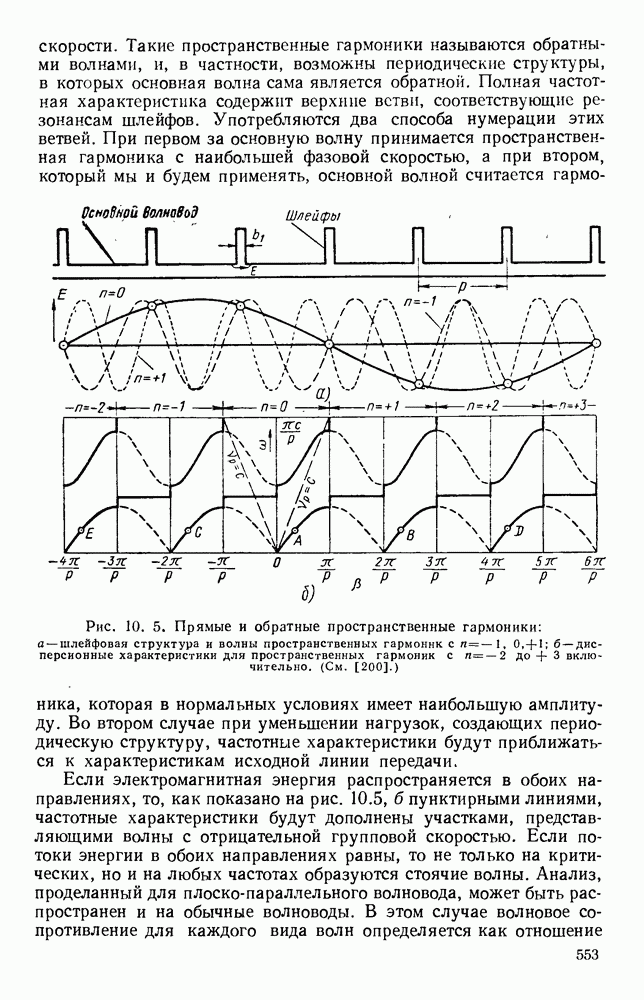
- 10.1.2. Пространственные гармоники
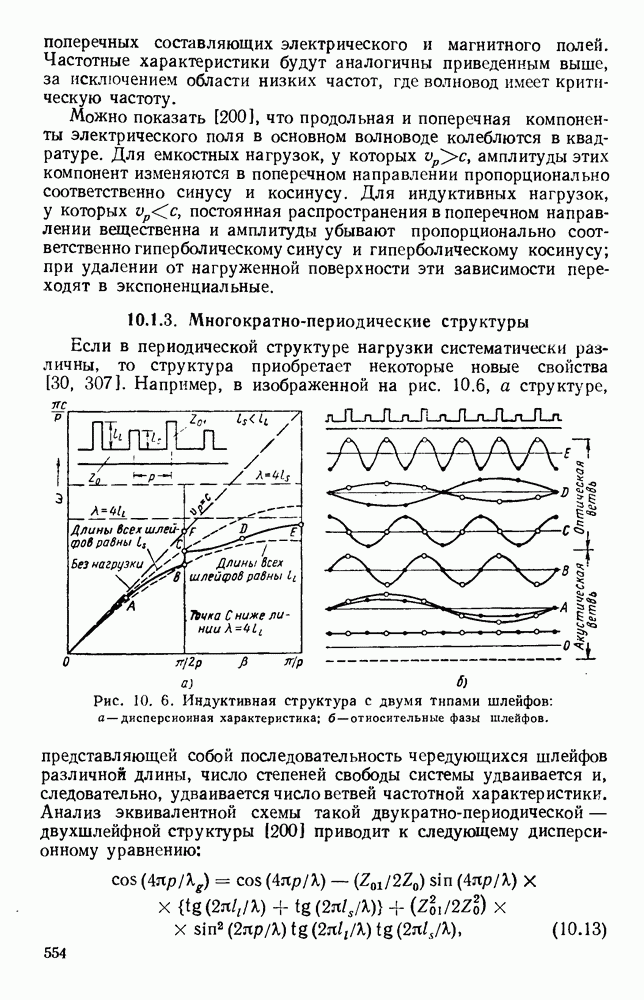
- 10.1.3. Многократно-периодические структуры
- 10.2. МЕТАЛЛИЧЕСКИЕ СТРУКТУРЫ С ДИЭЛЕКТРИЧЕСКИМ ПОКРЫТИЕМ
- 10.2.2. Радиальные волны над плоскими поверхностями
- 10.2.3. Продольные цилиндрические волны
- 10.3. ЛИНИИ ПЕРЕДАЧИ ПОВЕРХНОСТНЫХ ВОЛН
- 10.3.2. Влияние кривизны
- 10.3.3. Возбудители и другие устройства
- 10.4. ВОЛНЫ В ДИЭЛЕКТРИЧЕСКИХ ЛИНИЯХ
- 10.4.2. Цилиндрические стержни
- 10.4.3. Многослойные среды
- 10.4.4. Линии с зеркальным изображением
- 10.5. СТРУКТУРЫ ИЗ СВЯЗАННЫХ РЕЗОНАТОРОВ
- 10.5.2. Объемные резонаторы
- 10.6. СПИРАЛЬНЫЕ СТРУКТУРЫ
- 10.6.2. Практические варианты
- ГЛАВА 11. ЛАМПЫ С СЕТОЧНЫМ УПРАВЛЕНИЕМ И ЛАМПЫ С ПРОСТРАНСТВЕННЫМ ЗАРЯДОМ
- 11.1.2. Лампы с сеточным управлением
- 11.2. ВЗАИМОДЕЙСТВИЕ ПУЧКА И РЕЗОНАТОРА
- 11.2.2. Усилительные клистроны
- 11.2.3. Отражательные клистроны
- 11.3. ВЗАИМОДЕЙСТВИЕ ПУЧКА И КОНТУРА
- 11.3.1. Электронно-волновые лампы
- 11.3.2. Лампы с бегущей волной
- 11.3.3. Лампы обратной волны
- ГЛАВА 12. ЛАМПЫ СО СКРЕЩЕННЫМИ ПОЛЯМИ И ГЕНЕРАЦИЯ ВОЛН МИЛЛИМЕТРОВОГО ДИАПАЗОНА
- 12.1.2 Карсинотрон типа М
- 12.2. МАГНЕТРОНЫ
- 12.2.2. Резонаторные системы
- 12.2.3. Взаимодействие между электронным потоком и резонансной системой
- 12.2.4. Рабочие характеристики
- 12.3. ГЕНЕРАЦИЯ ВОЛН МИЛЛИМЕТРОВОГО ДИАПАЗОНА
- 12.3.2. Высокочастотный предел когерентного излучения
- 12.4. ИСТОЧНИКИ ЭЛЕКТРОНОВ
- 12.4.1. Термоэлектронные катоды
- 12.4.2. Фокусированные пучки
- ГЛАВА 13. ТЕХНИКА ОПТИЧЕСКОГО ТИПА
- 13.1.2. Типы дифракции
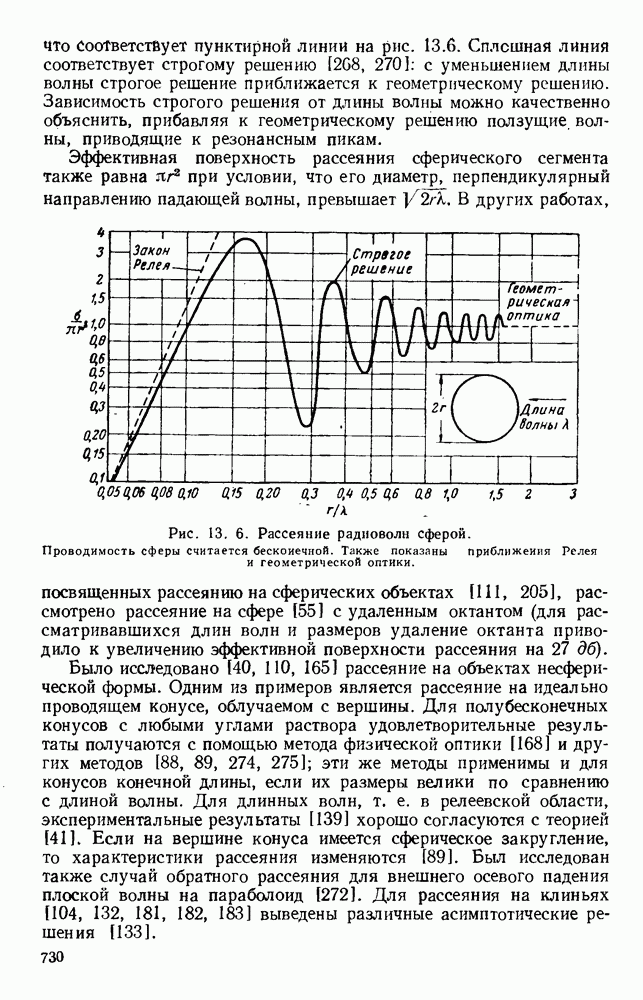
- 13.1.3. Рассеяние
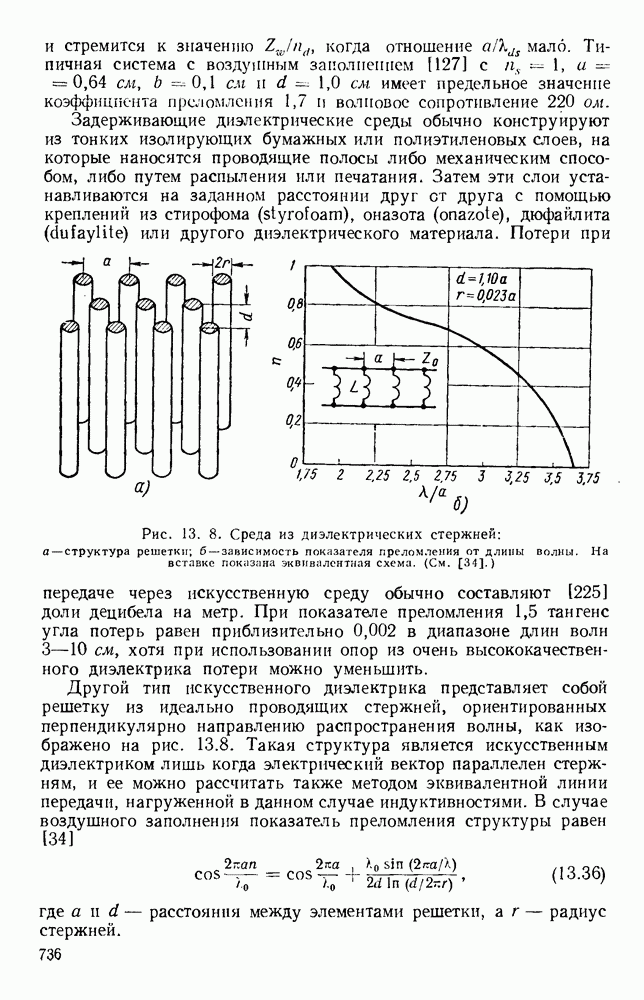
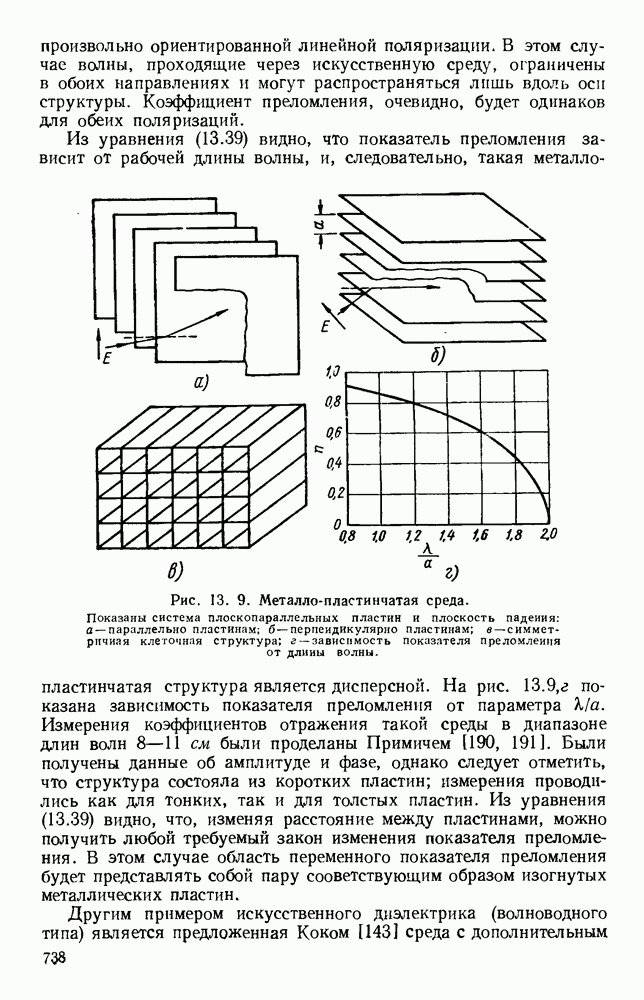
- 13.2. ИСКУССТВЕННЫЕ ДИЭЛЕКТРИКИ
- 13.2.2. Структуры волноводного типа
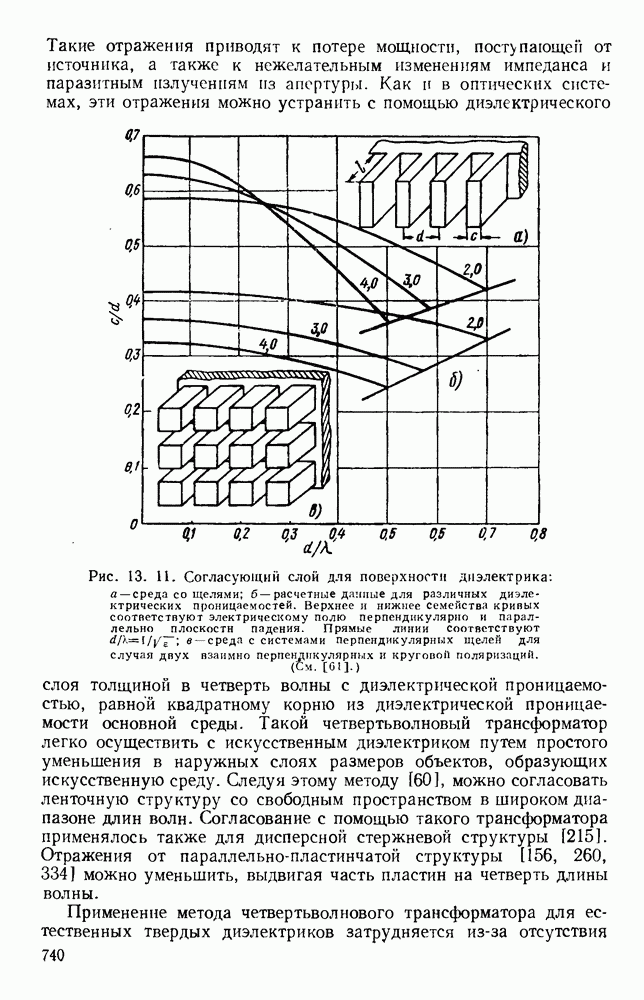
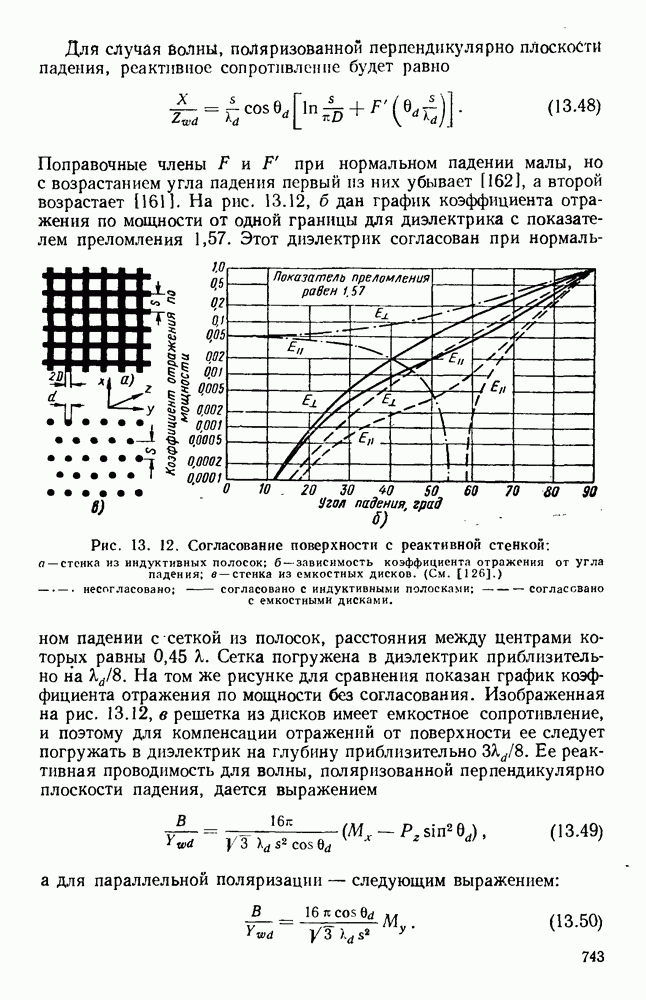
- 13.3. КОНТРОЛЬ ОТРАЖЕНИЙ ОТ ПОВЕРХНОСТИ
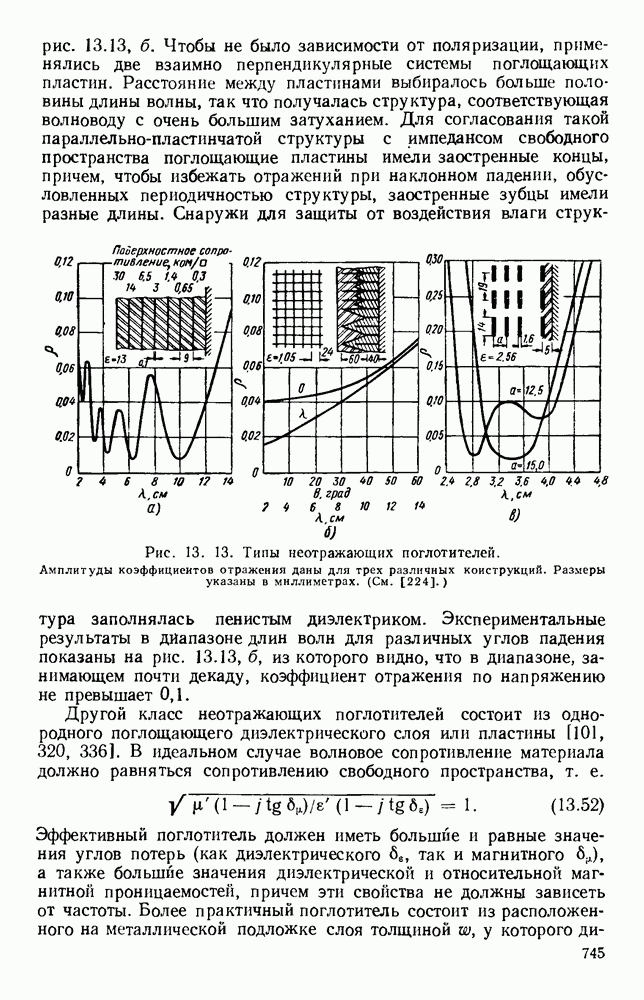
- 13.3.2. Неотражающие поглотители
- 13.3.3. Увеличение отражающей способности
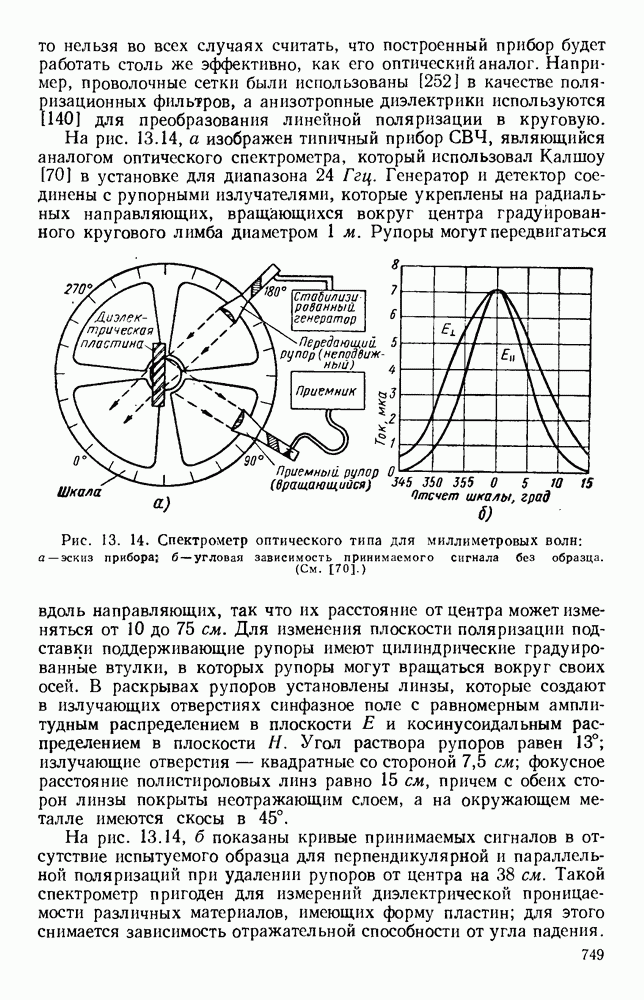
- 13.4. ПРИБОРЫ И СИСТЕМЫ
- 13.4.1. Спектрометры
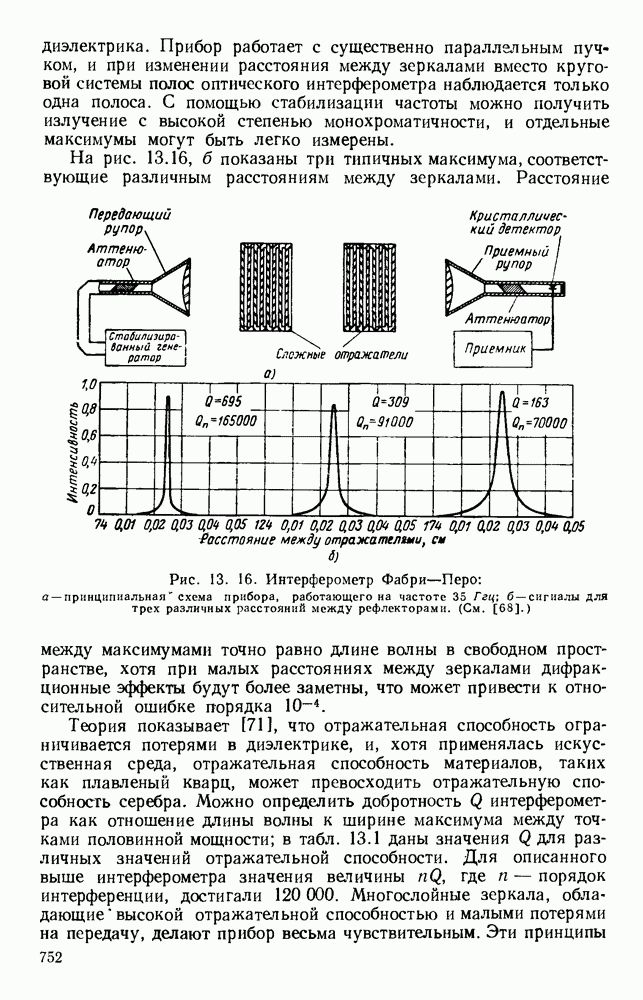
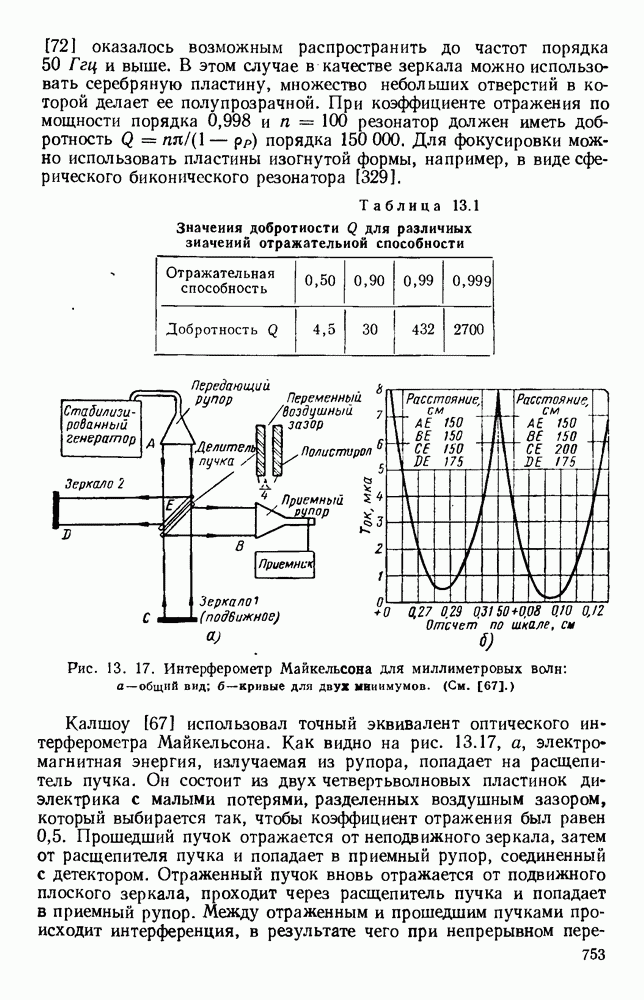
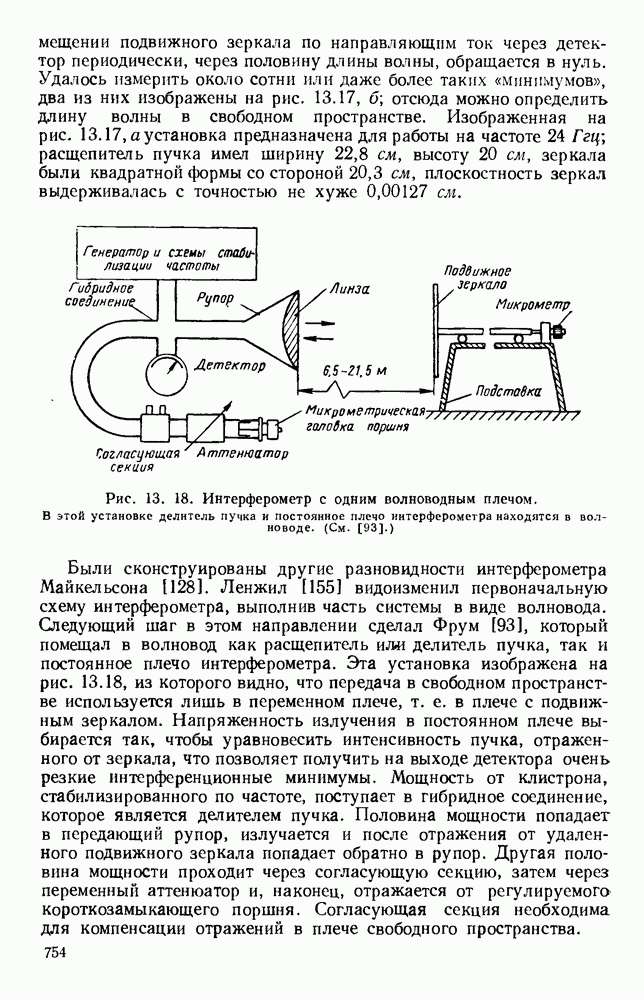
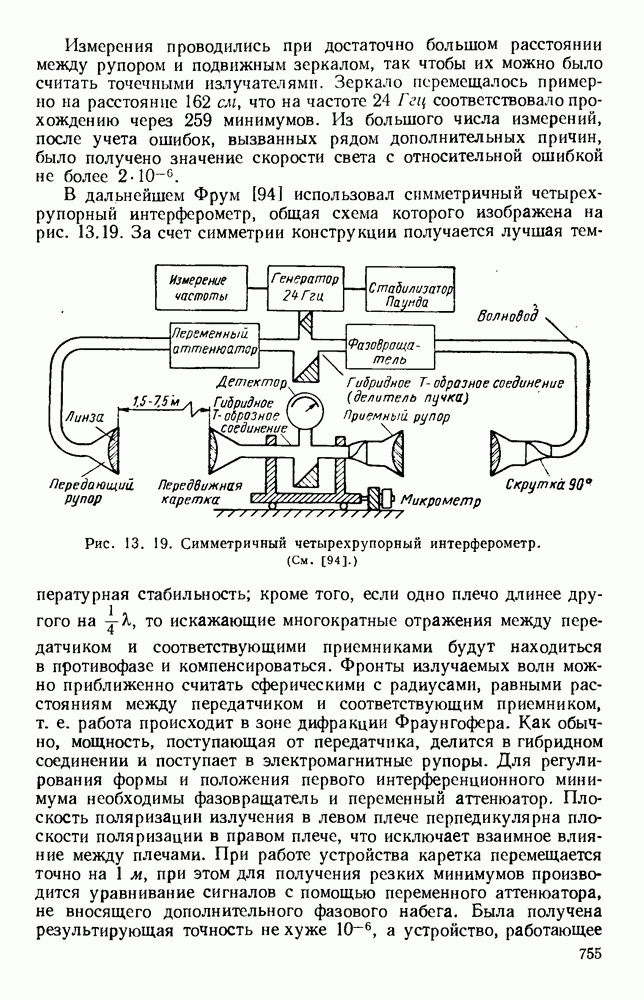
- 13.4.2. Интерферометры
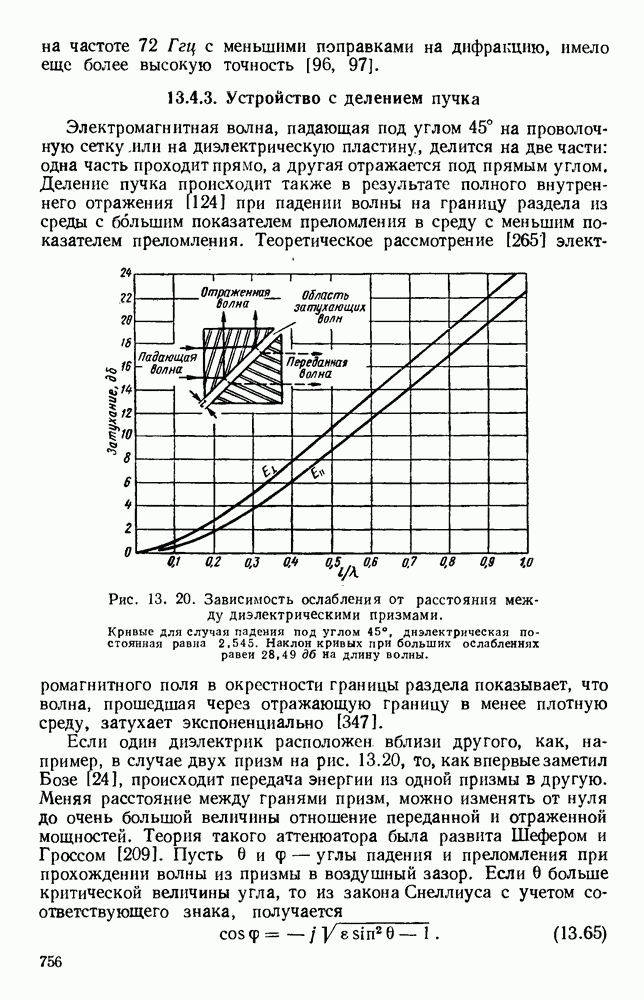
- 13.4.3. Устройство с делением пучка